ПНСТ 697-2024 Нефтяная и газовая промышленность. Системы подводной добычи. Расчет сопротивления усталости морских стальных сооружений. Методические указания

        ПНСТ 697-2024

ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Нефтяная и газовая промышленность

СИСТЕМЫ ПОДВОДНОЙ ДОБЫЧИ

Расчет сопротивления усталости морских стальных сооружений. Методические указания

Petroleum and natural gas industry. Subsea production systems. Fatigue design of offshore steel structures. Recommended practice

ОКС 75.020

Срок действия с 2024-06-30

до 2027-06-30

Предисловие

1 РАЗРАБОТАН Обществом с ограниченной ответственностью "Газпром 335" (ООО "Газпром 335")

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 023 "Нефтяная и газовая промышленность"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 марта 2024 г. № 14-пнст

Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16-2011 (разделы 5 и 6).

Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за 4 мес до истечения срока его действия разработчику настоящего стандарта по адресу: [email protected] и/или в Федеральное агентство по техническому регулированию и метрологии по адресу: 123112 Москва, Пресненская набережная, д.10, стр.2.

В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе "Национальные стандарты" и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)

Введение

Создание и развитие отечественных технологий и техники для освоения глубоководных шельфовых нефтегазовых месторождений должно быть обеспечено современными стандартами, устанавливающими требования к проектированию, строительству и эксплуатации систем подводной добычи. Для решения данной задачи Министерством промышленности и торговли Российской Федерации и Федеральным агентством по техническому регулированию и метрологии реализуется "Программа по обеспечению нормативной документацией создания отечественной системы подводной добычи для освоения морских нефтегазовых месторождений". В объеме работ программы предусмотрена разработка национальных стандартов и предварительных национальных стандартов, областью применения которых являются системы подводной добычи углеводородов.

Целью разработки настоящего предварительного национального стандарта является разработка методических указаний для выполнения расчетов сопротивления усталости морских стальных сооружений, входящих в состав систем подводной добычи углеводородов.

1 Область применения

1.1 Настоящий стандарт применяют для расчета сопротивления усталости морских стальных конструкций, входящих в состав систем подводной добычи углеводородов.

1.2 Положения настоящего стандарта применимы для стальных сооружений, включая их стальные конструкции, крепежные изделия и сварные соединения, при температуре эксплуатации, не превышающей 100°С. Допускается применение положений настоящего стандарта для более высоких температур эксплуатации с использованием понижающего коэффициента, см. также [1].

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие документы:

ГОСТ 23207 Сопротивление усталости. Основные термины, определения и обозначения

ГОСТ Р 59304 Нефтяная и газовая промышленность. Системы подводной добычи. Термины и определения

ГОСТ Р ИСО 2394 Конструкции строительные. Основные принципы надежности

СП 16.13330 "Актуализированная редакция СНиП II-23-81 Стальные конструкции"

СП 20.13330 "Актуализированная редакция СНиП 2.01.07-85 Нагрузки и воздействия"

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов (сводов правил) в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный документ, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого документа с учетом всех внесенных в данную версию изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то рекомендуется использовать версию этого документа с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку. Сведения о действии сводов правил целесообразно проверить в Федеральном информационном фонде стандартов.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 59304 и ГОСТ 23207, а также следующие термины с соответствующими определениями:

3.1 распределение Вейбулла: Двухпараметрическое или трехпараметрическое распределение, применяемое в теории вероятности.

3.2 S-N кривая: Кривая усталости, получаемая из данных компьютерного моделирования испытаний на усталость и применяемая для расчета сопротивления усталости морских стальных сооружений.

4 Сокращения и обозначения

В настоящем стандарте использованы следующие сокращения и обозначения:

КЭ	-	конечные элементы;
МКЭ	-	метод конечных элементов;
СПД	-	системы подводой добычи;
С	-	эмпирический параметр материала в механике разрушения;
d	-	диаметр;
	-	диаметр цилиндрической части вблизи конического перехода;
E	-	модуль упругости материала;
h	-	параметр формы в распределении Вейбулла;
	-	катет сварного шва;
I	-	момент инерции сечения трубы;
K	-	коэффициент интенсивности напряжений;
k	-	число блоков нагружения/показатель толщины;
L	-	длина эксцентриситета;
l	-	длина сегмента трубы;
m	-	эмпирический параметр, характеризующий обратный наклон расчетной S-N кривой;
	-	изгибающий момент, действующий в плоскости конструкции;
	-	изгибающий момент, действующий вне плоскости конструкции;
N	-	циклическая долговечность;
	-	число циклов до разрушения при постоянном размахе напряжений ;
	-	число циклов нагружения в блоке i;
	-	понижающий коэффициент, учитывающий влияние температуры;
S	-	амплитуда напряжений цикла;
SCF	-	коэффициент концентрации напряжений (stress concentration factor);
	-	толщина конического перехода;
	-	расчетное время, с;
	-	эталонная толщина;
	-	толщина листа;
Q	-	вероятность превышения размаха напряжения цикла;
q	-	параметр масштаба в распределении Вейбулла;
	-	угол наклона конуса;
A	-	глубина трещины;
	-	расчетная ширина сварного шва;
	-	параметр, характеризующий пересечение расчетной S-N кривой с осью log N;
	-	параметр, характеризующий соотношение диаметров распорки и пояса;
Г	-	Гамма-функция;
	-	параметр, характеризующий соотношение радиуса пояса и его толщины;
K	-	коэффициент концентрации напряжений;
	-	размах напряжений цикла;
	-	наибольший размах напряжений из циклов;
	-	коэффициент использования;
	-	эксцентриситет;
	-	характерная величина отклонения от соосности, учитываемая в S-N кривых;
	-	изгибные напряжения;
	-	напряжения в критической области;
	-	мембранные напряжения;
	-	максимальное номинальное напряжение, вызванное изгибающим моментом в плоскости конструкции;
	-	максимальное номинальное напряжение, вызванное изгибающим моментом вне плоскости конструкции;
	-	номинальные напряжения;
	-	максимальное номинальное напряжение, вызванное осевым усилием;
	-	касательное напряжение;
v	-	коэффициент Пуассона;
	-	средняя частота пересечения нулевого значения.

5 Общие положения

5.1 Расчет сопротивления усталости морских стальных сооружений выполняют в соответствии с положениями настоящего стандарта, СП 16.13330 и СП 20.13330 (см. также [1] и [2]).

5.2 Для расчета сопротивления усталости морских стальных сооружений СПД применяют метод расчета на основе кривых усталости (S-N кривых), учитывающих результаты компьютерного моделирования испытаний на усталость с применением МКЭ.

5.3 При выполнении МКЭ листов, труб и полых конструкций выделяют напряжения в критической области для данной геометрии.

5.4 Расчет сопротивления усталости морских стальных сооружений СПД может выполняться методами проверочного расчета или расчета на основании механики разрушения (см. также правила [3] и [4]).

6 Расчет сопротивления усталости на основе кривых усталости

6.1 Общие сведения

6.1.1 Расчет сопротивления усталости может выполняться с применением кривых усталости, которые являются эмпирическими S-N кривыми. При расчете сопротивления усталости учитывают дополнительные напряжения, возникающие вследствие допусков изготовления, сварных швов и крестообразных соединений (см. также [1]).

6.1.2 Для получения циклов до разрушения вычисленное напряжение в критической области сравнивается с S-N кривой.

6.1.3 На рисунке 1 приведены основные виды разрушения при усталостном повреждении:

- рост усталостной трещины от кромки лицевой поверхности сварного шва в основном материале (усталостная трещина начинается на малых дефектах или ослаблениях на кромке лицевой поверхности сварного шва, где реализуются самые высокие напряжения из-за геометрии дефекта сварного шва);

- рост усталостной трещины от корня сварного шва через угловой сварной шов;

- рост усталостной трещины от корня сварного шва в сечении под данным сварным швом;

- рост усталостной трещины от неоднородности поверхности или от дефекта в основном материале (усталостные трещины часто начинаются от надрезов, канавок или небольших дефектов/неравномерностей поверхности).

а) Рост усталостной трещины от кромки лицевой поверхности сварного шва в основном материале	б) Рост усталостной трещины от корня сварного шва через угловой сварной шов

в) Рост усталостной трещины от корня сварного шва в сечении под данным сварным швом	г) Рост усталостной трещины от неоднородности поверхности или от надреза в основном материале

Рисунок 1 - Примеры основных видов разрушения

6.2 Накопление усталостных повреждений

6.2.1 Усталостную долговечность можно вычислять с использованием кривых усталости (S-N кривых) и гипотезы суммирования усталостных повреждений (гипотезы Пальмгрена-Майнера) (см. также учебное пособие [5]).

6.2.2 Если распределение размахов напряжений цикла во времени выражено в виде гистограммы напряжений, которая состоит из некоторого числа блоков с постоянным размахом напряжений цикла

, каждый из которых имеет число повторений

, то критерий усталости может быть выражен по формуле

, (1)

где D - накопленная усталостная повреждаемость;

- параметр, характеризующий пересечение расчетной S-N кривой с осью log

N

;

m - параметр, характеризующий обратный наклон расчетной S-N кривой;

k - число блоков нагружения;

- число циклов нагружения в блоке

i

;

- число циклов до разрушения при постоянном размахе напряжений цикла

;

- коэффициент использования.

6.2.3 При расчетах с использованием гистограммы напряжений для достижения достаточной численной точности число блоков нагружения к должно быть не менее 20.

6.2.4 Вычисление усталостной повреждаемости с использованием расчетных графиков, основанных на двухпараметрическом распределении размахов напряжений цикла, приведено в разделе 9.

6.3 Методология расчета сопротивления усталости

6.3.1 Виды S-N кривых

6.3.1.1 Для расчета сопротивления усталости применяют несколько видов S-N кривых:

- S-N кривая номинальных напряжений;

- S-N кривая напряжений в критической области (для листовых конструкций или трубных соединений);

- S-N кривая напряжений с учетом наличия дефекта (см. также [1]).

6.3.1.2 Под номинальным напряжением следует понимать напряжение в компоненте, которое можно получить, используя классическую теорию, такую как теория балок или оболочек.

6.3.1.3 Под напряжением в критической области следует понимать геометрическое напряжение, которое реализуется непосредственно рассчитываемым элементом (не является напряжением, которое включает в себя влияние дефекта).

6.3.1.4 Под напряжением в дефекте следует понимать общее напряжение, появляющееся в результате геометрии данного элемента, и нелинейное напряжение вследствие наличия дефекта.

6.3.2 Листовые конструкции, использующие S-N кривые номинальных напряжений

6.3.2.1 Классификация соединений и соответствующие S-N кривые позволяют учитывать концентрацию локальных напряжений, формируемых самими соединениями и профилем сварного шва. Поэтому расчетное напряжение может рассматриваться как номинальное напряжение вблизи рассматриваемого сварного шва, если он не расположен в зоне концентрации напряжений, обусловленной общей формой конструкции.

6.3.2.2 На рисунке 2 а) локальными напряжениями для расчета усталости будут растягивающие напряжения

. При этом на рисунке 2 б) следует учитывать коэффициент концентрации напряжений из-за отверстия. Таким образом, локальные напряжения определяются по формуле

, (2)

где SCF - коэффициент концентрации напряжений;

- локальные напряжения, которые следует использовать вместе с соответствующими S-N кривыми в зависимости от классификации соединения.

а) Листовая конструкция без зоны концентрации напряжений	б) Листовая конструкция с зоной концентрации напряжений

Рисунок 2 - Примеры листовой конструкции с зоной концентрации напряжений и без нее

6.3.2.3 При расчете роста усталостной трещины важным параметром является максимальное главное напряжение. При оценке усталостной трещины вдоль кромки лицевой поверхности сварного шва определяют размах напряжения цикла. Если направление главных напряжений отличается от перпендикуляра к кромке, то данный подход является консервативным. Пример главных напряжений и трещины, расположенной вдоль кромки сварного шва, показан на рисунке 3.

6.3.2.4 При увеличении угла между перпендикуляром к сварному шву и направлением главных напряжений

усталостное повреждение может реализоваться не вдоль кромки сварного шва, а перпендикулярно главным напряжениям, как показано на рисунке 4.

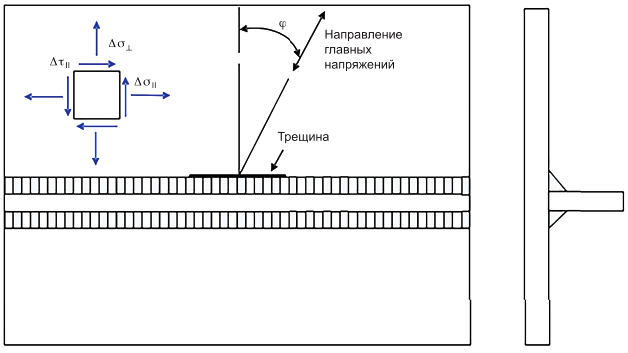Рисунок 3 - Трещина вдоль кромки сварного шва

Рисунок 4 - Трещина, перпендикулярная направлению главных напряжений

6.3.3 Листовые конструкции, использующие S-N кривые напряжений в критической области

6.3.3.1 При КЭ расчете усталостной долговечности сварных плоских соединений, за исключением трубных соединений, целесообразно рассматривать напряжения в критических областях.

6.3.3.2 Зависимость между номинальным напряжением и напряжением в критической области можно определить по формуле

. (3)

6.3.4 Трубные соединения

6.3.4.1 Для трубных соединений (соединение связи и пояса фермы, например) определяется размах напряжений цикла в критической области путем экстраполяции главных напряжений, вычисленных в нескольких точках за пределами области, на которую оказывает влияние сварной шов.

6.3.4.2 Напряжение в критической области трубных соединений определяется аналогично

. (4)

6.3.5 Угловые сварные швы в несущих соединениях

6.3.5.1 Размах напряжений цикла для потенциальных трещин в несущих соединениях, сваренных угловыми швами и швами с неполным проплавлением, можно вычислять по формуле

, (5)

где

,

,

- компоненты тензора напряжений.

6.3.5.2 Компоненты тензора напряжений приведены на рисунке 5.

Рисунок 5 - Компоненты тензора напряжений в угловом сварном шве

6.3.6 Угловые сварные швы на накладных листах

6.3.6.1 Угловые сварные швы на накладных листах, приведенные на рисунке 6, будут испытывать изгибающие напряжения по всей расчетной толщине сварного шва, если данный накладной лист нагружен осевым усилием или изгибающим моментом.

6.3.6.2 Оценку усталости данных соединений рекомендуется выполнять на основании КЭ расчета. Изгибающее напряжение в сварном шве можно определять, моделируя данный шов минимум двумя твердотельными конечными элементами второго порядка на расчетную толщину сварного шва.

6.3.6.3 Напряжения в корне сварного шва определяются экстраполяцией напряжений, вычисленных в точках

и

, где

- расчетная ширина сварного шва. Данные напряжения используются для вычисления главных напряжений и соответствующих размахов напряжений цикла, необходимых для оценки сопротивления усталости по соответствующей S-N кривой.

Рисунок 6 - Пример накладного листа

6.3.7 Несущие опоры, приваренные угловыми сварными швами

6.3.7.1 В случае приварки несущих опор угловыми сварными швами необходимо оценивать усталость данных сварных швов.

6.3.7.2 Если соединение работает только на сжатие, то при оценке усталости следует считать, что сжимающие напряжения реализуются только в сварных швах.

6.3.7.3 Если предполагается, что сжимающие нагрузки передаются через контактирующие поверхности деталей, следует убедиться в наличии данного контакта в процессе сварки деталей с учетом всех допусков.

6.4 S-N кривые

6.4.1 Общие сведения

6.4.1.1 Расчет усталости основывается на S-N кривых, которые получаются в результате усталостных испытаний.

6.4.1.2 Расчетные S-N кривые получают на основании экспериментальных данных как среднее значение минус два среднеквадратических отклонения.

6.4.2 S-N кривые и классификация соединений листовых конструкций

6.4.2.1 Сварные соединения принято разделять на несколько классов, для каждого из которых получена расчетная S-N кривая.

6.4.2.2 Все трубные соединения принято относить к классу Т, для которого параметры S-N кривых могут быть приняты по таблице 3.

6.4.2.3 Остальные типы соединений, включая соединение трубы с листом, могут попадать в один из 14 классов, для которых параметры S-N кривых могут быть приняты по таблицам 1, 2, 4 в зависимости от геометрического положения детали, направления действия усилия относительно рассматриваемой детали, а также способа изготовления деталей и методов инспектирования узлов.

6.4.2.4 Кривая усталости (S-N кривая) описывается уравнением

, (6)

где

N

- прогнозируемое число циклов до разрушения при размахе напряжений цикла

;

- размах напряжений цикла, МПа;

m - параметр, характеризующий обратный наклон расчетной S-N кривой;

- точка пересечения S-N кривой и оси log

N

.

6.4.2.5 Величина

определяется по формуле

, (7)

где log a - точка пересечения средней S-N кривой (экспериментальной) и оси log N;

- среднеквадратическое отклонение.

6.4.2.6 Сопротивление усталости сварных соединений зависит от толщины листа. Этот эффект возникает из-за локальной геометрии кромки лицевой поверхности сварного шва в зависимости от толщины присоединяемых листов. Влияние толщины учитывается изменением размаха напряжений цикла следующим образом:

, (8)

где

- эталонная толщина, равная 25 мм для сварных соединений и болтов, 16 мм для трубных соединений;

t

- толщина листа, через которую предполагается рост трещины (если

, то в расчетах принимается

);

k - показатель толщины, приведенный в таблицах 1, 2, 3, 4.

6.4.2.7 Как правило, k=0,1 для трубных стыковых швов, выполненных с одной стороны; и k=0,25 для болтов, испытывающих колебания осевых напряжений.

6.4.2.8 Показатель толщины учитывается в расчетах в том случае, если реальный размер элемента конструкции отличается от образца, для которого была получена S-N кривая. Показатель толщины не учитывает длину сварного шва или длину рассматриваемого элемента.

6.4.2.9 Влияние толщина элемента может зависеть от ширины стыковочных сварных швов и от длины крестообразных соединений, пример которых приведен на рисунке 7, где эти параметры обозначены

. Для стыковочных сварных швов, где ширина

может быть разной на двух сторонах листа, следует использовать ширину

для рассматриваемой в расчете стороны.

6.4.2.10 Для коротких длин

влияние толщины становится незначительным, поэтому толщину

t

в уравнении 8 для стыковочных сварных швов и крестообразных соединений можно заменять эффективной толщиной

, определяемой по формуле

, (9)

где

,

T

- параметры, приведенные на рисунке 7, мм.

6.4.2.11 Значение

должно быть не ниже значения

.

Рисунок 7 - Определение параметров

и

T

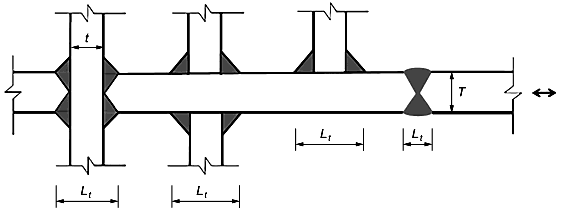6.4.3 S-N кривые для элементов, эксплуатируемых в воздушной среде

6.4.3.1 S-N кривые для соединений, эксплуатируемых в воздушной среде, приведены на рисунке 8. Параметры данных S-N кривых могут быть приняты по таблице 1.

6.4.3.2 Максимальный размах напряжений цикла соответствует кривой В1. При этом для морских сооружений, испытывающих воздействия волновых нагрузок и ветра, усталостная повреждаемость находится в диапазоне числа циклов

N

>10

, и можно использовать билинейные S-N кривые, параметры которых определены в таблице 1.

Рисунок 8 - S-N кривые для элементов, эксплуатируемых в воздушной среде

Таблица 1 - Параметры S-N кривых для элементов, эксплуатируемых в воздушной среде

S-N кривая	Число циклов N 10		для числа циклов N >10 и	Предел усталости при N =10 , МПа	Показатель толщины k	K
			5
B1	4,0	15,117	17,146	106,97	0	-
B2	4,0	14,885	16,856	93,59	0	-
C	3,0	12,592	16,320	73,10	0,05	-
C1	3,0	12,449	16,081	65,50	0,10	-
C2	3,0	12,301	15,835	58,48	0,15	-
D	3,0	12,164	15,606	52,63	0,20	1,00
E	3,0	12,010	15,350	46,78	0,20	1,13
F	3,0	11,855	15,091	41,52	0,25	1,27
F1	3,0	11,699	14,832	36,84	0,25	1,43
F3	3,0	11,546	14,576	32,75	0,25	1,61
G	3,0	11,398	14,330	29,24	0,25	1,80
W1	3,0	11,261	14,101	26,32	0,25	2,00
W2	3,0	11,107	13,845	23,39	0,25	2,25
W3	3,0	10,970	13,617	21,05	0,25	2,50

6.4.4 S-N кривые для элементов, эксплуатируемых в морской воде при наличии катодной защиты

S-N кривые для соединений, эксплуатируемых в морской воде при наличии катодной защиты, приведены на рисунке 9. Параметры данных S-N кривых могут быть приняты по таблице 2.

Рисунок 9 - S-N кривые для элементов, эксплуатируемых в морской воде при наличии катодной защиты

Таблица 2 - Параметры S-N кривых для элементов, эксплуатируемых в морской воде при наличии катодной защиты

S-N кривая	Число циклов N 10		для числа циклов N >10 и	Предел усталости при N =10 , МПа	Показатель толщины k	K
			5
B1	4,0	14,917	17,146	106,97	0
B2	4,0	14,685	16,856	93,59	0
C	3,0	12,192	16,320	73,10	0,05
C1	3,0	12,049	16,081	65,50	0,10
C2	3,0	11,901	15,835	58,48	0,15
D	3,0	11,764	15,606	52,63	0,20	1,00
E	3,0	11,610	15,350	46,78	0,20	1,13
F	3,0	11,455	15,091	41,52	0,25	1,27
F1	3,0	11,299	14,832	36,84	0,25	1,43
F3	3,0	11,146	14,576	32,75	0,25	1,61
G	3,0	10,998	14,330	29,24	0,25	1,80
W1	3,0	10,861	14,101	26,32	0,25	2,00
W2	3,0	10,707	13,845	23,39	0,25	2,25
W3	3,0	10,570	13,617	21,05	0,25	2,50

6.4.5 S-N кривые для трубных соединений

6.4.5.1 S-N кривые для трубных соединений, эксплуатируемых в воздушной среде, в морской воде при наличии катодной защиты и без коррозионной защиты, приведены на рисунке 10. Параметры данных S-N кривых могут быть приняты по таблице 3.

6.4.5.2 Приведенные кривые относятся к критическим областям, которые находятся вблизи сварных швов на внешней стороне трубных соединений.

Рисунок 10 - S-N кривые для трубных соединений

Таблица 3 - Параметры данных S-N кривых для трубных элементов

Среда					Предел усталости при N =10 , МПа	Показатель толщины k
Воздух	Число циклов N 10		Число циклов N >10
	3,0	12,48	5,0	16,13	67,09	0,25
Морская вода при наличии катодной защиты	Число циклов N 1,8 ·10		Число циклов N >1,8 ·10
	3,0	12,18	5,0	16,13	67,09	0,25
Морская вода без коррозионной защиты	3,0	12,03	3,0	12,03	0	0,25

6.4.6 S-N кривые для отливок

6.4.6.1 Для отливок рекомендуется использовать кривую C. Кривая C рекомендуется для того, чтобы обеспечить возможность выполнять ремонтные сварочные работы после появления возможных дефектов литья и возможных усталостных трещин через некоторое время эксплуатации. Возможность ремонта на протяжении срока службы зависит от накопленной усталостной повреждаемости.

6.4.6.2 Для отливок допускается применять эталонную толщину

38 мм при условии, что любой из возможных ремонтных сварных швов отшлифован до гладкой поверхности.

6.4.6.3 Для оценки влияния толщины допускается использовать сниженную эффективную толщину в формуле (8), определяемую следующим образом:

, (10)

где

- размах напряжений цикла на поверхности в критической области;

- размах напряжений цикла в зоне, расположенной ниже на 38 мм от поверхности в критической области;

- толщина отлитой детали в рассматриваемой критической области, измеренная перпендикулярно к поверхности;

- эффективная толщина, которая не должна быть ниже значения 38 мм;

k=0,15 - показатель толщины.

6.4.7 S-N кривые для листовых конструкций без коррозионной защиты

Параметры S-N кривых для листовых конструкций без коррозионной защиты приведены в таблице 4.

Таблица 4 - Параметры S-N кривых для листовых конструкций без коррозионной защиты

6.4.8 S-N кривые для свай

6.4.8.1 Переход от сварного шва к основному материалу на наружной поверхности кольцевого сварного шва, как правило, допускается классифицировать S-N кривой E. Если сварка выполняется в нижнем положении, этот переход допускается классифицировать S-N кривой D. Если сварка выполняется только снаружи, этот переход может классифицироваться S-N кривой F3 для корня данного сварного шва.

6.4.8.2 S-N кривая E применяется к однопроходному сварному шву.

6.4.8.3 S-N кривые для элементов, эксплуатируемых в воздушной среде, допускается использовать для этапа забивки свай.

6.4.8.4 S-N кривые для элементов, эксплуатируемых в морской воде при наличии катодной защиты, допускается использовать для режима эксплуатации, если данная конструкция имеет катодную защиту выше поверхности морского дна.

6.5 Влияние напряжений на сопротивление усталости

6.5.1 Основной материал без остаточных напряжений

6.5.1.1 Расчетный размах напряжений цикла, определяемый для областей основного материала, на которые не оказывают значительного влияния остаточные напряжения, допускается умножать на понижающий коэффициент, определяемый по формуле

, (11)

где

- максимальное растягивающее напряжение (положительное значение);

- максимальное сжимающее напряжение (отрицательное значение).

6.5.1.2 Зависимость понижающего коэффициента от средних напряжений

приведена на рисунке 11.

Рисунок 11 - Понижающий коэффициент для основного материала

6.5.1.3 В частности,

равен 1,0, если материал растягивается во время всего цикла нагружения, 0,8 - если материал испытывает нулевые средние напряжения, и 0 - если в течение всего цикла нагружения материал испытывает сжатие при условии, что низкие остаточные напряжения можно подтвердить документально.

6.5.1.4 Если остаточное напряжение известно, то перед вычислением понижающего коэффициента по формуле 11 это напряжение необходимо прибавить к растягивающим напряжениям и вычесть из сжимающих напряжений.

6.5.1.5 Если напряжения в цикле локально превышают предел текучести (в том числе и при сжатии), то остаточные напряжения необходимо также учитывать, а понижающий коэффициент не включать в расчет.

6.5.2 Сварные соединения без остаточных напряжений

6.5.2.1 При расчете усталости в областях, расположенных в сварных конструкционных элементах, которые были термообработаны после сварки или для которых можно подтвердить наличие низких остаточных напряжений, размах напряжений цикла может быть уменьшен с помощью понижающего коэффициента.

6.5.2.2 Соответствующий понижающий коэффициент определяется по формуле

, (12)

где

- максимальное растягивающее напряжение (положительное значение);

- максимальное сжимающее напряжение (отрицательное значение).

6.5.2.3 Зависимость понижающего коэффициента от средних напряжений

приведена на рисунке 12.

Рисунок 12 - Понижающий коэффициент для сварных соединений

6.5.2.4 В частности,

равен 1,0, если материал растягивается во время всего цикла нагружения, 0,9 - если материал испытывает нулевые средние напряжения, и 0,8 - если в течение всего цикла нагружения материал испытывает сжатие при условии, что низкие остаточные напряжения можно подтвердить документально.

6.5.2.5 Если напряжения в цикле локально превышают предел текучести (в том числе и при сжатии), то остаточные напряжения необходимо также учитывать, а понижающий коэффициент не включать в расчет.

6.6 Влияние допусков

6.6.1 В расчетах усталости следует учитывать напряжения, вызванные наличием допусков при изготовлении конструкций.

6.6.2 Особое внимание следует уделять допускам при изготовлении простых стыковых сварных швов в листовых и трубных элементах, так как они вносят значительный вклад в напряженное состояние конструкции.

6.7 Угловые сварные швы и швы с неполным проплавлением

6.7.1 Проектирование сварных швов следует выполнять таким образом, чтобы усталостное повреждение от корня сварного шва было менее вероятным, чем от кромки лицевой поверхности, т.к. усталостная трещина у кромки лицевой поверхности сварного шва может быть обнаружена при осмотре.

6.7.2 Пример сварных швов с неполным проплавлением приведен на рисунке 13.

Рисунок 13 - Сварные швы с неполным проплавлением

6.7.3 Зависимости геометрических параметров сварных швов с неполным проплавлением приведены на рисунке 14.

Рисунок 14 - Зависимости геометрических параметров сварных швов с неполным проплавлением

6.8 Болтовые соединения

6.8.1 Напряжение в болтовых соединениях следует вычислять на основании рабочей площади поперечного сечения тела болта, которая отличается от площади у основания витка резьбы.

6.8.2 Резьбы болтов, подверженных сдвиговой нагрузке, не рекомендуется располагать в плоскости сдвига. При этом знакопеременная сдвиговая нагрузка в расчете не рассматривается.

6.8.3 Число циклов до разрушения болта, подверженного сдвиговой нагрузке, определяется по формуле

, (13)

где

- касательные напряжения в болте.

6.9 Напряжения в кольцевых сварных швах трубопроводов и райзеров

6.9.1 Сварные швы в трубопроводах обычно выполняются с симметричной разделкой кромок под сварку и свариваются только снаружи. Допускается эксцентриситет менее 0,1·t (t - толщина стенки трубопровода), но не более 3 мм.

6.9.2 Если для трубопроводов с большей толщиной стенки используются те же критерии приемки, которые применяются для эталонной толщины 25 мм, то показатель толщины k=0 можно использовать для критической области у корня сварного шва, а k=0,15 - для кромки лицевой поверхности сварного шва, не подвергавшегося шлифовке.

6.9.3 Классификация кольцевых сварных швов трубопроводов и соответствующие типы S-N кривых, показателей толщины и коэффициенты концентрации приведены в таблице 5.

Таблица 5 - Классификация сварных швов трубопроводов

Сварка	Геометрия сварного шва и зона нагружения	Требования к допускам	S-N кривая	Показатель толщины k
С одной стороны			D	0,15
С одной стороны		мм	E	0,00
		1 мм мм	F
		2 мм мм	F1
С двух сторон		-	D	0,15
Отшлифованный с двух сторон сварной шов	-	-	C	0,00

7 Коэффициенты концентрации напряжений

7.1 Коэффициенты концентрации напряжений в листовых конструкциях

7.1.1 Общие сведения

Допуски изготовления конструкций увеличивают размахи напряжений цикла на сварных швах. Значения величины отклонения от соосности

для стыковых сварных швов некоторых конструкций приведены в таблице 6.

Таблица 6 - Значения величины отклонения от соосности

Элемент конструкции	После сварки	После шлифовки заподлицо
Листовые конструкции	0,10 t*	0,05 t*
Кольцевые швы в конструкциях	0,05 t	0
Кольцевые швы в тросах	0	0
Кольцевые швы в трубопроводах и райзерах	0	0
Примечание - Если значение допуска известно, то для вычисления К необходимо использовать значение для листовых конструкций и 0 для отшлифованных сварных швов.

7.1.2 Коэффициенты концентрации напряжения для стыковых сварных швов

7.1.2.1 Коэффициент концентрации напряжений для стыковых сварных швов в неподкрепленном листе или для стыковых швов, выполняемых в трубах большого диаметра, может быть определен по формуле

, (14)

где

- эксцентриситет;

- характерная величина отклонения от соосности, учитываемая в S-N кривых для стыковых сварных швов;

t - толщина листа или трубы.

7.1.2.2 Коэффициент концентрации напряжений для сварного шва, выполняемого между листами с разной толщиной, на стороне перехода толщины может быть определен по формуле

, (15)

где

- максимальный эксцентриситет;

- эксцентриситет вследствие изменения толщины (допускается использовать для переходов с наклоном 1:4);

- характерная величина отклонения от соосности, учитываемая в S-N кривых для стыковых сварных швов;

T - толщина толстого листа в соединении;

t - толщина тонкого листа в соединении.

7.1.2.3 Коэффициент концентрации напряжений для сварного шва, выполняемого между листами с разной толщиной, на противоположной стороне (относительно стороны перехода толщины) может быть определен по формуле

. (16)

7.1.2.4 Формула (16) применима для сварного шва на противоположной стороне относительно стороны перехода толщины при

, если стыковой сварной шов выполняется с обеих сторон. Если сварной шов является односторонним, то в этом случае принимается

0.

7.1.3 Коэффициенты концентрации напряжения для крестообразных соединений

7.1.3.1 Коэффициент концентрации напряжений для крестообразного соединения в листе толщиной

может быть определен по формуле

, (17)

где

- общий эксцентриситет;

- характерная величина отклонения от соосности, учитываемая в S-N кривых для крестообразных соединений;

- толщина рассматриваемого листа (

i

=1,2);

- длина рассматриваемого листа (

i

=1,2).

7.1.3.2 Пример расчетной схемы крестообразного соединения приведен на рисунке 15.

Рисунок 15 - Расчетная схема крестообразного соединения

7.1.4 Коэффициенты концентрации напряжений для скругленных отверстий прямоугольной формы

7.1.4.1 Коэффициенты концентрации напряжений для скругленных отверстий прямоугольной формы, полученные на основании аналитических вычислений, приведены на рисунке 16.

Рисунок 16 - Коэффициенты концентрации напряжений для скругленных отверстий прямоугольной формы

7.1.4.2 Если сварное соединение расположено вблизи какого-либо отверстия, необходимо учитывать влияние данного отверстия на напряжения, которое может быть оценено на основании рисунка 17.

Рисунок 17 - Распределение напряжений вблизи отверстия

7.1.5 Коэффициенты концентрации напряжений для отверстий с усилением кромок

7.1.5.1 Коэффициенты концентрации напряжений для отверстий с усилением приведены в [1].

7.1.5.2 Усталостное повреждение вокруг кольцевого сварного шва может возникать в различных местах листов вблизи укрепляющих колец в зависимости от геометрии кольца и размера сварного шва:

- усталостное повреждение поперек кромки лицевой поверхности сварного шва в зоне нагружения приводит к возникновению высокого уровня напряжений, действующих параллельно сварному шву. В этом случае

, причем коэффициент концентрации учтен в значении напряжений

(

). Пример приведен в таблице 7;

- усталостное повреждение параллельно кромке лицевой поверхности сварного шва. Зарождение усталостной трещины начинается от кромки лицевой поверхности сварного шва. Рост главного напряжения

приводит к дальнейшему росту трещины. В этом случае

. Также необходимо выполнять проверку при

. Пример приведен в таблице 7;

- усталостное повреждение от корня сварного шва. В некоторых местоположениях сварных швов имеются нормальные напряжения в листе поперек углового сварного шва

и касательные напряжения в листе параллельно данному сварному шву

. В этом случае для данного шва определяются комбинированные напряжения по формуле

, (18)

где t - толщина листа;

a - толщина сварного шва в случае двустороннего углового сварного шва.

Следует также проводить оценку усталости угловых сварных швов в положениях

0

°,

45

°.

Пример приведен в таблице 7.

Таблица 7 - Потенциальные места расположения усталостных трещин

Положение трещины		Комментарии
А		Рекомендуется использовать вместе с S-N кривой C. S-N кривую выбирать в соответствии с критериями, приведенными в 6.4
Б		Рекомендуется использовать вместе с S-N кривой D. S-N кривую выбирать в соответствии с критериями, приведенными в 6.4
В		Зарождение усталостной трещины начинается от корня сварного шва в угловых сварных швах в зоне с наибольшими нормальными и касательными напряжениями. Этот режим разрушения вероятен для малых угловых сварных швов в сравнении с толщиной вставляемого трубного элемента или кольцевого ребра жесткости и основного листа. Усталостное разрушение наблюдается в испытаниях на усталость при 45 °, 0 °

7.1.5.3 Все потенциальные зоны усталостного повреждения следует оценивать при проектировании, используя соответствующие коэффициенты концентраций напряжений для отверстий с усилением.

7.1.6 Коэффициенты концентрации напряжений для выемок

7.1.6.1 Коэффициенты концентрации напряжений для выемок приведены на рисунке 18.

7.1.6.2 Коэффициенты концентрации напряжений применимы к ребрам жесткости, находящихся под действием осевых нагрузок.

Примечания:

а) SCF=2,4 в точке A без учета отклонения от соосности; SCF=1,27 в точке B;

б) SCF=1,17 в точке A без учета отклонения от соосности; SCF=1,27 в точке B;

в) SCF=1,27 в точке A без учета отклонения от соосности; SCF=1,27 в точке B;

г) SCF=1,17 в точке A без учета отклонения от соосности; SCF=1,27 в точке B.

Рисунок 18 - Коэффициенты концентрации напряжений для выемок

7.2 Коэффициенты концентрации напряжений для деталей судов

Коэффициенты концентрации напряжений для деталей судов приведены в правилах РМРС [6].

7.3 Трубные соединения и элементы

7.3.1 Коэффициенты концентрации напряжений для простых трубных соединений

Коэффициенты концентрации напряжений для простых трубных соединений приведены в [1].

7.3.2 Суперпозиция напряжений в трубных соединениях

7.3.2.1 Напряжения в трубных соединениях вследствие действия нагрузок вычисляются в выпуклых (пята и носок сварного шва, например) и вогнутых (седло сварного шва, например) зонах, приведенных на рисунке 19.

N

- осевое усилие;

- изгибающий момент, действующий вне плоскости конструкции;

- изгибающий момент, действующий в плоскости конструкции

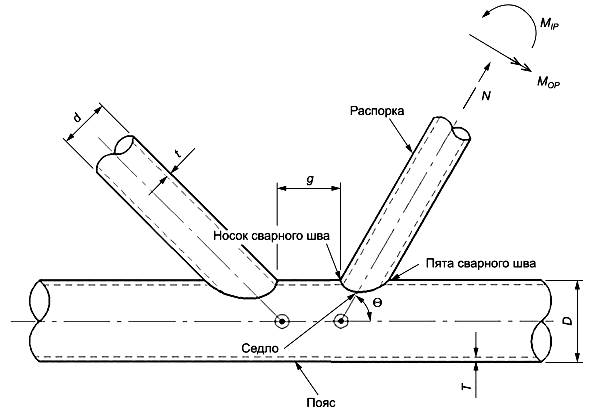Рисунок 19 - Пример трубного соединения

7.3.2.2 Напряжение в критической области получаются суммированием отдельных составляющих напряжений, получаемых от действия осевого усилия, изгибающего момента в плоскости и изгибающего момента, действующего вне плоскости конструкции. Напряжение в критической области следует оценивать в восьми местах, приведенных на рисунке 20, см. также [1].

Рисунок 20 - Точки для определения напряжений

7.3.3 Трубные соединения, выполненные с помощью стыковых сварных швов

7.3.3.1 Концентрация напряжений в трубных соединениях, выполненных стыковыми сварными швами, вызвана наличием эксцентриситетов. Источниками эксцентриситетов труб могут служить:

- концентричность (разница диаметров соединяемых труб);

- разница толщин соединяемых труб;

- овальность;

- смещение центров соединяемых труб.

7.3.3.2 Примеры эксцентриситетов приведены на рисунке 21.

а) Концентричность	б) Разница толщин соединяемых труб

в) Овальность	г) Смещение центров соединяемых труб

Рисунок 21 - Примеры эксцентриситетов

7.3.3.3 Результирующий эксцентриситет можно консервативно оценивать прямым суммированием всех эксцентриситетов. Самый большой вклад в результирующий эксцентриситет

вносит эксцентриситет, вызванный овальностью.

7.3.3.4 Коэффициент концентрации напряжений для кромок лицевой поверхности стыковых сварных швов между элементами равной толщины может быть определен по формуле

, (19)

где

- характерная величина отклонения от соосности, учитываемая в S-N кривых для стыковых сварных швов (не отшлифованных);

- параметр;

L - ширина сварного шва у поверхности.

7.3.3.5 В случае очень жестких производственных допусков рекомендуется принимать

0.

7.3.3.6 Дополнительные напряжения вблизи корня сварного шва с V-образной разделкой кромок, вызванные наличием производственных допусков, имеют низкие значения. В этом случае значение коэффициента концентрации может быть принято SCF=1.

7.3.3.7 Коэффициент концентрации напряжений для наружной стороны стыковых сварных швов с эксцентриситетом может быть определен по формуле

, (20)

где

- параметр;

- характерная величина отклонения от соосности, учитываемая в S-N кривых для стыковых сварных швов (не отшлифованных);

D - наружный диаметр трубы;

- параметр;

L - длина эксцентриситета, приведенная на рисунке 22.

а) Сварка выполнена снаружи

б) Двусторонний сварной шов

Рисунок 22 - Примеры перехода толщин на сварных швах

7.3.3.8 Концентрация напряжений снижается по мере увеличения L и/или снижения D.

7.3.3.9 Переход данного сварного шва к основному материалу на наружной стороне данной трубы можно классифицировать S-N кривой E. Если сварка выполняется в нижнем положении, его можно классифицировать как D. Это означает, что данную трубу необходимо проворачивать в процессе сварки.

7.3.3.10 Формула (20) может использоваться для определения коэффициента концентрации напряжений для наружной стороны сварного шва, если переход расположен снаружи.

7.3.3.11 Для определения коэффициента концентрации напряжений для внутренней стороны сварного шва, если переход расположен снаружи, следует применять формулу

. (21)

7.3.3.12 В формуле (20) предполагается, что сварка выполняется с обеих сторон. Если сварка выполняется только снаружи, необходимо принимать

0 и использовать данное уравнение для вычисления коэффициента концентрации напряжений в области корня сварного шва.

7.3.3.13 В трубных элементах корневая сторона сварных швов, выполняемых с одной стороны, как правило, классифицируется S-N кривой F3.

7.3.3.14 Локальные напряжения при изгибе по толщине трубы в сварном соединении возникают вследствие мембранного напряжения, действующего на данную трубу. Данные мембранные напряжения необходимо использовать для вычисления дополнительных напряжений, возникающих в результате концентрации напряжений на сварном шве. Более подробные рекомендации по определению напряжений приведены в [1].

7.3.4 Коэффициенты концентрации напряжений для соединений элементов квадратного сечения

7.3.4.1 Коэффициенты концентрации напряжений для соединений элементов квадратного сечения следует определять для конкретных конструкций, используя например конечно-элементный метод.

7.3.4.2 Данные коэффициенты концентрации напряжений допускается использовать с S-N кривой D.

7.3.4.3 В случае, если пояс и распорки имеют одинаковое квадратное сечение, то допускается принимать следующие значения коэффициентов концентрации:

- 1,90 при осевой нагрузке;

- 4,00 при действии момента при изгибе в плоскости конструкции;

- 1,35 при действии момента при изгибе вне плоскости конструкции.

7.3.4.4 Данные коэффициенты концентрации напряжений следует использовать с S-N кривой F.

7.3.5 Коэффициенты концентрации напряжений для соединений с косынками

7.3.5.1 В соединениях трубных деталей и балок часто используются стальные косынки. Пример данных соединений приведен на рисунке 23.

а) Рекомендуемая форма косынки	б) Упрощенная форма косынки

Рисунок 23 - Пример соединений с косынками

7.3.5.2 При действии динамических нагрузок в данных соединениях рекомендуется выполнять сварные швы с полным проплавлением.

7.3.5.3 Также рекомендуется выбирать форму косынки таким образом, чтобы поле напряжений в области перехода косынки в трубу было плавным. Пример рекомендуемой формы косынки приведен на рисунке 23 а).

7.3.5.4 Расчеты данных соединений рекомендуется выполнять методом конечных элементов. При оценке усталостной долговечности на внешней стороне допускается пользоваться S-N кривой D. При оценке усталостной долговечности на внутренней стороне допускается пользоваться S-N кривыми F3 и W3 при отсутствии проварки корня шва.

7.3.5.5 Использование оболочечных КЭ моделей для расчетов данных соединений допускается ввиду консервативности результатов по сравнению с твердотельными КЭ моделями.

8 Расчет напряжений в критических областях

8.1 Сварные трубные соединения

8.1.1 Размах напряжений цикла в критических областях трубных соединений принято сравнивать с кривой T. Для получения более достоверных результатов рекомендуется при моделировании учитывать сварные швы, т.е. выполнять моделирование с помощью твердотельных конечных элементов.

8.1.2 Также напряжения в критических областях трубных соединений допускается определять посредством линейной экстраполяции напряжений, полученных в соответствующих точках на расстояниях a и b. Пример трубного соединения с указанием точек определения напряжений приведен на рисунке 24.

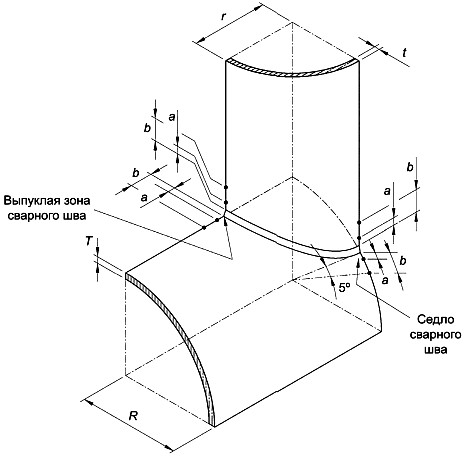Рисунок 24 - Пример трубного соединения

8.1.3 Значения размеров a и b на распорке определяются по формулам:

; (22)

. (23)

8.1.4 Значения размеров a и b на поясе в выпуклой зоне сварного шва определяются по формулам:

; (24)

. (25)

8.1.5 Значения размеров a и b в седле сварного шва определяются по формулам:

; (26)

. (27)

8.1.6 Также допускается определять напряжения в Гауссовых точках конечных элементов (точках интегрирования), если они находятся на расстоянии

от сварного шва. Данные значения напряжений могут непосредственно использоваться при оценке усталости.

8.2 Сварные соединения в листовых конструкциях

8.2.1 Распределение напряжений в сварной детали

8.2.1.1 Характерное распределение напряжений вблизи сварного шва листовой конструкции приведено на рисунке 25.

8.2.1.2 Влияние дефекта (местное напряжение) учитываются в S-N кривой, поэтому напряжения в критической области получаются экстраполяцией напряжений в конструкции, вычисленных на расстоянии 0,5t и 1,5t от кромки сварного шва, как показано на рисунке 25.

Рисунок 25 - Характерное распределение напряжений вблизи сварного шва листовой конструкции

8.2.1.3 Для экстраполяции выбираются напряжения на внешней поверхности рассматриваемой детали.

8.2.2 Конечно-элементное моделирование

8.2.2.1 Напряжения в критической области определяют в предположении, что материал является линейно-упругим и в конструкции отсутствуют заводские отклонения. Размеры локальной модели выбираются исходя из принципа Сен-Венана: влияние граничных условий на рассматриваемую зону концентрации напряжений должно быть минимальным.

8.2.2.2 В листовых конструкциях можно идентифицировать три типа критических областей на кромках лицевых поверхностей сварных швов:

- у кромки лицевой поверхности сварного шва основной детали вблизи приваренного листа (тип a);

- у кромки лицевой поверхности сварного шва приваренного листа вблизи основной детали (тип b);

- вдоль сварного шва у кромок лицевых поверхностей сварного шва как на основной, так и на привариваемой детали соединения (тип c).

Примеры трех типов критических областей приведены на рисунке 26.

Рисунок 26 - Примеры критических областей

8.2.2.3 Допускается выполнять моделирование листовых соединений оболочечными конечными элементами, срединная плоскость которых совпадает со срединной плоскостью конструкции. Пример оболочечной модели с линиями, вдоль которых выполняется экстраполяция напряжений, приведен на рисунке 27.

Рисунок 27 - Пример оболочечной модели

8.2.2.4 В случае высоких градиентов напряжений рекомендуются использовать квадратичные конечные элементы, особенно при оценке в критических зонах, типа b.

8.2.2.5 Сварные швы обычно не моделируются, за исключением особых случаев, когда на результаты значительно влияет локальный изгиб. В этом случае сварной шов допускается учитывать, как слой конечных элементов привариваемого листа с соответствующей жесткостью.

8.2.2.6 При использовании линейных оболочечных элементов (с 4-мя узлами) и дополнительными степенями свободы для уточненного описания поведения элемента в плоскости и для квадратичных оболочечных элементов (с 8 узлами) допускается использовать размер сетки от

t

t

до 2

t

2

t

. Использование более грубой сетки в критической области может дать неконсервативные результаты.

8.2.2.7 Также допускается выполнять моделирование листовых соединений квадратичными твердотельными конечными элементами (с 20 узлами) с одним элементом по толщине листа. При использовании линейных твердотельных конечных элементов (с 8 узлами) необходимо выполнять более мелкую сетку - не менее четырех элементов по толщине листа. При данном подходе рекомендуется моделировать сварной шов, как показано в примере (с линиями, вдоль которых выполняется экстраполяция напряжений) на рисунке 28.

Рисунок 28 - Пример твердотельной модели

8.2.3 Напряжения в точках 0,5t и 1,5t

8.2.3.1 Рекомендуемые точки определения напряжений расположены на расстоянии 0,5t и 1,5t от рассматриваемой критической области, где t - толщина листа.

8.2.3.2 Если в критической области используется сетка с характерным размером конечных элементов

t

t

, то напряжения допускается оценивать следующим образом:

- при использовании оболочечных конечных элементов напряжения можно вычислить в средних точках сторон соответствующих элементов, как показано на рисунке 29;

- при использовании твердотельных конечных элементов сперва вычисляются напряжения на поверхностях листа путем экстраполяции значений, полученных в точках интегрирования. Далее вычисляются напряжения на срединной поверхности листа путем интерполяции значений с поверхностей. И значения напряжений на срединной поверхности используются для определения напряжений в критической области.

Рисунок 29 - Пример определения напряжений на оболочечной модели

8.2.3.3 При использовании оболочечных конечных элементов с характерным размером больше, чем

t

t

, необходимо подбирать полином второго порядка при экстраполяции, чтобы определить напряжения в точках 0,5

t

и 1,5

t

на основании значений напряжений в первых трех конечных элементах. Пример полинома приведен на рисунке 30. Данный подход также допускается использовать при моделировании линейными твердотельными элементами.

Рисунок 30 - Пример экстраполяции напряжений на основании результатов в трех конечных элементах

8.2.4 Определение размаха напряжений цикла в критической области

8.2.4.1 При моделировании оболочечными конечными элементами без учета в модели сварного шва значения напряжений в критической области (на линии пересечения) получают линейной экстраполяцией напряжений, полученных на расстоянии 0,5t и 1,5t от линии пересечения.

8.2.4.2 При моделировании твердотельными конечными элементами с учетом сварного шва значения напряжений в критической области (на кромке лицевой поверхности сварного шва) получают линейной экстраполяцией напряжений, полученных на расстоянии 0,5t и 1,5t от кромки лицевой поверхности сварного шва.

8.2.4.3 Эффективный размах напряжений цикла в критической области, который используется вместе с S-N кривой критической области, может быть определен по формуле

, (28)

где

0,90, если рассматривается S-N кривая C2 и напряжение параллельно сварному шву вблизи критической области;

0,80, если рассматривается S-N кривая C1 и напряжение параллельно сварному шву вблизи критической области;

0,72, если рассматривается S-N кривая C и напряжение параллельно сварному шву вблизи критической области.

8.2.4.4 Размахи главных напряжений определяются по формулам:

; (29)

. (30)

8.2.4.5 Данный метод предполагает, что усталостное повреждение происходит вдоль кромки лицевой поверхности сварного шва, как показано на рисунке 3, а также в случае, когда направление главных напряжений практически параллельно лицевой кромке поверхности сварного шва, как показано на рисунке 4.

8.2.5 Определение размаха напряжений цикла в критической области

8.2.5.1 При моделировании оболочечными конечными элементами без учета в модели сварного шва значения напряжений в критической области (на линии пересечения) принимают равными значениям напряжений на расстоянии 0,5t от линии пересечения.

8.2.5.2 При МКЭ с учетом сварного шва значения напряжений в критической области (на кромке лицевой поверхности сварного шва) принимают равными значениям напряжений на расстоянии 0,5t от кромки лицевой поверхности сварного шва.

8.2.5.3 Эффективный размах напряжений цикла в критической области может быть определен по формуле

, (31)

где

,

и

аналогичны методу А.

8.2.5.4 Данный метод предполагает, что усталостное повреждение происходит по поверхности сварного шва.

8.2.6 S-N кривая для критической области

8.2.6.1 Напряжения в критической области, определенные МКЭ, сравнивают с S-N кривой D.

8.2.6.2 Расчет простых соединений (крестообразных, Т-образных или простых стыковых) с использованием оболочечных моделей будет давать значения напряжений в критических областях, равные номинальным напряжениям. Например, в простом соединении, приведенном на рисунке 31, при возникновении напряжений в корпусе, параллельных направлению I, не будет возникать напряжений поперек листа корпуса. При этом будут реализовываться напряжения, параллельные направлению II.

Рисунок 31 - Пример простого сварного соединения

8.2.6.3 В предложенном примере S-N кривая номинальных напряжений для направления I ниже, чем S-N кривая D, в отличие от направления II. В этом случае для критической области "с" консервативнее применять метод номинальных напряжений.

8.2.6.4 Для простых крестообразных соединений, простых Т-образных соединений в листовых конструкциях или простых стыковых сварных швов, которые свариваются только с одной стороны, рекомендуется использовать метод критических областей (вычислять напряжения методом конечных элементов) совместно с соответствующими номинальными S-N кривыми.

8.2.6.5 Производственные допуски оказывают значительное влияние на данные соединения (стыковые сварные швы и крестообразные соединения), поэтому их нужно учитывать при оценке усталости. Если отклонения от соосности превышают значения, которые уже включены в S-N кривую, рекомендуется уточнять полученные результаты с помощью соответствующих коэффициентов концентрации напряжений.

8.2.7 Определение размаха напряжений цикла в критической области на основании результатов конечно-элементного расчета

8.2.7.1 В критических областях, где реализуется значительный изгиб листа, размах напряжения цикла для оценки усталости может быть получен по формуле

, (32)

где

- размах мембранного напряжения;

- размах напряжения при изгибе.

8.2.7.2 Коэффициент снижения напряжения при изгибе, равный 0,6, применяют для перераспределения напряжений во время роста трещины.

8.2.8 Процедура расчета крестообразных соединений, усиленных перемычками

8.2.8.1 Примеры крестообразных соединений, усиленных перемычками, приведены на рисунках 32, 33 и 34.

Рисунок 32 - Пример крестообразного соединения в бункере танкера

Рисунок 33 - Пример крестообразного соединения основания колонны танкера

Рисунок 34 - Пример крестообразного соединения в соединении балок

8.2.8.2 Расчет крестообразных соединений выполняется только для критических областей, приведенных на рисунках 32, 33 и 34.

8.2.8.3 Напряжение в критической области определяется по формуле

, (33)

где

- поправочный коэффициент.

8.2.8.4 Напряжения при изгибе определяют по формуле

. (34)

8.2.8.5 Если в соединении пластины сварены под углом 45°, то поправочный коэффициент составляет

. (35)

8.2.8.6 Если в соединении пластины сварены под углом 60°, то поправочный коэффициент составляет

. (36)

8.2.8.7 Если в соединении пластины сварены под прямым углом, то поправочный коэффициент составляет

. (37)

8.2.8.8 При оценке других критических областей, приведенных рисунках 32, 33 и 34, следует использовать максимальное главное напряжение на поверхности листов, определенное на расстоянии

(

- толщина перемычки,

- наименьшая из длин катетов угловых сварных швов) от линии пересечения элементов, но не ближе к самим элементам, чем величина

.

8.2.8.9 Полученные значения напряжений необходимо сравнивать с S-N кривыми номинальных напряжений E и F для крестообразных соединений. Пример данной процедуры приведен на рисунке 35.

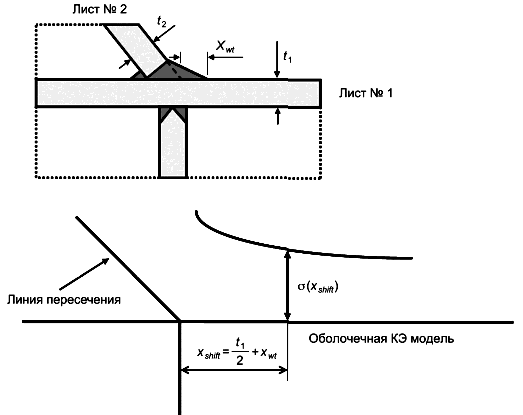Рисунок 35 - Пример процедуры расчета в зоне концентрации напряжений

8.2.9 Расчет сварных швов с проплавлением

8.2.9.1 Сварные швы с проплавлением, как правило, не включают в КЭ модели из-за значительного увеличения расчетного времени. При моделировании листовых конструкций в месте проплавления поле напряжения вычисляется с использованием оболочечных элементов: определяются нормальные напряжений

,

и касательные напряжения

. На основании полученных напряжений размахи напряжений циклов могут быть вычислены по формулам:

; (38)

. (39)

8.2.9.2 Связь главных напряжений с нормальными и касательными, а также местоположения критических областей приведены на рисунке 36.

Рисунок 36 - Элементарная площадка и местоположения критических областей

Напряжение в положении a рассматриваемой критической области, приведенной на рисунке 36, будет определяться первыми главными напряжениями и вторыми главными напряжениями, которые могут быть вычислены независимо друг от друга, как показано на рисунке 37. Затем полученные напряжения суммируются, и результат сравнивается с S-N кривой C.

а) Следует вычислять с использованием	б) Следует вычислять с использованием

Рисунок 37 - Примеры действия главных напряжений в положении a

8.2.9.3 Напряжение в положении

b

рассматриваемой критической области, приведенной на рисунке 36, будет определяться на основании главных нормальных напряжений (перпендикулярных

и параллельных

кромке) и касательных

, на основании которых вычисляются размахи напряжений цикла по формулам:

; (40)

. (41)

8.2.9.4 Размах эффективных напряжений в положении b рассматриваемой критической области определяется по формуле

. (42)

8.2.9.5 Напряжение в положении c рассматриваемой критической области, приведенной на рисунке 36, будет определяться первыми главными напряжениями и вторыми главными напряжениями, которые могут быть вычислены независимо друг от друга, как показано на рисунке 38. Затем полученные напряжения суммируются, и результат сравнивается с S-N кривой D.

а) Следует вычислять с использованием	б) Следует вычислять с использованием

Рисунок 38 - Примеры действия главных напряжений в положении c

9 Метод проверочного расчета сопротивления усталости

9.1 Общие сведения

9.1.1 Проверочный расчет сопротивления усталости является упрощенным и косвенным методом расчета сопротивления усталости, т.к. результатом данного метода расчета не является значение циклической долговечности, см. также правила [3] и [4].

9.1.2 Особенность метода проверочного расчета сопротивления усталости заключается в том, что двухпараметрическое распределения Вейбулла представляют как долговременное распределение размаха напряжений цикла по следующей формуле:

, (43)

где

Q

- вероятность превышения размаха напряжений цикла

;

h - параметр формы в распределении Вейбулла;

q - параметр масштаба в распределении Вейбулла.

9.1.3 Параметр масштаба в распределении Вейбулла определяется на основании размаха напряжений цикла

по формуле

, (44)

где

- наибольших размах напряжений из

циклов.

9.1.4 Если долговременное распределение размаха напряжений цикла представлено распределением Вейбулла и используется S-N кривая с одним наклоном, то усталостная повреждаемость может быть вычислена по формуле

, (45)

где

- расчетное время, с;

- средняя частота пересечения нулевого значения;

- Гамма-функция, значения которой для различных величин

h

и

m

=3 приведены в таблице 8.

9.1.5 Использование S-N кривых с одним наклоном приводит к получению консервативных результатов.

Таблица 8 - Значения Гамма-функции

9.2 Графики расчета усталости

9.2.1 Расчетные графики для стальных элементов, эксплуатируемых в воздушной среде в воздухе и в морской воде при наличии катодной защиты, показаны на рисунках 39 и 40 соответственно. Значения приведены в таблицах 9 и 10.

9.2.2 Расчетные графики получены в предположении, что допустимая усталостная повреждаемость составляет

1 при количестве циклов 10

(20-летний срок службы, который соответствует среднему периоду цикла 6,3 с).

9.2.3 Коэффициент использования, как функция долговечности и DFF, приведен в таблице 15.

9.2.4 Приведенные значения допускаемых напряжений получены для заготовок с эталонной толщиной. Для учета толщин, превышающих эталонное значение, допустимые напряжения при количестве циклов 10

могут быть уточнены по формуле

, (46)

где k - показатель толщины, приведенный в таблицах 1, 2, 3;

- допускаемый размах напряжений цикла, приведенный в таблицах 9 и 10.

Рисунок 39 - Допускаемый размах напряжений цикла для компонентов, эксплуатируемых в воздушной среде

Таблица 9 - Допускаемый размах напряжений цикла в МПа для компонентов, эксплуатируемых в воздушной среде

Рисунок 40 - Допускаемый размах напряжений цикла для компонентов, эксплуатируемых в морской воде при наличии катодной защиты

Таблица 10 - Допускаемый размах напряжений цикла в МПа для компонентов, эксплуатируемых в морской воде при наличии катодной защиты

Таблица 11 - Понижающие коэффициенты для S-N кривых B1 и B2 и компонентов, эксплуатируемых в воздушной среде

	Параметр формы в распределении Вейбулла
	0,50	0,60	0,70	0,80	0,90	1,00	1,10	1,20
0,1	0,57	0,575	0,581	0,587	0,592	0,597	0,602	0,603
0,2	0,674	0,678	0,682	0,686	0,69	0,694	0,698	0,701
0,22	0,69	0,693	0,697	0,701	0,705	0,709	0,712	0,715
0,27	0,725	0,728	0,731	0,735	0,738	0,742	0,745	0,748
0,30	0,744	0,747	0,75	0,753	0,756	0,759	0,762	0,765
0,33	0,762	0,764	0,767	0,77	0,773	0,776	0,778	0,781
0,40	0,798	0,8	0,803	0,805	0,808	0,81	0,812	0,815
0,50	0,843	0,845	0,846	0,848	0,85	0,852	0,854	0,856
0,60	0,882	0,883	0,884	0,886	0,887	0,888	0,89	0,891
0,67	0,906	0,907	0,908	0,909	0,91	0,911	0,912	0,913
0,70	0,916	0,917	0,917	0,919	0,92	0,92	0,921	0,922
0,80	0,946	0,947	0,947	0,948	0,949	0,949	0,95	0,95
1,00	1	1	1	1	1	1	1	1

Таблица 12 - Понижающие коэффициенты для S-N кривых C - W3 и компонентов, эксплуатируемых в воздушной среде

	Параметр формы в распределении Вейбулла
	0,50	0,60	0,70	0,80	0,90	1,00	1,10	1,20
0,1	0,497	0,511	0,526	0,54	0,552	0,563	0,573	0,582
0,2	0,609	0,62	0,632	0,642	0,652	0,661	0,67	0,677
0,22	0,627	0,638	0,648	0,659	0,668	0,677	0,685	0,692
0,27	0,661	0,676	0,686	0,695	0,703	0,711	0,719	0,725
0,30	0,688	0,697	0,706	0,715	0,723	0,73	0,737	0,743
0,33	0,708	0,717	0,725	0,733	0,741	0,748	0,754	0,76
0,40	0,751	0,758	0,765	0,772	0,779	0,785	0,79	0,795
0,50	0,805	0,81	0,816	0,821	0,826	0,831	0,835	0,839
0,60	0,852	0,856	0,86	0,864	0,868	0,871	0,875	0,878
0,67	0,882	0,885	0,888	0,891	0,894	0,897	0,9	0,902
0,70	0,894	0,897	0,9	0,902	0,905	0,908	0,91	0,912
0,80	0,932	0,934	0,936	0,938	0,939	0,941	0,942	0,944
1,00	1	1	1	1	1	1	1	1

Таблица 13 - Понижающие коэффициенты для S-N кривых B1 и B2 и компонентов, эксплуатируемых в морской воде при наличии катодной защиты

	Параметр формы в распределении Вейбулла
	0,50	0,60	0,70	0,80	0,90	1,00	1,10	1,20
0,1	0,583	0,593	0,602	0,61	0,617	0,621	0,625	0,627
0,2	0,684	0,691	0,699	0,705	0,711	0,715	0,718	0,72
0,22	0,699	0,706	0,714	0,72	0,725	0,729	0,732	0,735
0,27	0,733	0,74	0,746	0,752	0,757	0,76	0,763	0,766
0,30	0,751	0,758	0,764	0,769	0,773	0,777	0,78	0,782
0,33	0,768	0,774	0,78	0,785	0,789	0,792	0,795	0,792
0,40	0,804	0,809	0,814	0,818	0,822	0,825	0,827	0,829
0,50	0,848	0,851	0,855	0,858	0,861	0,864	0,866	0,867
0,60	0,885	0,888	0,891	0,893	0,896	0,897	0,899	0,9
0,67	0,909	0,911	0,913	0,915	0,917	0,919	0,92	0,921
0,70	0,918	0,92	0,922	0,924	0,926	0,927	0,928	0,929
0,80	0,948	0,949	0,95	0,952	0,953	0,954	0,955	0,955
1,00	1	1	1	1	1	1	1	1

Таблица 14 - Понижающие коэффициенты для S-N кривых C - W3 и компонентов, эксплуатируемых в морской воде при наличии катодной защиты

	Параметр формы в распределении Вейбулла
	0,50	0,60	0,70	0,80	0,90	1,00	1,10	1,20
0,1	0,535	0,558	0,577	0,593	0,605	0,613	0,619	0,623
0,2	0,64	0,659	0,676	0,689	0,699	0,707	0,713	0,717
0,22	0,657	0,675	0,691	0,703	0,713	0,721	0,727	0,731
0,27	0,694	0,71	0,725	0,736	0,745	0,752	0,758	0,762
0,30	0,714	0,729	0,743	0,754	0,763	0,769	0,775	0,779
0,33	0,732	0,747	0,76	0,77	0,779	0,785	0,79	0,794
0,40	0,772	0,785	0,796	0,805	0,812	0,818	0,822	0,825
0,50	0,821	0,831	0,84	0,847	0,853	0,858	0,862	0,864
0,60	0,864	0,872	0,879	0,885	0,889	0,893	0,896	0,898
0,67	0,892	0,898	0,903	0,908	0,912	0,915	0,917	0,919
0,70	0,903	0,908	0,913	0,917	0,921	0,924	0,926	0,927
0,80	0,938	0,941	0,945	0,947	0,949	0,951	0,953	0,954
1,00	1	1	1	1	1	1	1	1

Таблица 15 - Значения коэффициента использования

9.3 Расчет соединений

При проектировании соединений могут использоваться два подхода:

- использование метода конечных элементов при решении линейной задачи с упругими моделями материалов. В этом случае полученный размах напряжений сравнивается с S-N кривой B1, а требования к проведению испытаний на усталость отсутствуют;

- использование метода конечных элементов при решении нелинейной задачи (с учетом контактных взаимодействий и нелинейных моделей материалов с упрочнением). Полученный размах напряжений может сравниваться с S-N кривой для высокопрочных материалов, приведенной в [1]. Результаты данного подхода рекомендуется верифицировать испытаниями на усталость.

10 Метод расчета сопротивления усталости на основании механики разрушения

10.1 При расчете сопротивления усталости может применяться метод расчета, основанный на механике разрушения в соответствии с ГОСТ Р ИСО 2394, см. также правила [3] и [4].

10.2 Метод расчета сопротивления усталости, основанный на механике разрушения, заключается в подтверждении того, что усталостные трещины, которые могут возникать в процессе эксплуатации, не приведут к разрушению стального сооружения.

10.3 Расчет сопротивления усталости выполняют с учетом следующего:

- параметр роста трещины C определяется как среднее значение плюс два среднеквадратических отклонения;

- выполнена детальная оценка начальных дефектов конструкции;

- используются геометрические функции, которые определены с погрешностями в безопасную сторону.

10.4 Размер начальной трещины, задаваемый при вычислениях, необходимо рассчитывать в каждом случае с учетом известных опытных размеров дефектов для разных сварных изделий или геометрий. Для поверхностных трещин, начинающихся от перехода сварного шва/основного материала, допускается принимать глубину 0,5 мм, если отсутствует иная информация.

10.5 Для прогнозирования распространения трещины может применяться уравнение Париса

, (47)

где

;

A - глубина трещины в предположении, что отношение глубины к длине трещины ниже, чем величина 1:5.

10.6 Коэффициент K может приниматься в значениях, приведенных в разделе 6, см. также [7].

Библиография