ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

пнет 614—
2023
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Нефтяная и газовая промышленность
СИСТЕМЫ ПОДВОДНОЙ ДОБЫЧИ
Моделирование и расчет морских операций. Методические указания
Издание официальное
Москва Российский институт стандартизации 2023
Предисловие
1 РАЗРАБОТАН Обществом с ограниченной ответственностью «Газпром 335» (ООО «Газпром 335»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 023 «Нефтяная и газовая промышленность»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 марта 2023 г. № 16-пнст
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТР 1.16—2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за 4 мес до истечения срока его действия разработчику настоящего стандарта по адресу: inf@gazprom335.ru и/или в Федеральное агентство по техническому регулированию и метрологии по адресу: 123112 Москва, Пресненская набережная, д. 10, стр. 2.
В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе «Национальные стандарты» и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
© Оформление. ФГБУ «Институт стандартизации», 2023
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
Содержание
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Сокращения
5 Общие методы расчета
6 Спуско-подъемные операции в волновой зоне. Общие положения
7 Спуско-подъемные операции в волновой зоне. Упрощенный метод
8 Глубоководные работы по опусканию/подниманию
9 Опускание на морское дно и извлечение
10 Буксировка
11 Расчет погодных критериев и пригодности
12 Спуско-подъемные операции
Приложение А (справочное) Коэффициенты присоединенной массы
Приложение Б (справочное) Коэффициенты лобового сопротивления
Приложение В (справочное) Постоянные физические величины
Библиография
Введение
Создание и развитие отечественных технологий и техники для освоения шельфовых нефтегазовых месторождений должно быть обеспечено современными стандартами, устанавливающими требования к проектированию, строительству и эксплуатации систем подводной добычи. Для решения данной задачи Министерством промышленности и торговли Российской Федерации и Федеральным агентством по техническому регулированию и метрологии реализуется Программа по обеспечению нормативной документацией создания отечественной системы подводной добычи для освоения морских нефтегазовых месторождений. В объеме работ данной программы предусмотрена разработка национальных стандартов и предварительных национальных стандартов, областью применения которых являются системы подводной добычи углеводородов.
Цель разработки настоящего стандарта — регламентирование методики определения расчетных нагрузок, необходимых для планирования и выполнения морских операций, связанных со строительством и эксплуатацией систем подводной добычи углеводородов.
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Нефтяная и газовая промышленность
СИСТЕМЫ ПОДВОДНОЙ ДОБЫЧИ
Моделирование и расчет морских операций. Методические указания
Petroleum and natural gas industry. Subsea production systems. Modelling and calculation of marine operations. Methodology guide
Срок действия — с 2023—07—01 до 2026—07—01
1 Область применения
Настоящий стандарт распространяется на методику математического моделирования и расчеты (определение предельных состояний и допустимых нагрузок) морских операций при грузоподъемных работах, выполняемых в зоне периодического смачивания, при работах по спуску объектов на большие глубины и при установке на морское дно, производимых при строительстве систем подводной добычи углеводородов.
Оценку влияния ледовых условий, а также снега и обледенения на морские операции выполняют в соответствии с требованиями ГОСТ Р 57148.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 55311 Нефтяная и газовая промышленность. Сооружения нефтегазопромысловые морские. Термины и определения
ГОСТ Р 57148 (ИСО 19901-1:2015) Нефтяная и газовая промышленность. Сооружения нефтегазопромысловые морские. Проектирование и эксплуатация с учетом гидрометеорологических условий
ГОСТ Р 59304 Нефтяная и газовая промышленность. Системы подводной добычи. Термины и определения
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
Издание официальное
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 59304 и ГОСТ Р 55311, а также следующие термины с соответствующими определениями:
3.1
зона периодического смачивания (splash zone): Участок сооружения, который находится в зоне воздействия волн и колебаний уровня моря.
[ГОСТ Р 58772—2019, пункт 3.30]
3.2
характерная высота волны (significant wave height): Статистическая мера высоты волн при определенном состоянии моря.
[ГОСТ Р 57148—2016, пункт 3.39]
4 Сокращения
В настоящем стандарте использованы следующие сокращения:
КС — число Келегана—Карпентера;
КЭ — конечные элементы;
ПМ — спектр Пирсона—Московица;
ТИПА — телеуправляемый необитаемый подводный аппарат;
ВЕМ — метод граничных элементов;
CFD — вычислительная гидродинамика;
DAF — коэффициент динамичности;
HF — высокая частота;
НМРЕ — сверхмолекулярный полиэтилен;
LF — низкая частота;
LTF — линейная передаточная функция;
NRT — реальный масштаб времени;
RAO — оператор амплитуды отклика;
RT — реальное время;
VIV — вызванные вихреобразованием вибрации;
WF — частота волны.
5 Общие методы расчета
5.1 Общие положения
5.1.1 Волны имеют неправильные и случайные форму, высоту, длину и скорость распространения. Фактическое состояние моря наиболее наглядно представлено моделью случайной волны.
5.1.2 Линейная модель случайной волны представляет собой сумму многих малых линейных компонентов волны с разными амплитудой, частотой и направлением. Фазы являются случайными относительно друг друга.
5.1.3 Нелинейная модель случайной волны учитывает суммарные и разностные частотные составляющие волны, вызванные нелинейным взаимодействием между отдельными компонентами волны.
5.1.4 Волновые условия, учитываемые для целей расчета конструкции, можно описать, применяя или детерминированные методы расчетной волны, или вероятностные методы, использующие волновые спектры.
5.1.5 Для оценки квазистатического поведения конструкций достаточно использовать детерминированные регулярные волны, характеризуемые длиной волны и соответствующими периодом волны, высотой волны, высотой гребня. Детерминированные параметры волны могут быть спрогнозированы статистическими методами.
5.1.6 Конструкции со значительным динамическим откликом требуют стохастического моделирования поверхности моря и его кинематики посредством временных рядов. Состояние моря задается спектром частоты волны с заданной высотой характерной волны, репрезентативной частотой, средним направлением распространения и функцией распространения. Состояние моря также можно описать в виде продолжительности его спокойного состояния, в качестве этого значения берут 3 ч (см. [1]).
5.1.7 Морские волны можно разделить на два класса: ветровые волны и зыбь. Ветровые волны образуются локальным ветром, в то время как зыбь не имеет отношения к локальному ветру. Зыбь — это волны, ушедшие с участков их образования. Умеренные и спокойные состояния моря на участках открытого моря часто определяются как ветровыми волнами, так и зыбью.
5.1.8 На некоторых участках могут возникать внутренние одиночные волны. Они появляются на глубине в связи с быстрым изменением плотности воды в силу меняющейся температуры или солености. Такие волны могут влиять на глубоководные работы по опусканию конструкций.
5.1.2 Регулярное волнение
5.1.2.1 У регулярной волны при перемещении форма остается неизменной. Такая волна имеет определенные длину, период и высоту.
5.1.2.2 Регулярную волну описывают следующими основными характеристиками:
- длина волны: длина волны X представляет собой расстояние между последовательными гребнями;
- период волны: период волны Т — это временной интервал между последовательными гребнями, проходящими через определенную точку;
- фазовая скорость: скорость распространения формы волны — фазовая скорость, скорость распространения волны или скорость волны, обозначаемая с = МТ = ш/к;
- частота волны, обратная периоду волны: f= МТ;
- угловая частота волны: ш = 2л/Т;
- волновое число: к = 2л:/Х;
- подъем поверхности: подъем поверхности z = r|(x,y,f) представляет собой расстояние между уровнем неподвижной воды и поверхностью волны;
- высота гребня волны АС — это расстояние от уровня неподвижной воды до гребня волны;
- глубина подошвы волны АТ — расстояние от уровня неподвижной воды до подошвы волны;
- высота волны: высота волны Н— вертикальное расстояние от подошвы до гребня. Н = АС + АТ;
- глубина воды d.
Характеристики повторяющейся перемещающейся волны отражены на рисунке 1.
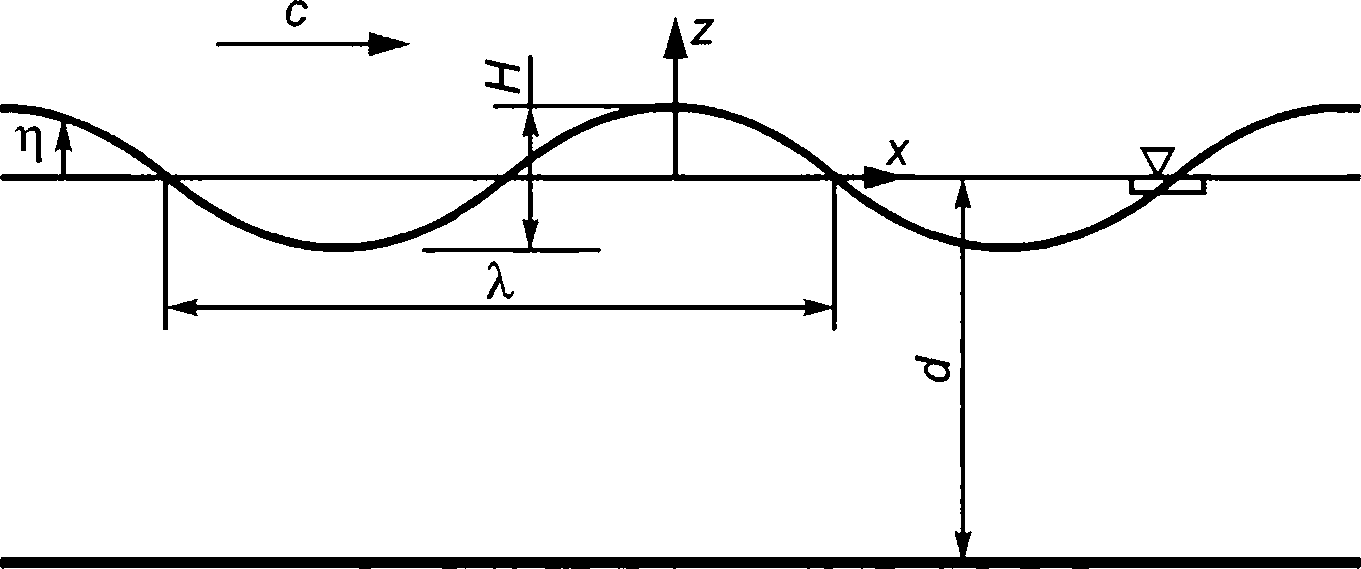
Н — высота волны, м; с — скорость волны, м/с; ?. — длина волны, м; d — глубина воды, м; г, — подъем поверхности, м
Рисунок 1 — Характеристики волны
5.1.2.3 Нелинейные регулярные волны являются асимметричными Ас > Ат, их фазовая скорость зависит от высоты волны.
5.1.2.4 Для заданной регулярной волны с периодом Т, высотой Н и глубиной воды d двухмерную кинематику можно рассчитать с использованием соответствующей теории волн, которая действительна для волны с заданными параметрами.
5.1.3 Моделирование нерегулярного волнения
5.1.3.1 Характеризующие фактическое состояние моря нерегулярные случайные волны могут моделироваться как сумма синусоидальных компонентов волны. Простейшей моделью случайной волны является модель линейной волны с длинным гребнем, задаваемая следующим выражением:
N
Hi(0 = £4C0S(>V + ^). <1)
к=1
где т|1 — возвышение водной поверхности относительно невозмущенного уровня моря;
t — время, с;
к — номер волны;
Ак — детерминированная амплитуда, м;
а)к — частота волны к, Гц;
&к — случайные фазы, равномерно распределенные между 0 и 2л случайными фазами, взаимно независимыми друг от друга и от случайных амплитуд, которые принимаются распределенными в соответствии с распределением Рэлея j со среднеквадратичным значением
E[42] = 2S(<ok)Ao>k, (2)
где S(a)k) — спектр волны. Использование детерминированных амплитуд Ак = <зк может дать неконсервативные оценки;
\<£>к — частотный интервал.
5.1.3.2 Наименьший частотный интервал Асо регулируется общей продолжительностью моделирования t: Асо =2n/t. Количество частот для моделирования типичного кратковременного состояния моря определено длительностью моделирования, но должно быть не менее 1000, чтобы фиксировать свойства экстремальных волн. Для моделирования движений плавучей установки случайность, как правило, обеспечивают использованием порядка 100 частот. Необходимо изучить влияние максимальной частоты tomax. Это особенно важно при моделировании скоростей нерегулярной жидкой среды.
5.1.4 Предел дробящейся волны
5.1.4.1 Высота волны ограничена разрушением волны. Максимальную высоту дробящейся волны Нь вычисляют по выражению
—— = 0,142 tan/?----,
X X
где X — длина волны, м, соответствующая d;
d — глубина воды, м;
tan/? — гиперболический тангенс.
5.1.4.2 На больших глубинах предел дробящейся волны соответствует максимальной крутизне Smax = мелководье предел высоты волны может приниматься как 0,78 от локальной глу
бины воды.
5.1.5 Краткосрочные состояния волны
5.1.5.1 Краткосрочные неизменные нерегулярные состояния моря можно описать с помощью спектра волны, то есть с использованием функции спектральной плотности мощности вертикального смещения поверхности моря.
5.1.5.2 Обычной практикой является допущение того, что поверхность моря неизменна в течение от 20 мин до 3—6 ч. Неизменное состояние моря можно охарактеризовать набором параметров окружающей среды, таких как высота характерной волны Hs и период пика спектра Г Спектр волны часто определяют через значения Hs и Т .
5.1.5.3 Высота характерной волны Hs примерно равна средней высоте (от подошвы до гребня) одной трети наиболее высоких волн за указанный период времени.
5.1.5.4 Период пика спектра Тр представляет собой период волны, значение которого определяют как обратное к той частоте, при которой спектр энергии волны имеет максимальное значение.
5.1.5.5 Период колебания через нулевую точку Tz — это средний интервал времени между двумя последовательными колебаниями через точку среднего уровня моря.
5.1.5.6 Спектры волны могут быть заданы в табличном виде как измеренные значения спектров или с помощью параметризованной аналитической формулы. Наиболее подходящий спектр волны зависит от географического района с местными батиметрическими данными и от сложности состояния моря.
5.1.5.7 Для ветровых волн часто применяют спектр ПМ и спектр JONSWAP. Спектр ПМ первоначально предложен для полностью развитого волнения. Спектр JONSWAP расширяет спектр ПМ путем включения волн с ограниченным разгоном волны. Оба спектра описывают условия ветровых волн, часто возникающих при наиболее сложных состояниях моря.
5.1.5.8 Умеренные и спокойные состояния на участках открытого моря часто формируются как ветровыми волнами, так и зыбью. Для учета и ветровых волн, и зыби можно использовать спектр с двумя пиками. Спектрами с двумя пиками являются спектр Гяйза-Хаббла и спектр Торсетаугена.
5.1.6 Спектры Пирсона—Московица и JONSWAP
5.1.6.1 Спектр ПМ Spy (со) задается следующим образом:
г
^РмМ^ ^Ор Ф^ехр ■
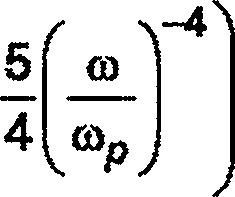
(4)
где со — частота волны, Гц;
Hs — высота характерной волны, м; сор = 2л/7р — угловая частота пика спектра, Гц;
Тр — период пика спектра.
5.1.6.2 Спектр JONSWAP Sj(co) представляется как модификация спектра ПМ для развивающегося состояния моря в ситуации с ограниченным разгоном волны:
I <1>-С0п ехр -0,5 -----
(5)
где А = 1 - 0,287 Iny — коэффициент нормализации;
Spy (со) — спектр Пирсона—Московица;
у — безразмерный параметр формы пика;
со — частота волны, Гц;
сор = 2п/Тр — угловая частота пика спектра, Гц;
о — параметр спектральной ширины;
су — су _ для со со.,, d
СУ = <5Ь ДЛЯ СО > СОр.
5.1.6.3 Соответствующий спектральный момент Мп спектров волны составляет:
Mn = JconS(co)cton.
о
5.1.6.4 Для спектра JONSWAP спектральные моменты Мо, Mv М2 задаются как:
=
5 + у
М2 = нгюгЦ±1.
z s р 5 + у
5.1.6.5 Следующие параметры состояния моря могут быть определены в виде спектральных моментов.
Высоту характерной волны Hs определяют как
(Ю)
Период колебания Тт02 через нулевую точку Tz может быть оценен как
(11)
(12)
Лп02 - 2к.
Средний период 7ш01 волны может быть оценен как
Т — 2тг ^0
5.1.6.6 Константами JONSWAP, определенными экспериментальным путем, являются у = 3,3; оа = 0,07; сь = 0,09. При у = 1 спектр JONSWAP сводится к спектру ПМ.
5.1.6.7 Модель спектра JONSWAP находится в пределах неравенства
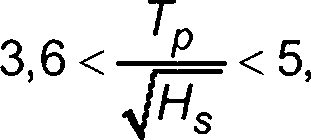
(13)
где Тр— период пика спектра
и вне данного интервала не должна быть использована. Влияние параметра у формы пика показано на рисунке 2.

Рисунок 2 — Спектр JONSWAP для Hs = 4,0 м; Тр = 8,0 с для у=1,у = 2иу = 5
5.1.6.8 Период колебания волны через нулевую точку Tz и средний период волны 71 могут быть связаны с периодом пика с помощью следующих приблизительных отношений (1 < у < 7):
= 0,6673 + 0,05037у - 0,00623у2 + 0,0003341у3; (14)
ТР
-Ь- = 0,7303 + 0,04936у - 0,006556у2 + 0,000361у3, (15)
ТР
где Tz — период колебания волны через нулевую точку;
Тр — период пика спектра;
71 — средний период волны.
Для у = 3,3; Тр = 1,28597z, а Т1 = 1,07347z.
Для у = 1,0 (спектр ПМ): Тр = 1,40497z, а 71 = 1,0867Tz.
5.1.6.9 Если для безразмерного параметра у формы пика не задано определенных значений, то может быть применено следующее значение:
при у = 5
-JL<3,6;
№
(
при у - exp 5,75 -1,15
I
3,6<-^=<5;
№
при у = 1
5S-JL,
№
где Тр — период пика спектра;
Hs — высота характерной волны, м.
5.1.7 Направленное распределение ветровых волн и зыби
5.1.7.1 Спектры направленной волны с коротким гребнем S(co,0) могут быть выражены в виде спектров однонаправленной волны
S(w,0) = S(co) D(0,co) = S(co) 0(0), (19)
где 0(0,co), D(0) — функции направленности;
0 — угол между направлением серий элементарной волны и направлением главной волны.
5.1.7.2 Функция направленности отвечает следующему требованию:
fD(eI<»)de=i. (20)
5.1.7.3 Для выраженного как сумма компонента зыби и компонента ветровой волны спектра с двумя пиками общий направленный спектр частоты S(co,0) может быть выражен как
S(co,0) = SB в(со) DB в(0) + S3(co) О3(0),
(21)
где SB в(со), Ов в(0) — компоненты ветровой волны спектра с двумя пиками; S3(w), £>3(0) — компоненты зыби.
5.1.7.4 Часто используемой для ветровой волны общей функцией направленности является 0(0), вычисляемая по формуле
о(е) =
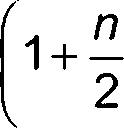
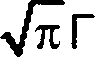
(1 o'! --I--
I2 2J
cosn
(22)
где — Г — гамма
5.1.7.5 При отсутствии данных направленной волны главное направление 0р может быть задано равным направлению преобладающего ветра.
5.1.7.6 Фактическое состояние моря характеризуется постоянной п, указанной в формуле (22). Типичными для ветровой волны являются значения л от 2 до 4. В случае зыби более подходящим является значение п > 6.
5.1.8 Максимальная высота волны в неподвижном состоянии моря
Для неподвижного узкополосного состояния моря с N независимыми местными максимальными высотами волны крайние максимумы в состоянии моря могут быть представлены в таблице 1.
Таблица 1—Максимумы состояния моря
Количество | Hmax/HS(M —большое) |
Наиболее вероятное наибольшее | /-In N V2 |
Срединное значение | 1 1 1. л, 0.367 ¥ ч-InW- 1+<— у 2 In? ) |
Ожидаемое крайнее значение | 1 1. ..Л 0,577> 4 — 1пЛИ 1+—--- Р InT J |
Крайнее значение р-квантиля | р InW J |
Для узкополосного состояния моря число максимумов может быть принято как N = t/Tz, где t является продолжительностью состояния моря.
5.2 Волновые нагрузки на крупнообъемные конструкции
5.2.1 Общие положения5.2.1.1 Как правило, морские конструкции характеризуются как крупнообъемные или как малообъемные. Вблизи крупнообъемных конструкций в открытом море образовываются волны, вклад которых учитывают при расчете усилия, в то время как для малообъемных конструкций волна является несущественной.
5.2.1.2 Малообъемные конструкции могут быть подразделены на конструкции, в которых преобладает усилие лобового сопротивления, и конструкции, в которых преобладает усилие инерции (массы). На рисунке 3 показаны различные режимы, где участки I, III, V и VI охватывают малообъемные конструкции.
5.2.1.3 Термин «крупнообъемная конструкция» используется для конструкций с размерами D величиной такого же порядка, как и типичные длины волны X возбуждающих сооружение морских волн, обычно D > Х/6. Это соответствует показанным на рисунке 3 режимам дифракционной волновой нагрузки II и IV, где данная граница эквивалентно определяется как iiD/k > 0,5.
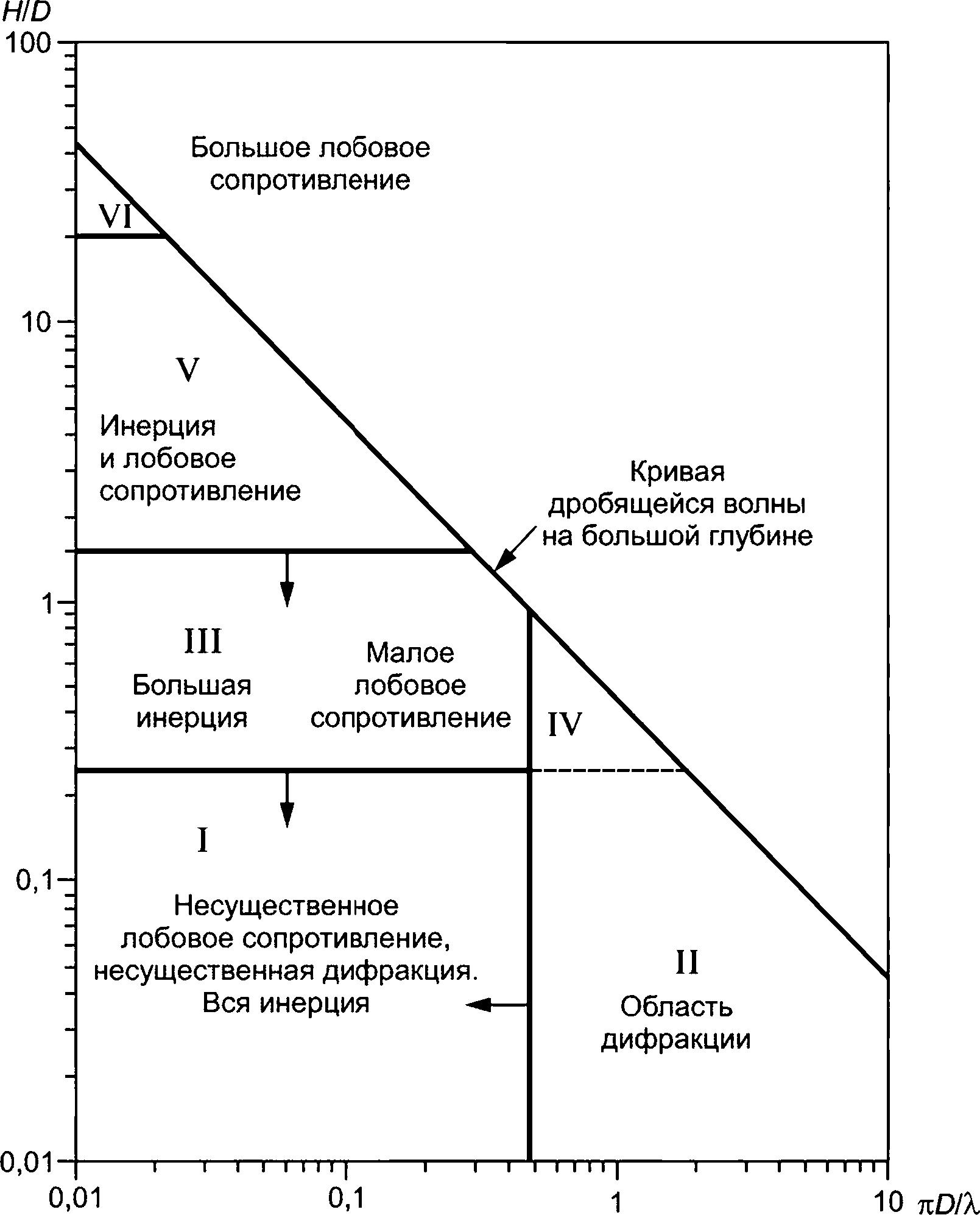
D — характерный размер объекта; Н — высота волны; X — длина волны
Рисунок 3 — Различные режимы волновой нагрузки
5.2.2 Масштаб времени периода движения
5.2.2.1 Плавучая заякоренная конструкция может реагировать на ветер, волны и течение путем движения. В зависимости от частоты движения объекта относительно частоты волнения моря выделяют следующие типы движения:
- с высокой частотой (HF);
- частотой волны (WF);
- низкой частотой (LF).
5.2.2.2 Наибольшие волновые нагрузки на морские конструкции возникают на частотах, совпадающих с волновой частотой, вызывая движения конструкции с указанной WF. Для предотвращения крупных резонансных эффектов морские конструкции и их системы швартовых часто проектируют таким образом, чтобы резонансные частоты существенно сместились за пределы диапазона частот волны.
5.2.2.3 Плавучее сооружение реагирует на нагрузку главным образом движениями в шести направлениях, включая поступательные движения, продольно-горизонтальную качку, поперечно-горизонтальную, вертикальную качки и угловые движения, бортовую качку, килевую качку, рыскание. Кроме того, вызванные волной нагрузки могут привести к высокочастотному (HF) упругому перемещению и волновой вибрации судов. Течение может индуцировать высокочастотную (HF), вызванную вихреобра-зованием вибрацию (VIV) на удлиненных конструктивных элементах.
5.2.2.4 В силу нелинейных результатов действия нагрузки некоторые перемещения плавучего сооружения проявляются при собственных частотах колебания. Медленно изменяющиеся волновые и ветровые нагрузки являются источником низкочастотных (LF) резонансных горизонтальных движений, также называемых движения медленного дрейфа.
5.2.2.5 Движения с частотой волны (WF) управляются главным образом воздействиями невязкой текучей среды, в то время как воздействия вязкой текучей среды являются относительно значимыми для движений LF. Воздействия вязкой текучей среды могут быть важными для близких к резонансным движениям с частотой волны (WF). Типичный пример — резонансное движение бортовой качки. Различные гидродинамические воздействия следует учитывать для каждого типа плавучей установки.
5.2.3 Периоды собственных колебаний
5.2.3.1 Как правило, периоды собственных колебаний крупной заякоренной морской конструкции при продольно-горизонтальной качке, поперечно-горизонтальной качке и рыскании превышают 100 с. Обычно периоды собственных колебаний при вертикальной качке, бортовой и килевой качках полупо-груженных конструкций превышают 20 с.
5.2.3.2 Несвязанные периоды собственных колебаний Tj, j = 1,2,...6 заякоренной морской конструкции аппроксимируются выражением:
T,=2n[Mll+Ail ]2, (23)
где Mjj, Ajj, Cjj, Kjj, — составляющие элементы матриц массы.
5.2.3.3 Периоды собственных колебаний зависят от связи между различными режимами и от величины демпфирования.
5.2.3.4 Несвязанный период собственных колебаний при вертикальной качке Т3 для свободно плавающего морского судна вычисляют по формуле
2
7>2,/М + М2 (24)
3 I P9S J
где М — масса, кг;
Д33 — присоединенная масса при вертикальной качке, кг;
S — площадь зеркала воды, кг;
р — плотность, кг/м3;
д — ускорение свободного падения, м/с2.
5.2.3.5 Несвязанный период собственных колебаний при килевой качке Т5 для свободно плавающего морского судна вычисляют по формуле
т of ^^55 + Аэ5
(25)
(26)
Тс = 2 л ----22- ,
b [ pgVGML )
где г55 — радиус вращения килевой качки;
Д55 — момент присоединенной массы при килевой качке;
GMl — продольная метацентрическая высота;
М — масса, кг;
V — объем, м3.
Несвязанный период собственных колебаний при бортовой качке Т4 вычисляют по формуле
т _ о_f Mr44 + А44 12 4 I pgVGMT I
где г44 — радиус вращения бортовой качки;
Д44 — момент присоединенной массы при бортовой качке;
GMT — поперечная метацентрическая высота;
М — масса, кг;
V — объем, м3;
р — плотность, кг/м3;
д — ускорение свободного падения, м/с2.
5.2.4 Расчет в частотной области
5.2.4.1 Вызванные волнами нагрузки при нерегулярном волнении моря могут быть получены путем использования линейно наложенных нагрузок от компонентов регулярных волн. Расчет крупнообъемной конструкции при регулярных набегающих волнах называют расчетом в частотной области.
5.2.4.2 Допуская стабильное состояние и пренебрегая всеми переходными режимами, можно считать, что нагрузки и динамический отклик сооружения гармонически колеблются с такой же частотой, как и волны, или в случае поступательных перемещений с частотой соударения.
5.2.4.3 В рамках линейного расчета гидродинамическую задачу обычно делят на две подзадачи:
- радиационная задача, когда сооружение вынуждено колебаться с частотой волны в режиме движения твердого тела без набегающих волн. Результирующие нагрузки как правило, определяют в виде нагрузок присоединенной массы, демпфирования и возвращения по формуле
Fkr}=-A^+B^-C^l- (27>
где Akj, Bkj представляют собой присоединенную массу и демпфирование;
Су — движение жесткого тела;
Ckj — коэффициенты гидростатического возвращения;
- задача дифракции, когда сооружение удерживается от движений и возбуждается набегающими волнами. Получившиеся нагрузки являются нагрузками усилия внешнего возбуждающего воздействия волны
F^ = fk((d)e-i(0t, <28)
где к = 1,6;
e~lwt— базисная функция распределения Фурье.
5.2.4.4 Заданную нераспределенным давлением в набегающей волне часть нагрузок усилия внешнего возбуждающего воздействия волны называют усилиями/моментами Фруда—Крылова; остальную часть — усилиями/моментами дифракции.
5.2.4.5 Крупнообъемные конструкции находятся под влиянием инерции, то есть общие нагрузки, обусловленные дифракцией волн, значительно выше, чем общие нагрузки, вызванные усилием лобового сопротивления. Для предотвращения чрезмерного увеличения числа элементов/панелей на удлиненных элементах/раскосах конструкции в численном расчете дифракции к модели радиации/диф-ракции может быть добавлена модель нагрузки Морисона с заранее определенными коэффициентами присоединенной массы.
Для некоторых типов крупнообъемных плавучих морских установок, таких как полупогружные конструкции с понтонами и колоннами прямоугольной формы, кромки могут привести к разделению потока и привнести существенное демпфирование вязкостью воды. Для таких плавучих морских установок можно применить двойную гидродинамическую модель, когда на один и тот же конструктивный элемент добавляют вязкостные нагрузки типа Морисона и нагрузки радиации/дифракции.
5.2.4.6 Как правило, использование линейного расчета обеспечивает достаточную точность при прогнозировании общих нагрузок волновой частоты. В связи с этим целью настоящего раздела является изучение влияния волновых нагрузок первого порядка. Термин «линейный» означает, что динамическое давление жидкой среды и получившиеся нагрузки пропорциональны амплитуде волны. То есть нагрузки от отдельных волн в произвольном состоянии моря могут быть просто наложены друг на друга.
5.2.4.7 Учитывают только смачиваемую область плавучей установки вплоть до средней ватерлинии. Результатом расчета являются усилия внешнего возбуждающего воздействия первого порядка, гидростатика, потенциальное демпфирование волны, присоединенная масса, движения первого порядка
в степенях свободы твердого тела и средние усилия/моменты смещения. Среднее усилие и моменты смещения волны — это величины второго порядка, но они зависят только от величин первого порядка.
5.2.4.8 Результаты расчета в частотной области — функции передачи рассматриваемых переменных, например возбуждающих усилий/моментов и движения платформы на единицу амплитуды волны.
Первый порядок линейной передаточной функции (LTF) усилия/момента, как правило, обозначают Н(со).
Функция линейной передачи движения ^1\со) также обозначает функцию передачи отклика. Как правило, эти величины задают как комплексные числа. Функция линейной передачи движения дает отклик на единицу амплитуды внешнего возбуждающего воздействия как функцию от частоты волны:
^1)(w) = H1(oj) (29)
где /-У1 (со) — первый порядок функции линейного переноса;
L(co) — линейный структурный оператор, характеризующий уравнение движения:
Цсо) = - w2 [М + Д(со)] + /о)в(о)) + С, (30)
где М — масса и инерция конструкции;
А — присоединенная масса;
/ — направление движения;
В — демпфирование волны;
С — жесткость, включая гидростатическую и конструктивную жесткость.
Уравнениями движения твердого тела являются в общем случае шесть связанных уравнений для трех поступательных (продольно-горизонтальная, поперечно-горизонтальная и вертикальная качка) и трех угловых (бортовая качка, килевая качка и рыскание) движений. Модуль функции передачи движения обозначает оператор амплитуды отклика (RAO).
5.2.4.9 Концепция RAO также может быть использована для полученных из движений твердого тела общих усилий и моментов, высоты поверхности дифракционной волны, давления и кинематики жидкой среды.
5.2.4.10 Метод частотной области подходит для систем, подвергающихся воздействию случайных волновых сред, так как спектр случайного отклика S^w) может быть рассчитан с использованием непосредственно функции передачи и спектра волны по формуле
SR(M) = I I2 S(o>), (31)
где со — угловая частота волны, равная 2л/Т;
^(1\со) — функция передачи отклика;
S(w) — спектр волны.
5.2.4.11 На основании спектра отклика можно оценить краткосрочную статистику отклика. Ограничения метода состоят в том, что уравнения движения линейные, и возбуждающее внешнее воздействие тоже является линейным.
5.2.4.12 Линейное допущение также применяют в используемой для интерпретации решения теории вероятностного процесса. Это не подходит для таких нелинейных воздействий, как нагрузки от усилия лобового сопротивления, демпфирование и возбуждающее внешнее воздействие, изменяющаяся со временем геометрия, горизонтальные усилия возвращения и переменный подъем поверхности. Эти нелинейности можно линеаризовать (см. [1]).
5.2.4.13 Расчет в частотной области, включая расчет движений и усилий, широко используют для плавучих установок. Обычно его применяют при расчете усталостной прочности, а также при расчетах более умеренных условий окружающей среды, в которых линеаризация дает удовлетворительные результаты. Основным преимуществом данного метода является то, что по сравнению с методами расчета по временной области вычисления относительно простые и эффективные.
5.2.4.14 Низкочастотные движения заякоренной плавучей конструкции вызваны усилиями медленно изменяющихся волны, ветра и течения. Вызванное волной усилие дрейфа может быть смоделировано как сумма невязкого усилия и вязкого усилия. Усилие дрейфа невязкой волны является усилием 12
волны второго порядка, пропорционального квадрату амплитуды волны. В случайном состоянии моря, представленном суммой N компонентов волны со,-, где / = 1, усилие дрейфа волны N колеблется при разности частот со,- минус соуИ задано выражением
N •/ \
= (32)
ij
где Re обозначает действительную часть;
Aj, Aj — индивидуальные амплитуды волны;
Н — квадратичная функция передачи разности частот.
Матрица QTF обычно представляется как комплексная величина для учета соответствующей фазы относительно компонентов волны. Re обозначает действительную часть. Среднее усилие дрейфа получается сохранением только диагональных элементов (со,- = Wy) в приведенной выше сумме.
5.2.4.15 Если собственные частоты горизонтального движения плавучей установки намного ниже характеристических частот состояния моря, для аппроксимации нагрузки от дрейфа волны можно использовать так называемое приближение Ньюмена. В данном приближении матрица QTF может быть аппроксимирована с помощью диагональных элементов следующим образом:
+ (33)
5.2.5 Межкорпусное гидродинамическое взаимодействие
5.2.5.1 Гидродинамические взаимодействия между находящимися в непосредственной близости несколькими плавучими морскими установками и между плавучей морской установкой и крупным неподвижным сооружением в окрестностях плавучей установки можно рассчитывать с использованием программного обеспечения радиации/дифракции посредством соответствующих возможностей моделирования множественных объектов. N плавучих морских установок рассчитываются в интегрированной системе сдвижениями шести степеней свободы.
5.2.5.2 Примером системы из двух частей являются плавучий кран и расположенная борт о борт баржа во время подъемных работ, где может быть сильное гидродинамическое взаимодействие между двумя плавучими морскими установками. Взаимодействие может стать проблемой из-за нежелательного сильного отклика относительного перемещения между двумя плавучими морскими установками.
5.2.5.3 Существенным эффектом взаимодействия является близкая к резонансу канальная волна между плавучими морскими установками, способная возбудить поперечно-горизонтальную и бортовую качку. Данная канальная волна не затухает в соответствии с потенциальной теорией. Некоторые стандарты радиации/дифракции предписывают гашение таких канальных волн. Дискретизация смачиваемых поверхностей на участке между плавучими морскими установками должна быть достаточно точной для улавливания изменений в канальной волне. Дополнительные резонансные пики также появляются в связанных движениях вертикальной, бортовой и килевой качек.
В случае узкого зазора между соседними, расположенными борт о борт конструкциями при определенной частоте волны в зоне всплеска волны может быть возбуждено движение в резонансном поршневом режиме. Собственная частота ю0 поршневого режима находится в пределах диапазона частот, заданного с помощью следующего выражения:
, 2 G сорР 2 । 71 13 (34)
л D д 2D'
где G — ширина зазора, м;
D — осадка конструкции (судна), м;
со0 — собственная частота, Гц.
Кроме того, в зазоре могут возникнуть движения поперечного и продольного колебательного режимов.
5.2.5.4 При расчете гидродинамического взаимодействия между несколькими плавучими морскими установками с использованием панельных методов радиации/дифракции необходимо различать
собственные частоты близких к резонансу канальных режимов и характерные для численного метода возможные нерегулярные частоты.
5.2.5.5 Еще одним эффектом взаимодействия является эффект затенения, который приводит к более мелким движениям на подветренной стороне по сравнению с наветренной. Эффекты гидродинамического взаимодействия между несколькими конструкциями, проходящими сквозь поверхность, следует учитывать, если на нагрузки от возбуждающего внешнего воздействия на каждое сооружение существенно влияет присутствие других конструкций.
5.2.5.6 При расчете отдельных усилий дрейфа, действующих на несколько плавучих морских установок, требуется непосредственное интегрирование давления жидкости по схеме второго порядка на каждое тело. Обычно применяемый импульсный подход для отдельной плавучей установки дает только общее усилие дрейфа на общую систему. При расчете усилия дрейфа вблизи частот канальных режимов необходимо учитывать недемпфированное движение свободной поверхности, которое может привести к ошибочным прогнозам усилия дрейфа.
5.2.6 Расчет по временной области
5.2.6.1 Некоторые воздействия гидродинамических нагрузок могут быть линеаризованы и включены в метод частотной области, в то время как другие являются крайне нелинейными и могут быть обработаны только по временной области.
5.2.6.2 Преимущество расчета по временной области заключается в том, что таким образом может уловить нелинейные воздействия гидродинамических нагрузок и нелинейные воздействия взаимодействия между объектами, включая кранцы с нелинейными отношениями «усилие—перемещение». Кроме того, расчет по временной области дает статистику отклика без создания допущений касательно распределения отклика.
5.2.6.3 Расчет по временной области включает в себя численное интегрирование уравнений движения и должен быть использован в случае значимости нелинейных воздействий. Примерами являются:
- переходный отклик воздействия волны;
- моделирование низкочастотных движений (медленный дрейф);
- связанный отклик плавучей установки, райзера и якорного крепления.
5.2.6.4 Как правило, методы расчета по временной области используют для прогнозирования воздействий экстремальной нагрузки. Когда расчет по временной области занимает значительное количество времени, критические события можно рассчитывать путем использования уточненной модели для продолжительности, определенной по упрощенной модели.
5.2.6.5 Расчет временного интервала между реакциями конструкции, испытывающей влияние случайных нагрузок, должен быть достаточным для получения постоянных статистических данных.
5.2.7 Численные методы
5.2.7.1 Нагрузки на крупнообъемные конструкции, вызванные волной, можно прогнозировать на основании потенциальной теории, то есть выводить нагрузки из потенциала скорости невихревого течения несжимаемой и невязкой жидкости.
5.2.7.2 Наиболее распространенным численным методом для решения потенциального потока является метод граничных элементов (ВЕМ), при котором потенциал скорости в области жидкости представлен распределением источников по средней смачиваемой поверхности тела. Функция источника удовлетворяет условию свободной поверхности и называется функцией свободной поверхности Грина. Удовлетворение граничного состояния на поверхности тела дает интегральное уравнение для силы источника.
5.2.7.3 Альтернативой является использование элементарных источников Ренкина (1/Г?), распределенных как по средней смачиваемой поверхности, так и по средней свободной поверхности. Метод источника Ренкина является предпочтительным для задач поступательной скорости.
5.2.7.4 Другими формами представления являются использование смешанного распределения источников и нормальных диполей и решение непосредственно для потенциала скорости на границе.
5.2.7.5 Средняя смачиваемая поверхность дискретизируется в плоские или криволинейные панели, в связи с чем данные методы также называют панельными методами. Панельный метод низкого порядка использует плоские панели, а панельный метод более высокого порядка — криволинейные панели. Метод более высокого порядка дает такую же точность с меньшим числом панелей.
5.2.7.6 Задача потенциального потока также может быть решена конечно-элементным методом (FEM) расчета, дискретизируя объем области жидкости по элементам. Для бесконечных областей используют аналитическое представление на расстоянии от тела для снижения числа элементов. Альтер-14
нативой может быть применение так называемого конечного элемента для моделирования бесконечной области.
5.2.7.7 Для стационарных или плавучих конструкций с простой геометрией по типу сферы, цилиндра, сфероида, эллипсоида, тора и т. п. для решения проблемы потенциального потока могут быть выведены полуаналитические выражения. Для определенных морских конструкций такие решения могут стать полезными аппроксимациями.
5.2.7.8 Вызванные волной нагрузки на удлиненные, подобные судам крупнообъемные конструкции можно прогнозировать с помощью теории полос. В этом случае нагрузка аппроксимируется суммой нагрузок на двухмерные полосы. Следует учитывать, что численная реализация теории полос должна включать надлежащую обработку нагрузок от возбуждающего внешнего воздействия волны (0 = 180°).
5.2.7.9 Демпфирование движения крупнообъемных конструкций осуществляется вследствие радиационного демпфирования волны, трения обшивки корпуса, вихреобразования корпуса, вязкостного демпфирования от скуловых килей и других дополнительных деталей, а также вязкостного демпфирования от райзера и швартовых. Радиационное демпфирование волны рассчитывают на основе потенциальной теории. Воздействия вязкостного демпфирования, как правило, оценивают путем применения упрощенных гидродинамических моделей или экспериментальным способом. Для простых геометрий для оценки вязкостного демпфирования может быть использована вычислительная гидродинамика (CFD).
5.2.8 Требования к частоте и сетке панели
5.2.8.1 Несколько периодов и направлений волны следует выбирать так, чтобы движения и уси-лия/моменты можно было описать максимально точно. Необходимо надлежащим образом отмечать воздействия отмены, усиления и резонанса.
5.2.8.2 Следует придерживаться принципов моделирования, связанных с точностью сетки панели. Для панельного метода граничных элементов (ВЕМ) с постоянным значением потенциала на протяжении панели применяют следующие принципы:
- диагональная длина сетки панели должна быть менее 1/6 от наименьшей длины рассчитываемой волны;
- на участках с резкими изменениями геометрии (кромки, углы) следует применять мелкую сетку;
- при моделировании тонкостенных конструкций с водой с обеих сторон размер панели не должен превышать 3-, 4-кратной толщины моделируемой стенки;
- при расчете усилий сдвига внешнего возбуждающего воздействия волны в направлении ватерлинии следует применять более мелкую сетку панели;
- площадь зеркала воды и объем дискретизированной модели должны соответствовать реальному сооружению.
5.2.8.3 Для гарантирования точности вычисленных нагрузок необходимо проводить проверки на сходимость путем увеличения числа панелей. Сравнение усилий дрейфа, вычисленных путем метода интегрирования давления и импульсного метода, дает полезную проверку численного схождения для данной дискретизации.
5.2.8.4 По сравнению с расчетом общего отклика для расчета подъема поверхности волны и скоростей частиц жидкости требуется еще более мелкая сетка. Диагональ типичной панели должна быть менее 1/10 самой короткой рассчитываемой длины волны. Для ВЕМ кинематика жидкости и подъем поверхности необходимо рассчитывать, как минимум, на расстоянии одного размера сетки панели в сторону от границы тела, предпочтительно ближе к центру панелей.
5.2.8.5 Для расчета движения плавучей установки в частотной области вычисления, как правило, выполняют не менее чем для 30 частот. В особых случаях может потребоваться большее количество, в частности в случаях нахождения пика узкополосного резонанса в пределах спектрального диапазона частот волны. Шаг частот должен быть менее цо)0 для достижения менее чем = 5 % изменения в стандартном отклонении отклика. С, — это коэффициент демпфирования, а со0 — частота.
5.2.9 Нерегулярные частоты
5.2.9.1 При расчетах радиации/дифракции с использованием методов решения функции свободной поверхности Грина для крупнообъемных конструкций с большой площадью зеркала воды типа судов и барж следует обратить внимание на существование так называемых нерегулярных частот.
5.2.9.2 Нерегулярные частоты соответствуют мнимым собственным колебаниям решения внутренней задачи (внутри математической модели конструкции) и не имеют какого-либо прямого физического смысла. Это является недостатком используемого метода интегральных уравнений для решения потенциала скорости.
5.2.9.3 Поблизости от нерегулярных частот стандартный метод БЕМ может дать ненадежные значения для присоединенной массы и демпфирования, следовательно, и для прогнозируемых RAO и усилий дрейфа. Метод источников Ренкина позволяет избежать нерегулярных частот.
5.2.9.4 Числа нерегулярного волнения v прямоугольной баржи длиной L, шириной В и осадкой Т задаются отношениями
v = Vjj = kjj cot h (kjj,
rfle^- = 7c^£j +^J;/J = 0,1,2,...; /+/2»1.
5.2.9.5 Числа нерегулярного волнения v вертикального цилиндра с радиусом R и осадкой Т задаются отношениями
v “ vms ~ к ms со^ ^ms 7)’
где kms = jms /R заданы нулями m-го порядка функции Бесселя = 0; т = 0, 1, 2, ...; з = 1, 2, ... Самыми нижними нулями являются/01 = 2,405,/^ = 3,832, у21 = 5,136,/02 = 5,520.
Соответствующие нерегулярные частоты тогда задаются дисперсионным уравнением
со2 = gv tan/7 (vd),
где о» — угловая частота;
д — ускорение свободного падения;
v — номер нерегулярной волны;
d — глубина воды.
5.3 Волновые нагрузки на малообъемные конструкции
5.3.1 Малообъемные трехмерные конструкции
5.3.1.1 Термин «малообъемная конструкция» используется для конструкций с размерами D, меньшими, чем типичные длины волны А, возбуждающих сооружение морских волн. Обычно D < А/5 (см. рисунок 3).
5.3.1.2 Для оценки нагрузок от усилия лобового сопротивления и инерции на трехмерные объекты при волнении и течении можно использовать формулу типа Морисона. Для неподвижной конструкции нагрузку от усилия лобового сопротивления и инерции на трехмерные объекты при волнении и течении F(t) определяют следующим выражением:
, ч , х 1 I. (38)
F(0 = PV(l + CA)v+jpCDSv|4
где р — плотность воды, кг/м3;
V — вытесненный объем, м3;
СА — коэффициент присоединенной массы;
v — ускорение частиц жидкости, м/с2;
CD — коэффициент лобового сопротивления;
S — поперечная к направлению усилия площадь проекции, м2;
v — скорость частиц жидкости (волн и/или течения), м/с.
Коэффициенты присоединенной массы для некоторых трехмерных объектов (см. таблицу А.2 приложения А). Коэффициенты лобового сопротивления приведены в приложении Б.
5.3.1.3 Для некоторых типичных подводных конструкций с перфорированными отверстиями (каналами) присоединенная масса может зависеть от амплитуды движения или, равнозначно, от числа КС.
5.3.2 Усилие на сечение, применимое к удлиненным конструкциям
5.3.2.1 Прилагаемое к удлиненной конструкции гидродинамическое усилие в общем потоке жидкости может быть оценено путем суммирования усилий на сечение, действующих на каждую полосу конструкции. Как правило, вектор действующего на полосу усилия может быть разложен на поперечное усилие fN, осевое усилие fT и подъемное усилие fL, являющееся нормалью как к fN, так и к fT (см. рисунок 4). Кроме того, на некруглые поперечные сечения будет действовать крутящий момент тт.
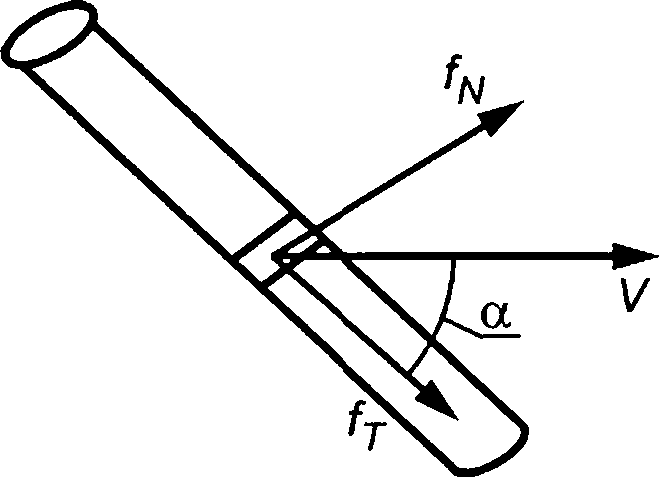
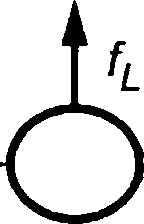
Рисунок 4 — Определение поперечного усилия, осевого усилия и подъемного усилия, действующих на удлиненную конструкцию
5.3.2.2 Для удлиненных конструктивных элементов (цилиндров) с размерами поперечного сечения, достаточно малыми для получения возможности пренебрежения градиентами скорости и для ускорения частиц жидкости в параллельном элементу направлении, волновые нагрузки могут быть рассчитаны с использованием формулы нагрузки Морисона. Усилие на сечение fN(t), действующее на неподвижную удлиненную конструкцию поперек оси элемента, может быть определено по формуле
WO = P0 + CaMv+—pCDDv|v|, (39)
где р — массовая плотность текучей среды, кг/м3;
СА — коэффициент присоединенной массы (с площадью поперечного сечения как базовой площадью);
А — площадь поперечного сечения, м2;
v — ускорение частиц жидкости, м/с2;
CD — коэффициент лобового сопротивления;
D — диаметр или типичный размер в поперечном сечении, м;
у — скорость частиц жидкости (волн и/или течения), м/с.
5.3.2.3 Обычно формула нагрузки Морисона применима при выполнении следующего условия:
X > 50, (40)
где X — длина волны;
О — диаметр или проекция другого размера поперечного сечения элемента.
5.3.2.4 Для комбинированных условий волны и течения потока вызванные волной и течением скорости частиц должны быть добавлены как векторные величины. Необходимо вычисление общих скоростей и ускорений частиц на основе более точных теорий взаимодействия волны/течения.
5.3.3 Определение коэффициентов усилия
5.3.3.1 Коэффициент лобового сопротивления CD является безразмерным усилием лобового сопротивления, который вычисляют по формуле
Р ^drag
где fdrag — усилие сопротивления сечения, Н/м; р — плотность текучей среды, кг/м3;
D — диаметр (или типичный размер), м;
v — скорость, м/с.
5.3.3.2 В общем случае вектор скорости жидкости будет находиться в направлении о относительно оси удлиненного элемента (см. рисунок 4). Усилие лобового сопротивления fdrag раскладывается на поперечное усилие fN и осевое усилие fT.
5.3.3.3 Коэффициент присоединенной массы СА представляет собой безразмерную присоединенную массу, вычисляемый по формуле
сд=^. <42>
рД
где та — присоединенная масса на единицу длины, кг/м;
р — плотность присоединяемой среды, кг/м3;
А — площадь поперечного сечения, м2.
5.3.3.4 Коэффициент массы См определяется как
См=1+Сд. (43)
5.3.3.5 Коэффициент подъема CL определяют как безразмерное подъемное усилие
= (44)
IpDv2
где fiift — подъемное усилие на сечение, Н/м;
р — плотность текучей среды, кг/м3;
D — диаметр (или типичный размер), м;
v — скорость, м/с.
5.3.4 Перемещающаяся конструкция в неподвижной воде
Усилие на сечение на движущейся удлиненной конструкции в неподвижной воде может быть записано как
(45)
где р — плотность текучей среды, кг/м3;
СА — коэффициент присоединенной массы;
А — площадь поперечного сечения, м2;
г — ускорение элемента по нормали к оси, м/с2;
Cd — коэффициент гидродинамического демпфирования;
D — диаметр, м;
г — скорость элемента по нормали к оси, м/с.
5.3.5 Перемещающаяся конструкция при волнах и течении
5.3.5.1 Усилие на сечение fN(t), действующее на движущуюся удлиненную конструкцию по двухмерному неравномерному (волны и течение) потоку поперек оси элемента, вычисляют по формуле
fN(0 = -pC^r+p(1 + CA)4v+|pCDDv|v|-lpCdDr|r|, (46)
где р — плотность воды, кг/м3;
СА — коэффициент присоединенной массы;
А — площадь поперечного сечения, м2;
г — ускорение элемента по нормали к оси, м/с2;
v — ускорение частиц жидкости, м/с2;
CD — коэффициент лобового сопротивления;
D — диаметр или типичный размер в поперечном сечении, м;
v — скорость частиц жидкости (волн и/или течения), м/с;
Cd — коэффициент гидродинамического демпфирования;
г — скорость элемента по нормали к оси, м/с.
5.3.5.2 Данная форма известна как независимая модель поля потока. При расчете отклика для r= r(f) усилие присоединенной массы добавляют к массе конструкции ms, умноженной на ускорение г по формуле (46).
Коэффициент лобового сопротивления CD может быть получен экспериментально во время испытаний с возбуждающим внешним воздействием волны на неподвижном цилиндре, в то время как коэффициент гидродинамического демпфирования Cd может быть получен во время испытаний демпфирования цилиндра в спокойной воде. Для большинства областей применения отсутствует необходимость различать эти два коэффициента.
5.3.6 Формула относительной скорости
При выражении усилия лобового сопротивления в виде относительной скорости достаточно одного коэффициента лобового сопротивления. Вследствие этого наиболее часто применяют формулу относительной скорости. Таким образом, усилие на сечение fN(t) можно определить в значениях относительной скорости по формуле
fN(t) = - PC4Af+p(1+Cx)Av+|pCoDvfPr|, (47)
или при введении также относительного ускорения в эквивалентной форме:
(0 = Р^а + рСдАаг + 2 PCDD vr | vr | • (48)
где а = v — ускорение жидкости, м/с;
ar = v-f — относительное ускорение, м/с2;
Vr = v-r — относительная скорость, м/с.
При использовании формулы относительной скорости для усилия лобового сопротивления дополнительное гидродинамическое демпфирование, как правило, не должно включаться.
5.3.7 Применимость формулы относительной скорости
5.3.7.1 Использование формулы относительной скорости для усилия лобового сопротивления правомерно,если
£>1 (49)
D ’
где г — амплитуда смещения элемента; D — диаметр элемента.
5.3.7.2 Когда < 1,, правомерность зависит от значения параметра VR = следующим образом:
- 20 < VR— применение относительной скорости;
- 10 < VR < 20 — если смещение меньше диаметра элемента, то относительная скорость может привести к переоценке демпфирования. В этом случае полевая модель независимого потока будет применена с равными коэффициентами лобового сопротивления CD и демпфирования Cd,
- VR < 10 — скорость конструкции не учитывают тогда, когда смещение меньше одного диаметра.
5.3.7.3 Для проходящего сквозь поверхность вертикального элемента в поле объединенных волны и течения параметр VR может быть рассчитан по формуле
Hs TZ
In.
D ’
(50)
где vc — скорость течения, м/с;
Hs — высота характерной волны, м;
Tz — период колебания через нулевую точку, с;
Тп — период колебаний конструкции, с;
D — диаметр элемента, м.
5.3.8 Усилие лобового сопротивления, действующее на наклонный цилиндр
Для набегающего потока с углом атаки от 45° до 90° следует соблюдать принцип поперечного потока. Поперечное усилие, действующее на цилиндр, может быть рассчитано с использованием поперечного компонента скорости частиц воды vn = v sin а, где а — угол между осью цилиндра и вектором скорости. Усилие по нормали к лобовому сопротивлению цилиндра fdN в этом случае определяют с помощью выражения
fdN = ^PGDnDvn Ы> (51)
где р — массовая плотность текучей среды, кг/м3;
СОл — коэффициент, который зависит от числа Рейнольдса и угла падения;
D — диаметр или типичный размер в поперечном сечении, м;
vn — поперечная компонента скорости частиц воды.
В целом, CDn зависит от числа Рейнольдса и угла падения. Для подкритичного и надкритичного потока CDn может считаться независимым от угла а.
5.3.9 Гидродинамические коэффициенты нормального потока
5.3.9.1 При использовании формулы нагрузки Морисона для вычисления гидродинамических нагрузок на сооружение необходимо учитывать изменение CD и СА как функцию от числа Рейнольдса, числа КС и шероховатости:
CD = CD(Re, КС, А);
Сд = C^(Re, КС, А).
Параметры определяют как:
- число Рейнольдса: Re = VD/v,
- число КС: КС = Vm T/D;
- безразмерная шероховатость: Д = k/D, где D — диаметр, м;
Т — период волны или период колебания, с;
к — высота шероховатости, м;
V — общая скорость потока, м/с;
v — кинематическая вязкость жидкости, м2/с;
Vm — максимальная орбитальная скорость частиц, м/с.
5.3.9.2 Для волновой нагрузки при случайных волнах использованная в определении числа Рейнольдса и числа КС скорость должна быть учтена какд/2 cv, где vv— стандартное отклонение скорости жидкости. Период волны должен быть учтен как период колебания через нулевую точку Tz.
5.3.9.3 Для колебательного потока жидкости вместо числа Рейнольдса часто используют частотный параметр вязкости. Данный параметр р определяют как отношение между числом Рейнольдса и числом КС:
р = Re/KC = D2/vT = wD2 (2ttv), (52)
где D — диаметр, м;
v — кинематическая вязкость жидкости, м2/с;
Т — период волны или период колебания конструкции, с;
со - 2л/Т = угловая частота, рад/с.
Так как период колебания Т является постоянным и, следовательно, 0 является константой для каждой модели; полученные при испытаниях в П-образной трубе экспериментальные данные для CD и См часто задают как функцию от КС и 0.
5.3.9.4 Для цилиндра круглого сечения отношение максимального усилия лобового сопротивления fDmax к максимальному усилию инерции f/max определяют по выражению
^тах =---Со---кс (53)
^/тах Я^(1 + Сд)
где CD — коэффициент гидродинамического демпфирования;
СА — коэффициент присоединенной массы;
КС — число Келегана—Карпентера.
Выражение (53) может быть использовано в качестве индикатора определения того, какое усилие преобладает: лобового сопротивления или инерции. Когда f/max > 2- fD тах, усилие лобового сопротивления не будет влиять на максимальное общее усилие.
5.3.9.5 Для комбинированных условий волны и течения определяющими параметрами являются число Рейнольдса при максимальной скорости у = vc + vm, при максимальной орбитальной скорости vm число КС и отношение скорости потока течения, определяемое как:
ac=vc,(vc+vml <54)
где vc— скорость течения.
5.3.9.6 Для синусоидального (гармонического) потока число КС также может быть определено как
кс = 2лпо (55)
D
где г|0 — амплитуда колебательного потока.
Вследствие этого число КС является мерой расстояния, пройденного частицами жидкости в течение полупериода относительно диаметра элемента.
5.3.9.7 Для потока жидкости в волновой зоне амплитуду тдо в формуле (55) можно принять как амплитуду волны. Таким образом число КС определяют следующим образом:
КС=^_, (56)
D
где Н— высота волны.
5.3.9.8 Для колеблющейся конструкции в спокойной воде, что, например, применимо к нижней части райзера в глубокой воде, число КС определено выражением
х Т кс=-^-, D
(57)
где хт — максимальная скорость конструкции;
Т — период колебания;
D — диаметр цилиндра.
6 Спуско-подъемные операции в волновой зоне. Общие положения
6.1 Общая часть
6.1.1 Общие положения6.1.1.1 При опускании подводных конструкций через волновую зону требуется определить расчетные нагрузки. Точное прогнозирование этих расчетных нагрузок может уменьшить риск затратного простоя по погодным условиям, увеличить количество подходящих судов для установки, а также повысить уровень безопасности работы.
6.1.1.2 Цель данного раздела — предоставить руководство по усовершенствованию методов моделирования расчета с целью получения более точного прогнозирования расчетных нагрузок.
6.1.2 Этапы подводного спуско-подъема
Типичный подводный спуско-подъем состоит из следующих основных этапов:
- подъем с палубы и вывод объекта с транспортного судна;
- опускание через волновую зону;
- дальнейшее опускание вниз на морское дно;
- размещение и посадка.
Оценке подлежат все этапы подводной подъемной операции.
6.1.3 Применение
6.1.3.1 В данном разделе представлено общее руководство по моделированию и расчету этапа подъема через волновую зону.
6.1.3.2 Приведено описание только типичных подводных подъемов. Другие методы установки, такие как маятниковый монтаж свободного падения, не представлены.
6.2 Нагрузки и влияния нагрузок
6.2.1 Общие положения6.2.1.1 Опускаемый в воду или поднимаемый из воды объект подвергают нескольким действующим на сооружение различным усилиям (см. DNVGL-RP-N103 [1]). В целом при оценке отклика объекта необходимо учитывать следующие усилия:
F//ne — усилие в подъемном канате/тросе;
И/о — вес объекта (в воздухе);
FB — выталкивающее усилие;
Fc — постоянное усилие вследствие течения;
F/ — сила инерции;
Fwd — усилие демпфирования волны;
Fd — усилие лобового сопротивления;
Fw — усилие внешнего возбуждающего воздействия волны;
Fs — усилие при слеминге;
Fe — усилие выхода из воды.
6.2.1.2 Усилие Fljne в подъемном канате/тросе является суммой среднего значения усилия Fo и динамического усилия Fdyn(t) из-за движения оконечности крана и внешнего возбуждающего воздействия волны на объект. Среднее значение усилия фактически является медленно изменяющимся усилием, частично вследствие скорости опускания и попадания воды в объект после погружения.
6.2.2 Вес объекта
6.2.2.1 Вес объекта в воздухе Wo принимается как
% = м9, (58)
где М — масса объекта, включая предварительно залитую в объект воду, кг;
д — ускорение свободного падения, м/с2.
Толкование терминов «вес» и «конструктивная масса» иногда бывает неверным. Вес — это статическая сила на объекте из-за гравитации. Результирующая статической силы, влияющая на погруженный объект, является суммой действующего вниз веса объекта и действующего вверх выталкивающего 22
усилия. Конструктивная масса, будучи динамическим свойством объекта, не изменяется в зависимости от места расположения объекта. Усилие инерции — это произведение массы (включая присоединенную массу) и ускорения тела.
6.2.2.2 Дополнительная вода, втекающая в (частично или полностью) погруженный объект, должна быть учтена.
6.2.3 Выталкивающее усилие
6.2.3.1 Выталкивающее усилие для погруженного объекта FB(t) равно весу вытесненной воды:
FB(t) = Рд У(0, (59)
где р — плотность воды, кг/м3;
д — ускорение свободного падения, м/с2;
V(t) — объем вытесненной воды, м3.
Массовая плотность воды изменяется в зависимости от солености и температуры.
6.2.3.2 Во время входа опускаемого через свободную поверхность объекта в воду выталкивающее усилие определено весом вытесненной в данный момент воды.
6.2.3.3 Для полностью погруженного объекта в случае продолжения попадания воды в объект выталкивающее усилие может изменяться со временем.
6.2.3.4 Направление выталкивающего усилия противоположно направлению силы тяжести. Если центр плавучести не находится вертикально над центром тяжести, то выталкивающее усилие будет создавать крутящий момент на поднимаемый объект.
Центр плавучести Хв определяют как геометрический центр вытесненного объема воды.
6.2.3.5 Для частично погруженного объекта в длинных (по сравнению с характеристическим горизонтальным размером) волнах выталкивающее усилие изменяется с подъемом волны. Изменяющаяся во времени из-за волн часть выталкивающего усилия тогда может быть учтена как усилие внешнего возбуждающего воздействия волны.
6.2.3.6 Вес объекта в погруженном состоянии W(t) определяют следующим образом:
W(t)=W0-FB(t) = [M-PV(t)]g, (60)
где И/о — вес объекта;
FB(f) — выталкивающее усилие для погруженного объекта;
р — массовая плотность воды, кг/м3;
V(t) — объем вытесненной воды, м3;
д — ускорение свободного падения, м/с2.
6.2.4 Постоянное усилие вследствие течения
6.2.4.1 Постоянное усилие вследствие морского течения Fc может быть принято как квадратичное лобовое сопротивление и определено следующим образом:
Fc=^fCDsiApiUc(z0)2, (61)
где р — массовая плотность воды, кг/м3;
CDSj — коэффициент лобового сопротивления стабильного состояния в направлении течения /;
Apj — площадь проекции в направлении /, м2;
C/c(z0) — скорость течения на глубине объекта z0, м/с.
6.2.4.2 Постоянному усилию вследствие течения противостоит горизонтальный компонент усилия подъемного троса.
6.2.5 Усилие инерции из-за движущегося объекта
6.2.5.1 Усилие инерции в направлении / (/ = 1,2, 3) Ftj на движущийся поступательно объект может быть рассчитано по формуле
где М — конструктивная масса, кг;
Г1, если /' = j .
О;; — >
J [0, если/*;
Ajj — присоединенная масса в направлении / из-за ускорения в направлении j, кг;
Xj — ускорение объекта в направлении j, м/с2.
Присоединенная масса в направлении / из-за ускорения в направлении J А^, кг, как правило, выражена в значениях коэффициента присоединенной массы, определяемого следующим образом:
Л = рфк.
(63)
где р — массовая плотность воды, кг/м3,
— коэффициент присоединенной массы;
VR — относительный объем объекта, м3.
При отсутствии симметрии тела взаимосвязанные коэффициенты присоединенной массы Д12, Д13 и ^23 являются ненулевыми, так что усилие гидродинамической инерции может отличаться по направлению от ускорения. Коэффициенты присоединенной массы являются симметричными: А- = Ajt. Вследствие этого для трехмерного объекта произвольной формы существует в целом 21 различный коэффициент присоединенной массы для трех поступательных и трех вращательных движений. Коэффициенты присоединенной массы для общих компактных неперфорированных конструкций могут определяться с помощью теории потенциального течения с использованием метода источников и стоков.
Схематичное изображение погруженного объекта, поднимаемого через волновую зону, представлен на рисунке 5.
SWL — безопасная рабочая нагрузка
Рисунок 5 — Погруженный объект, поднимаемый через волновую зону
6.2.5.2 Для пересекающих поверхность воды объектов объем в погруженном состоянии и вертикальная присоединенная масса Д33 должны приниматься для уровня спокойной воды z, равного 0.
6.2.5.3 Для вращательного движения (как правило, движения рыскания) поднимаемого объекта воздействия инерции задаются массовыми моментами инерции и добавленными моментами инерции А-, где /, j = 4, 5, 6, а также коэффициентами взаимодействия с умноженной на длину размерной массой.
Для перфорированных конструкций может быть важным влияние вязкости, а коэффициенты присоединенной массы будут зависеть от амплитуды движения, определенной с помощью числа КС. На присоединенную массу также будет влиять крупнообъемное сооружение в ее непосредственной близости.
6.2.5.4 Объект общего характера в простом поступательном движении может быть дестабилизирован из-за момента Мунка, который можно выразить в значениях коэффициентов поступательной присоединенной массы.
6.2.6 Усилие демпфирования волнообразования
6.2.6.1 Как правило, когда объект движется вблизи свободной поверхности, будут создаваться отходящие поверхностные волны. Энергия этих волн поступает от работы, выполненной по демпфированию движения объекта. Образующееся усилие, действующее на объект, является усилием демпфирования волнообразования.
6.2.6.2 Усилие демпфирования волны Fwd пропорционально скорости объекта, вычисляемое по формуле
Fwd=BijXj’ ($4)
где Bjj— коэффициент демпфирования волнообразования, кг/с; Xj — скорость поднимаемого объекта, м/с.
6.2.6.3 Для колебательного движения объекта усилие демпфирования волнообразования стремится к нулю для высоких и низких частот. Демпфированием волнообразования можно пренебречь, если:
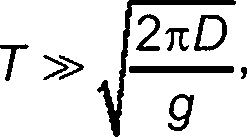
(65)
где Т — период колебательного движения;
D — характеристический размер перпендикулярно направлению движения;
д — ускорение свободного падения.
Для проницаемых конструкций, состоящих из нескольких удлиненных элементов, характеристическим размером является размер поперечного сечения удлиненных элементов.
6.2.7 Усилие внешнего возбуждающего воздействия волны
6.2.7.1 Усилия и моменты внешнего возбуждающего воздействия волны являются нагрузками на сооружение, когда оно удерживается от какого-либо отклика передвижения и при наличии набегающих волн.
6.2.7.2 Когда характеристический размер существенно меньше длины волны, усилие внешнего возбуждающего воздействия волны в направлении / FWj на полностью погруженный объект вычисляют по формуле
% = Р v[fy + С*) vj + FDh (66)
где p — массовая плотность воды, кг/м3;
V — объем погруженного объекта (принятый к уровню спокойной воды z = 0), м3;
1, если / = /
5//= п .
J |_0, если / * j
— коэффициент присоединенной массы;
Vj — ускорение частиц воды в направлении j, м/с2;
FDj— усилие внешнего возбуждающего воздействия вязкостного лобового сопротивления, Н.
6.2.7.3 Для частично погруженного объекта усилие внешнего возбуждающего воздействия в направлении / FWj вычисляют по формуле
%=р9А»ОД8й+ру(мсЗ)У+/Ъ. <67)
где pgAwC>(t) 8/3 — гидростатическое усилие, связанное с подъемом набегающей волны в месте нахождения объекта;
Aw — площадь зеркала воды;
£(?) — высота поверхности волны, м;
р — массовая плотность воды, кг/м3;
V — объем погруженного объекта (принятый к уровню спокойной воды z = 0), м3;
5/з =
1, если i = 3 (по вертикали)
0, если / = 1 или 2 (по горизонтали);
— коэффициент присоединенной массы;
vj — ускорение частиц воды в направлении /, м/с2;
FDj — усилие внешнего возбуждающего воздействия вязкостного лобового сопротивления, Н.
Так как в длинных волнах увеличение в погруженном объеме для объекта может быть аппроксимировано с помощью Aw ^(0, гидростатическая составляющая в усилии внешнего возбуждающего воздействия волны для частично погруженного объекта также может рассматриваться как часть зависимого от времени выталкивающего усилия (действующего вверх). Это правомерно только для объектов с вертикальными бортами.
6.2.8 Усилие вязкостного лобового сопротивления
6.2.8.1 Усилие вязкостного лобового сопротивления в направлении / Fdj может быть определено по формуле
Fa=jpCDAp\vr\vri, (68)
где р — массовая плотность воды, кг/м3;
CD — коэффициент лобового сопротивления в колеблющейся жидкости;
Ар — поперечная к направлению движения/потока площадь проекции, м2;
vr — общая относительная скорость, м/с;
vrj — компонента относительной скорости в направлении /, м/с.
В зависимости от относительной величины и направления скорости объекта и скорости частиц жидкости, усилие вязкостного лобового сопротивления может быть либо усилием возбуждающего внешнего воздействия волны, либо усилием демпфирования.
6.2.8.2 Если демпфирование колеблющегося объекта вычисляют с помощью формулы квадратичного лобового демпфирования, коэффициент лобового сопротивления CD зависит от амплитуды колебания. Обычно амплитуда колебания выражается в значениях безразмерного числа КС, определяемого как
КС = -^2-, (69)
D
где zm — амплитуда колебания, м;
D — характеристическая длина объекта, как правило, наименьший размер поперечно направлению колебания, м.
Для синусоидального движения число КС также может быть определено как
КС = vmT/D, где vm = 2nzm IT, а Т — период колебания. Число КС является мерой расстояния, пройденного частицами жидкости в течение полупериода относительно размера объекта.
6.2.8.3 Зависимость числа КС для коэффициентов усилия (инерции и демпфирования) также применяют к объектам, подвергающимся колебательному движению частиц воды в волновой зоне. Для регулярных волн число КС может быть представлено как:
кс=^, <7°)
о
где Н — высота регулярной волны;
D — характеристическая длина объекта, как правило, наименьший размер поперечно направлению колебания, м.
Для нерегулярного волнения число КС может быть представлено как
KC_(V2av)Tz (71)
D
где cv — стандартное отклонение скорости частиц воды, м/с;
Tz — период колебания через нулевую точку, с;
D — характеристическая длина объекта, как правило, наименьший размер поперечно направлению колебания, м.
6.2.8.4 Для малых чисел КС (как правило, менее 10) может оказаться удобным выразить лобовое сопротивление и усилие демпфирования FDj как сумму линейного и квадратичного демпфирований
FDi = + &2vri I vr I’ (^2)
где vr — общая относительная скорость, м/с;
vrj — компонента относительной скорости в направлении /, м/с.
6.2.8.5 Верхняя диаграмма на рисунке 6 показывает типичное изменение CD с числом КС. Коэффициент лобового сопротивления для устойчивого потока обозначен CDS, что соответствует значению CD для большого числа КС.
Полученные в ходе испытаний пульсирующего потока типовых подводных модулей для числа КС в диапазоне 0 < КС < 10 коэффициенты демпфирования могут быть в несколько раз больше коэффициента лобового сопротивления для данных устойчивого потока. Вследствие этого при использовании коэффициентов лобового сопротивления устойчивого потока CDS вместо зависимых от числа КС коэффициентов лобового сопротивления CD можно недооценить усилие демпфирования и переоценить резонансные движения объекта.
6.2.8.6 При оценке коэффициента демпфирования и его зависимости от числа КС на основе испытаний пульсирующего потока произведение CDKC наносят на график в зависимости от числа КС. Тогда через значительную часть экспериментальных данных в этом представлении часто можно провести прямую линию (см. нижнюю диаграмму на рисунке 6).
Влияние числа КС на коэффициенты демпфирования также можно определить численным моделированием с использованием вычислительной гидродинамики CFD потока жидкости после объектов при вынужденных колебаниях.
6.2.8.7 Пересечение с вертикальной осью задано с помощью где Ъ1 представляет собой переменную линейного демпфирования, а переменная квадратичного демпфирования Ь2 равна уклону прямой линии. Параметр со'представляет собой безразмерную частоту колебания и определяется следующим образом:
оУ = со^/О / 2д , (73>
где со'— безразмерная частота колебания;
D — характеристическая длина объекта, м.
Коэффициент демпфирования CDKC тогда может быть определен следующим образом:
С0КС = -^ + Ь2КС, (74)
со'
где — переменная линейного демпфирования;
со'— безразмерная частота колебания;
Ь2 — переменная квадратичного демпфирования.
Эти постоянные параметры могут заменить зависимый от амплитуды CD для реалистического диапазона амплитуд, что необходимо для динамического расчета нерегулярного движения (см. [1]).
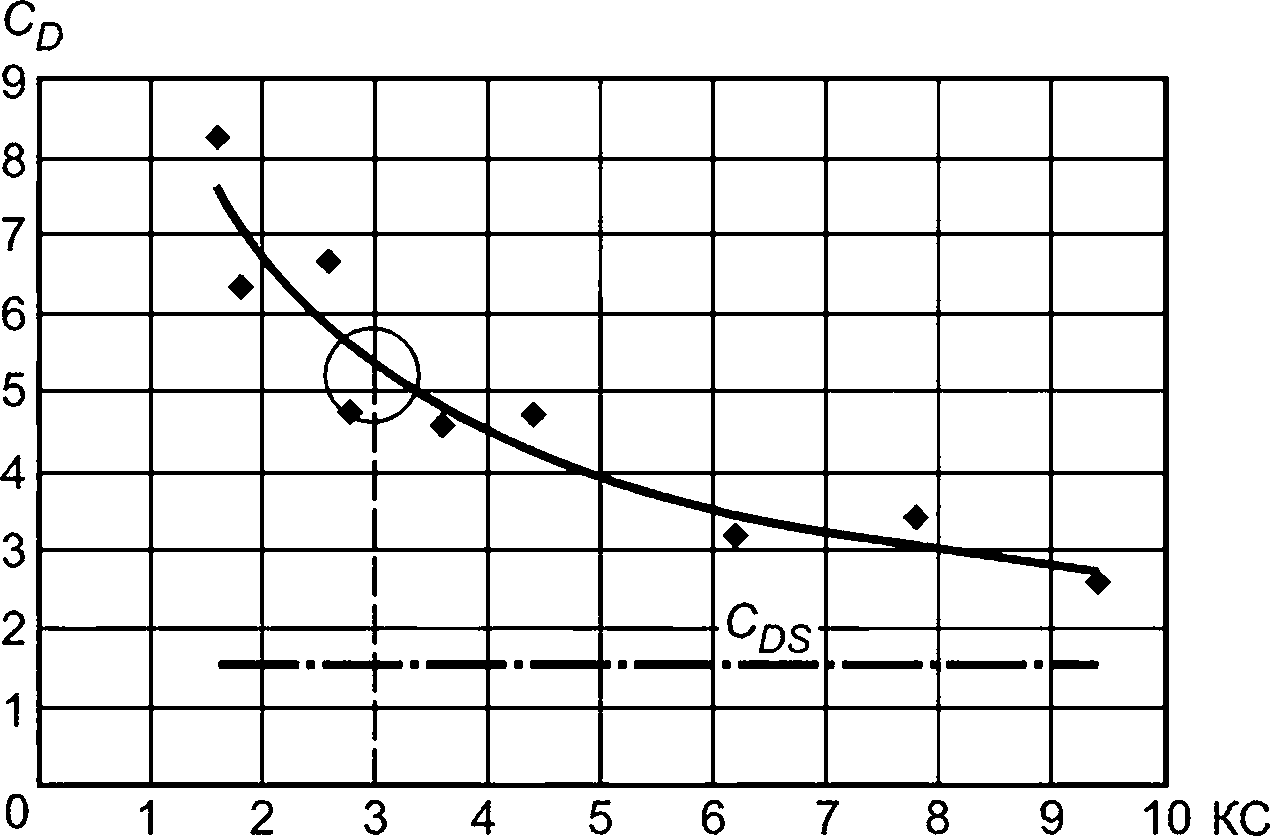
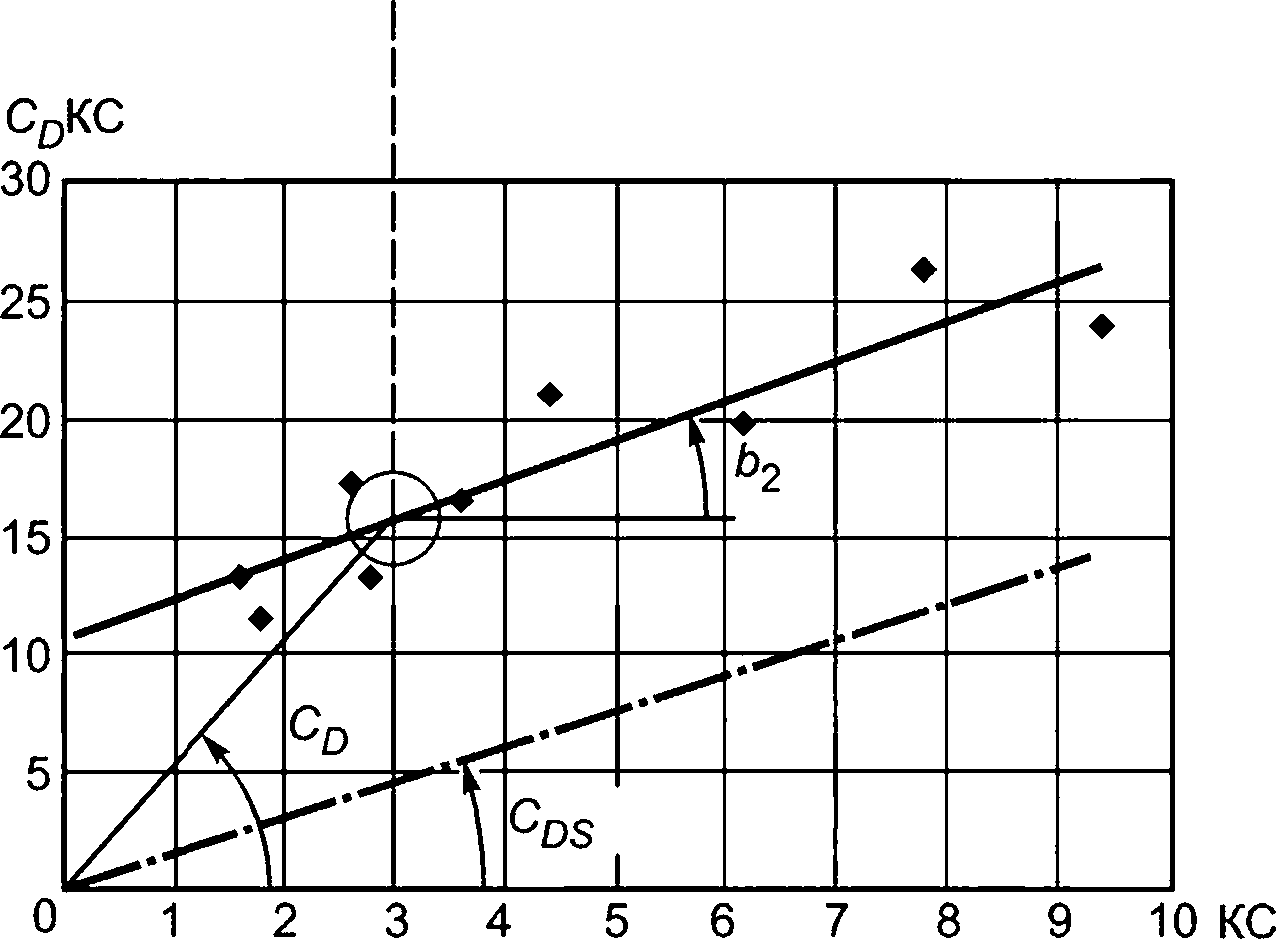
Рисунок 6 — Оценка коэффициентов демпфирования по экспериментальным значениям
В данном примере С0КС = 10,62 +1.67КС.
6.2.8.8 Когда определены Ь1 и Ь2, коэффициенты линейного демпфирования В1 и коэффициент квадратичного демпфирования В2 в выражении могут быть вычислены на основе формул:
В, = 2рД V2go bi ОТТ
(75)
S2-—рДрЬ2, (76)
где р — массовая плотность воды, кг/м3;
Ар — поперечная к направлению движения/потока площадь проекции, м2;
д — ускорение свободного падения, м/с2;
D — характеристическая длина объекта, м;
Ъ1 — переменная линейного демпфирования;
Ь2 — переменная квадратичного демпфирования.
Линейное демпфирование может быть физически связано с поверхностным трением, а квадратичное демпфирование — с демпфированием формы.
6.2.9 Усилие при слеминге
6.2.9.1 Усилие при слеминге Fs(t) на опускаемый через свободную поверхность объект с постоянной скоростью удара при слеминге vs (предполагается положительной) в спокойной воде может быть выражено как скорость изменения импульса жидкости и определено следующим образом:
(77) dt s dt
где 433(f)— моментальная высокочастотная граница присоединенной массы при вертикальной качке;
\/s — постоянная скорость волны.
Использование высокочастотной границы присоединенной массы основано на допущении того, что локальные ускорения жидкости из-за входа объекта в воду намного сильнее, чем ускорение свободного падения д. Это соответствует высокочастотной границе для колеблющегося вместе со свободной поверхностью тела.
6.2.9.2 Усилие при слеминге Fs(t) может быть вычислено в значениях коэффициента Cs при сле-минге по формуле
М0=^рсл>^2> <78)
где Cs вычисляют по формуле
q _ 2 dA^(t) _ 2 #*зз(0 (79)
s pApva dt рАр dh
с/Дзз(/)
где —— скорость изменения присоединенной массы при погружении; dt
р — массовая плотность воды, кг/м3;
Ар — площадь горизонтальной проекции объекта, м2;
vs — постоянная скорость волны, м/с;
h — погружение относительно высоты поверхности, м.
Скорость изменения присоединенной массы при погружении может быть выведена из данных зависимой от расположения присоединенной массы, рассчитанных методом источников и стоков, или оценена на основе испытаний на модели. Высокочастотная граница присоединенной массы при вертикальной качке для частично погруженного объекта составляет половину присоединенной массы соответствующего двойного тела в безграничной текучей среде, где погруженная часть объекта зеркально отображается над свободной поверхностью.
6.2.9.3 При входе в воду при волнении относительная скорость между опускаемым объектом и поверхностью моря должна применяться так, чтобы усилие при слеминге Fs(f) могло быть вычислено по формуле
Fsm=ipCA(s-r|)2, (80)
где 5 — вертикальная скорость поверхности моря, м/с;
П — вертикальное движение объекта, м/с.
6.2.9.4 Следует отметить, что при измерении вертикального усилия, действующего на объект во время входа в воду, частями измеряемого усилия будут выталкивающее усилие и усилие вязкостного лобового сопротивления. Тем не менее во время первоначального входа в воду может преобладать усилие при слеминге.
6.2.10 Уравнение вертикального движения поднимаемого объекта при опускании в волновой зоне
6.2.10.1 Объединяя выражения для усилий выталкивания, инерции, внешнего возбуждающего воздействия волны, удара при слеминге и демпфирования лобового сопротивления, действительные для длин волны, намного превышающих размеры объекта, уравнение вертикального движения п(0 для опускаемого объекта можно записать как
М + =Bg(V3-fi) + 41)(v3-T|)|,<3-f|| + (pV + /i33)v3+^^(4-f|)2 +
(81)
(82)
+pgV(t)-Mg + Fline(t),
где — коэффициент линейного демпфирования, кг/с;
— коэффициент квадратичного демпфирования, кг/м;
v3 — скорость частиц воды, м/с;
v3 — ускорение частиц воды, м/с2;
РцПе^) — усилие в подъемном тросе, Н.
6.2.10.2 Усилие в подъемном тросе Fljne{t) вычисляют по формуле
F//ne(0 = Мд- pgV(t) + K(zcf- и),
где К — жесткость подъемного троса, Н/м;
zct — движение оконечности крана;
П — движение объекта, м.
6.2.10.3 Скорость fi и ускорение т] опускаемого объекта составляют
(83) (84)
где — скоРость объекта, движение которого обусловлено движением волн, м/с;
vc — постоянная скорость опускания, м/с.
6.2.10.4 Для объекта с вертикальными боковыми стенками на среднем уровне воды выталкивающее усилие в данный момент pgV(t) может быть разделено на медленно изменяющийся (средний) компонент, компонент внешнего возбуждающего воздействия волны и компонент гидростатического возвращения из-за вызванного волной движения объекта и вычислено по формуле
рд\/ (/) = pg[V0 + Awq(t) - >Vi(f)],
(85)
где Уо — вытесненный объектом объем в неподвижной воде, м3;
Aw — мгновенная площадь зеркала воды, м2.
Мгновенная площадь зеркала воды Aw представляет собой зависимую от скорости опускания медленно изменяющуюся функцию времени vc.
6.2.10.5 Допуская, что вертикальная скорость vc опускаемого объекта постоянна, и пренебрегая движением оконечности крана, усилие в подъемном тросе F/jne(t), Н, можно рассчитать по формуле
%®(0=M9-P^(f)-(pV+433)y3--^ffi(g-vc)2-Bj(y3-vc)-
(86)
где В1 — коэффициент линейного демпфирования;
В2 — коэффициент квадратичного демпфирования;
A^(t)— моментальная высокочастотная граница присоединенной массы при вертикальной качке; vc — постоянная скорость опускания, м/с.
Усилия удара при слеминге и внешнего возбуждающего воздействия волны могут вызвать провисание (F = 0) в подъемном канате с последующими высокими нагрузками рывка.
6.2.10.6 Воздействие волны по верхней пластине задавливаемой самопогружной сваи приведет к изменению скорости сваи. Изменение скорости Аус определяют по формуле
Дис=^г-(5-ис0). <87>
где М — масса задавливаемой самопогружной сваи, кг;
А33 — масса водяной пробки (присоединенная масса) внутри задавливаемой самопогружной сваи, кг;
с; — вертикальная скорость водной поверхности внутри задавливаемой самопогружной сваи перед событием удара, м/с;
vc0 — вертикальная скорость задавливаемой самопогружной сваи перед событием удара, м/с.
6.2.10.7 Уменьшение усилия в подъемном тросе из-за удара при слеминге AF//ne может быть представлено как
^Рию=к^-. <88)
где К — жесткость грузоподъемной системы, Н/м;
со0 — собственная частота движения сваи, рад/с.
6.2.11 Усилие выхода из воды
6.2.11.1 Усилие выхода из воды Fe(t) на полностью погруженном объекте, поднимаемом под свободной поверхностью с постоянной скоростью подъема ve (положительной вверх), в спокойной воде может быть выражено через скорость изменения кинетической энергии жидкости с помощью отношения
(89)
где Е„ =1/2Z^3 ve2;
д0
Азз — моментальная низкочастотная граница присоединенной массы при вертикальной качке.
6.2.11.2 Усилие выхода из воды Fe(f) тогда может быть записано следующим образом:
₽ т- 1 (Ад» у 2' к»&,, ' vg а г^33 ’) 2 at ’’
(90)
где ve — скорость подъема;
Дзз — моментальная низкочастотная граница присоединенной массы при вертикальной качке.
Использование низкочастотной границы присоединенной массы основано на допущении того, что локальные ускорения жидкости во время выхода из воды намного меньше ускорения свободного падения д. Это соответствует низкочастотной границе для колеблющегося под свободной поверхностью тела. Выходная скорость может быть выражена в значениях выходного числа Фруда Fn = vel JgD, где D — характеристический горизонтальный размер объекта. Вследствие этого формула действительна для малого числа Фруда, Fn « 1.
6.2.11.3 Присоединенная масса при вертикальной качке увеличивается по мере приближения полностью погруженного объекта к свободной поверхности. Вследствие этого усилие выхода из воды действует вниз, в направлении, противоположном скорости выхода.
Схематичное изображение выхода ТПНА из воды представлено на рисунке 7.

Рисунок 7 — Выход ТИПА из воды
6.2.11.4 Как правило, усилием выхода из воды на поднимаемом частично погруженном объекте можно пренебречь. Усилия выхода из воды могут учитываться при значительной площади горизонтальных поверхностей поднимаемых объектов.
6.2.11.5 Усилие выхода из воды Fe(?) может быть определено в значениях коэффициента выхода из воды Се следующим образом:
/ъ(0 = --рСеАоУе2,
где Се— коэффициент выхода из воды, который определяется как:
С 1 1
• pApve dt рАр dh
dA^ -
где —— — скорость изменения присоединенной массы по мере погружения, кг/м;
dh
р — массовая плотность воды, кг/м3;
Ар — площадь горизонтальной проекции объекта, м2;
h — погружение относительно высоты поверхности, м.
Следует учитывать, что скорость изменения присоединенной массы является отрицательной.
6.2.11.6 Учитывают находящуюся в объекте воду и выпуск воды на стадии выхода. Выпуск воды может изменить распределение веса во время выхода.
6.2.11.7 При выходе из воды при волнении относительная скорость между поднимаемым объектом и поверхностью моря применяется так, чтобы усилие выхода Fe(t) можно было вычислить по формуле
Р,(() = -^рСеДр(?-п)2, (93)
где 5 — вертикальная скорость поверхности моря, м/с;
П — вертикальное движение объекта (положительное вверх), м/с;
р — массовая плотность воды, кг/м3;
Ар — площадь горизонтальной проекции объекта, м2;
Се — коэффициент выхода из воды.
6.2.12 Уравнение вертикального движения поднимаемого объекта при подъеме из волновой зоны
Объединяя выражения для усилий выталкивания, инерции, внешнего возбуждающего воздействия волны и выхода из воды, уравнение вертикального движения п(/) для поднимаемого объекта можно записать как
(М+Aj3)n = 4з (v3 - n)+(у3 - п)|и3 - л|+(р V+Aj3) V3 -
1 9 (94)
" 2 - П) + P9V (0 - Mg + Fline (t),
где^з — коэффициент линейного демпфирования, кг/с;
— коэффициент квадратичного демпфирования, кг/м;
|/3 — скорость частиц воды, м/с;
v3 — ускорение частиц воды, м/с2;
F//ne(f) — усилие в подъемном тросе, Н;
Й — скорость поднимаемого объекта, которая определяется как:
n = Vv'e- (95)
Сила в подъемном тросе задается с помощью 6.2.10.2.
6.2.13 Гидродинамические нагрузки на удлиненные элементы
6.2.13.1 Прилагаемое к удлиненному объекту гидродинамическое усилие может быть оценено путем суммирования действующих на каждую полосу конструкции усилий на сечение. Для удлиненных конструктивных элементов со значительно меньшими, чем длина волны, размерами поперечного сечения волновые нагрузки можно рассчитать с использованием формулы нагрузки Морисона, представляя как сумму пропорциональной ускорению силы инерции и пропорциональной квадрату скорости силы лобового сопротивления.
6.2.13.2 Как правило, формулу нагрузки Морисона применяют в том случае, когда длина волны превышает пятикратный характеристический размер поперечного сечения.
Поперечное усилие, тангенциальное и подъемное усилия, действующие на удлиненную конструкцию, представлены на рисунке 8.
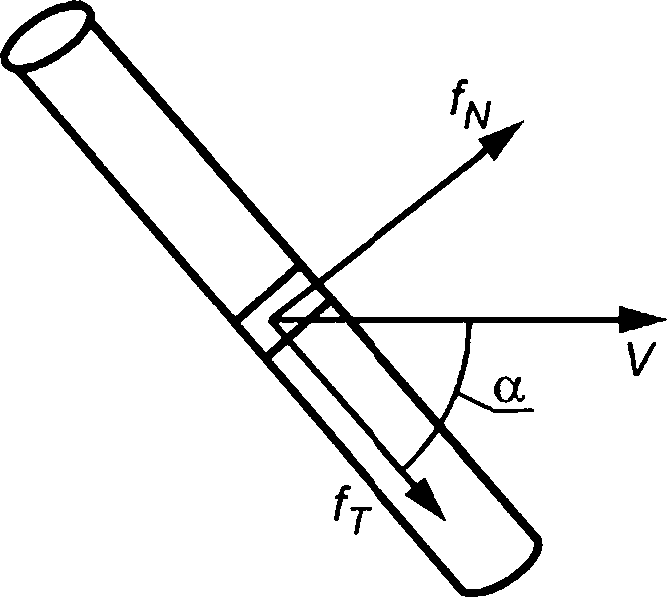
Рисунок 8 — Поперечное усилие fN, тангенциальное усилие fT и подъемное усилие fL, действующие на удлиненную конструкцию
6.2.13.3 Поперечное усилие на сечение, действующее на удлиненную конструкцию, fN задается с помощью выражения:
= -pCAAxN 4- р (1 + СА) A vN + ^pCDD | vrN |, (96)
где p — массовая плотность воды, кг/м3;
СА — коэффициент присоединенной массы;
А — площадь поперечного сечения, м2;
Хдг — продольное элементу ускорение элемента, м/с2;
v/y — ускорение частиц воды в поперечном направлении, м/с2;
CD — коэффициент лобового сопротивления;
D — диаметр или характеристический размер в поперечном сечении, м;
vrN — поперечная элементу относительная скорость, м/с.
Формула относительной скорости для лобового сопротивления действительна тогда, когда движение xN элемента в поперечном направлении превышает характеристический размер поперечного сечения D. Использование поперечной скорости в формуле скорости правомерно, если угол атаки а (см. рисунок 8) находится в диапазоне 45°—90°. Коэффициент лобового сопротивления может быть принят как независимый от угла атаки.
6.2.13.4 Местная (двухмерная) присоединенная масса для удлиненного элемента составляет aij = pCAAR, i,j= 1,2, где AR— относительная площадь, обычно принимаемая как площадь поперечного сечения.
6.2.13.5 Для открытых цилиндров тангенциальное усилие лобового сопротивления ft присутствует главным образом вследствие поверхностного трения и по сравнению с поперечным усилием лобового сопротивления является малой. Тем не менее для протяженных удлиненных элементов с преобладающим компонентом тангенциальной скорости тангенциальное усилие лобового сопротивления может быть значимым.
6.2.13.6 Подъемное усилие fL в поперечном к направлению вектора относительной скорости направлении может присутствовать в силу несимметричного поперечного сечения, попутной вихревой зоны, непосредственной близости к большому сооружению (влияние стенок) и вихревого потока.
6.2.13.7 Усилие при слеминге на сечение, действующее на горизонтальный цилиндр, fs(t) может быть определено в значениях коэффициента Cs при слеминге следующим образом:
^0) = ^pCsDvs2, (97)
где р — массовая плотность воды, кг/м3;
С„ — коэффициент, который определяется как: Cs =--
s pD dh
D — диаметр цилиндра, м;
h — глубина погружения, м;
— скорость изменения местной присоединенной массы по мере погружения, кг/м2; dh
vs — скорость удара при слеминге, м/с.
Погружение h — это расстояние от центра цилиндра до свободной поверхности, определяемое таким образом, что h = - г в начальный момент времени, когда цилиндр ударяется о поверхность воды.
Высокочастотный коэффициент вертикальной присоединенной массы как функция погружения представлена на рисунке 9.
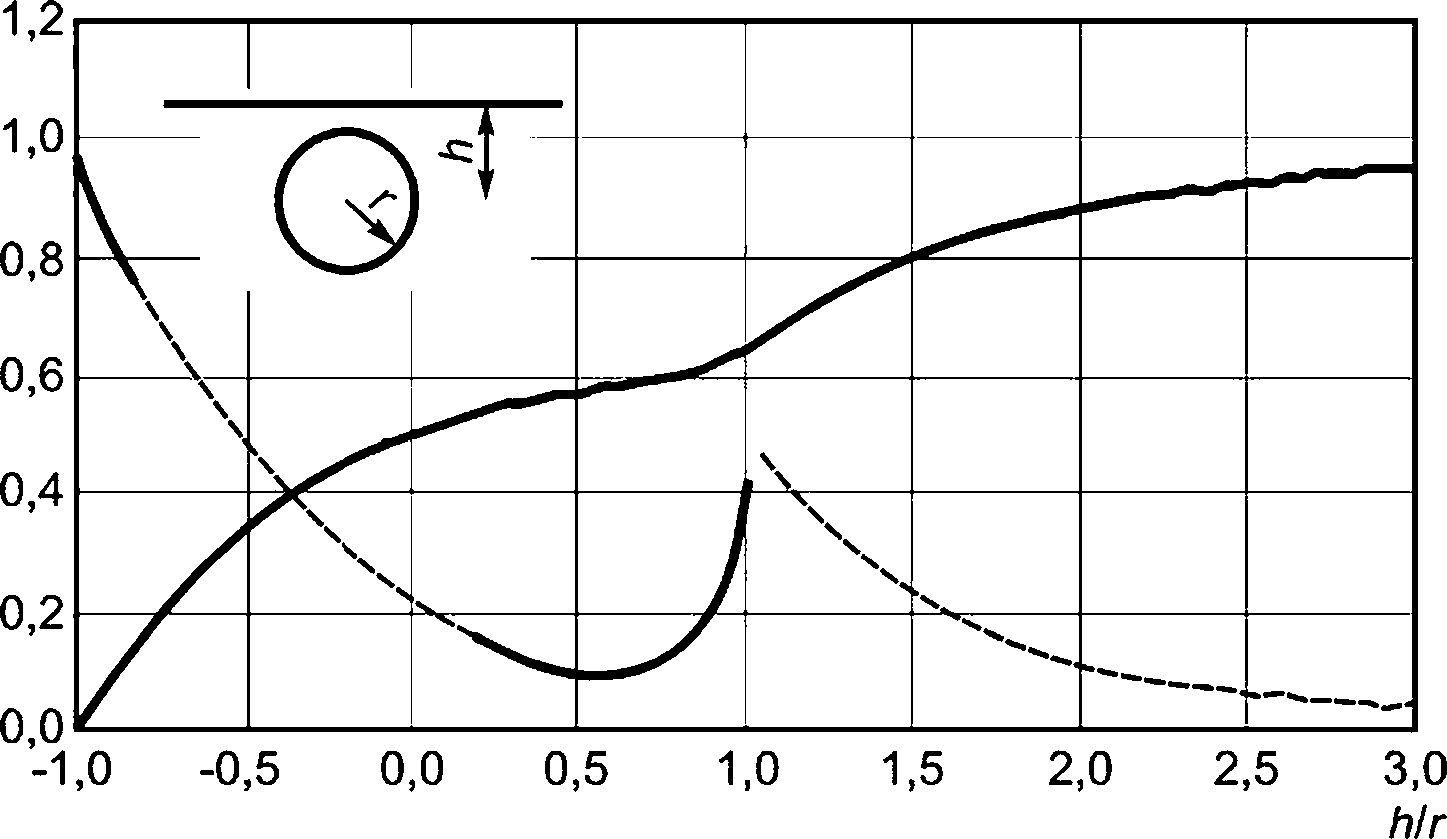
Примечание — Сплошная линия — а^/pnr2; пунктирная линия — (da33ldh)lpitr.
Рисунок 9 — Высокочастотная граница коэффициента вертикальной присоединенной массы и ее производная вблизи свободной поверхности как функция глубины воды
6.2.13.8 Коэффициент присоединенной массы СА выделяют по формуле
СЛ=^, (98)
p7trZ
где СА — коэффициент присоединенной массы;
р — массовая плотность воды, кг/м3.
6.2.13.9 Усилие на сечение выхода из воды, действующее на горизонтальный цилиндр Fe(t), может быть определено в значениях коэффициента выхода из воды Се следующим образом:
^(0 = 4pC®Dve- <99)
где Се определено по формуле
С 1 da33 (100)
е pD dh
— скорость изменения местной низкочастотной присоединенной массы по мере погружения, кг/м2;
р — массовая плотность воды, кг/м3;
h — погружение относительно высоты поверхности, м.
Следует учитывать, что коэффициент выхода может напрямую зависеть от выходного числа Фруда: рп = vely/gD, а формула в значениях скорости изменения присоединенной массы действительна только для Fn« 1.
6.2.13.10 Коэффициент при слеминге для цилиндра круглого сечения Cs(s) может вычисляться на основе экспериментальных значений Кэмпбелла и Уайнберга для гладкого цилиндра следующим образом: где s = h + D/2 — величина погружения цилиндра, м;
Cs(s) = 5,15
D 0,107s
D + 19s+ D
(101)
D — диаметр цилиндра, м;
h — расстояние от центра цилиндра до уровня спокойной воды, м (см. рисунок 9).
Следует отметить, что воздействия выталкивающего усилия включены в данную формулу таким образом, чтобы она использовалась только для s/D менее 0,5 или h/r менее 0.
Начальное значение данного эмпирического коэффициента при слеминге Cs(0), равного 5,15, находится между теоретическими значениями, полученными с помощью двух классических решений задачи входа в воду: л (фон Карман) и 2л (Вагнер).
6.3 Гидродинамические коэффициенты
6.3.1 Общие положенияКак правило, коэффициенты гидродинамического усилия (коэффициент присоединенной массы, коэффициент лобового сопротивления и демпфирования, коэффициент подъема) зависят от следующих факторов:
- геометрии;
- числа Рейнольдса (Re = vmD/v) на основе максимальной скорости vm;
- число КС (КС = vmT/D), где D — диаметр, м;
v — кинематическая вязкость жидкости, м/с2;
Т — период волны или период колебания.
Кроме того, на эти коэффициенты могут влиять соотношение сторон, угол наклона к потоку, шероховатость поверхности, коэффициент перфорации, частота колебания, близость к свободной поверхности и близость к границе твердого тела.
Вблизи свободной поверхности присоединенная масса и демпфирование могут изменяться в зависимости от частоты и расстояния до свободной поверхности. На морском дне коэффициенты зависят от близости, а не от частоты (см. [1]).
6.3.2 Коэффициенты присоединенной массы и лобового сопротивления для простых тел
6.3.2.1 Коэффициенты присоединенной массы и лобового сопротивления для 2- и 3-мерных тел с простой геометрией приведены в приложениях А и Б.
6.3.2.2 Следует принять во внимание, что представленные в приложениях А и Б коэффициенты присоединенной массы не учитывают воду внутри тела. Вода внутри тела может включаться либо в присоединенную массу, либо в массу тела. В случае ее включения в массу тела плавучесть должна включать в себя внутренний объем.
Простым руководством является следующее: при подъеме объекта из воды содержащуюся в сооружении воду следует принимать как часть массы тела. В ином случае вода должна быть включена в присоединенную массу. Например, вода внутри заполняемых через небольшие отверстия трубчатых рам может, как правило, приниматься как часть массы тела, в то время как вода внутри задавливаемых самопогружных свай чаще всего включается в присоединенную массу.
6.3.3 Присоединенная масса и демпфирование для типичных подводных конструкций
6.3.3.1 Большинство подводных конструкций, таких как дистанционно управляемые инструменты, опорные плиты и защитные конструкции, имеют сложную геометрию. Следовательно, трудно определить гидродинамические коэффициенты аналитическими методами или с использованием программ источников и стоков.
6.3.3.2 В настоящее время наиболее точным методом определения гидродинамического коэффициента для сложных трехмерных подводных конструкций являются испытания на модели. Используют один из методов испытаний: либо испытание свободного колебания, либо испытание вынужденного колебания.
6.3.3.3 Присоединенная масса и демпфирование открытой подводной конструкции могут быть оценены как сумма дополнительных факторов от его отдельных конструктивных элементов. Однако вызванные ограничениями потока эффекты взаимодействия между элементами могут привести к значительному увеличению присоединенной массы и демпфирования.
Эффектами взаимодействия можно пренебречь, если поперечная к направлению колебания (в пределах типичной амплитуды либо колебания тела, либо колебания частиц волны) сплошная площадь проекции менее 50 % от площади контура.
6.3.4 Присоединенная масса и демпфирование проницаемых конструкций
6.3.4.1 В данном контексте проницаемые конструкции включают в себя конструкции, в которых поперечная направлению колебания плоскость либо сделана с отверстиями или щелями, либо состоит из параллельных удлиненных элементов. Примерами являются горизонтальная верхняя пластина вакуумной сваи с отверстиями и верхний участок защитной конструкции (см. рисунок 10). Проницаемые конструкции в настоящем стандарте также определяют и как другие части трехмерной конструкции со значительным ограничением потока.

Рисунок 10 — Пример проницаемой конструкции.
Защитная крышка, используемая для прикрытия подводных модулей на морском дне
6.3.4.2 Для оценки воздействия амплитуды колебания на коэффициенты усилия для проницаемых конструкций число КС может быть определено как
КС = ^-^1. (102)
° 2мр2
где zm — амплитуда колебания, м;
D — характеристический горизонтальный размер, м;
р — коэффициент перфорации 0 < р < 1;
ц — коэффициент расхода.
Коэффициент перфорации р определяют как деленную на общую площадь открытую площадь. Коэффициент расхода ц, как правило, находится в диапазоне от 0,5 до 1,0.
6.3.4.3 На рисунке 11 показаны результаты испытания на модели для присоединенных масс пяти вентилируемых конструкций, представляющих стандартные защитные конструкции, с коэффициентом перфорации, изменяющимся от 0,15 до 0,47. Присоединенная масса А33 нормализована с присоединенной массой сплошной конструкции А330 (с такими же размерами перпендикулярно направлению колебания). Изменение присоединенной массы в зависимости от амплитуды колебания является значительным (с коэффициентом 2—3) для всех объектов.
6.3.4.4 Асимптотическое значение для А33 в пределе нулевых амплитуд (КС = 0) может быть найдено на основе потенциальной теории и рассчитано с помощью панельной программы источников и стоков. Следующая приближенная формула найдена путем подбора кривой через результаты для пластин с круглыми отверстиями и признана применимой для пластин с вентиляционными отверстиями:
Азз
р 0,28
Азз.о кс=0
(ЮЗ)
Однако, как видно на рисунке 11, данное асимптотическое значение при КС, равном 0, может дать неточные значения для конструкций в колеблющемся потоке жидкости.
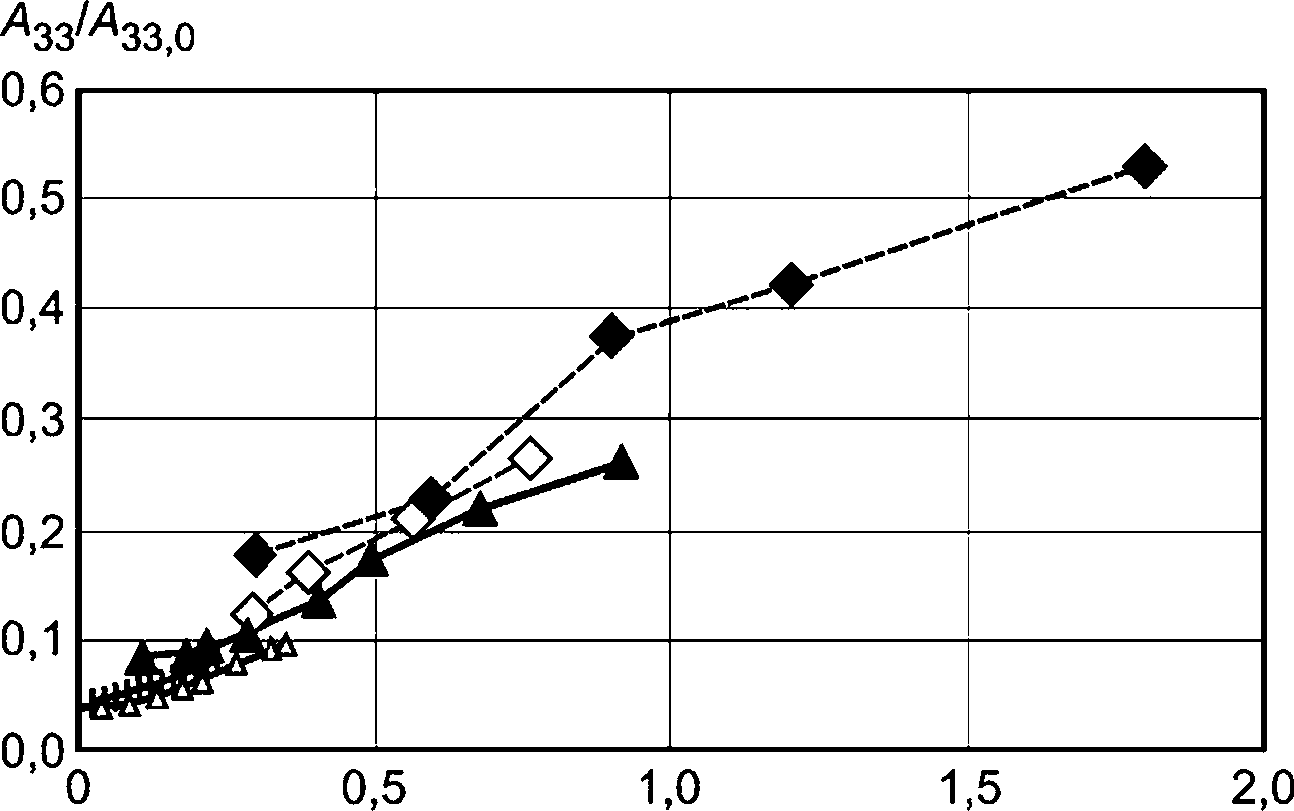
----+-----люк 20, р = 0,15;
----О-----люк 18, р = 0,25;
----А--верхнее покрытие #1, р = 0,267;
-----1--верхнее покрытие #2, р = 0,47;
----Д--верхнее покрытие #3, р = 0,375
Рисунок 11 — Присоединенная масса пяти сравниваемых перфорированных объектов
6.3.5 Коэффициенты сопротивления для цилиндров круглого сечения
6.3.5.1 Коэффициент сопротивления для цилиндров круглого сечения напрямую зависит от шероховатости цилиндра к. Для высокого числа Рейнольдса (Re > 10) и числа КС коэффициент постоянного сопротивления CDS может быть определен следующим образом:
cds(д)-
0,65 ;Д<10"4,
(29 + 4 1од10(д))/20 ; Ю"4 < Д < 10"2,
1,05 : д> ю-2,
(104)
где Д = k/D является безразмерной шероховатостью.
Указанные выше значения применяют для расчета как нерегулярного, так и регулярного волнения.
6.3.5.2 Изменение коэффициента лобового сопротивления CD в зависимости от числа КС для цилиндров круглого сечения может быть аппроксимировано по выражению
Cq ~ ^ds ' v(KC),
(Ю5)
где CDS— коэффициент сопротивления для устойчивого потока после цилиндра, определяемый как:
Cds ~ v(KC),
(Юб)
где у(КС) — коэффициент динамичности.
На рисунке 12 показана зависимость коэффициента динамичности от числа КС с учетом изменения шероховатости поверхности а.
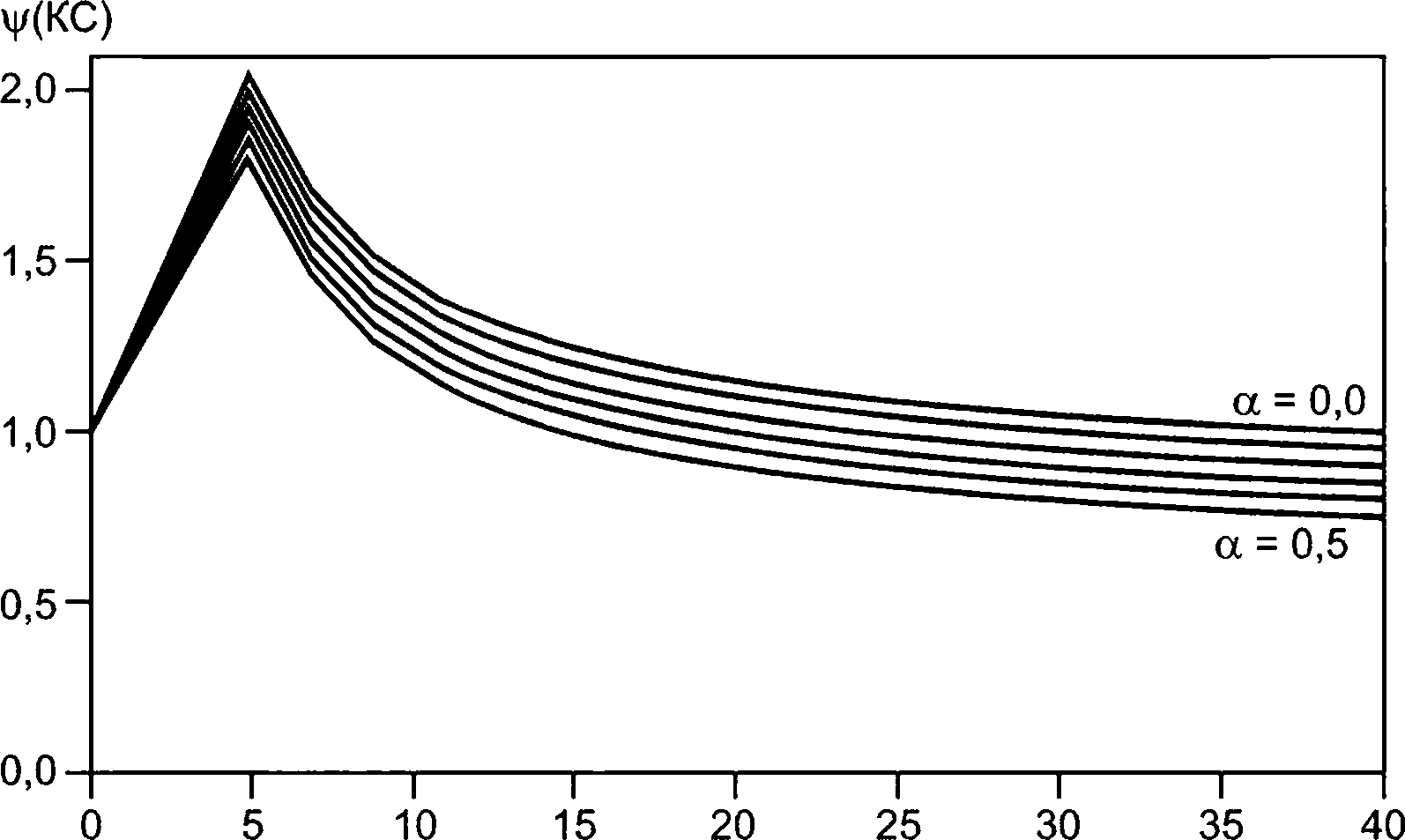
Рисунок 12 — Зависимость коэффициента динамичности от числа Келегана-Карпентера
6.3.6 Оценка коэффициентов присоединенной массы и демпфирования по результатам испытаний на модели или по данным расчета CFD
6.3.6.1 При испытаниях вынужденного колебания сооружение подвергают к синусоидальному колебанию с частотой со.
6.3.6.2 Временные ряды для движения z(f) и усилия F(f) рассчитывают, а общую колеблющуюся массу М + Д33 и линеаризированное демпфирование В можно оценить с помощью метода наименьших квадратов. Усилие F(t) вычисляют по уравнению
(Ю7)
где М — колеблющаяся масса;
А — присоединенная масса;
В — линеаризированное демпфирование;
z — ускорение колебаний, м/с2;
z — скорость колебаний, м/с.
6.3.6.3 Присоединенную массу А расссчитывают путем вычитания конструктивной массы конструкции и элементов подвески из общей колеблющейся массы. Коэффициент присоединенной массы СА извлекают из присоединенной массы по выражению
(108)
СА =—, Pvr
где р — массовая плотность воды, кг/м3;
VR — относительный объем объекта, м3.
6.3.6.4 Выведенное линеаризированное демпфирование В может быть отображено на графике как функция амплитуды колебания z. Если можно подобрать относительно прямую линию, то демпфирование можно разделить на линейное и квадратичное демпфирования:
В1 = В при z = 0, кг/с.
Квадратичное демпфирование В2, кг/м, вычисляют по формуле
<109>
где В — линеаризированное демпфирование;
В1 — линейное демпфирование, кг/с;
Т — период колебания, с;
z — амплитуда колебания.
6.3.6.5 Альтернативным уравнением для вычисления усилия F(t) применяют уравнение
F = -(M + A)z-Bz\z\. (110)
6.3.6.6 После этого коэффициент лобового сопротивления CD вычисляют по формуле
Со=^-. (111)
° рАр
где В — коэффициент демпфирования;
р — массовая плотность воды, кг/м3;
Ар — поперечная к направлению колебания площадь проекции, м2.
6.3.6.7 После определения коэффициентов лобового сопротивления для нескольких амплитуд колебания можно рассчитать (в случае получения прямой линии) линейный и квадратичный коэффициенты В1 и В2 (6.2.8.6).
6.3.6.8 Эти методы являются более надежными, чем оценка двух коэффициентов демпфирования, осуществляемая на одном этапе. Похожий подход применяют для оценки присоединенной массы и демпфирования на основании расчетов CFD.
6.3.6.9 При испытании демпфирования свободного движения общую массу находят на основании периода каждого цикла движения, а демпфирование выводят из затухающих амплитуд колебания.
6.3.6.10 Применяемые для оценки коэффициентов усилия испытательные модели масштабируют путем использования определяемого числом Фруда правила масштабирования Фруда. Как правило, масштаб выбирают между 1:30 и 1:100. При значительных вязких усилиях число Рейнольдса также правомерно применять в связи с вихревым потоком, а также может потребоваться внести исправления в масштабирование Фруда. Обычно такие исправления называются воздействиями масштабирования. Следует иметь в виду, что воздействия масштабирования могут быть значимыми для перфорированных конструкций.
6.4 Методы вычисления для оценки гидродинамических усилий
6.4.1 Упрощенный метод6.4.1.1 Упрощенный метод можно использовать для оценки гидродинамических усилий, действующих на объекты, опускаемые сквозь поверхность воды и далее на дно моря.
6.4.1.2 Упрощенный метод также можно применять при расчете возврата объекта с морского дна обратно на судно-укладчик.
6.4.1.3 Цель упрощенного метода — предоставление простых консервативных оценок действующих на объект усилий.
6.4.1.4 Упрощенный метод предполагает, что горизонтальная протяженность поднимаемого объекта незначительна по сравнению с длиной волны. Если протяженность объекта признана существенной, следует использовать метод регулярной расчетной волны или выполнить расчет по временной области.
6.4.1.5 Упрощенный метод предполагает, что вертикальное движение конструкции равно вертикальному движению оконечности крана. В случае присутствия усиления из-за вертикального резонанса необходимо выполнить расчет по временной области.
6.4.2 Метод регулярной расчетной волны
6.4.2.1 Работы по подъему и опусканию можно рассчитывать путем применения к сооружению метода регулярной расчетной волны с использованием электронной таблицы или языка программирования, как описано в данном пункте.
6.4.2.2 Полученная при использовании данного метода документация должна быть детально описана во всех подробностях, что позволит при необходимости повторить все расчеты.
6.4.2.3 Для простоты изложения в данный пункт не включены сведения о влиянии мелководья.
Конечная глубина воды d может быть учтена путем вывода скорости v = grad ср и ускорения а = dv/dt частиц воды из потенциала скорости ф для линейных волн Эйри.
Таким образом, потенциал скорости ф вычисляют по формуле
ф = COS^Z + ^cos((of-/acosp-/(ysinp) , (^2)
со coshkd ' 7
где д — ускорение свободного падения, равное 9,81, м/с2;
£а — амплитуда волны;
со — угловая частота волны;
d — глубина воды;
t — время, изменяющееся от 0 до Г с типовыми шагами в 0,1, с;
к — волновое число, м-1;
х, у — горизонтальные координаты центра тяжести для индивидуальных основных частей поднимаемого объекта, м;
Р — направление распространения волны, измеренное от оси х, и положительное против часовой стрелки, рад.
6.4.2.4 Общая геометрия конструкции как по горизонтали, так и по вертикали должна быть разделена на отдельные основные элементы, каждый из которых является дополнительным фактором при гидродинамических усилиях (см. рисунок 13).
6.4.2.5 Отдельные расчеты выполняют для каждого определенного направления волны и для каждого определенного случая нагрузки, где уровень спокойной воды расположен либо под областью удара при слеминге, либо слегка выше главной части опускаемой конструкции.
6.4.2.6 Применяют регулярную волну. Расчеты выполняют для получения допустимых пределов как для высоты характерной волны, так и для периода колебания волны через нулевую точку.
6.4.2.7 Высота регулярной волны не должна быть меньше наиболее вероятной высоты наибольшей волны. Если опускание через волновую зону проводят в пределах 30 мин, наибольшая характеристическая высота волны может быть равной 1,80 высоты характерной волны.
6.4.2.8 Когда планируемое время выполнения операции (включая непредвиденное время) превышает 30 мин, применяемая высота регулярной волны должна в два раза превышать высоту характерной волны.
6.4.2.9 Период регулярной волны должен быть равным периоду колебания через нулевую точку Tz для соответствующего состояния моря.
6.4.2.10 На рисунке 13 показано определение системы координат для приведенного в 6.4.2.11 описания волны. Волны распространяются в направлении р относительно оси х. Исходной точкой системы координат является уровень спокойной воды.
В данном случае сооружение может быть приблизительно разделено на четыре задавливаемые самопогружные сваи (Д, В, С и D) и две половины манифольда (левая сторона и правая сторона).
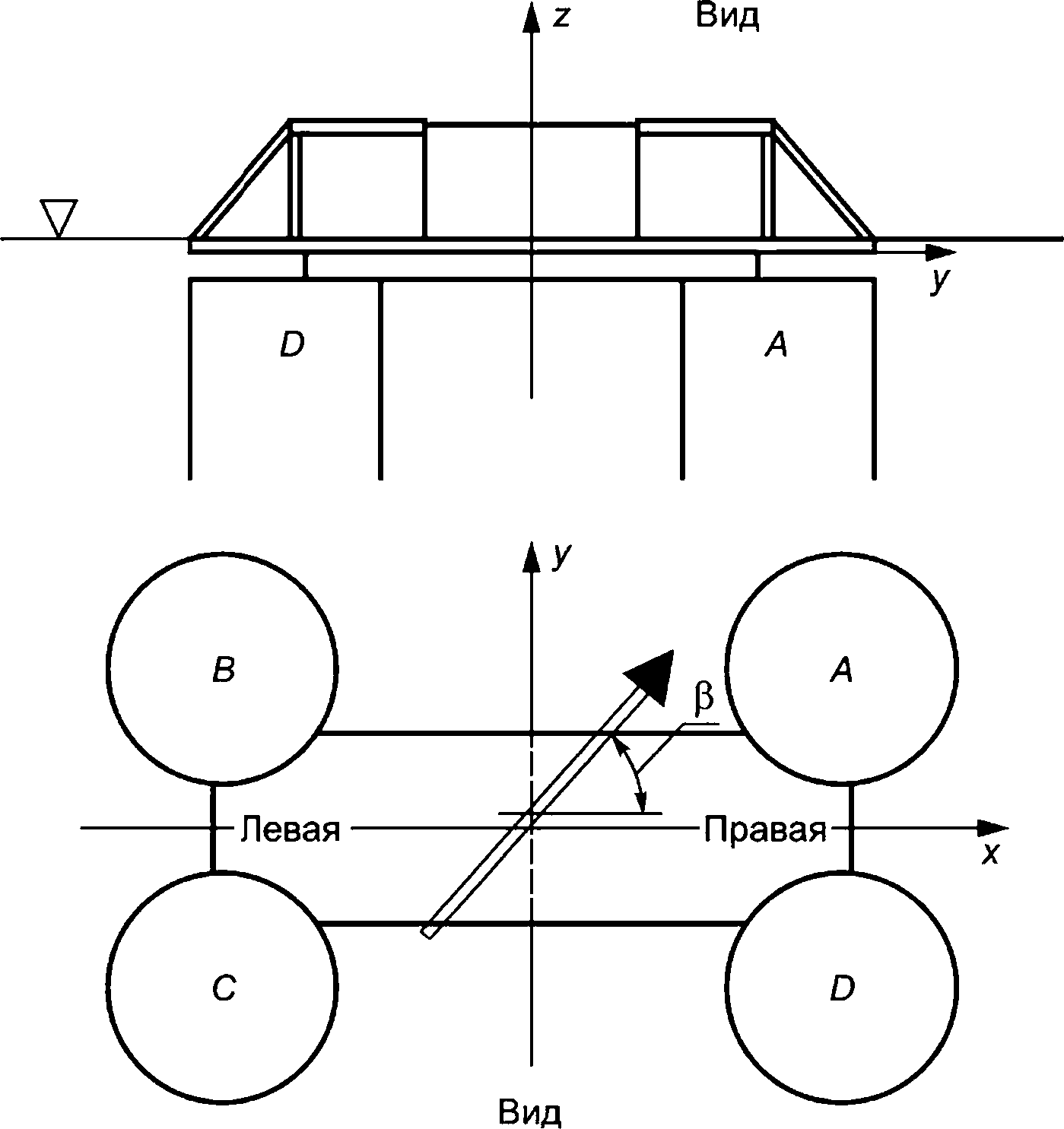
Рисунок 13 — Пример подводного модуля. Основные элементы, система координат и направление волны
6.4.2.11 Амплитуду регулярной волны С вычисляют по формуле = ^а sin (со/- kxcosp - kysinp), (113)
где Qa — амплитуда волны, т. е. Са = 0,9/7s для работ продолжительностью менее 30 мин и С,а = Hs для работ продолжительностью более 30 мин, м;
со — угловая частота волны;
t — время, изменяющееся от 0 до Г с типовыми шагами в 0,1, с;
к — волновое число, м-1;
х, у — горизонтальные координаты центра тяжести для индивидуальных основных частей поднимаемого объекта, м;
р — направление распространения волны, измеренное от оси х, и положительное против часовой стрелки, рад.
На мелководье угловая частота волны ш определена общим дисперсионным уравнением со2 = дк ianh(kd), (114)
где к — волновое число, м-1;
d — глубина воды.
6.4.2.12 Вертикальные скорость v, м/с, и ускорение частицу, м/с2, волны могут быть определены по формулам:
v = w^e^cos (со/ - kxcosp - kysinp), (115)
й = m2^aetesin(®t-Axcosp-/cysinp), (116)
где со — угловая частота волны;
к — волновое число, м-1;
z — вертикальная координата для центра тяжести индивидуальных основных частей поднимаемого объекта (отрицательная вниз), м;
Са — амплитуда волны;
х, у — горизонтальные координаты центра тяжести для индивидуальных основных частей поднимаемого объекта, м;
Р — направление распространения волны, измеренное от оси х, и положительное против часовой стрелки, рад.
6.4.2.13 В данном способе вычисления допускается, что вертикальное движение поднимаемого объекта следует за движением оконечности крана, а вертикальное движение оконечности крана гармонически колеблется с амплитудой т|а и регулярным периодом Tct.
В случаях неправомерности данного допущения необходимо выполнить расчет по временной области.
6.4.2.14 В качестве наиболее вероятной наибольшей отдельной вертикальной амплитуды движения оконечности крана г|а для примененного периода волны Tz может быть принято следующее значение:
г|а = 3,6 о м — для работ продолжительностью менее 30 мин;
г|а = 4,0 а , м — для работ продолжительностью свыше 30 мин, где о — стандартное отклонение спектра отклика вертикального движения оконечности крана.
6.4.2.15 Таким образом, вертикальное движение т|, м, скорость-q, м/с, и ускорение поднимаемого объекта т), м/с2, вычисляют по формулам:
Л = т|а sin(wn t + s),
^w^acosfeo^ + s),
f| = - co2nr|asin((on/ + s),
где r|a — отдельная вертикальная амплитуда движения поднимаемого объекта, предполагаемая равной наиболее вероятной наибольшей отдельной амплитуде оконечности крана, м;
а)л — угловая частота вертикального движения поднимаемого объекта, рад/с; t — время, изменяющееся от 0 до Г с типовыми шагами в 0,1, с;
8 — фазовый угол между волной и движением оконечности крана, рад.
6.4.2.16 Необходимо применять фазовый угол, вызывающий наибольшие амплитуды динамического натяжения в подъемных стропах и подъемном канате.
Фазовый угол можно найти путем применения набора фазовых углов в диапазоне от е = 0 до 8 = 2л с шагами, например, 0,1л. Следует применять фазовые углы, приводящие к наибольшему риску провисания стропы или наибольшему DAFconv.
6.4.2.17 Действующее на каждый из основных компонентов конструкции вертикальное гидродинамическое усилие Fhvd, Н, может быть вычислено по формуле
Fhvd= Fp + Fm + Fs+ Fd’ (12°)
где Fp — переменное выталкивающее усилие, H;
Fm — гидродинамическое массовое усилие, Н;
Fs — сила удара при слеминге, Н;
Fd — гидродинамическое усилие лобового сопротивления, Н.
6.4.2.18 Переменное выталкивающее усилие Fp для пересекающих поверхность воды компонентов вычисляют по формуле
Fp = pgbV^-^, (121)
где SVfc - г|) — изменение в вытесненном объеме в силу относительного вертикального движения, £ - т| (см. 6.2.10.2 и рисунок 14), м3;
£ — амплитуда поверхности воды в примененной регулярной волне, как определено в 6.4.2.11, м;
т| — вертикальное движение поднимаемого объекта (см. 6.4.2.15), м;
р — плотность морской воды, обычно 1025, кг/м3;
д — ускорение свободного падения, равное 9,81, м/с2.
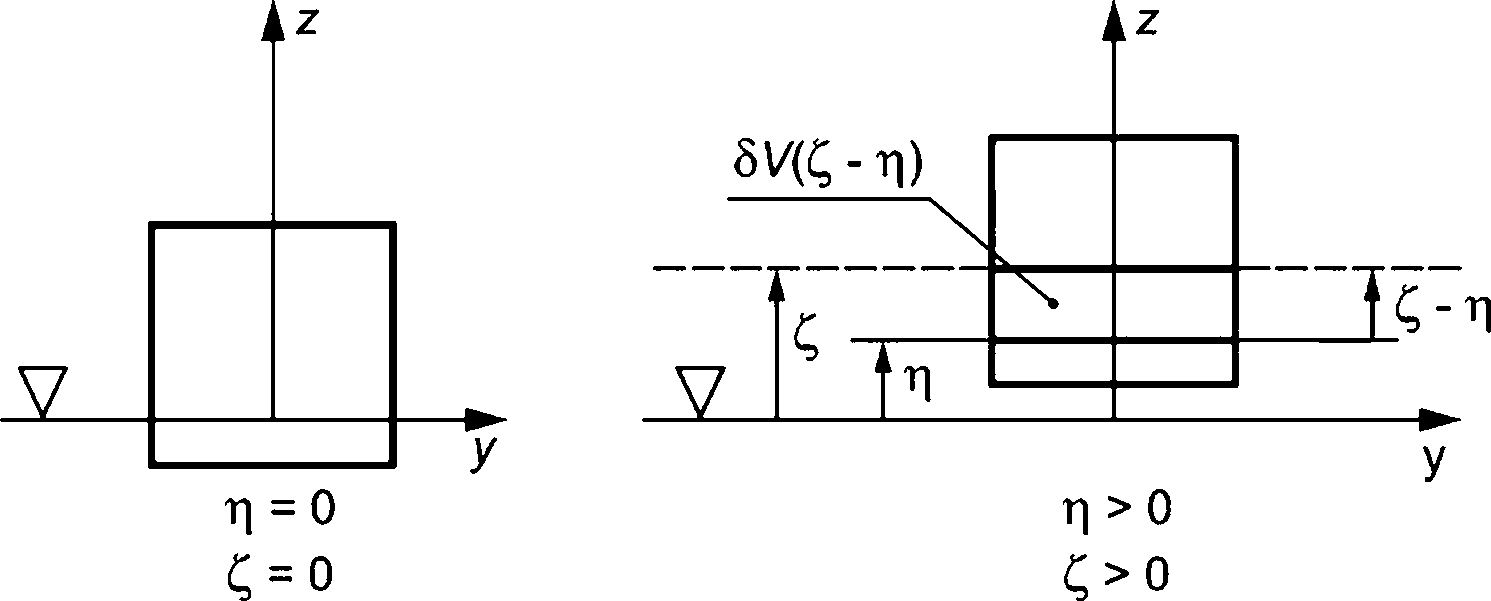
Рисунок 14 — Изменение водоизмещения 5У((^ - г|)
6.4.2.19 Массовое усилие в данном упрощенном методе регулярной расчетной волны Fm, Н, вычисляют по выражению
(122)
Гт=рУу + Дзз
где р — плотность морской воды, обычно 1025, кг/м3;
V — объем вытесненной воды компонента объекта, м3;
v — вертикальное ускорение частиц воды (см. 6.4.2.12), м/с2;
Д33 — присоединенная масса компонента объекта, кг;
i] — вертикальное ускорение поднимаемого объекта (см. 6.4.2.15), м/с2;
М — масса компонента объекта в воздухе, кг;
Массовое усилие является суммой усилия инерции (см. 6.2.5.1) и усилия внешнего возбуждающего воздействия волны (см. 6.2.7.2).
Для пересекающих поверхность воды компонентов объем вытесненной воды должен приниматься как объем на уровне спокойной воды.
6.4.2.20 Усилие удара при слеминге Fs на проходящие сквозь поверхность воды компоненты вычисляют по формуле
(123)
Гв=0,5рСзДв(1/-т|)2,
где р — плотность морской воды, кг/м3;
Cs — коэффициент при слеминге, который может быть определен теоретическими и/или экспериментальными методами. Для гладких цилиндров круглого сечения значение Cs должно быть не менее 3,0. В ином случае значение Cs должно быть не менее 5,0;
Д5 — проекция площади воздействия удара при слеминге на горизонтальной плоскости, м;
у — вертикальная скорость частиц воды в области воздействия удара при слеминге, z = 0, если область воздействия удара при слеминге находится на уровне спокойной воды (см. 6.4.2.12), м/с;
Л — вертикальная скорость поднимаемого объекта, м/с.
6.4.2.21 Лобовое сопротивление Fd вычисляют по формуле
(124)
Fd =0,5рСоДр(1/-п)р-т1|,
где CD — коэффициент лобового сопротивления компонента объекта;
Ар — проекция площади компонента объекта на горизонтальной плоскости, м2, а также иным образом, как определено в 6.4.2.20;
v — вертикальная скорость частиц воды в области воздействия удара при слеминге, м/с;
q — вертикальная скорость поднимаемого объекта, м/с.
Лобовое сопротивление Fd можно вычислить по формуле
Fd =Bl(v-Г\) + В2(у-Т|)|у-Г||, (125)
где В1 — коэффициент линейного демпфирования объекта, кг/с;
В2 — коэффициент квадратичного демпфирования объекта, кг/м;
v — вертикальная скорость частиц воды в области воздействия удара при слеминге, м/с;
q — вертикальная скорость поднимаемого объекта, м/с.
6.4.2.22 Выполняемые расчеты должны включать следующий диапазон периода колебания волны через нулевую точку для заданной высоты характерной волны Hs:
8,9^<TZ<13, <126>
где Hs — высота характерной волны, м;
Tz — период колебания волны через нулевую точку.
6.4.2.23 Если это отражено в критериях монтажа в процедурах эксплуатации, можно применить более ограниченный диапазон Tz.
6.4.2.24 Вертикальное движение оконечности крана находят в соответствии с 7.3.3.
6.4.2.25 Движения, скорости и ускорения рассчитывают для каждого этапа времени на каждом определенном основном компоненте.
6.4.2.26 Некоторые компьютерные программы расчета отклика передвижения способны определить точки вне корпуса на поверхности волны и напрямую сформировать относительное движение. В данном случае можно принять эти точки.
6.4.2.27 Переменное выталкивающее усилие, массовое усилие, усилие при слеминге и усилие лобового сопротивления рассчитывают для каждого этапа времени на каждом определенном основном компоненте.
6.4.2.28 Затем данные усилия суммируют. Статический вес применяют как минимальное и максимальное значения в соответствии с 7.2.2. Усилия отклика в стропах и крюках крана находят путем применения равновесия усилия и момента. Должен быть удовлетворен критерий провисания стропы, как описано в 7.4.3. Сооружение и подъемное оборудование должны быть проверены в соответствии с положениями, представленными в 7.4.4.
6.4.3 Расчеты по временной области
6.4.3.1 Для более точных вычислений можно использовать компьютерные программы, применяющие нелинейное моделирование временной области многокомпонентных систем.
6.4.3.2 При расчетах необходимо использовать полный 3-часовой период моделирования для каждого случая нагрузки.
6.4.3.3 В расчетах чувствительности можно выполнять несколько более коротких, например 30-минутных, моделирований.
6.4.3.4 Следует фиксировать наибольшую и наименьшую наблюдаемые нагрузки, например в стропах и канате, во время периода моделирования.
6.4.3.5 Допуская, что динамические нагрузки могут иметь распределение Рэлея, наиболее вероятную наибольшую максимальную нагрузку Ятах можно вычислить по следующему уравнению:
/?тах =arJ2lnf—У (127)
П1с1л 'Al i "7~ I
V \ z )
где <зг— стандартное отклонение динамической нагрузки, Н;
t — продолжительность работы, включая непредвиденное время, не менее 30 мин, с;
Tz — период колебания через нулевую точку для динамической нагрузки, с.
Период колебания через нулевую точку для динамической нагрузки Tz, с, вычисляют по формуле
где Мо и М2 — нулевой и второй моменты спектра нагрузки.
В большинстве динамических нелинейных случаев отклик в недостаточной степени соответствует распределению Рэлея. Следовательно, оцениваемую максимальную нагрузку должны постоянно сравнивать с наибольшей наблюдаемой в моделировании нагрузкой.
6.4.3.6 Если расчеты основаны на выбранных сериях волн короткой продолжительности, то желательно, чтобы выбор был основан на максимальном вертикальном относительном движении между оконечностями крана и поверхностью воды. Амплитуда, скорость и ускорение относительного движения должны быть решающими параметрами при выборе серий волн.
6.4.3.7 При моделировании работ по спуску необходимо поддерживать объект зафиксированным в выбранных положениях в течение не менее 30 мин. В случае моделирования непрерывного опускания объекта для получения должной статистической достоверности требуется большое количество реализаций.
6.4.3.8 Значения демпфирования и присоединенной массы следует тщательно выбирать при расчетах, гарантируя также правильное моделирование значений момента инерции.
6.4.4 Расчеты вычислительной гидродинамики
6.4.4.1 На подводных подъемных работах можно выполнять расчеты волновой нагрузки на основании CFD. Движение жидкости в таком случае описывают с помощью уравнений Навье—Стокса.
6.4.4.2 Примерами численных методов, применимых для моделирования взаимодействия волна—сооружение, включая вход в воду (удар при слеминге) и выход из воды, являются:
- метод объема жидкости (VOF);
- метод функции уровня (LS);
- метод ограниченного интерполяционного профиля (CIP);
- метод сглаженных частиц (SPH).
6.4.4.3 Первые три метода (VOF, LS, CIP) являются методами сеток, в то время как SPH — метод частиц, при котором сетка не требуется.
6.4.4.4 Примененные граничные условия и размер области вычислений должны гарантировать, что отражения от границ области не будут влиять на гидродинамические усилия на объект.
6.4.4.5 Для установления достаточности примененного количества ячеек или частиц (для методов частиц) в модели должны быть проведены проверки на сходимость.
6.4.4.6 Растягивание ячеек может повлиять на набегающую волну. Вследствие этого данный фактор необходимо обязательно учитывать.
6.4.4.7 В некоторых случаях расстояние от границы набегающего потока до конструкции может повлиять на действие волны на сооружение.
6.4.4.8 Для тех моделирований, где образованные волны начинаются от состояния покоя, с целью предотвращения переходных эффектов должно быть образовано достаточное число последующих волн.
6.4.4.9 Аппроксимация фактической геометрии конструкции из-за ограничения в имеющихся вычислительных мощностях должна быть выполнена с применением правильных общих площадей. Отверстия и перфорации могут быть суммированы в меньшее число и большие отверстия.
Аппроксимация геометрии может дать недостаточное представление местных усилий и давлений. Проверки на сходимость необходимо проводить на постоянной основе.
6.4.4.10 Дополнительную плавучесть из-за аппроксимации модели следует учитывать при оценке вычисленных общих вертикальных усилий.
6.4.4.11 Для решения задач удара волны необходимо двухфазное моделирование, так как при однофазном моделировании вычисленные нагрузки от удара могут быть завышенными.
6.4.4.12 Рассчитанные экспериментальные усилия, давления и скорости необходимо проверять и сравнивать с приближенными ручными вычислениями.
6.4.4.13 При наличии результатов испытания на модели результаты численного моделирования необходимо сравнить с экспериментальными и подтвердить в ходе испытаний на модели.
6.4.4.14 На рисунке 15 показан пример прогноза коэффициентов присоединенной массы и демпфирования для модели геометрий опорного башмака с тремя различными коэффициентами перфорации (0 %, 15 % и 25 %). Расчеты проведены с использованием двух различных моделей CFD и подтверждены экспериментальными результатами (см. [1]).

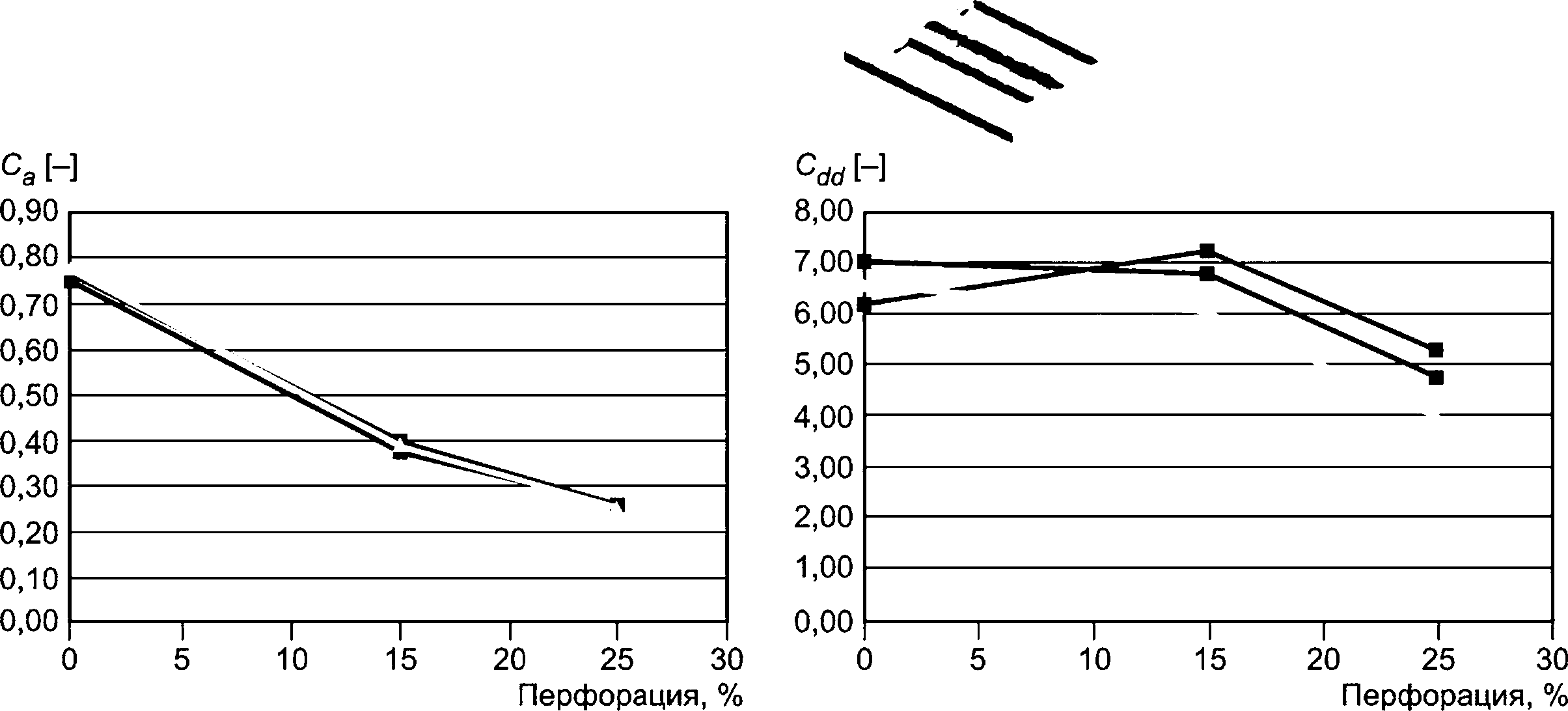
Рисунок 15 — Пример использования CFD для прогноза коэффициентов присоединенной массы и лобового сопротивления для модели геометрий опорного башмака
6.5 Работы в буровой шахте
6.5.1 Общие положенияДля небольших подводных модулей и инструментов часто предпочтителен монтаж через буровую шахту судна. Это может уменьшить динамические усилия, увеличить предельное состояние поверхности моря и сократить стоимость монтажных и геолого-технических работ. Типовой областью применения являются работы по техническому обслуживанию и ремонту установок подводной добычи.
6.5.2 Упрощенный расчет подъема через буровую шахту
Описанный в данном пункте упрощенный расчет основан на следующих ограничивающих допущениях:
- размеры буровой шахты являются малыми по сравнению с шириной судна;
- рассматривают только движение воды и объекта в вертикальном направлении;
- блокирующее воздействие поднимаемого объекта на воду в буровой шахте является умеренным;
- механические визиры предотвращают удар о стенки буровой шахты. Учитывают только вертикальные усилия, параллельные оси буровой шахты.
6.5.3 Уравнение движения
6.5.3.1 Рассматривают подвешенный внутри буровой шахты объемный объект (см. рисунок 16). Буровая шахта может иметь переменную площадь поперечного сечения A(z). Осадка судна составляет D. Вертикальное движение поднимаемого тела может отличаться от вертикального движения судна из-за работы лебедки и/или динамичности в подъемной системе.
6.5.3.2 Уравнение движения для водяной пробки можно записать следующим образом:
( M + A33)i;+cs|^-;s|(c-;s) + c()|;-^|(;-^) + ^ = F(t), (129)
где М — масса водяной пробки, кг;
Д33 — присоединенная масса водяной пробки, кг;
Cs — коэффициент демпфирования для относительного движения между водяной пробкой и судном, кг/м;
Cs — движение вертикальной качки судна, м;
Сь — коэффициент полноты водоизмещения, кг/м;
— движение тела в буровой шахте, м;
К = рдА — жесткость зеркала воды, кг/с2;
С, — движение водяной пробки, м;
F(f) — усилие внешнего возбуждающего воздействия волны, действующее на водяную пробку, Н.
Движение вертикальной качки судна £s, м, связано с высотой поверхности моря с помощью функции передачи Gs (амплитуда и фаза) и рассчитано по формуле
^S=GS^ (13°)
где Gs — функция передачи;
— высота поверхности моря за пределами буровой шахты, м.
Действующее на водяную пробку усилие гидродинамического давления F(f) также может быть связано с высотой поверхности моря с помощью функции передачи Gw (амплитуда и фаза) и рассчитано по формуле
Ftf)=Gw^w, (131)
где Gw — функция передачи;
'Qw — высота поверхности моря за пределами буровой шахты, м.
6.5.3.3 Gw можно найти путем интегрирования давления р, полученного с помощью программы дифракции источников и стоков над поперечным сечением буровой шахты при z = -D. Gs и Gw являются функциями частоты волны и направления волны.
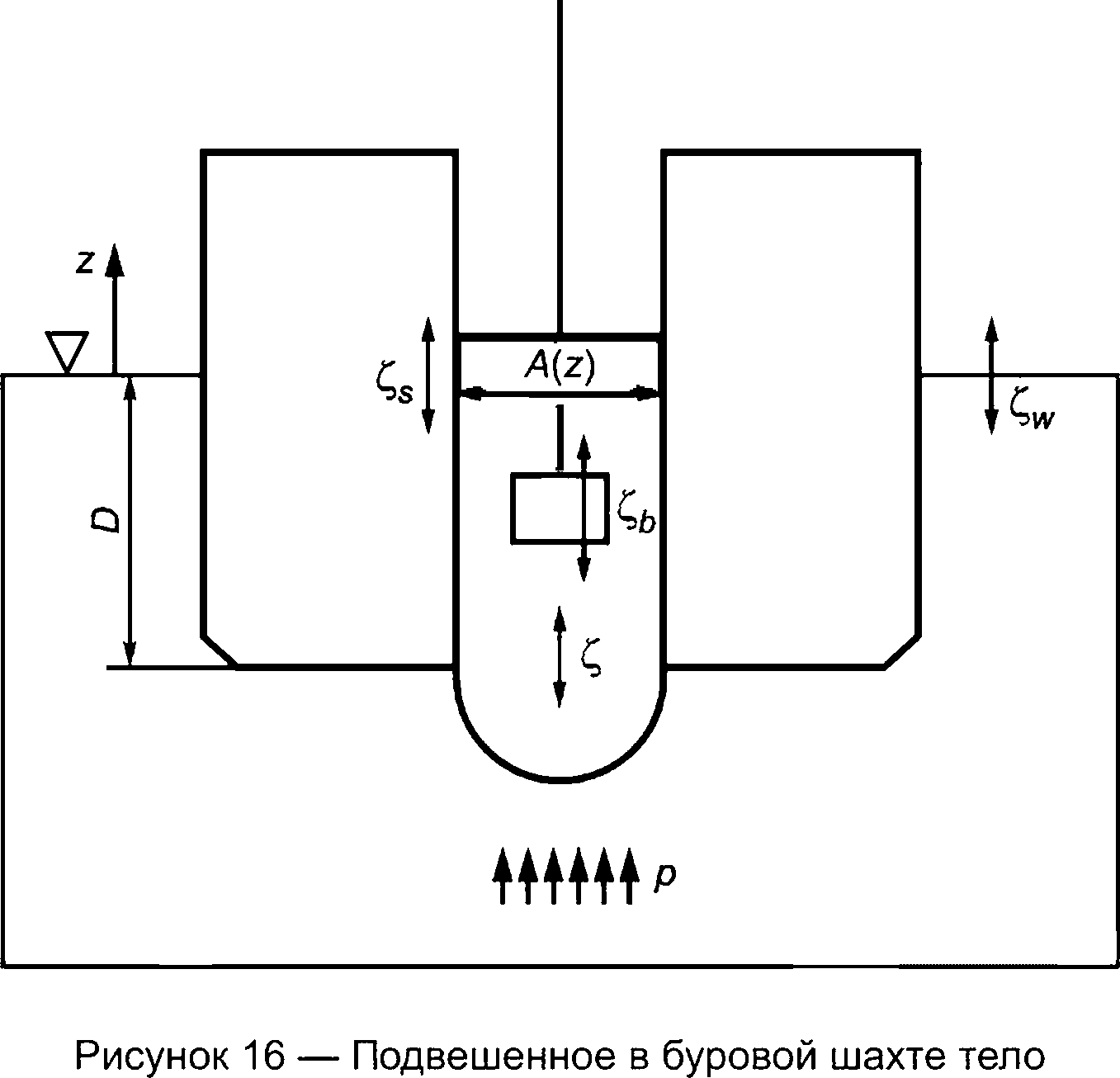
6.5.4 Период резонанса
6.5.4.1 Заданные конструкцией буровой шахты собственный период вертикальных движений водяной пробки и условия демпфирования существенны для динамических усилий, влияющих на объект внутри буровой шахты.
6.5.4.2 В целом площадь поперечного сечения буровой шахты А является функцией от вертикального положения z. Допуская отсутствие движения стенок буровой шахты, в соответствии с требованием непрерывности определяют
Д(г)Ч(г) = Д(0)Ч(0),
(132)
где z — значение вертикального положения шахты, м.
6.5.4.3 В соответствии с требованием сохранения энергии определяют
—(£к+Еп) = 0, dr к р)
(133)
где Ек— кинетическая энергия жидкости, вычисляемая по формуле
я и л
f A(z);2(z)dz+433^2(-D) =
-° (134)
= 1рД(0);2(0)П 4%-^ —^4 ,
2 V v 7|-оД(2) A(~D) PA(~D)
Ер — потенциальная энергия жидкости, вычисляемая по формуле
Ер=^Р<?Л(0К2(0).
(135)
6.5.4.4 А33 является присоединенной массой для вертикального движения водяной пробки, которая может быть вычислена по формуле
(136)
Дзз=р/<Д(-О)7А(-О),
где к— коэффициент коррекции шахты судна.
6.5.4.5 Параметр к определен как лежащий в пределах между 0,45 и 0,47 для прямоугольных буровых шахт со значениями соотношения сторон в пределах между 0,4 и 1,0. Таким образом, для всех реальных прямоугольных буровых шахт можно использовать к, равный 0,46. Для буровой шахты круглого сечения к равен 0,48.
6.5.4.6 Период резонанса находят из выражения сохранения энергии:
(137)
или
—y~dz+
(138)
6.5.4.7 Энергетически эквивалентную массу Meq, кг (масса плюс присоединенная масса), движущуюся с поверхностной скоростью, вычисляют по формуле где Ек — кинетическая энергия жидкости;
|С2(0)
(139)
к — коэффициент коррекции шахты судна.
6.5.4.8 Если буровая шахта имеет постоянную площадь поперечного сечения A(z) = А, то приведенные выше выражения упрощаются до следующего:
T0=-^D+kjA , (140)
49
Meq=pA(D+k4A), (141)
1,421
6.5.5 Демпфирование движения воды в буровой шахте
6.5.5.1 Амплитуда движения воды в буровой шахте, в частности для близкого к периоду резонанса TQ внешнего возбуждающего воздействия волны, зависит от уровня демпфирования. Кроме невязкостного демпфирования из-за волнообразования демпфирование обеспечено демпфированием вязкостного лобового сопротивления, вызванным такими структурами, как направляющие конструкции, арматура, коффердам или обшивка днища.
6.5.5.2 Движение воды внутри буровой шахты исследовали в модельных испытаниях нескольких морских судов для выполнения водолазных работ и рабочих судов с различными успокоительными устройствами. В ходе этих испытаний измерено относительное движение между водяной пробкой и судном на центральной оси буровой шахты. Амплитуду RAO для относительного движения определяют следующим образом:
RAO =
(143)
где £ — движение водяной пробки, м;
— движение вертикальной качки судна, м;
— высота поверхности моря за пределами буровой шахты, м.
6.5.5.3 На рисунке 17 показана измеренная амплитуда RAO для различных конструкций, вызывающих демпфирование движения воды в буровой шахте.
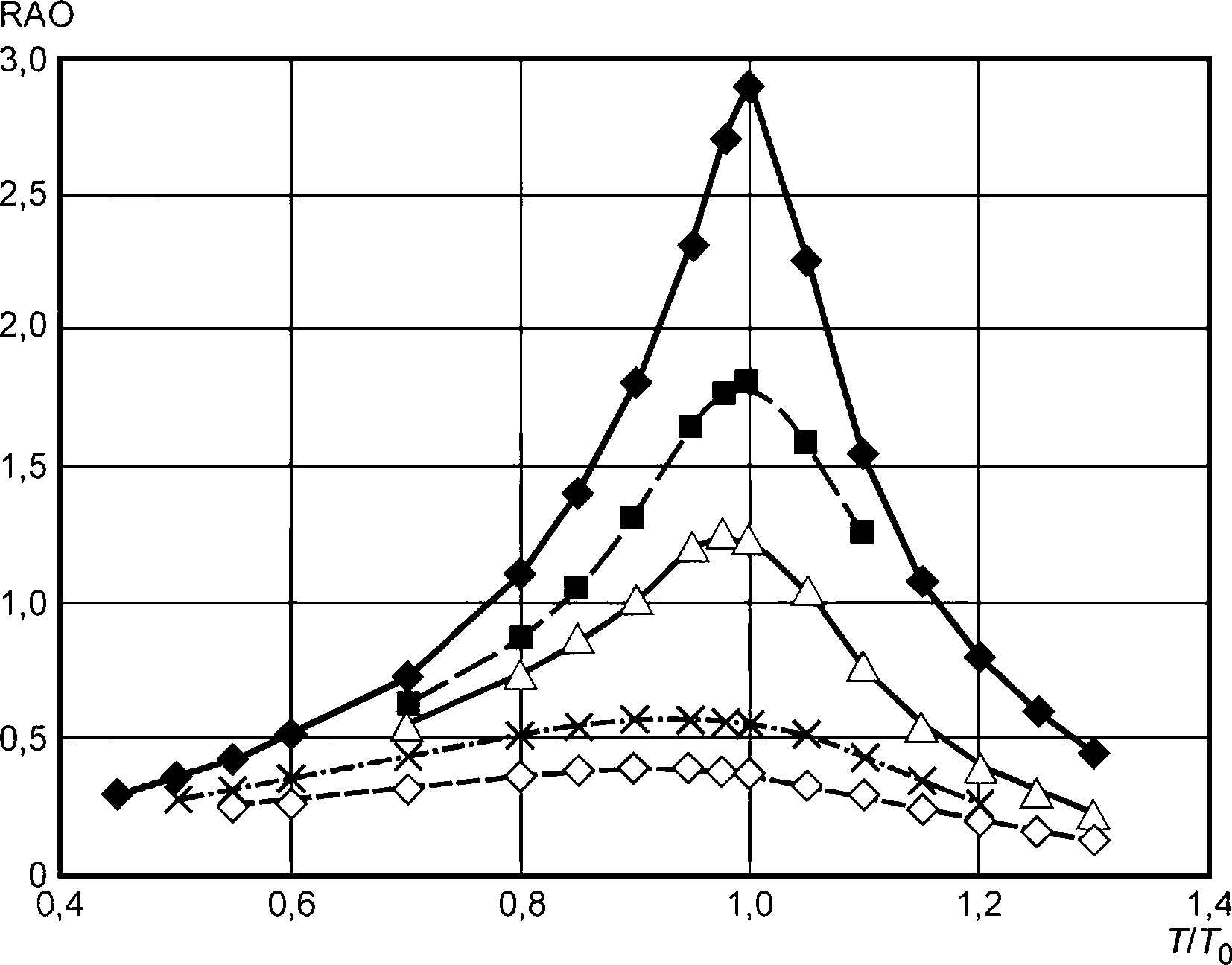
- открытая буровая шахта;--■---приварные пластины;
- направляющая конструкция; —X----коффердам;
——Q—--днищевое закрытие
Рисунок 17 — Измеренная относительная высота воды в буровой шахте на единицу амплитуды набегающей волны
6.5.5.4 Водяная пробка возбуждается как набегающими волнами, так и вертикальным движением судна, вследствие этого определенная сложность возникает с выведением данных демпфирования непосредственно из таких кривых. С целью оценки демпфирования, заданного разными схемами демпфирования, использован аппроксимационный подход. Приближенное линеаризированное комплексное уравнение движения водяной пробки в свободной буровой шахте (без поднимаемого объекта) представлено следующим образом:
м ;+ cs1 (; - ;s) + к; = f (t) => -«2м<; + /<oCs1 (; - Gsi^ )+кс = gwi;w,
(144)
гДе M = pA\D + kslA] — общая масса водяной пробки, включая присоединенную массу, кг;
Cs1 = 2г\у/км — линеаризированное демпфирование, кг/с;
Л — коэффициент демпфирования (относительно критического демпфирования);
К = рдА — жесткость зеркала воды, кг/с2;
Gs — функция передачи для вертикального движения буровой шахты, м/м;
— функция передачи от высоты волны к усилию внешнего возбуждающего воздействия волны, Н/м.
6.5.5.5 Отношение между движением водяной пробки и подъемом поверхности воды за пределами буровой шахты составляет:
Gw 'у ®
£ _ /mCs1Gs + Gw
® Л4 + /соC$1 + К
—— + 2/Gsr|--
Р9Д“0
(145)
г х2
. (О ] „.со
1- — +2/Г] —
I ю0 ) %
6.5.5.6 Для получения отношения между функциями передачи Gw и Gs сделаны некоторые упрощающие допущения:
- размеры буровой шахты являются малыми по сравнению с шириной судна;
- усилия внешнего возбуждающего воздействия набегающих волн F1 и перемещения судна Р2 может быть оценена так же, как и для судна без буровой шахты;
- можно использовать правомерные для длинных волн выражения давления жидкости;
- предполагается значительная глубина.
В таком случае можно применять следующие приближенные выражения для усилия внешнего возбуждающего воздействия волны:
F(f) = F, (f) + F2(t) = pFK • A+Дзз + kpjAAt>s =
(146)
= pA^w [g&~kD -a?k JAG$ j,
где pFK — динамическое давление в свободном (Фруд—Крылов) потоке, Н/м2;
F^f) — усилие внешнего возбуждающего воздействия набегающих волн;
F2(t) — усилие от перемещения судна;
Д33 — присоединенная масса водяной пробки, как задано в 6.5.4.4, кг. Таким образом
G# =^^ = pA(ge~kD-ш2 k4AGs\, (147)
bw
где k = ы21д, коэффициент коррекции шахты судна;
Qw — высота поверхности моря за пределами буровой шахты, м;
Gw — функция передачи от высоты волны к усилию внешнего возбуждающего воздействия волны,
Н/м.
6.5.5.7 Отношение амплитуды относительного подъема водяной пробки к подъему набегающей волны определено выражением
RAO =
(148)
где RAO — оператор амплитуды отклика;
— движение водяной пробки, м;
— движение вертикальной качки судна, м;
Gs — функция передачи для вертикального движения буровой шахты, м/м;
Cw — высота поверхности моря за пределами буровой шахты, м.
6.5.5.8 На рисунке 18 представлен пример относительного уровня воды внутри буровой шахты. Использованы функции передачи движения типичного судна длиной 80 м для выполнения водолазных работ. В приведенные выше выражения вставлена Gs для вертикального движения буровой шахты, а кривые RAO вычислены для переменного относительного демпфирования г|.
6.5.5.9 Результаты являются неопределенными для наиболее коротких периодов волны (Т/То < 0,8), где формы кривых отличаются от результатов испытания на модели.
6.5.5.10 Найденные при резонансе максимальные значения RAO показаны на рисунках 18 и 19 как функция относительного демпфирования для случаев без обшивки днища.
Относительный уровень воды в буровой шахте
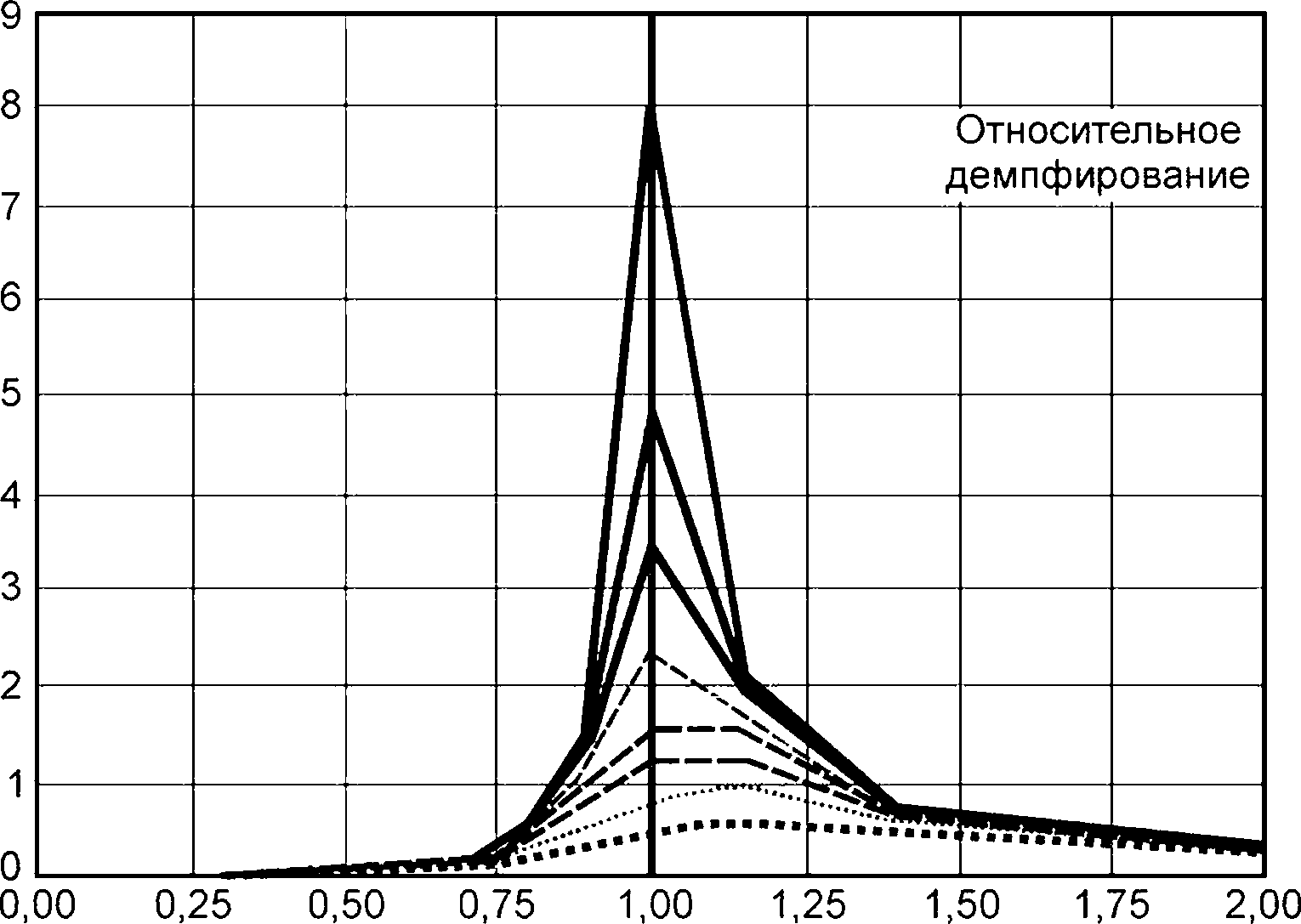
--0,03;--0,05;--0,07;-----0,10; Т1Т0
----0,15;----0,20;............-0,30;......-0,50
--0,03;--0,05;--0,07;-----0,10; Т1Т0
----0,15;----0,20;............-0,30;......-0,50
Рисунок 18 — Расчетный относительный подъем воды без обшивки днища (р = 1)
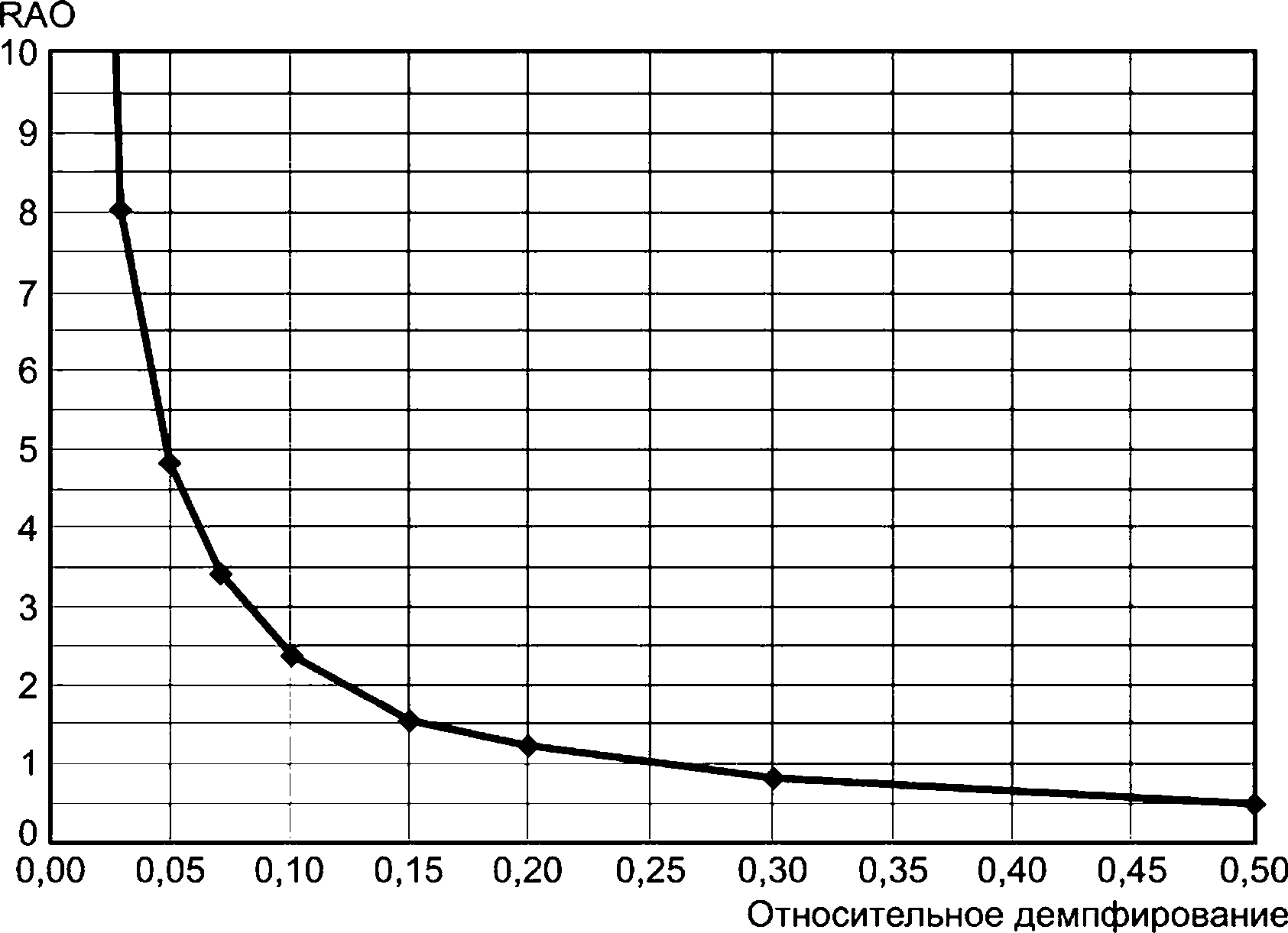
Рисунок 19 — Расчетный относительный подъем воды при резонансе
6.5.5.11 Приближенные значения относительного демпфирования для случаев без обшивки днища получены путем сравнения максимальных значений RAO на рисунках 18 и 19. Анализируют следующие приближенные значения относительного демпфирования:
- неприкрытая буровая шахта: ц — от 8 % до 9 %;
- арматура небольшого размера: г| — от 13 % до 14 %;
- направляющая конструкция: q — от 18 % до 19 %;
- направляющая конструкция + 50 % обшивка днища: г| — от 40 % до 45 %;
- коффердам: г| « 45 %.
6.5.5.12 Анализ квадратичного коэффициента демпфирования Cs можно провести на основании относительного демпфирования и движения. Допускается использование следующего приближения:
Cs=^0.2nVKM, <149>
о
где — амплитуда относительного движения.
6.5.6 Коэффициенты усилия в буровой шахте
6.5.6.1 Ограниченный поток вокруг объекта внутри буровой шахты ведет к увеличенным гидродинамическим усилиям. Подлежащие использованию при вычислении увеличенные коэффициент лобового сопротивления CD и коэффициент присоединенной массы СА вычисляют по формулам:
С Г) 1 — 0,5Ак /А Л/Л^-ПО /И СП\
—=!—2—- при AJA < 0,8; (150)
cdo (1-Аь/А)2
9
.£a_ = 1 + 19(V|4 при AJA <0,8, (151)
СД0 v А )
где CD0 — коэффициент лобового сопротивления для неограниченного потока;
Сдо — коэффициент присоединенной массы для неограниченного потока;
Аь — сплошная площадь проекции объекта, м2;
А — площадь поперечного сечения буровой шахты (на вертикальном уровне объекта), м2. При Аь/А > 0,8 следует применять более подробный метод вычисления.
6.5.6.2 Динамические характеристики поднимаемого объекта при выходе из нижнего конца буровой шахты при опускании или перед входом при подъеме должны быть рассчитаны в нерегулярных волнах с помощью метода временной области.
6.5.6.3 Для объекта вблизи нижнего конца буровой шахты консервативным подходом будет расчет динамики с использованием гидродинамических усилий на основании кинематики волны невозмущенных волн и гидродинамических коэффициентов для неограниченного состояния потока.
6.5.6.4 Реальные ударные усилия между поднимаемым телом и стенками буровой шахты требуют точных данных жесткости для системы механического визира.
6.5.7 Подробный метод вычисления
Более подробный метод вычисления необходимо использовать, либо если сплошная площадь проекции покрывает более 80 % площади сечения буровой шахты, либо если вертикальное движение поднимаемого объекта отличается от вертикального движения судна у буровой шахты, то есть:
- при нахождении поднимаемого объекта внутри буровой шахты применяется система управления движением или
- объект подвешен на мягкой пружине, такой как пневматический цилиндр.
6.5.7.1 Необходимо выполнить следующие этапы вычисления:
а) следует рассчитать функции передачи давления волны первого порядка у устья буровой шахты, используя программу теории дифракции с панельной моделью судна с буровой шахтой. Особое внимание необходимо уделить получению численной устойчивости для режима движения буровой шахты;
б) необходимо выполнить нелинейный расчет по временной области системы с моделью, как описано ниже. Расчет должен быть выполнен для соответствующих нерегулярных состояний волнения моря. Следует рассчитать движение поднимаемого объекта и усилия в подъемном оборудовании.
6.5.7.2 Предлагается следующая модель расчета:
а) смоделировать поднимаемый объект с массой, гидродинамической массой и демпфированием;
б) смоделировать подъемную систему с компенсатором движения или, если применимо, с мягкой пружиной;
в) смоделировать водную пробку внутри буровой шахты как движущееся только в вертикальном направлении тело жидкости с массой, равной энергетически эквивалентной массе;
г) пласт воды нужно возбуждать давлением воды, умноженным на площадь сечения отверстия буровой шахты;
д) смоделировать взаимодействие между водной пробкой и стенками буровой шахты как связь квадратичного демпфирования в вертикальном направлении;
е) силу взаимодействия между водной пробкой и поднимаемым объектом F следует вычислять по формуле
F = ^CDAbvr\vr\ + (<PV + A33Kw~A33^b ’ <152)
где Аь — сплошная площадь проекции поднимаемого объекта, м2;
vr— относительная скорость между поднимаемым объектом и водной пробкой, м/с;
V — объем поднимаемого тела, м3;
Д33 — присоединенная масса поднимаемого тела, кг;
— вертикальное ускорение водной пробки, м/с2;
с;/, — вертикальное ускорение поднимаемого объекта, м/с2.
6.5.7.3 Использование CFD не следует применять для расчета динамики буровой шахты. Даже несмотря на то, что с помощью CFD может рассчитывать динамическое взаимодействие жидкости между поднимаемым объектом и водной пробкой внутри буровой шахты, сложно связать динамические характеристики судна на волнах и отклик подъемной системы. Следовательно, прогнозы усилия могут быть неопределенными.
6.6 Стабильность спуско-подъемных операций
6.6.1 Общая частьСитуации, в которых стабильность во время спуско-подъемных операций особенно значима, включают в себя:
- наклон частично наполненных воздухом объектов при опускании;
- воздействия свободной поверхности воды внутри объекта.
6.6.2 Частично наполненные воздухом объекты
6.6.2.1 Данный случай также относится к подъему тех объектов, в которых плавучесть распределена от массы иным образом. На рисунке 20 показано погруженное тело, в котором центр тяжести CG и центр плавучести Св не совпадают.
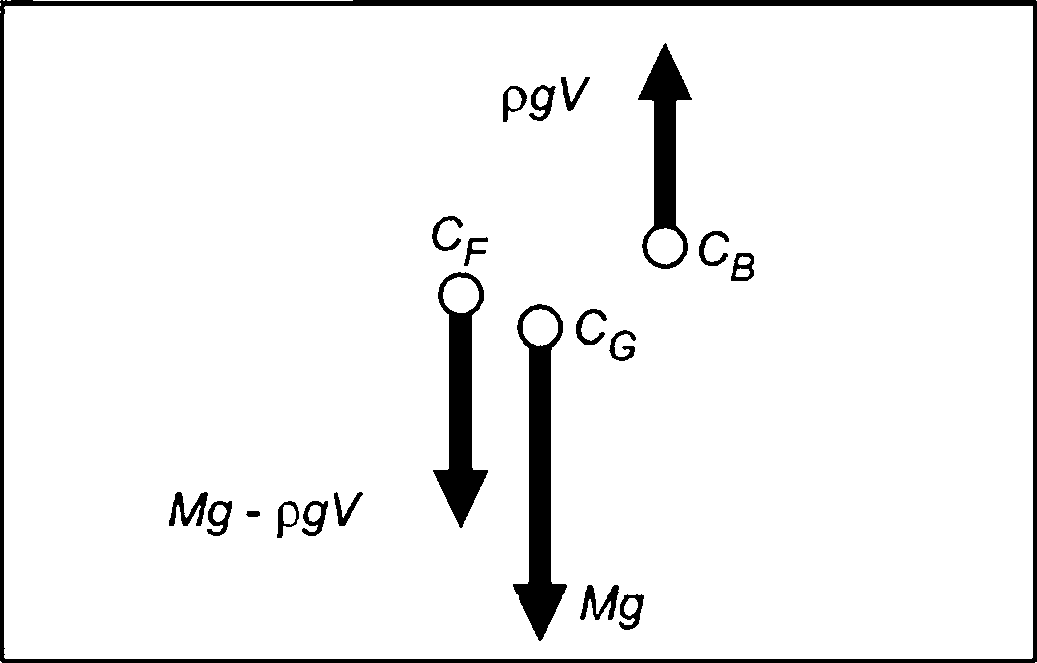
Рисунок 20 — Определение CG, Св и CF
6.6.2.2 Центр усилия CF находится на основе равновесия момента и определяется следующим образом:
q _ MgCG -pgVCB _ Cq - аСв (153)
F Mg-pgV 1-а
где М — масса объекта, кг;
д — ускорение свободного падения 9,81, м/с2;
V — объем поднимаемого тела, м3;
Gg — центр тяжести;
Ge — центр плавучести;
„ P9V
а = -г/— — ускорение частиц жидкости.
6.6.2.3 Если на объект не действуют другие усилия, он будет вращаться до тех пор, пока Св не окажется вертикально над CG. Если объект подвешен, то для предотвращения наклона подъемный трос должен быть закреплен вертикально над CF.
6.6.2.4 Регулировки требуемой для горизонтальной посадки на морское дно длины стропы могут таким образом дать угол наклона при нахождении объекта в воздухе (в силу горизонтального расстояния CF—CG).
6.6.3 Влияние свободной поверхности воды внутри объекта
В случае свободной поверхности воды внутри тела вертикальное расстояние GB между CG и Св должно быть достаточно большим, чтобы дать выравнивающий момент, превышающий обеспечиваемый свободной поверхностью воды переворачивающий момент (см. рисунок 21).
MgGB>pgl, (154)
где М — масса объекта, кг;
/ — момент инерции площади свободной поверхности, м4.
Момент инерции площади изменяется в соответствии с заполнением, геометрией и углом наклона.
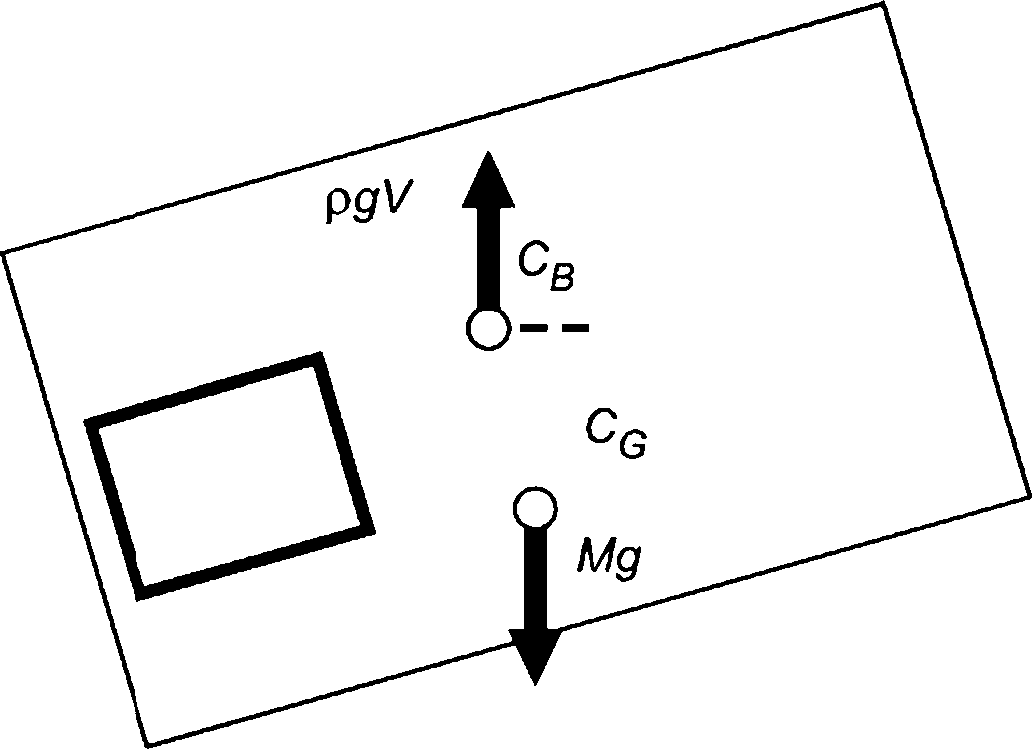
Рисунок 21 — Спуско-подъемные операции со свободной поверхностью внутри объекта
7 Спуско-подъемные операции в волновой зоне.
Упрощенный метод7.1 Общая часть
7.1.1 Цель7.1.1.1 В данном разделе представлен упрощенный метод для оценки характеристических гидродинамических усилий на объекты, опускаемые сквозь поверхность воды и далее на дно моря.
7.1.1.2 Цель упрощенного метода — доступный консервативный анализ действующих на объект усилий.
7.1.2 Применение
7.1.2.1 Если не указано иное, знак значений передвижения, скорости, ускорения и усилия в упрощенном методе должен быть положительным.
7.1.2.2 В целом упрощенный метод описывает усилия, действующие при опускании с воздуха объекта вниз через волновую зону. Данный метод, однако, также применим и к случаю извлечения из воды.
7.1.3 Главные допущения
7.1.3.1 Упрощенный метод основан на следующих главных допущениях:
- горизонтальная протяженность поднимаемого объекта (в направлении распространения волны) относительно мала по сравнению с длиной волны;
- вертикальное движение объекта следует за движением оконечности крана;
- расчетный случай определяется относительным вертикальным движением между объектом и водой, другими типами движений можно пренебречь.
7.1.3.2 Если основные допущения не выполнены, необходимо проводить более точные расчеты (см. раздел 6).
7.1.3.3 В упрощенный метод не включено увеличенное движение вертикальной качки поднимаемого объекта вследствие влияний резонанса (см. 7.3.3.3).
7.2 Статический вес
7.2.1 Общие положения7.2.1.1 Статический вес погруженного объекта FCT определяют по формуле
FCJ = Mg-pVg, (155)
где М — масса объекта в воздухе, кг;
д — ускорение свободного падения 9,81, м/с2;
р — плотность морской воды, обычно 1025, кг/м3;
V — объем вытесненной воды во время различных этапов при прохождении сквозь поверхность воды, м3.
7.2.1.2 Статический вес вычисляют относительно поверхности неподвижной воды.
7.2.1.3 Коэффициент неточности веса следует применять к массе объекта в воздухе.
7.2.2 Минимальный и максимальный статический вес
7.2.2.1 Заполнение водой подводных конструкций после погружения может занять определенное время. В таких случаях статический вес следует рассчитывать, применяя как его минимальное, так и максимальное значения.
7.2.2.2 Минимальный FCTmjn и максимальный FCTmax статический вес для заполняемых водой после погружения подводных конструкций вычисляют по формулам:
^ст min “ Mmin^ - Р^/> 056)
^"ст max - ^max^ — Р057)
где /Wmin — минимальная масса, равная массе объекта в воздухе (т. е. сооружение погружено, но заполнение водой еще не началось), кг;
Мтах — максимальная масса, равная массе объекта в воздухе, включая полный вес воды, заполняющей конструкцию (т. е. сооружение полностью заполнено водой после погружения), кг.
Объем вытесненной воды V одинаков для обоих случаев.
7.2.2.3 Коэффициент неточности веса следует применять как снижение минимальной массы и как увеличение максимальной массы.
7.2.2.4 Предварительно залитая до подъема вода должна быть учтена как часть массы объекта в воздухе.
7.2.2.5 Оставшаяся во время извлечения внутри поднимаемого объекта вода должна быть учтена как часть массы объекта в воздухе.
7.2.2.6 В случае значимости возможный захваченный воздух следует оценивать и включать в расчеты. Необходимо исследовать и потерю стабильности, и риск сплющивания, и риск провисания строп.
7.3 Гидродинамические усилия
7.3.1 Общие положенияВ данном подразделе представлены упрощенный способ оценки нагрузок от воздействия окружающей среды и результаты действия нагрузок.
7.3.2 Периоды волны
7.3.2.1 Влияние периода волны может быть принято во внимание. В таком случае выполняемые расчеты должны включать следующий диапазон периода колебания через нулевую точку для заданной высоты характерной волны /-/s:
on /ЙГ -г ИО
(158)
8,9• — <Т7 <13, v в
где Hs — высота характерной волны расчетного состояния моря, м;
д — ускорение свободного падения 9,81, м/с2;
Tz — периоды колебания волны через нулевую точку, с.
В большинстве случаев достаточными являются значения Tz с шагами 1,0 с.
Здесь используется нижняя граница в Нтах= 1,8 • Hs = Х/7 с длиной волны X = дТ 2/2л.
Отношение между периодом колебания волны через нулевую точку Tz и периодом пика волны Тр можно учитывать, применяя спектр JONSWAP. Для спектра ПМ отношение можно определить как 7-p=1,4Tz.
7.3.2.2 Примененные Tz диапазоны или признанные допустимыми отклоняющиеся от значений в 7.3.2.1 Tz диапазоны должны быть показаны в погодных критериях в инструкции по эксплуатации.
7.3.2.3 Как вариант, можно применить независимые от периода волны уравнения кинематики волны. В таком случае инструкции по эксплуатации должны показывать, что расчеты правомерны только для тех волн, продолжительность периода которых больше, чем следующий допустимый предел, то есть:
Т2>10,6.Д (159)
где Tz — период колебания волны через нулевую точку;
Hs — высота характерной волны, м.
Периоды колебания волны через нулевую точку менее указанного выше допустимого предела крайне редкие, поэтому в большинстве случаев данное эксплуатационное ограничение не подразумевает какого-либо практического снижения эксплуатационных качеств.
В данном случае использована нижняя граница Hmax = 1,8/7S = Х/10 с длиной волны X = д-Тг2/2л.
7.3.3 Движения оконечности крана
7.3.3.1 Для того чтобы установить относительное движение между волнами и поднимаемой конструкцией, необходимо найти движение оконечности крана судна.
7.3.3.2 Упрощенный метод предполагает, что вертикальное движение конструкции равно вертикальному движению оконечности крана. В случае присутствия усиления из-за вертикального резонанса должны быть выполнены более точные расчеты.
7.3.3.3 Резонансное усиление может присутствовать, если период движений оконечности крана или период волны близки к периоду резонанса То подъемной системы, вычисляемому по формуле
IM + А33 + 6mL (160)
0 V к
где М — масса объекта в воздухе, кг;
А33 — присоединенная масса при вертикальной качке объекта, кг;
О — поправочный коэффициент с учетом влияния массы подъемного каната и возможных гибких строп (например, ведущего механизма крана) (см. 5.3.5.2);
m — масса подъемного каната на единицу длины, кг/м;
L — длина подъемного каната, м;
К — жесткость грузоподъемной системы, Н/м.
В большинстве случаев То меньше соответствующих периодов волны. Вызванным волной усилением резонанса, расположенного в волновой зоне объекта, в таких случаях можно пренебречь, если пиковый период волны Тр значительно больше периода резонанса подъемной системы, как правило: тр> 1,3-То.
Усилением резонанса из-за движения оконечности крана можно пренебречь, если пиковый период спектра отклика для вертикального движения оконечности крана Тр _ct больше периода резонанса подъемной системы:
Tp-ct^J- То, (161)
где Tp_ct — пиковый период спектра отклика для вертикального движения оконечности крана (рассчитывают для диапазона Tz, как описано в 7.3.2.1);
TQ — период резонанса.
Период резонанса для подъемной системы 70 увеличивается вместе с длиной подъемного троса. Следовательно, усиление резонанса из-за движения оконечности крана может возникнуть при опускании объектов вниз на очень большую глубину, и на это следует обратить особое внимание (см. 7.7.7 и раздел 8).
7.3.3.4 Как правило, активные или пассивные системы компенсации вертикальной качки не следует учитывать в упрощенном методе при расчете гидродинамических нагрузок. Более точные расчеты относительно временной области приведены в разделе 6.
Воздействие пассивных систем компенсации вертикальной качки можно реализовать как эффект мягких пружин в жесткости подъемной системы при выполнении расчетов нагрузок рывка и при проверке риска усиления резонанса.
7.3.3.5 Характеристические вертикальные движения оконечности крана на установочном судне должны быть рассчитаны для проектных условий окружающей среды либо путем уточненного расчета, либо с помощью приемлемо документированных упрощенных расчетов.
7.3.3.6 Для подводных подъемных работ необходимо рассчитывать отклики судна для всех направлений волнения.
7.3.3.7 Для подводных подъемных работ, которые могут проводить независимо от курсов судна, отклик судна следует рассчитывать для направлений волнения не менее ± 15° в стороны от установленного в инструкции курса судна.
7.3.3.8 В расчете можно применять волны с длинным гребнем.
В некоторых случаях с целью нахождения наиболее критичного состояния может быть удобно использовать волны с коротким гребнем. Вертикальное движение оконечности крана может быть, например, определено движением бортовой качки во встречном волнении ± 15°. Тогда движение бортовой качки в волнах с коротким гребнем может быть большим, чем движение в волнах с длинным гребнем. Вследствие этого в таких случаях требуется исследовать влияние волн с коротким гребнем.
Если для упрощения применяют волны с длинным гребнем, то для учета дополнительного влияния волн с коротким гребнем необходимо использовать курсовой угол ± 20°. Курсовой угол ± 15° в комбинации с волнами с длинным гребнем следует применять только в том случае, если вертикальное движение оконечности крана не определено движением бортовой качки или если на судне не могут документально подтвердить способность судна удерживаться в пределах ± 10° в расчетном состоянии волнения.
7.3.3.9 Для нахождения вертикального движения оконечности крана вычисленные амплитуды RAO вертикальной качки, бортовой и килевой качки нужно объединить с положением оконечности крана в общей координатной системе судна.
7.3.3.10 Использованные значения для скорости и ускорения оконечности крана должны представлять наиболее вероятные наибольшие характеристические амплитудные отклики.
7.3.3.11 Если ожидается, что опускание через волновую зону (включая непредвиденное время) будет выполнено в пределах 30 мин, то наиболее вероятные наибольшие характеристические отклики могут быть учтены как превышающие значимые отклики в 1,8 раза.
7.3.3.12 Выполненные расчеты отклика передвижения должны включать диапазон периода колебания волны через нулевую точку, как описано в 7.3.2.
7.3.4 Кинематика волны
7.3.4.1 В данном пункте рассмотрены случаи, когда опускание через волновую зону (включая непредвиденное время) выполнено в пределах 30 мин.
7.3.4.2 Если ожидается, что продолжительность операции подъема превысит 30 мин, высота характерной волны Hs в приведенных ниже уравнениях для амплитуды волны, скорости частиц волны и ускорений частиц волны должна быть умножена на коэффициент 1,10.
7.3.4.3 Характеристическая амплитуда волны С,а, м, может быть учтена как
C>a = WHs’ (162)
где Hs— высота характерной волны, м.
7.3.4.4 В данном упрощенном методе могут применяться следующие характеристические вертикальные скорость частиц воды vw, м/с, и ускорение частиц воды aw, м/с2, вычисляемые по формулам:

4яг</
/гЛ ,
2
е"^,
где Са — характеристическая амплитуда волны согласно 7.3.4.3, м;
Tz — периоды колебания волны через нулевую точку (см. 7.3.2.1), с;
d — расстояние от зеркала воды до центра тяжести погруженной части объекта, м;
д — ускорение свободного падения 9,81, м/с2;
Tz — периоды колебания волны через нулевую точку (см. 7.3.2.1), с.
7.3.4.5 Как вариант, можно применить следующие независимые от периода волны уравнения кинематики волны:
0,Э5</ vw = Q,3y]ngHse н* ,
(165)
(166)
0,35d aw=0,1rcge н° ,
где д — ускорение свободного падения 9,81, м/с2,
Hs — высота характерной волны расчетного состояния моря, м;
d — расстояние от зеркала воды до центра тяжести погруженной части объекта, м.
В данном случае использована нижняя граница /7тах = 1,8 /-/s = 7/10 с длиной волны
X = g-Tz /2л.
7.3.4.6 В документации расчетов должно быть четко указано, включено влияние периода волны или не включено. Два варианта упрощенного метода не должны чередоваться в пределах расчетов.
7.3.5 Сила удара при слеминге
7.3.5.1 Характеристическую силу удара при слеминге Fs на проходящие сквозь поверхность воды компоненты объекта можно учитывать как
F =0,5рС„Д„у 2 (167)
где р — плотность морской воды, кг/м3;
Cs — коэффициент при слеминге, который может определяться теоретическими и/или экспериментальными методами. Для гладких цилиндров круглого сечения Cs должен составлять не менее 3,0. В ином случае Cs должен составлять не менее 5,0;
— площадь воздействия удара при слеминге, т. е. часть конструкции, проецируемая на горизонтальную плоскость, которая будет подвергнута нагрузке от удара при слеминге о волну во время пересечения поверхности воды, м2;
vs — скорость удара при слеминге, м/с.
7.3.5.2 Скорость удара при слеминге v рассчитывают по формуле
(168)
+ vw2>
где vc — скорость опускания крюка, как правило, 0,50, м/с;
vct — характеристическая отдельная амплитуда вертикальной скорости оконечности крана, м/с;
vw — характеристическая вертикальная скорость частиц воды, как определено в 7.3.4.4 или 7.3.4.5 путем применения расстояния d, равного нулю, м/с.
7.3.5.3 Отдельно может быть учтена увеличенная скорость удара при слеминге из-за внешнего возбуждающего воздействия водного столба внутри задавливаемых самопогружных свай.
Может быть применена упрощенная оценка местной скорости удара при слеминге vs внутри за-давливаемой самопогружной сваи, вычисляемой по формуле
vs = vc+^vct +vwk2>
(169)
где vc — скорость опускания крюка, как правило, 0,50, м/с;
vct — характеристическая отдельная амплитуда вертикальной скорости оконечности крана, м/с;
vw — характеристическая вертикальная скорость частиц воды, м/с;
к — коэффициент усиления, как правило, 1,0 < к < 2,0.
В данной упрощенной оценке не учтены сжатие и сплющивание воздушных подушек. Влияние воздушной подушки из-за ограниченного отвода воздуха через вентиляционные отверстия может являться дополнительным фактором, влияющем на уменьшение усилия при слеминге.
Воздействие волнения на устанавливаемую самопогружную сваю представлено на рисунках 22 и 23.

Рисунок 22 — Верхняя пластина пересекающей поверхность воды, задавливаемой самопогружной сваи (Брызги воды из вентиляционного отверстия)
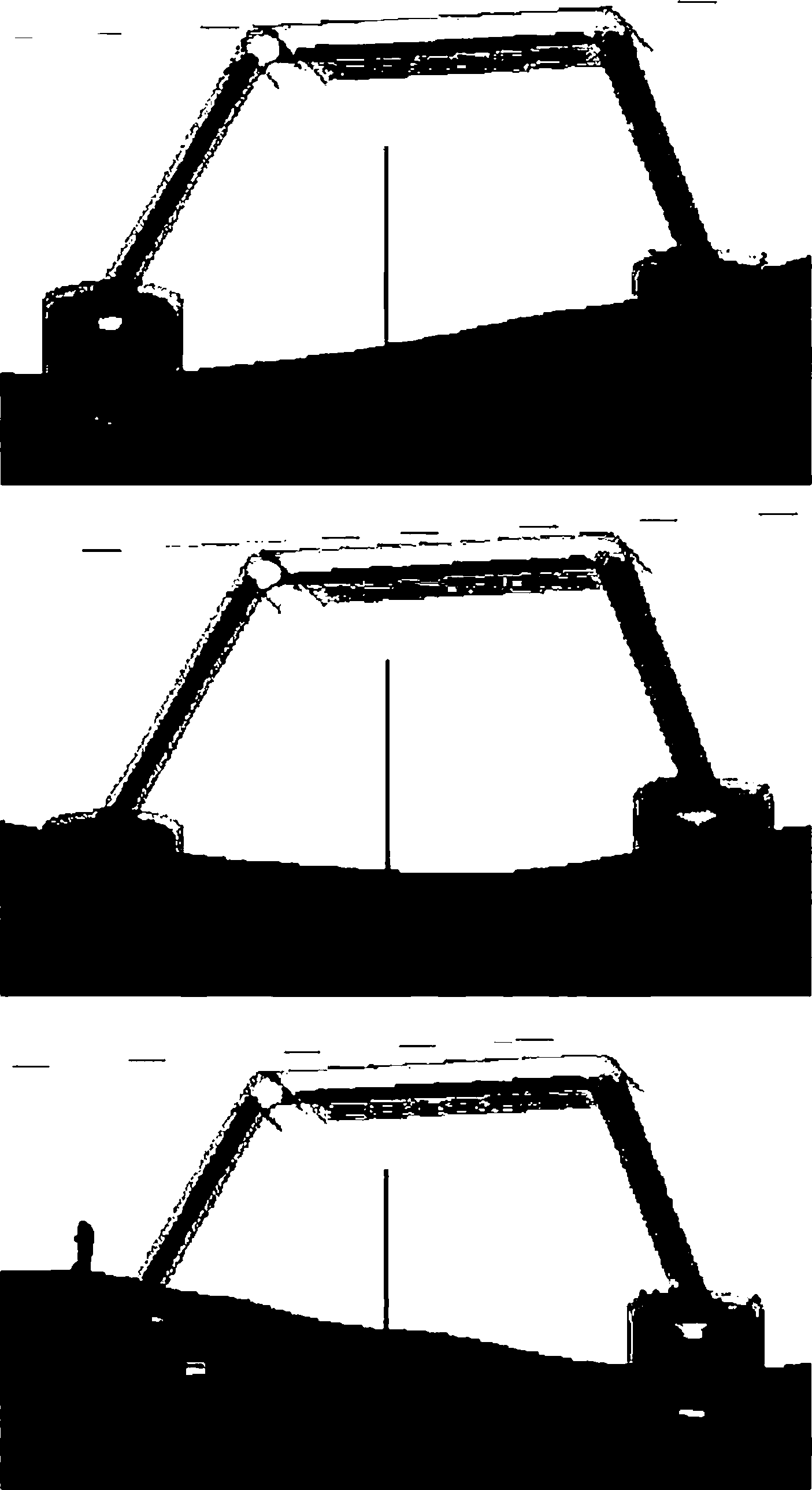
Примечание — На основе расчета CFD. Размеры башмака — 3,5 х 0 4,0 м. Вентиляционные отверстия диаметром 0,8 м. Регулярная волна — Н= 3,5 м,Т = 5,5 с. Скорость опускания — 0,25 м/с. Между снимками 1 с.
Рисунок 23 — Внутреннее воздействие волны на верхнюю пластину опорного башмака
7.3.6 Переменное выталкивающее усилие
7.3.6.1 Статический вес объекта связан с поверхностью неподвижной воды. Изменение в плавучести из-за подъема поверхности волны может быть учтено следующим образом:
Fp = p8VU (170)
где р — плотность морской воды, обычно 1025, кг/м3;
&V — изменение объема вытесненной воды от поверхности неподвижной воды до гребня волны или подошвы волны, м3;
д — ускорение свободного падения, м/с2.
7.3.6.2 Изменение объема вытесненной воды <5V, м3, можно вычислить по формуле
<171>
где Aw — площадь среднего уровня воды в зоне поверхности волны, м2;
^а — характеристическая амплитуда волны (см. 7.3.4.3), м;
r|cf— характеристическая отдельная амплитуда вертикального движения оконечности крана, м.
7.3.6.3 Изменение объема вытесненной воды может быть асимметричным относительно поверхности неподвижной воды.
Если изменение вытеснения является сильно нелинейным, непосредственное вычисление объема от поверхности неподвижной воды до гребня волны или до подошвы волны можно выполнить с применением диапазона поверхности воды
ХГ-+ /г24.п2 <172)
где Са — характеристическая амплитуда волны, м;
r|cf— характеристическая отдельная амплитуда вертикального движения оконечности крана, м.
7.3.7 Массовое усилие
7.3.7.1 Характеристическое массовое усилие компонента объекта FMj, Н, из-за объединенного ускорения объекта и частиц воды вычисляют по формуле
FMi = + A33i)'act~\ + [(PV/' +^33/)'aiv] ’ (173)
где Mj — масса компонента объекта в воздухе, кг;
Д33/- — присоединенная масса при вертикальной качке компонента объекта, кг;
act — характеристическая отдельная амплитуда вертикального ускорения оконечности крана, м/с2; р — плотность морской воды, обычно 1025, кг/м3;
Vj — объем вытесненной компонентом объекта воды относительно уровня неподвижной воды, м3; aw — характеристическое вертикальное ускорение частиц воды (см. 7.3.4.4 или 7.3.4.5), м/с2.
Конструкция может быть разделена на основные компоненты. Тогда массу, присоединенную массу, вытесненный объем и площадь проекции для каждого отдельного основного компонента применяют в соответствии с положениями, изложенными в 7.3.7.1 и 7.3.8.1. Впоследствии массовые усилия и усилия лобового сопротивления суммируют, как описано в 7.3.9.6.
В настоящем стандарте термин «массовое усилие» следует понимать как комбинацию дополнительных факторов усилия инерции и гидродинамического усилия на основе усилия Фруда—Крылова и усилий дифракции (связанных с относительным ускорением). Допускается, что ускорение оконечности крана и ускорение частиц воды статистически независимые.
7.3.7.2 Оценка присоединенной массы может быть выполнена в соответствии с 7.6.3, 7.6.4.
7.3.8 Усилие лобового сопротивления
7.3.8.1 Характеристическое усилие лобового сопротивления компонента объекта FDj, Н, может быть учтено как
FDj = 0,5 р CDApj V2, (174)
где р — плотность морской воды, обычно 1025, кг/м3;
CD — коэффициент лобового сопротивления погруженной части объекта в колеблющемся потоке;
Apj — площадь проекции погруженной части компонента объекта на горизонтальной плоскости, м2; vr — характеристическая вертикальная относительная скорость между объектом и частицами воды, м/с.
7.3.8.2 Оценка коэффициентов лобового сопротивления может быть выполнена в соответствии с положениями 7.6.2.
7.3.8.3 Характеристическую вертикальную относительную скорость vr, м/с, между объектом и частицами воды вычислена по формуле
vr = vc + 'lvct+vw ■
(175)
где vc — скорость подъема/опускания крюка, как правило, 0,50, м/с;
vct — характеристическая отдельная амплитуда вертикальной скорости оконечности крана, м/с;
vw — характеристическая вертикальная скорость частиц воды (см. 7.3.4.4 или 7.3.4.5), м/с.
7.3.9 Гидродинамическое усилие
7.3.9.1 Характеристическое гидродинамическое усилие, действующее на объект при опускании сквозь поверхность воды, является зависимой от времени функцией силы удара при слеминге, от усилий переменной плавучести, гидродинамического массового усилия и от усилия лобового сопротивления.
7.3.9.2 В данном упрощенном методе приемлемы следующие комбинации различных компонентов нагрузки при характеристическом гидродинамическом усилии Fxap гид, вычисляемом по формуле
^"хар.гмд “ у (FO + ^~s ) + ^"р ) »
(176)
где Fd — характеристическое гидродинамическое усилие лобового сопротивления, Н;
Fs — характеристическая сила удара при слеминге, Н;
FM — характеристическое гидродинамическое массовое усилие, Н;
Fp — характеристическая переменная выталкивающая сила, Н.
При опускании сквозь поверхность воды конструкция может иметь как полностью погруженные части, так и компоненты в зоне всплеска волны. Таким образом, действующее на компонент, пересекающий поверхность, усилие при слеминге является синфазным с усилием лобового сопротивления, действующим на полностью погруженную часть. Аналогично массовое и переменное выталкивающие усилия на 180° не синфазны.
7.3.9.3 Сила удара при слеминге, действующая на часть конструкции, ударяемую поверхностью волны, может быть принята как единственный действующий на эту часть компонент нагрузки (см. 7.5.2).
7.3.9.4 Данный метод предполагает, что горизонтальная протяженность поднимаемого объекта незначительна по сравнению с длиной волны. Если протяженность объекта признана значимой, необходимо выполнить его более точную оценку (см. раздел 6).
7.3.9.5 Сооружение может быть разделено на являющиеся дополнительным фактором в гидродинамическую силу основные компоненты и поверхности.
7.3.9.6 При вычислении массового усилия и лобового сопротивления скорость и ускорение частиц воды должны быть связаны с вертикальным центром тяжести каждого основного компонента. Дополнительные факторы этих усилий FM и FD вычисляют следующим образом:
FM=^FMi и Fd=XF0, , (177)
/■ /■
где FMj и FDj — дополнительные факторы отдельного усилия от каждого основного компонента (см. 7.5.2).
7.4 Критерии приемлемости
7.4.1 Общие положения7.4.1.1 В данном подразделе представлены критерии приемлемости для вычисленных гидродинамических усилий.
7.4.2 Характеристическое общее усилие
7.4.2.1 Характеристическое общее усилие Fxapo6lM на опускаемый сквозь поверхность воды объект должно учитываться как
^"хар.общ - ^”ст + ^"хар.гид’ (178)
где FCT — статический вес объекта, 7.2.2, Н;
Fxap гид — характеристическое гидродинамическое усилие (см. 7.3.9), Н.
7.4.2.2 Когда возникают нагрузки рывка, характеристическое общее усилие на объект вычисляют по формуле
Т’хар.общ - ЕСу + ^рыв’ (179)
где FCT — статический вес объекта (см. 7.2.2), Н;
Fpb|B — характеристическое усилие рывка (см. 7.7.2), Н.
7.4.3 Критерий провисания стропы
7.4.3.1 Действие усилий рывка следует предотвращать в максимально возможной степени. Для обеспечения этого необходимо скорректировать факторы погоды.
7.4.3.2 Усилия рывка в стропах или в подъемном тросе могут возникнуть в том случае, если гидродинамическое усилие превышает статический вес объекта.
7.4.3.3 Для предотвращения нагрузок рывка в стропах и в подъемном тросе должен быть выполнен следующий критерий:
^хар.гид - 0’9 ^ст min’ (180)
где Fxap гид — характеристическое гидродинамическое усилие, Н;
F„T min — статический вес объекта, Н, vl I I III I
В настоящем стандарте допускается 10 %-ный запас на рывок провисания строп, являющийся достаточным уровнем безопасности относительно факторов нагрузки и комбинаций нагрузки.
Подлежащие применению и приведенные в 7.4.3.3 гидродинамические усилия действуют по направлению вверх.
В случаях с участием объектов с большой протяженностью по горизонтали, например, таких протяженных удлиненных конструкций, как трубные секции, для определения нагрузок в отдельных стропах требуются более точные расчеты. Как правило, для данной цели требуются расчеты по временной области. Более простым и более консервативным подходом может быть применение метода регулярной расчетной волны, как описано в 6.4.2. В данном методе допускается, что вызванный волной отклик перемещения поднимаемого объекта пренебрежимо мал.
7.4.3.4 Минимальный статический вес поднимаемого объекта должен рассчитываться в соответствии с 7.2.2.
7.4.4 Проверка прочности
7.4.4.1 В дополнение к критерию провисания стропы следует проверять прочность поднимаемой конструкции и подъемного оборудования.
7.4.4.2 Характеристическое общее усилие, действующее на объект, должно быть рассчитано с применением максимального статического веса.
7.4.4.3 Проверки прочности относятся к весу объекта в воздухе. Вследствие этого следует применять преобразованный коэффициент динамичности, эквивалентный коэффициенту, применяемому в воздухе (DAF), и использовать следующее отношение:
nAP _/\ар.общ (181)
иАЬдин" Мд ’
где DAFflMH — преобразованный коэффициент динамичности;
М — масса объекта в воздухе, кг;
д — ускорение свободного падения 9,81, м/с2;
^харобщ — характеристическое большее усилие, большее из суммы FCT max + Fxaprk|fl или суммы F + F Н 'ст max 'рыв’ '
7.4.4.4 Максимальный статический вес поднимаемого объекта должен рассчитываться в соответствии с 7.2.2.
7.5 Типовые случаи нагрузки при опускании сквозь поверхность воды
7.5.1 Общие положения7.5.1.1 При опускании сквозь поверхность воды будут присутствовать различные гидродинамические нагрузки, действующие на различные части конструкции. Следовательно, расчет работы должен включать в себя несколько различных вариантов нагрузки.
7.5.1.2 При определении вариантов нагрузки необходимо определить основные компоненты объекта, вносящие дополнительные факторы в гидродинамические усилия. Уровни неподвижной воды могут быть расположены в соответствии со следующим общим руководством:
- немного ниже площади воздействия удара при слеминге на основной компонент;
- немного выше верхней части погруженного основного компонента.
7.5.1.3 Примеры типичных случаев нагрузки приведены в 7.5.2 и представлены в качестве руководства. Типовые случаи нагрузки и комбинации нагрузки должны быть установлены отдельно для всех конструкций.
7.5.1.4 Общее гидродинамическое усилие, действующее на сооружение, следует рассчитывать согласно 7.3.9.2.
7.5.2 Случаи нагрузки для защитной конструкции
7.5.2.1 Как показано на рисунках 24—27, опускание типичной защитной конструкции сквозь поверхность воды может быть разделено на четыре случая нагрузки.
7.5.2.2 Первым случаем нагрузки являются воздействия в зоне бочек (см. рисунок 24).
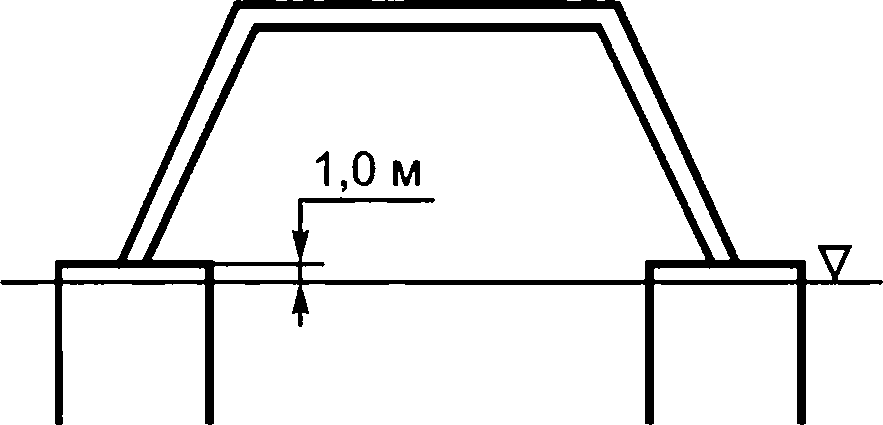
Рисунок 24 — Уровень неподвижной воды ниже верхней части бочек
При этом:
- сила удара при слеминге Fs действует вверх на внешнюю поверхность бочек. При этом должна быть учтена только площадь бочек. Как правило, если объект имеет четыре бочки, то достаточно рассматривать воздействие на две бочки;
- допуская, что горизонтальная площадь проекции стенок юбки является небольшой, переменное выталкивающее усилие F , массовое усилие FM и усилие лобового сопротивления FD можно считать пренебрежимо малыми.
7.5.2.3 Второй случай нагрузки имеет место, когда бочки полностью погружены (см. рисунок 25).
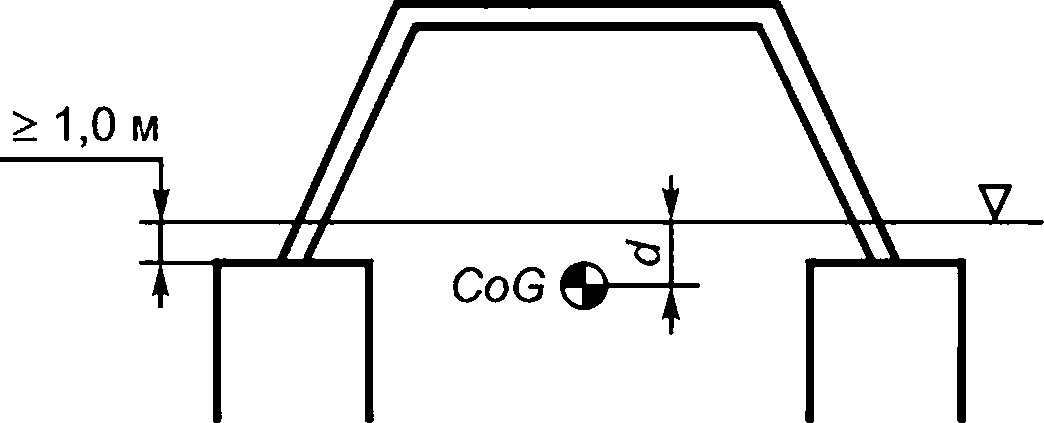
CoG — центр тяжести; d — расстояние от центра тяжести до уровня неподвижной воды Рисунок 25 — Опоры полностью погружены
При этом:
- сила удара при слеминге Fs равна нулю;
- рассчитывают переменное выталкивающее усилие F массовое усилие FM и усилие лобового сопротивления FD. Характеристические вертикальные, относительная скорость и ускорение связаны с центром тяжести погруженной части конструкции.
7.5.2.4 В третьем случае нагрузки верхнее покрытие защитной конструкции находится немного над уровнем неподвижной воды (см. рисунок 26).
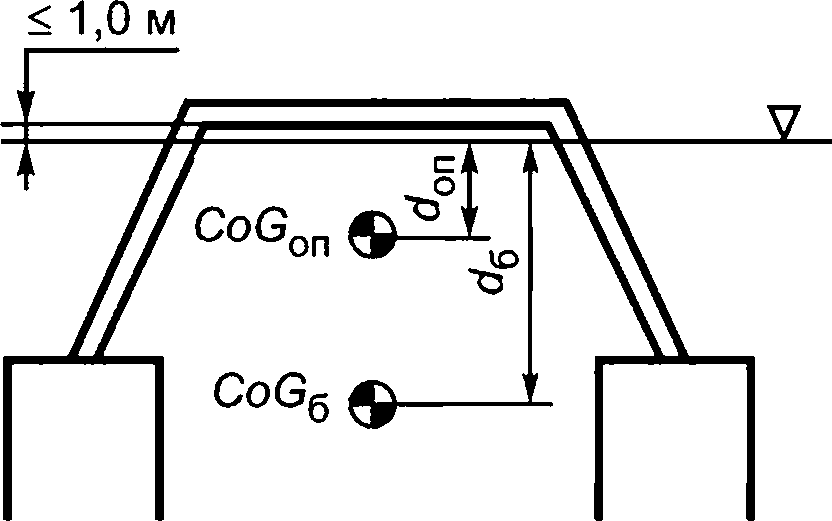
CoGon — центр тяжести опор; с/оп — расстояние от центра тяжести опор до уровня неподвижной воды; CoG6 — центр тяжести бочек; с/б — расстояние от центра тяжести бочек до уровня неподвижной воды
Рисунок 26 — Уровень неподвижной воды ниже верхней части защитной конструкции
При этом вычисляют:
- силу удара при слеминге Fs на верхнем покрытии;
- переменное выталкивающее усилие Fp в зоне поверхности волны;
- массовые усилия FMj для бочек и опор отдельно, с применением характеристического вертикального ускорения частиц воды для центра тяжести бочек и опор по отдельности. Общее массовое усилие является суммой двух компонентов нагрузки (см. 7.3.9.6);
- усилие лобового сопротивления FDj для бочек и опор отдельно с применением правильных центров тяжести. Общее усилие лобового сопротивления является суммой двух компонентов нагрузки.
7.5.2.5 Четвертый случай нагрузки наблюдается, когда конструкция полностью погружена (см. рисунок 27).

CoGBepxnoKp — центр тяжести верхнего покрытия; dBepxn0Kp — расстояние от центра тяжести верхнего покрытия до уровня неподвижной воды; CoGon — центр тяжести опор; don — расстояние от центра тяжести опор до уровня неподвижной воды;
CoG6 — центр тяжести бочек; d& — расстояние от центра тяжести бочек до уровня неподвижной воды
Рисунок 27 — Четвертый случай нагрузки: уровень неподвижной воды выше верхнего покрытия
При этом:
- сила удара при слеминге Fs равна нулю;
- переменное выталкивающее усилие Fp равно нулю;
- массовые усилия FMj рассчитывают для бочек, опор и верхнего покрытия отдельно, с применением характеристического вертикального ускорения частиц воды для центра тяжести бочек, опор и верхнего покрытия защитной конструкции по отдельности. Общее массовое усилие является суммой трех компонентов нагрузки;
- усилия лобового сопротивления FDl также рассчитывают для бочек, опор и верхнего покрытия отдельно с применением правильных центров тяжести. Общее усилие лобового сопротивления является суммой трех компонентов нагрузки (см. 7.3.9.6).
7.6 Оценка гидродинамических характеристик
7.6.1 Общие положения7.6.1.1 Гидродинамические характеристики могут быть определены теоретическими и/или экспериментальными методами.
7.6.1.2 Гидродинамические характеристики могут зависеть от нескольких факторов:
- геометрии конструкции;
- перфорации;
- острых кромок;
- близости к поверхности воды или морскому дну;
- высоты волны или периода волны;
- частоты колебаний;
- амплитуды колебаний.
7.6.1.3 Приведенные в настоящем упрощенном методе коэффициенты лобового сопротивления и значения присоединенной массы не полностью учитывают все перечисленные выше параметры.
7.6.1.4 Испытания на модели показали, что присоединенная масса может существенно зависеть от амплитуды колебаний типичных подводных конструкций.
7.6.2 Коэффициенты лобового сопротивления
7.6.2.1 В колеблющемся потоке необходимо использовать коэффициенты гидродинамического лобового сопротивления.
7.6.2.2 Коэффициент лобового сопротивления CD в колеблющемся потоке изменяется в зависимости от числа КС и, как правило, может в два-три раза превышать коэффициент лобового сопротивления CDS в устойчивом потоке.
7.6.2.3 Волны, течение или вертикальный поток жидкости из-за скорости опускания могут частично снести часть попутного потока. Это может снизить коэффициент лобового сопротивления в колеблющемся потоке по сравнению с полученными без этого влияния данными испытания на модели.
Под волновой зоной коэффициент лобового сопротивления уменьшается с увеличением скорости опускания, так как опускаемое сооружение направляют ко входу в менее возмущенную жидкость. Если скорость опускания превышает максимальную скорость колебания, коэффициент лобового сопротивления будет стремиться к достижению значения коэффициента лобового сопротивления в устойчивом потоке.
7.6.2.4 Если специальные исследования CFD или испытания на модели не проводились, то коэффициент лобового сопротивления на типичных подводных конструкциях в пульсирующем потоке определяют по условию
CD> 2,5. (182)
7.6.2.5 При отсутствии влияния гидродинамических взаимодействий для протяженных удлиненных элементов можно применять коэффициент лобового сопротивления, равный двойному коэффициенту лобового сопротивления CDS стабильного состояния (см. приложение Б).
7.6.2.6 Чтобы оценить применимость более точных методов, таких как исследования CFD или испытания на модели, необходимо выполнить исследование чувствительности присоединенной массы и демпфирования.
Коэффициент лобового сопротивления может быть значительно выше приведенного в 7.6.2.4 значения.
При проведении испытаний на модели и расчетов CFD сложных подводных конструкций при соответствующих числах КС, коэффициенты лобового сопротивления в колеблющемся потоке в диапазоне CD ~ 4—8 можно получить, если пренебречь сносом попутного потока из-за волн, течения или скорости опускания.
Следует отметить, что при чрезвычайно малых числах КС коэффициент лобового сопротивления в примененном в 7.3.8.1 виде по мере снижения скорости жидкости до нуля стремится к бесконечности.
7.6.3 Присоединенная масса для неперфорированных конструкций
7.6.3.1 Коэффициенты гидродинамической присоединенной массы для различных тел и форм поперечного сечения приведены в приложении А (таблицы А.1, А.2).
7.6.3.2 Присоединенная масса при вертикальной качке конструкции, проходящей сквозь поверхность, может быть учтена как половина присоединенной массы при вертикальной качке (в области безграничной текучей среды) объекта, образованного погруженной частью конструкции, плюс ее зеркальное отражение над свободной поверхностью.
Данное приближение основано на высокочастотном пределе и, следовательно, применимо только в случаях пренебрежимо малых излучающих поверхностных волн.
7.6.3.3 При вертикальной качке для трехмерного тела с вертикальными сторонами можно применить следующую упрощенную аппроксимацию присоединенной массы:
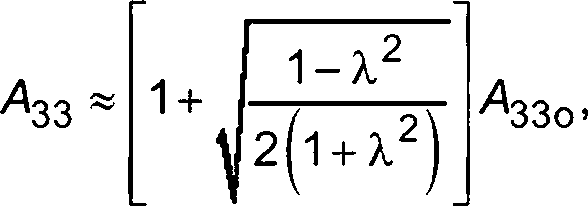
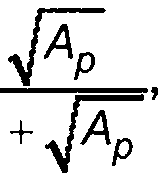
(183)
(184)
где А33о — присоединенная масса для плоской пластины с формой, равной площади горизонтальной проекции объекта, кг;
h — высота объекта, м;
Ар — площадь проецируемой на горизонтальную плоскость погруженной части объекта, м2.
7.6.3.4 Конструкция, содержащая частично изолированный объем воды, перемещающейся вместе с конструкцией, может быть представлена как трехмерное тело, в котором частично изолированный объем воды включен в присоединенную массу.
Например, имеющая форму цилиндра задавливаемая самопогружная свая с диаметром, равным высоте, будет согласно 7.6.3.3 иметь присоединенную массу, равную сумме 1,57-кратной присоединенной массы круглого диска и массы объема воды внутри цилиндра.
В рамках данного упрощенного метода затапливаемые компоненты, такие как трубчатые рамы или трубные секции, должны быть использованы при расчетах статического веса в соответствии с 7.2.2. Массу данного объема воды не следует включать в присоединенную массу, так как она уже включена в массу тела.
7.6.3.5 Расчеты присоединенной массы на основе сложения дополнительных факторов каждого компонента не допускают в случае плотно составленной конструкции. Рассчитанные значения могут быть недооценены из-за влияний взаимодействия и зависимости от амплитуды колебаний.
Влияниями взаимодействия можно пренебречь, если поперечная к направлению движения (в пределах типичной амплитуды либо движения тела, либо движения частицы волны) сплошная площадь проекции менее 50 %.
7.6.4 Влияние перфорации
7.6.4.1 Влияние перфорации на присоединенную массу можно с наименьшей степенью достоверности оценить следующим образом:
если р< 5
Д33 = Д33з’
(185)
(186)
если 5 < р < 34
если 34 < р < 50
10-р
(187)
Д33 = Д33зе 28 > где Д335 — сплошная присоединенная масса (присоединенная масса при вертикальной качке для неперфорированной конструкции), кг;
р — коэффициент (процент) перфорации.
Например, имеющая форму цилиндра задавливаемая самопогружная свая с вентиляционным отверстием, соответствующим перфорации 5 %, будет иметь присоединенную массу, равную сплошной присоединенной массе, т. е. в данном случае вентиляционное отверстие не влияет на присоединенную массу.
Данное требование основано на ограниченном количестве данных модельных испытаний, и, следовательно, используется коэффициент запаса. Такой подход неприменим для коэффициентов перфорации выше 50 %. Применимая кривая зависимости присоединенной массы от перфорации показана на рисунке 28 (верхняя кривая). Затемненная область представляет данные модельных испытаний для различных подводных конструкций при переменных числах КС. Кривая ехр(-Р/28) выведена из численных моделей (на основе теории потенциального потока) перфорированных пластин и включена для сравнения. Как показано, кривая ехр(-Р/28) может дать неконсервативные значения.
7.6.4.2 Фактический понижающий коэффициент (светлая область на рисунке 28) может изменяться в зависимости от геометрии и амплитуды колебания. В большинстве случаев указанная в 7.6.4.1 методика будет значительно переоценивать присоединенную массу. При необходимости более точных оценок требуется проводить исследования CFD или испытания на модели (см. [1]).
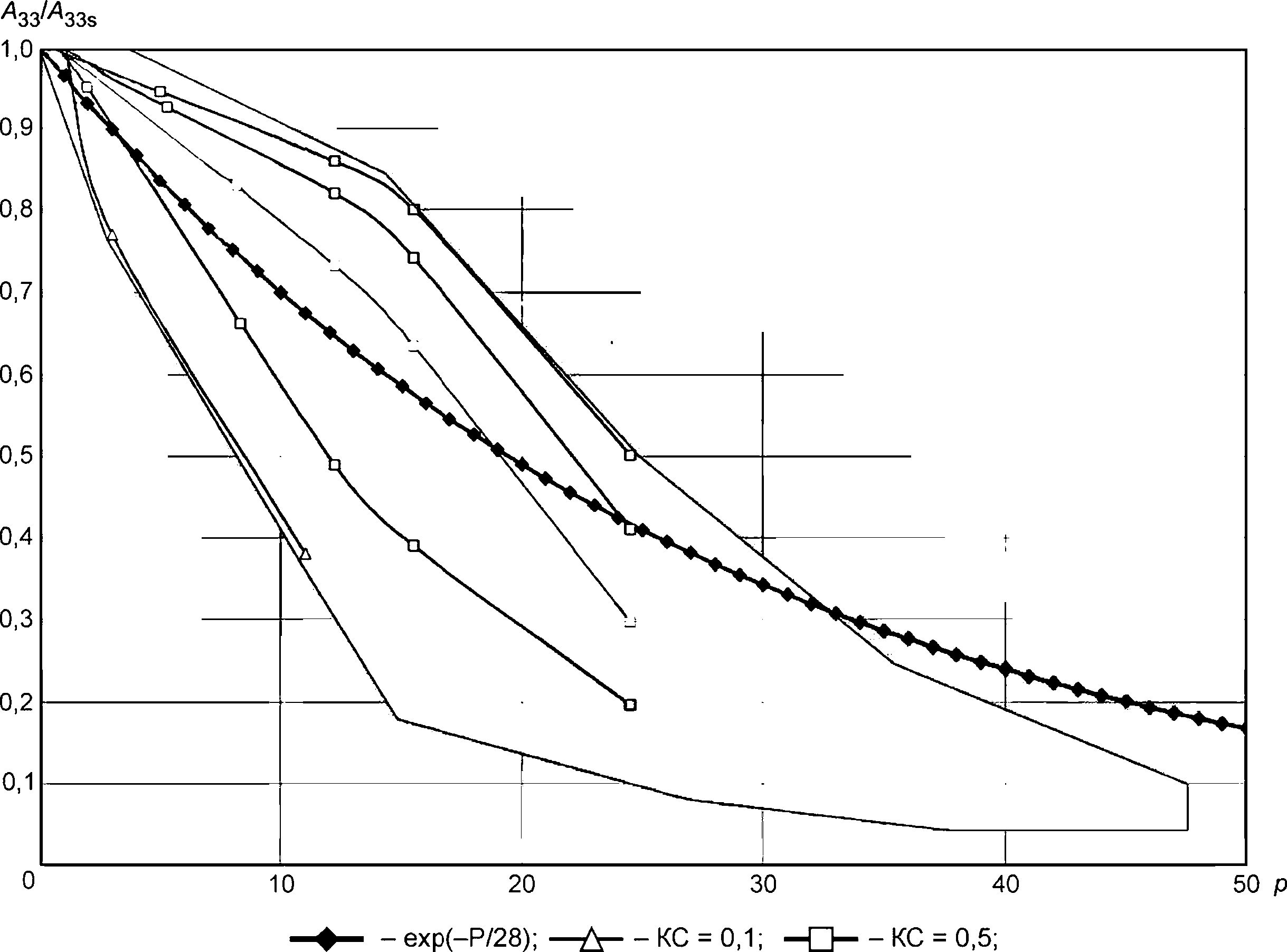
- КС = 1,5;
-КС = 2,5; —□--КС = 3,5
Рисунок 28 — Зависимости присоединенной массы от коэффициента перфорации
7.7 Усилия рывка в стропах или подъемном канате
7.7.1 Общие положения7.7.1.1 Усилия рывка необходимо предотвращать в максимально возможной степени. Для обеспечения этого следует учитывать метеорологические факторы, которые определяют характеристическую вертикальную скорость частиц воды.
7.7.1.2 Усилия рывка могут возникнуть в случае неудовлетворения критерия провисания стропы.
7.7.2 Усилие рывка
7.7.2.1 Характеристическая нагрузка рывка Ерыв может быть вычислена по формуле
----------- (188)
^ыв ='/рыву^(^ + ^3з)>
где урыв — характеристическая скорость рывка, м/с;
К — жесткость грузоподъемной системы, Н/м;
М — масса объекта в воздухе, кг;
Д33 — присоединенная масса при вертикальной качке объекта, кг.
7.7.2.2 Характеристическая нагрузка рывка должна быть применена в соответствии с 7.4.2.2 и 7.4.4.3.
7.7.3 Скорость рывка
7.7.3.1 Характеристическая скорость рывка урыв может быть учтена как
vPVB=vff+C vr- <189)
где vff— скорость свободного падения объекта (см. 7.7.3.5), м/с;
vr — характеристическая вертикальная относительная скорость между объектом и частицами воды (см. 7.7.3.2), м/с;
С — поправочный коэффициент (см. 7.7.3.4).
7.7.3.2 Характеристическая вертикальная относительная скорость между объектом и частицами воды vr, м/с, может быть представлена как
(190)
где vc — скорость подъема/опускания крюка (см. 7.7.3.3, м/с);
vct — характеристическая отдельная амплитуда вертикальной скорости оконечности крана, м/с;
vw — характеристическая вертикальная скорость частиц воды (см. 7.3.4.4 или 7.3.4.5), м/с.
7.7.3.3 Следует применять два значения скорости опускания крюка: vc, равная 0 м/с, и vc — типичная скорость опускания. Кроме того, должен быть включен случай извлечения путем применения vc, равной типичной скорости подъема. В расчете усилия рывка нужно использовать наивысшую скорость рывка для трех вариантов.
Если типичная скорость подъема/опускания неизвестна, можно применять значение vc, равное ± 0,50 м/с.
7.7.3.4 Для Vff < 0,2 vr поправочный коэффициент С = 1.
Для 0,2 vr< Vff< 0,7 vr, поправочный коэффициент С вычисляют по формуле
С = cos
(191)
где Vff— скорость свободного падения объекта, м/с;
vr — характеристическая вертикальная относительная скорость между объектом и частицами воды (см. 7.7.3.2), м/с.
Для Vff > 0,2 vr поправочный коэффициент С = 0.
7.7.3.5 Скорость свободного падения объекта vff, м/с, может быть вычислена по формуле
v„ = (192)
урАрсо
где FCT — минимальный и максимальный статический вес (см. 7.2.2.2), Н;
р — плотность морской воды, обычно 1025, кг/м3;
Ар — площадь проецируемой на горизонтальную плоскость погруженной части объекта, м2;
CD — коэффициент лобового сопротивления погруженной части объекта.
7.7.3.6 Если нагрузка рывка вызвана силой удара при слеминге, пока объект находится в воздухе, скорость рывка может допускаться равной приведенной в 7.3.5.2 скорости удара при слеминге.
В настоящем стандарте предполагается, что максимальная скорость свободного падения после удара не превысит максимальную относительную скорость между объектом и поверхностью воды.
7.7.4 Усилие рывка вследствие запуска или остановки
Усилие рывка вследствие запуска или остановки может быть рассчитано согласно 7.7.2.1 с применением характеристической скорости рывка 1/рыв, равной максимальной скорости опускания, как правило, 1,0 м/с.
7.7.5 Усилие рывка вследствие отрыва
7.7.5.1 Следует должным образом учитывать усилия рывка вследствие отрыва, например от баржи.
7.7.5.2 Нагрузки рывка во время отрыва могут быть рассчитаны согласно 7.7.2.1 с применением характеристической скорости рывка 1/рыв, вычисляемой по формуле
^рыв _ vc + vrct’ (193)
где vc — скорость подъема крюка, как правило, 0,50, м/с;
vrct — характеристическая вертикальная относительная скорость между объектом и оконечностью крана, м/с.
7.7.5.3 Характеристическую вертикальную относительную скорость между объектом и оконечностью крана следует рассчитывать с применением проектных состояний моря согласно 7.3.2.1 и в соответствии с 7.3.3.
7.7.6 Жесткость подъемной системы
7.7.6.1 Жесткость подъемной системы К, Н/м, может быть рассчитана с помощью выражения
К к к к к к к
гх посн Атр Астроп Абл Астр пдоп
где /госн — жесткость такелажной оснастки, траверса и т. п.;
ктр — жесткость подъемного(ых) троса(ов);
/<СТроп — жесткость мягкой стропы или при использовании пассивной системы компенсации вертикальной качки (см. 7.7.7);
кбл — жесткость при использовании нескольких тросов в одном блоке;
кстр — жесткость стрелы крана;
кдоп — дополнительные факторы, при наличии.
7.7.6.2 Жесткость троса ктр может быть рассчитана по формуле к (195)
ктр - L >
где Е — модуль упругости троса, Н/м2;
А — эффективное поперечное сечение троса(ов) (см. 7.7.6.3) (площади суммируют, если они являются несколькими параллельными тросами), м2;
L — длина троса(ов); в случае нескольких тросов применяют, как правило, расстояние от блока до оконечности крана, м.
7.7.6.3 Эффективное поперечное сечение одного троса Дтр находят следующим образом: где D — диаметр троса, м;
cF — коэффициент заполнения троса.
Коэффициент заполнения cF необходимо определить в соответствии с Дтр, D и Е. Типичными значениями, например, для троса с сердечником из стальной проволоки размером 6 * 37 могут быть CF= 0,58 и Е= 85-109 Н/м2.
7.7.7 Применение пассивных систем компенсации вертикальной качки с ограниченной длиной хода
7.7.7.1 Пассивные системы компенсации вертикальной качки могут иметь определенную доступную длину хода.
7.7.7.2 Превышающие доступную длину хода динамические движения поднимаемого объекта могут вызвать огромные пиковые нагрузки и отказ подъемной системы.
Если упрощенный метод указывает на риск нагрузок рывка, требуется выполнить более точный расчет подъемной операции.
7.7.7.3 Оценка доступной длины хода должна учитывать изменение в статическом весе по мере перемещения поднимаемого объекта из воздуха в погруженное состояние. В каждом случае нагрузки следует применять наименьшую доступную амплитуду длины хода.
Положение равновесия (и вследствие этого доступная длина хода) будет изменяться во время подъемной операции по мере изменения статического веса объекта при опускании сквозь поверхность воды.
Также следует проверить случаи нагрузки при извлечении.
7.7.7.4 При проверке доступной длины хода необходимо учитывать захваченную воду, вызывающую увеличение веса объекта в воздухе при извлечении.
7.7.7.5 Если требуется, можно учитывать изменения в положении равновесия из-за увеличенного давления воды находящихся под давлением поршней.
7.7.7.3 Для упрощенной проверки доступной отдельной амплитуды длины хода 5Х, можно применить следующий критерий:
gx> I(M+Ai3)vx. (197)
I ^стр
где М — масса объекта в воздухе, кг,
Д33 — присоединенная масса при вертикальной качке объекта, кг,
vx — скорость хода, допускаемая равной относительной скорости vr (см. 7.7.3.2), пока не возникли усилия рывка, при которых следует применять мгновенную скорость у (см. 7.7.3.1 или 7.7.5.2), м/с;
/гстр — жесткость пассивной системы компенсации вертикальной качки, Н/м.
Если заказаны характеристики системы, то требуется более точная оценка доступной длины хода. Потери энергии, вызываемые сопротивлением воды, не включены в 7.7.7.3.
8 Глубоководные работы по опусканию/подниманию
8.1 Общая часть
8.1.1 Общие положения8.1.1.1 При подъемных работах в глубоких водах должны быть учтены следующие факторы:
- растянутая длина троса в силу собственного веса троса и веса поднимаемого объекта;
- горизонтальное смещение из-за течения, где скорость течения может быть зависимой от времени, а значение и направление течения могут изменяться при погружении в воду;
- динамика поднимаемого объекта из-за вызванного волнением движения оконечности крана на судне;
- способы управления вертикальным перемещением поднимаемого объекта.
8.1.1.2 В дальнейшем изложении термин «трос» используется для обозначения подъемного троса от крана до поднимаемого объекта. Трос может состоять из стальной проволоки, волоконного троса, цепи или их комбинации.
8.1.2 Применение
8.1.2.1 Если не обозначено иное, знак значений движения, скорости, ускорения и усилия в данном разделе должен применяться как положительный.
8.1.2.2 В данном разделе приведено описание усилий, действующих на вертикальный трос и опускаемый объект из-под волновой зоны вниз до морского дна. Данный метод и формулы также применимы и в случае извлечения. Усилия, действующие на поднимаемые/опускаемые объекты в волновой зоне, рассмотрены в разделах 6 и 7.
8.1.2.3 Статические и динамические отклики опускаемых или поднимаемых объектов в глубокой воде можно прогнозировать с помощью общепринятых коммерческих компьютерных программ. Для проверки или подтверждения прогнозов на основании таких численных расчетов могут быть использованы представленные в данном разделе аналитические формулы.
8.2 Статические усилия, действующие на трос
8.2.1 Растянутая длина тросаВертикальный трос растянется из-за собственного веса и веса подвешенного объекта на конце троса. Растянутую длину Ls, м, троса вычисляют по формуле
H/+-WL
LS=L 1 +
2 ЕА
(198)
где L — первоначальная длина троса, м;
И/, равный Мд - pgV, — вес поднимаемого объекта в полностью погруженном состоянии, Н, где М — масса поднимаемого объекта, кг;
д — ускорение свободного падения 9,81 м/с2;
р — плотность воды, кг/м3;
V — вытесненный поднимаемым объектом объем, м3.
и/, равный тд - рдА, — вес в полностью погруженном состоянии на единицу длины троса, Н/м, где т — масса на единицу длины троса, кг/м;
А — номинальная площадь поперечного сечения троса, м2 (см. 8.2.4);
Е — модуль упругости троса, Н/м2.
8.2.2 Горизонтальное смещение из-за течения
8.2.2.1 Для жесткого в осевом направлении троса с пренебрежимо малой жесткостью на изгиб, горизонтальное смещение при вертикальном тросе £(z), м, с тяжелым грузом И/о на конце троса на глубине z со скоростью течения Uc(z) вычисляют по формуле
CD„Oo[yc{z2)]2dz2
(199)
W+wfa+L)
где Fdq — усилие гидродинамического лобового сопротивления на поднимаемый объект, вычисляемое по формуле
FD0=^PCDxAx[_Uc(~L)\ > (200) где р — плотность воды, кг/м3;
CDx — коэффициент лобового сопротивления для горизонтального потока через поднимаемый объект;
Ах — площадь х-проекции поднимаемого объекта, м2;
Uc(-L) — скорость течения на глубине, равной длине нерастянутого троса, м/с;
L — нерастянутая длина троса, м;
СОл — коэффициент лобового сопротивления для поперечного потока через трос;
Dc — диаметр троса, м;
И/ — вес подвешенного объекта в погруженном состоянии, Н;
w — вес в погруженном состоянии на единицу длины троса, Н/м;
Z1’ z2 — переменные интегрирования, м.
Допускается, что сумма веса троса wL и веса подвешенного объекта в погруженном состоянии И/ настолько велика, что угол между тросом и вертикальной линией является малым (см. рисунок 29).
Диаметр троса Dc(z) и коэффициент лобового сопротивления для поперечного потока CDn(z) могут изменяться при погружении. Данное изменение учтено при расчете смещения.
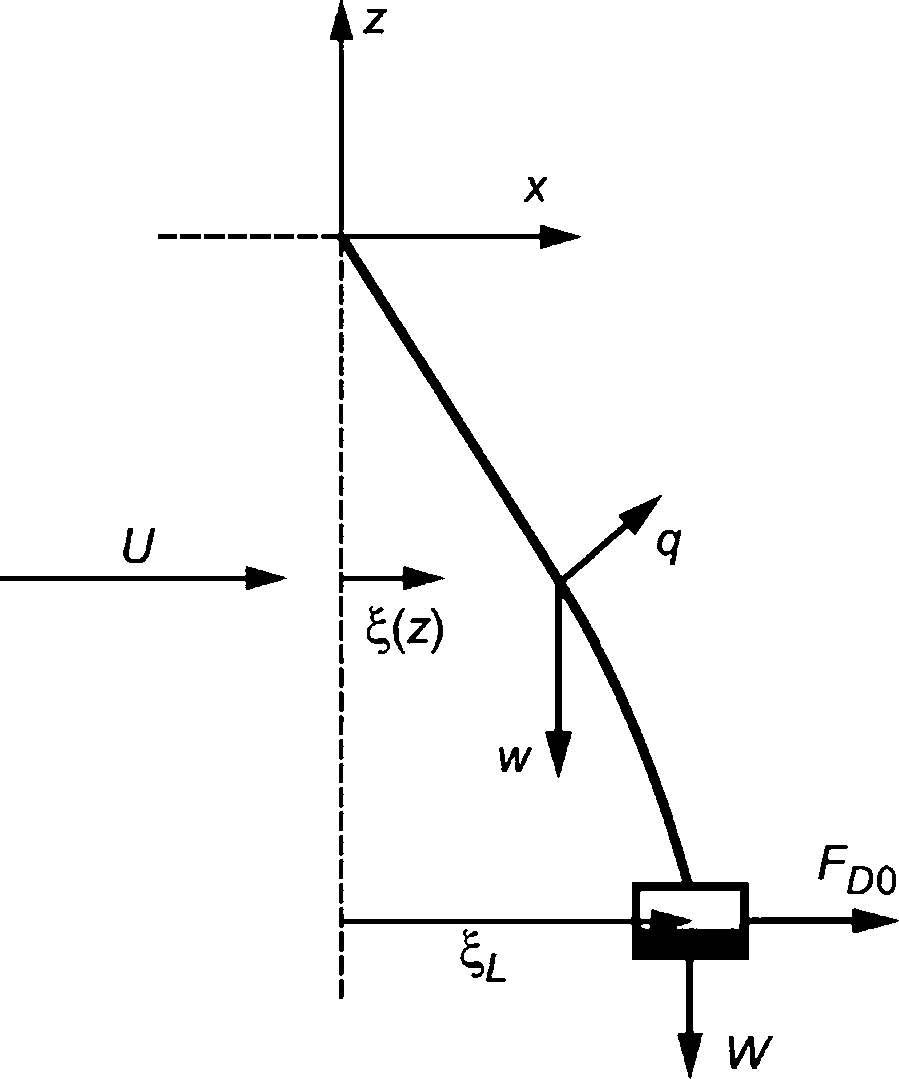
c(z) — горизонтальное смещение при вертикальном положении z, м;
— горизонтальное смещение троса, м;
Fdo — усилие гидродинамического лобового сопротивления на поднимаемый объект;
W— вес подвешенного объекта в погруженном состоянии, Н;
w— вес в погруженном состоянии на единицу длины троса, Н/м; q — усилие на сечение лобового сопротивления течения;
z1t z2 — переменные интегрирования, м;
Горизонтальное смещение c,L на конце троса z = - L, м
Рисунок 29 — Горизонтальное смещение ^(z) из-за равномерного течения
8.2.2.2 Для равномерного течения Uc и свойств троса Dc, CDn горизонтальное смещение £(z), м, может быть вычислено по формуле где L — нерастянутая длина троса, м;
$(z) = ZJ ^-к-к jin
Vw J
z
+ —f
L
k + 1
— —Z, W
(201)
и/ — вес в полностью погруженном состоянии на единицу длины троса, Н/м;
к — отношение между весом подвешенного объекта IV и весом троса;
X — отношение между лобовым сопротивлением на подвешенном объекте FDQ и весом троса.
Горизонтальное смещение подвешенного объекта
tL = l_\^-к-Х In
I w J
к
/с + 1
qL w
(202)
где L — нерастянутая длина троса, м;
и/ — вес в полностью погруженном состоянии на единицу длины троса, Н/м;
к — отношение между весом подвешенного объекта И/ и весом троса, определяемое как:
к=—, (203)
wL
к— отношение между лобовым сопротивлением на подвешенном объекте FDQ и весом троса, определяемое как:
х = ^о_. (204)
wL
Силу гидродинамического лобового сопротивления q на единицу длины троса вычисляют по формуле
(205)
Поправкой для учета вертикальной составляющей лобового сопротивления является замена w на и/— qc,L/L в формуле (204) для горизонтального смещения, где cL— нескорректированное смещение в конце троса, рассчитанное по формуле (205).
8.2.2.3 При изменении направления скорости течения и свойств троса с глубиной воды для нахождения смещения выполняют статический расчет с использованием конечно-элементного метода с полным численным интегрированием.
8.2.3 Вертикальное смещение
8.2.3.1 При установке модулей на морском дне необходимо управлять расстоянием от морского дна до нижней части подвешенного объекта на конце троса. Разница Az вертикального положения нижнего конца троса между фактическим состоянием и вертикальным нерастянутым состоянием имеет две составляющие:
Az = AzG + AzE, (206)
где AzG — вертикальное геометрическое смещение из-за кривизны троса; AzE — вертикальное упругое смещение из-за растяжения троса.
Геометрический эффект увеличивает просвет до морского дна, в то время как растяжение его уменьшает.
8.2.3.2 Для постоянного однонаправленного течения и постоянных свойств троса вдоль длины троса вертикальное смещение из-за кривизны троса может быть учтено как
(207)
где параметры q, w, к и к определены в 8.2.2.1 и 8.2.2.2.
8.2.3.3 Вертикальное смещение из-за растяжения троса может быть представлено как
az£ ~ 1 ~Т~ Х~~ЁА
W+^wL-q^)
(208)
8.2.3.4 В случае изменения направления скорости течения и свойств троса при погружении в воду для нахождения смещения выполняют трехмерный статический расчет с использованием конечно-элементного метода.
8.2.4 Вертикальная жесткость троса
8.2.4.1 Вертикальная жесткость троса kv представляет собой вертикальное усилие, которое должно быть применено к подвешенному объекту на нижнем конце троса на единицу вертикального смещения, и вычисляется по формуле
(209)
dz
где Fv — вертикальное усилие;
z — вертикальное сопротивление.
8.2.4.2 Вертикальная жесткость является суммой двух составляющих: упругой жесткости кЕ и геометрической жесткости kG. Вертикальную жесткость ку вычисляют по формуле
_L-_L 1
(210)
ку кЕ kG
где kv — вертикальная жесткость троса; кЕ — упругая жесткость;
kG — геометрическая жесткость.
8.2.4.3 Упругую жесткость кЕ вычисляют по формуле
(211)
где Е — модуль упругости троса, Н/м2;
А — эффективное поперечное сечение троса, м2;
L — длина троса (тросов), м.
Причем А, определенная как А = S-cF, — номинальная площадь поперечного сечения троса, где S — площадь поперечного сечения (описанной окружности), cF— коэффициент заполнения (см. разделы 7, 10).
8.2.4.4 Геометрическую жесткость kG вычисляют по формуле
J_^_d(AZG2^_q2_ Г к ~| । 1 2k + 3 kG dW0 w3 n|_A + lJ + 2(/< + 1)2
(212)
q X 1 1 f X Л2 2k +1
w3 к (k + 1)2 w[k J 2(k + l)2 ’
где L — нерастянутая длина троса, м;
w — вес в полностью погруженном состоянии на единицу длины троса, Н/м;
к — отношение между весом подвешенного объекта И/ и весом троса.
Определенная выше жесткость троса действительна для статических нагрузок и изменяет положение нижнего конца троса для примененной на конце единицы усилия.
Геометрическая жесткость уменьшается с увеличением скорости течения пропорционально Uc. Вследствие этого геометрическая жесткость становится значимой при более высокой скорости течения.
8.2.5 Горизонтальная жесткость
8.2.5.1 Горизонтальная жесткость кн подвешенного объекта представляет собой горизонтальное усилие, прилагаемое к нижнему концу троса, на единицу горизонтального смещения. Горизонтальную жесткость вычисляют по формуле
_dFH н~~
(213)
где FH — горизонтальное усилие;
х — горизонтальное сопротивление.
8.2.5.2 Кроме того, горизонтальную жесткость кн определяют по выражению
1 Ж,, 1, Г к +1
(214)
— = —-^ =—In --
кн dFDo w [ к
где — горизонтальное смещение на конце троса z = - L, м;
FD0 — усилие гидродинамического лобового сопротивления на поднимаемый объект; w — вес в погруженном состоянии на единицу длины троса, Н/м;
к — отношение между весом подвешенного объекта И/ и весом троса.
Следует учитывать то, что на горизонтальную жесткость не влияет лобовое сопротивление течению троса и подвешенного объекта, а также то, что выражение для горизонтальной жесткости справедливо только для статических нагрузок.
8.2.5.3 Когда подвешенный объект намного тяжелее веса троса, горизонтальная жесткость троса уменьшается до жесткости математического маятника:
И/ W
(215)
к - — »1=>kH - wk - — , wL н L
где кн — горизонтальная жесткость троса;
и/ — вес в полностью погруженном состоянии на единицу длины троса, Н/м;
L — нерастянутая длина троса, м;
к — отношение между весом подвешенного объекта W и весом троса.
8.2.6 Разматывание троса. Квазистатические нагрузки
Квазистатическое растяжение T(s) на верхнем конце троса во время разматывания для операции глубоководного опускания вычисляют по формуле
1 1 (216)
Т (s) = W + ws+-рС^ tcDcs vc | vc |+-p CDzAp vc | vc |,
где W — вес подвешенного объекта в погруженном состоянии, Н;
w — вес в погруженном состоянии на единицу длины троса, Н/м;
s — величина разматывания троса, м;
р — плотность воды, кг/м3;
CDf— коэффициент продольного трения троса;
Dc — диаметр троса, м;
vc — постоянная скорость разматывания троса при подъеме, являющаяся положительной, а при опускании — отрицательной, м/с;
CDz — коэффициент лобового сопротивления для вертикального потока через поднимаемый объект;
Ар — площадь горизонтальной проекции подвешенного объекта, м2.
Для величины разматывания троса s необходимую для получения состояния провисания скорость разматывания определяют путем задания T(s) = 0 в формуле (216). В формуле (216) не учтено влияние течения и скорости частиц воды из-за волн, и, следовательно, данная формула действительна только для неподвижной воды.
Примечание —Данные, описывающие коэффициенты трения для потока, тангенциального относительно троса (см. [2]).
8.3 Динамические усилия, действующие на трос и поднимаемый/опускаемый объект
8.3.1 Общие положенияДля типичной спуско-подъемной операции с плавучего судна допускается, что движение объекта не влияет на движение судна (см. [1]). Это упрощение основано на следующем:
- масса и присоединенная масса поднимаемого/опускаемого объекта намного меньше водоизмещения судна;
- дополнительные факторы объектов в момент инерции вокруг центра тяжести/плоскости симметрии судна намного меньше, чем момент инерции судна;
- движение оконечности крана является вертикальным;
- влиянием течения можно пренебречь.
Несвязанные RAO судна дают консервативные результаты, так как в большинстве случаев объект имеет тенденцию уменьшать вертикальное движение оконечности крана.
8.3.2 Динамические усилия лобового сопротивления
В силу движения оконечности крана и поднимаемого объекта на трос будут действовать динамические усилия лобового сопротивления. Усилия лобового сопротивления ограничивают изменение формы троса. По мере увеличения скорости/ускорений оконечности крана упругая жесткость приобретает все большее значение.
8.3.3 Применение
При глубоководных работах по подъему и опусканию динамический отклик объекта зависит от его вертикального положения (глубины). С целью осуществления управляемого опускания объекта при заданном состоянии моря в процессе планирования операции следует выполнить оценку динамического отклика объекта на всех глубинах.
8.3.4 Собственные частоты, прямой вертикальный трос
8.3.4.1 Собственную угловую частоту прямого вертикального троса соу, рад/с, определяют по формуле
e">
где j = 0, 1,2, ...;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2; т — масса на единицу длины троса, кг/м.
8.3.4.2 Точное решение для волновых чисел vy, 1/м, определено уравнением (с допущением недемпфированных колебаний): где L — длина троса, м;
vyLtan(vyL) = е =
mL
М + А33
(218)
£ — отношение масс, равное mU(M + А33);
т — масса на единицу длины троса, кг/м;
М — масса поднимаемого объекта в воздухе, кг;
А33 — присоединенная масса для движения в вертикальном направлении, кг.
Вертикальную присоединенную массу для трехмерных тел в безграничной текучей среде определяют как А33 = pCAVR, где СА — коэффициент присоединенной массы, a VR— относительный объем, как правило, вытесненный. На присоединенную массу поднимаемого объекта влияют близость к свободной поверхности и близость к морскому дну.
Следует отметить, что в случае сложных, частично перфорированных подводных модулей присоединенная масса также зависит от амплитуды движений, что дополнительно влияет на период собственных движений поднимаемого объекта (см. разделы 6, 7). Коэффициенты присоединенной массы для определенных трехмерных тел приведены в таблице А.2.
8.3.4.3 Для небольших отношений масс основное волновое число определяют с помощью приближения
(219)
где е — отношение масс.
Разница между точным решением и приблизительным решением показана на рисунке 30. Приведенное выше приближение близко к точному решению даже для отношений масс £ вплоть до 3. Таким образом, установленный в 8.3.5.1 период собственных движений (выведенный на основании 8.3.4.3) должен быть действительным для большинства практических случаев. Для отношений масс выше 3 в знаменателе приведенного выше приближенного решения вместо е/3 необходимо использовать 2е/5.
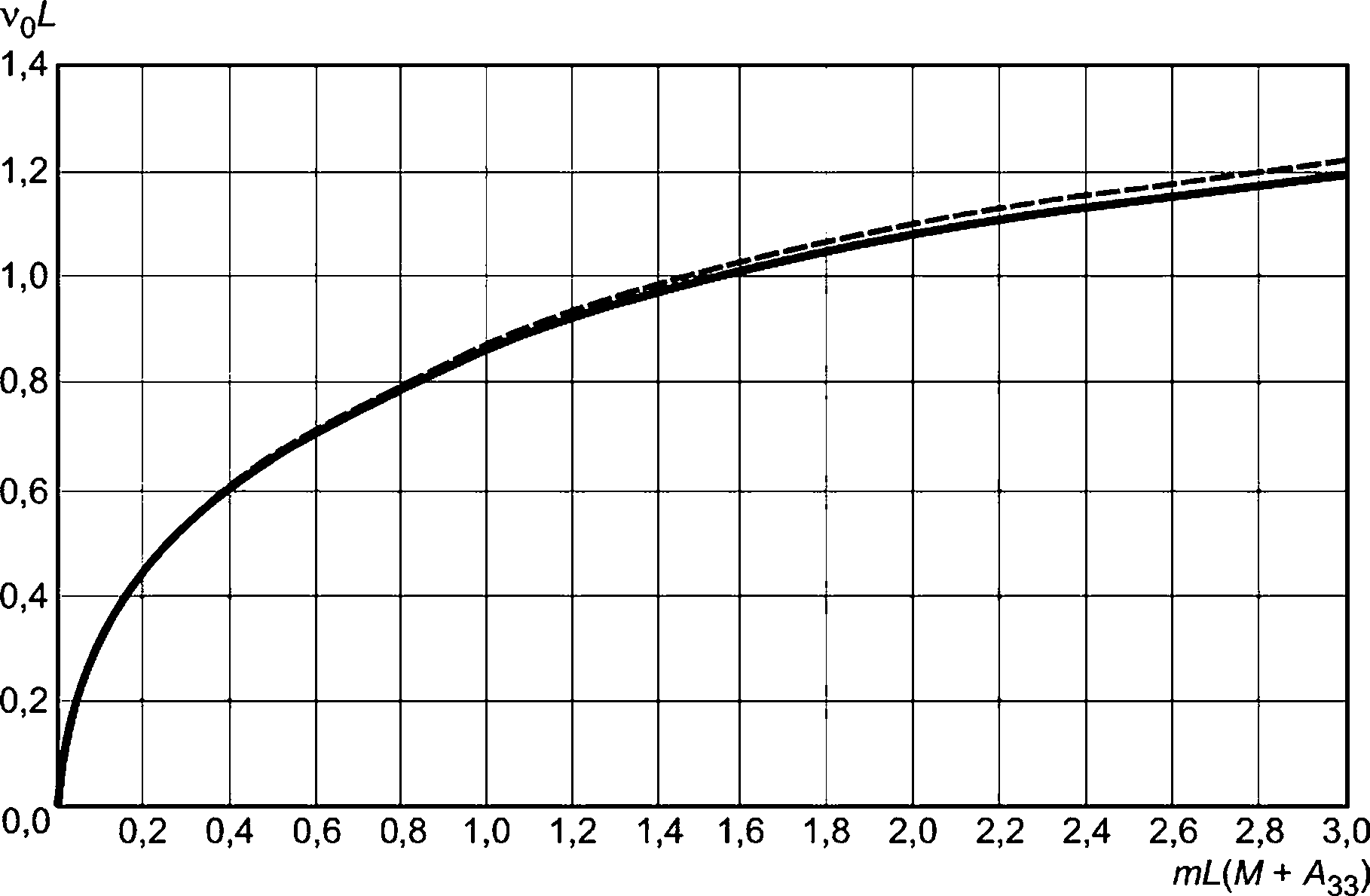
Примечание — Сплошная линия представляет точное решение, а пунктирная линия является приближением для малого отношения масс £.
Рисунок 30 — Точное решение и приближенное решение основного волнового числа v0L как функции от отношения масс (соответствующего первой собственной частоте вертикальных колебаний)
8.3.4.4 Для малых отношений масс £ более высокие собственные частоты можно оценить с помощью соответствующих волновых чисел v-, вычисленных по формуле
, mix’;L ~ jn + —--------
(220)
7 ;л(М + Д33)
где/= 1, 2, ...;
т — масса на единицу длины троса, кг/м;
М — масса поднимаемого объекта в воздухе, кг;
Д33 — присоединенная масса для движения в вертикальном направлении, кг.
Как правило, основная частота связана с колебанием поднимаемого/опускаемого объекта (с изменениями в силу массы троса), в то время как более высокие режимы связаны с продольными волнами давления в тросе (см. 8.3.6).
8.3.5 Периоды собственных колебаний
8.3.5.1 Первый (основной) период собственных колебаний для недемпфированных колебаний поднимаемого/опускаемого объекта в присутствии ведущего механизма крана и/или гибких строп (см. рисунок 31) может быть представлен как
2 я о /Л4 + Ajq + 0 * mL — = ----
®0 V К
(221)
где М — масса поднимаемого объекта в воздухе, кг;
Д33 — присоединенная масса для движения в вертикальном направлении, кг;
0 — поправочный коэффициент для учета массы троса;
т — масса на единицу длины троса, кг/м;
L — длина троса, м;
К — жесткость всей грузоподъемной системы, кг/с2, вычисляемая по формуле
_1__J_ 1 L
К~ кс + ks + ЕА’
(222)
где кс — жесткость ведущего механизма крана в верхней части троса, кг/с2;
ks — жесткость гибкой стропы или ведущего механизма крана у поднимаемого объекта, кг/с2;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2.
8.3.5.2 Поправочный коэффициент 0 для учета массы троса вычисляют по формуле
3
ч2 С )
S J
(223)
где с — скорость движения волны, м/с;
s — величина погружения цилиндра, м, вычисляемая по формуле
ksL
(224)
ЕА
где L — длина троса, м;
ks — жесткость гибкой стропы или ведущего механизма крана у поднимаемого объекта, кг/с2;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2.
8.3.5.3 Для поправочного коэффициента 0 можно применять следующие ограничивающие значения:
- 0-1/3, если жесткость троса ЕА/L является доминирующей гибкой жесткостью (и с, и s — большие числа);
- 0 - 0, если доминирующая гибкая пружина находится непосредственно над поднимаемым объектом (s «1 и с > 1);
- 0 - 1, если доминирующая гибкая пружина находится у оконечности крана (с «1 и s >1).
В случае гибких пружин с обоих концов троса (s «1 и с «1) поправочный коэффициент 0 может быть аппроксимирован с помощью выражения
• (225)
ls + c 7
В случае глубоководных работ, где грузоподъемная система главным образом состоит из одного длинного троса (каната, кабеля), допускается, что К может быть равным упругой жесткости троса кЕ (см. 8.2.4). В этом случае для заданного поднимаемого/опускаемого объекта и грузоподъемной системы период собственных колебаний увеличивается на значение, равное квадратному корню от длины троса.
Как правило, влиянием демпфирования на период собственных колебаний можно пренебречь.
8.3.5.4 Для прямых вертикальных тросов более высокие периоды собственных колебаний Tj задаются с помощью выражения
(226)
где/= 1,2, ...;
wy определено в 8.3.4.4.
Вынужденные колебания поднимаемого/опускаемого на тросе объекта с ведущим механизмом крана у верхней части троса и гибким стропом у верхней части поднимаемого/опускаемого объекта представлены на рисунке 31.
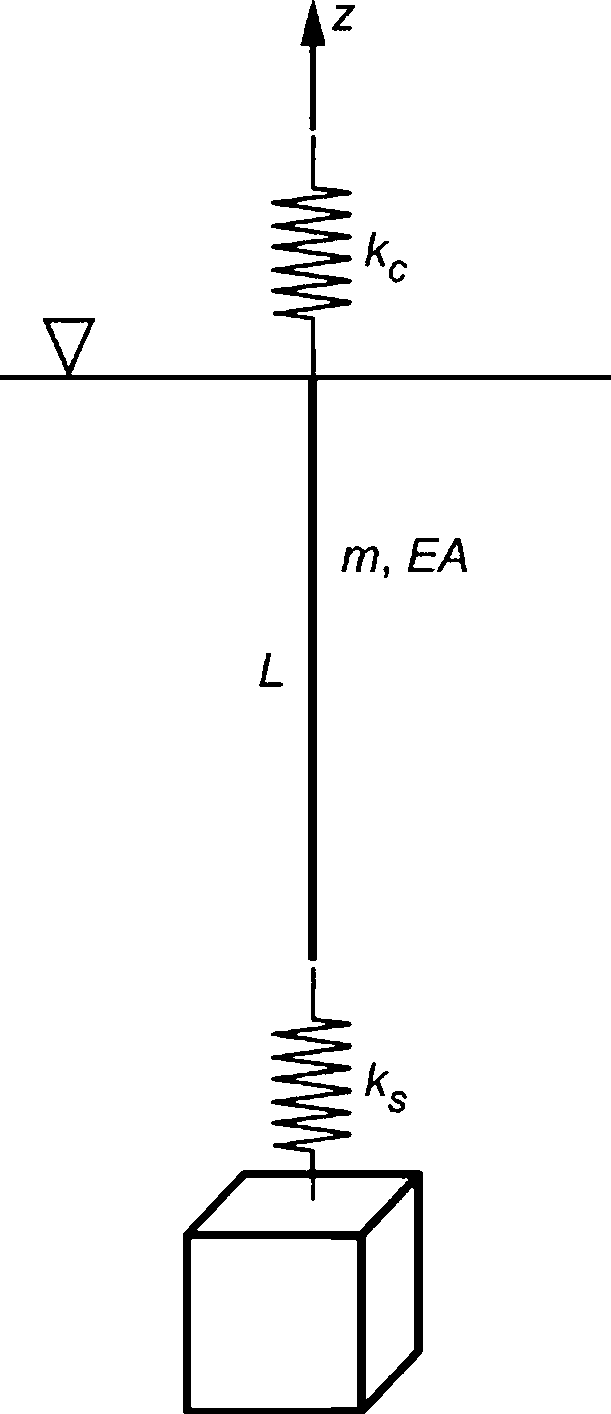
Рисунок 31 — Вынужденные колебания поднимаемого/опускаемого на тросе объекта с ведущим механизмом крана у верхней части троса и гибким стропом у верхней части поднимаемого объекта
8.3.6 Продольные волны давления
8.3.6.1 Скорость продольных волн давления в тросе (или скорость звука) cL, м/с, задается с помощью выражения
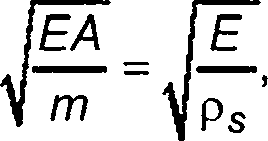
(227)
где Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2;
т — масса на единицу длины троса, кг/м;
ps — массовая плотность троса, кг/м.
8.3.6.2 Из-за продольных волн давления будут возникать динамические воздействия, когда трос возбуждается с характеристическим периодом Т, который меньше либо равен:
2L
CL
(228)
где т — время, требуемое для прохождения сигнала давления от верхней части троса вниз до конца и обратно;
cL — скорость звука, м/с.
Для стального троса с модулем упругости Е, равным 0,85-10 Н/м2, и ps, равной 7800 кг/м3, значение cL равно 3300 м/с. Для троса из полиэстера cL может быть порядка 1000 м/с, что означает, что для глубины 3000 м сигналу давления потребуется 6 с для прохождения от верхней части троса вниз до поднимаемого объекта и обратно.
8.3.7 Отклик объекта, поднимаемого на прямом вертикальном тросе, подвергающемся вынужденным вертикальным колебаниям
8.3.7.1 При подъеме глубоко погруженного объекта с судна, находящегося под действием волн, вертикальное движение объекта управляется движением верхней части закрепленного на качающемся судне троса.
Движение верхней части троса или движение оконечности крана в заданном состоянии моря выводится из характеристик движения плавучего крана с помощью линейной комбинации RAO судна, определенной расположением оконечности крана относительно центра вращения судна.
Движения оконечности крана в направлениях х, у и z могут быть объединены со спектром волны для получения временной диаграммы движения оконечности крана. При работах по опусканию в глубоких водах интерес представляет только вертикальное движение.
8.3.7.2 Вертикальное движение прямого вертикального троса с поднимаемым объектом в вертикальном положении z = -L, вызванное вынужденным колебанием верхней части троса с частотой оэ и амплитудой па, задается с помощью формулы
|n(z)| ^cos[k(z + L)] + <о2М' + /cozjsin[k(z + L)]
Ha kEcos[kL] + (-a>2M' + /coz)sin(RL)
где | | — абсолютное значение (или модуль) комплексного числа;
1 — определенный эквивалентной линеаризацией коэффициент линейного демпфирования для движения троса и движения поднимаемого объекта, соответственно;
М' — масса, равная М + Д33 (см. 8.3.4.2).
8.3.7.3 Комплексное волновое число к, м-1, определяют по формуле, где предполагается положительный квадратный корень
I I -I 1~т~ 12 • { к - к, + ik: - .—— /со —
(230)
г ' \ЕАу {mJ
где т — масса на единицу длины троса;
/ = •7^1 — мнимая единица;
о — определенные эквивалентной линеаризацией коэффициенты линейного демпфирования для движения троса и движения поднимаемого объекта, соответственно.
Вынужденное колебание поднимаемого на тросе объекта представлено на рисунке 32.
т, ЕА
Рисунок 32 — Вынужденное колебание поднимаемого/опускаемого на тросе объекта
8.3.7.4 Коэффициент линейного демпфирования о для движения троса определяют по формуле а = ^РсоА®Па. (231)
где CDf— коэффициент продольного трения троса;
Dc — диаметр троса;
г|а — амплитуда колебаний.
Продольную силу трения троса на единицу длины fv определяют по формуле
fv = 0,5р CDfDcr\|ц|, (232)
где CDf— коэффициент продольного трения троса;
Dc — диаметр троса; fi — вертикальное движение вдоль троса, определяемое как:
• ап (233)
1 dt ‘
Использование амплитуды движения у верхней части троса в определении коэффициента линейного демпфирования для движения троса является приближением. В реальности линеаризированное демпфирование изменяется на всем протяжении троса.
8.3.7.5 Коэффициент линейного демпфирования I для движения поднимаемого объекта определяют следующим образом:
s=Y-pCDzV4i- (234)
Вертикальное усилие лобового сопротивления Fv для поднимаемого объекта вычисляют по формуле
Fv = 0,5pCDzApni.|n1.|, <235>
где р — массовая плотность воды, кг/м3;
CDz — коэффициент вертикального лобового сопротивления для поднимаемого объекта;
Ар — площадь проекции z поднимаемого объекта, м2;
f]£ — движение поднимаемого объекта, равное п(—Z_), м.
Так как линеаризированные коэффициенты демпфирования зависят от амплитуды движения Ht, для нахождения фактического отклика необходим итеративный подход. При этом должны быть учтены колебательные влияния Кс на CDz (см. 6.3.5.2). Кроме того, конструкционное демпфирование не включено в данный упрощенный расчет.
8.3.7.6 Амплитуду вертикального движения поднимаемого объекта, вызванную вынужденным колебанием верхней части троса с частотой со и амплитудой г|а, определяют по формуле
hl
Па
___________кЕА____________
kEAcosfW.] + а>2М' + /coz) sin (kL)
(236)
где r|L — движение поднимаемого объекта, м;
к — комплексное волновое число;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2;
М' — общая масса, кг.
8.3.7.7 Отношение между движением поднимаемого объекта и движением у верхней части троса является функцией передачи движения /-/Jco), вычисляемой по формуле
(237)
где г|£ — движение поднимаемого объекта, м;
г|а — амплитуда колебаний.
Типовая кривая отклика поднимаемого объекта в глубокой воде, проведенная относительно периода колебания Т = 2л/со, показана на рисунке 33.
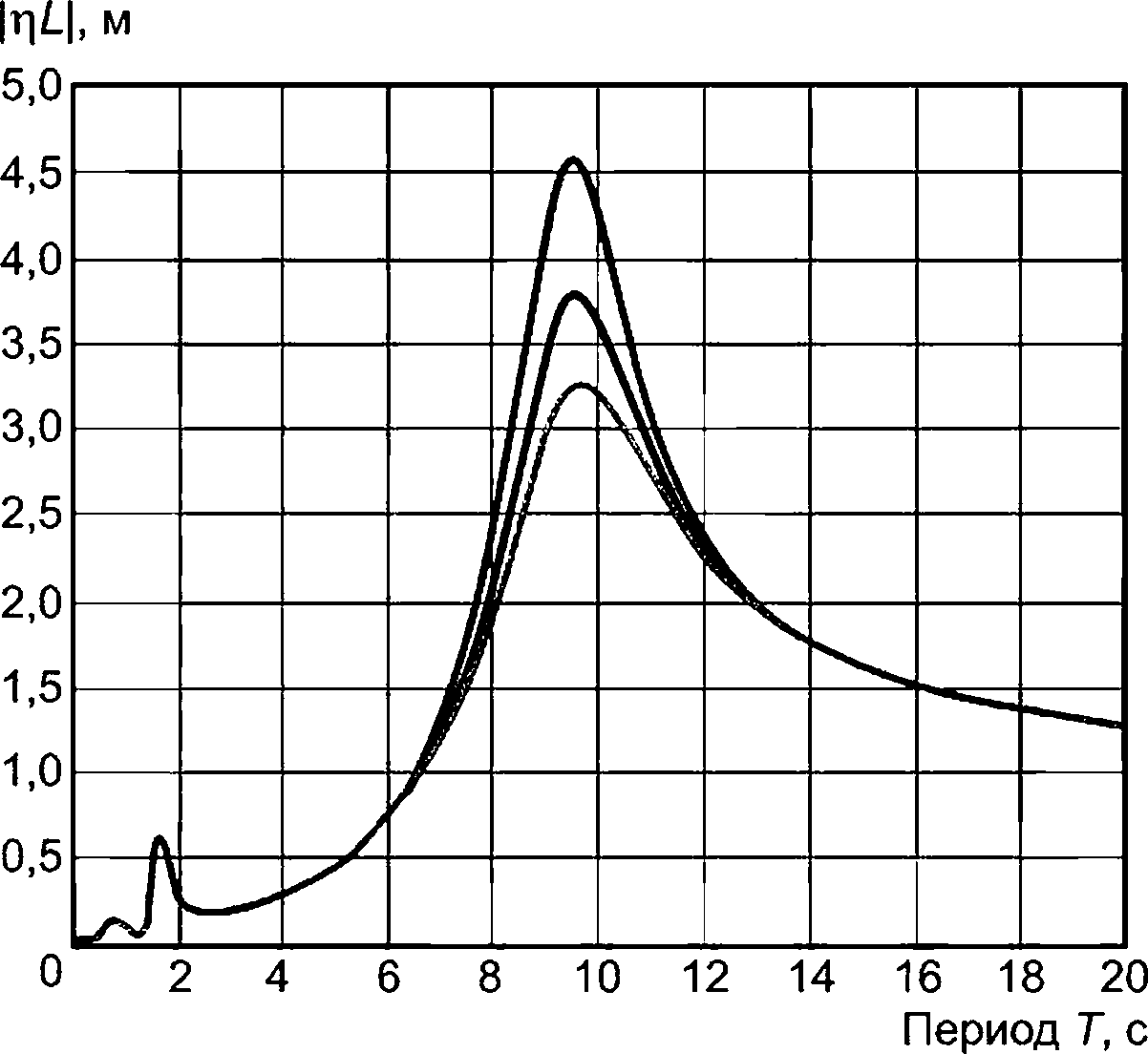
— - CDz - 1,0; — - CDz - 1,5; " - CDz - 2,0
Рисунок 33 — Типовая амплитуда отклика поднимаемого объекта в глубокой воде в силу вынужденного движения г|а = 1 м у верхнего конца троса
для трех различных коэффициентов лобового сопротивления CDz— 1,0; 1,5; 2,0
В расчетах использовались следующие параметры:
М'=М + А33 = 190 0 00 кг;
m = 25,0 кг/м;
L = 3000 м;
ЕА = 3,00Е + 08 Н;
р = 1025 кг/м3;
Dc = 0,04 м;
CDf= 0,02;
CDz= 1,0-2,0;
Ар = 25 м2;
Па= 1 м.
Сильный отклик наблюдался вблизи периода собственных колебаний 70, равного 9,2 с [как задано формулой (221) для недемпфированных колебаний]. Также может наблюдаться расширенный отклик у периода собственных колебаний Tv равного 1,7 с.
Для длительных периодов колебания объединенная система троса и поднимаемого объекта колеблется как жесткое тело, где поднимаемый объект следует за движением верхней части троса Int/Hal ~ 1-
8.3.7.8 Амплитуда динамического усилия Fd(z) в тросе на длине z определяют по выражению
Fd (z) ~(kL)2 кЕ sin[k(z + L)] + (kL)/7(co)cos[k(z + L)]
(238)
4akE
(kL)kE cos(kL) + /7(«)sin(kL)
где r|a — амплитуда колебаний;
kE — упругая жесткость троса, Н/м;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2;
к — комплексное волновое число;
/7(w) — функция передачи движения.
Амплитуду динамического усилия Fd(z) у верхней части троса определяют путем задания z = 0 в выражении (238). Аналогично амплитуду динамического усилия Fdl_ на поднимаемом объекте определяют путем задания z = - L,
(239)
где г|а — амплитуда колебаний;
кЕ — упругая жесткость троса, Н/м;
к — комплексное волновое число.
8.3.7.9 Динамическое усилие на единицу движения верхней части троса HF(co;z), Н/м, является функцией передачи усилия, вычисляемой по формуле
(240)
Hf(<d;z) = —, ^а
где Fd — динамическое усилие;
Па — амплитуда колебаний.
8.3.7.10 Движение поднимаемого объекта из-за вызванного нерегулярным волнением верхней части троса формируется путем объединения функций передачи для движения поднимаемого объекта и движения верхней части троса у оконечности крана. Спектр отклика поднимаемого объекта SJw) вычисляют по формуле
SL(<o) = [HL(o>) Ha(M)]2 S(<o), где — функция передачи движения;
(241)
/7а(со) — функция передачи движения оконечности крана; S(w) — спектр волны.
Аналогично динамическое усилие в тросе из-за вызванного волнением общего движения верхней части троса SF(w;z) вычисляют по формуле
SF(co;z) = [HF((o;z) Ha(w)]2 S(w),
(242)
где HF(u;z) — динамическое усилие на единицу движения, Н/м;
/-/а(со) — функция передачи движения крана;
S(w) — спектр волны.
8.3.8 Состояния слабо натянутого троса
8.3.8.1 В общем случае динамическое усилие изменяется вдоль длины троса из-за влияний инерции в тросе. Если амплитуда динамического усилия превышает статическое растяжение в тросе, возникает состояние слабо натянутого троса. Как вариант трос будет слабо натянут, если относительное движение между поднимаемым объектом и оконечностью крана выше статического растяжения троса:
ht - Па1 - Пет ■ (243)
где т|£ — перемещение поднимаемого объекта;
г|а — вертикальная отдельная амплитуда перемещения оконечности крана;
Пст — статическое растяжение, определяемое как: где И/ — вес подвешенного объекта в погруженном состоянии, Н;
L — длина троса, м;
w — вес в погруженном состоянии на единицу длины троса, Н/м;
Е — модуль упругости, Н/м2;
А — номинальная площадь поперечного сечения троса, м2.
8.3.8.2 Если пренебречь демпфированием из-за трения по длине кабеля (о = 0), критерий слабо натянутого троса определяют по уравнению
\1(а1а2 ? + (а1ь)2 + (а2ь)2 + ь4 т
а2 + Ь2
где безразмерные параметры определены следующим образом:
а1 — коэффициент перемещения, вычисляемый по формуле
а1 = ЛЕ cos ЛЕ - Л2 sin ЛЕ,
а2 — коэффициент перемещения, вычисляемый по формуле
a2 = \~av
b — коэффициент перемещения, вычисляемый по формуле
b = 2^Л sin ЛЕ,
где Л — безразмерная частота, вычисляемая по формулам:
(249)
(250)
где е — случайная фаза, отношение масс, вычисляемое по формуле
М'
(251)
£ — безразмерное демпфирование (коэффициент демпфирования), вычисляемое по формуле
(252)
(253)
£ = , s 2 УЕАМ'
где т — коэффициент перемещения, вычисляемый по формуле
I = г*ст Па ’
где Z — линеаризированное демпфирование (см. 8.3.7.5).
Области состояний натянутого и провисающего тросов показаны на рисунке 34 для соотношений масс с коэффициентов демпфирования равных 0; 0,4 и 1,0.
Пренебрежение демпфированием из-за трения вдоль длины троса сокращает область провисания (Л, т). Для учета этого необходимо провести сравнение между усилием лобового сопротивления Fvl_ на поднимаемом объекте и общей силой трения fvL вдоль длины троса (см. 8.3.7.4) и увеличить коэффициент демпфирования на коэффициент 1 + fvL/Fv в критерии т. Критерий слабо натянутого троса, подобный для общего случая, включая демпфирование из-за трения вдоль длины троса, может быть выведен из общего критерия г|ст с использованием формул (230) и (236) соответственно.
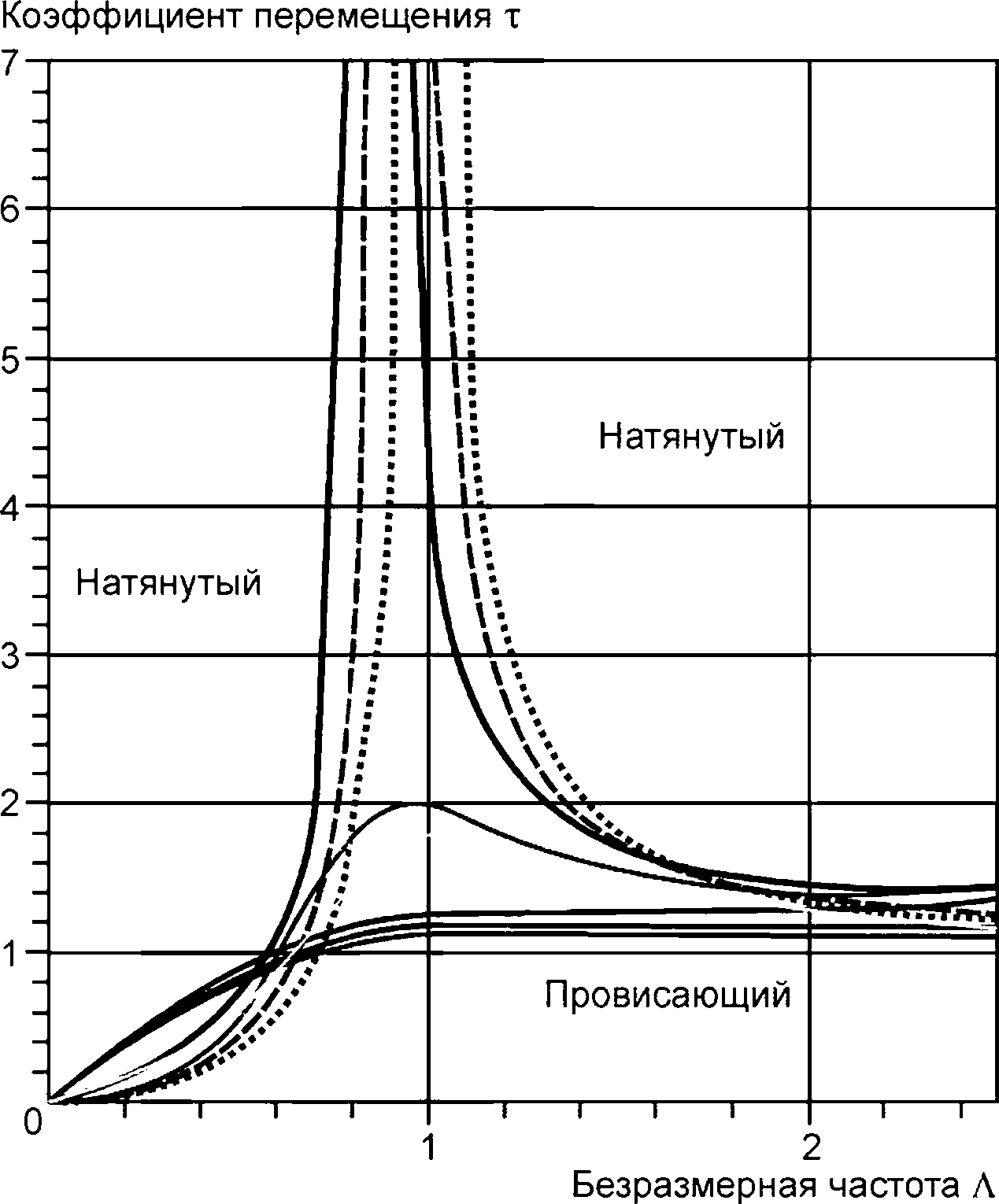
.......8 = 0,0; § = 0,0;---s = 0,0; 4 = 0,4; -----s = 0,0; £, = 1,0; e = 0,4; § = 0,0;
-----8 = 0,4; £ = 1,0; -----8 = 1,0; c = 0,0; -----s = 1,0; £ = 0,4; -----e = 1,0; £ = 1,0
Рисунок 34 — Области состояний натянутого и провисающего тросов для заданных частоты и амплитуды колебания
Области зависят от отношения масс и демпфирования поднимаемого объекта.
8.3.8.3 В случае пренебрежимо малой массы троса критерий для предстоящего провисания в тросе может быть выражен как:
Л4 +(2£Л)2
(254)
'Л4 (л2 + 4£2 -l)2 + (2£Л)2
где Л — безразмерная частота;
£ — безразмерное демпфирование (коэффициент демпфирования);
т — коэффициент перемещения.
Для исследования состояний провисания могут быть прямо использованы следующие приближения. Для небольших значений демпфирования £ < 0,01 состояние можно аппроксимировать следующим образом:
(255)
где Л — безразмерная частота;
т — коэффициент перемещения.
Для небольших коэффициентов перемещения т < 0,04 состояние можно аппроксимировать следующим образом:
^л4 +(2£Л)2 > т, где Л — безразмерная частота;
(256)
£ — безразмерное демпфирование (коэффициент демпфирования);
т — коэффициент перемещения.
8.3.9 Отклик горизонтального перемещения объекта, поднимаемого на прямом вертикальном тросе
8.3.9.1 Первый (основной) период собственных колебаний для недемпфированных колебаний поднимаемого объекта TOh может быть определен как
Л)/?
(257)
где М — масса поднимаемого объекта, кг;
А^ — присоединенная масса продольно-горизонтальной качки поднимаемого объекта, кг;
т — масса на единицу длины троса, кг/м;
L — длина троса, м;
И/ — вес поднимаемого объекта в погруженном состоянии, равный Мд - pgV, Н;
w — вес в погруженном состоянии на единицу длины троса, равный тд - рдА, Н/м.
8.3.9.2 Применение присоединенной массы А22 при поперечно-горизонтальной качке в уравнении (243) обеспечит период собственных движений поперечно-горизонтальной качки поднимаемого объекта.
8.3.9.3 Если спектр энергии океанского течения отличается от нуля в близком к f0 = ^\/Т0Ь диапазоне частот, то могут быть возбуждены горизонтальные колебания поднимаемого объекта. Аналогично колебания могут быть возбуждены горизонтальным движением оконечности крана. Такие колебания могут быть существенно снивелированы из-за вязкостного лобового сопротивления на тросе и поднимаемом объекте.
8.4 Компенсация вертикальной качки
8.4.1 Общие положения8.4.1.1 Для компенсации вертикального движения судна могут быть использованы различные устройства управления движением (см. [1]). Наиболее часто применяемым устройством является компенсатор вертикальной качки.
8.4.1.2 Компенсатор вертикальной качки может быть использован для управления движением поднимаемого объекта на тросе во время подъемной операции.
8.4.1.3 Компенсаторы вертикальной качки могут быть разделены на три основные группы:
- пассивные компенсаторы вертикальной качки;
- активные компенсаторы вертикальной качки;
- совмещенные пассивные/активные системы.
8.4.1.4 Пассивный компенсатор вертикальной качки представляет собой пружинную демпферную систему, которая не требует поступления энергии во время работы. При работе активного компенсатора вертикальной качки могут быть задействованы активно управляемые лебедки и гидравлические поршни. Активная система управляется опорным сигналом. В совмещенной системе активная система работает параллельно с пассивной.
8.4.1.5 Примерами входных опорных сигналов на активный компенсатор вертикальной качки являются:
- натяжение кабеля;
- движение верхней части крана;
- движение лебедки или гидравлического поршня;
- положение поднимаемого объекта;
- движение судна;
- высота волны/скорость течения.
8.4.2 Динамическая модель для компенсации вертикальной качки (типовой случай)
8.4.2.1 В качестве типового случая показана упрощенная динамическая модель для находящегося на оконечности крана пассивного компенсатора вертикальной качки (см. на рисунок 35). Уравнения движения у верхней части кабеля т|зр и у поднимаемого объекта г|3 могут быть представлены следующим образом:
тс Пзр + сс’1зр + кс^ЗР + kw (Пзр _ Пз)= F3T (О- (258)
где тс — масса компенсатора вертикальной качки, кг;
Лзя — ускорение вертикального движения у верхней части кабеля, м/с2;
сс — линейное демпфирование компенсатора вертикальной качки, кг/с;
ЛЗТ — скорость вертикального движения у верхней части кабеля, м/с;
кс — жесткость компенсатора вертикальной качки, Н/м;
Пзр — вертикальное движение у верхней части кабеля, м;
kw — жесткость кабеля, равная EA/L, Н/м;
г|3 — вертикальное движение поднимаемого объекта, м;
F3T(/) — вертикальное усилие у оконечности крана (т. е. у верхней части компенсатора), Н;
(Л4 + Дзз)пз+сг]3 + kw (т|3 - г|3р) = F3M (/), (259)
где М — масса поднимаемого объекта, кг;
Д33 — присоединенная масса поднимаемого объекта, кг;
Лз — ускорение вертикального движения поднимаемого объекта, м/с2;
с — линейное демпфирование поднимаемого объекта, кг/с;
Лз — скорость вертикального движения поднимаемого объекта, м/с;
kw — жесткость кабеля, равная EA/L, Н/м;
П3 — вертикальное движение поднимаемого объекта, м;
П3р— вертикальное движение у верхней части кабеля (т. е. ниже компенсатора), м;
F3/W(f) — вертикальное усилие у поднимаемого объекта, Н.
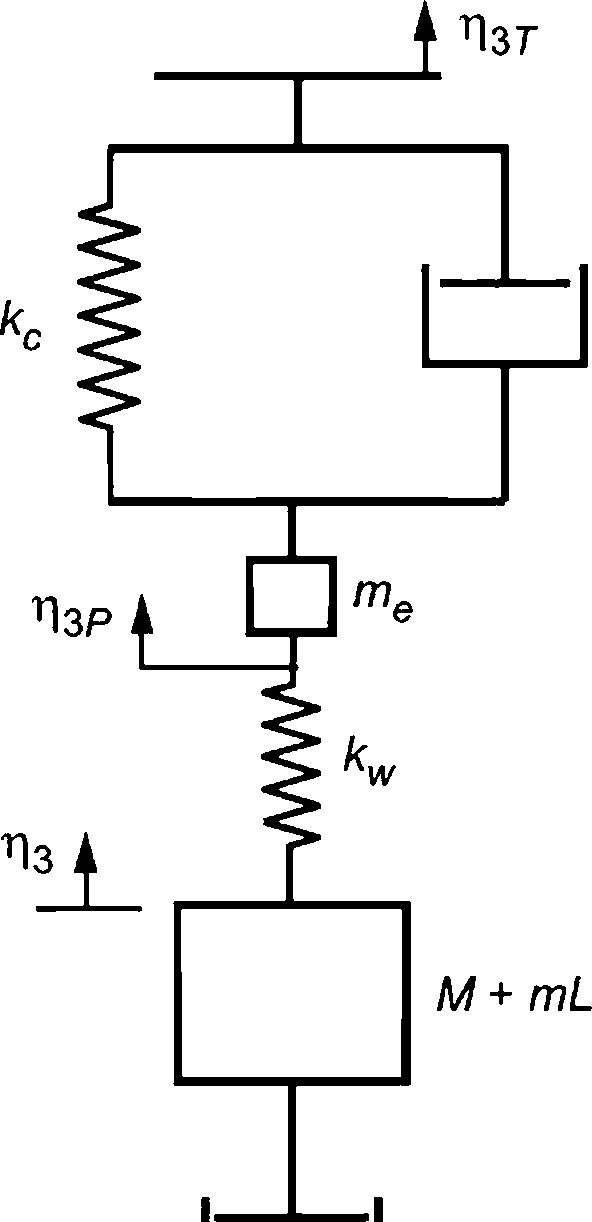
Рисунок 35 — Упрощенная динамическая модель пассивного компенсатора вертикальной качки
Следует учитывать, что демпфирование компенсатора и поднимаемого объекта в целом происходит из-за квадратичного вязкостного демпфирования, а жесткость компенсатора, в целом, является нелинейной. Оценки линейного демпфирования можно получить путем эквивалентной линеаризации. Жесткость компенсатора может быть обусловлена сжатием объема газа в пневматических цилиндрах.
8.4.2.2 В случае вынужденного движения верхней части компенсатора при движении судна усилие на компенсатор F3T, Н, вычисляют по формуле
= Пзт^с + ссПзт> (26°)
где г|37- — вертикальное движение у оконечности крана (т. е. у верхней части компенсатора), м;
кс — жесткость компенсатора вертикальной качки, Н/м;
сс — линейное демпфирование компенсатора вертикальной качки, кг/с;
Лзт — скорость вертикального движения у верхней части компенсатора, м/с.
8.4.2.3 Вертикальное усилие F3M(t), действующее на поднимаемый объект, связано с движением верхней части кабеля т|зр = т|а с помощью функции передачи (см. 8.3.7.2).
8.4.2.4 В операции опускания длина кабеля изменяется со временем. Вследствие этого жесткость кабеля kw будет функцией от времени.
8.4.2.5 Для заданных временных рядов F37[t) и F3M(t) уравнения движения (258), (259) могут быть интегрированы по времени путем замены двух уравнений на четыре дифференциальных уравнения первого порядка и использования стандартной схемы интегрирования, т. е. метода Рунге—Кутта 4-го порядка.
8.4.2.6 Гармоническое внешнее возбуждающее воздействие верхней части компенсатора F3T(t), Н, вертикальной качки вычисляют по формуле
F3tW = F3Ta cos (261)
8.4.2.7 Отношение между откликом поднимаемого объекта и возбужденным движением можно определить через комплексную функцию передачи:
Лзт
(262)
где т|3 — вертикальное движение поднимаемого объекта, м;
г|37-— вертикальное движение у оконечности крана (т. е. у верхней части компенсатора), м; G(co) — комплексная функция передачи.
Эффективность компенсатора вертикальной качки определяют как
e=1-|G(co)|,
(263)
где G(co) — комплексная функция передачи.
8.4.2.8 Как правило, для управления разматыванием троса лебедки активные системы компенсации вертикальной качки используют информацию от датчика движения судна. Движение вертикальной качки у оконечности крана рассчитывают исходя из движений судна в шести степенях свободы, а сигнал подают на блок компенсатора.
8.4.2.9 Измерения движения и система управления неизбежно вносят погрешности и задержки по времени. Вследствие этого для получения реалистичных результатов теоретическая модель активной компенсации вертикальной качки должна учитывать физические несовершенства. Такие несовершенства должны быть основаны на эксплуатационных данных для реальной системы.
8.4.2.10 Отклонения из-за несовершенных измерений движения и управления слежением могут привести к остаточному движению подъемного троса в точке подвеса на судне. Данное остаточное движение может вызывать низкоамплитудные колебания поднимаемого объекта с частотой резонанса.
8.4.2.11 Как правило, активный компенсатор вертикальной качки неодинаково эффективно уменьшает колебания на всех частотах: на одних частотах он будет более эффективным, чем на других.
8.5 Свойства волоконного троса
8.5.1 Общие положенияВолоконные тросы состоят из материалов, демонстрирующих вязкоупругие свойства. Это означает, что характеристики отклика значительно отличаются от идеального упруго-пластического отклика для стали. К основным различиям относят следующие:
- отклик является нелинейным и неупругим;
- отсутствует возврат в первоначальный случай статической нагрузки;
- наблюдается связанное с динамическими нагрузками рассеяние энергии (гистерезис). При подъеме и спуске существуют разные схемы вытягивания под нагрузкой. Гистерезис зависит от истории нагружения;
- со временем происходит непрерывное удлинение троса под действием статической или динамической нагрузки (ползучесть).
Выбор волоконного материала зависит от области применения. Для систем глубоководного размещения применен сверхвысокомолекулярный полиэтилен (НМРЕ) в силу его высокой удельной прочности и высоких жесткостных характеристик. Другим вариантом является арамид, имеющий более высокую жаростойкость, чем НМРЕ. Ограничивающие срок службы НМРЕ факторы включают в себя гидролиз, нагрев (из-за нагрузки изгиба над шкивом) и внутреннее истирание, усталость при растяжении, осевую усталость при сжатии и расползание.
8.5.2 Удлинение и жесткость
8.5.2.1 Характеристики изменения в длине волоконных тросов являются более сложными, чем аналогичные характеристики стального троса. Поскольку деформация для такого же уровня нагрузки может отличаться, жесткость может быть нелинейной. Остаточная деформация может быть значительной. Как жесткость, так и деформация зависят от истории нагружений и даже от частоты колебаний нагрузок.
8.5.2.2 Растяжение AL = Ls - L определяют как изменение длины троса. Деформацию е определяют как изменение длины, разделенное на длину L до изменения натяжения, и вычисляют по формуле
£ = ^l, (264)
L
где AL — растяжение троса;
L — длина троса до изменения натяжения.
Безразмерную жесткость S определяют как прирастающее натяжение троса AF/F0
AF
S = A_. (265)
1-0
где AF — изменение нагрузки;
Fo — минимальная разрушающая нагрузка, разделенная на деформацию s.
Прочность троса Fo также обозначается MBL (минимальная разрушающая нагрузка).
8.5.2.3 Характеристики изменения в длине полиэфирных тросов в целом могут быть описаны шестью элементами:
ер — деформация полимера при ползучести, функция от времени под натяжением;
ес— конструктивная деформация троса, функция от наиболее высокого приложенного натяжения;
So — первоначальная жесткость во время нагружения до нагрузки, которая превышает любую предыдущую нагрузку;
Ss — статическая жесткость во время последующих нагружений менее самой высокой предыдущей нагрузки или вплоть до нее;
Sd— динамическая жесткость после нескольких относительно быстрых циклов нагружения;
sse — длительная упругая деформация, которая возникает в течение циклического повторения и возвращается в исходное состояние после циклического повторения.
8.5.2.4 Коэффициент упругости К для волоконного троса определяют по выражению
K = AF) (266)
AL
где AF — изменение нагрузки;
AL — растяжение троса.
Для коэффициента упругости используют следующие обозначения:
KQ — первоначальный коэффициент упругости;
Ks — статический коэффициент упругости;
Kd — динамический коэффициент упругости.
8.5.2.5 Обычно используемой для записи жесткости на основании результатов испытания величи-Е
нои является удельный модуль упругости —, который устраняет влияние изменения площади попереч-Ps
ного сечения и который вычисляют по формуле
= (267)
Ps т
где Е — модуль упругости Юнга, Н/м2;
ps — массовая плотность волоконного троса, кг/м3;
Д — площадь поперечного сечения, м2ж;
т — масса на единицу длины троса, кг/м.
Следует учитывать, что скорость продольных волн давления в волоконном тросе равна квадратному корню из удельного модуля упругости.
8.5.2.6 При колебании подвешенного груза удельный модуль упругости для волоконного троса в целом зависит от средней нагрузки и амплитуды нагружения, а также от частоты колеблющейся нагрузки. В этом случае удельный модуль упругости — вычисляют по формуле
р
— = a + pFm-yFa + 5log10(f), (268)
р
где Fm — средняя нагрузка, Н;
Fa — амплитуда нагружения, Н;
f— частота внешнего возбуждающего воздействия, Гц;
а, р, у, 8 — постоянные.
8.5.2.7 Так как зависимость от частоты нагружения является только логарифмической, дополнительные факторы элемента частоты не существенны и ими можно пренебречь. Следует отметить, что влияния амплитуды и частоты нагружения обычно стремятся к нулю в условиях сложных циклов нагрузки (соответствующих фактическим волновым нагрузкам).
8.5.2.8 Постоянное растяжение влияет на изменение длины волоконного троса. Оно вызывает затруднения при определении длины волоконного троса во время операции опускания и подъема.
8.5.2.9 Связанное с первоначальным нагружением нового волоконного троса дополнительное удлинение, когда трос втягивается в более тугую и, следовательно, более жесткую конструкцию. Во время первоначальных установки и натяжения определить общую жесткость затруднительно. После полного принятия начальной нагрузки в течение установленного периода времени трос в какой-то степени возвращается в исходное состояние. После натяжения троса для возможности приработки, возникновения циклической нагрузки и ослабления на определенное время жесткость волоконных тросов стремится в направлении линейной функции средней нагрузки и диапазона нагрузки.
8.5.3 Ползучесть
8.5.3.1 Удлинение в волоконных тросах возникает из-за приработки в структуре и концах троса, а также как от первоначального расширения, так и от ползучести в пучках волокон. Ползучесть может негативно влиять на НМРЕ под действием сильных натяжений.
8.5.3.2 Ползучесть полиэфирного троса вычисляют по формуле
t/=u0+aclog10 1 + -^—М , V го )
(269)
где и0 — удлинение при t = tQ, измеренное от начала нагружения;
t0 — начало отсчета времени, т. е. начало плоского участка нагрузки;
ас — ползучесть на декаду.
8.5.3.3 Ползучесть может быть разделена на три вида:
- первичная ползучесть (восстанавливаемая часть удлинения);
- вторичная ползучесть (постоянная часть удлинения);
- расползание (наиболее повреждающая форма ползучести).
8.5.3.4 Первичная ползучесть также называется отложенным упругим удлинением и является восстановимой. Для большинства волоконных тросов скорость ползучести снижается со временем и становится примерно одинаковой для равных приращений логарифмического времени.
8.5.3.5 Вторичная ползучесть является результатом постоянного увеличения длины волоконного троса, находящегося под длительной нагрузкой в течение времени, и представляет собой часть, которая является значимой для используемых при глубоководном размещении волоконных тросов, изготовленных из НМРЕ. Вторичная ползучесть не подчиняется такой же логарифмической функции времени, как и первичная ползучесть, а линейно увеличивается со временем.
8.5.3.6 Защиту от расползания можно обеспечить посредством использования основанного на постоянном удлинении троса критерия отбраковки (предложено 10 %).
8.5.4 Осевое демпфирование
8.5.4.1 Осевое демпфирование троса является значимым параметром для прогнозирования динамического отклика системы при действии полезной нагрузки и троса, а также при анализе нагрузок рывка и резонансного отклика. В таких случаях осевое демпфирование волоконного троса определяет пиковое натяжение в тросе.
8.5.4.2 Коэффициент демпфирования для волоконных тросов может зависеть от массы подвешенного груза. Относящиеся к осевому демпфированию волоконных тросов данные являются недостаточными.
8.5.5 Усталостная стойкость волоконных тросов, совершающих цикл через шкивы
Усталостная стойкость волоконных тросов, совершающих цикл через шкивы, ограничена следующими факторами:
- вызывающее риск проскальзывания и обгорания низкое трение тросов о стальные шкивы;
- риск истирания и врезания, при которых несколько слоев троса наматываются друг поверх друга;
- ведущий к ползучести или плавлению троса внутренний нагрев.
9 Опускание на морское дно и извлечение
9.1 Общие положения
9.1.1 Типы конструкций и основанийВ настоящем разделе приведены требования по оценке спуска на морское дно и по извлечению любой подводной конструкции с постоянным или временным основанием, состоящим из плоских оснований, которые могут быть как с юбками, так и без них. Сюда включаются такие решения по основаниям, как задавливаемые самопогружные сваи, также называемые цилиндрическими основаниями или башмаками. Монтаж или извлечение забивных свай или буронабивных и набивных свай не рассмотрены.
9.1.2 Инженерно-геологические данные
Требуемые для данных оценок инженерно-геологические данные будут, как правило, включены в данные, собранные и определенные для расчета основания.
9.2 Опускание на морское дно
9.2.1 Общие положения
9.2.1.1 Целью оценки опускания на морское дно должно быть обеспечение того, что:
- при опускании не произойдет разрушения фундамента;
- не будет повреждено чувствительное к ускорению оборудование.
Таким образом, необходимы критерии приемлемости для сравнения с рассчитанными/оцененны-ми откликами по отношению к допустимым смещениям или допустимым ускорениям (замедлениям).
9.2.1.2 Оснащение решения по основанию (например, размер плоских оснований) юбками напрямую зависит от типа и характеристик подводной конструкции и свойств грунта. Решение по основанию также влияет на задачи при опускании и на то, как это будет учтено.
9.2.1.3 Некоторые основания на твердых грунтах имеют существенную способность выдерживать без юбок вес в погруженном состоянии, в силу чего оценка опускания должна сконцентрироваться на усилии динамического воздействия и максимальных замедлениях. Для других оснований на мягком грунте может потребоваться значительное проникновение юбок до того, как грунт сможет выдержать даже статический вес конструкции в погруженном состоянии. В таком случае, чтобы давление воды не превышало несущей способности грунта, основной проблемой проектирования является обеспечение достаточной площади отверстий для отвода захваченной внутри юбки воды по мере их проникновения.
9.2.1.4 В следующих пунктах рассмотрен вопрос относительно удара при опускании, включая описание задействованных физических воздействий и параметров. Затем представлены оптимальное решение с учетом всех возникающих воздействий и упрощенные методы проверки удара при опускании основания без юбок на твердый грунт и методы требуемого отвода воды при опускании оснований с юбками на предельно мягкий грунт.
9.2.2 Определение проблемы удара при опускании
9.2.2.1 В настоящем пункте рассмотрен метод моделирования опускания цилиндра на морское дно с одной степенью свободы — вертикальным движением.
9.2.2.2 Пока центр тяжести и центр реакции для других усилий совпадают с геометрическим центром оснований, данный метод также может быть использован для решения вертикального удара конструкций с несколькими основаниями. В данном случае массы и усилия могут быть равно поделены на каждое из оснований, и удар может быть рассчитан для одного основания.
9.2.2.3 Основание башмака без юбки, модель которого представлена на рисунке 36, является отдельным случаем для расчета.
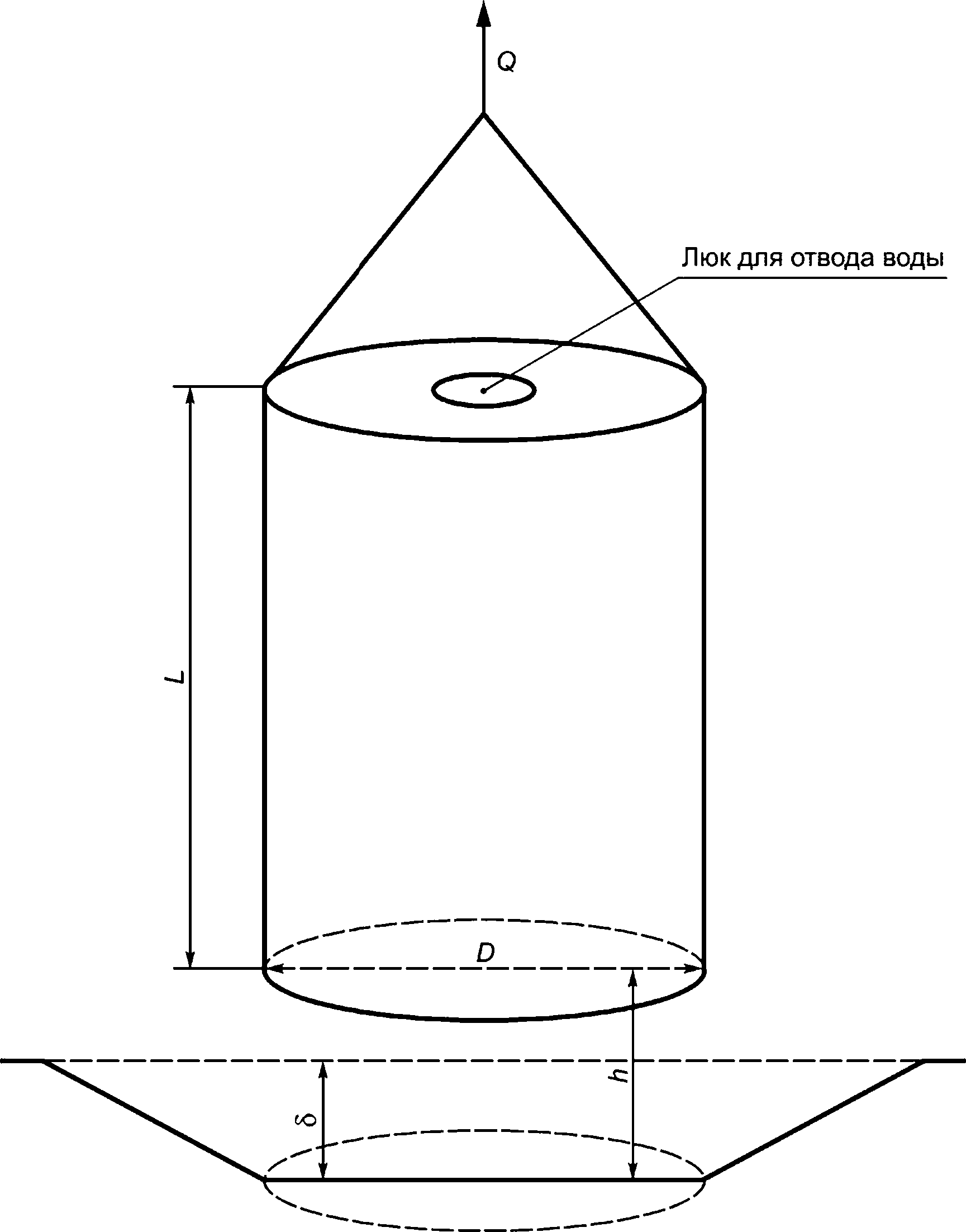
Q — вертикальная сила, действующая на цилиндр;
8 — скорость изменения смещения грунта
Рисунок 36 — Модель опорного башмака без юбки
9.2.2.4 Свая опускается вниз на морское дно на стропе с подвергающегося действию волн судна-укладчика.
9.2.2.5 При опускании вертикальное движение сваи определено направленной вниз постоянной скоростью плюс колебательным движением вертикальной качки в результате вызванного волнами движения судна-укладчика.
9.2.2.6 Геометрия башмака упрощена до вертикальной цилиндрической поверхности с диаметром D и высотой L. Люк для отвода воды расположен в верхней части сваи.
9.2.2.7 Удар должен быть вычислен путем интегрирования по времени общего уравнения движения, что может быть выполнено как обеспечивающее сохранение энергии интегрированием по времени.
Все действующие на основание соответствующие усилия следует рассматривать в интегрировании по времени мгновенными зависимыми от времени значениями. Такими усилиями являются сила тяжести, выталкивающее усилие, усилия в стропах, динамическое давление воды внутри цилиндра и сопротивление грунта, действующее на юбки по мере их проникновения.
9.2.3 Подлежащие рассмотрению физические характеристики и воздействия
9.2.3.1 В имитационной модели задействованы нижеприведенные физические характеристики. Если башмак состоит только из стальной емкости, вес в погруженном состоянии IV вычисляют по формуле
(270)
W=Mgt^—В, Ps
где М — конструкционная масса, кг;
д — ускорение свободного падения, м/с2;
ps — массовая плотность стали, кг/м3;
р — массовая плотность воды, кг/м3.
9.2.3.2 Конструкционная масса М должна включать в себя массу конструктивных элементов и оборудования на верхней части сваи.
9.2.3.3 Для типового цилиндрического фундаментного основания присоединенную массу для вертикального движения, включая массу захваченной внутри юбок воды, Д33, кг, вычисляют по формуле
(271)
где Аь = лО2/4 — площадь основания цилиндра, м2;
D — диаметр цилиндра, м;
L — длина цилиндра, м.
Для представления вызванной конструктивными элементами и оборудованием на верхней части сваи присоединенной массы, возможно, потребуется добавление дополнительной присоединенной массы.
На присоединенную массу при вертикальной качке могут повлиять высота цилиндра и размер вентиляционного отверстия. Более точная оценка представлена в 7.6.3.
9.2.3.4 Общую динамическую массу М' вычисляют по формуле
(272)
М' = М + д33, где Д33 — присоединенная масса для вертикального движения, кг.
Первоначальную кинетическую энергию Ек0 вычисляют по формуле
(273)
Ек0 = ус0 ’
где М'— общая динамическая масса;
vc0 — первоначальная скорость в начале расчетов.
9.2.3.5 Для вертикального движения предельно близкого ко дну моря объекта присоединенная масса будет изменяться вместе с расстоянием до морского дна. При этом воздействует направленное вверх усилие величиной
0,5
dh
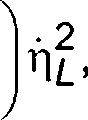
(274)
где dA33/dh — скорость изменения присоединенной массы относительно h, кг/м;
h — расстояние до морского дна, м;
— скорость объекта, м/с.
В данной оценке гидродинамического усилия для присоединенной массы использован такой же подход, как для выхода из воды (см. 6.2.11.2).
9.2.3.6 Гидродинамическое давление воды увеличивается по мере приближения цилиндра к морскому дну, а площадь для отвода воды уменьшается. Подъем давления воды также зависит от взаимодействия с грунтом (мобилизация несущей способности грунта). Должно быть учтено увеличение несущей способности при проникновении юбки, а сопротивление проникновению юбки должно быть включено в расчеты.
9.2.3.7 Сумма сопротивления проникновению и усилия от давления воды внутри цилиндра должна быть ограничена несущей способностью.
9.2.3.8 Гидродинамическое усилие от давления воды под башмаком и внутри башмака pw, Н/м2, рассчитывают с использованием уравнения Бернулли
„ _lk BV2 (275)
"и/ ~ 2 кпотР''пот ’
где кпот — коэффициент падения давления;
р — массовая плотность воды, кг/м3;
упот — скорость выходящей из цилиндра воды, м/с.
9.2.3.9 Когда длина цилиндра больше его диаметра, вычисляют коэффициент падения давления кпот по формуле
*пот =1 + 1/2
/ . \2~|2 1-рп
I D J
+ /п£.ц / ф,
(276)
где dj — диаметр потока, м;
f— коэффициент трения;
п — количество потоков;
/_ц — длина цилиндра, м.
9.2.3.10 Также коэффициент кпот может быть рассчитан для разных геометрий выходного отверстия.
9.2.3.11 Скорость выходящей из цилиндра воды упор м/с, вычисляют по формуле
., _ Фют
(277)
пот " А 'тот
где дпот — расход воды, выходящей из цилиндра, м3/с;
Дпот — площадь, равная Ah + nD-h, м2;
Ah — площадь имеющихся в башмаке отверстий, м2;
h — просвет между грунтом и краем юбки, который уменьшается по мере приближения башмака к морскому дну, м.
9.2.3.12 Если вода является несжимаемой жидкостью, то расход выходящей в любое время изнутри и снизу цилиндра воды дпот вычисляют по формуле
(278)
^пот — Ab ' (— $гр ) ’ где Аь — площадь основания цилиндра, м2;
vc — вертикальная скорость цилиндра, а;
§ — изменение смещения грунта из-за изменения в несущем давлении, происходящее в течение отрезка времени dt, вычисляемое по формуле
с/5Го
(279)
(280)
5 ____[В.
гр dt
9.2.3.13 Передаваемое на грунт в любое время общее усилие Qrp вычисляют по формуле
О = О + О с
^гр WK)6’
где — вытекающее из гидродинамического давления воды усилие;
ОЮб — усилие, передаваемое от заглубляющихся юбок грунту.
9.2.3.14 Мобилизация несущей способности грунта как зависимость между Qrp и 8гр показана на рисунке 37. Принимая, что мобилизация сопротивления грунта является параболической функцией, можно использовать следующее соотношение Qrp и 8гр:
й™ 8гр<8мо6. (281>
V $МОб
где Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н;
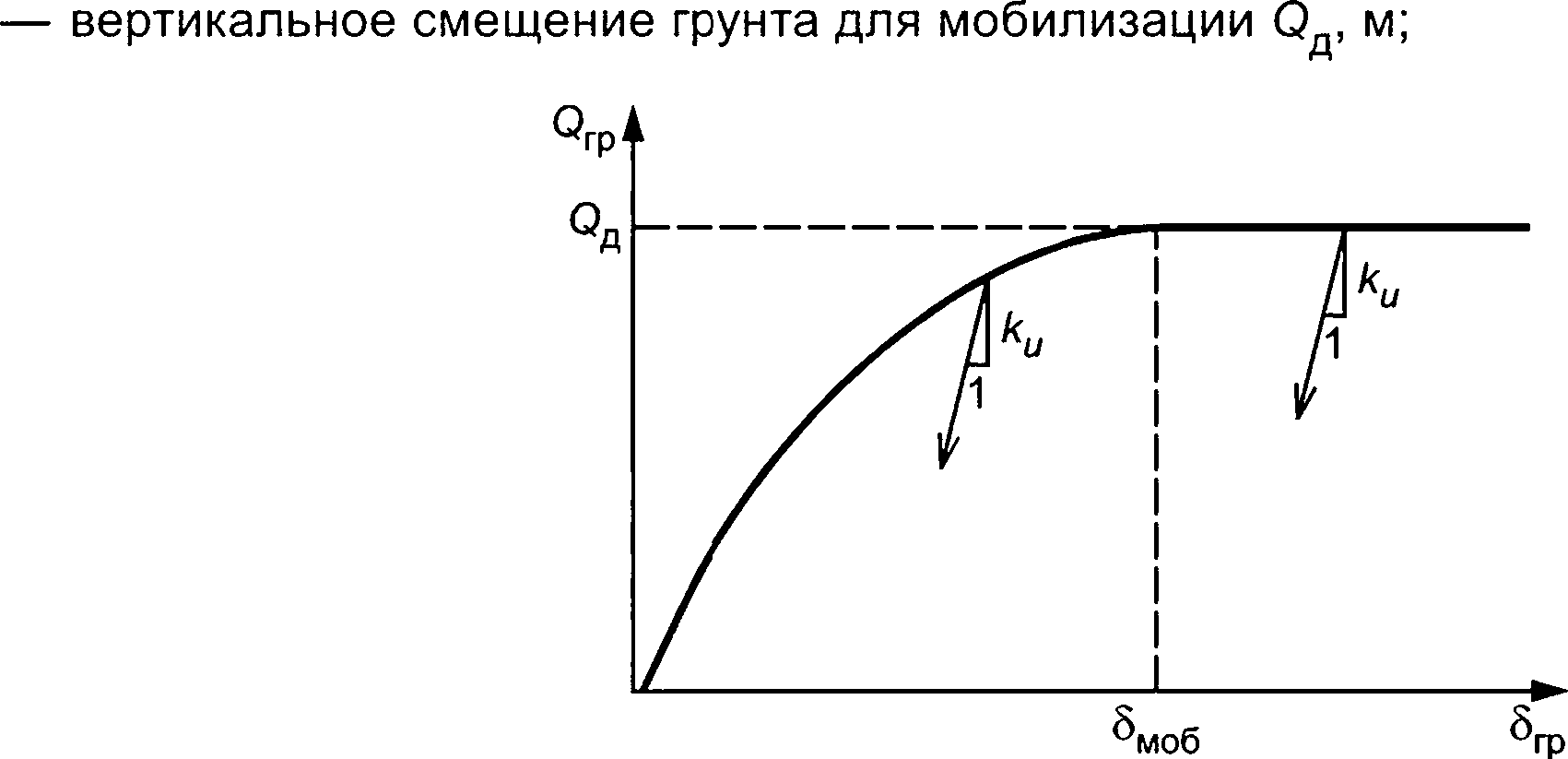
Примечание — При Srp > 5моб Qrp принимают равным Од; ки — разгрузочная жесткость, Н/м.
1 — направление действия нагрузки
Рисунок 37 — Мобилизация несущей способности грунта
9.2.3.15 Характеристическое статическое сопротивление грунта Qsc для использования в расчетах переводят в расчетное сопротивление грунта при помощи формулы
Qsd = О«с—• (282>
Ут
где уг — коэффициент воздействия скорости для учета увеличенной прочности на сдвиг вследствие быстрой нагрузки;
ут — коэффициент материала грунта.
9.2.3.16 Несущая способность грунта может быть определена на основании формул несущей способности или с помощью компьютерных программ, использующих методы предельного равновесия или конечных элементов. Сопротивление проникновению юбки может быть рассчитано согласно 9.2.8.
9.2.3.17 Задача удара опорного башмака может быть решена путем интегрирования по времени с итеративным решением на каждом шаге по времени. Расчеты должны начинаться на расстоянии от морского дна, где умеренное нарастание гидродинамического давления смещения грунта.
9.2.3.18 Для грузоподъемного оборудования учитывают ограничения по скорости опускания, а также амплитуду и период синусоидального движения вертикальной качки. Исходными данными являются значения фазового угла для начала расчетов. Просвет с морским дном в начале расчетов /?нач, при t = 0, м, связан с заданным минимальным просветом и с амплитудой вертикальной качки и фазовым углом начала, как показано на рисунке 38:
^нач = ^min + П/. (1 + sincp), (283)
где /7mjn — требуемый для начала расчета минимальный просвет, м;
T|L — амплитуда вертикальной качки основания (на конце троса крана длиной L), м; Ф — фазовый угол.
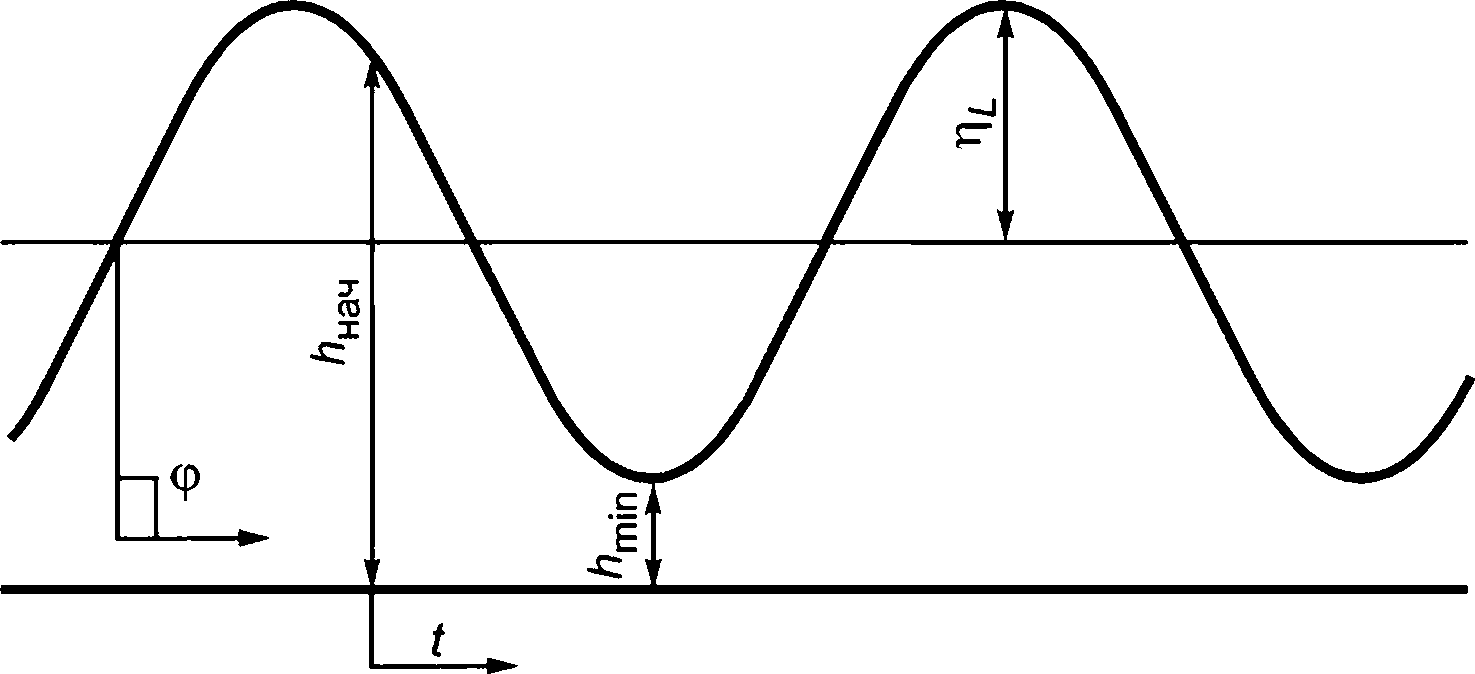
Морское дно
Рисунок 38 — Положение для начала расчета
9.2.3.19 Движение вертикальной качки может быть учтено путем расчета удара для постоянной скорости опускания, представленной как сумма скорости опускания крана и максимальной скорости вертикальной качки основания. Это является вариантом синхронизации вертикальных движений, который необходимо рассмотреть для возможности управления синхронизацией.
9.2.3.20 При значительной продолжительности удара так же, как при глубоком проникновении юбок в грунт до достижения пика удара, учитывают совместные движения опускания крана и вертикальной качки. При этом рассматривают несколько фазовых углов движений вертикальной качки.
9.2.3.21 Для описанного метода расчета допускается, что движения вертикальной качки связаны с движением r|L близкого к морскому дну основания. С целью учета движений крана движение на конце троса со стороны судна т|а может быть установлено с учетом недемпфированного колебания смоделированной общей динамической массы на тросе, вычисляемой следующим образом:
1 , (284)
Па | . со2
1-~2
I “0 )
где r|L — амплитуда вертикальной качки основания (на конце троса крана длиной L), м;
Па — движение на конце троса со стороны судна;
Mf— коэффициент динамичности;
со — угловая частота вертикальных движений, рад/с;
o)q — угловая частота собственных колебаний, рад/с.
Для условий резонанса, когда характеристическая частота движений оконечности крана близка к частоте собственных колебаний грузоподъемной системы, заданный по формуле (284) недемпфированный отклик может быть чрезмерно консервативным. Тогда могут быть применены результаты динамического расчета, включающие соответствующие влияния демпфирования. Динамический отклик опускаемого объекта из-за действия волны описан в разделе 8.
9.2.4 Процедура итеративного расчета
9. 2.4.1 Для каждого этапа времени в предложенном итеративном расчете по временной области с целью учета нелинейного поведения сопротивления грунта используют следующую процедуру:
а) выбирают прирастающее смещение грунта А8гр, м;
б) рассчитывают просвет ht между краем юбки и морским дном по формуле
hj = - Az,- + А8гр, (285)
где Д8гр — прирастающее смещение грунта, м;
Az,- — ускорение опускания крана, вычисляемое по формуле
(286)
Az,- = vcj Af,
где vcj — скорость опускания крана, м/с;
А/ — время опускания крана, с.
При этом при проникновении юбки в грунт просвет Л, имеет отрицательные значения;
в) рассчитывают площадь для выхода воды Afj по формуле
Afj= ^h + max (nDh^O), (287)
где Ah — площадь имеющихся в башмаке отверстий, м2;
D — гидродинамический диаметр буксирного троса, м;
hj — просвет между краем юбки и морским дном, м;
г) рассчитывают соответствующую реакцию давления воды на грунт и опорный цилиндрический башмак 0^,-по формулам
Qw>/ = sign (vci) kflow ^-Ab = sign (vc/-) kf ( vci - W | (288)
Z Z Ш jr+f
где vcj — скорость опускания крана, м/с;
kf— коэффициент падения давления;
2
vfj — скорость потока воды, м/с;
р — массовая плотность воды, кг/м3;
Аь — площадь основания цилиндра, м;
А8гр — прирастающее смещение грунта;
Af— площадь для выхода воды;
д) рассчитывают общую реакцию на грунт Qrp,-no формуле
^гр,/_ ®w,i + ®юб,/’ (289)
где Qwj — усилие гидродинамического давления воды;
Оюб/- — усилие, передаваемое от заглубляющихся юбок грунту;
е) рассчитывают смещения грунта 8гр j и Д8гр ,■ по формулам:
1) при Огр/< Од
/
$гр,/= $моб ■
I ид )
Д$гр,/ = $ гр, / “ $ гр, / -1 ’
2) при Огр > Од, когда h, > 0 (до заглубления юбки)
д5гр = -/7/-1 +/7/ + Azr
где hj— просвет между краем юбки и морским дном, рассчитываемый по формуле
(293)
где Afj— площадь для выхода воды, рассчитываемая по формуле
Мгр ) л L Аьр де Пу*2ОД
(294)
где vcj— вертикальная скорость цилиндра, м/с;
Д8гр — прирастающее смещение грунта;
Д/— время опускания цилиндра, с;
Аь — площадь основания цилиндра, м2;
kf— коэффициент падения давления;
р — массовая плотность воды, кг/м3;
Од — расчетная несущая способность грунта.
Следует отметить, что для нахождения неизвестной Af jтребуется итерация по А8гр/, вычисляемая по формуле
(295)
$гр,/ Д$гр,/ + $гр,7 —1 •
Когда hj < 0 (т. е. юбки заглубляются), прирастающее смещение грунта Д8гр/- вычисляют по формуле
Д8гр,/ —
Af,i 12(^Д Ооб,/) Ab V kfAbP
д/,
7
(296)
где ус/-— вертикальная скорость цилиндра, м/с;
Afj — площадь для выхода воды;
Аь — площадь основания цилиндра, м2;
Од — расчетная несущая способность дна;
ОЮб у — усилие, передаваемое от юбок грунту; kf — коэффициент падения давления; р — массовая плотность воды, кг/м3;
3) при разгрузке Д6гр/
, (°гр,/ Qrp,/-1)
(297)
^гр,/ =------7-------
ки
где ки — разгрузочная жесткость, Н/м;
ж) повторяют шаги по перечислениям а)—е) до схождения;
и) рассчитывают общее изменение длины троса крана 6w/ no формуле
- LAZ;
vct+dQ—(sin(erf+(p)-sin(p) ,
(298)
где Az,- — ускорение опускания крана, м/с2;
vc — скорость опускания крана, м/с;
t — время изменения длины троса, с;
сУ0 — диаметр троса, м;
Mf— коэффициент динамичности;
со — угловая частота вертикальных движений, рад/с;
Ф — фазовый угол;
к) рассчитывают новое усилие троса 0^,-по формуле
(299)
®w,i $и/,0 + &w,i - 0’
где kw — жесткость троса крана;
л) рассчитывают потерю кинетической энергии АЕ,-по формуле где Аь — площадь основания цилиндра, м2;
=| +О«Р; W
I J
(300)
Ah — площадь имеющихся в башмаке отверстий, м2;
ОЮб / — усилие, передаваемое от заглубляющихся юбок грунту, Н;
QCTp / — сила, передаваемая от строп на точку подъема, Н;
W — вес в погруженном состоянии на единицу длины троса/буксирного троса;
Az,- — расстояние между нижними положениями троса, м.
Допускается, что кинетическая энергия воды Ekj внутри опорного цилиндрического башмака не действует на выпускные отверстия в верхней части цилиндра Ah, при этом Ekj вычисляют по формуле
^k,i ~ Ek,i-1 ~ ^^k,i> (301)
где Ekj_^ — кинетическая энергия воды под опорным башмаком, Дж;
АЕ^,- — потеря кинетической энергии;
м) рассчитывают новое значение скорости vc/+1 по формуле
vw+i=72Ew/mB , (302)
где Ekj— кинетическая энергия воды, Н;
тв — масса воды, кг.
9.2.4.2 По мере проникновения юбок сопротивление проникновению и общее сопротивление грунта следует уточнять для учета увеличенного сопротивления при увеличенном проникновении.
9.2.4.3 Необходимо отметить, что требованиями для использования указанного выше метода являются поддержание постоянной скорости опускания крана до опирания основания и отсутствие ее увеличения при начале проникновения юбок.
9.2.5 Упрощенный метод для оснований без юбок
9.2.5.1 В упрощенном подходе к проверке несущей способности основания для ситуации опускания на морское дно оснований без юбок можно пренебречь благоприятными воздействиями водной подушки под опорным башмаком и благоприятным влиянием выполненной тросом крана работы.
9.2.5.2 Примененными к задаче граничными условиями тогда являются конструкция с заданными динамической массой и весом в погруженном положении, скорость при ударе о морское дно и нелинейная мобилизация несущей способности. Упрощенным уравнением для решения задачи удара при опускании тогда становится следующее:
(303)
jQp(8)d8,
где М' — общая динамическая масса;
vimp — скорость в момент касания дна;
VV — вес в погруженном состоянии на единицу длины троса/буксирного троса;
Qrp — передаваемое усилие на грунт;
8гр — скорость изменения смещения грунта.
9.2.5.3 Допуская нелинейное сопротивление грунта, получают правую сторону уравнения (303) в следующем виде:
при 8гр < 8М, м;
(304)
где Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н;
8гр — скорость изменения смещения грунта;
8моб — вертикальное смещение грунта для мобилизации Одна, м,
при 8гР > 8моб-м;
(305)
9.2.5.4 В соответствующих случаях коэффициенты нагрузки должны быть включены в расчетную динамическую массу и вес в погруженном положении, а коэффициенты материала — в сопротивление грунта. Как правило, критерием приемлемости является 8гр < 8моб, м.
В таком случае требованием к скорости удара при опускании vjmp становится:
где Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н;
W — вес в погруженном состоянии на единицу длины троса/буксирного троса;
8МОб — вертикальное смещение грунта для мобилизации Од, м;
М'— общая динамическая масса.
9.2.5.5 Тем не менее на основании оценки последствий могут быть использованы другие критерии.
9.2.6 Упрощенный метод для оснований с юбками на мягком грунте
9.2.6.1 Для оснований с юбками на мягком грунте, где требуется, чтобы юбки заглубились до того, как грунт сможет сопротивляться динамическому воздействию опускания (или даже весу установленной подводной конструкции с основанием в погруженном состоянии), необходимо обеспечить достаточную площадь для отвода воды таким образом, чтобы гидродинамическое давление не превышало несущую способность (см. [1]).
9.2.6.2 Консервативное проектирование можно выполнить, пренебрегая благоприятными воздействиями на удар податливости троса крана и грунта. Граничными условиями для задачи в этом случае становятся скорость удара по мере начала проникновения юбки, полная площадь основания, площадь для отвода воды, а также несущая способность грунта для поверхностной нагрузки на полную площадь основания. Отношение между скоростью удара и требуемой для отвода воды площадью определено следующим уравнением:
/ \2
где Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н;
Аь — площадь основания цилиндра, м2;
Ah — площадь имеющихся в башмаке отверстий, м2;
pw — гидравлическое давление внутри башмака;
kf— коэффициент падения давления;
р — массовая плотность воды;
vimp — скорость в момент касания дна.
9.2.6.3 Площадь для отвода воды Ah для необходимой скорости опускания определена следующим уравнением:
, > pWmp Л3 (308)
V 2qa ’
где kf— коэффициент падения давления;
р — массовая плотность воды;
vimp — скорость в момент касания дна;
Аь — площадь основания цилиндра, м2;
Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н,
или, если площадь для отвода воды установлена, скорость опускания vjmp определена следующим уравнением:
где Од — расчетная несущая способность для нагрузки в пределах площади Ар на уровне морского дна или края юбки, Н;
Ah — площадь имеющихся в башмаке отверстий, м2;
kf— коэффициент падения давления;
р — массовая плотность воды;
Аь — площадь основания цилиндра, м2.
9.2.7 Применение коэффициентов безопасности
Применение коэффициентов безопасности следует оценивать относительно последствий превышения выбранных предельных значений. Коэффициенты нагрузки могут быть применены к массам и соответствующим весам в погруженном положении, а коэффициенты материала должны быть использованы в отношении сопротивления грунта. Когда последствия считают внушительными, применяют коэффициент нагрузки yf, равный 1,3, и коэффициент материала ут, равный 1,25.
9.2.8 Расчет сопротивления проникновению юбки
9.2.8.1 Расчет сопротивления проникновению юбки требуется в качестве исходных данных для расчета опускания на морское дно, а также с целью оценки необходимости в проникновении с помощью разрежения и определения указанного разрежения.
9.2.8.2 Усилие, передаваемое от заглубляющихся юбок грунту Оюб, Н, рассчитывают как сумму сопротивления вертикальному сдвигу, часто обозначаемому как поверхностное трение вдоль обеих сторон юбок и сопротивления края юбки по формуле
d
QW6=Ajf(z)^+'Mf(d)> (31°)
о
где Д5 — площадь трения на 1 м глубины, м2/м;
d — глубина проникновения, м;
f(z) — поверхностное трение на глубине z, Н/м2;
At — площадь края юбки, м2;
qt(d) — сопротивление края на глубине проникновения, Н/м2.
9.2.8.3 В песке и сверхуплотненных глинах поверхностное трение на глубине z, f(z), Н/м2 и qt(z) можно наиболее надежно спрогнозировать путем корреляции с сопротивлением вдавливанию конуса зонда по формулам:
f(z) = kfQc(z); (311)
qt(z) = ktqc(z), (312)
где kf— коэффициент корреляции поверхностного трения;
qc(z) — сопротивление грунта вдавливанию конуса зонда, как измерено в испытании конусной пенетрометрией (СРТ), Н;
kt— коэффициенты корреляции сопротивления края.
9.2.8.4 Наиболее вероятные и наиболее ожидаемые значения для коэффициента корреляции поверхностного трения kf и коэффициента корреляции сопротивления края kt для глины и песка (условия Северного моря) приведены в таблице 2.
Таблица 2 — Коэффициенты корреляции для поверхностного трения и сопротивления края в песке и сверхуплотненной глине
Коэффициент корреляции | Глина | Песок | ||
Наиболее вероятный | Наиболее ожидаемый | Наиболее вероятный | Наиболее ожидаемый | |
Поверхностное трение kf | 0,03 | 0,05 | 0,001 | 0,003 |
Сопротивление края kt | 0,4 | 0,6 | 0,3 | 0,6 |
9.2.8.5 В качестве альтернативы в менее сверхуплотненных глинах поверхностное трение может быть принято равным пределу прочности на сдвиг для нарушенного состояния. Погрешности должны быть учтены путем назначения диапазона для предела прочности на сдвиг для нарушенного состояния. Сопротивление края в глинах может быть учтено как 7,5-кратная прочность недренированной глины на сдвиг в ненарушенном состоянии.
9.3 Установка с помощью разрежения и выравнивания
9.3.1 Установка с помощью разрежения9.3.1.1 Когда для установки оснований с юбками требуется разрежение, для обеспечения подходящего оборудования и проектирования основания с юбками на сопротивление разрежению необходимо рассчитать диапазон ожидаемого необходимого разрежения.
9.3.1.2 Сопротивление проникновению юбки можно рассчитать по 9.2.8 и для обеспечения необходимого усилия проникновения (превышающего вес в погруженном состоянии) применить в оценке необходимого разрежения.
9.3.1.3 При проектировании юбки и опорного башмака следует учитывать потерю устойчивости для необходимого разрежения по верхней оценке.
9.3.1.4 В качестве части проектирования основания должна быть выполнена проверка того, что при использовании разрежения не произошло оседания грунтового ядра. Такое нарушение произойдет в том случае, когда общее поверхностное трение на внешней стороне юбок превысит обратную несущую способность на уровне края юбки. Это может относиться к задавливаемым самопогружным сваям с большим отношением длины к диаметру, также часто называемым вакуумными сваями.
9.3.1.5 Применяемое во время установки фактическое разрежение следует постоянно контролировать и регистрировать для выполнения установки.
9.3.2 Выравнивание применением разрежения или избыточного давления
9.3.2.1 Опирающаяся на три или более (как правило, четыре) отдельных основания с юбками подводная конструкция может быть выровнена путем приложения давления на пустое пространство между опорным башмаком и грунтом в нижних углах или приложением разрежения у верхних углов.
9.3.2.2 Процедуры должны быть детально спланированы, а необходимые для осуществления выравнивания разрежение или избыточное давление — рассчитаны.
9.3.2.3 При выравнивании подводной конструкции с четырьмя основаниями для предотвращения заклинивания конструкции разрежение или избыточное давление следует прилагать на двух соседних основаниях одновременно.
9.3.2.4 Выпрямляющий момент для достижения выравнивания происходит от дифференциальных давлений в юбках основания. Преодолеваемым сопротивлением является:
- вертикальное поверхностное трение грунта и сопротивление края из-за проникновения или подъема юбок;
- сопротивление на поворот юбок внутри грунта;
- вес конструкции, являющийся дополнительным фактором увеличения избыточного давления или уменьшения разрежения.
9.3.2.5 Вертикальное поверхностное трение грунта и сопротивление края могут быть рассчитаны согласно 9.2.8. Поверхностное трение может быть принято равным в обоих направлениях. В глине дополнительный фактор разрежения ниже края должен быть учтен при движении юбок в направлении вверх.
9.3.2.6 Сопротивление на поворот основания с юбками внутри грунта будет наименьшим из определяемых для местного режима, при котором сопротивление грунта мобилизуется с каждой стороны стенок юбки, и для глобального режима, при котором основание с юбкой вращается, как свая с повторяющим движения сваи грунтовым ядром. Оба режима могут быть исследованы с применением простой модели сваи, в которой на любом уровне над краем юбки максимальное горизонтальное сопротивление равно объединенному сопротивлению пассивных и активных давлений и сопротивлению горизонтальному сдвигу вокруг периферии юбки.
9.3.2.7 Для местного режима должно быть включено сопротивление к обеим сторонам стенки юбки, в то время как для глобального режима должно быть включено сопротивление только к внешней стороне. Для глобального режима должно быть включено отражающее сдвиг грунтового ядра на уровне края юбки горизонтальное сопротивление у края юбки. Сопротивление может быть реализовано как кривые ply. Граничным условием для расчета должен быть приложенный момент без горизонтального усилия на оголовке сваи.
9.3.2.8 В качестве альтернативы сопротивление на поворот юбок внутри грунта можно рассчитывать с помощью конечно-элементного метода.
9.3.2.9 Конструкция включающего опорный башмак основания с юбкой должна пройти проверку на максимальное прогнозируемое разрежение или избыточное давление. Аналогичным образом должен быть проверен режим возможного оседания грунтового ядра в случае нарушения обратной несущей способности для высокого разрежения или направленной вниз несущей способности для высокого избыточного давления.
9.3.2.10 Для оснований с длинными юбками, требующих разрежения для проникновения, выравнивание, как правило, должно быть проведено после этапа самостоятельного проникновения с последующей частой регулировкой уровня в течение дальнейшего проникновения.
9.3.2.11 Процесс выравнивания следует тщательно контролировать и регистрировать в документации о выполнении установки.
9.4 Извлечение оснований
9.4.1 Извлечение оснований с юбкой9.4.1.1 Извлечение оснований с юбкой может быть осуществлено с помощью комбинации подъема и приложения давления снизу опорного башмака. Преодолеваемым общим усилием является сумма весов в погруженном состоянии и сопротивления грунта.
9.4.1.2 Для предотвращения прилипания к грунту и для обеспечения распределения прилагаемого давления по всей площади между опорным башмаком и грунтом предназначенные для извлечения основания с юбкой должны быть оснащены прикрепленной к нижней поверхности опорного башмака фильтрационной сеткой. В этом случае сопротивлением грунта будет только вертикальное сопротивление вдоль юбок.
9.4.1.3 Первоначальное внешнее и внутреннее поверхностное трение можно рассчитать с использованием методов, разработанных для расчета осевой нагрузки забивных свай. В глине также необходимо направленное вниз сопротивление края. После начала движения сопротивление грунта может упасть по отношению к использованному для расчета проникновения юбки.
9.4.2 Извлечение оснований без юбки
9.4.2.1 При извлечении оснований без юбки должно быть учтено разрежение от грунта. Даже на песчаных грунтах из-за быстрого подъема возникнет разрежение. В зависимости от размера площадки и проницаемости песка для сброса разрежения может потребоваться несколько секунд или минут, что следует учитывать при создании процедур подъема.
9.4.2.2 При подъеме оснований без юбки с глинистого морского дна разрежение длится настолько долго, что, как правило, сброс разрежения нереалистичным не представляется. В дополнение к подъему веса конструкции в погруженном положении придется преодолеть обратную несущую способность грунта. Значение этого дополнительного сопротивления грунта будет, как минимум, равным весу конструкции в погруженном положении.
9.4.2.3 Если конструкция установлена с высокой скоростью посадки на грунт, преодолеваемое сопротивление может быть близким к динамической ударной нагрузке на грунт во время установки. Данная ударная нагрузка может, например, оцениваться с помощью предложенного в 9.2.5 метода. В частности, если ударная нагрузка в два раза превышает вес конструкции в погруженном положении, необходимая для освобождения подъемная нагрузка в три раза превысит вес в погруженном положении, что должно быть учтено при выборе и проектировании подъемного оборудования. Требуемое подъемное усилие может быть снижено путем подъема с одного конца конструкции или использования струйного размывания в комбинации с подъемом.
10 Буксировка
10.1 Общие положения
10.1.1 Буксировка является одной из самых распространенных морских работ. Большинство проектов разработки морских месторождений включают в себя буксировку на одном или нескольких своих этапах. Примерами буксировки являются:
- перемещение буровой установки;
- транспортирование на место и размещение большой плавучей установки;
- транспортирование объектов на барже;
- буксировка мокрым способом подводных модулей;
- буксировка на плаву протяженных удлиненных элементов, обладающих положительной плавучестью.
10.1.2 Классическая надводная буксировка описана в 10.2; буксировка погруженных малообъемных конструкций или протяженных удлиненных конструкций — в 10.3.
10.1.3 Ограничения, обусловленные воздействием окружающей среды
10.1.3.1 Из-за малой скорости перемещения буксировка может занять несколько дней и может быть классифицирована как ограничиваемая или не ограничиваемая погодными условиями.
10.1.3.2 Для регламентированного периода выполнения операции TR менее 72 ч может быть определено погодное окно (операция в ограничиваемых погодных условиях). Начало операции зависит от приемлемого прогноза погоды.
Регламентированный период выполнения операции TR должен включать как плановый период операции, так и расчетное непредвиденное время, TR вычисляют по формуле
TR= Тп.0.п+ТС, (313)
где Тп 0 п — плановый период операции;
Тс — расчетное непредвиденное время.
10.1.3.3 При TR, длящихся более 72 ч, операция может быть определена как операция в ограничиваемых погодных условиях при условии, что:
- в порядке работы установлено непрерывное наблюдение фактических и прогнозных погодных условий;
- на протяжении маршрута установлены безопасные условия для буксируемого объекта (например, посадка на грунт морского дна);
- система соответствует требованиям для неограничиваемых погодных условий.
10.1.3.4 При операциях с TR, длящихся более 72 ч, операция, как правило, должна быть определена как операция в неограничиваемых погодных условиях. Критерии окружающей среды для таких операций должны быть основаны на статистике по экстремумам.
10.2 Надводная буксировка больших плавучих установок
10.2.1 Определение системы10.2.1.1 Для динамического расчета буксировки требуется информация по геометрическим и массовым характеристикам буксируемого объекта и буксира, данные буксирного троса (вес, диаметр, жесткость, устройство для крепления и т. п.), а также эксплуатационные данные, включая информацию об условиях окружающей среды (волнение, ветер и течение).
10.2.1.2 На рисунке 39 показаны местная и глобальная системы координат и определение углов для ориентации буксира, буксируемого объекта и буксирного троса, подлежащие использованию при статическом и динамическом расчетах буксирного троса в распространяющемся в направлении 0 волнении.
10.2.1.3 Вызванный волной отклик буксира и буксируемого объекта (а следовательно, и динамическое натяжение в буксирном тросе) является функцией направления волны относительно объектов.
Рисунок 39 — Определение углов для ориентации буксира, буксируемого объекта и буксирного троса относительно общих осей XG,YG
10.2.2 Данные для моделирования и расчета буксировок
10.2.2.1 Исходные данные для расчета надводных буксировок подразделяют на данные буксира и буксируемого объекта, данные буксирного троса и эксплуатационные данные.
Данные буксира и буксируемого объекта:
Н'бук(со,е) — функция передачи движения в шести степенях свободы (/ = 1,6) для буксира;
/7убук(со,0) — функция передачи движения в шести степенях свободы (/ = 1,6) буксируемого объекта;
гобук— местное положение конца буксировочного троса на буксируемом объекте, м;
В — ширина буксируемого объекта, м;
Lb — длина буксируемого объекта, м;
Ть — осадка буксируемого объекта, м.
10.2.2.2 Данные буксирного троса, применяемые в настоящем стандарте:
D — гидродинамический диаметр буксирного троса, м;
CD — коэффициент гидродинамического лобового сопротивления;
См— коэффициент гидродинамической инерции;
А — номинальная площадь буксирного конца (площадь стали), м2;
S — площадь описанной окружности, равная tiD2/4, м2;
cF = A/S — коэффициент заполнения;
Е — модуль упругости буксирного троса, Н/м2;
ps— массовая плотность стали, кг/м3;
m — масса на единицу длины буксирного троса, кг/м;
та — присоединенная масса на единицу длины буксирного троса, кг/м;
w— вес в погруженном состоянии на единицу длины троса, Н/м;
W— общий вес буксирного троса в погруженном состоянии, Н.
Общий вид поперечного сечения буксирного троса представлен на рисунке 40 (см. также [1]).
D
Рисунок 40 — Общий вид поперечного сечения буксирного троса из стальной проволоки с коэффициентом заполнения cF = 0,58
Следует учитывать, что модуль упругости буксирного троса из стальной проволоки составляет, как правило, приблизительно 40 % от модуля упругости сплошной стали.
10.2.2.3 Вес в погруженном состоянии на единицу длины троса w определяют по формуле
w = (m - cF Spw) д ,
(314)
где т — конструкционная масса на единицу длины в воздухе;
pw — плотность воды;
д — ускорение свободного падения.
Общий вес буксирного троса в погруженном состоянии обозначается IV = wL.
10.2.2.4 Входными эксплуатационными данными для расчета буксируемого судна являются следующие:
U — скорость буксировки, м/с;
То — натяжение буксирного троса, Н;
L — длина буксирного троса, м;
а — направление буксирного троса, град;
Hs— высота характерной волны, м;
Тр — период пика спектра, с;
S(co, 0) — спектр волны;
0 — среднее направление волны, град;
vc— скорость течения, м/с;
vw— скорость ветра, м/с.
10.2.3 Статическая конфигурация буксирного троса
10.2.3.1 Для буксирного троса с намного превышающим вес троса натяжением в буксирном тросе 7q/W » 1, горизонтальная x(s) и вертикальная z(x) координаты вдоль буксирного троса могут быть аппроксимированы с помощью следующих параметрических уравнений:
x(s) = | 1 + -^-Is—— | — | s3, (315)
v < еа) 6^Т0J
z(s)~~zm
1 ws2 (. Та >
+--1 + —У- ,
2 То I ЕА)
(316)
где То — натяжение буксирного троса, Н;
Е — модуль упругости буксирного троса, Н/м2;
А — номинальная площадь поперечного сечения буксирного троса, м2;
s — координата вдоль буксирного троса (-L/2 < s < L/2);
L — длина буксирного троса, м;
w — вес в погруженном состоянии на единицу длины троса;
zm — провисание буксирного троса, вычисляемое по формуле
_L( wL
u-М.
ЕА )
(317)
10.2.3.2 Применение формул (315)—(317) обеспечивает достоверные оценки, даже когда То сравнимо с весом буксирного троса И/. Обычно То « ЕА, поэтому в данных формулах элементом Т0/ЕА можно пренебречь. Типичная статическая геометрия буксирного троса показана на рисунке 41.
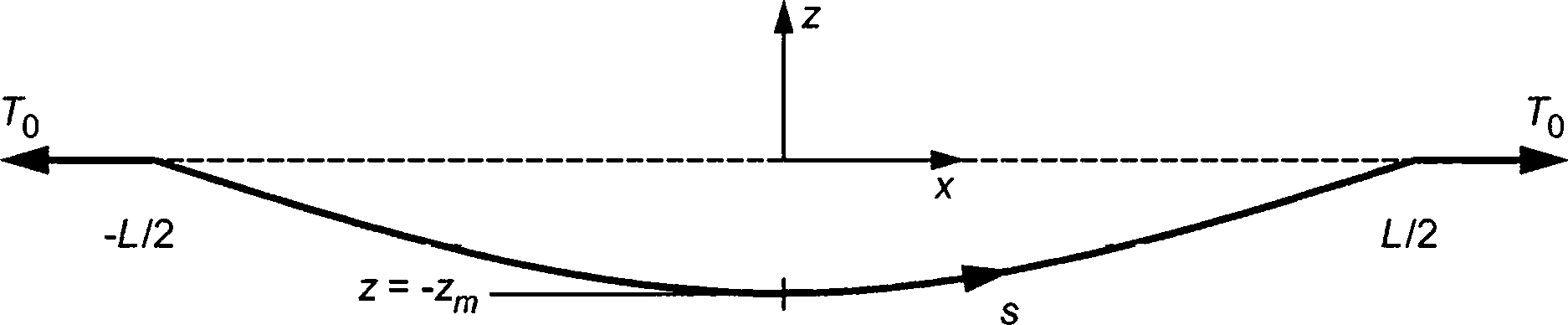
Рисунок 41 — Геометрия буксирного троса
10.2.3.3 При буксировке на мелководье длину и натяжение буксирного троса необходимо контролировать, чтобы имелся достаточный просвет между буксирным тросом и морским дном:
zm < д' где d— глубина воды, м.
Трущийся контакт между буксирным тросом и морским дном может привести к существенному снижению прочности буксирного троса.
10.2.4 Жесткость буксирного троса
10.2.4.1 Жесткость буксирного троса можно разделить на два компонента: один определен упругим удлинением троса; другой — изменением геометрии кривой провисания буксирного троса.
10.2.4.2 Жесткость для компонента упругого удлинения буксирного троса кЕ, Н/м, определяют по формуле
к£^. (318)
где Е — модуль упругости буксирного троса, Н/м2;
Д — номинальная площадь поперечного сечения буксирного троса, м2;
L — длина буксирного троса, м.
10.2.4.3 Жесткость для компонента изменения геометрии kG, Н/м, определяют по формуле
, _ 127-р3 ;
(319)
(320)
(321)
(wL)2L
где То — натяжение буксирного троса, Н;
w — вес в погруженном состоянии на единицу длины троса, Н/м;
L — длина буксирного троса, м.
10.2.4.4 Общую жесткость к, Н/м, определяют по формуле
1 1 1
— —--1--
k кЕ kG
или
к= kGkE = кЕ , kG + кЕ 1 + кЕ / kG
где kG — жесткость для компонента изменения геометрии;
кЕ — жесткость для компонента упругого удлинения буксирного троса.
Для предельно высокого натяжения буксирного троса kG » кЕ, а общая жесткость может быть аппроксимирована с помощью упругой жесткости к ~ кЕ.
10.2.4.5 Следует отметить, что заданное выше объединенной жесткостью отношение «усилие— перемещение» действительно только для медленных движений конечных точек буксирного троса. Для типичных буксирных тросов это означает движения с периодами более 30 с. Для движений волновой частоты будут существенными динамические воздействия из-за инерции и демпфирования.
10.2.5 Блокировка лобовым сопротивлением
При буксировке во время волнения получившееся вертикальное движение буксирного троса может быть частично ограничено из-за усилия лобового сопротивления, действующего на буксирный трос так, как если бы буксирный трос был ограничен в пределах узкой изогнутой трубы. Вследствие этого заблокирована геометрическая упругость. Данное явление называется блокировкой лобовым сопротивлением. Блокировка лобовым сопротивлением вызывает увеличение предполагаемой жесткости троса, а динамическое усилие приближенно является усилием, полученным с учетом только упругой жесткости.
10.2.6 Среднее буксировочное усилие
10.2.6.1 При нулевой скорости и отсутствии ветра, с учетом волнения и течения, буксир будет иметь максимальное буксировочное усилие, равное непрерывной тяге на крюке. Если буксир имеет поступательную скорость, часть тяги используют для преодоления сопротивления неподвижной воды движению буксира. Данное сопротивление частично связано с вязкостным сопротивлением трения, давлением от усилия лобового сопротивления и волнового сопротивления. Имеющееся буксировочное усилие уменьшается с поступательной скоростью. Также, если буксир направляется против волнения, ветра или течения, имеющееся буксировочное усилие уменьшается из-за увеличенных усилий, действующих непосредственно на буксир.
10.2.6.2 Кроме усилий от ветра и сопротивления неподвижной воды, буксируемый объект подвергается усилиям дрейфа волны Fwd, которые могут являться существенным дополнительным фактором в сопротивлении при буксировке. Усилие дрейфа волны, действующее на плавучую установку, может быть рассчитано с помощью программы дифракции волны с использованием панельной дискретизации смачиваемой поверхности.
10.2.6.3 Воздействие волнения можно учитывать путем умножения непрерывной тяги на крюке на коэффициент эффективности в зависимости от длины буксира и высоты характерной волны.
10.2.6.4 Усилие дрейфа волны при нулевой скорости буксировки Fwd может быть аппроксимировано с помощью следующего упрощенного выражения:
F^=^gR2BH2s, (322>
О
где типичными коэффициентами отражения R являются коэффициенты, представленные в таблице 3.
Таблица 3 — Типичные коэффициенты отражения
Показатель | Значение R |
Квадратная грань (Square face) | 1,00 |
Бетонное основание (Condeep base) | 0,97 |
Вертикальный цилиндр (Vertical cylinder) | 0,88 |
Баржа с носом с наклонным форштевнем (Barge with raked bow) | 0,67 |
Баржа с ложкообразным носом (Barge with spoon bow) | 0,55 |
Hoc судна (Ship bow) | 0,45 |
p(V— плотность морской воды, обычно 1025, кг/м3;
д — ускорение свободного падения, м/с2;
R — коэффициент отражения;
В — ширина буксируемого объекта, м;
Hs— высота характерной волны, м.
В большинстве случаев использование данного упрощенного выражения усилия дрейфа волны обеспечивает консервативные результаты. При необходимости получить более точные результаты необходим расчет с помощью программы дифракции волны.
10.2.6.5 Усилие дрейфа волны Fwd(U), Н, линейно изменяется со скоростью буксировки согласно формуле
(323)
где U — скорость буксировки, м/с;
В^ — демпфирование дрейфа волны.
10.2.7 Низкочастотные движения
10.2.7.1 Вследствие медленно изменяющихся усилий от волн и ветра буксир и буксируемый объект могут испытывать низкочастотные (медленного смещения) движения. При низкочастотных движениях буксирный трос будет иметь свойства пружины.
10.2.7.2 Период собственных колебаний медленного смещения определяют по формуле
Г0=21г
(324)
к 1+ где к — определенная в 10.2.4.4 жесткость буксирного троса, кг-с-2;
— конструкционная масса буксира, кг;
к — жесткость буксирного троса, кг с-2;
— присоединенная масса буксира в направлении буксирного троса, кг;
— конструкционная масса буксируемого объекта, кг;
— присоединенная масса буксируемого объекта в направлении троса.
10.2.7.3 В большинстве случаев при надводной буксировке масса и присоединенная масса буксируемого объекта намного превышают массу и присоединенную массу буксира, поэтому период собственных колебаний может быть аппроксимирован по формуле
(325)
Формулы для периода собственных колебаний медленного смещения допускают, что масса буксирного троса намного меньше массы буксира и буксируемого объекта.
10.2.8 Короткие буксирные тросы/струя за гребным винтом
10.2.8.1 В случае применения коротких буксирных тросов скорость потока от гребного винта буксира может воздействовать на буксируемую конструкцию, что значительно увеличивает сопротивление при буксировке.
10.2.8.2 При малом по сравнению со струей за гребным винтом буксируемом сооружении усилие на каждый элемент конструкции буксируемой конструкции можно оценить на основе местной скорости потока с учетом увеличенной скорости в струе за гребным винтом и коэффициентов лобового сопротивления для обычного потока.
10.2.8.3 Для глубоко погруженных поворотных движителей струю за гребным винтом можно аппроксимировать с помощью осесимметричной турбулентной струи с радиальным распределением скорости:
21 2
(r;x) = Um(x) 1 + 0,4142
(326)
где Um(x) — функция скорости, вычисляемая по формуле
Um(x) = Uo [0,89 + 0,149x/D]-1, (327)
г0 5(х) — функция радиуса турбулентной струи, вычисляемая по формуле
г0 5(х) = 0,390 + 0,0875х, (328)
где г — радиальное расстояние до центральной оси струи;
D — диаметр диска гребного винта;
UQ — скорость потока через диск гребного винта, предполагаемая равномерной (см. рисунок 42).
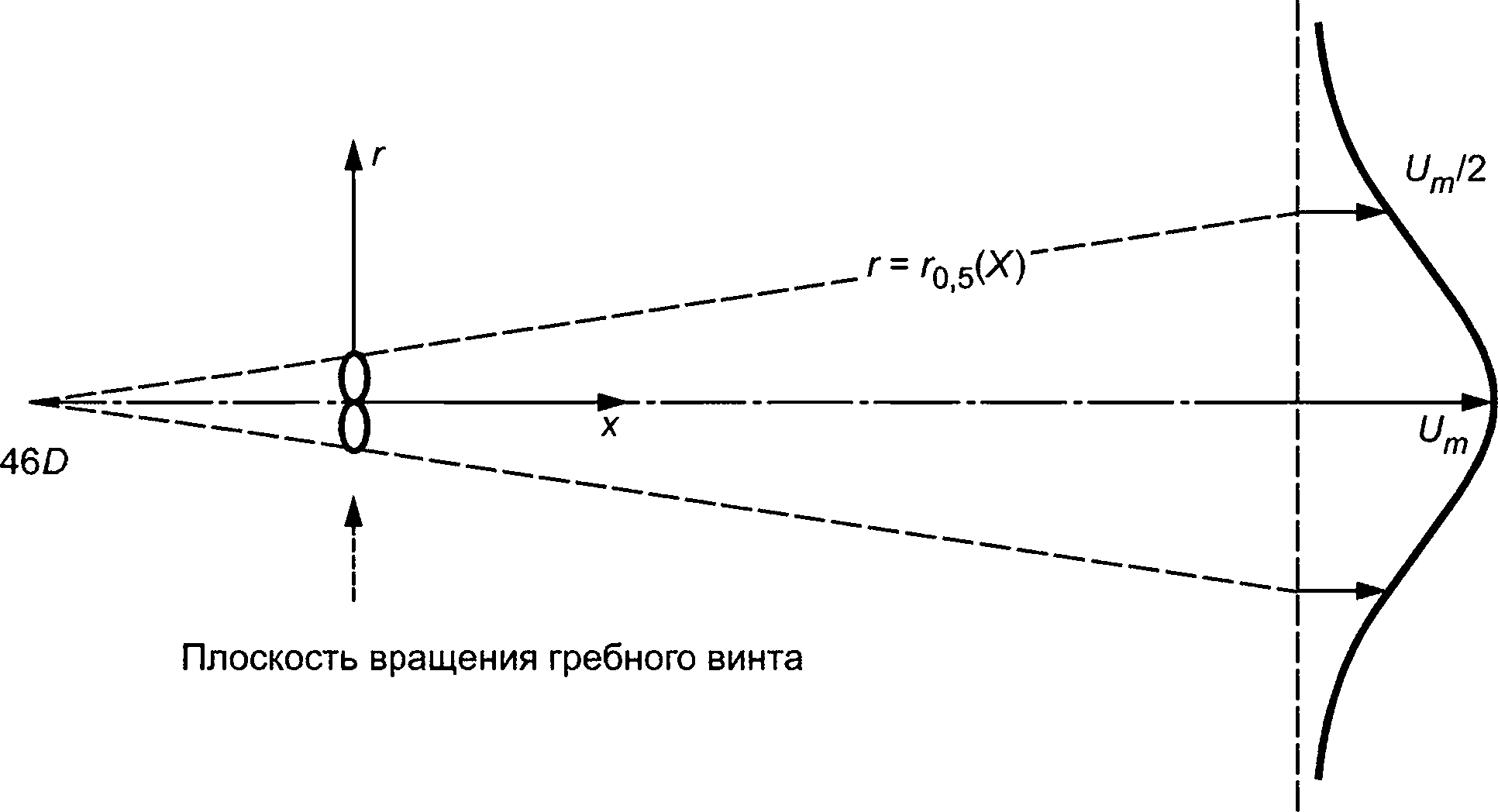
Рисунок 42 — Струя за гребным винтом, смоделированная как осесимметричная струя
10.2.8.4 Для буксирных тросов длиной более 30 м влияние струи за гребным винтом учитывают путем снижения имеющейся тяги на крюке на коэффициент эффективности взаимодействия ajnt, вычисляемый по формуле где Аехр — площадь проекции поперечного сечения буксируемого объекта, м2;
a/nt -
1 I 0,015.4^
(329)
L — длина буксирного троса, м;
Л — 2,1 для барж стандартной формы.
10.2.8.5 Когда буксируемый объект более крупный по сравнению с размерами гребного винта на буксире, большая часть струи гребного винта может быть обращена буксируемым объектом в обратном направлении, что снижает чистую поступательную тягу системы. Фактически из-за данного воздействия чистая поступательная тяга может стать отрицательной, так что система из буксира и буксируемого судна может двигаться назад. Подробный расчет данного воздействия можно выполнить с помощью CFD.
10.2.9 Распределение усилия в буксирной оттяжке
10.2.9.1 Когда буксируемая конструкция поворачивается под углом а, усилия в каждом оттяжном тросе будут разными (см. рисунок 42). Допуская, что каждый оттяжной трос образует с буксирным тросом угол р, а буксировочное усилие равно 7"0, распределение усилий в каждом оттяжном тросе для малых углов поворота можно определить следующим образом:
Г1 _ sin(P + a + Y), (330)
То sin2p
т2 = sin(p-a-r) (зз 1)
То sin2p
где Tj — усилие в оттяжке на левом борту, Н (для поворота буксируемого объекта в направлении левого борта) (см. рисунок 43);
То — буксировочное усилие, Н;
Р — угол между каждым оттяжным тросом и осевой линией судна, рад;
a — угол поворота буксируемой конструкции, рад;
R
у — угол, равный —а, рад;
Т2 — усилие в оттяжке на правом борту, Н (для поворота буксируемого объекта в направлении правого борта) (см. рисунок 43);
L — длина буксирного троса, измеренная от оттяжки, м.
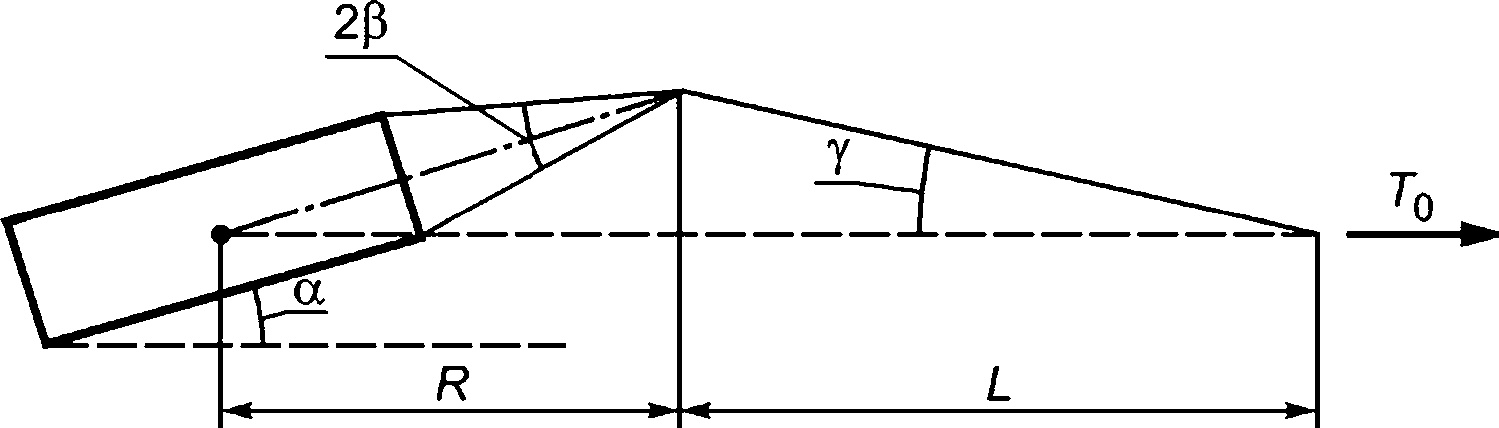
R — расстояние от центра тяжести буксируемого объекта до конца оттяжных тросов, м
Рисунок 43 — Расположение буксирного троса и оттяжных тросов
10.2.9.2 Усилие в оттяжном тросе становится нулевым, когда угол поворота буксируемой конструкции а
а = _£Р_, (332)
L + R
где L — длина буксирного троса, измеренная от оттяжки, м;
R — расстояние от центра тяжести буксируемого объекта до конца оттяжных тросов, м;
Р — угол между каждым оттяжным тросом и осевой линией судна, рад.
10.2.9.3 Для превышающих данное значение углов поворота один оттяжной трос провиснет, и нагрузка будет действовать только на другой оттяжной трос.
10.2.9.4 Момент буксировочного усилия вокруг центра поворота буксируемой конструкции MG вычисляют по формуле
А
(333)
MG =TqR 1 + у. а ,
где То — буксировочное усилие, Н;
R — расстояние от центра тяжести буксируемого объекта до конца оттяжных тросов, м;
L — длина буксирного троса, измеренная от оттяжки, м;
а — угол поворота буксируемой конструкции, рад.
Вращательную жесткость С66 из-за буксировочного усилия вычисляют по формуле
С66=Т0К^1-Д), <334>
где То — буксировочное усилие, Н;
R — расстояние от центра тяжести буксируемого объекта до конца оттяжных тросов, м;
L — длина буксирного троса, измеренная от оттяжки, м.
Следовательно, оттяжка является существенным дополнительным фактором во вращательную жесткость, положительно влияя на продольную устойчивость буксируемого судна.
10.2.10 Воздействия мелководья
В силу увеличенной скорости позади объекта, вызывающей уменьшение давления на смачиваемую поверхность, буксируемый объект будет подвергаться воздействию осаживания (погружения). Данное воздействие может значительно увеличиваться в ограниченных водах, таких как русла или каналы траншейного типа. Осадка объекта также изменится. Данное объединенное воздействие погружения и осадки на мелководье называется явлением проседания. Полуэмпирическое отношение проседания zmax’ м’ подобного судну буксируемого объекта к осадке объекта Т, м, вычисляют по формуле
7 О
£тах _ 2 /| b __h__ т ■'ив^
(335)
где Сь — коэффициент полноты водоизмещения, равный V/LBT, где V — объем вытесненной воды; L — длина объекта, м;
В — ширина объекта при максимальной площади, м;
Fh — число Фруда для глубины, вычисляемое по формуле
V fgh
(336)
где V = U — Uc — относительная скорость, м/с;
U — скорость буксировки, м/с;
Uc — скорость течения (например, в реке), являющаяся положительной в направлении колебания буксируемого судна, м/с;
д — ускорение свободного падения, м/с2;
h — глубина воды, м.
10.2.11 Динамика буксирных тросов
10.2.11.1 Расчет динамики буксирного троса включает в себя независимый расчет движения буксира и буксируемого объекта в заданном состоянии моря и полученный отклик буксирного троса. Для снижения натяжения в буксирном тросе на буксире может быть использована тяговая лебедка. Отклик тяговой лебедки и буксирного троса является выражением нелинейной зависимости (см. 10.2.13).
10.2.11.2 Расчет динамики буксирного троса может быть выполнен в частотной области или по временной области. Метод частотной области является вычислительно выгодным, но требует линеаризированной модели системы. Метод временной области может учитывать нелинейности в системе, вызванный волнением нелинейный отклик, а также нелинейную динамику буксирного троса.
10.2.11.3 Вызванный волнением отклик буксируемого объекта и буксира четко описан с помощью линейных уравнений. Ни буксир, ни буксируемый объект не подвергаются значительному воздействию буксирного троса применительно к вызванному волнением отклику первого порядка. Расчет в частотной области может быть использован для получения относительного движения между буксиром и буксируемым судном.
10.2.11.4 Может быть применен следующий метод решения в частотной области:
- вначале рассчитывают статическую конфигурацию буксирного троса. Статическая конфигурация является основой для расчета динамики динамичного буксирного троса. На основании статического расчета определяют максимальную глубину провисания;
- функции передачи движения для мест крепления троса рассчитывают на буксире и буксируемом объекте соответственно, кроме того, может быть определена передаточная функция для относительного движения мест крепления буксирного троса. Если буксируемый объект намного крупнее буксира, относительное движение будет определено откликом буксира, а передаточные функции буксируемого объекта могут быть отброшены.
10.2.11.5 Передаточную функцию для относительного движения п между буксиром и буксируемым объектом в направлении, пересекающем буксирный трос /-/^(оф), определяют путем линейного преобразования (см. рисунок 39) по формуле
Н„ (“■₽) = Hseo ) - Н™ (Ю,₽ГО), <337)
гден™^) — передаточная функция преобразования движения буксира;
^sec(®>₽T0) — передаточная функция преобразования движения буксируемого объекта.
10.2.11.6 Функция передачи относительного движения буксирного троса объединена с характеризующим фактическое состояние моря спектром волны. Спектр отклика относительного движения Зл(<о) в направлении, пересекающем буксирный трос, определяют по формуле 118
S„(») = |Hn(<o,p)|2 S(<o), (338)
где /-/^(€0,3) — передаточная функция для относительного движения г| между буксиром и буксируемым объектом в направлении, пересекающем буксирный трос;
S(co) — спектр волны.
Допуская вызванные волнами небольшие развороты (бортовая качка, килевая качка и рыскание) буксира и буксируемого объекта, функцию передачи движения для конечной точки буксирного троса можно задать с помощью линейной комбинации функций передачи движения жесткого тела. Функция передачи движения в направлении, пересекающем буксирный трос, является элементом вектора движения в этом направлении.
10.2.11.7 Крайнее представление относительного движения может быть сформировано на основе спектра отклика. Наиболее вероятным крайним значением для относительного движения во временном интервале Tr|max, обычно задаваемом как 3 ч, является
Птах * anJ2lnf?"l ’ (339)
V \ z )
где — стандартное отклонение относительного движения, м;
Tz — период колебания через нулевую точку, с.
10.2.11.8 Оценка крайнего натяжения буксирного троса при буксировке в условиях волнения Ттах может быть получена в предположении блокировки лобовым сопротивлением (см. 10.2.5) таким образом, что эффективной жесткостью становится упругая жесткость, вычисляемая по формуле
Тщах ” Л) + Лщах (340)
где То — среднее буксировочное усилие;
кЕ — жесткость буксирного троса (см. 10.2.4.2);
r|max — наиболее вероятное крайнее значение для относительного движения во временном интервале Т.
Вследствие этого крайнее упругое натяжение буксирного троса уменьшается с увеличением длины буксирного троса.
10.2.12 Нелинейный расчет по временной области
10.2.12.1 Альтернативным подходом к описанному выше методу в частотной области являются моделирование буксирного троса в программе нелинейного расчета методом конечных элементов и предписание вынужденных движений конечных точек буксирного троса на буксире и буксируемом объекте соответственно.
10.2.12.2 Временные диаграммы для движений конечных точек буксирного троса xp(t), yp(t), zp(t) определяют корректным преобразованием функции передачи движения жесткого тела как для буксира, так и для буксируемого объекта и объединением со спектром волны. Например, временную диаграмму движения конечной точки р в направлении х вычисляют по формуле
Хр (0 = ХАк И (“* )|cos(rak( + )• (341)
к
где (t»k) — функция передачи для движения в направлении х конечной точки р;
Акм гк — случайные амплитуда и фаза соответственно, вычисляемые по формуле
---- <342>
Ак =^S(dk)^G)k , где 5(0)^) — спектр волны к.
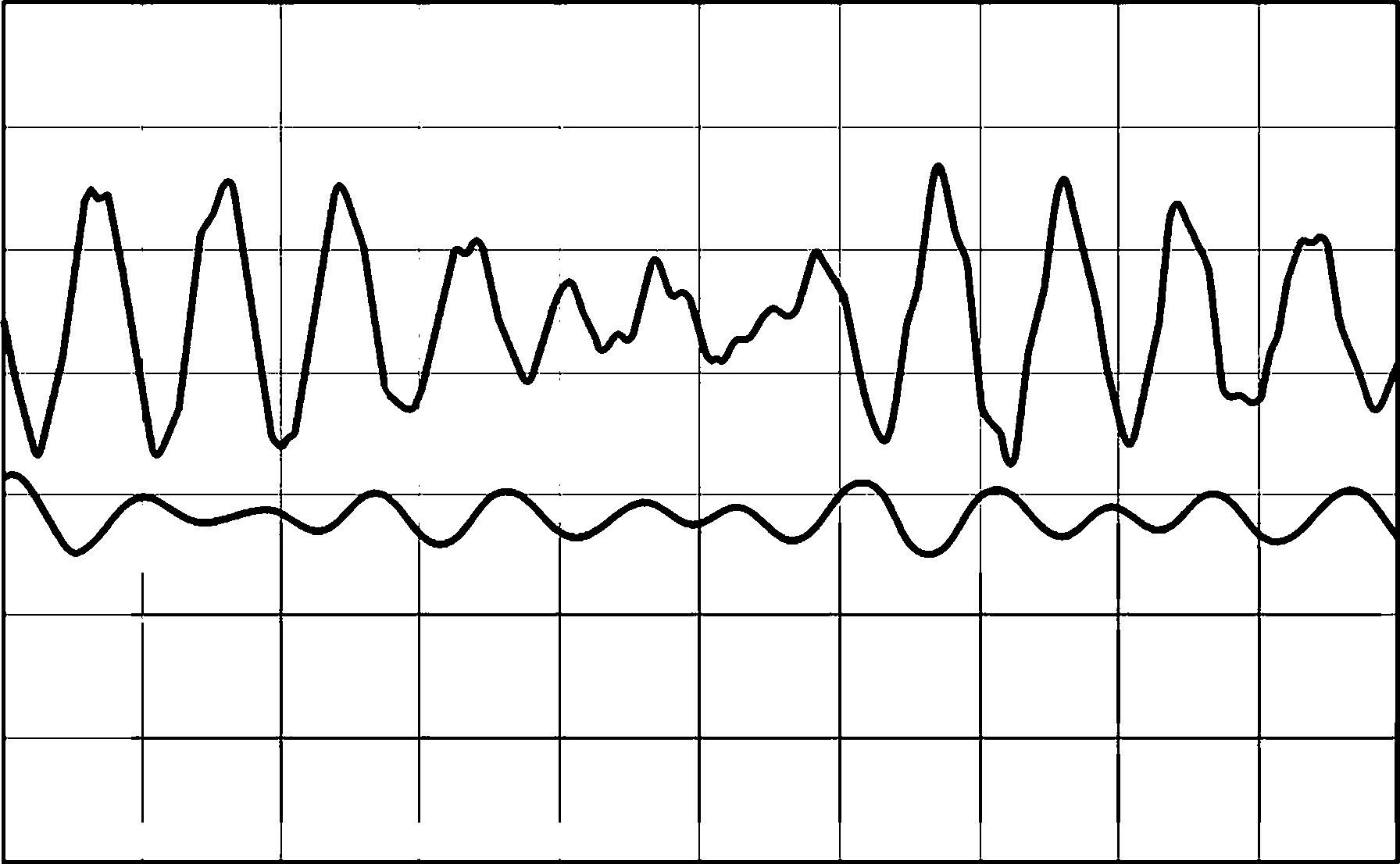
Примеры смоделированных движений концов буксирного троса у буксира и буксируемого объекта для встречных волн и отсутствия течения показаны на рисунках 44, 45.
Небольшие различия между двумя кривыми у пиков возникли в силу динамических воздействий в буксирном тросе.
15
10
5
0
-5
-10
-15
-20
200 210 220 230 240 250 260 270 280 290 300
Время, с
Рисунок 44 — Пример смоделированного вертикального движения буксируемого объекта (нижняя кривая) и буксира (верхняя кривая) в заданном состоянии моря
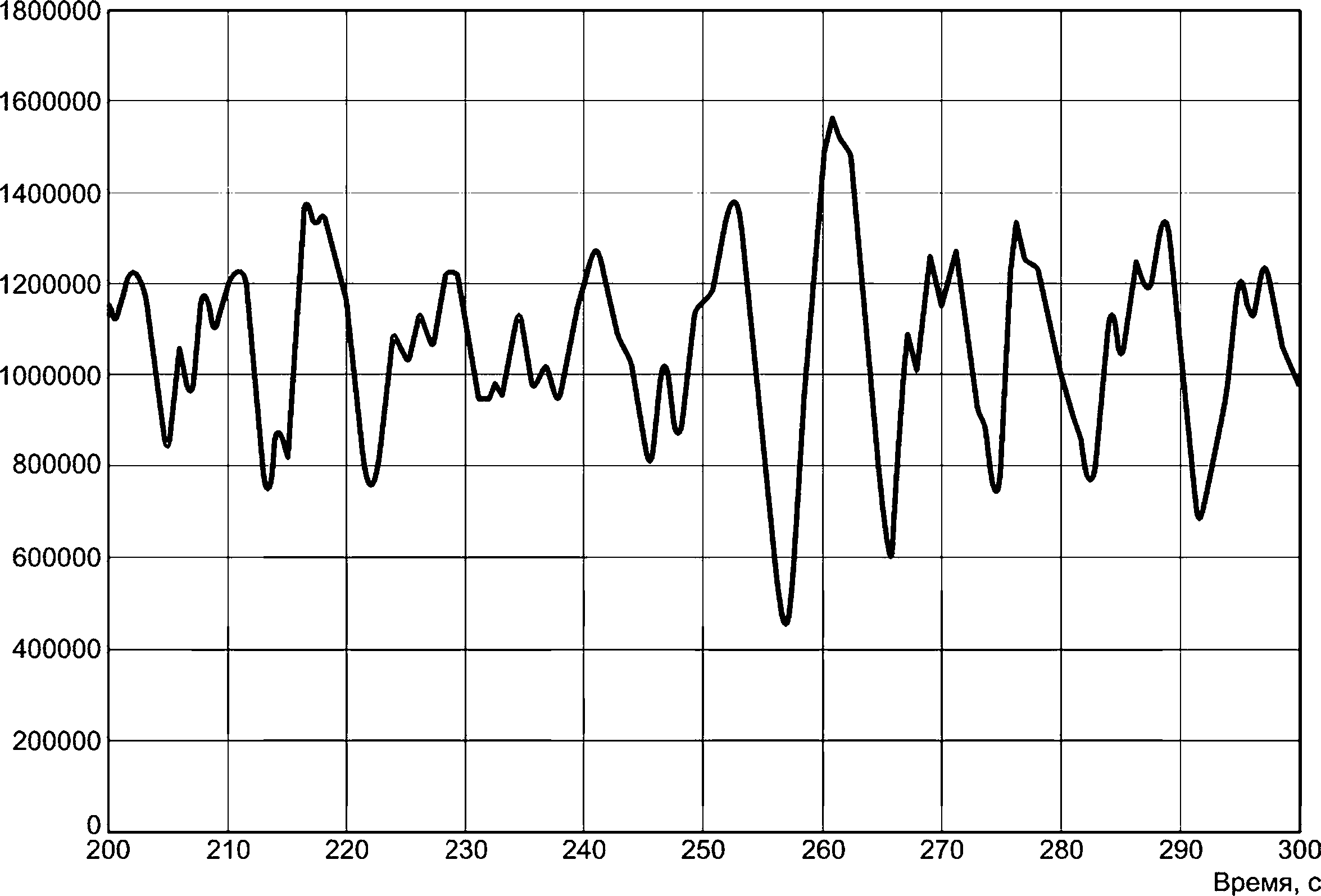
Рисунок 45 — Пример смоделированного осевого натяжения буксирного троса в конечных точках. Среднее натяжение равно TQ = 1,0 МН (т. е. =100 т тяги на крюке)
10.2.13 Лебедка
10.2.13.1 Для уменьшения крайнего натяжения буксирного троса может быть сконструирована автоматическая лебедка (см. рисунок 46). Лебедка предназначена для ослабления натяжения буксирного троса при превышении установленного значения.
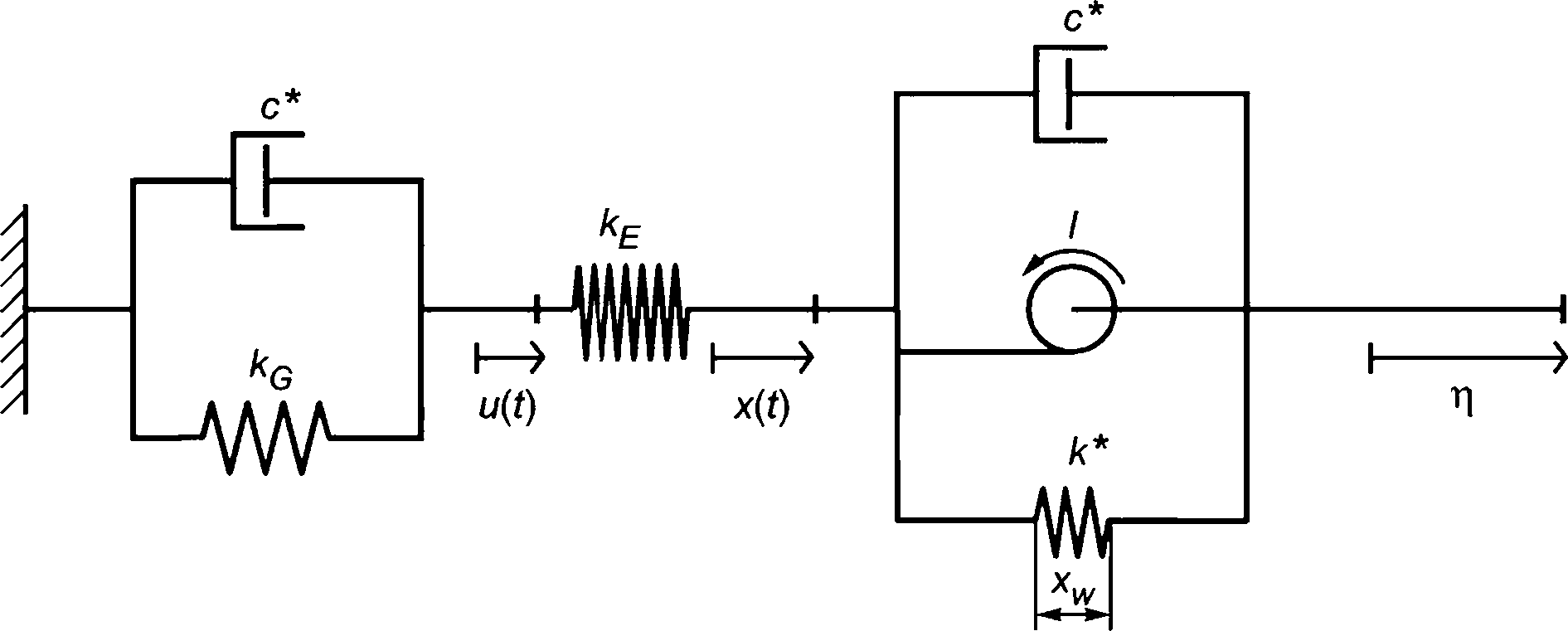
Рисунок 46 — Связанная модель буксирный трос — лебедка
10.2.13.2 Упрощенная модель буксирного троса основана на допущении того, что форма динамического движения равна изменению в статической геометрии буксирного троса. Массовые усилия не учитывают. Движение троса вычисляют по следующему уравнению:
(343)
с*й|й| + к* и = кЕх ,
где с* — обобщенное демпфирование троса, кг/м;
й — относительная скорость движения троса, м/с;
к* — обобщенная жесткость буксирного троса, Н/м, равная кЕ + kG;
кЕ — упругая жесткость, Н/м (см. 10.2.4.2);
kG — геометрическая жесткость, Н/м (см. 10.2.4.3);
и — смещение буксирного троса, м;
х — внешнее возбуждающее воздействие тангенциального движения на конце буксирного троса, м.
10.2.13.3 Травящую лебедку моделируют с помощью эквивалентной массы, демпфирования и жесткости и определяют, когда лебедка травит, по уравнению движения
m'xw+c'xw + k'xw = То + (f),
(344)
где m' — эквивалентная масса лебедки (равная 1/г2, где /— момент инерции массы лебедки, г— радиус лебедки), кг;
Xw — ускорение травления лебедки, м/с2;
с'— зависимый от скорости эквивалентный коэффициент демпфирования лебедки, равный cjr2, где cw— коэффициент демпфирования лебедки, кг/с;
xw — скорость травления лебедки, м/с;
к'—зависимый от положения эквивалентный коэффициент жесткости лебедки, равный к Jr, где kw— коэффициент жесткости лебедки, Н/м.
То — статическое натяжение, Н;
Td(t) — динамическое натяжение, Н;
xw — координата разматывания лебедки, м.
Если лебедка остановлена, то xw = 0 м/с.
10.2.13.4 Лебедку начинают травить, когда общее натяжение 7"0 + Td(t) превышает предельное значение травления лебедки F.
10.2.13.5 Допуская, что буксирный трос выходит из лебедки горизонтально, тангенциальное движение конца буксирного троса х можно вычислить по формуле
х = П-х„, (345)
где г| — относительное движение между буксиром и буксируемым судном;
xw — координата разматывания лебедки, м.
Динамическое натяжение буксирного троса Td вычисляют по формуле
Td = kE(x-u), (346)
где кЕ — упругая жесткость, Н/м;
х — тангенциальное движение конца буксирного троса;
и — смещение буксирного троса, м.
10.2.13.6 Объединяя уравнения (343) и (344), получают функцию движения для модели «буксирный трос — лебедка»:
f(t) = m х + сх + (к' + к)х, (347)
где х — ускорение движения троса, м/с2;
х — скорость поднимаемого объекта, м/с;
к' — коэффициент жесткости лебедки;
к — волновое число, высота неровностей;
х — тангенциальное движение конца буксирного троса.
Также /(/) вычисляют по формуле
f(/) = kEu(t) + + с'п(Г) + k'r|(f) - To, (348)
где кЕ — упругая жесткость, Н/м;
u(t) — смещение буксирного троса, м;
т'— эквивалентная масса лебедки;
Л — вертикальное ускорение объекта, м/с2;
с'— зависимый от скорости эквивалентный коэффициент демпфирования лебедки;
т] — вертикальная скорость объекта, м/с;
к'— зависимый от положения эквивалентный коэффициент жесткости лебедки;
П — относительное движение между буксиром и буксируемым судном;
То — среднее буксировочное усилие.
Данное уравнение связано с моделью отклика буксирного троса, приведенной в 10.2.12, и определяет отклик буксирного троса и как функцию смещения конечной точки х.
10.3 Буксировка трехмерных объектов и протяженных удлиненных конструкций в погруженном положении
10.3.1 Общие положения
10.3.1.1 В данном подразделе рассмотрены три разные конфигурации буксировки:
а) подводная буксировка прикрепленных к судну объектов;
б) подводная буксировка прикрепленных к буксируемому бую объектов;
в) надводная или полупогруженная буксировка протяженных удлиненных элементов, например связок труб.
10.3.1.2 Подводная буксировка объектов является альтернативой морскому подъемному монтажу. Причинами для выбора такого метода монтажа могут быть:
- использование судов-укладчиков с ограниченным палубным пространством или недостаточной грузоподъемностью крана;
- увеличение эксплуатационного рабочего времени путем исключения морских операций с низкими ограничивающими критериями, таких как подъем с барж и/или опускание через зону всплеска волны.
10.3.1.3 Надводная и полупогруженная буксировки протяженных удлиненных элементов являются признанными методами для транспортирования к месторождению. Должен обеспечиваться приемлемо низкий риск повреждения в течение этапа транспортирования.
10.3.1.4 В операцию буксировки включают следующие этапы:
а) прибрежный перевод в буксировочную конфигурацию;
б) буксировка к месту морской установки;
в) морской перевод в монтажную конфигурацию.
В данном подразделе рассмотрена буксировка к месту морской установки.
10.3.2 Критические параметры
Примерами подлежащих рассмотрению при моделировании и расчете подводной буксировки критических параметров могут быть:
- характеристики движения судна;
- свойства троса;
- скорость буксировки;
- прокладка маршрута операции буксировки (ограниченное пространство для маневров, изменяющиеся условия течения);
- продольная устойчивость буксируемого объекта как функция курса;
- усилия в подвешенном тросе, стропах и буксирной оттяжке;
- просвет между объектом и буксирным судном;
- просвет между такелажной оснасткой и судном;
- VIV связок труб и протяженных удлиненных конструкций (например, трубных секций, конструк-ций/трубопроводов);
- влияние подъемного усилия на буксируемые в полупогруженном положении конструкции;
- волновые нагрузки на буксируемые над поверхностью связки (предельная и усталостная нагрузки).
Для расчета/моделирования этих воздействий необходим расчет по временной области.
10.3.3 Прикрепленные к судну объекты
10.3.3.1 На прикрепленные к судну объекты, например в раме устройства вывешивания (см. рисунок 47), воздействуют главным образом поступательная скорость и вертикальное периодическое волновое движение (вертикальная, бортовая и килевая качки) судна-укладчика.
10.3.3.2 Первоначально необходимо определить, что является консервативным для рассматриваемого расчета — волны с длинным гребнем или волны с коротким гребнем. При встречном волнении волны с короткими гребнями дадут увеличенное по сравнению с волнами с длинными гребнями движение бортовой качки, в то время как волны с длинными гребнями — увеличенное по сравнению с волнами с короткими гребнями движение килевой качки.
10.3.3.3 Исходя из моделирований очевидно, что эффекты взаимодействия могут быть значимыми даже для малоразмерных объектов. В результате объект стремится демпфировать движения судна с уменьшенным усилием в подъемном тросе. Несвязанный расчет, таким образом, будет консервативным.
10.3.3.4 При увеличенном размере (масса, присоединенная масса) объекта несоответствия могут быть значительными, и связанный расчет, таким образом, более точно определит поведение судна.
10.3.3.5 Если объект находится, например, на раме устройства вывешивания на борту судна, вес объекта приведет к крену судна. Данное накренение может быть уравновешено включением в расчеты возвращающего момента. В результате это моделирует балластировку, которая будет выполнена для сохранения судна на ровном киле.
10.3.3.6 Если объект подвешен на такелажном оборудовании через буровую шахту судна, особое внимание необходимо обратить на проверку просвета между такелажным оборудованием и краями буровой шахты.
10.3.4 Прикрепленные к буксируемому бую объекты
10.3.4.1 Для прикрепленных к буксируемому бую объектов (см. рисунки 48, 49) динамические усилия, действующие на объект, и такелажное оборудование не подвергаются воздействию вызванных волнами вертикальных движений судна.
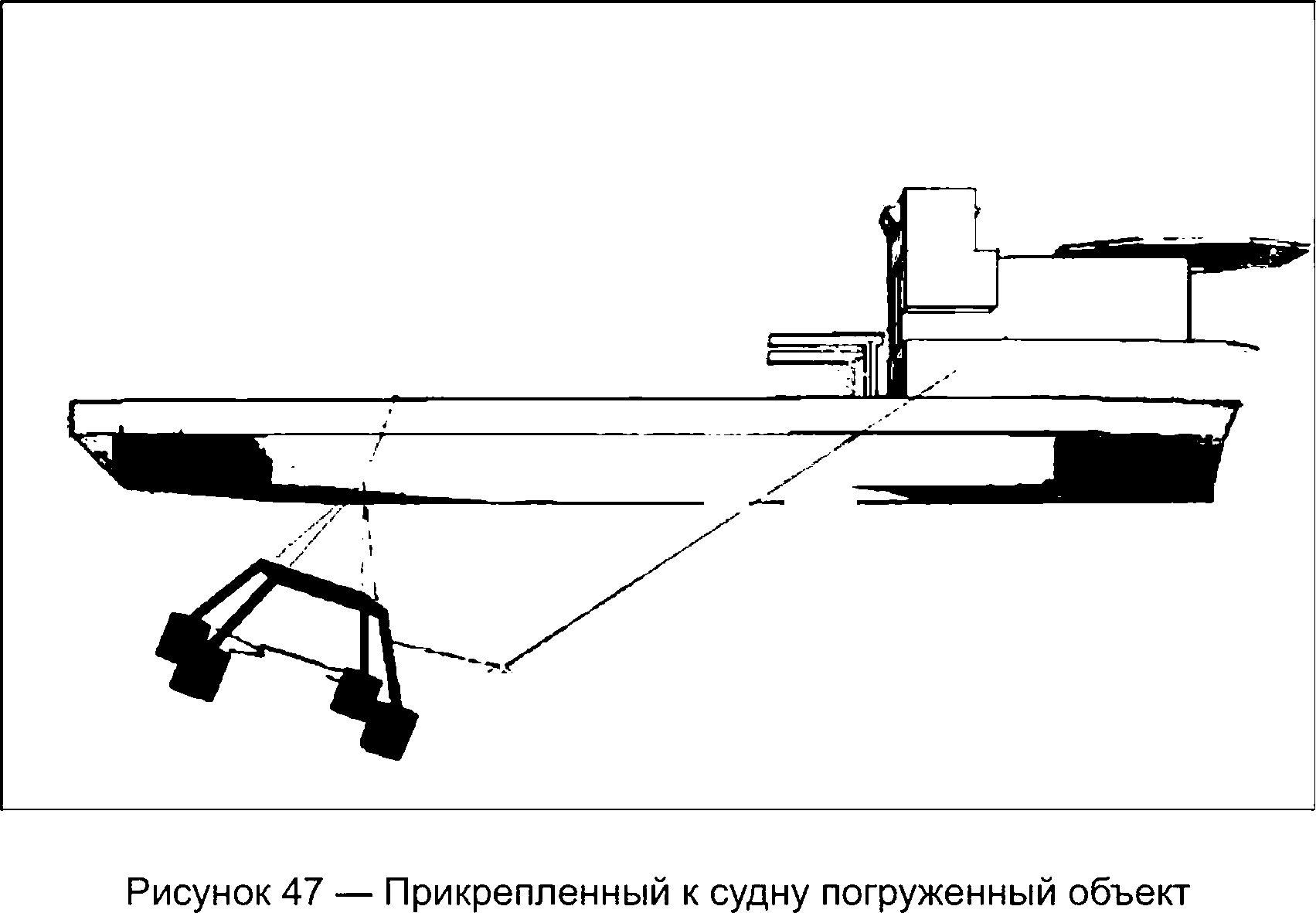
Рисунок 48 — Прикрепленный к буксируемому бую погруженный объект (не в масштабе)
10.3.4.2 Буй может быть сконструирован с малой относительно его водоизмещения площадью зеркала воды, снижающей вызванное волнами вертикальное движение буя.
10.3.4.3 Так как движения бортовой качки судна не влияют на поведение буя, волны с длинными гребнями будут консервативными для данного расчета.
10.3.5 Буксировка протяженных удлиненных элементов
10.3.5.1 Примерами удлиненных объектов, которые можно буксировать к месторождению, являются:
- трубопроводы, связки, трубные секции;
- растяжки платформ с натяжными опорами;
- колонны райзеров/гибридные райзеры.
Несколько удлиненных объектов можно буксировать в виде пучка (связанными вместе или внутри защитного кожуха).
10.3.5.2 Как правило, буксировку протяженных удлиненных элементов проводят одним из следующих методов:
а) при буксировке над дном комбинацию плавучести и балластных цепей используют таким образом, чтобы буксируемый объект был поднят над морским дном. Балластные цепи применяют для удержания буксируемого объекта поблизости от морского дна и обеспечения достаточного веса и устойчивости в погруженном положении;
б) метод буксировки с глубоким погружением, или буксировки с регулируемой глубиной (CDT), является дальнейшим развитием метода буксировки над дном. Путем тщательного проектирования длины буксирного троса, противонатяжения, плавучести, балластных и тяговых цепей со специфическими гидродинамическими свойствами буксируемый объект будет поднят с морского дна на критически малой скорости для буксировки на регулируемой глубине над препятствиями на морском дне, но ниже области с сильным влиянием волнения;
в) методы надводной или подповерхностной буксировки для транспортирования протяженных удлиненных элементов на короткие или длинные расстояния. При надводных буксировках на буксируемый объект будут воздействовать волновые нагрузки. Часто используют элементы плавучести (см. рисунок 49).
а) Надводная буксировка
б) Подповерхностная буксировка
Направление буксировки

в) Буксировка на регулируемой глубине (во время буксировки)
Рисунок 49 — Различные методы буксировки протяженных удлиненных объектов
10.3.5.3 Конфигурация буксировки зависит:
- от веса в погруженном состоянии в воде;
- использования временной плавучести/веса;
- скорости буксировки и длины буксирного троса;
- обеспечиваемого тянущим буксиром противонатяжения;
- нагрузки лобового сопротивления из-за течения.
10.3.5.4 Влияние подъемного усилия и устойчивость могут помешать контролю над буксируемой под поверхностью связкой. Особое внимание требуется обратить на несимметричное относительно оси поперечное сечение, буксирные головки или другие прикрепленные к связке конструкции.
10.3.5.5 Необходимо до минимума снизить усталостную нагрузку на трубу из-за движений буксира и прямого воздействия волн. С целью минимизации прямого воздействия волн при буксировке в условиях волнения с высокими периодами пиков глубина буксировки буксируемого объекта должна быть больше, так как длинные волны воздействуют глубже в водной толще.
Вызванная волной скорость снижается с коэффициентом ekz вниз в водной толще, где к = 2л/Х — волновое число, X— длина волны. Вследствие этого при равной Х/2 глубине буксировки энергия составляет только 4 % от значения на поверхности.
10.3.6 Характеристики системы
Для выполнения расчета по временной области концепции буксировки в погруженном состоянии необходимы следующие данные системы:
- судна: массовые характеристики (масса, плавучесть, центр тяжести, радиус инерции, водоизмещение, осадка) и геометрия корпуса. Эти данные будут исходными для расчета трехмерной дифракции;
- буя: массовые характеристики (масса, плавучесть, центр тяжести, радиус инерции, водоизмещение) и геометрия корпуса;
- буксируемого объекта: массовые характеристики (масса, плавучесть, центр тяжести, радиус инерции) и чертеж общей компоновки (включая размер конструктивных элементов) для определения расчетной модели, жесткостных характеристик, влияний усилия лобового сопротивления и подъемного усилия;
- такелажного оборудования: массовые характеристики (масса, плавучесть) любых сосредоточенных масс, таких как крюк. Геометрия и жесткость;
- буксирного троса/оттяжки: массовые характеристики (масса, плавучесть), геометрия и жесткость, любые сосредоточенные массы;
- эксплуатационные: скорость буксировки, курс судна, скорость/направление течения, направления волн и состояния моря.
10.3.7 Моделирование системы
10.3.7.1 Функции передачи движения и гидродинамические коэффициенты судна для всех шести степеней свободы следует рассчитывать путем трехмерного расчета дифракции волны.
10.3.7.2 Что касается буя, то в концепции буксируемого буя следует применять модель, правильно описывающую объединенное движение продольно-горизонтальной/килевой качки. В дополнение к этому также должно быть включено влияние осадки на движение вертикальной качки. Для того чтобы уловить эти воздействия, можно использоватья модель Морисона. Это правомерно для протяженных и удлиненных буев. Должны быть включены возможные воздействия поступательной скорости.
10.3.7.3 Для прикрепленных к судну или буксируемому бую буксируемых объектов в модели КЭ такелажного оборудования (строп и подъемного троса) и/или буксирного троса и оттяжки, как правило, необходимость отсутствует. В таких случаях может быть достаточно смоделировать тросы с использованием пружин.
10.3.7.4 В большинстве случаев буксируемый объект моделируется с помощью элементов Морисона со свойствами присоединенной массы и усилия лобового сопротивления для различных основных компонентов, таких как цилиндры, пластины и т. п. Необходимо обеспечить получение правильного распределения массы и плавучести. Для улавливания корректного распределения динамической нагрузки между стропами буксируемый объект следует моделировать как тело с шестью степенями свободы, с распределенными по всей конструкции элементами Морисона.
10.3.7.5 Для буксировки протяженных удлиненных объектов типа связок конструкция должна быть смоделирована в программе КЭ. В данном случае решающими могут быть усталостные нагрузки и потребуется оценить общее поведение конструкции под динамической нагрузкой.
10.3.8 Вызванные вихреобразованием вибрации
10.3.8.1 В случае удлиненных конструкций, таких как связки, трубные секции, трубопроводы и т. п., особое внимание должно быть обращено на определение того, возникнут ли затруднения, VIV.
10.3.8.2 Для удлиненных конструкций собственные колебания могут быть рассчитаны в программе КЭ. Собственные колебания являются «мокрыми», включающими влияние присоединенной массы от окружающей воды. Если одна из собственных частот fn конструкции близка к частоте вихревого потока, могут возникнуть VIV, а возможная усталостная нагрузка вследствие VIV во время операции буксировки в море должна быть проанализирована VIV дополнительно.
Для погруженных в воду протяженных удлиненных конструкций VIV могут возникнуть, если 3 < Vp < 16,
где vR — сниженная скорость, равная U/(fnD);
U — относительная скорость между скоростью буксировки и течением, м/с;
fn— собственная частота, Гц;
D — диаметр удлиненного элемента, м.
Первую собственную частоту свободно опертой балки вычисляют по формуле
= 1,57
1 + 0,8
(349)
где El — жесткость на изгиб;
т'— общая масса на единицу длины (включая присоединенную массу);
L — длина вылета;
8 — статический прогиб (провисание);
D — характеристический размер поперечного сечения (диаметр).
Статический прогиб 8 из-за равномерного течения вычисляют по формуле
g_ 5 gL4 (350)
384 El ’
где q — усилие на сечение лобового сопротивления течения.
10.3.8.3 Если обнаружено, что буксируемый объект предрасположен к VIV, необходимо либо документально подтвердить, что причиненные этим повреждения являются приемлемыми, либо изменить конфигурацию таким образом, чтобы периоды собственных колебаний уменьшились для предотвращения VIV. Это можно осуществить путем поддержки конструкции или его предрасположенной к VIV части, для того чтобы сделать ее жестче.
Если иное не подтверждено документально, независимо от класса безопасности необходимо, чтобы на этапе монтажа использовалось не более 10 % от допустимого усталостного повреждения, что соответствует отраслевой практике.
10.3.9 Требования к расчету
10.3.9.1 Для того чтобы определить существенные физические воздействия, необходимо использовать расчет по временной области (см. 10.3.2). Расчет в частотной области может быть применен на этапе планирования для изучения параметров и для получения быстрых оценок отклика для различных буксировочных конфигураций. Расчет в частотной области также может быть использован для расчета усталости продолжительных по времени буксировок, сталкивающихся во время буксировки с различными состояниями моря.
10.3.9.2 Продолжительность временного моделирования должна быть достаточной для предоставления достоверных статистических данных. Требуется выполнить 3-часовые моделирования в нерегулярных состояниях моря.
10.3.9.3 Для некоторых программ расчета может потребоваться максимальное время моделирования для полного 3-часового моделирования, и, следовательно, полновременные моделирования для широкого диапазона состояний моря и курсов волнения могут быть непрактичными. Для таких программ может быть применен метод с выбором характеристических серий волн.
10.3.9.4 Последовательностью для выбора является расчет зависимого от времени вертикального движения в точке подвеса (например, в раме устройства вывешивания), а затем — выбор серии волн, совпадающих с возникновением максимальной вертикальной скорости и максимального вертикального ускорения.
10.3.9.5 Особое внимание также необходимо обратить на выбор серий волн для расчета минимального просвета до борта судна и краев буровой шахты.
10.3.9.6 Для того чтобы убедиться в том, что способ выбора дает результаты с примерно правильной величиной, требуется провести одну 3-часовую проверку для наихудших предельных случаев.
10.3.9.7 Следует установить проектные ограничения для каждого прогноза погодных условий.
10.3.9.8 Держащее курс управляемое судно будет неспособно постоянно сохранять абсолютно такое же направление, в связи с чем необходимо, чтобы расчеты выполнялись для предполагаемого направления ± 15°.
Если применяются волны с длинным гребнем, то с целью учета дополнительного влияния волн с коротким гребнем используют курсовой угол ± 20°.
10.3.9.9 Необходимо проверить результаты в сравнении с установленными критериями приемлемости, такими как:
- минимальное и максимальное усилия в стропах;
- просвет между объектом и судном;
- устойчивость во время буксировки;
- VIV удлиненных конструкций. В случае связок VIV могут причинить значительные усталостные повреждения.
10.3.9.10 Для протяженных удлиненных элементов существенным результатом расчетов будет определение оптимальной конфигурации буксировки (глубина буксировки, использование временной плавучести/веса, натяжение в связке и т. п.).
10.3.9.11 Целесообразной является визуализация результатов. Таким образом может быть обнаружено нефизическое поведение, такое как сильные прогибы относительно первоначального положения и сильные угловые движения.
10.3.10 Мокрое анкерное закрепление
Буксировки над дном протяженных удлиненных объектов на дальние расстояния могут быть прекращены ввиду неблагоприятных погодных условий, а связка оставлена в закрепленном анкером положении вблизи морского дна (см. рисунок 50). Как правило, анкеры крепят к концу связки. В закрепленном анкером положении связка будет подвергаться действию усилий от течения. Связка стабилизируется с помощью сил трения между балластными цепями и морским дном. Типичные коэффициенты трения для цепи анкера приведены в таблице 4.
Таблица 4 — Коэффициенты трения между цепью и морским дном
Состояние морского дна | Коэффициент трения | |
статический | скольжения | |
Песок | 0,98 | 0,74 |
Ил с песком | 0,92 | 0,69 |
Твердый ил | 1,01 | 0,62 |
Мягкий ил | 0,90 | 0,56 |
Глина | 1,25 | 0,81 |
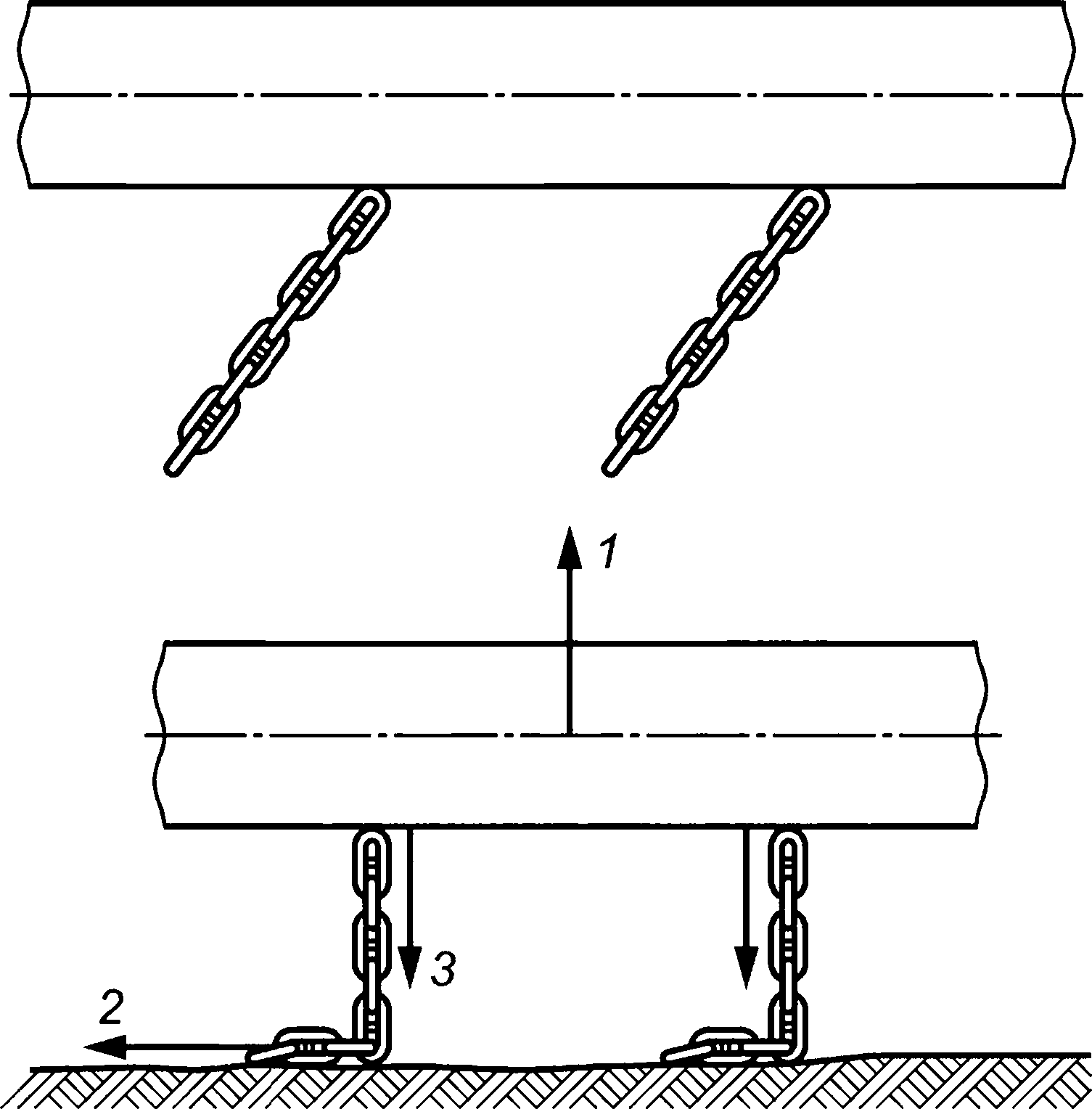
1 — плавучесть; 2 — сила трения; 3 — вес цепи в погруженном состоянии
Рисунок 50 — Цепи во время буксировки (вверху) и в режиме над дном (внизу)
11 Расчет погодных критериев и пригодности
11.1 Общая часть
11.1.1 Погодные условияИнформация о требуемых для выполнения морских работ погодных условиях зависит от типа работ, например: бурение, прокладка трубопровода, морская отгрузка, установка платформы, крановые работы или подводная установка.
11.1.2 Планирование и выполнение
11.1.2.1 Морские операции состоят из двух этапов:
- проектирование и планирование;
- выполнение работ.
11.1.2.2 На этапе проектирования и планирования должны быть выбраны сезоны выполнения морских работ и определены критерии погодных условий для начала и прерывания операций (расчет пригодности). Расчет должен быть основан на статистических данных, включающих в себя период не менее 5—10 лет.
11.1.2.3 Выполнение морских работ должно быть быть основано на прогнозе погоды, данных почти в реальном масштабе времени (NRT) (данные с динамикой изменений в 1—5 ч) и, если оправданно, на данных в реальном времени (RT) (данные с динамикой изменений в 0—1 ч).
11.2 Условия окружающей среды
11.2.1 Общие положения11.2.1.1 Для морских работ ключевыми параметрами являются динамика изменений погодных условий и продолжительность метеорологических явлений. Расчет погодных критериев и пригодности должен включать в себя критически важные для операции установленные условия окружающей среды и предоставление продолжительности явлений для превышения и непревышения пороговых значений для этих условий.
11.2.1.2 До начала операции необходимо установить критически важные для проведения операции и ее вспомогательных действий пороговые значения условий окружающей среды, время для подготовки операции, а также продолжительность каждого вспомогательного действия. Эти значения будут зависеть от типа операции и от критичных откликов.
Если для операции определено максимальное пороговое значение отклика Хтах, то устанавливают соответствующие пределы (пороговые значения) высоты характерной волны для переменных периода волны и направления волны. Если в качестве спектра использован спектр ПМ, а также линейный отклик, постоянный период колебания волны через нулевую точку Tz и направление распространения волны, то получают отклик, пропорциональный высоте характерной волны Hs. Также можно будет рассчитать отклик для Hs, равный 1 м для всех наблюдаемых в статистических данных периодов колебания волны через нулевую точку. Максимальную высоту Hs для каждой точки Tz тогда масштабируют согласно формуле
Hsn^(Tz)= HS(TZ), (351)
xvz)hs=i
где Xmax — максимальное пороговое значение отклика;
Hs — высота характерной волны;
Tz — период колебаний через нулевую точку.
11.2.2 Первичные характеристики
11.2.2.1 Чаще всего первичным параметром будет превышающая заданный пороговый уровень, как показано на рисунке 51, высота характерной волны. Существенные для выполнения морских работ пороговые значения для других условий окружающей среды (например, соответствующие периоды колебания волны) могут быть установлены на основании совместных вероятностей.
Высота характерной волны /7S', м
*2 *з *4 *5 *7
Время, ч
Рисунок 51 — Пример изменения высоты характерной волны во времени
11.2.2.2 Продолжительность метеорологического явления определяют как время между пересечением уровня для данного параметра и следующим пересечением аналогичного уровня (см. рисунок 51). Явление может быть определено как выше уровня (от до t2, Hs > так и ниже уровня (от t2 до t3, Hs < Н^. Явления ниже порогового уровня часто называют периодами покоя, а выше порогового уровня — периодами шторма. Попадающие в конец ряда данных явления не должны включаться в статистику.
11.2.3 Выбор оптимальных маршрутов в зависимости от погодных условий для неограничиваемых операций
11.2.3.1 Для включающих в себя операций транспортирования, например буксировка морских работ, необходимо определить оптимальный маршрут. В расчете должны быть представлены и использованы необходимые для оценки критичных откликов по различным альтернативным маршрутам условия окружающей среды. Как правило, они представляют собой диаграммы разброса высоты характерной волны и периода (или пика спектра) колебания волны через нулевую точку.
11.2.3.2 На этапе проектирования и планирования требуется выбрать оптимальный маршрут, основанный на оценке откликов и усталостного повреждения по различным альтернативным маршрутам. Для данной цели могут быть использованы общие базы данных условий окружающей среды.
11.2.3.3 Выбор оптимальных маршрутов в зависимости от погодных условий также может быть сделан во время транспортирования на основании прогнозирования погоды. Путем изменения скорости и направления движения судно может избежать или минимизировать нахождение в районах с плохими погодными условиями. В силу скрытых вероятностей человеческих ошибок или ошибочного прогнозирования существует тем не менее определенная опасность принятия ошибочных решений.
11.3 Точность данных
11.3.1 Общие требованияРасчет погодных критериев и пригодности должен быть основан на надежных данных и должна быть указана точность этих данных. Примененные данные должны быть представлены для места или участка моря, в котором проводят операцию. Требуется использование надежных данных технических средств или данных, подготовленных с помощью общепризнанных моделей прогнозирования погоды. В дополнение к этому необходимо, чтобы данные собирались как минимум каждый 3-й час и интерполировались между интервалами выборки. Общие требования к сбору данных гидрометеорологических условий определяют в процессе работы.
11.3.2 Данные приборов
11.3.2.1 Точность данных условий окружающей среды может значительно изменяться и тесно связана со способом наблюдений.
11.3.2.2 Общие наблюдения за ветром включают в себя среднюю скорость ветра, среднее направление ветра и максимальную скорость ветра в пределах интервала наблюдения. Стандартная информация о ветре представляет собой измеренную или калиброванную 10-минутную среднюю скорость на высоте 10 м над уровнем земли или средним уровнем моря. Приборы измерения ветра на буях обычно устанавливают на высоте примерно 4 м над уровнем моря. Систематическая инструментальная погрешность при оценке средней скорости и направления ветра может считаться пренебрежимо малой. Кроме того, могут быть использованы данные спутниковых измерителей разброса.
11.3.2.3 Приборная точность наблюдений за волнами зависит от типа используемого прибора. Волновые буи считают высокоточными приборами, и погрешность в оценке высоты характерной волны и периода колебания волны через нулевую точку может быть пренебрежимо малой для большинства состояний моря. Во время неблагоприятных морских условий присутствие сильного поверхностного 130
течения или внешних усилий, действующих на буй (например, дробящихся волн, швартовых), может стать причиной систематической погрешности измерений буя.
11.3.2.4 Проведенные за последние годы несколько исследований показывают обещающие результаты, подтверждающие использование спутниковых данных. В диапазоне высот характерной волны 1—8 м полученные со спутникового альтиметра высоты характерной волны были почти такими же точными, как и значения, полученные от измерений поверхностного буя.
11.3.2.5 В случае крутых волн разница между записанными с помощью фиксированного (эйлерова) зонда или лазера колебаниями поверхности моря и данными, полученными с помощью плывущего по течению (лагранжева) буя, может быть значительной. Данные волнового буя не должны быть использованы для оценки профилей волнения при крутых волнах. При наблюдении за профилем волнения необходимо применять лазер.
11.3.2.6 Установленные на платформе волномеры и другие устройства измерения волн имеют преимущество, которое позволяет напрямую измерять смещение поверхности моря, а не ускорение, что осуществляется с помощью буев. Положение волномера может повлиять на точность данных.
11.3.2.7 Судовой самопишущий волномер (SBWR) осуществляет непосредственные измерения высоты волны, но не дает информацию о направлении. Главной неопределенностью является отклик судна на волны. Сравнение с данными волнового буя предлагает среднюю точность высоты волны около 8 % — 10 %. В среднем высоты характерной волны SBWR выше, чем высота волны буя, с большим процентом разницы при малых высотах волны и с меньшим при больших высотах волны. Периоды колебания через нулевую точку от двух приборов приблизительно одинаковы.
11.3.2.8 Морские радиолокаторы предоставляют спектры направленной волны и вычисляют высоту волны опосредованным методом. Для применения морского радиолокатора в морских операциях необходимо учитывать его точность.
11.3.2.9 Для зафиксированной приборами изменчивости выборки данных волнения время вносит значительный вклад в погрешность выполнения замеров. Для вариабельности замеров спектров JONSWAP и ПМ для 20-минутного интервала измерения коэффициенты изменения высоты характерной волны и периода колебания волны через нулевую точку приближенно составляют 4 % — 6 % и 1,5 % — 2,5 % соответственно.
11.3.2.10 Набор инструментальных данных течения может быть ошибочным из-за отказа прибора, например ротора, или из-за обрастания морскими организмами. Перед применением набора данных в планировании и выполнении морских работ следует удостовериться в проведении проверки качества данных. Погрешность данных течения указывается.
11.3.2.11 Сбор данных уровня воды осуществляют с помощью либо механических приборов, либо датчиков давления, волновых буев, волновых радиолокаторов и лазеров. Точность таких фиксаций составляет 2—3 см. Для использования рассчитанных данных уровня воды необходимо установить допущения и ограничения модели. Данные, как правило, представлены как остаточные уровни морской воды, т. е. уменьшенные на прилив общего уровня морской воды.
11.3.3 Данные численного моделирования
11.3.3.1 Численно моделированные данные волнения получают на регулярной основе от крупных национальных метеорологических служб и сохраняют в центрах хранения и обработки данных. Точность этих данных может быть непостоянной и зависит от точности примененной модели прогнозирования волнения, а также от принятого поля скоростей ветра. Могут быть использованы данные ретроспективного прогноза, когда лежащий в основе ретроспективный прогноз откалиброван с измеренными данными, а точность этих данных имеет документальное подтверждение.
11.3.3.2 Часто применяют собранные находящимися в обычной эксплуатации по всему миру судами визуальные наблюдения Всемирной волновой статистики (GWS) начиная с 1949 г. Эти данные представляют собой среднюю ветровую и волновую обстановку для 104 областей океанских волн. Они имеют достаточно долгую историю наблюдений, для того чтобы иметь надежную всемирную статистику ветровой и волновой обстановки. Точность таких данных тем не менее по-прежнему подвергается сомнению, особенно касательно периода волны.
11.3.3.3 Недавно созданы несколько всемирных баз данных условий окружающей среды. Они включают в себя откалиброванные измерениями (данными на месте, спутниковыми данными) численные данные ветра и волн (некоторые предоставляют уровень течения и/или морской воды), комбинацию численных и инструментальных данных или инструментальные (спутниковые) данные. Перед применением данных их точность должна быть подтверждена документально.
11.3.4 Климатическая неопределенность
11.3.4.1 На статистические данные, используемые для определения критериев погодных условий операции, может повлиять климатическая неопределенность. Климатическая неопределенность возникает тогда, когда данные получены от временного интервала, который не является полностью репрезентативным для долговременных изменений условий окружающей среды. Это может выразиться в переоценке или недооценке критериев погодных условий операции. Для учета изменчивости климата база данных должна охватывать не менее 20 лет из предпочтительно 30 лет или более.
11.3.4.2 При наличии данных за 20—30 лет необходимо установить климатическую характеристику, например распределение высоты характерной волны для периодов повторяемости в 1, 3, 5, 10 и 25 лет.
11.3.5 Источники данных
В силу неточности данных в расчете (при наличии) необходимо использовать несколько источников данных, указывая критерии погодных условий для сравнения. Особое внимание требуется обратить на области океана с плохой обеспеченностью данными.
11.4 Прогнозирование погоды
11.4.1 Операции, ограничиваемые погодойМорские операции с регламентированным периодом выполнения менее 72 ч могут быть определены как ограничиваемые погодой. Эти работы могут планироваться при выбранных независимо от статистических данных погодных условиях, т. е. заданных заказчиком, эксплуатантом и т. п.
11.4.2 Неопределенность метеорологических прогнозов
Для ограничиваемых погодой работ необходимо учитывать неопределенность в прогнозах погоды. Эксплуатационные пределы условий окружающей среды (например, высота характерной волны, скорость ветра) должны быть меньше проектных значений.
11.5 Статистика изменчивости
11.5.1 Не ограничиваемые погодой операции11.5.1.1 Морские операции с превышающим 72 ч регламентированным периодом выполнения, как правило, определяют в качестве неограничиваемых работ. Эти работы должны планироваться на основании статистики по экстремумам, установленной по статистическим данным или моделированиям временной области.
11.5.1.2 Статистика изменчивости должна быть определена согласно ранее установленным проектным эксплуатационным критериям.
11.5.1.3 Нестационарное стохастическое моделирование, пригодное для моделирования многомерного временного ряда данных условий окружающей среды, может быть использовано в качестве вспомогательного инструмента для формирования долговременных данных.
11.5.2 Статистика на основании данных за прошедшие периоды
11.5.2.1 Статистика должна содержать следующие параметры:
Ttot — общий период времени рассматриваемых климатических временных рядов;
Nc— количество периодов покоя;
тс— средняя продолжительность периодов покоя;
ts — средняя продолжительность периодов шторма;
Тс — общая продолжительность всех периодов покоя;
Ts— общая продолжительность всех периодов шторма.
Соответственно общую продолжительность всех периодов покоя Тс вычисляют по формуле
Nc
Tc=%ci, (352)
/=1
где тс/-— средняя продолжительность периодов покоя;
Nc — количество периодов покоя.
Общую продолжительность всех периодов шторма Ts вычисляют по формуле
Nc
(353)
Ts = ^Si’
где ts/- — средняя продолжительность периодов шторма.
Общий перевод времени рассматриваемых климатических временных рядов Тобщ вычисляют по формуле
(354)
Г « = Т + Т 'общ 'с 's’
11.5.2.2 Для маргинального распределения периода покоя t может допускаться 2-параметриче-ское распределение Вейбулла вычисляемое по формуле
Ет(Г) = 1-ехр
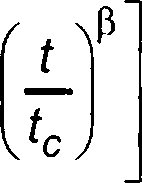
(355)
где tc — параметр масштаба;
Р — параметр формы.
Параметры распределения определены на основании конкретных данных места с помощью указанных методов подбора.
11.5.2.3 Средняя продолжительность тс выражена как
(356) а
где FT— частное (маргинальное) распределение периода покоя.
Для 2-параметрического распределения Вейбулла среднюю продолжительность тс вычисляют по формуле
fc=tc-rfl+l), (357)
с с (р J
где tc — параметр масштаба;
Г — математическая гамма-функция;
Р — параметр формы.
11.5.2.4 Если установлена интегральная функция распределения Hs, то средняя продолжительность периодов тсс высотой характерной волны h может быть аппроксимирована следующим образом:
(358)
где FHs(h) — интегральная функция распределения Hs;
7"Общ — общий период времени рассматриваемых климатических временных рядов;
Nc — количество периодов покоя;
г / tn— (359)
Te=A[-|n(f>,s {/>))] 9.
где FH (/?) — интегральная функция распределения Hs;
Дир — параметры, установленные на основании относящихся к конкретному месту данных.
Для Северного моря могут быть приняты следующие значения: А = 20 ч, р = 1,3.
11.5.2.5 Распределение для h < Hs и продолжительность t < t' составляют:
Fhs\T(л<н;|*> *’)= FHs(h<н;)(1-1),
где X — длина волны, рассчитываемая по формуле
х=4
J *М) О
11.5.2.6 Количество периодов, когда h < Hs. \л t < t', может быть выражено следующим образом:
=
где N’c — количество периодов;
Л/с — количество периодов покоя.
Средняя продолжительность периодов ?с для h < Hs,wt< t' составляет:
(363)
В качестве примера эксплуатационные качества оценивают для судна с буровой шахтой. Рассматривают три чувствительные к движению операции с максимальной характерной амплитудой в буровой шахте, равной 0,5; 0,75 и 1,0 м. Рассчитанные значимые амплитуды вертикального движения для судна определяют ограничивающее значение Hs для этих трех операций, как показано на рисунке 52.
Для того чтобы показать рабочие и нерабочие состояния моря, эти ограничения состояния моря объединены с диаграммой разброса (см. таблицу 5). Эксплуатационная пригодность для каждой из разных рабочих задач показана в таблице 6. Рассчитанные эксплуатационные ограничения должны быть объединены с эксплуатационными ограничениями на основе практических соображений и требований персонала, который будет выполнять работу.
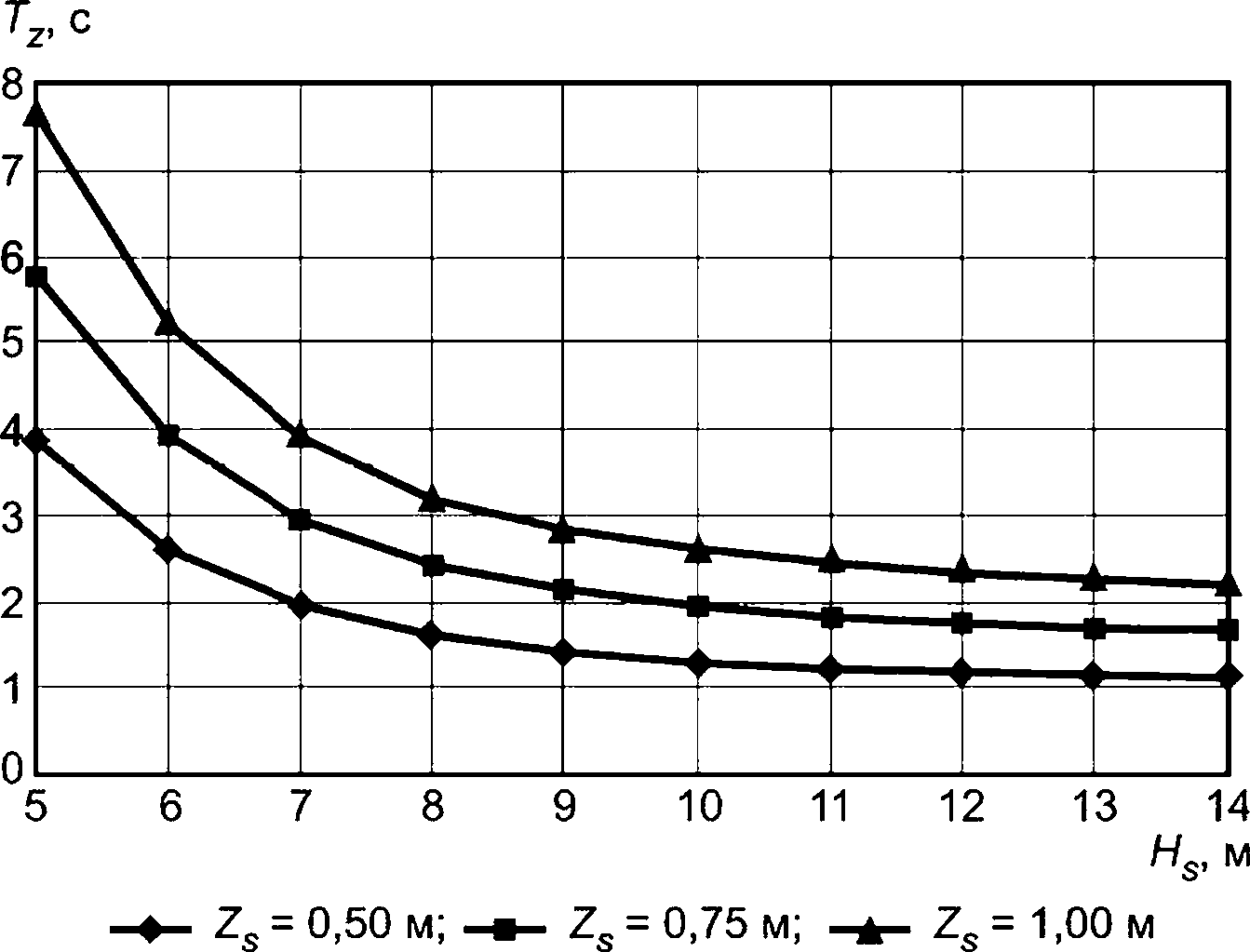
Tz — период колебания через нулевую точку для относительного движения, с; Hs — высота характерной волны, м; Zs— максимальная характерная амплитуда в буровой шахте, м
Рисунок 52 — Ограничивающее значение Hs для работ с Zs = 0,5; 0,75 и 1,0 м
Таблица 5 — Эксплуатационные ограничения в зависимости от волнения моря
Hs, м | 7-z,c | Сумма Tz, с | |||||||||
5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
6,8 | |||||||||||
0,5 | 4,9 | 1,3 | 1,3 | 1,1 | 0,2 | 1,6 | 0,9 | 1,6 | 1,6 | 1,1 | 16,1 |
1,0 | 10,4 | 4,8 | 2,2 | 1,1 | 0,9 | 1,5 | 0,5 | 2,0 | 1,6 | 2,6 | 27,7 |
1,5 | 4,6 | 2,4 | 1,8 | 2,0 | 0,4 | 0,7 | 0,7 | 0,2 | 1,3 | 0,7 | 14,8 |
2,0 | 3,3 | 3,1 | 1,8 | 2,0 | 0,4 | 0,7 | 0,7 | 0,5 | — | 1,8 | 14,5 |
2,5 | 2,2 | 2,4 | 1,5 | 2,2 | 0,4 | 0,9 | — | 0,2 | 0,2 | 0,4 | 10,3 |
3,0 | 0,4 | 0,2 | 1,1 | 1,8 | 0,5 | 0,2 | 0,2 | — | — | 0,2 | 4,8 |
3,5 | 0,4 | — | — | 1,3 | — | 0,2 | — | — | — | — | 1,8 |
4,0 | 0,5 | 0,2 | 0,4 | 0,2 | — | 0,5 | 0,2 | — | — | — | 2,0 |
4,5 | 0,4 | — | 0,2 | 0,4 | 0,2 | 0,2 | — | — | — | — | 1,3 |
Сумма Hs, м | 27,3 | 14,7 | 10,3 | 12,1 | 2,9 | 6,6 | 3,3 | 4,6 | 4,8 | 6,8 | 100 |
Таблица 6 — Вероятность эксплуатационных ограничений
Критерий Zs0, м | Нерабочее состояние моря, % | Рабочее состояние моря, % |
0,5 | 35,0 | 65,0 |
0,75 | 19,4 | 80,6 |
1,0 | 6,6 | 93,4 |
11.5.3 Моделирование временной области
11.5.3.1 В качестве альтернативы, описанной в статистике по 11.5.2, расчет погодных критериев и пригодности может быть исследован путем использования моделирований временной области выполнения работы. При расчете учитывают погодные условия в форме измеренных или вычисленных временных рядов. Любое заданное количество условий окружающей среды, как правило, может быть обработано по временным рядам.
11.5.3.2 Программы моделирования морских работ должны включать параметры продолжительности, погодных ограничений и последовательности действий. Они могут быть использованы для предварительного планирования и во время выполнения работ.
11.5.3.3 Разработав график работ и установив временные ряды погоды, программное обеспечение для выполнения работы сканирует временные ряды погоды и находит выполнение заданного графика работ исходя из заданного дня начала в течение года.
11.5.3.4 Преимуществами использования временных рядов и нестатистических данных по сравнению с приведенными в 11.5.2 являются:
- более простой способ выведения статистического разброса;
- на временных рядах более доступная проверка эксплуатационных ограничений;
- проверка в облегченном режиме графиков работ на соответствие временным рядам;
- доступное объединение предельных значений нескольких погодных параметров;
- возможность установки статистических данных определенных погодных параметров. Для получения надежных результатов следует рассчитывать достаточно продолжительные хронологические временные ряды;
- прямой учет продолжительности работ.
11.5.3.5 Каждая операция должна быть разделена на последовательность небольших и, насколько возможно, независимых вспомогательных операций.
11.5.3.6 Для предотвращения начала критической операции, которая должна быть запущена, но не сможет завершиться до возникновения неприемлемых погодных условий, может потребоваться дополнительная продолжительность прогнозируемого погодного окна. Максимальные пределы более длительного времени будут зависеть от точности оценок продолжительности. Как вариант, погрешность в моделированиях прогноза можно учесть путем введения случайной погрешности (и/или систематической ошибки) в запись фактических условий окружающей среды, т. е. регистрацию волнения.
11.5.4 Сезонные колебания
Статистика изменчивости должна содержать информацию о сезонных изменениях погодной обстановки. Проектирование и планирование морских работ должны быть основаны на средних погодных условиях, в течение одного года, 3 мес и более короткого периода времени.
11.6 Контроль погодных условий и откликов
11.6.1 Контроль явлений окружающей среды11.6.1.1 Для морских работ, особенно чувствительных к определенным условиям окружающей среды, таким как волнение, зыбь, течение, прилив и т. п., до и во время работы должен быть организован систематический контроль за этими условиями.
11.6.1.2 Значимые системы контроля должны иметь резервные системы. О любых непредусмотренных результатах контроля необходимо немедленно докладывать.
11.6.1.3 Выполнению морских работ может содействовать установленная на борту морских конструкций система поддержки принятия решений, если надежность системы представлена и одобрена официальным или классификационным органом. Система поддержки принятия решений может быть основана на данных практически в NRT и/или на данных RT, которые могут быть предоставлены метеослужбами, частными компаниями или исследовательскими институтами. Данные NRT и RT могут представлять собой данные численного моделирования, комбинацию численных данных и показаний приборов (данные измерений на месте, данные морского радара и спутниковые данные) или только показаний приборов, если частота выборки последних достаточна для рассматриваемой операции. Движения судна могут быть использованы системой поддержки принятия решений, а условия окружающей среды — оценены на основании движений судна. Необходимо обратить внимание на точность прогнозирования комбинированных волнений (ветровая волна и зыбь).
11.6.1.4 Требуемый интервал выборки для временного мониторинга будет зависеть от типа работы и ее продолжительности.
11.6.2 Приливные изменения
Приливные изменения следует дополнительно наблюдать в период с такой же фазой Луны, как и планируемая работа.
Приливные изменения должны быть нанесены в зависимости от установленных графиков астрономических приливов. Любые противоречия необходимо анализировать должным образом, принимая во внимание барометрическое давление и другие влияния погодных условий.
11.6.3 Мониторинг откликов
Мониторинг откликов следует проводить с помощью документально подтвержденных надежных приборов.
11.6.4 Проводят связанный с альфа-коэффициентом мониторинг.
12 Спуско-подъемные операции
12.1 Общие положения
12.1.1 Как правило, в спускоподъемных операциях задействованы кран, плавучий кран, транспортное судно/баржа и поднимаемый объект.
12.1.2 Во время спускоподъемной операции следует принимать во внимание следующие функциональные особенности:
- просвет между поднимаемым объектом и стрелой крана;
- просвет между стрелой крана и любым другим объектом/сооружением;
- просвет между поднимаемым объектом и другим объектом/сооружением;
- просвет между нижней поверхностью поднимаемого объекта и крепежными средствами или конструкцией раскрепления на транспортном судне/барже;
- донный просвет между плавучим краном и морским дном при подъемных работах на малых глубинах воды.
12.1.3 Перечисленные в 12.1.2 просветы должны быть определены на основании ожидаемой продолжительности работы, порядков выполнения работы и условий окружающей среды.
12.1.4 Должен быть рассчитан просвет между поднимаемым объектом или транспортным судном/ баржей и плавучим краном или стрелой крана. Рассчитанный просвет должен учитывать движения плавучего крана и транспортного судна/баржи. Расчеты движения должны основываться на проектных условиях окружающей среды, и следует выполнить оценку максимальных значений.
12.1.5 Как правило, спускоподъемные операции крана разделяют на две категории:
- легкие подъемы, при которых поднимаемый объект предельно мал по сравнению с плавучим краном.
Вес поднимаемого объекта составляет менее 1 % — 2 % от водоизмещения плавучего крана — как правило, менее нескольких сотен тонн. В данном случае поднимаемый объект не влияет на характеристики движения судна (на оконечности крана);
- тяжелые подъемы, при которых вес поднимаемого объекта составляет более 1 % — 2 % от водоизмещения судна и, как правило, более 1000 т. Для таких подъемов следует принимать во внимание связанную динамику судна и поднимаемого объекта.
12.1.6 Во время легких подъемов часто используют компенсацию вертикальной качки. Для тяжелых подъемов применение компенсации вертикальной качки в целом невозможно. Моделирование систем компенсации вертикальной качки рассмотрено в разделе 8.
12.2 Легкие подъемы
12.2.1 Движение оконечности крана12.2.1.1 В случае легких подъемов стрела крана может быть рассмотрена как жесткая конструкция. В связи с этим движение оконечности крана может быть напрямую определено на основании вызванного волнами движения жесткого тела плавучего крана.
12.2.1.2 Вызванные волнами поступательные движения (продольно-горизонтальная, поперечногоризонтальная и вертикальная качки) оконечности крана xct, yct и zct заданы на основании RAO судна для движения в шести степенях свободы, обычно определяемых для центра тяжести судна.
Горизонтальное движение продольно-горизонтальной качки оконечности крана определено RAO продольно-горизонтальной качки, килевой качки и рыскания судна; горизонтальное движение поперечно-горизонтальной качки оконечности крана — RAO поперечно-горизонтальной качки, бортовой качки и рыскания судна; движение вертикальной качки оконечности крана — RAO вертикальной качки, бортовой качки и килевой качки судна. RAO движения должны быть объединены с положением оконечности крана в общей системе координат судна. В случае учета всех возможных периодов волны Tz характеристические значения для движений оконечности крана xct, yct, zct в состоянии моря с заданной Hs могут быть приняты как наибольший отклик передвижения.
12.2.1.3 Характеристическую отдельную амплитуду вертикального движения оконечности крана r|cf, м, при заданных состоянии моря и направлении волн вычисляют по формуле
Псе = аЙ + (bsintu)2 + (/sirn]5)2 , <364>
где г|3 — характеристическая отдельная амплитуда движения вертикальной качки судна, м;
b — горизонтальное расстояние от осевой линии судна до оконечности крана, м;
т|4 — характеристическая отдельная амплитуда угла бортовой качки судна, град;
/ — горизонтальное расстояние от миделя до оконечности крана, м;
г|5 — характеристическая отдельная амплитуда угла килевой качки судна, град.
Значения характеристических амплитуд вертикальной качки, бортовой качки и килевой качки приняты как абсолютные значения.
12.2.1.4 Характеристическая отдельная амплитуда вертикальной скорости оконечности крана vct, м/с, при заданных состоянии моря и направлении волн может быть представлена как
Г А2 Лк • \2 Л/ ■ л2
vc. = 2 J + ^5 . (365)
W I Т4 ) I. Т5 J
где т|3 — характеристическая отдельная амплитуда движения вертикальной качки судна, м;
Т3 — собственный период вертикальной качки, с;
b — горизонтальное расстояние от осевой линии судна до оконечности крана, м;
г|4 — характеристическая отдельная амплитуда угла бортовой качки судна, град;
Т4 — собственный период бортовой качки, с;
I — горизонтальное расстояние от миделя до оконечности крана, м;
г|5 — характеристическая отдельная амплитуда угла килевой качки судна, град;
Т5 — собственный период килевой качки, с.
12.2.1.5 Для данного движения оконечности крана движение поднимаемого объекта в воздухе может быть решено как задача принудительного маятника. Перед входом в воду на движение объекта может повлиять усилие от неустойчивого ветра. При использовании для управления горизонтальным движением поднимаемого объекта направляющих тросов в уравнениях движения для поднимаемого объекта они должны быть смоделированы как ограничители или горизонтальные пружины.
12.2.1.6 Период собственных колебаний для горизонтального движения TOh поднимаемого объекта в воздухе вычисляют по формуле
Tnh = 2л ЬУ'М + О.ЗЗ'пЦ (366)
У(д)(м + О,45т1_)’
где L — длина подъемного троса, м;
д — ускорение свободного падения, м/с2;
М — масса поднимаемого объекта, кг;
т — масса на единицу длины подъемного троса, кг/м.
В том случае, когда масса подъемного троса меньше массы поднимаемого объекта, влиянием массы подъемного троса можно пренебречь.
12.2.1.7 Период собственных колебаний для вращательного движения (рыскания) ТОг поднимаемого двумя параллельными тросами объекта [тандемная подъемная система (см. рисунок 53)] вычисляют по формуле
(367)
где гд — радиус вращения при рыскании для поднимаемого объекта, м;
а — расстояние между тросами, м;
L — длина подъемного троса, м;
д — ускорение свободного падения, м/с2.
Резонансное движение рыскания поднимаемого объекта может быть возбуждено как действием волнения, так и переменным ветром.
Рисунок 53 — Тандемная подъемная система
12.2.2 Гидродинамическое взаимодействие
12.2.2.1 На RAO плавучего крана могут влиять другие, находящиеся в непосредственной близости, стационарные или плавучие конструкции. Как правило, рассчитанные для плавучего крана в неограниченной воде RAO не могут применяться для подъемных работ без поправки на гидродинамическое взаимодействие между плавучим краном и другими близко расположенными конструкциями.
12.2.2.2 Для подъема с транспортного судна или на транспортное судно/баржу в непосредственной близости необходимо рассчитать RAO для обоих судов. Связанная гидродинамическая проблема должна быть решена как система с 12 степенями свободы. Примененная для вызванной волнами отклика крана и транспортных судов компьютерная программа должна иметь опцию для расчета многочастичных систем.
12.2.2.3 При подъемных работах в мелкой воде на движение плавучего крана, а следовательно, и на движение оконечности крана может оказывать значительное влияние гидродинамическое взаимодействие с морским дном.
12.2.2.4 Численное моделирование гидродинамического взаимодействия между плавающими телами приведено в 5.3.5.
12.3 Тяжелые подъемы
12.3.1 Общие положения12.3.1.1 Тяжелые подъемы обычно выполняют полупогружными плавучими крановыми судами (SSCV). Для противодействия возникающим во время подъема и установки груза моментам осадки и бортовой качки плавучие краны с большой грузоподъемностью, как правило, оснащены управляемой компьютером балластной системой.
12.3.1.2 Для операции отрыва крановое судно с установленными на носу кранами предварительно осаживают в положение кормой вверх. В предподъемной операции крюк поднимают вверх, перенося примерно 80 % тяжелого груза с баржи на SSCV. В данном состоянии с натянутыми стропами баржа и SSCV представляют собой почти жестко соединенную в вертикальном направлении систему. Путем регулировки балластной воды в танках дифферент судна меняется на противоположный, и груз поднимается на высоту 4—5 м в течение 90 с, что соответствует скорости подъема около 5 см/с.
12.3.2 Степени свободы
12.3.2.1 Перед отрывом от баржи для учета гидродинамического взаимодействия между полупо-гружным судном и баржей система из плавучего крана и баржи может быть смоделирована как система с 12 степенями свободы. После отрыва тяжелый поднимаемый объект будет влиять на движение полу-погружного судна таким образом, что общая система должна моделироваться как система с 18 степенями свободы.
12.3.2.2 В состоянии маятника, когда груз оторван от баржи, динамический режим системы является достаточно сложным, так как груз и плавучий кран выполняют связанные колебания. Горизонтальные относительные движения между грузом и плавучим краном могут быть критическими. Такие движения можно уменьшить с помощью натянутых тросов. Вертикальные движения также будут уменьшены из-за сниженного влияния взаимодействия.
12.3.2.3 Гидродинамическое взаимодействие между SSCV и баржей может быть существенным, поскольку колонны и характеристические длины волн в условиях работы являются сравнимыми с размерами судна.
12.3.3 Связанное динамическое движение
12.3.3.1 Плавучий кран с тяжелым грузом, подвешенным на вертикальном подъемном тросе с оконечности крана, в целом является системой с 12 степенями свободы. Как правило, вращения поднимаемого объекта контролируют с помощью проходящих от груза к судну направляющих тросов или буксировочных канатов. В полностью численных моделированиях связанной системы такие направляющие тросы моделируют как пружины. При упрощенном расчете вращениями поднимаемого объекта можно пренебречь, а число степеней свободы уменьшить с 12 до 9.
Модель плавучего крана с поднимаемым объектом представлена на рисунке 54.
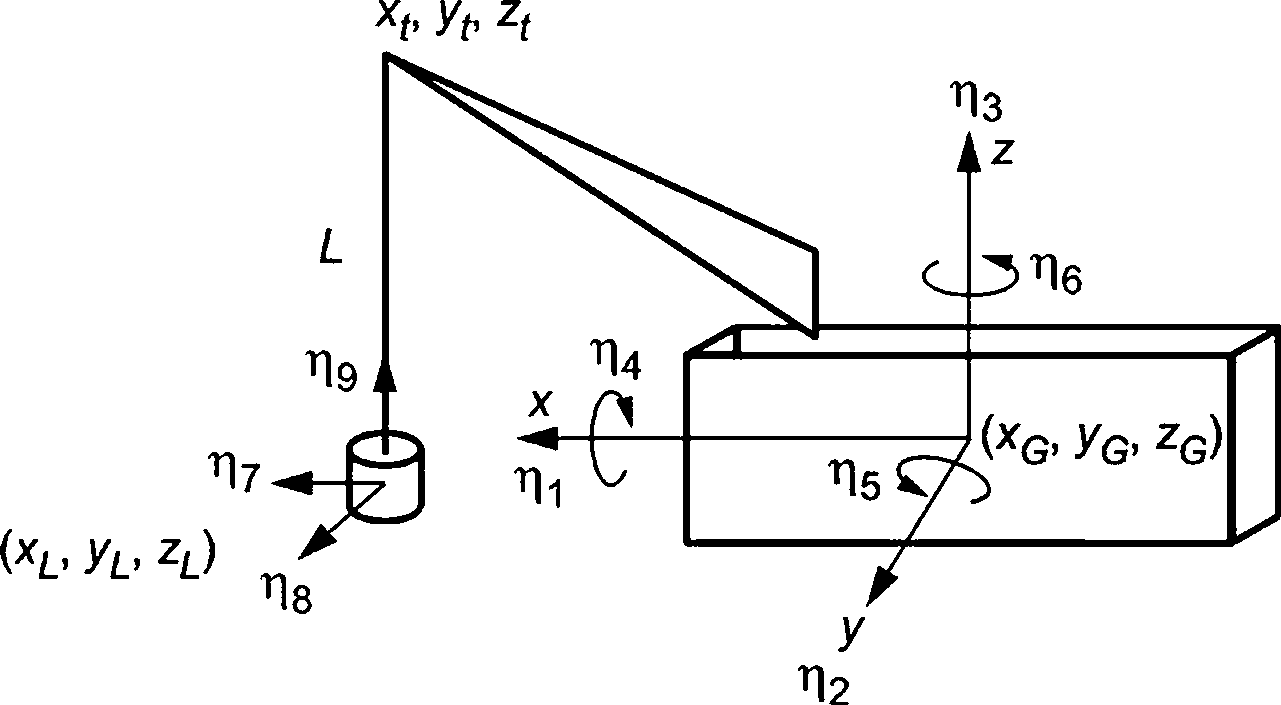
Рисунок 54 — Модель плавучего крана с поднимаемым объектом
12.3.3.2 Девять степеней свободы движения обозначены т|/, / = 1, 2, ..., 9, где / = 1, 2, ...6 являются движениями твердого тела плавучего крана с тремя поступательными и тремя вращательными движениями (см. рисунок 54). г|7 — движение поднимаемого объекта в направлении х; г|8 — движение поднимаемого объекта в направлении у; г|9 — движение в направлении z.
12.3.3.3 Поднимаемый объект может быть смоделирован как точечная масса с массой т и может быть погруженным. В этом случае включается присоединенная масса поднимаемого объекта. В целом поднимаемый объект будет иметь различную присоединенную массу а/7для движения продольно-горизонтальной качки (/= 1), поперечно-горизонтальной качки (/ = 2) и движения вертикальной качки (/' = 3).
12.3.3.4 Матрицу массы М, кг, размером 9*9 вычисляют по формуле где Mv — матрица размером 6><6 массы тела для плавучего крана, кг;
(Mv+A
Л4 = v 0
о
т0 +а
(368)
А — матрица размером 6x6 присоединенной массы для плавучего крана, кг;
т0 — матрица размером 3 х з массы для поднимаемого объекта, кг;
а — матрица размером 3 х з присоединенной массы для поднимаемого объекта, кг.
И матрица массы М, и матрица присоединенной массы А являются симметричными. Значения, связывающие инерцию судна и поднимаемый объект, отсутствуют. Пренебрегая недиагональными (/1 j) элементами присоединенной массы, матрицу массы для поднимаемого объекта можно представить как
т0 + а = (т + Э//)
(369)
где т0 — матрица размером 3x3 массы для поднимаемого объекта, кг;
а — матрица размером 3x3 присоединенной массы для поднимаемого объекта, кг.
12.3.3.5 Как правило, существует гидродинамическое взаимодействие между погруженным поднимаемым объектом и плавучим краном. Такое взаимодействие обеспечивает ненулевые значения связанной присоединенной массы (между Д и а), но, как правило, настолько мало, что может игнорироваться при связанном расчете.
12.3.3.6 Матрица жесткости С для связанной системы может быть разделена на три дополнительных фактора:
С - Ch + Ст + Сс,
(370)
где Ch — матрица гидростатической жесткости;
Ст — матрица жесткости швартовых;
Сс — матрица жесткости сочленения.
Жесткость швартовых является дополнительным фактором только при горизонтальных движениях плавучего крана. Обычно при сравнении с гидростатическими воздействиями вертикальные усилия якорных креплений можно игнорировать.
12.3.3.7 Матрица гидростатической жесткости Ch размером 9x9 может быть записана как
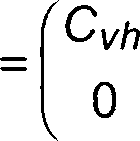
(371)
где Cvh — гидростатическая матрица размером 6x6 для плавучего крана задана следующим образом:
' 0 | 0 | 0 | 0 | 0 | 0 | ||
0 | 0 | 0 | 0 | 0 | 0 | ||
0 | 0 | ch,33 | ch,34 | C/?,35 | 0 | ||
Cvh ~ | 0 | 0 | O?,34 | C/,,44 | 0 | C/7,46 | |
0 | 0 | Qj,35 | 0 | G?,55 | Qj,56 | ||
< 0 | 0 | 0 | C/1,46 | C/7,56 | 0 |
(372)
Когда плавучий кран является симметричным относительно у = 0 и когда вертикальные усилия якорных креплений можно игнорировать, СЛ34, Ch45 и СЛ56 можно установить в ноль.
12.3.3.8 Матрица жесткости швартовых Ст размером 9x9 может быть записана как
(373)
где Cvm—матрица жесткости швартовых размеров 6x6 для плавучего крана. Матрица жесткости швартовых является симметричной, единственные ненулевые элементы:
(374)
cvm11’ cum12’ Cvm22> Cvto16> Ci/m26’ Ci/m66’
Эти элементы можно анализировать с помощью программы расчета швартовых. Если система швартовых симметричная, то ненулевыми элементами являются только диагональные элементы. Если плавучий кран не закреплен швартовыми, а использует динамическую стабилизацию (DP), система DP может быть приближенно выражена с помощью линейной пружинной системы демпфирования с матрицей возвращения, подобной указанной выше.
12.3.3.9 Симметричная матрица жесткости сочленения Сс размером 9х 9 задана с помощью:
** о о
0
ks2t
"Vf
ks
0
0 "
0
~kSZt
0
М
0
~ks
0
ке
кеУ1
0
0
0
~ke
Сс =
$с44
Сс55
-ksWt Ссбб
0 ~kszt кзУ1
ks
0
-ksxf 0 ks
keYt kext
0
0
0
ke >
(375)
где ks - w/Ls, Н/м;
ke-AE/Le, Н/м;
w — вес груза в погруженном состоянии, Н;
Ls — длина подъемного троса от оконечности крана до центра груза, м;
АЕ — жесткость троса на единицу длины, Н;
Le — эффективная длина подъемного троса, включая гибкость общей длины от груза до лебедки, а также гибкость крана, м;
Cc44 = kszt2 + keyt2’ н’м=
Cc55 = kszt2 + kext2’ Н'м;
GC66 = ks У2 + ке У2’ ^’м;
xt— положение оконечности крана х, м; yt— положение оконечности крана у, м; zt— положение оконечности крана z, м.
12.3.3.10 Недемпфированные собственные частоты coz, /= 1, 2, ..., 9 и собственные векторы сочлененной системы могут быть рассчитаны на основе
(-w2 М+ С)х = 0,
(376)
где С — матрица жесткости для связанной системы;
М — матрица массы размером 9 х 9.
В силу связи между режимами движения собственные векторы являются дополнительными факторами от различных степеней свободы.
12.3.3.11 Для вызванного синусоидальным внешним возбуждающим воздействием волны судна вектор нагрузки F может быть записан по сложной форме:
F = Re {Fa ei(ot}, (377)
где Fa — вектор усилия комплексного внешнего возбуждающего воздействия, определяемый по формуле
Fa = (F1.........F6,0,0,0)T, (378)
где со — частота колебания;
Re — действительная часть выражения.
12.3.3.12 Отклик передвижения сочлененной системы судно—груз определяют следующим образом:
П = (-со2 М + /мВ + C)“1F, (379)
где / = 1,2, 9;
ш — частота колебания;
М — матрица массы размером 9x9;
В — матрица линейного деформирования;
С — матрица жесткости для связанной системы;
F — вектор нагрузки.
12.3.4 Моделирование тяжелых подъемов во временной области
12.3.4.1 Операции тяжелого подъема могут быть рассчитаны путем моделирований во временной области на основании ранее сформированной зависимой от частоты функции передачи усилия внешнего возбуждающего воздействия, присоединенной массы и демпфирования волнообразования для плавучего крана, транспортной баржи и поднимаемого объекта (в погруженном положении). Демпфирование волнообразования представлено во временной области с помощью интеграла свертки, где предыдущие значения скоростей умножены на функции замедления.
12.3.4.2 Для заданного состояния моря ранее сформированные зависимые от частоты усилия волнообразования, действующие на плавучий кран, транспортную баржу и поднимаемый объект (в погруженном положении), преобразованы во временные диаграммы усилия, применяемые в связанных уравнениях движения для системы.
12.3.4.3 Когда элементы конструкции поднимаемого объекта малы по сравнению с характеристическими длинами волн, возбуждающее усилие и демпфирование для погруженного объекта могут быть приближенно выражены с помощью формулы нагрузки Морисона в значениях кинематики частиц волны (скорость и ускорение жидкости).
12.3.4.4 Для моделирований переходной характеристики, где во время операции происходят изменения осадки объекта, необходимо обратить внимание на обеспечение правильного моделирования гидростатических усилий, присоединенной массы и демпфирования волнообразования. Вместо этого для каждого этапа можно использовать несколько стационарных шагов с различными гидродинамическими моделями.
12.3.4.5 Изменяющаяся со временем сила сопротивления ветра, действующая на поднимаемый объект в воздухе, определена коэффициентом усилия ветра и мгновенной относительной скоростью между ветром и поднимаемым объектом. Как правило, при расчете относительной скорости скоростью поднимаемого объекта можно пренебречь.
12.4 Гидродинамическое взаимодействие
12.4.1 Если два судна расположены борт к борту, в просвете между двумя суднами может возникнуть гидродинамический резонанс. Необходимо учитывать три типа резонансных движений:
- поршневой режим движения;
- продольное колебание;
- поперечное колебание.
12.4.2 Соответствующие гидродинамическим резонансам в просвете собственные частоты а>п вычисляют по формуле
. 1 + JnOtanbV? (380)
соп = ул
горая рассчит
pf г2
П ^no + tan^n^
ывается по формуле
з
чо и24г2+и2
1
—
1 I 1 i W IJwwwt Jf/vU 9 wllilirJwM f
ПК
. _ . 1 + cos0o^
И + 2г n--------У- .
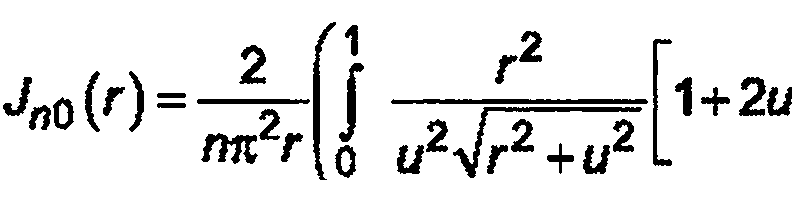
h — осадка судов (полагается равная осадка), м;
д — ускорение свободного падения, м/с2;
= пл//, м-1;
0о = tan -1 (1 /г), рад.
Функция Jn в сопоставлении с ляг показана на рисунке 55. Соответствующие периоды собственных колебаний Тп вычисляют по формуле
(382)
где соп — соответствующие гидродинамическим резонансам в просвете собственные частоты.
12.4.3 При поршневом режиме движения объем воды между судами качается вверх и вниз более или менее как твердое тело. Данную форму движения также называют качанием или формой Гельмгольца. Частоту собственных колебаний поршневого режима определяют путем задания п = 1 в 12.4.2.
12.4.4 Упрощенное выражение для частоты собственных колебаний поршневого режима задается с помощью выражения
„2 д С04 = ---------7---------------!
(383)
и ■ В
d + —\ 1,5 +In— я( 2Ь
где w1 — частота собственных колебаний поршневого режима;
В — общая ширина двух судов, включая просвет между судами.
12.4.5 В формах продольных колебаний вода между судами движется вперед и назад, в продольном направлении частоты собственных колебаний форм колебаний определяют путем задания п = 2, 3, 4... в 12.4.2 (см. рисунок 55).
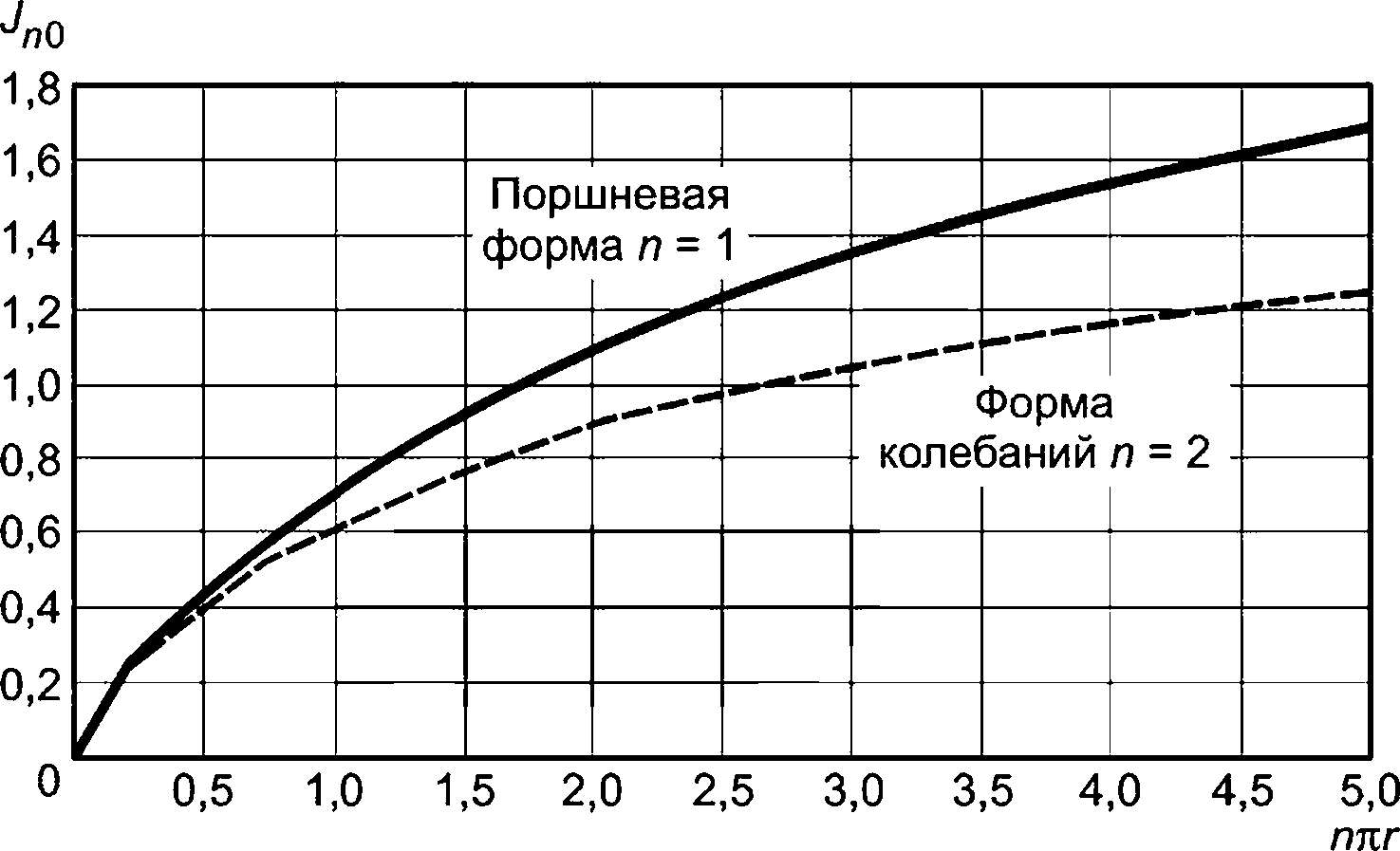
Рисунок 55 — Функция Jn0 в сопоставлении с ляг для поршневого режима (л = 1, сплошная линия) и наименьшей формы горизонтальных колебаний (л = 2, пунктирная линия)
Пример — Для просвета между двумя баржами размерами I = 80 м, b = 4 м и осадкой h = 10 м, г = Ь/1 = 0,05, л1 - 0,03927, х2 = 0,07854, J10 = 0,2067 и J20 = 0,3089 определяют в результате период собственных колебаний Т1 - 7,43 с для поршневого режима и Т2- 6,41 с для наименьшей формы горизонтальных колебаний.
12.4.6 В форме поперечного колебания движение воды между судами представляет собой стоячую волну между судами с длиной волны порядка ширины просвета. Когда суда расположены в непосредственной близости, с узким просветом, собственные частоты поперечного колебания воды в просвете являются высокими и ими можно пренебречь.
12.4.7 Гидродинамические резонансы в поршневом режиме и при формах продольного/попереч-ного колебания могут быть определены путем дифракционного расчета как пики в функции передачи для подъема поверхности в произвольных точках просвета между судами.
12.5 Отрыв объекта
12.5.1 Общие положения12.5.1.1 Так как спуско-подъемные операции выполняют в относительно безветренную погоду, движения баржи и плавучего крана могут быть рассчитаны на основе теории линейной волны и движения можно будет считать нормально распределенными (см. также [1]).
12.5.1.2 В случае осуществления транспортирования на плавучем кране операция отрыва является простой, так как относительное движение между верхней частью крана и судном незначительное.
12.5.1.3 При подъеме объекта с баржи с помощью крана на борту расположенного борт о борт с баржей кранового судна критическим параметром является относительное движение между крюком крана и баржей в месте поднимаемого объекта. Статистика относительного движения определяет вероятность удара баржи о поднимаемый объект после отрыва.
12.5.1.4 Определяющими выполнимость операции отрыва параметрами являются следующие:
- скорость подъема крана (зависит от веса подлежащего подъему объекта, нижний предел, как правило, принимает значение порядка 0,1 м/с);
- суммарные характеристики движения баржи и плавучего крана;
- погодные условия в совокупности с ориентацией двух судов.
12.5.1.5 После отрыва объекта от транспортного судна (баржи) объект будет на кране подчиняться движению верхней части крана. Поскольку в данном случае трос короткий, динамический отклик системы «объект—трос» будет незначительным, а усилие в тросе можно оценить на основе вертикального ускорения только верхней части крана.
12.5.2 Вероятность удара баржи о поднимаемый объект
12.5.2.1 Критерием квалификации безопасности подъемной операции является то, что после отрыва объект снова не ударит по барже. Безопасность операции можно определить путем оценки вероятности удара баржи по поднимаемому объекту и обеспечения того, что вероятность составляет менее предписанного значения.
12.5.2.2 Для статистического расчета сделаны следующие упрощающие допущения:
- отклики передвижения двух судов — узкополосные;
- во время подъема скорость подъема U является постоянной;
- поднимаемый объект покидает баржу при максимальном относительном вертикальном движении а между баржей и крюком крана;
- вероятность того, что баржа ударит поднимаемый объект более одного раза, практически равна нулю. Вследствие этого рассматривают только первый возможный удар.
12.5.2.3 Вероятность Р(т) того, что баржа ударит поднимаемый объект при следующем максимальном значении относительного движения, может быть приближенно выражена следующим образом:
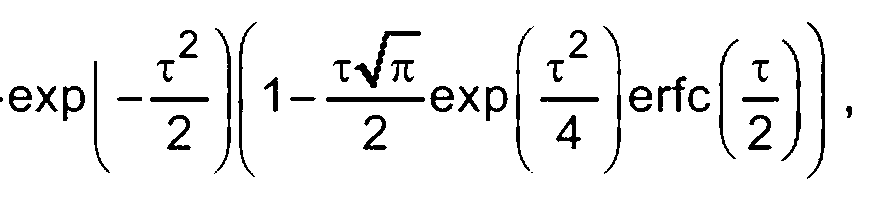
где Р(т) — вероятность того, что баржа ударит поднимаемый объект при следующем максимальном
значении относительного движения
(385)
где U — скорость подъема, м/с;
Tz — период колебания через нулевую точку для относительного движения, с; а — стандартное отклонение относительного движения, м;
erfc — функция ошибок;
т — средняя продолжительность подъема, с.
Вероятность Р представлена на рисунке 56.
12.5.2.4 Вероятность удара поднимаемого объекта о баржу является функцией от безразмерного числа т, вычисляемой по формуле
(386)
где U — скорость подъема, м/с;
Tz — период колебания через нулевую точку для относительного движения, с;
о — стандартное отклонение относительного движения, м.
Требование к вероятности быть менее заданного числа £ косвенно дает значение для максимального стандартного отклонения относительного движения о, которое пропорционально высоте характерной волны Hs.
В течение серии из 10 подъемных операций может потребоваться, чтобы общая приемлемая вероятность составила 0,01. Вследствие этого требуемая вероятность Р для каждого подъема должна быть менее 0,001. Исходя из рисунка 56 для этого требуется UTz/v > 2,9.
При допущении скорости подъема U = 0,3 м/с, Tz = 7,0 с требование к стандартному отклонению относительного движения составит о < 0,72 м, что относится к высоте характерной волны состояния моря через функцию передачи относительного движения. Если относительное движение как частный случай равно движению волны, то в этом случае предельную высоту Hs операции определяют как m„Y = 4g = 2,9 м. о 111с1Л
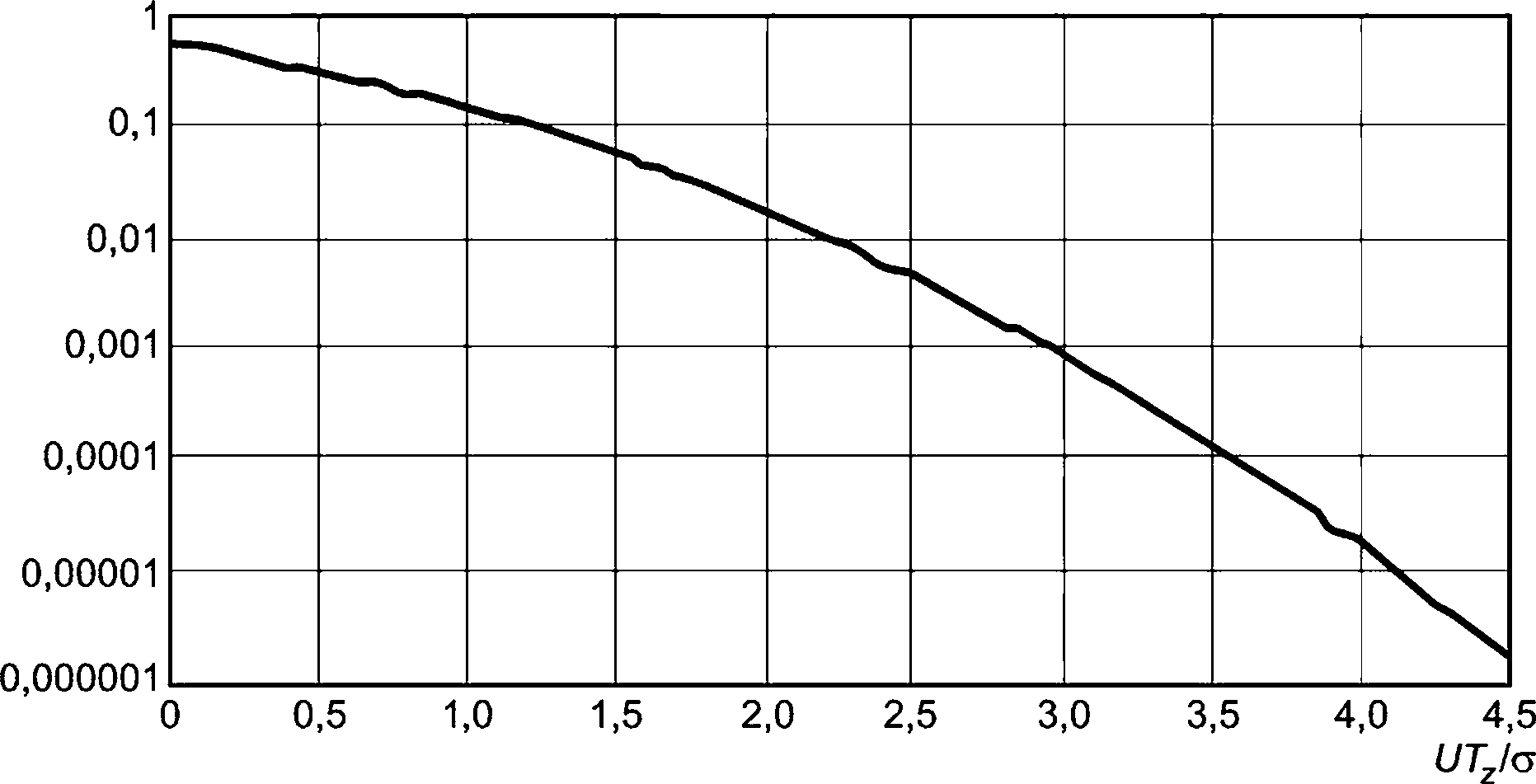
Рисунок 56 — Вероятность удара баржи о поднимаемый объект
Приложение А (справочное)
Коэффициенты присоединенной массы
Аналитические коэффициенты присоединенной массы для двухмерных тел представлены в таблице А.1 (см. [1]).
Таблица А.1 — Аналитический коэффициент присоединенной массы для двухмерных тел, т. е. протяженных цилиндров в безграничной текучей среде (вдали от границ)
Поперечное сечение тела | Направление движения | Сд | ar | Момент инерции присоединенной массы (кг/м)*м2 | |||||
«2а. | Горизонтальное или вертикальное | 1,0 | л ■ а2 | 0 | |||||
«2а. | о | Вертикальное | 1,0 | л ■ а2 | 00 | а го 1 0) го to | ||||
Горизонтальное | 1,0 | л • Ь2 | |||||||
Вертикальное | 1,0 | л • а2 | Со| Я | ||||||
2а | |||||||||
Цилиндр круглого сечения с двумя ребрами | <2а» | -Q | Вертикальное | 1,0 | л • а2 | pa4 (esc4 af(a) - л2)/2л, где f(a) = 2a2 — asin 4a + 0,5 sin2 a и sina = 2abl(a2 + b2) л/2 < a < л | |||
Горизонтальное | I Ст | 0) 4 м + О-1 £0 | л • Ь2 | |||||||
-а> | сч | Горизонтальное или вертикальное | 1,0 | л • а2 | 2 -pa л | ||||
Окончание таблицы А. 1
Поперечное сечение тела | Направление движения | сА | ar | Момент инерции присоединенной массы, (кг/м)*м2 | ||||||||
а/b = °° а/Ь =10 а/b = 5 а/Ь = 2 а/b = 1 а/Ь = 0,5 а/b = 0,2 а/b = 0,1 | Вертикальное | 1,0 1,14 1,21 1.36 1,51 1,70 1,98 2,23 | л ■ а2 | Р1 рла4 или р2 рлЬ4 | ||||||||
а/Ь | ₽1 | ₽2 | ||||||||||
■с о | 0,1 0,2 0,5 1,0 2,0 5,0 СО | 0,234 0,15 0,15 0,125 | 0,147 0,15 0,15 0,234 | |||||||||
- 2а . | ||||||||||||
d/a = 0,05 с//а = 0,10 d/a = 0,25 | Вертикальное | 1,61 1,72 2,19 | л ■ а2 | Р рла4 | ||||||||
d/a | ₽ | |||||||||||
0,05 0,10 0,10 | 0,31 0,40 0,69 | |||||||||||
св CN | ||||||||||||
',2а. | ||||||||||||
tf | а л2аг | ■Q О1 | а/Ь = 2 а/Ь = 1 а/Ь = 0,5 а/Ь = 0,2 | Вертикальное | 0,85 0,76 0,67 0,61 | л ■ а2 | 0,059 рла4 для а = Ь | |||||
Жидкая среда | Горизонтальное | --1 3 | л ■ а2 | — | ||||||||
У | Мелководье 2Ь | о | Ь 2. Л 2 СЕ 71 71 2b Ь --+ £—+ С с 2 2 +—£ Зя d . — - 1-Е с | 2рс? | — | Мелководье | ||||||
— | V | 2Ь | ||||||||||
о | ||||||||||||
Примечание — Присоединенная масса (на единицу длины) составляет = pCAAR, кг/м, где AR — базовая площадь, м2.
Аналитические коэффициенты присоединенной массы для трехмерных тел представлены в таблице А.2.
Таблица А.2 — Аналитический коэффициент присоединенной массы для трехмерных тел в безграничной текучей среде (вдали от границ)
Форма тела | Направление движения | С | Vr | |||||||
Плоские пластины | Круглый диск | Вертикальное | 2/я | со ГО t=i ’Т | со | ||||||
Эллиптический диск 2а | Вертикальное | Ь/а | СА | Ь/а | СА | 71 2. — аЬ 6 | ||||
ОО 14,3 12,8 10,0 7,0 6,0 | 1,000 0,991 0,989 0,984 0,972 0,964 | 5,0 4,0 3,0 2,0 1,5 1,0 | 0,952 0,933 0,900 0,826 0,758 0,637 | |||||||
Прямоугольные пластины ь/ | Вертикальное | Ь/а | СА | Ь/а | сА | л 2r 4Э6 | ||||
1,00 1,25 1,50 1,59 2,00 2,50 3,00 | 0,579 0,642 0,690 0,704 0,757 0,801 0,830 | 3,17 4,00 5,00 6,25 8,00 10,00 ОО | 0,840 0,872 0,897 0,917 0,934 0,947 1,000 | |||||||
Тр( | эугольные пла< | зтины | Вертикальное | 1 л\3/2 —(tan0) 7Г | 3 | |||||
а | ||||||||||
Тела вращения | Сферы | Любое направление | 1/2 | 4 з —л-а 3 | ||||||
IO | ||||||||||
Сфероиды | Поперечное или осевое | а/Ь | Осевое | Поперечное | 4 2 —л-Ь а 3 | |||||
1,0 1,5 2,0 2,5 4,0 5,0 6,0 7,0 8,0 | 0,500 0,304 0,210 0,156 0,082 0,059 0,045 0,036 0,029 | 0,500 0,622 0,704 0,762 0,860 0,894 0,917 0,933 0,945 | ||||||||
СЮ | ||||||||||
2а | ||||||||||
Окончание таблицы А. 2
Форма тела | Направление движения | ||||||||||
Эллипсоид | -Q см | ж 2а Ось а > b > с | Осевое | X V- |СМ + 3 см "О о со см ^0 53 1 со | см Y -Q ^2 ° ' Ф 1 1, II О СМ с£ '—' 3 и II 3 + w " " + + ф с<5 Ч т- ™ С[ О у' Т° X W II г? | abc 3 | ||||||
Квадратные призмы | 1э/ | - | •Q | ^а. | Вертикальное | Ь/а 1,0 2,0 3,0 4,0 5,0 6,0 7,0 10,0 | Сд 0,68 0,36 0,24 0,19 0,15 0,13 0,11 0,08 | а2 • b | |||
b « а | 0,45 | а3 | |||||||||
Прямой круговой цилиндр | \ / — | Вертикальное | Ы2а | Сд | я ■ а2 b | ||||||
1,2 2,5 5,0 9,0 ОО | 0,62 0,78 0,90 0,96 1,00 | ||||||||||
Приложение Б (справочное)
Коэффициенты лобового сопротивления
Коэффициенты лобового сопротивления на некруглых поперечных сечениях представлены в таблице Б.1.
Таблица Б.1 — Коэффициент лобового сопротивления на некруглых поперечных сечениях для устойчивого потока CDS
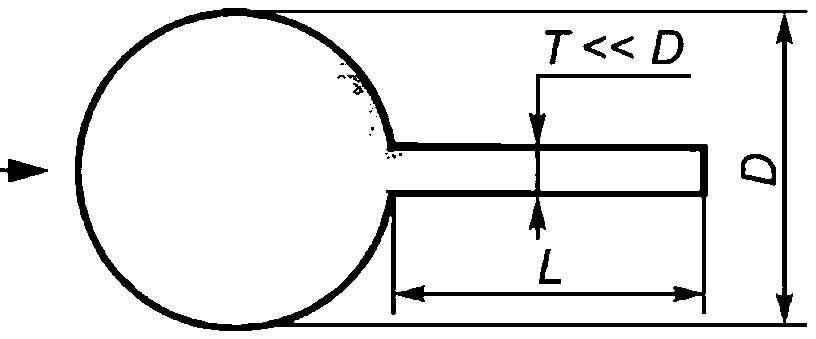
Re ~ 105
3 Прямоугольник с тонкой разделительной перегородкой
/-/ < 0/10
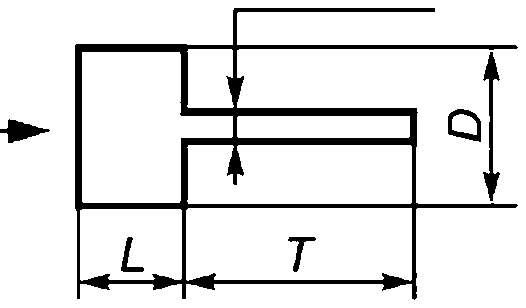
L/D | T/D | ||
0 | 5 | 10 | |
0,1 | 1,9 | 1,4 | 1,38 |
0,2 | 2,1 | 1,4 | 1,43 |
0,4 | 2,35 | 1,39 | 1,46 |
0,6 | 1,8 | 1,38 | 1,48 |
0,8 | 2,3 | 1,36 | 1,47 |
1,0 | 2,0 | 1,33 | 1,45 |
1,5 | 1,8 | 1,30 | 1,40 |
2,0 | 1,6 | — | 1,33 |
Коэффициент лобового сопротивления CDS
Геометрия
1 Трос и цепи | Тип (Re = 104- 107) | CDS | |||||||
Трос, шесть жил Трос спиральный без оболочки Трос спиральный с оболочкой Цепь с распоркой (относительно диаметра цепи) Цепь без распорки (относительно диаметра цепи) | 1,5—1,8 1,4—1,6 1,0—1,2 2,2—2,6 2,0—2,4 | ||||||||
—8 В Q | |||||||||
2 Цилиндр круглого сечения с тонким ребром | LID | 0 | 0,33 | 0,67 | 1,0 | 1,5 | 2,0 | 2,5 | |
CDS | 1,25 | 1,2 | 1,15 | 1,1 | 1,07 | 1,02 | 1,0 | ||
Продолжение таблицы Б. 1
Геометрия | Коэффициент лобового сопротивления CDS |
Re ~ 5 х 104 | |
CDS = (1 - D/H)~n CD | H = °° для 0 < D/H < 0,25 | |
—1 Q 1 | LID 0,1 0,25 0,50 1,0 2,0 |
n 2,3 2,2 2,1 1,2 0,4 | |
7////7//7////////Л | |
Re > 103 | |
LID RID CDS LID RID CDS | |
0 2,5 0 1,6 | |
0,021 2,2 0,042 1,4 | |
5 Прямоугольник со скругленными углами | 0,5 2,0 |
0,083 1,9 0,167 0,7 | |
0,250 1,6 0,50 0,4 | |
—Q | |
в,ш " | 0 2,2 |
[_ | 0,021 2,0 0 0,89 |
1,0 6,0 | |
0,167 1,2 0,5 0,29 | |
0,333 1,0 | |
Re ~ 105 | |
0 0 5 10 15 20 25 30 35 40 45 | |
CDS 2,2 2,1 1,8 1,3 1,9 2,1 2,2 2,3 2,4 2,4 | |
7 <д/" | Re ~ 4,7 ■ 104 |
Lo/Do ^/Do ^ds | |
0.021 1,8 Передний | |
0,5 0,083 1,7 и задний углы | |
7 Ромб со скругленными углами | |
0 167 17 не скруглены | |
0,015 1,5 | |
—Q° | 1,0 0,118 1,5 — |
0,235 1,5 | |
Lq | 0,040 1,1 |
20 0 167 Поперечные углы | |
’ ’ ’ не скруглены | |
0,335 1,1 | |
Re ~ 105 |
Продолжение таблицы Б. 1
Геометрия
Коэффициент лобового сопротивления CDS
8 Закругленная передняя часть
L/D
CDS
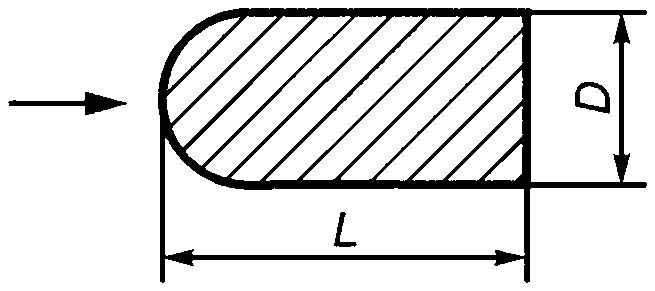
0,5
1,0
2,0
4,0
6,0
1,16
0,90
0,70
0,68
0,64
9 Перпендикулярная к потоку тонкая плоская пластина
CDS = 1,9; Re > 104
10 Наклонная к потоку тонкая плоская пластина
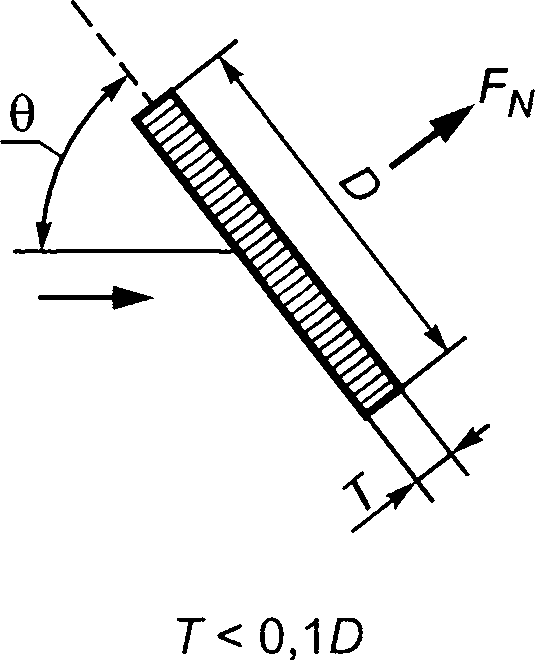
Cw = <
2лЛап0, е<8° 1 ,90°se>12
0,222+0,283/sine
С £ — Сду cos 0, С ds = s'n ®
11 Тонкий подъемный аэродинамический профиль
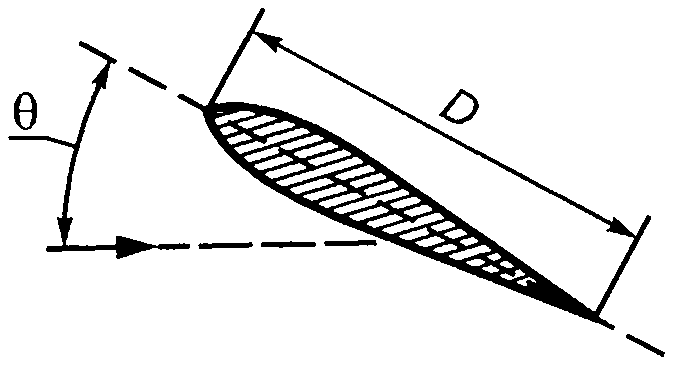
С ds ~ 0,01;
CL = 2л sin 9;
См = (л/4) sin 20 (момент относительно передней кромки);
См = 0 относительно точки D/4 позади передней кромки
12 Две тонкие пластины в одном ряду
D | UJ | |
жж D | ||
E/D | CDS | |
0,5 | 1,42 или 2,20 | Несколько значений |
1,0 | 1,52 или 2,13 | в силу изменения |
2,0 | 1,9 или 2,10 | струи. |
3,0 | 2,0 | Лобовое |
5,0 | 1,96 | сопротивление на каждой пластине |
10,0 | 1,9 | |
15,0 | 1,9 |
Re ~ 4•103
Окончание таблицы Б. 1
Коэффициент лобового сопротивления CDS
Геометрия
E/D | CDS1 | CDS2 | ||||
13 Две расположенные последовательно | 2 | 1,80 | 0,10 | |||
тонкие пластины | 3 | 1,70 | 0,67 | |||
4 | 1,65 | 0,76 | ||||
Q | 6 | 1,65 | 0,95 | |||
10 | 1,9 | 1,00 | ||||
L__Е__. | 20 | 1,9 | 1,15 | |||
30 | 1,9 | 1,33 | ||||
1 | 2 | ОО | 1,9 | 1,90 | ||
Re ~ 4•103
14 Тонкая пластина, частично выступающая поперек канала
1,4
\2,85 ’
УУ/////////////У/.
для 0 < D/H < 0,25; Re > 103
D/L
Cos(Re~105)
15 Эллипс
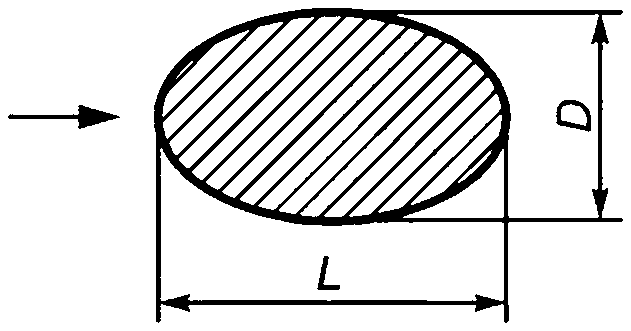
0,125 0,25 0,50 1,00 2,0
0,22 0,3 0,6 1,0 1,6
16 Равнобедренный треугольник
CDS (Re -104)
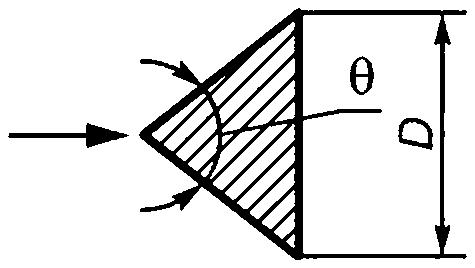
30
60
90
120
1,1
1,4
1,6
1,75
17 Равнобедренный треугольник
CDS (Re ~104)
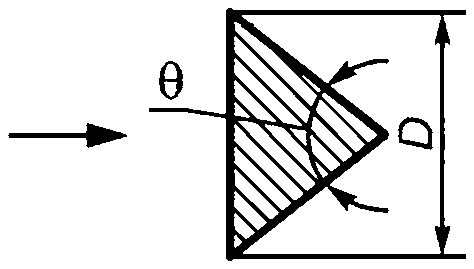
30
60
90
120
1,9
2,1
2,15
2,05
Таблица Б.2 — Коэффициент лобового сопротивления на трехмерных объектах для устойчивого потока CDS
Геометрия | Размеры | CDS | ||||||||
Поперечная направлению прямоугольная пласти | ПО1 1на т- | гока | В/Н 1 5 10 | 1,16 1,20 1,50 1 QD | ||||||
и | ||||||||||
к— | Re > 103 | |||||||||
Цилиндр круглого сечения. Ось параллельна потоку Il J Y L | D | L/D 0 1 2 4 7 | 1,12 0,91 0,85 0,87 0,99 Re > 103 | |||||||
Параллельный потоку квадратнь стержень | 1Й Q | L/D 1,0 1,5 2,0 2,5 3,0 4,0 5,0 | 1,15 0,97 0,87 0,90 0,93 0,95 0,95 Re = 1,7- 105 | |||||||
и | ||||||||||
L | ||||||||||
Поперечный потоку цилиндр круглого сечения | L/D | Докритический поток Re < 105 | Сверхкритический поток Re < 105 | |||||||
и ---► | D | — | 2 5 10 20 40 50 100 | К 0,58 0,62 0,68 0,74 0,82 0,87 0,98 | К 0,80 0,80 0,82 0,90 0,98 0,99 1,00 | |||||
CDS - kCpS, где к— коэффициент ослабления в силу конечной длины; — двухмерный коэффициент устойчивого лобового сопротивления | ||||||||||
Примечания
1 Лобовое сопротивление определено как FD = % pCDS Su.
2 S— поперечная к направлению потока площадь проекции, м1.
3 Re — VD/v— число Рейнольдса, где D — характеристический размер.
Коэффициенты сопротивления—подъема на двухмерных профилях представлены в таблице Б.З.
Таблица Б.З — Усилие сопротивления—подъема на двухмерных профилях для устойчивого потока
Профиль | а, град | Cd2 | Профиль | а, град | Cd | Cd2 | ||||||||||
4? | Pd2 | 0 45 90 135 180 | 1,9 1,8 2,0 -1,8 -2,0 | 1,0 0,8 1,7 -0,1 0,1 | 0 45 90 135 180 | 2,1 1,9 0,0 -1,6 -1,8 | 0,0 0,6 0,6 0,4 0 | |||||||||
-Q | 4—,-Q аД/ | PdA 0,5b | ||||||||||||||
0,5b | ||||||||||||||||
X /У У /Рхч rf2 Х4^>Р | 0 45 90 135 180 | 1,8 2,1 -1,9 -2,0 -1,4 | 1,8 1,8 -1,0 0,3 -1,4 | <4 | 12 pdl 0,5b | 0 45 90 | 2,1 2,0 0,0 | 0,0 0,6 0,9 | ||||||||
, i—। | _i | |||||||||||||||
u | ||||||||||||||||
Л | Pd2 | 0 45 90 135 180 | 1,7 0,8 0,0 -0,8 -1,7 | 0,0 0,8 1,7 0,8 0,0 | —12! | 0 45 90 | 1,6 1,5 0,0 | 0,0 1,5 1,9 | ||||||||
4г | ||||||||||||||||
0,2b | pdl | |||||||||||||||
b | b | |||||||||||||||
4г, | 1 ftPd2 | 0 45 90 135 180 | 2,0 1,2 -1,6 -1,1 -1,7 | 0 0,9 2,2 -2,4 0,0 | — | 0Pd2 Pd1 | 0 180 | 1,8 -1,3 | 0 0 | |||||||
J, 1b | 0,87b | |||||||||||||||
Примечание— Компоненты усилия определяют как Pd^ = Уг pCd^bU и Pd2 = pCd2bU (следует отметить, что один и тот же характеристический размер b использован для обоих компонентов), где U— скорость набегания под углом а. Если, как показано, подъемное усилие является положительным, общие коэффициенты лобового сопротивления и подъема на профиле определяют следующим образом: CD = Cd1 cos а + sin а; CD = -Cd1 cos а + Cd2 cos a. | ||||||||||||||||
Приложение В (справочное)
Постоянные физические величины
Плотность и вязкость пресной воды, морской воды и сухого воздуха представлены в таблице В.1 (см. также [1]).
Таблица В.1 — Плотность и вязкость пресной воды, морской воды и сухого воздуха
Температура, °C | Плотность р, кг/м3 | Кинематическая вязкость v, м2/с | ||||
Пресная вода | Соленая вода | Сухой воздух | Пресная вода | Соленая вода | Сухой воздух | |
0 | 999,8 | 1028,0 | 1,293 | 1,79 • 10-6 | 1,83 • 10"6 | 1,32 • IO"5 |
5 | 1000,0 | 1027,6 | 1,270 | 1,52 | 1,56 | 1,36 |
10 | 999,7 | 1026,9 | 1,247 | 1,31 | 1,35 | 1,41 |
15 | 999,1 | 1025,9 | 1,226 | 1,14 | 1,19 | 1,45 |
20 | 998,2 | 1024,7 | 1,205 | 1,00 | 1,05 | 1,50 |
25 | 997,0 | 1023,2 | 1,184 | 0,89 | 0,94 | 1,55 |
30 | 995,6 | 1021,7 | 1,165 | 0,80 | 0,85 | 1,60 |
Библиография
[1] DNVGL-RP-N103—2017 Моделирование и анализ морских операций. Рекомендуемая практика
[2] DNVGL-RP-C205—2019 Условия окружающей среды и экологические загрузки. Рекомендуемая практика
УДК 622.276.04:006.354
ОКС 75.020
Ключевые слова: нефтяная и газовая промышленность, системы подводной добычи, моделирование, расчет, морские операции, методические указания
Редактор Л. С. Зимилова Технический редактор В.Н. Прусакова Корректор Е.Д. Дульнева Компьютерная верстка Е.А. Кондрашовой
Сдано в набор 20.03.2023. Подписано в печать 29.03.2023. Формат 60х841/8. Гарнитура Ариал. Усл. печ. л. 18,60. Уч.-изд. л. 16,84.
Подготовлено на основе электронной версии, предоставленной разработчиком стандарта
Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.
1
2D — характеристическая ширина, м.
