ГОСТ Р ИСО 7870-9-2023
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
КОНТРОЛЬНЫЕ КАРТЫ
Часть 9
Контрольные карты для стационарных процессов
Statistical methods. Control charts. Part 9. Control charts for stationary processes
ОКС 03.120.30
Дата введения 2024-03-01
Предисловие
1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 сентября 2023 г. N 967-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 7870-9:2020* "Контрольные карты. Часть 9. Контрольные карты для стационарных процессов" (ISO 7870-9:2020 "Control charts - Part 9: Control charts for stationary processes", IDT).
Международный стандарт разработан Техническим комитетом ТК 69 Международной организации по стандартизации (ИСО).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
Введение
Методы статистического управления процессами (SPC) широко используют в промышленности для мониторинга процессов и повышения качества продукции. Для мониторинга среднего и изменчивости процесса разработаны различные статистические контрольные карты. Традиционная методология SPC основана на фундаментальном предположении, что данные процесса статистически независимы. Однако это предположение не всегда выполняется. В отраслях непрерывного производства, таких как химическое производство, большая часть данных о характеристиках качества коррелированы во времени или автокоррелированы. В общем случае автокорреляция может быть вызвана особенностями системы измерений, динамики процесса или и тем, и другим. Во многих случаях данные могут демонстрировать дрейф процесса. В биологии случайные биологические изменения, например случайный всплеск секреции какого-либо вещества, влияющего на кровяное давление, могут иметь устойчивый эффект, то есть на несколько последовательных измерений влияет одно и то же случайное явление. При сборе данных, когда интервал отбора выборки невелик, автокорреляция, особенно положительная автокорреляция данных, требует изучения. В таких условиях традиционные процедуры SPC не подходят для мониторинга, контроля и улучшения качества процесса.
Автокоррелированные процессы можно разделить на два вида: стационарные и нестационарные.
1) Стационарный процесс - прямое продолжение независимой и одинаково распределенной последовательности. Автокоррелированный процесс является стационарным, если он находится в состоянии "статистическое равновесие". Это означает, что изменчивость процесса не меняется со временем. В частности, стационарный процесс всегда имеет идентичные средние и дисперсии.
2) Нестационарный процесс.
Подробная информация о случайном процессе и временных рядах приведена в приложении А.
Для учета автокоррелированных данных разработаны некоторые методологии SPC. В основном, существует два подхода. Первый подход заключается в использовании карт остатков процесса после подбора модели временных рядов или другой математической модели, соответствующей данным. Другой, более прямой подход состоит в изменении существующих карт, например путем корректировки контрольных границ на основе данных об автокорреляции процесса.
Целью настоящего стандарта является описание основных контрольных карт управления процессом для мониторинга среднего и дисперсии автокоррелированного процесса.
1 Область применения
Настоящий стандарт описывает построение и применение контрольных карт для стационарных процессов.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт [для датированной ссылки применяют только указанное издание ссылочного стандарта, для недатированной - последнее издание (включая все изменения)]:
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
3 Термины, определения, обозначения и сокращения
3.1 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-2, а также следующие термины с соответствующими определениями.
ИСО и МЭК ведут терминологические базы данных для использования в области стандартизации по следующим адресам:
- платформа онлайн-просмотра ИСО: доступна по адресу http://www.iso.org/obp;
- Электропедия МЭК: доступна по адресу http://www.electropedia.org/.
3.1.1 автоковариация (autocovariance): Внутренняя ковариация между элементами серии наблюдений, упорядоченных по времени.
3.1.2 контрольная карта для автокоррелированного процесса (control charts for autocorrelated processes): Контрольная карта статистического управления процессами, применяемая к автокоррелированному процессу.
3.2 Обозначения и сокращения
3.2.1 Сокращения
В настоящем стандарте использованы следующие сокращения:
ARL - средняя длина серии;
i.i.d. - независимый и одинаково распределенный;
SPC - статистическое управление процессом;
ACF - функция автокорреляции;
AR(1) - процесс авторегрессии первого порядка;
EWMA - экспоненциально взвешенное скользящее среднее;
EWMAST - экспоненциально взвешенное скользящее среднее для стационарных процессов;
EWMS - экспоненциально взвешенное среднеквадратическое отклонение;
CUSUM - кумулятивная сумма.
3.2.2 Обозначения
В настоящем стандарте использованы следующие обозначения:
T | - набор индексов для случайного процесса; |
- истинное среднее процесса; | |
- истинное стандартное отклонение процесса; | |
- нормальное распределение со средним и дисперсией ; | |
- автоковариация; | |
- оценка автоковариации; | |
- автокорреляция; | |
- оценка автокорреляции; | |
- зависимый параметр процесса авторегрессии первого порядка; | |
- параметр сглаживания для EWMA; | |
r | - параметр сглаживания для EWMS; |
- интервал времени между двумя точками (лаг); | |
- EWMS в момент времени t; | |
- начальное значение ; | |
- случайная переменная X в момент времени t; | |
- случайная переменная a в момент времени t для процесса авторегрессии первого порядка; | |
- изменение среднего шага, кратное среднеквадратичному отклонению процесса; | |
- среднее арифметическое последовательности x; | |
s | - стандартное отклонение последовательности x; |
- оценка прогнозирования ; | |
- остаток в момент времени t; | |
- среднее арифметическое ; | |
- стандартное отклонение ; | |
- статистика EWMA в момент времени t; | |
- начальное значение ; | |
- значение контрольной границы для (выраженное в количестве стандартных отклонений ); | |
- стандартное отклонение статистики EWMA; | |
- стандартное отклонение случайных величин белого шума в процессе авторегрессии первого порядка. |
4 Контрольные карты автокоррелированных процессов для мониторинга среднего процесса
4.1 Общие положения
Многие специалисты в области статистики и статистического управления процессами обнаружили, что автокорреляция данных процесса оказывает влияние на работу традиционных карт SPC. Подобно автоковариации (см. 3.1.1), автокорреляция - это внутренняя корреляция между элементами серии наблюдений, упорядоченными по времени. Автокорреляция может быть вызвана особенностями системы измерений, динамики процесса или и тем, и другим. В приложении B показано влияние положительной автокорреляции на работу различных традиционных контрольных карт.
4.2 Карты остатков
Карты остатков используют для отслеживания возможных изменений среднего процесса. Для построения карты остатков по данным процесса необходимо применить временные ряды или другие методы математического моделирования.
Предполагают, что модель верна и остатки статистически не коррелируют друг с другом. Теперь к остаткам можно применить традиционные карты SPC, такие как X-карты, CUSUM-карты и EWMA-карты. В случае применения X-карты к остаткам ее, как правило, называют X-картой остатков. Как только обнаружено изменение среднего в процессе остатков, делают вывод о том, что среднее исходного процесса вышло из-под контроля.
Аналогичным образом используют карту остатков CUSUM и карту остатков EWMA [2], [3]. Для сравнения карт остатков с другими контрольными картами см. [4].
Преимущество карт остатков:
- карта остатков может быть применена к любым автокоррелированным данным, даже если они нестационарны. Обычно модель формируют с помощью временных рядов или программного обеспечения для подбора других моделей.
Недостатки карт остатков:
- карты остатков не обладают теми же свойствами, что и традиционные карты. X-карта остатков для процесса авторегрессии первого порядка (см. A.3.3) может иметь низкую способность обнаруживать смещение среднего. В [5] показано, что при положительной автокорреляции процесса X-карта остатков работает плохо. В [6] показано, что способность обнаружения у X-карты остатков иногда невелика по сравнению с обычной X-картой;
- карты остатков требуют применения временных рядов или других моделей. Пользователь карты остатков должен периодически контролировать достоверность модели, чтобы уменьшить общее влияние ошибки моделирования и изменения процесса.
 |
X - номер наблюдения; Y - вязкость
Рисунок 1 - Пример
 |
X - лаг; Y - автокорреляция
Рисунок 2 - Выборочные автокорреляции для серии ежедневных измерений вязкости и приближенный доверительный интервал с уровнем доверия 95%
 |
X - время; Y - остаток
 |
X - лаг; Y - автокорреляция
Рисунок 4 - Выборочная автокорреляция остатков серии измерений вязкости и приближенный доверительный интервал с уровнем доверия 95%
4.3 Традиционные контрольные карты со скорректированными контрольными границами
4.3.1 Модифицированная EWMA-карта
По сравнению с картами остатков более прямой подход заключается в изменении существующих карт путем корректировки контрольных границ без моделирования временных рядов. Однако применение некоторых методов, основанных на этом подходе, ограничено из-за особенностей конкретных процессов, например процессами авторегрессии первого порядка [9]. В [10] предложено для мониторинга EWMA стационарного процесса использовать EWMAST-карту, которая в общем случае может быть применена к стационарному процессу. Карту формируют путем построения графика статистики EWMA [10]:
 |
X - время
Рисунок 5 - Реализация процесса авторегрессии первого порядка, используемого для иллюстрации EWMAST-карты
 |
X - время; Y - EWMA
Рисунок 6 - EWMAST-карта применительно к моделируемым данным, показанным на рисунке 5, с увеличением среднего
4.3.2 Модифицированная CUSUM-карта
В [12] рассмотрено построение графиков необработанных данных непосредственно с помощью CUSUM-карты при низкой автокорреляции процесса. Если автокорреляция высока, следует рассмотреть возможность использования преобразованных наблюдений. В [9], [13] предложены другие подходы для применения модифицированных CUSUM-карт к процессам авторегрессии первого порядка и некоторые другие временные ряды.
4.4 Сопоставление карт для автокоррелированных данных
Возможно сопоставление некоторых контрольных карт для автокоррелированных данных. В [9] и [4] проведено сопоставление X-карты, X-карты остатков, CUSUM-карты остатков, EWMA-карты остатков и EWMAST-карты для стационарных процессов авторегрессии первого порядка с помощью моделирования. EWMAST-карта работает лучше, чем CUSUM-карта остатков и EWMA-карта остатков. В целом, она также работает лучше, чем X-карта и X-карта остатков. Сравнение также показывает, что CUSUM-карта остатков и EWMA-карта остатков работают почти одинаково. CUSUM-карта остатков и EWMA-карта остатков работают лучше, чем X-карта остатков, при низкой автокорреляции процесса. Напротив, когда автокорреляция высока, X-карта остатков работает лучше, чем другие карты остатков. Если автокорреляция процесса очень высокая, т.е. процесс близок к нестационарному, EWMAST-карта по-прежнему работает лучше, чем другие карты.
Очевидным преимуществом использования EWMAST-карт является то, что нет необходимости строить модель временных рядов для данных стационарного процесса. Формирование EWMAST-карты требует только оценки среднего, стандартного отклонения и автокорреляций процесса, полученных по данным, когда процесс находился в стабильном состоянии. Таким образом, если процесс является автокоррелированным и стационарным, для мониторинга среднего процесса рекомендуется использовать EWMAST-карту.
5 Мониторинг изменчивости стационарных процессов
В [14] рассмотрены две контрольные карты для мониторинга изменчивости процесса: одна основана на экспоненциально взвешенном среднеквадратичном отклонении от целевого значения [карта экспоненциально взвешенного среднеквадратичного отклонения (EWMS) или EWMS-карта], а другая основана на экспоненциально взвешенной скользящей дисперсии, в которой среднее значение процесса оценивают с использованием EWMA-карты наблюдений [карта экспоненциально взвешенной скользящей дисперсии (EWMV) или EWMV-карта].
где t=1, 2, ...;
В [16] применение EWMS-карты распространено на случай стационарных процессов. В сочетании с EWMAST-картой EWMS-карта может быть использована для определения возможного изменения дисперсии стационарного процесса.
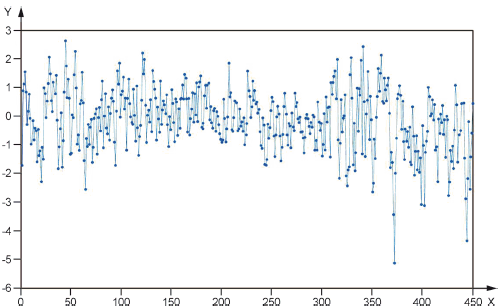 |
X - время; Y - значение статистики
Рисунок 7 - Реализация процесса авторегрессии первого порядка, используемого для иллюстрации процедуры EWMS, когда среднее процесса равно 0, но дисперсия процесса изменяется два раза
 |
X - время; Y - EWMA
Рисунок 8 - EWMAST-карта с контрольными границами для временных рядов, показанных на рисунке 7
 |
X - время; Y - EWMS
Рисунок 9 - EWMS-карта с контрольными границами для временных рядов, показанных на рисунке 7
6 Другие подходы при работе с автокоррелированными процессами
В разделах 4 и 5 рассмотрены различные контрольные карты, которые могут быть скорректированы к данным автокоррелированного процесса. В качестве альтернативы адаптации моделей влияние автокорреляции может быть уменьшено с помощью подходящего способа обработки данных. В [17] рассмотрено влияние выбора интервала отбора выборки на некоторые данные процесса. Если процесс является стационарным и выборку отбирают реже, автокорреляция выборочных данных снижается.
Таким образом, если интервал отбора выборки достаточно велик, данные кажутся некоррелированными. Однако такой подход не учитывает промежуточные данные и, следовательно, увеличивает вероятность пропуска важных изменений процесса. Вместо применения большого интервала отбора выборки можно формировать скользящее среднее процесса с фиксированным размером "окна". В [18] показано, что если процесс является стационарным и удовлетворяет некоторым условиям регулярности, неперекрывающиеся средние или средние партий являются асимптотически независимыми и нормально распределенными. Таким образом, если объем партии достаточно велик, среднее партий можно рассматривать как белый шум. Для некоторых конкретных стационарных процессов во многих статьях рассматривают средние подвыборок или средние партий, а также соответствующие карты для средних партий. В [19] рассмотрены последствия использования общих скользящих средних стационарного процесса для снижения автокорреляции процесса и их применение к контрольным картам процесса.
Приложение A
(справочное)
Случайный процесс и временные ряды
A.1 Общие положения
A.2 Автоковариация и автокорреляция временного ряда
A.3 Стационарные временные ряды и модели стационарных временных рядов
A.3.1 Общие положения
A.3.2 Белый шум
Временной ряд называют белым шумом, если:
A.3.3 Авторегрессионные процессы первого порядка [AR(1)]
A.4 Оценка среднего, автоковариации и автокорреляции для стационарных временных рядов
A.5 Проверка наличия автокорреляции данных временных рядов
Важно проверить, являются ли данные процесса автокоррелированными. Часто используют два простых теста.
1) Использование графика выборочной автокорреляционной функции с доверительной полосой
2) Тест длины серии
Использование выборочной автокорреляционной функции основано на предположении о том, что процесс является стационарным, это означает, что среднее процесса постоянно. Однако график автокорреляционной функции может ложно показывать значительные автокорреляции, если исследуемый случайный процесс не имеет постоянного среднего. В этом случае использование автокорреляционной функции для проверки того, является ли процесс автокоррелированным, может ввести в заблуждение. Данный тест можно использовать как дополнение к графику автокорреляционной функции. Данный тест является непараметрическим, он основан на увеличении и уменьшении длины серии [21]. В [21] (стр.99-101) представлен пример, показывающий использование данного теста.
Приложение B
(справочное)
Формирование традиционных контрольных карт для автокоррелированных данных
 |
X - время
 |
X - время
 |
X - время
 |
X - время
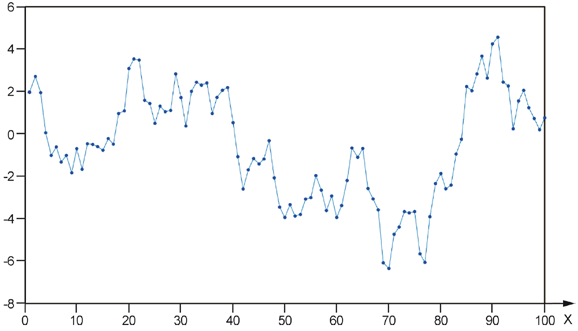 |
X - время
Таблица B.1 - Результаты исследований
в единицах | X-карта L=3 | CUSUM-карта при h=5,0, k=0,5 | EWMA-карта при 0,2, 3 | |
0 | 0 | 370,40 | 465,00 | 547,71 |
(автокорреляция | 0,5 | 155,21 | 38,40 | 44,60 |
отсутствует) | 1 | 43,89 | 10,40 | 10,75 |
2 | 6,30 | 4,01 | 3,73 | |
3 | 2,00 | 2,57 | 2,38 | |
0,25 | 0 | 381,60 | 119,35 | 139,50 |
(автокорреляция | 0,5 | 160,53 | 30,02 | 32,81 |
слабая) | 1 | 46,61 | 10,58 | 10,72 |
2 | 7,25 | 4,16 | 3,85 | |
3 | 2,21 | 2,64 | 2,41 | |
0,5 | 0 | 400,74 | 49,23 | 56,00 |
(автокорреляция | 0,5 | 181,15 | 25,76 | 26,96 |
средняя) | 1 | 56,42 | 11,43 | 10,79 |
2 | 9,16 | 4,34 | 4,00 | |
3 | 2,60 | 2,64 | 2,50 | |
0,75 | 0 | 496,04 | 30,98 | 31,45 |
(автокорреляция | 0,5 | 235,98 | 22,74 | 21,82 |
умеренно высокая) | 1 | 74,33 | 12,67 | 11,30 |
2 | 14,42 | 4,73 | 4,56 | |
3 | 3,59 | 2,83 | 2,58 | |
0,9 | 0 | 833,59 | 29,02 | 26,24 |
(автокорреляция | 0,5 | 413,03 | 24,40 | 21,09 |
высокая) | 1 | 157,72 | 15,38 | 13,19 |
2 | 27,09 | 5,84 | 5,08 | |
3 | 6,24 | 2,85 | 2,72 |
Здесь приведены результаты только для положительно автокоррелированных рядов, поскольку положительная автокорреляция на сегодняшний день является наиболее распространенной на практике, например в биологии. Для изучения влияния отрицательной автокорреляции см. [4]. Рассмотрены только поэтапные изменения среднего.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандарта: - IDT - идентичный стандарт. | ||
Библиография
[1] | ALWAN L.C., ROBERT H.V. (1988), Time-series modelling for statistical process control, Journal of Business & Economic Statistics, 6(1), 87-95 |
[2] | RUNGER G.C., WILLEMAIN T.R., PRABHU, S. (1995), Average run lengths for CUSUM control charts applied to residuals, Communication in Statistics - Theory and Methods, 24(1), 273-282 |
[3] | LU C.W., REYNOLDS M.R. (1999), EWMA control charts for monitoring the mean of autocorrelated processes, Journal of Quality Technology, 31(2), 166-188 |
[4] | ZHANG N.F. (2000), Statistical control charts for monitoring the mean of a stationary process, Journal of Statistical Computation and Simulation, 66(3), 249-258 |
[5] | WARDELL D.G., MOSKOWWITZ H., PLANTE R.D. (1994), Run-length distributions of special-cause control charts for correlated processes, Technometrics, 36, 3-17 |
[6] | ZHANG N.F. (1997), Detection capability of residual chart for autocorrelated data, Journal of Applied Statistics, 24(4), 475-492 |
[7] | DODSON B. (1995), Control charting dependent data: A case study, Quality Engineering, 7(4), 757-768 |
[8] | WOODWARD W.A., GRAY H.L., ELLICOTT A.C. (2012), Applied time series analysis. Boca Raton, FL: CRC Press. |
[9] | VANBRACKLE L., REYNOLDS M.R. (1997), EWMA and CUSUM control charts in the presence of correlation, Communications in Statistics - Simulation and computation, 26(3), 979-1008 |
[10] | ZHANG N.F. (1998), A statistical control chart for stationary process data, Technometrics, 40(1), 24-38 |
[11] | BOX G.E.P., JENKINS G.M., REINSEL G.C. (1994), Time series analysis: Forecasting and control (3rd ed.), Englewood Cliffs, NJ: Prentice Hall |
[12] | YASHCHIN E. (1993), Performance of CUSUM control schemes for serially correlated observations, Technometrics, 35(1), 37-52 |
[13] | LU C.W., REYNOLDS M.R. (2001), CUSUM charts for monitoring an autocorrelated process, Journal of Quality Technology, 33(3), 316-334 |
[14] | MACGREGOR J.F., HARRIS T.J. (1993), The exponentially weighted moving variance, Journal of Quality Technology, 25(2), 106-118 |
[15] | LU C.W., REYNOLDS M.R. (1999), Control charts for monitoring the mean and the variance of autocorrelated processes, Journal of Quality Technology, 31(2), 259-274 |
[16] | ZHANG N.F., PINTAR A.L. (2015), Monitoring process variability for stationary process data, Quality and Reliability Engineering International, 31(8), 1383-1396 |
[17] | MACGREGOR J.F. (1976), Optimal choice of the sampling interval for discrete process control, Technometrics, 18(2), 151-160 |
[18] | BRILLINGER D.R. (1973), Estimation of the mean of a stationary time series by sampling, Journal of Applied Probability, 10, 419-431 |
[19] | ZHANG N.F. (2006), The batched moving averages of measurement data and their applications in data treatment, Measurement, (39), 864-875 |
[20] | BROCKWELL P.J., DAVIS R.A. (1991), Time series: Theory and methods (2nd ed.). New York, NY: Springer-Verlag |
[21] | WINKEL P., & ZHANG N.F. (2007), Statistical development of quality in medicine. Chichester, UK: John Wiley & Sons, Ltd. |
[22] | ISO 7870-4:2011*, Control charts - Part 4: Cumulative sum charts |
_______________ * Заменен на ISO 7870-4:2021. | |
[23] | LUCAS J.M. (1976), The design and use of V-Mask control schemes, Journal of Quality Technology, 8(1), 1-12 |
УДК 658.562.012.7:65.012.122:006.352 | ОКС 03.120.30 |
Ключевые слова: статистическое управление процессом, контрольная карта, контрольная карта для стационарных процессов, автокорреляция, автоковариация, карта остатков | |
