ГОСТ Р ИСО 7870-7-2023 Статистические методы. Контрольные карты. Часть 7. Многомерные контрольные карты

        ГОСТ Р ИСО 7870-7-2023

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

КОНТРОЛЬНЫЕ КАРТЫ

Часть 7

Многомерные контрольные карты

Statistical methods. Control charts. Part 7. Multivariate control charts

ОКС 03.120.30

Дата введения 2024-03-01

Предисловие

1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 сентября 2023 г. N 966-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 7870-7:2020* "Контрольные карты. Часть 7. Многомерные контрольные карты" (ISO 7870-7:2020 "Control charts - Part 7: Multivariate control charts", IDT).

Международный стандарт разработан Техническим комитетом ТК 69 Международной организации по стандартизации (ИСО).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)

Введение

При необходимости одновременного контроля нескольких характеристик качества продукции, как правило, используют несколько отдельных (одномерных) контрольных карт. К сожалению, при наличии сильной корреляции между контролируемыми характеристиками это может привести к ошибочным результатам. Мониторинг процессов, в которых одновременно рассматривают несколько взаимосвязанных переменных, называется многомерным статистическим управлением процессами (MSPC). Наиболее полезным способом многомерного статистического управления процессами является применение многомерных контрольных карт. Многомерные контрольные карты используют для статистической оценки и контроля процесса с учетом зависимости между контролируемыми характеристиками.

Назначение системы многомерного статистического управления процессом состоит в подаче сигнала при наличии заданных причин изменчивости. Систематическое устранение указанных причин чрезмерных отклонений путем постоянных целенаправленных усилий переводит процесс в состояние статистической управляемости (стабильности). Если процесс находится в состоянии статистической управляемости, его работа предсказуема, а его воспроизводимость и соответствие установленным требованиям можно оценить.

Основной целью настоящего стандарта является демонстрация способов использования многомерных контрольных карт для управления процессом с точки зрения SPC и методов оценки состояния стабильности процесса. В ИСО 22514-6 приведен метод расчета статистик воспроизводимости для параметров процесса или характеристик продукции, подчиняющихся многомерному нормальному распределению.

Многомерные карты основаны на многомерных характеристиках при необходимости мониторинга двух и более характеристик, связанных между собой. На практике многомерную контрольную карту всегда применяют при использовании программного обеспечения, такого как Minitab, JMP и Q-DAS

.

_______________

MINITAB - это торговое название продукта, поставляемого Minitab Inc. JMP - это торговое название продукта, поставляемого SAS Institute Inc. Q-DAS - это торговое название продукта, поставляемого Q-DAS GmbH. Данная информация приведена для удобства пользователей данного документа и не является одобрением ИСО этих продуктов.

1 Область применения

Настоящий стандарт устанавливает требования к построению и использованию многомерных контрольных карт для статистического управления процессами (SPC), а также методы использования и понимания этого обобщенного подхода к контрольным картам, когда измеряемые характеристики - данные о переменных.

Использование метода главных компонент (PCA) и частичных наименьших квадратов (PLS) в области многомерного статистического управления процессами в настоящем стандарте не представлено.

Примечание - В настоящем стандарте описано существующее состояние многомерных контрольных карт, применяемых на практике. В стандарте не описано современное состояние научных исследований в этой области.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт [для датированной ссылки применяют только указанное издание ссылочного стандарта, для недатированной - последнее издание (включая все изменения)]:

ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)

3 Термины и определения

В настоящем стандарте применены термины по ИСО 3534-2, а также следующие термины с соответствующими определениями.

ИСО и МЭК ведут терминологические базы данных для использования в области стандартизации по следующим адресам:

- платформа онлайн-просмотра ИСО: доступна по адресу http://www.iso.org/obp;

- Электропедия МЭК: доступна по адресу http://www.electropedia.org/.

3.1 многомерная характеристика (multivariate characteristics): Многомерная величина, состоящая из d самостоятельных величин или величин, характеризующих качество продукции.

Примечание 1 - В соответствии с ИСО 7870-2 эти величины обозначают как характеристики качества

, где

i

=1, 2, ...,

d

.

Примечание 2 - Результаты наблюдений многомерных характеристик могут быть представлены в виде вектора

. Таким образом, многомерную величину можно рассматривать как вектор характеристик продукции. Значение многомерной величины представляет собой точку в

d

-мерном пространстве.

Примечание 3 - Все единичные величины, объединенные в многомерный вектор, могут быть определены на одной и той же единице продукции или на одном и том же объекте.

Примечание 4 - Если многомерная величина описана статистически, вектор рассматривают как случайный вектор, подчиняющийся d-мерному многомерному распределению.

3.2 доверительная область (confidence region): d-мерная область, накрывающая оцениваемый d-мерный параметр с заданным уровнем доверия.

Примечание 1 - Область ограничена линиями, поверхностями или гиперповерхностями в d-мерном пространстве.

Примечание 2 - Форму и размер области определяют один или несколько параметров.

4 Обозначения и сокращения

4.1 Сокращения

В настоящем стандарте использованы следующие сокращения:

SPC - статистическое управление процессом;

MSPC - многомерное статистическое управление процессом;

PCA - метод главных компонент;

PLS - метод частичных наименьших квадратов;

UCL - верхняя контрольная граница;

LCL - нижняя контрольная граница;

ARL - средняя длина серии;

EWMA - экспоненциально взвешенное скользящее среднее;

MEWMA - многомерное экспоненциально взвешенное скользящее среднее.

4.2 Обозначения

В настоящем стандарте использованы следующие обозначения:

	- квантиль бета-распределения уровня с числом степеней свободы и ;
d	- количество измерений многомерных характеристик;
	- статистика, отражаемая на контрольной карте этапа II;
E(|S|)	- среднее |S|;
	- квантиль F -распределения уровня с числом степеней свободы и ;
h	- верхняя контрольная граница контрольной карты MEWMA;
	- нижняя контрольная граница;
m	- количество подгрупп;
n	- объем каждой подгруппы;
	- d -мерное нормальное распределение с параметрами и ;
	- ковариация между характеристиками a и b при n=1;
	- ковариация между характеристиками a и b в j-й подгруппе при n>1;
	- оценка дисперсии i-й характеристики при n=1;
	- оценка дисперсии i-й характеристики в j-й подгруппе при n>1;
	- выборочное среднее значений , по всем m подгруппам для i -й характеристики при n >1;
	- выборочное среднее значений по всем m подгруппам с ковариацией между характеристиками a и b при n >1;
S	- выборочная дисперсионно-ковариационная матрица с n=1;
	- выборочная дисперсионно-ковариационная матрица с n>1;
|S|	- определитель выборочной дисперсионно-ковариационной матрицы S;
	- статистика, отражаемая на карте этапа I;
	- статистика, отражаемая на карте этапа II;
tr	- оператор определения следа матрицы;
	- верхняя контрольная граница;
V(|S|)	- дисперсия |S|;
	- j-е наблюдение i-й характеристики при n=1;
	- k-е наблюдение i-й характеристики в j-й подгруппе при n>1;
	- выборочное среднее i-й характеристики в j-й подгруппе при n>1;
	- выборочное среднее значений по всем m подгруппам для i -й характеристики при n >1;
x	- вектор наблюдений;
	- вектор j-го наблюдения при n=1;
	- вектор будущего индивидуального наблюдения при n=1;
	- вектор выборочного среднего при n=1;
	- выборочное среднее j-й рациональной подгруппы при n>1;
	- среднее будущей рациональной подгруппы при n>1;
	- вектор выборочных средних при n>1;
	- i -й элемент вектора ;
	- статистика, отражаемая на контрольной карте MEWMA;
	- статистика MEWMA;
	- квантиль распределения уровня с числом степеней свободы ;
	- размер сдвига вектора среднего;
	- вектор скользящих параметров MEWMA;
	- скользящий параметр MEWMA, 0 1;
	- вектор среднего многомерных характеристик;
	- заранее заданный вектор среднего многомерных характеристик;
	- коэффициент корреляции между и ;
	- дисперсионно-ковариационная матрица многомерных характеристик;
	- заранее заданная дисперсионно-ковариационная матрица многомерных характеристик;
	- дисперсионно-ковариационная матрица MEWMA статистики ;
( ·)	- оператор обратной матрицы;
( ·)	- оператор транспонирования матрицы.

5 Назначение и классификация многомерных контрольных карт

5.1 Назначение и условия применения многомерных контрольных карт

Существует много ситуаций, в которых необходим одновременный мониторинг или контроль двух и более взаимосвязанных характеристик. Сложность использования независимых одномерных контрольных карт показана на рисунке 1. Для простоты рассмотрены только две характеристики (

,

).

Предположим, что в ситуации, когда процесс находится в состоянии статистической управляемости (стабильности), при наличии только общей причины изменчивости,

и

подчиняются нормальному распределению, с корреляцией (

-0,94), как показано на совместном графике

и

на рисунке 1. Эллипс представляет собой контур стабильного процесса с квантилем уровня 0,9973, соответствующим риску ложной тревоги 0,0027 на карте Шухарта, а точки представляют собой набор отдельных наблюдений изданного распределения. Те же наблюдения показаны на рисунке 1 на отдельных контрольных картах Шухарта для

и

с соответствующим количеством наблюдений (время) и соответствующими верхней и нижней контрольными границами (квантили уровня 0,998 65).

По результатам анализа каждой из отдельных контрольных карт Шухарта процесс явно находится в состоянии статистической управляемости, и ни одна из точек не указывает на наличие проблем. Истинная ситуация раскрывается только на двумерном графике

и

, где видно, что партия продукции, обозначенная знаком

, находится за пределами доверительной области и существенно отличается от стабильной нормальной совокупности продукции.

Если характеристики не являются независимыми, что обычно имеет место, если они относятся к одному и тому же объекту, не существует простого способа измерения искажения в процедуре совместного контроля. Проблемы мониторинга процесса, в которых рассматривают несколько взаимосвязанных переменных, иногда называют проблемами многомерного контроля качества. Этот вопрос особенно важен, поскольку процедуры автоматизированного контроля позволяют относительно легко измерять множество параметров на каждой единице продукции. Например, многие химические и технологические предприятия, а также изготовители полупроводников регулярно ведут производственные базы данных о процессе и качестве продукции по сотням переменных. Мониторинг или анализ этих данных с помощью одномерных процедур SPC часто нерезультативны. Многомерные контрольные карты применяют для статистической оценки и управления процессом с учетом зависимости между наблюдаемыми характеристиками.

- выборочное среднее

;

- выборочное среднее

;

j

- номер наблюдения;

- верхняя контрольная граница

;

- нижняя контрольная граница

;

- верхняя контрольная граница

;

- нижняя контрольная граница

;

- точка, соответствующая

;

- точка, соответствующая

;

- точка, соответствующая (

,

)

Рисунок 1 - Контроль качества по двум переменным

Применение многомерных контрольных карт удобно, когда количество переменных процесса не слишком велико - десять или менее. Однако по мере увеличения количества переменных традиционные многомерные контрольные карты теряют результативность в отношении обнаружения сдвигов процесса. Популярный подход в такой ситуации состоит в уменьшении размерности задачи. Это может быть сделано с использованием методов прогнозирования, таких как анализ главных компонент (РСА) или метод частичных наименьших квадратов (PLS). Эти два метода основаны на построении модели на основе набора ранее полученных данных, которые, как предполагается, соответствуют состоянию статистической управляемости процесса. После того, как модель построена, следующее наблюдение проверяют на предмет его соответствия модели.

В одномерном случае в SPC для описания непрерывной характеристики обычно используют нормальное распределение. Тот же подход может быть использован и в многомерном случае. Многомерное нормальное распределение применяют в качестве основного предположения при рассмотрении многомерных характеристик.

5.2 Классификация многомерных контрольных карт

Если многомерные характеристики рассматривают как случайный вектор из многомерного нормального распределения, распределение характеризуют вектором средних

и матрицей ковариаций и дисперсий

(см. приложение C). С точки зрения применения многомерного управления процессом, многомерные контрольные карты могут быть применены для мониторинга среднего сдвига и рассеивания процесса отдельно. Таким образом, многомерные контрольные карты могут быть классифицированы следующим образом:

a) многомерные контрольные карты сдвига среднего;

b) многомерные контрольные карты рассеивания процесса.

Для контроля сдвига среднего многомерные контрольные карты с невзвешенными средними аналогичны карте Шухарта

или карте индивидуальных значений. Они используют информацию только из текущей выборки и относительно нечувствительны к небольшим и умеренным сдвигам вектора среднего. Для решения этой проблемы можно использовать многомерные контрольные карты взвешенных средних, такие как многомерная контрольная карта EWMA. Так же, как карты EWMA обычно используют для обнаружения небольших сдвигов среднего процесса, их обычно используют для обнаружения сдвигов от 0,5 до 2

. Таким образом, многомерные контрольные карты среднего можно классифицировать следующим образом:

i) многомерные контрольные карты взвешенных средних (см. раздел 6), такие как карты

и

;

ii) многомерные контрольные карты взвешенных средних (см. раздел 7), такие как многомерная контрольная карта EWMA.

На рисунке 2 показано, как следует выбирать многомерную контрольную карту.

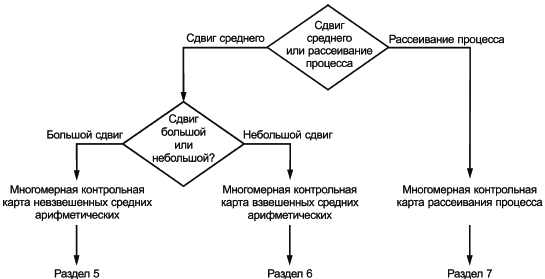Рисунок 2 - Блок-схема выбора многомерной контрольной карты

6 Многомерные контрольные карты невзвешенных средних для контроля сдвига среднего процесса

6.1 Общие положения

Для каждой из многомерных контрольных карт возможны две различные ситуации, когда:

a) заданы установленные значения параметров процесса;

b) значения параметров процесса не заданы.

В качестве предварительно установленных или известных значений параметров процесса могут быть заданы целевые значения, требования или оценки значений, определенные на основе данных в условиях стабильного процесса.

Существует два различных этапа составления контрольных карт:

i) этап I: контрольные карты используют для ретроспективной проверки того, что процесс находился в состоянии статистической управляемости, при отборе первых подгрупп. Как только это будет сделано, контрольную карту используют для определения того, что следует понимать под процессом, находящимся в стабильном состоянии. Это называется ретроспективным использованием контрольных карт;

ii) этап II: контрольные карты используют для проверки того, что процесс находится в стабильном состоянии при составлении будущих подгрупп. На этом этапе карту используют в качестве вспомогательного средства при мониторинге процесса на предмет любых изменений и выхода процесса из стабильного состояния.

Другим важным вопросом является объем n каждой рациональной подгруппы. Если n=1, то необходимо соблюдать особую осторожность. Таким образом, рассматривают четыре возможности:

- этап I, n=1, работа с индивидуальными наблюдениями;

- этап I, n>1, работа с рациональными подгруппами;

- этап II, n=1, работа с индивидуальными наблюдениями;

- этап II, n>1, работа с рациональными подгруппами.

6.2 Контрольные карты среднего процесса (n>1)

6.2.1 Контрольная карта

, когда установленные значения параметров известны

Предположим, что вектор x подчиняется

d

-мерному нормальному распределению

, и из процесса отобрано

m

подгрупп объемом

n

>1 каждая. Кроме того, предположим, что векторы наблюдений x не зависят от времени. Контрольная карта может быть основана на последовательности следующих статистик:

,

j

=1, 2, ...,

m

. (1)

Здесь

- вектор средних

j

-й рациональной подгруппы,

и

- известный вектор средних и известная дисперсионно-ковариационная матрица соответственно.

Статистика

представляет собой взвешенное расстояние (расстояние Махаланобиса) от любой точки на карте до цели,

. Если значение статистики

превышает верхнюю контрольную границу, это указывает на возможность выхода процесса из стабильного состояния. Как правило, контрольные карты имеют как верхние, так и нижние контрольные границы. Однако в этом случае используют только верхнюю контрольную границу, поскольку экстремальные значения статистики соответствуют точкам, удаленным от целевого значения

, точкам, близким к целевому значению

, соответствуют малые или нулевые значения статистики.

Статистика

подчиняется

-распределению с

d

степенями свободы. Таким образом, многомерная контрольная карта Шухарта для среднего процесса с известным вектором среднего

и известной дисперсионно-ковариационной матрицей

имеет следующую верхнюю контрольную границу:

. (2)

Для определения верхней контрольной границы уровень вероятности

может быть выбран из ряда 0,1%, 0,2%, 0,5% или 1% с учетом особенностей практического применения. Например, выбор 0,2% означает, что существует риск ложной тревоги, приблизительно равный 0,2%, или процесс находится в стабильном состоянии в среднем два раза из тысячи случаев, когда точка статистики

на графике находится за пределами верхней контрольной границы.

Такую контрольную карту называют контрольной картой

этапа II.

6.2.2 Контрольная карта

, когда значения параметров процесса не известны

Если получены наблюдения 20 подгрупп, многомерные контрольные карты используют для мониторинга процесса и вектор выборочного среднего

оценивают как среднее арифметическое всех средних в подгруппах. Матрицу выборочных дисперсий и ковариаций

оценивают как

d

d

матрицу средних дисперсий и ковариаций подгрупп. См. C.1.

Если

заменить на

, а

- на

, с

n

>1, где

- среднее

j

-й рациональной подгруппы, контрольная карта может быть основана на последовательности значений следующей статистики [4]:

,

j

=1, 2, ...,

m

. (3)

Статистика

подчиняется

F

-распределению с числом степеней свободы

d

и (

mn

-

m

-

d

+1). Здесь

.

Таким образом, многомерная контрольная карта Шухарта для среднего значения процесса с неизвестными параметрами имеет следующую верхнюю контрольную границу:

. (4)

Эту контрольную карту называют контрольной картой

этапа I.

Если

заменить на

, а

- на

, с

n

>1, где

- среднее будущей рациональной подгруппы, контрольная карта может быть основана на последовательности значений следующей статистики:

. (5)

Статистика

подчиняется

F

-распределению с числом степеней свободы

d

и (

mn

-

m

-

d

+1), где

и

m

- количество подгрупп, относящихся к этапу I.

Таким образом, многомерная контрольная карта Шухарта для среднего процесса с неизвестными параметрами процесса имеет следующую верхнюю контрольную границу:

. (6)

Эта контрольная карта называется контрольной картой Т2 этапа II.

6.3 Контрольные карты среднего процесса (n=1)

6.3.1 Контрольная карта

, когда установленные значения параметров известны

Для карт, построенных с использованием отдельных наблюдений (n=1), контрольная карта может быть основана на последовательности значений следующей статистики:

,

j

=1, 2, ...,

m

, (7)

где

-

j

-е наблюдение,

j

=1, 2, ...,

m

, из

, где

и

- известный вектор средних и известная дисперсионно-ковариационная матрица соответственно. Более того, предположим, что наблюдения

не зависят от времени. Статистика

подчиняется

-распределению с числом степеней свободы

d

. Таким образом, многомерная контрольная карта Шухарта для среднего процесса с известным вектором среднего

и известной дисперсионно-ковариационной матрицей

имеет следующую верхнюю контрольную границу:

. (8)

Такая контрольная карта называется контрольной картой

этапа II.

6.3.2 Контрольная карта

, когда значения параметров процесса не известны

Если получены наблюдения более 20 наблюдаемых векторов по многомерным характеристикам и для мониторинга процесса используют многомерные контрольные карты, оценивают вектор среднего выборки

и вектор дисперсии-ковариации выборки S. См. С.2.

Если

заменяют на

,

- на S, где

является

j

-м индивидуальным наблюдением, которое не является независимым от оценок

и S, контрольная карта может быть основана на последовательности следующей статистики:

,

j

=1, 2, ...,

m

. (9)

Статистика

подчиняется бета-распределению с числом степеней свободы

d

/2 и

, где

.

Таким образом, многомерная контрольная карта Шухарта для среднего процесса с неизвестными параметрами имеет следующую верхнюю контрольную границу:

. (10)

Такая контрольная карта называется контрольной картой

этапа I.

Если

заменить на

,

- на S, где

- будущее индивидуальное наблюдение, которое не зависит от оценок

и S, контрольная карта может быть основана на последовательности значений следующей статистики:

. (11)

Статистика

подчиняется F-распределению с числом степеней свободы

d

и (

m-d

), где

и

m

- количество наблюдаемых векторов, относящихся к этапу I.

Таким образом, многомерная контрольная карта Шухарта для среднего процесса с неизвестными параметрами имеет следующую верхнюю контрольную границу:

. (12)

Такая контрольная карта называется контрольной картой Т2 этапа II.

6.4 Обобщение и выбор многомерных контрольных карт с невзвешенными средними арифметическими сдвигов среднего

В таблице 1 приведены статистики и верхние контрольные границы в различных случаях многомерных контрольных карт с невзвешенным средним для сдвигов среднего процесса, а на рисунке 3 показано, как выбирать эти контрольные карты.

Таблица 1 - Многомерные контрольные карты с невзвешенными средними

Состояние		Статистика		Наименование карты
n>1	параметры известны			Карта этапа II при n >1
	этап I			Карта этапа I при n >1
	этап II			Карта этапа II при n >1
n=1	параметры известны			Карта этапа II при n =1
	этап 1			Карта этапа I при n =1
	этап II			Карта этапа II при n =1

Рисунок 3 - Блок-схема выбора контрольной карты

Во многих ситуациях требуется большое количество предварительных выборок, прежде чем будут точно определены контрольные границы этапа II. Рекомендуемое количество m предварительных выборок всегда более 20, а часто и более 50, особенно для подгрупп с объемом более 10.

6.5 Проверка на наличие установленных причин

В картах Шухарта

и

X

-картах для выявления небольших сдвигов, не достаточных для быстрого появления точек за пределами контрольных границ, часто используют набор признаков изменения кривой на карте, таких как серии и тренды. Поскольку статистика для контрольных карт

и

характеризует квадрат расстояния от соответствующей точки до цели

, она не выявляет точки, расположенные выше или ниже центральной линии, как на картах Шухарта и

X

-картах. Для контрольных карт

и

нижней контрольной границы не существует. Таким образом, меньшие сдвиги не могут привести к появлению серий и трендов на контрольных картах

и

в отличие от карт Шухарта и

X

-карт. Для контрольных карт

и

сигналом о возможном выходе процесса из стабильного состояния является только превышение статистикой верхней контрольной границы.

Для проверки меньших сдвигов среднего многомерных характеристик применяют многомерные контрольные карты взвешенного среднего.

7 Многомерные контрольные карты взвешенных средних для контроля сдвига среднего процесса

Карты

и

, описанные в разделе 6, являются контрольными картами типа карт Шухарта. Они используют только информацию текущей выборки, поэтому относительно нечувствительны к небольшим и умеренным сдвигам вектора среднего. Карты

можно использовать в ситуациях как первого, так и второго этапа. Контрольные карты EWMA были разработаны для обеспечения большей чувствительности к небольшим сдвигам в одномерном случае, их можно распространить на многомерные задачи контроля. Как и в одномерном случае, многомерную версию этих карт всегда используют в качестве процедуры этапа II.

MEWMA является логическим продолжением одномерного EWMA, его определяют следующим образом [5]:

,

j

=1, 2, ..., (13)

где

, при контроле среднего

, 0

1. (14)

Как правило, предполагают, что

одинаковы и

. MEWMA можно записать:

,

j

=1, 2, ... . (15)

Константа

, 0

1, является скользящим параметром EWMA. Статистика MEWMA сокращается до

, когда

1.

Карта MEWMA выдает сигнал о нарушении стабильного состояния, когда:

, (16)

где

h

- верхняя контрольная граница MEWMA, а дисперсионно-ковариационная матрица

статистики MEWMA

имеет вид:

(17)

аналогично одномерному EWMA. Если

1, карта MEWMA сокращается до многомерной контрольной карты Шухарта. Если известны вектор среднего

и дисперсионно-ковариационная матрица

от

, карта MEWMA превращается в карту

при

1.

Анализ ARL контрольной карты MEWMA может быть использован для выбора

и

h

на основе моделирования с учетом объема подгруппы, размера сдвига, установленного значения

и ARL, соответствующего заданному размеру сдвига

. Значения

h

выбирают для достижения установленной

. Значение

выбирают для минимизации

в соответствии с размером сдвига вектора среднего следующим образом (см. таблицу 2):

- значение

менее 0,05 предпочтительно для обнаружения величины сдвига

0,5. Несмотря на то, что количество переменных имеет важное значение, рекомендуется использовать

0,03;

- для сдвига, приблизительно равного

1,

0,1 близко к наилучшему выбору в широком диапазоне

d

;

- для сдвигов

от 1,5 до 2 хорошим выбором являются значения

от 0,15 до 0,25;

- для сдвигов с

3,

0,4 является рациональным.

Таблица 2 - Определение

на основе величины сдвига

Величина сдвига	0,5	1	От 1,5 до 2	3
	0,03	0,1	От 0,15 до 0,25	0,4

Примечание - В таблице 2 приведены значения

на основе сдвига

. Однако точный размер сдвига легко определить заранее. Более того, разумно вести мониторинг небольших сдвигов процесса вместо сдвига уникального размера. В ИСО 7870-6 рекомендовано, чтобы наиболее часто используемые значения

находились в диапазоне от 0,25 до 0,5 включительно.

Применение контрольной карты MEWMA описано в приложении В.

8 Контрольные карты разброса процесса

Изменчивость процесса суммируют с помощью дисперсионно-ковариационной матрицы

размера

d

d

. Основными диагональными элементами этой матрицы являются дисперсии отдельных переменных процесса, а недиагональными элементами являются ковариации. Прямая процедура мониторинга разброса процесса является расширением одномерной контрольной карты и эквивалентна повторным проверкам гипотезы о том, что ковариационная матрица процесса равна матрице

. Статистика, отображаемая на контрольной карте

j

-й подгруппы, имеет вид [6]:

, (18)

где

,

- дисперсионно-ковариационная матрица

j

-й подгруппы, а tr - оператор определения следа матрицы. След матрицы - сумма основных диагональных элементов. Если значение

расположено выше верхней контрольной границы

, процесс выходит из стабильного состояния.

Другой подход при мониторинге разброса процесса основан на дисперсии обобщенной выборки |S|, которая представляет собой определитель выборочной дисперсионно-ковариационной матрицы S. Например, один из методов состоит в использовании для определения верхней и нижней контрольных границ при мониторинге разброса процесса среднего и дисперсии |S|, то есть

E

(|S|) и

V

(|S|), а также того, что большую часть распределения вероятностей |S| накрывает интервал

. В приложении А приведен пример, показывающий применение контрольной карты, основанное на обобщенной дисперсии отдельных наблюдений (

n

=1).

Многомерное расширение контрольных карт разброса процесса не так просто, как карт среднего процесса. Общая модель и методы, охватывающие широкий спектр проблем, возникающих на практике, отсутствуют. В большинстве случаев конкретные задачи необходимо решать уникальным образом.

Были внедрены различные альтернативные методы мониторинга разброса процесса, которые получили широкое признание на практике. Несмотря на то, что распространение этих методов на многомерный случай имеет большое значение, процедурам мониторинга корреляций между характеристиками многомерного процесса уделяется очень мало внимания. Возможно, это отсутствие прогресса связано с тем, что статистические выводы по дисперсионно-ковариационной матрице, как правило, довольно сложны. Кроме того, в отличие от задачи контроля среднего процесса, нелегко однозначно определить сдвиги в дисперсионно-ковариационной матрице, которые необходимо обнаружить. Другой трудностью при разработке такой многомерной процедуры является идентификация параметра (параметров) нестабильности процесса, когда на контрольной карте появляется сигнал о нестабильном состоянии процесса. В многомерном случае необходимость мониторинга изменчивости процесса становится еще более очевидной.

Применение многомерных контрольных карт среднего процесса и разброса процесса рассмотрено в приложении A.

9 Интерпретация сигнала о нестабильном состоянии процесса

Многомерные контрольные карты способны распознавать процесс, вышедший из стабильного состояния.

Если одномерная контрольная карта выдает сигнал о нестабильности процесса, то, как правило, можно легко обнаружить проблему и найти решение, поскольку одномерная карта связана с одной переменной. Это неверно для многомерной контрольной карты, поскольку задействован набор переменных и между ними существуют корреляционные зависимости.

Идентификация нестабильной переменной при появлении сигнала на многомерной контрольной карте - интересная тема для академических исследований. Очевидный подход состоит в использовании соответствующих одномерных контрольных карт. Иногда методы декомпозиции применяют для идентификации конкретных подмножеств, которые вызывают соответствующий сигнал. Для анализа того, какие из переменных ответственны за появление сигнала, также может быть использован метод главных компонент. Однако проблема интерпретации сигнала о нестабильности процесса остается открытой и требует дальнейшего исследования.

Приложение A

(справочное)

Пример многомерного статистического контроля процесса

A.1 Общие положения

Для оценки качества ультразвуковой сварки контролируют глубину проплавления шва. Для анализа взаимосвязанных характеристик, влияющих на глубину проплавления шва, применяют многомерную контрольную карту. На основе предыдущего опыта были определены три характеристики: глубина сварочного кольца, глубина вставки и диаметр входного отверстия раструба.

A.2 Наблюдаемые данные

Каждый месяц выбирают и анализируют одну деталь. Объем подгруппы равен 1. Собранные данные наблюдений о глубине сварочного кольца, глубине вставки и диаметре входного отверстия раструба приведены в таблице A.1. Их используют для анализа того, был ли процесс стабильным (этап I). Корреляционная матрица, полученная на основе наблюдаемых данных, приведена в таблице A.2.

Таблица A.1 - Исходные данные по показателям сварки

Таблица A.2 - Корреляционная матрица

A.3 Многомерный анализ

j

- текущий номер подгруппы; |S| - обобщенная дисперсия;

- значение статистики

Рисунок A.1 - Контрольная карта

и контрольная карта, основанная на обобщенной дисперсии

На рисунке A.1 видно, что все точки расположены внутри контрольных границ. Независимо от контрольной карты

и контрольных карт разброса процесса, процесс является стабильным.

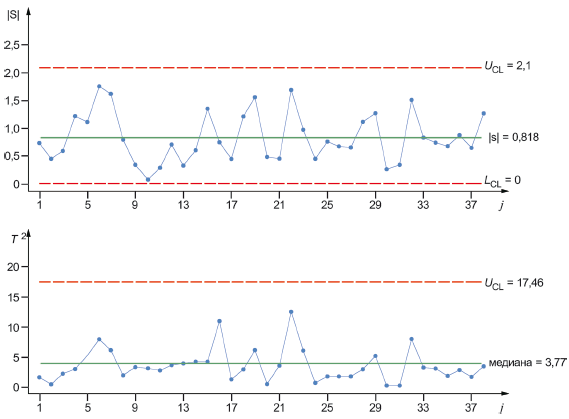Приложение B

(справочное)

Пример контрольной карты MEWMA

B.1 Общие положения

В процессе сборки электронной продукции качество электронных изделий в значительной степени определяют качество и безотказность паяных соединений. Данные мониторинга качества паяного соединения включают в себя скорость и температуру пайки.

B.2 Наблюдаемые данные

Данные мониторинга собирают с помощью автоматизированного оборудования. В таблице B.1 приведено 125 пар данных непрерывных наблюдений. Затем определяют корреляционную матрицу (см. таблицу B.2).

Таблица B.1 - Исходные данные

Таблица B.2 - Корреляционная матрица

B.3 Выбор параметров контрольной карты MEWMA

Существуют две характеристики

d

=2. Средняя длина серии при определении стабильного состояния процесса равна 200. Контрольная карта MEWMA выбрана в качестве процедуры этапа II для обнаружения небольшого сдвига процесса. Скользящий параметр MEWMA

и верхняя контрольная граница MEWMA

h

должны быть определены с помощью моделирования [7]. Однако эти параметры могут быть получены с помощью программного обеспечения непосредственно на практике.

B.4 Контрольная карта MEWMA

Контрольная карта MEWMA, полученная с помощью Minitab, показана на рисунках B.1-B.3 с различными

от 0,1 до 0,3 и соответствующей верхней контрольной границей

h

. Сравнение результатов на рисунках B.1-B.3 показывает, что при

0,3 точка 41 (10,21) находится за пределами

10,08, что является сигналом о нестабильном состоянии процесса. Анализ показал, что скорость является ключевым фактором, вызывающим выход процесса из стабильного в точке 41.

j

- текущий номер подгруппы;

- квадрат расстояния MEWMA от среднего в стабильном состоянии

Рисунок B.1 - Контрольная карта MEWMA для скорости и температуры при

0,1

j

- текущий номер подгруппы;

- квадрат расстояния MEWMA от среднего в стабильном состоянии

Рисунок B.2 - Контрольная карта MEWMA для скорости и температуры при

0,2

j

- текущий номер подгруппы;

- квадрат расстояния MEWMA от среднего в стабильном состоянии

Рисунок B.3 - Контрольная карта MEWMA для скорости и температуры при

0,3

Приложение C

(справочное)

Оценка

и

C.1 Оценка

и

(

n

>1)

На практике обычно необходимо оценить

и

на основе анализа предварительных подгрупп объема

n

, отобранных в условиях, когда предполагается, что процесс находился в стабильном состоянии. В данном приложении

-

k

-е наблюдение в

j

-й подгруппе по

i

-й характеристике,

k

=1, 2, ...,

n

;

j

=1, 2, ...

m

;

i

= 1, 2, ...,

d

.

Предположим, что имеется m таких подгрупп, средние и дисперсии вычисляют следующим образом для каждой подгруппы:

, (C.1)

. (C.2)

Ковариация между a-й и b-й характеристиками в j-й подгруппе имеет вид:

,

. (C.3)

,

и

затем усредняют по всем

m

подгруппам и определяют:

, (C.4)

, (C.5)

,

. (C.6)

является

i

-м элементом вектора выборочных средних

, а выборочная дисперсионно-ковариационная матрица

представляет собой матрицу

d

d

, сформированную следующим образом:

. (C.7)

Вектор выборочного среднего

и выборочная дисперсионно-ковариационная матрица

при

n

>1 являются несмещенными оценками

и

, когда процесс находится в стабильном состоянии.

C.2 Оценка

и

(

n

=1)

Предположим, имеется случайная выборка из многомерного нормального распределения:

,

, ...,

,

где

j

-й вектор наблюдения

содержит

d

переменных

,

, ...,

. Тогда вектор выборочного среднего имеет вид:

, (C.8)

а выборочная дисперсионно-ковариационная матрица [8] имеет вид:

. (C.9)

То есть выборочную дисперсию на главной диагонали матрицы S и выборочные ковариации вычисляют следующим образом:

, (C.10)

,

. (C.11)

Вектор выборочного среднего

и выборочная дисперсионно-ковариационная матрица S при

n

=1 являются несмещенными оценками

и

, когда процесс находится в стабильном состоянии.

Приложение ДА

(справочное)

Сведения о соответствии ссылочных международных стандартов национальным стандартам

Таблица ДА.1

Библиография