ГОСТ Р ИСО 7870-4-2013
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
КОНТРОЛЬНЫЕ КАРТЫ
Часть 4
Карты кумулятивных сумм
Statistical methods. Control charts. Part 4. Cumulative sum charts
ОКС 03.120.30
Дата введения 2014-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 декабря 2013 г. N 2334-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 7870-4:2011* "Контрольные карты. Часть 4. Карты кумулятивных сумм" (ISO 7870-4:2011 "Control charts - Part 4: Cumulative sum charts", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ Р 50779.45-2002
6 ПЕРЕИЗДАНИЕ. Март 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
Введение
В настоящем стандарте рассмотрен универсальный и полезный, но очень простой и достаточно мощный графический метод интерпретации данных, расположенных в любой установленной последовательности. Эти данные могут отражать общие экономические показатели, такие как прибыль, издержки, данные выполнения конкретной технологической операции, параметры процесса и характеристики продукции. Данные могут представлять собой последовательные, количественные данные, измеряемые в соответствии с непрерывной шкалой (например, 24,60, 31,21, 18,97...), неколичественные данные вида "да"/"нет", "хорошо"/"плохо", "успех", "отказ" или статистику (например, среднее, размах, количество событий).
Метод называется методом кумулятивных сумм или "cusum-методом". Это вызвано тем, что метод предусматривает вычитание из полученных данных заданного значения, например целевого, предпочтительного или опорного значения, и их суммирование с накоплением. График таких сумм называется cusum-картой. Такой простой арифметический процесс обеспечивает хорошую визуальную интерпретацию данных.
Сusum-метод используют игроки в гольф во всем мире, прибавляя 4 при выигрыше и вычитая 2 при проигрыше к своему счету и накапливая полученные баллы. Это - cusum-метод в действии. Однако метод еще недостаточно известен и, следовательно, недостаточно широко применяется в бизнесе, промышленности, торговле и т.п.
Настоящий стандарт направлен на обеспечение широкого применения этого метода. Преимущество данного метода перед широко известными картами Шухарта состоит в том, что cusum-метод позволяет обнаружить изменения приблизительно в три раза быстрее, чем карты Шухарта.
Сusum-карты могут быть использованы как дополнение к картам Шухарта и EWMA-картам (картам экспоненциально взвешенного скользящего среднего). Каждая точка на карте EWMA включает информацию обо всех предыдущих подгруппах или наблюдениях, при этом веса предыдущих наблюдений убывают по экспоненте. Аналогично cusum-карте, EWMA-карта может быть усовершенствована и стать более чувствительной для обнаружения изменений процесса.
1 Область применения
В настоящем стандарте установлены статистические процедуры определения кумулятивной суммы (cusum) для процесса и контроля качества с использованием количественных данных. В стандарте установлены общие методы принятия решений, использующие кумулятивную сумму (cusum) для мониторинга, контроля, управления и ретроспективного анализа.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах)
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
3 Термины и определения, сокращения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, а также следующие термины с соответствующими определениями:
3.1.1 целевое значение (target value );
: Значение, от которого должно быть обнаружено отклонение среднего уровня процесса.
Примечание 1 - При использовании cusum-карты отклонения от целевого значения суммируют.
Примечание 2 - При использовании V-маски целевое значение часто является опорным значением или номинальным значением. Необходимо подчеркнуть, что целевое значение не обязательно является самым желательным или предпочтительным значением. Это лишь удобное значение для разработки cusum-карты.
3.1.2 начальное значение (datum value): Значение (для cusum-таблиц), по отношению к которому вычисляют разности.
Примечание - Верхнее начальное значение равно ![]() для мониторинга смещения вверх. Нижнее начальное значение равно
для мониторинга смещения вверх. Нижнее начальное значение равно ![]() для мониторинга смещения вниз.
для мониторинга смещения вниз.
3.1.3 опорный сдвиг (для cusum-таблиц) (reference shift); ,
: Разность между целевым значением (3.1.1) и начальным значением (3.1.2).
Примечание - Необходимо различать , относящийся к стандартизованному опорному сдвигу, и
, относящийся к наблюдаемому опорному сдвигу
![]() .
.
3.1.4 опорный сдвиг (для V-маски) (reference shift); ,
: Угловой коэффициент линии маски (тангенс угла наклона линии маски).
Примечание - Необходимо различать , относящийся к стандартизованному опорному сдвигу, и
, относящийся к наблюдаемому опорному сдвигу,
![]() .
.
3.1.5 интервал решений (для cusum-таблиц ,
) (decision interval);
,
: Совокупная сумма отклонений от начального значения (3.1.2), приводящая к появлению сигнала.
Примечание - Необходимо различать , относящийся к стандартизованному интервалу решений, и
, относящийся к наблюдаемому интервалу решений,
![]() .
.
3.1.6 интервал решения (для усеченной V-маски ,
) (decision interval);
,
: Полувысота в точке отсчета маски.
Примечание - Необходимо различать , относящийся к стандартизованному интервалу решений и
относящийся к наблюдаемому интервалу решения,
![]() .
.
3.1.7 средняя длина серии (average run length); : Среднее количество выборок, отобранных до точки появления сигнала.
Примечание - Среднюю длину серии () обычно связывают с определенным уровнем процесса. При этом
означает среднюю длину серии процесса на целевом уровне, т.е. с нулевым сдвигом.
3.2 Сокращения
ARL - средняя длина серии;
CS1 - cusum-схема с большой ARL при нулевом сдвиге;
CS2 - cusum-схема с меньшей ARL при нулевом сдвиге;
DI - интервал решений;
EWMA - экспоненциально взвешенное скользящее среднее;
FIR - быстрая начальная реакция;
LCL - нижняя контрольная граница;
RV - опорное значение;
UCL - верхняя контрольная граница.
3.3 Обозначения
- коэффициент масштаба; | |
- значение кумулятивной суммы; | |
- разность cusum-значений в ведущей точке и неконтролируемой точке; | |
- коэффициент для определения оценки стандартного отклонения в пределах подгруппы; | |
- изменение, которое должно быть обнаружено; | |
- стандартизованное количество изменений, которые должны быть обнаружены; | |
- ведущее расстояние; | |
- коэффициент для определения оценки стандартного отклонения в пределах подгруппы; | |
- наблюдаемый опорный сдвиг; | |
- стандартизованный опорный сдвиг; | |
- наблюдаемый интервал решений | |
- стандартизованный интервал решений; | |
- индекс; | |
- размер корректировки процесса; | |
- начальное значение cusum для дискретных данных; | |
- количество подгрупп; | |
- средняя длина серии при нулевом сдвиге; | |
- средняя длина серии при сдвиге | |
- среднее (математическое ожидание) совокупности; | |
- среднее биномиальной величины; | |
- объем подгруппы; | |
- вероятность "успеха"; | |
- средний размах подгруппы; | |
- количество точек на графике между ведущей точкой и неконтролируемой точкой; | |
- стандартное отклонение процесса; | |
- стандартное отклонение в пределах подгруппы; | |
- оценка стандартного отклонения в пределах подгруппы; | |
- стандартная ошибка; | |
- выборочное стандартное отклонение в пределах подгруппы; | |
- среднее арифметическое стандартных отклонений подгрупп; | |
- стандартная ошибка среднего по | |
- целевое значение; | |
- опорная или целевая интенсивность событий; | |
- опорная или целевая пропорция; | |
- истинная точка изменения; | |
- наблюдаемая точка изменения; | |
- среднее напряжение; | |
- оценка среднего напряжения; | |
- разность между выборочными средними последовательных подгрупп; | |
- результат наблюдений; | |
- выборочное среднее (подгруппы); | |
- среднее арифметическое выборочных средних подгрупп. |
4 Основные функции cusum-карт
Кумулятивная сумма представляет собой сумму отклонений от некоторого установленного опорного значения. Среднее любой группы последовательных значений может быть представлено визуально с помощью угла наклона графика данных. Основные особенности cusum-карты следующие.
a) Cusum-карта чувствительна к обнаружению изменений среднего.
b) Любые изменения среднего и степень этих изменений на карте визуально проявляются изменениями угла наклона графика данных:
1) горизонтальный график указывает на соответствие среднего процесса целевому или опорному значению;
2) наклон графика вниз указывает на то, что среднее процесса меньше опорного или целевого значения (чем больше угол наклона, тем больше разность);
3) наклон графика данных вверх указывает на то, что среднее процесса больше опорного или целевого значения (чем больше угол наклона, тем больше разность).
c) Cusum-карта может быть использована ретроспективно для исследовательских целей и прогнозирования состояния процесса в ближайшем будущем.
В соответствии с перечислением b) cusum-карта может указать точки произошедших изменений. Это точки изменения градиента cusum-графика. Сusum-карта обладает огромным преимуществом для управления процессами. Она позволяет быстро и точно определить момент изменений процесса, когда необходимы корректирующие действия.
Полезная функция cusum-карты состоит в том, что она может быть обработана без графического изображения, т.е. в табличной форме. Это очень полезно при контроле процесса, когда количество параметров процесса и характеристик продукции велико. Данные о состоянии процесса могут быть получены автоматически и загружены в соответствующее программное обеспечение для автоматического cusum-анализа. Менеджер процесса может быть предупрежден об изменениях по многим характеристикам одновременно. Пример метода приведен в приложении B.
5 Основные этапы построения cusum-карты. Графическое представление
При построении cusum-карты для отдельных значений необходимо выполнить следующие действия.
Этап 1. Выбирают опорное, целевое, контрольное или предпочтенное значение. Среднее арифметическое последних результатов обычно обеспечивает карте хорошую дискриминацию.
Этап 2. Заносят в таблицу результаты в значимой последовательности (например, хронологической). Вычитают опорное значение из каждого результата.
Этап 3. Последовательно суммируют значения, полученные на этапе 2. Последовательные суммы изображают на cusum-карте.
Этап 4. Для большей наглядности устанавливают масштаб по горизонтальной оси не более 2,5 мм между точками.
Этап 5. Для разумной дискриминации, без излишней чувствительности, рекомендуется:
а) выбрать удобный интервал между точками на горизонтальной оси и выбрать интервал на вертикальной оси, равный 2 (или 2
для cusum-карты среднего), округляя в соответствии с правилами;
б) если необходимо обнаружить известное изменение, скажем , выбрать вертикальный масштаб так, чтобы отношение единицы масштаба по вертикальной оси к единице масштаба по горизонтальной оси составляло от
до 2
с округлением в соответствии с правилами.
Примечание - Выбор масштаба очень важен, так как неудачный масштаб может создать ошибочное впечатление о состоянии процесса. Масштаб, выбранный в соответствии с перечислениями а) и b), показывает обоснованные изменения и не является ни слишком чувствительным, ни слишком инертным.
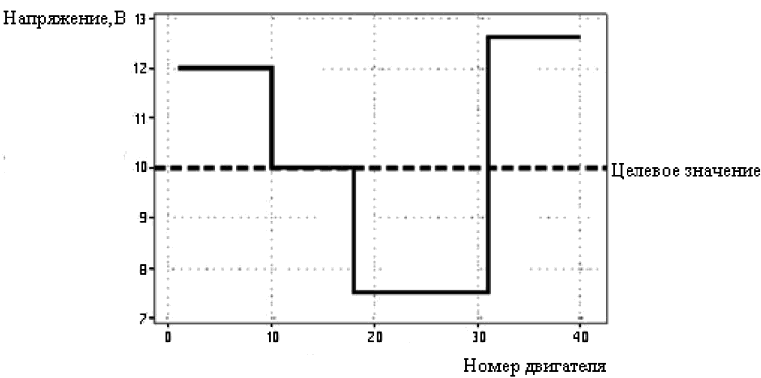
6 Пример cusum-графика. Напряжение на двигателе
6.1 Процесс
Получен набор из 40 значений контролируемой характеристики в хронологической последовательности. Контролируемой характеристикой является напряжение на электродвигателях мощностью не более одной лошадиной силы на ранней стадии производства. Измерения выполнены в непрерывном масштабе на двигателях в последовательности их изготовления. Результаты измерений:
9, 16, 11, 12, 16, 7, 13, 12, 13, 11, 12, 8, 8, 11, 14, 8, 6, 14, 4, 13, 3, 9, 7, 14, 2, 6, 4, 12, 8, 8, 12, 6, 14, 13, 12, 14, 13, 10, 13, 13.
Опорное или целевое значение напряжения составляет 10 В.
6.2 Простой график результатов
Для лучшего понимания основных свойств процесса с помощью стандартного подхода необходимо графически представить эти значения в естественном порядке [см. рисунок 1 а)].
На графике заметно общее уменьшение среднего в средней части от более высокого начального уровня с такими же значениями в конце. Рисунок 1 а) не позволяет четко уловить тенденции изменения контролируемой характеристики вследствие высокой изменчивости данных.
6.3 Стандартная контрольная карта индивидуальных значений
Затем составляют стандартную контрольную карту индивидуальных значений [см. рисунок 1 b)].
Рисунок 1 b) не добавляет ясности. Он даже вводит в заблуждение. Стандартные критерии статистического управления процессом для проверки стабильности и управляемости процесса включают следующее:
a) отсутствие точек выше верхней (UCL) или нижней (LCL) контрольных границ;
b) отсутствие семи или более последовательных точек монотонно убывающих или возрастающих значений cusum;
c) отсутствие семи точек выше или ниже центральной линии процесса.
В рассматриваемом примере все перечисленные критерии выполняются, следовательно, можно сделать вывод, что данный процесс является устойчивым вокруг его среднего уровня 10 В, который является целевым значением. Дальнейший стандартный анализ показал, что, несмотря на стабильность, процесс не удовлетворяет установленным требованиям. Сам по себе анализ не дает объяснения причин несоответствия требованиям.
Причина неспособности стандартной контрольной карты индивидуальных значений выявлять причины изменчивости процесса состоит в том, что контрольные границы основаны на фактическом состоянии процесса, а не на установленных требованиях. Следовательно, если процессу присуща высокая изменчивость, контрольные границы являются достаточно широкими. Необходим метод, который лучше выявляет тенденции изменений процесса и позволяет определить и удалить их основные причины.
Примечание - Использование дополнительно контрольных карт скользящего размаха позволяет исследовать другие проблемы изменчивости.
6.4 Cusum-карта. Общий обзор
Затем данные представляют на cusum-карте. На рисунке 1 с) представлена cusum-карта для рассмотренных выше данных.
|
а) График значений напряжения на электродвигателях
|
b) Стандартная контрольная карта индивидуальных значений
|
с) Cusum-карта
Рисунок 1 - Пример. Напряжение на электродвигателе
Предыдущие карты не дают ответа на вопрос, где произошли существенные изменения уровня процесса. График cusum-карты позволяет определить эту область. Визуальный анализ указывает на четыре изменения уровня процесса в точках 10-го, 18-го и 31-го двигателей.
В разделе 4 установлено, что наклон графика вверх/вниз указывает на значение уровня процесса выше/ниже предпочтительного значения, а горизонтальная линия указывает, что уровень процесса соответствует предпочтительному значению. Следовательно, процесс находится на уровне целевого значения только в течение короткого периода времени между 11-м и 18-м двигателями. У двигателей с 1-го по 10-й и с 33-го до конца наблюдается повышение уровня процесса. У двигателей с 19-го по 32-й - понижение уровня процесса.
Эти изменения рассмотрены и интерпретированы в 6.6.
В реальной ситуации на следующем этапе необходимо определить, что произошло в этих точках процесса и вызвало такие изменения напряжения. Это заставляет поставить некоторые вопросы для улучшения стабильности процесса на уровне 10 В. Например, чем сборка двигателя 32 отличается от сборки двигателя 33? Или что произошло с испытательным оборудованием в этой точке? Это соответствует сдвигу уровня процесса или изменениям в партии? И так далее. Используемая таким образом cusum-карта обеспечивает диагностику состояния процесса и позволяет определять возможности его улучшения.
6.5 Построение cusum-карты
Построение cusum-карты индивидуальных значений, как в рассматриваемом примере, основано на выполнении этапов, установленных в разделе 5.
Этап 1. Выбирают опорное значение RV. В примере предпочтительное и опорное значения равны 10 В.
Этап 2. Заносят в таблицу результаты измерений напряжения в последовательности изготовления напротив номера двигателя в таблице 1 (столбцы 2 и 6). Вычитают значение 10 (опорное значение) из каждого результата измерений (см. таблицу 1, столбцы 3 и 7).
Этап 3. Последовательно суммируют значения из таблицы 1 (столбцы 3 и 7) и сумму указывают в столбцах 4 и 8. Изображают в виде графика данные столбцов 4 и 8 в соответствии с номером двигателя [см. рисунок 1 c)], учитывая рекомендации относительно масштаба на этапах 4 и 5 раздела 5.
Таблица 1 - Табличное представление вычислений для cusum-карты на основе последовательности измерений напряжения
Номер двигателя | Напря- | Напряжение минус 10В | Cusum- | Номер двигателя | Напря- | Напряжение минус 10 В | Cusum- |
1 | 9 | -1 | -1 | 21 | 3 | -7 | +11 |
2 | 16 | +6 | +5 | 22 | 9 | -1 | +10 |
3 | 11 | +1 | +6 | 23 | 7 | -3 | +7 |
4 | 12 | +2 | +8 | 24 | 14 | +4 | +11 |
5 | 16 | +6 | +14 | 25 | 2 | -8 | +3 |
6 | 7 | -3 | +11 | 26 | 6 | -4 | -1 |
7 | 13 | +3 | +14 | 27 | 4 | -6 | -7 |
8 | 12 | +2 | +16 | 28 | 12 | +2 | -5 |
9 | 13 | +3 | +19 | 29 | 8 | -2 | -7 |
10 | 11 | +1 | +20 | 30 | 8 | -2 | -9 |
11 | 12 | +2 | +22 | 31 | 12 | +2 | -7 |
12 | 8 | -2 | +20 | 32 | 6 | -4 | -11 |
13 | 8 | -2 | +18 | 33 | 14 | +4 | -7 |
14 | 11 | +1 | +19 | 34 | 13 | +3 | -11 |
15 | 14 | +4 | +23 | 35 | 12 | +2 | -7 |
16 | 8 | -2 | +21 | 36 | 14 | +4 | -4 |
17 | 6 | -4 | +17 | 37 | 13 | +3 | -2 |
18 | 14 | +4 | +21 | 38 | 10 | 0 | +2 |
19 | 4 | -6 | +15 | 39 | 13 | +3 | +5 |
20 | 13 | +3 | +18 | 40 | 13 | +3 | +5 |
6.6 Интерпретация cusum-карты
6.6.1 Введение
При использовании cusum-карты для ретроспективного анализа, как в рассматриваемом примере, обычно лучше не сосредотачиваться на отдельных точках графика, а провести минимальное количество прямых линий, которые являются линиями наилучшего визуального приближения представленных данных [см. рисунок 1 c)].
Не следует интерпретировать наклон этих прямых и их расположение относительно вертикальной оси. Необходимо отметить, что вертикальная ось не представляет фактические данные напряжения.
Прямая линия с наклоном вверх/вниз не указывает, как раньше, на увеличение/уменьшение уровня процесса, а лишь означает, что он постоянен и его значение больше/меньше опорного значения. Чем более крутой наклон прямой, тем больше разность с опорным значением. Горизонтальная линия указывает на то, что уровень процесса является постоянным и равен опорному значению. Интерпретация cusum-карты для двигателей более подробно рассмотрена ниже.
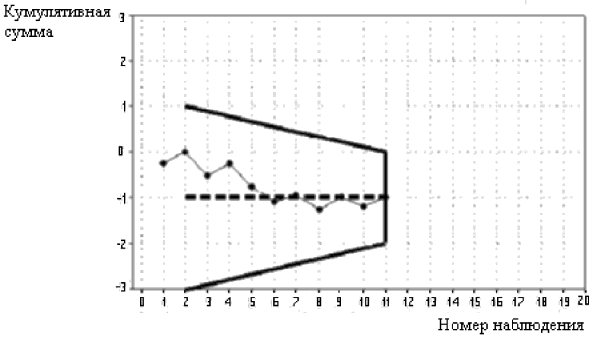
6.6.2 Основы интерпретации cusum-карты, используя "воображаемые данные без помех"
Пусть последовательность первых 18 измерений напряжения на двигателе имеет вид: 10, 10, 10, 13, 13, 13, 10, 10, 10, 9, 9, 9, 10, 10, 10, 8, 8, 8 (см. таблицу 2, столбец 2), а опорное значение равно 10 В.
Таблица 2 - Воображаемые данные измерений напряжения на электродвигателях для иллюстрации интерпретации cusum-карты
Номер двигателя | Напряжение | Напряжение - 10 В | Cusum-карта |
(1) | (2) | (3) | (4) |
1 | 10 | 0 | 0 |
2 | 10 | 0 | 0 |
3 | 10 | 0 | 0 |
4 | 13 | +3 | +3 |
5 | 13 | +3 | +6 |
6 | 13 | +3 | +9 |
7 | 10 | 0 | +9 |
8 | 10 | 0 | +9 |
9 | 10 | 0 | +9 |
10 | 9 | -1 | +8 |
11 | 9 | -1 | +7 |
12 | 9 | -1 | +6 |
13 | 10 | 0 | +6 |
14 | 10 | 0 | +6 |
15 | 10 | 0 | +6 |
16 | 8 | -2 | +4 |
17 | 8 | -2 | +2 |
18 | 8 | -2 | 0 |
Полученная cusum-карта представлена на рисунке 2.
|
Рисунок 2 - Cusum-карта для воображаемых данных
Из сопоставления данных таблицы 2 (столбец 2) и cusum-карты (см. рисунок 2) можно заметить, что:
a) двигатели 1-3, 7-9 и 13-15 все соответствуют опорному значению 10 В и лежат на горизонтальных отрезках прямой на cusum-карте. Положение этих горизонтальных отрезков относительно вертикальной оси не связано с реально измеряемыми значениями, а лишь с предыдущими значениями;
b) двигателям 4-6 соответствуют значения выше опорного, а именно 13 В, эти точки расположены на отрезке возрастающей прямой на cusum-карте. Здесь нет изменчивости данных. При отсутствии помех для вычисления среднего арифметического для конкретного отрезка на графике следует использовать следующую формулу:
![]() .
.![]() ;
;
c) аналогично для двигателей 9-12
![]() ;
;
d) для двигателей 16-18
![]() .
.
Таким образом, различные углы наклона графика на cusum-карте указывают, что:
- у двигателей 1-3, 7-9 и 13-15 напряжение оставалось постоянным на уровне 10 В;
- у двигателей 4-6 напряжение также оставалось постоянным, но на уровне 13 В;
- у двигателей 9-12 напряжение оставалось постоянным на уровне 9 В;
- у двигателей 16-18 напряжение оставалось постоянным на уровне 8 В.
Для данных "без помех" выводы очевидны. Для реальных данных таблицы 1 (столбцы 2 и 6) выводы не столь очевидны.
6.6.3 Интерпретация для реальных данных
Cusum-карта, представленная на рисунке 1 с), показывает, что:
a) выборочное среднее результата измерений двигателей 1-10 больше опорного значения и равно:

![]() В;
В;
b) для двигателей 11-18 выборочное среднее равно 10 В, поскольку соответствующие точки находятся на горизонтальном отрезке прямой;
c) для двигателей 19-31
![]() В.
В.
d) для двигателей 32-40
![]() В.
В.
Таким образом, cusum-карта позволяет вычислить скользящие средние для периодов изменчивости процесса. Это является существенным улучшением по сравнению с негибким подходом карты скользящего среднего. Общие результаты приведены в таблице 3.
Таблица 3 - Средние напряжения для двигателей в периоды сохранения или изменения уровня процесса
Номер двигателя | Среднее напряжение |
1-10 | 12,0 |
11-18 | 10,0 |
19-31 | 7,5 |
32-40 | 12,6 |
В качестве альтернативы этому методу можно просто вычислить локальные средние для каждого отрезка cusum-карты.
Например, для двигателей 1-10
![]() .
.
Результаты таких вычислений могут иногда давать несколько отличающиеся результаты по сравнению с предыдущим методом. Это вызвано сглаживанием данных при проведении прямой линии через отдельные точки.
6.7 Манхэттенская схема
После проведения исследований часто бывает удобно построить еще одну схему, обеспечивающую более простое представление данных в форме "без помех". Это представление под влиянием прямоугольных очертаний Манхэттена получило наименование манхэттенской схемы.
Это представление данных, приведенных в 6.6.3 а), b), с) и d) в виде установленного графика напряжений на двигателях в соответствии с последовательностью их изготовления. Схема представлена на рисунке 3 для сравнения с кумулятивными суммами исходными данными, представленными на рисунках 1 с) и 1 а).
Рисунки 3, 1 с) и 1 а) объединяют функции и значение cusum-метода в режиме ретроспективного анализа функционирования процесса. Рисунки показывают простой метод визуального представления данных без использования специальных математических символов и статистических выражений.
|
Рисунок 3 - Манхэттенская схема для данных напряжений на электродвигателях
Простота и однозначность манхэттенской схемы обеспечивают понимание и возможность получения технических выводов. Cusum-карту можно рассматривать как промежуточный этап и представление данных для составления манхэттенской схемы.
7 Принципы принятия решений на основе cusum-карты
7.1 Правила принятия решения
Правила принятия решений необходимы для интерпретации cusum-карты. Если правила принятия решений установлены в зависимости от свойств процесса, то на основе cusum-карты могут быть предприняты необходимые действия. Обычно эти действия включают:
a) для управления процессом: корректировки условий функционирования процесса;
b) для улучшения: исследование первопричин изменчивости;
c) для прогнозирования: анализ и, при необходимости, корректировки модели прогнозирования или ее параметров.
7.2 Основы принятия решений
Необходимо установить основные критерии принятия решений.
Для обеспечения эффективных основ обнаружения сигнала об изменении состояния процесса необходимо установление количественных характеристик "шума" в системе. Что представляют собой шум и сигнал, определяет принятая стратегия контроля, которая устанавливает необходимое количество наблюдений, частоту отбора и способ составления выборки или подгруппы. Следует учитывать, что мера, используемая для количественной оценки изменчивости процесса, как правило, влияет на результат.
Собственную изменчивость обычно измеряют c помощью одной из следующих статистик.
а) Стандартное отклонение: если для построения cusum-карты использованы отдельные наблюдения.
Отдельные наблюдения для вычисления стандартного отклонения процесса обычно отбирают от гомогенного сегмента данных. Это требование является достаточно жестким. Изменчивость больше собственной изменчивости процесса рассматривают как результат действия специальных причин, что указывает на сдвиг среднего серии данных или изменение собственной изменчивости или того и другого.
b) Стандартная ошибка: если некоторая функция подгруппы наблюдений, такая как среднее, медиана или размах позволяет построить cusum-карту.
Понятие подгруппы основано на том, что изменчивость в пределах подгруппы является результатом воздействия общих, а между подгруппами - специальных причин. Основной ролью cusum-карты является выявление общих и особых причин изменчивости. Следовательно, правильный выбор подгруппы имеет огромное значение. Например, составление подгруппы путем отбора четырех последовательно изготовленных единиц продукции производственного процесса каждый час, в противоположность отбору одной единицы продукции через каждые четверть часа, может дать совершенно разные оценки изменчивости. Стандартная ошибка в первом случае меньше, чем во втором. Одна cusum-карта характеризует изменчивость последовательных единиц продукции, а другая изменчивость - через 15 минут. Выбор соответствующей меры изменчивости зависит от того, о какой изменчивости должна сигнализировать карта.
Однако требование наличия стабильности процесса в течение периода, достаточного для установления количественных показателей изменчивости, таких как стандартное отклонение или стандартная ошибка, является слишком жестким для некоторых областей применения cusum-метода.
Например, наблюдения непрерывного процесса могут показать незначительные отклонения среднего уровня. Требуется, чтобы именно по этим отклонениям были приняты решения о систематической или постоянной изменчивости. Иллюстрации:
a) процессом управляет термостат или другое устройство автоматического управления;
b) качество исходного сырья может подвергаться незначительным изменениям, не нарушая установленных требований;
c) при мониторинге отзывов о лечении пациента могут быть выявлены незначительные изменения обмена веществ, связанные с пищей, пребыванием в больнице или домашними делами и т.д., но по всем последствиям лечения должны быть приняты решения об общей изменчивости.
С другой стороны, выборка может включать продукцию или наблюдения из нескольких источников (административных областей, заводов, машин и операторов). Также может присутствовать слишком большая локальная изменчивость, что не позволит принять адекватные решения о смещении общего среднего. Поэтому данные, полученные из нескольких источников, следует обрабатывать осторожно, поскольку все особенности отдельных источников данных могут быть пропущены. Кроме того, изменчивость между источниками данных может быть замаскирована изменениями, происходящими во всей системе во времени.
Одним из важных предположений в cusum-процедуре является то, что стандартное отклонения процесса предполагается постоянным. Поэтому прежде чем применять cusum-процедуру, процесс должен быть исследован на наличие статистической управляемости (с помощью
-карты,
-карты или карты скользящих размахов), а затем определяют оценку
.
Может также проявиться последовательная корреляция между наблюдениями, когда одно наблюдение оказывает влияние на следующее. Иллюстрацией отрицательной последовательной корреляции являются последовательные значения массы использованного сыпучего материала, когда нивелируются ошибки предыдущего и последующего исследований. Другим примером является ситуация, когда недостаточный или избыточный заказ в одном месяце компенсируется заказом в следующем месяце. Появление положительной корреляции возможно в некоторых производственных процессах, когда одна партия материала частично смешивается с предыдущей и последующей партиями.
Аналогичное явление можно наблюдать в финансовых отчетах, когда отдельные показатели переходят в следующий отчетный период.
В силу сказанного необходимо рассмотреть другие количественные меры изменчивости в серии или последовательностях данных и условия, в которых эти меры являются адекватными.
Такие меры изменчивости, на которых основано принятие решений с использованием cusum-карт, приведены в приложении А. Кроме того, там даны рекомендации относительно их выбора в зависимости от ситуации.
7.3 Эффективность правил принятия решения
7.3.1 Основные понятия
Идеальное выполнение правила принятия решения состоит в том, чтобы реальные изменения не менее чем на заданную величину были обнаружены, а процесс без таких изменений мог работать неопределенно долго без ложных сигналов. В действительности это не достижимо. Простой и удобной мерой эффективности правила принятия решений является средняя длина серии (ARL).
ARL представляет собой математическое ожидание количества выборок, необходимого для принятия решений о наличии изменений.
Если реальные изменения отсутствуют, идеальное значение ARL равно бесконечности. Практическая цель в такой ситуации состоит в том, чтобы сделать ARL большим. Наоборот, при наличии реального изменения идеальное значение ARL равно 1, когда изменение обнаружено при отборе следующей выборки. Выбор ARL - компромисс между этими двумя требованиями. Принятие ошибочного решения действовать, когда процесс не изменился, приводит к "сверхуправлению" и еще большему увеличению изменчивости. Принятие соответствующих мер, когда процесс изменился, способствует обеспечению стабильности процесса. В действительности это тоже увеличивает изменчивость процесса и приводит к увеличению стоимости производства.
Значение ARL также подвержено изменчивости. Иногда ложный сигнал может быть получен после большой серии данных или изменение обнаружено очень быстро. В некоторых случаях неудачный отбор выборок может вызвать появление ложных сигналов или так замаскировать реальное изменение, что оно не приведет к появлению сигнала. Время от времени фактическую изменчивость ARL необходимо исследовать. Обычно ARL рассматривают как меру эффективности правила принятия решений.
Истинное состояние процесса | Требуемый cusum | Идеальное значение ARL |
Уровень процесса равен целевому значению или близок | Значение ARL достаточно велико | Бесконечность |
Существенное отклонение уровня процесса от целевого значения | Значение ARL мало (быстрое обнаружение изменений) | 1 |
7.3.2 Пример вычисления ARL
Понятие ARL не определено по отношению к cusum. На рисунке 4 показана стандартная контрольная карта Шухарта с контрольными границами на уровне ±3 стандартных отклонения от центральной линии для нормального распределения.
Это распределение называют "нормированным", поскольку у него нулевое среднее и стандартное отклонение, равное единице.
В соответствии с рисунком 4 приблизительно 0,135% наблюдений в среднем попадают вне каждой из границ, если среднее процесса находится на центральной линии или на целевом значении. На основе этого можно легко подсчитать ARL: 1/0,00135=741. Другими словами, в среднем выше верхней контрольной границы попадает одно из 741 наблюдения. Это частота ошибки сигнала об изменении уровня процесса, когда фактически это не произошло.
|
Рисунок 4 - График плотности нормированного нормального распределения
Следовательно, для практических целей необходимо разработать систему контроля, обеспечивающую высокое значение ARL, когда уровень процесса совпадает с целевым значением.
Если заданы две границы и среднее процесса совпадает с целевым значением, ARL делят на два, т.е. он равен 1/(0,00135+0,00135)=370.
Если среднее процесса смещено на стандартное отклонение к верхней контрольной границе, то в среднем 2,28% наблюдений будут находиться выше верхней контрольной границы. Тогда ARL по отношению к UCL становится 1/0,0228=44 для этой односторонней границы. Другими словами, в среднем потребуется приблизительно 44 интервала наблюдения, чтобы выявить сдвиг среднего на одно стандартное отклонение.
При наличии двух границ ожидается, что ниже LCL будет находиться только 0,0032% наблюдений, поскольку значение, равное среднему процесса минус четыре стандартных отклонения, находится достаточно далеко от LCL. Так как 1/(0,000032+0,0228) существенно не влияет на значение ARL, вычисленное для единственной контрольной границы и сдвига среднего процесса на одно стандартное отклонение, ARL в случае двух контрольных границ приблизительно такое же, как и в случае одной контрольной границы, а именно 44.
Суммирование:
Среднее процесса равно целевому значению | В случае двух контрольных границ значение ARL равно половине ARL для одной контрольной границы |
Сдвиг среднего вверх | В случае двух контрольных границ значение ARL равно ARL для одной контрольной границы |
На практике часто применяют дополнительно предупреждающие границы выше и ниже среднего процесса, которые защищают от слишком быстрого обнаружения сдвига среднего процесса, за счет увеличения количества ложных сигналов, когда среднее процесса равно целевому значению. Карта Шухарта очень привлекательна и популярна из-за ее простоты и эффективности обнаружения отдельных специальных причин, вызывающих большие сдвиги среднего процесса.
Однако общеизвестно, что контрольная карта Шухарта дает мало сигналов при небольших сдвигах среднего, даже если они сохраняются. Это указывает на другой метод более быстрого обнаружения сдвига среднего при высоких значениях ARL, когда среднее процесса находится рядом с целевым значением. Для этого хорошо подходит cusum-метод.
8 Типы решений по cusum-карте
8.1 Формы V-масок
Самые простые правила решения на основе cusum-карты представлены формами V-масок. Существуют различные формы V-масок. Они идентичны по принципу построения и одинаково эффективны:
a) усеченная V-маска;
b) полупараболическая маска;
c) укороченная V-маска;
d) полная V-маска.
8.2 Усеченная V-маска
8.2.1 Конфигурация и размеры
Усеченная V-маска общего назначения показана на рисунке 5. Она содержит точку начала отсчета, обозначенную О. Два вертикальных отрезка ОВ и ОС длиной 5 каждый расположены по обе стороны от точки начала отсчета (т.е.
![]() ). Эти два отрезка называют интервалами решений. Два наклонных отрезка ВА и CD, называемые разрешающими линиями, охватывают cusum-график. Размер ЕО равен десяти интервалам наблюдений, а вертикальные отрезки ЕА и ED равны 10
). Эти два отрезка называют интервалами решений. Два наклонных отрезка ВА и CD, называемые разрешающими линиями, охватывают cusum-график. Размер ЕО равен десяти интервалам наблюдений, а вертикальные отрезки ЕА и ED равны 10 (т.е.
![]() ).
).
*
|
Рисунок* 5 - Форма и размеры усеченной V-маски общего назначения
__________________
* Рисунок соответствует оригиналу. - .
Усеченная V-маска в реальном масштабе показана на рисунке 6 для контролируемой характеристики процесса со стандартным отклонением 0,2. Здесь использовано стандартное отклонение, а не стандартная ошибка, поскольку данная маска разработана для контроля отдельных наблюдений, а не среднего.
|
Рисунок 6 - V-маска в реальном масштабе для характеристики процесса (стандартное отклонение собственной изменчивости 0,2)
8.2.2 Применение усеченной V-маски
Для использования маски на линии начала отсчета, расположенной горизонтально на cusum-карте, указывают точку начала отсчета. В ситуации продолжающегося управления процессом это самая последняя точка.
Если cusum-график находится внутри разрешающих линий маски (или их продления до точек A и D), то существенный сдвиг в среднем на этом графике не выявлен. В этом случае процесс находится в состоянии статистической управляемости относительно целевого значения. Если график изменения cusum выходит за разрешающие линии маски, это указывает на существенное отклонение от целевого значения. В этом случае процесс является неуправляемым.
На рисунке 7 показаны cusum-графики процесса в состоянии статистической управляемости, когда существенные отклонения от целевого значения не выявлены, и двух неконтролируемых процессов, когда имеются существенные увеличение и уменьшение значений контролируемой характеристики. Во всех случаях на рисунке 7 использовано стандартное отклонение. Целевое значение, используемое при построении cusum-карты, равно целевому среднему процесса.
Текущую ситуацию определяют наложением V-маски на cusum-карту по мере накопления данных.
Хотя рисунок 7 a) показывает, что среднее процесса меньше целевого значения, V-маска еще не регистрирует это изменение как существенное отклонение.
По рисунку 7 b) видно, что среднее процесса значительно меньше целевого значения. В то время как существенное отклонение не обнаружено до десятого наблюдения, с визуальной точки зрения среднее процесса имеет тенденцию снижения с первого наблюдения. Отмечая наклон линии наблюдений, можно определить оценку фактического среднего процесса. Это обеспечивает возможность необходимой корректировки для возвращения процесса к его целевому значению и диагностику определения причин в точке наблюдения 1, вызвавших стойкое снижение уровня процесса.
Из рисунка 7 c) видно, что среднее процесса значительно меньше целевого значения. Это отклонение не зарегистрировано как существенное отклонение среднего до наблюдения 14. Можно заметить, что уровень процесса был ниже целевого значения до наблюдения 6, но этого было недостаточно для появления сигнала о неконтролируемости процесса. Затем в точке наблюдения 6 уровень процесса изменился на более высокий по отношению к целевому значению. Измерение наклона cusum-линии до и после наблюдения 6 позволяет корректировать процесс и выявить причины изменений процесса.
При наличии только верхней или только нижней границы допустимых значений применяют односторонний контроль. В этом случае может быть использована полумаска. При контроле сдвига вверх/вниз необходима лишь соответствующая половина маски. Однако все же предпочтительно использовать маску целиком для получения большего количества информации. Все сдвиги в другом направлении могут быть проигнорированы.
|
а) Отсутствие существенных изменений среднего процесса по отношению к целевому значению
Рисунок 7, лист 1 - Примеры использования усеченной V-маски для обнаружения существенного изменения среднего процесса
|
b) Существенное уменьшение среднего процесса по отношению к целевому значению
|
с) Существенное увеличение среднего процесса по отношению к целевому значению
Рисунок 7, лист 2
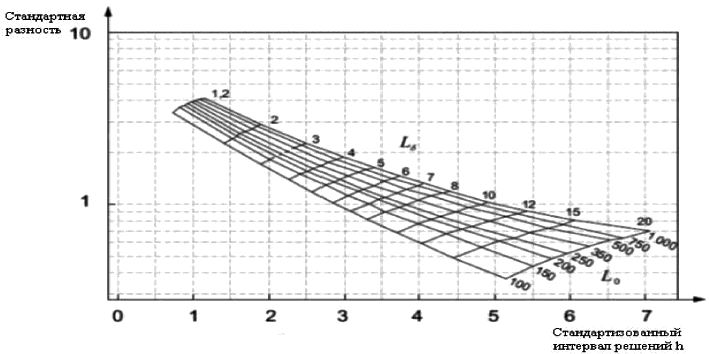
8.2.3 Средняя длина серии
Свойства средней длины серии (ARL) для усеченной V-маски общего назначения, представленной на рисунке 8, приведены в таблице 4 в единицах, кратных стандартному отклонению или стандартной ошибке контролируемой характеристики. Значение ARL приведено для cusum-карты и карт Шухарта с двумя правилами принятия решений.
Правила принятия решений:
- Правило Шухарта 1. Если точка оказывается за границами ±3 стандартных отклонения от центральной линии, а именно за границами действия или контрольными границами, принимают решение о наличии отклонения среднего процесса от целевого значения;
- Правило Шухарта 2. Если последовательные точки оказываются за границами ±2 стандартных отклонения контролируемой переменной от центральной линии, а именно за границами предупреждения, принимают решение об отклонении среднего процесса.
Примечание 1 - Предполагается, что контролируемая переменная подчиняется нормальному распределению со стандартным отклонением .
Примечание 2 - Средняя длина серии соответствует контролю среднего процесса по отношению к одной границе. Если контроль осуществляют относительно двух границ с единственным целевым значением, то ARL для двух границ вдвое больше (количество ложных сигналов удваивается), но для больших отклонений процесса значение ARL в среднем сохраняется.
Примечание 3 - Для стандартной cusum-карты высота интервала решений h и угловой коэффициент разрешающей линии удовлетворяют условиям
=5,0 и
=0,5 (см. рисунок 4). Граница действий карты Шухарта относится только к правилу 1. Границы действия и предупреждения применяют в комбинации правил 1 и 2.
|
Рисунок 8 - Средняя длина серии для обнаружения сдвига среднего процесса от целевого значения для усеченной V-маски общего назначения и стандартных контрольных карт Шухарта
Таблица 4 - Средняя длина серии для обнаружения сдвига среднего процесса от целевого значения для усеченной V-маски общего назначения (см. рисунок 5) и двух видов стандартных контрольных карт Шухарта
Сдвиг среднего | Средняя длина серии | ||
процесса от целевого значения | Стандартная усеченная V-маска | Контрольная карта Шухарта с границами действия | Контрольная карта Шухарта с границами действия и предупреждения |
0,0 | 931,0 | 741,0 | 556,0 |
0,2 | 198,0 | 308,0 | 223,0 |
0,4 | 60,0 | 200,0 | 134,0 |
0,6 | 27,0 | 120,0 | 75,0 |
0,8 | 15,0 | 72,0 | 43,0 |
1,0 | 10,0 | 44,0 | 26,0 |
1,2 | 7,8 | 28,0 | 16,0 |
1,4 | 6,3 | 18,0 | 11,0 |
1,6 | 5,3 | 12,0 | 7,4 |
1,8 | 4,6 | 8,7 | 5,4 |
2,0 | 4,0 | 6,3 | 4,1 |
2,2 | 3,6 | 4,7 | 3,2 |
2,4 | 3,3 | 3,7 | 2,6 |
2,6 | 3,0 | 2,9 | 2,2 |
2,8 | 2,8 | 2,4 | 1,9 |
3,0 | 2,6 | 2,0 | 1,7 |
Значение ARL является индикатором эффективности метода принятия решений:
- чем больше значение ARL для целевого значения, тем ниже вероятность ложных сигналов;
- чем меньше ARL при выявлении отклонения среднего от его целевого значения, тем быстрее обнаруживаются изменения процесса.
В соответствии с рисунком 8 и таблицей 4 можно сделать следующие выводы:
a) Значение (ARL при нулевом сдвиге) для cusum-карты больше, чем для карты Шухарта с пределами действия, однако для карты Шухарта с границами действия и предупреждения значение
существенно меньшее. Таким образом, cusum-карта обладает самым низким уровнем ошибочных сигналов.
b) Для сдвигов среднего процесса менее 2 ARL cusum-карты меньше, чем ARL любых других карт с наиболее быстрой реакцией на сдвиг процесса. Это особенно проявляется в области от 0,4
до 1,4
.
c) Для сдвигов среднего процесса более 2 карта Шухарта с границами действия и предупреждения быстрее реагирует на сдвиг процесса, чем cusum-карта. Для сдвига среднего процесса более 2,4
карта Шухарта с границами действия и предупреждения быстрее реагирует на сдвиг процесса, чем cusum-карта. Однако при этом карты Шухарта обладают более высоким уровнем ошибочных сигналов.
8.2.4 Общие комментарии к ARL
Во-первых, размерности стандартной усеченной V-маски общего назначения разработаны для обнаружения сдвигов процесса в области не более одной стандартной ошибки (1). При контроле других сдвигов используют другие значения
и
. Кроме того, для улучшения свойств ARL и, следовательно, обнаружения сдвига среднего процесса могут быть выбраны V-маски различной конфигурации или формы. Примеры полупараболической V-маски и усеченной V-маски рассмотрены в 8.4 и 8.5 соответственно.
Во-вторых, вместе с контрольной картой Шухарта часто используют дополнительные правила. Эти правила включают "7 последовательных точек с одной стороны от целевого значения" и "7 последовательно возрастающих или убывающих точек". Эти правила существенно уменьшают значение ARL, если среднее процесса совпадает с целевым значением, что значительно увеличивает вероятность ложных сигналов.
В-третьих, большое количество факторов влияет на устойчивость ARL. К ним относятся форма предполагаемой модели изменчивости, значение и независимость наблюдаемых характеристик. Значения ARL, приведенные в таблице 4 и на рисунке 8, основаны на трех предположениях:
a) наблюдения подчиняются нормальному распределению;
b) стандартное отклонение известно точно;
c) последовательные наблюдения статистически независимы.
Нормальное распределение симметрично. Асимметрия с более длинным хвостом в направлении возможного сдвига при одной контрольной границе приводит к уменьшению ARL и имеет слабое влияние на значение ARL при больших сдвигах среднего. Наоборот, при асимметрии с более коротким хвостом в направлении возможного сдвига значение ARL значительно возрастает со слабым влиянием на значение ARL при больших сдвигах среднего.
Стандартное отклонение или стандартную ошибку обычно оценивают по тем же наблюдениям, которые используют для представления на cusum-карте. Ошибки 10% и более весьма распространены в этом случае. Завышенная оценка увеличивает значение ARL, заниженная оценка уменьшает ARL. Это искажение ARL является самым явным для значений среднего процесса, равных целевому значению или близких к нему, и имеет небольшое влияние при больших сдвигах. В таблице 5 показательно искажение ARL для 10%-ой ошибки оценки
.
Таблица 5 - Иллюстрация влияния на ARL неправильной оценки стандартной ошибки
Сдвиг среднего процесса от целевого | Средняя длина серии (ARL) | ||
значения, единицы истинного | Оценка | Корректная оценка | Оценка |
0,0 | 3000,0 | 930,0 | 410,0 |
0,5 | 45,0 | 38,0 | 35,0 |
1,0 | 10,0 | 10,5 | 10,0 |
1,5 | 6,0 | 5,8 | 6,0 |
2,0 | 4,4 | 4,1 | 4,5 |
Положительная автокорреляция приводит к уменьшению значения ARL, а отрицательная - к его увеличению.
Необходимо отметить, что влияние трех упомянутых предположений не характерно только для cusum-карты, оно относится к другим методам построения диаграмм.
8.3 Альтернативные подходы
Альтернативным подходом улучшения показателей контроля для более широкого диапазона сдвигов среднего процесса являются использование полупараболической V-маски (см. 8.4), усеченной V-маски (см. 8.5) или усеченной V-маски с быстрой начальной реакцией (FIR)(см. 8.7).
Данные сопоставления этих масок со стандартной усеченной V-маской приведены в таблице 6.
Таблица 6 - Средняя длина серии (ARL) для различных cusum-масок
Сдвиг среднего от целевого значения (в единицах | Усеченная V-маска ( | Полупараболическая V-маска (см. таблицу 7) | Усеченная V-маска ( | Усеченная V-маска FIR ( |
0,00 | 465,0 | 235,0 | 300,0 | 448,0 |
0,25 | 142,0 | 113,0 | 114,0 | 125,0 |
0,50 | 38,0 | 36,0 | 36,0 | 29,0 |
1,00 | 10,0 | 10,0 | 10,0 | 6,4 |
1,50 | 5,8 | 5,3 | 5,3 | 3,4 |
2,00 | 4,0 | 3,3 | 3,3 | 2,4 |
2,50 | 3,1 | 2,3 | 2,3 | 1,9 |
3,00 | 2,6 | 1,7 | 1,8 | 1,5 |
3,50 | 2,2 | 1,4 | 1,5 | 1,3 |
4,00 | 2,0 | 1,2 | 1,3 | 1,2 |
8.4 Полупараболическая V-маска
Стандартной усеченной V-маске общего назначения соответствуют параметры 5 и
0,5. Могут быть выбраны различные значения
и
усеченной V-маски для обеспечения быстрой реакции на сдвиг среднего определенного размера. В других случаях для некоторых отраслей промышленности, таких как пищевая промышленность, необходимо повышать скорость обнаружения больших сдвигов среднего процесса, что требует изменения типа маски.
Единственным решением является применение полупараболической маски, кривая профиля которой вписана в усеченную V-маску около ее узкого конца (см. рисунок 9).
|
Рисунок 9 - Полупараболическая маска
Основой полупараболической маски, представленной на рисунке 9, является усеченная V-маска общего назначения, представленная на рисунке 5. В последних пяти интервалах наблюдений в узком конце ширина маски составляет 1,25 вместо 5
для V-маски. Данные для построения полупараболической приведены в таблице 7.
Таблица 7 - Данные для построения полупараболической маски
Расстояние от точки отсчета | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
Полуширина маски в точке | 1,25 | 3,10 | 4,65 | 5,90 | 6,85 | 7,50 | 10,00 | 15,00 |
Детали |
| Прямая линия | ||||||
Характеристика свойств полупараболической маски:
a) превосходит V-маску по всему диапазону сдвигов среднего процесса. Это достигается за счет увеличения почти вдвое уровня ложных сигналов при среднем процесса на уровне целевого значения;
b) уступает стандартной усеченной V-маске FIR и по уровню ложных сигналов и по уровню сдвигов среднего процесса, кроме сдвигов, не превосходящих 0,5 стандартного отклонения;
c) уступает усеченной V-маске по уровню ложных сигналов и сопоставима по обнаружению сдвигов среднего процесса.
Эти свойства приведены в таблице 6, где показано сравнение значений ARL для различных правил принятия решений.
8.5 Усеченная V-маска
Усеченная V-маска предназначена для обеспечения тех же преимуществ, что и полупараболическая V-маска, но является более простой. Таким образом, она полезна в тех случаях, когда требуется более ранняя реакция на большие сдвиги. Это достигается суперпозицией двух или более усеченных V-масок. На рисунке 10 показана укороченная V-маска, полученная суперпозицией усеченной V-маски с 2,05 и
1,5 и стандартной V-маски c
5,0 и
0,5. В таблице 6 показано, что эта усеченная маска обладает почти такими же хорошими свойствами, как полупараболическая маска на широком диапазоне сдвигов и существенно лучше стандартной усеченной V-маски.
|
Рисунок 10 - Усеченная V-маска
8.6 Полная V-маска
Правила принятия решений могут также быть применены при использовании полной V-маски (см. рисунок 11). По своим свойствам эта маска идентична усеченной V-маске.
На рисунке 11 показано, что разрешающие линии полной V-маски продлены к вершине О. Это означает, что у маски нет начала отсчета и вершина О расположена на cusum-карте на расстоянии ОА вперед (направо) от последней точки наблюдений. Отрезок ОА называют ведущим расстоянием . Идентичные характеристики те же, что и у стандартной усеченной V-маски,
![]() и
и 10 единиц наблюдений.
|
Рисунок 11 - Полная V-маска
8.7 Усеченная V-маска FIR
Усеченная V-маска FIR предназначена для уменьшения значения ARL при выявлении сдвигов среднего без существенного уменьшения ARL при сохранении среднего процесса на целевом значении. Это относится к сопоставлению критериев принятия решения. Таким образом, цель состоит в более быстрой реакции на сдвиги при сохранении уровня ложных сигналов.
Сравнение значений ARL в столбцах 2 и 5 таблицы 6 показывает, что схеме FIR соответствует более быстрая реакция на сдвиг среднего по всему диапазону (29 вместо 38 в 0,5 и 6,4 вместо 10 в 1
) при сохранении значения ARL при среднем процесса на целевом значении 448 по сравнению с 465.
Таблица 6 также показывает, что схема FIR обладает более быстрой реакцией на сдвиги по сравнению с полупараболической и усеченной масками по всему диапазону и одновременно имеет существенно большее значение ARL, если среднее процесса совпадает с целевым значением (448 по сравнению с 235 и 300).
Суммирование начинается с FIR, а не с нуля. Обычно это значение равно половине интервала решения .
Анализ FIR-схемы показывает, что она позволяет ускорить получение сигнала о сдвиге среднего. Однако при отсутствии сдвига процесса кумулятивная сумма будет убывать до нуля, так же как обычная кумулятивная сумма.
При использовании вместе со схемами табличных решений (см. 8.8) начальное значение часто используют для верхней и нижней кумулятивных сумм.
8.8 Cusum-таблицы
8.8.1 Обоснование
Иногда основная цель cusum-процедуры состоит в том, чтобы просто выявить нестандартные условия, а не обеспечить наглядное представление последовательных данных. В этом случае данные могут быть записаны в форме таблицы. Численное правило тогда заменяет маску, используемую стандартной cusum-картой.
Такие схемы называют cusum-таблицами.
V-маска обнаруживает изменения угла наклона кривой. Ее интервал решения учитывает степень рассеяния cusum-точек. Угловой коэффициент разрешающих линий маски соответствует среднему уровню процесса: целевое значение
![]() .
.
В табличной схеме вместо вычисления и графического представления кумулятивной суммы разности наблюдаемых и целевых значений вычисляют и сводят в таблицу кумулятивную сумму следующих ( - наблюдаемое значение):
;
![]() ,
,
(при этом кумулятивной сумме присваивают значение 0, если она становится отрицательной для верхней cusum, чтобы обнаружить увеличение среднего).
![]() ,
,
(при этом кумулятивной сумме присваивают значение 0, если она становится положительной для нижней cusum, чтобы обнаружить уменьшение среднего).
Это дает горизонтальные линии решений на уровне ![]() , вместо разрешающих линий с угловым коэффициентом
, вместо разрешающих линий с угловым коэффициентом , выходящих из точки
(\/-маска).
Статистические решения совпадают с решениями по сопоставимой V-маске.
8.8.2 Табличный cusum-метод
Для установки и интерпретации интервала решений двухсторонней cusum-схемы, если контролируемая характеристика подчиняется нормальному распределению, необходимо выполнить следующие действия:
Этап 1. Установление параметров cusum-карты:
a) интервала решений ;
b) углового коэффициента разрешающей линии ;
c) целевого значения ;
d) оценки стандартной ошибки характеристики .
Этап 2. Вычисление cusum-критериев:
![]() и
и ![]() .
.
Этап 3. Подготовка cusum-таблицы для верхней табличной cusum по обнаружению увеличения среднего уровня. Таблица должна иметь следующие колонки:
e) номер наблюдения;
f) значение наблюдаемой характеристики;
g) ![]() ;
;
h) кумулятивная сумма величины ![]() .
.
Примечание - Эта таблица аналогична используемой для стандартного cusum-графика, за исключением того, что ![]() заменяет значение
заменяет значение , а
является угловым коэффициентом эквивалентной разрешающей линии V-маски.
Этап 4. Подготовка cusum-таблицы для нижней табличной cusum по выявлению уменьшения среднего. Таблица должна включать колонки, аналогичные таблице этапа 3, кроме следующих:
i) ![]() ;
;
j) кумулятивная сумма величины ![]() .
.
Этап 5. Ввод данных
k) Вводят данные и выполняют вычисления;
I) для положительных значений cusum: вычисляют и записывают значения cusum для ![]() . Если cusum становится отрицательной в любой точке, сброс обнуляют и продолжают до тех пор, пока cusum снова не станет положительной. Если cusum касается границы решения
. Если cusum становится отрицательной в любой точке, сброс обнуляют и продолжают до тех пор, пока cusum снова не станет положительной. Если cusum касается границы решения или превышает ее, фиксируют сдвиг вверх;
m) для отрицательных значений cusum: вычисляют и записывают значения cusum для ![]() . Если cusum становится положительной в любой точке, ее обнуляют и продолжают до тех пор, пока cusum снова не станет отрицательной. Если cusum касается границы решения
. Если cusum становится положительной в любой точке, ее обнуляют и продолжают до тех пор, пока cusum снова не станет отрицательной. Если cusum касается границы решения или опускается ниже, фиксируют сдвиг вниз.
Пример метода показан в таблице 8. Другой пример табличного метода приведен в приложении В.
Таблица 8 - Пример табличной cusum
Наблюдаемое значение |
| Cusum (верхняя) |
| Cusum (нижняя) | Примечание |
10 | -1 | 0 | +1 | 0 | Обе суммы равны нулю, среднее |
10 | -1 | 0 | +1 | 0 | процесса равно целевому |
10 | -1 | 0 | +1 | 0 | значению |
14 | +3 | +3 | +5 | 0 | Среднее процесса выше целевого |
14 | +3 | +6 | +5 | 0 | значения, нижняя cusum равна нулю |
3 | -8 | 0 | -6 | -6 | |
3 | -8 | 0 | -6 | -12 |
|
10 | 0 | +1 | -11 | ||
10 | 0 | +1 | -10 | ||
10 | 0 | +1 | -9 | ||
10 | 0 | +1 | -8 | ||
10 | 0 | +1 | -7 | ||
17 | +6 | +6 | +8 | 0 | |
17 | +6 | + 12 | +8 | 0 |
|
Примечание 1 - Целевое значение - Примечание 2 - В колонке 2 следует записывать значения Примечание 3 - В колонке | |||||
9 Cusum-методы для управления процессом и контроля качества продукции
9.1 Причины изменений
9.1.1 Величина изменений
При разработке cusum-системы для контроля параметров процесса или характеристик продукции должен быть установлен размер сдвига или изменения параметра процесса или характеристики продукции, который важно обнаружить. Эта величина влияет на форму V-маски, которая может быть использована для выявления неконтролируемых состояний. На практике в качестве такого значения часто выбирают наименьший сдвиг, при котором может быть проведена корректировка процесса. Однако следует учитывать, что назначение слишком малого сдвига может привести к появлению рысканья (см. 9.1.5).
Все изменения могут быть отнесены к одному из следующих типов шаговые, дрейф или "циклические:
9.1.2 Шаговые изменения
При шаговых изменениях данные об измерениях параметра процесса или характеристики продукции внезапно переходят на новый уровень. Примером является использование новой партии сырья, которая отличается от используемой ранее, или когда неопытный служащий, заменяя коллегу, делает больше ошибок, чем опытный служащий. В таких случаях cusum-карта идентифицирует это изменение, показывая существенный сдвиг среднего процесса.
9.1.3 Дрейф
Этот тип изменений часто связывают с износом оборудования, инструментов и т.п. Cusum-график в этом случае выглядит как возрастающий или убывающий.
9.1.4 Циклические изменения
При наличии циклических изменений участок cusum-графика периодически повторяется. Например, это может произойти в организации, где имеется три рабочих смены, которые выполняют одни и те же задачи, но по-своему. При наличии циклических изменений повторяется некоторая последовательность сдвигов, например, сдвиг В всегда следует за сдвигом А. На cusum-графике периоды возрастания чередуются с периодами убывания.
9.1.5 Рысканье
Рысканье (нерегулярные колебания) контролируемой характеристики происходят, когда параметр или характеристика не могут быть точно скорректированы и установлены на целевое значение, а после сигнала о потере стабильности процесса корректировка устанавливает значение параметра или характеристики, при котором знак отклонения от целевого значения меняется на противоположный. Cusum-график меняет направление изменений на противоположное, затем появляется сигнал, требующий исправить сделанную корректировку и т.д.
Таким образом, на cusum-графике появляется зигзагообразный участок. Это самая неудовлетворительная ситуация. Ее можно избежать с помощью выбора исходного целевого значения\== и последующих минимальных корректировок [см. 9.3.1, этап 13 с)] для устранения рысканья.
9.2 Выбор целевых значений
9.2.1 Общие положения
Правильный выбор целевого значения имеет главное значение при установке cusum-схемы.
Целевое значение между двух возможных значений может привести к рысканью (см. 9.1.5).
9.2.2 Стандартное заданное значение как целевое значение
Самым простым выбором целевого значения является выбор в качестве целевого значения заданного или установленного значения. В этом случае целевое значение часто устанавливают равным некоторому указанному в требованиях значению, такому как номинальное значение или значение середины поля допуска. Эти значения установлены в документированных требованиях или на чертежах. Если cusum-метод применяют в непроизводственной сфере, целевое значение может быть некоторым уровнем выполнения, таким как среднее время обработки счета или ежемесячные расходы подразделения организации.
Целевое значение может быть изменено. Например, при продаже мороженого целевое значение может изменяться в течение года. В среднем больше мороженого продают в течение летних месяцев. Таким образом, могут быть использованы различные целевые значения для каждого месяца. Использование постоянного целевого значения в течение всего года приводит к ложным выводам. Значение cusum в течение одного периода года повышается, затем убывает. Если целевые значения различны, то cusum лучше указывает существенные изменения уровня продаж мороженого.
Неудачно выбранное целевое значение может привести к появлению рысканья, описанному в 9.1.5. Поэтому выбор целевого значения является важной задачей cusum-метода.
Номинальное значение выбирают в качестве целевого значения при контроле среднего или среднего уровня (положения) параметра или характеристики. Хотя тот же подход мог бы быть использован для установления целевого значения при контроле изменчивости (дисперсии) в виде стандартного отклонения подгруппы или диапазона, эта практика не рекомендуется в стандартах серии ИСО 7870. Предпочтительно использовать рекомендации, приведенные в 9.2.3 и следующих подразделах.
9.2.3 Функциональное целевое значение
Целевое значение может быть установлено на основе текущих уровней функционирования. Этот подход совместим с функциональными контрольными картами, когда средства управления установлены в соответствии с предыдущим состоянием параметра процесса или характеристики продукции.
Для контроля положения или разброса важно получить данные испытаний или сбора данных. Такой период для анализа собственной изменчивости должен быть достаточно продолжительным. Как правило, испытания должны обеспечить получение 25 точек на cusum-графике. По этим данным должны быть получены оценки среднего и стандартного отклонения.
Установленные целевые значения должны быть использованы для вычисления кумулятивных сумм, но спустя некоторое время может потребоваться изменение целевого значения, если cusum-карта указывает на изменение уровня процесса. Если невозможно выполнить корректировку процесса или если новый уровень является приемлемым, то единственным, что может быть сделано, является изменение целевого значения. Это обычно делают после проверки, что новый уровень соответствует следующим данным, и устанавливают его в качестве целевого значения. Далее cusum-метод контролирует параметр или характеристику относительно нового целевого значения.
9.3 Cusum-схемы для контроля положения
9.3.1 Стандартная схема
Последовательность этапов выполнения стандартной cusum-схемы приведена на рисунке 12.
Этап 1. Определение объекта для построения cusum-карты
Определение контролируемого параметра процесса или характеристики продукции.
Примечание 1 - Это могут быть ключевой параметр процесса или значимая характеристика продукции, или они могут быть установлены потребителем. Объект может быть также идентифицирован при выборе контролируемого параметра или характеристики.
Этап 2. Определение объема подгруппы
Определение рациональной подгруппы для cusum-карты идентично аналогичному процессу при разработке любой карты Шухарта.
Если параметр процесса является выбранным объектом, то самым подходящим объемом подгруппы является объем, равный единице. Это вызвано тем, что параметры, например температура или давление в транспортном средстве, изменяются в течение достаточно продолжительного времени. Выполнение нескольких последовательных повторных измерений вряд ли покажет какие-либо различия. Это приводит к техническим проблемам с определением стандартного отклонения и корректной установкой cusum-маски.
Если данные действительно единичны, такие как показатель за месяц, то размер рациональной подгруппы будет таким же.
Для характеристики продукции объем рациональной подгруппы часто больше единицы и равен обычно пяти. В соответствии со здравым смыслом выбранный объем подгруппы позволяет представить случайную изменчивость процесса.
Этап 3. Выбор cusum-схемы
В таблице 9 приведен набор стандартных схем, охватывающих весь диапазон типичных требований для cusum-схемы. В таблице приведены две основные схемы: схема CS1 с достаточно высоким значением ARL при нулевом сдвиге и с более низким значением ARL - схема CS2. Другими словами, схема CS2 обнаруживает сдвиг уровня процесса быстрее, чем схема CS1, но за счет большего количества ложных сигналов. При выборе схемы необходимо определить, какой сценарий более важен. В таблице 10 показаны различия этих стандартных схем.
Таблица 9 - Стандартные cusum-схемы для среднего подгруппы
Значимый сдвиг среднего, который должен быть | Схема CS1 | Схема CS2 | ||
обнаружен | ||||
i) <0,75 | 8,0 | 0,25 | 5,0 | 0,25 |
ii) от 0,75 до 1,50 | 5,0 | 0,50 | 3,5 | 0,50 |
iii) >1,50 | 2,5 | 1,00 | 1,8 | 1,00 |
Примечание 1 - Схеме CS1 соответствует средняя длина серии Примечание 2 - Схеме CS2 соответствует средняя длина серии | ||||
| ||||
Как только выбрана cusum-схема (CS1 или CS2), необходимо установить размер значимого сдвига. В таблице приведены три типичных значения значимого сдвига. В зависимости от выбранного значения сдвига значения и
могут быть определены по таблице.
Если неясно, какую схему необходимо выбрать, практика показывает, что хорошей начальной схемой является схема CS1 ii), т.е. =5,0 и
=0,50.
Таблица 10 - Сопоставление стандартных cusum-схем для среднего подгруппы
Значения средней длины серии (ARL) | ||||||
Отклонение среднего от целевого | Схема CS1 | Схема CS2 | ||||
значения (в единица ( | (i) | (ii) | (iii) | (i) | (ii) | (iii) |
0,00 | 730,0 | 930,0 | 715,0 | 140,0 | 200,0 | 170,0 |
0,75 | 16,4 | 17,0 | 27,0 | 10,5 | 11,5 | 15,0 |
1,00 | 11,4 | 10,5 | 13,4 | 7,4 | 7,4 | 8,8 |
1,50 | 7,1 | 5,8 | 5,4 | 4,7 | 4,3 | 4,0 |
Примечание - Значение ARL является заданным. Следует помнить, что фактическое значение ARL для обнаружения фактического сдвига может быть больше или меньше ARL. При необходимости следует исследовать распределение значений ARL для определенных отклонений среднего от целевого значения, чтобы знать средний диапазон значений ARL, которые могут быть рассмотрены. | ||||||
Независимо от того, какая схема выбрана, значения параметров должны быть умножены на (или
) для определения фактических размеров и формы маски. Это установлено в этапе 8.
Этап 4. Сбор данных испытательного периода
Как указано в 9.2.3, должны быть собраны данные, характеризующие изменчивость процесса, необходимые для построения cusum-схемы и установления целевого значения при необходимости.
Определяют период, в течение которого все источники изменчивости процесса будут проявлены. Этот период должен быть достаточно продолжительным или частота отбора выборки достаточно высокой для получения не менее 25 подгрупп данных.
Не следует вводить дополнительные источники изменчивости процесса, например регулировки процесса в течение этого периода, поскольку это исказит данные об изменчивости процесса. Если есть необходимость в прерывании сбора данных, должно быть принято решение о необходимости повторения наблюдений или достаточности данных. Если количество подгрупп было 20 или более и если все потенциальные источники изменчивости процесса воздействовали в процессе сбора данных, то это количество подгрупп является достаточным и сбор данных может быть прекращен. Собранные данные должны быть использованы для установления уровня изменчивости для cusum-схемы. Это установлено на этапах 5 и 6.
Этап 5. Оценка по данным испытательного периода
а) Общие положения
Ниже описан метод определения оценки . В некоторых случаях может возникнуть необходимость применения другого подхода. Этот другой подход может потребовать определения оценки стандартного отклонения средних подгрупп.
|
Рисунок 12 - Последовательность этапов выполнения стандартной cusum-схемы
b) Объем подгрупп больше единицы (1)
i. Вычисляют размах (разность наибольшего и наименьшего наблюдений) для каждой подгруппы.
ii. Вычисляют средний размах () по подгруппам.
iii. Определяют оценку стандартного отклонения в подгруппе () делением среднего размаха на соответствующее значение
, приведенное в таблице 11.
iv. Определяют делением
на квадратный корень из объема подгруппы, т.е.
![]() .
.
Таблица 11 - Значение коэффициента для оценки стандартного отклонения подгрупп по размаху подгруппы
Объем подгруппы | |
2 | 1,128 |
3 | 1,693 |
4 | 2,059 |
5 | 2,326 |
6 | 2,534 |
7 | 2,704 |
8 | 2,847 |
9 | 2,970 |
10 | 3,078 |
Примечание - Для подгрупп, объем которых больше 10, другие методы могут быть более эффективны при определении оценки стандартного отклонения подгруппы. | |
Вместо размаха подгруппы может быть определено выборочное стандартное отклонение подгруппы (). В этом случае вместо
и
определяют среднее стандартное отклонение подгрупп
и оценку
. Значения
приведены в таблице 18.
с) Объем подгруппы 1
Для определения оценки должен быть использован метод последовательных разностей (иногда называемый скользящим размахом).
Данные, собранные за испытательный период, должны быть использованы в той последовательности, в которой они были собраны. Должны быть вычислены размах (разность) между первым и вторым наблюдениями, затем размах между вторым и третьим наблюдениями, и т.д. Если имеется подгрупп, должны быть получены значения (
)-го размаха. Вычисляют средний размах (
).
Оценку определяют делением среднего размаха на 1,128.
Этап 6. Определение целевого значения
В соответствии с 9.2 в качестве целевого значения может быть заданное значение, определенное на основе данных наблюдений.
a) Заданное значение
Целевое значение может быть выбрано на основе установленных требований или чертежа или является номинальным размером или значением характеристики продукции или некоторым средним уровнем параметра управления в случае непроизводственного процесса.
b) Значение, выбранное на основе наблюдений
Целевое значение определяют по данным наблюдений, полученных во время испытательного периода.
i. Вычисляют выборочное среднее () для каждой подгруппы.
ii. Вычисляют общее среднее () средних подгрупп.
iii. Выбирают в качестве целевого значения .
Этап 7. Установление параметров cusum-карты
a) Общие положения
В разделе 5 приведены рекомендации по установлению параметров cusum-карт.
b) Cusum-таблица.
Устанавливают подходящую cusum-таблицу для записи результатов вычислений. Часть такой таблицы приведена в таблице 12.
Таблица 12 - Таблица вычислений для cusum-метода
Номер подгруппы | Значение кумулятивной суммы | ||
и т.д. |
Если объем подгруппы равен единице, в таблице заменяют на
.
с) Cusum-бумага
Выбирают линованную бумагу с удобными интервалами между линиями сетки. Выбор зависит от предполагаемого использования бумаги, например для вывешивания на стену.
Выбирают подходящий масштаб. Масштаб зависит от расположения графика. Например, для графиков, предназначенных для вывешивания на стену, интервал на горизонтальной оси может быть 10 мм, тогда как для графика, предназначенного для использования на столе, достаточно интервала 5 мм.
Подходящий интервал для оси кумулятивной суммы выбирают таким же, как интервал для горизонтальной оси, приблизительно равный 2, с округлением. Это масштабирование вряд ли "сгладит" существенные изменения или преувеличит незначительные.
Отмечают центральную точку 0 на cusum-оси и проводят полужирную горизонтальную линию через эту точку. Различают вертикальную ось cusum в соответствии с масштабом.
Пример такой бумаги показан на рисунке 13.
Этап 8. Установление cusum-маски
В подразделе 8.2.1 описана геометрия стандартной cusum-маски, а на рисунке 5 показаны элементы маски и необходимый масштаб.
Значения ,
и
должны быть определены в соответствии с настоящим подразделом.
a) Вычисляют ![]() .
.
b) Вычисляют ![]() .
.
Маска должна быть начерчена в соответствии с масштабом, выбранным для cusum-бумаги. Это важно для принятия правильного решения о наличии изменения установленного размера.
Примечание 2 - Иногда маски делают из прозрачного материала, такого как ацетат, на который маску наносят при помощи несмываемых чернил. Иногда маска может быть вырезана из части карты со значениями и
в масштабе cusum-бумаги.
Примечание 3 - Существуют компьютерные программы, которые выводят на экран cusum-график с маской.
Этап 9. Вычисление кумулятивной суммы для данных испытательного периода
Используя целевое значение, определенное на этапе 6, и таблицу, аналогичную таблице 12, вычисляют значения кумулятивной суммы для данных испытательного периода.
Этап 10. Cusum-график для данных испытательного периода
Представленные в таблице значения кумулятивной суммы должны быть изображены на бумаге, аналогичной представленной на рисунке 13. График начинается слева и продолжается направо. Соединяют все изображенные точки, это делает все тенденции более наглядными.
Этап 11. Анализ cusum-графика
Накладывают маску на cusum-график.
Это делают, определяя положение точки отсчета, указанной на рисунке 7 а), по последней точке кумулятивной суммы. При этом необходимо совмещать центральную линию маски с нулевой осью на бумаге. Это гарантирует, что маска правильно ориентирована.
Любая точка, выходящая за разрешающие линии маски, указывает на выход процесса из управляемого состояния, даже если такая точка не последняя и даже если следующие точки возвращаются в пределы разрешающих линий маски [см. рисунок 7 b)].
|
Рисунок 13 - Пример cusum-бумаги
Этап 12. Идентификация и устранение специальных причин
a) Общие положения
Важно проанализировать все точки за разрешающими линиями на cusum-карте и идентифицировать соответствующую специальную причину.
b) Идентификация и предотвращение возникновения специальных причин
Как только идентифицирована специальная причина и предприняты действия по ее предотвращению в будущем, необходимо рассмотреть и изменить, при необходимости, целевое значение и стандартную ошибку (или стандартное отклонение). Если имеется только одна несоответствующая точка и причина была удовлетворительно устранена, то установленные целевое значение и стандартная ошибка или стандартное отклонение могут быть изменены на основе данных испытательного периода, а не данных для неконтролируемой подгруппы. Необходимо заново определить масштаб cusum-бумаги и размерности маски и повторно начертить маску.
Если имеется несколько неконтролируемых точек в данных испытательного периода, это указывает на большее количество проблем с процессом. В таком случае рекомендуется проанализировать процесс, внести корректировки и затем провести испытательный период и собрать новые данные.
c) Идентификация специальных причин без предотвращения их повторного возникновения
Бывают ситуации, когда невозможно предотвратить появление специальных причин в будущем в силу экономных или технических соображений.
В этом случае cusum-параметры, основанные на всех данных испытательного периода, используют для контроля. Другими словами, эти специальные причины рассматривают как часть случайной изменчивости процесса.
d) Невозможность выявления специальных причин
Некоторые специальные причины могут остаться не идентифицированными. Это отрицательный результат, поскольку он препятствует улучшению процесса. Необходимо приложить все усилия для выявления специальных причин, в том числе использовать другие методы и решения проблемы. Одним из наиболее мощных методов является метод статистического планирования экспериментов.
Если специальные причины остаются не выявленными, необходимо выполнить действия в соответствии с перечислением с).
Этап 13. Продолжение построения карты
a) Общие положения
Если данные испытательного периода соответствуют стабильному состоянию или когда собраны новые данные после удовлетворительного сокращения специальных причин, cusum-карта готова к продолжению контроля параметра процесса или характеристики продукции. Масштабированную бумагу и параметры маски теперь используют для контроля данных будущих подгрупп.
Если появляется неконтролируемая точка, необходимо решить, что делать с процессом. Действия могут включать регулировку процесса, принятие нового целевого значения, если процесс переместился в более желательное положение.
b) Регулировки процесса
Количество необходимых регулировок может быть определено по cusum-графику. Для этого:
i. Определяют значение кумулятивной суммы в последней точке графика.
ii. Определяют значение кумулятивной суммы в месте, где cusum-график вышел за границы маски. В случае нескольких нарушений берут неконтролируемую точку, наиболее близкую к точке отсчета на маске.
iii. Вычисляют разность значений в этих двух точках.
iv. Подсчитывают количество точек на графике между точкой отсчета и неконтролируемой точкой.
v. Делят разность, вычисленную на этапе iii, на количество точек, подсчитанных на этапе iv, т.е. вычисляют локальный градиент cusum-графика. Это - оценка сдвига процесса от целевого значения.
vi. Корректируют процесс на ту же величину. Записывают на cusum-графике выполненные изменения.
vii. Обнуляют кумулятивную сумму и продолжают контроль.
Примечание 4 - Вместо выполнения описанных вычислений можно построить графики "поиска" для определения величины сдвига от целевого значения. Пример приведен на рисунке 14.
|
Рисунок 14 - Схематический пример графика поиска величины сдвига целевого значения
с) Регулировки процесса - антирысканье
Понятие "рысканья" введено в 9.1.5. Применение cusum-метода предполагает, что регулировка процесса на величину, равную 100% полученного сдвига от целевого значения, может ввести рысканье. После такой регулировки cusum-карта может потребовать далее выполнить следующую регулировку процесса, но в противоположном направлении. Если процесс скорректирован в обратную сторону на величину последнего сдвига, он может быть позже скорректирован в противоположном направлении. Это явление называют рысканьем.
Рысканье может быть вызвано быстрым изменением кумулятивной суммы, преувеличивающим реальный сдвиг, который может быть исправлен модификацией маски, или фактической корректировкой.
Одно практическое решение состоит в том, чтобы выполнить регулировку процесса, корректирующую сдвиг меньше чем на 100%. Этот процент называют коэффициентом антирысканья. Этот коэффициент снижает рысканье кумулятивной суммы. Пользователи и практики вместе с некоторыми исследователями указывают, что коэффициент антирысканья, равный 75%, работает очень хорошо. Поэтому рекомендуется, по крайней мере в начале, корректировать только 75% сдвига.
Такие графики, как представленные на рисунке 14, могут быть построены с использованием коэффициента анти рысканья. В некоторых случаях это бывает необходимо.
Альтернативным коэффициентом, подавляющим рысканье, является ![]() , где
, где - количество точек между ведущей и неконтролируемой точками. Используя этот коэффициент, размер корректировки характеристики процесса
определяют по следующей формуле:
![]() ,
,
где - разность значений кумулятивной суммы в ведущей и неконтролируемой точками. Использование
во многих случаях позволяет предотвратить рысканье.
9.3.2 Стандартные схемы. Ограничения
Основные cusum-схемы, установленные в 9.3.1, обеспечивают хорошее начало работы и во многих случаях не требуют дальнейших изменений. Для некоторых приложений можно заметить, по истечении некоторого времени, что основная выбранная схема должна быть улучшена, потому что ARL для обнаружения сдвига значимого размера слишком велика или потому, что частота ложных сигналов слишком высока.
9.3.3 Специальные cusum-схемы
Примечание - Разработка конкретной cusum-схемы требует больших знаний и исходных данных, чем основные схемы, установленные в 9.3.1. В этом случае необходима консультация со специалистом.
a) Определение (значимого) размера отклонения от целевого значения, которое должно быть обнаружено ().
b) Определение оценки стандартной ошибки (или стандартного отклонения, если объем подгруппы равен единице), как установлено выше.
c) Определение исходной ARL, если сдвиг имеет величину, указанную в 9.3.1, этап 3, .
d) Определение исходной ARL, если сдвиг равен нулю, т.е. частота ложных сигналов равна .
e) Вычисление стандартного сдвига ![]() .
.
f) Нанесение данных на карту, представленную на рисунке 15, и определение по расчетному значению
с учетом значений
и
.
g) Значение для также может быть определено по графику, соответствующему расчетному значению
.
h) Изменение cusum-маски в соответствии с новыми значениями и
в соответствии с изложенным.
|
Рисунок 15 - Карта для определения параметров маски (для нормального распределения)
9.4 Cusum-схемы для контроля изменчивости
9.4.1 Общие положения
Кроме контроля положения процесса важно контролировать его изменчивость, которая в большинстве случаев будет краткосрочной.
Двумя наиболее подходящими мерами изменчивости являются размах и стандартное отклонение в пределах подгруппы. Выбор зависит от легкости вычислений и уровня понимания персоналом выполняемых вычислений. Часто при работе с контрольными картами для обеспечения простоты вычислений выбирают карты размаха, а объем подгруппы часто выбирают равным пяти. Эффективность использования размаха и стандартного отклонения практически не различима.
Если объем подгруппы равен единице, используемой мерой изменчивости должен быть размах, вычисляемый как разность последовательных результатов.
9.4.2 Cusum-схемы для размахов
Для установления подходящей схемы контроля изменчивости процесса на основе размаха в пределах подгруппы необходимо выполнить следующие действия. Некоторые из этапов действий будут завершены, если выполнена cusum-схема контроля среднего.
Этап 1. Определение объекта для построения cusum-карты
См. 9.3.1, этап 1.
Этап 2. Определение объема подгруппы
См. 9.3.1, этап 2.
Этап 3. Выбор cusum-схемы для размаха
В таблице 13 установлены стандартные схемы, которые обеспечивают выполнение типичных требований к cusum-карте размаха. В соответствии с 9.3.1 в таблице приведены две основные схемы: CS1, которой соответствуют большие значения ARL на ожидаемом уровне изменчивости, и CS2, которой соответствуют меньшие значения ARL. Схема CS2 обнаруживает сдвиг уровня процесса быстрее, чем соответствующая схема CS1, но за счет большего количества ложных сигналов. В таблице 14 приведены различия этих стандартных схем.
Таблица 13 - Стандартные cusum-схемы размаха подгруппы
Объем подгруппы | Схема CS1 | Схема CS2 | ||
2 | 2,50 | 0,85 | 2,50 | 0,55 |
3 | 1,75 | 0,55 | 1,75 | 0,35 |
4 | 1,25 | 0,50 | 1,25 | 0,30 |
5 | 1,00 | 0,45 | 1,00 | 0,30 |
6 | 0,85 | 0,45 | 0,85 | 0,30 |
7 | 0,70 | 0,45 | 0,70 | 0,30 |
8 | 0,55 | 0,40 | 0,55 | 0,25 |
9 | 0,55 | 0,40 | 0,55 | 0,25 |
10 | 0,50 | 0,35 | 0,50 | 0,25 |
Примечание 1 - Схеме CS1 соответствует средняя длина серии Примечание 2 - Схеме CS2 соответствует средняя длина серии | ||||
Выбирают одну из схем, CS1 или CS2. При этом используют те же критерии выбора, которые были использованы при выборе схемы для среднего подгруппы. Если требуется схема с большим значением ARL, при отсутствии изменений процесса выбирают схему CS1. В противном случае выбирают схему CS2.
Независимо от выбранной схемы для определения фактического размера и формы маски, значения для этих параметров должны быть умножены на оценку изменчивости (см. этап 8).
Этап 4. Сбор данных испытательного периода
Здесь применяют также инструкции для оценки положения процесса
Этап 5. Оценка по данным испытательного периода
Вычисляют , используя один из методов, описанных в 9.3.1, этап 5.
Таблица 14 - Сравнение ARL стандартных cusum-схем размаха для подгруппы
Объем подгруппы | Уровень изменчивости фактического процесса | Схема CS1 | Схема CS2 |
2 | 779,0 | 170,0 | |
2 | 7,2 | 5,5 | |
4 | 2,3 | 2,1 | |
3 | 893,0 | 196,0 | |
2 | 4,5 | 3,6 | |
4 | 1,6 | 1,5 | |
4 | 918,0 | 157,0 | |
2 | 3,3 | 2,7 | |
4 | 1,3 | 1,2 | |
5 | 771,0 | 179,0 | |
2 | 2,7 | 2,3 | |
4 | 1,2 | 1,1 | |
6 | 942,0 | 204,0 | |
2 | 2,4 | 2,0 | |
4 | 1,1 | 1,1 | |
8 | 893,0 | 162,0 | |
2 | 2,0 | 1,7 | |
4 | 1,0 | 1,0 | |
10 | 635,0 | 184,0 | |
2 | 1,7 | 1,5 | |
4 | 1,0 | 1,0 | |
Примечание - Данные значения являются ARL. Необходимо знать, что фактическая длина серии для обнаружения изменения может быть больше или меньше ARL. При необходимости следует проверить распределение для определенных сдвигов от целевого значения, чтобы знать средний размах длин серий. | |||
Этап 6. Определение целевого значения
a) Данное значение
При статистическом контроле качества продукции или процесса, наиболее распространен метод установки целевого значения размаха, описанный в b) ниже. Однако в некоторых случаях предпочтительно установить целевое значение на некотором предполагаемом уровне. Если это так, целевое значение размаха равно заданному значению размаха.
Если изменчивость описана с помощью стандартного отклонения, целевое значение размаха может быть вычислено по формуле
![]() .
.
Значение определяют по таблице 11. Оно зависит от объема подгруппы.
b) Функционально обоснованное значение
По данным, полученным за испытательный период, устанавливают целевое значение размаха, равное .
Этап 7. Установление cusum-бумаги
Устанавливают cusum-таблицу (или добавляют данные к существующей cusum-таблице) и разрабатывают cusum-бумагу, как установлено в 9.3.1, этап 7. Cusum-бумага для размаха может иметь масштаб, отличный от масштаба бумаги для контроля среднего. Подходящий масштаб может быть вычислен по формуле . Значение
приведено в таблице 15.
Таблица 15 - Коэффициент масштаба для cusum-бумаги размаха
Объем подгруппы | |
2 | 1,50 |
3 | 1,00 |
4 | 0,85 |
5 | 0,75 |
6 | 0,65 |
8 | 0,55 |
10 | 0,50 |
Этап 8. Установление cusum-маски
Используя значения и
, выбранных на этапе 3, вычисляют:
a) ![]() ;
;
b) ![]() .
.
Разрабатывают маску, используя расчетные значения и
в соответствии с масштабом cusum-бумаги.
Этап 9. Вычисление кумулятивной суммы для данных испытательного периода
Используя целевое значение, определенное на этапе 6, и таблицу, аналогичную таблице 12, вычисляют значение кумулятивной суммы для размаха по данным испытательного периода.
Этап 10. Построение cusum-графика для данных испытательного периода
Графически изображают кумулятивную сумму для размаха на cusum-бумаге, как описано в 9.3.1, этапах 7 и 10.
Этап 11. Анализ cusum-графика для данных испытательного периода
Анализ cusum-графика выполняют, как установлено в 9.3.1, этап 11.
Этап 12. Идентификация и устранение специальных причин изменчивости
a) Общие положения
Важно исследовать все точки, расположенные за контрольными границами на cusum-графике и идентифицировать соответствующую причину специальной изменчивости.
Если необходимо пересмотреть значения целевого размаха в соответствии с одним из следующих подпунктов, то необходимо пересмотреть маску и возможно cusum-бумагу для контроля среднего.
b) Идентифицированная и устраненная специальная причина изменчивости
Как только специальная причина идентифицирована и выполнены действия по ее устранению, в будущем значение целевого размаха может быть изменено (по необходимости). При наличии только одной точки вне зоны управляемости, которая обработана в соответствии с перечислением а), ранее присвоенное целевое значение может быть пересмотрено с использованием данных испытательного периода, за исключением данных, содержащих точку вне зоны управляемости подгруппы. Пересматривают вычисления для масштабирования cusum-бумагии маски и повторно масштабируют бумагу и маску при необходимости.
Если данные испытательного периода содержат несколько точек, это указывает на наличие проблем с процессом. Рекомендуется проанализировать и отрегулировать процесс и затем провести новый испытательный период с регистрацией новых данных.
c) Идентифицированная, но не устраненная специальная причина
Существуют случаи, когда специальная причина не может быть устранена вследствие экономических или технических трудностей.
В этом случае cusum-параметры определяют на основе всех данных испытательного периода и используют для продолжающегося контроля. Другими словами, такие специальные причины рассматривают как часть изменчивости случайного процесса.
d) Не выявленная специальная причина
Если специальная причина остается не выявленной, должны быть выполнены действия в соответствии с перечислением с).
Это крайне нежелательная ситуация, поскольку она не способствует улучшению процесса. Необходимо сделать все возможное для исследования специальных причин.
Этап 13. Продолжение построения карты
a) Общие положения
Выполнение действий по построению карты в соответствии с 9.3.1, этап 13.
b) Действия с процессом
Как при контроле среднего, если появляется сигнал о потере управляемости, то размер изменения можно оценить по градиенту cusum-графика. В этом случае интерпретация сводится к определению, насколько изменилась изменчивость, представленная в виде .
Если cusum-график, относящийся к оборудованию или машине, указывает на увеличение размаха, необходимо провести техническое обслуживание для восстановления оборудования. Если эти мероприятия успешны, предпринятые действия должны быть записаны, значение кумулятивной суммы обнулено, а процесс может продолжать функционировать. Если процесс возвратился к своему предыдущему уровню изменчивости, cusum-карта может применяться для контроля.
Если cusum-график показывает уменьшение размаха, то это обычно рассматривают как позитивное событие. Специальная причина и необходимые действия должны быть идентифицированы. Маски среднего и размаха (и, возможно, бумага) должны быть скорректированы для отражения новой ситуации. Целевое значение должно также быть заменено на новое меньшее значение. Для продолжения составления графика необходимо обнулить кумулятивную сумму размаха.
Обнуление кумулятивной суммы для среднего необходимо, поскольку анализ, сделанный с использованием пересмотренной маски для среднего, показал, что размах действительно уменьшился. Новые неконтролируемые точки теперь можно наблюдать на графике среднего.
c) Оценка изменчивости. Антирысканье
Как в случае кумулятивной суммы, при контроле положения, если необходимы меры по снижению рысканья, рекомендуется использовать регулировки на величину 75% целевого размаха.
9.4.3 Cusum-схемы стандартных отклонений подгруппы
Процедура разработки cusum-схемы контроля стандартных отклонений очень похожа на аналогичную процедуру контроля размаха подгруппы. Поэтому ниже приведены положения, отличные от установленных в 9.4.2.
Рассмотренные ниже схемы контроля стандартных отклонений подгруппы предполагают, что в каждой подгруппе сделано не менее двух наблюдений. Если собранные данные содержат по одному наблюдению, в подгруппе следует использовать метод последовательных размахов.
Этап 3. Выбор cusum-схемы стандартного отклонения
В таблице 16 установлены стандартные схемы, соответствующие типовым требованиям контроля стандартного отклонения. В таблице приведены две основных схемы: CS1 c большим значением ARL на ожидаемом уровне изменчивости и CS2 c меньшим значением ARL. Схема CS2 даст некоторое количество ложных сигналов и обнаруживает значимое изменение стандартного отклонения быстрее, чем соответствующая схема CS1. В таблице 17 показана разница этих стандартных схем.
Таблица 16 - Стандартные cusum-схемы для стандартных отклонений подгруппы
Объем подгруппы | Схема CS1 | Схема CS2 | ||
2 | 2,00 | 0,50 | 2,00 | 0,25 |
3 | 1,60 | 0,35 | 1,60 | 0,15 |
4 | 1,15 | 0,35 | 1,15 | 0,20 |
4 | 1,15 | 0,35 | 1,15 | 0,20 |
5 | 0,90 | 0,35 | 0,90 | 0,20 |
6 | 0,80 | 0,32 | 0,80 | 0,20 |
7 | 0,70 | 0,30 | 0,70 | 0,20 |
8 | 0,60 | 0,30 | 0,60 | 0,20 |
9 | 0,55 | 0,30 | 0,55 | 0,20 |
10 | 0,50 | 0,30 | 0,50 | 0,20 |
12 | 0,40 | 0,30 | 0,40 | 0,20 |
15 | 0,35 | 0,27 | 0,35 | 0,18 |
20 | 0,30 | 0,23 | 0,30 | 0,16 |
Примечание 1 - Схеме CS1 соответствует средняя длина серии Примечание 2 - Схеме CS2 соответствует средняя длина серии | ||||
________________
* Текст документа соответствует оригиналу. - .
Выбирают одну из схем, CS1 или CS2. При этом должны быть использованы те же самые критерии выбора, которые были использованы при выборе схемы для среднего подгруппы. Если требуется схема с большим значением ARL, при отсутствии изменений процесса выбирают схему CS1, в противном случае выбирают схему CS2.
Независимо от выбранной схемы, значения маски фактического размера и формы должны быть умножены на оценку , чтобы определить новые маски. Это описано ниже (см. этап 5).
Этап 5. Определение оценки по данным испытательного периода
a) Для каждой подгруппы вычисляют выборочное стандартное отклонение () подгруппы.
b) Вычисляют среднее стандартное отклонение () подгруппы.
Определяют оценку стандартного отклонения подгруппы ![]() , где
, где определяют по таблице 18.
Таблица 17 - Сравнение ARL стандартных cusum-схем стандартных отклонений подгруппы
Объем подгруппы | Уровень изменчивости фактического процесса | Схема CS1 | Схема CS2 |
2 | 920,0 | 185,0 | |
2 | 7,4 | 5,6 | |
4 | 2,3 | 2,1 | |
3 | 920,0 | 155,0 | |
2 | 4,4 | 3,7 | |
4 | 1,6 | 1,5 | |
4 | 840,0 | 180,0 | |
2 | 3,2 | 2,6 | |
4 | 1,3 | 1,2 | |
5 | 820,0 | 155,0 | |
2 | 2,6 | 2,2 | |
4 | 1,1 | 1,1 | |
6 | 850,0 | 190,0 | |
2 | 2,2 | 1,9 | |
4 | <1,1 | <1,1 | |
8 | 720,0 | 180,0 | |
2 | 1,7 | 1,6 | |
4 | 1,0 | 1,0 | |
10 | 930,0 | 200,0 | |
2 | 1,5 | 1,4 | |
4 | 1,0 | 1,0 | |
12 | 840,0 | 170,0 | |
2 | 1,3 | 1,2 | |
4 | 1,0 | 1,0 | |
15 | 860,0 | 170,0 | |
2 | 1,2 | 1,1 | |
4 | 1,0 | 1,0 | |
Примечание - Данные значения являются ARL. Необходимо учитывать, что фактическая длина серии для обнаружения фактического изменения может быть больше или меньше ARL. При необходимости следует проверить вид распределения длины серии для сдвигов от целевого значения, чтобы знать средний размах длины серий. | |||
Таблица 18 - Коэффициент для определения оценки стандартного отклонения подгруппы
Объем подгруппы | |
2 | 0,7979 |
3 | 0,8862 |
4 | 0,9213 |
5 | 0,9400 |
6 | 0,9515 |
7 | 0,9594 |
8 | 0,9650 |
9 | 0,9693 |
10 | 0,9727 |
12 | 0,9776 |
15 | 0,9823 |
20 | 0,9869 |
| |
Этап 6. Определение целевого значения
а) Заданное значение
При статистическом контроле качества продукции или процессов наиболее распространенный метод установки целевого значения стандартного отклонения подгруппы описан в b) ниже. Однако могут быть случаи установки целевого значения на основе заданного значения . В этом случае целевое стандартное отклонение подгруппы вычисляют по формуле
![]() . Значение
. Значение определяют по таблице 18.
b) Значение, выбранное на основе наблюдений
На основе данных испытательного периода устанавливают целевое значение стандартного отклонения подгруппы .
Этап 7. Установление cusum-бумаги
Устанавливают cusum-таблицу (или дополняют существующую cusum-таблицу) и разрабатывают cusum-бумагу. Cusum-бумага для стандартного отклонения подгруппы может иметь другой масштаб, чем бумага для контроля среднего. Масштаб может быть выбран с использованием округления вверх или вниз до ближайшего удобного значения.
Интервал шкалы cusum-карты для стандартного отклонения подгруппы составляет . Значение
определяют по таблице 19.
Таблица 19 - Коэффициенты масштаба cusum-бумаги для стандартного отклонения подгруппы
Объем подгруппы | |
2 | 1,50 |
3 | 1,00 |
4 | 0,85 |
5 | 0,75 |
6 | 0,65 |
8 | 0,55 |
10 | 0,50 |
15 | 0,40 |
20 | 0,35 |
Этап 8. Установление cusum-маски
Используя значения и
, установленные на этапе 3, вычисляют:
a) ![]() ;
;
b) ![]() .
.
Разрабатывают маску, используя расчетные значения и
и масштаб маски, равный масштабу cusum-бумаги.
9.5 Особые ситуации
9.5.1 Большая изменчивость между подгруппами
В некоторых случаях важно часть изменчивости средних между подгруппами рассматривать как случайную изменчивость. Примером являются небольшие колебания среднего, выявленные cusum-картой, устранение которых не планируется. Для предотвращения ситуаций, когда cusum-карта непрерывно показывает неконтролируемое состояние, эти небольшие колебания должны быть включены в оценку изменчивости.
Вычисляют среднее стандартное отклонение между подгруппами (стандартная ошибка среднего) . Для этого могут быть использованы данные испытательного периода или некоторого другого периода, который является репрезентативным для изменчивости. Используют значение
в качестве шкалы cusum-бумаги и маски, вместо
для средних. В приложении А приведен метод, позволяющий идентифицировать пригодность такого подхода.
Эта процедура должна приводить к сокращению неконтролируемых точек на cusum-графике.
9.5.2 "Одиночные" данные
Для некоторых объектов контроля данные наблюдений по своей природе появляются по одному, и понятие подгруппы для таких данных не имеет смысла. Примерами являются ежемесячный объем продаж, температура резервуара с химикатами, используемыми в производственном процессе, когда данные повторных измерений температуры сделаны приблизительно в одно и то же время и не могут показывать наличие изменчивости между измерениями. В этом случае изменчивость в пределах подгруппы равна нулю, и ,таким образом, маска не может быть построена.
Другим примером является определение счета при игре в гольф. Лункам соответствует различное среднее количество ударов, и игрок в гольф определяет результат по сравнению со средним количеством ударов для каждой лунки. Совокупная сумма разностей представляет собой кумулятивную сумму.
Объемы подгрупп, равные единице, появляются в случаях, когда отбор и/или анализ выборок очень дороги.
В соответствии с принятым подходом необходимо установить объем подгруппы, равный единице, и затем действовать в соответствии с этапами, установленными в 9.3 для 1. Таким образом, контроль положения (среднего уровня) проводят по отдельным результатам наблюдений, а контроль изменчивости - по размаху между последовательными результатами наблюдений.
Целевое значение среднего должно быть ![]() , причем выборочное среднее должно быть определено по данным испытательного периода или в качестве целевого значения должно быть выбрано заданное значение. Целевое значение размаха должно быть или
, причем выборочное среднее должно быть определено по данным испытательного периода или в качестве целевого значения должно быть выбрано заданное значение. Целевое значение размаха должно быть или , определенное по последовательным разностям за испытательный период, или
![]() , если стандартное отклонение является заданным значением. Хотя объем подгруппы равен единице, эффективный объем подгруппы равен двум.
, если стандартное отклонение является заданным значением. Хотя объем подгруппы равен единице, эффективный объем подгруппы равен двум.
9.5.3 Зависимость наблюдений в серии
Одним из основных предположений, используемых при построении cusum-карты, как и для любой контрольной карты, является предположение о независимости точек на графике. В некоторых случаях независимость отсутствует, примером являются процессы с обратной связью, такой как передача информации от термостата к нагревающемуся устройству, или процессы с выраженной сезонностью, такой как в данных об объемах продаж.
Влияние cusum-графика может быть существенным и в некоторых случаях может приводить к ложным сигналам и неверным оценкам значимых изменений.
Существуют статистические критерии, позволяющие выявить наличие положительной или отрицательной зависимости данных. Прямой метод оценивает корреляцию между исходными данными в их последовательности появления, т.е. первого результата в исходных данных со вторым, второго с третьим, и т.д. Если оценка коэффициента корреляции намного больше нуля, это указывает на непосредственную связь между наблюдениями. Если коэффициент корреляции намного меньше нуля, то имеется отрицательная зависимость, которая предполагает, что при увеличении результата по сравнению с предыдущим последующий результат изменится в противоположном направлении. Это процессы с избыточным управлением. Такие корреляции легко могут быть вычислены с применением программных средств.
Диапазон значений коэффициентов корреляции - [-1; +1]. Пороговое значение, указывающее на существенное отличие коэффициента корреляции от нуля, зависит от количества точек, использованных в исследовании. Если объем набора данных небольшой, то даже большое численное значение коэффициента корреляции может быть статистически незначащим, тогда как для большого набора данных коэффициент корреляции может быть близок к нулю и интерпретирован как статистически существенный. В таблице 20 приведены приближенные значения коэффициентов корреляции.
Таблица 20 - Интервалы критических значений коэффициента корреляции
Количество пар данных | Критический интервал для коэффициента корреляции |
10 | [-0,45; 0,45] |
15 | [-0,37; 0,37] |
20 | [-0,33; 0,33] |
25 | [-0,30; 0,30] |
| |
Если вычисленное значение коэффициента корреляции находится в интервале, указанном в таблице 20, нет причин предполагать, что имеется последовательная зависимость данных. Возможно, имеется некоторая слабая последовательная зависимость, для выявления которой объем выборки слишком мал.
Если выявлена последовательная зависимость данных, необходима помощь специалиста. Дальнейшие действия могут включать более глубокий анализ процесса для выявления причин зависимости. Решение проблемы может быть простым или сложным. Если зависимость вызвана сезонностью, она может быть преодолена изменением целевого значения в каждом временном периоде. В результате значение кумулятивной суммы станет независимым от сезона.
9.5.4 Выбросы
Применение cusum-карт требует защиты от выбросов. Влияние выбросов на значение кумулятивной суммы может быть большим и может привести к появлению сигнала о неуправляемости процесса. Рекомендуется следующий простой, но эффективный метод для защиты от выбросов.
a) Результат является выбросом, если:
1) среднее подгруппы больше целевого значения плюс 3 или меньше целевого значения минус 3
;
2) отдельный результат больше целевого значения плюс 3 или меньше целевого значения минус 3
.
Такой результат фиксируют как выброс и не используют его при вычислении кумулятивной суммы, если последующий результат не является подозрительным на выброс.
b) Результат является подозрительным на выброс, если:
1) среднее подгруппы больше целевого значения плюс 2 или меньше целевого значения минус 2
;
2) отдельный результат больше целевого значения плюс 2 или меньше целевого значения минус 2
.
Если два последовательных результата находятся вне границ подозрения на выброс, их оба используют при вычислении кумулятивной суммы. Это почти всегда приводит к получению сигнала о неконтролируемости процесса.
Примечание - Более строгие методы обнаружения выбросов приведены в ИСО 5727-5. Они не очень применимы в режиме реального времени. Метод, установленный в настоящем стандарте, является простым, применимым на практике.
9.6 Cusum-схемы для дискретных данных
9.6.1 Количество событий. Распределение Пуассона
9.6.1.1 Общие положения
Иногда данные представляют собой количество событий, а каждый элемент данных - количество событий за определенный период времени или количество продукции. Такими данными являются: количество несчастных случаев или количество отсутствующих за месяц, количество срабатываний или вылетов в день, количество входящих телефонных звонков в минуту или число несоответствий на единицу продукции или партию.
Распределение Пуассона имеет два важных значения для cusum-анализа:
a) это распределение является приближением более громоздкого биномиального распределения (см. 9.6.2), при большом и малом
, например
20 и
;
b) распределение используется самостоятельно, когда случайные события происходят во времени или пространстве, а наблюдением является количество событий в заданном интервале времени или объеме.
Для распределения Пуассона характерны независимость событий и постоянная интенсивность их реализации (в отсутствие специальных причин).
Поскольку плотность распределения Пуассоном (а также биномиального) не симметрична, для выявления сдвига процесса вверх и вниз необходимо использовать различные правила принятия решения. Поэтому усеченная V-маска в этом случае не симметрична, имеет различные значения угловых коэффициентов и интервалы решений в верхней и нижней частях.
Для обеспечения простоты вычислений в некоторых случаях используют аппроксимацию одних распределений другими. Например, распределение Пуассона или нормальное распределение используют как аппроксимацию биномиального распределения, а нормальное распределение - как аппроксимацию распределения Пуассона.
В 9.3 и 9.4 значения ARL для данных, подчиняющихся нормальному распределению, определены на основе нормированного нормального распределения со средним 0 и стандартным отклонением 1. Для дискретных распределений каждый параметр должен быть вычислен отдельно. Поэтому для дискретных распределений рассмотрены только ситуации, связанные со смещением процесса вверх. В настоящее время программное обеспечение позволяет решить эту задачу и для сдвига процесса вниз.
9.6.1.2 Общие правила решений для дискретных данных
Cusum-схема для дискретных данных неоднозначно определяется видом распределения данных и двумя параметрами: значением показателя и интервалом принятия решений
. При выборе параметров необходимо руководствоваться следующим.
а) Разработка cusum-схемы включает два этапа:
1) выбор комбинации и
для обеспечения желательного значения ARL;
2) определение скорости появления сигнала при различных сдвигах среднего.
b) Значение должно быть выбрано на основе заданного значения среднего, которое дает сигнал. Удобным значением
является значение между средним управляемого процесса и средним неуправляемого процесса, для которых кумулятивная сумма должна быть максимально чувствительной. Значение
зависит от вида распределения данных и приемлемого значения среднего.
9.6.1.3 Cusum-схемы для дискретных данных
Этап 1. Определение фактических средней интенсивности и стандартного отклонения
.
Этап 2. Выбор опорной или целевой интенсивности . Часто
![]() .
.
Этап 3. Выбор наиболее подходящего правила принятия решений на основе выбора применимой схемы. Предпочтительными вариантами являются схемы CS1 с ARL не менее 1000 для процесса уровня целевого значения или схема CS2 с ARL не менее 200 для процесса уровня целевого значения (см. таблицу 21).
Этап 4. Определение значений и
:
a) для выбранного значения (0,1
![]() 25,0) по таблице 21 определяют значения
25,0) по таблице 21 определяют значения и
. При необходимости используют линейную интерполяцию между значениями
от 10,0 до 25,0;
b) если 25,0 для определения
и
используют таблицы 9.3 для нормального распределения с
![]() (нормальное приближение распределения Пуассона).
(нормальное приближение распределения Пуассона).
Например, если 25, для нормальной переменной со средним 25 и стандартным отклонением 5
24 и
28. Соответствующее значение ARL приблизительно равно 1500. Истинное значение ARL для переменной из распределения Пуассона с
24 и
28 равно 1085. Это уменьшение значения ARL является следствием несимметричности распределения Пуассона.
Этап 5. Построение и применение V-маски или таблицы:
a) на cusum-карте строят cusum-график разностей (![]() ) и используют усеченную V-маску с интервалом решения
) и используют усеченную V-маску с интервалом решения и угловым коэффициентом
![]() ;
;
b) для табличного cusum формируют сумму разностей (![]() ), обнуляя ее всякий раз, когда накопленная сумма становится отрицательной. Проверяют
), обнуляя ее всякий раз, когда накопленная сумма становится отрицательной. Проверяют на наличие сигнала о сдвиге.
Этап 6. Определение ARL для выбранной схемы при исследуемых сдвигах от номинала в соответствии с таблицей 22.
Пример
Этап 2. Опорная средняя интенсивность =4.
Этап 3. Используемая схема CS1.
Этап 4. В соответствии с таблицей 21 для =4,0,
=8 и
=6.
Этап 5 а). Изображение cusum-графика и применение V-маски (=8,
=2).
Этап 5 b). Разработка cusum-таблицы (=8,
=6).
Этап 6. Выполнение схемы показано ниже. Для процесса на целевом уровне ARL () равен 1736. Однако ARL уменьшается на 10 для интенсивности 6,60.
ARL | 1000 | 500 | 200 | 100 | 50 | 20 | 10 | 5 | 2 | |||||
8,0 | 6,00 | 4,000 | 1736 | m | 4,160 | 4,380 | 4,710 | 5,000 | 5,300 | 5,90 | 6,60 | 7,80 | 11,50 |
Примечание - Данные взяты из таблицы 22.
9.6.2 Биномиальные данные
9.6.2.1 Общие положения
Возможна ситуация, когда каждый элемент данных относится к одной из нескольких категорий. Часто категорий две. Это случай биномиального распределения, когда результат обычно выражается в виде 0 или 1 и соответствует работоспособному/неработоспособному состоянию, прибыли/убыткам, наличию/отсутствию определенного свойства.
Такие данные называют биномиальными данными. Иногда данные характеризуют попадание другой количественной меры в некоторый интервал, например телефонные переговоры могут быть разделены по продолжительности менее или более 10 минут.
Таблица 21 - Значения и
схем CS1 и CS2 для распределения Пуассона
Целевое значение | Схема CS1 | Схема CS2 | ||
0,100 | 1,5 | 0,75 | 2,0 | 0,25 |
0,125 | 2,5 | 0,50 | 2,5 | 0,25 |
0,160 | 3,0 | 0,50 | 2,0 | 0,50 |
0,200 | 3,5 | 0,50 | 2,5 | 0,50 |
0,250 | 4,0 | 0,50 | 3,0 | 0,50 |
0,320 | 3,0 | 1,00 | 4,0 | 0,50 |
0,400 | 2,5 | 1,50 | 3,0 | 1,00 |
0,500 | 3,0 | 1,50 | 2,0 | 1,50 |
0,640 | 3,5 | 1,50 | 2,0 | 2,00 |
0,800 | 5,0 | 1,50 | 3,5 | 1,50 |
1,000 | 5,0 | 2,00 | 5,0 | 1,50 |
1,250 | 4,0 | 3,00 | 5,0 | 2,00 |
1,600 | 5,0 | 3,00 | 4,0 | 3,00 |
2,000 | 7,0 | 3,00 | 5,0 | 3,00 |
2,500 | 7,0 | 4,00 | 5,0 | 4,00 |
3,200 | 7,0 | 5,00 | 5,0 | 5,00 |
4,000 | 8,0 | 6,00 | 6,0 | 6,00 |
5,000 | 9,0 | 7,00 | 7,0 | 7,00 |
6,400 | 9,0 | 9,00 | 9,0 | 8,00 |
8,000 | 9,0 | 11,00 | 9,0 | 10,00 |
10,000 | 11,0 | 13,00 | 11,0 | 12,00 |
15,000 | 16,0 | 18,00 | 11,0 | 18,00 |
20,000 | 20,0 | 23,00 | 14,0 | 23,00 |
25,000 | 24,0 | 28,00 | 17,0 | 28,00 |
Примечание 1 - Схеме CS1 обычно соответствуют значения ARL от 1000 до 2000 наблюдений. Схеме CS2 обычно соответствуют значения ARL от 200 до 400 наблюдений. Примечание 2 - Для Примечание 3 - Значение Примечание 4 - Интервал значений | ||||
Таблица 22 - Значения ARL для cusum-схем (распределение Пуассона)
Схема CS1 | Схема CS2 | Среднее значение ARL | ||||||||||||
1000 | 500 | 200 | 100 | 50 | 20 | 10 | 5 | 2 | ||||||
2,0 | 0,25 | - | - | 0,100 | 212 | 0,057 | 0,072 | 0,102 | 0,135 | 0,179 | 0,29 | 0,43 | 0,74 | 1,99 |
2,5 | 0,25 | - | - | 0,125 | 227 | 0,078 | 0,097 | 0,131 | 0,166 | 0,220 | 0,33 | 0,49 | 0,82 | 2,12 |
2,0 | 0,50 | - | - | 0,160 | 230 | 0,095 | 0,121 | 0,168 | 0,220 | 0,280 | 0,42 | 0,59 | 0,91 | 2,09 |
1,5 | 0,75 | 0,100 | 1033 | - | - | 0,120 | 0,130 | 0,181 | 0,240 | 0,320 | 0,46 | 0,66 | 0,99 | 2,11 |
2,5 | 0,50 | 0,125 | 1371 | 0,200 | 278 | 0,138 | 0,167 | 0,220 | 0,280 | 0,350 | 0,49 | 0,68 | 1,05 | 2,32 |
3,0 | 0,50 | 0,160 | 1609 | 0,250 | 264 | 0,179 | 0,210 | 0,270 | 0,330 | 0,400 | 0,56 | 0,77 | 1,12 | 2,74 |
3,5 | 0,50 | 0,200 | 1461 | - | - | 0,220 | 0,250 | 0,310 | 0,370 | 0,440 | 0,60 | 0,84 | 1,31 | 3,02 |
4,0 | 0,50 | 0,250 | 966 | 0,320 | 271 | 0,250 | 0,280 | 0,340 | 0,400 | 0,470 | 0,65 | 0,91 | 1,41 | 3,37 |
3,0 | 1,00 | 0,320 | 1174 | 0,400 | 446 | 0,330 | 0,390 | 0,480 | 0,570 | 0,690 | 0,91 | 1,17 | 1,63 | 3,08 |
2,0 | 1,50 | - | - | 0,500 | 260 | 0,360 | 0,420 | 0,540 | 0,640 | 0,780 | 1,04 | 1,32 | 1,78 | 3,17 |
2,5 | 1,50 | 0,400 | 1103 | - | - | 0,410 | 0,490 | 0,610 | 0,730 | 0,890 | 1,15 | 1,46 | 1,93 | 3,37 |
2,0 | 2,00 | - | - | 0,640 | 221 | 0,420 | 0,510 | 0,650 | 0,790 | 0,970 | 1,27 | 1,58 | 2,09 | 3,44 |
3,0 | 1,50 | 0,500 | 1475 | - | - | 0,540 | 0,620 | 0,740 | 0,860 | 1,010 | 1,28 | 1,60 | 2,12 | 3,85 |
3,5 | 1,50 | 0,640 | 833 | 0,800 | 249 | 0,620 | 0,700 | 0,830 | 0,950 | 1,100 | 1,38 | 1,70 | 2,26 | 3,74 |
4,0 | 1,50 | 0,640 | 1843 | - | - | 0,700 | 0,790 | 0,920 | 1,040 | 1,190 | 1,47 | 1,81 | 2,38 | 4,44 |
5,0 | 1,50 | 0,800 | 1439 | 1,000 | 274 | 0,840 | 0,920 | 1,040 | 1,160 | 1,310 | 1,60 | 1,95 | 2,64 | 5,25 |
5,0 | 2,00 | 1,000 | 1904 | 1,250 | 259 | 1,090 | 1,190 | 1,350 | 1,500 | 1,680 | 2,00 | 2,37 | 3,09 | 5,90 |
4,0 | 3,00 | 1,250 | 1867 | 1,600 | 354 | 1,380 | 1,530 | 1,750 | 1,950 | 2,200 | 2,61 | 3,04 | 3,76 | 6,35 |
5,0 | 3,00 | 1,600 | 1118 | 2,000 | 188 | 1,640 | 1,770 | 1,940 | 2,180 | 2,420 | 2,83 | 3,29 | 4,07 | 6,60 |
7,0 | 3,00 | 2,000 | 894 | - | - | 1,980 | 2,110 | 2,310 | 2,490 | 2,710 | 3,09 | 3,57 | 4,59 | 7,55 |
8,0 | 3,00 | 2,000 | 1927 | - | - | 2,110 | 2,330 | 2,430 | 2,600 | 2,810 | 3,23 | 3,78 | 4,80 | 8,40 |
5,0 | 4,00 | - | - | 2,500 | 300 | 2,170 | 2,350 | 2,600 | 2,870 | 3,160 | 3,63 | 4,16 | 5,00 | 7,60 |
7,0 | 4,00 | 2,500 | 1761 | - | - | 2,620 | 2,800 | 3,050 | 3,260 | 3,450 | 3,99 | 4,53 | 5,60 | 8,85 |
5,0 | 5,00 | - | - | 3,200 | 245 | 2,730 | 2,940 | 3,270 | 3,560 | 3,890 | 4,45 | 5,00 | 6,00 | 8,50 |
7,0 | 5,00 | 3,200 | 1318 | - | - | 3,280 | 3,480 | 3,780 | 4,030 | 4,320 | 4,88 | 5,50 | 6,50 | 9,80 |
6,0 | 6,00 | - | - | 4,000 | 373 | 3,640 | 3,880 | 4,240 | 5,550 | 4,930 | 5,50 | 6,20 | 7,20 | 10,40 |
8,0 | 6,00 | 4,000 | 1736 | - | - | 4,160 | 4,380 | 4,710 | 5,000 | 5,300 | 5,90 | 6,60 | 7,80 | 11,50 |
7,0 | 7,00 | - | - | 5,000 | 348 | 4,600 | 4,840 | 5,200 | 5,600 | 5,900 | 6,60 | 7,30 | 8,50 | 11,60 |
9,0 | 7,00 | 5,000 | 1268 | - | - | 5,100 | 5,300 | 5,700 | 6,000 | 6,400 | 6,90 | 7,70 | 9,10 | 13,50 |
9,0 | 8,00 | - | - | 6,400 | 226 | 5,800 | 6,100 | 6,500 | 6,800 | 7,200 | 7,90 | 8,60 | 10,00 | 14,20 |
9,0 | 9,00 | 6,400 | 1351 | - | - | 6,500 | 6,800 | 7,200 | 7,600 | 8,100 | 8,80 | 9,60 | 11,10 | 15,20 |
9,0 | 10,00 | - | - | 8,000 | 213 | 7,200 | 7,600 | 8,000 | 8,400 | 8,900 | 9,70 | 10,50 | 11,90 | 16,20 |
9,0 | 11,00 | 8,000 | 946 | - | - | 8,000 | 8,300 | 8,800 | 9,300 | 9,800 | 10,50 | 11,40 | 13,00 | 16,40 |
11,0 | 12,00 | - | - | 10,000 | 234 | 9,300 | 9,600 | 10,100 | 10,500 | 11,000 | 11,90 | 12,80 | 14,60 | 19,80 |
11,0 | 13,00 | 10,000 | 1052 | - | - | 10,000 | 10,400 | 11,000 | 11,400 | 11,900 | 12,70 | 13,70 | 15,50 | 20,30 |
11,0 | 18,00 | - | - | 15,000 | 214 | 13,900 | 14,300 | 15,100 | 15,600 | 16,300 | 17,40 | 18,50 | 20,40 | 25,90 |
16,0 | 18,00 | 15,000 | 1289 | - | - | 15,100 | 15,500 | 16,100 | 16,500 | 17,200 | 18,20 | 19,40 | 21,70 | 29,10 |
14,0 | 23,00 | - | - | 20,000 | 215 | 18,800 | 19,300 | 20,100 | 20,700 | 21,400 | 22,60 | 24,00 | 26,20 | 32,90 |
20,0 | 23,00 | 20,000 | 1140 | - | - | 20,100 | 20,500 | 21,100 | 21,700 | 22,300 | 23,50 | 24,90 | 27,60 | 36,80 |
17,0 | 28,00 | - | - | 25,000 | 222 | 23,700 | 24,300 | 25,100 | 25,800 | 26,500 | 27,80 | 29,30 | 31,90 | 40,00 |
24,0 | 28,00 | 25,000 | 1085 | - | - | 25,100 | 25,500 | 26,200 | 26,700 | 27,400 | 28,70 | 30,40 | 33,50 | 44,90 |
Примечание - Таблица относится к сдвигам среднего вверх. | ||||||||||||||
Условия, при выполнении которых данные могут быть отнесены к биномиальному распределению:
a) фиксированное количество испытаний ;
b) в каждом испытании возможны лишь два исхода;
c) испытания независимы;
d) в каждом испытании вероятность "успеха" постоянная;
e) наблюдение представляет собой общее количество "успехов" в испытаниях.
Биномиальное распределение является очень громоздким для вычислений, поэтому для вычисления ARL и критериев принятия решений могут быть использованы аппроксимации биномиального распределения другими распределениями.
Из-за большого диапазона возможных значений параметров биномиального распределения и
составление таблиц для всех возможных комбинаций невозможно. Однако во многих случаях могут быть применены приближенные процедуры:
- ситуация 1. 0,1 (т.е. целевое или опорное значение равно 10%), используют соответствующую схему для распределения Пуассона с
![]() .
.
- ситуация 2. 20 (т.е. среднее количество событий на выборку в целевых условиях превышает 20), используют соответствующую схему для нормального распределения.
9.6.2.2 ситуация 1: 0,1
В данном случае используют аппроксимацию биномиального распределения распределением Пуассона. Может быть применим метод, установленный в 9.6.1.3, для ![]() . Использование распределения Пуассона всегда дает значение ARL меньше, чем использование биномиального распределения. Однако при существенных отклонениях от целевых условий значения ARL близки друг к другу.
. Использование распределения Пуассона всегда дает значение ARL меньше, чем использование биномиального распределения. Однако при существенных отклонениях от целевых условий значения ARL близки друг к другу.
Пример
Этап 2. Пусть n=20 и p=0,025. Таким образом, np=0,5 и =0,5.
Этап 3. Использована схема CS1.
Этап 4. В соответствии с таблицей 21 для =0,5,
=3 и
=1,5.
Этап 5 а). Строят cusum-график, разрабатывают и применяют V-маску (=3,
=1,0).
Этап 5 b). Разрабатывают cusuт-таблицу (=3,
=1,5).
Этап 6. Выполнение схемы показано ниже. Если процесс работает на целевом уровне, ARL () равно 1475. Однако ARL снижается на 10, если интенсивность повышается до 1,60, т.е. p=0,080.
ARL | 1000 | 500 | 200 | 100 | 50 | 20 | 10 | 5 | 2 | |||||
3,0 | 1,50 | 0,500 | 1475 | m | 0,540 | 0,620 | 0,740 | 0,860 | 1,010 | 1,28 | 1,60 | 2,12 | 3,85 |
Примечание - Данные взяты из таблицы 22.
9.6.2.3 Ситуация 2: 20
В ситуации 2 выбирают подходящую пару параметров ,
, например, 5 и 0,5, для соответствующей нормальной переменной. Cusum-параметры для биномиального распределения определяют по следующим формулам:
![]() с округлением
с округлением до ближайшего целого числа.
![]() с округлением
с округлением до ближайшего целого числа.
![]() с округлением
с округлением до ближайшего целого числа.
Пример
Этап 2. Пусть n=80 и =0,3, h=5 и
=0,5.
Этап 4. ![]() .
.
![]() .
.
![]() .
.
Этап 5 а). Графическое представление кумулятивной суммы, разработка и применение V-маски (H=20, F=2).
Этап 5 b). Разработка cusum-таблицы ( =20,
=26).
Этап 6. Если процесс находится на целевом уровне, ARL () равна приблизительно 930. Однако, ARL уменьшится приблизительно на 10, если p увеличится до 0,35.
Приложение А
(справочное)
Метод Неймана
При разработке cusum-карты для представления данных, как правило, выбор процедуры измерения изменчивости основывают на свойствах и особенностях данных метода отбора выборки и удобства вычислений. Однако при использовании статистических критериев для выявления точек изменения или сдвига процесса должна быть изучена возможность наличия зависимости последовательных данных.
Полезный общий критерий выявления аномальных наблюдений в серии, по которой определяют оценку стандартной ошибки, состоит в следующем.
1. Вычисляют .
2. Вычисляют ![]() .
.
3. Определяют количество подгрупп .
4. Вычисляют  .
.
5. Вычисляют ![]() .
.
Если значение, вычисленное на этапе 4, больше верхней границы интервала, вычисленного на этапе 5, имеется отрицательная последовательная корреляция данных, например сверх управление или чередование. Значение ниже нижней границы интервала, вычисленного на этапе 5, может быть результатом циклического повторения или других форм положительной последовательной корреляции, например, отдельных воздействий на средний уровень в пределах последовательности наблюдений, регулярных или нерегулярных изменений дрейфа или тренда.
Наоборот, расчетное значение на этапе 4 может быть оценено по таблице А.1 для точек вероятности 0,05 (с двумя хвостами).
Таблица А.1 - Вероятностные точки (с двумя хвостами) критерия Неймана
Количество подгрупп | Нижнее критическое значение | Верхнее критическое значение |
20 | 0,58 | 1,42 |
30 | 0,65 | 1,35 |
50 | 0,73 | 1,27 |
75 | 0,78 | 1,22 |
150 | 0,84 | 1,16 |
200 | 0,86 | 1,14 |
Приложение В
(справочное)
Пример табличного cusum
Среднее 35 и стандартное отклонение 6 были получены по предыдущим данным и использованы в качестве параметров для карты Шухарта и cusum-карты. Было установлено целевое значение 35.
Были собраны данные за двадцать четыре дня: 25,8; 33,4; 31,6; 26,0; 36,4; 33,0; 35,8; 41,8; 44,2; 37,2; 35,0; 41,8; 33,4; 38,4; 30,2; 33,8; 42,6; 39,6; 32,0; 48,4; 44,6; 43,0; 40,8 и 50,6.
Карта Шухарта показана на рисунке B.1. С помощью стандартных критериев карты Шухарта не получено никаких сигналов.
|
Рисунок В.1 - Карта Шухарта для среднего
Cusum-график данных показан на рисунке В.2. Он показывает "сигнал" в день N 24. Карта Шухарта на рисунке В.1 не обнаруживает это изменение.
|
Рисунок В.2 - Cusum-график и V-маска для среднего
Табличная версия этой cusum-карты показана в таблице В.1.
Таблица В.1 - Cusum-таблица для средних
(1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
День | Среднее за день ( | ( | Сумма "Hi" | Номер "Hi" | ( | Сумма "Lo" | Номер "Lo" |
0 | 15,0 | 0 | -15,0 | 0 | |||
1 | 25,8 | -12,2 | 2,8 | 1 | -6,2 | -21,2 | 1 |
2 | 33,4 | -4,6 | 0,0 | 0 | 1,4 | -19,8 | 2 |
3 | 31,6 | -6,4 | 0,0 | 0 | -0,4 | -20,2 | 3 |
4 | 26,0 | -12,0 | 0,0 | 0 | -6,0 | -26,2 | 4 |
5 | 36,4 | -1,6 | 0,0 | 0 | 4,4 | -21,8 | 5 |
6 | 33,0 | -5,0 | 0,0 | 0 | 1,0 | -20,8 | 6 |
7 | 35,8 | -2,2 | 0,0 | 0 | 3,8 | -17,0 | 7 |
8 | 41,8 | 3,8 | 3,8 | 1 | 9,8 | -7,2 | 8 |
9 | 44,2 | 6,2 | 10,0 | 2 | 12,2 | 0,0 | 0 |
10 | 37,2 | -0,8 | 9,2 | 3 | 5,2 | 0,0 | 0 |
11 | 35,0 | -3,0 | 6,2 | 4 | 3,0 | 0,0 | 0 |
12 | 41,8 | 3,8 | 10,0 | 5 | 9,8 | 0,0 | 0 |
13 | 33,4 | -4,6 | 5,4 | 6 | 1,4 | 0,0 | 0 |
14 | 38,4 | 0,4 | 5,8 | 7 | 6,4 | 0,0 | 0 |
15 | 30,2 | -7,8 | 0,0 | 0 | -1,8 | -1,8 | 1 |
16 | 33,8 | -4,2 | 0,0 | 0 | 1,8 | 0,0 | 0 |
17 | 42,6 | 4,6 | 4,6 | 1 | 10,6 | 0,0 | 0 |
18 | 39,6 | 1,6 | 6,2 | 2 | 7,6 | 0,0 | 0 |
19 | 32,0 | -6,0 | 0,2 | 3 | 0,0 | 0,0 | 0 |
20 | 48,4 | 10,4 | 10,6 | 4 | 16,4 | 0,0 | 0 |
21 | 44,6 | 6,6 | 17,2 | 5 | 12,6 | 0,0 | 0 |
22 | 43,0 | 5,0 | 22,2 | 6 | 11,0 | 0,0 | 0 |
23 | 40,8 | 2,8 | 25,0 | 7 | 8,8 | 0,0 | 0 |
24 | 50,6 | 12,6 | 37,6 | 8 | 18,6 | 0,0 | 0 |
Примечание - | |||||||
В этой cusum-таблице использован "быстрый начальный отклик" (FIR), таким образом, начальное значение помещено в "День 0" в "Сумму Hi" и "Сумму Lo". Это значение равно +2,5 и -2,5
соответственно, или +15,0 и -15,0. Аналогично 0 помещен в столбцы "Номер Hi" и "Номер Lo" в "День 0". Таким образом,
![]() , границы сигнала составляют +30 и -30, соответственно.
, границы сигнала составляют +30 и -30, соответственно.
Значение для "Дня 1" равно 25,8. Вычисления для колонки (3) следующие:
25,8-35-3=-12,2.
Значение (-12,2) прибавляют к предыдущему значению 15,0 в колонке "Сумма Hi" (-12,2+15,0=2,8). Так как 2,8 положительно, к предыдущему значению колонки "Номер Hi" добавляют единицу. Новое значение в колонке "Номер Нi" равно 1.
Вычисления для столбца (6):
25,8-35+3=-6,2.
Значение (-6,2) прибавляют к предыдущему значению колонки "Сумма Lo" (-15,0), получая (-21,2). Так как (-21,2) отрицательно, добавляют 1 к предыдущему значению в колонке "Номер Lo", т.е. 0. Новый номер Lo равен 1.
Для вычислений рекомендуется использовать компьютер.
Среднее за "День 2" составило 33,4. Вычисления для столбца (3) следующие:
33,4-35-3=-4,6 .
Значение (-4,6) прибавляют к предыдущему значению (2,8) колонки "Сумма Hi", получая в результате (-1,8). Так как это значение отрицательно, значение в колонке "Сумма Hi" изменяют на 0, и "Номер Hi" также изменяют на 0, т.е. для этой стороны cusum-карты считаются только положительные значения cusum.
Вычисления для столбца (6):
33,4-35+3=1,4.
Значение 1,4 прибавляют к предыдущему значению (-21,2) в колонке "Сумма Hi", получают (-19,8). Поскольку (-19,8) отрицательно, к предыдущему значению колонки "Номер Lo" прибавляют 1 (значение в колонке "Номер Lo" равно 2).
Эту процедуру продолжают до тех пор, пока значение в колонках "Сумма Hi" или "Сумма Lо" не превысит значение (30 или -30 в данном примере). Это происходит на 24-й день, когда "Сумма Hi" принимает значение 37,6.
Анализ того, когда произошел сдвиг, и определение его величины могут быть выполнены по таблице. Из таблицы В.1 видно, что "Сумма Hi" и "Сумма Lо" уменьшаются достаточно быстро, если уровень процесса находится вблизи целевого значения. Если это не так, то обычно "Сумма Hi" и "Сумма Lо" дают сигнал об изменении процесса.
В данном примере сигнал дает "Сумма Hi". При этом "Номер Hi" равен 8. Это означает, что изменение произошло между 16-м и 17-м днем. Оценка сдвига в предположении отсутствия FIR равна
![]() .
.
Если выявленный сдвиг отрицателен, оценка равна
![]() .
.
Так как "Сумма Hi" превысила значение 30, оценка сдвига
![]() .
.
Примечание - Последние восемь значений исходных данных смещены вверх приблизительно на одно стандартное отклонение, т.е. на 6 единиц. Таким образом, кумулятивная сумма выявила место сдвига и позволила оценить его величину (7,7), которая не существенно отличается от 6.
На рисунке В.3 представлен cusum-график, соответствующий таблице.
|
Рисунок В.3 - Cusum-график, соответствующий таблице В.1
Приложение С
(справочное)
Определение точки изменений
Управляемость процесса может быть определена по контрольным картам при использовании определенных критериев, но контрольные карты не могут выявить неслучайную причину изменчивости процесса. Однако анализ предыдущих графиков на контрольных картах может дать информацию для поиска неслучайных причин. Это важная роль, которую выполняет оценка точки изменения.
В случае изменения среднего процесса , точку изменения можно описать системой уравнений:
![]() .
.
Cusum-карта обладает возможностью определения точки изменения процесса. Точка изменения - это момент времени, когда cusum-график выходит за границы V-маски, как показано на рисунке С.1.
|
Рисунок С.1 - Точка изменения на усеченной V-маске
На рисунке С.2 показано распределение точки изменения на cusum-карте при использовании схемы CS1 (0,5,
0,5). Ошибка первого рода должна быть учтена, поскольку изменения определяют только после того, как карта выявляет сигнал об изменении процесса. Поэтому распределение, представленное на рисунке С.2 получено при условии отсутствия ошибки первого рода.
Распределение является унимодальным, и его мода указывает на истинную точку изменения 10. Несмотря на то что величина сдвига не велика (см. рисунок С.2) и составляет
![]() , такой подход предпочтителен.
, такой подход предпочтителен.
|
Примечание - Для усеченной V-маски с параметрами 5,0,
0,5,
1,0 и
10.
Рисунок С.2 - Распределение точки изменения процесса при использовании cusum-карты
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | Nishina K. Estimation of the change-point from cumulative sum tests. Reports of Statistical Application Research, JUSE, 33(4), 1986 | |
[2] | Nishina K. Estimation of the amount of shift using cumulative sum tests. Reports of Statistical Application Research, JUSE, 35(3), 1988 | |
[3] | Nishina K. A comparison of control charts from the viewpoint of change-point estimation. Quality and Reliability Engineering International, 8, 1992 | |
[4] | ISO 5725-5 | Accuracy (trueness and precision) of measurement methods and results - Part 5: Alternative methods for the determination of the precision of a standard measurement method |
[5] | ISO 7870-1 | Control charts - Part 1: General guidelines |
[6] | ISO 7870-2 | Control charts - Part 2: Shewhart control charts |
[7] | ISO 9000 | Quality management systems - Fundamentals and vocabulary |
[8] | BS 5703 | Guide to data analysis, quality control and improvement using cusum techniques |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: статистический приемочный контроль, контроль по альтернативному признаку, контрольная карта, контрольная карта Шухарта, приемочная контрольная карта, статистическое управление процессом, приемлемость процесса, выборка, отбор выборки, единица продукции, несоответствие, несоответствующая единица продукции, процент несоответствующих единиц продукции, объем выборки | |
Электронный текст документа
и сверен по:
, 2020