ГОСТ Р ИСО 28596-2024 Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Двухступенчатые планы для аудита и контроля при наличии априорной информации

ГОСТ Р ИСО 28596-2024

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

ПРОЦЕДУРЫ ВЫБОРОЧНОГО КОНТРОЛЯ ПО АЛЬТЕРНАТИВНОМУ ПРИЗНАКУ

Двухступенчатые планы для аудита и контроля при наличии априорной информации

Statistical methods. Sampling procedures for inspection by attributes. Two-stage plans for auditing and for inspection under prior information

ОКС 03.120.30

Дата введения 2025-01-01

Предисловие

1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 июля 2024 г. № 1004-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 28596:2022* "Процедуры выборочного контроля по альтернативному признаку. Двухступенчатые планы для аудита и контроля при наличии априорной информации" (ISO 28596:2022 "Sampling procedures for inspection by attributes - Two-stage sampling plans for auditing and for inspection under prior information", IDT).

Международный стандарт разработан Техническим комитетом ТК 69 Международной организации по стандартизации (ИСО).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА.

Дополнительная сноска в тексте стандарта, выделенная курсивом, приведена для пояснения текста оригинала

5 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)

Введение

Настоящий стандарт имеет несколько сфер применения: финансовый аудит, контроль качества партий, аудит качества продукции, функциональные испытания, проверка соответствия и приемо-сдаточные испытания. Во всех этих сферах возникает проблема принятия решения о приемке или отклонении гипотезы о соответствии объекта проверки установленной цели.

Двухступенчатая схема контроля, приведенная в настоящем стандарте, охватывает три области контроля:

a) определение объема выборки в соответствии с априорной информацией о состоянии объекта;

b) обеспечение возможности быстрого принятия решения по выборкам небольшого объема, если контролируемая совокупность на самом деле находится в очень хорошем или очень плохом состоянии, и использование большого объема выборки только в том случае, если контролируемая совокупность находится в среднем состоянии;

c) защита от ошибок двух видов:

1) ошибочного отклонения приемлемого (в соответствии с целью) объекта;

2) ошибочного принятия неприемлемого (в соответствии с целью) объекта.

Для выполнения требования, приведенного в перечислении а), планы выборочного контроля проиндексированы по показателю доверия с тремя уровнями (низким, средним, высоким), при этом повышение уровня доверия соответствует уменьшению объема выборки. Для выполнения требования, приведенного в перечислении b), в настоящем стандарте установлены двухступенчатые планы контроля с небольшим объемом выборки на первом этапе и большим объемом выборки на втором, когда решение обычно принимают уже на первом этапе, если контролируемая совокупность, находится где-то посередине между наихудшим и наилучшим состояниями.

Схема выборочного контроля, приведенная в настоящем стандарте, особенно подходит для финансового аудита, как для аудита системы внутреннего контроля (ICS), так и для проверки деталей существующих процедур финансового аудита. Оба эти варианта обычно основаны на выборочном, а не на сплошном контроле. Соответствующий стандарт ISA 530 требует, чтобы выборочный контроль позволял делать выводы о всей совокупности. Следует отметить, что схемы статистического выборочного контроля являются обязательными.

Результаты предыдущего контроля являются важной основой при выборе уровня показателя доверия для последующих проверок. Таким образом, дальнейшее использование схемы выборочного контроля, установленной в настоящем стандарте, служит стимулом для поставки объектов с соответствующими целевыми показателями, например для органов, ответственных за ICS (систему внутреннего контроля) в организации, а также для повышения качества целевых совокупностей.

Процедура принятия решения на основе выборочного контроля максимально проста. От пользователя не требуется применения сложных формул.

Целевую совокупность считают приемлемой, если доля несоответствующих единиц в совокупности не превышает заданного значения

, в противном случае совокупность считают неприемлемой. Соответственно, цель выборочного контроля состоит в том, чтобы обеспечить возможность принятия одного из двух решений: "о приемке" или "об отклонении". Поскольку в разных областях применения термины "приемка" и "отклонение" имеют различное толкование, см. пояснения в разделе 5.

Процедуру выборочного контроля начинают с первой выборки объема

со следующим правилом принятия решения: приемка возможна только тогда, когда среди

отобранных единиц не обнаружено несоответствующих единиц; отклонение возможно только тогда, когда среди

отобранных единиц обнаружено не менее

несоответствующих единиц (браковочное число этапа 1); к следующему этапу контроля переходят только тогда, когда не менее одной и не более (

-1) несоответствующих единиц обнаружено среди

отобранных единиц. На втором этапе отбирают

единиц и принимают решение о приемке только тогда, когда количество несоответствующих единиц в объединенной выборке (с объемом

+

) менее или равно приемочному числу

второго этапа, в противном случае принимают решение об отклонении. Двухступенчатая процедура принятия решения может быть выражена эквивалентно путем сравнения границ двустороннего доверительного интервала, соответствующего номинальной доверительной вероятности

для доли несоответствующих единиц, с допуском

.

Планы выборочного контроля индексированы по трем величинам:

i) значению

,

ii) номинальному значению доверительной вероятности

, которое равно соответственно 0,7, 0,8, 0,9, 0,95 или 0,99;

iii) трем уровням показателя доверия: низкому, среднему, высокому.

Уровни показателя доверия выражают степень уверенности пользователя в состоянии целевой совокупности.

Цель настоящего стандарта состоит в установлении процедур, позволяющих быстро и экономично принимать решение, если доля несоответствующих единиц совокупности мала или высока. В последнем случае процедура контроля в большинстве случаев завершается на этапе 1 при небольших объемах выборки

. Только при промежуточных значениях доли несоответствующих единиц в целевой совокупности вероятность перехода ко второму этапу контроля высока. Два объема выборки на этапах 1 и 2 выбраны таким образом, чтобы минимизировать средний объем выборки для заданной доверительной вероятности и заданного уровня показателя доверия.

1 Область применения

Настоящий стандарт устанавливает двухступенчатые планы выборочного контроля по альтернативному признаку для контроля доли несоответствующих единиц в целевой совокупности, состоящей из дискретных единиц, в частности:

a) доли несоответствующих единиц в партии;

b) доли несоответствий в системе внутреннего контроля (ICS);

c) доли ошибок в совокупности бухгалтерских записей или журналов;

d) доли несоответствующих характеристик объекта на приемо-сдаточных испытаниях, например при аудите продукции и процессов.

Эти планы предпочтительнее планов одноступенчатого контроля, когда затраты на контроль высоки или когда задержка и неопределенность, вызванные возможной необходимостью отбора и контроля второй выборки, несущественны. Статистическая теория, лежащая в основе планов, таблиц и рисунков настоящего стандарта, приведена в приложениях А-К.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты [для датированных стандартов применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения)]:

ISO 2859-2, Sampling procedures for inspection by attributes - Part 2: Sampling plans indexed by limiting quality (LQ) for isolated lot inspection [Процедуры выборочного контроля по альтернативному признаку. Часть 2. Планы выборочного контроля отдельных партий на основе предельного качества (LQ)]

ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей)

ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)

3 Термины, определения, обозначения и сокращения

3.1 Термины и определения

В настоящем стандарте применены термины по ИСО 2859-2, ИСО 3534-1, ИСО 3534-2, а также следующие термины с соответствующими определениями.

- ИСО и МЭК ведут терминологические базы данных для использования в области стандартизации по следующим адресам:

- платформа онлайн-просмотра ИСО: доступна по адресу http://www.iso.org/obp;

- Электропедия МЭК: доступна по адресу http://www.electropedia.org/.

3.1.1 приемочное число Ac (acceptance number): Наибольшее число несоответствий или несоответствующих единиц в выборке при статистическом приемочном контроле (3.1.2) по альтернативному признаку, допускающее приемку партии в соответствии с планом приемочного контроля (3.1.3).

[ИСО 3534-2:2006, 4.4.2]

3.1.2 статистический приемочный контроль (acceptance sampling): Выборочный контроль, после проведения которого принимают решение о приемке или отклонении партии или другой совокупности продукции, материалов или услуг на основе результатов отбора выборки.

[ИСО 3534-2:2006, 1.3.17]

3.1.3 план статистического приемочного контроля (acceptance sampling plan): План, который устанавливает необходимые объем(ы) выборки и соответствующие критерии приемки партии.

[ИСО 3534-2:2006, 4.3.3]

3.1.4 Условные вероятности

3.1.4.1

ошибка первого рода, риск первого рода

(conditional risk type I): Вероятность того, что по результатам контроля будет принята гипотеза

:

p

при условии, что

p

>

.

Примечание 1 - Термины "ошибка первого рода" и "риск первого рода" являются синонимами.

Примечание 2 - При аудите ошибка первого рода определяет степень, в которой цель аудита не достигнута. Следовательно, ошибку первого рода также можно рассматривать как условный показатель эффективности аудита.

Примечание 3 - Подробное математическое объяснение ошибки первого рода приведено в приложении D.

3.1.4.2

ошибка второго рода, риск второго рода

(conditional risk type II): Условная вероятность того, что по результатам контроля будет отклонена гипотеза

:

p

при условии, что

.

Примечание 1 - Термины "ошибка второго рода" и "риск второго рода" являются синонимами.

Примечание 2 - При аудите в этом случае имеют в виду ошибочное отклонение хорошей партии. Таким образом, ошибка второго рода характеризует экономические потери. Следовательно, ошибку второго рода можно также рассматривать как условный показатель эффективности аудита.

Примечание 3 - Подробное математическое объяснение ошибки второго рода приведено в приложении D.

3.1.5 доверительный интервал (confidence interval): Интервал, границы которого рассчитаны по данным выборки, указывающий область, которая с заданной вероятностью накрывает значение неизвестного параметра p.

Примечание 1 - Достоверность доверительного интервала как интервальной оценки

p

характеризует доверительная вероятность, т.е. вероятность того, что доверительный интервал накрывает истинное значение

p

. Для доверительного интервала с номинальным значением доверительной вероятности

фактическая вероятность охвата имеет нижнюю границу

в точке

p

. Длина доверительного интервала соответствует точности статистических выводов о

p

. Таким образом, наиболее интересны кратчайшие доверительные интервалы.

Примечание 2 - См. приложение А.

3.1.6 вероятность охвата (coverage probability): Вероятность того, что случайная доверительная область накрывает истинное значение p.

Примечание - Подробное математическое объяснение вероятности охвата приведено в приложении G.

3.1.7 финансовая отчетность (financial statement): Формальные записи о финансовой деятельности и положении организации, относящиеся к одному моменту времени или к изменениям в течение определенного периода времени.

3.1.8 контроль по альтернативному признаку (inspection by attributes): Контроль, основанный на регистрации наличия или отсутствия одной или нескольких характеристик у каждой единицы в рассматриваемой группе или подсчете числа единиц, обладающих или не обладающих этой характеристикой, или числа таких событий в единице, группе или совокупности.

[ИСО 3534-2:2006, 4.1.3]

3.1.9 средний объем объединенной выборки I.ASN (integrated average sample number I.ASN): Число, характеризующее средний объем объединенной выборки в соответствии с планом выборочного контроля для заданной доли несоответствующих единиц p с весами в соответствии с априорной информацией о p.

Примечание 1 - Подробное математическое объяснение I.ASN приведено в приложении F.

Примечание 2 - Если указаны затраты на контроль отдельной единицы, то

I.ASN

допускается использовать для оценки средних затрат на выборочный контроль по двухступенчатому плану (

;

).

3.1.10

общая вероятность применения второго этапа

(integrated second stage probability

): Вероятность того, что потребуется применение второго этапа контроля.

Примечание - Подробное математическое объяснение

приведено в приложении E.

3.1.11 партия (lot): Часть генеральной совокупности, составленная в соответствии с теми же условиями, что и генеральная совокупность для целей отбора выборки.

[ИСО 3534-2:2006, 1.2.4]

3.1.12 ошибка (misstatement): Различие между требуемой суммой, классификацией, представлением или раскрытием финансовой отчетности и фактически наблюдаемой величиной.

3.1.13 несоответствующий объект, несоответствующая единица (nonconforming item, nonconforming unit): Объект или единица с одним или несколькими несоответствиями.

[ИСО 3534-2:2006, 1.2.12, изменено - было добавлено слово "объект"]

3.1.14 несоответствие (nonconformity): Невыполнение требования.

[ИСО 3534-2:2006, 3.1.11]

3.1.15 оперативная характеристика OC (operating characteristic OC): Вероятность приемки в соответствии с планом выборочного контроля, как функция истинного значения доли несоответствующих единиц p.

Примечание - См. приложение В.

3.1.16 сопоставляемые OC (OC matched): Одинаковые оперативные характеристики для различных планов выборочного контроля.

Примечание - См. приложение С.

3.1.17 априорная информация (prior information): Знания о параметре до получения фактических данных выборки.

Примечание - Источниками априорных знаний являются, например, результаты предыдущих аудитов и оценки окружающей среды организации.

3.1.18 совокупность (генеральная) (population): Множество всех рассматриваемых единиц.

[ИСО 3534-2:2006, 1.2.1]

3.1.19 браковочное число Re (rejection number): Наименьшее число несоответствий или несоответствующих единиц в выборке при статистическом приемочном контроле по альтернативному признаку, при котором партия должна быть отклонена в соответствии с планом контроля.

[ИСО 3534-2:2006, 4.4.1]

3.1.20 выборка (sample): Подмножество генеральной совокупности, состоящее из одной или нескольких выборочных единиц.

[ИСО 3534-2:2006, 1.2.17, изменено - удалено примечание]

3.1.21 основная процедура (substantive procedure): Процедура аудита с целью выявления ошибок на уровне утверждений.

Примечание - Существует два типа основных процедур:

a) проверка деталей (классов транзакций, остатков на счетах и раскрытия информации);

b) аналитические основные процедуры.

3.1.22 проверка средств контроля (test of controls): Процедура аудита с целью оценки результативности средств контроля при предотвращении или выявлении и исправлении существенных ошибок на уровне утверждений.

3.1.23

допустимая доля

(tolerance proportion): Наибольшее значение

доли несоответствующих единиц

p

, при котором целевую совокупность считают приемлемой.

3.2 Обозначения и сокращения

- объем выборки на этапе

i

;

- объем выборки одноэтапного плана с той же OC, что и при двухэтапном плане;

- количество несоответствующих единиц, обнаруженных в выборке объема

;

D - доверительный интервал доли несоответствующих единиц;

p - доля несоответствующих единиц;

- нижняя граница доверительного интервала

D

;

- верхняя граница доверительного интервала

D

;

- допустимое значение

p

;

I.cp - общая фактическая вероятность охвата;

- номинальное значение доверительной вероятности;

a, b - параметры формы бета-распределения;

- приемочное число этапа

i

;

- браковочное число этапа

i

;

c.type I - ошибка первого рода (условная вероятность ошибочной приемки);

c.type II - ошибка второго рода (условная вероятность ошибочного отклонения);

- общая вероятность применения второго этапа контроля;

I.ASN - средний объем объединенной выборки;

N - объем партии;

OC - функция оперативной характеристики;

- вероятность приемки (функция OC при заданном значении

p

).

4 Выбор и применение двухступенчатого плана выборочного контроля при наличии априорной информации

4.1 Общие положения

В таблицах 1 и 5 раздела 7 приведены параметры двухступенчатых планов выборочного контроля [

, (

;

),

(

;

)], индексированных по значениям

(допустимой доле несоответствующих единиц),

(доверительной вероятности) и соответствующей априорной информации (соответствующему уровню показателя доверия).

Целями применения двухступенчатого плана выборочного контроля являются:

a) обеспечение возможности принятия решения о том, превышает ли фактическая доля несоответствующих единиц

p

допустимое значение

. В статистической терминологии задача принятия решения представляет собой проверку гипотезы

H

:

p

против альтернативы

K

:

p

>

;

b) определение доверительного интервала для фактической доли несоответствующих единиц p.

Разработка планов выборочного контроля гарантирует, что вероятности обеих ошибок принятия решения: 1) ошибочного отклонения H и 2) ошибочного принятия H ограничены.

4.2 Определение плана выборочного контроля

План выборочного контроля можно определить по таблицам 1-5 раздела 7. Записи в ячейках этих таблиц означают следующее:

a) вверху слева указан объем выборки

на этапе 1;

b) справа вверху указаны значения приемочного и браковочного чисел (

и

) на этапе 1;

c) слева внизу указан объем выборки

на этапе 2;

d) справа внизу указаны значения приемочного и браковочного чисел (

и

) на этапе 2.

Планы выборочного контроля индексированы по

(допустимой доле несоответствующих единиц),

(номинальному значению доверительной вероятности) и уровню показателя доверия.

Номинальное значение доверительной вероятности

определяет достоверность окончательного решения, принимаемого в соответствии с алгоритмом, описанным в 5.3, в том смысле, что вероятность охвата

P

(

p

D

) превышает

для широкого диапазона фактических значений

p

, за исключением небольшого интервала около

, (рисунки G.1-G.5). Соответственно, вероятности обеих ошибок принятия решения: 1) ошибочного отклонения

H

:

p

и 2) ошибочного принятия

H

:

p

ограничены и не превышают (1-

) для широкого диапазона фактических значений

p

.

Уровень предварительной информации в виде уровня показателя доверия должен быть определен по порядковой шкале, путем выбора одного из трех значений уровня (низкий, средний, высокий). Низкий уровень доверия следует использовать при отсутствии предшествующего опыта или при плохих результатах предшествующего опыта работы с контролируемыми совокупностями. Высокий уровень показателя доверия следует использовать при наличии убедительных свидетельств хорошей работы. Средний уровень показателя доверия следует использовать, если существуют слабые доказательства хорошей работы или убедительные доказательства промежуточного качества.

Дополнительная техническая информация о модели априорной информации и шкале показателя доверия приведена в приложении H.

4.3 Процедура выборочного контроля и принятия решения

При принятии решения на основе двухступенчатого плана выборочного контроля [

, (

;

),

(

;

)] необходимо действовать в соответствии со следующим алгоритмом

=0.

Этап 1

Отбирают случайную выборку объема

, определяют количество

несоответствующих единиц среди

отобранных единиц. Принимают решение в соответствии с правилами a), b) и c):

a) если

, принимают гипотезу

H

:

p

, т.е. считают, что значение

p

не превышает допустимого значения

;

b) если

, отклоняют гипотезу

H

:

p

, т.е. считают, что

p

превышает допустимое значение

,

c) если

, то необходимо перейти к выполнению этапа 2.

Этап 2

Если на этапе 1 возникает ситуация c), приводящая к переходу на этап 2, необходимо действовать следующим образом.

Проверяют вторую случайную выборку объема

и определяют количество

несоответствующих единиц среди

отобранных единиц. Решение принимают в соответствии со следующими правилами:

a) если

, принимают гипотезу

H

:

p

, т.е. считают, что значение

p

не превышает допустимого значения

;

b) если

, отклоняют гипотезу

H

:

p

, т.е. считают, что значение

p

превышает допустимое значение

.

4.4 Оценка фактической доли несоответствующих единиц

Выборочная оценка доли несоответствующих единиц имеет вид:

- несмещенная оценка фактической доли несоответствующих единиц

p

в совокупности. Неопределенность, присущую оценке

p

, выражают в виде доверительного интервала. Двусторонний доверительный интервал

D

=[

;

], соответствующий номинальной доверительной вероятности

, удовлетворяет неравенству

, т.е. с вероятностью не менее

можно утверждать, что фактическая доля

p

имеет значение от

до

. Двусторонний доверительный интервал

D

для фактической доли

p

несоответствующих единиц может быть определен с помощью функции confint в пакете программ для ИСО 28596 по следующим входным данным: 1) номинальная доверительная вероятность

и уровень показателя доверия, выбранный для плана выборочного контроля; 2) количество

несоответствующих единиц в выборке на этапе 1; 3) если был введен этап 2, то количество

несоответствующих единиц на этапе 2.

5 Варианты применения: контроль партий и финансовый аудит

Ниже подробно описаны два стандартных примера применения двухступенчатой процедуры принятия решений:

- контроль партий отдельных единиц продукции, см. 6.1;

- финансовый аудит с двумя целями: проверка соответствия системы внутреннего контроля (проверка средств контроля) и проверка деталей основных процедур, см. 6.2.

5.1 Контроль партий

5.1.1 Отбор выборки

Выборки должны быть отобраны из партии путем простого случайного отбора выборки. Если партия состоит из подгрупп или слоев, сформированных по какому-либо рациональному критерию, необходимо использовать репрезентативную выборку, сформированную таким образом, чтобы количество отобранных единиц было пропорционально количеству единиц в подгруппе или слое.

5.1.2 Приемка партии

Все единицы в выборке должны быть проверены, а количество несоответствующих единиц должно быть подсчитано.

Приемлемость партии определяют путем использования планов выборочного контроля. Если количество несоответствующих единиц, обнаруженных в выборке, равно или менее приемочных чисел

и

соответственно, партия должна быть принята, в противном случае партию не принимают.

5.1.3 Распоряжение непринятыми партиями

Распоряжение непринятыми партиями должно быть заранее согласовано всеми заинтересованными сторонами.

5.1.4 Партии с одной или несколькими несоответствующими единицами

Если партия была принята, не следует принимать ни одной несоответствующей единицы, выявленной при приемо-сдаточном выборочном контроле.

5.1.5 Повторно представленные партии

Партия, которая была проконтролирована, но не была принята, может быть повторно представлена на проверку только в том случае, если:

a) покупатель удовлетворен тем, что все несоответствующие единицы удалены или заменены соответствующими единицами;

b) все заинтересованные стороны согласны.

Ответственный орган должен определить метод выполнения повторной проверки.

5.2 Финансовый аудит

5.2.1 Цели аудита, ориентированного на риски

Соответствующими целями в процессе аудита, ориентированного на риски, являются:

1) проверка средств контроля, т.е. проверки на соответствие требованиям, применяемым при оценке системы внутреннего контроля (ICS);

2) проверка деталей для выбранных целей при выполнении основных процедур.

В любом случае аудитор уведомляет о результатах процедуры отбора выборки и последующем решении в документации об аудите.

5.2.2 Целевая совокупность, доля несоответствующих единиц и допустимое значение

При оценке ICS целевая совокупность представляет собой совокупность событий внутреннего контроля за определенный период времени. Доля несоответствующих единиц - это количество событий контроля, которые в течение установленного периода времени отклоняются от предписанных процедур внутреннего контроля. Допустимая доля

- это количество отклонений от предписанных процедур внутреннего контроля, которое считают допустимым для целей финансового аудита в течение определенного периода времени.

В рамках проверки деталей процедуры целевая совокупность представляет собой совокупность выписок по указанному балансу счета или классу транзакций. Доля несоответствующих единиц - доля ошибок в документах целевой совокупности. Допустимая доля

- количество ошибок за установленный период, которое считают допустимым для целей финансового аудита.

5.2.3 Принятие и отклонение в случае проверки соответствия ICS

Как принятие, так и отклонение влияют на оценку аудитором вероятностей ошибок контроля. В случае принятия аудитор склоняется к выбору более низкого значения вероятностей ошибок. Как следствие, объем усилий аудитора в ходе последующих основных процедур уменьшается. В случае отклонения аудитор склоняется к выбору более высокого значения вероятностей ошибок. Как следствие, объем усилий аудитора в ходе последующих основных процедур увеличивается.

5.2.4 Принятие и отклонение в случае проверки деталей

Как принятие, так и отклонение влияют на заключение аудитора о наличии существенных искажений в целевой аудиторской совокупности. Однако на окончательное заключение аудитора влияют различные дополнительные факторы, в частности, дальнейшая проверка деталей, аналитические процедуры, качественная оценка вида несоответствий.

6 Примеры

6.1 Пример 1. Контроль партии

Потребитель покупает набор винтов и может допустить 3% несоответствующих единиц. Предположим, уверенность потребителя в том, что в партии низкое значение

p

является средним, т.е. уровень показателя доверия средний (Trust=mid). Кроме того, выбрана номинальная доверительная вероятность 0,80, т.е.

=0,80. Следует использовать таблицу 2, в которой указано, что объем выборки на этапе 1

=63. Кроме того, в соответствии с таблицей 2, приемочное и браковочное числа на данном этапе равны

=0 и

=5. Если контроль не выявил несоответствующих единиц, партия может быть принята на первом этапе. Если в результате контроля в выборке из 63 единиц обнаружено 5 или более несоответствующих единиц, партия должна быть отклонена и отобрана вторая выборка. В соответствии с таблицей 2 объем выборки на этапе 2

составляет 228,

=8 и

=9.

В таблице I.2 приведена также дополнительная информация:

c.type I

=0,0630,

c.type

II

=0,0988,

I.ASN

=161,67,

=0,4328 и

I.cp

=0,8078.

6.2 Пример 2. Аудит системы внутреннего контроля (процесс закупки)

Аудитор проверяет процесс закупки офисного оборудования розничным продавцом, чтобы оценить эффективность соответствующей части ICS. За год осуществляется большое количество закупок у большого количества различных поставщиков. На первом этапе аудитор оценивает целесообразность разработки процесса. В результате собеседования и наблюдения выяснилось, что процесс закупки состоит из следующих этапов: оценка потребностей, заказ на покупку, поступление товаров, получение и проверка счета-фактуры, обработка платежей, корректировка записей в главной книге. На этих этапах было выявлено много различных средств контроля, которые должны гарантировать, что процесс закупки выполнен надлежащим образом. После оценки соответствия структуры процесса на каждом этапе аудитор определяет вид средств контроля, подлежащих дальнейшему изучению. Например, на этапе "входящие товары" аудитор выбирает контроль за тем, соответствуют ли доставленные товары заказанным товарам по количеству и качеству. Поэтому аудитор предлагает розничному продавцу доказать, что ответственный персонал должным образом подписал накладные на все поступающие товары. Подпись должна указывать на то, что количество и качество каждого поступающего товара проверено (например, информация из заказа на покупку), и они являются приемлемыми. Целью аудита являются оценка доли

p

отсутствующих, неподписанных или ненадлежащим образом подписанных накладных. Аудитор предполагает, что допустимая доля отклонений составляет 5% (

=0,05).

Ввиду большого количества поступающих товаров аудитор приступает к выборочной проверке. Для расчетов в рамках аудита, ориентированного на риск, для аудита системы внутреннего контроля (ICS) устанавливают номинальную доверительную вероятность

=0,80. Исходя из предыдущего опыта работы с объектом аудита, у аудитора возникает высокое доверие к ICS, и он применяет высокий уровень показателя доверия. В соответствии с таблицей 2 объем первой выборки равен

=32, с приемочным числом

=0 и браковочным числом

=6.

Аудитор отбирает случайную выборку объема

=32 событий поступления товаров из ERP-системы. Проверка 32 событий поступления товаров показывает, что все соответствующие поставки были должным образом подписаны, т.е. количество несоответствующих единиц в выборке равно нулю

=0. Сравнивая

с приемочным числом

=0, аудитор принимает гипотезу

H

:

p

, т.е. принимает решение, что доля

p

недостающих, неподписанных или ненадлежащим образом подписанных накладных во всей совокупности не превышает допустимого значения

. В заключение аудитор классифицирует рассмотренную конкретную процедуру внутреннего контроля как эффективную.

6.3 Пример 3. Аудит общей системы контроля (процесс продаж)

Аудитор проверяет процесс продаж в розничной сети металлопродукции продавцом, чтобы оценить эффективность соответствующей части системы внутреннего контроля (ICS). Ежегодно происходит большое количество продаж с большим количеством различных потребителей. На первом этапе аудитор оценивает целесообразность разработки процесса продаж. В результате собеседования и собственных наблюдений аудитор выяснил, что процесс продаж состоит из следующих этапов: подача заявок, прием заказов, отправка товаров, выставление счетов, обработка платежей, выполнение записей в главной книге. На этих этапах определено много различных средств контроля, которые должны обеспечить надлежащее функционирование процесса продаж. После оценки соответствия структуры процесса аудитор определяет вид средств контроля на каждом этапе, которые подлежат дальнейшему изучению. Например, аудитор рассматривает на этапе "выставление счетов" контроль за тем, был ли надлежащим образом соблюден принцип реализации. Следовательно, аудитор просит розничного продавца доказать, что в отношении всех единичных продаж реализация товарооборота была зафиксирована за указанный период времени. Аудитор принял 3% неправильно зафиксированных оборотов как допустимый уровень несоответствий.

Ввиду большого количества исходящих счетов-фактур за год аудитор приступает к выборочной проверке. По каждому отобранному счету-фактуре аудитор проверяет, правильно ли был отражен оборот. Расчеты по предыдущим экспериментам в рамках процесса аудита, ориентированного на риск, устанавливают для этапа аудита системы внутреннего контроля (ICS) доверительную вероятность

=0,70. Исходя из предыдущего опыта работы с объектом аудита, у аудитора возникает высокое доверие к ICS, и он принимает высокий уровень показателя доверия. В соответствии с таблицей 1 объем первой выборки равен

=40, с приемочным числом

=0 и браковочным числом

=6. На первом этапе аудитор наблюдает

=7 неправильно отраженных оборотов. Сравнивая

с браковочным числом

=6, аудитор отвергает гипотезу

H

:

p

, т.е. принимает решение, что доля

p

неправильно отраженных оборотов во всей совокупности превышает допустимое значение

=0,03, т.е. 3%. В заключение аудитор классифицирует рассматриваемую конкретную процедуру внутреннего контроля как неэффективную.

6.4 Пример 4. Аудиторская проверка деталей (дебиторская задолженность)

Аудитор проверяет дебиторскую задолженность розничного продавца офисного оборудования на предмет точности отчета баланса на отчетную дату. Аудитор устанавливает допустимый уровень

=0,05, т.е. 5% ошибок на отчетную дату он считает допустимым.

Ввиду большого количества дебиторской задолженности аудитор приступает к выборочной проверке. Для расчетов в рамках процесса аудита, ориентированного на риск, для этапа проверки деталей устанавливают доверительную вероятность

=0,70. Исходя из предыдущего опыта общения с проверяемым лицом, у аудитора возникает низкое доверие к бухгалтерскому учету организации, он принимает низкий уровень показателя доверия. В соответствии с таблицей 1 объем первой выборки равен

=36, с приемочным числом

=0 и браковочным числом

=4. В первой выборке аудитор наблюдает

=0. Сравнивая

с приемочным числом

=0, аудитор принимает гипотезу

H

:

p

, т.е. принимает решение, что доля

p

ошибочных счетов во всей совокупности документов о дебиторской задолженности не превышает допустимого значения

.

6.5 Пример 5. Аудиторская проверка деталей (исходных материалов)

Аудитор проверяет запасы сырья у розничного продавца металлопродукции на предмет точной оценки стоимости на отчетную дату. Аудитор устанавливает допустимую долю

=0,05, т.е. он считает допустимым 5% неточных оценок стоимости на отчетную дату.

Ввиду большого разнообразия сырья аудитор приступает к выборочной проверке. Аудитор устанавливает для проверки деталей доверительную вероятность

=0,90. На основе предыдущего опыта работы с объектом у аудитора возникает средняя уверенность в оценке материалов организации, он применяет средний уровень показателя доверия. В соответствии с таблицей 3 объем первой выборки равен

=52, с приемочным числом

=0 и браковочным числом

=7. В первой выборке аудитор выявляет 4 ошибки оценок стоимости, т.е.

=4. В результате аудитор переходит ко второй выборке с объемом

=185, которая содержит

=7 неточных оценок стоимости. На втором этапе приемочное число равно

=11, а браковочное число

=12. Совокупное количество неточных оценок стоимости равно (

+

)=11. В заключение аудитор принимает гипотезу

H

:

p

, т.е. считает, что доля

p

неточных оценок стоимости во всей совокупности данных инвентаризации не превышает допустимого значения

.

7 План выборочного контроля

Планы выборочного контроля с приемочным и браковочными числами для различных номинальных значений доверительной вероятности и данными этапов, указанными по строкам ячейки, приведены в таблицах 1-5

.

________________

См. также 4.2.

Таблица 1 - Планы выборочного контроля для номинальной доверительной вероятности

=0,70

Уровень показателя	(доля совокупности)
доверия	0,01		0,02		0,03		0,04		0,05		0,06
Низкий	181	(0; 4)	91	(0; 4)	60	(0; 4)	45	(0; 4)	36	(0; 4)	30	(0; 4)
	797	(9; 10)	449	(10; 11)	393	(13; 14)	299	(13; 14)	260	(14; 15)	217	(14; 15)
Средний	148	(0; 4)	74	(0; 4)	49	(0; 4)	37	(0; 4)	30	(0; 4)	25	(0; 4)
	599	(7; 8)	299	(7; 8)	200	(7; 8)	150	(7; 8)	120	(7; 8)	100	(7; 8)
Высокий	120	(0; 7)	60	(0; 6)	40	(0; 6)	30	(0; 6)	24	(0; 5)	20	(0; 5)
	557	(6; 7)	278	(6; 7)	147	(5; 6)	126	(6; 7)	103	(5; 6)	82	(5; 6)
Уровень показателя	(доля совокупности)
доверия	0,07		0,08		0,09		0,1		0,15		0,2
Низкий	26	(0; 4)	22	(0; 4)	20	(0; 4)	18	(0; 4)	12	(0; 4)	9	(0; 4)
	185	(14; 15)	150	(13; 14)	121	(12; 13)	109	(12; 13)	58	(10; 11)	44	(10; 11)
Средний	22	(0; 4)	19	(0; 4)	17	(0; 4)	15	(0; 4)	10	(0; 4)	8	(0; 4)
	85	(7; 8)	75	(7; 8)	66	(7; 8)	50	(6; 7)	41	(7; 8)	29	(7; 8)
Высокий	17	(0; 5)	15	(0; 5)	13	(0; 5)	12	(0; 5)	8	(0; 4)	6	(0; 4)
	64	(5; 6)	59	(5; 6)	56	(5; 6)	38	(4; 5)	34	(5; 6)	23	(5; 6)

Таблица 2 - Планы выборочного контроля для номинальной доверительной вероятности

=0,80

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04			0,05			0,06		0,07
Низкий	110	(0; 5)	74	(0; 5)	55	(0; 5)		44		(0; 5)	37	(0; 5)	31	(0; 5)
	600	(13; 14)	460	(15; 16)	343	(15; 16)		275		(15; 16)	229	(15; 16)	197	(15; 16)
Средний	94	(0; 5)	63	(0; 5)	47	(0; 5)		38		(0; 5)	32	(0; 5)	27	(0; 5)
	392	(9; 10)	228	(8; 9)	169	(8; 9)		135		(8; 9)	112	(8; 9)	97	(8; 9)
Высокий	80	(0; 7)	53	(0; 8)	40	(0; 7)		32		(0; 6)	27	(0; 6)	23	(0; 6)
	333	(7; 8)	214	(7; 8)	151	(7; 8)		113		(6; 7)	94	(6; 7)	81	(6; 7)
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15				0,2
Низкий	27	(0; 5)	24	(0; 5)	22	(0; 5)	15		(0; 5)		11	(0; 5)
	160	(14; 15)	142	(14; 15)	128	(14; 15)	76		(13; 14)		48	(11; 12)
Средний	24	(0; 5)	21	(0; 5)	19	(0; 5)	13		(0; 5)		10	(0; 5)
	85	(8; 9)	76	(8; 9)	57	(7; 8)	52		(9; 10)		33	(8; 9)
Высокий	20	(0; 6)	18	(0; 6)	16	(0; 6)	10		(0; 6)		8	(0; 5)
	71	(6; 7)	64	(6; 7)	52	(6; 7)	37		(6; 7)		26	(6; 7)

Таблица 3 - Планы выборочного контроля для номинальной доверительной вероятности

=0,90

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05		0,06		0,07
Низкий	150	(0; 7)	100	(0; 7)	75	(0; 7)	60	(0; 7)	50	(0; 7)	43	(0; 7)
	710	(16; 17)	547	(18; 19)	407	(18; 19)	306	(17; 18)	255	(17; 18)	219	(17; 18)
Средний	131	(0; 7)	88	(0; 7)	66	(0; 7)	52	(0; 7)	44	(0; 7)	38	(0; 7)
	463	(11; 12)	309	(11; 12)	232	(11; 12)	185	(11; 12)	154	(11; 12)	132	(11; 12)
Высокий	114	(0; 11)	76	(0; 9)	57	(0; 8)	45	(0; 9)	38	(0; 8)	32	(0; 8)
	440	(10; 11)	275	(9; 10)	211	(9; 10)	163	(9; 10)	139	(9; 10)	119	(9; 10)
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	37	(0; 7)	33	(0; 7)	30	(0; 7)	17	(0; 6)	13	(0; 6)
	192	(17; 18)	171	(17; 18)	141	(16; 17)	83	(14; 15)	51	(12; 13)
Средний	33	(0; 7)	29	(0; 7)	26	(0; 7)	16	(0; 7)	12	(0; 6)
	116	(11; 12)	92	(10; 11)	72	(9; 10)	62	(11; 12)	42	(10; 11)
Высокий	28	(0; 8)	25	(0; 7)	22	(0; 8)	15	(0; 7)	11	(0; 6)
	104	(9; 10)	81	(8; 9)	63	(7; 8)	53	(9; 10)	37	(9; 10)

Таблица 4 - Планы выборочного контроля для номинальной доверительной вероятности

=0,99

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05		0,06		0,07
Низкий	188	(0; 9)	126	(0; 9)	94	(0; 9)	76	(0; 9)	63	(0; 9)	54	(0; 9)
	802	(18; 19)	631	(21; 22)	472	(21; 22)	357	(20; 21)	298	(20; 21)	240	(19; 20)
Средний	169	(0; 9)	112	(0; 9)	84	(0; 9)	67	(0; 9)	56	(0; 8)	48	(0; 8)
	553	(13; 14)	363	(13; 14)	271	(13; 14)	216	(13; 14)	201	(14; 15)	184	(15; 16)
Высокий	149	(0; 11)	99	(0; 10)	74	(0; 10)	59	(0; 10)	49	(0; 10)	42	(0; 10)
	500	(11; 12)	332	(11; 12)	253	(11; 12)	199	(11; 12)	177	(12; 13)	166	(13; 14)
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	47	(0; 9)	38	(0; 8)	34	(0; 8)	23	(0; 8)	17	(0; 8)
	208	(19; 20)	189	(19; 20)	171	(19; 20)	99	(17; 18)	64	(15; 16)
Средний	42	(0; 8)	35	(0; 8)	32	(0; 8)	21	(0; 8)	16	(0; 8)
	165	(15; 16)	144	(15; 16)	130	(15; 16)	72	(13; 14)	49	(12; 13)
Высокий	36	(0; 11)	32	(0; 10)	29	(0; 10)	19	(0; 9)	14	(0; 8)
	148	(13; 14)	132	(13; 14)	117	(13; 14)	58	(10; 11)	44	(10; 11)

Таблица 5 - Планы выборочного контроля для номинальной доверительной вероятности

=0,99

Уровень показателя	(доля совокупности)
доверия	0,03		0,04		0,05		0,06		0,07
Низкий	177	(0; 13)	133	(0; 13)	107	(0; 13)	89	(0; 13)	76	(0; 13)
	806	(27; 28)	603	(27; 28)	481	(27; 28)	402	(27; 28)	343	(27; 28)
Средний	165	(0; 13)	123	(0; 13)	99	(0; 13)	82	(0; 13)	70	(0; 12)
	578	(20; 21)	408	(19; 20)	302	(18; 19)	283	(20; 21)	263	(21; 22)
Высокий	152	(0; 17)	113	(0; 15)	90	(0; 15)	75	(0; 17)	64	(0; 16)
	540	(18; 19)	374	(17; 18)	284	(16; 17)	268	(18; 19)	240	(19; 20)
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	62	(0; 12)	55	(0; 12)	50	(0; 12)	33	(0; 12)	23	(0; 11)
	305	(27; 28)	259	(26; 27)	222	(25; 26)	126	(22; 23)	91	(21; 22)
Средний	59	(0; 12)	52	(0; 12)	47	(0; 12)	31	(0; 12)	22	(0; 11)
	231	(21; 22)	192	(20; 21)	152	(18; 19)	94	(17; 18)	56	(14; 15)
Высокий	56	(0; 16)	49	(0; 16)	44	(0; 15)	29	(0; 15)	21	(0; 13)
	209	(19; 20)	178	(18; 19)	129	(15; 16)	86	(15; 16)	48	(12; 13)

Приложение А

(справочное)

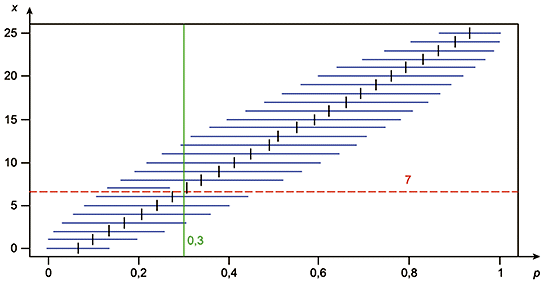
Доверительный интервал

Методология процедуры принятия решения, приведенная в 4.3, основана на построении кратчайших двусторонних доверительных интервалов при наличии априорной информации о неизвестной доле несоответствующих единиц. Технические подробности о кратчайших доверительных интервалах при наличии априорной информации приведены в [5]. При проверке гипотез доверительный интервал сопоставляют с желаемым допустимым значением

.

Процедура принятия решения на этапах 1 и 2 приведена на рисунке A.1.

На этапе 1, после проверки

единиц и определения

несоответствующих единиц, вычисляют границы доверительного интервала для

p

. Принятие решения на этапе 1 происходит в соответствии со следующими правилами:

1.1 если доверительный интервал полностью находится левее допустимого значения, партию принимают;

1.2 если доверительный интервал полностью находится правее допустимого значения, партию отклоняют;

1.3 если допустимое значение находится в пределах границ доверительного интервала, то решение не может быть принято на первом этапе и необходимо выполнение второго этапа выборочного контроля (этап 2).

На этапе 2 в выборке с объемом

определяют количество несоответствующих единиц

. Новый доверительный интервал для

p

рассчитывают на основе общего числа (

+

) несоответствующих единиц. Принятие решения на этапе 2 происходит в соответствии со следующими правилами:

2.1 если доверительный интервал полностью находится левее или правее допустимого значения, принимают решение о принятии или отклонении, соответственно, по аналогии с первым этапом;

2.2 если интервал включает допустимое значение, решение принимают на основе того, где находится большая часть доверительного интервала (левее или правее допустимого значения), что приводит к принятию или отклонению.

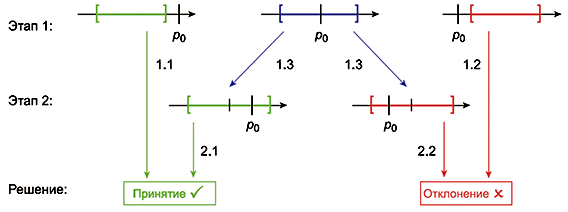Рисунок A.1 - Иллюстрация двухступенчатой процедуры принятия решения на основе доверительного интервала

Взаимосвязь между доверительными интервалами и процедурой принятия решения проиллюстрирована на рисунках A.2 и A.3. Горизонтальные отрезки представляют доверительные интервалы для

p

на основе выборочного значения

x

на вертикальной оси. На первом этапе доверительные интервалы пересекаются с допуском

=0,3. На рисунке A.2 показано наибольшее значение

, при котором

более или равно верхней границы доверительного предела, и наименьшее значение

х

, при котором

менее нижней границы доверительного интервала. Это приводит к приемочному числу

=3 и браковочному числу

=12. На втором этапе наивысшая точка менее или равна

, что соответствует

=7 и

=8, см. рисунок A.3.

Рисунок A.2 - Доверительные интервалы для

p

(горизонтальная ось) в зависимости от значения

(вертикальная ось) для объема выборки

=25

Рисунок A.3 - Доверительные интервалы для

p

(горизонтальная ось) с отмеченными средними точками в зависимости от значения (

+

) (вертикальная ось) для объема выборки

+

=25

В результате применения двухступенчатой процедуры значение доверительной вероятности конечного доверительного интервала ниже назначенного значения номинальной доверительной вероятности

в небольшой окрестности

. См. рисунки G.1-G.5 приложения G.

Приложение B

(справочное)

Кривая оперативной характеристики (OC)

Кривая оперативной характеристики (OC) представляет собой вероятность приемки по результатам статистического контроля. В данном случае для набора параметров

, (

;

),

,

и

~

Bi

(

,

p

),

~

Bi

(

,

p

) функцию оперативной характеристики можно записать следующим образом:

.

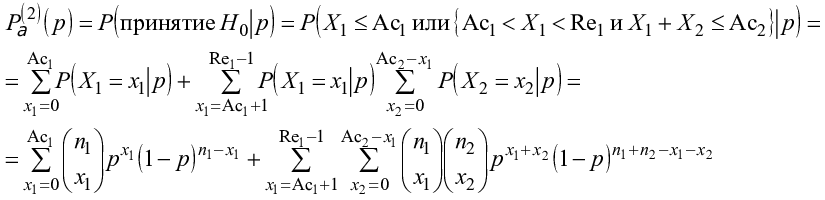
Приложение С

(справочное)

Сопоставимые кривые OC

Функция OC, описанная в приложении В, может быть использована для двух различных планов выборочного контроля одинаково успешно, если соответствующие им функции OC почти равны. Так называемый принцип соответствия OC использован для получения одноступенчатого плана выборочного контроля, который соответствует заданному двухступенчатому плану выборочного контроля.

Для (n, Ac) и X~Bi (n, p) OC одноступенчатого плана представляет собой:

.

То есть она является биномиальной OC. Чтобы найти объем выборки

, соответствующий по ОС двухступенчатому плану

,

, необходимо минимизировать квадрат остатков:

.

Значения, менее или равные

, не считаются допустимыми для

n

, поскольку они делают рассчитанный двухступенчатый план выборочного контроля ненужным. Значения более (

+

) также не следует рассматривать, поскольку они делают бесполезным план одноступенчатого выборочного контроля.

Приложение D

(справочное)

Ошибки (риски) первого и второго рода

Для

, (

;

),

,

,

a

,

b

,

~

Bi

(

,

y

),

~

Bi

(

,

y

) и

p

=

y

c

Y

~

Beta

(

a

,

b

) ошибки первого и второго рода могут быть получены следующим образом:

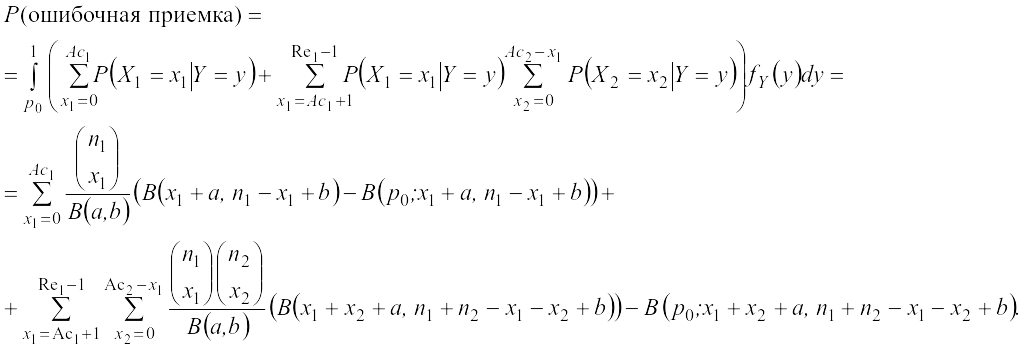
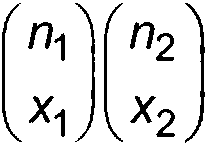
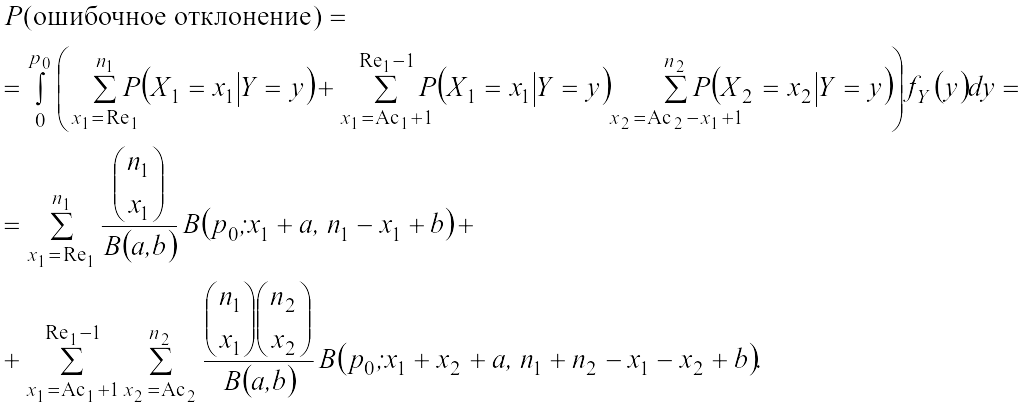
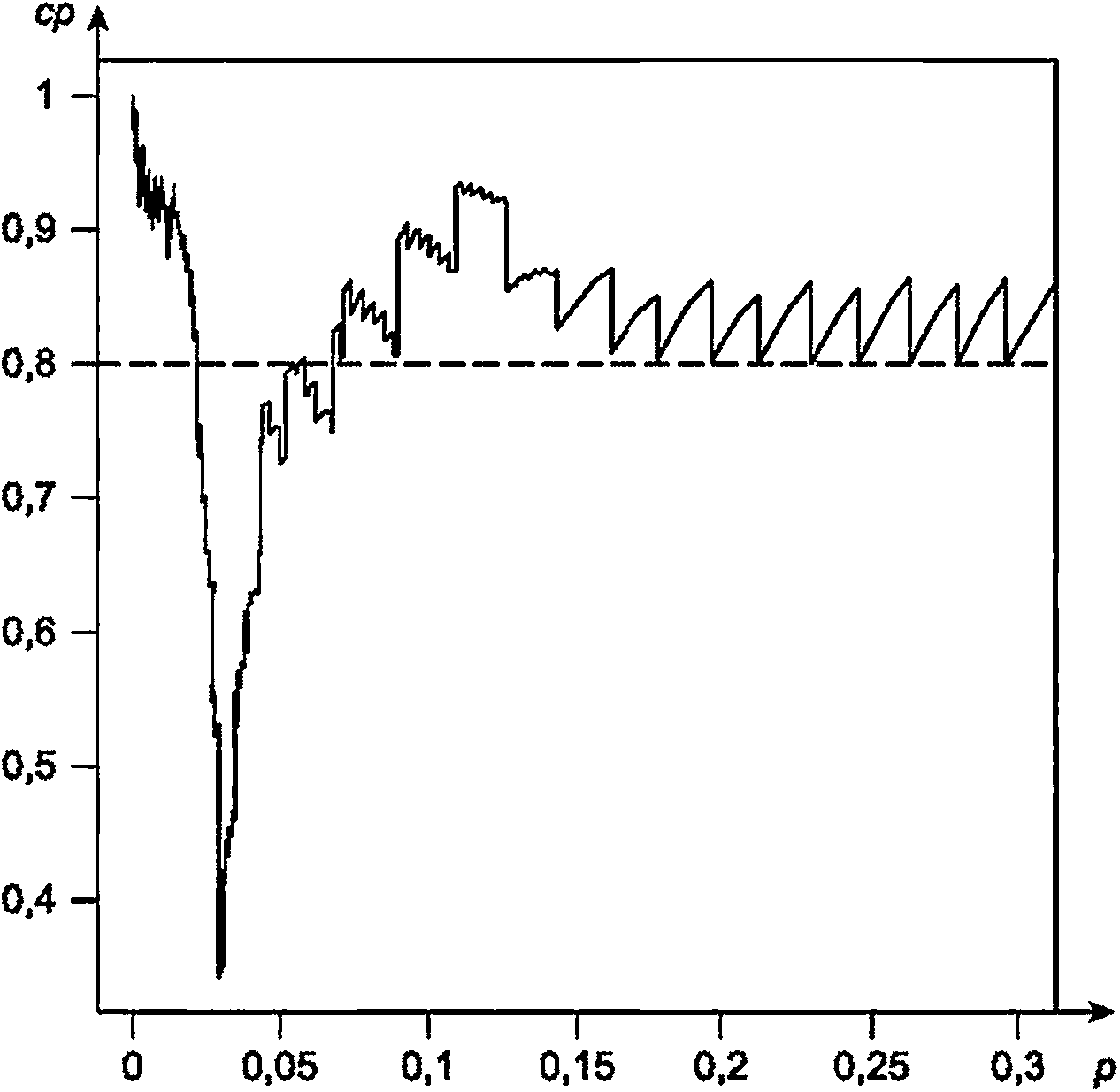
Приложение E

(справочное)

Общая вероятность применения второго этапа контроля

Если общая вероятность применения второго этапа

близка к 1, первый этап и контроль выборки объема

не требуются, поскольку почти каждый раз необходим контроль выборки объема (

+

).

Значение

уменьшается с увеличением

.

При

,

a

,

b

,

,

~

Bi

(

,

y

) и заданных значениях (

;

) эту вероятность можно получить следующим образом:

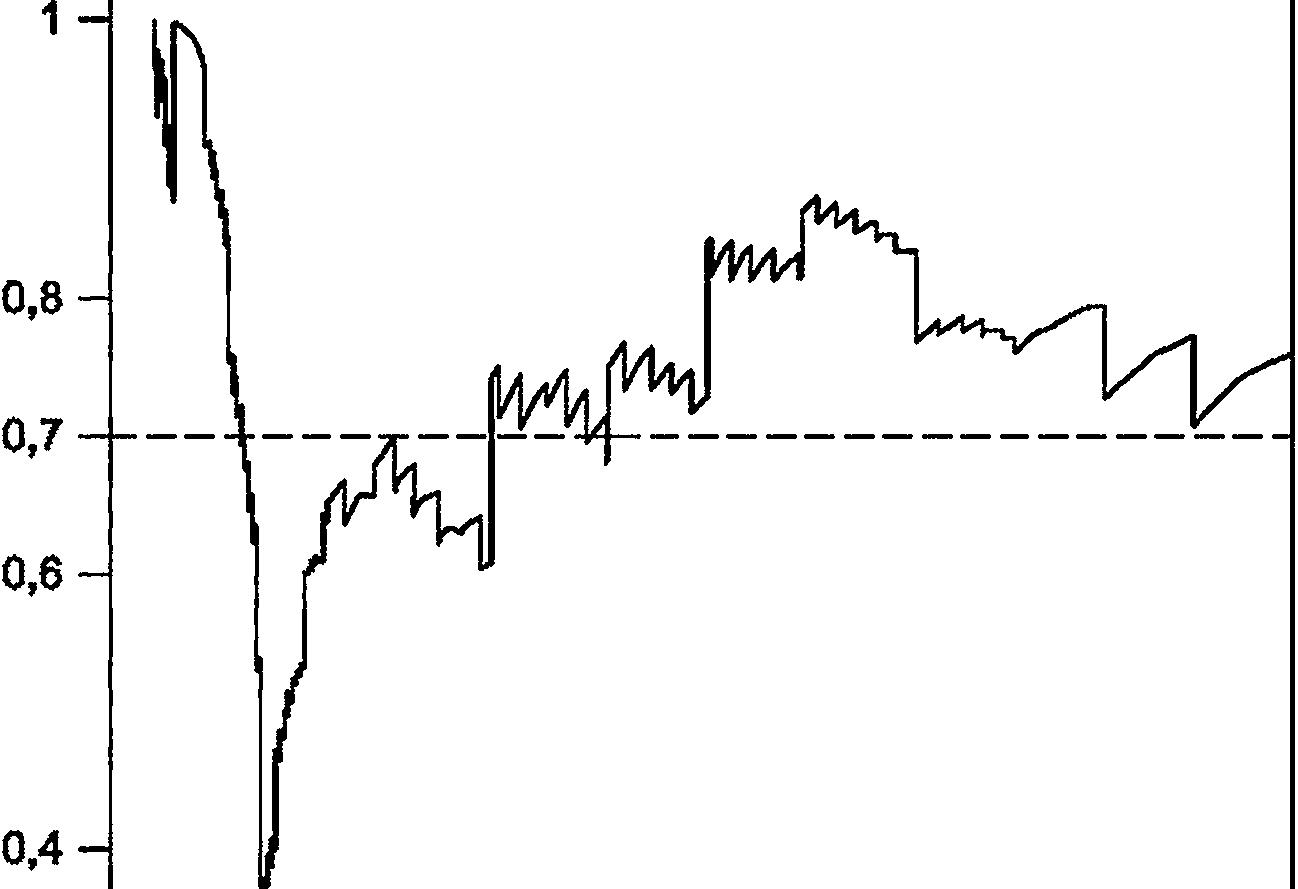
Приложение F

(справочное)

Общий средний объем объединенной выборки

Общее среднее количество выборок, т.е.

I.ASN

(

,

), можно вычислить с использованием общей вероятности перехода на второй этап, т.е.

в соответствии с приложением E:

Приложение G

(справочное)

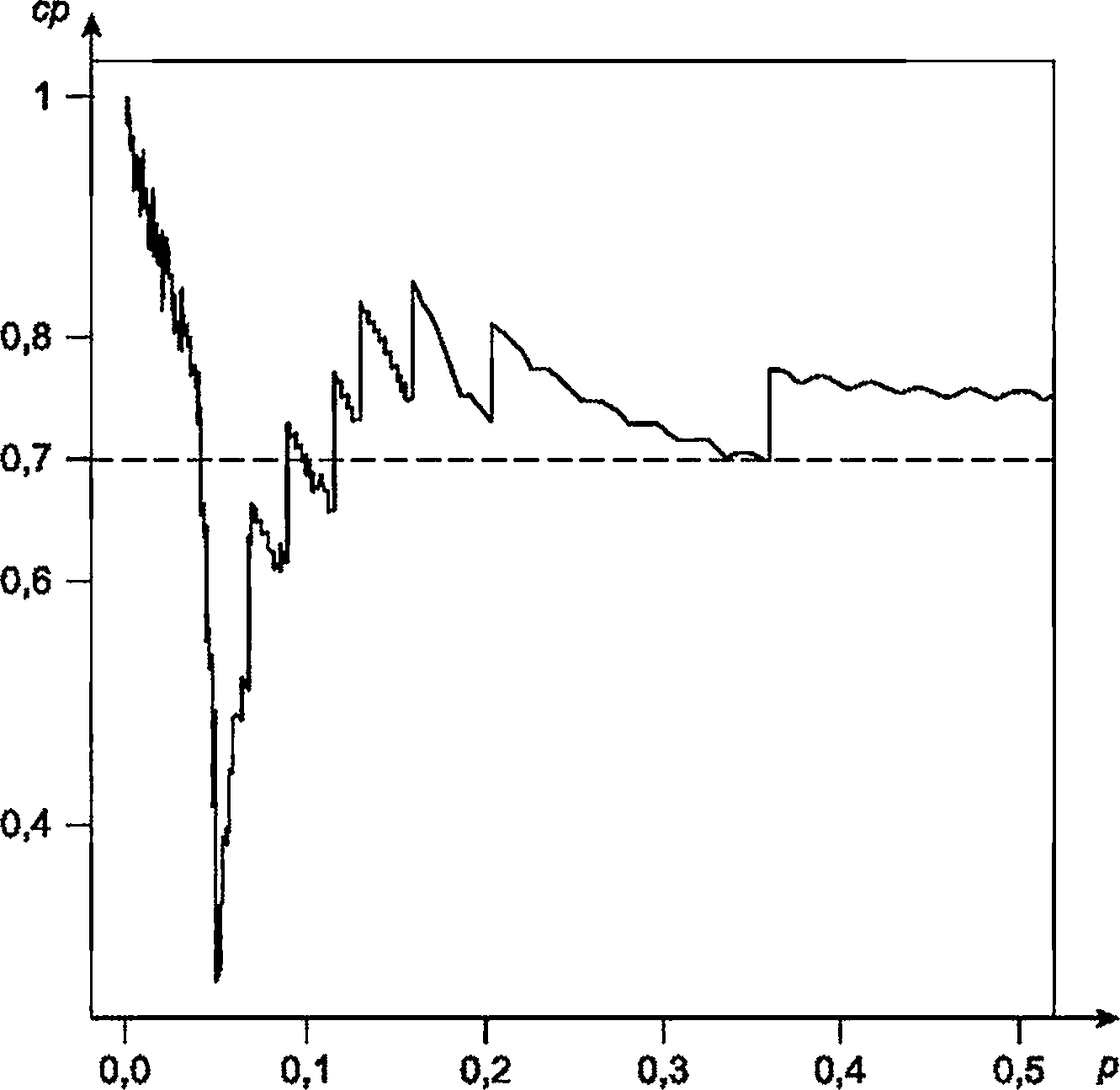
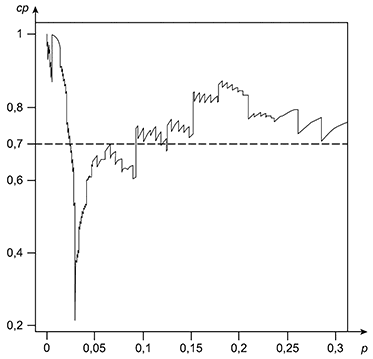
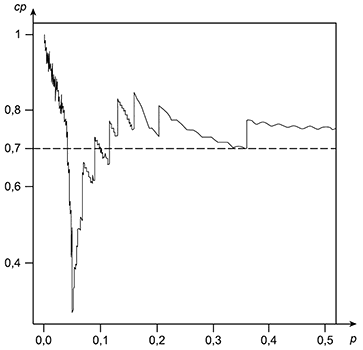
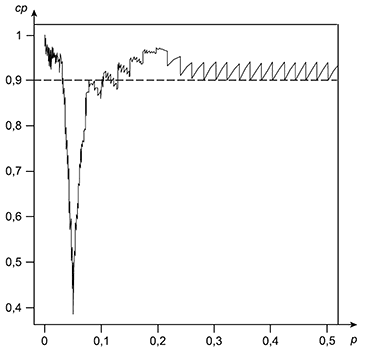
Фактическая вероятность охвата

Пусть

- доверительный интервал, рассчитанный по реализации

первого этапа контроля с выборкой объема

,

- доверительный интервал, рассчитанный по реализации

на первом этапе контроля и по реализации

на втором этапе контроля с объемом выборки второго этапа

. Фактическая вероятность охвата

cp

для заданных

p

,

, (

;

),

,

имеет вид:

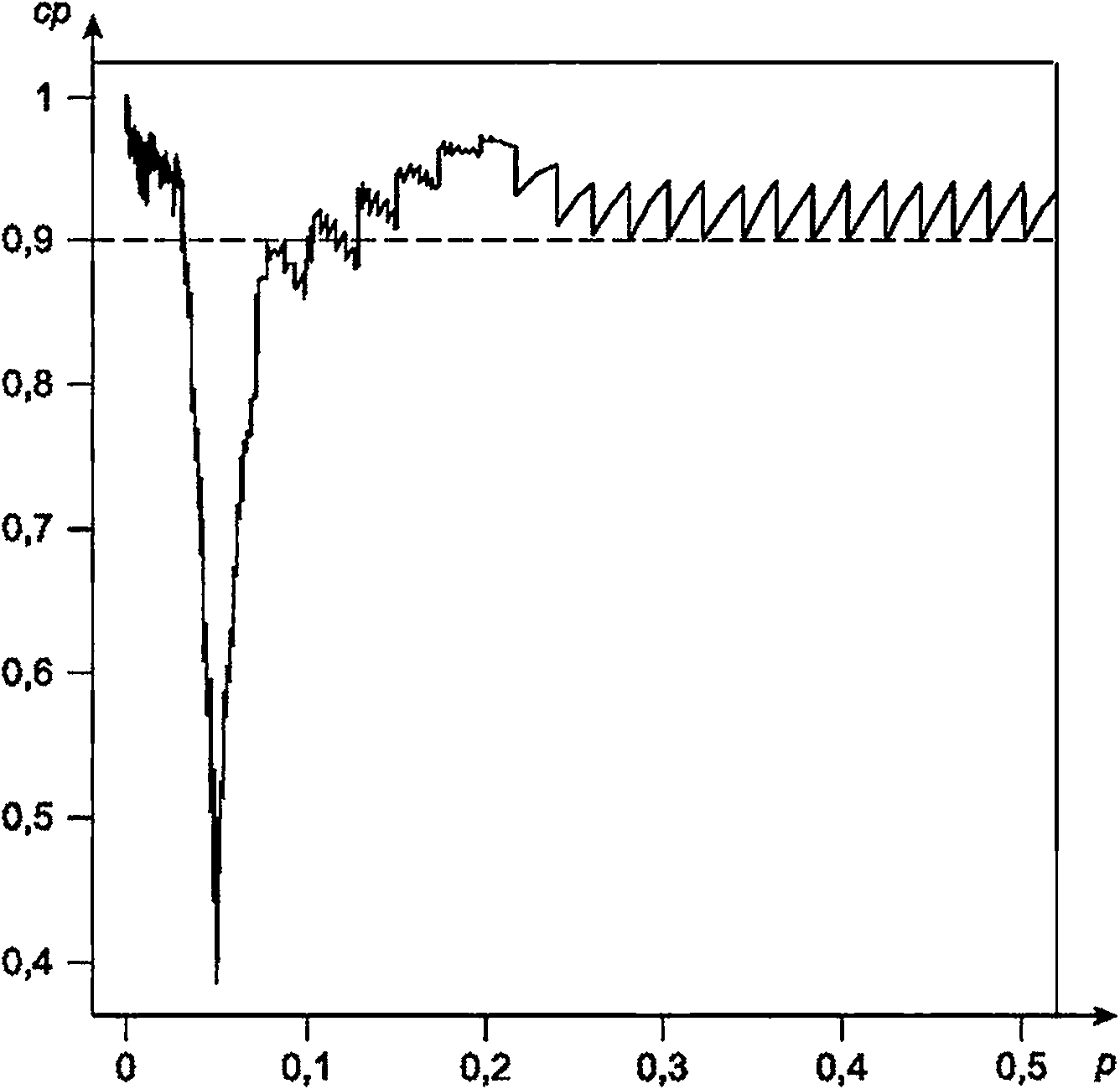
В общем виде вероятность охвата можно записать следующим образом:

,

где || - индикаторная функция:

.

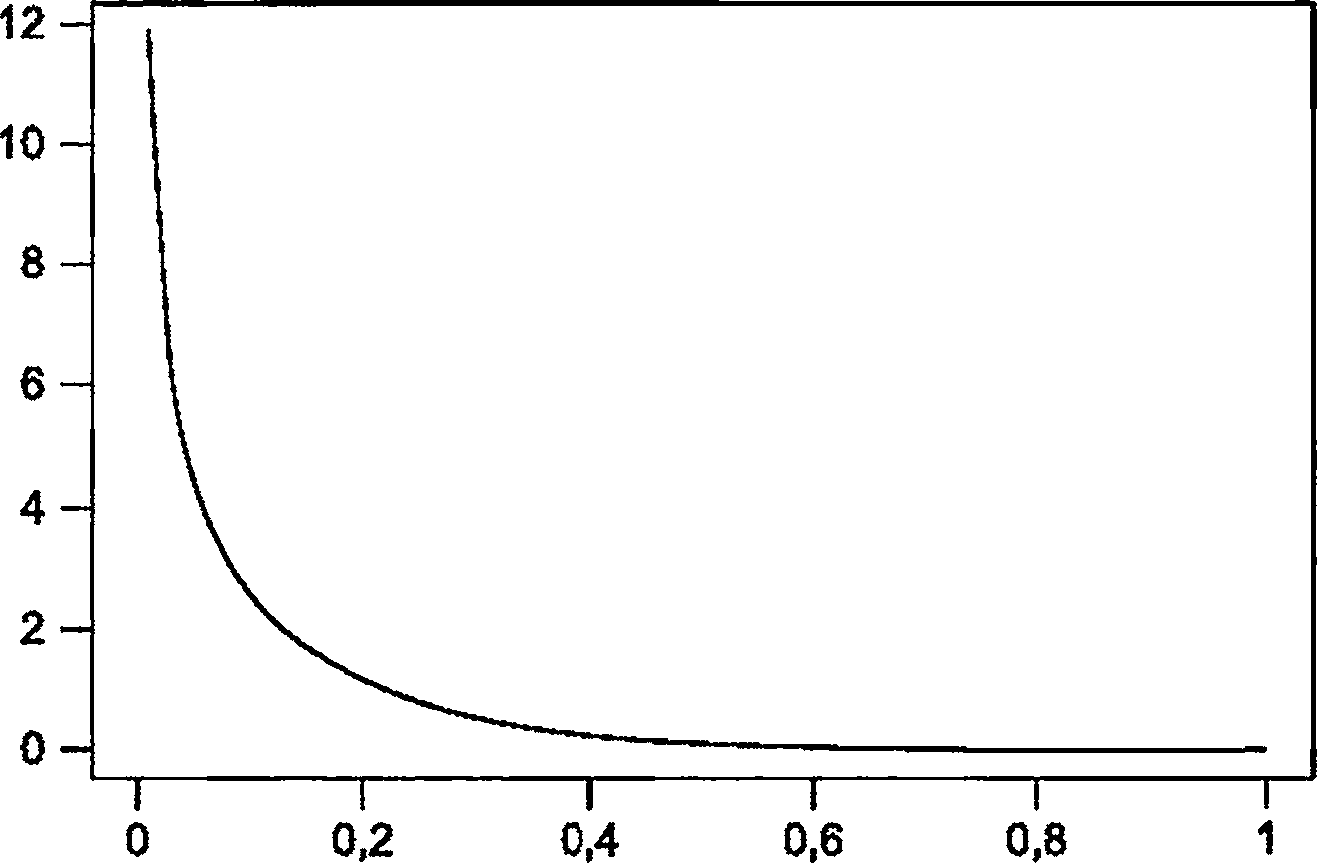
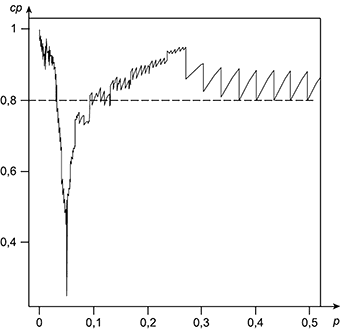
Некоторые графики вероятности охвата, а также функции программного обеспечения для их генерации приведены на рисунках G.1-G.5.

Рисунок G.1 - Фактическая вероятность охвата в примере 1 [при среднем уровне показателя доверия, номинальном значении доверительной вероятности

=0,80 и допустимой доле несоответствующих единиц

=0,03, график сгенерирован для параметров (Trust="Mid", gamma=0,80,

=0,03, p_capped=TRUE)]

Рисунок G.2 - Фактическая вероятность охвата в примере 2 [при высоком уровне показателя доверия, номинальном значении доверительной вероятности

=0,80 и допустимой доле несоответствующих единиц

=0,05, график сгенерирован для параметров (Trust="High", gamma=0,80,

=0,05, p_capped=TRUE)]

Рисунок G.3 - Фактическая вероятность охвата в примере 3 [при высоком уровне показателя доверия, номинальном значении доверительной вероятности

=0,70 и допустимой доле несоответствующих единиц

=0,03, график сгенерирован для параметров (Trust="High", gamma=0,70,

=0,03, p_capped=TRUE)]

Рисунок G.4 - Фактическая вероятность охвата в примере 4 [при низком уровне показателя доверия, номинальном уровне доверительной вероятности

=0,70 и допустимой доле несоответствующих единиц

=0,05, график сгенерирован для параметров (Trust="Low", gamma=0,70,

=0,05, p_capped=TRUE)]

Рисунок G.5 - Фактическая вероятность охвата в примере 5 [при среднем уровне показателя доверия, номинальном уровне доверительной вероятности

=0,90 и допустимой доле несоответствующих единиц

=0,05, график сгенерирован для параметров (Trust="Mid", gamma=0,90,

=0,05, p_capped=TRUE)]

Приложение H

(справочное)

Модель априорной информации

Уровень априорных знаний, используемый для выбора плана контроля по таблицам 1-5, представлен двумя параметрами a и b. Эти параметры однозначно определяют бета-распределение, которое моделирует предварительные знания о доле несоответствующих единиц, т.е. насколько вероятны низкие значения p, высокие значения и т.д. В зависимости от выбора a и b необходимо различать две формы.

а) Выбор a=b=1 приводит к равномерному распределению p, т.е. все значения p являются равновероятными. Этот случай свидетельствует об отсутствии конкретных предварительных знаний и соответствует низкому уровню показателя доверия в таблицах для планов выборочного контроля. См. рисунок H.1.

Рисунок H.1 - Плотность равномерного бета-распределения, соответствующая низкому уровню доверия

b) Выбор

a

1 и

b

1 (но не

а=b

=1) приводит к строго убывающей бета-кривой, которая может быть использована для представления среднего и высокого уровней доверия. Это означает, что низкие значения

p

более вероятны, чем высокие. Высокий уровень показателя доверия представляет наилучшую возможную ситуацию по наличию статистической априорной информации, что приводит к максимально возможному сокращению объема выборки. Средний уровень показателя доверия выбирают таким образом, что размер первой выборки представляет собой среднее геометрическое объема первой выборки высокого и низкого уровней показателя доверия, округленное в большую сторону. См. рисунок H.2.

Рисунок H.2 - Плотность строго убывающего бета-распределения; пример среднего или высокого уровней показателя доверия

Менеджер по качеству, который планирует провести проверку партии, может выбрать уровень показателя доверия, основываясь на прошлых записях результатов проверки партии. Аудитор может выбрать уровень показателя доверия, учитывая прошлый опыт работы с объектом аудита и наблюдения, сделанные на предыдущих этапах аудита.

Приложение I

(справочное)

Параметры планов выборочного контроля

Таблицы 1-5 разработаны для использования процедуры принятия решений, описанной в настоящем стандарте. В таблицах I.1-I.5 приведены статистические параметры планов выборочного контроля, приведенных в таблицах 1-5.

Элементы ячеек в таблицах I.1-I.5 поясняют рисунок I.1. Обозначения и сокращения приведены в разделе 3.

(доля совокупности)
c.type I ошибка первого рода (условная вероятность ошибочной приемки)	c.type II ошибка второго рода (условная вероятность ошибочного отклонения)
I.ASN средний объем объединенной выборки	общая вероятность применения второго этапа контроля
объем выборки одноэтапного плана с той же ОС, что и для двухэтапного плана	I.cp общая фактическая вероятность охвата
a первый параметр формы бета-распределения	b второй параметр формы бета-распределения

Рисунок I.1 - Записи в ячейках таблиц I.1-I.5

Таблица I.1 - Параметры планов, приведенных в таблице 1 для номинальной доверительной вероятности

=0,70

Уровень показателя	(доля совокупности)
доверия	0,01		0,02		0,03		0,04		0,05		0,06
Низкий	0,001 9	0,114 5	0,003 7	0,111 2	0,005 4	0,096 1	0,006 9	0,099 7	0,008 4	0,097 9	0,010 0	0,098 0
	194,14	0,016 5	105,64	0,032 6	79,33	0,049 2	64,50	0,065 2	57,08	0,081 1	51.0	0,096 8
	754,00	0,722 1	427,00	0,729 1	313,00	0,737 2	237,00	0,737 4	210,00	0,749 7	175.0	0,749 7
	1	1	1	1	1	1	1	1	1	1	1	1
Средний	0,083 8	0,091 2	0,086 0	0,090 7	0,086 3	0,090 8	0,085 4	0,091 5	0,081 8	0,093 2	0,083 8	0,093 0
	378,19	0,384 3	191,37	0,392 6	128,45	0,397 3	96,94	0,399 6	77,50	0,395 9	65,44	0,404 4
	520,00	0,738 4	260,00	0,740 0	174,00	0,740 4	131,00	0,738 2	105,00	0,740 8	88,00	0,742 7
	1	35	1	18	1	12	1	9	1	7	1	6
Высокий	0,099 8	0,003 9	0,099 7	0,012 7	0,099 6	0,012 1	0,099 4	0,008 4	0,100 0	0,049 4	0,099 0	0,043 7
	153,67	0,060 4	105,66	0,164 2	62,58	0,153 6	47,91	0,142 2	58,23	0,332 3	46,48	0,322 9
	418,00	0,972 4	209,00	0,923 0	109,00	0,924 5	100,00	0,930 0	71,00	0,837 4	58,00	0,842 5
	0,03	8	0,1	5	0,09	3	0,08	2	0,31	4	0,29	3
Уровень показателя	(доля совокупности)
доверия	0,07		0,08		0,09		0,1		0,15		0,2
Низкий	0,011 5	0,097 3	0,014 0	0,097 1	0,015 8	0,099 2	0,017 5	0,099 2	0,028 7	0,098 0	0,036 5	0,099 4
	46,56	0,111 1	41,57	0,130 4	37,29	0,142 9	35,21	0,157 9	25,38	0,230 8	22,20	0,300 0
	150,00	0,757 8	118,00	0,745 6	105,00	0,754 9	95,00	0,763 5	56,00	0,765 5	42,00	0,768 0
	1	1	1	1	1	1	1	1	1	1	1	1
Средний	0,080 0	0,094 2	0,074 2	0,095 8	0,082 9	0,093 1	0,095 1	0,097 6	0,095 9	0,096 3	0,089 8	0,091 7
	55,83	0,398 0	48,13	0,388 4	44,18	0,411 9	36,87	0,437 3	29,50	0,475 5	21,53	0,466 7
	88,00	0,742 0	66,00	0,739 2	69,00	0,740 7	53,00	0,741 7	42,00	0,749 9	31,00	0,753 2
	1	5	1	4	1	4	1	4	1	3	1	2
Высокий	0,098 5	0,032 7	0,099 5	0,032 0	0,098 6	0,039 5	0,073 6	0,037 6	0,099 4	0,008 4	0,100 0	0,049 4
	36,08	0,298 2	31,45	0,278 7	30,07	0,304 8	22,33	0,272 0	47,91	0,142 2	58,23	0,332 3
	47,00	0,848 3	43,00	0,865 2	39,00	0,857 6	35,00	0,856 7	100,00	0,930 0	71,00	0,837 4
	0,25	2	0,22	2	0,25	2	0,21	1	0,08	2	0,31	4

Таблица I.2 - Параметры планов, приведенных в таблице 2 для номинальной доверительной вероятности

=0,80

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05		0,06		0,07
Низкий	0,002 6	0,109 1	0,003 9	0,098 5	0,005 3	0,095 5	0,006 6	0,095 9	0,007 8	0,096 3	0,009 2	0,095 1
	131,62	0,036 0	98,53	0,053 3	79,50	0,071 4	68,44	0,088 9	61,11	0,105 3	55,63	0,125 0
	594,00	0,821 6	425,00	0,823 7	317,00	0,828 0	274,00	0,829 8	229,00	0,827 1	196,00	0,833 2
	1	1	1	1	1	1	1	1	1	1	1	1
Средний	0,058 4	0,094 1	0,063 0	0,098 8	0,065 1	0,095 7	0,062 8	0,096 9	0,064 1	0,096 6	0,062 4	0,098 1
	258,08	0,418 6	161,67	0,432 8	120,97	0,437 7	96,54	0,433 6	81,38	0,440 9	69,96	0,442 9
	420,00	0,806 5	249,00	0,807 8	185,00	0,808 1	148,00	0,809 4	124,00	0,810 1	106,00	0,809 5
	1	17	1	12	1	9	1	7	1	6	1	5
Высокий	0,099 7	0,029 4	0,099 7	0,006 7	0,099 0	0,017 4	0,099 6	0,065 5	0,099 3	0,068 2	0,099 1	0,067 5
	176,66	0,290 3	72,65	0,091 8	75,39	0,234 4	82,65	0,448 2	70,18	0,459 4	60,05	0,457 4
	285,00	0,912 3	185,00	0,973 2	157,00	0,928 9	115,00	0,855 0	96,00	0,853 0	83,00	0,852 5
	0,22	15	0,05	7	0,15	5	0,48	8	0,5	7	0,49	6
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	0,010 8	0,097 4	0,012 2	0,096 7	0,013 0	0,098 7	0,021 5	0,091 8	0,029 3	0,100 5
	49,86	0,142 9	46,72	0,160 0	44,26	0,173 9	34,00	0,250 0	27,00	0,333 3
	159,00	0,832 0	141,00	0,837 0	128,00	0,832 1	77,00	0,831 4	53,00	0,834 8
	1	1	1	1	1	1	1	1	1	1
Средний	0,056 2	0,101 2	0,062 9	0,099 8	0,075 0	0,099 4	0,071 8	0,093 8	0,070 3	0,096 4
	60,10	0,424 7	55,73	0,457 0	46,39	0,480 5	39,93	0,517 9	27,00	0,515 2
	94,00	0,811 5	83,00	0,810 3	64,00	0,807 6	57,00	0,810 4	42,00	0,815 9
	1	4	1	4	1	4	1	3	1	2
Высокий	0,098 5	0,061 7	0,097 8	0,070 8	0,099 3	0,045 5	0,098 6	0,034 2	0,096 8	0,077 5
	50,95	0,435 9	47,78	0,465 2	37,03	0,404 5	22,02	0,324 9	21,56	0,521 5
	72,00	0,859 8	65,00	0,852 4	55,00	0,874 0	37,00	0,904 2	28,00	0,827 7
	0,44	5	0,5	5	0,36	3	0,24	2	0,65	2

Таблица I.3 - Параметры планов, приведенных в таблице 3 для номинальной доверительной вероятности

=0,90

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05		0,06		0,07
Низкий	0,002 0	0,099 6	0,002 7	0,098 7	0,003 7	0,0956	0,004 7	0,098 5	0,005 6	0,098 3	0,006 5	0,099 1
	178,21	0,039 7	132,50	0,059 4	107,13	0,078 9	90,10	0,098 4	80,00	0,1176	72,86	0,136 4
	799,00	0,909 1	566,00	0,910 1	449,00	0,910 8	339,00	0,909 6	283,00	0,910 5	257,00	0,909 2
	1	1	1	1	1	1	1	1	1	1	1	1
Средний	0,049 3	0,092 5	0,047 6	0,093 9	0,048 6	0,094 0	0,055 8	0,090 1	0,051 6	0,092 3	0,051 1	0,093 1
	365,13	0,505 7	243,18	0,502 2	184,83	0,512 2	152,97	0,545 8	125,89	0,531 8	108,53	0,534 3
	537,00	0,877 1	359,00	0,876 4	270,00	0,876 3	214,00	0,873 6	179,00	0,876 5	168,00	0,875 7
	1	20	1	13	1	10	1	9	1	7	1	6
Высокий	0,099 5	0,004 1	0,099 9	0,046 5	0,102 3	0,096 3	0,099 5	0,036 4	0,099 3	0,088 0	0,098 4	0,077 1
	144,70	0,069 8	197,57	0,442 1	190,28	0,631 6	107,85	0,385 6	123,64	0,616 1	101,21	0,581 6
	491,00	0,988 0	299,00	0,914 8	224,00	0,865 4	179,00	0,928 9	133,00	0,872 3	114,00	0,882 0
	0,04	21	0,44	25	1	29	0,34	13	0,89	17	0,76	13
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	0,007 5	0,098 2	0,008 3	0,099 0	0,010 2	0,095 4	0,017 7	0,096 9	0,026 4	0,096 9
	67,32	0,157 9	63,18	0,176 5	57,29	0,193 5	40,06	0,277 8	31,21	0,357 1
	212,00	0,908 3	177,00	0,911 0	159,00	0,907 6	92,00	0,904 5	64,00	0,898 9
	1	1	1	1	1	1	1	1	1	1
Средний	0,048 8	0,094 5	0,066 9	0,09 27	0,067 3	0,096 0	0,095 8	0,075 4	0,055 5	0,095 8
	94,47	0,529 9	83,88	0,596 5	68,38	0,588 6	57,14	0,663 5	35,08	0,549 5
	135,00	0,877 9	120,00	0,869 9	97,00	0,868 7	77,00	0,870 3	53,00	0,875 3
	1	5	1	6	1	5	1	5	1	2
Высокий	0,097 9	0,072 8	0,099 4	0,099 0	0,099 7	0,075 6	0,100 0	0,092 4	0,092 0	0,084 6
	86,91	0,566 5	75,25	0,620 3	55,89	0,538 0	49,92	0,658 9	34,38	0,631 9
	112,00	0,885 7	88,00	0,863 1	69,00	0,887 1	66,00	0,863 5	47,00	0,865 2
	0,71	11	0,94	11	0,62	8	1	6	1	3

Таблица I.4 - Параметры планов, приведенных в таблице 4 для номинальной доверительной вероятности

=0,95

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05		0,06		0,07
Низкий	0,002 0	0,099 6	0,002 7	0,098 7	0,003 7	0,095 6	0,004 7	0,098 5	0,005 6	0,098 3	0,006 5	0,099 1
	178,21	0,039 7	132,50	0,059 4	107,13	0,078 9	90,10	0,098 4	80,0	0,117 6	72,86	0,136 4
	799,00	0,909 1	566,00	0,910 1	449,00	0,910 8	339,00	0,909 6	283,00	0,910 5	257,00	0,909 2
	1	1	1	1	1	1	1	1	1	1	1	1
Средний	0,049 3	0,092 5	0,047 6	0,093 9	0,048 6	0,094 0	0,055 8	0,090 1	0,051 6	0,092 3	0,051 1	0,093 1
	365,13	0,505 7	243,18	0,502 2	184,83	0,512 2	152,97	0,545 8	125,89	0,531 8	108,53	0,534 3
	537,00	0,877 1	359,00	0,876 4	270,00	0,876 3	214,00	0,873 6	179,00	0,876 5	168,00	0,875 7
	1	20	1	13	1	10	1	9	1	7	1	6
Высокий	0,099 5	0,004 1	0,099 9	0,046 5	0,102 3	0,096 3	0,099 5	0,036 4	0,099 3	0,088 0	0,098 4	0,077 1
	144,70	0,069 8	197,57	0,442 1	190,28	0,631 6	107,85	0,385 6	123,64	0,616 1	101,21	0,581 6
	491,00	0,988 0	299,00	0,914 8	224,00	0,865 4	179,00	0,928 9	133,00	0,872 3	114,00	0,882 0
	0,04	21	0,44	25	1	29	0,34	13	0,89	17	0,76	13
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15		0,2
Низкий	0,007 5	0,098 2	0,008 3	0,099 0	0,010 2	0,095 4	0,017 7	0,096 9	0,026 4	0,096 9
	67,32	0,157 9	63,18	0,176 5	57,29	0,193 5	40,06	0,277 8	31,21	0,357 1
	212,00	0,908 3	177,00	0,911 0	159,00	0,907 6	92,00	0,904 5	64,00	0,898 9
	1	1	1	1	1	1	1	1	1	1
Средний	0,048 8	0,094 5	0,066 9	0,092 7	0,067 3	0,096 0	0,095 8	0,075 4	0,055 5	0,095 8
	94,47	0,529 9	83,88	0,596 5	68,38	0,588 6	57,14	0,663 5	35,08	0,549 5
	135,00	0,877 9	120,00	0,869 9	97,00	0,868 7	77,00	0,870 3	53,00	0,875 3
	1	5	1	6	1	5	1	5	1	2
Высокий	0,097 9	0,072 8	0,099 4	0,099 0	0,099 7	0,075 6	0,100 0	0,092 4	0,092 0	0,084 6
	86,91	0,566 5	75,25	0,620 3	55,89	0,538 0	49,92	0,658 9	34,38	0,631 9
	112,00	0,885 7	88,00	0,863 1	69,00	0,887 1	66,00	0,863 5	47,00	0,865 2
	0,71	11	0,94	11	0,62	8	1	6	1	3

Таблица I.5 - Параметры планов, приведенных в таблице 5 для номинальной доверительной вероятности

=0,99

Уровень показателя	(доля совокупности)
доверия	0,02		0,03		0,04		0,05			0,06		0,07
Низкий	0,001 5	0,108 9	0,002 2	0,098 1	0,002 9	0,096 4	0,003 7	0,099 1		0,004 4	0,099 1	0,005 4	0,099 8
	221,95	0,042 3	165,75	0,063 0	133,75	0,084 2	113,09	0,103 9		100,25	0,125 0	88,91	0,145 5
	899,00	0,952 7	733,00	0,952 3	524,00	0,951 6	399,00	0,951 2		333,00	0,950 9	257,00	0,950 3
	1	1	1	1	1	1	1	1		1	1	1	1
Средний	0,035 1	0,102 2	0,042 0	0,095 3	0,042 0	0,094 4	0,048 1	0,091 0		0,041 1	0,095 4	0,037 9	0,089 9
	466,04	0,537 1	319,58	0,571 9	238,71	0,570 9	197,70	0,605 1		167,37	0,554 1	144,82	0,526 2
	649,00	0,912 5	433,00	0,904 9	349,00	0,909 5	279,00	0,905 6		233,00	0,909 2	214,00	0,914 3
	1	20	1	15	1	11	1	10		1	8	1	6
Высокий	0,100 3	0,079 2	0,099 7	0,079 9	0,080 3	0,094 2	0,099 2	0,080 2		0,100 4	0,074 8	0,099 5	0,070 8
	471,69	0,645 4	313,70	0,646 7	246,00	0,679 9	188,46	0,650 6		168,00	0,672 3	153,59	0,672 2
	499,00	0,899 3	333,00	0,898 3	249,00	0,890 7	219,00	0,897 7		183,00	0,899 6	171,00	0,902 8
	1	79	1	51	1	31	1	30		1	22	1	19
Уровень показателя	(доля совокупности)
доверия	0,08		0,09		0,1		0,15			0,2
Низкий	0,006 5	0,095 4	0,007 4	0,095 7	0,008 1	0,097 1	0,013 4		0,097 0	0,019 5	0,099 3
	81,67	0,166 7	71,92	0,179 5	68,20	0,200 0	51,88		0,291 7	41,89	0,388 9
	237,00	0,949 3	211,00	0,948 0	189,00	0,948 3	113,00		0,941 7	79,00	0,934 5
	1	1	1	1	1	1	1		1	1	1
Средний	0,013 6	0,108 5	0,035 0	0,088 6	0,028 5	0,093 3	0,048 5		0,088 1	0,044 4	0,095 8
	89,62	0,288 6	109,14	0,514 9	92,76	0,467 4	64,08		0,598 3	45,14	0,594 8
	187,00	0,935 8	166,00	0,917 6	149,00	0,922 3	93,00		0,908 4	64,00	0,908 3
	1	2	1	4	1	3	1		3	1	2
Высокий	0,098 1	0,037 4	0,099 5	0,070 8	0,097 6	0,043 4	0,096 8		0,087 8	0,094 8	0,089 2
	105,48	0,469 5	118,70	0,656 8	90,01	0,521 5	58,67		0,684 0	43,75	0,676 2
	162,00	0,940 0	133,00	0,904 5	129,00	0,932 2	73,00		0,891 5	49,00	0,890 7
	0,5	14	1	16	0,58	11	1		8	1	6

Приложение J

(справочное)

Алгоритм выбора плана контроля

Планы, приведенные в таблицах 1-5, рассчитаны с помощью алгоритма с использованием следующих данных и этапов.

Данные:

,

1000,

200,

a

[0,01,1],

b

[1,100],

{0,70, 0,80, 0,90, 0,95, 0,99},

{0,01,0,02,0,03,0,04,0,05,0,06,0,07,0,08,0,09,0,10,0,15,0,20}.

Этап 0. Вычисление

и

(см. приложение А) для всех

n

[2; 200].

Этап I. Определение:

;

.

Вычисление

.

Если одно из трех приведенных выше уравнений не имеет решения, соответствующую пару (

,

) отбрасывают.

Этап II. Определение:

и

;

и

;

.

Этап III (должен быть выполнен последовательно для низкого, среднего, высокого уровней показателя доверия, здесь приведен пример для высокого уровня доверия).

Этап IIIa. Для каждой пары (

a

,

b

)

находят

.

Затем для каждого значения

вычисляют

и

.

Этап IIIb. Если для любых (

a

,

b

) существует по крайней мере одно значение

, для которого

,

тогда

- наименьшее.

Если для (

a

,

b

) не существует хотя бы одного значения

, повторяют этап IIIb с 0,125 вместо 0,1. При необходимости затем повторяют процедуру со значениями 0,15, 0,175 и 0,2 до тех пор, пока не будет найдено хотя бы одно значение

.

Этап IIIc. Из всех найденных значений

выбирают то, у которого наибольший результат

I.ASN

.

В некоторых случаях результаты, полученные с помощью приведенного алгоритма, были немного изменены в таблицах для согласованности объема выборки с точки зрения пользователя, а именно:

a) объемы выборки должны уменьшаться по строкам таблиц 1-5;

b) объемы выборки должны уменьшаться по графам таблиц 1-5.

Приложение K

(справочное)

Прилагаемое программное обеспечение. Руководство по использованию

Для поддержки применения настоящего стандарта и удобства пользователей было разработано сопутствующее программное обеспечение, доступное по адресу https://standards.iso.org/iso/28596/ed-1/en.

Целью программного обеспечения является вычисление:

a) точечной оценки и доверительного интервала для доли несоответствующих единиц p в целевой совокупности по результатам двухступенчатой процедуры выборочного контроля, см. приложение A;

b) функции OC для двухступенчатой процедуры выборочного контроля, см. приложение B;

c) кривой вероятности охвата для двухступенчатой процедуры выборочного контроля, см. приложение G. Программное обеспечение поставлено в виде пакета программ на языке R (см. [10] для получения информации о языке программирования R).

Все примеры, приведенные в настоящем приложении, соответствуют примерам из раздела 6.

K.1 Доверительные интервалы

Функция confint вычисляет двусторонние доверительные интервалы для доли несоответствующих единиц в партии.

	Данные (Trust="Low", gamma=0,70, p0=0,01, x1=NULL, x2=NULL)
Аргументы
Trust	Уровень показателя доверия для доли несоответствующих единиц "низкий". Значение по умолчанию="Низкий". Доступные уровни: "Низкий", "Средний", "Высокий".
gamma	Номинальная доверительная вероятность. Значение по умолчанию=0,70. Доступные значения: 0,70, 0,80, 0,90, 0,95, 0,99.
p0	Допустимое значение, на соответствие которому выполняют контроль. Значение по умолчанию=0,01. Доступные значения: 0,01, 0,02, 0,03, 0,04, 0,05, 0,06, 0,07, 0,08, 0,09, 0,10, 0,15, 0,20.
x1	Количество несоответствующих единиц на первом этапе контроля. Значение по умолчанию=NULL. По умолчанию функция проведет вас через весь процесс контроля и запросит результат после первого этапа отбора выборки. Возможные значения: 0 x 1 .
x2	Количество несоответствующих единиц на втором этапе контроля. Значение по умолчанию=NULL. По умолчанию функция проведет вас через весь процесс контроля и запросит результат после второго этапа контроля. Возможные значения: 0 x 2 .
Выход
	Вектор, содержащий 1) оценку доли несоответствующих единиц, 2) нижнюю доверительную границу, 3) верхнюю доверительную границу.
Примеры
Пример 7.1	Данные (Trust="Mid", gamma=0,80, p0=0,03, x1=NULL)
Пример 7.2	Данные (Trust="High", gamma=0,80, p0=0,05, x1=0, x2=NULL)
Пример 7.3	Данные (Trust="High", gamma=0,70, p0=0,03, x1=7)
Пример 7.4	Данные (Trust="Low", gamma=0,70, p0=0,05, x1=0)
Пример 7.5	Данные (Trust="Mid", gamma=0,90, p0=0,05, x1=4, x2=7)

K.2 Функция OC

Функция OC вычисляет кривую OC для двухступенчатой процедуры выборочного контроля и долю несоответствующих единиц p. Если установлено, функция OC также выводит на график кривую OC.

	Функция OC (p=NULL, Trust="Low", gamma=0,70, p0=0,01, plot=TRUE, plotpoints=1 001, p_capped=FALSE)
Аргументы
p	Доля несоответствующих единиц, для которой должна быть рассчитана кривая OC. Значение по умолчанию=NULL. При значении по умолчанию никакое конкретное значение OC вычисляться не будет. Возможные значения: 0 p 1.
Trust	Уровень показателя доверия для доли несоответствующих единиц "низкий". Значение по умолчанию="Низкий". Доступные уровни: "Низкий", "Средний", "Высокий".
gamma	Номинальная доверительная вероятность. Значение по умолчанию=0,70. Доступные значения: 0,70, 0,80, 0,90, 0,95, 0,99.
p0	Допустимое значение, которое необходимо проверить. Значение по умолчанию=0,01. Доступные значения: 0,01, 0,02, 0,03, 0,04, 0,05, 0,06, 0,07, 0,08, 0,09, 0,10, 0,15, 0,20.
plot	Указывает, следует ли чертить график ОС. Значение по умолчанию=TRUE.
plotpoints	Количество точек, которое необходимо вычислить для построения графика кривой OC. Значение по умолчанию=1001.
p_capped	Указывает, должен ли график охватывать весь диапазон значений p или должен быть нанесен в более узком диапазоне. Значение по умолчанию=FALSE. По умолчанию график будет построен на всем диапазоне.
Выход
Примеры
Пример 7.1	Функция OC (p=0,06, Trust="Mid", gamma=0,80, p0=0,03, график=FALSE)
Пример 7.2	Функция OC (p=0,025, Trust="High", gamma=0,80, p0=0,05, plot=TRUE, plotpoints=101, p_capped=FALSE)
Пример 7.3	Функция OC (p=NULL, Trust="High", gamma=0,70, p0=0,03)
Пример 7.4	Функция OC (p=0,10, Trust="Low", gamma=0,70, p0=0,05, plot=TRUE, p_capped=TRUE)
Пример 7.5	Функция OC (p=0,01, Trust="Mid", gamma=0,90, p0=0,05, plot=FALSE)

K.3 Функция покрытия

Функция покрытия вычисляет и строит график вероятности охвата для двухступенчатого плана выборочного контроля.

Приложение ДА

(справочное)

Сведения о соответствии ссылочных международных стандартов национальным стандартам

Таблица ДА.1

Библиография

[1]	ISO 2859-1, Sampling procedures for inspection by attributes - Part 1: Sampling schemes indexed by acceptance quality limit (AQL) for lot-by-lot inspection
[2]	FINANCIAL REPORTING COUNCIL International Standard on Auditing (UK) 200. Overall Objectives of the Independent Auditor and the Conduct of an Audit in Accordance with Internationals Standards on Auditing. Revised June 2016
[3]	FINANCIAL REPORTING COUNCIL International Standard on Auditing (UK) 320. Materiality in Planning and Performing an Audit. Revised June 2016.
[4]	FINANCIAL REPORTING COUNCIL International Standard on Auditing (UK) 530. Audit sampling. Revised June 2016.
[5]	RLURZ K (2014), Shortest two-sided confidence intervals for a probability under prior information. Metrika: International Journal for Theoretical and Applied Statistics, Springer, vol. 77(3), pages 389-413, April.
[6]	ISA 200, Overall Objectives of the Independent Auditor and the Conduct of an Audit in Accordance with Internationals Standards on Auditing
[7]	ISA 320, Materiality in Planning and Performing an Audit
[8]	ISA 530, Audit Sampling
[9]	LURZ K. Confidence and Prediction under Covariates and Prior Information. PhD Thesis, University of , Germany. : 2015.
[10]	R CORE TEAM (2014). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL http://www.R-project.org/