ГОСТ Р 50779.23-2005
(ИСО 3301:1975)
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Сравнение двух средних в парных наблюдениях
Statistical methods. Statistical interpretation of data. Comparison of two means
in the case of paired observations
ОКС 03.120.10
Дата введения 2005-07-01
Предисловие
Задачи, основные принципы и правила проведения работ по государственной стандартизации в Российской Федерации установлены ГОСТ Р 1.0-92 "Государственная система стандартизации Российской Федерации. Основные положения" и ГОСТ Р 1.2-92 "Государственная система стандартизации Российской Федерации. Порядок разработки государственных стандартов"
Сведения о стандарте
1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" и Научно-исследовательским центром контроля и диагностики технических систем на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением технического регулирования и стандартизации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 мая 2005 г. N 112-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 3301:1975 "Статистическое представление данных. Сравнение двух средних в парных наблюдениях" (ISO 3301:1975 "Statistical interpretation of data - Comparison of two means in the case of paired observations", MOD) путем включения отдельных фраз, которые выделены в тексте курсивом, с целью гармонизации с национальными стандартами.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5 (подраздел 3.6)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в указателе "Национальные стандарты", а текст изменений - в информационных указателях "Национальные стандарты". В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе "Национальные стандарты"
1 Область применения
Настоящий стандарт устанавливает метод проверки статистической гипотезы о равенстве среднего распределения (далее - среднее) разностей парных наблюдений нулю (предположение о несущественности расхождения между рядами наблюдений) или какому-либо другому заданному значению.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения (ИСО 3534-1:1993, IDT)
Примечания
1 Настоящий раздел является дополнительным по отношению к содержанию международного стандарта ИСО 3301:1975 (ISO 3301:1975) и включен для учета основополагающих национальных стандартов в области статистических методов.
2 При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов по указателю "Национальные стандарты", составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяют в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 50779.10, а также следующий термин с соответствующим определением:
парные наблюдения (paired observations): Два результата наблюдений определенных свойств или характеристик объекта и
называются парными, если они получены:
- как результаты наблюдений над одним и тем же объектом (из совокупности), причем данные наблюдения относятся к различным условиям получения этих наблюдений (например, сравнение двух методов анализа свойств одного и того же объекта);
- как результаты наблюдений над объектами, идентичными во всех отношениях, кроме предполагаемого систематического различия в некотором интересующем аспекте; в отношении значимости этого различия проводят проверку статистической гипотезы (например, сравнение урожайности двух соседних участков, засеянных семенами различных сортов).
Во втором случае эффективность проверки гипотез зависит от степени уверенности в отсутствии каких-либо других систематических различий между объектами, кроме некоторого возможного различия, в отношении которого проверяют гипотезу.
4 Применение метода для сравнения двух способов обработки экспериментальных данных
Установленный в настоящем стандарте метод проверки статистической гипотезы может быть применен с целью подтвердить различие двух способов обработки. В этом случае можно считать, что результаты наблюдений получены одним способом обработки, а результаты наблюдений
- некоторым другим способом. Две серии результатов наблюдений не являются независимыми, поскольку каждому
первой серии (первый способ обработки) ставится в соответствие вполне определенное
второй серии (второй способ обработки). Термин "способ обработки" понимают в широком смысле. При выявлении возможного систематического расхождения два сравниваемых способа обработки могут относиться к двум методам испытаний, к двум измерительным устройствам или к двум лабораториям. Два способа обработки, выполненные над одним и тем же экспериментальным материалом, могут влиять друг на друга, и полученное значение может зависеть от последовательности обработки. Оптимальный план эксперимента должен устранять возможные систематические смещения. В качестве альтернативы сравнению способов обработки можно рассмотреть воздействие одного способа обработки по сравнению со случаем полного отсутствия обработки.
5 Условия применения метода
Для корректного применения метода необходимо выполнение следующих двух условий:
- последовательность разностей ![]() является выборкой независимой случайной величины;
является выборкой независимой случайной величины;
- распределение величин ![]() является нормальным или близким к нормальному.
является нормальным или близким к нормальному.
Если распределение разностей отклоняется от нормального, метод проверки гипотез применим при условии, что объем выборки достаточно велик. При больших отклонениях от нормальности требуется соответственно большая выборка. Однако даже в предельных случаях отклонения от нормальности выборки объемом 100 могут быть достаточными для корректного применения метода в большинстве прикладных задач.
6 Расчетные формулы и правила принятия решения
Изучаемая проблема | ||||
Условия проведения эксперимента | ||||
Статистические данные | Расчетные формулы | |||
Объем выборки |
| |||
Заданное значение (среднее случайных разностей парных наблюдений): |
| |||
Правило принятия решения
| ||||
Примечание - ![]() - квантиль уровня
- квантиль уровня статистики Стьюдента с (
) степенями свободы. Значения
![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1 - Значения отношения ![]() для
для ![]()
| Двусторонняя гипотеза | Односторонняя гипотеза | ||
|
|
|
| |
1 | 8,985 | 45,013 | 4,465 | 22,501 |
2 | 2,434 | 5,730 | 1,686 | 4,021 |
3 | 1,591 | 2,920 | 1,177 | 2,270 |
4 | 1,242 | 2,059 | 0,953 | 1,676 |
5 | 1,049 | 1,646 | 0,823 | 1,374 |
6 | 0,925 | 1,401 | 0,734 | 1,188 |
7 | 0,836 | 1,237 | 0,670 | 1,060 |
8 | 0,769 | 1,118 | 0,620 | 0,966 |
9 | 0,715 | 1,028 | 0,580 | 0,892 |
10 | 0,672 | 0,956 | 0,546 | 0,833 |
11 | 0,635 | 0,897 | 0,518 | 0,785 |
12 | 0,604 | 0,847 | 0,494 | 0,744 |
13 | 0,577 | 0,805 | 0,473 | 0,708 |
14 | 0,554 | 0,769 | 0,455 | 0,678 |
15 | 0,533 | 0,737 | 0,438 | 0,651 |
16 | 0,514 | 0,708 | 0,423 | 0,626 |
17 | 0,497 | 0,683 | 0,410 | 0,605 |
18 | 0,482 | 0,660 | 0,398 | 0,586 |
19 | 0,468 | 0,640 | 0,387 | 0,568 |
20 | 0,455 | 0,621 | 0,376 | 0,552 |
21 | 0,443 | 0,604 | 0,367 | 0,537 |
22 | 0,432 | 0,588 | 0,358 | 0,523 |
23 | 0,422 | 0,573 | 0,350 | 0,510 |
24 | 0,413 | 0,559 | 0,342 | 0,498 |
25 | 0,404 | 0,547 | 0,335 | 0,487 |
26 | 0,396 | 0,535 | 0,328 | 0,477 |
27 | 0,388 | 0,524 | 0,322 | 0,467 |
28 | 0,380 | 0,513 | 0,316 | 0,458 |
29 | 0,373 | 0,503 | 0,310 | 0,449 |
30 | 0,367 | 0,494 | 0,305 | 0,441 |
40 | 0,316 | 0,422 | 0,263 | 0,378 |
50 | 0,281 | 0,375 | 0,235 | 0,337 |
60 | 0,256 | 0,341 | 0,214 | 0,306 |
70 | 0,237 | 0,314 | 0,198 | 0,283 |
80 | 0,221 | 0,293 | 0,185 | 0,264 |
90 | 0,208 | 0,276 | 0,174 | 0,248 |
100 | 0,197 | 0,261 | 0,165 | 0,235 |
200 | 0,139 | 0,183 | 0,117 | 0,165 |
500 | 0,088 | 0,116 | 0,074 | 0,104 |
0 | 0 | 0 | 0 | |
Пример - Приведенные в таблице 2 данные собраны в процессе исследований, спланированных с целью определить, зависит ли скорость изнашивания шеек коленчатого вала двигателя внутреннего сгорания от типа материала металлических вкладышей подшипников скольжения этого вала.
Таблица 2 - Износ шеек коленчатых валов в течение заданной наработки, измеренный в стотысячных долях дюйма
Номер вала | Износ вала | Разность | |
Медно-свинцовые вкладыши | Алюминиевые вкладыши | ||
1 | 3,5 | 1,5 | 2,0 |
2 | 2,0 | 1,3 | 0,7 |
3 | 4,7 | 4,5 | 0,2 |
4 | 2,8 | 2,5 | 0,3 |
5 | 6,5 | 4,5 | 2,0 |
6 | 2,2 | 1,7 | 0,5 |
7 | 2,5 | 1,8 | 0,7 |
8 | 5,8 | 3,3 | 2,5 |
9 | 4,2 | 2,3 | 1,9 |
Сумма | 34,2 | 23,4 | 10,8 |
Технические характеристики _ | |
Статистические данные | Вычисления |
Объем выборки: |
|
Выводы
| |
7 Ошибка второго рода
Вероятность отклонения нулевой гипотезы, когда она верна, равна уровню значимости . Отклонение нулевой гипотезы, когда она верна, называется ошибкой первого рода, и поэтому выбор значения
ограничивает риск такой ошибки.
С другой стороны, можно совершить ошибку второго рода, то есть проверить нулевую гипотезу, когда она неверна. Вероятность отклонения нулевой гипотезы, когда она неверна, называется мощностью критерия статистической проверки гипотезы. Вероятность ошибки второго рода в таком случае равна
.
Для заданной выборки и ошибки первого рода вероятность
зависит не только от истинного среднего
наблюдаемых разностей
![]() , для которых устанавливают различные альтернативные гипотезы, но также и от стандартного отклонения
, для которых устанавливают различные альтернативные гипотезы, но также и от стандартного отклонения этих разностей. Это стандартное отклонение неизвестно, и, если
мало, выборка может обеспечить только плохую оценку. В результате невозможно устанавливать верхний предел вероятности ошибки второго рода.
На графиках (рисунки 1 и 2) показаны зависимости между мощностью критерия проверки гипотез и истинным средним совокупности, деленным на соответствующее стандартное отклонение (
![]() ) для случая односторонней гипотезы
) для случая односторонней гипотезы ![]() , различных значений
, различных значений и уровней значимости 0,05 и 0,01 соответственно.

Рисунок 1 - Мощность критерия для одной выборки (односторонний критерий), = 0,01
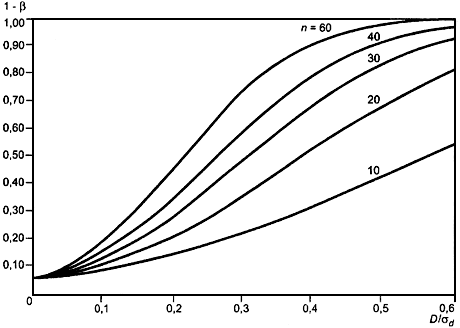
Рисунок 2 - Мощность критерия для одной выборки (односторонний критерий), = 0,05
На основании этих графиков можно сделать следующие заключения:
1) Мощность критерия проверки гипотез однозначно определяется истинным средним совокупности разностей, измеренных в единицах стандартного отклонения
, уровнем значимости
и объемом выборки.
2) Функция мощности является монотонно возрастающей функцией истинного среднего совокупности разностей. Она также монотонно возрастает с ростом объема выборки и уровня значимости при условии, что
>0 и
отличается от 0 и 1.
3) Для уровня значимости 0,05 и при объеме выборки 50 достигается мощность 0,95, если истинное среднее разностей превышает половину стандартного отклонения разностей. Для =20 такая мощность достигается для
![]() =0,78 и больших значений.
=0,78 и больших значений.
Текст документа сверен по:
, 2005
