ГОСТ 27872-88
(СТ СЭВ 5892-87)
Группа Т80
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
МЕТРОЛОГИЯ
СТАНДАРТНЫЕ ОБРАЗЦЫ
Методика изготовления и аттестации стандартных образцов состава горных пород и минерального сырья
Metrology. Reference materials. Methods of production and calibration of reference materials of rocks and mineral raw materials
ОКСТУ 0008
Дата введения 1989-01-01
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. ВНЕСЕН Министерством геологии СССР
РАЗРАБОТЧИКИ
Е.П.Осико, канд.хим.наук; Т.Я.Белова, канд. хим. наук; Л.Е.Беренштейн, канд. техн. наук; Г.В.Остроумов, д-р. техн. наук
2. Постановлением Государственного комитета СССР по стандартам от 28.10.88 N 3582 стандарт Совета Экономической Взаимопомощи СТ СЭВ 5892-87 "Метрология. Стандартные образцы. Методика изготовления и аттестации стандартных образцов состава горных пород и минерального сырья" введен в действие непосредственно в качестве государственного стандарта СССР с 01.01.89
3. ВВЕДЕН ВПЕРВЫЕ
4. Переиздание. Январь 1994 г.
Настоящий стандарт распространяется на стандартные образцы (далее - СО) состава горных пород и минерального сырья и устанавливает порядок изготовления СО, оценки их однородности, а также порядок проведения аттестационных анализов, статистической обработки аналитических результатов и аттестации содержаний компонентов СО.
1. ПОРЯДОК ИЗГОТОВЛЕНИЯ СО
1.1. Исходным материалом для изготовления СО является геологическая проба, которая должна быть достаточно однородной и иметь состав, характерный для данного типа горной породы или минерального сырья.
1.2. Количество материала геологической пробы должно гарантировать изготовление СО массой не менее 200 кг.
Минимальная масса материала геологической пробы для изготовления СО с повышенным содержанием золота, серебра и других благородных металлов должна быть не менее 500 кг.
Минимальная масса пробы для изготовления СО изотопного состава устанавливается для каждого образца.
1.3. Материал геологической пробы для изготовления СО должен быть тщательно отобран и упакован с целью исключения его случайного загрязнения.
1.4. После оценки пригодности материала геологической пробы для изготовления СО материал пробы дробят, измельчают и гомогенизируют. При этом должен быть, по возможности, достигнут гранулометрический состав, при котором 95% массы пробы должно иметь размер зерен менее 0,074 мм и 100% массы - размер зерен менее 0,100 мм.
В отдельных случаях при изготовлении СО (например, для обеспечения достаточной однородности СО) допускается использовать только отобранные фракции геологической пробы.
1.5. После гомогенизации и установления достаточной однородности материал пробы расфасовывают. Если материал пробы не соответствует требованиям однородности, проводят дополнительную гомогенизацию и повторную оценку однородности.
1.6. Материал геологической пробы, отобранный для изготовления СО, не должен изменять своего состава под воздействием влаги, кислорода и других веществ. В случае опасности такого изменения следует принимать необходимые меры при упаковке, транспортировании и хранении.
2. ИССЛЕДОВАНИЕ ОДНОРОДНОСТИ МАТЕРИАЛА СО
2.1. Исследование однородности материала СО проводят до начала аттестационных анализов.
2.2. Оценку характеристик однородности выполняют для элементов-индикаторов. В качестве элементов-индикаторов выбирают из числа аттестуемых элементы, которые наиболее неравномерно распределены в исходном материале геологической пробы. Элементы-индикаторы должны представлять различные группы элементов.
2.3. Исследование однородности заключается в следующем. От гомогенизированного материала СО случайным образом отбирают проб (
![]() ). В каждой пробе выполняют
). В каждой пробе выполняют определений элемента-индикатора (обычно
![]() ). Все определения проводят в одинаковых условиях.
). Все определения проводят в одинаковых условиях.
2.4. При определении однородности следует иметь в виду, что результат исследования однородности распределения компонентов зависит от массы навески, взятой для исследования, и что разные компоненты в одном и том же материале СО могут иметь различный характер распределения. На практике обычно минимальную представительную навеску устанавливают по компоненту, наиболее неравномерно распределенному в данном материале, за исключением золота и благородных металлов.
2.5. Для определения компонентов при исследовании однородности выбирают, прежде всего, те методы, которые обладают высокой чувствительностью и высокой воспроизводимостью.
При этом
![]() , (1)
, (1)
где ![]() - относительное среднее квадратическое отклонение метода, использованного для исследования однородности;
- относительное среднее квадратическое отклонение метода, использованного для исследования однородности;
![]() - относительное среднее квадратическое отклонение, вносимое остаточной неоднородностью;
- относительное среднее квадратическое отклонение, вносимое остаточной неоднородностью;
![]() - относительное среднее квадратическое отклонение результатов рядовых анализов (табл.21).
- относительное среднее квадратическое отклонение результатов рядовых анализов (табл.21).
2.6. Остаточная неоднородность СО (![]() ) не должна вносить значимого вклада в ошибку воспроизводимости рядовых методов анализа и ее значение не должно превышать 1/3 относительного среднего квадратического отклонения результатов анализа (
) не должна вносить значимого вклада в ошибку воспроизводимости рядовых методов анализа и ее значение не должно превышать 1/3 относительного среднего квадратического отклонения результатов анализа (), полученных аналитическими методами, для исследования которых предназначен СО, т.е.:
![]() . (2)
. (2)
2.7. Полученные данные об однородности обрабатывают с применением дисперсионного анализа, целью которого является разложение суммарной дисперсии () на две составляющие:
1) дисперсию между пробами (), обусловленную неоднородностью материала;
2) дисперсию внутри проб (), обусловленную техникой эксперимента.
Рассчитывают
дисперсию между пробами ():
![]() , (3)
, (3)
где
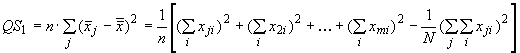 ; (4)
; (4)
дисперсию внутри проб ():
![]() , (5)
, (5)
где
![]() ; (6)
; (6)
суммарную дисперсию ():
![]() , (7)
, (7)
где
![]() (8)
(8)
В формулах (3)-(8) приняты обозначения:
-
-й образец,
-й результат (
=1...
,
=1...
);
- среднее результатов в
-м образце;
- среднее всех
результатов;
- число образцов, исследуемых на однородность;
- число параллельных результатов в
-м образце;
- суммарное число результатов (
![]() );
);
,
,
- суммы квадратов.
Результаты дисперсионного анализа при исследовании однородности СО записывают в виде табл.1.
Таблица 1
Рассеяние результатов | Сумма квадратов | Число степеней свободы | Дисперсия |
Между пробами |
|
| |
Внутри проб |
|
| |
Сумма |
|
|
|
2.8. Распределение исследуемого компонента в СО можно считать однородным, если выполнены условия:
1) критерий Фишера , рассчитанный по формуле:
![]() , (9)
, (9)
меньше чем табличное, взятое для доверительной вероятности
=0,95 и для степеней свободы
и
, т.е.
![]() , (10)
, (10)
где ![]() ;
;
![]() ;
;
2) среднее квадратическое отклонение между пробами () не должно превышать 1/3 среднего квадратического отклонения результатов анализа, полученных методами, для контроля которых предназначен СО и погрешность которых характеризуется
,
![]() ; (11)
; (11)
![]() , (12)
, (12)
где - содержание исследуемого компонента-индикатора.
Если выполнены условия (9, 11), то, согласно критерию ничтожной погрешности, можно пренебречь погрешностью неоднородности.
Если среднее квадратическое отклонение между пробами значимо по сравнению с величиной
, т.е.
![]() , (13)
, (13)
то погрешность неоднородности () оценивают по формуле
![]() . (14)
. (14)
Распределение исследуемого компонента в СО можно считать однородным, если
![]() . (15)
. (15)
Примеры проверки однородности распределения железа и серебра в СО флюорита приведены в приложении 11.
3. ПОРЯДОК ПРОВЕДЕНИЯ АТТЕСТАЦИОННЫХ АНАЛИЗОВ
3.1. При рассылке СО на аттестационный анализ одновременно направляют:
1) материал СО;
2) краткую петрографо-минералогическую характеристику СО;
3) данные предварительного анализа химического состава СО и перечень компонентов, подлежащих аттестации, с указанием диапазона содержаний;
4) сведения об условиях выполнения анализа и аналитических особенностях СО.
3.2. Перед началом аналитического исследования проводят дополнительную гомогенизацию материала СО, если предполагается, что при транспортировании он претерпел изменения.
3.3. Для аналитических методов исследования, в которых используют навески СО массой меньше минимальной представительной навески, поступают следующим образом: отбирают пробу массой равной или больше минимальной представительной навески, дополнительно растирают в агатовой ступке, перемешивают и берут для анализа необходимую часть материала.
Материал СО, из которого взята часть для аттестационных анализов, сохраняют до конца аттестации для контроля и обмена материала.
Отобранную, но неиспользованную часть стандартного образца не следует возвращать обратно в упаковку.
3.4. Для аттестационного анализа используют методы, основанные на различных физических и химических принципах. Для каждого компонента каждым методом выполняют четыре определения из отдельных навесок, по возможности разной массы. В случае, когда для определения данного компонента нет независимых методов анализа, определения выполняют одним методом в разных лабораториях в различные интервалы времени.
3.5. Аттестационные анализы выполняют в условиях, которые обеспечивают правильность и максимальную воспроизводимость результатов анализа. Для обеспечения правильности результатов анализа следует принимать специальные меры (теоретическая оценка возможных погрешностей и мероприятия по их уменьшению, одновременный анализ СО, применение реактивов особой чистоты, выполнение холостого опыта при определении микрокомпонентов и т.д.).
3.6. Одновременно с проведением аттестационных анализов определяют содержание гигроскопической влаги для последующего пересчета аттестованных содержаний на сухое вещество.
3.7. Результаты аттестационных анализов приводят с числом десятичных цифр, которое обеспечивается метрологическими характеристиками методики.
Если содержание определяемого элемента меньше, чем предел обнаружения метода, результат анализа приводится в виде: , г/т (где
- предел обнаружения метода по критерию 3
).
3.8. Результаты аттестационных анализов направляют изготовителю СО по форме, приведенной в приложении 1. В примечании к таблице приводят краткое описание метода определения и ссылку на использованный источник.
Описание метода должно содержать информацию о массе навески, способе подготовки СО к анализу, способе отделения мешающих компонентов и др. В графе "Обозначение" указывают химический символ или формулу компонента.
4. СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ АТТЕСТАЦИОННЫХ АНАЛИЗОВ И УСТАНОВЛЕНИЕ АТТЕСТУЕМЫХ ХАРАКТЕРИСТИК СО
4.1. Данные аттестационных анализов оценивают вначале с аналитико-методических позиций. Учитывают корректность выполнения измерений содержаний компонентов, правильность применения методики анализа, соблюдение пределов измерений, выполнение процедуры анализа, влияние мешающих компонентов, независимость результатов, полученных в лаборатории различными методами, и т.д.
При этом может быть принято решение об исключении или объединении нескольких результатов или о необходимости проведения дополнительных исследований.
4.2. Статистическая обработка результатов аттестационных анализов сводится к обработке средних независимых значений
, рассчитанных по формуле
![]() , (16)
, (16)
где - число параллельных определений;
-
-й результат,
-й лаборатории или
-го метода;
- среднее значение
-й лаборатории или
-го метода, рассчитанное из
параллельных определений.
При использовании двух методов в одной лаборатории принимают ![]() для данной лаборатории.
для данной лаборатории.
4.3. При статистической обработке результатов аттестационных анализов следует выполнить проверку аномальных результатов, установить вид распределения, рассчитать метрологические характеристики стандартного образца.
4.3.1. Проверку аномальных результатов выполняют в зависимости от объема выборки при помощи критерия Диксона (![]() ) или критерия Смирнова-Груббса (
) или критерия Смирнова-Груббса (![]() ).
).
В случае выявления аномальных результатов в проверяемой выборке необходимо провести методический анализ и установить по возможности причины появления недостоверных результатов.
Проверка аномальных результатов по критерию Диксона заключается в следующем. Средние независимые результаты упорядочивают по мере возрастания:
![]() .
.
Затем проверяют ![]() и
и ![]() на аномальность.
на аномальность.
Рассчитывают или
по формулам, приведенным в табл.2.
Таблица 2
От 3 до 7 |
|
|
От 8 до 10 |
|
|
От 11 до 13 |
|
|
От 14 до 25 |
|
|
Полученные значения или
сравнивают с табличными значениями
![]() , взятыми для доверительной вероятности
, взятыми для доверительной вероятности и для объема выборки
. Для
![]() берут
берут ![]() и для
и для ![]() берут
берут ![]() . Значения
. Значения ![]() приведены в табл.4.
приведены в табл.4.
Если ![]() или
или ![]() , можно
, можно (или
) считать аномальным результатом и исключить из выборки. Максимальное число исключенных результатов - 15%.
В случае выявления аномальных результатов в проверяемой выборке перед их исключением рекомендуется проводить методический анализ и по возможности установить причины появления недостоверных результатов.
Пример проверки аномальных результатов по критерию Диксона приведен в приложении 12.
Проверка аномальных результатов по критерию Смирнова-Груббса заключается в следующем.
Имеется выборка средних результатов. Максимальный и минимальный результаты
и
проверяют на аномальность следующим образом.
Для выборки находят среднее значение и среднее квадратическое отклонение
по формулам:
![]() , (17)
, (17)
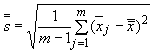 . (18)
. (18)
Для рассчитывают отношение
![]() , (19)
, (19)
а для отношение
![]() . (20)
. (20)
Рассчитанные значения и
сравнивают с табличным значением
![]() для определенной доверительной вероятности
для определенной доверительной вероятности и числа измерений
. Значения
![]() приведены в табл.4.
приведены в табл.4.
Если ![]() , значение
, значение считают аномальным результатом и исключают его из выборки. Если
![]() , значение
, значение считают аномальным результатом и исключают его из выборки. Максимальное число исключенных результатов - 15%.
В случае выявления аномальных результатов в проверяемой выборке необходимо проводить методический анализ.
Пример проверки аномальных результатов по критерию Смирнова-Груббса приведен в приложении 12.
4.3.2. Установление вида распределения результатов аттестационных анализов.
Проверку соответствия распределения результатов нормальному закону в зависимости от объема выборки выполняют по -критерию (критерий Шапиро-Уилка) при
![]() и по асимметрии и эксцессу при
и по асимметрии и эксцессу при ![]() .
.
Проверка нормальности распределения по -критерию заключается в следующем. Результаты
, оставшиеся после методического анализа и исключения аномальных результатов, располагают в порядке возрастания:
![]() .
.
Вычисляют сумму квадратов
![]() , (21)
, (21)
где
![]() . (22)
. (22)
Затем вычисляют
![]() , (23)
, (23)
где ![]() - если
- если четное число;
![]() - если
- если нечетное число.
Значения коэффициентов ![]() приведены в табл.5.
приведены в табл.5.
Вычисляют критерий
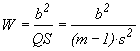 , (24)
, (24)
где - дисперсия, рассчитанная по формуле
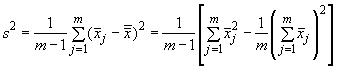 . (25)
. (25)
Полученное значение сравнивают с табличным
![]() , взятым для
, взятым для =0,95 и для соответствующего
. Если
![]() , распределение результатов считают нормальным. Значения
, распределение результатов считают нормальным. Значения ![]() приведены в табл.6.
приведены в табл.6.
Примеры проверки нормальности распределения с помощью -критерия приведены в приложении 12.
Для выборки объемом 51 результат и более проверяют нормальность их распределения при помощи асимметрии и эксцесса.
Проверка нормальности распределения результатов по асимметрии и эксцессу выборки заключается в следующем.
Для случайной выборки объемом ![]() вычисляют выборочную асимметрию
вычисляют выборочную асимметрию по формуле
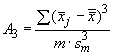 , (26)
, (26)
где
![]() . (27)
. (27)
Среднее квадратическое отклонение (), рассчитанное по формуле (25), и величина
связаны следующим соотношением:
![]() . (28)
. (28)
Одновременно вычисляют выборочный эксцесс () по формуле
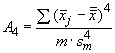 . (29)
. (29)
Гипотезу нормальности распределения принимают, если абсолютное значение асимметрии () меньше табличного значения
![]() приведенного в табл.7, и одновременно, если значение эксцесса (
приведенного в табл.7, и одновременно, если значение эксцесса () находится в пределах табличного
![]() , приведенного в табл.8.
, приведенного в табл.8.
Пример проверки нормальности распределения результатов с помощью асимметрии и эксцесса приведен в приложении 12.
4.4. Если гипотезу соответствия нормальному закону распределения не отвергают, дальнейшую обработку проводят в соответствии с требованиями п.4.5.
4.5. Установление метрологических характеристик СО при нормальном законе распределения результатов.
4.5.1. В качестве аттестованного содержания принимают среднее арифметическое
ряда независимых средних результатов
.
Значение рассчитывают по формуле (17) после исключения аномальных результатов.
4.5.2. Оценку среднего квадратического отклонения аттестованного содержания компонента вычисляют по формуле (18) после исключения аномальных результатов.
4.5.3. Характеристику погрешности аттестации стандартного образца вычисляют по формуле
![]() , (30)
, (30)
где - квантиль распределения Стъюдента. Значения отношений
![]() приведены в табл.9.
приведены в табл.9.
4.5.4. Рассчитывают коэффициент точности установления аттестованных характеристик , являющийся отношением погрешности
к допустимой погрешности серийных анализов содержания компонента:
![]() (31)
(31)
![]() (32)
(32)
![]() . (33)
. (33)
Значения отношения ![]() приведены в табл.9.
приведены в табл.9.
Компонент может быть аттестован, если выполнены условия:
1) для аттестации компонентов с массовой долей более 0,1% значение коэффициента ![]() при числе независимых результатов
при числе независимых результатов ![]() ;
;
2) для аттестации компонентов, массовая доля которых не более 0,1%, значение коэффициента ![]() при
при ![]() .
.
В табл.3 приведена классификация СО состава горных пород и минерального сырья по точности аттестации и регламентированы требования к точности установления аттестованных характеристик в СО разных разрядов точности.
Таблица 3
Разряд точности СО | Максимальное значение коэффициента | Минимальное число определений |
СО высшего разряда | 0,2 | 25 |
СО первого разряда | 0,3 | 11 |
СО второго разряда | 0,4 | 6 |
Серийные измерения | 1 | 1 |
| ||
Пример обработки результатов при нормальном распределении приведен в приложении 12.
4.6. Установление метрологических характеристик СО при логарифмически нормальном распределении результатов.
К статистической обработке результатов анализа по логарифмически нормальному распределению прибегают в случае, если невозможно было принять гипотезу о их нормальном распределении. Ход обработки результатов следующий.
Преобразуют результаты в их логарифмы
по формуле
![]() . (34)*
. (34)*
________________
* Формула соответствует оригиналу. - .
Рассчитывают среднее арифметическое преобразованных величин и их дисперсию
.
Проверяют нормальность распределения при помощи
-критерия. Если гипотеза о нормальном распределении
не отвергается, то распределение исходных результатов
является логарифмически нормальным. В этом случае в качестве аттестованной характеристики принимают среднее геометрическое
, которое рассчитывают по формуле:
![]() . (35)
. (35)
Рассчитывают относительное среднее квадратическое отклонение
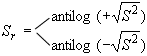 . (36)
. (36)
Затем рассчитывают доверительный интервал среднего геометрического, который асимметричен.
Верхнюю границу определяют по формуле
![]() , (37)
, (37)
нижнюю границу - по формуле
![]() . (38)
. (38)
Коэффициент - по формуле
![]() . (39)
. (39)
Условия аттестации метрологических характеристик те же, что и при нормальном распределении, т.е. для содержания ![]() %:
%:
![]() и для
и для ![]() %:
%:![]() .
.
Пример обработки данных при логарифмически нормальном распределении приведен в приложении 12.
4.7. Установление метрологических характеристик СО при несимметричном распределении результатов с использованием -преобразования.
Цель -преобразования данных выборки со значимой асимметрией - устранение асимметрии при помощи алгоритма.
![]() , (40)
, (40)
где - преобразованные данные;
- исходные данные.
Коэффициент следует выбирать так, чтобы достичь ничтожной асимметрии преобразованных данных. Затем рассчитывают среднее арифметическое преобразованных результатов (
) и их среднее квадратическое отклонение
.
В качестве аттестованного содержания принимают среднее значение исходных результатов (), которое определяют по формуле
![]() . (41)
. (41)
Доверительный интервал среднего значения преобразованных результатов () - по формуле
![]() . (42)
. (42)
Доверительный интервал среднего значения исходных данных асимметричен.
Верхнюю границу определяют по формуле
![]() , (43)
, (43)
нижнюю границу - по формуле
![]() . (44)
. (44)
Коэффициент - по формуле
![]() . (45)
. (45)
Условия аттестации метрологических характеристик: для содержания компонентов ![]() %:
%: ![]() ,
, ![]() и для
и для ![]() %:
%: ![]() ,
, ![]() .
.
Пример обработки результатов после -преобразования приведен в приложении 12.
4.8. Установление метрологических характеристик СО при неизвестном типе распределения.
Если нельзя принять модель определенного типа распределения результатов, используют статистические модели, не требующие знания характера распределения. В качестве оценки значений аттестованных характеристик используют выборочную медиану или значения медианы, рассчитанной по Гаствирту или Ходжесу-Леману.
4.8.1. Для расчета выборочной медианы средние независимые результаты располагают по возрастанию
![]() . (46)
. (46)
Выборочную медиану ряда рассчитывают по формулам:
![]() (
(- четное), (47)
![]() (
(- нечетное). (48)
В качестве характеристики погрешности аттестации принимают доверительный интервал медианы ряда (46):
![]() .
.
Порядковые номера и
членов ряда (46) определяют по табл.10 для доверительной вероятности
=0,95 и для числа результатов
от 6 до 50. Доверительный интервал медианы асимметричен.
Коэффициент рассчитывают по формуле
![]() . (49)
. (49)
Условия аттестации метрологических характеристик: для содержания компонентов ![]() %:
%: ![]() ,
, ![]() и для
и для ![]() %:
%: ![]() ,
, ![]() .
.
4.8.2. Для выборки результатов с большой асимметрией в качестве значения аттестованной характеристики рекомендуется применять медиану по Гаствирту, которую рассчитывают по формуле
![]() , (50)
, (50)
где - выборочная медиана упорядоченного по возрастанию ряда результатов;
и
- члены этого ряда с порядковыми номерами
и
. Нижнее значение
рассчитывают по формуле
![]() (округляют до нижнего целого числа). (51)
(округляют до нижнего целого числа). (51)
Верхнее значение - по формуле
![]() (округляют до верхнего целого числа). (52)
(округляют до верхнего целого числа). (52)
Значения и
для упорядоченного по возрастанию ряда результатов приведены в табл.11.
Доверительный интервал и коэффициент
рассчитывают, как в п.4.8.1.
4.8.3. Для выборки результатов малого объема в качестве значения аттестованной характеристики рекомендуется применять медиану по Ходжесу-Леману. Из членов ряда (46) образуют все возможные полусуммы вида
![]() , (53)
, (53)
где ![]()
![]()
![]() .
.
Общее число полусумм
![]() . (54)
. (54)
Полученный ряд полусумм () упорядочивают по возрастанию
![]() . (55)
. (55)
В качестве значения аттестованной характеристики принимают медиану упорядоченного ряда полусумм по формуле
![]() , (
, (- четное); (56)
![]() , (
, (- нечетное). (57)
В качестве характеристики погрешности аттестации принимают доверительный интервал медианы ряда (55):
![]()
Порядковые номера и
членов ряда (55) определяют по табл.12 для доверительной вероятности
=0,95 и для числа результатов
от 6 до 50.
Примеры обработки результатов аттестационных анализов и установления аттестованных характеристик с применением медианы приведены в приложении 12.
4.9. Представление результатов аттестации.
Числовое значение аттестованной характеристики СО должно оканчиваться цифрой того же разряда, что и значение доверительного интервала.
Значения максимально допустимых относительных средних квадратических отклонений рядовых анализов приведены в приложении 13.
ПРИЛОЖЕНИЕ 1
Рекомендуемое
ФОРМА ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ЛАБОРАТОРИЯМИ, УЧАСТВУЮЩИМИ В АТТЕСТАЦИОННЫХ АНАЛИЗАХ
Страна | ||||||
Наименование лаборатории | ||||||
Дата | ||||||
Результаты исследования пробы N | ||||||
стандартного образца | ||||||
(наименование) | ||||||
подготовленного | ||||||
(наименование изготовителя и страна) | ||||||
Обозначение компонента | Метод определения | Результаты определений в пересчете на сухое вещество | |||
1 | 2 | 3 | 4 | ||
FeO, % | Объемный | 5,20 | 5,18 | 5,15 | 5,25 |
Au, г/т | Атомно-абсорбционный | 10,2 | 11,0 | 11,5 | 9,5 |
руководитель подразделения | Личная | Расшифровка |
ПРИЛОЖЕНИЕ 2
Справочное
Таблица 4
Значения ![]() критерия Диксона и
критерия Диксона и ![]() - критерия Смирнова-Груббса для проверки аномальных результатов
- критерия Смирнова-Груббса для проверки аномальных результатов
|
| |||
|
|
|
| |
6 | 0,482 | 0,560 | 1,729 | 1,822 |
7 | 0,434 | 0,507 | 1,829 | 1,938 |
8 | 0,479 | 0,554 | 1,909 | 2,032 |
9 | 0,441 | 0,512 | 1,977 | 2,110 |
10 | 0,409 | 0,477 | 2,036 | 2,176 |
11 | 0,517 | 0,576 | 2,088 | 2,234 |
12 | 0,490 | 0,546 | 2,134 | 2,285 |
13 | 0,467 | 0,521 | 2,175 | 2,331 |
14 | 0,492 | 0,546 | 2,213 | 2,371 |
15 | 0,472 | 0,525 | 2,247 | 2,409 |
16 | 0,454 | 0,507 | 2,279 | 2,443 |
17 | 0,438 | 0,490 | 2,309 | 2,475 |
18 | 0,424 | 0,475 | 2,335 | 2,504 |
19 | 0,412 | 0,462 | 2,361 | 2,532 |
20 | 0,401 | 0,450 | 2,385 | 2,557 |
21 | 0,391 | 0,440 | 2,408 | 2,580 |
22 | 0,382 | 0,430 | 2,429 | 2,603 |
23 | 0,374 | 0,421 | 2,448 | 2,624 |
24 | 0,367 | 0,413 | 2,467 | 2,644 |
25 | 0,360 | 0,406 | 2,486 | 2,663 |
30 | - | - | 2,563 | 2,745 |
35 | - | - | 2,638 | 2,811 |
40 | - | - | 2,682 | 2,866 |
45 | - | - | 2,727 | 2,914 |
50 | - | - | 2,768 | 2,956 |
60 | - | - | 2,837 | 3,025 |
70 | - | - | 2,893 | 3,082 |
80 | - | - | 2,940 | 3,130 |
90 | - | - | 2,981 | 3,171 |
100 | - | - | 3,017 | 3,207 |
ПРИЛОЖЕНИЕ 3
Справочное
Таблица 5
Коэффициенты ![]() для расчета
для расчета -критерия по методу Шапиро-Уилке
Значение коэффициента | |||||||||
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 0,7071 | 0,7071 | 0,6872 | 0,6646 | 0,6431 | 0,6233 | 0,6052 | 0,5888 | 0,5739 |
2 | - | 0,0000 | 0,1677 | 0,2413 | 0,2806 | 0,3031 | 0,3164 | 0,3244 | 0,3291 |
3 | - | - | - | 0,0000 | 0,0875 | 0,1401 | 0,1743 | 0,1976 | 0,2141 |
4 | - | - | - | - | - | 0,0000 | 0,0561 | 0,0947 | 0,1224 |
5 | - | - | - | - | - | - | - | 0,0000 | 0,0399 |
Продолжение табл.5
Значение коэффициента | ||||||||||
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
1 | 0,5601 | 0,5475 | 0,5359 | 0,5251 | 0,5150 | 0,5056 | 0,4968 | 0,4986 | 0,4808 | 0,4734 |
2 | 0,3315 | 0,3325 | 0,3325 | 0,3318 | 0,3306 | 0,3290 | 0,3273 | 0,3253 | 0,3232 | 0,3211 |
3 | 0,2260 | 0,2347 | 0,2412 | 0,2460 | 0,2495 | 0,2521 | 0,2540 | 0,2553 | 0,2561 | 0,2565 |
4 | 0,1429 | 0,1586 | 0,1707 | 0,1802 | 0,1878 | 0,1939 | 0,1988 | 0,2027 | 0,2059 | 0,2085 |
5 | 0,0695 | 0,0922 | 0,1099 | 0,1240 | 0,1353 | 0,1447 | 0,1524 | 0,1587 | 0,1641 | 0,1686 |
6 | 0,0000 | 0,0303 | 0,0539 | 0,0727 | 0,0880 | 0,1005 | 0,1109 | 0,1197 | 0,1271 | 0,1334 |
7 | - | - | 0,0000 | 0,0240 | 0,0433 | 0,0593 | 0,0725 | 0,0837 | 0,0932 | 0,1013 |
8 | - | - | - | - | 0,0000 | 0,0196 | 0,0359 | 0,0496 | 0,0612 | 0,0711 |
9 | - | - | - | - | - | - | 0,0000 | 0,0163 | 0,0303 | 0,0422 |
10 | - | - | - | - | - | - | - | - | 0,0000 | 0,0140 |
Продолжение табл.5
Значение коэффициента | ||||||||||
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
1 | 0,4643 | 0,4590 | 0,4542 | 0,4493 | 0,4450 | 0,4407 | 0,4366 | 0,4328 | 0,4291 | 0,4254 |
2 | 0,3185 | 0,3156 | 0,3126 | 0,3098 | 0,3069 | 0,3043 | 0,3018 | 0,2992 | 0,2968 | 0,2944 |
3 | 0,2578 | 0,2571 | 0,2563 | 0,2554 | 0,2543 | 0,2533 | 0,2522 | 0,2510 | 0,2499 | 0,2487 |
4 | 0,2119 | 0,2131 | 0,2139 | 0,2145 | 0,2148 | 0,2151 | 0,2152 | 0,2151 | 0,2150 | 0,2148 |
5 | 0,1736 | 0,1764 | 0,1787 | 0,1807 | 0,1822 | 0,1836 | 0,1848 | 0,1857 | 0,1864 | 0,1870 |
6 | 0,1399 | 0,1443 | 0,1480 | 0,1512 | 0,1539 | 0,1563 | 0,1584 | 0,1601 | 0,1616 | 0,1630 |
7 | 0,1092 | 0,1150 | 0,1201 | 0,1245 | 0,1283 | 0,1316 | 0,1346 | 0,1372 | 0,1395 | 0,1415 |
8 | 0,0804 | 0,0878 | 0,0941 | 0,0997 | 0,1046 | 0,1089 | 0,1128 | 0,1162 | 0,1192 | 0,1219 |
9 | 0,0530 | 0,0618 | 0,0696 | 0,0764 | 0,0823 | 0,0876 | 0,0923 | 0,0965 | 0,1002 | 0,1036 |
10 | 0,0263 | 0,0368 | 0,0459 | 0,0539 | 0,0610 | 0,0672 | 0,0728 | 0,0778 | 0,0822 | 0,0862 |
11 | 0,0000 | 0,0122 | 0,0228 | 0,0321 | 0,0403 | 0,0476 | 0,0540 | 0,0598 | 0,0650 | 0,0697 |
12 | - | - | 0,0000 | 0,0107 | 0,0200 | 0,0284 | 0,0358 | 0,0424 | 0,0483 | 0,0537 |
13 | - | - | - | - | 0,0000 | 0,0094 | 0,0178 | 0,0253 | 0,0320 | 0,0381 |
14 | - | - | - | - | - | - | 0,0000 | 0,0084 | 0,0159 | 0,0227 |
15 | - | - | - | - | - | - | - | - | 0,0000 | 0,0076 |
Продолжение табл.5
Значение коэффициента | ||||||||||
31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |
1 | 0,4220 | 0,4188 | 0,4156 | 0,4127 | 0,4096 | 0,4068 | 0,4040 | 0,4015 | 0,3989 | 0,3964 |
2 | 0,2921 | 0,2898 | 0,2878 | 0,2854 | 0,2834 | 0,2813 | 0,2794 | 0,2774 | 0,2755 | 0,2737 |
3 | 0,2475 | 0,2463 | 0,2451 | 0,2439 | 0,2427 | 0,2415 | 0,2403 | 0,2391 | 0,2380 | 0,2368 |
4 | 0,2145 | 0,2141 | 0,2137 | 0,2132 | 0,2127 | 0,2121 | 0,2116 | 0,2110 | 0,2104 | 0,2098 |
5 | 0,1874 | 0,1878 | 0,1880 | 0,1882 | 0,1883 | 0,1883 | 0,1883 | 0,1881 | 0,1880 | 0,1878 |
6 | 0,1641 | 0,1651 | 0,1660 | 0,1667 | 0,1673 | 0,1678 | 0,1683 | 0,1686 | 0,1689 | 0,1691 |
7 | 0,1433 | 0,1449 | 0,1463 | 0,1475 | 0,1487 | 0,1496 | 0,1505 | 0,1513 | 0,1520 | 0,1526 |
8 | 0,1243 | 0,1265 | 0,1284 | 0,1301 | 0,1317 | 0,1331 | 0,1344 | 0,1356 | 0,1366 | 0,1376 |
9 | 0,1066 | 0,1093 | 0,1118 | 0,1140 | 0,1160 | 0,1179 | 0,1196 | 0,1211 | 0,1225 | 0,1237 |
10 | 0,0899 | 0,0931 | 0,0961 | 0,0988 | 0,1013 | 0,1036 | 0,1056 | 0,1075 | 0,1092 | 0,1108 |
11 | 0,0739 | 0,0777 | 0,0812 | 0,0844 | 0,0873 | 0,0900 | 0,0924 | 0,0947 | 0,0967 | 0,0986 |
12 | 0,0585 | 0,0629 | 0,0669 | 0,0706 | 0,0739 | 0,0770 | 0,0798 | 0,0824 | 0,0848 | 0,0870 |
13 | 0,0435 | 0,0485 | 0,0530 | 0,0572 | 0,0610 | 0,0645 | 0,0677 | 0,0706 | 0,0733 | 0,0759 |
14 | 0,0289 | 0,0344 | 0,0395 | 0,0441 | 0,0484 | 0,0523 | 0,0559 | 0,0592 | 0,0622 | 0,0651 |
15 | 0,0144 | 0,0206 | 0,0262 | 0,0314 | 0,0361 | 0,0404 | 0,0444 | 0,0481 | 0,0515 | 0,0546 |
16 | 0,0000 | 0,0068 | 0,0131 | 0,0187 | 0,0239 | 0,0287 | 0,0331 | 0,0372 | 0,0409 | 0,0444 |
17 | - | - | 0,0000 | 0,0062 | 0,0119 | 0,0172 | 0,0220 | 0,0264 | 0,0305 | 0,0343 |
18 | - | - | - | - | 0,0000 | 0,0057 | 0,0110 | 0,0158 | 0,0203 | 0,0244 |
19 | - | - | - | - | - | - | 0,0000 | 0,0053 | 0,0101 | 0,0146 |
20 | - | - | - | - | - | - | - | - | 0,0000 | 0,0049 |
Продолжение табл.5
Значение коэффициента | ||||||||||
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | |
1 | 0,3940 | 0,3917 | 0,3894 | 0,3874 | 0,3850 | 0,3830 | 0,3808 | 0,3789 | 0,3770 | 0,3751 |
2 | 0,2719 | 0,2701 | 0,2684 | 0,2667 | 0,2851 | 0,2635 | 0,2620 | 0,2604 | 0,2589 | 0,2574 |
3 | 0,2357 | 0,2345 | 0,2334 | 0,2323 | 0,2313 | 0,2302 | 0,2291 | 0,2281 | 0,2271 | 0,2260 |
4 | 0,2091 | 0,2085 | 0,2078 | 0,2072 | 0,2065 | 0,2058 | 0,2052 | 0,2045 | 0,2038 | 0,2032 |
5 | 0,1876 | 0,1874 | 0,1871 | 0,1868 | 0,1865 | 0,1862 | 0,1859 | 0,1855 | 0,1851 | 0,1847 |
6 | 0,1693 | 0,1694 | 0,1695 | 0,1695 | 0,1695 | 0,1695 | 0,1695 | 0,1693 | 0,1692 | 0,1691 |
7 | 0,1531 | 0,1535 | 0,1539 | 0,1542 | 0,1545 | 0,1548 | 0,1550 | 0,1551 | 0,1553 | 0,1554 |
8 | 0,1384 | 0,1392 | 0,1398 | 0,1405 | 0,1410 | 0,1415 | 0,1420 | 0,1423 | 0,1427 | 0,1430 |
9 | 0,1249 | 0,1259 | 0,1269 | 0,1278 | 0,1286 | 0,1293 | 0,1300 | 0,1306 | 0,1312 | 0,1317 |
10 | 0,1123 | 0,1136 | 0,1149 | 0,1160 | 0,1170 | 0,1180 | 0,1189 | 0,1197 | 0,1205 | 0,1212 |
11 | 0,1004 | 0,1020 | 0,1035 | 0,1049 | 0,1062 | 0,1073 | 0,1085 | 0,1095 | 0,1105 | 0,1113 |
12 | 0,0891 | 0,0909 | 0,0927 | 0,0943 | 0,0959 | 0,0972 | 0,0986 | 0,0998 | 0,1010 | 0,1020 |
13 | 0,0782 | 0,0804 | 0,0824 | 0,0842 | 0,0860 | 0,0876 | 0,0892 | 0,0906 | 0,0919 | 0,0932 |
14 | 0,0677 | 0,0701 | 0,0724 | 0,0745 | 0,0765 | 0,0783 | 0,0801 | 0,0817 | 0,0832 | 0,0846 |
15 | 0,0575 | 0,0602 | 0,0628 | 0,0651 | 0,0673 | 0,0694 | 0,0713 | 0,0731 | 0,0748 | 0,0764 |
16 | 0,0476 | 0,0506 | 0,0534 | 0,0560 | 0,0584 | 0,0607 | 0,0628 | 0,0648 | 0,0667 | 0,0685 |
17 | 0,0379 | 0,0411 | 0,0442 | 0,0471 | 0,0497 | 0,0522 | 0,0546 | 0,0568 | 0,0588 | 0,0608 |
18 | 0,0283 | 0,0318 | 0,0352 | 0,0383 | 0,0412 | 0,0439 | 0,0465 | 0,0489 | 0,0511 | 0,0532 |
19 | 0,0188 | 0,0227 | 0,0263 | 0,0296 | 0,0328 | 0,0357 | 0,0385 | 0,0411 | 0,0436 | 0,0459 |
20 | 0,0094 | 0,0136 | 0,0175 | 0,0211 | 0,0245 | 0,0277 | 0,0307 | 0,0335 | 0,0361 | 0,0386 |
21 | 0,0000 | 0,0045 | 0,0087 | 0,0126 | 0,0163 | 0,0197 | 0,0229 | 0,0259 | 0,0288 | 0,0314 |
22 | - | - | 0,0000 | 0,0042 | 0,0081 | 0,0118 | 0,0153 | 0,0185 | 0,0215 | 0,0244 |
23 | - | - | - | - | 0,0000 | 0,0039 | 0,0076 | 0,0111 | 0,0143 | 0,0174 |
24 | - | - | - | - | - | - | 0,0000 | 0,0037 | 0,0071 | 0,0104 |
25 | - | - | - | - | - | - | - | - | 0,0000 | 0,0035 |
ПРИЛОЖЕНИЕ 4
Справочное
Таблица 6
Критические значения (
=0,95,
от 6 до 50) - критерий Шапиро-Уилке
6 | 0,786 |
7 | 0,803 |
8 | 0,818 |
9 | 0,829 |
10 | 0,842 |
11 | 0,850 |
12 | 0,859 |
13 | 0,866 |
14 | 0,874 |
15 | 0,881 |
16 | 0,887 |
17 | 0,892 |
18 | 0,897 |
19 | 0,901 |
20 | 0,905 |
21 | 0,908 |
22 | 0,911 |
23 | 0,914 |
24 | 0,916 |
25 | 0,918 |
26 | 0,920 |
27 | 0,923 |
28 | 0,924 |
29 | 0,926 |
30 | 0,927 |
31 | 0,929 |
32 | 0,930 |
33 | 0,931 |
34 | 0,933 |
35 | 0,934 |
36 | 0,935 |
37 | 0,936 |
38 | 0,938 |
39 | 0,939 |
40 | 0,940 |
41 | 0,941 |
42 | 0,942 |
43 | 0,943 |
44 | 0,944 |
45 | 0,945 |
46 | 0,945 |
47 | 0,946 |
48 | 0,947 |
49 | 0,947 |
50 | 0,947 |
ПРИЛОЖЕНИЕ 5
Справочное
Таблица 7
Критические значения асимметрии (
=0,95,
от 5 до 1000)
5 | 1,05 |
10 | 0,92 |
15 | 0,84 |
20 | 0,79 |
25 | 0,711 |
30 | 0,662 |
35 | 0,621 |
40 | 0,587 |
45 | 0,558 |
50 | 0,534 |
60 | 0,492 |
70 | 0,459 |
80 | 0,432 |
90 | 0,409 |
100 | 0,389 |
125 | 0,350 |
150 | 0,321 |
175 | 0,298 |
200 | 0,280 |
250 | 0,251 |
300 | 0,230 |
350 | 0,213 |
400 | 0,200 |
500 | 0,179 |
750 | 0,146 |
1000 | 0,127 |
ПРИЛОЖЕНИЕ 6
Справочное
Таблица 8
Критические значения эксцесса (
=0,95,
от 5 до 1000)
5 | - | 2,89 |
10 | - | 3,85 |
15 | - | 4,07 |
20 | - | 4,15 |
25 | - | 4,00 |
50 | 2,15 | 3,99 |
75 | 2,27 | 3,87 |
100 | 2,35 | 3,77 |
125 | 2,40 | 3,71 |
150 | 2,45 | 3,65 |
200 | 2,51 | 3,57 |
250 | 2,55 | 3,52 |
400 | 2,64 | 3,41 |
500 | 2,67 | 3,37 |
700 | 2,72 | 3,31 |
1000 | 2,76 | 3,26 |
ПРИЛОЖЕНИЕ 7
Справочное
Таблица 9
Значения отношений ![]() и
и ![]() (
(=0,95,
от 6 до 50)
|
| |
6 | 1,0494 | 53,54 |
7 | 0,9248 | 47,18 |
8 | 0,8360 | 42,65 |
9 | 0,7687 | 39,22 |
10 | 0,7154 | 36,49 |
11 | 0,6718 | 34,28 |
12 | 0,6354 | 32,42 |
13 | 0,6043 | 30,83 |
14 | 0,5774 | 29,46 |
15 | 0,5538 | 28,25 |
16 | 0,5329 | 27,19 |
17 | 0,5142 | 26,23 |
18 | 0,4973 | 25,37 |
19 | 0,4820 | 24,59 |
20 | 0,4680 | 23,88 |
21 | 0,4552 | 23,22 |
22 | 0,4434 | 22,62 |
23 | 0,4324 | 22,06 |
24 | 0,4224 | 21,54 |
25 | 0,4128 | 21,06 |
26 | 0,4039 | 20,60 |
27 | 0,3956 | 20,18 |
28 | 0,3878 | 19,79 |
29 | 0,3804 | 19,41 |
30 | 0,3734 | 19,05 |
31 | 0,3668 | 18,71 |
32 | 0,3605 | 18,39 |
33 | 0,3546 | 18,09 |
34 | 0,3489 | 17,80 |
35 | 0,3435 | 17,53 |
36 | 0,3384 | 17,27 |
37 | 0,3334 | 17,01 |
38 | 0,3287 | 16,77 |
39 | 0,3242 | 16,54 |
40 | 0,3198 | 16,32 |
41 | 0,3156 | 16,10 |
42 | 0,3116 | 15,90 |
43 | 0,3078 | 15,70 |
44 | 0,3040 | 15,51 |
45 | 0,3004 | 15,32 |
46 | 0,2970 | 15,15 |
47 | 0,2936 | 14,98 |
48 | 0,2904 | 14,82 |
49 | 0,2872 | 14,65 |
50 | 0,2842 | 14,50 |
ПРИЛОЖЕНИЕ 8
Справочное
Таблица 10
Номера членов упорядоченного ряда для определения границ доверительного интервала для медианы (=0,95,
от 6 до 50)
6 | 1-6 |
7 | 1-7 |
8 | 1-8 |
9 | 2-8 |
10 | 2-9 |
11 | 2-10 |
12 | 3-10 |
13 | 3-11 |
14 | 3-12 |
15 | 4-12 |
16 | 4-13 |
17 | 5-13 |
18 | 5-14 |
19 | 5-15 |
20 | 6-15 |
21 | 6-16 |
22 | 6-17 |
23 | 7-17 |
24 | 7-18 |
25 | 8-18 |
26 | 8-19 |
27 | 8-20 |
28 | 9-20 |
29 | 9-21 |
30 | 10-21 |
31 | 10-22 |
32 | 10-23 |
33 | 11-23 |
34 | 11-24 |
35 | 12-24 |
36 | 12-25 |
37 | 13-25 |
38 | 13-26 |
39 | 13-27 |
40 | 14-27 |
41 | 14-28 |
42 | 15-28 |
43 | 15-29 |
44 | 16-29 |
45 | 16-30 |
46 | 16-31 |
47 | 17-31 |
48 | 17-32 |
49 | 18-32 |
50 | 18-33 |
Между и
справедливо соотношение
![]() .
.
Если медианой является -й результат, то
и
для
![]() рассчитывают по формулам:
рассчитывают по формулам:
![]() (округляют до нижнего целого числа),
(округляют до нижнего целого числа),
![]() (округляют до верхнего целого числа).
(округляют до верхнего целого числа).
ПРИЛОЖЕНИЕ 9
Справочное
Таблица 11
Номера членов упорядоченного ряда для расчета значений медианы по Гаствирту ( от 6 до 50)
6 | 3 | 4 |
7 | 3 | 5 |
8 | 3 | 6 |
9 | 4 | 6 |
10 | 4 | 7 |
11 | 4 | 8 |
12 | 5 | 8 |
13 | 5 | 9 |
14 | 5 | 10 |
15 | 6 | 10 |
16 | 6 | 11 |
17 | 6 | 12 |
18 | 7 | 12 |
19 | 7 | 13 |
20 | 7 | 14 |
25 | 9 | 17 |
30 | 11 | 20 |
35 | 12 | 24 |
40 | 14 | 27 |
45 | 16 | 30 |
50 | 17 | 34 |
ПРИЛОЖЕНИЕ 10
Справочное
Таблица 12
Номера членов упорядоченного ряда для определения границ доверительного интервала при расчете медианы по Ходжесу-Леману при доверительной вероятности =0,95
6 | 1 | 21 |
7 | 3 | 26 |
8 | 4 | 33 |
9 | 6 | 40 |
10 | 9 | 47 |
11 | 11 | 56 |
12 | 14 | 65 |
13 | 18 | 74 |
14 | 22 | 84 |
15 | 26 | 95 |
16 | 30 | 107 |
17 | 35 | 119 |
18 | 41 | 131 |
19 | 47 | 144 |
20 | 53 | 158 |
21 | 59 | 173 |
22 | 66 | 188 |
23 | 74 | 203 |
24 | 82 | 219 |
25 | 90 | 236 |
26 | 99 | 253 |
27 | 108 | 271 |
28 | 117 | 290 |
29 | 127 | 309 |
30 | 138 | 328 |
31 | 148 | 349 |
32 | 160 | 369 |
33 | 171 | 391 |
34 | 183 | 413 |
35 | 196 | 435 |
36 | 209 | 458 |
37 | 222 | 483 |
38 | 236 | 506 |
39 | 250 | 531 |
40 | 265 | 556 |
41 | 280 | 582 |
42 | 295 | 611 |
43 | 311 | 636 |
44 | 328 | 663 |
45 | 344 | 692 |
46 | 362 | 720 |
47 | 379 | 750 |
48 | 397 | 780 |
49 | 416 | 810 |
50 | 435 | 841 |
ПРИЛОЖЕНИЕ 11
Справочное
ПРИМЕРЫ ПРОВЕРКИ ОДНОРОДНОСТИ РАСПРЕДЕЛЕНИЯ ОКИСИ ЖЕЛЕЗА И СЕРЕБРА В СО ФЛЮОРИТА
Пример 1. Проверка однородности распределения окиси железа в СО флюорита при помощи рентгеноспектрального метода анализа.
Случайным образом было взято 30 проб СО флюорита (=30) и рентгеноспектральным методом измерена интенсивность излучения железа (в импульсах). В каждой пробе выполнено по 4 определения (
=4), всего
=30·4=120 определений. Полученные результаты
(где
=1, 2;...30,
=1, 2, 3, 4) приведены в табл.13.
Перед статистической обработкой результатов полученные данные были преобразованы по уравнению
![]() .
.
Преобразованные результаты приведены в табл.14.
Определение дисперсии между пробами :
![]() ;
;
![]() ;
;
![]() .
.
Определение дисперсии внутри проб :
![]() ;
;
![]() ;
;
![]() .
.
Определение суммарной дисперсии :
![]() ;
;![]() ;
;
![]()
Таблица 13
Интенсивность излучения железа в СО флюорита (в импульсах)
| |||||
|
|
|
| ||
1 | 11875 | 11720 | 11802 | 11797 | 47194 |
2 | 11699 | 11820 | 11751 | 11769 | 47039 |
3 | 11788 | 11688 | 11739 | 11724 | 46939 |
4 | 11878 | 11778 | 11700 | 11724 | 47080 |
5 | 11806 | 11606 | 11797 | 11700 | 46909 |
6 | 11787 | 11682 | 11815 | 11788 | 47072 |
7 | 11773 | 11797 | 11896 | 11845 | 47311 |
8 | 11795 | 11716 | 11816 | 11775 | 47102 |
9 | 11828 | 12013 | 11842 | 11778 | 47461 |
10 | 11770 | 11918 | 11979 | 11945 | 47612 |
11 | 11727 | 11824 | 11788 | 11816 | 47155 |
12 | 11842 | 11784 | 11699 | 11673 | 46998 |
13 | 11755 | 11774 | 11695 | 11781 | 47005 |
14 | 11693 | 11777 | 11720 | 11890 | 47080 |
15 | 11739 | 11835 | 11766 | 11877 | 47217 |
16 | 11748 | 11681 | 11748 | 11796 | 46973 |
17 | 11868 | 11950 | 11720 | 11860 | 47398 |
18 | 11773 | 11703 | 11793 | 11716 | 46985 |
19 | 11795 | 11758 | 11764 | 11732 | 47050 |
20 | 11698 | 11692 | 11829 | 11730 | 46939 |
21 | 11760 | 11700 | 11737 | 11861 | 47058 |
22 | 11784 | 11814 | 11886 | 11836 | 47320 |
23 | 11845 | 11795 | 11780 | 11872 | 47292 |
24 | 11634 | 11893 | 11788 | 11847 | 47162 |
25 | 11887 | 11765 | 11787 | 11796 | 47234 |
26 | 11805 | 11855 | 11688 | 11883 | 47231 |
27 | 11880 | 11742 | 11859 | 11879 | 47360 |
28 | 11729 | 11866 | 11741 | 11861 | 47197 |
29 | 11792 | 11798 | 11694 | 11840 | 47124 |
30 | 11649 | 11817 | 11710 | 11804 | 46980 |
| |||||
| |||||
Таблица 14
Преобразованные значения импульсов
|
| ||||
|
|
|
| ||
1 | +88 | -67 | +15 | +10 | +46 |
2 | -88 | +33 | -36 | -18 | -109 |
3 | +1 | -99 | -48 | -63 | -209 |
4 | +91 | -9 | -87 | -63 | -68 |
5 | +19 | -181 | +10 | -87 | -239 |
6 | 0 | -105 | +28 | +1 | -76 |
7 | -14 | +10 | +109 | +58 | +163 |
8 | +8 | -71 | +29 | -12 | -46 |
9 | +41 | +226 | +55 | -9 | +313 |
10 | -17 | +131 | +192 | +158 | +464 |
11 | -60 | +37 | +1 | +29 | +7 |
12 | +55 | -3 | -88 | -114 | -150 |
13 | -32 | -13 | -92 | -6 | -143 |
14 | -94 | -10 | -67 | +103 | -68 |
15 | -48 | +48 | -21 | +90 | +69 |
16 | -39 | -106 | -39 | +9 | -175 |
17 | +81 | +163 | -67 | +73 | +250 |
18 | -14 | -84 | +6 | -71 | -163 |
19 | +8 | -29 | -23 | -55 | -99 |
20 | -89 | -95 | +42 | -67 | -209 |
21 | -27 | -87 | -50 | +74 | -90 |
22 | -3 | +27 | +99 | +49 | +172 |
23 | +58 | +8 | -7 | +85 | +144 |
24 | -153 | +106 | +1 | +60 | +14 |
25 | +100 | -22 | 0 | +9 | +87 |
26 | +18 | +68 | -99 | +96 | +83 |
27 | +93 | -45 | +72 | +92 | +212 |
28 | -58 | +79 | -46 | +74 | +49 |
29 | +5 | +11 | -93 | +53 | -24 |
30 | -138 | +30 | -77 | +17 | -168 |
| |||||
| |||||
Результаты, полученные при проверке однородности распределения окиси железа в СО флюорита, приведены в табл.15.
Таблица 15
Рассеяние результатов | Сумма квадратов | Число степеней свободы | Дисперсия |
Между пробами |
|
|
|
Внутри проб |
|
|
|
Сумма |
|
|
|
Расчет критерия :
![]() .
.
Табличное значение :
![]() .
.
Так как ![]() , нет значимой разницы между дисперсиями между пробами и внутри проб.
, нет значимой разницы между дисперсиями между пробами и внутри проб.
Среднее число импульсов, соответствующее содержанию в СО флюорита, равно 11787. Среднее квадратическое отклонение между пробами :
![]() .
.
Относительное среднее квадратическое отклонение между пробами равно:
![]() ,
,
![]() (для 0,2-0,499%,
(для 0,2-0,499%, ![]() )=13,5%.
)=13,5%.
Так как ![]() , можно считать содержание
, можно считать содержание ![]() в СО флюорита равномерно распределенным на уровне массы навески, взятой для рентгено-спектрального метода анализа.
в СО флюорита равномерно распределенным на уровне массы навески, взятой для рентгено-спектрального метода анализа.
Пример 2. Проверка однородности распределения серебра в СО флюорита при помощи спектрального анализа.
Условия эксперимента те же, что в примере 1, т.е. =30,
=4,
=120. Содержание серебра определено спектральным методом; результаты приведены в табл.16.
Таблица 16
Результаты определения содержания серебра в СО флюорита
| |||||
|
|
|
| ||
1 | 8,14 | 9,54 | 5,88 | 7,97 | 31,53 |
2 | 8,25 | 11,50 | 10,10 | 10,10 | 39,85 |
3 | 10,30 | 9,80 | 14,30 | 9,30 | 43,70 |
4 | 7,34 | 11,40 | 9,87 | 13,20 | 41,81 |
5 | 7,65 | 9,84 | 10,10 | 10,20 | 37,79 |
6 | 11,30 | 13,40 | 14,60 | 7,06 | 46,36 |
7 | 7,77 | 5,72 | 9,78 | 7,67 | 30,94 |
8 | 9,30 | 9,04 | 8,20 | 9,30 | 35,84 |
9 | 13,50 | 10,80 | 8,57 | 7,92 | 40,79 |
10 | 13,70 | 10,70 | 17,80 | 16,10 | 58,30 |
11 | 9,48 | 23,70 | 18,70 | 8,76 | 60,64 |
12 | 10,60 | 11,50 | 10,30 | 9,81 | 42,21 |
13 | 15,30 | 7,50 | 8,04 | 11,40 | 42,24 |
14 | 13,40 | 7,53 | 10,80 | 11,00 | 42,73 |
15 | 11,20 | 12,60 | 13,20 | 11,30 | 48,30 |
16 | 12,70 | 14,30 | 12,70 | 10,50 | 50,20 |
17 | 10,10 | 13,60 | 7,99 | 11,10 | 42,79 |
18 | 6,80 | 15,30 | 12,90 | 10,70 | 45,70 |
19 | 6,85 | 9,48 | 9,05 | 8,11 | 33,49 |
20 | 8,60 | 7,46 | 13,50 | 23,10 | 52,66 |
21 | 11,00 | 7,70 | 13,90 | 8,41 | 41,01 |
22 | 10,50 | 9,84 | 7,55 | 6,71 | 34,60 |
23 | 8,75 | 6,78 | 10,40 | 6,67 | 32,60 |
24 | 7,98 | 8,51 | 7,62 | 6,74 | 30,85 |
25 | 7,95 | 9,35 | 7,85 | 9,46 | 34,61 |
26 | 9,55 | 8,11 | 8,57 | 6,38 | 32,61 |
27 | 20,60 | 14,60 | 17,70 | 8,85 | 61,75 |
28 | 9,41 | 18,90 | 13,20 | 17,10 | 58,61 |
29 | 14,70 | 15,10 | 10,30 | 13,20 | 53,30 |
30 | 13,20 | 10,50 | 9,32 | 11,10 | 44,12 |
| |||||
| |||||
Результаты, полученные при проверке однородности распределения серебра в СО флюорита, приведены в табл.17.
Таблица 17
Рассеяние результатов | Сумма квадратов | Число степеней свободы | Дисперсия |
Между пробами |
|
|
|
Внутри проб |
|
|
|
Сумма |
|
|
|
Расчет критерия :
![]() .
.
Табличное значение ![]() .
.
Так как ![]() , есть значимая разница между дисперсиями
, есть значимая разница между дисперсиями и
. В таком случае оценивают погрешность неоднородности (
):
![]() .
.
Содержание серебра в СО флюорита 10,77 г/т. Относительное среднее квадратическое отклонение, вызванное неоднородностью:
![]() .
.
![]() серебра в интервале концентраций от 10 до 19 г/т - 7,5%. Так как
серебра в интервале концентраций от 10 до 19 г/т - 7,5%. Так как
![]() ,
,
нельзя считать распределение серебра в СО флюорита однородным на уровне навески, взятой для спектрального анализа.
ПРИЛОЖЕНИЕ 12
Справочное
ПРИМЕРЫ ПРОВЕРКИ АНОМАЛЬНЫХ РЕЗУЛЬТАТОВ И ОБРАБОТКИ РЕЗУЛЬТАТОВ
Пример 1. Проверка аномальных результатов по критерию Диксона.
В СО каолина было определено следующее содержание меди (, г/т): 4; 7; 7; 7,5; 8; 8,3; 8,4; 9,4; 9,5; 10; 10; 10,5; 12; 12,8; 13; 22; 23. Проверить результаты 22 и 23 на аномальность по критерию Диксона.
Проверка результата 23:
![]() ;
;![]() ;
;
![]() - результат 23 является аномальным и исключается из выборки.
- результат 23 является аномальным и исключается из выборки.
Проверка результата 22:
![]() ;
;![]() ;
;
![]() - результат 22 исключается из выборки.
- результат 22 исключается из выборки.
Общее число исключенных результатов равно 2, т.е. 11,8%.
Пример 2. Проверка аномальных результатов по критерию Смирнова-Груббса.
В СО гранита было определено следующее содержание фтора (, %): 1,25; 1,27; 1,29; 1,30; 1,30; 1,34; 1,53; 1,54; 1,55; 1,58; 1,69; 1,69; 1,70; 1,70; 1,70; 1.71; 1,78; 1,79; 1,80; 1,86; 1,88; 1,88; 1,90; 1,90; 1,94; 2,30.
Проверить результат 2,30 на аномальность по критерию Смирнова-Груббса.
Проверка:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() - результат 2,30%
- результат 2,30% нельзя исключить как аномальный.
Пример 3. Проверка нормальности распределения с помощью -критерия.
Проверить нормальность распределения результатов определения меди в СО каолина после исключения двух максимальных результатов 22 и 23 г/т при помощи
-критерия (данные из примера 1).
Проверка:
| |
Расчет | (13-4)·0,5150=4,6350 |
(12,8-7)·0,3306=1,9175 | |
(12-7)·0,2496=1,2480 | |
(10,5-7,7)·0,1878=0,5634 | |
(10-8)·0,1353=0,2706 | |
(10-8,3)·0,0880=0,1496 | |
(9,5-8,4)·0,0433=0,0476 | |
|
![]() ;
;
![]() ;
;
![]() . Гипотеза о нормальном распределении остальных результатов определения меди в СО каолина не отвергается.
. Гипотеза о нормальном распределении остальных результатов определения меди в СО каолина не отвергается.
Пример 4. Проверка аномальных результатов с помощью асимметрии и эксцесса.
В СО гранита было определено следующее содержание хрома: 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 12; 12; 12; 12; 13; 13; 13; 13; 14; 14; 14; 15; 17; 17; 17; 17; 17; 18; 18; 20; 20; 20; 20; 20; 20; 20; 20; 20; 22; 22; 22; 22; 22; 30; 46. Проверить симметричность распределения результатов с помощью асимметрии и эксцесса.
Расчет асимметрии :
![]() ,
, ![]() ,
, ![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ; распределение результатов несимметрично.
; распределение результатов несимметрично.
Расчет эксцесса :
![]() ;
;
![]() ;
;
![]() ;
;
![]() ; результаты имеют значительный эксцесс.
; результаты имеют значительный эксцесс.
На основе проверки асимметрии и эксцесса можно сделать заключение, что распределение результатов определения хрома в СО гранита отлично от нормального.
Пример 5. Обработка результатов при нормальном распределении.
Рассчитать аттестованные значения и категорию точности определения меди в СО каолина. Данные из примера 1.
После исключения результатов 22 и 23 г/т оценивают следующую выборку упорядоченных результатов:
4; 7; 7; 7,5; 8; 8,3; 8,4; 9,4; 9,5; 10; 10; 10,5; 12; 12,8; 13.
Распределение представленных результатов нормально, что следует из значений -критерия и эксцесса
и
.
=0,965,
![]() ,
, ![]() ;
;
=0,18,
![]() ,
, ![]() ;
;
=2,81,
![]() до 4,07,
до 4,07, ![]() .
.
.
Аттестованные значения:
![]() ;
;
![]() ;
;
![]() .
.
Коэффициент :
![]() .
.
Условия аттестации выполнены (![]() ,
, ![]() ). Аттестация меди в СО каолина после исключения двух недостоверных результатов соответствует первой категории точности.
). Аттестация меди в СО каолина после исключения двух недостоверных результатов соответствует первой категории точности.
Пример 6. Обработка данных по логарифмически нормальному распределению.
В СО каолина было определено следующее содержание (г/т): 4; 7; 7; 7,5; 8; 8,3; 8,4; 9,4; 9,5; 10; 10; 10,5; 12; 12,8; 13; 22; 23.
Распределение результатов отлично от нормального, обработку выполняют по модели логарифмического нормального распределения.
Преобразование результатов в их логарифмы : 0,6021; 0,8451; 0,8451; 0,8751; 0,9031; 0,9191; 0,9243; 0,9731; 0,9777; 1,0000; 1,0000; 1,0212; 1,0792; 1,1072; 1,1139; 1,3424; 1,3617 (
=17).
Среднее арифметическое преобразованных данных =0,99355. Среднее квадратическое отклонение
=0,18087. Проверка нормальности
при помощи
-критерия:
![]() ;
;![]() .
.
![]() ; распределение исходных результатов логарифмически нормальное. Среднее геометрическое аналитических данных:
; распределение исходных результатов логарифмически нормальное. Среднее геометрическое аналитических данных:
![]() ;
;
![]()
Доверительный интервал среднего геометрического:
![]()
![]()
Для 9,9 г/т ![]() =30%:
=30%:
Коэффициент :
![]()
Условия аттестации выполнены (![]() ,
, ![]() ).
).
Аттестация содержания меди в СО каолина, выполненная по модели логарифмически нормального распределения с учетом всех результатов, соответствует второй категории точности.
Пример 7. Обработка результатов после -преобразования.
Провести -преобразование данных из примера 6 и рассчитать аттестованные характеристики.
-преобразование результатов проводят по уравнению (40) (
=-0,18).
![]() .
.
Расчеты приведены в табл.18.
Таблица 18
Вспомогательная таблица для расчетов,
и
.....* | ||
1 | 4 | 1,2269 |
2 | 7 | 1,6417 |
3 | 7 | 1,6417 |
4 | 7,5 | 1,6900 |
5 | 8 | 1,7346 |
6 | 8,3 | 1,7598 |
7 | 8,4 | 1,7680 |
8 | 9,4 | 1,8439 |
9 | 9,5 | 1,8510 |
10 | 10 | 1,8850 |
11 | 10 | 1,8850 |
12 | 10,5 | 1,9171 |
13 | 12 | 2,0035 |
14 | 12,8 | 2,0446 |
15 | 13 | 2,0543 |
16 | 22 | 2,3707 |
17 | 23 | 2,3961 |
|
| |
|
____________________
* Брак оригинала. - .
Асимметрия преобразованных результатов =0,003 достигает почти теоретического значения.
![]()
Доверительный интервал средней величины :
![]()
![]()
![]()
Для 9,7 г/т ![]() =30%:
=30%:
Коэффициент
![]()
Требования аттестации выполнены (![]() ,
, ![]() ).
).
Аттестация меди в СО каолина, выполненная при помощи -преобразования с учетом всех результатов, соответствует второй категории точности.
Пример 8. Обработка результатов с применением разных видов медианы.
В СО силиката было определено следующее содержание марганца (%):
0,050; 0,051; 0,051; 0,051; 0,051; 0,052, 0,052; 0,053; 0,056; 0,060; 0,060; 0,061. По -критерию нельзя считать выборку результатов нормально распределенной. Нельзя принять и модель логарифмически нормального распределения.
Оценка аттестуемых характеристик выполняется по медиане и ее доверительному интервалу.
Оценка аттестованных характеристик с применением выборочной медианы
![]()
![]()
![]() ;
;
![]() для 0,052%
для 0,052% - 17%;
![]() .
.
Условия аттестации выполнены (![]() ,
, ![]() ). Аттестация марганца в СО силиката соответствует первой категории точности.
). Аттестация марганца в СО силиката соответствует первой категории точности.
Оценка аттестованных характеристик с применением медианы по Гаствирту
![]()
![]() ;
;
![]() .
.
При расчете медианы по Гаствирту получаются те же аттестованные значения, что и при использовании выборочной медианы.
Оценка аттестованных характеристик с применением медианы по Ходжесу-Леману.
Вычисление всех возможных полусумм результатов определения содержания марганца приведено в табл.19. В табл.20 приведены рассчитанные значения полусумм в порядке возрастания.
Таблица 19
Расчет полусумм по Ходжесу-Леману
| 0,050 | 0,051 | 0,051 | 0,051 | 0,051 | 0,052 | 0,052 | 0,053 | 0,056 | 0,060 | 0,060 | 0,061 |
0,050 | 0,0500 | 0,0505 | 0,0505 | 0,0505 | 0,0505 | 0,0510 | 0,0510 | 0,0515 | 0,0530 | 0,0550 | 0,0550 | 0,0555 |
0,051 | - | 0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0515 | 0,0515 | 0,0520 | 0,0535 | 0,0555 | 0,0555 | 0,0560 |
0,051 | - | - | 0,0510 | 0,0510 | 0,0510 | 0,0515 | 0,0515 | 0,0520 | 0,0535 | 0,0555 | 0,0555 | 0,0560 |
0,051 | - | - | - | 0,0510 | 0,0510 | 0,0515 | 0,0515 | 0,0520 | 0,0535 | 0,0555 | 0,0555 | 0,0560 |
0,051 | - | - | - | - | 0,0510 | 0,0515 | 0,0515 | 0,0520 | 0,0535 | 0,0555 | 0,0555 | 0,0560 |
0,052 | - | - | - | - | - | 0,0520 | 0,0520 | 0,0525 | 0,0540 | 0,0560 | 0,0560 | 0,0565 |
0,052 | - | - | - | - | - | - | 0,0520 | 0,0525 | 0,0540 | 0,0560 | 0,0560 | 0,0565 |
0,053 | - | - | - | - | - | - | - | 0,0530 | 0,0545 | 0,0565 | 0,0565 | 0,0570 |
0,056 | - | - | - | - | - | - | - | - | 0,0560 | 0,0580 | 0,0580 | 0,0585 |
0,060 | - | - | - | - | - | - | - | - | 0,0600 | 0,0600 | 0,0605 | |
0,060 | - | - | - | - | - | - | - | - | - | 0,0600 | 0,0605 | |
0,061 | - | - | - | - | - | - | - | - | - | - | - | 0,0610 |
Общее число полусумм ![]()
Таблица 20
Упорядочение полусумм по возрастанию
0,0500 | 0,0505 | 0,0505 | 0,0505 | 0,0505 | 0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0510 |
0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0510 | 0,0515 | 0,0515 | 0,0515 |
0,0515 | 0,0515 | 0,0515 | 0,0515 | 0,0515 | 0,0515 | 0,0520 | 0,0520 | 0,0520 | 0,0520 |
0,0520 | 0,0520 | 0,0520 | 0,0525 | 0,0525 | 0,0530 | 0,0530 | 0,0535 | 0,0535 | 0,0535 |
0,0535 | 0,0540 | 0,0540 | 0,0545 | 0,0550 | 0,0550 | 0,0555 | 0,0555 | 0,0555 | 0,0555 |
0,0555 | 0,0555 | 0,0555 | 0,0555 | 0,0555 | 0,0560 | 0,0560 | 0,0560 | 0,0560 | 0,0560 |
0,0560 | 0,0560 | 0,0560 | 0,0560 | 0,0565 | 0,0565 | 0,0565 | 0,0565 | 0,0570 | 0,0580 |
0,0580 | 0,0585 | 0,0600 | 0,0600 | 0,0600 | 0,0605 | 0,0605 | 0,0610 |
В качестве значения аттестованного содержания принимают медиану ряда полусумм, упорядоченных по возрастанию (табл.20).
![]()
Доверительный интервал медианы
![]()
Значение доверительного интервала для медианы, рассчитанной по Ходжесу-Леману меньше, чем для выборочной медианы и медианы, расcчитанной по Гаствирту.
![]() для 0,052%
для 0,052% - 17%
Коэффициент
![]() .
.
Условия аттестации выполнены (![]() ,
, ![]() ).
).
ПРИЛОЖЕНИЕ 13
Обязательное
Таблица 21
Максимально допустимые относительные средние квадратические отклонения результатов рядовых анализов
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||||
|
|
|
| ||||||
1 | 60,0-69,9 | 1,1 | - | - | - | - | - | - | - |
2 | 50,0-59,9 | 1,2 | - | - | - | - | - | - | |
3 | 40,0-49,9 | 1,6 | 2,8 | - | - | - | - | - | - |
4 | 30,0-39,9 | 2,1 | 4,0 | - | 1,6 | - | - | - | - |
5 | 20,0-29,9 | 2,8 | 5,4 | - | 2,1 | - | - | - | 1,4 |
6 | 10,0-19,9 | 3,5 | 7,0 | 1,8 | 2,8 | - | - | 2,1 | 2,1 |
7 | 5,0-9,9 | 5,4 | 9,0 | 2,5 | 4,0 | - | - | 3,5 | 3,5 |
8 | 2,0-4,9 | 8,0 | 11 | 3,5 | 6,0 | 6,0 | 6,0 | 5,4 | 5,4 |
9 | 1,0-1,9 | 11 | 13 | 4,6 | 9,0 | 8,0 | 6,5 | 7,0 | 7,0 |
10 | 0,50-0,99 | 15 | 16 | 6,0 | 12 | 10 | 7,0 | 9,0 | 9,0 |
11 | 0,20-0,49 | 20 | 19 | 8,0 | 15 | 12 | 8,6 | 11 | 11 |
12 | 0,10-0,19 | 25 | 21 | 10 | 19 | 16 | 10 | 14 | 14 |
13 | 0,050-0,099 | 28 | 27 | 12 | 24 | 18 | 12 | 21 | 21 |
14 | 0,020-0,049 | 30 | 28 | 16 | 27 | 21 | 16 | - | - |
15 | 0,010-0,019 | 30 | 30 | 20 | 28 | 25 | 21 | - | - |
16 | 0,0050-0,0099 | 30 | 30 | 27 | 30 | 30 | 27 | - | - |
17 | 0,0020-0,0049 | 30 | 30 | 30 | 30 | 30 | 30 | - | - |
18 | 0,0010-0,0019 | 30 | 30 | 30 | 30 | 30 | 30 | - | - |
19 | 0,00050-0,00099 | 30 | 30 | 30 | 30 | 30 | 30 | - | |
20 | 0,00020-0,00049 | 30 | 30 | 30 | 30 | 30 | 30 | - | |
21 | 0,00005-0,00019 | 30 | 30 | 30 | 30 | 30 | 30 | - | - |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | - | - |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | ||||||
| ||||||||
1 | 60,0-69,9 | - | - | - | - | - | 0,7 | - |
2 | 50,0-59,9 | - | - | - | - | 1,1 | 0,8 | - |
3 | 40,0-49,9 | - | - | - | - | 1,4 | 0,9 | 0,7 |
4 | 30,0-39,9 | - | - | - | - | 1,8 | 1,1 | 0,8 |
5 | 20,0-29,9 | - | - | - | - | 2,3 | 1,4 | 1,0 |
6 | 10,0-19,9 | - | - | - | - | 2,8 | 2,1 | 1,6 |
7 | 5,0-9,9 | 6,0 | 5,4 | - | - | 4,3 | 4,3 | 3,0 |
8 | 2,0-4,9 | 7,0 | 6,5 | - | - | 6,5 | 7,0 | 5,6 |
9 | 1,0-1,9 | 8,0 | 7,5 | - | - | 9,3 | 10 | 9,0 |
10 | 0,50-0,99 | 9,0 | 8,6 | - | - | 14 | 13 | 11 |
11 | 0,20-0,49 | 11 | 10 | - | - | 20 | 17 | 15 |
12 | 0,10-0,19 | 13 | 12 | 7,0 | 7,0 | 25 | 21 | 20 |
13 | 0,050-0,099 | 15 | 14 | 9,0 | 9,0 | 30 | 25 | 23 |
14 | 0,020-0,049 | 19 | 18 | 11 | 11 | 30 | 28 | 27 |
15 | 0,010-0,019 | 25 | 23 | 12 | 13 | 30 | 30 | 30 |
16 | 0,0050-0,0099 | 30 | 28 | 15 | 16 | 30 | 30 | 30 |
17 | 0,0020-0,0049 | 30 | 30 | 18 | 20 | 30 | 30 | 30 |
18 | 0,0010-0,0019 | 30 | 30 | 21 | 23 | 30 | 30 | 30 |
19 | 0,00050-0,00099 | 30 | 30 | 25 | 26 | 30 | 30 | 30 |
20 | 0,00020-0,00049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||||
| |||||||||
1 | 60,0-69,9 | - | - | - | - | - | - | - | - |
2 | 50,0-59,9 | - | - | - | - | - | - | 1,2 | - |
3 | 40,0-49,9 | - | - | - | - | - | - | 1,4 | - |
4 | 30,0-39,9 | - | - | - | - | - | - | 1,8 | - |
5 | 20,0-29,9 | - | - | - | - | - | - | 2,1 | - |
6 | 10,0-19,9 | - | - | - | - | - | 3,5 | 3,2 | - |
7 | 5,0-9,9 | - | - | - | - | - | 5,4 | 5,0 | - |
8 | 2,0-4,9 | - | - | - | - | - | 8,0 | 6,8 | - |
9 | 1,0-1,9 | - | - | - | - | 4,6 | 10 | 9,0 | 2,1 |
10 | 0,50-0,99 | - | - | - | - | 5,7 | 12 | 12 | 2,8 |
11 | 0,20-0,49 | - | - | - | - | 7,5 | 16 | 16 | 4,3 |
12 | 0,10-0,19 | - | - | - | - | 10 | 20 | 21 | 5,4 |
13 | 0,050-0,099 | - | - | - | 11 | 13 | 23 | 28 | 8,0 |
14 | 0,020-0,049 | - | - | - | 14 | 18 | 28 | 30 | 14 |
15 | 0,010-0,019 | - | - | - | 17 | 21 | 30 | 30 | 20 |
16 | 0,0050-0,0099 | 3,2 | 6,5 | 9,0 | 21 | 25 | 30 | 30 | 30 |
17 | 0,0020-0,0049 | 5,4 | 9,0 | 12 | 24 | 30 | 30 | 30 | 30 |
18 | 0,0010-0,0019 | 8,2 | 12 | 20 | 28 | 30 | 30 | 30 | 30 |
19 | 0,00050-0,00099 | 12 | 18 | 27 | 30 | 30 | 30 | 30 | 30 |
20 | 0,00020-0,00049 | 18 | 27 | 30 | 30 | 30 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 27 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||||
| |||||||||
1 | 60,0-69,9 | 0,7 | - | - | - | - | - | - | - |
2 | 50,0-59,9 | 0,8 | - | 1,4 | - | - | - | - | - |
3 | 40,0-49,9 | 1,0 | - | 1,7 | - | - | - | - | - |
4 | 30,0-39,9 | 1,3 | - | 1,8 | - | - | - | - | - |
5 | 20,0-29,9 | 1,9 | - | 2,5 | 1,1 | - | - | - | - |
6 | 10,0-19,9 | 3,2 | - | 3,4 | 1,4 | - | - | - | 3,5 |
7 | 5,0-9,9 | 5,0 | - | 4,6 | 2,0 | 2,1 | - | - | 5,4 |
8 | 2,0-4,9 | 6,8 | 5,4 | 6,5 | 2,8 | 3,5 | - | 2,3 | 8,0 |
9 | 1,0-1,9 | 9,3 | 6,8 | 9,0 | 3,4 | 5,0 | 2,8 | 4,0 | 10 |
10 | 0,50-0,99 | 12 | 8,5 | 13 | 5,4 | 7,0 | 5,4 | 5,4 | 12 |
11 | 0,20-0,49 | 17 | 11 | 16 | 8,0 | 11 | 8,0 | 8,0 | 16 |
12 | 0,10-0,19 | 21 | 14 | 21 | 11 | 14 | 11 | 10 | 20 |
13 | 0,050-0,099 | 27 | 18 | 27 | 17 | 20 | 15 | 13 | 24 |
14 | 0,020-0,049 | 30 | 22 | 30 | 21 | 25 | 19 | 18 | 28 |
15 | 0,010-0,019 | 30 | 25 | 30 | 24 | 30 | 24 | 25 | 30 |
16 | 0,0050-0,0099 | 30 | 26 | 30 | 28 | 30 | 30 | 30 | 30 |
17 | 0,0020-0,0049 | 30 | 28 | 30 | 30 | 30 | 30 | 30 | 30 |
18 | 0,0010-0,0019 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
19 | 0,00050-0,00099 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
20 | 0,00020-0,00049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | ||||||||
|
|
| ||||||||
1 | 60,0-69,9 | - | - | - | - | - | - | - | - | - |
2 | 50,0-59,9 | - | - | - | - | - | - | - | - | - |
3 | 40,0-49,9 | - | - | - | - | - | - | - | - | - |
4 | 30,0-39,9 | - | - | - | - | - | - | - | - | - |
5 | 20,0-29,9 | - | - | 1,4 | 1,4 | - | - | - | - | - |
6 | 10,0-19,9 | - | - | 1,8 | 2,1 | - | - | - | 2,1 | - |
7 | 5,0-9,9 | - | 5,4 | 2,8 | 3,5 | 3,5 | - | - | 2,8 | - |
8 | 2,0-4,9 | - | 6,0 | 4,3 | 5,4 | 4,7 | - | - | 4,7 | - |
9 | 1,0-1,9 | 5,0 | 7,5 | 5,7 | 7,0 | 6,5 | - | 5,4 | 6,8 | 10 |
10 | 0,50-0,99 | 7,1 | 9,3 | 7,5 | 9,0 | 8,5 | - | 6,0 | 9,0 | 12 |
11 | 0,20-0,49 | 9,6 | 11 | 9,6 | 11 | 11 | - | 7,0 | 11 | 14 |
12 | 0,10-0,19 | 13 | 13 | 12 | 14 | 16 | - | 9,0 | 14 | 18 |
13 | 0,050-0,099 | 17 | 16 | 16 | 21 | 21 | - | 11 | 17 | 21 |
14 | 0,020-0,049 | 20 | 19 | 20 | - | 25 | - | 14 | 21 | 25 |
15 | 0,010-0,019 | 23 | 22 | 24 | - | 30 | - | 17 | 25 | 30 |
16 | 0,0050-0,0099 | 25 | 27 | 30 | - | 30 | - | 21 | 30 | 30 |
17 | 0,0020-0,0049 | 30 | 30 | 30 | - | 30 | 16 | 26 | 30 | 30 |
18 | 0,0010-0,0019 | 30 | 30 | 30 | - | 30 | 18 | 30 | 30 | 30 |
19 | 0,00050-0,00099 | 30 | 30 | 30 | - | 30 | 20 | 30 | 30 | 30 |
20 | 0,00020-0,00049 | 30 | 30 | 30 | - | 30 | 22 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 30 | 30 | 30 | - | 30 | 25 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | 30 | 30 | - | 30 | 30 | 30 | 30 | 30 |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||||
| |||||||||
1 | 60,0-69,9 | - | - | - | - | - | - | - | - |
2 | 50,0-59,9 | - | - | - | - | - | - | - | - |
3 | 40,0-49,9 | - | 0,8 | - | - | - | - | - | - |
4 | 30,0-39,9 | - | 1,0 | - | - | - | - | - | - |
5 | 20,0-29,9 | - | 1,2 | - | - | - | - | - | - |
6 | 10,0-19,9 | - | 1,5 | 5,0 | - | - | - | - | - |
7 | 5,0-9,9 | - | 3,3 | 6,5 | - | - | - | 3,5 | - |
8 | 2,0-4,9 | - | 5,4 | 8,0 | - | 4,3 | - | 4,3 | - |
9 | 1,0-1,9 | - | 7,5 | 10 | - | 6,8 | - | 5,0 | - |
10 | 0,50-0,99 | 3,5 | 10 | 13 | - | 10 | - | 6,5 | 3,5 |
11 | 0,20-0,49 | 4,3 | 12 | 16 | - | 13 | - | 8,5 | 5,0 |
12 | 0,10-0,19 | 5,0 | 14 | 19 | - | 17 | 7,1 | 11 | 5,7 |
13 | 0,050-0,099 | 6,5 | 17 | 23 | 2,5 | 19 | 9,0 | 14 | 8,0 |
14 | 0,020-0,049 | 9,0 | 21 | 29 | 5,0 | 24 | 11 | 18 | 11 |
15 | 0,010-0,019 | 12 | 26 | 30 | 7,0 | 28 | 13 | 21 | 14 |
16 | 0,0050-0,0099 | 16 | 28 | 30 | 9,0 | 30 | 16 | 26 | 18 |
17 | 0,0020-0,0049 | 21 | 30 | 30 | 12 | 30 | 18 | 30 | 21 |
18 | 0,0010-0,0019 | 28 | 30 | 30 | 15 | 30 | 21 | 30 | 28 |
19 | 0,00050-0,00099 | 30 | 30 | 30 | 18 | 30 | 25 | 30 | 30 |
20 | 0,00020-0,00049 | 30 | 30 | 30 | 20 | 30 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 30 | 30 | 30 | 25 | 30 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||||
1 | 60,0-69,9 | - | - | - | - | - | - | - | - |
2 | 50,0-59,9 | 0,8 | - | - | 0,9 | - | - | - | - |
3 | 40,0-49,9 | 1,0 | - | - | 1,1 | - | - | - | - |
4 | 30,0-39,9 | 1,2 | - | - | 1,4 | - | - | - | 1,1 |
5 | 20,0-29,9 | 1,5 | - | - | 1,8 | - | - | - | 1,6 |
6 | 10,0-19,9 | 2,1 | - | - | 3,0 | - | - | - | 2,7 |
7 | 5,0-9,9 | 3,5 | - | - | 4,3 | - | - | - | 3,2 |
8 | 2,0-4,9 | 5,4 | - | - | 6,5 | - | 3,2 | - | - |
9 | 1,0-1,9 | 7,0 | 3,4 | - | 10 | 2,5 | 4,3 | 2,1 | - |
10 | 0,50-0,99 | 9,0 | 4,3 | 7,0 | 14 | 3,2 | 6,0 | 3,2 | - |
11 | 0,20-0,49 | 11 | 5,0 | 10 | 20 | 3,5 | 8,2 | 5,0 | - |
12 | 0,10-0,19 | 14 | 6,0 | 14 | 25 | 4,6 | 9,3 | 7,5 | - |
13 | 0,050-0,099 | 18 | 7,5 | 20 | 27 | 5,7 | 12 | 10 | - |
14 | 0,020-0,049 | 21 | 9,0 | 25 | 29 | 6,8 | 16 | 13 | - |
15 | 0,010-0,019 | 27 | 11 | 27 | 30 | 9,0 | 21 | 20 | - |
16 | 0,0050-0,0099 | 29 | 15 | 30 | 30 | 12 | 24 | 23 | - |
17 | 0,0020-0,0049 | 30 | 18 | 30 | 30 | 14 | 27 | 25 | - |
18 | 0,0010-0,0019 | 30 | 24 | 30 | 30 | 16 | 29 | 27 | - |
19 | 0,00050-0,00099 | 30 | 30 | 30 | 30 | 18 | 30 | 29 | - |
20 | 0,00020-0,00049 | 30 | 30 | 30 | 30 | 20 | 30 | 30 | - |
21 | 0,00005-0,00019 | 30 | 30 | 30 | 30 | 25 | 30 | 30 | - |
22 | 0,000020-0,000049 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | - |
Продолжение табл.21
Номер интер- | Интервалы содержаний, % | Элемент или оксид | |||||
|
| ||||||
1 | 60,0-69,9 | - | - | - | - | - | - |
2 | 50,0-59,9 | - | - | - | - | - | - |
3 | 40,0-49,9 | - | - | 1,0 | - | - | - |
4 | 30,0-39,9 | - | 2,0 | 1,2 | - | - | - |
5 | 20,0-29,9 | - | 2,5 | 1,5 | 1,4 | - | 1,2 |
6 | 10,0-19,9 | - | 3,5 | 2,0 | 2,1 | - | 1,7 |
7 | 5,0-9,9 | - | 5,0 | 2,5 | 2,8 | - | 2,1 |
8 | 2,0-4,9 | 6,5 | 7,0 | 3,5 | 4,6 | - | 3,2 |
9 | 1,0-1,9 | 8,0 | 9,0 | 4,5 | 6,8 | 10 | 5,0 |
10 | 0,50-0,99 | 10 | 12 | 6,0 | 9,0 | 12 | 7,0 |
11 | 0,20-0,49 | 12 | - | 7,0 | 11 | 14 | 9,0 |
12 | 0,10-0,19 | 14 | - | 8,5 | 14 | 18 | 12 |
13 | 0,050-0,099 | 17 | - | 10 | 18 | 21 | 16 |
14 | 0,020-0,049 | 20 | - | 11 | 21 | 25 | 18 |
15 | 0,010-0,019 | 22 | - | 14 | 25 | 30 | 21 |
16 | 0,0050-0,0099 | 25 | - | 18 | 27 | 30 | 24 |
17 | 0,0020-0,0049 | 27 | - | 21 | 29 | 30 | 27 |
18 | 0,0010-0,0019 | 29 | - | 28 | 30 | 30 | 30 |
19 | 0,00050-0,00099 | 30 | - | 30 | 30 | 30 | 30 |
20 | 0,00020-0,00049 | 30 | - | 30 | 30 | 30 | 30 |
21 | 0,00005-0,00019 | 30 | - | 30 | 30 | 30 | 30 |
22 | 0,000020-0,000049 | 30 | - | 30 | 30 | 30 | 30 |
| |||||||
ПРИЛОЖЕНИЕ 14
Справочное
ПОЯСНЕНИЕ ТЕРМИНОВ, ИСПОЛЬЗУЕМЫХ В НАСТОЯЩЕМ СТАНДАРТЕ
Стандартный образец (СО) состава горных пород и минерального сырья | - материал, подготовленный специальным способом, в котором с необходимой точностью установлено содержание всех важнейших компонентов или их частей и к которому прилагается свидетельство, выдаваемое аттестующей организацией |
Геологическая проба | - исходный материал для приготовления СО, достаточно однородный и имеющий состав, характерный для данного типа горной породы или минерального сырья |
Лабораторная проба | - порошкообразный материал, соответствующий среднему составу геологической пробы, из которого берут навески для аттестационных анализов |
Минимальная представительная навеска СО | - масса СО, на уровне которой гарантируется однородность лабораторной пробы |
Аттестационный анализ | - межлабораторный анализ, выполняемый с целью установления содержания компонентов при использовании принципиально различных методов |
Электронный текст документа
и сверен по:
М.: Издательство стандартов, 1994
