ГОСТ Р ИСО 21748-2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
Statistical methods. Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation
ОКС 17.020
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1419-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 21748:2010* "Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений" (ISO 21748:2010 "Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВЗАМЕН Р 50.1.060-2006
6 ПЕРЕИЗДАНИЕ. Июль 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Знание неопределенности результатов измерений крайне важно для принятия решений. Без количественных оценок неопределенности невозможно решить, превышают ли наблюдаемые отклонения результатов измерений заданную изменчивость, соответствуют ли объекты испытаний установленным требованиям. При отсутствии информации о неопределенности результатов измерений велика вероятность ошибочного принятия решений, которые могут привести к непредусмотренным расходам в процессе производства, неправильным судебным выводам, неблагоприятным последствиям для здоровья человека или неблагоприятным социальным последствиям.
Лаборатории, аккредитованные в соответствии с ИСО/МЭК 17025:2005, обязаны оценивать неопределенность результатов измерений и испытаний и составлять соответствующий отчет (см. ГОСТ ИСО 17025-2009*, пункт 5.4.6). Эта работа может быть выполнена с использованием настоящего стандарта, Руководства ИСО/МЭК 98-3:2008
или другой нормативной документации. В ИСО/МЭК Руководство 98-3:2008 установлен стандартный подход к оценке неопределенности результатов измерений. Приведенный в этом документе подход относится к ситуации, когда известна модель процесса измерений. Широкий диапазон стандартных методов испытаний может быть подвергнут совместному исследованию в соответствии с ИСО 5725-2:1994
. Настоящий стандарт устанавливает методы оценки неопределенности результатов измерений и испытаний, основанные на анализе данных полученных при межлабораторном исследовании.
_______________
ИСО/МЭК 17025:2005 "Общие требования к компетентности испытательных и поверочных лабораторий" (ISO/IEC 17025:2005 "General requirements for the competence of testing and calibration laboratories").
Руководство ИСО/МЭК 98-3:2008 "Неопределенность измерений. Часть 3. Руководство по выражению неопределенности измерений (GUM:1995)" [ISO/IEC Guide 98-3:2008, "Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)"].
ИСО 5725-2:1994 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерения" [ISO 5725-2:1994 "Accuracy (trueness and precision) of measurement methods and results. Part 2. Basic method for the determination of repeatability and reproducibility of a standard measurement method"]
* Вероятно, ошибка оригинала. Следует читать: ГОСТ ИСО/МЭК 17025-2009. - .
Общий подход, используемый в настоящем стандарте, требует, чтобы:
- оценки повторяемости, воспроизводимости и правильности метода, полученные при межлабораторном исследовании в соответствии с ИСО 5725-2:1994, могли быть получены из опубликованной информации об использовании метода испытаний. Эти оценки позволяют получать внутрилабораторные и межлабораторные составляющие неопределенности, а также оценку неопределенности результатов, связанную с правильностью метода;
- лаборатория подтвердила на основе проверок присущих ей смещения и прецизионности, что качество выполнения ею метода испытаний соответствует установленным требованиям к методу испытаний, то есть подтвердила, что опубликованные данные о применении метода согласуются с результатами измерений и испытаний, полученными лабораторией;
- любые воздействия на результаты измерений, не охваченные межлабораторными исследованиями, были идентифицированы, а отклонения, вызванные этими воздействиями, определены количественно.
Оценку неопределенности определяют объединением оценок дисперсии, полученных в результате межлабораторных исследований в соответствии с GUM.
Для контроля полного понимания метода разброс результатов, полученных в межлабораторном исследовании, полезно сравнивать с оценками неопределенности измерений, полученными с использованием процедур GUM. Такие сравнения будут более эффективны при использовании последовательных оценок одного и того же параметра, полученных на основе данных совместных исследований.
Применяемый в настоящем стандарте международный стандарт разработан Техническим комитетом ИСО/ТС 69 "Применение статистических методов".
1 Область применения
В настоящем стандарте приведено руководство для:
- оценки неопределенности измерений на основе данных, полученных в результате исследований, проводимых в соответствии с ИСО 5725-2;
- сравнения результатов, полученных в межлабораторном исследовании, с оценками неопределенности измерений исследуемого параметра, полученными с использованием принципов переноса неопределенности (см. раздел 13).
В ИСО 5725-3 установлены дополнительные модели для анализа промежуточной прецизионности. Однако оценка неопределенности с использованием этих моделей не включена в настоящий стандарт, хотя этот общий подход может быть применен к более широкой группе моделей.
Настоящий стандарт применим во всех областях измерений и испытаний, когда должна быть определена неопределенность результатов.
В настоящем стандарте не приведено описание применения данных повторяемости в отсутствии данных воспроизводимости.
В настоящем стандарте использовано предположение, что признанные значимыми систематические воздействия устранены либо путем численной корректировки результатов, включенной в метод измерений, либо путем анализа и устранения причины воздействий.
В настоящем стандарте приведено общее руководство. Представленный подход к оценке неопределенности применим во многих случаях, однако возможно применение и других методов.
В общем случае информация, приведенная в настоящем стандарте, относительно результатов, методов и процессов измерений, относится также к результатам, методам и процессам испытаний.
2 Термины и определения
В настоящем стандарте применены термины по ИСО 5725-3, а также следующие термины с соответствующими определениями:
2.1 смещение (bias): Разность между математическим ожиданием результатов наблюдений испытаний и измерений и истинным значением.
Примечания
1 Смещение представляет собой систематическую ошибку в противоположность случайной ошибке. Могут существовать одна или несколько причин, вызывающих систематическую ошибку. Большее систематическое отклонение от истинного значения соответствует большему значению смещения.
_______________
Применительно к измерениям под ошибкой следует понимать "погрешность".
2 Смещение измерительного прибора обычно оценивают с помощью среднего арифметического ошибок его показаний по соответствующему количеству повторных измерений. Ошибка показания - "показания измерительного прибора минус истинное значение соответствующей величины".
3 На практике применяют вместо истинного значения принятое опорное значение.
[ИСО 3534-2:2006, определение 3.3.2]
2.2 суммарная стандартная неопределенность (combined standard uncertainty); : Стандартная неопределенность результата измерений, полученного через значения ряда других величин, равная положительному квадратному корню из суммы членов, представляющих собой дисперсии или ковариации этих величин, взятых с весами, соответствующими степени влияния этих величин на результат измерений.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.4]
2.3 коэффициент охвата (coverage factor); : Числовой коэффициент, на который умножают суммарную стандартную неопределенность при определении расширенной неопределенности.
Примечание - Коэффициент охвата обычно принимает значения от 2 до 3.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.6]
2.4 расширенная неопределенность (expanded uncertainty); : Величина, определяющая интервал вокруг математического ожидания результатов измерений, охватывающий большую долю распределения значений, которые обоснованно могут быть приписаны измеряемой величине.
Примечания
1 Долю распределения, охватывающую интервалом, характеризует вероятность охвата или уровень доверия интервала.
2 Чтобы связать определенный уровень доверия с интервалом расширенной неопределенности, необходимы предположения (в явной или неявной форме) о форме распределения вероятностей результатов измерений и их суммарной стандартной неопределенности. Уровень доверия, который соответствует этому интервалу, может соответствовать действительности только в той степени, в какой могут быть справедливы предположения.
3 В рекомендациях [20] расширенную неопределенность называют общей неопределенностью.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.5]
2.5 прецизионность (precision): Близость независимых результатов наблюдений, полученных при определенных принятых условиях.
Примечания
1 Прецизионность зависит от распределения случайных ошибок и не связана ни с истинным, ни с заданным значениями.
2 Меру прецизионности обычно выражают в терминах изменчивости и вычисляют как стандартное отклонение результатов наблюдений (испытаний/измерений). Малой прецизионности соответствует большое стандартное отклонение.
3 Количественные меры прецизионности существенным образом зависят от принятых условий. Условия повторяемости и условия воспроизводимости являются примерами крайних вариантов принятых условий.
[ИСО 3534-2:2006, определение 3.3.4]
2.6 повторяемость (repeatability): Прецизионность в условиях повторяемости.
Примечание - Повторяемость может быть выражена количественно в виде характеристики разброса результатов наблюдений.
[ИСО 3534-2:2006, определение 3.3.5]
2.7 условия повторяемости (repeatability conditions): Условия наблюдений, при которых независимые результаты наблюдений (испытаний/измерений) получают одним и тем же методом на идентичных объектах наблюдений, в одной и той же лаборатории, с применением одних и тех же средств испытаний/измерений, одним и тем же оператором, с использованием одного и того же оборудования в течение короткого интервала времени.
Примечание - Условия повторяемости предполагают использование одних и тех же:
- процедур измерений или испытаний;
- операторов;
- измерительного и испытательного оборудования, используемых в одних и тех же условиях;
- расположения оборудования;
- повторений в течение короткого интервала времени.
[ИСО 3534-2:2006, определение 3.3.6]
2.8 стандартное отклонение повторяемости (repeatability standard deviation): Стандартное отклонение результатов наблюдений (испытаний/измерений), полученных в условиях повторяемости.
Примечания
1 Стандартное отклонение повторяемости является мерой рассеяния результатов наблюдений в условиях повторяемости.
2 Аналогично "дисперсия повторяемости" и "коэффициент вариации повторяемости" могут быть определены и использованы в качестве меры рассеяния результатов наблюдений в условиях повторяемости.
[ИСО 3534-2:2006, определение 3.3.7]
2.9 воспроизводимость (reproducibility): Прецизионность в условиях воспроизводимости.
Примечания
1 Воспроизводимость может быть выражена количественно в виде характеристик разброса результатов.
2 Под результатами обычно понимают исправленные (скорректированные) результаты.
[ИСО 3534-2:2006, определение 3.3.10]
2.10 условия воспроизводимости (reproducibility conditions): Условия, при которых независимые результаты наблюдений (испытаний/измерений) получены одним методом, на идентичных объектах наблюдений, в разных лабораториях, с применением различных средств испытаний/измерений, разными операторами, с использованием различного оборудования.
[ИСО 3534-2:2006, определение 3.3.11]
2.11 стандартное отклонение воспроизводимости (reproducibility standard deviation): Стандартное отклонение результатов наблюдений (испытаний/измерений), полученных в условиях воспроизводимости.
Примечания
1 Стандартные отклонения воспроизводимости являются мерой рассеяния результатов наблюдений в условиях воспроизводимости.
2 Аналогично "дисперсия воспроизводимости" и "коэффициент вариации воспроизводимости" могут быть определены и использованы как меры рассеяния результатов наблюдений в условиях воспроизводимости.
[ИСО 3534-2:2006, определение 3.3.12]
2.12 стандартная неопределенность (standard uncertainty); : Неопределенность результатов измерений, выраженная в виде стандартного отклонения.
[Руководство ИСО/МЭК 98-3:2008, определение 2.3.1]
2.13 правильность (trueness): Близость математического ожидания результатов наблюдений (испытаний/измерений) к истинному значению.
Примечания
1 В качестве меры правильности обычно используют смещение.
2 Правильность иногда трактуют как "точность среднего". Применение такого термина не рекомендуется.
3 На практике в качестве истинного значения обычно используют принятое опорное значение.
[ИСО 3534-2:2006, определение 3.3.3]
2.14 неопределенность (измерения) (uncertainty): Параметр, относящийся к результату измерения, характеризующий разброс значений, которые обоснованно могут быть приписаны измеряемой величине.
Примечания
1 Параметром может быть, например, стандартное отклонение (или величина, кратная ему) или полуширина интервала, которому соответствует установленный уровень доверия.
2 Неопределенность измерения включает в себя в общем случае несколько составляющих. Некоторые из этих составляющих могут быть оценены по статистическим распределениям результатов серии измерений и могут быть охарактеризованы экспериментальными стандартными отклонениями. Другие составляющие, которые также могут быть характеризованы стандартными отклонениями, оценивают исходя из предположений о виде распределения, основанных на экспериментальной или другой информации.
3 Очевидно, что результат измерений является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая те, которые являются результатом систематических воздействий (таких как поправки, корректировки, применение эталона), вносят свой вклад в разброс результатов измерений.
[Руководство ИСО/МЭК 98-3:2008, определение 2.2.3]
2.15 бюджет неопределенности (uncertainty budget): Перечень источников неопределенности с соответствующими им стандартными неопределенностями, составленный для определения оценки суммарной стандартной неопределенности результата измерений.
Примечание - Перечень обычно включает в себя дополнительную информацию, такую как коэффициент чувствительности (изменчивость результатов в зависимости от изменчивости воздействия на результат), число степеней свободы, соответствующее каждой стандартной неопределенности, и идентификацию методов оценки каждой стандартной неопределенности в терминах оценок типа А или типа В.
2* Условные обозначения
________________
* Нумерация соответствует оригиналу. - .
- | свободный член эмпирической функции | |
- | лабораторная составляющая смещения; | |
- | коэффициент наклона эмпирической функции | |
- | коэффициент эмпирической функции | |
- | коэффициент чувствительности | |
- | показатель степени эмпирической функции | |
- | случайная погрешность результата измерений в условиях повторяемости; | |
- | числовой коэффициент, на который умножают суммарную стандартную неопределенность | |
- | количество лабораторий; | |
- | математическое ожидание (среднее) измеряемой величины; | |
- | количество составляющих, используемых при вычислении неопределенности; | |
- | количество объединяемых составляющих при вычислении суммарной неопределенности в дополнение к совместно исследуемым данным; | |
- | количество повторений, выполняемых лабораторией | |
- | количество повторений измерения; | |
- | количество лабораторий; | |
- | количество объектов испытаний из большей (по количеству) партии; | |
- | количество назначенных величин в соответствии с принятым соглашением в процесс совместных исследований; | |
- | коэффициент корреляции | |
- | стандартное отклонение межгрупповой составляющей дисперсии; | |
- | межгрупповая составляющая дисперсии; | |
- | оценочное или экспериментальное стандартное отклонение результатов наблюдений, полученных повторными измерениями на образце сравнения, используемом при контроле смещения; | |
- | неопределенность, соответствующая неоднородности образца; | |
- | составляющая дисперсии, соответствующая неоднородности образца; | |
- | оценка стандартного отклонения повторяемости c | |
- | экспериментальное или оцененное внутрилабораторное стандартное отклонение; | |
- | скорректированная оценка стандартного отклонения типа | |
- | оценка дисперсии типа | |
- | оценка внутрилабораторного стандартного отклонения; оценка стандартного отклонения для | |
- | скорректированная оценка внутрилабораторного стандартного отклонения, когда вклад зависит от выходной переменной; | |
- | оценка дисперсии | |
- | оценка стандартного отклонения воспроизводимости; | |
- | оценка стандартного отклонения воспроизводимости, скорректированная для лабораторной оценки стандартного отклонения повторяемости; | |
- | скорректированная оценка стандартного отклонения воспроизводимости, вычисленная по эмпирической модели, когда вклады зависят от выходной переменной; | |
- | оценка внутрилабораторного стандартного отклонения, полученная на основе повторных измерений или других исследований повторяемости; | |
- | оценка компонента дисперсии внутри группы (часто внутрилабораторный компонент дисперсии); | |
- | оценка стандартного отклонения оценки смещения | |
| - | лабораторное стандартное отклонение разностей, определяемых при сравнении обычного для лаборатории метода с заданным методом или с величинами, назначенными в соответствии с принятым соглашением; |
- | неопределенность, соответствующая | |
- | неопределенность, соответствующая паспортному значению | |
- | неопределенность, соответствующая входному значению | |
- | суммарная стандартная неопределенность, соответствующая | |
- | вклад в суммарную неопределенность | |
- | суммарная стандартная неопределенность результата или назначенного значения | |
- | суммарная неопределенность для результата | |
| - | суммарная стандартная неопределенность, соответствующая |
- | неопределенность, соответствующая неоднородности выборки; | |
- | расширенная неопределенность, равная стандартной неопределенности | |
- | расширенная неопределенность | |
- | значение | |
- | отклонение | |
- | объединенный результат, представляющий собой функцию других результатов | |
- | результат испытаний | |
- | результат испытаний | |
- | заданное значение для проверки квалификации; | |
- | лабораторное смещение; | |
- | оценка смещения | |
- | среднее смещение лаборатории при сравнении обычного метода с заданным методом или со значениями, назначенными в соответствии с принятым соглашением; | |
- | смещение, присущее используемому методу измерений; | |
- | оценка смещения метода измерений; | |
- | неизвестное математическое ожидание идеального результата; | |
- | паспортное значение образца сравнения; | |
- | стандартное отклонение для проверки квалификации; | |
- | истинное значение стандартного отклонения результатов наблюдений, полученных на основе повторных измерений на образце сравнения, используемом при контроле смещения; | |
- | межлабораторное стандартное отклонение; стандартное отклонение типа | |
- | дисперсия | |
- | внутрилабораторное стандартное отклонение, стандартное отклонение | |
- | дисперсия | |
- | стандартное отклонение в пределах группы; | |
- | стандартное отклонение, необходимое для адекватной работы (см. Руководство ИСО 33); | |
- | число эффективных степеней свободы для стандартного отклонения или неопределенности, соответствующей результату | |
- | число степеней свободы, соответствующее | |
- | число степеней свободы, соответствующее оценке |
4 Принципы
4.1 Отдельные результаты и свойства процесса измерений
4.1.1 Неопределенность измерений относят к отдельным результатам измерений. Повторяемость, воспроизводимость и правильность относят к выполнению процесса измерений или испытаний. При проведении анализа неопределенности в соответствии с ИСО 5725 (все части) процесс измерений или испытаний должен быть единым методом измерений, используемым всеми лабораториями, принимающими участие в исследовании. Следует заметить, что в настоящем стандарте под методом измерений понимают единственную полностью детализированную процедуру (как определено в Руководстве ИСО/МЭК 99:2007, п.2.6). В настоящем стандарте предполагается, что графики, полученные при исследовании метода, отражают все полученные отдельные результаты измерений. Это предположение требует подтверждающих доказательств в виде соответствующих данных контроля и качества выполнения процесса измерений (раздел 6).
4.1.2 В некоторых случаях может потребоваться учитывать различия между отдельными объектами испытаний. Однако в этом случае нет необходимости в проведении специальных детальных исследований неопределенности для каждого объекта испытаний при наличии устойчивого процесса измерений с хорошими характеристиками.
4.2 Применение данных воспроизводимости
Применение данного стандарта основано на двух принципах:
- стандартное отклонение воспроизводимости, полученное при совместных исследованиях, является основой для оценки неопределенности измерений (см. А.2.1);
- воздействия, не наблюдаемые в процессе совместных исследований, должны быть незначительными или должны быть учтены. Данный принцип является расширением основной модели, используемой для совместных исследований (см. А.2.3).
4.3 Основные уравнения статистической модели
4.3.1 Статистическая модель, на которой основаны изложенные в настоящем стандарте методы оценки неопределенности, может быть записана в виде уравнения
![]() , (1)
, (1)
где - результат измерений, относительно которого предполагается, что он может быть вычислен по соответствующей функции;
- (неизвестное) математическое ожидание идеальных результатов;
- смещение, присущее методу измерений;
- лабораторная составляющая смещения;
- отклонение от номинального значения
;
- коэффициент чувствительности, равный
![]() ;
;
- случайная погрешность в условиях повторяемости.
Предполагается, что и
подчиняются нормальному распределению с нулевым средним и дисперсиями
и
соответственно. Эти предположения формируют модель, используемую в ИСО 5725-2 для совместного анализа данных.
Так как наблюдаемые стандартные отклонения смещения метода , лабораторного смещения
и случайных ошибок
полностью описывают разброс в условиях совместного исследования, сумма
![]() учитывает воздействия, которые вызывают отклонения, не включенные в
учитывает воздействия, которые вызывают отклонения, не включенные в ,
или
, и, таким образом, эта сумма позволяет учесть влияние действий, которые не выполнялись в ходе совместных исследований.
Примерами таких действий являются:
a) подготовка объекта испытаний, выполняемая для каждого испытываемого объекта, выполненная до проведения совместных исследований;
b) влияние подвыборки в случае, когда объекты, подвергаемые совместному исследованию, были гармонизированы до проведения совместного исследования. Предполагается, что подчиняются нормальному распределению с нулевым математическим ожиданием и дисперсией
![]() .
.
Пояснения к этой модели приведены в приложении А.
Примечание - Ошибка обычно определяется как разность между установленным значением и результатом измерений. В GUM [16], "ошибку" (значение) отличают от "неопределенности" (разброса значений). При оценке неопределенности, однако, важно характеризовать разброс значений, вызванный случайными воздействиями, и включить его в модель. Для этого в уравнение (1) включают член с нулевым математическим ожиданием, характеризующий "ошибку".
4.3.2 Учитывая модель, описываемую уравнением (1), неопределенность наблюдений можно оценить, применяя уравнение
![]() , (2)
, (2)
где - оценка дисперсии
;
- оценка дисперсии
;
- неопределенность, вызванная неопределенностью оценки
, полученной на основе измерений эталона или образца сравнения с паспортным значением
;
- неопределенность, соответствующая
.
Учитывая, что стандартное отклонение воспроизводимости , задаваемое равенством
![]() ,
, можно заменить на
![]() , уравнение (2) можно привести к уравнению
, уравнение (2) можно привести к уравнению
![]() . (3)
. (3)
4.4 Данные повторяемости
Данные повторяемости использованы в настоящем стандарте, прежде всего, для проверки прецизионности, которая вместе с другими проверками подтверждает, что конкретная лаборатория может применять данные воспроизводимости и правильности при оценке неопределенности. Данные повторяемости используют также при вычислении составляющей воспроизводимости в неопределенности (см. 6.3 и раздел 10).
5 Оценка неопределенности с использованием оценок повторяемости, воспроизводимости и правильности
5.1 Процедура оценки неопределенности измерений
Принципы, на которых основан настоящий стандарт (см. 4.1), приводят к следующей процедуре оценки неопределенности измерений:
a) получение оценок повторяемости, воспроизводимости и правильности метода на основе опубликованной информации о методе;
b) проверка не превышения лабораторным смещением, рассчитанным по измерениям смещения, определенного на основе данных, полученных в соответствии с перечислением а);
c) проверка не превышения прецизионностью, полученной по текущим измерениям прецизионности, полученной на основе оценок повторяемости и воспроизводимости, определенных в соответствии с перечислением а);
d) идентификация любых воздействий на измерение, которые не были учтены в процессе исследований в соответствии с перечислением а), и определение количественной оценки отклонений, которые могут вызывать эти воздействия, учитывая коэффициент чувствительности и неопределенность каждого из воздействий;
e) объединение оценки воспроизводимости [см. перечисление а)] с неопределенностью, соответствующей правильности [см. перечисления а) и b)] и результатами дополнительных воздействий [см. перечисление d)], для формирования оценки суммарной неопределенности, когда смещение и прецизионность находятся под контролем в соответствии с перечислениями b) и с).
Этапы этой процедуры описаны более подробно в разделах 6-10.
Примечание - В настоящем стандарте предполагается, что в случае когда смещение является не контролируемым, выполняют корректирующие действия для приведения процесса в устойчивое состояние.
5.2 Различия между фактической прецизионностью и ее математическим ожиданием
Если фактическая прецизионность отличается от математического ожидания прецизионности, полученного на основе исследований в соответствии с перечислением 5.1 а), должны быть учтены соответствующие вклады в неопределенность. В 7.5 описаны корректировки оценок воспроизводимости для общего случая, когда прецизионность приближенно пропорциональна уровню отклика.
6 Установление соответствия данных выполнения метода результатам измерений для конкретного процесса измерений
6.1 Общие положения
На основе результатов совместных исследований (,
и в некоторых случаях оценки смещения метода) формируют требования к выполнению метода. При применении метода для установленных целей ожидается, что лаборатория продемонстрирует выполнение этих требований. В большинстве случаев для этого проводят исследования, направленные на подтверждение выполнения требований к повторяемости (см. 6.3) и лабораторной составляющей смещения (см. 6.2), а также регулярно проводят проверки правильности выполнения метода [контроль и обеспечение качества исполнения метода (см. 6.4)].
6.2 Демонстрация контролируемости лабораторной составляющей смещения
6.2.1 Общие требования
6.2.1.1 Лаборатория должна продемонстрировать, что соответствующее ей смещение при выполнении метода является контролируемым, то есть лабораторная составляющая смещения не выходит за пределы смещения, полученного при совместных исследованиях. Далее предполагается, что контроль смещения выполнен на образцах материалов, значения характеристик которых близки к объектам исследования при обычных испытаниях. В тех случаях, когда материалы, используемые для проверки смещения, имеют значения характеристик, значительно отличающиеся от материалов, исследуемых при обычных испытаниях, итоговые вклады смещения в неопределенность должны быть скорректированы в соответствии с 7.4 и 7.5.
6.2.1.2 В общем случае проверка лабораторной составляющей смещения сводится к сравнению результатов, полученных в лаборатории, с некоторыми эталонными значениями и представляет собой оценку . Уравнение (2) показывает, что неопределенность, связанная с изменениями
, характеризуется
, непосредственно входящей в
. Однако проверке смещения соответствует своя неопределенность, поэтому неопределенность сравнения в общем случае увеличивает неопределенность результатов, которые могут быть получены при применении метода. По этой причине важно гарантировать, что неопределенность, связанная с проверкой смещения, мала по сравнению с
(в идеале меньше чем
![]() ) и, следовательно, соответствующее увеличение неопределенности является незначительным. В этом случае, если свидетельства чрезмерной лабораторной составляющей смещения не обнаружены, уравнение (3) применяют без изменений. Если неопределенность, соответствующая проверке смещения, является большой, целесообразно увеличивать неопределенность, оцененную на основе уравнения (3), например, путем включения в суммарную неопределенность дополнительных членов (см. 2.15).
) и, следовательно, соответствующее увеличение неопределенности является незначительным. В этом случае, если свидетельства чрезмерной лабораторной составляющей смещения не обнаружены, уравнение (3) применяют без изменений. Если неопределенность, соответствующая проверке смещения, является большой, целесообразно увеличивать неопределенность, оцененную на основе уравнения (3), например, путем включения в суммарную неопределенность дополнительных членов (см. 2.15).
Если на основе совместных исследований правильности известно, что метод имеет незначительное смещение, известное смещение метода следует учитывать при оценке лабораторного смещения, например, путем корректировки результатов на известное смещение метода.
6.2.2 Методы демонстрации контролируемости лабораторной составляющей смещения
6.2.2.1 Общие положения
Контролируемость смещения может быть продемонстрирована одним из методов, приведенных в 6.2.2.2-6.2.2.4. Для всех тестов на смещение, приведенных в настоящем стандарте, последовательно используют одни и те же общие критерии. Допускается применение более строгих тестов и проверок.
6.2.2.2 Исследование образца сравнения или эталона стандартного метода измерений
Лаборатория должна выполнить
повторных измерений на эталоне сравнения в условиях повторяемости, чтобы получить оценку смещения на нем
(равную среднему лаборатории
минус паспортное значение
). При этом
следует выбирать так, чтобы неопределенность удовлетворяла неравенству
![]() . Следует заметить, что эталон сравнения в общем случае не является тем же эталоном, который использовали при оценке правильности метода. Кроме того,
. Следует заметить, что эталон сравнения в общем случае не является тем же эталоном, который использовали при оценке правильности метода. Кроме того, , как правило, не равно
. Следуя Руководству ИСО/МЭК 33 (с соответствующим изменением обозначений), процесс измерений выполняется адекватно, если
![]() . (4)
. (4)
Для оценки из неравенства (4) используют оценку
, заданную уравнением (5)
_______________
См. п.4.3 ГОСТ Р ИСО 5725-2-2002 и п.4.2.3 ГОСТ Р ИСО 5725-6-2002.
![]() , (5)
, (5)
где - количество повторений лаборатории
;
- внутрилабораторное стандартное отклонение, полученное на основе
повторений или других исследований повторяемости;
- межлабораторное стандартное отклонение, полученное при совместных исследованиях.
Выполнение неравенства (4) является подтверждением того, что лабораторная составляющая смещения находится в интервале значений, установленном при совместных исследованиях. Следует обратить внимание на то, что образец или эталон сравнения используют здесь для независимой проверки или в качестве контрольного материала, а не для калибровки.
Примечания
1 Лаборатория может применять более строгий критерий, чем неравенство (4), используя коэффициент охвата менее 2 или выполняя более чувствительный метод на выявление смещения.
2 Эти процедуры предполагают, что неопределенность, соответствующая эталонному значению, мала по сравнению с .
6.2.2.3 Сравнение с заданным методом испытаний, обладающим известной неопределенностью
Лаборатории необходимо проверить соответствующее количество
объектов испытаний, применяя заданный метод испытаний и метод, используемый лабораторией, получив, таким образом,
пар (
,
) (
- результат применения заданного метода к
-му объекту, а
- значение, полученное применением обычного для лаборатории метода испытаний для
-го объекта). Затем лаборатория должна вычислить соответствующее среднее смещение
, используя уравнение (6) и стандартное отклонение разностей
![]() [см. (7)]:
[см. (7)]:
![]() , (6)
, (6)
 , (7)
, (7)
где ![]() .
.
На практике значение должно быть выбрано так, чтобы выполнялось неравенство
![]() . По аналогии с (4) и (5) процесс измерений удовлетворяет требованиям, если
. По аналогии с (4) и (5) процесс измерений удовлетворяет требованиям, если ![]() , где
, где ![]() . В этом случае (3) используют без изменений.
. В этом случае (3) используют без изменений.
Примечания
1 Лаборатория может выбирать более строгий критерий, чем неравенство (4), используя коэффициент охвата менее 2 или применяя более чувствительный метод выявления смещения.
2 Эти процедуры предполагают, что стандартная неопределенность, соответствующая эталонному методу, мала по сравнению с и отклонения
![]() принадлежат к совокупности с постоянной дисперсией.
принадлежат к совокупности с постоянной дисперсией.
6.2.2.4 Использование метода при сравнении с другими лабораториями
Если -я лаборатория участвует в дополнительных совместных исследованиях (например, при проверке квалификации в соответствии с ИСО/МЭК 17043), для которых она может оценивать смещение, данные этих исследований можно использовать для контроля смещения. Применяют два возможных варианта.
а) При выполнении испытаний используют эталон или образец сравнения с независимо назначенными значением и неопределенностью. Затем применяют процедуру 6.2.2.2 без изменений.
b) Проводят последовательную проверку соответствия (
1) заданных значений
,
, ...,
. Лаборатория по результатам
,
, ...,
должна рассчитать среднее смещение
в соответствии с (8) и стандартное отклонение
![]() [см. уравнение (9)]:
[см. уравнение (9)]:
![]() , (8)
, (8)
 , (9)
, (9)
где ![]() .
.
Процесс измерений удовлетворяет требованиям, если ![]() , где
, где ![]() . В этом случае (3) используют без изменений.
. В этом случае (3) используют без изменений.
Примечания
1 Эта процедура предполагает, что заданные значения основаны на количестве результатов, превышающем , и обладают незначительной неопределенностью, а отклонения
принадлежат совокупности с постоянной дисперсией.
2 В некоторых схемах проверки квалификации все значения преобразуют в
-значения
![]() , вычитая из
, вычитая из назначенное значение
и деля разность на стандартное отклонение
(см. ИСО/МЭК 17043)
. В этом случае для проверки квалификации стандартное отклонение меньше или равное
для метода и среднее
-значений в пределах
![]() для
для назначенных значений обеспечивают достаточное свидетельство контролируемости смещения. Это удобно для вычислений и обеспечивает меньшую чувствительность к предположению о постоянстве дисперсии (см. примечание 1). Однако это обычно более строгий критерий, чем описанный в 6.2.2.4. Лаборатория может использовать более строгий критерий (см. примечание 3), но вычисления, установленные в 6.2.2.4, необходимы для проверки эквивалентности.
_______________
См. также ГОСТ Р ИСО 13528-2011*.
* Вероятно, ошибка оригинала. Следует читать: ГОСТ Р ИСО 13528-2010. - .
3 Лаборатория может использовать более строгий критерий, чем описанный в 6.2.2.4.
6.2.3 Выявление существенной лабораторной составляющей смещения
Как отмечено в разделе 1, настоящий стандарт применим только в тех случаях, когда лабораторная составляющая смещения находится под контролем. Если обнаружено чрезмерное смещение, предполагается, что должны быть предприняты необходимые действия для приведения смещения в границы требуемого диапазона до продолжения выполнения измерений. Такие действия обычно требуют проведения исследований и устранения причины, вызывающей смещение.
6.3 Верификация повторяемости
6.3.1 Испытательная лаборатория должна продемонстрировать, что ее повторяемость совместима со стандартным отклонением повторяемости, полученным при совместных исследованиях. Для демонстрации этого проводят анализ одного или более соответствующих испытываемых материалов и получают (объединяя результаты при необходимости) стандартное отклонение повторяемости
с
степенями свободы. Значение
необходимо сравнить, используя F-тест с 95% уровнем доверия, со стандартным отклонением повторяемости
, полученным при совместных исследованиях. На практике для получения
15 следует выполнить достаточное количество повторений.
6.3.2 Если значительно больше
, лаборатория должна или идентифицировать и устранить соответствующие причины, либо использовать
вместо
во всех оценках неопределенности, рассчитанных с использованием настоящего стандарта. Следует обратить внимание, что это вызывает увеличение оценки стандартного отклонения повторяемости
, так как
![]() будет заменено на
будет заменено на ![]() (
( является скорректированной оценкой стандартного отклонения воспроизводимости). Если
значительно меньше
, лаборатория может также использовать
вместо
, получая меньшую оценку неопределенности.
Во всех исследованиях прецизионности важно подтверждать, что данные свободны от неизвестных смещений, и проверять постоянство стандартного отклонения для различных объектов испытаний. Если стандартное отклонение
не постоянно, может быть полезно оценивать прецизионность отдельно для каждого класса объектов или построить общую модель (см. 7.5) для этой зависимости.
Примечание - Если требуется сравнение с заданным значением прецизионности, Руководство ИСО 33 более детально описывает соответствующий тест, основанный на ![]() , в котором
, в котором соответствует требуемому значению прецизионности.
6.4 Проверка верификации исполнения метода
Кроме предварительной оценки смещения и прецизионности лаборатория должна принимать необходимые меры для обеспечения статистической контролируемости процедуры измерений. Для этого проводят:
- соответствующий контроль качества исполнения метода измерений, включая регулярные проверки смещения и прецизионности. Для этих проверок могут быть использованы любые уместные устойчивые гомогенные объекты испытаний или материалы. Настоятельно рекомендуется использование контрольных карт (см. [10] и [11]);
_______________
См. также ГОСТ ИСО 5725-6-2002*.
* Вероятно, ошибка оригинала. Следует читать: ГОСТ Р ИСО 5725-6-2002. - .
- мероприятия по обеспечению качества выполнения метода измерений, включая привлечение обученного и квалифицированного персонала, предусмотренные системой менеджмента качества.
Примечание - При использовании контрольных карт стандартное отклонение наблюдений за рассматриваемый период времени должно быть меньше , вычисленного в соответствии с 6.3.2, если прецизионность и смещение находятся под контролем.
7 Учет особенностей объекта испытаний
7.1 Общие положения
В совместных исследованиях или оценке промежуточных показателей прецизионности в соответствии с ИСО 5725-2 и ИСО 5725-3 обычно проводят измерения на гомогенных материалах или объектах небольшого количества типов. Это является обычной практикой для разделения подготовленных для измерений материалов. Однако объекты испытаний могут иметь широкий диапазон возможных изменений, что может требовать дополнительной их обработки до испытаний. Например, образцы для экологических испытаний часто поставляют высушенными и гомогенизированными. Обычные образцы, как правило, являются влажными, неоднородными и грубо разделенными. Соответственно необходимо исследовать образцы и, если необходимо, учитывать различие их состояния.
7.2 Отбор выборки
7.2.1 Процесс отбора выборки
Совместные исследования редко включают этап отбора выборки. Если метод, используемый внутри лаборатории, включает формирование подвыборки или оценивается свойство материала большого объема по образцу малого объема, то влияние отбора выборки необходимо исследовать. При этом возможно использование документации по отбору выборки, например ИСО 11648-1 или других стандартов.
_______________
В соответствии с ГОСТ Р 50779.10-2000 (4.2).
7.2.2 Негомогенность
Негомогенность (неоднородность) обычно исследуют экспериментально с применением дисперсионного анализа (ANOVA) к нескольким объектам испытаний, для которых составляющая дисперсии
, описывающая разброс между объектами, характеризует негомогенность. Если после всех установленных действий по гомогенизации испытываемые материалы признаны существенно неоднородными, эту оценку дисперсии следует преобразовать непосредственно в стандартную неопределенность (то есть
![]() ). В некоторых обстоятельствах, особенно когда стандартное отклонение негомогенности найдено для выборки по
). В некоторых обстоятельствах, особенно когда стандартное отклонение негомогенности найдено для выборки по -объектам, взятым из партии, а средний результат предполагается применять к другим объектам партии, вклад в неопределенности оценивают на основе предикционного интервала [то есть
![]() ]. Можно также теоретически оценивать влияние негомогенности, используя знание процесса отбора выборки и предположений о распределении, соответствующем выборке.
]. Можно также теоретически оценивать влияние негомогенности, используя знание процесса отбора выборки и предположений о распределении, соответствующем выборке.
_______________
Принятая в международной практике аббревиатура для обозначения дисперсионного анализа (Analysis of Variance).
7.3 Подготовка и предварительная обработка
В большинстве исследований образцы являются гомогенными и могут быть дополнительно стабилизированы. Могут потребоваться исследования, позволяющие учитывать воздействия специфических процедур предварительной обработки внутри лаборатории. Как правило, такие исследования устанавливают воздействие этой процедуры на результаты измерений на исследуемых материалах с приблизительно или точно установленными свойствами. Результатом воздействия может быть изменение разброса или появление систематических воздействий. Существенные изменения разброса следует устранять прибавлением соответствующей составляющей к бюджету неопределенности (предполагая, что воздействия увеличивают разброс). Если выявлены существенные систематические воздействия, наиболее удобно устанавливать соответствующий верхний предел. Следуя рекомендациям GUM [16], этот предел можно рассматривать как границу прямоугольного или другого ограниченного симметричного распределения, а оценку стандартной неопределенности можно задавать в виде половины длины области изменений функции распределения, деленной на соответствующий коэффициент.
7.4 Изменение типа объекта испытаний
При необходимости следует исследовать неопределенность, являющуюся результатом изменения типа или состава объекта испытаний по сравнению с используемыми в совместных исследованиях. Как правило, подобные воздействия должны быть предсказаны на основе установленных воздействий, объемных свойств материала (которые дают оценку неопределенности, полученную в соответствии с GUM) или исследованы введением систематических или случайных изменений типа или состава объекта испытаний (см. приложение В).
7.5 Изменение неопределенности в зависимости от уровня отклика
7.5.1 Корректировка
Обычно некоторые или большая часть составляющих неопределенности измерений зависят от измеренного значения. В ИСО 5725-2 рассмотрено три простых случая, когда стандартное отклонение воспроизводимости для положительной величины может быть приближенно описано одной из следующих моделей:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() ; (12)
; (12)
где - скорректированная оценка стандартного отклонения воспроизводимости, рассчитанная по приближенной модели;
,
,
и
- эмпирические коэффициенты, полученные на основе пяти или большего количества различных объектов испытаний с различными средними откликов
(
,
и
являются положительными).
При использовании уравнений (10)-(12) неопределенность должна основываться на оценке воспроизводимости, рассчитанной с использованием соответствующей модели.
В условиях 6.3 оценка должна учитывать измененный вклад члена
, отражающего вклад повторяемости. В большинстве случаев имеет место простое пропорциональное изменение
 , (13)
, (13)
где имеет то же самое значение, как и в 6.3.
7.5.2 Изменение других вкладов в неопределенность
В общем случае, если любая составляющая неопределенности изменяется в соответствии с измеренным откликом предсказуемым способом, соответствующая стандартная неопределенность должна быть откорректирована соответственно.
Примечание - Если вклады в неопределенность прямо пропорциональны , часто бывает удобно выражать все существенные воздействия в терминах мультипликативных воздействий на
, а всю неопределенность - в форме относительных стандартных отклонений.
8 Дополнительные факторы
В разделе 7 рассмотрены основные факторы, различающиеся в совместных исследованиях и обычных испытаниях. Возможно, что в специфических случаях могут проявляться другие воздействия. Это может быть вызвано тем, что контролируемые переменные случайно или преднамеренно рассматривались как постоянные в процессе совместного исследования, или тем, что полный диапазон условий, достижимых в обычной практике, не был охвачен при совместных исследованиях.
Воздействия факторов, которые считаются постоянными или которые недостаточно изменяются при совместных исследованиях, следует оценивать отдельно либо в процессе экспериментального изменения, либо в соответствии с прогнозом на основе теоретических моделей. В тех случаях, когда воздействия являются существенными, неопределенность, связанную с соответствующими факторами, необходимо оценить, зарегистрировать и объединить с другими вкладами обычным способом [то есть суммировать в соответствии с уравнением (3)].
9 Общее выражение для суммарной стандартной неопределенности
При оценке суммарной стандартной неопределенности , соответствующей результату
, и необходимости использовать скорректированную оценку
вместо
, для учета факторов, рассматриваемых в разделе 7, уравнение (3) принимает вид
![]() . (14)
. (14)
Значение подсчитывают в соответствии с уравнением (15) [см. также уравнение (А.8)].
 , (15)
, (15)
где - количество лабораторий;
- количество повторений в каждой лаборатории;
![]() - неопределенность, соответствующая паспортному значению
- неопределенность, соответствующая паспортному значению , используемому для оценки смещения в лабораторных исследованиях.
Переменная не использована в уравнении (14), потому что неопределенность
, соответствующая
, уже включена в
. Индекс
охватывает воздействия, идентифицированные в разделах 7 и 8 (индексы изменяются от 1 до
). Очевидно, что если воздействия и соответствующие им неопределенности малы по сравнению с
, то ими можно пренебречь для большинства практических целей. Например, неопределенность менее
![]() ведет к изменению менее чем на
ведет к изменению менее чем на ![]() оценки полной неопределенности.
оценки полной неопределенности.
10 Бюджет неопределенности, основанный на данных совместных исследований
Настоящий стандарт использует только одну, приведенную в уравнении (3), модель для описания результатов измерений или испытаний. Информация, подтверждающая справедливость модели, может быть получена из различных источников, но если неопределенность, соответствующая испытаниям, остается незначительной, используют уравнение (3). Однако существует несколько различных ситуаций, для которых уравнение (3) принимает несколько иной вид, например, в случае, когда параметры воспроизводимости или повторяемости зависят от отклика. Бюджет неопределенности, если неопределенность совсем не зависит от отклика в исследуемом диапазоне, приведен в таблице 1, а для случая, когда неопределенность зависит от отклика, - в таблице 2.
Таблица 1 - Составляющие неопределенности, не зависящие от отклика
Источник воздействия | Стандартная неопределенность | Примечание |
Используют в случае, если смещение, выявленное при совместных исследованиях, устранено, а неопределенность является существенной | ||
См. таблицу 2 | ||
Если среднее, полученное по | ||
| См. раздел 7 и приложение В | |
| ||
Таблица 2 - Составляющие неопределенности, зависящие от отклика
Источник воздействия | Стандартная неопределенность | Примечание |
| Используют только в случае, когда выявленное при совместном исследовании смещение устранено, а неопределенность является существенной. (Производную используют, чтобы охватить случаи, когда устранение смещения не сводится к простому сложению или вычитанию) | |
|
Данная форма применима только в случае, когда установлена зависимость | |
|
Если среднее, полученное по Эта форма применима только в случае, когда установлена зависимость | |
|
|
Эту объединенную оценку следует использовать вместо отдельных оценок |
| См. раздел 7 и приложение В | |
| ||
11 Оценка неопределенности комбинированного результата
11.1 Комбинированный результат формируют из совокупности результатов различных испытаний, каждый из которых охарактеризован совместными исследованиями. Например, анализ состава мяса обычно включает определение содержания в мясе белка (рассчитанного путем определения содержания в мясе азота), жира и воды. При этом содержание каждой составляющей определяют соответствующим стандартным методом.
11.2 Неопределенность для каждого результата
может быть получена на основе принципов, установленных в настоящем стандарте или непосредственно, используя уравнения (А.1) или (А.2) соответственно. Если величины
независимы, суммарную неопределенность
для результата
![]() вычисляют по формуле
вычисляют по формуле
![]() . (16)
. (16)
Если не являются независимыми, должны быть сделаны предположения относительно корреляции в соответствии с GUM [также использующим уравнение (А.2)].
12 Представление информации о неопределенности
12.1 Общие положения
Неопределенность может быть представлена в виде суммарной стандартной неопределенности или расширенной неопределенности
![]() (
( - коэффициент охвата) (см. 12.2 и GUM). В некоторых случаях удобно представить неопределенность в относительных величинах в виде коэффициента вариации или расширенной неопределенности в процентах от зарегистрированных значений результатов.
12.2 Выбор коэффициента охвата
12.2.1 Общие положения
При оценке суммарной расширенной неопределенности применяют следующие исследования для выбора коэффициента охвата .
12.2.2 Уровень доверия
Для практических целей должно быть указано значение суммарной расширенной неопределенности, соответствующее уровню доверия 95%. Однако выбор уровня доверия зависит от диапазона факторов, таких как критичность и последствия применения неправильных результатов. Эти факторы вместе с любыми рекомендациями или юридическими требованиями, касающимися применения, должны быть рассмотрены при выборе .
12.2.3 Число степеней свободы, соответствующих оценке
12.2.3.1 Для большинства практических целей, когда требуется 95%-ный уровень доверия и число степеней свободы в доминирующих составляющих неопределенности превышает 10 (10), выбор
2 обеспечивает достаточно надежный охват вероятного диапазона значений. Однако есть обстоятельства, в которых это приводит к существенно заниженной оценке, особенно когда один или более значимых членов уравнения (14) имеют число степеней свободы менее 7.
12.2.3.2 Если один такой член с
степенями свободы доминирует [признаком является выполнение неравенства
![]() ], обычно достаточно выбрать в качестве
], обычно достаточно выбрать в качестве , эффективное число степеней свободы
, соответствующее
.
12.2.3.3 Если несколько значимых членов имеют приблизительно равную величину и число степени свободы, удовлетворяющее условию 10, для получения эффективных значений числа степеней свободы
следует применять уравнение Велча - Саттервейта [см. уравнение (17)]
 . (17)
. (17)
Значение в этом случае выбирают на основе
, используя значение квантиля двустороннего распределения Стьюдента
для требуемого уровня доверия и
степеней свободы. Это наиболее безопасно при округлении нецелых значений
до ближайшего меньшего целого числа.
Примечание - Во многих областях измерений и испытаний для нормального распределения частота статистических выбросов является достаточно высокой, поэтому применение высоких уровней доверия (95%) без хорошего знания распределения не рекомендуется.
13 Сравнение данных выполнения метода и неопределенности
13.1 Основные предположения
Оценка неопределенности измерений в соответствии с настоящим стандартом обеспечивает стандартную неопределенность, которая хотя и основывается прежде всего на оценках воспроизводимости или промежуточной прецизионности, отдает должное факторам, которые не изменяются в процессе исследований, в которых эти оценки прецизионности получены. В идеале итоговая стандартная неопределенность должна быть идентична неопределенности, полученной на основе детальной математической модели процесса измерений. Сравнение этих двух оценок, если это возможно, обеспечивает полезную проверку качества оценки. Рекомендованная процедура описана в 13.2.
Процедура основана на двух важных предположениях:
- во-первых, оценку стандартной неопределенности с
степенями свободы обычно определяют в предположении о нормальном распределении наблюдений [это означает, что
![]() подчиняется
подчиняется -распределению с
![]() степенями свободы]. Это предположение позволяет использовать F-критерий. Однако, поскольку суммарная неопределенность может включать неопределенность, связанную с величинами, описываемыми распределениями различной формы с различными дисперсиями, результаты испытаний необходимо рассматривать как индикатор, а уровень доверия следует выбирать с необходимой осторожностью;
степенями свободы]. Это предположение позволяет использовать F-критерий. Однако, поскольку суммарная неопределенность может включать неопределенность, связанную с величинами, описываемыми распределениями различной формы с различными дисперсиями, результаты испытаний необходимо рассматривать как индикатор, а уровень доверия следует выбирать с необходимой осторожностью;
- во-вторых, обычно предполагают, что две оценки неопределенности, которые будут сравнивать, полностью независимы. Это также маловероятно на практике, так как некоторые факторы могут быть общими для обеих оценок. Более тонкие воздействия являются предметом исследований для выявления влияния составляющей неопределенности, соответствующей выполнению работ в разных лабораториях. Предполагается, что приняты необходимые меры предосторожности, чтобы избежать этого воздействия. Если значимые факторы являются общими для обеих оценок неопределенности, очевидно, что оценки будут подобны значительно чаще. В этом случае, если последовательные испытания не позволяют выявлять существенных различий, результаты не следует трактовать как свидетельство адекватности модели измерений.
13.2 Процедура сравнения
Для сравнения двух оценок и
![]()
![]() с эффективными числами степеней свободы
с эффективными числами степеней свободы и
соответственно и уровнем доверия
(например, для 95%-ного уровня доверия
0,05) необходимо выполнить следующие действия.
a) Вычислить ![]() .
.
b) Найти по таблицам или получить с помощью программного обеспечения одностороннее верхнее критическое значение ![]() . Если даны верхнее и нижнее значения, выбирают верхнее значение, которое всегда больше 1;
. Если даны верхнее и нижнее значения, выбирают верхнее значение, которое всегда больше 1;
c) Если ![]() , то
, то следует считать значительно больше
![]() .
.
13.3 Причины различий
Существует много причин для существенного различия между оценками суммарной неопределенности. Они включают:
- наличие различий в работе лабораторий;
- использование модели, не учитывающей влияния всех существенных воздействий на измерения;
- неверное определение оценки значимости вклада в неопределенность.
Приложение А
(справочное)
Подходы к оценке неопределенности
А.1 Подход GUM
В руководстве по выражению неопределенности измерений (GUM) установлена методология оценки неопределенности измерений результата в соответствии с моделью процесса измерений. Методология GUM основана на рекомендациях Международной палаты мер и весов (BIPM) [20], в соответствии с которыми составляющие неопределенности оценивают либо на основе статистического анализа серии наблюдений (оценка типа А), либо другими способами (оценка типа В), например, используя данные публикаций о неопределенности измерений образцов или эталонов сравнения или мнения специалистов. Отдельные составляющие выражают в виде стандартных отклонений и при необходимости затем объединяют.
Выполнение рекомендаций BIPM в GUM начинается с построения модели измерений в виде функции ![]() , связывающей результат измерений
, связывающей результат измерений со входными величинами
. Тогда в случае независимых входных величин GUM дает неопределенность
в соответствии с уравнением
 , (A.1)
, (A.1)
где - коэффициент чувствительности, оцениваемый в соответствии с уравнением
![]() , (частная производная
, (частная производная по
);
и
- стандартные неопределенности (неопределенности измерений в виде стандартных отклонений)
и
соответственно.
Если входные величины не являются независимыми, выражение для неопределенности является более сложным и определяется уравнением
 , (А.2)
, (А.2)
где ![]() - ковариация между
- ковариация между и
;
и
- коэффициенты чувствительности, соответствующие уравнению (А.1).
На практике часто ковариацию выражают через коэффициент корреляции
![]() , (А.3)
, (А.3)
где - 1![]() 1.
1.
В случаях, учитывающих нелинейность модели измерений, в уравнение (А.1) включают члены более высокого порядка. Эта ситуация более подробно описана в GUM.
После вычисления комбинированной стандартной неопределенности с использованием уравнений (А.1)-(А.3) расширенную неопределенность определяют умножая на коэффициент охвата
, который выбирают на основе числа степеней свободы для
. Более подробно это описано в разделе 12.
В подходе GUM существует неявное предположение, что входные данные измерены или назначены. Если существуют воздействия (например, воздействие оператора), которые могут быть не определены через измеримые величины, удобно сформировать суммарную стандартную неопределенность , которая учитывает такие воздействия, или ввести дополнительные переменные в
![]() .
.
Из-за ориентации на входные величины этот подход иногда называют восходящим подходом оценки неопределенности.
Физическая интерпретация не является однозначной. Поскольку при оценке неопределенности могут быть использованы экспертные оценки, то
можно рассматривать как функцию, характеризующую степень доверия. Однако можно получить более прямую физическую интерпретацию, определив стандартное отклонение результатов вычисления
, которое было бы получено, если бы все входные переменные изменялись случайным образом в соответствии с принятыми для них распределениями.
А.2 Принцип совместных исследований
А.2.1 Основная модель
Планирование эксперимента при совместных исследованиях, их организация и статистическая обработка подробно описаны в ИСО 5725-1 - ИСО 5725-6. Самая простая модель, лежащая в основе статистической обработки данных совместных исследований, задается уравнением (обозначения по ИСО 5725)
![]() , (А.4)
, (А.4)
где - математическое ожидание
;
- лабораторная составляющая смещения в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением
;
- случайная погрешность в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением
.
Кроме того, предполагается, что и
некоррелированы.
Применение уравнения (А.1) к простой модели дает уравнение (А.5) для единственного результата
![]() . (А.5)
. (А.5)
Поскольку и
являются дисперсиями, соответствующими
и
, и их оценивают с помощью дисперсии между лабораториями
и дисперсии повторяемости
, полученных в процессе межлабораторных исследований, так что
![]() и
и ![]() , возможно получить уравнение (А.6) для суммарной стандартной неопределенности результата
, возможно получить уравнение (А.6) для суммарной стандартной неопределенности результата
![]() . (А.6)
. (А.6)
По сравнению с ИСО 5725-2 уравнение (А.6) представляет собой лишь оценку стандартного отклонения воспроизводимости .
Так как этот подход ориентируется на полное выполнение метода, его называют иногда нисходящим подходом.
Следует учитывать, что каждая лаборатория вычисляет свою оценку по уравнению ![]() , полагая ее наилучшей оценкой измеряемой величины
, полагая ее наилучшей оценкой измеряемой величины для лаборатории. Тогда, если
![]() - общая модель, используемая для описания поведения измерительной системы, то, следовательно, при вычислении
- общая модель, используемая для описания поведения измерительной системы, то, следовательно, при вычислении предполагается, что дисперсии, характеризующиеся оценками
и
, являются результатом изменения величин
![]() . Если предполагается, что условия воспроизводимости обеспечиваются для случайной величины при всех существенных воздействиях и применяется физическая интерпретация
. Если предполагается, что условия воспроизводимости обеспечиваются для случайной величины при всех существенных воздействиях и применяется физическая интерпретация , приведенная выше, то из этого следует, что
в уравнении (А.6) является оценкой
, описанной уравнениями (А.1) или (А.2).
Стандартное отклонение воспроизводимости, полученное в совместном исследовании, является основой для оценки неопределенности измерений (первый принцип, на котором основан настоящий стандарт).
А.2.2 Включение данных правильности
Правильность в общем случае измеряется смещением относительно принятого опорного значения. В некоторых совместных исследованиях правильность метода в конкретной системе измерений (обычно СИ) исследуют путем анализа образца сравнения (CRM) или эталона единицы физической величины с паспортным значением
, выраженным в единицах этой системы (ИСО 5725-4). Итоговая статистическая модель определяется уравнением
_______________
CRM - certified material.
![]() , (А.7)
, (А.7)
где - паспортное значение;
- смещение метода.
Совместное исследование может дать оценку смещения со стандартным отклонением
, рассчитанным по формуле
 , (А.8)
, (А.8)
где - количество лабораторий;
- количество повторений в каждой лаборатории.
Неопределенность , соответствующая этому смещению, задается уравнением
![]() , (A.9)
, (A.9)
где - неопределенность, соответствующая паспортному значению
, используемому для оценки правильности при совместном исследовании.
Если смещение, оцененное в процессе испытаний, используют при вычислении результатов в лабораториях, соответствующую ему неопределенность (если она является значительной) следует включать в бюджет неопределенности.
А.2.3 Другие воздействия. Объединенная модель
На практике и
необязательно включают все изменения, влияющие на результаты измерений. Отсутствие некоторых важных факторов вызвано характером совместных исследований; некоторые факторы могут отсутствовать или не оцениваться случайно или в соответствии с планом эксперимента. Второй принцип, на котором основан настоящий стандарт, состоит в том, что воздействия, не наблюдаемые в процессе совместного исследования или являются незначительными, или должны быть учтены.
Проще всего учесть эти воздействия, рассматривая воздействия отклонений от номинальных значений
, необходимых для получения оценки
, предполагая приближенную линейность этих воздействий. Объединенная модель описывается уравнением
![]() . (А.10)
. (А.10)
Суммирование ведется по всем воздействиям, кроме представленных в ,
,
.
Примеры включают воздействие отбора выборки, подготовки испытаний объекта и изменения состава или типа отдельных объектов испытаний. В строгом смысле это линеаризованная форма самой общей модели. При необходимости можно включать в нее члены более высокого порядка или члены, учитывающие корреляцию, как описано в [1].
Очевидно, что центрирование не оказывает влияния на
, так как
![]() из чего следует, что для оценки неопределенности, соответствующей
из чего следует, что для оценки неопределенности, соответствующей , можно использовать уравнение (А.10) и следующее уравнение
![]() . (A.11)
. (A.11)
Суммирование ведется по воздействиям, не учтенным в других членах уравнения.
Следует отметить, что при оценке выполнения метода условия промежуточной прецизионности также могут быть описаны уравнением (А.10), хотя число членов суммы соответственно будет больше, поскольку по сравнению с условиями воспроизводимости в промежуточных условиях меньшее количество переменных будет меняться случайным образом. В общем случае уравнение (А.10) можно применять к любым условиям прецизионности, учитывая, что воздействия суммируются. В случае, когда и
равны нулю, а неопределенность общего смещения не определена, уравнение (А.11) становится идентичным уравнению (А.1).
Из этого следует два вывода:
- во-первых, необходимо продемонстрировать, что количественные данные, доступные для совместного исследования, согласуются с рассматриваемыми результатами испытаний;
- во-вторых, даже при согласованности данных совместного исследования для определения реальной оценки неопределенности с учетом дополнительных воздействий [ в уравнении (А.10)] могут быть необходимы дополнительные исследования и предположения. При учете дополнительных воздействий предполагается применение уравнения (А.1).
И, наконец, в настоящем стандарте для утверждения, что надежную оценку неопределенности измерений можно получить на основе анализа данных повторяемости, воспроизводимости и правильности, полученных в соответствии с ИСО 5725-1 - ИСО 5725-6, использованы те же предположения, что и в перечисленных стандартах.
a) Если используются данные воспроизводимости, предполагается, что все лаборатории подобны по выполнению работ. В частности, их прецизионность повторяемости для данного объекта испытаний одинакова, а лабораторная составляющая смещения в уравнении (А.10) соответствует тому же распределению, что и при совместных исследованиях.
b) Испытываемые материалы, используемые в исследовании, являются гомогенными и стабильными.
А.3 Сопоставление подходов
Приведенные рассуждения описывают два различных подхода к оценке неопределенности. Подход GUM описывает неопределенность в виде дисперсии, полученной на основе дисперсий входных данных, соответствующих математической модели. Другой подход использует факт, что, если одни и те же воздействия заметно изменяются в процессе исследования воспроизводимости, наблюдаемая дисперсия является оценкой исследуемой неопределенности. На практике значения неопределенности, полученные на основе различных подходов, различны для разных целей, включая:
a) неполные математические модели (т.е. при наличии неизвестных воздействий);
b) неполное или несущественное изменение всех воздействующих факторов в процессе оценки воспроизводимости.
Сравнение двух различных оценок поэтому полезно для оценки полноты модели измерений. Однако следует обратить внимание, что наблюдаемую повторяемость или другую оценку прецизионности очень часто рассматривают как отдельную составляющую неопределенности даже в подходе GUM. Точно так же индивидуальные воздействия обычно проверяют на их значимость или оценивают количественно до оценки воспроизводимости. На практике для оценки неопределенности часто используют некоторые элементы обоих подходов.
Когда оценка неопределенности для интерпретации сопровождается результатами, важно, чтобы пробелы в каждом подходе были заполнены. Возможности неполных моделей на практике обычно дополняют гарантированными оценками, расширяющими неопределенность модели. В настоящих рекомендациях для устранения неадекватных изменений входных воздействий рекомендуется определять оценки дополнительных воздействий. Это является гибридным подходом, объединяющим элементы и нисходящего и восходящего подходов.
Приложение В
(справочное)
Экспериментальная оценка неопределенности
В.1 Процедура оценки коэффициента чувствительности
Если входные величины могут изменяться непрерывно по всему диапазону значений, рекомендуется исследовать воздействие таких изменений. Простая процедура, предполагающая приблизительно линейную зависимость результатов от
следующая:
a) выбирают диапазон изменения переменной который должен быть ориентирован на лучшую оценку (или на значение, характерное для указанного метода);
b) выполняют всю процедуру измерений (или ту часть, которая касается ) в каждом из пяти или более уровней
с повторением при необходимости;
c) рассчитывают и изображают линейную модель в соответствии с результатами, используя в качестве абсциссы, а результат измерений в качестве ординаты;
d) используют коэффициент чувствительности, равный угловому коэффициенту в уравнениях (А.1) или (14).
Этот подход может дать различные коэффициенты чувствительности для различных объектов испытаний.
Это может быть преимуществом во всесторонних исследованиях конкретного объекта или класса объектов. При этом если коэффициент чувствительности должен быть применен к большому диапазону различных ситуаций, важно убедиться, что различные объекты ведут себя аналогично.
В.2 Простая процедура оценки неопределенности, вызванной случайным воздействием
Если входные величины являются дискретными и/или неконтролируемыми, соответствующую неопределенность можно получить на основе анализа экспериментов, в которых переменная изменяется случайным образом. Например, состав почвы в экологических исследованиях может иметь непредсказуемое воздействие на результаты анализа. Если случайные ошибки не зависят от уровня исследуемой величины, можно исследовать дисперсию ошибки, являющейся результатом таких изменений, используя серию объектов, для которых заданное значение или доступно, или, если изменение известно, может быть получено теоретически.
Общая процедура включает в себя:
a) выполнение полного измерения на представительном наборе объектов испытаний в условиях повторяемости, используя равное количество повторений для каждого объекта;
b) вычисление разности с заданным значением для каждого наблюдения;
c) проведение анализа результатов (ранжированных по величине) в соответствие с ANOVA с использованием суммы квадратов для формирования оценок внутригрупповой составляющей дисперсии и межгрупповой составляющей дисперсии
. Стандартная неопределенность
![]() являющаяся результатом изменения
являющаяся результатом изменения , равна
.
Примечание - Если различные объекты или классы объектов по-разному реагируют на исследуемую величину (то есть существует взаимосвязь величины и класса исследуемых объектов), взаимодействие увеличивает значение . Детальное исследование этой ситуации в настоящем стандарте не приводится.
Приложение С
(справочное)
Примеры расчета неопределенности
С.1 Измерение содержания монооксида углерода (CO) в выхлопных газах автомобиля
С.1.1 Введение
До поставки на рынок легковые автомобили должны проходить испытания типа транспортного средства для проверки выполнения обязательных требований относительно количества угарного газа в выхлопных газах. (Верхний допустимый предел составляет 2,2 г/км). Метод испытаний описан в Директиве ЕН 70/220 [21], где введены следующие требования:
- цикл двигателя задается как функция скорости (км/ч), времени (с) и оборотов двигателя. Исследуемый автомобиль помещают на специальный стенд для выполнения заданного количества циклов;
- измерительное оборудование - газоанализатор ;
- контроль окружающей среды проводят с использованием специальной камеры мониторинга загрязнений;
- персонал имеет специальную подготовку.
Такие испытания на соответствие установленным требованиям можно выполнять в испытательной лаборатории предприятия по производству автомобилей или в независимой испытательной лаборатории.
С.1.2 Данные совместных исследований
Перед принятием и использованием такого метода испытаний необходимо оценить факторы или источники, влияющие на результаты испытаний (и, следовательно, на неопределенность результатов испытаний). Такая оценка выполнялась по данным экспериментов, проводимых в различных лабораториях. Для контроля метода испытаний межлабораторный эксперимент проводился в соответствии с ИСО 5725-2. Цель межлабораторного эксперимента состоит в том, чтобы оценить прецизионность метода испытаний при применении его в данном наборе испытательных лабораторий. Оценка прецизионности получена на основе данных, собранных в межлабораторном эксперименте со статистическим анализом в соответствии с ИСО 5725-2. Исследования проведены так, чтобы каждый участник выполнял все необходимые процессы измерений и учитывал воздействующие факторы.
Было установлено, что повторяемость в лабораториях значимо не различается, а оценка стандартного отклонения повторяемости метода испытаний равна 0,22 г/км. Оценка стандартного отклонения воспроизводимости метода испытаний равна 0,28 г/км.
С.1.3 Контроль смещения
Оценка правильности (контроль смещения по отношению к эталону) включает методологические и технические вопросы. Не существует "эталонного автомобиля" как образца сравнения. Правильность следует контролировать при калибровке оборудования системы испытаний. Например, калибровку анализатора можно выполнять с помощью эталонного газа, а калибровку испытательного стенда можно выполнять для таких величин, как время, расстояние, скорость и ускорение. Знание норм выбросов выхлопных газов для различных скоростей и наличие другой аналогичной информации подтверждают, что неопределенность, связанная с этими калибровками, не дает существенных вкладов в неопределенность, связанную с результатами измерений (то есть вся расчетная неопределенность много меньше, чем стандартное отклонение воспроизводимости). Смещение находится под контролем.
С.1.4 Прецизионность
Повторные испытательные пробеги в лаборатории показали, что разброс содержания в выхлопных газах (повторяемость) не превышает 0,20 г/км и находится в пределах диапазона повторяемости, найденного при межлабораторном исследовании. Таким образом, прецизионность находится под контролем.
С.1.5 Соответствие объектов испытаний
Метод признают подходящим для всех транспортных средств, относящихся к легковым автомобилям. Поскольку неопределенность имеет тенденцию уменьшаться для более низких уровней выхлопных газов, неопределенность наиболее важна на уровнях, близких к установленной границе. Поэтому было решено использовать оценку неопределенности, равную установленной границе, как корректную и несколько консервативную (гарантированную) оценку неопределенности для более низких уровней выделения . Необходимо заметить, если испытания транспортного средства показывают выхлоп существенно больше установленной границы, может оказаться необходимым проведение дополнительных исследований неопределенности, если сравнения являются критичными. На практике, однако, такое транспортное средство нельзя предлагать для продажи без его модернизации.
С.1.6 Оценка неопределенности
Поскольку предшествующие исследования установили хорошую контролируемость смещения и прецизионности в пределах испытательной лаборатории, а также отсутствие воздействующих факторов, не учтенных при совместных исследованиях, стандартное отклонение воспроизводимости, используемое для оценки стандартного отклонения неопределенности, дает расширенную неопределенность 0,56 г/км (
2) для уровня доверия 95%.
Примечание - Интерпретация неопределенности результатов в области проверки соответствия рассмотрена в ИСО 10576-1.
______________
См. также п.4.2.2 (примечание 2) ГОСТ Р ИСО 5725-6-2002.
С.2 Определение состава мяса
С.2.1 Введение
Для продукции из мяса необходимо гарантировать, что состав мяса соответствует заявленному. Состав мяса определяют как комбинацию содержания азота (преобразованного к общему белку) и жира. Представленный пример показывает принцип объединения различных составляющих неопределенности, каждую из которых непосредственно определяют из оценок воспроизводимости, как описано в разделе 11.
С.2.2 Основные уравнения
Полный состав мяса определяют в соответствии с уравнением
![]() , (C.1)
, (C.1)
где - общий белок в мясе, выраженный в виде процента массы;
- общее содержание жира, выраженное в виде процента массы.
Белок в мясе вычисляют по формуле
![]() , (C.2)
, (C.2)
где - коэффициент содержания азота, соответствующий исследуемому материалу;
- полное содержание азота в мясе.
В этом случае идентично общему содержанию азота
, определяемому в соответствии с анализом Кьельдаля.
С.2.3 Этапы эксперимента по определению состава мяса
При определении состава мяса выполняют следующие действия:
a) определяют содержание жира ;
b) определяют содержание азота по Кьельдалю (среднее дублированных измерений);
c) вычисляют содержание обезжиренного мяса и
[уравнение (С.2)];
d) вычисляют общий состав мяса [уравнение (С.1)].
С.2.4 Составляющие неопределенности
Составляющие неопределенности соответствуют каждой из величин, перечисленных в С.2.3. Наиболее существенным является , составляющий приближенно 90% массы
. Наибольшая неопределенность, соответствующая
, является результатом:
a) неопределенности коэффициента , вызванной неполным знанием исследуемого материала;
b) отклонений метода в условиях воспроизводимости при повторении метода и при точном выполнении метода в течение длительного времени;
c) неопределенности, вызванной смещением метода;
d) неопределенности, соответствующей содержанию жира .
Примечание - Неопределенности, указанные в перечислениях а), b) и с) относятся к образцу лаборатории и методу соответственно. Часто бывает полезно грубо рассмотреть каждую из этих трех составляющих при идентификации неопределенности, а также неопределенность, соответствующую отдельным этапам процедуры.
С.2.5 Оценка составляющих неопределенности
С.2.5.1 Неопределенность, соответствующая
Неопределенность, соответствующая , может быть оценена по приведенным в публикациях значениям. В [22] приведены результаты исследований содержания азота в говядине, которые показывают четкие различия между данными, полученными при исследовании образцов мяса от различных поставщиков и кусков мяса. В [22] также даны рекомендации по вычислению наблюдаемого стандартного отклонения для
0,052 и относительного стандартного отклонения 0,014 для большого диапазона типов выборок.
Примечание - Непосредственно применены данные содержания азота, определенные в [22], полученные с использованием метода Кьельдаля.
С.2.5.2 Неопределенность, соответствующая
Информация о двух совместных испытаниях [22], [23] позволяет получить оценку неопределенности, вызванной низкой воспроизводимостью или ошибками выполнения метода. Тщательная проверка условий испытаний показывает, во-первых, что каждое исследование проводят по широкому диапазону типов выборки и с хорошим репрезентативным набором компетентных лабораторий, а во-вторых, что стандартное отклонение воспроизводимости хорошо коррелирует с уровнем азота. Для обоих испытаний наиболее подходящая линейная функция задается уравнением
![]() . Кроме того, исследование показывает, что стандартное отклонение повторяемости пропорционально
. Кроме того, исследование показывает, что стандартное отклонение повторяемости пропорционально с
![]() и
и ![]() .
.
Метод таков, что каждое измерение повторяют и определяют выборочное среднее. Член, соответствующий повторяемости, который представляет собой оценку повторяемости единственного результата, должен быть соответствующим образом приспособлен для учета воздействия среднего двух результатов в лаборатории (см. комментарий, относящийся к в таблице 1). Неопределенность
![]() , соответствующая содержанию азота, имеет вид
, соответствующая содержанию азота, имеет вид
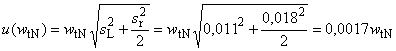 . (C.3)
. (C.3)
Уравнение (С.3) дает лучшую оценку неопределенности с , соответствующей разумным изменениям при выполнении метода.
Воспроизводимость также используют в качестве критерия оценки прецизионности отдельной лаборатории. Метод устанавливает, что результаты должны быть отброшены, если данные попадают вне 95%-ного доверительного интервала (с границами приблизительно равными ![]() ). Эта проверка гарантирует, что внутрилабораторная прецизионность соответствует прецизионности совместного исследования.
). Эта проверка гарантирует, что внутрилабораторная прецизионность соответствует прецизионности совместного исследования.
Примечание - Если эта проверка показывает отрицательный результат чаще, чем в 5% случаев, вероятно, что контролируемость прецизионности недостаточна и необходимы действия по корректировке процедуры.
Необходимо также рассмотреть неопределенность, соответствующую и являющуюся результатом воздействия неизвестного смещения метода. В отсутствии надежных образцов сравнения сравнение с альтернативными методами, использующими другие принципы, является установленным средством оценки смещения. Сравнение метода Кьельдаля с методом анализа при сжигании образца для определения полного азота и различных типов выборки установило различие
![]() . Это удовлетворяет критерию
. Это удовлетворяет критерию [см. Руководство ИСО 33, уравнение (4)], подтверждающему, что неопределенность, вызванная смещением, адекватно подсчитана для данных воспроизводимости.
С.2.5.3 Неопределенность, соответствующая
Дополнительные данные совместных испытаний для анализа жира [25] дают оценку стандартного отклонения воспроизводимости ![]() . Анализ снова выполняют дважды, а результаты принимают только в случае, если разность находится в соответствующих пределах повторяемости, гарантируя, что лабораторная прецизионность находится под контролем. Предшествующая верификация работы на соответствующем образце сравнения для определения жира устанавливает, что неопределенность, связанная со смещением, адекватна значениям воспроизводимости.
. Анализ снова выполняют дважды, а результаты принимают только в случае, если разность находится в соответствующих пределах повторяемости, гарантируя, что лабораторная прецизионность находится под контролем. Предшествующая верификация работы на соответствующем образце сравнения для определения жира устанавливает, что неопределенность, связанная со смещением, адекватна значениям воспроизводимости.
С.2.6 Суммарная неопределенность
В таблице С.1 приведены значения и неопределенность, подсчитанная с использованием этих значений.
Таблица С.1 - Бюджет неопределенности для состава мяса
Наименование показателя | Значение показателя | ||
|
| ||
Содержание жира | 5,50 | 0,110 | 0,020 |
Содержание азота | 3,29 | 0,056 | 0,017 |
Коэффициент | 3,65 | 0,052 | 0,014 |
Белок | 90,1 | 90,1·0,022=1,98 |
|
Общий состав мяса | 95,6 |
| 0,021 |
При определении расширенной неопределенности для уровня доверия 95% суммарную стандартную неопределенность умножают на коэффициент охвата , равный 2. При округлении до двух знаков после запятой получают расширенную неопределенность на состав мяса
4,0%; то есть
![]() (95,6±4,0)%.
(95,6±4,0)%.
Примечание - В соответствии с приведенными расчетами в некоторых случаях содержание мяса может превышать 100%.
С.3 Неопределенность метода АОАС 990.12 (с применением пластин для подсчета аэробных бактерий)
С.3.1 Введение
Метод представляет собой микробиологический метод анализа микробной деятельности в продуктах [27]. Метод использует пластины для бактериальной культуры в виде сухой среды и растворимого в воде геля. Пробы наносят на пластины в количестве 1,0 мл на пластину и распределяют по площади приблизительно на 20 см. После инкубации подсчитывают количество колоний. Измеряемой величиной является количество формирующихся колоний. Для получения значений, отличных от нуля, в качестве результатов использован
(количество колоний)
полученного количества колоний, т.е. логарифм с основанием 10 от количества формирующихся колоний (CFU
). Оценка неопределенности необходима для трех изготовителей продуктов питания: поставщиков моллюсков, муки и овощей.
_______________
![]() .
.
CFU - colony-forming units.
Пример основан на данных документа [28]. (Руководства A2LA).
С.3.2 Совместные данные исследования
Метод утвержден на основе совместных исследований восьмью лабораториями, шести образцов продуктов с различными уровнями загрязнения, по две пробы на образце продукта и два повторения на пробу. Проведение анализа данных в соответствии с требованиями ИСО 5725-2 и исследование ратификации включало все этапы проверки за исключением этапа определения точного размера подвыборки (измеренные пробы были получены в совместном исследовании). В таблице С.2 приведены зафиксированные оценки стандартных отклонений для повторяемости и воспроизводимости, соответствующие этим трем видам продуктов в процентах.
Таблица С.2 - Данные совместных исследований аэробных бактерий в пределах
Пища | Стандартное отклонение воспроизводимости, % | Стандартное отклонение повторяемости, % |
Креветки | 11,1 | 9,8 |
Овощи | 9,2 | 6,3 |
Мука | 5,8 | 5,3 |
Данные повторяемости и воспроизводимости представлены в виде стандартных отклонений относительно среднего наблюдаемого значения для (количество колоний). Это удобно для данного метода, у которого разброс значений приблизительно пропорционален наблюдаемым значениям и относительное стандартное отклонение является приблизительно устойчивым.
С.3.3 Контроль смещения
Чтобы установить, находится ли лабораторное смещение в ожидаемых пределах, лаборатория выполняет сравнение своих результатов с результатами эталонной лаборатории. Результаты для овощей и креветок всегда находятся в пределах ±10% (![]() ,
, - среднее соответствующих наблюдений). Сравнение результатов для муки показывает результат ±5% (
![]() ). Эти отклонения совместимы со стандартным отклонением воспроизводимости, поэтому смещение является приемлемым.
). Эти отклонения совместимы со стандартным отклонением воспроизводимости, поэтому смещение является приемлемым.
С.3.4 Контроль прецизионности
Чтобы установить, находится ли прецизионность в пределах ожидаемых границ, в лаборатории определяют оценки стандартного отклонения повторяемости по сериям из 10 повторений. Стандартное отклонение повторяемости для всех видов продукции составляет не более 5% (![]() ). Поэтому принято решение, что повторяемость является не только приемлемой, но и является ниже соответствующей скорректированной воспроизводимости (см. 6.3.2). Стандартные отклонения воспроизводимости приведены в таблице С.3.
). Поэтому принято решение, что повторяемость является не только приемлемой, но и является ниже соответствующей скорректированной воспроизводимости (см. 6.3.2). Стандартные отклонения воспроизводимости приведены в таблице С.3.
Таблица С.3 - Скорректированные стандартные отклонения воспроизводимости
Продукт | Стандартное отклонение воспроизводимости, % | Относительное стандартное отклонение между лабораториями, % | Относительное стандартное отклонение повторяемости, % | Скорректированное стандартное отклонение воспроизводимости, % |
Креветки | 11,1 | 5,2 | 5,0 | 7,2 |
Овощи | 9,2 | 6,7 | 5,0 | 8,4 |
Мука | 5,8 | 2,4 | 5,0 | 5,5 |
С.3.5 Обоснование выбора объекта испытаний
С.3.5.1 Подготовка образцов и предварительная обработка
Совместное исследование исключило стадию отбора проб. С учетом этого подготовка образцов (отбор подвыборки, взвешивание) вносит дополнительно 3,0% в суммарную стандартную неопределенность (на основе мнений экспертов). Этот вклад приведен в таблице С.4.
С.3.5.2 Изменение неопределенности в зависимости от уровня отклика
Воспроизводимость, повторяемость и вклад дополнительных этапов подготовки образцов приблизительно пропорциональны количеству колоний аэробных бактерий на пластине. Поэтому основная модель может иметь форму уравнения (10), в котором коэффициент равен скорректированному относительному стандартному отклонению воспроизводимости, а дополнительный вклад отбора выборки включен как пропорциональный вклад. Это эквивалентно простому подходу (используемому выше) представления всех вкладов в неопределенность в виде относительных членов.
С.3.6 Суммарная стандартная неопределенность
Суммарная стандартная неопределенность (в виде относительного стандартного отклонения) для каждого типа продуктов приведена в таблице С.4.
Таблица С.4 - Относительное стандартное отклонение воспроизводимости
Продукт | Межлабораторное относительное стандартное отклонение, % | Относительное стандартное отклонение повторяемости, % | Вклад подготовки образцов в стандартную неопределенность, % | Суммарная стандартная неопределенность |
Креветки | 5,2 | 5,0 | 3,0 | 7,8 |
Овощи | 6,7 | 5,0 | 3,0 | 8,9 |
Мука | 2,4 | 5,0 | 3,0 | 6,4 |
С.3.7 Расширенная неопределенность
Расширенную неопределенность вычисляют, используя коэффициент охвата 2, который соответствует уровню доверия приблизительно 95%. Расширенная неопределенность составила 15,6%, 17,8% и 12,8% [как процент от (количество колоний) для креветок, овощей и муки, соответственно].
С.3.8 Дополнительный анализ
Результаты метода традиционно получают в виде десятичного логарифма от количества колоний аэробных бактерий. Однако для единственного объекта испытаний часто более полезно определить расширенный интервал неопределенности (в тех же единицах). Для значений с неопределенностью в области значений это лучше всего сделать, вычисляя расширенную неопределенность в области значений
(см. С.3.7) и преобразуя значение CFU впоследствии. Это можно проиллюстрировать вычислением расширенных интервалов неопределенности для исследуемых материалов с 150 CFU. Соответствующие вычисления приведены в таблице С.5.
Таблица С.5 - Скорректированное стандартное отклонение воспроизводимости
Продукт | Стандартная неопреде- | Расширенная неопреде- |
| Расширенная неопреде- | Интервал неопреде- | Итоговый интервал неопреде- |
Креветки | 7,8 | 15,6 | 2,1761 | 0,3395 | 1,8366-2,5156 | 68-328 |
Овощи | 8,9 | 17,8 | 2,1761 | 0,3873 | 1,7888-2,5634 | 61-366 |
Мука | 6,4 | 12,8 | 2,1761 | 0,2785 | 1,8976-2,4546 | 79-285 |
С.4 Неопределенность при определении количества грубых волокон
С.4.1 Введение
Метод используют при определении количества грубых волокон в кормах для животных. Под грубыми волокнами понимают количество обезжиренных органических веществ, нерастворимых в кислых и щелочных средах. Содержание волокон в кормах для животных обычно изменяется в интервале от 2% до 12% от массы корма.
С.4.2 Вычисление концентрации волокон
Содержание волокон , как процент от массы пробы (то есть массовую долю в процентах) вычисляют по формуле
![]() , (С.4)
, (С.4)
где - масса пробы (для анализа взята проба массой 1 г), в граммах;
- масса тигля и пробы после высушивания постоянной массы, в граммах;
- масса тигля и пробы после озоления, в граммах;
- масса тигля и пустой пробы после высушивания до постоянной массы
, в граммах;
- масса тигля и пустой пробы после озоления, в граммах.
_______________
Пустая проба предполагает использование пустого тигля на всех стадиях метода.
Блок-схема, иллюстрирующая основные этапы метода, представлена на рисунке С.1.
С.4.3 Данные совместных исследований
Метод был объектом совместных исследований в соответствии с ИСО 5725-2. Пять различных видов корма для животных, представляющих типичные концентрации грубых волокон и жира, были исследованы в процессе испытаний. Участники испытаний выполнили все этапы метода, включая размол проб. Полученные оценки повторяемости и воспроизводимости приведены в таблице С.6.
Таблица С.6 - Данные совместных исследований содержания грубых волокон
Объект испытаний | Среднее содержание волокон, % | Стандартное отклонение воспроизводимости | Относительное стандартное отклонение воспроизводимости | Стандартное отклонение повторяемости, |
А | 2,3 | 0,293 | 0,127 | 0,198 |
В | 12,1 | 0,563 | 0,0465 | 0,358 |
С | 5,4 | 0,390 | 0,0722 | 0,264 |
D | 3,4 | 0,347 | 0,102 | 0,232 |
Е | 10,1 | 0,575 | 0,0569 | 0,391 |
С.4.4 Контроль смещения
Чтобы установить, находится ли лабораторное смещение в ожидаемых пределах, лаборатория выполняет сравнение с образцом сравнения, сертифицированным рассматриваемым методом (это существенно, поскольку измеряемая величина определена заданным методом анализа). Паспортное значение составляет (93±14) г/кг (9,3%). Лаборатория получила значение 9,16%, соответствующее лабораторному смещению минус 0,14%. Оно находится в пределах ожидаемого интервала, исходя из стандартного отклонения воспроизводимости на уровне 9%. Стандартная неопределенность паспортного значения составляет приблизительно 0,07 г/кг (0,7% массовой доли). Она невелика по сравнению со стандартным отклонением воспроизводимости для аналогичных уровней содержания грубых волокон в таблице С.6. Поэтому смещение является приемлемым.
|
Рисунок С.1 - Действия по оценке содержания грубых волокон
С.4.5 Контроль прецизионности
Как часть верификации метода в лаборатории были выполнены эксперименты для оценки повторяемости (в пределах партии) кормов, концентрация грубых волокон в которых аналогична концентрации в некоторых пробах, проанализированных в совместных исследованиях. Результаты приведены в таблице С.7. Сравнение с таблицей С.6 показывает, что лаборатория получает прецизионность очень близкую к найденной в совместных исследованиях.
Таблица С.7 - Данные повторяемости для концентрации грубых волокон
Объект испытаний | Среднее содержание волокон, % | Стандартное отклонение повторяемости |
F | 3,0 | 0,198 |
G | 5,5 | 0,264 |
Н | 12,0 | 0,358 |
С.4.6 Изменение неопределенности в зависимости от отклика
Стандартные отклонения повторяемости и воспроизводимости, приведенные в таблице С.6, увеличиваются с увеличением концентрации грубых волокон. Однако очевидно несоответствие относительного стандартного отклонения воспроизводимости простой пропорциональной модели. Поэтому лаборатория при определении неопределенности на различных наблюдаемых уровнях концентрации волокон использует воспроизводимость, найденную на аналогичных уровнях в совместных исследованиях; например, для уровней концентрации волокон не выше 2,5% (массовая доля) стандартное отклонение воспроизводимости 0,29% (массовая доля) выбрано из таблицы С.6.
С.4.7 Дополнительные факторы
Лаборатория провела экспериментальные и другие исследования влияния различных величин на результаты для типичных объектов испытаний. Полученные оценки неопределенности приведены в таблице С.8. Ни один из вкладов не является существенным кроме влияния высушивания до постоянной массы. Неопределенность, соответствующая этому этапу процесса, получена, исходя из требования постоянной массы, установленного лабораторией; постоянная масса не определена в стандартном методе, и лаборатория приняла решение использовать метод высушивания, приводящий к массе в пределах 0,002 г массы. Деление этого максимального отклонения на дает оценку неопределенности 0,115% (массовая доля) содержания волокон, если для анализа взят 1 г пробы.
Таблица С.8 - Влияние различных величин на определение содержания грубых волокон
Источник неопределенности | Значение | Стандартная неопределенность | Соответствующая неопределенность в виде стандартного отклонения повторяемости | Источник информации |
Масса пробы | 1,0 г | 0,00020 г | 0,00020 | Свидетельство о калибровке |
Концентрация кислоты | - | - | 0,00030 | Опубликованные данные об изменении содержания волокна в зависимости от концентрации кислоты |
Концентрация щелочи | - | - | 0,00048 | Опубликованные данные об изменении содержания волокна в зависимости от концентрации щелочи |
Время разрушения в кислой среде | - | - | 0,0090 | Опубликованные данные об изменении содержания волокна в зависимости от времени вываривания |
Время разрушения в щелочной среде | - | - | 0,0072 | Опубликованные данные об изменении содержания волокна в зависимости от времени вываривания |
Высушивание до постоянной массы | - | 0,00115 г | - | Лабораторные требования постоянной массы |
Температура и время озоления | - | Незначительная | - | Опубликованные данные об отсутствии существенных изменений содержания волокон в зависимости от изменения температуры и времени озоления |
Потеря массы после озоления для холостой пробы | - | Незначительная | - | Экспериментальные исследования |
С.4.8 Суммарная стандартная неопределенность
Поскольку неопределенность, соответствующая высушиванию до постоянной массы, не пропорциональна уровню грубых волокон, невозможно принять простую пропорциональную модель для оценки неопределенности. Вместо этого удобно оценивать неопределенность, соответствующую типичным уровням грубых волокон. Оценки неопределенности приведены в таблице С.9.
Таблица С.9 - Скорректированное стандартное отклонение воспроизводимости
Содержание волокон, % | Стандартное отклонение воспроизводимости | Дополнительный вклад высушивания, % | Суммарная стандартная неопределенность |
| 0,293 | 0,115 | 0,31 |
2,5 к 5 | 0,390 | 0,115 | 0,41 |
5 к 10 | 0,575 | 0,115 | 0,59 |
С.4.9 Расширенная неопределенность
Расширенная неопределенность вычислена с коэффициентом охвата 2, который соответствует уровню доверия, приблизительно равному 95%, дает расширенную неопределенность 0,6%, 0,8% и 1,2% соответственно для различных диапазонов содержания волокон в таблице С.9.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов, указанных в библиографии настоящего стандарта, национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1:2006 | - | * |
ISO 3534-2:2006 | - | * |
ISO 3534-3:1999 | IDT | * |
ISO 5725-1:1994 | IDT | ГОСТ Р ИСО 5725-1-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения" |
ISO 5725-2:1994 | IDT | ГОСТ Р ИСО 5725-2-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений" |
ISO 5725-3:1994 | IDT | ГОСТ Р ИСО 5725-3-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений" |
ISO 5725-4:1994 | IDT | ГОСТ Р ИСО 5725-4-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений" |
ISO 5725-5:1998 | IDT | ГОСТ Р ИСО 5725-5-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений" |
ISO 5725-6:1994 | IDT | ГОСТ Р ИСО 5725-6-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике" |
ISO 7870-2:2013 | IDT | ГОСТ Р ИСО 7870-2-2015 "Статистические методы. Контрольные карты. Часть 2. Контрольные карты Шухарта" |
ISO 7870-4:2011 | IDT | ГОСТ Р ИСО 7870-4-2013 "Статистические методы. Контрольные карты. Часть 4. Карты кумулятивных сумм" |
ISO 10576-1:2003 | IDT | ГОСТ Р ИСО 10576-1-2006 "Статистические методы. Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы" |
ISO 11648-1:2003 | IDT | ГОСТ Р ИСО 11648-1-2009 "Статистические методы. Выборочный контроль нештучной продукции. Часть 1. Общие принципы" |
ISO 11648-2:2001 | IDT | ГОСТ Р ИСО 11648-2-2009 "Статистические методы. Выборочный контроль нештучной продукции. Часть 2. Отбор выборки сыпучих материалов" |
ISO/IEC 17025:2005 | IDT | ГОСТ Р ИСО/МЭК 17025-2009* "Общие требования к компетентности испытательных и калибровочных лабораторий" |
________________ * Вероятно, ошибка оригинала. Следует читать: ГОСТ ИСО/МЭК 17025-2009. - . | ||
ISO/IEC 17043:2010 | IDT | ГОСТ ISO/IEC 17043-2013 "Оценка соответствия. Основные требования к проведению проверки квалификации" |
ISO/IEC Guide 33:2000 | - | * |
ISO/IEC Guide 98-3:2008 | IDT | ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения" |
ISO/IEC Guide 99:2007 | - | * |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. - IDT - идентичные стандарты. | ||
Библиография
[1] | ISO 3534-1 | Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability |
[2] | ISO 3534-2:2006 | Statistics - Vocabulary and symbols - Part 2: Applied statistics |
[3] | ISO 3534-3 | Statistics - Vocabulary and symbols - Part 3: Design of experiments |
[4] | ISO 5725-1:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 1: General principles and definitions |
[5] | ISO 5725-2:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method |
[6] | ISO 5725-3:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 3: Intermediate measures of the precision of a standard measurement method |
[7] | ISO 5725-4:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 4: Basic methods for the determination of the trueness of a standard measurement method |
[8] | ISO 5725-5:1998 | Accuracy (trueness and precision) of measurement methods and results - Part 5: Alternative methods for the determination of the precision of a standard measurement method |
[9] | ISO 5725-6:1994 | Accuracy (trueness and precision) of measurement methods and results - Part 6: Use in practice of accuracy values |
[10] | ISO/TR 7871:1997 | Cumulative sum charts - Guidance on quality control and data analysis using CUSUM techniques |
________________
| ||
[11] | ISO 8258:1991 | Shewhart control charts |
________________ | ||
[12] | ISO 10576-1 | Statistical methods - Guidelines for the evaluation of conformity with specified requirements - Part 1: General principles |
[13] | ISO 11648 (all parts) | Statistical aspects of sampling from bulk materials |
[14] | ISO Guide 33 | Uses of certified reference materials |
[15] | ISO/IEC 17025 | General requirements for the competence of testing and calibration laboratories |
[16] | ISO/IEC Guide 98-3:2008 | Uncertainty of measurement - Guide to the expression of uncertainty in measurement (GUM:1995) |
[17] | ISO/IEC Guide 99:2007 | International vocabulary of metrology - Basic and general concepts and associated terms (VIM) |
[18] | ISO/IEC 17043 | Conformity assessment - General requirements for proficiency testing |
[19] | AFNOR FD X07-021 (October 1999), Normes fondamentales - Metrologie et applications de la statistique - Aide a la demarche pour l'estimation et l'utilisation de l'incertitude des mesures et des resultats d'essais | |
[20] | Recommendation INC-1 (1980), BIPM | |
[21] | European Directive 70/220, Measures to be taken against air pollution by emissions from motor vehicles | |
[22] | Kaarls R. Proc.-Verbal Com. Int. Poids et Mesures, 49, BIPM, 1981, p. A.1-A.12 References for Example C.2 | |
[23] | Analytical Methods Committee. Analyst, 118, 1993, p. 1217 | |
[24] | Shure B., Corrao, P.A., Glover, A. and Malinowski A.J. J. AOAC Int., 65, 1982, p. 1339 | |
[25] | King-Brink M. and Sebranek J.G. J. AOAC Int., 76, 1993, p. 787 | |
[26] | Breese Jones D. US Department of Agriculture Circular No. 183 (August 1931) References for Example C.3 | |
[27] | Official Methods of Analysis, 18th Ed., AOAC INTERNATIONAL, Gaithersburg, MD, 2007 | |
[28] | Mettler D. and Tholen D. A2LA Guidance Document G108 - Guidelines for Estimating Uncertainty for Microbiological Counting Methods. American Association for Laboratory Accreditation, 2007 | |
УДК 658.562.012.7:65.012.122:006.354 |
| ОКС 17.020 |
Ключевые слова: оценки неопределенности, повторяемости, воспроизводимости, правильности, математическое ожидание, прецизионность, стандартное отклонение, дисперсия, смещение | ||
Электронный текст документа
и сверен по:
, 2019