ГОСТ Р 54500.3.1-2011/Руководство ИСО/МЭК 98-3:2008/Дополнение 1:2008
Группа Т80
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Часть 3
Руководство по выражению неопределенности измерения
Дополнение 1
Трансформирование распределений с использованием метода Монте-Карло
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement. Supplement 1. Propagation of distributions using a Monte Carlo method
ОКС 17.020
Дата введения 2012-10-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт метрологии им. Д.И.Менделеева" (ФГУП "ВНИИМ") и Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного аутентичного перевода на русский язык международного документа, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 16 ноября 2011 г. N 555-ст
4 Настоящий стандарт идентичен международному документу Руководство ИСО/МЭК 98-3:2008/Дополнение 1:2008* "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 1. Трансформирование распределений с использованием метода Монте-Карло" [ISO/IEC Guide 98-3:2008/Supplement 1:2008 "Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) - Supplement 1: Propagation of distributions using a Monte Carlo method"].
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
В стандарт введены технические изменения 1, подготовленные техническим управляющим комитетом (ТМВ) ИСО, которые выделены двойной вертикальной линией, расположенной слева от соответствующего текста.
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные и межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
0.1 Общие сведения
В настоящем стандарте рассматривается трансформирование распределений для заданной математической модели измерений [Руководство ИСО/МЭК 98-3 (3.1.6)] с целью получения оценки неопределенности измерений и реализация этой процедуры методом Монте-Карло. Метод применим к моделям с произвольным числом входных величин и единственной выходной величиной.
Метод Монте-Карло является практической альтернативой способу оценки неопределенности по GUM [Руководство ИСО/МЭК 98-3 (3.4.8)]. Метод имеет особое значение, когда:
a) линеаризация модели не обеспечивает ее адекватного представления;
b) распределение выходной величины, например вследствие своей выраженной асимметрии, не может быть описано нормальным распределением (распределением Гаусса) или масштабированным смещенным -распределением.
В случае а) оценки выходной величины и соответствующей стандартной неопределенности, полученные в соответствии с GUM, могут оказаться недостоверными. В случае b) при оценке неопределенности могут быть получены недостоверные интервалы охвата (обобщение понятия расширенной неопределенности, используемого в GUM).
GUM [Руководство ИСО/МЭК 98-3 (3.4.8)] "...устанавливает общую методологию оценивания неопределенности...", основанную на использовании закона трансформирования неопределенностей [Руководство ИСО/МЭК 98-3 (раздел 5)], когда выходная величина подчиняется нормальному распределению или масштабированному смещенному -распределению [Руководство ИСО/МЭК 98-3 (G.6.2, G.6.4)]. При этом закон трансформирования неопределенностей позволяет учесть неопределенности входных величин и вычислить стандартную неопределенность оценки выходной величины на основе:
1) наилучших оценок входных величин;
2) стандартных неопределенностей оценок входных величин;
3) числа степеней свободы для стандартных неопределенностей оценок входных величин;
4) всех ненулевых ковариаций пар этих оценок.
Кроме того, полученная плотность распределения вероятностей выходной величины позволяет определить для выходной величины интервал охвата с заданной вероятностью.
Наилучшие оценки входных величин, их стандартные неопределенности, ковариации и числа степеней свободы представляют собой ту информацию, которая необходима для применения метода расчета неопределенности по GUM. Метод, устанавливаемый настоящим стандартом, основан на использовании плотностей распределения вероятностей входных величин для последующего расчета плотности распределения вероятностей выходной величины.
В то время как для применения способа оценивания неопределенности по GUM существуют некоторые ограничения, трансформирование распределений всегда позволяет получить плотность распределения вероятностей выходной величины на основе распределений входных величин. Плотность распределения вероятностей выходной величины представляет собой выражение знания об этой величине, полученного на основе знаний о входных величинах в виде сопоставленных им распределений. После получения плотности распределения вероятностей выходной величины могут быть определены математическое ожидание, используемое в качестве оценки выходной величины, и стандартное отклонение, используемое в качестве стандартной неопределенности этой оценки. Кроме того, плотность распределения вероятностей может быть использована для получения интервала охвата для выходной величины, соответствующего заданной вероятности.
Использование плотностей распределения вероятностей в соответствии с настоящим стандартом в основном согласуется с принципами GUM. Плотность распределения вероятностей величины отражает состояние знаний об этой величине, т.е. она численно определяет степень доверия тем значениям, которые могут быть приписаны упомянутой величине на основе доступной информации. Информация обычно состоит из необработанных статистических данных, результатов измерения, научных выводов, профессиональных суждений.
Для построения плотности распределения вероятностей случайной величины на основе наблюдений может быть применена теорема Байеса [27, 33]. Информация о систематических эффектах может быть преобразована в соответствующую плотность распределения вероятностей на основе принципа максимума энтропии [51, 56].
Трансформирование распределений имеет более широкую область применения, чем способ оценивания неопределенности по GUM. Метод трансформирования распределений использует более обширную информацию, чем та, что содержится в наилучших оценках и соответствующих стандартных неопределенностях (а также в числах степеней свободы и ковариациях).
Исторический обзор приведен в приложении А.
Примечание 1 - В GUM рассматривается случай, когда линеаризация модели измерения неприменима [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)]. Однако это рассмотрение ограничено использованием только основных нелинейных членов в ряде Тейлора для функции измерения, а также предположением о нормальности распределения входных величин.
Примечание 2 - Строго говоря, в GUM -распределение описывает не выходную величину
, а величину
![]() [точнее, как указано в GUM,
[точнее, как указано в GUM, ![]() ], где
], где - оценка
,
- стандартная неопределенность оценки
[Руководство ИСО/МЭК 98-3 (G.3.1)]. Такое представление использовано и в настоящем стандарте.
Примечание 3 - Плотность распределения вероятностей не следует понимать в смысле частотного описания вероятности.
Примечание 4 - "Оценивание неопределенности нельзя рассматривать как типовую задачу, требующую применения стандартных математических процедур. От пользователя требуется детальное знание природы измеряемой величины и процедуры измерения. Поэтому качество оценки неопределенности, приписанной результату измерений, зависит, в конечном счете, от понимания, критического анализа и профессиональной добросовестности всех лиц, принимающих участие в ее получении" [17].
0.2 Основные сведения о JCGM
В 1997 г. семью международными организациями, подготовившими в 1993 г. "Руководство по выражению неопределенности измерения" (GUM) и "Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины" (VIM), был образован Объединенный комитет по руководствам в метрологии (JCGM), возглавляемый директором Международного бюро мер и весов (МБМВ), который принял на себя ответственность за указанные документы от Технической консультативной группы по метрологии (ИСО/ТАГ 4).
Учредителями JCGM, помимо МБМВ, являются Международная электротехническая комиссия (МЭК), Международная федерация клинической химии и лабораторной медицины (МФКХ), Международное сотрудничество по аккредитации лабораторий (ИЛАК), Международная организация по стандартизации (ИСО), Международный союз теоретической и прикладной химии (ИЮПАК), Международный союз теоретической и прикладной физики (ИЮПАП) и Международная организация по законодательной метрологии (МОЗМ).
В рамках JCGM созданы две Рабочие группы (РГ). Задачей РГ 1 "Выражение неопределенности измерения" является содействие использованию Руководства (GUM), подготовка дополнений к Руководству и иных документов, способствующих его широкому применению. Задачей РГ 2 "Рабочей группы по Международному словарю основных и общих терминов в метрологии (VIM)" является пересмотр VIM и содействие его применению. Более подробную информацию о деятельности JCGM можно найти на сайте www.bipm.org.
Дополнения к GUM, подобные тому, что положен в основу настоящего стандарта, имеют целью распространить руководство на те аспекты, которые в этом руководстве в полной мере не отражены. При этом, однако, разрабатываемые дополнения соответствуют, насколько это возможно, общей методологии, изложенной в GUM.
1 Область применения
В настоящем стандарте установлен численный метод, согласующийся с основными принципами GUM [Руководство ИСО/МЭК 98-3 (G.1.5)] и предназначенный для получения оценки неопределенности измерения. Этот метод может быть применен к любым моделям, имеющим единственную выходную величину, в которых входные величины характеризуются любыми заданными функциями распределения вероятностей [Руководство ИСО/МЭК 98-3 (G.1.4, G.5.3)].
Также как GUM, настоящий стандарт посвящен вопросам определения выражения для неопределенности измерения хорошо определенной физической величины, характеризуемой единственным значением [Руководство ИСО/МЭК 98-3 (1.2)].
В настоящем стандарте установлены также методы, применимые в ситуациях, когда условия применения способа расчета неопределенности по GUM [Руководство ИСО/МЭК 98-3 (G.6.6)] не выполняются или информация об их выполнении отсутствует. Стандарт также может быть применен в ситуациях, когда возникают трудности при оценке неопределенности по GUM, например вследствие сложности модели. Методы изложены в виде, облегчающем их программирование для расчетов на компьютере.
Настоящий стандарт может быть использован для определения плотности распределения вероятностей выходной величины, что позволяет получить:
a) оценку выходной величины;
b) стандартную неопределенность, ассоциированную с этой оценкой;
c) интервал охвата для выходной величины, соответствующий заданной вероятности охвата.
При заданных (i) модели, описывающей взаимосвязь входных величин с выходной величиной, и (ii) плотностях распределения вероятностей входных величин существует единственная плотность распределения вероятностей выходной величины. Как правило, последняя не может быть определена аналитически. Настоящий стандарт позволяет определить величины, указанные в перечислениях а), b) и с) с приемлемой точностью, не используя приближений, которые нельзя оценить количественно.
Настоящий стандарт позволяет получить интервал охвата для заданной вероятности охвата, в том числе вероятностно симметричный и наименьший интервалы.
Настоящий стандарт применим к статистически независимым входным величинам с соответствующими функциями плотности распределения вероятностей, а также к статистически зависимым случайным величинам, описанным совместной плотностью распределения.
Как правило, настоящий стандарт применяют в случаях, когда:
- вклад разных составляющих неопределенности может быть существенно неодинаков [Руководство ИСО/МЭК 98-3 (G.2.2)];
- трудно или неудобно находить частные производные от функции измерения, как того требует закон трансформирования неопределенностей;
- распределение выходной величины нельзя считать ни нормальным, ни масштабированным смещенным -распределением [Руководство ИСО/МЭК 98-3 (G.6.5)];
- оценка выходной величины и соответствующая стандартная неопределенность имеют приблизительно одинаковое значение [Руководство ИСО/МЭК 98-3 (G.2.1)];
- модель является достаточно сложной [Руководство ИСО/МЭК 98-3 (G.1.5)];
- плотности распределения вероятностей входных величин асимметричны [Руководство ИСО/МЭК 98-3(G.5.3)].
Прежде чем применять метод, установленный настоящим стандартом, рекомендуется проверить, позволяют ли условия измерительной задачи использовать способ оценивания неопределенности по GUM. Если условия позволяют, то основным методом расчета остается оценивание неопределенности способом, установленным в GUM.
Значение для неопределенности измерений, как правило, достаточно приводить с одной или двумя значащими цифрами. Методы, установленные настоящим стандартом, позволяют получить оценки с указанной точностью.
Применение стандарта иллюстрировано подробными примерами.
Настоящий стандарт служит дополнением к GUM и должен быть использован вместе с ним. Он не исключает использования других методов расчета неопределенности, не противоречащих GUM.
Примечание 1 - Настоящий стандарт неприменим к моделям, описываемым многозначными функциями (например, в виде решения квадратного уравнения без указания, какой из корней должен быть выбран).
Примечание 2 - В настоящем стандарте не рассмотрен случай, когда априорно известна плотность распределения вероятностей выходной величины, однако установленный в нем метод может быть модифицирован и для этой ситуации [16].
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие документы:
Руководство ИСО/МЭК 98-3:2008 Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения (GUM:1995)[ISO/IEC Guide 98:2008, Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)]
Руководство ИСО/МЭК 99:2007 Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины (VIM) [ISO/IEC Guide 99:2007 International vocabulary of metrology - Basic and general concepts and associated terms (VIM)]
3 Термины и определения
В настоящем стандарте применены термины по Руководству ИСО/МЭК 98-3 и Руководству ИСО/МЭК 99, некоторые из которых (при необходимости, модифицированных) приведены в настоящем разделе.
Обозначения, использованные в настоящем стандарте, приведены в приложении G.
3.1 распределение (вероятностей) (probability distribution): Функция, устанавливающая вероятность того, что случайная величина принимает заданное значение или принадлежит к заданному множеству значений.
Примечание - Сумма вероятностей принятия случайной величиной всех возможных значений равна 1.
[Модифицировано по отношению к ИСО 3534-1:1993, словарная статья 1.3, Руководство ИСО/МЭК 98-3, словарная статья С.2.3]
Примечание 1 - Распределение вероятностей называется одномерным, если оно описывает поведение единственной (скалярной) случайной величины, и многомерным, если оно описывает поведение вектора случайных величин. Многомерное распределение вероятностей описывается также совместным распределением этих случайных величин.
Примечание 2 - Распределение вероятностей может быть представлено в виде функции распределения и плотности распределения вероятностей.
3.2 функция распределения (вероятностей) (distribution function): Функция, устанавливающая для каждого значения вероятность того, что случайная переменная
меньше или равна
:
![]() .
.
[Модифицировано по отношению к ИСО 3534-1:1993, словарная статья 1.4; Руководство ИСО/МЭК 98-3:2008, словарная статья С.2.4]
3.3 плотность распределения (вероятностей) (probability density function): Первая производная, если она существует, функции распределения непрерывной случайной величины
![]() .
.
Примечание - ![]() , называется "элементом вероятности":
, называется "элементом вероятности":
![]() .
.
[Модифицировано по отношению к ИСО 3534-1:1993, словарная статья 1.5; Руководство ИСО/МЭК 98-3:2008, словарная статья С.2.5]
3.4 нормальное распределение (вероятностей) (normal distribution): Распределение вероятностей непрерывной случайной величины такое, что соответствующая плотность распределения вероятностей для
![]() имеет вид:
имеет вид:
 .
.
Примечание - - математическое ожидание
,
- стандартное отклонение
.
[Модифицировано по отношению к ИСО 3534-1:1993, словарная статья 1.37; Руководство ИСО/МЭК 98-3:2008, словарная статья С.2.14]
Примечание - Нормальное распределение называют также распределением Гаусса.
3.5 -распределение (
-distribution): Распределение вероятностей непрерывной случайной величины
, плотность распределения вероятностей которой для
![]() имеет вид
имеет вид
 ,
,
где - число степеней свободы (положительное целое число);
 - гамма-функция,
- гамма-функция, 0.
3.6 математическое ожидание (expectation): Характеристика случайной величины, которая для непрерывной случайной величины с плотностью распределения вероятностей
![]() имеет вид
имеет вид
![]() .
.
Примечание 1 - Не всякая случайная величина имеет математическое ожидание.
Примечание 2 - Математическое ожидание случайной величины ![]() имеет вид:
имеет вид:
![]() .
.
3.7 дисперсия (variance): Характеристика случайной величины, которая для непрерывной случайной величины с плотностью распределения вероятностей
![]() имеет вид
имеет вид
![]() .
.
Примечание - Не всякая случайная величина имеет дисперсию.
3.8 стандартное отклонение (standard deviation): Положительный квадратный корень из дисперсии ![]() .
.
3.9 момент порядка (moment of order
): Математическое ожидание
-й степени случайной величины
![]() .
.
Примечание 1 - Центральным моментом порядка является математическое ожидание случайной величины
![]() .
.
Примечание 2 - Математическое ожидание ![]() представляет собой момент первого порядка. Дисперсия
представляет собой момент первого порядка. Дисперсия ![]() является центральным моментом второго порядка.
является центральным моментом второго порядка.
3.10 ковариация (covariance): Характеристика двух случайных величин, которая в случае непрерывных случайных величин и
с совместной плотностью распределения
![]() , где
, где ![]() ,
, ![]() имеет вид
имеет вид
![]() .
.
Примечание - Не все пары случайных величин имеют ковариацию.
3.11 матрица неопределенности (uncertainty matrix): Матрица размерности , на главной диагонали которой расположены квадраты стандартных неопределенностей, соответствующих оценкам-компонентам векторной величины размерности
, а остальные элементы представляют собой ковариации для соответствующих оценок.
Примечание 1 - Матрица неопределенности размерности
, соответствующая вектору оценок
векторной величины
, имеет вид:
 ,
,
где ![]() - дисперсия (квадрат стандартной неопределенности) оценки
- дисперсия (квадрат стандартной неопределенности) оценки ;
![]() - ковариация
- ковариация и
;
![]() 0, если элементы
0, если элементы и
вектора
некореллированны.
Примечание 2 - Ковариации также можно трактовать как совместные неопределенности.
Примечание 3 - Матрицу неопределенности также называют матрицей ковариации или дисперсионно-ковариационной матрицей.
3.12 интервал охвата* (coverage interval): Интервал, построенный на основе имеющейся информации и содержащий значение случайной величины с заданной вероятностью.
_______________
* В отечественных нормативных документах интервал охвата иногда называют интервалом неопределенности.
Примечание 1 - Интервал охвата иногда называют байесовским интервалом.
Примечание 2 - В общем случае для заданной вероятности существует более одного интервала охвата.
Примечание 3 - Интервал охвата не следует называть доверительным интервалом, чтобы избежать путаницы с термином, имеющим строгую статистическую интерпретацию [Руководство ИСО/МЭК 98-3 (6.2.2)].
Примечание 4 - Данное определение отличается от определения, приведенного в Руководстве ИСО/МЭК 99, поскольку в настоящем стандарте не использован термин "истинное значение" по причинам, изложенным в GUM [Руководство ИСО/МЭК 98-3 (Е.5)].
3.13 вероятность охвата (coverage probability): Вероятность того, что значение случайной величины находится в границах интервала охвата.
Примечание - Вероятность охвата иногда называют уровнем доверия [Руководство ИСО/МЭК 98-3 (6.2.2)].
3.14 длина интервала охвата (length of a coverage interval): Разность наибольшего и наименьшего значений интервала охвата.
3.15 вероятностно симметричный интервал охвата (probabilistically symmetric coverage interval): Интервал охвата, для которого вероятность того, что значение случайной величины меньше наименьшего значения (нижней границы) интервала охвата, равна вероятности того, что значение случайной величины больше наибольшего значения (верхней границы) интервала.
3.16 наименьший интервал охвата (shortest coverage interval): Интервал охвата, имеющий наименьшую длину среди всех возможных интервалов охвата для данной случайной величины с одинаковой вероятностью охвата.
3.17 трансформирование распределений (propagation of distributions): Метод, используемый для определения функции распределения выходной величины на основе функций распределения входных величин, от которых выходная величина зависит функционально.
Примечание - Метод может быть аналитическим или численным, точным или приближенным.
3.18 способ оценивания неопределенности по GUM (GUM uncertainty framework): Применение закона трансформирования неопределенностей и описание выходной величины с помощью нормального распределения или масштабированного смещенного -распределения, по которым может быть рассчитан соответствующий интервал охвата.
3.19 метод Монте-Карло (Monte Carlo method): Метод трансформирования распределений на основе моделирования случайных выборок из этих распределений.
3.20 предел погрешности вычисления (numerical tolerance): Половина длины наименьшего интервала, содержащего все числа, отражающие результат вычислений, которые могут быть корректно представлены заданным числом значащих цифр.
Пример - При использовании в представлении результата вычисления двух значащих цифр записи 1,8 соответствуют все числа более 1,75 и менее 1,85. Тогда предел погрешности вычисления будет равен (1,85-1,75)/2=0,05.
Примечание - Расчет предела погрешности вычисления - см. 7.9.2.
4 Соглашения и условные обозначения
В настоящем стандарте использованы следующие соглашения и условные обозначения.
4.1 Математическая модель измерения [Руководство ИСО/МЭК 98-3 (4.1)] одномерной (скалярной) величины может быть представлена в виде функции :
![]() , (1)
, (1)
где - выходная скалярная величина, а
- вектор
входных величин
![]() . Каждая величина
. Каждая величина рассматривается в качестве случайной величины, принимающей значения
, с математическим ожиданием
.
- случайная величина, принимающая значения
, с математическим ожиданием
.
Примечание 1 - В настоящем стандарте один и тот же символ использован для физической величины и случайной величины, которая эту величину представляет [см. Руководство ИСО/МЭК 98-3 (4.1.1, примечание 1)].
Примечание 2 - Хотя многие модели измерений могут быть представлены формулой (1), более общим представлением является
![]() ,
,
где и
связаны между собой неявной функцией. В любом случае для применения метода Монте-Карло достаточно, чтобы каждому допустимому
было поставлено в соответствие значение
.
4.2 Настоящий стандарт отступает от обозначений, часто используемых для обозначения плотностей распределения вероятностей и функций распределения [24]. В GUM одно и то же обозначение использовано как для функции измерения, так и для плотности распределения вероятностей, чем создается некоторая путаница. Поскольку в настоящем стандарте моделям уделено особое внимание, для плотности распределения вероятностей и функции распределения вместо обозначений
и
использованы, соответственно,
и
. Используемые в обозначениях индексы соответствуют случайной величине, о которой идет речь. Обозначение
оставлено для описания функции измерения.
Примечание - Определения, приведенные в разделе 3, даны в соответствии с изложенным соглашением об обозначениях.
4.3 В настоящем стандарте плотности распределения вероятностей могут быть определены для скалярной или векторной
случайных величин. Для скалярной случайной величины
плотность распределения вероятностей обозначена
![]() , где
, где - возможное значение
. Случайной величине
соответствуют математическое ожидание
![]() и дисперсия
и дисперсия ![]() (см. 3.6, 3.7).
(см. 3.6, 3.7).
4.4 Плотность распределения вероятностей векторной случайной величины обозначают
![]() , где
, где ![]() - вектор возможных значений величины
- вектор возможных значений величины . Вектор
рассматривают как вектор случайных величин, которому соответствуют вектор математических ожиданий
![]() и ковариационная матрица
и ковариационная матрица ![]() .
.
4.5 Плотность распределения вероятностей нескольких случайных величин часто называют совместной, даже если все входные величины являются независимыми.
4.6 Если элементы вектора
независимы, плотность распределения вероятностей
обозначают
![]() .
.
4.7 Плотность распределения вероятностей и функцию распределения для обозначают
![]() и
и ![]() соответственно.
соответственно.
4.8 В настоящем стандарте случайную величину обозначают прописной буквой, а ее математическое ожидание или оценку - соответствующей строчной буквой. Например, оценку величины (оценку ее математического ожидания) обозначают буквой
. Такое обозначение часто неудобно в случае физических величин, для которых традиционно используют иные символы, например
для температуры и
для времени. Поэтому в некоторых примерах (раздел 9) использованы другие обозначения. В этом случае случайная величина обозначена своим общепринятым символом, а ее оценка (оценка ее математического ожидания) - тем же символом с "крышкой". Например, отклонение калибруемой концевой меры длины от номинального значения при 20 °С (см. 9.5) обозначено
, а его оценка -
.
Примечание - Символ с "крышкой" в литературе по математической статистике используют для обозначения оценки.
4.9 В настоящем стандарте термин "закон трансформирования неопределенностей" используют в смысле аппроксимации функции измерения рядом Тейлора первого порядка. Этот термин также может быть применен при использовании разложения в ряд более высокого порядка.
4.10 Подстрочный индекс "с" для суммарной стандартной неопределенности [Руководство ИСО/МЭК 98-3 (5.1.1)] в настоящем стандарте рассматривается как излишний. Стандартная неопределенность оценки у выходной величины может быть записана как
, хотя использование обозначения
![]() остается допустимым, если это помогает заострить внимание на том, что имеется в виду суммарная стандартная неопределенность. Определение "суммарная" в данном контексте также является излишним и может быть опущено, поскольку присутствие символа "
остается допустимым, если это помогает заострить внимание на том, что имеется в виду суммарная стандартная неопределенность. Определение "суммарная" в данном контексте также является излишним и может быть опущено, поскольку присутствие символа "" в
уже указывает на оценку, с которой ассоциирована данная стандартная неопределенность. Еще более неуместным становится использование нижнего индекса "с" и определения "суммарная", когда результаты одного или нескольких измерений и соответствующие оценки неопределенности являются исходными данными для получения оценки неопределенности последующей величины.
4.11 В настоящем стандарте использованы термины "интервал охвата" и "вероятность охвата". В GUM в качестве синонима "вероятности охвата" использован термин "уровень доверия" с предупреждением, что это не то же самое, что "доверительная вероятность" [Руководство ИСО/МЭК 98-3 (6.2.2)], поскольку последний термин имеет специальное определение в математической статистике. Т.к. в некоторых языках перевод с английского терминов "уровень доверия" и "доверительная вероятность" совпадает, в настоящем стандарте термин "уровень доверия" не используется.
4.12 Для обозначения десятичной дроби используется запятая*.
_______________
* В оригинале на английском языке в данном подразделе указывается на использование в качестве десятичного знака точки вместо запятой.
4.13 Если не определено иначе, то числа представляют с заданным количеством значащих цифр.
Пример - Числа 0,060, 0,60, 6,0 и 60 представлены с точностью до двух значащих цифр. В этом случае запись с точностью только до одной значащей цифры: 0,06, 0,6, и 6·10 - будет некорректной.
4.14 Некоторые символы, использованные в настоящем стандарте, имеют более одного значения (см. приложение G). Однако их смысл понятен из контекста.
4.15 В настоящем стандарте использованы следующие сокращения:
CGPM - Генеральная конференция по мерам и весам;
IEEE - Институт инженеров электротехники и электроники;
JCGM - Объединенный комитет по руководствам в метрологии;
GUM - Руководство по выражению неопределенности измерения;
VIM - Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины.
5 Общие принципы
5.1 Основные этапы оценки неопределенности
5.1.1 Основные этапы оценки неопределенности включают в себя формулировку измерительной задачи, трансформирование распределений и получение окончательного результата:
a) формулировка измерительной задачи включает в себя:
1) задание выходной величины (измеряемой величины);
2) выявление входных величин ![]() , от которых зависит выходная величина
, от которых зависит выходная величина ;
3) составление модели измерения, определяющей взаимосвязь с входными величинами
;
4) приписывание распределений вероятностей (нормального, прямоугольного и т.д.) входным величинам (или совместного распределения вероятностей входным величинам, не являющимся независимыми) на основе имеющейся информации;
b) трансформирование распределений предусматривает определение плотности распределения вероятностей выходной величины на основе плотностей распределения вероятностей входных величин
и используемой модели измерения;
c) получение окончательного результата предполагает использование плотности распределения вероятностей выходной величины для определения:
1) оценки математического ожидания величины в виде оценки
;
2) оценки стандартного отклонения величины в виде стандартной неопределенности
, ассоциированной с
[Руководство ИСО/МЭК 98-3 (Е.3.2)];
3) интервала охвата для величины , соответствующего заданной вероятности (вероятности охвата).
Примечание 1 - В некоторых случаях оценка выходной величины в виде математического ожидания может оказаться неприемлемой [см. Руководство ИСО/МЭК 98-3 (4.1.4)].
Примечание 2 - Некоторые величины, например подчиняющиеся распределению Коши, не имеют математического ожидания и стандартного отклонения. Однако интервал охвата для выходной величины всегда может быть построен.
5.1.2 При оценке неопределенности по GUM функции распределения входных величин в явном виде не используют. Однако в соответствии с Руководством ИСО/МЭК 98-3 (3.3.5) "...стандартную неопределенность типа А рассчитывают по плотности распределения вероятностей,... полученной из распределения частот..., а стандартную неопределенность типа В - по предполагаемой плотности распределения вероятностей, отражающей степень уверенности в появлении того или иного события.... Оба подхода используют общепринятые интерпретации понятия вероятности".
Примечание - Трактовка распределения вероятностей при определении оценки неопределенности типа В характерна для байесовского анализа [21, 27]. В настоящее время продолжаются исследования [22] границ применимости формулы Уэлча-Саттертуэйта для расчета числа степеней свободы, приписываемых стандартной неопределенности.
5.1.3 Формулировку измерительной задачи осуществляет метролог с возможным участием специалиста в той области знаний, в которой проводят измерение. В настоящем стандарте приведены рекомендации по выбору плотности распределения вероятностей [стадия 4) этапа а) в соответствии с 5.1.1] для некоторых общих случаев (см. 6.4). Этапы трансформирования распределений и получения окончательных результатов [б) и в) в соответствии с 5.1.1], для которых приведены подробные указания, не требуют дополнительной метрологической информации и могут быть выполнены с любой допустимой точностью для поставленной задачи.
Примечание - Как только этап постановки задачи а) в соответствии с 5.1.1 выполнен, тем самым плотность распределения вероятностей для выходной величины формально полностью определена. Однако вычисление математического ожидания, стандартного отклонения и интервала охвата может потребовать применения численных методов, обладающих некоторой степенью приближения.
5.2 Трансформирование распределений
В настоящем стандарте рассматривается общий эффективный способ определения (численным методом) функции распределения случайной величины :
![]() .
.
Этот способ основан на применении метода Монте-Карло для трансформирования распределений входных величин (см. 5.9).
Примечание - Формально плотность распределения вероятностей случайной величины можно представить в виде [9]
![]() ,
,
где - дельта функции Дирака, и применять численные методы вычисления
-кратного интеграла (поскольку в общем случае он не может быть взят аналитически). Однако такой способ численного вычисления плотности распределения вероятностей
неэффективен.
5.3 Получение окончательного результата
5.3.1 Оценка входной величины
представляет собой оценку математического ожидания
. Стандартная неопределенность
оценки
представляет собой оценку стандартного отклонения
, т.е. положительный квадратный корень из дисперсии
.
5.3.2 Интервал охвата для может быть определен на основе
![]() . Если задать требуемую вероятность охвата
. Если задать требуемую вероятность охвата и взять любое число
из интервала от нуля до
![]() , то границами
, то границами %-ного интервала охвата для
будут значения
![]() и
и ![]() , т.е. квантили распределения
, т.е. квантили распределения ![]() уровней
уровней и
![]() соответственно.
соответственно.
5.3.3 Выбор ![]() позволяет определить вероятностно симметричный
позволяет определить вероятностно симметричный %-ный интервал охвата, границами которого являются квантили уровней
![]() и
и ![]() .
.
Примечание - Если плотность распределения вероятностей для симметрична относительно математического ожидания
, то полученный интервал будет совпадать с интервалом
![]() , где расширенная неопределенность
, где расширенная неопределенность [Руководство ИСО/МЭК 98-3 (2.3.5)] равна произведению стандартной неопределенности
на коэффициент охвата, соответствующий данной плотности распределения вероятностей. В общем случае плотность распределения вероятностей выходной величины не может быть выражена в аналитическом виде.
5.3.4 Если плотность распределения вероятностей асимметрична, то более подходящим может быть выбор , отличающийся от
![]() , например позволяющий получить наименьший
, например позволяющий получить наименьший %-ный интервал охвата. Если плотность распределения вероятностей унимодальна, то оно обладает таким свойством, что наименьший интервал охвата будет включать в себя моду этого распределения. Данному интервалу будет соответствовать значение
, удовлетворяющее соотношению
![]() . В случае распределения общего вида значение
. В случае распределения общего вида значение , соответствующее наименьшему
%-ному интервалу охвата, должно быть таким, чтобы разность
![]() была минимальна.
была минимальна.
5.3.5 Для симметричной плотности распределения вероятностей, например для нормального или масштабированного смещенного -распределения, используемых при оценивании неопределенности по GUM, вероятностно симметричный и наименьший
%-ные интервалы охвата совпадают между собой. Поэтому в способе оценивания неопределенности по GUM эти интервалы не различают.
5.3.6 На рисунке 1 показана функция распределения ![]() , соответствующая асимметричной плотности распределения вероятностей. Пунктирными вертикальными линиями показаны границы вероятностно симметричного 95%-ного интервала охвата, а пунктирными горизонтальными линиями - соответствующие значения вероятности 0,025 и 0,975. Сплошными линиями показаны границы наименьшего 95%-ного интервала охвата и соответствующие значения вероятности, которые в данном случае равны 0,006 и 0,956. Длина этих двух интервалов охвата для данного примера составляет соответственно 1,76 и 1,69.
, соответствующая асимметричной плотности распределения вероятностей. Пунктирными вертикальными линиями показаны границы вероятностно симметричного 95%-ного интервала охвата, а пунктирными горизонтальными линиями - соответствующие значения вероятности 0,025 и 0,975. Сплошными линиями показаны границы наименьшего 95%-ного интервала охвата и соответствующие значения вероятности, которые в данном случае равны 0,006 и 0,956. Длина этих двух интервалов охвата для данного примера составляет соответственно 1,76 и 1,69.
- величина (безразмерная);
- функция распределения
Рисунок 1 - Функция распределения ![]() , вероятностно симметричный и наименьший 95%-ные интервалы охвата
, вероятностно симметричный и наименьший 95%-ные интервалы охвата
5.4 Способы трансформирования распределений
5.4.1 Трансформирование распределений осуществляют несколькими способами:
a) аналитическими методами, обеспечивающими определение плотности распределения вероятностей для за счет применения математических преобразований;
b) применением закона трансформирования неопределенностей, основанного на замене функции измерения ее аппроксимацией рядом Тейлора с членами первого порядка [Руководство ИСО/МЭК 98-3 (5.1.2)];
c) применением того же закона трансформирования неопределенностей [см. перечисление b) выше], но с учетом членов разложения более высокого порядка [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)];
d) численными методами [Руководство ИСО/МЭК 98-3 (G.1.5)], в том числе с использованием метода Монте-Карло (см. 5.9).
Примечание 1 - Аналитические методы превосходят все прочие с той точки зрения, что они не используют приближений. Однако они применимы только в простых случаях. Применение аналитических методов и примеры их использования приведены в [8, 13]. Далее эти методы в настоящем стандарте рассматриваются только в примерах (см. раздел 9).
Примечание 2 - Метод Монте-Карло в настоящем стандарте используется для получения распределения выходной величины, а не в качестве метода имитационного моделирования. При оценке неопределенности на этапе трансформирования распределений решаемая задача является детерминированной, поэтому в имитационном моделировании случайного процесса нет необходимости.
5.4.2 GUM допускает применение подходов к оценке неопределенности, отличных от того, что использован в самом GUM [см. Руководство ИСО/МЭК 98-3 (G.1.5)]. Однако самым общим из этих подходов является тот, что установлен в настоящем стандарте и основан на трансформировании распределений. Для линейных и линеаризованных функций измерения и входных величин, подчиняющихся нормальному распределению, такой подход согласуется с подходом GUM. Однако в случаях, когда условия применения подхода GUM не выполняются (см. 5.7 и 5.8), подход, установленный в настоящем стандарте, позволяет получить обоснованные заключения о неопределенности.
5.4.3 Трансформирование распределений требует выбора подходящего метода. Если можно продемонстрировать, что условия, необходимые для получения достоверных результатов в соответствии с GUM, выполнены, то может быть использован подход GUM. Если имеются основания полагать, что оценка неопределенности, полученная по GUM, окажется недостоверной, то должен быть применен другой подход. Может возникнуть ситуация, когда сложно оценить обоснованность применения способа оценивания неопределенности по GUM. Однако во всех трех вышеописанных случаях хороший результат может быть получен с использованием метода Монте-Карло. В первом случае метод Монте-Карло может быть проще в применении, например, вследствие трудностей вычисления коэффициентов чувствительности [Руководство ИСО/МЭК 98-3 (5.1.3)]. Во втором случае метод Монте-Карло позволит получить достоверный результат, т.к. его применение не требует использования дополнительных предположений. В третьем случае метод Монте-Карло может быть применен как собственно для получения оценки неопределенности, так и для оценки качества результатов, полученных способом расчета неопределенности по GUM.
5.4.4 Трансформирование моделью измерений плотностей распределения вероятностей ![]() ,
, 1, ...,
входных величин
для получения плотности распределения вероятностей
![]() выходной величины
выходной величины , показано на рисунке 2 для трех независимых
(
3). Рисунок 2 можно сравнить с рисунком 3, иллюстрирующим закон трансформирования неопределенностей. На рисунке 2 функции
![]() ,
, 1, 2, 3 представляют собой плотности распределения вероятностей случайных величин, подчиняющихся соответственно нормальному, треугольному и нормальному законам. Соответственно функция
![]() показана асимметричной, что обычно имеет место в случае нелинейных моделей или асимметрии функций
показана асимметричной, что обычно имеет место в случае нелинейных моделей или асимметрии функций ![]() .
.
Рисунок 2 - Трансформирование распределений трех (3) независимых входных величин
5.4.5 На практике только в самых простых случаях преобразование распределений может быть выполнено без приближений. При оценке неопределенности по GUM применяется один метод приближения, в методе Монте-Карло - другой. Для небольшой, но важной подгруппы задач оценки неопределенности в соответствии с GUM не требуется применения приближений (решение является точным). Метод Монте-Карло не позволяет получить точные результаты, но для широкого класса задач он будет более обоснованным, чем подход GUM.
5.5 Представление результатов
5.5.1 После выполнения трансформирования распределений должна быть отражена, как правило, следующая информация:
a) оценка выходной величины
;
b) стандартная неопределенность оценки
;
c) заданная %-ная (например, 95%-ная) вероятность охвата;
d) границы выбранного %-ного (например, 95%-ного) интервала охвата для
;
e) другая значимая информация, такая как тип интервала охвата (вероятностно симметричный или наименьший).
5.5.2 Значения ,
и границ
%-ного интервала охвата для
должны быть указаны с таким количеством значащих цифр, чтобы низший разряд записи значения этих величин совпадал с низшим разрядом, используемым для записи
[Руководство ИСО/МЭК 98-3 (7.2.6)]. Обычно для представления
достаточно одной или двух значащих цифр.
Примечание 1 - Представляемое численное значение обычно получают путем округления числа, содержащего большее количество значащих цифр.
Примечание 2 - Фактором, влияющим на выбор представления результатов одной или двумя значащими цифрами, является значащая цифра высшего разряда в значении . Если это 1 или 2, то погрешность округления
будет сопоставима с самим значением величины. Если же первая значащая цифра равна 9, то относительная погрешность округления будет меньше.
Примечание 3 - Если полученные результаты должны быть использованы в дальнейших вычислениях, следует определить, есть ли необходимость в сохранении большего числа значащих цифр.
Пример - Результаты для ,
и границ интервала охвата в случае, когда интервал охвата асимметричен относительно
, а
имеет две значащие цифры, приведены в виде: "
1,024 В;
![]() 0,028 В; наименьший 95%-ный интервал охвата: [0,983, 1,088] В".
0,028 В; наименьший 95%-ный интервал охвата: [0,983, 1,088] В".
Те же результаты в случае, когда выражен одной значащей цифрой, имеют вид: "
1,02 В,
![]() 0,03 В, наименьший 95%-ный интервал охвата: [0,98, 1,09] В".
0,03 В, наименьший 95%-ный интервал охвата: [0,98, 1,09] В".
5.6 Оценивание неопределенности по GUM
5.6.1 В GUM установлено общее руководство, распространяющееся на разные аспекты последовательного оценивания неопределенности в соответствии с 5.1.1, и установлен способ оценивания неопределенности для этапов трансформирования распределений и получения окончательных результатов измерения. Общая схема оценивания неопределенности, установленная GUM, принята многими организациями, нашла широкое практическое применение, используется в стандартах и руководствах, в которых рассматриваются вопросы оценки неопределенности измерения, и реализована в программных средствах.
5.6.2 Способ оценивания неопределенности по GUM включает в себя следующие этапы. Каждая входная величина модели характеризуется математическим ожиданием и стандартным отклонением плотности распределения вероятностей, поставленной в соответствие этой величине [Руководство ИСО/МЭК 98-3 (4.1.6)]. Оценку математического ожидания принимают в качестве наилучшей оценки
величины
, а оценку стандартного отклонения - в качестве стандартной неопределенности
оценки
. На основе этих данных в соответствии с законом трансформирования неопределенностей [Руководство ИСО/МЭК 98-3 (5.1.2)] через разложение функции измерения в ряд Тейлора с сохранением членов первого или более высокого порядка малости, получают:
a) оценку выходной величины
,
b) стандартную неопределенность оценки
.
Оценку определяют как значение функции измерения в точке
. При определении интервала охвата для
используют предположение, что
подчиняется нормальному распределению или, если число степеней свободы, соответствующее
, конечно [Руководство ИСО/МЭК 98-3 (приложение G)], масштабированному смещенному
-распределению.
Примечание - В число характеристик входной величины может входить также число степеней свободы для [Руководство ИСО/МЭК 98-3 (4.2.6)], а также, при необходимости, попарные ковариации оценок входных величин [Руководство ИСО/МЭК 98-3 (5.2.5)].
5.6.3 Этапы трансформирования распределений и получения окончательных результатов по GUM [этапы b) и с) в 5.1.1] включают в себя следующие компьютерные расчеты [см. рисунок 3, иллюстрирующий закон трансформирования неопределенностей для модели с тремя (3) независимыми входными величинами
![]() , соответствующими оценками
, соответствующими оценками и стандартными неопределенностями этих оценок
,
1, 2, 3; оценкой выходной величины
является
с соответствующей стандартной неопределенностью
]:
Рисунок 3 - Трансформирование неопределенностей для трех (3) независимых входных величин
a) в соответствии с плотностью распределения вероятностей для входных величин ![]() определяют оценки математического ожидания
определяют оценки математического ожидания ![]() и стандартного отклонения (стандартные неопределенности)
и стандартного отклонения (стандартные неопределенности) ![]() . Если
. Если являются статистически зависимыми (имеют ненулевую ковариацию), то используют совместную плотность распределения
;
b) определяют число степеней свободы (бесконечное или конечное) для каждой ;
c) для каждой пары зависимых величин и
на основе совместной плотности распределения
и
определяют ковариацию (взаимную неопределенность)
![]() для
для и
;
d) определяют частные производные первого порядка от ![]() по
по ;
e) вычисляют оценку, подставляя в функцию измерения ![]() ;
;
f) вычисляют коэффициенты чувствительности модели [Руководство ИСО/МЭК 98-3 (5.1.3)] через значения вычисленных частных производных в точке ;
g) вычисляют стандартную неопределенность , объединяя
,
![]() и коэффициенты чувствительности модели [Руководство ИСО/МЭК 98-3, формулы (10), (13)];
и коэффициенты чувствительности модели [Руководство ИСО/МЭК 98-3, формулы (10), (13)];
h) вычисляют [число эффективных степеней свободы для
] по формуле Уэлча-Саттертуэйта [Руководство ИСО/МЭК 98-3, формула (G.2b)];
i) вычисляют расширенную неопределенность и соответствующий интервал охвата (для заданной вероятности охвата
) для
(рассматриваемой в качестве случайной величины) посредством выбора множителя для
в виде квантиля распределения функции
![]() , предполагаемого стандартным нормальным распределением (для
, предполагаемого стандартным нормальным распределением (для ![]() ) или
) или -распределением (для
![]() ).
).
5.7 Условия применимости способа оценивания по GUM в случае линейной модели
5.7.1 В случае линейных моделей (функция измерения линейна относительно ) применение закона трансформирования неопределенностей всегда корректно.
5.7.2 Интервал охвата может быть определен в соответствии с GUM при выполнении следующих условий:
a) применима формула Уэлча-Саттертуэйта для вычисления числа эффективных степеней свободы [Руководство ИСО/МЭК 98-3 (G.4.1)], если одной или нескольким
соответствует конечное число степеней свободы;
b) если стандартной неопределенности оценки какой-либо входной величины соответствует конечное число степеней свободы, то эта оценка не зависит от оценок других входных величин;
c) плотность распределения вероятностей для может быть аппроксимирована нормальным распределением или масштабированным смещенным
-распределением.
Примечание 1 - Условие а) обеспечивает возможность описания масштабированным смещенным
-распределением.
Примечание 2 - Условие b) связано с тем, что GUM не рассматривает возможность оценивания неопределенности в случае зависимых с конечным числом степеней свободы.
Примечание 3 - Условие с) заведомо выполняется, если каждая случайная величина подчиняется нормальному распределению. Оно выполняется также в случае, когда выполнены условия центральной предельной теоремы [Руководство ИСО/МЭК 98-3 (G.2)].
Примечание 4 - Способ оценивания неопределенности по GUM не может быть применен, если величина , вклад которой в
является доминирующим, не подчиняется нормальному распределению.
5.8 Условия применимости способа оценивания неопределенности по GUM для нелинейных моделей
5.8.1 Закон трансформирования неопределенностей может быть применен для нелинейных моделей при выполнении следующих условий:
a) функция имеет непрерывную производную по компонентам
вектора
в окрестностях оценок
;
b) условие а) справедливо в отношении производных всех порядков, используемых в законе трансформирования неопределенностей;
c) величины , входящие в значимые члены разложения функции
![]() в ряд Тейлора высших порядков, независимы;
в ряд Тейлора высших порядков, независимы;
d) величины , входящие в члены разложения функции
![]() в ряд Тейлора высших порядков, подчиняются нормальному распределению;
в ряд Тейлора высших порядков, подчиняются нормальному распределению;
е) члены высших порядков, не включенные в аппроксимацию ![]() рядом Тейлора, пренебрежимо малы.
рядом Тейлора, пренебрежимо малы.
Примечание 1 - Условие а) необходимо для применения закона трансформирования неопределенностей, основанного на аппроксимации ![]() рядом Тейлора первого порядка, когда нелинейность
рядом Тейлора первого порядка, когда нелинейность ![]() незначительна [Руководство ИСО/МЭК 98-3 (5.1.2)].
незначительна [Руководство ИСО/МЭК 98-3 (5.1.2)].
Примечание 2 - Условие b) необходимо для применения закона трансформирования неопределенностей, основанного на аппроксимации ![]() рядом Тейлора более высокого порядка [Руководство ИСО/МЭК 98-3 (5.1.2)]. Выражение для наиболее важных членов более высокого порядка, которые необходимо учесть, приведено в GUM [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)].
рядом Тейлора более высокого порядка [Руководство ИСО/МЭК 98-3 (5.1.2)]. Выражение для наиболее важных членов более высокого порядка, которые необходимо учесть, приведено в GUM [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)].
Примечание 3 - Условие с) относится к рассматриваемому в GUM случаю, когда в разложении в ряд Тейлора учитываются члены высших порядков, определяемых независимыми [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)]. Возможность учета членов высших порядков, определяемых зависимыми
, в GUM не рассматривается.
Примечание 4 - Условие d) представляет собой уточнение утверждения GUM [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)] о том, что закон трансформирования неопределенностей, учитывающий члены высших порядков, основан на предположении о симметричности плотностей распределения вероятностей для [19, 27].
Примечание 5 - Если требуемое для существенно нелинейной функции измерения аналитическое определение частных производных высших порядков представляет трудности или может привести к ошибкам, то допускается применение методов численного дифференцирования с использованием соответствующего программного обеспечения. Как вариант, частные производные могут быть аппроксимированы численно методом конечных разностей [5]. (В GUM приведена формула конечно-разностной аппроксимации для вычисления частных производных первого порядка [Руководство ИСО/МЭК 98-3 (примечание 2 к 5.1.3)].) Однако следует соблюдать осторожность, оперируя конечными разностями для близких значений функции, поскольку погрешности округления чисел при использовании арифметики с конечной точностью способны привести к значительным ошибкам в расчетах.
5.8.2 Интервал охвата может быть определен в соответствии с GUM, если выполнены условия а), b) и с), установленные в 5.7.2, а примечание 3 из 5.8.1 заменено на следующее: "Условие с) необходимо для того, чтобы интервал охвата мог быть определен из распределений этих величин".
5.8.3 Если условия 5.8.1 или 5.8.2 выполнены (что справедливо для многих практических ситуаций), то этого обычно достаточно для корректного применения способа оценивания неопределенности по GUM.
5.9 Метод Монте-Карло для этапов трансформирования распределений и получения окончательных результатов
5.9.1 Метод Монте-Карло обеспечивает получение приближенного численного представления математического объекта , которым может быть, в частности, функция распределения
![]() для [32, стр.75]. Основным принципом этого подхода является получение повторных выборок из плотностей распределения вероятностей для входных величин
для [32, стр.75]. Основным принципом этого подхода является получение повторных выборок из плотностей распределения вероятностей для входных величин и получение соответствующей выборки на выходе модели.
5.9.2 Поскольку ![]() содержит в себе всю известную информацию об
содержит в себе всю известную информацию об , то на основе приближения
может быть получена аппроксимация любой характеристики
, такой как математическое ожидание, дисперсия или интервал охвата. Качество полученных результатов улучшается по мере увеличения числа выборок.
5.9.3 Математическое ожидание и дисперсия (а также более высокие моменты распределения) могут быть определены непосредственно по выборке на выходе модели. Для определения интервала охвата необходимо предварительно эту выборку упорядочить.
5.9.4 Если ,
1, ...,
, представляют собой
значений на выходе модели, взятых независимо из плотности распределения вероятностей для
, то приближенные значения математического ожидания
и дисперсии
могут быть получены по этим выборочным значениям
. В общем случае все моменты
[включая
и
] могут быть аппроксимированы их выборочными значениями. Если обозначить
число значений выборки, не превышающих некоторого произвольно выбранного значения
, то вероятность
![]() можно приближенно определить равной
можно приближенно определить равной ![]() . Таким образом по выборке
. Таким образом по выборке можно построить ступенчатую функцию, аппроксимирующую функцию распределения
![]() .
.
5.9.5 Каждое значение определяют на основе случайной выборки входных величин
из их распределений вероятностей и последующего преобразования этих входных величин моделью измерения. Приближение
, полученное методом Монте-Карло, представляет собой выборочные значения
, расположенные в строго возрастающем порядке.
Примечание - Существует небольшая вероятность того, что найдутся элементы выборки , совпадающие по значению. В этом случае построить строго возрастающую последовательность можно, внося в совпадающие элементы выборки малые случайные возмущения (см. 7.5.1).
5.9.6 Применение метода Монте-Карло для трансформирования распределений схематически показано на рисунке 4 для случая заранее заданного значения (случай, когда
не задается заранее, рассматривается в 7.9). Поэтапная процедура метода Монте-Карло включает в себя:
a) выбор числа испытаний (см. 7.2);
b) формирование в каждом из испытаний
-мерного вектора входных величин
в соответствии с их законами распределения (см. 7.3);
c) получение для каждого такого вектора значения на выходе модели измерения (см. 7.4);
d) расположение полученных значений
в строго возрастающем порядке, обеспечивающее построение приближения
(см. 7.5);
e) получение на основе оценки
для
и ее стандартной неопределенности
(см. 7.6);
f) построение на основе интервала охвата для
, соответствующего заданной вероятности охвата
(см. 7.7).
Рисунок 4 - Этапы трансформирования распределений и получения окончательных результатов оценивания неопределенности методом Монте-Карло
Примечание 1 - Формирование выборки из распределений вероятностей рассматривается в 6.4 и в приложении С.
Примечание 2 - Среднее арифметическое из значений на выходе модели является случайной величиной с математическим ожиданием
и дисперсией
![]() . Таким образом, близость среднего арифметического к
. Таким образом, близость среднего арифметического к пропорциональна
![]() .
.
Примечание 3 - На этапе е) можно использовать неупорядоченных реализаций
. Однако для определения интервала охвата на этапе f) значения выборки выходных значений модели необходимо упорядочить.
5.9.7 Эффективность метода Монте-Карло при определении ,
и интервала охвата для
зависит от адекватного выбора числа испытаний
[этап а) в 5.9.6]. Рекомендации по определению достаточного значения
и по другим вопросам реализации метода Монте-Карло приведены в [7] (см. также 7.2 и 7.9).
5.10 Условия применимости метода Монте-Карло
5.10.1 Применение метода Монте-Карло для трансформирования распределений с получением результатов оценивания неопределенности требует выполнения следующих условий:
a) функция измерения - непрерывна по всем
вектора
в окрестности наилучших оценок
входных величин
;
b) функция распределения для непрерывна и строго возрастающая;
c) плотность распределения вероятностей для :
1) непрерывна на интервале, где ее значения строго положительны,
2) унимодальна (т.е. имеет единственный максимум),
3) равна нулю или монотонно возрастает слева от моды и монотонно убывает или равна нулю справа от моды;
d) и
существуют;
e) выбранное значение является достаточно большим.
Примечание 1 - В отличие от требования а) непрерывности самой функции измерения никаких условий на производные этой функции не налагается.
Примечание 2 - Условия а) и b) обеспечивают однозначность функции обратной функции распределения и, следовательно, позволяют определить интервал охвата. Если определение интервала охвата не требуется, то необходимым является только условие а).
Примечание 3 - Условие с) необходимо только в случае определения наименьшего интервала охвата. Тогда условие с) обеспечивает единственность наименьшего интервала охвата, соответствующего заданной вероятности охвата. Если мода является граничной точкой интервала, на котором плотность распределения вероятностей отлична от нуля, то одно из двух условий перечисления 3) является лишним.
Примечание 4 - Условие d) необходимо для обеспечения сходимости по вероятности оценок, полученных методом Монте-Карло, при увеличении (см. 7.2).
Примечание 5 - Условие е) необходимо для обеспечения достоверности результатов оценивания неопределенности (см. 8.2).
5.10.2 Если условия, указанные в 5.10.1, выполнены, то результаты оценивания неопределенности с использованием метода Монте-Карло можно считать достоверными. Эти условия менее жесткие, чем те, выполнение которых необходимо для оценивания неопределенности по GUM (см. 5.7 и 5.8).
5.11 Сравнение способов оценивания неопределенности по GUM и методом Монте-Карло
5.11.1 Целью подраздела является сравнение принципов, лежащих в основе оценивания неопределенности по GUM и методом Монте-Карло, используемого для преобразования распределений. В настоящем подразделе приведены некоторые обоснования использования метода Монте-Карло в условиях, когда обоснованность применения способа оценивания неопределенности по GUM остается неясной.
5.11.2 Для сравнения способа оценивания неопределенности по GUM с методом Монте-Карло полезно сделать обзор основных положений GUM, касающихся оценок неопределенности типов А и В. При определении оценки неопределенности типа A GUM позволяет получить наилучшую оценку величины и соответствующей стандартной неопределенности в виде среднего арифметического и выборочного стандартного отклонения, полученных на основе независимых наблюдений. При определении оценки неопределенности типа В используют априорные знания о величине для описания с ее помощью плотности распределения вероятностей, на основе которых определяют наилучшую оценку величины и соответствующую стандартную неопределенность. В соответствии с GUM оба типа оценок основаны на использовании распределений вероятностей [Руководство ИСО/МЭК 98-3 (3.3.4)] и общепризнанных интерпретаций вероятности [Руководство ИСО/МЭК 98-3 (3.3.5)]. В подходе GUM оценивание неопределенности подразумевает трансформирование распределений вероятностей, поскольку входной и выходной величинам в нем ставятся в соответствие случайные величины, обладающие своими распределениями вероятностей [Руководство ИСО/МЭК 98-3 (G.6.6)] (см. также 5.1.2).
5.11.3 В методе оценивания неопределенности по GUM плотность распределения вероятностей выходной величины в явном виде не определяют. Ссылки настоящего стандарта при рассмотрении подхода GUM на распределение выходной величины исходят из того, что существование такого распределения обусловлено смыслом процедуры оценивания.
5.11.4 Метод, устанавливаемый настоящим стандартом, в максимально возможной степени совместим с GUM, особенно в отношении использования плотностей распределения вероятностей для описания всех входящих в модель измерения величин, но может отличаться от него в следующем:
a) всем входным величинам в явном виде приписаны соответствующие плотности распределения вероятностей (а не стандартные неопределенности оценок
этих величин) на основе имеющейся информации об этих величинах. Классификация оценок на оценки типов А и В не используется;
b) вычисление коэффициентов чувствительности [Руководство ИСО/МЭК 98-3 (5.1.3)] не является неотъемлемой частью метода, и, следовательно, вычисление или численная аппроксимация частных производных функции измерения по не требуется. Тем не менее, метод позволяет получить приближенные значения коэффициентов чувствительности, которые, однако, не будут соответствовать коэффициентам разложения функции измерения в ряд Тейлора первого порядка, а будут учитывать все члены высшего порядка этого разложения (см. приложение В);
c) численное представление функции распределения выходной величины , полностью определяемое видом модели измерения и плотностями распределения вероятностей для
, не ограничивается нормальным распределением или масштабированным смещенным
-распределением;
d) поскольку плотность распределения вероятностей для не является в общем случае симметричной, интервал охвата для
также не всегда симметричен относительно ее оценки. Следовательно, для выбора интервала охвата, соответствующего заданной вероятности охвата, необходима дополнительная информация.
5.11.5 Так как способ оценивания неопределенности по GUM оперирует только наилучшими оценками и соответствующими стандартными неопределенностями (а также, при необходимости, ковариациями и числами степеней свободы), предоставляемая им информация о выходной величине
ограничена. По существу, он позволяет лишь получить оценку
для
и соответствующую
стандартную неопределенность
, а также, в ряде случаев, оценку числа эффективных степеней свободы. Если функция измерения линейна по
, то оценки
и соответствующей неопределенности
будут достоверны. Всю остальную информацию об
, в том числе интервалы охвата, получают на основе дополнительных предположений о виде распределения
(оно является либо нормальным, либо масштабированным смещенным
-распределением).
5.11.6 Метод Монте-Карло обладает следующими преимуществами:
a) сокращаются аналитические расчеты в случае более сложных или нелинейных моделей, особенно вследствие того, что не требуется определение частных производных первого или более высоких порядков, необходимых для оценки коэффициентов чувствительности в соответствии с законом трансформирования неопределенности;
b) в общем случае улучшаются оценки для нелинейных моделей [Руководство ИСО/МЭК 98-3 (4.1.4)];
c) улучшаются оценки стандартной неопределенности оценки для нелинейных моделей, особенно когда
приписано негауссово (а, например, асимметричное) распределение, без необходимости определения производных высших порядков [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)];
d) существует возможность построения интервала охвата в соответствии с заданной вероятностью охвата, когда плотность распределения вероятностей для не может быть адекватно аппроксимирована нормальным распределением или масштабированным смещенным
-распределением, т.е. когда центральная предельная теорема неприменима [Руководство ИСО/МЭК 98-3 (G.2.1, G.6.6)]. Аппроксимация нормальным распределением или масштабированным смещенным
-распределением может быть неадекватной, когда (1) распределение, приписанное доминирующей входной величине
, не является нормальным распределением или масштабированным смещенным
-распределением, (2) функция модели нелинейна, (3) ошибка аппроксимации, обусловленная используемой формулой Уэлча-Саттертуэйта для расчета числа эффективных степеней свободы, является существенной;
е) для определения интервала охвата не требуется использования коэффициента охвата [Руководство ИСО/МЭК 98-3 (2.3.6)].
6 Плотности распределения вероятностей входных величин
6.1 Общие положения
6.1.1 Настоящий раздел содержит рекомендации по выбору в некоторых типичных ситуациях плотностей распределения вероятностей для входных величин на этапе формулировки задачи оценивания неопределенности. Выбор плотности распределения вероятностей может быть основан на теореме Байеса [20] или на принципе максимума энтропии [8, 26, 51, 56].
Примечание - В некоторых случаях выбор приписываемой плотности распределения вероятностей может быть основан на иных соображениях. Но всегда должны быть зафиксированы основания, положенные в основу этого выбора.
6.1.2 В общем случае входным величинам ![]() соответствует совместная плотность распределения вероятностей
соответствует совместная плотность распределения вероятностей ![]() (см. 6.4.8.4, примечание 2).
(см. 6.4.8.4, примечание 2).
6.1.3 Если независимы, то каждой величине
может быть поставлена в соответствие плотность распределения вероятностей
![]() , вид которой выбирают, основываясь на анализе наблюдений (оценка неопределенности типа А) или научных суждениях с использованием (см. [50]) истории наблюдений, данных калибровки и экспертных оценок (оценка неопределенности типа В) [Руководство ИСО/МЭК 98-3 (3.3.5)].
, вид которой выбирают, основываясь на анализе наблюдений (оценка неопределенности типа А) или научных суждениях с использованием (см. [50]) истории наблюдений, данных калибровки и экспертных оценок (оценка неопределенности типа В) [Руководство ИСО/МЭК 98-3 (3.3.5)].
6.1.4 В случае, когда независимы только некоторые из , индивидуальные плотности распределения вероятностей приписывают только этим входным величинам, а для остальных применяют совместную плотность распределения.
Примечание - В ряде случаев от всех или некоторых зависимостей между входными величинами можно избавиться посредством их замены на другие переменные величины [Руководство ИСО/МЭК 98-3 (F.1.2.4, Н.1.2)]. Такая замена может упростить как применение закона трансформирования неопределенностей, так и закона трансформирования распределений. Более подробно этот вопрос с иллюстрацией примерами рассмотрен в [15].
6.1.5 Значимая информация для выбора плотности распределения вероятностей для приведена в GUM [Руководство ИСО/МЭК 98-3 (4.3)].
6.1.6 В настоящем стандарте не приводятся подробные рекомендации по выбору плотностей распределения вероятностей индивидуальных или совместных. Вид выбранной плотности распределения вероятностей в неявном виде включает в себя знания и практический опыт метролога, составляющего модель измерения, который в конечном счете несет ответственность за качество конечных результатов.
6.1.7 Справочным руководством по видам распределения вероятностей может служить [18].
6.2 Теорема Байеса
6.2.1 Если информация о некоторой входной величине содержится в серии наблюдений, рассматриваемых как реализации независимых одинаково распределенных случайных величин с заданной формой плотности распределения вероятностей, но с неизвестными математическим ожиданием и дисперсией, то приписываемая входной величине
плотность распределения вероятностей может быть рассчитана по теореме Байеса. Расчет включает в себя два этапа. Сначала неизвестным математическому ожиданию и дисперсии приписывают неинформативное совместное распределение (априорное). Затем, используя теорему Байеса, совместную плотность распределения вероятностей уточняют на основе данных серии наблюдений, в результате чего получают совместную плотность распределения (апостериорную) для двух неизвестных параметров. После этого искомую апостериорную плотность распределения вероятностей неизвестного математического ожидания, которую рассматривают как плотность распределения, приписываемую
, вычисляют интегрированием совместной плотности распределения по области возможных значений неизвестной дисперсии (см. 6.4.9.2).
6.2.2 В соответствии с теоремой Байеса для уточнения плотности распределения вероятностей используют произведение априорной плотности распределения вероятностей на функцию правдоподобия [20]. Функция правдоподобия в случае независимых наблюдений является произведением значений плотностей распределения вероятностей (например, гауссовых с неизвестным математическим ожиданием и дисперсией) для полученных наблюдений. Апостериорную плотность распределения вероятностей получают интегрированием произведения априорной плотности распределения вероятностей и функции правдоподобия по всем возможным значениям дисперсии с последующей нормировкой.
Примечание 1 - Иногда (например, как в 6.4.11) случайные величины, для которых получены наблюдения, описываются плотностью распределения с единственным параметром распределения. В таких случаях математическому ожиданию этого распределения приписывают неинформативную априорную плотность распределения вероятностей, а апостериорное распределение, понимаемое как распределение , формируют непосредственно в соответствии с теоремой Байеса без последующего интегрирования.
Примечание 2 - Теорема Байеса может быть также применена для разных предположений о виде распределения наблюдаемых случайных величин, например, когда их неизвестные математическое ожидание и стандартное отклонение полагают равными между собой.
6.3 Принцип максимума энтропии
6.3.1 При использовании принципа максимума энтропии, введенного Джейнсом [25], выбирают единственную плотность распределения вероятностей из всех возможных распределений с заданными свойствами, например заданными центральными моментами различного порядка или заданными интервалами, на которых плотность распределения вероятностей не равна нулю. Этот метод особенно полезен для выбора плотности распределения вероятностей величин, для которых данные наблюдений недоступны, или величин, которые невозможно измерить.
6.3.2 При применении принципа максимума энтропии в качестве плотности распределения вероятностей ![]() , которая адекватно характеризует неполноту знания о величине
, которая адекватно характеризует неполноту знания о величине , выбирают такую, для которой функционал
![]() ,
,
представляющий собой энтропию по Шеннону [48], достигает максимума при ограничениях, определяемых имеющейся информацией об .
6.4 Выбор плотности распределения в некоторых типичных условиях
6.4.1 Общие положения
Информация, приведенная в 6.4.2-6.4.11, позволяет выбрать плотности распределения вероятностей случайных величин на основе различной имеющейся информации об этих величинах. Вид плотности распределения вероятностей ![]() определяет:
определяет:
a) формулы для математического ожидания и дисперсии ;
b) способ получения выборки из ![]() .
.
Сведения, приведенные в 6.4.2-6.4.11, и графическое представление распределений, к которым эти сведения относятся, собраны в таблице 1.
Таблица 1 - Информация о случайной величине и вид соответствующей плотности распределения вероятностей
Информация о величине | Распределение вероятностей | Пункт | |
Нижняя и верхняя границы: | Равномерное |
| 6.4.2 |
Неточно известные нижняя и верхняя границы: | Криволинейно-трапецеидальное |
| 6.4.3 |
Сумма двух равномерно распределенных величин с границами ( | Трапецеидальное |
| 6.4.4 |
Сумма двух равномерно распределенных величин с границами ( | Треугольное |
| 6.4.5 |
Гармоническое колебание между нижней ( | Арксинусное (U-образное) |
| 6.4.6 |
Наилучшая оценка | Нормальное (гауссово)
|
| 6.4.7 |
Наилучшая оценка | Многомерное нормальное (гауссово) | 6.4.8 | |
Выборка независимых наблюдений |
|
| 6.4.9.2 |
Наилучшая оценка |
|
| 6.4.9.7 |
Наилучшая оценка | Экспоненциальное |
| 6.4.10 |
Число | Гамма-распределение |
| 6.4.11 |
Примечание - Графики плотностей распределения вероятностей в таблице 1 даны без соблюдения масштаба. График многомерного нормального распределения не показан. | |||
6.4.2 Равномерное (прямоугольное) распределение
6.4.2.1 Если единственной доступной информацией о величине являются нижняя
и верхняя
(
) границы возможных значений этой величины, то в соответствии с принципом максимума энтропии
следует описывать равномерным распределением
![]() на интервале [
на интервале [,
].
6.4.2.2 Плотность распределения вероятностей для в этом случае имеет вид:
 .
.
6.4.2.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() . (2)
. (2)
6.4.2.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , необходимо случайные значения
, необходимо случайные значения , полученные из стандартного равномерного распределения
![]() (см. С.3.3), преобразовать следующим образом:
(см. С.3.3), преобразовать следующим образом:
![]() .
.
6.4.3 Равномерное распределение с неточно известными границами
6.4.3.1 О величине может быть известно, что она находится в интервале с границами
и
,
![]() , таком, что средняя точка интервала
, таком, что средняя точка интервала ![]() фиксирована, а длина интервала
фиксирована, а длина интервала ![]() точно не определена, но известно, что
точно не определена, но известно, что лежит в интервале
![]() , а
, а - в интервале
![]() , где
, где ,
и
заданы и при этом
0,
![]() . Если никакой другой информации о
. Если никакой другой информации о ,
и
нет, то в соответствии с принципом максимума энтропии случайная величина
может быть описана криволинейно-трапецеидальным распределением
![]() .
.
6.4.3.2 Плотность распределения вероятностей для в этом случае имеет вид:
 (3)
(3)
где ![]() и
и ![]() являются, соответственно, средней точкой и полушириной интервала [
являются, соответственно, средней точкой и полушириной интервала [,
] [Руководство ИСО/МЭК 98-3 (примечание 2 к 4.3.9)]. Эта плотность распределения вероятностей похожа на трапецеидальную, но боковые стороны трапеции не являются прямыми линиями.
Примечание - Формула (3) может быть представлена в следующем виде, удобном для программирования:
 .
.
6.4.3.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() . (4)
. (4)
Примечание 1 - Дисперсия, полученная по формуле (4), всегда больше дисперсии соответствующего равномерного распределения, полученной по формуле (2), т.е. когда 0.
Примечание 2 - В GUM информация об , аналогичная приведенной в 6.4.3.1, используется для приписывания числа степеней свободы для стандартной неопределенности, связанной с наилучшей оценкой
[Руководство ИСО/МЭК 98-3 (G.4.2)].
6.4.3.4 Для получения выборочного значения из распределения
![]() независимо выбирают два значения
независимо выбирают два значения и
из стандартного равномерного распределения
(0, 1) (см. С.3.3) и формируют величины
и
:
![]() ,
, ![]() ,
,
и
![]() .
.
Примечание - - выборочное значение из прямоугольного распределения с границами
, a
формируют таким образом, чтобы средняя точка между
и
совпала с заданным значением
![]() .
.
Пример - В сертификате указано, что значение напряжения находится в интервале 10,0 В ±0,1 В. Какая-либо другая информация относительно
в сертификате не приведена, однако можно предположить, что значения границ интервала являются результатом корректного округления некоторого числового значения (см. 3.20). Поскольку значение 0,1, указанное в сертификате, могло быть получено в результате округления до одной значащей цифры любого числа из интервала (0,05; 0,15), то за интервал неточного задания границ, в пределах которых находится, можно принять интервал от 0,05 до 0,15 В. С учетом сказанного положение интервала можно считать фиксированным, а его длину известной неточно. Наилучшей оценкой
будет
10,0 В, и, используя выражение (4) для
9,9 В,
10,1 В и
0,05 В, можно получить значение соответствующей стандартной неопределенности
:
![]() .
.
Следовательно, ![]() (0,0036)
(0,0036)=0,060 В, что сопоставимо с
![]() 0,058 В в случае известных точных границ, которые получаются заменой d на ноль. Использование точных границ в этом случае дает значение
0,058 В в случае известных точных границ, которые получаются заменой d на ноль. Использование точных границ в этом случае дает значение на 4% меньше, чем в случае неточных границ. Значимость такого расхождения следует рассматривать в контексте измерительной задачи.
6.4.4 Трапецеидальное распределение
6.4.4.1 В GUM [Руководство ИСО/МЭК 98-3 (4.3.9)] рассмотрено применение симметричного трапецеидального распределения. Если случайная величина является суммой двух независимых случайных величин
и
, каждая из которых подчиняется равномерному распределению
![]() с нижней границей
с нижней границей и верхней границей
(
1, 2), то
подчиняется симметричному трапецеидальному распределению
![]() с нижней границей
с нижней границей , верхней границей
и параметром
, равным отношению длины верхнего основания трапеции к длине ее нижнего основания. Параметры трапецеидального распределения связаны с параметрами равномерного распределения следующими соотношениями:
![]() ,
, ![]() ,
, ![]() , (5)
, (5)
где
![]() ,
, ![]() ,
, ![]() . (6)
. (6)
6.4.4.2 Плотность распределения вероятностей для (рисунок 5), полученная в результате свертки двух распределений [42, стр.93], имеет вид:
 (7)
(7)
где ![]() .
.
Примечание - Формула (7) может быть представлена в следующем виде, удобном для программирования:
 .
.
Рисунок 5 - Плотность трапецеидального распределения суммы ![]() равномерно распределенных случайных величин
равномерно распределенных случайных величин и
6.4.4.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() .
.
6.4.4.4 Для получения выборочного значения из распределения
![]() независимо выбирают два значения
независимо выбирают два значения и
из стандартного равномерного распределения
![]() (см. С.3.3) и формируют
(см. С.3.3) и формируют
![]() .
.
6.4.5 Треугольное распределение
6.4.5.1 Если величина является суммой двух независимых случайных величин, каждая из которых подчиняется равномерному распределению (см. 6.4.4), и
![]() , то из выражений (5) и (6) следует, что
, то из выражений (5) и (6) следует, что 0 и
0. Таким образом, трапецеидальное распределение
![]() превращается в симметричное треугольное распределение
превращается в симметричное треугольное распределение ![]() на интервале [
на интервале [,
].
6.4.5.2 Плотность распределения вероятностей для в этом случае имеет вид:
 , (8)
, (8)
где ![]() и
и ![]() .
.
Примечание - Формула (8) может быть представлена в следующем виде, удобном для программирования:
 .
.
6.4.5.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() .
.
6.4.5.4 Для получения выборочного значения из распределения
![]() независимо выбирают два значения
независимо выбирают два значения и
из стандартного равномерного распределения
![]() (см. С.3.3) и формируют
(см. С.3.3) и формируют
![]() .
.
6.4.6 Арксинусное (U-образное) распределение
6.4.6.1 Если известно, что величина изменяется по гармоническому закону между предельными значениями
и
,
, но в момент наблюдения фаза
процесса неизвестна, то в соответствии с принципом максимума энтропии для описания
следует использовать равномерное распределение
![]() . Тогда распределение
. Тогда распределение , получаемое в результате преобразования
![]() ,
,
где подчиняется распределению
![]() , будет арксинусным (U-образным) распределением
, будет арксинусным (U-образным) распределением ![]() [18].
[18].
6.4.6.2 Плотность распределения вероятностей для в этом случае имеет вид:

Примечание - Посредством замены переменной
![]()
можно от распределения ![]() перейти к стандартному распределению
перейти к стандартному распределению ![]() для величины
для величины :
 (9)
(9)
Случайная величина имеет математическое ожидание 1/2 и дисперсию 1/8. Распределение (9) называют арксинусным, т.к. соответствующая ему функция распределения имеет вид
![]() .
.
Это частный случай бета-распределения, когда оба параметра распределения равны одной второй.
6.4.6.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() .
.
6.4.6.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , необходимо случайные значения
, необходимо случайные значения , полученные из стандартного равномерного распределения
![]() (см. С.3.3), преобразовать следующим образом:
(см. С.3.3), преобразовать следующим образом:
![]() .
.
6.4.7 Нормальное распределение (распределение Гаусса)
6.4.7.1 Если наилучшая оценка и соответствующая стандартная неопределенность
являются единственной доступной информацией о величине
, то в соответствии с принципом максимума энтропии случайную величину
следует описывать нормальным распределением
![]() .
.
6.4.7.2 Плотность распределения вероятностей для имеет вид:
 . (10)
. (10)
6.4.7.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() .
.
6.4.7.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , необходимо случайные значения
, необходимо случайные значения , полученные из стандартного нормального распределения
![]() (см. раздел С.4), преобразовать следующим образом:
(см. раздел С.4), преобразовать следующим образом:
![]() .
.
6.4.8 Многомерное нормальное распределение
6.4.8.1 Ситуация, описанная в 6.4.7.1, может быть распространена на -мерную случайную величину
![]() . Если единственной доступной информацией об
. Если единственной доступной информацией об является наилучшая оценка
![]() и соответствующая невырожденная положительно определенная матрица неопределенностей
и соответствующая невырожденная положительно определенная матрица неопределенностей
 ,
,
то случайная величина может быть описана многомерным нормальным распределением
![]() .
.
6.4.8.2 Совместная плотность распределения имеет вид
![]() . (11)
. (11)
6.4.8.3 Математическое ожидание и ковариационная матрица имеют вид:
![]() ,
, ![]() .
.
6.4.8.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , независимо выбирают
, независимо выбирают значений
,
1, ..,
, случайной величины, имеющей стандартное нормальное распределение
![]() (см. раздел С.4) и формируют
(см. раздел С.4) и формируют
![]() ,
,
где ![]() , a
, a - верхняя треугольная матрица, полученная разложением Холецкого
![]() , (см. раздел С.5).
, (см. раздел С.5).
Примечание 1 - Вместо разложения Холецкого ![]() может быть использован любой другой способ факторизации матрицы неопределенностей.
может быть использован любой другой способ факторизации матрицы неопределенностей.
Примечание 2 - Из многомерных распределений в настоящем стандарте рассматривается только многомерное нормальное распределение, часто применяемое на практике. Процедура получения выборки из многомерного нормального распределения приведена выше (а также в разделе С.5). Если необходимо использовать многомерное распределение, отличное от нормального, то необходимо определить процедуру формирования выборки из этого распределения.
Примечание 3 - В случае независимых случайных величин плотность многомерного нормального распределения (11) превращается в произведение плотностей одномерных нормальных распределений вероятностей. В этом случае
![]() ,
,![]() ,
, .
.
6.4.9 -распределение
6.4.9.1 Обычно -распределение появляется в двух случаях: при оценке ряда наблюдений (см. 6.4.9.2) и интерпретации данных, приводимых в сертификатах о калибровке (см. 6.4.9.7).
6.4.9.2 Если имеется серия из независимых наблюдений
, ...,
случайной величины, подчиняющейся нормальному распределению с неизвестным математическим ожиданием
и неизвестной дисперсией
,
![]() , и за входную величину
, и за входную величину принимают оценку математического ожидания
, то, приписывая
и
совместное неинформативное априорное распределение и используя теорему Байеса, можно получить безусловное одномерное распределение для
, которым в данном случае будет масштабированное смещенное
-распределение
![]() с
с ![]() степенями свободы, где
степенями свободы, где
![]() ,
, ![]()
представляют собой, соответственно, выборочное среднее и выборочную дисперсию [20].
6.4.9.3 Плотность распределения вероятностей для имеет вид:
 , (12)
, (12)
где - гамма-функция:
 ,
, .
6.4.9.4 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() ,
,
где ![]() определено только для
определено только для 2, a
![]() - только для
- только для 3. Таким образом, для
3 наилучшая оценка
и соответствующая ей стандартная неопределенность имеют вид:
,
![]() . (13)
. (13)
Примечание 1 - В соответствии с GUM [Руководство ИСО/МЭК 98-3 (4.2)] стандартную неопределенность , соответствующую среднему арифметическому
независимых наблюдений, следует вычислять по формуле
![]() , а не по формуле (13). В качестве меры достоверности
, а не по формуле (13). В качестве меры достоверности использовано число степеней свободы
![]() . Кроме того, оценкам неопределенности типа В также предложено ставить в соответствие число степеней свободы, основанное на субъективном суждении о степени доверия к этой оценке [Руководство ИСО/ МЭК 98-3 (G.4.2)] (см. также 6.4.3.3, примечание 2). Знание числа степеней свободы, соответствующих неопределенности
. Кроме того, оценкам неопределенности типа В также предложено ставить в соответствие число степеней свободы, основанное на субъективном суждении о степени доверия к этой оценке [Руководство ИСО/ МЭК 98-3 (G.4.2)] (см. также 6.4.3.3, примечание 2). Знание числа степеней свободы, соответствующих неопределенности , необходимо для определения числа эффективных степеней свободы
, соответствующих неопределенности
, по формуле Уэлча-Саттертуэйта.
Примечание 2 - В байесовской интерпретации вероятности, использованной в настоящем стандарте, такого понятия как надежность оценки неопределенности не существует. Соответственно, в настоящем стандарте число степеней свободы оценки неопределенности типа А не рассматривается как мера этой неопределенности, а понятие числа степеней свободы для оценки неопределенности типа В не используется.
6.4.9.5 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , выбирают значения
, выбирают значения случайной величины, подчиняющейся центральному
-распределению с
![]() степенями свободы [Руководство ИСО/МЭК 98-3 (раздел G.3)] (см. также раздел С.6) и формируют
степенями свободы [Руководство ИСО/МЭК 98-3 (раздел G.3)] (см. также раздел С.6) и формируют
![]() .
.
6.4.9.6 Если вместо оценки стандартного отклонения , вычисленной по одной выборке наблюдений, используют объединенную оценку стандартного отклонения
c
степенями свободы, полученную по
сериям наблюдений:
 ,
, ![]() ,
,
то число степеней свободы ![]() для масштабированного смещенного
для масштабированного смещенного -распределения, приписанного
, необходимо заменить числом степеней свободы
для объединенной оценки стандартного отклонения
. В результате формулу (12) необходимо заменить на
 ,
,
а формулы (13) - на
![]() ,
,  .
.
6.4.9.7 Если источником информации о величине является сертификат о калибровке [Руководство ИСО/МЭК 98-3 (4.3.1)], в котором указаны наилучшая оценка
, расширенная неопределенность
, коэффициент охвата
и число эффективных степеней свободы
, то величина
может быть описана масштабированным смещенным
-распределением
![]() с
с ![]() степенями свободы.
степенями свободы.
6.4.9.8 Если бесконечно или неопределенно (а при отсутствии соответствующей информации его следует считать бесконечным), то
может быть приписано нормальное распределение
![]() (см. 6.4.7.1).
(см. 6.4.7.1).
Примечание - Это нормальное распределение будет предельным случаем масштабированного смещенного -распределения
![]() при
при стремящемся к бесконечности.
6.4.10 Экспоненциальное распределение
6.4.10.1 Если единственной доступной информацией о неотрицательной величине является ее наилучшая оценка
0, то в соответствии с принципом максимума энтропии величина
может быть описана экспоненциальным распределением
![]() .
.
6.4.10.2 Плотность распределения вероятностей для в этом случае имеет вид
![]()
6.4.10.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() .
.
6.4.10.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() , выбирают значения
, выбирают значения случайной величины, подчиняющейся стандартному равномерному распределению
![]() (см. С.3.3), и формируют
(см. С.3.3), и формируют
![]() .
.
Примечание - Дополнительную информацию в отношении приписывания плотности распределения вероятностей неотрицательной величине можно найти в [14].
6.4.11 Гамма-распределение
6.4.11.1 Величина может представлять собой среднее число объектов, обладающих определенным свойством (далее - объектов), в выборке фиксированного объема (например, среднее число частиц в образце воздуха, взятом из чистой комнаты, или среднее число фотонов, излученных источником за установленный промежуток времени). Если
- число объектов, подсчитываемых в выборке заданного объема, - является случайной величиной с неизвестным математическим ожиданием, подчиняющейся распределению Пуассона, то в соответствии с теоремой Байеса (после приписывания математическому ожиданию априорного равномерного распределения на бесконечном интервале) распределение
будет подчиняться гамма-распределению
![]() .
.
6.4.11.2 Плотность распределения вероятностей для в этом случае имеет вид:
 (14)
(14)
6.4.11.3 Математическое ожидание и дисперсия имеют вид:
![]() ,
, ![]() . (15)
. (15)
6.4.11.4 Для формирования выборки значений случайной величины, подчиняющейся распределению ![]() независимо выбирают
независимо выбирают значений
,
1, ...,
, случайной величины, подчиняющейся стандартному равномерному распределению
![]() (см. С.3.3), и формируют (см. [18])
(см. С.3.3), и формируют (см. [18])
![]() .
.
Примечание 1 - Если подсчет осуществляют по нескольким выборкам (соответствующим одному и тому же распределению Пуассона), a - число объектов, обнаруженных в
-й выборке объема
, то распределением среднего количества объектов в выборке объема
![]() будет
будет ![]() с
с ![]() и
и 1. Формулы (14) и (15) в этом случае применяют для
![]() .
.
Примечание 2 - Гамма-распределение является обобщением распределения хи-квадрат и используется для анализа информации, относящейся к дисперсиям.
Примечание 3 - Специфическое гамма-распределение в 6.4.11.4 - это распределение Эрланга, представляющее собой распределение суммы случайных величин, подчиняющихся экспоненциальному распределению с параметром 1 [18].
6.5 Распределения, получаемые по предшествующим расчетам неопределенности
Выполненные ранее вычисления неопределенности могут быть использованы для приписывания распределения выходной величине, которая в последующих расчетах неопределенности может выступать в качестве входной величины. Такое распределение может иметь аналитическое представление, например в виде нормального распределения. Оно может также иметь вид аппроксимации функции распределения для величины, полученной, например, при предшествующем применении метода Монте-Карло. Способы описания такой функции распределения приведены в 7.5.1 и разделе D.2.
7 Применение метода Монте-Карло
7.1 Общие положения
Данный раздел содержит сведения о применении метода Монте-Карло для трансформирования распределений (см. процедуру, описанную в 5.9.6 и графически изображенную на рисунке 4).
7.2 Число испытаний при применении метода Монте-Карло
7.2.1 Для применения метода Монте-Карло необходимо выбрать число испытаний , т.е. число наблюдений выходных значений модели. Это число может быть выбрано заблаговременно (до проведения испытаний), но тогда будет исключена возможность управления точностью результатов, полученных с помощью данного метода. Причиной этому служит то, что число испытаний, необходимое для получения результата вычисления с заданной точностью, зависит от формы плотности распределения вероятностей выходной величины и от заданного значения вероятности охвата. Кроме того, метод вычисления является стохастическим по своей природе, поскольку зависит от случайной выборки.
Примечание - Как правило, выбор 10
позволяет построить 95%-ный интервал охвата для выходной величины с точностью до одной или двух значащих цифр.
7.2.2 Рекомендуется выбирать значение достаточно большим (например, превышающим в 10
раз) по сравнению с
![]() . Тогда можно ожидать, что
. Тогда можно ожидать, что обеспечит приемлемое дискретное представление
![]() вблизи границ 100
вблизи границ 100%-ного интервала охвата для
.
7.2.3 Поскольку нельзя заранее гарантировать, что выбранное значение обеспечит достаточную точность приближения, можно использовать процедуру адаптивного выбора, уточняя значение
в процессе испытаний. Некоторые рекомендации по адаптивной процедуре выбора
приведены в [2]. Адаптивная процедура, установленная в 7.9, позволяет оптимальным образом получить значение
, соответствующее заданной точности вычислений.
Примечание - Для сложной модели, например, требующей получения решения методом конечных элементов, применение большого числа испытаний может оказаться невозможным. В этом случае рекомендуется представить плотность распределения вероятностей выходной величины ![]() в виде гауссовского приближения (как в GUM). Это позволяет использовать относительно небольшое число испытаний
в виде гауссовского приближения (как в GUM). Это позволяет использовать относительно небольшое число испытаний , например 50 или 100, а полученные по результатам испытаний выборочное среднее и выборочное стандартное отклонение принять, соответственно, за оценки
и
. Для описания
и построения интервала охвата используют плотность нормального распределения
![]() . Хотя уменьшение числа испытаний неизбежно ухудшает свойства метода в части аппроксимации распределения выходной величины, оно все же позволяет учесть нелинейность модели измерения.
. Хотя уменьшение числа испытаний неизбежно ухудшает свойства метода в части аппроксимации распределения выходной величины, оно все же позволяет учесть нелинейность модели измерения.
7.3 Выборка из распределения вероятностей
Для применения метода Монте-Карло формируют векторов
,
1, ...,
(см. 7.2) в соответствии с плотностями распределения вероятностей
![]() для
для входных величин
или, если это необходимо, из совместной (многомерной) плотности распределения
![]() . Рекомендации по формированию выборки для наиболее распространенных распределений (равномерного, нормального, многомерного нормального и
. Рекомендации по формированию выборки для наиболее распространенных распределений (равномерного, нормального, многомерного нормального и -распределения) приведены в приложении С (см. также 6.4). Однако возможно получение выборок, соответствующих и другим распределениям (см. раздел С.2). Некоторые распределения могут быть аппроксимированы распределениями, полученными в результате применения метода Монте-Карло при предыдущих вычислениях неопределенности (см. 6.5, 7.5 и приложение D).
Примечание - Для достоверности результатов применения метода Монте-Карло необходимо, чтобы генераторы псевдослучайных чисел, используемые для формирования выборок из заданных распределений, обладали соответствующими свойствами. В С.3.2 приведены некоторые критерии проверки сформированных выборок на случайность.
7.4 Оценка выходной величины
7.4.1 Выходную величину определяют для каждой из выборок по
значениям входных величин в каждой, полученных в соответствии с заданными плотностями распределения вероятностей. Если обозначить
выборок через
, …,
, где
-й вектор состоит из случайных значений
,...,
, и каждое такое значение
получено в соответствии с плотностью распределения вероятностей для входной величины
, то выход модели можно представить в виде
![]() ,
, 1, ...,
.
7.4.2 Если являются зависимыми величинами, то в 7.4.1 необходимо использовать совместную плотность распределения.
Примечание - При использовании закона трансформирования неопределенностей, когда аналитические выражения производных функции измерения по входным величинам известны точно, значения выходной величины и этих производных получают в точке наилучших оценок входных величин. Если аналитические выражения для производных неизвестны, и для их оценок используют приближение в виде конечных разностей, то получают значения только выходной величины. Согласно рекомендации GUM [Руководство ИСО/МЭК 98-3 (примечание 2 к 5.1.3)] значения функции измерения берут в точках наилучших оценок входных величин, а также в точках, отстоящих по обе стороны от этих наилучших оценок на расстоянии одной стандартной неопределенности (варьируя по очереди для каждой входной величины). В методе же Монте-Карло значения выходной величины получают при варьировании входных величин в окрестности их наилучших оценок, так что в отдельной выборке значение входной величины может отстоять от ее наилучшей оценки на несколько стандартных отклонений. Тот факт, что в методе Монте-Карло значения функции измерений получают в разных точках, может породить вопрос о свойствах вычислительной процедуры, в частности, о ее устойчивости и (в случае применения адаптивной процедуры) сходимости. При возникновении сомнений пользователю следует убедиться в том, что метод дает достоверные оценки выходной величины для достаточно больших окрестностей наилучших оценок входных величин. Однако следует ожидать, что вопросы устойчивости и сходимости численного метода могут стать критическими только в исключительных случаях.
7.5 Дискретное представление функции распределения выходной величины
7.5.1 Дискретное представление функции распределения
![]() выходной величины
выходной величины может быть получено следующим образом:
a) значения выходной величины ,
1, ...,
, полученные в соответствии с методом Монте-Карло, располагают в неубывающем порядке, обозначая их
,
1, ...,
;
b) если среди значений есть совпадающие, то в них вносят минимальные случайные возмущения, чтобы полученная в результате последовательность
,
1, ...,
была строго возрастающей [см. условие b) в 5.10.1];
c) полученная последовательность ,
1, ...,
, определяет
.
Примечание 1 - Из возможных алгоритмов сортировки, применяемой на этапе а), рекомендуется выбирать такой, в котором число операций пропорционально ![]() [47]. В обычных алгоритмах сортировки число операций пропорционально
[47]. В обычных алгоритмах сортировки число операций пропорционально , что необоснованно увеличивает время вычислений (см. 7.8).
Примечание 2 - В перечислении а) использован термин "неубывающий", а не "возрастающий" вследствие возможного равенства между собой некоторых значений выходной величины.
Примечание 3 - Внесение в совпадающие значения выходной величины только очень малых возмущений [см. перечисление b)] обеспечивает неизменность статистических свойств .
Примечание 4 - Необходимость внесения малых возмущений на этапе b) в действительности маловероятна из-за огромного множества различных чисел с плавающей запятой, появляющихся на выходе модели при подаче на ее вход данных с генератора случайных чисел. Тем не менее, возможность внесения малых возмущений должна быть предусмотрена применяемыми программными средствами.
Примечание 5 - Из построенного на этапе с) приближения можно извлечь разнообразную дополнительную информацию. Так, помимо оценок математического ожидания и стандартного отклонения, могут быть получены оценки коэффициентов асимметрии и эксцесса, а также другие статистики, например оценки моды или медианы.
Примечание 6 - Если выходная величина будет в дальнейшем рассматриваться как входная величина при оценивании неопределенности другого измерения, то выборку из ее распределения легко получить случайным (равновероятным) выбором значений из
,
1, ...,
(см. 6.5).
7.5.2 Последовательность (или
) может быть представлена в виде гистограммы (при соответствующем выборе ширины классов), представляющей собой распределение частот появления выходной величины. После нормирования, обеспечивающего равенство площади под гистограммой единице, ее можно рассматривать как аппроксимацию плотности распределения вероятностей
![]() . Вычисления характеристик распределения обычно проводят по приближению
. Вычисления характеристик распределения обычно проводят по приближению , а не по построенной гистограмме, поскольку разрешение последней зависит от выбора ширины классов. Тем не менее, гистограмма может быть полезна с точки зрения понимания особенностей плотности распределения вероятностей выходной величины, например степени ее асимметрии (см. также примечание 1 к 7.8.3 в части использования гистограммы при больших значениях
).
7.5.3 В ряде случаев требуется аппроксимация ![]() непрерывной функцией. Этот вопрос рассматривается в приложении D.
непрерывной функцией. Этот вопрос рассматривается в приложении D.
7.6 Оценка выходной величины и ее стандартной неопределенности
В качестве оценки выходной величины
используют выборочное среднее
![]() , (16)
, (16)
а в качестве оценки ее стандартной неопределенности - выборочное стандартное отклонение
:
![]() . (17)
. (17)
Примечание 1 - Для численных вычислений следует использовать формулу (17), а не эквивалентную ей математически формулу
 .
.
Это связано с тем, что очень часто в метрологии много меньше по модулю, чем
, и, как следствие, числа в последовательности
в их десятичном представлении имеют много совпадающих цифр в старших разрядах. В этом случае погрешности округления в арифметике с конечной точностью (при вычитании близких по значению величин) могут привести к большим ошибкам в расчетах (доходящим даже до того, что выражение в круглых скобках станет отрицательным, т.е. средний квадрат будет меньше квадрата среднего). Результаты таких вычислений будут иметь неудовлетворительную точность (см. [4]).
Примечание 2 - В некоторых особых случаях, когда одной из входных величин приписано -распределение с числом степеней свободы менее трех, математическое ожидание и стандартное отклонение
, соответствующие плотности распределения вероятностей
![]() , могут не существовать. Как следствие, формулы (16) и (17) не способны обеспечить получение содержательных результатов. Однако интервал охвата для
, могут не существовать. Как следствие, формулы (16) и (17) не способны обеспечить получение содержательных результатов. Однако интервал охвата для (см. 7.7), построенный на основе
, будет сохранять свое содержательное значение.
Примечание 3 - В общем случае не будет согласовываться с оценкой выходной величины, полученной по наилучшим оценкам входных величин, т.к. для нелинейной функции измерения
![]() математическое ожидание
математическое ожидание ![]() (см. [Руководство ИСО/МЭК 98-3 (4.1.4)]). Независимо от линейности или нелинейности функции
(см. [Руководство ИСО/МЭК 98-3 (4.1.4)]). Независимо от линейности или нелинейности функции ![]() при
при , стремящемся к бесконечности,
стремится к
![]() , если последняя величина существует.
, если последняя величина существует.
7.7 Интервал охвата для выходной величины
7.7.1 Интервал охвата для может быть получен на основе дискретного приближения
для
![]() аналогично тому, как он был построен для
аналогично тому, как он был построен для ![]() в 5.3.2.
в 5.3.2.
7.7.2 Если - целое число, то берут
![]() , в противном случае в качестве
, в противном случае в качестве можно выбрать целую часть
![]() . Тогда [
. Тогда [,
] является 100
%-ным интервалом охвата для
, где
![]() ,
, ![]() для любого
для любого из ряда
1, ...,
![]() . Вероятностно симметричный 100
. Вероятностно симметричный 100%-ный интервал охвата можно получить, выбрав
![]() , если
, если ![]() - целое число, или
- целое число, или ![]() в противном случае. Для определения наименьшего 100
в противном случае. Для определения наименьшего 100%-ного интервала охвата следует выбрать такое
, чтобы для всех
, принадлежащих ряду
1, ...,
![]() , выполнялось неравенство
, выполнялось неравенство
![]() .
.
Примечание - Поскольку численные значения, полученные в результате применения метода Монте-Карло, случайны по своей природе, то некоторые из построенных ![]() интервалов будут меньше, чем в среднем (при многократном применении метода), а некоторые - больше. Поэтому при выборе наименьшего 100
интервалов будут меньше, чем в среднем (при многократном применении метода), а некоторые - больше. Поэтому при выборе наименьшего 100%-ного интервала охвата следует иметь в виду, что его длина будет, как правило, меньше, чем если бы он был рассчитан на основе
![]() , или, что то же самое, что вероятность охвата для построенного эмпирического наименьшего 100
, или, что то же самое, что вероятность охвата для построенного эмпирического наименьшего 100%-ного интервала охвата будет в действительности меньше, чем 100
. Однако для больших
этим отличием можно пренебречь.
Пример - С помощью генератора псевдослучайных чисел для равномерного распределения в интервале [0,1] были получены 10 псевдослучайных значений, и по этой выборке вышеописанным способом был построен наименьший 95%-ный интервал охвата. Всего эта процедура была повторена 1000 раз. Средняя вероятность охвата составила 94,92%, а выборочное стандартное отклонение вероятности охвата по 1000 реализациям процедуры составило 0,06%.
7.8 Время вычислений
7.8.1 Большая часть времени вычислений по методу Монте-Карло расходуется на выполнение следующих трех этапов:
a) генерирование случайных значений в соответствии с заданной плотностью распределения вероятностей для каждой входной величины
(или совместной плотности распределения для
);
b) определение соответствующих значений на выходе модели;
c) расположение значений выходной величины в неубывающем порядке.
7.8.2 Время, необходимое на выполнение этих трех этапов, прямо пропорционально для этапов а) и b) и
![]() для этапа с) (при использовании эффективного алгоритма сортировки [47]).
для этапа с) (при использовании эффективного алгоритма сортировки [47]).
7.8.3 В случае простой модели и независимых входных величин время, необходимое для выполнения этапа с), будет преобладающим, а общее время вычислений на персональном компьютере с тактовой частотой процесса в несколько гигагерц при 10
составит несколько секунд. Если же процедура сортировки не является затратной по времени, то, обозначив
время вычисления одного псевдослучайного значения в соответствии с заданной плотностью распределения вероятностей для входных величин, а
- время вычисления одного значения выходной величины, получим приближенную оценку общего времени вычислений в виде
![]() . Для сложной модели преобладающим будет слагаемое
. Для сложной модели преобладающим будет слагаемое .
Примечание 1 - Если модель проста, а - очень большое число, например 10
или 10
, то время сортировки может быть значительно больше времени вычисления значения на выходе модели. В таком случае предпочтительным может быть оценивание неопределенности не по экспериментальной функции распределения, а по гистограмме, построенной для ряда
.
Примечание 2 - Ориентировочно оценку времени вычислений методом Монте-Карло можно выполнить на примере, задав модель измерения в виде суммы пяти членов:
![]() .
.
Каждой входной величине приписано нормальное распределение. Число испытаний метода выбрано равным
10
. Относительное время выполнения операций:
a) генерирования случайных чисел;
b) вычисления значений на выходе модели;
c) сортировки значений выходной величины, - составляет, соответственно, 20%, 20% и 60% общего времени вычислений, равного приблизительно нескольким секундам при выполнении расчетов на персональном компьютере с тактовой частотой в несколько гигагерц.
7.9 Адаптивная процедура реализации метода Монте-Карло
7.9.1 Общие положения
Суть адаптивной процедуры состоит в последовательном увеличении числа испытаний до тех пор, пока полученные числовые оценки статистических характеристик не станут установившимися. Численный результат считается установившимся, если соответствующее ему удвоенное стандартное отклонение станет меньше заданной точности вычисления стандартной неопределенности (см. 7.9.2).
7.9.2 Точность вычисления числовых значений
Если обозначить через число существенных значащих цифр в числовом представлении величины
, то предел погрешности вычисления
значения
определяют следующим образом:
a) представляют значение в виде
, где
- целое число, состоящее из
значащих цифр,
- целое число;
b) определяют по формуле
![]() . (18)
. (18)
Пример 1 - Оценка выходной величины для эталона массы номиналом 100 г [Руководство ИСО/МЭК 98-3 (7.2.2)] составляет 100,02147 г. Стандартная неопределенность
![]() 0,00035 г, причем обе значащие цифры рассматриваются как существенные. Таким образом,
0,00035 г, причем обе значащие цифры рассматриваются как существенные. Таким образом, ![]() 2, и
2, и может быть представлена в виде 35·10
г, следовательно,
35 и
-5. Таким образом,
![]() 10
10=0,000005 г.
Пример 2 - Условия те же, что и в примере 1, за исключением того, что только одна значащая цифра в является существенной;
![]() 1 и
1 и ![]() 0,0004 г = 4·10
0,0004 г = 4·10 г. Это дает
4 и
-4. Следовательно,
![]() 10
10= 0,00005 г.
Пример 3 - При измерениях температуры ![]() 2 К. Тогда
2 К. Тогда ![]() 1,
1, ![]() 2·10 К, что дает
2·10 К, что дает 2 и
0. Таким образом,
![]() 10 К = 0,5 К.
10 К = 0,5 К.
7.9.3 Назначение адаптивной процедуры
В результате применения адаптивной процедуры, приведенной в 7.9.4, должны быть определены:
a) оценка величины
;
b) стандартная неопределенность ;
c) границы и
интервала охвата для
, соответствующего заданной вероятности охвата.
При этом числовые значения каждой из вышеуказанных четырех величин должны в среднем удовлетворять заданной точности вычисления.
Примечание 1 - То, что выполнение требования к точности вычислений может быть гарантировано не безусловно, а только в среднем, обусловлено природой случайности, на которой основан метод Монте-Карло.
Примечание 2 - С увеличением числа испытаний скорость сходимости оценок и
обычно гораздо выше, чем оценок
и
.
Примечание 3 - Как правило, чем больше вероятность охвата, тем большее число испытаний требуется для определения и
с заданной точностью вычисления.
7.9.4 Процедура
Практическая реализация адаптивной процедуры метода Монте-Карло с последовательным увеличением числа испытаний состоит в следующем:
a) задают ;
b) задают ![]() , где
, где - наименьшее целое, больше или равное
![]() ;
;
c) задают 1 (счетчик итераций метода Монте-Карло);
d) выполняют испытаний методом Монте-Карло (см. 7.3 и 7.4);
e) используют полученных на выходе модели значений
, ...,
для вычислений в соответствии с 7.5-7.7 очередной,
-й оценки
величины
, ее стандартной неопределенности
![]() левой
левой и правой
границ 100
%-ного интервала охвата;
f) если 1, то увеличивают счетчик
на единицу и выполняют этап d);
g) вычисляют выборочное стандартное отклонение среднего значения полученных в результате итераций оценок
, ...,
по формуле:
![]() ,
,
где ![]() ;
;
h) аналогичным образом вычисляют выборочное стандартное отклонение для средних значений оценок ,
и
;
i) используют все значений выходной величины для вычисления
;
j) определяют предел погрешности вычисления для
(см. 7.9.2);
k) если хотя бы одно из значений ,
![]() ,
, ![]() ,
, ![]() превышает
превышает , то увеличивают значение счетчика
на единицу и возвращаются к этапу d);
l) если возврата к этапу d) не произошло, и значения всех вычисляемых оценок можно считать установившимися, то на основе полученных значений выходной величины в соответствии с 7.5-7.7 вычисляют
,
и 100
%-ный интервал охвата.
Примечание 1 - Обычно на этапе а) задают ![]() 1 или
1 или ![]() 2.
2.
Примечание 2 - На этапе b) выбор произволен, но должен основываться на практических соображениях.
Примечание 3 - На этапе g) можно рассматривать как реализацию случайной величины со стандартным отклонением
.
Примечание 4 - Стандартные отклонения, полученные в соответствии с g) и h), имеют тенденцию к уменьшению по закону (см. 5.9.6, примечание 2).
Примечание 5 - В тех случаях, когда определять интервал охвата не требуется, проверку точности вычислений на этапе k) достаточно выполнять только для и
![]() .
.
Примечание 6 - Множитель 2, используемый на этапе k), основан на представлении выборочных средних в виде случайных величин, подчиняющихся нормальному распределению, и соответствует вероятности охвата, приблизительно равной 95%.
Примечание 7 - Альтернативный неадаптивный подход для построения 95%-ного вероятностно симметричного интервала охвата, основанный на использовании статистик биноминального распределения [10], состоит в следующем. Выбирают 10
или
10
. Формируют интервал [
,
], где для
10
2420,
97581, а для
10
24747,
975254. Этот интервал будет 95%-ным толерантным интервалом для уровня доверия 0,99 (см. [Руководство ИСО/МЭК 98-3 (С.2.30)], [55]), т.е. вероятность охвата составит не менее 95% в 99%, как минимум, случаев применения метода Монте-Карло. Средняя вероятность охвата для такого интервала будет равна
![]() , что превышает 95% на величину, уменьшающуюся с ростом
, что превышает 95% на величину, уменьшающуюся с ростом . Так для
10
средняя вероятность охвата будет 95,16%, а для
10
- 95,05%. (Возможен и другой выбор значений
и
, и при этом не обязательно, чтобы их сумма составляла
![]() . Достаточно [10, раздел 2.6], чтобы разность
. Достаточно [10, раздел 2.6], чтобы разность ![]() удовлетворяла условию
удовлетворяла условию
![]() ,
,
где ![]() . Наилучший результат соответствует ситуации, когда левая часть этого неравенства достигает максимального значения, при котором неравенство еще выполняется.) Эти результаты могут быть распространены на другие значения вероятности охвата и другие значения
. Наилучший результат соответствует ситуации, когда левая часть этого неравенства достигает максимального значения, при котором неравенство еще выполняется.) Эти результаты могут быть распространены на другие значения вероятности охвата и другие значения .
8 Проверка результатов
8.1 Проверка результатов оценивания неопределенности по GUM сравнением с методом Монте-Карло
8.1.1 Способ оценивания неопределенности по GUM во многих случаях работает хорошо. Однако не всегда можно сразу определить, соблюдены ли все условия для его применения (см. 5.7 и 5.8). Обычно гораздо проще оценить неопределенность с использованием метода Монте-Карло (при наличии соответствующего программного обеспечения), чем выяснить, выполнены ли все условия оценивания по GUM [8]. При наличии сомнений в обоснованности применения способа оценивания по GUM полученные с его помощью результаты нуждаются в проверке, а поскольку диапазон условий, при которых может быть применен метод Монте-Карло, значительно шире, чем для метода по GUM, то для такой проверки рекомендуется сопоставить результаты оценивания по GUM с результатами оценивания методом Монте-Карло. Если сравнение подтвердит обоснованность применения GUM, то способ оценивания неопределенности по GUM можно будет применять в будущем для схожих задач. В противном случае следует рассмотреть возможность замены на другой способ оценивания неопределенности, включая тот же метод Монте-Карло.
8.1.2 При сравнении двух методов рекомендуется руководствоваться следующей двухэтапной процедурой:
a) применить способ оценивания неопределенности по GUM (возможно с учетом членов высшего порядка разложения функции измерения в ряд Тейлора в законе трансформирования неопределенностей) (см. 5.6), для определения 100%-ного интервала охвата
![]() , где
, где - заданная вероятность охвата;
b) применить адаптивную процедуру Монте-Карло (см. 7.9.4) для получения стандартной неопределенности и границ
и
заданного 100
%-ного интервала охвата для выходной величины (вероятностно симметричного или наименьшего) (см. также 8.2).
8.1.3 Процедура сравнения позволяет определить, согласуются ли интервалы охвата, полученные в соответствии со способом оценивания неопределенности по GUM и методом Монте-Карло, в пределах заданной точности вычислений. Точность вычислений для границ интервалов охвата определяют через точность выражения стандартной неопределенности числом существенных значащих цифр в ее десятичном представлении (сравни с 7.9.2). Для этого:
a) определяют предел погрешности вычисления для
, как указано в 7.9.2;
b) сравнивают интервалы охвата, полученные в соответствии со способом оценивания неопределенности по GUM и методом Монте-Карло, чтобы определить, получено ли в значениях границ интервала охвата, вычисленных по GUM, необходимое число верных значащих цифр. При этом определяют:
![]() , (19)
, (19)
![]() , (20)
, (20)
т.е. абсолютные значения разности соответствующих границ двух интервалов охвата. Если как , так и
не превышают
, то способ оценивания неопределенности по GUM в этом случае можно считать применимым.
Примечание - Результат сравнения будет зависеть от того, какой вероятности охвата соответствуют сравниваемые интервалы. Поэтому проверку выполняют только для конкретной заданной вероятности охвата .
8.2 Применение метода Монте-Карло при проведении проверки
Для выполнения проверки по 8.1 метод Монте-Карло должен быть реализован для достаточно большого числа испытаний (см. 7.2). Если обозначить через
число существенных значащих цифр в десятичном представлении
при проверке применимости способа оценивания по GUM, а через
- допустимую погрешность вычисления
(см. 7.9.2), то для получения в целях проверки результатов методом Монте-Карло рекомендуется использовать его адаптивный вариант (см. 7.9.4) до достижения погрешности вычисления
[т.е. в 7.9.4 на этапе k)
следует заменить на
].
Примечание - В среднем уменьшение погрешности вычисления до требует повышения числа испытаний
в 25 раз. Выполнение операций с векторами столь большой размерности может представлять собой серьезную проблему для ряда компьютеров. В этом случае для вычисления статистических оценок рекомендуется использовать приближение
![]() гистограммой для ряда
гистограммой для ряда . При этом частота попаданий в соответствующий класс гистограммы уточняется в ходе итераций (см. 7.8.3, примечание 1).
9 Примеры
9.1 Иллюстрация положений настоящего стандарта
9.1.1 Приведенные в настоящем разделе примеры иллюстрируют различные вопросы применения положений настоящего стандарта, включая использование способа оценивания неопределенности по GUM с учетом и без учета членов разложения функции измерения в ряд Тейлора высших порядков и сопоставление полученных с его помощью результатов с результатами:
a) метода Монте-Карло с использованием заданного числа испытаний ;
b) адаптивной процедуры метода Монте-Карло (см. 7.9.4), в которой необходимое значение определяется в ходе итераций;
c) сочетающими перечисленное в а) и b).
9.1.2 Некоторые из примеров посвящены вопросу, подтверждают ли результаты, указанные в 9.1.1, перечисление b), результаты оценивания неопределенности по GUM. Для целей сравнения результатов используется соответствующим образом выбранный предел погрешности вычисления (см. 7.9.2) для оценки
. Результаты с использованием адаптивной процедуры метода Монте-Карло получены для погрешности вычисления
(см. 8.2). В некоторых случаях результаты сравниваются с решениями, полученными аналитически.
9.1.3 Как правило, результаты представлены в виде, установленном в 5.5. Однако для облегчения сравнения результатов, полученных разными методами, часто использовано более рекомендованных одной или двух значащих цифр.
9.1.4 В качестве генератора псевдослучайных чисел из равномерного распределения (см. С.З) использован вихрь Мерсенна [34]. Этот генератор прошел всестороннюю проверку статистических свойств получаемой выборки из равномерного распределения [30] и реализован в пакете МАТLАВ* [36], который использован для получения результатов в примерах настоящего раздела.
_______________
* MATLAB является коммерческим продуктом, удобным для числовых расчетов, требуемых в примерах настоящего стандарта. Информация об используемом средстве приведена только для удобства пользователей настоящего стандарта. Ее не следует рассматривать как рекомендацию использовать именно этот коммерческий продукт в практических вычислениях.
9.1.5 Первый пример (см. 9.2) представляет собой аддитивную модель. Он демонстрирует совпадение результатов, полученных с применением метода Монте-Карло, с теми, что получены способом оценивания неопределенности по GUM в случае выполнения условий применимости последнего (см. 5.7). Эта модель рассмотрена для различных плотностей распределения вероятностей для входных величин, что позволяет показать некоторые отклонения результатов в ситуациях, когда выполнены не все условия применимости способа оценивания неопределенности по GUM.
9.1.6 Второй пример (см. 9.3) представляет собой задачу калибровки при измерении массы. Он показывает, что способ оценивания неопределенности по GUM дает достоверные результаты для данного примера только в том случае, когда учтены вклады членов разложения функции измерения в ряд Тейлора высших порядков.
9.1.7 Третий пример (см. 9.4) относится к области электрических измерений. Он показывает, что плотность распределения вероятностей для выходной величины может быть существенно асимметричной, и, таким образом, способ оценивания неопределенности по GUM может дать недостоверные результаты даже при учете членов разложения функции измерения в ряд Тейлора высших порядков. Рассмотрены случаи как независимых, так и зависимых входных величин.
9.1.8 Четвертый пример (см. 9.5) - это пример калибровки концевой меры длины, взятый из GUM [Руководство ИСО/МЭК 98-3 (раздел Н.1)]. Даны пояснения относительно используемых в примере входных величин модели и плотностях распределения вероятностей для этих величин, а также приведено сравнение результатов, получаемых по GUM, с полученными с использованием метода Монте-Карло. Результаты получены как для приближения, использованного в GUM, так и без использования этого приближения для данной измерительной задачи.
9.2 Аддитивная модель
9.2.1 Постановка задачи
В настоящем примере рассмотрена аддитивная модель
![]() , (21)
, (21)
представляющая собой частный случай общей линейной модели, рассмотренной в GUM, для трех различных сочетаний плотностей распределения вероятностей ![]() для входных величин
для входных величин , рассматриваемых как независимые. Входные величины
и, следовательно, выходная величина
безразмерны. В первом сочетании каждая из
![]() является плотностью стандартного нормального распределения (каждая входная величина
является плотностью стандартного нормального распределения (каждая входная величина имеет нулевое математическое ожидание и единичное стандартное отклонение). Во втором сочетании все
![]() являются плотностями равномерного распределения с нулевым математическим ожиданием и единичным стандартным отклонением. Третий набор идентичен второму, за исключением того, что для плотности распределения вероятностей
являются плотностями равномерного распределения с нулевым математическим ожиданием и единичным стандартным отклонением. Третий набор идентичен второму, за исключением того, что для плотности распределения вероятностей ![]() стандартное отклонение равно 10.
стандартное отклонение равно 10.
Примечание - Более подробная информация об аддитивных моделях, подобных описываемым формулой (21), где входные величины распределены либо по нормальному, либо по равномерному закону, либо частью по нормальному, а частью по равномерному закону, приведена в [13].
9.2.2 Нормально распределенные входные величины
9.2.2.1 Каждой входной величине приписано стандартное нормальное распределение. Наилучшими оценками
являются
0,
1, 2, 3, 4 с соответствующими стандартными неопределенностями
![]() 1.
1.
9.2.2.2 Полученные результаты [с тремя значащими цифрами для облегчения их сопоставления (см. 9.1.3)] приведены в первых пяти столбцах таблицы 2.
Таблица 2 - Применение к модели (21) в случае нормального распределения , (а) в соответствии со схемой оценки неопределенности по GUM (GUF), (b) методом Монте-Карло и (с) аналитическим методом (9.2.2.2, 9.2.2.7, 9.2.3.4).
Метод | Вероятностно симметричный 95%-ный интервал охвата | Достоверность результатов по GUM ( | |||||
GUM | - | 0,00 | 2,00 | [-3,92, 3,92] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,00 | [-3,94, 3,92] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,00 | [-3,92, 3,92] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,00 | [-3,92, 3,92] | - | - | - |
Монте-Карло, адаптивный | 1,23·10 | 0,00 | 2,00 | [-3,92, 3,93] | 0,00 | 0,01 | Да |
Монте-Карло, адаптивный | 1,02·10 | 0,00 | 2,00 | [-3,92, 3,92] | 0,00 | 0,00 | Да |
Аналитический | - | 0,00 | 2,00 | [-3,92, 3,92] | - | - | - |
Примечание - Поскольку в данном случае, также как и в других случаях, рассматриваемых в настоящем примере, известно, что плотность распределения вероятностей для симметрична, то рассматривается вероятностно-симметричный (95%-ный) интервал охвата.
9.2.2.3 В соответствии с законом трансформирования неопределенностей [Руководство ИСО/МЭК 98-3 (5.1.2)] наилучшей оценкой будет
0,0 с соответствующей стандартной неопределенностью
![]() 2,0 при оставлении в результате оценивания для
2,0 при оставлении в результате оценивания для двух значащих цифр (
0,05) (см. 5.5). Вероятностно симметричный 95%-ный интервал охвата для
, основанный на коэффициенте охвата 1,96, будет [-3,9, 3,9].
9.2.2.4 Применение метода Монте-Карло (раздел 7) с числом испытаний 10
дает
0,0;
![]() 2,0 и вероятностно симметричный интервал охвата [-3,9, 3,9]. Два последующих применения метода Монте-Карло для
2,0 и вероятностно симметричный интервал охвата [-3,9, 3,9]. Два последующих применения метода Монте-Карло для 10
дали результаты, согласующиеся с полученным ранее в рамках установленной точности вычислений. Эти два применения (с различными случайными выборками из тех же распределений) понадобились, чтобы продемонстрировать вариации получаемых результатов. Четвертое и пятое значения (1,23·10
и 1,02·10
) представляют собой числа испытаний, полученные в результате двух применений адаптивной процедуры Монте-Карло (см. 7.9) для погрешности вычисления
(см. 8.2).
9.2.2.5 Плотность распределения вероятностей для , полученная аналитически, представляет собой плотность нормального распределения с математическим ожиданием, равным нулю, и стандартным отклонением, равным двум.
9.2.2.6 На рисунке 6 показана плотность распределения вероятностей для (гауссова), полученная способом оценивания неопределенности по GUM. На рисунке показана также одна из аппроксимаций (гистограмма) для
10
значений выходной величины
дискретным приближением
(см. 7.5) для данной плотности распределения, полученная методом Монте-Карло. Границы вероятностно симметричного 95%-ного интервала охвата, полученные обоими методами, показаны вертикальными линиями. Нормальная плотность распределения и ее аппроксимация визуально неразличимы, также как и границы соответствующих интервалов охвата. Для данного примера такое согласие является ожидаемым, т.к. соблюдаются все условия применимости способа оценивания неопределенности по GUM (см. 5.7) и задано достаточно большое значение
.
- величина (безразмерная);
- плотность распределения вероятностей
Рисунок 6 - Приближения плотности распределения вероятностей для при нормальном распределении входных величин, полученных способом оценивания по GUM и методом Монте-Карло
9.2.2.7 В столбцах 6-8 таблицы 2 приведены результаты применения процедур проверки по 8.1 и 8.2. В соответствии с 7.9.2 ![]() 2, поскольку
2, поскольку определяют с двумя значащими цифрами. Таким образом,
![]() 2,0=20·10
2,0=20·10,
20 и
-1. Следовательно, в соответствии с 7.9.2 предел погрешности вычисления составляет
![]() .
.
В таблице 2 приведены также абсолютные значения разности верхних и нижних границ интервалов охвата, полученных способом оценивания по GUM и с помощью адаптивной процедуры метода Монте-Карло, и
соответственно [см. формулы (19) и (20)]. Показано, что проверкой с помощью адаптивной процедуры подтверждена достоверность результатов, полученных способом оценивания по GUM для
0,05.
9.2.2.8 На рисунке 7 показана зависимость длины ![]() 95%-ного интервала охвата (см. 7.7) от значения функции вероятности (определенной по
95%-ного интервала охвата (см. 7.7) от значения функции вероятности (определенной по ) в точке его левой границы. Как и следовало ожидать для симметричной плотности распределения вероятностей, интервал имеет наименьшую длину, если он симметричен относительно математического ожидания.
- значение функции вероятности для левой границы интервала охвата;
- длина интервала охвата
Рисунок 7 - Длина 95%-ного интервала охвата в зависимости от значения функции вероятности для его левой границы в дискретном представлении , полученном методом Монте-Карло для модели, описываемой формулой (21)
9.2.2.9 В 9.4 дан пример асимметричной плотности распределения вероятностей, для которой наименьший интервал охвата существенно отличается от вероятностно симметричного.
9.2.3 Входные величины, описываемые равномерными распределениями с одинаковым носителем
9.2.3.1 Каждой входной величине приписано равномерное распределение с нулевым математическим ожиданием и единичным стандартным отклонением (в отличие от 9.2.2.1, где входным величинам приписано нормальное распределение). Наилучшими оценками
являются
0,
1, 2, 3, 4 с соответствующими стандартными неопределенностями
![]() 1.
1.
9.2.3.2 Аналогично 9.2.2.3-9.2.2.5 получены результаты, представленные в таблице 3. Аналитическое решение для границ вероятностно симметричного 95%-ного интервала охвата, а именно, ![]() , было получено в соответствии с приложением Е.
, было получено в соответствии с приложением Е.
Таблица 3 - То же, что и в таблице 2, для равномерных плотностей распределения вероятностей для с одинаковыми математическими ожиданиями и стандартными отклонениями
Метод | Вероятностно симметричный 95%-ный интервал охвата | Достоверность результатов по GUM ( | |||||
GUM | - | 0,00 | 2,00 | [-3,92, 3,92] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,01 | [-3,90, 3,89] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,00 | [-3,89, 3,88] | - | - | - |
Монте-Карло | 10 | 0,00 | 2,00 | [-3,88, 3,88] | - | - | - |
Монте-Карло, адаптивный | 1,02·10 | 0,00 | 2,00 | [-3,88, 3,89] | 0,04 | 0,03 | Да |
Монте-Карло, адаптивный | 0,86·10 | 0,00 | 2,00 | [-3,87, 3,87] | 0,05 | 0,05 | Нет |
Аналитический | - | 0,00 | 2,00 | [-3,88, 3,88] | - | - | - |
9.2.3.3 Рисунок 8, построенный для данного случая, аналогичен рисунку 6, но в отличие от рисунка 6 можно заметить небольшие различия между аппроксимациями плотности распределения вероятностей. Способ оценивания неопределенности по GUM дает одну и ту же плотность распределения вероятностей для и в случае нормального, и в случае равномерного распределения
, поскольку и в том, и в другом случае и математические ожидания, и стандартные отклонения равны между собой. Плотность распределения вероятностей для
, полученная методом Монте-Карло, меньше плотности распределения вероятностей, полученной по GUM, в окрестности математического ожидания и, в меньшей степени, в области "хвостов" распределения и, наоборот, несколько выше в промежуточных областях на "склонах" распределения. Границы полученных интервалов охвата снова почти неразличимы визуально, но в числовых значениях, приведенных в таблице 3, можно увидеть небольшие различия.
- величина (безразмерная);
- плотность распределения вероятностей
Рисунок 8 - То же, что и на рисунке 6, но для равномерно распределенных входных величин с одинаковыми математическими ожиданиями и одинаковыми стандартными неопределенностями
9.2.3.4 Вероятностно симметричный 95%-ный интервал охвата, определенный по GUM, в данном случае несколько превышает интервал, полученный аналитическим расчетом. Как и в случае нормально распределенных входных величин, применена процедура проверки (таблица 3, столбцы 6-8). Как и ранее, ![]() 2,
2, ![]() 2,0=20·10
2,0=20·10,
20,
-1 и
0,05. Разности между границами
и
в данном случае больше, чем для нормально распределенных величин (таблица 2). Первая проверка с помощью адаптивной процедуры метода Монте-Карло показала, что результаты, полученные способом оценивания неопределенности по GUM, являются достоверными. Однако вторая проверка этот вывод не подтвердила, хотя полученные в ходе проверок значения
и
близки к пределу погрешности вычисления
0,05 (несоответствие заявленной точности вычислений можно обнаружить, если использовать большее число значащих цифр, чем показано в таблице 3). Различие в результатах двух проверок методом Монте-Карло объясняются стохастической природой этого метода.
9.2.4 Входные величины, описываемые равномерными распределениями с различными параметрами
9.2.4.1 В таблице 4 представлены результаты для примера, аналогичного рассмотренному в 9.2.3, но когда стандартное отклонение для равно десяти.
Таблица 4 - То же, что и в таблице 3, в случае, когда четвертая входная величина имеет стандартное отклонение, равное десяти, и нет аналитического решения
Метод | Вероятностно симметричный 95%-ный интервал охвата | Достоверность результатов по GUM ( | |||||
GUM | - | 0,00 | 10,1 | [-19,9, 19,9] | - | - | - |
Монте-Карло | 105* | 0,00 | 10,2 | [-17,0, 17,0] | - | - | - |
Монте-Карло | 106* | 0,00 | 10,2 | [-17,0, 17,0] | - | - | - |
Монте-Карло | 106* | 0,00 | 10,1 | [-17,0, 17,0] | - | - | - |
Монте-Карло, адаптивный | 0,03·10 | 0,01 | 10,2 | [-17,1, 17,1] | 2,8 | 2,8 | Нет |
Монте-Карло, адаптивный | 0,08·10 | 0,00 | 10,1 | [-17,0, 17,0] | 2,9 | 2,9 | Нет |
________________
* Текст документа соответствует оригиналу. - .
9.2.4.2 Число испытаний , полученное при реализации адаптивной процедуры метода Монте-Карло (0,03·10
и 0,08·10
), намного меньше, чем в двух предыдущих случаях для данного примера. Основная причина состоит в том, что в данном случае предел погрешности вычисления
0,5, полученный, как и ранее, из условия представления
двумя значащими цифрами, в десять раз больше ее значения в двух предыдущих случаях. Если бы использовалось предыдущее значение
0,05, то значения были примерно в 100 раз больше указанных в таблице 4.
9.2.4.3 На рисунке 9 показаны две аппроксимации плотности распределения вероятностей для . Видно, что они сильно различаются между собой. Доминирующая роль распределения для
очевидна - плотность распределения вероятностей для
похожа на плотность распределения вероятностей для
, но имеет более покатые "склоны", что обусловлено влиянием плотностей распределения вероятностей других входных величин
,
1, 2, 3.
- величина (безразмерная);
- плотность распределения вероятностей
Рисунок 9 - То же, что и на рисунке 8, за исключением того, что стандартное распределение четвертой входной величины равно 10
9.2.4.4 На рисунке 9 показаны также границы вероятностно симметричного 95%-ного интервала охвата для , полученного на основе аппроксимаций. Внутренняя пара вертикальных линий (сплошные линии) показывает границы вероятностно симметричного 95%-ного интервала охвата, определенного методом Монте-Карло. Внешняя пара (пунктирные линии) получена на основе оценивания неопределенности по GUM с коэффициентом охвата
1,96.
9.2.4.5 Вероятностно симметричный 95%-ный интервал охвата, определенный способом оценивания неопределенности по GUM, в этом случае существенно больше полученного с использованием метода Монте-Карло. Как и ранее, применена процедура проверки (таблица 4, столбцы 6-8). В данном случае ![]() 2,
2, ![]() 1,0·10
1,0·10, 10·10
,
10,
0 и
0,5. Проведенная дважды проверка с помощью адаптивного метода Монте-Карло показала, что результаты оценивания неопределенности по GUM являются недостоверными. Однако результаты проверки были бы положительными при условии сохранения одной значащей цифры в десятичном представлении
, т.е. когда
![]() 1 и
1 и 5. В этом случае все интервалы охвата, полученные разными способами, имели бы один и тот же вид: [-2·10
, 2·10
] (см. 4.13).
Примечание - Условия центральной предельной теоремы [Руководство ИСО/МЭК 98-3 (G.6.5)] в этом случае выполняются не в полной мере из-за доминирующего влияния равномерного распределения для (см. 5.7.2), что должно было исключить возможность применения способа оценивания неопределенности по GUM. В настоящем пункте результаты применения данного способа приведены для сопоставления, поскольку на практике пользователи зачастую пренебрегают выполнением условий центральной предельной теоремы и полагают выходную величину
подчиняющейся нормальному закону (особенно когда пользуются собственными программными средствами расчета неопределенности - см. 9.4.2.5, примечание 3).
9.3 Калибровка массы
9.3.1 Постановка задачи
9.3.1.1 Рассмотрена калибровка гири с массовой плотностью
сравнением с эталоном
той же номинальной массы с массовой плотностью
путем взвешивания на весах в воздухе с массовой плотностью
[39]. Поскольку
и
в общем случае различны, необходимо учитывать действие выталкивающей силы. С учетом закона Архимеда модель измерения имеет следующий вид:
![]() , (22)
, (22)
где - масса гири;
- масса эталона;
- масса малого дополнительного груза с плотностью
, добавленного к эталону
, чтобы уравновесить его с гирей
.
9.3.1.2 Обычно при калибровке масс используют понятие условной массы. Условная масса - это масса воображаемой гири с массовой плотностью
8000 кг/м
, которая при взвешивании в воздухе с плотностью воздуха
![]() 1,2 кг/м
1,2 кг/м уравновесит гирю
. Таким образом,
![]() .
.
9.3.1.3 В обозначениях условных масс ,
и
![]() c формула (22) принимает вид
c формула (22) принимает вид
![]() . (23)
. (23)
Формулу (23) можно представить в приближенном виде, пригодном для большинства практических ситуаций:
 .
.
Если обозначить через ![]() отклонение условной массы гири
отклонение условной массы гири от номинальной массы гири
![]() 100 г, то модель измерения для данного примера будет иметь вид:
100 г, то модель измерения для данного примера будет иметь вид:
 . (24)
. (24)
Примечание - Применение закона трансформирования неопределенности к "точной" модели, задаваемой формулой (23), затруднительно из-за сложного вида частных производных. К "точной" модели проще применить метод Монте-Карло, поскольку в этом случае необходимо только сформировать выходные значения модели.
9.3.1.4 Единственная доступная информация относительно эталона заключается в том, что
и
![]() - это, соответственно, наилучшие оценки массы эталона и ее стандартной неопределенности. В соответствии с 6.4.7.1 каждой из этих величин приписывают нормальное распределение с наилучшими оценками в качестве математического ожидания соответствующих величин и их стандартными неопределенностями в качестве стандартных отклонений. Единственная доступная информация о
- это, соответственно, наилучшие оценки массы эталона и ее стандартной неопределенности. В соответствии с 6.4.7.1 каждой из этих величин приписывают нормальное распределение с наилучшими оценками в качестве математического ожидания соответствующих величин и их стандартными неопределенностями в качестве стандартных отклонений. Единственная доступная информация о ,
и
- это нижняя и верхняя границы возможных значений для каждой из этих величин. Соответственно (см. 6.4.2.1), каждой из этих величин приписывают равномерное распределение в пределах границ возможных значений. В таблице 5 представлены входные величины и приписанные им плотности распределения вероятностей. В этой таблице нормальное распределение
![]() задано математическим ожиданием
задано математическим ожиданием и стандартным отклонением
, а равномерное распределение
![]() с границами интервала
с границами интервала и
![]() - математическим ожиданием
- математическим ожиданием ![]() и половиной длины интервала
и половиной длины интервала ![]() .
.
Примечание - Для величины в модели, задаваемой формулой (24), установлено значение 1,2 кг/м
без соответствующей неопределенности.
Таблица 5 - Входные величины с соответствующими плотностями распределения вероятностей для модели калибровки массы
Распределение | Параметры | ||||
Математическое ожидание | Стандартное отклонение | Математическое ожидание | Половина длины носителя | ||
| 100000,000 мг | 0,050 мг | |||
|
| 1,234 мг | 0,020 мг | ||
| 1,20 кг/м | 0,10 кг/м | |||
| 8·103* кг/м | 1·103* кг/м | |||
| 8,00·103* кг/м | 0,05·103* кг/м | |||
________________
* Текст документа соответствует оригиналу. - .
9.3.2 Трансформирование распределений и получение результатов
9.3.2.1 Способ оценивания неопределенности по GUM и адаптивная процедура метода Монте-Карло (см. 7.9) были использованы для получения оценки величины
, ее стандартной неопределенности
![]() и наименьшего 95%-ного интервала охвата для
и наименьшего 95%-ного интервала охвата для . Полученные результаты приведены в таблице 6.
Таблица 6 - Результаты вычислений для калибровки массы
Метод |
|
| Наименьший 95%-ный интервал охвата, мг |
|
| Достоверность результатов по GUM ( |
GUM, с использованием членов 1-го порядка | 1,2340 | 0,0539 | [1,1285, 1,3395] | 0,0451 | 0,0430 | Нет |
Монте-Карло | 1,2341 | 0,0754 | [1,0834, 1,3825] | |||
GUM, с использованием членов более высокого порядка | 1,2340 | 0,0750 | [1,0870, 1,3810] | 0,0036 | 0,0015 | Да |
9.3.2.2 Для достижения погрешности вычисления (см. 8.2) с
, соответствующей одной значащей цифре в
![]() , было выполнено 0,72·10
, было выполнено 0,72·10 испытаний в соответствии с адаптивной процедурой метода Монте-Карло (см. 9.3.2.6).
9.3.2.3 На рисунке 10 показана аппроксимация плотностей распределения вероятностей для , полученных применением способа оценивания неопределенности по GUM с использованием членов первого порядка в представлении функции измерения рядом Тейлора и методом Монте-Карло. Непрерывная кривая соответствует плотности нормального распределения с параметрами, определенными способом оценивания неопределенности по GUM. Внутренняя пара (пунктирных) вертикальных линий показывает наименьший 95%-ный интервал для
, построенный на основе этой плотности распределения вероятностей. Гистограмма представляет собой аппроксимацию плотности распределения вероятностей, построенную методом Монте-Карло. Внешняя пара (непрерывных) вертикальных линий показывает наименьший 95%-ный интервал охвата для
, построенный на основе дискретного представления функции распределения в соответствии с 7.5.
- отклонение
условной массы гири от ее номинального значения, мг;
- плотность распределения вероятностей, мг
Рисунок 10 - Аппроксимации плотности распределения вероятностей для выходной величины , полученные с использованием способа оценивания неопределенности по GUM с учетом членов первого порядка и методом Монте-Карло
9.3.2.4 Результаты показывают, что, хотя способ оценивания неопределенности по GUM (с учетом членов первого порядка) и метод Монте-Карло дают очень близкие оценки , значения соответствующих стандартных неопределенностей заметно различаются. Значение (0,0754 мг) для
![]() , полученное методом Монте-Карло, на 40% больше значения (0,0539 мг) для той же величины, полученного способом оценивания неопределенности по GUM (с учетом членов первого порядка). Т.е. оценка, полученная по GUM, в данном случае будет излишне оптимистичной. В то же время хорошо согласуются между собой оценка
, полученное методом Монте-Карло, на 40% больше значения (0,0539 мг) для той же величины, полученного способом оценивания неопределенности по GUM (с учетом членов первого порядка). Т.е. оценка, полученная по GUM, в данном случае будет излишне оптимистичной. В то же время хорошо согласуются между собой оценка ![]() , полученная с использованием метода Монте-Карло, и значение (0,0750 мг), полученное способом оценивания неопределенности по GUM с учетом членов более высокого порядка в разложении функции измерения в ряд Тейлора.
, полученная с использованием метода Монте-Карло, и значение (0,0750 мг), полученное способом оценивания неопределенности по GUM с учетом членов более высокого порядка в разложении функции измерения в ряд Тейлора.
9.3.2.5 В таблице 7 приведены частные производные первого порядка функции измерения [формула (24)] по входным величинам и коэффициенты чувствительности, т.е. значения этих производных в точках наилучших оценок входных величин. Эти данные показывают, что для рассматриваемого примера при применении способа оценивания неопределенности по GUM с учетом членов первого порядка разложения может быть использована аддитивная модель
![]() .
.
Таблица 7 - Коэффициенты чувствительности для модели измерения [формула (24)] в примере калибровки массы
Частная производная | Коэффициент чувствительности | |
| 1 | |
|
| 1 |
| 0 | |
| 0 | |
| 0 |
Метод Монте-Карло такой аппроксимации не требует.
9.3.2.6 В трех правых столбцах таблицы 6 приведены результаты проверки (см. 8.1 и 8.2) при сохранении одной значащей цифры в ![]() , т.е.
, т.е. ![]() 1. Следовательно,
1. Следовательно, ![]() 0,08 = 8·10
0,08 = 8·10, тогда (см. 7.9.2)
8 и
-2. Таким образом,
1/2·10
=0,005. Значения
и
показывают разности в оценках, соответственно, для нижней и верхней границы интервала охвата [см. формулы (19) и (20), где вместо
нужно подставить
]. В последнем столбце таблицы 6 приведены итоги проверки достоверности результатов, полученные при условии сохранения одной значащей цифры в представлении
![]() . Если в представлении функции измерения рядом Тейлора учтены только члены первого порядка, то применение способа оценивания неопределенности по GUM дает недостоверные результаты. Если учтены члены более высокого порядка [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)], то применение способа оценивания неопределенности по GUM обосновано. Следовательно, в данном примере нелинейность модели такова, что учета только членов первого порядка в разложении функции измерения недостаточно.
. Если в представлении функции измерения рядом Тейлора учтены только члены первого порядка, то применение способа оценивания неопределенности по GUM дает недостоверные результаты. Если учтены члены более высокого порядка [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)], то применение способа оценивания неопределенности по GUM обосновано. Следовательно, в данном примере нелинейность модели такова, что учета только членов первого порядка в разложении функции измерения недостаточно.
9.4 Определение коэффициента рассогласования для калибровки измерителя мощности СВЧ-сигнала методом сравнения
9.4.1 Постановка задачи
9.4.1.1 При калибровке сравнением калибруемый и эталонный измерители мощности поочередно помещают в поле стабильного генератора СВЧ-сигнала. Поглощаемая измерителями мощность в общем случае будет разной ввиду несовпадения их комплексных коэффициентов отражения по напряжению. Отношение мощности
, поглощенной калибруемым измерителем, к мощности
, поглощенной эталонным измерителем, имеет вид [43]:
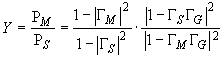 , (25)
, (25)
где - коэффициент отражения по напряжению генератора сигнала;
- коэффициент отражения по напряжению калибруемого измерителя;
- коэффициент отражения по напряжению эталонного измерителя.
Отношение, определенное формулой (25), называют коэффициентом рассогласования, знание которого необходимо для проведения калибровки методом сравнения [1, 28].
9.4.1.2 В настоящем примере рассматривается случай отсутствия отражения эталонным измерителем и генератором сигнала, т.е. когда ![]() 0, и значения измеряемой величины определяются действительной
0, и значения измеряемой величины определяются действительной и мнимой
частями величины
![]() , где
, где -1. Поскольку
![]() , формула (25) принимает вид
, формула (25) принимает вид
![]() . (26)
. (26)
9.4.1.3 На основе измерений получены наилучшие оценки и
величин
и
и соответствующие им стандартные неопределенности
и
![]() . Зачастую
. Зачастую и
не являются независимыми. Ковариация
![]() , связанная с оценками
, связанная с оценками и
, может быть представлена в виде
![]() , где
, где ![]() - коэффициент корреляции [Руководство ИСО/МЭК 98-3 (5.2.2)].
- коэффициент корреляции [Руководство ИСО/МЭК 98-3 (5.2.2)].
Примечание - На практике инженер-электрик может затрудняться в числовом определении ковариации. В таких случаях оценивание неопределенности может быть повторено в испытаниях с различными численными значениями коэффициента корреляции, чтобы изучить его влияние. В данном примере проведены вычисления с коэффициентом корреляции, равным нулю и 0,9 (см. 9.4.1.7).
9.4.1.4 В соответствии с 6.4.8.1 вектору случайных величин ![]() приписана двумерная плотность нормального распределения с математическим ожиданием и ковариационной матрицей соответственно
приписана двумерная плотность нормального распределения с математическим ожиданием и ковариационной матрицей соответственно
 . (27)
. (27)
9.4.1.5 Т.к. величины и
, входящие в формулу (26), на практике малы по сравнению с единицей, соответствующее значение
будет близко к единице. Поэтому в качестве модели измерения можно принять
![]() . (28)
. (28)
В соответствии с физическим смыслом 01 и, следовательно, 0
![]() 1.
1.
9.4.1.6 Оценка величины
, ее стандартная неопределенность
и интервал охвата для
должны быть получены для различных
,
,
,
![]() и
и ![]() . Все эти величины безразмерны.
. Все эти величины безразмерны.
9.4.1.7 Рассматриваются шесть случаев, в каждом из которых 0,
![]() 0,005. В первых трех случаях
0,005. В первых трех случаях принимает значения
0,
0,010 и
0,050 при
![]() 0. Остальные три случая соответствуют тем же значениям
0. Остальные три случая соответствуют тем же значениям , но при
![]() 0,9. Различные значения
0,9. Различные значения (сопоставимые с наблюдаемыми на практике) использованы с целью исследовать, до какой степени могут различаться результаты оценивания неопределенности, полученные разными методами.
9.4.1.8 В случаях, когда ![]() 0, ковариационная матрица [см. формулу (27)] становится диагональной:
0, ковариационная матрица [см. формулу (27)] становится диагональной: ![]() , а соответствующее совместное распределение
, а соответствующее совместное распределение и
превращается в произведение двух одномерных нормальных распределений
,
1, 2, с математическим ожиданием
и стандартным отклонением
.
9.4.2 Трансформирование распределений и получение результатов при нулевой ковариации между входными величинами
9.4.2.1 Общие положения
9.4.2.1.1 Оценивание неопределенности основано на трансформировании распределений, реализованном:
a) аналитически (в целях сравнения);
b) использованием способа оценивания неопределенности по GUM;
c) с использованием метода Монте-Карло.
Примечание - Все указанные методы не обеспечивают получение такого распределения вероятностей для , чтобы, как это диктуют физические соображения, вероятность значений
, превышающих единицу, была равна нулю. Однако для достаточно малых неопределенностей
и
![]() , как в данном примере, можно указанным физическим ограничением пренебречь и аппроксимировать плотность распределения вероятностей для
, как в данном примере, можно указанным физическим ограничением пренебречь и аппроксимировать плотность распределения вероятностей для более простой функцией, определенной на множестве всех неотрицательных значений
. Более строгий результат [не зависящий от условия малости значений
и
![]() ] мог бы быть получен в рамках байесовского подхода [51], учитывающего априорную информацию об измеряемой величине, однако его рассмотрение выходит за рамки настоящего стандарта (см. раздел 1, примечание 2).
] мог бы быть получен в рамках байесовского подхода [51], учитывающего априорную информацию об измеряемой величине, однако его рассмотрение выходит за рамки настоящего стандарта (см. раздел 1, примечание 2).
9.4.2.1.2 Оценки и
могут быть получены аналитически как математическое ожидание и стандартное отклонение плотности распределения вероятностей для
(см. раздел F.1). В свою очередь, плотность распределения вероятностей для
может быть получена аналитически и использована для определения границ наименьшего 95%-ного интервала охвата в случае, когда
0 (см. раздел F.2).
9.4.2.1.3 Способ оценивания неопределенности по GUM с использованием членов первого порядка и членов более высокого порядка разложения в ряд Тейлора применен для каждой из трех оценок при
![]() 0 (см. раздел F.3). Оценка
0 (см. раздел F.3). Оценка выходной величины
каждый раз была получена по формуле [Руководство ИСО/МЭК 98-3 (4.1.4)]
![]() .
.
9.4.2.1.4 Метод Монте-Карло был применен в каждом из случаев с числом испытаний 10
.
9.4.2.2 Оценка входной величины 0
9.4.2.2.1 Для случая, когда оценка входной величины 0, при применении закона трансформирования неопределенностей необходимо учитывать члены высших порядков, поскольку частные производные
по
и
в точке
![]() ,
, ![]() при
при ![]() 0 равны нулю. Следовательно, если в законе трансформирования неопределенностей учитывать только члены разложения первого порядка, то получаемая оценка стандартной неопределенности для выходной величины будет некорректной (равной нулю).
0 равны нулю. Следовательно, если в законе трансформирования неопределенностей учитывать только члены разложения первого порядка, то получаемая оценка стандартной неопределенности для выходной величины будет некорректной (равной нулю).
Примечание - Аналогичная трудность возникает и при оценке , не равной, но достаточно близкой к нулю.
9.4.2.2.2 На рисунке 11 показана плотность распределения вероятностей для , полученная на основе трансформирования распределений:
a) аналитически (экспоненциально убывающая кривая для 0 и ноль для
0);
b) с использованием способа оценивания неопределенности по GUM с учетом членов более высокого порядка для того, чтобы охарактеризовать выходную величину нормальной плотностью распределения (колоколообразная кривая);
c) с использованием метода Монте-Карло (гистограмма).
- отклонение
коэффициента рассогласования от единицы (умноженное на 10
);
- плотность распределения вероятностей (умноженная на 10
)
Рисунок 11 - Результаты оценивания для модели коэффициента рассогласования, применяемого при калибровке измерителей мощности СВЧ-сигнала, в случае ![]() 0,
0, ![]() 0,005,
0,005, ![]() 0
0
9.4.2.2.3 Из рисунка 11 видно, что использование способа оценивания неопределенности по GUM с учетом членов более высокого порядка для описания выходной величины нормальным распределением дает плотность распределения вероятностей, которая существенно отличается от полученной аналитическим решением. Аналитическое решение представляет собой частный случай распределения -квадрат (распределение суммы квадратов двух случайных величин, каждая из которых подчиняется стандартному нормальному распределению) (см. раздел F.2).
9.4.2.2.4 Т.к. все частные производные функции измерения [формула (28)] порядка выше двух равны нулю, полученное решение, по существу, соответствует учету всех членов ряда Тейлора, т.е. полному учету нелинейности рассматриваемой модели. Следовательно, полученное нормальное распределение является наилучшим приближением среди всех возможных, определяемых по GUM, для описания свойств выходной величины.
9.4.2.2.5 Можно сделать вывод, что причина расхождения результатов применения аналитического метода и способа оценивания неопределенности по GUM в том, что в последнем случае для описания выходной величины использовано нормальное распределение, которое, однако, не может адекватно аппроксимировать аналитическое решение для данной конкретной задачи.
9.4.2.2.6 Из рисунка 11 видно также, что плотность распределения вероятностей, полученная методом Монте-Карло, полностью согласуется с аналитическим решением.
9.4.2.2.7 Оценки математического ожидания
получены:
а) аналитически;
b) с использованием способа оценивания неопределенности по GUM;
c) с применением метода Монте-Карло.
Значения оценок приведены в столбцах 2-4 строки, соответствующей 0,000, таблицы 8. В столбцах 5-8 приведены соответствующие значения
, полученные по GUM с учетом только членов первого порядка разложения (
) и с учетом членов более высокого порядка (
).
Таблица 8 - Оценки коэффициента рассогласования, полученные для входных величин с нулевой ковариацией аналитически (), способом оценивания неопределенности по GUM с членами первого порядка (
) и членами более высокого порядка (
), методом Монте-Карло (M)
|
| Наименьший 95%-ный интервал охвата | |||||||||
А | G | М | А | G1 | G2 | М | А | G1 | G2 | М | |
0,000 | 50 | 0 | 50 | 50 | 0 | 50 | 50 | [0, 150] | [0,0] | [-98, 98] | [0, 150] |
0,010 | 150 | 100 | 150 | 112 | 100 | 112 | 112 | - | [-96, 296] | [-119, 319] | [0, 367] |
0,050 | 2550 | 2500 | 2551 | 502 | 500 | 502 | 502 | - | [1520, 3480] | [1515, 3485] | [1590, 3543] |
9.4.2.2.8 Оценка 0, получаемая при подстановке оценок входных величин в функцию измерения, является некорректной. Правильный (полученный аналитически) вид плотности распределения вероятностей
![]() показывает, что
показывает, что ![]() 0 для всех
0 для всех 0. Таким образом, оценка
0 лежит на границе области значений, где функция
![]() отлична от нуля. Оценка, полученная методом Монте-Карло, согласуется с аналитическим решением. Закон трансформирования неопределенностей с учетом членов разложения первого порядка дает уже упомянутое неверное, нулевое значение для
отлична от нуля. Оценка, полученная методом Монте-Карло, согласуется с аналитическим решением. Закон трансформирования неопределенностей с учетом членов разложения первого порядка дает уже упомянутое неверное, нулевое значение для . Значение
![]() 50·10
50·10, полученное с использованием закона трансформирования неопределенностей при учете членов более высокого порядка согласуется со значением, полученным аналитически и методом Монте-Карло.
Примечание - Оценки для , полученные в результате нескольких повторных применений метода Монте-Карло, дают некоторый разброс в окрестности значения 50·10
. После повторений метода Монте-Карло еще несколько раз, но уже с большим значением числа испытаний М, результаты вновь находились в окрестности 50·10
, но уже с меньшим разбросом. Такое уменьшение разброса является ожидаемым и наблюдается для разных вычислений, использующих метод Монте-Карло. Чтобы увидеть реальные изменения численных результатов применения метода необходимо использовать для их представления большее число значащих цифр.
9.4.2.2.9 На рисунке 11 показаны наименьшие 95%-ные интервалы охвата для соответствующих аппроксимаций функции распределения . Интервал, обозначенный пунктирными вертикальными линиями и полученный на основе способа оценивания неопределенности по GUM, некорректен - он симметричен относительно
0 и, таким образом, допускает 50%-ную вероятность существования отрицательных значений
, не имеющих физического смысла. Непрерывные вертикальные линии указывают границы наименьшего 95%-ного интервала охвата, полученные на основе аналитического решения, как описано в F.2. Границы наименьшего 95%-ного интервала, определенные с использованием метода Монте-Карло, от них на рисунке 11 неотличимы.
9.4.2.2.10 Границы наименьших интервалов охвата, соответствующие оценкам стандартной неопределенности, приведенным в столбцах 5-8 строки, соответствующей 0,000, указаны в столбцах 9-12 таблицы 8.
9.4.2.2.11 На рисунке 12 показана зависимость длины ![]() 95%-ного интервала охвата (см. 7.7) от вероятности его левой границы, определенной по аппроксимации плотности распределения вероятностей, полученной методом Монте-Карло и показанной на рисунке 11. В данном примере 95%-ный интервал охвата, расположенный симметрично относительно математического ожидания, не является наименьшим 95%-ным интервалом охвата. Наименьший 95%-ный интервал охвата очень сильно отличается и от вероятностно-симметричного 95%-ного интервала охвата. Если для последнего площади под плотностью распределения вероятностей слева от
95%-ного интервала охвата (см. 7.7) от вероятности его левой границы, определенной по аппроксимации плотности распределения вероятностей, полученной методом Монте-Карло и показанной на рисунке 11. В данном примере 95%-ный интервал охвата, расположенный симметрично относительно математического ожидания, не является наименьшим 95%-ным интервалом охвата. Наименьший 95%-ный интервал охвата очень сильно отличается и от вероятностно-симметричного 95%-ного интервала охвата. Если для последнего площади под плотностью распределения вероятностей слева от и справа от
равны и составляют 0,025 (или 2,5%), то для наименьшего 95%-ного интервала охвата эти значения будут равны, соответственно, 0 и 0,05 (или 0% и 5%). Этот рисунок можно сравнить с рисунком 7 для аддитивной модели (см. 9.2), в которой плотность распределения вероятностей для
симметрична относительно математического ожидания.
- значение функции вероятности для левой границы интервала охвата;
- длина интервала охвата (умноженная на 10
)
Рисунок 12 - Длина 95%-ного интервала охвата в зависимости от значения функции вероятности для левой границы интервала охвата, построенного с использованием метода Монте-Карло для модели, описываемой формулой (28)
9.4.2.3 Оценка входной величины 0,010
9.4.2.3.1 На рисунке 13 показаны плотности распределения вероятностей, полученные способом оценивания неопределенности по GUM с использованием членов разложения только первого порядка и с использованием членов разложения более высокого порядка, а также методом Монте-Карло для случая оценки входной величины 0,010 и коэффициента корреляции
![]() 0.
0.
- отклонение
коэффициента рассогласования от единицы (умноженное на 10
);
- плотность распределения вероятностей (умноженная на 10
)
Рисунок 13 - То же, что и на рисунке 11, но для 0,010 и с двумя кривыми, полученными способом оценивания по GUM (высокий пик - учтены только члены 1-го порядка; низкий пик - учтены члены более высокого порядка)
9.4.2.3.2 Плотность распределения вероятностей, полученная методом Монте-Карло, имеет небольшой левый склон, несмотря на то, что она обрезана в нуле, наименьшем возможном значении . По сравнению с результатами для
0 она более близка по форме к плотностям нормального распределения, полученным с применением способа оценивания неопределенности по GUM. Плотности нормального распределения, в свою очередь, достаточно близки друг к другу, имеют математическое ожидание величины
, равное 1,0·10
, и стандартные отклонения 1,0·10
и 1,1·10
соответственно.
9.4.2.3.3 На рисунке 13 показаны границы наименьших 95%-ных интервалов охвата, полученных с использованием вышеуказанных трех методов. Сплошные вертикальные линии показывают границы интервала, полученного методом Монте-Карло, пунктирные вертикальные линии - интервала, полученного на основе способа оценивания неопределенности по GUM с учетом членов разложения только первого порядка, а штрих-пунктирные вертикальные линии - интервала, полученного на основе того же способа по GUM, но с учетом членов разложения более высокого порядка. Интервалы, полученные на основе способа оценивания неопределенности по GUM, несколько смещены влево по сравнению с интервалом, полученным методом Монте-Карло. Как и в предыдущем случае, они включают в себя физически невозможные значения . Интервал, полученный методом Монте-Карло, имеет левую границу в нуле, наименьшем из возможных значений, и смещен относительно интервалов, полученных по GUM, приблизительно на 70% стандартной неопределенности.
9.4.2.3.4 Соответствующие значения границ интервалов приведены в предпоследней строке таблицы 8.
9.4.2.4 Оценка входной величины 0,050
9.4.2.4.1 Рисунок 14 аналогичен рисунку 13, но отражает результаты, полученные для 0,050. На рисунке 14 плотности распределения вероятностей, полученные в соответствии с обоими вариантами способа оценивания неопределенности по GUM, визуально почти неотличимы друг от друга. Кроме того, они намного ближе к аппроксимации плотности распределения вероятностей, полученной методом Монте-Карло. Последняя имеет незначительную асимметрию, особенно заметную на хвостах распределения. Интервалы охвата, полученные в соответствии с двумя вариантами способа оценивания неопределенности по GUM, визуально также почти неразличимы, но все еще смещены относительно интервалов, построенных методом Монте-Карло. Смещение составляет приблизительно 10% стандартной неопределенности. Интервалы, полученные на основе оценки неопределенности по GUM, теперь не являются физически некорректными.
- отклонение
коэффициента рассогласования от единицы (умноженное на 10
);
- плотность распределения вероятностей (умноженная на 10
)
Рисунок 14 - То же, что и на рисунке 13, но для 0,050
9.4.2.4.2 Соответствующие значения границ интервалов приведены в последней строке таблицы 8.
9.4.2.5 Анализ результатов
По мере удаления от нуля результаты, полученные на основе способа оценивания неопределенности по GUM с учетом членов разложения первого порядка и членов более высокого порядка, все более приближаются к результатам, полученным на основе метода Монте-Карло.
Примечание 1 - Случай ![]() 0 не относится к предельным, "экзотическим" ситуациям, но, наоборот, представляет наибольший интерес для инженера-электрика, поскольку он соответствует отсутствию рассогласования между калибруемым измерителем мощности и эталоном.
0 не относится к предельным, "экзотическим" ситуациям, но, наоборот, представляет наибольший интерес для инженера-электрика, поскольку он соответствует отсутствию рассогласования между калибруемым измерителем мощности и эталоном.
Примечание 2 - Поскольку модель симметрична относительно и
, те же самые результаты были бы получены при варьировании значения
, а не
.
Примечание 3 - Одной из причин, почему способ оценивания неопределенности по GUM с учетом только членов разложения первого порядка используется на практике, является легкодоступность соответствующих программных средств. Причем в некоторых ситуациях результаты, получаемые в рамках такого подхода, не вызывают вопросов. Для случая же, когда ![]() 0 (рисунок 11), опасность применения такого подхода очевидна, поскольку он дает нулевую оценку стандартной неопределенности
0 (рисунок 11), опасность применения такого подхода очевидна, поскольку он дает нулевую оценку стандартной неопределенности и, следовательно, нулевой интервал охвата для
при любой заданной вероятности охвата. В случае
0 (или
0) и
, длина интервала охвата для
отлична от нуля, т.е. полученный результат не является заведомо абсурдным, и о его возможной некорректности трудно судить, не имея априорной информации о реальных возможных значениях указанных величин. Таким образом, опасность применения программных средств, реализующих способ оценивания неопределенности по GUM, состоит в том, что при малых значениях
и
полученные с их помощью результаты, будучи недостоверными, могут быть, тем не менее, непредумышленно приняты за достоверные.
9.4.3 Трансформирование распределений и получение результатов при ненулевой ковариации между входными величинами
9.4.3.1 Общие положения
9.4.3.1.1 Описанные выше методы (см. 9.4.2) были применены для случая, когда коррелированны и
![]() 0,9. Однако использованный способ оценивания неопределенности по GUM учитывал только члены разложения функции измерения в ряд Тейлора первого порядка. Это связано с тем, что, в отличие от случая, когда
0,9. Однако использованный способ оценивания неопределенности по GUM учитывал только члены разложения функции измерения в ряд Тейлора первого порядка. Это связано с тем, что, в отличие от случая, когда некоррелированны, при наличии ковариаций способ оценивания неопределенности по GUM с учетом членов более высокого порядка не применяют ввиду отсутствия в GUM соответствующих формул (см. 5.8). Все остальные вопросы вычислений аналогичны 9.4.2.
9.4.3.1.2 Оценку по GUM с учетом членов разложения первого порядка определяют в соответствии с F.3.2. Применение для данного примера формулы (F.7) позволяет получить выражение для
![]() при
при 0 в виде
![]() .
.
Следовательно, не зависит от
![]() , и способ оценивания неопределенности по GUM с учетом членов разложения первого порядка даст те же результаты, что и в 9.4.2. В частности, как и в 9.4.2.2.1, для случая
, и способ оценивания неопределенности по GUM с учетом членов разложения первого порядка даст те же результаты, что и в 9.4.2. В частности, как и в 9.4.2.2.1, для случая 0, вновь будет получен тот же некорректный результат:
![]() 0.
0.
9.4.3.1.3 Метод Монте-Карло основан на формировании случайных элементов вектора выборкой из двумерного нормального распределения с заданным математическим ожиданием и ковариационной матрицей [см. формулу (27)]. Использована процедура в соответствии с разделом С.5.
Примечание - Не принимая во внимание необходимость формирования случайной выборки из многомерного распределения, реализация метода Монте-Карло для случая коррелированных входных величин будет не намного сложнее, чем для не коррелированных.
9.4.3.2 Оценки входных величин 0,
0,010,
0,050
9.4.3.2.1 Полученные результаты приведены в таблице 9. Результаты, полученные на основе метода Монте-Карло, показывают, что, хотя не зависит от корреляции между
, оценка
от нее зависит, причем в большей степени для малых
. Соответственно, зависят и границы 95%-ных интервалов охвата.
Таблица 9 - Оценки коэффициента рассогласования, полученные для входных величин с ненулевой ковариацией [![]() 0,9] аналитически (А), способом оценивания неопределенности по GUM (G) и методом Монте-Карло (М)
0,9] аналитически (А), способом оценивания неопределенности по GUM (G) и методом Монте-Карло (М)
|
| Наименьший 95%-ный интервал охвата | |||||||
А | G | М | А | G | М | А | G | М | |
0,000 | 50 | 0 | 50 | 67 | 0 | 67 | - | [0, 0] | [0, 185] |
0,010 | 150 | 100 | 150 | 121 | 100 | 121 | - | [-96, 296] | [13, 398] |
0,050 | 2550 | 2500 | 2551 | 505 | 500 | 504 | - | [1520, 3480] | [1628, 3555] |
9.4.3.2.2 На рисунках 15 и 16 показаны плотности распределения вероятностей, полученные на основе способа оценивания неопределенности по GUM с учетом членов разложения первого порядка (колоколообразные кривые) и методом Монте-Карло (гистограммы) для случаев 0,010 и
0,050, соответственно. Границы наименьших 95%-ных интервалов охвата показаны штриховыми вертикальными линиями для способа оценивания неопределенности по GUM и сплошными вертикальными линиями для метода Монте-Карло.
Примечание - Строго говоря, условия, при которых могла бы быть описана нормальным распределением, не выполняются при применении для данных случаев способа оценивания неопределенности по GUM (см. 5.8) [Руководство ИСО/МЭК 98-3 (G.6.6)]. Однако ввиду частого использования этого способа на практике полученные с его помощью плотности распределения вероятностей и границы 95%-ного интервала охвата показаны на рисунках 15 и 16.
- отклонение
коэффициента рассогласования от единицы (умноженное на 10
);
- плотность распределения вероятностей (умноженная на 10
)
Рисунок 15 - Результаты оценивания для модели коэффициента рассогласования, применяемого при калибровке измерителей мощности СВЧ-сигнала, в случае 0,010,
0,
![]() 0,005,
0,005, ![]() 0,9
0,9
- отклонение
коэффициента рассогласования от единицы (умноженное на 10
);
- плотность распределения вероятностей (умноженная на 10
)
Рисунок 16 - То же, что и на рисунке 15, но для 0,050
9.4.3.3 Анализ результатов
В случае 0,010 (рисунок 15) корреляция заметно повлияла на результаты, полученные методом Монте-Карло (ср. с рисунком 13). Изменилась сама форма аппроксимирующей плотности распределения вероятностей, и, кроме того, соответствующий интервал охвата уже не имеет левосторонней границы в нуле. В случае
0,050 (рисунок 16) разница в результатах для случаев некоррелированных и коррелированных входных величин (ср. с рисунком 14) менее заметна.
9.5 Калибровка концевой меры длины
9.5.1 Постановка задачи: модель измерения
9.5.1.1 Длину концевой меры номиналом 50 мм определяют ее сопоставлением с известным эталоном того же номинала. Непосредственный результат сопоставления длин двух концевых мер представляет собой разность :
![]() , (29)
, (29)
где - измеряемая величина, т.е. длина калибруемой концевой меры при 20 °С;
- длина эталона при 20 °С, приведенная в сертификате о калибровке;
и
- коэффициенты теплового расширения соответственно калибруемой концевой меры длины и эталона;
и
- отклонения температуры соответственно калибруемой концевой меры и эталона от нормальной температуры 20 °С.
Примечание 1 - В GUM рассматривается та же измерительная задача (раздел Н.1).
Примечание 2 - Для длины концевой меры в настоящем подразделе применено обозначение вместо обозначения
использованного в GUM.
9.5.1.2 В соответствии с формулой (29) выходная величина может быть определена как
![]() , (30)
, (30)
а в качестве приближения формулы (30), применимого в большинстве практических ситуаций, может быть использована формула
![]() . (31)
. (31)
Если разность температур калибруемой концевой меры и эталона обозначить как ![]() , а разность их коэффициентов теплового расширения как
, а разность их коэффициентов теплового расширения как ![]() , то формулы (30) и (31) принимают вид соответственно
, то формулы (30) и (31) принимают вид соответственно
![]() , (32)
, (32)
![]() . (33)
. (33)
9.5.1.3 Оценку разности длин калибруемой концевой меры и эталона определяют как выборочное среднее по пяти наблюдениям, полученным независимо с использованием калиброванного компаратора. Разность
можно представить в виде:
![]() , (34)
, (34)
где - случайная величина, для которой получено выборочное среднее по пяти наблюдениям;
и
- величины, описывающие, соответственно, случайные и систематические эффекты, связанные с использованием компаратора.
9.5.1.4 Величина , представляющая собой отклонение температуры калибруемой концевой меры длины от 20 °С, может быть представлена в виде:
![]() , (35)
, (35)
где - среднее отклонение температуры концевой меры длины от 20 °С;
- величина, описывающая циклические колебания отклонения температуры от
.
9.5.1.5 Подставляя формулы (34) и (35) в формулы (32) и (33) и введя обозначение для отклонения
от номинальной длины
![]() 50 мм концевой меры, можно записать
50 мм концевой меры, можно записать
![]() (36)
(36)
или
![]() . (37)
. (37)
Эти зависимости могут быть рассмотрены как модели измерительной задачи.
9.5.1.6 Выходной величиной для моделей (36) и (37) является , а входными величинами -
,
,
,
,
,
,
,
и
. Эта модель отличается от приведенной в GUM (раздел Н.1) тем, что в GUM модели, описываемые формулами (34) и (35) настоящего стандарта, рассматриваются как подмодели моделей, описываемых формулами (32) и (33), т.е. в GUM вначале оценивание неопределенности выполнено для подмоделей, соответствующих формулам (34) и (35), после чего полученные оценки неопределенности для
и
были использованы для описания этих входных величин в моделях, соответствующих формулам (32) и (33). В настоящем примере, где для получения оценок используется метод Монте-Карло, такое двухэтапное оценивание не применяется.
9.5.2 Постановка задачи: приписывание плотностей распределения вероятностей входным величинам
9.5.2.1 Общие положения
В последующих подпунктах приведена информация о каждой входной величине моделей, соответствующих формулам (36) и (37). Используемая информация основана на описании, приведенном в GUM, и каждый раз дается ссылка на соответствующий структурный элемент GUM, откуда эта информация взята. Кроме того, показано, каким образом указанная информация используется при выборе распределения входных величин. Все сведения, связанные с приписыванием распределений входным величинам моделей измерений, собраны в таблицу 10.
Таблица 10 - Плотности распределения вероятностей для входных величин для моделей концевых мер длины (36) и (37) на основе доступной информации (9.5.2.1). (Основная информация о плотностях распределения вероятностей приведена в таблице 1)
Вели- | Плотность распределения | Параметры распределения | |||||
| 50000623 нм | 25 нм | 18 | ||||
| 215 нм | 6 нм | 24 | ||||
| 0 нм | 4 нм | 5 | ||||
| 0 нм | 7 нм | 8 | ||||
| 9,5·10 | 13,5·10 | |||||
| -0,1 °С | 0,2 °С | |||||
| -0,5 °С | 0,5 °С | |||||
| -1,0·10 | 1,0·10 | 0,1·10 | ||||
| -0,050 °С | 0,050 °С | 0,025 °С | ||||
9.5.2.2 Длина эталона
9.5.2.2.1 Исходная информация
В сертификате о калибровке для эталона указана оценка его длины при 20 °С 50,000623 мм [Руководство ИСО/МЭК 98-3 (Н.1.5)] и расширенная неопределенность этой оценки
0,075 мкм для коэффициента охвата
3 [Руководство ИСО/МЭК 98-3 (Н.1.3.1)]. В сертификате указано, что число эффективных степеней свободы для суммарной стандартной неопределенности, на основе которой была получена упомянутая расширенная неопределенность,
![]() 18 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
18 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
9.5.2.2.2 Выбор распределения
Величине было приписано масштабированное смещенное
-распределение
![]() (см. 6.4.9.7) со значениями параметров
(см. 6.4.9.7) со значениями параметров
50000623 нм,
 25 нм,
25 нм, 18.
9.5.2.3 Средняя разность длин
9.5.2.3.1 Исходная информация
Выборочное среднее по пяти наблюдениям разности длин калибруемой концевой меры длины и эталона составляет 215 нм [Руководство ИСО/МЭК 98-3 (Н.1.5)]. Объединенное стандартное отклонение, характеризующее разность
и
, определено по 25 независимым наблюдениям разности длин двух эталонных концевых мер длины и составляет 13 нм [Руководство ИСО/МЭК 98-3 (Н.1.3.2)].
9.5.2.3.2 Выбор распределения
Величине было приписано масштабированное смещенное
-распределение
![]() (см. 6.4.9.2 и 6.4.9.6) со значениями параметров
(см. 6.4.9.2 и 6.4.9.6) со значениями параметров
215 нм,
![]() 6 нм,
6 нм, 24.
9.5.2.4 Случайное влияние компаратора
9.5.2.4.1 Исходная информация
Согласно сертификату о калибровке компаратора, используемого для сравнения и
, неопределенность, связанная со случайными эффектами и оцененная по шести независимым наблюдениям, составляет 0,01 мкм для вероятности охвата 95% [Руководство ИСО/МЭК 98-3 (Н.1.3.2)].
9.5.2.4.2 Выбор распределения
Величине было приписано масштабированное смещенное
-распределение
![]() (см. 6.4.9.7) со значениями параметров
(см. 6.4.9.7) со значениями параметров
0 нм,
![]() 4 нм,
4 нм, 5.
Значение получено по GUM (таблица G.2) для
5 степеней свободы и
0,95.
9.5.2.5 Систематическое влияние компаратора
9.5.2.5.1 Исходная информация
В сертификате указана неопределенность компаратора, связанная со систематическими эффектами. Она составила 0,02 мкм "на уровне трех сигма" [Руководство ИСО/МЭК 98-3 (Н.1.3.2)]. Возможную неточность в заявленном значении неопределенности можно принять равной 25%, и, таким образом, число эффективных степеней свободы составит ![]() 8 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
8 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
9.5.2.5.2 Выбор распределения
Величине было приписано масштабированное смещенное
-распределение
![]() (см. 6.4.9.7) со значениями параметров
(см. 6.4.9.7) со значениями параметров
0 нм,
 7 нм,
7 нм, 8.
9.5.2.6 Коэффициент температурного расширения
9.5.2.6.1 Исходная информация
Оценка коэффициента температурного расширения эталона указана в виде 11,5·10
°С
с возможными значениями этой величины в интервале ±2·10
°С
и равномерным распределением [Руководство ИСО/МЭК 98-3 (Н.1.3.3)].
9.5.2.6.2 Выбор распределения
Величине было приписано равномерное распределение
![]() (см. 6.4.2) с границами
(см. 6.4.2) с границами
9,5·10
°С
,
13,5·10
°С
.
Примечание - Из-за отсутствия информации о достоверности границ распределения выбрано равномерное распределение с точно известными границами. Информация о границах распределения могла быть опущена в описании примера, рассмотренном в GUM, по той причине, что соответствующий данной входной величине коэффициент чувствительности был принят равным нулю, и, таким образом, данная величина не могла оказать влияния на результат оценивания неопределенности по GUM с учетом только членов разложения первого порядка.
9.5.2.7 Среднее отклонение температуры
9.5.2.7.1 Исходная информация
Температура измерительного стола указана равной (19,9±0,5) °С. Указано также, что оценка среднего отклонения температуры -0,1 °С имеет неопределенность, связанную с неопределенностью средней температуры измерительного стола,
![]() 0,2 °С [Руководство ИСО/МЭК 98-3 (Н.1.3.4)].
0,2 °С [Руководство ИСО/МЭК 98-3 (Н.1.3.4)].
9.5.2.7.2 Выбор распределения
Величине было приписано нормальное распределение
![]() (см. 6.4.7) со значениями параметров
(см. 6.4.7) со значениями параметров
-0,1 °С,
0,2 °С.
Примечание - Нормальное распределение выбрано из-за отсутствия информации об источнике оценки неопределенности для (см. также примечание к 9.5.2.6.2).
9.5.2.8 Влияние циклических колебаний температуры
9.5.2.8.1 Исходная информация
Температура измерительного стола указана равной (19,9±0,5) °С. Указано также, что максимальный сдвиг температуры 0,5 °С представляет собой амплитуду почти гармонических изменений температуры в изолированной термодинамической системе. Гармонические колебания температуры во времени соответствуют U-образному (арксинусному) распределению значений температуры [Руководство ИСО/МЭК 98-3 (Н.1.3.4)].
9.5.2.8.2 Выбор распределения
Величине было приписано U-образное распределение
![]() (см. 6.4.6) с границами
(см. 6.4.6) с границами
-0,5 °С,
0,5 °С.
Примечание - Из-за отсутствия информации о достоверности границ выбрано U-образное распределение с точно известными границами. Такая информация могла быть в GUM опущена по той же причине, что указана в примечании к 9.5.2.6.2.
9.5.2.9 Разность коэффициентов расширения
9.5.2.9.1 Исходная информация
Оценки границ изменчивости составляют ±1·10
°С
с равной вероятностью принятия величиной
любого значения внутри этих границ [Руководство ИСО/МЭК 98-3 (Н.1.3.5)]. Возможную неточность в заявленном значении границ принимают за 10%, что дает
![]() 50 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
50 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
9.5.2.9.2 Выбор распределения
Величине приписано равномерное распределение с неточно заданными границами (см. 6.4.3) с параметрами распределения
-1,0·10
°С
,
1,0·10
°С
,
0,1·10
°С
.
Основой для выбора значения параметра послужила информация о возможной неточности границ распределения в 10%.
9.5.2.10 Разность температур
9.5.2.10.1 Исходная информация
Эталон и калибруемая концевая мера в среднем имеют одну и ту же температуру, однако разность их температур может с одинаковой вероятностью лежать в любой точке интервала от - 0,05 °С до 0,05 °С [Руководство ИСО/МЭК 98-3 (Н.1.3.6)]. Возможную неточность этой разности оценивают в 50%, что дает
![]() 2 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
2 [Руководство ИСО/МЭК 98-3 (Н.1.6)].
9.5.2.10.2 Выбор распределения
Величине приписано равномерное распределение с неточно заданными границами (см. 6.4.3) с параметрами распределения
-0,050 °С
,
0,050 °С,
0,025 °С.
Основой для выбора значения параметра послужила информация о возможной неточности границ распределения в 50%.
9.5.3 Трансформирование распределений и получение результатов
9.5.3.1 Способ оценивания неопределенности по GUM
Применение способа оценивания неопределенности по GUM основано на:
- использовании членов первого порядка в аппроксимации функции измерения [формула (36) или (37)] рядом Тейлора;
- вычислении неопределенности на основе закона трансформирования неопределенностей с использованием формулы Уэлча-Саттертуэйта для оценки числа эффективных степеней свободы (с округлением в сторону уменьшения);
- использовании для выходной величины масштабированного смещенного -распределения с числом степеней свободы, полученным по формуле Уэлча-Саттертуэйта.
9.5.3.2 Метод Монте-Карло
Применение метода Монте-Карло включает в себя:
- формирование выборок из равномерного распределения (см. 6.4.2.4 и С.3.3), нормального распределения (см. 6.4.7.4 и раздел С.4), -распределения (см. 6.4.9.5 и С.6), U-образного распределения (см. 6.4.6.4) и равномерного распределения с неточно заданными границами (см. 6.4.3.4);
- использование адаптивной процедуры метода Монте-Карло (см. 7.9) с погрешностью вычисления (0,5), соответствующей числу
![]() 2 значащих цифр в представлении стандартной неопределенности.
2 значащих цифр в представлении стандартной неопределенности.
9.5.4 Результаты
9.5.4.1 В таблице 11 приведены результаты, полученные для модели, описанной формулой (37), с использованием информации, приведенной в таблице 10. На рисунке 17 показаны плотности распределения вероятностей для , полученные на основе применения способа оценивания неопределенности по GUM (сплошная кривая) и метода Монте-Карло (гистограмма). Распределение, полученное оцениванием неопределенности по GUM, представляет собой
-распределение с
16 степенями свободы. Границы наименьших 99%-ных интервалов охвата для
для двух методов оценивания показаны в виде вертикальных линий и визуально неразличимы.
Таблица 11 - Результаты, полученные для модели, описываемой формулой (37), с использованием информации, приведенной в таблице 10
Метод |
|
| Наименьший 99%-ный интервал охвата для |
GUM | 838 | 32 | [746, 931] |
Монте-Карло | 838 | 36 | [745, 932] |

- отклонение длины калибруемой концевой меры длины от номинала, нм;
- плотность распределения вероятностей, нм
Рисунок 17 - Распределение , полученное способом оценивания неопределенности по GUM (колоколообразная кривая) и методом Монте-Карло (гистограмма) для модели по формуле (37) с данными таблицы 10
9.5.4.2 В адаптивной процедуре метода Монте-Карло было выполнено 1,26·10 испытаний. Были проведены также вычисления для вероятности охвата 95%, при которых было сделано 0,53·10
испытаний.
9.5.4.3 Результаты, полученные для нелинейной модели [формула (36)], идентичны результатам таблицы 11 для заданного числа значащих цифр.
9.5.4.4 В полученных результатах существуют умеренные различия. В случае применения метода Монте-Карло ![]() на 4 нм больше, чем при использовании способа оценивания неопределенности по GUM, а длина 99%-ного интервала охвата для
на 4 нм больше, чем при использовании способа оценивания неопределенности по GUM, а длина 99%-ного интервала охвата для больше на 1 нм. Эти результаты равно справедливы как для нелинейной, так и для аппроксимированной моделей. Важны ли эти различия, зависит от того, каким образом предполагается использовать полученные результаты.
Приложение А
(справочное)
Историческая справка
А.1 GUM представляет собой документ, охватывающий многие вопросы, в той или иной степени связанные с оценкой неопределенности. Несмотря на то, что в нем отсутствуют явные ссылки на метод Монте-Карло, использование этого метода изначально предполагалось при разработке GUM. Проект GUM (первое издание) от июня 1992 г., выпущенный ISO/TAG 4/WG 3, констатирует [G.1.5]:
"Если зависимость между и входными величинами нелинейна или если известные значения параметров вероятностных характеристик
(математического ожидания, дисперсии, моментов более высокого порядка) сами являются оценками, характеризующимися соответствующими распределениями, а представление зависимости в виде ряда Тейлора с членами первого порядка не является допустимым приближением, тогда распределение для
не может быть выражено в виде свертки. В этом случае, как правило, необходимо использовать более сложные вычисления с применением численного метода (такого, как метод Монте-Карло)".
А.2 В опубликованной версии GUM этот подраздел был заменен на следующий:
"Если функциональная зависимость между и входными величинами нелинейна и представление этой зависимости рядом Тейлора первого порядка не является допустимым приближением (см. 5.1.2 и 5.1.5), тогда распределение
не может быть получено через свертку распределений входных величин. В таких случаях необходимо использовать другие аналитические или численные методы расчета".
А.3 В настоящем стандарте внесенная формулировка "другие аналитические или численные методы" рассматривается как возможность использовать все подходящие методы оценивания неопределенности в дополнение к установленному в самом GUM. Это согласуется с позицией Национального Института стандартов и технологий США (НИСТ) [50]:
"[6.6] Позиция НИСТ предусматривает следующие исключения из упомянутого правила: (см. приложение С):
"Очевидно, что любой обоснованный статистический метод, применение которого технически оправдано в существующих условиях, может быть использован для определения эквивалента ,
или
. Кроме того, международные, национальные или договорные соглашения, в которых НИСТ принимает участие, могут потребовать отступления от общих правил НИСТ. В обоих случаях все выполненные действия по оцениванию неопределенности и их обоснование должны быть документированы"".
Приложение В
(справочное)
Коэффициенты чувствительности и бюджет неопределенности
В.1 Ни сам закон трансформирования распределений, ни его реализация с использованием метода Монте-Карло не предполагают получения значений коэффициентов чувствительности [Руководство ИСО/МЭК 98-3 (5.1.3)]. Однако зафиксировав все входные величины, кроме одной, в точке их наилучшей оценки, можно использовать метод Монте-Карло для получения плотности распределения вероятностей для выходной величины модели с единственной входной величиной в качестве независимой переменной [8]. Отношение стандартного отклонения значений на выходе модели (см. 7.6) к стандартной неопределенности для наилучшей оценки входной величины может быть принято за коэффициент чувствительности. Это отношение соответствует тому, которое было бы получено при использовании представления функции измерения рядом Тейлора с членами разложения всех высших порядков. Данный подход можно рассматривать как обобщение приближенной формулы с частными производными в GUM [Руководство ИСО/МЭК 98-3 (примечание 2 к 5.1.3)]. В общем случае и коэффициенты чувствительности, и вклады каждой входной величины в неопределенность оценки выходной величины будут отличаться от тех, что получены по GUM.
В.2 В практике многих измерений принято указывать перечень составляющих неопределенности ![]() ,
, 1, ...,
, где
-
-й коэффициент чувствительности, а
- стандартная неопределенность, соответствующая оценке
-й входной величины, вносящей вклад в
. Обычно такой перечень представляют в виде таблицы, называемой бюджетом неопределенности. Ее составление может быть полезно для идентификации членов, вносящих доминирующий вклад в неопределенность
оценки выходной величины. Однако в случаях, когда вместо трансформирования неопределенностей более обоснованно использовать трансформирование распределений, бюджет неопределенности следует рассматривать как некоторый вспомогательный инструмент.
Приложение С
(справочное)
Формирование выборок из распределений вероятностей
С.1 Общие положения
С.1.1 В настоящем приложении приведены рекомендации по формированию выборки в соответствии с заданной функцией распределения вероятностей. Формирование такой выборки представляет собой ключевой момент при трансформировании распределений с использованием метода Монте-Карло. В качестве источников информации можно использовать [37] (сборник таблиц математических функций) и [38] (библиотека соответствующих программ).
С.1.2 Генератор псевдослучайных чисел для любого распределения, в том числе, для рассмотренных в 6.4 (см. таблицу 1), может теоретически быть получен на основе заданной функции распределения и генератора выборки для равномерного распределения (см. С.2). Генератор для равномерного распределения рассматривается в С.3.3. Для некоторых распределений, таких как нормальное распределение или -распределение, более эффективным будет использование генераторов, специально разработанных именно для этих распределений (например, рассматриваемых в настоящем приложении). Общие рекомендации по формированию выборки в соответствии с заданным законом распределения приведены в 6.4.
Примечание - Настоящий стандарт не ограничивает возможности использования генераторов, отличных от описанных в данном приложении. Однако перед их использованием необходимо убедиться в том, что генерируемые ими последовательности обладают достаточно хорошими статистическими свойствами. Средства тестирования генератора псевдослучайных чисел для равномерного распределения указаны в С.3.2.
С.2 Распределения общего вида
Выборка для любой строго возрастающей одномерной непрерывной функции распределения ![]() может быть получена посредством выборки из равномерного распределения. Для этого:
может быть получена посредством выборки из равномерного распределения. Для этого:
a) выбирают случайное число из равномерного распределения
![]() ;
;
b) определяют , удовлетворяющее условию
![]() .
.
Примечание 1 - Требуемая на этапе b) обратная функция ![]() может быть найдена аналитически или определена численными методами.
может быть найдена аналитически или определена численными методами.
Пример - Входной величине приписано экспоненциальное распределение с математическим ожиданием
0, определяемое плотностью распределения вероятностей
![]() в области
в области 0 и
![]() 0 в области
0 в области 0 (см. 6.4.10). Полученная интегрированием плотности распределения вероятностей функция распределения имеет вид
![]() в области
в области 0 и
![]() 0 в области
0 в области 0. Аналитическое решение дает
![]() . Этот результат может быть несколько упрощен. Поскольку для случайной величины
. Этот результат может быть несколько упрощен. Поскольку для случайной величины , подчиняющейся равномерному распределению
![]() , случайная величина
, случайная величина ![]() также будет подчиняться равномерному распределению, то можно записать обратную функцию в виде
также будет подчиняться равномерному распределению, то можно записать обратную функцию в виде ![]() .
.
Примечание 2 - Численно значение обычно определяют как точку пересечения с нулем функции
![]() . Для определения
. Для определения может быть использован алгоритм поиска отрезка, на концах которого функция имеет разные знаки, такой, например, как метод деления отрезка пополам или, что более эффективно, комбинации линейной интерполяции и метода деления отрезка пополам [11].
Примечание 3 - При использовании генератора случайных чисел из равномерного распределения для получения выборки псевдослучайных чисел из другого распределения следует помнить, что выпадение значения 0 или
1 может привести к сбою генератора. Примером может служить экспоненциальное распределение (см. 6.4.10). Его плотность распределения [формула (9)] для указанных значений
не определена. Генератор, описанный в С.3.3, ошибок подобного рода не дает.
С.3 Равномерное распределение
С.3.1 Общие положения
С.3.1.1 Генератор для равномерного распределения является основой для получения псевдослучайных чисел из любого распределения (см. разделы С.2, С.4 и С.6) при наличии соответствующего алгоритма или формулы. При этом качество получаемой выборки из произвольного распределения зависит от качества работы генератора для равномерного распределения и свойств используемого алгоритма преобразования. Таким образом, только генератор, способный воспроизводить выборку из равномерного распределения с хорошими свойствами вместе с хорошим алгоритмом, обеспечивает генерирование псевдослучайных чисел, хорошо согласующихся с заданным распределением.
С.3.1.2 Отсюда вытекает важность тестирования генератора псевдослучайных чисел для равномерного распределения [31]. Если пользователь не уверен в качестве работы генератора, то его не следует использовать до тех пор, пока соответствующее тестирование не будет проведено. В противном случае не исключено получение ошибочных результатов. Рекомендуется использовать средства тестирования согласно [30]. В С.3.3 приведена процедура генерирования псевдослучайных чисел для равномерного распределения, которая успешно прошла указанное тестирование и проста в применении.
С.3.1.3 Параметры процедуры генерирования псевдослучайных чисел, соответствующих равномерному распределению ![]() , - входной, выходной, а также являющийся одновременно входным и выходным, - определены в таблице С.1.
, - входной, выходной, а также являющийся одновременно входным и выходным, - определены в таблице С.1.
Таблица С.1 - Процедура генерирования псевдослучайных чисел для стандартного равномерного распределения
Входной параметр |
|
Входной/выходной параметр |
|
Выходной параметр |
|
Примечание 1 - При задании одного и того же начального числа результатом может быть генерирование одной и той же последовательности случайных чисел. Этот факт является важным элементом регрессионного тестирования, используемого для определения согласованности результатов, полученных программным средством, с результатами предыдущих версий.
Примечание 2 - Некоторые генераторы псевдослучайных чисел при каждом обращении выдают одно случайное, а некоторые - последовательность значений.
С.3.1.4 Псевдослучайное число выборки из
![]() определяют преобразованием
определяют преобразованием ![]() , где
, где - элемент выборки из
![]() .
.
С.3.2 Проверка качества случайной выборки
С.3.2.1 Каждый генератор псевдослучайных чисел должен:
a) обладать хорошими статистическими свойствами;
b) предусматривать возможность реализации на любом языке программирования;
c) давать одни и те же результаты для одного и того же начального числа на любом компьютере.
Желательно также, чтобы он был компактным, т.е. простым при реализации. Одним из таких генераторов, близко приближающихся к удовлетворению перечисленных требований, является генератор Вихманна-Хилла [52, 53]. Он использовался во многих приложениях, включая вычисление неопределенности. Однако длина его цикла (количество генерируемых псевдослучайных чисел до их повторения) составляет 2, что сегодня считается для некоторых задач недостаточным. Более того, при его тестировании не по всем критериям были получены положительные результаты [35]. Наконец, этот генератор был разработан для 16-разрядных компьютеров, тогда как сегодня повсеместно используются 32-разрядные и 64-разрядные компьютеры.
Примечание - Период последовательности значений, полученных с помощью генератора псевдослучайных чисел, - это количество последовательных псевдослучайных чисел до их повторения.
С.3.2.2 Для комплексной проверки статистических свойств генератор тестируют пакетом программ TestU01 [30]. Этот программный продукт весьма детализирован и включает в себя большое количество статистических тестов, в том числе расширенный пакет краш-тестирования BigCrush. Некоторые генераторы, успешно выдержавшие это тестирование, приведены в списке, составленном Вихманном и Хиллом [54]. В их число входит и усовершенствованный генератор Вихманна-Хилла (см. С.3.3), обладающий следующими свойствами [54]:
a) его просто реализовать на любом языке программирования, он не зависит от побитовых операций, используемых в некоторых генераторах;
b) структура генератора (количество информации, сохраняемой генератором между запросами) невелика и легка в обращении (сравни с параметром в таблице С.1);
c) он позволяет легко получить несколько последовательностей, необходимых для высокопараллельных приложений, что, вероятно, будет особенностью вычислений неопределенности в будущем;
d) существуют варианты генератора для 32-разрядных и 64-разрядных компьютеров.
С.3.3 Процедура генерирования выборки псевдослучайных чисел из равномерного распределения
С.3.3.1 Как и его предшественник, улучшенный генератор Вихманна-Хилла представляет собой комбинацию конгруэнтных генераторов. Новый генератор сочетает в себе четыре таких генератора, тогда как предыдущая версия сочетала три. Новый генератор имеет период 2, приемлемый для любого возможного применения.
С.3.3.2 В таблице С.2 приведено описание улучшенного генератора Вихманна-Хилла для получения псевдослучайных чисел из ![]() для 32-разрядного компьютера.
для 32-разрядного компьютера.
Таблица С.2 - Улучшенный генератор Вихманна-Хилла для псевдослучайных чисел из равномерного распределения на интервале (0,1) для 32-разрядного компьютера
Входной параметр | |
Нет | |
Входные/выходные параметры | |
| Целочисленные параметры, которые требуются в качестве входных величин и изменяются в процессе выполнения процедуры. Перед первым обращением к процедуре им присваивают значения от 1 до 2147483647. Между обращениями значения параметров остаются неизменными. Пользователю обычно нет необходимости знать, как изменяются значения этих параметров, используемых в процедуре генерирования псевдослучайных чисел. Данные параметры могут быть реализованы как глобальные переменные и не входить явно в формальные параметры процедуры. |
Константы | |
| Четырехмерные векторы с целочисленными координатами, т.е. |
Между обращениями значения констант остаются неизменными. | |
Выходной параметр | |
Псевдослучайное число из | |
Алгоритм вычисления | |
а) Для | |
С.3.3.3 Для 64-разрядных компьютеров шаг а) вычисления, включая (i) и (ii), в таблице С.2 должен быть заменен более простым шагом:
"а) Для 1, ..., 4 вычисляют
![]() mod
mod ".
С.4 Нормальное распределение
Процедура, описанная в таблице С.3, обеспечивает выбор случайных значений из стандартного нормального распределения ![]() с использованием преобразования Бокса-Мюллера [3]. Случайное значение
с использованием преобразования Бокса-Мюллера [3]. Случайное значение из нормального распределения
![]() вычисляют по формуле
вычисляют по формуле ![]() , где
, где - случайное значение из
![]() .
.
Таблица С.3 - Генератор псевдослучайных чисел Бокса-Мюллера
Входной параметр | |
Нет | |
Выходной параметр | |
| Два случайных значения, полученных независимо из стандартного нормального распределения |
Алгоритм вычисления | |
а) Независимо генерируют случайные числа | |
С.5 Многомерное нормальное распределение
С.5.1 Из всех многомерных распределений наибольший интерес представляет совместное нормальное распределение ![]() , где
, где - вектор математического ожидания размерности
, а
- ковариационная матрица размерности
.
С.5.2 Значения случайной величины из ![]() [45, 49] могут быть получены путем использования процедуры, описанной в таблице С.4.
[45, 49] могут быть получены путем использования процедуры, описанной в таблице С.4.
Таблица С.4 - Генератор случайных чисел из многомерного нормального распределения
Входной параметр | |
Размерность многомерного нормального распределения | |
Вектор математических ожиданий размерности | |
Ковариационная матрица размерности | |
Число генерируемых векторов, состоящих из псевдослучайных чисел | |
Выходной параметр | |
Матрица размерности | |
Алгоритм вычисления | |
а) Для матрицы b) Генерируют массив с) Вычисляют где | |
Примечание 1 - Если - положительно определенная матрица (т.е. все ее собственные значения строго положительны), то множитель Холецкого
единственен [23, страница 204].
Примечание 2 - Если не является положительно определенной матрицей, то из-за возможных ошибок округления или других причин
может не существовать. Более того, в случаях, когда одно или несколько собственных значений
хотя и положительны, но очень малы, программная реализация алгоритма факторизации Холецкого может оказаться неспособной сформировать матрицу
из-за ошибок округления в арифметике с плавающей запятой. В любой из этих ситуаций рекомендуется вносить в
малые возмущения таким образом, чтобы множитель
для "возмущенной" матрицы
был хорошо определен. Простая процедура внесения возмущений описана в [49, страница 322] и реализована в генераторе MULTNORM [45].
Примечание 1 - Если положительно полуопределенная матрица, тогда ее можно представить в виде
![]() , где
, где - ортогональная матрица,
- диагональная матрица. Тогда матрица
![]() может быть использована вместо
может быть использована вместо для формирования выборки из
![]() даже в случае матрицы
даже в случае матрицы неполного ранга.
С.5.3 На рисунке С.1 показано 200 точек, полученных с использованием генератора MULTNORM [45] из![]() , где
, где
![]() и
и ![]() .
.
- величина 1;
- величина 2
Рисунок С.1 - Выборка значений из двумерного нормального распределения с положительной корреляцией
Это совместное распределение двух положительно коррелированных величин. Подобные генераторы описаны в других источниках [12].
С.5.4 На рисунке С.1 точки образуют вытянутый наклонный эллипс. Если недиагональные элементы матрицы заменить нулевыми значениями, то эти точки образуют круг. Если бы элементы главной диагонали были не равны между собой, а недиагональные элементы были равны нулю, то точки образовали бы эллипс с главными осями, параллельными осям графика. Если бы элементы главной диагонали были отрицательными числами (т.е. величины имели отрицательную корреляцию), то главная ось эллипса имела бы не положительный (как на рисунке С.1), а отрицательный наклон.
С.6 -распределение
Процедура, описанная в таблице С.5, представляет метод [29], [44, страница 63] генерирования выборки из -распределения с
степенями свободы.
Таблица С.5 - Генератор псевдослучайных чисел для -распределения
Входной параметр | |
Число степеней свободы | |
Выходной параметр | |
Выборка из | |
Алгоритм вычисления | |
а) Независимо генерируют случайные числа b) Если с) Если | |
Примечание - Чтобы стандартное отклонение -распределения с
степенями свободы было конечным, значение
должно быть больше двух.
Приложение D
(справочное)
Непрерывная аппроксимация функции распределения выходной величины
D.1 В некоторых случаях предпочтительнее работать не с дискретным представлением , а с непрерывной аппроксимацией
![]() функции распределения для выходной величины
функции распределения для выходной величины (см. 7.5).
Примечание - Преимущества работы с непрерывной аппроксимацией состоят, например, в том, что:
a) выборка из заданного распределения может быть выполнена без необходимости округления, как в случае дискретного представления;
b) для определения наименьшего интервала охвата могут быть использованы численные методы, требующие для своей работы непрерывность функции распределения.
D.2 Чтобы сформировать ![]() , используют дискретное представление
, используют дискретное представление ![]() для
для ![]() в соответствии с 7.5.1 после замены совпадающих значений модели для
в соответствии с 7.5.1 после замены совпадающих значений модели для [как того требует этап b) в 7.5.1] в соответствии со следующей процедурой:
a) значениям приписывают равномерно отстоящие друг от друга значения вероятностей
![]() ,
, 1, ...,
[8], которые представляют собой средние точки интервалов шириной
, покрывающих диапазон изменения вероятности от нуля до единицы;
b) формируют ![]() в виде непрерывной строго возрастающей кусочно-линейной функции, последовательно соединяющей
в виде непрерывной строго возрастающей кусочно-линейной функции, последовательно соединяющей точек
![]() ,
, 1, ...,
:
 ,
, ![]() ,
, 1, …,
. (Д.1)*
_______________
* Нумерация соответствует оригиналу. - .
Примечание - Формула (D.1) может быть использована как основа формирования выборки из ![]() для последующей оценки неопределенности (см. раздел С.2 в части формирования выборки на основе функции, обратной к функции распределения). Некоторые библиотеки и пакеты программ предоставляют средства такой кусочно-линейной интерполяции. Поскольку
для последующей оценки неопределенности (см. раздел С.2 в части формирования выборки на основе функции, обратной к функции распределения). Некоторые библиотеки и пакеты программ предоставляют средства такой кусочно-линейной интерполяции. Поскольку ![]() кусочно-линейна, то такой же вид имеет и обратная функция, что позволяет использовать для ее построения те же программные средства.
кусочно-линейна, то такой же вид имеет и обратная функция, что позволяет использовать для ее построения те же программные средства.
D.3 На рисунке D.1 показан график ![]() , построенный на основе 50 выборочных значений из нормального распределения для
, построенный на основе 50 выборочных значений из нормального распределения для с плотностью распределения вероятностей
![]() , математическим ожиданием, равным трем, и стандартным отклонением, равным единице.
, математическим ожиданием, равным трем, и стандартным отклонением, равным единице.
- выходная величина
;
- вероятность
Рисунок D.1 - Аппроксимация ![]() функции распределения
функции распределения ![]()
D.4 На основе приближения ![]() , задаваемого формулой (D.1), может быть построено приближение
, задаваемого формулой (D.1), может быть построено приближение ![]() для плотности распределения вероятностей выходной величины, представляющее собой кусочно-постоянную функцию с разрывами в точках
для плотности распределения вероятностей выходной величины, представляющее собой кусочно-постоянную функцию с разрывами в точках ![]() . Математическое ожидание
. Математическое ожидание и стандартное отклонение
величины
, описываемой плотностью распределения вероятностей
![]() , рассматриваются соответственно как оценка
, рассматриваются соответственно как оценка и ее стандартная неопределенность и имеют вид:
![]() , (D.2)
, (D.2)
![]() , (D.3)
, (D.3)
где двойной штрих справа от символа суммирования показывает, что первый и последний члены суммы необходимо брать с коэффициентом 1/2.
Примечание - Для достаточно больших значений (например, 10
или более)
и
, полученные с использованием формул (D.2) и (D.3), в общем случае с практической точки зрения неотличимы от оценок, полученных по формулам (16) и (17) соответственно.
D.5 Если - любое значение между нулем и
![]() , где
, где - требуемая вероятность охвата (например, 0,95), то границы 100
%-ного интервала охвата могут быть получены на основе
![]() с помощью обратной линейной интерполяции. Чтобы определить нижнюю границу
с помощью обратной линейной интерполяции. Чтобы определить нижнюю границу такую, что
![]() , необходимо найти индекс
, необходимо найти индекс , для которого точки
![]() и
и ![]() будут удовлетворять условию:
будут удовлетворять условию:
![]() .
.
Тогда посредством обратной линейной интерполяции получаем:
![]() .
.
Аналогично, верхнюю границу , для которой
![]() , вычисляют по формуле
, вычисляют по формуле
![]() ,
,
где индекс такой, что точки
![]() и
и ![]() удовлетворяют условию
удовлетворяют условию
![]() .
.
D.6 Значение 0,025 дает интервал охвата, ограниченный квантилями уровней 0,025 и 0,975. Этот выбор обеспечивает вероятностно симметричный 95%-ный интервал охвата для
.
D.7 Наименьший интервал охвата может в общем случае быть получен на основе ![]() путем определения
путем определения , для которого
![]() будет принимать минимальное значение. Прямой численный способ определения минимума - вычисление значений
будет принимать минимальное значение. Прямой численный способ определения минимума - вычисление значений ![]() для большой по объему выборки
для большой по объему выборки равномерно распределенных значений
в интервале от нуля до
![]() и выбор значения
и выбор значения из этой выборки, которому соответствует минимальное значение
![]() .
.
D.8 Вычисление интервала охвата становится проще, если - целое число. Тогда значение
, для которого
![]() минимально, равно
минимально, равно ![]() , где
, где - значение индекса
, для которого длина интервала
![]() минимальна среди всех
минимальна среди всех 1, ...,
![]() .
.
Приложение Е
(справочное)
Интервал охвата для свертки четырех прямоугольных распределений
Е.1 В 9.2.3.2 проведено аналитическое решение в виде
![]() ,
,
представляющее собой границы вероятностно симметричного 95%-ного интервала охвата для выходной величины , определяемой через модель в виде аддитивной функции четырех входных величин, каждой из которых приписано одно и то же равномерное распределение с математическим ожиданием, равным нулю, и стандартным отклонением, равным единице. В настоящем приложении приведено обоснование этого результата.
Е.2 Плотность равномерного распределения ![]() (см. 6.4.2) для случайной величины
(см. 6.4.2) для случайной величины равна постоянному значению
![]() на отрезке
на отрезке ![]() и нулю вне этого отрезка. Распределение суммы
и нулю вне этого отрезка. Распределение суммы независимых случайных величин представляет собой свертку их распределений и, если все случайные величины подчиняются распределению
![]() , имеет вид би-сплайна
, имеет вид би-сплайна ![]() порядка
порядка [т.е. суммы степенных функций с показателями степени до
![]() включительно] с узлами в точках 0, ...,
включительно] с узлами в точках 0, ..., [46]. Точное выражение для
![]() [6]:
[6]:
![]() ,
,
где ![]() ,
, ![]() .
.
В частности, на интервале 01 свертка четырех прямоугольных распределений будет иметь вид
![]()
(на интервалах между другими узлами искомое распределение также будет иметь вид кубических полиномов, но другой формы), следовательно,

(см. также [6]).
Е.3 Левая граница вероятностно симметричного 95%-ного интервала охвата заведомо лежит между нулем и единицей, поскольку для данной вероятности охвата площадь, лежащая под кривой плотности распределения вероятностей на интервале слева от
, равна 0,025, но
![]() .
.
Эту площадь можно записать в виде
 ,
,
таким образом, ![]() .
.
С учетом симметрии распределения для правой границы интервала охвата получаем
![]() .
.
Таким образом, вероятностно симметричный 95%-ный интервал охвата имеет вид:
![]() .
.
Распределение для каждой из входных величин с нулевым математическим ожиданием и единичным стандартным отклонением имеет вид ![]() . Это означает, что интервал охвата, полученный для свертки четырех распределений
. Это означает, что интервал охвата, полученный для свертки четырех распределений ![]() , нужно сместить на две единицы влево и умножить его границы на
, нужно сместить на две единицы влево и умножить его границы на , что и даст формулу (Е.1).
Приложение F
(справочное)
Задача определения коэффициента рассогласования
В настоящем приложении рассматриваются некоторые детали задачи определения коэффициента рассогласования при калибровке измерителя мощности (см. 9.4). В разделе F.1 получены математическое ожидание и стандартное отклонение (см. 9.4.2.1.2). В разделе F.2 аналитически получена плотность распределения вероятностей для
, когда
![]() 0 и
0 и ![]() 0 (см. 9.4.2.1.2). В разделе F.3 способ оценивания неопределенности по GUM применен для некоррелированных и коррелированных входных величин (см. 9.4.2.1.3 и 9.4.3.1.1).
0 (см. 9.4.2.1.2). В разделе F.3 способ оценивания неопределенности по GUM применен для некоррелированных и коррелированных входных величин (см. 9.4.2.1.3 и 9.4.3.1.1).
F.1 Аналитическое решение для математического ожидания и стандартного отклонения
F.1.1 Дисперсия величины может быть выражена через математические ожидания, как [42, стр.124]:
![]() .
.
Таким образом,
![]() ,
,
где - наилучшая оценка
, а
- стандартная неопределенность этой оценки. Таким образом, для модели, описываемой формулой (28)
![]() , имеет место
, имеет место
![]() .
.
Этот результат справедлив независимо от:
- функций распределения и
;
- наличия или отсутствия корреляции между и
.
F.1.2 Стандартная неопределенность для может быть получена на основе выражения
![]() ,
,
где для 1, 2
![]() и
и ![]() . Тогда, применяя теорему Прайса для нормальных распределений [40, 41], можно получить
. Тогда, применяя теорему Прайса для нормальных распределений [40, 41], можно получить
![]() . (F.1)
. (F.1)
Если 0 и
![]() , то, заменяя
, то, заменяя ![]() на
на ![]() можно получить
можно получить
![]() .
.
F.1.3 Если и
некоррелированны, т.е.
![]() 0, то формула (F.1) принимает вид
0, то формула (F.1) принимает вид
![]() . (F.2)*
. (F.2)*
_______________
* Формула соответствует оригиналу. - .
Формула (F.2) может быть проверена применением формулы (10) из GUM [Руководство ИСО/МЭК 98-3 (5.1.2)] и непосредственно следующей за ней формулой из GUM [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)].
F.2 Аналитическое решение для случая нулевой оценки коэффициента отражения по напряжению при нулевой ковариации
F.2.1 Для случая ![]() 0 и
0 и ![]() 0 и
0 и ![]() плотность распределения вероятностей
плотность распределения вероятностей ![]() для
для может быть получена аналитически. Такое решение полезно иметь для последующего расчета неопределенности калибровки измерителя мощности. В указанном предположении выходную величину можно представить в виде
 .
.
F.2.2 Член в квадратных скобках, который можно обозначить , представляет собой сумму квадратов двух независимых величин, каждая из которых подчиняется стандартному нормальному распределению. Следовательно, случайная величина
подчиняется распределению хи-квадрат с двумя степенями свободы [42, стр.177], так что
![]() ,
,
где имеет плотность распределения вероятностей
![]() .
.
F.2.3 Применение общей формулы для плотности распределения вероятностей функции случайной величины [42, стр.57-61] в случае дифференцируемой и строго возрастающей функции аргумента (в данном случае ) с заданным распределением позволяет получить плотность распределения вероятностей для выходной величины
в виде
 ,
, 0.
F.2.4 Это позволяет получить выражения для математического ожидания и дисперсии для :
 ,
,
 .
.
Таким образом, стандартное отклонение составляет ![]() , что согласуется с результатами, приведенными в F.1.
, что согласуется с результатами, приведенными в F.1.
F.2.5 Интегрирование плотности распределения вероятностей дает функцию распределения следующего вида:
 ,
, 0. (F.3)
F.2.6 Если - такое
в формуле (F.3), для которого
![]() для любого
для любого , удовлетворяющего условию
![]() , тогда
, тогда
![]() ,
,
и 100%-ный интервал охвата для
(см. 7.7) имеет вид:
![]() . (F.4)
. (F.4)
Длина этого интервала будет равна
![]() .
.
F.2.7 Наименьший 100-ный интервал охвата соответствует такому
, для которого
![]() минимально (см. 5.3.4). Так как
минимально (см. 5.3.4). Так как ![]() - строго возрастающая функция
- строго возрастающая функция для
![]() , то
, то ![]() достигает минимума в точке
достигает минимума в точке 0. Таким образом, наименьший 100
-ный интервал охвата для
имеет вид:
![]() .
.
Для ![]() 0,005 наименьший 95%-ный интервал охвата представляет собой [0; 0,00014998].
0,005 наименьший 95%-ный интервал охвата представляет собой [0; 0,00014998].
F.2.8 Вероятностно симметричный 95%-ный интервал охвата для соответствует
![]() (см. 5.3.3) и имеет вид
(см. 5.3.3) и имеет вид
![]() .
.
Он на 20% длиннее, чем наименьший 95%-ный интервал охвата.
Примечание - Приведенный выше анализ демонстрирует аналитический вывод, применимый к некоторым задачам подобного типа. В данном частном случае результаты могли бы быть получены быстрее, если принять во внимание факт, что ![]() - строго убывающая функция, а наименьший интервал охвата всегда включает в себя моду распределения.
- строго убывающая функция, а наименьший интервал охвата всегда включает в себя моду распределения.
F.3 Применение способа оценивания неопределенности по GUM к задаче определения коэффициента рассогласования
F.3.1 Некоррелированные входные величины
F.3.1.1 В задаче определения коэффициента рассогласования, рассмотренной в 9.4, в качестве модели измерения использована следующая:
![]() ,
,
где величинам и
приписаны нормальные распределения с математическими ожиданиями
и
дисперсиями
![]() и
и ![]() соответственно.
соответственно.
F.3.1.2 Применение GUM [Руководство ИСО/МЭК 98-3 (5.1.1)] дает
![]()
в качестве оценки . Частные производные от функции измерения по
для
1, 2 имеют вид
![]() ,
, 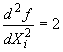 .
.
F.3.1.3 Следовательно, в соответствии с GUM [Руководство ИСО/МЭК 98-3 (5.1.2)] для стандартной неопределенности справедливо выражение:
 , (F.5)
, (F.5)
основанное на аппроксимации ![]() рядом Тейлора первого порядка. Если нелинейность
рядом Тейлора первого порядка. Если нелинейность ![]() значительна [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)], то к формуле (F.5) следует добавить член
значительна [Руководство ИСО/МЭК 98-3 (примечание к 5.1.2)], то к формуле (F.5) следует добавить член
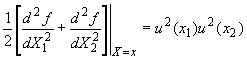 .
.
В результате формула (F.5) принимает вид
![]() . (F.6)
. (F.6)
F.3.1.4 Поскольку подчиняется нормальному распределению, 95%-ный интервал охвата для
имеет вид
![]() .
.
F.3.2 Коррелированные входные величины
F.3.2.1 Если входные величины коррелированны, то матрица неопределенностей для наилучших оценок входных величин определена формулой (27).
F.3.2.2 Применяя GUM [Руководство ИСО/МЭК 98-3 (5.2.2)], можно получить:
 (F.7)
(F.7)
Приложение G
(справочное)
Основные обозначения
случайная величина, представляющая собой нижнюю границу равномерного распределения с неточно заданными пределами | |
нижняя граница области, в пределах которой находится случайная величина | |
центральная точка интервала, о котором известно, что в нем лежит нижняя граница | |
случайная величина, представляющая собой верхнюю границу равномерного распределения с неточно заданными пределами | |
верхняя граница области, в пределах которой находится случайная величина | |
центральная точка интервала, о котором известно, что в нем лежит верхняя граница | |
| равномерное распределение с неточно заданными границами с параметрами |
| ковариация случайных величин |
целое десятичное число с | |
| |
половина длины интервалов, о которых известно, что в них лежат нижняя | |
абсолютная разность значений правосторонних границ интервалов охвата, полученных на основе способа оценивания неопределенности по GUM и по методу Монте-Карло | |
абсолютная разность значений левосторонних границ интервалов охвата, полученных на основе способа оценивания неопределенности по GUM и по методу Монте-Карло | |
| математическое ожидание случайной величины |
| вектор математического ожидания векторной случайной величины |
|
|
| экспоненциальное распределение с параметром |
функция измерения, связывающая выходную величину модели | |
дискретное представление функции распределения | |
| гамма-распределение с параметрами |
| плотность распределения вероятностей переменной |
| совместная (многомерная) плотность распределения переменной |
| плотность распределения вероятностей переменной |
| функция распределения переменной |
| непрерывная аппроксимация функции распределения |
| плотность распределения вероятностей переменной |
| производная от |
наименьшее целое, большее или равное | |
коэффициент охвата, соответствующий вероятности охвата | |
целое число в представлении | |
число испытаний метода Монте-Карло | |
число входных величин | |
| стандартное нормальное распределение |
| нормальное распределение с параметрами |
| многомерное нормальное распределение с параметрами |
число наблюдений | |
количество значащих цифр числа, рассматриваемых как достоверные | |
вероятность события | |
вероятность охвата | |
целая часть числа | |
число объектов в выборке (объем выборки) | |
верхняя треугольная матрица | |
| стандартное равномерное распределение на интервале [0, 1] |
| равномерное распределение на интервале |
| коэффициент корреляции оценок |
оценка стандартного отклонения по | |
объединенная оценка стандартного отклонения по нескольким сериям наблюдений | |
верхний индекс, обозначающий транспонирование матрицы | |
стандартное отклонение для среднего | |
| треугольное распределение на интервале |
| трапецеидальное распределение на интервале |
| |
| масштабированное смещенное |
| стандартное арксинусное ( |
| арксинусное ( |
расширенная неопределенность, соответствующая вероятности охвата | |
матрица неопределенности для вектора оценок | |
| вектор |
стандартная неопределенность оценки | |
| ковариация оценок |
стандартная неопределенность оценки | |
стандартная неопределенность | |
| суммарная стандартная неопределенность оценки |
| |
ковариационная (дисперсионно-ковариационная) матрица | |
| дисперсия случайной переменной |
| ковариационная матрица векторной случайной величины |
половина длины интервала | |
входная величина, рассматриваемая как случайная величина | |
вектор | |
| |
оценка (математическое ожидание) величины | |
векторная оценка (векторное математическое ожидание) | |
среднее арифметическое | |
оценка (математическое ожидание) величины | |
| |
| |
| |
(скалярная) выходная величина, рассматриваемая как случайная величина | |
оценка (математическое ожидание) величины | |
оценка величины | |
правосторонняя граница интервала охвата для | |
левосторонняя граница интервала охвата для | |
| |
| |
| |
значение вероятности | |
параметр гамма-распределения | |
параметр трапецеидального распределения, равный отношению длины верхнего основания трапеции к длине нижнего основания трапеции | |
параметр гамма-распределения | |
гамма-функция переменной | |
предел погрешности вычисления числового значения | |
дельта-функция Дирака переменной | |
переменная, описывающая возможные значения выходной величины | |
половина длины верхнего основания трапеции трапецеидального распределения | |
половина длины нижнего основания трапеции трапецеидального распределения | |
математическое ожидание случайной величины | |
число степеней свободы | |
число эффективных степеней свободы, соответствующих стандартной неопределенности | |
число степеней свободы для объединенной оценки стандартного отклонения | |
переменная, описывающая возможные значения случайной величины | |
векторная величина | |
переменная, описывающая возможные значения входной величины | |
стандартное отклонение случайной величины, характеризуемой распределением вероятностей | |
дисперсия (квадрат стандартного отклонения) случайной величины | |
фаза гармонически изменяющейся величины | |
распределение хи-квадрат с |
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных документов национальным стандартам Российской Федерации
Таблица ДА.1
Обозначение ссылочного международного документа | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
Руководство ИСО/МЭК 98-3:2008 | IDT | ГОСТ Р 54500.3-2011 (Руководство ИСО/МЭК 98-3:2008) "Неопределенность измерения. Часть 1. Руководство по выражению неопределенности измерения" |
Руководство ИСО/МЭК 99:2007 | - | * |
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | Beatty, R.W. Insertion loss concepts. Proc. IEEE 52, 1964, pp.663-671 |
[2] | Berthouex, P.M. and Brown, L.C. Statistics for Environmental Engineers. CRC Press, USA, 1994 |
[3] | Box, G. E. P. and Muller, M. A note on the generation of random normal variates. Ann. Math. Statist., 29, 1958, pp.610-611 |
[4] | Chan, A., Golub, G. and Leveque, R. Algorithms for computing the sample variance: analysis and recommendations. Amer. Stat., 37, 1983, pp.242-247 |
[5] | Conte, S.D. and De Boor, С. Elementary Numerical Analysis: An Algorithmic Approach. McGraw-Hill, 1972 |
[6] | Cox, M.G. The numerical evaluation of B-splines. J. Inst. Math. Appl. 10, 1972, pp.134-149 |
[7] | Cox, M.G. and Harris, P.M. Software specifications for uncertainty evaluation. Tech. Rep. DEM-ES-010, National Physical Laboratory, Teddington, UK, 2006 |
[8] | Cox, M.G. and Harris, P.M. SSfM Best Practice Guide No. 6, Uncertainty evaluation. Tech. Rep. DEM-ES-011, National Physical Laboratory, Teddington, UK, 2006 |
[9] | Cox, M.G. and Siebert, B. R. L. The use of a Monte Carlo method for evaluating uncertainty and expanded uncertainty. Metrologia, 43, 2006, pp.S178-S188 |
[10] | David, H.A. Order Statistics. Wiley, New York, 1981 |
[11] | Dekker, T.J. Finding a zero by means of successive linear interpolation. In: Constructive Aspects of the Fundamental Theorem of Algebra (eds Dejon B. and Henrici P.), Wiley Interscience, London, 1969 |
[12] | Devroye, L. Non-Uniform Random Number Generation. Springer, New York, 1986 |
[13] | Dietrich, C.F. Uncertainty, Calibration and Probability. Adam Hilger, Bristol, UK, 1991 |
[14] | Dowson, D.C. and Wragg, A. Maximum entropy distributions having prescribed first and second order moments. IEEE Trans. IT, 19, 1973, pp.689-693 |
[15] | EA. Expression of the uncertainty of measurement in calibration. Tech. Rep. EA-4/02, European Cooperation for Accreditation, 1999 |
[16] | Elster, С. Calculation of uncertainty in the presence of prior knowledge. Metrologia, 44, 2007, pp.111-116 |
[17] | EURACHEM/CITAC. Quantifying uncertainty in analytical measurement. Tech. Rep. Guide CG4, EURACHEM/CITEC, 2000. Second edition |
[18] | Evans, M., Hastings, N. and Peacock, B. Statistical distributions. Wiley, 2000 |
[19] | FRENKEL, R.B. Statistical background to the ISO 'Guide to the Expression of Uncertainty in Measurement'. Tech. Rep. Monograph 2, NML Technology Transfer Series, Publication number TIP P1242, National Measurement Laboratory, CSIRO, Australia, 2002 |
[20] | Gelman, A., Carlin, J.B., Stern, H.S. and Rubin, D.B. Bayesian Data Analysis. Chapman and Hall, London, 2004 |
[21] | Gleser, L.J. Assessing uncertainty in measurement. Stat. Sci., 13, 1998, pp.277-290 |
[22] | Hall, B.D. and Willink, R. Does "Welch-Satterthwaite" make a good uncertainty estimate? Metrologia, 38, 2001, pp.9-15 |
[23] | Higham, N.J. Accuracy and Stability of Numerical Algorithms. SIAM, Philadelphia, 1996 |
[24] | ISO 3534-1:19932) Statistics - Vocabulary and symbols - Part 1: Probability and general statistical terms |
[25] | Jaynes, E. T. Information theory and statistical mechanics. Phys. Rev, 106, 1957, pp.620-630 |
[26] | Jaynes, E.T. Where do we stand on maximum entropy? In Papers on Probability, Statistics, and Statistical Physics (Dordrecht, The Netherlands, 1989), R. D. Rosenkrantz, Ed., Kluwer Academic, pp.210-314. http://bayes.wustl.edu/ etj/articles/stand.on.entropy.pdf |
[27] | Kacker, R. and Jones, A. On use of Bayesian statistics to make the Guide to the Expression of Uncertainty in Measurement consistent. Metrologia, 40, 2003, pp.235-248 |
[28] | Kerns, D.M. and Beatty, R.W. Basic Theory of Waveguide Junctions and Introductory Microwave Network Analysis. Pergamon Press, London, 1967 |
[29] | Kinderman, A., Monahan, J. and Ramage, J. Computer methods for sampling from Student's t-distribution. Math. Comput, 31, 1977, pp.1009-1018 |
[30] | L'Ecuyer, P. and Simarf, R. TestU01: A software library in ANSI С for empirical testing of random number generators. http://www.iro.umontreal.ca/~simardr/testu01/tu01.html |
[31] | Leydold, J. Automatic sampling with the ratio-of-uniforms method. ACM Trans. Math. Software, 26, 2000, pp.78-98 |
[32] | Lira, I. Evaluating the Uncertainty of Measurement. Fundamentals and Practical Guidance. Institute of Physics, Bristol, UK, 2002 |
[33] | Lira, I.H. and Woger, W. Bayesian evaluation of the standard uncertainty and coverage probability in a simple measurement model. Meas. Sci. Technol., 12, 2001, pp.1172-1179 |
[34] | Matsumoto, M. and Nishimura, T. Mersenne Twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Modeling and Computer Simulation 8 (1998), pp.3-30 |
[35] | McCullough, B.D. and Wilson, B. On the accuracy of statistical procedures in Microsoft Excel 2003. Computational Statistics and Data Analysis, 2004 |
[36] | Moler, C.B. Numerical computing with MATLAB. SIAM, Philadelphia, 2004 |
[37] | NETLIB. The Netlib repository of freely available software, documents, and databases of interest to the numerical, scientific computing, and other communities contains facilities for sampling from probability distributions, http://www.netlib.org |
[38] | NIST. The NIST Digital Library of Mathematical Functions contains facilities for sampling from probability distributions, http://dlmf.nist.gov |
[39] | OIML. Conventional value of the result of weighing in air. Tech. Rep. OIML D 28, Organisation Internationale de Metrologie Legale, Paris, 2004 |
[40] | Papoulis, A. On an extension of Price's theorem. IEEE Trans. Inform. Theory IT-11, 1965 |
[41] | Price, R. A useful theorem for nonlinear devices having Gaussian inputs. IEEE Trans. Inform. Theory IT-4, 1958, pp.69-72 |
[42] | Rice, J. R. Mathematical Statistics and Data Analysis, second ed. Duxbury Press, Belmont, Ca., USA, 1995 |
[43] | Ridler, N.M. and Salter, M.J. Propagating S-parameter uncertainties to other measurement quantities. In: 58th ARFTG (Automatic RF Techniques Group) Conference Digest (2001) |
[44] | Robert, C.P. and Casella, G. Monte Carlo Statistical Methods. Springer-Verlag, New York, 1999 |
[45] | Salter, M.J., Ridler, N.M. and Cox, M.G. Distribution of correlation coefficient for samples taken from a bivariate normal distribution. Tech. Rep. CETM 22, National Physical Laboratory, Teddington, UK, 2000 |
[46] | Schoenberg, I.J. Cardinal interpolation and spline functions. J. Approx. Theory, 2, 1969, pp.167-206 |
[47] | Scowen, R.S. Algorithm 271: quickersort. Communications of the ACM, 8(11), 1965, pp.669-670 |
[48] | Shannon, C.E. A mathematical theory of information. Bell Systems Tech. J., 27, 1948, pp.623-656 |
[49] | Strang, G. and Borre, K. Linear Algebra, Geodesy and GPS. Wiley, Wellesley-Cambridge Press, 1997 |
[50] | Taylor, B.N. and Kuyatt, C.E. Guidelines for evaluating and expressing the uncertainty of NIST measurement results. Tech. Rep. TN1297, National Institute of Standards and Technology, USA, 1994 |
[51] | Weise, K., and Woger, W. A Bayesian theory of measurement uncertainty. Meas. Sci. Technol., 3, 1992, pp.1-11 |
[52] | Wichmann, B.A. and Hill, I.D. Algorithm AS183. An efficient and portable pseudo-random number generator. Appl. Statist., 31, 1982, pp.188-190 |
[53] | Wichmann, B.A. and Hill, I.D. Correction. Algorithm AS183. An efficient and portable pseudo-random number generator. Appl. Statist., 33, 1984, p.123 |
[54] | Wichmann, B.A. and Hill, I.D. Generating good pseudo-random numbers. Computational Statistics and Data Analysis, 51, 2006, pp.1614-1622 |
[55] | Willink, R. Coverage intervals and statistical coverage intervals. Metrologia, 41, 2004, L5-L6 |
[56] | Woger, W. Probability assignment to systematic deviations by the Principle of Maximum Entropy. IEEE Trans. Instr. Measurement IM-36, 1987, pp.655-658 |
Электронный текст документа
и сверен по:
, 2012