ГОСТ Р ИСО 18437-6-2021
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Вибрация и удар
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ МЕХАНИЧЕСКИХ СВОЙСТВ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ
Часть 6
Метод температурно-временной суперпозиции
Mechanical vibration and shock. Characterization of the dynamic mechanical properties of visco-elastic materials. Part 6. Method of time-temperature superposition
ОКС 17.160
Дата введения 2022-01-01
Предисловие
1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 183 "Вибрация, удар и контроль технического состояния"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 25 мая 2021 г. N 461-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 18437-6:2017* "Вибрация и удар. Определение динамических механических свойств вязко-упругих материалов. Часть 6. Температурно-временная суперпозиция" (ISO 18437-6:2017 "Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 6: Time-temperature superposition", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочного международного стандарта соответствующий ему национальный стандарт, сведения о котором приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
Введение
Вязкоупругие материалы широко используются в разных системах, в частности для снижения вибрации в конструкциях посредством потери энергии (демпфирования) или изоляции компонентов и в акустических приложениях, связанных с преобразованием, передачей и поглощением энергии. Для оптимального функционирования таких систем зачастую необходимо, чтобы их элементы обладали заданными динамическими свойствами. У большинства вязкоупругих материалов их свойства зависят от частоты, температуры и амплитуды деформации. Целью настоящего стандарта является представление руководства по сбору данных о динамических функциях вязкоупругости с учетом их последующей обработки и установление стандартного метода их анализа на основе принципа температурно-временной суперпозиции. Настоящий стандарт распространяется на термореологически простые материалы с линейным поведением при малых амплитудах деформации (напряжения). В настоящем стандарте предложен метод подтверждения термореологической простоты материала, а также выявления и исключения сомнительных данных, установлены минимальные критерии к сбору данных исходя из требований их последующей обработки и возможности объединения нескольких наборов данных о характеристиках вязкоупругих материалов, полученных при разных температурах, в одну обобщенную кривую на основе принципа температурно-временной суперпозиции. При достаточном объеме данных применяется стандартный аналоговый метод расчета в виде сдвигов участков кривой ([16], [17]).
Метод температурно-временной суперпозиции является наиболее широко используемым в ускоренных испытаниях, позволяющих предсказать долговременное поведение вязкоупругих материалов ([13]). Он позволяет получить значения характеристик упругости в той области частот, в которой реальное проведение испытаний не представляется возможным.
1 Область применения
Настоящий стандарт устанавливает метод сбора и анализа экспериментальных данных, полученных в результате испытаний по одному из следующих стандартов: ИСО 18437-1 - ИСО 18437-5, ИСО 6721-4 - ИСО 6721-7 или ИСО 6721-12.
Установленный метод применим к данным, полученным для термореологически простых материалов при их испытаниях в равновесном состоянии при каждой заданной температуре.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения к нему):
ISO 18437-1, Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 1: Principles and guidelines (Вибрация и удар. Определение динамических механических свойств вязкоупругих материалов. Часть 1. Общие принципы и руководство)
3 Термины и определения
В настоящем стандарте применены термины по ИСО 18437-1, а также следующие термины с соответствующими определениями:
ИСО и МЭК ведут терминологические базы данных для использования в стандартизации по следующим адресам:
- Платформа онлайн-просмотра ИСО: доступна на https://www.iso.org/obp;
- Электропедия МЭК: доступна на http://www.electropedia.org/.
3.1 динамическая функция (вязкоупругости) (dynamic visco-elastic function): Основная характеристика вязкоупругих свойств материала, состоящая из модуля накопления и модуля потерь и определяемая в виде модулей упругости при деформациях растяжения, сдвига или сжатия, а также в виде функции потерь как функция частоты и температуры.
3.2 модуль накопления M' (storage modulus): Действительная часть комплексного модуля упругости.
Примечание 1 - Является мерой энергии, накапливаемой и возвращаемой материалом при его циклическом нагружении.
Примечание 2 - Модули накопления для деформаций растяжения, сдвига и сжатия обозначают соответственно E', G' и K'.
Примечание 3 - Выражается в паскалях (Па).
[ИСО 472:2013, статья 2.998 с изменениями (добавлены примечания)]
3.3 модуль потерь M'' (loss modulus): Мнимая часть комплексного модуля упругости.
Примечание 1 - Является мерой потерь (диссипации) энергии в материале при его циклическом нагружении.
Примечание 2 - Модули потерь для деформаций растяжения, сдвига и сжатия обозначают соответственно E'', G" и K".
Примечание 3 - Выражается в паскалях (Па).
[ИСО 472:2013, статья 2.559 с изменениями (добавлены примечания)]
3.4 коэффициент потерь ![]() (loss factor): Отношение модуля потерь (3.3) к модулю накопления (3.2) для деформаций растяжения, сдвига, сжатия или продольного сжатия материала.
(loss factor): Отношение модуля потерь (3.3) к модулю накопления (3.2) для деформаций растяжения, сдвига, сжатия или продольного сжатия материала.
Примечание 1 - Вычисляется по формуле ![]() =M"/M'.
=M"/M'.
[ИСО 472:2013, статья 2.557 с изменениями (уточнено определение термина)]
3.5 температурно-временная суперпозиция (time-temperature superposition): Принцип эквивалентности для вязкоупругих материалов величин времени и температуры, согласно которому кривую, построенную по данным при одном значении температуры, распространяют на данные, соответствующие другой температуре, посредством сдвига соответствующей кривой вдоль оси времени в логарифмическом масштабе.
Примечание 1 - Настоящий термин в большей степени подходит для динамических испытаний, хотя для них он менее употребим. В качестве эквивалента используют также термин "метод приведенных величин".
[ИСО 18437-2:2005, пункт 3.3 с изменениями ("ось частот" заменена на "ось времени в логарифмическом масштабе" и добавлено примечание)]
3.6 термореологически простой материал (thermorheologically simple material): Материал, для которого справедлив принцип температурно-временной суперпозиции (3.5).
Примечание 1 - Материал, для которого принцип температурно-временной суперпозиции не выполняется, например вследствие множественных фазовых переходов, называют термореологически сложным.
Примечание 2 - В термореологически сложных системах отношение времен релаксации материала при разных температурах может не быть постоянной величиной. Таким образом, мультифазная система будет термореологически сложной, если фактор сдвига (3.7) зависит не только от температуры, но и от времени.
3.7 фактор (горизонтального) сдвига ![]() (shift factor): Величина сдвига вдоль логарифмической (по основанию 10) оси частот, при котором происходит совмещение кривой характеристики для одного постоянного значения температуры с кривой для другого постоянного значения температуры.
(shift factor): Величина сдвига вдоль логарифмической (по основанию 10) оси частот, при котором происходит совмещение кривой характеристики для одного постоянного значения температуры с кривой для другого постоянного значения температуры.
Примечание 1 - Выражение "фактор сдвига" обычно подразумевает сдвиг в горизонтальном направлении.
[ИСО 18437-2:2005, пункт 3.4 с изменениями (добавлено примечание)]
3.8 фактор вертикального сдвига ![]() (vertical shift factor): Величина сдвига вдоль логарифмической (по основанию 10) оси модуля упругости для учета влияния перехода от приведенной температуры к некоторой заданной температуре.
(vertical shift factor): Величина сдвига вдоль логарифмической (по основанию 10) оси модуля упругости для учета влияния перехода от приведенной температуры к некоторой заданной температуре.
3.9 обобщенная кривая (master curve): Кривая, построенная с применением температурно-временной суперпозиции (3.5), которая отражает динамическое поведение материала при температуре приведения в диапазоне частот более широком, чем тот, в котором были проведены испытания.
4 Определение диапазона вязкоупругости и описание данных
4.1 Принцип температурно-временной суперпозиции
Метод температурно-временной суперпозиции является наиболее широко используемым в ускоренных испытаниях, позволяющих предсказать долговременное поведение вязкоупругих материалов, и состоит в следующем. Для получения экспериментальных данных о механических свойствах материала проводят серию динамических испытаний при разных постоянных значениях температуры в заданном ограниченном диапазоне частот (часто называемом "окно эксперимента"). Это позволяет получить набор изотермических сегментов динамической функции вязкоупругости. Эти сегменты смещают вначале по вертикальной оси для учета изменения температуры и плотности материала, а затем вдоль горизонтальной оси частот (в логарифмическом масштабе) к сегменту кривой, полученной при температуре приведения ![]() . Кривую, составленную из таких сегментов, называют обобщенной кривой. Принцип температурно-временной суперпозиции утверждает, что результирующая обобщенная кривая будет совпадать с той кривой, которая была бы получена в результате проведения испытаний в широком диапазоне частот при температуре приведения. Таким образом, изотермы, полученные с применением практически и экономически обоснованного окна эксперимента, позволяют построить полную динамическую функцию вязкоупругости для испытуемого материала.
. Кривую, составленную из таких сегментов, называют обобщенной кривой. Принцип температурно-временной суперпозиции утверждает, что результирующая обобщенная кривая будет совпадать с той кривой, которая была бы получена в результате проведения испытаний в широком диапазоне частот при температуре приведения. Таким образом, изотермы, полученные с применением практически и экономически обоснованного окна эксперимента, позволяют построить полную динамическую функцию вязкоупругости для испытуемого материала.
Примечание 1 - Сдвиг сегментов в вертикальном направлении не требуется, если искомой динамической функцией является функция потерь ([17]).
Существуют несколько критериев применимости метода температурно-временной суперпозиции ([13]):
a) сегменты изотерм, полученных при разных температурах, хорошо совмещаются при наложении друг на друга в широком диапазоне частот;
b) фактор сдвига ![]() одинаковый для разных динамических функций;
одинаковый для разных динамических функций;
c) фактор сдвига ![]() представляет собой гладкую функцию температуры, не содержащую значительных флуктуаций и особенностей.
представляет собой гладкую функцию температуры, не содержащую значительных флуктуаций и особенностей.
Примечание 2 - Зависимость ![]() от температуры обычно моделируют теоретическими зависимостями Аррениуса ([14]) или Уильямса-Лэндела-Ферри ([13]). Дополнительная информация о модели Уильямса-Лэндела-Ферри приведена в [11] и [2].
от температуры обычно моделируют теоретическими зависимостями Аррениуса ([14]) или Уильямса-Лэндела-Ферри ([13]). Дополнительная информация о модели Уильямса-Лэндела-Ферри приведена в [11] и [2].
4.2 Получение данных
4.2.1 Новые данные
При получении экспериментальных данных следует обратить особое внимание на то, чтобы они были полны и обеспечивали достаточное перекрытие в точке сопряжения частот при сдвиге изотерм. Примером достаточно полного описания может служить сбор данных с интервалом 5°С на частотах 0,1; 0,2; 0,3; 0,5; 1; 2; 3; 5; 10; 20 и 30 Гц или динамических данных, обеспечивающих перекрытие в одну декаду (по логарифмической оси частот) между соседними изотермами.
Теоретически метод температурно-временной суперпозиции не налагает ограничений на выбор окна эксперимента. Однако диапазон частот испытаний должен быть согласован с другими стандартами и возможностями измерительного оборудования.
Диапазон температур при испытаниях также должен соответствовать возможностям экспериментальной установки с учетом того, что максимальная температура должна быть не выше той, при которой испытуемый образец материала начинает терять геометрическую форму под действием собственного веса.
4.2.2 Существующие данные
Если построение динамической функции вязкоупругости основывается на уже имеющихся данных, тогда эти данные должны удовлетворять требованиям 4.2.1. Если существующие данные не обеспечивают достаточного перекрытия соседних участков кривой, тогда для получения недостающих сегментов следует провести испытания в соответствии с требованиями настоящего стандарта.
Существует альтернативный способ восполнения недостающих данных без обращения к испытаниям (см. [15]), однако этот способ не должен рассматриваться как часть настоящего стандарта.
4.2.3 Разброс данных и подтверждение термореологической простоты
У термореологически простого материала ![]() является гладкой функцией температуры без значительных флуктуаций или особенностей, и существует только один фазовый переход во всем спектре частот и температур. Тогда график зависимости коэффициента потерь от модуля накопления будет иметь вид гладкой кривой, похожей на арку или перевернутую букву U ([15]).
является гладкой функцией температуры без значительных флуктуаций или особенностей, и существует только один фазовый переход во всем спектре частот и температур. Тогда график зависимости коэффициента потерь от модуля накопления будет иметь вид гладкой кривой, похожей на арку или перевернутую букву U ([15]).
Примечание - Если у полимера имеется более одной температуры фазового перехода, но всем им соответствует одна функция сдвига ![]() , тогда все данные по температуре и частоте будут ложиться на одну гладкую кривую, но ее вид будет отличен от перевернутой буквы U.
, тогда все данные по температуре и частоте будут ложиться на одну гладкую кривую, но ее вид будет отличен от перевернутой буквы U.
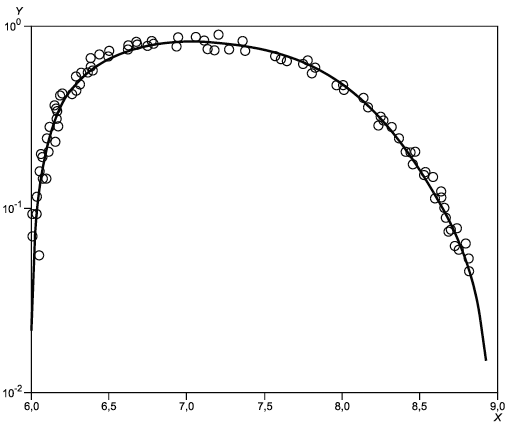
График экспериментальной зависимости коэффициента потерь от модуля накопления используется для количественного контроля разброса данных. Этот разброс характеризуется шириной полосы вокруг гладкой кривой, в которую попадает большинство экспериментальных точек, и выбросами отдельных точек. При наличии таких выбросов их следует удалить из рассмотрения или же повторить испытания для подтверждения достоверности результатов. По данному графику, однако, ничего нельзя сказать о точности измерений температуры и частоты, а также о наличии каких-либо систематических ошибок.
Пример графика зависимости коэффициента потерь от модуля накопления ("перевернутое U") приведен на рисунке 1.
|
X - модуль Юнга, Па; Y - коэффициент потерь
Рисунок 1 - Пример компьютерного моделирования графика зависимости коэффициента потерь от модуля упругости для материала с высокими диссипативными свойствами при погрешностях коэффициента потерь и модуля накопления, не превышающих 10%
4.3 Сдвиг изотерм
4.3.1 Вертикальный сдвиг
Подгонку данных по модулю накопления и коэффициенту потерь сначала выполняют в вертикальном направлении.
Для твердых вязкоупругих материалов фактор вертикального сдвига обычно мал, и при построении обобщенной кривой им можно пренебречь (см. [14]). Однако для ряда материалов и условий испытаний (например, проводившихся в широком диапазоне температур) его величина может быть значительна. В этом случае опускать операцию вертикального сдвига нельзя во избежание серьезных ошибок в поведении обобщенной кривой в широком диапазоне частот.
4.3.2 Горизонтальный сдвиг
После вертикального сдвига выполняют сдвиг в горизонтальном направлении. Фактор сдвига рассчитывают аналитическим методом ([16], [17]), для которого необходим определенный объем экспериментальных данных. Метод расчета исходит из предположения, что два соседних сегмента могут быть совмещены, если область их перекрытия равна нулю. Описание метода выходит за рамки настоящего стандарта, однако некоторые его подробности приведены для сведения в приложениях A и B. В приложении C приведен макрос, написанный в программе ![]()
![]() , для применения указанной методологии.
, для применения указанной методологии.
________________
![]() Excel - торговая марка продукта, принадлежащая компании
Excel - торговая марка продукта, принадлежащая компании ![]() . Данная информация приведена для удобства пользователей настоящего стандарта и не является рекламой указанного продукта со стороны ИСО. Вместо него может быть использован любой другой программный продукт, обеспечивающий получение аналогичных результатов.
. Данная информация приведена для удобства пользователей настоящего стандарта и не является рекламой указанного продукта со стороны ИСО. Вместо него может быть использован любой другой программный продукт, обеспечивающий получение аналогичных результатов.
4.3.3 Обобщенные кривые динамической функции вязкоупругости
Согласно критерию применимости метода температурно-временной суперпозиции b) [см. 4.1, перечисление b)] фактор сдвига должен быть одинаковым для всех динамических функций. Поскольку из всех динамических функций измерения обычно наиболее точны (имеют наименьший разброс данных) функции для модуля накопления, именно его выбирают для определения ![]() по 4.3.2 и построения обобщенной кривой. После этого полученное значение
по 4.3.2 и построения обобщенной кривой. После этого полученное значение ![]() применяют к другим динамическим функциям, таким как модуль потерь и коэффициент потерь (см. [9] и [10]). При этом следует помнить, что для всех указанных динамических функций горизонтальному сдвигу должен предшествовать вертикальный сдвиг.
применяют к другим динамическим функциям, таким как модуль потерь и коэффициент потерь (см. [9] и [10]). При этом следует помнить, что для всех указанных динамических функций горизонтальному сдвигу должен предшествовать вертикальный сдвиг.
Обобщенную кривую для модуля накопления, получаемую по результатам измерений при разных температурах, строят, откладывая значения ![]() относительно
относительно ![]() в логарифмическом масштабе (с основанием 10) по обеим осям.
в логарифмическом масштабе (с основанием 10) по обеим осям.
Примечание - Если график для модуля накопления имеет вид плоской функции, то более точное значение фактора сдвига может быть получено на основании данных для модуля потерь или коэффициента потерь. Соответствующий алгоритм приведен в [17].
5 Подтверждение пригодности данных
Контроль полученных экспериментальных данных выполняют, откладывая на графике значения коэффициента потерь относительно логарифма модуля накопления без учета температур и частот, при которых эти значения были получены. Данные должны находиться в пределах одной гладкой полосы (см. 4.3). Дополнительные сведения приведены в [11] и [8].
Сегменты изотерм должны удовлетворять критериям применимости по 4.1. Если эти критерии по какой-либо причине не выполняются, то метод температурно-временной суперпозиции так, как он описан в 4.1, не применяют, и построение обобщенной кривой требует более сложного анализа данных (см. [13]).
6 Основные источники ошибок
6.1 Общие положения
В настоящем разделе рассматриваются ошибки, связанные с алгоритмом построения обобщенной кривой, т.е. без учета неопределенности, обусловленной применяемым методом испытаний. Эти ошибки в основном вызваны недостатками организации испытаний (неправильное планирование испытаний, неправильная обработка выборки), несоблюдением требуемых граничных условий для испытуемого образца, неправильным применением полученных данных.
Основные источники ошибок описаны в 6.2-6.6.
6.2 Узкая область перекрытия сегментов
Если в результате испытаний получены изотермы с узким диапазоном перекрытия, то фактор сдвига может быть определен с меньшей точностью. В этом случае испытание рекомендуется повторить для получения лучшего перекрытия сегментов (см. 4.2.1).
6.3 Ошибки экспериментальных данных (более 10%) в пределах сегмента
Поскольку обобщенную кривую обычно строят из отдельных сегментов, ошибки сдвигов этих сегментов складываются в общую ошибку построения обобщенной кривой. В связи с этим наличие больших ошибок в экспериментальных данных приводит к тому, что ошибка построения обобщенной кривой превышает ошибки исходных сегментов. Рекомендуется повторить или изменить процедуру испытаний таким образом, чтобы обеспечить построение сегментов с большей точностью, т.е. с меньшими ошибками экспериментальных данных.
6.4 Малое число экспериментальных точек на сегменте
Низкая плотность экспериментальных точек не позволяет выполнить хорошую аппроксимацию в области перекрытия сегментов. Рекомендуется повторить или изменить процедуру испытаний таким образом, чтобы получить число экспериментальных точек, достаточное для описания всех особенностей отдельного сегмента.
6.5 Аномалии на краях сегментов
Если экспериментальные данные приводят к аномальному поведению изотермы в ее начале или конце, например вследствие локального перегрева ([18]) или эффектов инерции ([19]), то необходимо устранить эти аномалии, прежде чем выполнять операцию сдвига. Экспериментатору следует принять решение, исключить ли из построения сегмент полностью или только ту его часть на конце, где наблюдается аномалия.
6.6 Выбор температуры приведения
Процедура построения обобщенной кривой будет более надежной в том случае, если центральный сегмент, используемый при ее построении, получен при температуре приведения. В этом случае накапливаемая ошибка, связанная со сдвигами остальных сегментов, будет минимальной.
7 Представление результатов
7.1 Представление количественных данных
7.1.1 Количественные данные, полученные в соответствии с настоящим стандартом, должны быть представлены в виде графиков и таблиц, как указано в 7.1.2-7.1.6.
7.1.2 Исходные графики сегментов (перед выполнением операций сдвига) в логарифмическом масштабе (с основанием 10) по обеим осям для модулей накопления и потерь и в линейно-логарифмическом масштабе - для коэффициента потерь.
7.1.3 Графики обобщенной кривой для температуры приведения в логарифмическом масштабе (с основанием 10) по обеим осям для модулей накопления и потерь и в линейно-логарифмическом масштабе - для коэффициента потерь.
В целях единообразия и облегчения работы с данными при температурах, отличающихся от температуры приведения, рекомендуется представлять обобщенные кривые для модулей накопления и потерь, а также для коэффициента потерь в виде номограмм (см. [8]).
7.1.4 Таблица, содержащая:
a) логарифмы (по основанию 10) горизонтального фактора сдвига для каждого сегмента;
b) логарифмы (по основанию 10) вертикального фактора сдвига для каждого сегмента.
7.1.5 График зависимости логарифма (по основанию 10) горизонтального фактора сдвига от температуры.
7.1.6 График зависимости логарифма (по основанию 10) вертикального фактора сдвига от температуры.
7.2 Протокол испытаний
Протокол испытаний должен содержать:
a) ссылку на настоящий стандарт;
b) подробную информацию, позволяющую идентифицировать испытуемый материал (тип, изготовителя, марку);
c) подробности метода испытаний (форму образца, его подготовку к испытаниям);
d) оценку возможных ошибок (количественную оценку неопределенности) в экспериментальных данных;
e) таблицу исходных данных (экспериментальных точек);
f) использованные способы обработки данных, например исключение выбросов (если такие применялись);
g) температуру приведения, для которой были построены обобщенные кривые;
h) графики и таблицы, указанные в 7.1;
i) дату построения обобщенной кривой.
Приложение A
(справочное)
Алгоритм расчета факторов сдвига
A.1 Вертикальный сдвиг
Фактор вертикального сдвига ![]() определяют по формуле
определяют по формуле
![]() , (A.1)
, (A.1)
где ![]() - плотность материала при заданной температуре, кг/м
- плотность материала при заданной температуре, кг/м![]() ;
;
T - заданная температура, К;
![]() - плотность материала при температуре приведения, кг/м
- плотность материала при температуре приведения, кг/м![]() ;
;
![]() - температура приведения, К.
- температура приведения, К.
Если отношение плотностей в формуле (A.1) неизвестно, то ![]() определяют по формуле
определяют по формуле
![]() . (A.2)
. (A.2)
A.2 Горизонтальный сдвиг для наложения двух сегментов
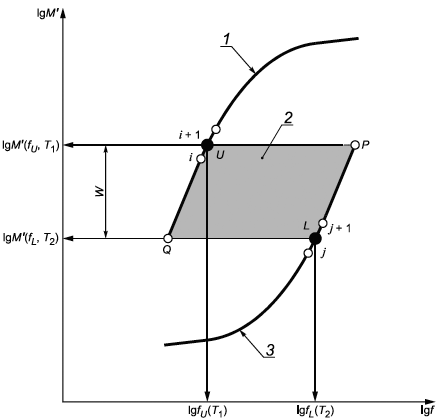
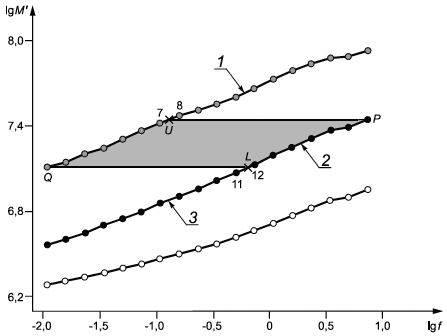
Алгоритм расчета горизонтального фактора сдвига исходит из предположения, что два соседних сегмента могут быть соединены, когда область их наложения друг на друга равна нулю ([16], [17]). Область наложения представляет собой область между двумя соседними сегментами, ограниченную с левой и правой сторон перекрывающимися частями сегментов, а сверху и снизу - прямыми горизонтальными линиями, проходящими через начало одного и конец другого сегмента (показана в виде затемненного участка A(![]() ,
, ![]() ) на рисунке A.1).
) на рисунке A.1).
|
1 - сегмент модуля накопления для температуры приведения ![]() ; 2 - область наложения сегментов A (
; 2 - область наложения сегментов A (![]() ,
, ![]() ); 3 - сегмент модуля накопления для температуры
); 3 - сегмент модуля накопления для температуры ![]() ,
, ![]() >
>![]()
Примечание - Обозначение lg f(![]() ) указывает на принадлежность значения частоты сегменту, полученному для температуры
) указывает на принадлежность значения частоты сегменту, полученному для температуры ![]() .
.
Рисунок А.1 - Схематичное изображение двух сегментов модуля накопления
При выполнении критериев применимости принципа температурно-временной суперпозиции (см. 4.1) ширина W области наложения сегментов модуля накопления (см. рисунок А.1) не должна быть меньше ![]() , где
, где ![]() - оценка погрешности получения экспериментальных данных ([16], [17]).
- оценка погрешности получения экспериментальных данных ([16], [17]).
На рисунке A.1 схематично изображены два сегмента в виде монотонно возрастающих функций, построенных для двух соседних температур испытаний ![]() и
и ![]() ,
, ![]() >
>![]() , по
, по ![]() и
и ![]() , экспериментальным точкам, соответственно.
, экспериментальным точкам, соответственно.
Согласно методу температурно-временной суперпозиции для построения обобщенной кривой при температуре приведения ![]() ,
, ![]() =
=![]() , сегмент, полученный при температуре
, сегмент, полученный при температуре ![]() , следует сдвинуть влево по логарифмической оси частот так, чтобы из двух сегментов составилась общая гладкая кривая (см. 4.1).
, следует сдвинуть влево по логарифмической оси частот так, чтобы из двух сегментов составилась общая гладкая кривая (см. 4.1).
Фактор горизонтального сдвига ![]() , соответствующий сегменту, полученному при температуре
, соответствующий сегменту, полученному при температуре ![]() , и в дальнейшем обозначаемый как "индивидуальный" фактор сдвига, рассчитывают по формуле
, и в дальнейшем обозначаемый как "индивидуальный" фактор сдвига, рассчитывают по формуле
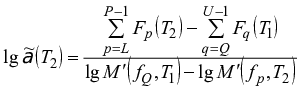 , (A.3)
, (A.3)
где
![]() , q=Q,...,U-1, (A.4)
, q=Q,...,U-1, (A.4)
![]() , p=L,...,P-1. (A.5)
, p=L,...,P-1. (A.5)
При наличии существенных ошибок эксперимента может оказаться так, что модуль накопления будет подвержен флуктуациям и тем самым отличаться от строго монотонной зависимости. Чтобы исключить влияние флуктуаций на вычисление фактора горизонтального сдвига, граничные точки Q, P, U и L области наложения должны быть определены следующим образом:
a) точка Q соответствует экспериментальной точке с минимальным значением модуля накопления на сегменте, полученном при температуре ![]() , т.е.
, т.е.
![]() ; (A.6)
; (A.6)
b) точка P соответствует экспериментальной точке с максимальным значением модуля накопления на сегменте, полученном при температуре ![]() , т.е.
, т.е.
![]() ; (A.7)
; (A.7)
c) точку U, которая соответствует верхней границе области наложения для сегмента, полученного при температуре ![]() , получают построением посредством постепенного горизонтального перемещения точки P до ее наложения на сегмент, полученный при температуре
, получают построением посредством постепенного горизонтального перемещения точки P до ее наложения на сегмент, полученный при температуре ![]() . Если при горизонтальном перемещении точки P она накладывается на указанный сегмент более одного раза, то в качестве точки U берут точку наложения, ближайшую (по частоте) к точке Q. Частотная координата точки U определяется формулой
. Если при горизонтальном перемещении точки P она накладывается на указанный сегмент более одного раза, то в качестве точки U берут точку наложения, ближайшую (по частоте) к точке Q. Частотная координата точки U определяется формулой
![]() , (A.8)
, (A.8)
где i и i+1 - ближайшие к U экспериментальные точки на сегменте, полученном при температуре ![]() (на рисунке А.1 они изображены незакрашенными точками на сегменте 1).
(на рисунке А.1 они изображены незакрашенными точками на сегменте 1).
Значение модуля накопления в точке U то же самое, что и в точке P, т.е.
![]() ; (A.9)
; (A.9)
d) точку L, которая соответствует нижней границе области наложения для сегмента, полученного при температуре ![]() , получают построением посредством постепенного горизонтального перемещения точки Q до ее наложения на сегмент, полученный при температуре
, получают построением посредством постепенного горизонтального перемещения точки Q до ее наложения на сегмент, полученный при температуре ![]() . Если при горизонтальном перемещении точки Q она накладывается на указанный сегмент более одного раза, то в качестве точки L берут точку наложения, ближайшую (по частоте) к точке P. Частотная координата точки L определяется формулой
. Если при горизонтальном перемещении точки Q она накладывается на указанный сегмент более одного раза, то в качестве точки L берут точку наложения, ближайшую (по частоте) к точке P. Частотная координата точки L определяется формулой
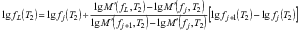 , (A.10)
, (A.10)
где j и j+1 - ближайшие к L экспериментальные точки на сегменте, полученном при температуре ![]() (на рисунке А.1 они изображены незакрашенными точками на сегменте 3).
(на рисунке А.1 они изображены незакрашенными точками на сегменте 3).
Значение модуля накопления в точке L то же самое, что и в точке Q, т.е.
![]() ; (A.11)
; (A.11)
A.3 Обобщенная кривая, построенная по трем и более сегментам
Испытания, в ходе которых получают экспериментальные данные, проводят при K разных температурах {![]() , k=1, ..., K}, K
, k=1, ..., K}, K3, где
![]() <
<![]() <...<
<...<![]() . На основе этих данных строят сглаженную обобщенную кривую для модуля накопления с использованием следующей процедуры:
. На основе этих данных строят сглаженную обобщенную кривую для модуля накопления с использованием следующей процедуры:
a) выбирают температуру приведения ![]() в пределах диапазона испытаний;
в пределах диапазона испытаний;
b) каждый сегмент сдвигают в вертикальном направлении на фактор вертикального сдвига b(![]() ), k=1,..., K, значение которого получено по формуле (A.1) или (A.2), преобразуя его тем самым в
), k=1,..., K, значение которого получено по формуле (A.1) или (A.2), преобразуя его тем самым в ![]() . Величину, которой соответствуют сдвинутые сегменты, называют приведенным модулем накопления;
. Величину, которой соответствуют сдвинутые сегменты, называют приведенным модулем накопления;
c) для каждой пары соседних сегментов:
1) определяют значения частоты и приведенного модуля накопления в точках Q и P с использованием формул (A.6) и (А.7);
2) определяют значения частоты и приведенного модуля накопления в точках U и L с использованием формул (A.8)-(А.11);
3) вычисляют индивидуальный фактор сдвига ![]() по формулам (А.3)-(А.5).
по формулам (А.3)-(А.5).
Сегменты пристраивают к цепочке других сегментов в порядке повышения их температуры;
d) для сегмента приведения, которому соответствует температура приведения ![]() , значение
, значение ![]() приводят к нулю, т.е.
приводят к нулю, т.е. ![]() =0. Это означает, что сегмент приведения останется в своем первоначальном положении;
=0. Это означает, что сегмент приведения останется в своем первоначальном положении;
e) соответствующим образом корректируют окончательные значения факторов горизонтального сдвига для сегментов с температурами выше температуры приведения, ![]() >
>![]() , суммируя их индивидуальные факторы горизонтального сдвига с окончательным сдвигом для сегмента приведения по формуле
, суммируя их индивидуальные факторы горизонтального сдвига с окончательным сдвигом для сегмента приведения по формуле
![]() ; (A.12)
; (A.12)
f) для сегментов с температурами ниже температуры приведения, ![]() <
<![]() , окончательные значения факторов горизонтального сдвига получают, вычитая их индивидуальные факторы горизонтального сдвига из окончательного сдвига для сегмента приведения по формуле
, окончательные значения факторов горизонтального сдвига получают, вычитая их индивидуальные факторы горизонтального сдвига из окончательного сдвига для сегмента приведения по формуле
![]() ; (A.13)
; (A.13)
g) для каждого сегмента получают "приведенную" частоту ее преобразованием к ![]() , k=1,..., K;
, k=1,..., K;
h) откладывают на графике в логарифмическом масштабе (с основанием 10) по обеим осям сегменты приведенных модулей накопления относительно приведенных частот, которые в совокупности составляют сглаженную обобщенную кривую.
Пример построения обобщенной кривой, иллюстрирующей процедуру по перечислениям a)-h), приведен в приложении B.
Приложение B
(справочное)
Пример построения обобщенной кривой для модуля накопления
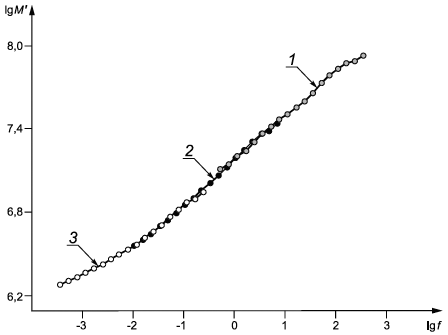
В настоящем приложении рассмотрен пример применения методологии сдвигов сегментов экспериментальных данных модуля накопления для построения обобщенной кривой. В примере использованы три сегмента, полученные в ходе испытаний при температурах ![]() =0°С;
=0°С; ![]() =10°С;
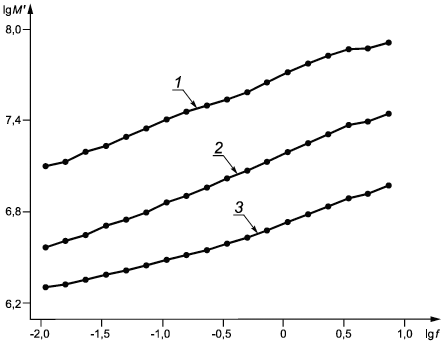
=10°С; ![]() =20°С. Сегменты составлены из 18 экспериментальных точек каждый (см. рисунок B.1), координаты которых даны в таблице B.1. Номер точки в пределах сегмента обозначен n, n=1,...,18;
=20°С. Сегменты составлены из 18 экспериментальных точек каждый (см. рисунок B.1), координаты которых даны в таблице B.1. Номер точки в пределах сегмента обозначен n, n=1,...,18; ![]() =
=![]() =
=![]() =18. Для всех сегментов использовано одно и то же окно эксперимента, т.е.
=18. Для всех сегментов использовано одно и то же окно эксперимента, т.е. ![]() .
.
|
1 - сегмент модуля накопления для температуры ![]() =0°С; 2 - сегмент модуля накопления для температуры
=0°С; 2 - сегмент модуля накопления для температуры ![]() =10°С; 3 - сегмент модуля накопления для температуры
=10°С; 3 - сегмент модуля накопления для температуры ![]() =20°С
=20°С
Рисунок B.1 - Три сегмента модуля накопления
Таблица B.1 - Экспериментальные данные для сегментов модуля накопления
n |
|
|
|
|
|
|
| ||
1 | -1,964 8 | 7,094 6 | 6,565 7 | 6,300 5 |
2 | -1,798 2 | 7,128 | 6,605 5 | 6,326 4 |
3 | -1,631 5 | 7,187 7 | 6,649 3 | 6,351 8 |
4 | -1,464 8 | 7,228 7 | 6,703 3 | 6,385 |
5 | -1,298 2 | 7,291 5 | 6,748 6 | 6,413 7 |
6 | -1,131 5 | 7,350 2 | 6,793 6 | 6,445 4 |
7 | -0,964 9 | 7,400 7 | 6,858 1 | 6,482 6 |
8 | -0,798 2 | 7,453 7 | 6,905 4 | 6,514 6 |
9 | -0,631 5 | 7,492 6 | 6,959 1 | 6,549 7 |
10 | -0,464 8 | 7,536 | 7,014 1 | 6,587 1 |
11 | -0,298 2 | 7,584 4 | 7,070 2 | 6,631 7 |
12 | -0,131 5 | 7,645 4 | 7,128 4 | 6,678 7 |
13 | 0,035 2 | 7,711 9 | 7,191 1 | 6,728 6 |
14 | 0,201 8 | 7,772 2 | 7,250 2 | 6,782 8 |
15 | 0,368 5 | 7,820 6 | 7,309 | 6,834 8 |
16 | 0,535 2 | 7,861 2 | 7,365 3 | 6,887 9 |
17 | 0,701 8 | 7,871 6 | 7,391 2 | 6,913 7 |
18 | 0,868 5 | 7,909 | 7,442 6 | 6,966 1 |
Из рисунка B.1 видно, что формы всех трех сегментов приблизительно одинаковые, что свидетельствует о выполнении критерия a) применимости метода температурно-временной суперпозиции (см. 4.1).
Построение обобщенной кривой выполнено в соответствии с процедурой по перечислениям a)-h), описанной в приложении A:
a) выбирают температуру приведения ![]() в пределах диапазона испытаний.
в пределах диапазона испытаний.
В примере в качестве сегмента приведения выбран средний, т.е. ![]() =
=![]() ;
;
b) каждый сегмент сдвигают в вертикальном направлении на фактор вертикального сдвига ![]() , k=1,..., K, значение которого получено по формуле (A.1) или (A.2), преобразуя его тем самым в
, k=1,..., K, значение которого получено по формуле (A.1) или (A.2), преобразуя его тем самым в ![]() .
.
Поскольку в рассматриваемом примере плотность материала при разных температурах неизвестна, вертикальный сдвиг выполнен с применением формулы (A.2), т.е. b(T)=T/![]() =T/
=T/![]() (температура в кельвинах). Таким образом, факторы вертикального сдвига будут равны:
(температура в кельвинах). Таким образом, факторы вертикального сдвига будут равны:
1) ![]() =(
=(![]() +237,15)/(
+237,15)/(![]() +237,15)=0,9647 - для сегмента с температурой
+237,15)=0,9647 - для сегмента с температурой ![]() ;
;
2) ![]() =(
=(![]() +237,15)/(
+237,15)/(![]() +237,15)=1 - для сегмента с температурой
+237,15)=1 - для сегмента с температурой ![]() (остается на своей позиции);
(остается на своей позиции);
3) ![]() =(
=(![]() +237,15)/(
+237,15)/(![]() +237,15)=1,0353 - для сегмента с температурой
+237,15)=1,0353 - для сегмента с температурой ![]() .
.
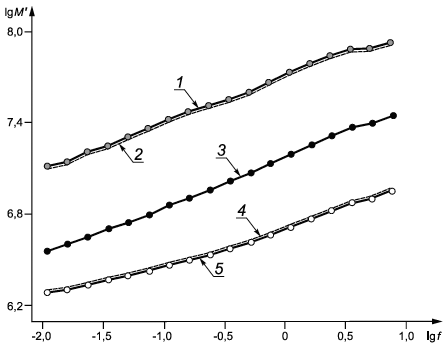
Вычитая фактор вертикального сдвига из значения модуля накопления (и та, и другая величины взяты как логарифмы по основанию 10) для каждой экспериментальной точки, получаем приведенные модули накопления (см. рисунок B.2 и таблицу B.2);
c) для каждой пары соседних сегментов:
1) определяют значения частоты и приведенного модуля накопления в точках Q и P с использованием формул (A.6) и (A.7);
2) определяют значения частоты и приведенного модуля накопления в точках U и L с использованием формул (A.8)-(A.11);
3) вычисляют индивидуальный фактор сдвига ![]() по формулам (A.3)-(A.5).
по формулам (A.3)-(A.5).
Вначале рассматривают выполнение указанных действий для первой пары приведенных сегментов с температурами (![]() ,
, ![]() )=(0°С, 10°С), выделенных цветом на рисунке B.3.
)=(0°С, 10°С), выделенных цветом на рисунке B.3.
|
1 - сегмент приведенного модуля накопления (![]() =0°С); 2 - сегмент исходного модуля накопления (
=0°С); 2 - сегмент исходного модуля накопления (![]() =0°С); 3 - сегмент исходного модуля накопления (
=0°С); 3 - сегмент исходного модуля накопления (![]() =10°С); 4 - сегмент исходного модуля накопления (
=10°С); 4 - сегмент исходного модуля накопления (![]() =20°С); 5 - сегмент приведенного модуля накопления (
=20°С); 5 - сегмент приведенного модуля накопления (![]() =20°С)
=20°С)
Рисунок B.2 - Сегменты исходного и приведенного модулей накопления
Таблица B.2 - Данные для сегментов приведенного модуля накопления
n |
|
|
|
|
|
|
| ||
1 | -1,964 8 | 7,110 2 | 6,565 7 | 6,285 4 |
2 | -1,798 2 | 7,143 6 | 6,605 5 | 6,311 3 |
3 | -1,631 5 | 7,203 3 | 6,649 3 | 6,336 7 |
4 | -1,464 8 | 7,244 3 | 6,703 3 | 6,369 9 |
5 | -1,298 2 | 7,307 1 | 6,748 6 | 6,398 6 |
6 | -1,131 5 | 7,365 8 | 6,793 6 | 6,430 3 |
7 | -0,964 9 | 7,416 3 | 6,858 1 | 6,467 5 |
8 | -0,798 2 | 7,469 3 | 6,905 4 | 6,499 5 |
9 | -0,631 5 | 7,508 2 | 6,959 1 | 6,534 6 |
10 | -0,464 8 | 7,551 6 | 7,014 1 | 6,572 |
11 | -0,298 2 | 7,6 | 7,070 2 | 6,616 6 |
12 | -0,131 5 | 7,661 | 7,128 4 | 6,663 6 |
13 | 0,035 2 | 7,727 5 | 7,191 1 | 6,713 5 |
14 | 0,201 8 | 7,787 8 | 7,250 2 | 6,767 7 |
15 | 0,368 5 | 7,836 2 | 7,309 | 6,819 7 |
16 | 0,535 2 | 7,876 8 | 7,365 3 | 6,872 8 |
17 | 0,701 8 | 7,887 2 | 7,391 2 | 6,898 6 |
18 | 0,868 5 | 7,924 6 | 7,442 6 | 6,951 |
|
1 - сегмент приведенного модуля накопления (![]() =0°С); 2 - область наложения сегментов А(
=0°С); 2 - область наложения сегментов А(![]() ,
, ![]() ); 3 - сегмент исходного модуля накопления (
); 3 - сегмент исходного модуля накопления (![]() =10°С);
=10°С);
Рисунок B.3 - Область наложения для сегментов модуля накопления при 0°С и 10°С
Точки Q и P.
Значение модуля накопления в точке Q, определяемое по формуле (A.6), равно ![]() Па.
Па.
Координата на логарифмической шкале частот: ![]() Гц.
Гц.
Значение модуля накопления в точке P, определяемое по формуле (A.7), равно ![]() Па.
Па.
Координата на логарифмической шкале частот: ![]() Гц.
Гц.
Точки U и L.
Исходя из рисунка B.3 и формулы (A.9) значение модуля накопления в точке U равно ![]() Па.
Па.
Координата точки на логарифмической шкале частот, вычисленная по формуле (A.8):
![]() Гц.
Гц.
Значение модуля накопления в точке L, вычисленное по формуле (A.11), равно ![]() Па.
Па.
Координата точки на логарифмической шкале частот, вычисленная по формуле (A.10):
![]() Гц.
Гц.
Индивидуальный фактор горизонтального сдвига ![]()
Суммы в числителе формулы (A.3) для данного примера могут быть записаны как ![]() , где
, где ![]() , и
, и ![]() , где
, где ![]() .
.
Подставляя соответствующие табличные значения, получаем ![]() и
и ![]() .
.
Далее для нахождения индивидуального фактора горизонтального сдвига между двумя сегментами подставляют полученные значения сумм в числитель формулы (A.3), что дает
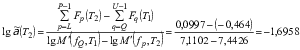 .
.
Теперь переходим к аналогичным вычислениям для второй пары приведенных сегментов с температурами (![]() ,
, ![]() )=(10°С, 20°С), выделенных цветом на рисунке B.4.
)=(10°С, 20°С), выделенных цветом на рисунке B.4.
|
1 - сегмент приведенного модуля накопления (![]() =10°С); 2 - область наложения сегментов А(
=10°С); 2 - область наложения сегментов А(![]() ,
, ![]() ); 3 - сегмент исходного модуля накопления (
); 3 - сегмент исходного модуля накопления (![]() =20°С)
=20°С)
Рисунок B.4 - Область наложения для сегментов модуля накопления при 10°С и 20°С
Точка Q: значение модуля накопления, определяемое по формуле (A.6), равно ![]() Па, координата на логарифмической шкале частот:
Па, координата на логарифмической шкале частот: ![]() Гц.
Гц.
Точка P: значение модуля накопления, определяемое по формуле (A.7), равно ![]() Па, координата на логарифмической шкале частот:
Па, координата на логарифмической шкале частот: ![]() Гц.
Гц.
Точка U: Значение модуля накопления равно ![]() , координату точки на логарифмической шкале частот рассчитывают по формуле (A.8) как линейную интерполяцию между 8-й и 9-й точками сегмента для температуры
, координату точки на логарифмической шкале частот рассчитывают по формуле (A.8) как линейную интерполяцию между 8-й и 9-й точками сегмента для температуры ![]() , т.е.
, т.е. ![]() Гц.
Гц.
Точка L: Значение модуля накопления равно ![]() , координату точки на логарифмической шкале частот рассчитывают по формуле (A.10) как линейную интерполяцию между 9-й и 10-й точками сегмента для температуры
, координату точки на логарифмической шкале частот рассчитывают по формуле (A.10) как линейную интерполяцию между 9-й и 10-й точками сегмента для температуры ![]() , т.е.
, т.е. ![]() Гц.
Гц.
Суммы для расчета индивидуальных факторов горизонтального сдвига в числителе формулы (A.3) могут быть записаны как ![]() , где
, где ![]() , и
, и ![]() , где
, где ![]() .
.
Расчет по формуле (A.3) дает значение индивидуального фактора горизонтального сдвига
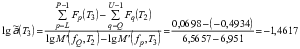 ;
;
d) для сегмента приведения, которому соответствует температура приведения ![]() , значение
, значение ![]() приводят к нулю, т.е.
приводят к нулю, т.е. ![]() =0. Это означает, что сегмент приведения останется в своем первоначальном положении;
=0. Это означает, что сегмент приведения останется в своем первоначальном положении;
e) соответствующим образом корректируют окончательные значения факторов горизонтального сдвига для сегментов с температурами выше температуры приведения, ![]() >
>![]() , с использованием формулы (A.12).
, с использованием формулы (A.12).
В рассматриваемом примере есть только один сегмент с температурой, превышающей температуру приведения, ![]() >
>![]() . Для него окончательное значение фактора горизонтального сдвига равно
. Для него окончательное значение фактора горизонтального сдвига равно
![]() ;
;
f) для сегментов с температурами ниже температуры приведения, ![]() <
<![]() , окончательные значения факторов горизонтального сдвига получают по формуле (A.13).
, окончательные значения факторов горизонтального сдвига получают по формуле (A.13).
В рассматриваемом примере есть только один сегмент с температурой ниже температуры приведения, ![]() <
<![]() . Для него окончательное значение фактора горизонтального сдвига равно
. Для него окончательное значение фактора горизонтального сдвига равно ![]() ;
;
g) для каждого сегмента получают "приведенную" частоту ее преобразованием к ![]() , k=1,..., K.
, k=1,..., K.
Значения приведенных частот даны в таблице B.3.
Таблица B.3 - Значения приведенных частот
n |
|
|
|
1 | -0,269 | -1,964 8 | -3,426 5 |
2 | -0,102 4 | -1,798 2 | -3,259 9 |
3 | 0,064 3 | -1,631 5 | -3,093 2 |
4 | 0,231 | -1,464 8 | -2,926 5 |
5 | 0,397 6 | -1,298 2 | -2,759 9 |
6 | 0,564 3 | -1,131 5 | -2,593 2 |
7 | 0,730 9 | -0,964 9 | -2,426 6 |
8 | 0,897 6 | -0,798 2 | -2,259 9 |
9 | 1,064 3 | -0,631 5 | -2,093 2 |
10 | 1,231 | -0,464 8 | -1,926 5 |
11 | 1,397 6 | -0,298 2 | -1,759 9 |
12 | 1,564 3 | -0,131 5 | -1,593 2 |
13 | 1,731 | 0,035 2 | -1,426 5 |
14 | 1,897 6 | 0,201 8 | -1,259 9 |
15 | 2,064 3 | 0,368 5 | -1,093 2 |
16 | 2,231 | 0,535 2 | -0,926 5 |
17 | 2,397 6 | 0,701 8 | -0,759 9 |
18 | 2,564 3 | 0,868 5 | -0,593 2 |
h) откладывают на графике в логарифмическом масштабе (с основанием 10) по обеим осям сегменты приведенных модулей накопления относительно приведенных частот, которые в совокупности составляют сглаженную обобщенную кривую.
График обобщенной кривой, построенный для данного примера, показан на рисунке B.5.
|
1 - сегмент приведенного модуля накопления для температуры ![]() =0°С, отображенный относительно приведенной частоты; 2 - исходный сегмент модуля накопления для температуры
=0°С, отображенный относительно приведенной частоты; 2 - исходный сегмент модуля накопления для температуры ![]() =10°С; 3 - сегмент приведенного модуля накопления для температуры
=10°С; 3 - сегмент приведенного модуля накопления для температуры ![]() =20°С, отображенный относительно приведенной частоты
=20°С, отображенный относительно приведенной частоты
Рисунок B.5 - Обобщенная кривая для температуры приведения 10°С
Приложение C
(справочное)
Листинг компьютерной программы
Разработан макрос на ![]() , демонстрирующий изложенную в 4.3.2 методологию аналитического расчета фактора горизонтального сдвига. Макрос доступен по ссылке http://standards.iso.org/iso/18437/-6/ed-1/en и допускает свободную загрузку и использование. Этот физический файл следует рассматривать как дополнение к настоящему стандарту.
, демонстрирующий изложенную в 4.3.2 методологию аналитического расчета фактора горизонтального сдвига. Макрос доступен по ссылке http://standards.iso.org/iso/18437/-6/ed-1/en и допускает свободную загрузку и использование. Этот физический файл следует рассматривать как дополнение к настоящему стандарту.
Все копии указанного файла (далее - Файл) и производные от него должны сопровождаться указанием о защите авторских прав и предупреждением следующего вида:
"![]() ISO 2017 - All rights reserved
ISO 2017 - All rights reserved
Permission is hereby granted, free of charge in perpetuity, to any person obtaining a copy of the File, to use, copy, modify, merge and distribute free of charge, copies of the File for the purposes of developing, implementing, installing and using software based on the File, and to permit persons to whom the File is furnished to do so, subject to the following conditions:
THE FILE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NON-INFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE FILE OR THE USE OR OTHER DEALINGS IN THE FILE."
("![]() ИСО 2017 - Все права сохраняются
ИСО 2017 - Все права сохраняются
Настоящим дается разрешение любому лицу на свободное получение копии настоящего Файла, его использование, копирование, модифицирование, слияние и распространение в целях разработки, применения и инсталляции программного обеспечения, основанного на данном Файле, а также разрешает указанное лицам, которым Файл предоставляется, при условии соблюдения следующего:
ФАЙЛ ПРЕДОСТАВЛЕН В ТОМ СОСТОЯНИИ, КАКОВ ОН ЕСТЬ, БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ, ЯВНО ВЫРАЖЕННЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ВКЛЮЧАЯ, НО НЕ ОГРАНИЧИВАЯСЬ ГАРАНТИЯМИ ПРИГОДНОСТИ ДЛЯ КОММЕРЧЕСКОГО ИСПОЛЬЗОВАНИЯ И ИНЫХ ЦЕЛЕЙ, И БЕЗ ОТВЕТСТВЕННОСТИ ЗА НАРУШЕНИЕ ЧЬИХ-ЛИБО АВТОРСКИХ ПРАВ. АВТОРЫ ИЛИ ВЛАДЕЛЬЦЫ АВТОРСКИХ ПРАВ НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ НЕ НЕСУТ ОТВЕТСТВЕННОСТИ ЗА ЧЬИ-ЛИБО ТРЕБОВАНИЯ, ЗА ПОНЕСЕННЫЙ УЩЕРБ ИЛИ В СВЯЗИ С ИНЫМИ ОБЯЗАТЕЛЬСТВАМИ, ВОЗНИКШИМИ ВСЛЕДСТВИЕ ИСПОЛНЕНИЯ КОНТРАКТА, НАРУШЕНИЙ ПРАВ ИЛИ ПО ИНОЙ ПРИЧИНЕ, СВЯЗАННЫЕ С ИСПОЛЬЗОВАНИЕМ ФАЙЛА ИЛИ СОДЕРЖАЩИХСЯ В НЕМ ЭЛЕМЕНТОВ ИЛИ ИНФОРМАЦИИ.")
Кроме того, любая модификация копии Файла должна сопровождаться извещением:
"THIS FILE HAS BEEN MODIFIED FROM THE FILE DEFINED IN ISO 18437-6, AND SHOULD NOT BE INTERPRETED AS COMPLYING WITH THAT DOCUMENT".
("Настоящий файл модифицирован по сравнению с файлом, определенным в ИСО 18437-6, и его не следует рассматривать в качестве соответствующего этому стандарту".)
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным и межгосударственным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального, межгосударственного стандарта |
ISO 18437-1 | IDT | ГОСТ Р ИСО 18437-1-2014 "Вибрация и удар. Определение динамических механических свойств вязкоупругих материалов. Часть 1. Общие принципы" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | ISO 472, | Plastics - Vocabulary |
[2] | ISO 4664-1, | Rubber, vulcanized or thermoplastic - Determination of dynamic properties - Part 1: General guidance |
[3] | ISO 6721-4, | Plastics - Determination of dynamic mechanical properties - Part 4: Tensile vibration - Non-resonance method |
[4] | ISO 6721-5, | Plastics - Determination of dynamic mechanical properties - Part 5: Flexural vibration - Non-resonance method |
[5] | ISO 6721-6, | Plastics - Determination of dynamic mechanical properties - Part 6: Shear vibration - Non-resonance method |
[6] | ISO 6721-7, | Plastics - Determination of dynamic mechanical properties - Part 7: Torsional vibration - Non-resonance method |
[7] | ISO 6721-12, | Plastics - Determination of dynamic mechanical properties - Part 12: Compressive vibration - Non-resonance method |
[8] | ISO 10112, | Damping materials - Graphical presentation of the complex modulus |
[9] | ISO 18437-2, | Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 2: Resonance method |
[10] | ISO 18437-3, | Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 3: Cantilever shear beam method |
[11] | ISO 18437-4, | Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 4: Dynamic stiffness method |
[12] | ISO 18437-5, | Mechanical vibration and shock - Characterization of the dynamic mechanical properties of visco-elastic materials - Part 5: Poisson ratio based on comparison between measurements and finite element analysis |
[13] | FERRY J.D. Visco-elastic properties of polymers. John Wiley&Sons, New York, Third Edition, 1980 | |
[14] | DEALY J. and PLAZEK D. Time-Temperature Superposition - A User Guide. Rheology Bulletin. 2009, 78 (2) pp.16-31 | |
[15] | MADIGOSKY W. et al. A method for modelling polymer viscoelastic data and the temperature shift function. J. Acoust. Soc. Am. 2006, 119 (6) pp.3760-3765 | |
[16] | GERGESOVA M. et al. The closed form t-T-P shifting (CFS) algorithm. J. Rheol. (N.Y.N.Y). 2011, 55 (1) pp.1-17 | |
[17] | GERGESOVA M. et al. Closed Form Solution for Horizontal and Vertical Shifting of Viscoelastic Material Functions in Frequency Domain. Rheologica Acta, 2016, ISSN: 0035-4511 (Print) 1435-1528 (Online) | |
[18] | DAO K.C. and DICKEN D.J. Fatigue failure mechanisms in polymers. Polym. Eng. Sci. 1987, 27 (4) pp.271-276 | |
[19] | MENARD K.P. Dynamic mechanical analysis: A practical introduction. CRC Press, Florida, 1999 | |
УДК 534.322.3.08:006.354 | ОКС 17.160 | ||
Ключевые слова: вязкоупругие материалы, термореологически простые материалы, модуль упругости, модуль накопления, модуль потерь, температурно-временная суперпозиция, обобщенная кривая | |||
Электронный текст документа
и сверен по:
М.: ФГБУ "РСТ", 2021