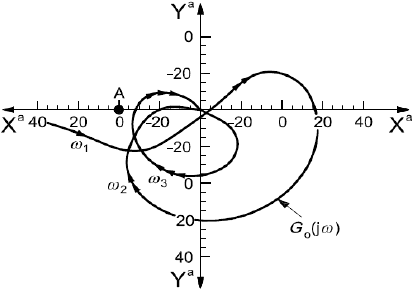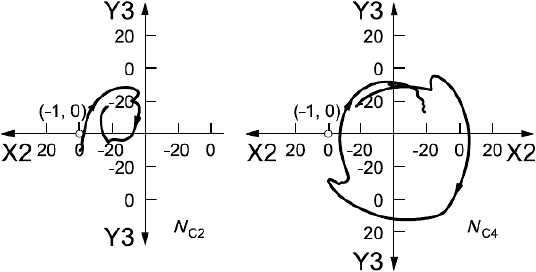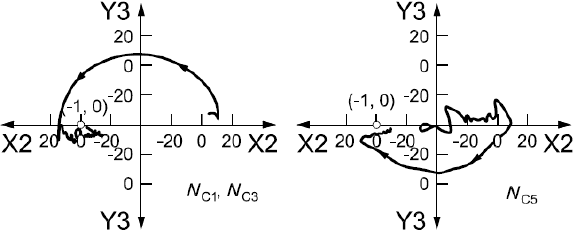ГОСТ Р ИСО 14839-3-2013 Вибрация. Вибрация машин вращательного действия с активными магнитными подшипниками. Часть 3. Определение запаса устойчивости

ГОСТ Р ИСО 14839-3-2013

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Вибрация

ВИБРАЦИЯ МАШИН ВРАЩАТЕЛЬНОГО ДЕЙСТВИЯ С АКТИВНЫМИ МАГНИТНЫМИ ПОДШИПНИКАМИ

Часть 3

Определение запаса устойчивости

Mechanical vibration. Vibration of rotating machinery equipped with active magnetic bearings. Part 3. Evaluation of stability margin

ОКС 17.160

Дата введения 2014-09-01

Предисловие

1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 183 "Вибрация, удар и контроль технического состояния"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 22 ноября 2013 г. N 1660-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 14839-3:2006* "Вибрация. Вибрация машин вращательного действия с активными магнитными подшипниками. Часть 3. Определение запаса устойчивости" (ISO 14839-3:2006 "Mechanical vibration - Vibration of rotating machinery equipped with active magnetic bearings - Part 3: Evaluation of stability margin", IDT).

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

6 ПЕРЕИЗДАНИЕ. Сентябрь 2019 г.

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Введение

В то время как пассивные опоры, такие как подшипники качения или скольжения, являются устойчивыми системами, магнитным подшипникам принципиально присуща неустойчивость поведения вследствие их отрицательной жесткости, обусловленной действием статических магнитных сил. Для обеспечения положительных значений жесткости и демпфирования и, соответственно, устойчивого равновесного вращения ротора в магнитных подшипниках вводят отрицательную обратную связь.

Для надежной и безопасной работы ротора в активных магнитных подшипниках помимо контроля вибрации (см. ИСО 14839-2) необходимо также контролировать запас устойчивости системы в соответствии с требованиями настоящего стандарта. Применение стандарта позволяет:

a) обеспечить заинтересованные стороны (поставщиков и пользователей, технических специалистов и пр.) информацией о работе системы;

b) определить методы оценки запаса устойчивости, используемые при составлении договоров, приемке машин и их техническом обслуживании;

c) установить общие стандарты обеспечения устойчивости при разработке и эксплуатации машин с активными магнитными подшипниками.

1 Область применения

Настоящий стандарт устанавливает требования к обеспечению устойчивой работы машин вращательного действия с активными магнитными подшипниками (АМП). Для оценки устойчивости вращения ротора машины введен показатель запаса устойчивости и приведен способ его измерения.

Настоящий стандарт распространяется на промышленные машины номинальной мощностью более 15 кВт с жесткими и гибкими роторами. Он не распространяется на машины с роторами малых размеров (шпиндели, роторы турбомолекулярных насосов и т.п.).

Оценка устойчивости осуществляется в нормальных установившихся режимах работы машины при испытаниях у изготовителя или на месте эксплуатации. Оценка запаса устойчивости при испытаниях у изготовителя является обязательным условием поставки машины. Оценка на месте эксплуатации осуществляется в зависимости от соглашения между поставщиком и пользователем.

В настоящем стандарте не рассматриваются резонансные колебания ротора, возникающие при прохождении критических частот вращения. Методы снижения вибрации на критических частотах вращения рассматриваются в ИСО 10814.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт:

ISO 10814, Mechanical vibration - Susceptibility and sensitivity of machines to unbalance (Вибрация. Подверженность и чувствительность машин к дисбалансу)

3 Предварительные исследования

Прежде всего необходимо исследовать характеристики демпфирования и устойчивости системы "ротор - АМП" для всех возможных режимов ее работы. Это исследование состоит из двух частей.

Во-первых, следует оценить поведение системы (через ее модальные чувствительности или модальные коэффициенты демпфирования) при разгоне ротора. Указанные характеристики определяют для всех собственных частот во всем диапазоне рабочих частот вращения ротора. Собственные частоты оценивают по вибрационному отклику системы в окрестностях критических частот вращения.

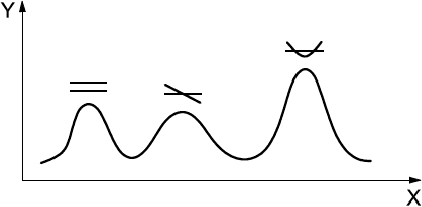
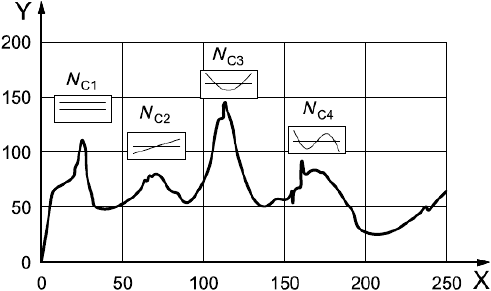
В примере, показанном на рисунке 1, кривая изменения амплитуды вибрации, обусловленной дисбалансом ротора, имеет три пика, соответствующих двум модам жесткого ротора и первой изгибной моде гибкого ротора. Ширина каждого пика определяется модальным коэффициентом демпфирования или добротностью. Требования к демпфированию системы "ротор - АМП" на резонансе устанавливает ИСО 10814, и в настоящем стандарте они не рассматриваются.

- частота вращения ротора; - амплитуда вибрации

Рисунок 1 - Оценка модального демпфирования

Задачей второй части исследования является определение способности системы управления обеспечить устойчивость поведения ротора на номинальной частоте вращения. При решении этой задачи определяются допустимые границы изменений в системе "ротор - АМП" (например, изменение коэффициента усиления из-за смещения датчика при изменении температуры) и сил, действующих на ротор (например, обусловленных дисбалансом или приводящих к появлению высших гармоник). Существуют разные характеристики устойчивости (по модулю, по фазе, по диаграмме Найквиста, по функции чувствительности и т.п.), на основе которых может быть определен запас устойчивости системы.

4 Принцип работы систем с обратной связью

4.1 Передаточные функции замкнутой и разомкнутой систем управления

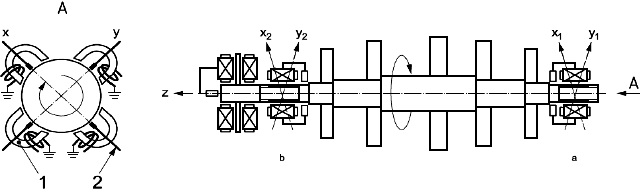
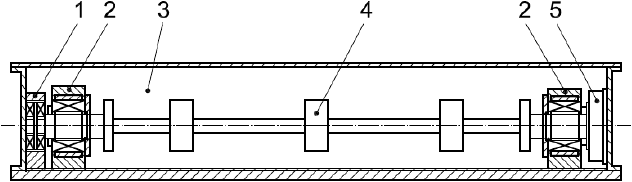
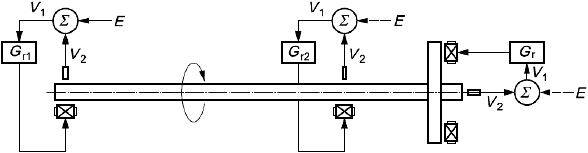
Активные магнитные подшипники поддерживают ротор без механического контакта с ним, как показано на рисунке 2. Обычно они расположены по обоим концам вала (стороны 1 и 2), включают в себя датчик перемещения и страхующий подшипник качения. Радиальные оси управления на стороне 1 обозначены и , на стороне 2 - и . Ось управления, совпадающая с осью вала, обозначена . Обычно управление системой "ротор - АМП" осуществляют по указанным пяти осям. Пример системы управления показан на рисунке 3.

Из рисунков 2 и 3 видно, что каждый датчик перемещения контролирует смещение цапфы вала в одном радиальном направлении вблизи подшипниковой опоры. Сигнал с датчика обеспечивает обратную связь в системе управления. Данные об отклонении положения ротора от центра АМП поступают в контроллер АМП. Выходной сигнал контроллера управляет работой усилителей мощности, т.е. током в катушках управления и в конечном счете магнитной силой, обеспечивающей левитацию ротора. Таким образом, система "ротор - АМП", как правило, представляет собой систему с обратной связью.

Замкнутую цепь управления рисунка 3 можно упрощенно описать (см. рисунок 4) через передаточную функцию цепи обратной связи и передаточную функцию прямого управления положением ротора. В некоторой точке цепи обратной связи можно ввести гармонический или случайный сигнал возбуждения и обозначить сигналы до и после этой точки как и соответственно. Тогда отношение изображений этих сигналов в частотной области даст передаточную функцию разомкнутой цепи (, - угловая частота вращения ротора):

1 - АМП; 2 - датчик перемещения; - сторона 1; - сторона 2

Рисунок 2 - Система "ротор - АМП"

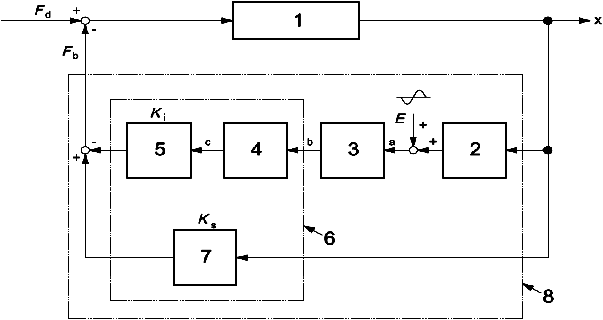
1 - ротор; 2 - датчик перемещения (В/м); 3 - контроллер АМП (В/В); 4 - усилитель мощности (А/В); 5 - электромагнит (Н/А); 6 - исполнительная часть АМП; 7 - отрицательная позиционная жесткость (Н/м); 8 - АМП; - сигнал датчика; - сигнал управления; - управляющий ток; - сигнал возбуждения; - магнитная сила, Н; - возмущающая сила, Н; - токовая жесткость (Н/А); - отрицательная позиционная жесткость (Н/м); - перемещение

Рисунок 3 - Блок-схема системы управления положением ротора

. (1)

Такое определение передаточной функции разомкнутой цепи не является общеупотребительным. Большинство систем "ротор - АМП" имеют несколько цепей управления (как правило, по числу осей управления). Работу системы анализируют в условиях, когда все эти цепи замкнуты, и передаточную функцию разомкнутой цепи для данной оси управления определяют по формуле (1) для этих же условий. Приведенное определение отличается от обычного определения элемента матрицы передаточной функции разомкнутой системы управления, получаемого в предположении, что участок цепи управления от ротора до контроллера разомкнут. Более подробно этот вопрос рассмотрен в приложении Е.

Передаточную функцию замкнутой цепи определяют по формуле

. (2)

Связь передаточных функций для разомкнутой и замкнутой цепей описывается формулой (для упрощения записи символ опущен)

или . (3)

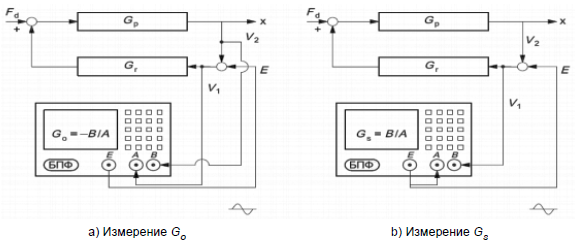
Передаточные функции и обычно получают, используя двухканальный БПФ-анализатор. Схема измерений показана на рисунке 4.

4.2 Диаграмма Боде

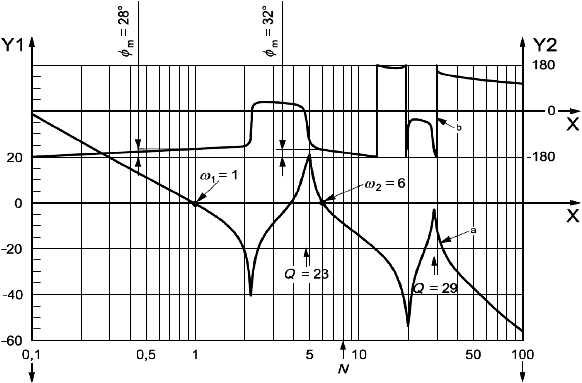
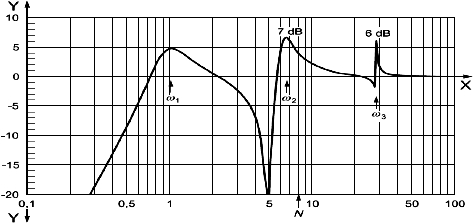
После измерения передаточной функции разомкнутой цепи (см. рисунок 5) она может быть преобразована в передаточную функцию замкнутой цепи (см. рисунок 6). На рисунках 5 и 6 показан пример диаграммы Боде, представляющей собой совокупность фазочастотной характеристики и амплитудно-частотной характеристики, выполненной в логарифмическом масштабе. В данном примере частота вращения ротора рассматривается как безразмерная величина и номинальная частота вращения =8. Таким образом, резонансные пики передаточной функции на частотах =1 и =6 попадают в рабочий диапазон частот вращения ротора, и острота (добротность ) этих пиков должна быть оценена в соответствии с ИСО 10814. В настоящем стандарте рассматриваются запасы устойчивости для всех пиков передаточной функции (в данном примере это =1, =6 и =30).

- передаточная функция цепи прямой связи управления положения ротора; - передаточная функция цепи обратной связи управления; - внешний переменный сигнал; - передаточная функция разомкнутой цепи; - функция чувствительности

Рисунок 4 - Двухканальная схема измерения и

- частота вращения ротора (безразмерная величина); - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -40 дБ =0,01; -20 дБ =0,1; 0 дБ =1; 20 дБ =10; 40 дБ =100); - фаза , в градусах; - номинальная частота вращения; - модуль передаточной функции; - фаза передаточной функции

Рисунок 5 - Передаточная функция разомкнутой цепи

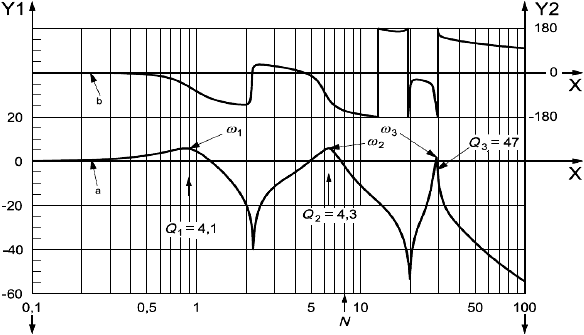
- частота вращения ротора (безразмерная величина); - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -40 дБ =0,01; -20 дБ =0,1; 0 дБ =1; 20 дБ =10; 40 дБ =100); - фаза , в градусах; - номинальная частота вращения; - модуль передаточной функции; - фаза передаточной функции

Рисунок 6 - Передаточная функция замкнутой цепи

4.3 Диаграмма Найквиста передаточной функции разомкнутой цепи

Кроме обычного представления в виде диаграммы Боде (см. рисунок 5) передаточная функция разомкнутой цепи может быть изображена на комплексной плоскости в виде диаграммы Найквиста, где каждой частоте вращения соответствует радиус-вектор передаточной функции, модуль которого равен модулю передаточной функции , а угол - ее фазе (см. рисунок 7, на котором модуль радиус-вектора дан в логарифмическом масштабе). Характеристическое уравнение системы имеет вид =0, а расстояние от кривой передаточной функции до критической точки с координатами (-1, 0) прямо зависит от демпфирования в системе и ее относительной устойчивости. В общем случае чем больше расстояние от кривой до точки , тем больше запас устойчивости системы.

________________

Чаще координаты этой точки указывают в виде (-1, j0), подчеркивая этим, что вторая координата представляет собой мнимую часть комплексного числа.

a) Диаграмма Найквиста, включающая частоты , и

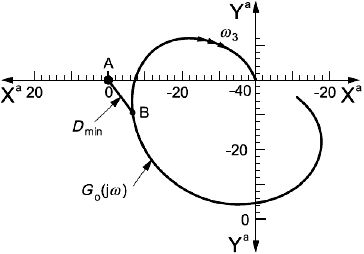
b) Диаграмма Найквиста в районе частоты (увеличенный масштаб)

________________

Отметки шкалы соответствуют следующим абсолютным значениям: -40 дБ =0,01; -20 дБ =0,1; 0 дБ =1; 20 дБ =10; 40 дБ =100.

Рисунок 7 - Диаграмма Найквиста передаточной функции разомкнутой цепи

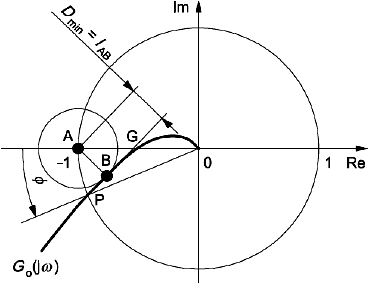
На рисунке 8 та же диаграмма Найквиста показана в линейном масштабе в области критической точки (-1, 0). Наименьшее расстояние от кривой передаточной функции до точки обозначено , где - радиус окружности с центром в точке , имеющей общую касательную с кривой в точке ее максимального приближения к точке . Для примера, показанного на рисунке 8, запас устойчивости по модулю определяется как расстояние между точкой и точкой пересечения касательной с действительной осью координат, а запас устойчивости по фазе - как угол между действительной осью координат и лучом, проходящим из центра координат в точку пересечения кривой и окружности единичного радиуса с центром в начале координат. В данном примере и , поэтому критерий устойчивости на основе минимального расстояния будет более строгим, чем критерии устойчивости по модулю и по фазе.

Примечание - Можно показать, что критерий на основе минимального расстояния от критической точки до кривой передаточной функции будет всегда более строгим, чем критерии устойчивости по модулю и по фазе.

Рисунок 8 - Диаграмма Найквиста передаточной функции разомкнутой цепи в линейном масштабе

4.4 Функция чувствительности

При анализе диаграммы Найквиста основное внимание уделяют определению минимального расстояния между кривой передаточной функции и критической точкой (-1, 0) или, другими словами, выяснению того, насколько малым может быть значение модуля функции . Тот же вопрос может быть переформулирован следующим образом: насколько большим может быть значение модуля функции , обратной , т.е.

. (4)

Функцию называют функцией чувствительности. Диаграмма Боде для функции чувствительности показана на рисунке 9.

- частота вращения ротора (безразмерная величина); - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; -10 дБ =0,315; 0 дБ =1; 1 дБ =3,15); - номинальная частота вращения

Рисунок 9 - Диаграмма Боде функции чувствительности

Существует две причины, по которым диаграммой Боде для функции чувствительности пользоваться удобнее, чем диаграммой Найквиста для передаточной функции. Во-первых, определить максимальное значение функции чувствительности по диаграмме Боде проще, чем определить минимальное расстояние по диаграмме Найквиста. Во-вторых, измерение функции чувствительности является простым. Как следует из рисунка 4 b), для измерения функции чувствительности достаточно в некоторую точку цепи обратной связи ввести сигнал возбуждения и измерить сигнал отклика непосредственно за этой точкой. Тогда функцию чувствительности можно рассчитать по формуле

. (5)

5 Измерения

5.1 Измерения передаточных функций

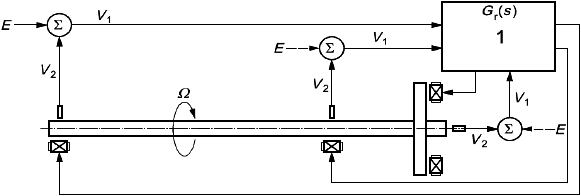
На первом этапе оценки запаса устойчивости системы "ротор - АМП" проводят измерения одной из передаточных функций, или , для каждой цепи обратной связи. На рисунке 10 показана общая схема контроллера, куда поступают все управляющие сигналы перемещения по пяти осям управления и выходной сигнал которого определяет магнитную силу, действующую в АМП.

Примечание - Схемы конкретных реализаций контроллеров представлены в приложении А.

1 - центральное процессорное устройство (ЦПУ)

Рисунок 10 - Общая схема контроллера АМП

На рисунке 10 одна из точек выбрана в качестве точки возбуждения . Измерения передаточной функции разомкнутой цепи проводят в соответствии с формулой (1) при отсутствии подаваемых сигналов в других входных точках. После измерения передаточной функции ее преобразуют в в соответствии с формулой (4).

Другим вариантом является непосредственное измерение в соответствии с формулой (5).

5.2 Определение показателя запаса устойчивости

При измерении передаточной функции разомкнутой цепи управления для данной контрольной оси цепи управления для всех контрольных осей должны быть замкнуты. Измерения повторяют последовательно для всех контрольных осей. Полученные в результате измерений передаточные функции разомкнутой цепи преобразуют в функции чувствительности. Другим вариантом является непосредственное измерение функций чувствительности.

Если число осей управления равно пяти, то должно быть получено пять функций чувствительности.

Измерения проводят при неподвижном роторе или при вращении ротора на номинальной частоте вращения. Передаточную функцию разомкнутой цепи (или функцию чувствительности) определяют в диапазоне частот от нуля до некоторой максимальной частоты.

Верхнюю границу диапазона частот определения передаточной функции устанавливать в принципе не требуется, поскольку модуль передаточной функции разомкнутой цепи для всех реальных систем уменьшается с ростом частоты (см. рисунок 5), так что, начиная с некоторой частоты, функция чувствительности обращается в нуль, а расстояние от кривой передаточной функции до критической точки - в единицу (см. рисунки 7 и 9). Это означает, что на очень высоких частотах поведение АМП всегда устойчиво. Однако в целях практических измерений обработку сигнала проводят в некоторой конечной полосе частот. В настоящем стандарте за верхнюю границу диапазона частот измерений , кГц, принимают максимальное из следующих значений:

a) утроенная номинальная частота вращения, обозначаемая "3";

b) 2 кГц,

т.е.

. (6)

В цифровых системах управления максимальная частота не должна превышать половину частоты выборки.

На основе измеренных функций чувствительности для каждой контрольной оси в диапазоне частот 0, , рассчитывают значение показателя запаса устойчивости по формуле

, (7)

где - номер контрольной оси.

Из формулы (7) следует, что общая оценка устойчивости системы определяется через "наихудшую" передаточную функцию среди всех пяти передаточных функций системы.

5.3 Условия измерений

Поведение системы "ротор - АМП" должно быть устойчивым к обычным возмущениям и ожидаемым возможным изменениям рабочих условий. Проверку поведения системы осуществляют на стендах изготовителя перед поставкой машины. Заказчик также может провести соответствующие испытания в условиях эксплуатации системы. Измерения выполняют в следующих условиях:

a) при неподвижном роторе - на стенде изготовителя;

b) при максимальной номинальной частоте вращения ротора или при номинальной нагрузке - на стенде изготовителя или в условиях эксплуатации.

Во втором случае место проведения испытаний должно быть согласовано между поставщиком и заказчиком машины.

6 Оценка запаса устойчивости

6.1 Критерий I

В таблице 1 приведены границы зон, применяемых при оценке запаса устойчивости работы системы "ротор - АМП". Определения зон сформулированы таким образом, чтобы быть максимально приближенными к определениям зон вибрационного состояния по ИСО 7919-1:

- зона A. В эту зону попадают пиковые значения функции чувствительности новых машин, вводимых в эксплуатацию;

- зона B. В эту зону попадают пиковые значения функции чувствительности машин, которые считают годными к долговременной работе без каких-либо ограничений;

- зона C. В эту зону попадают пиковые значения функции чувствительности машин, которые считают непригодными к долговременной работе (обычно работу таких машин допускают в течение ограниченного времени, пока не появится возможность проведения корректирующих мероприятий);

- зона D. Попадание пиковых значений функции чувствительности в эту зону обычно рассматривают как свидетельство опасности возможных повреждений машины.

Таблица 1 - Границы зон запаса устойчивости

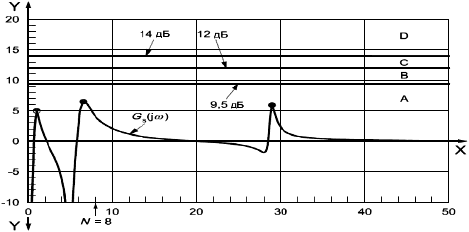
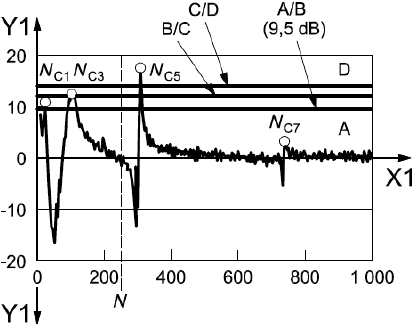
Пример оценки запаса устойчивости системы "ротор - АМП" приведен на рисунке 11, содержащем диаграмму Боде (см. рисунок 9) на фоне границ зон запаса устойчивости, установленных в таблице 1. Из рисунка 11 следует, что все пиковые значения функции чувствительности попадают в зону А.

6.2 Критерий II

Этот критерий основан на периодических измерениях запасов устойчивости и оценке их отклонения от средних значений. Наличие существенных отклонений может потребовать принятия мер даже в том случае, когда граница зоны C по критерию I еще не достигнута. Изменения запаса устойчивости, будь они скачкообразными или постепенно нарастающими во времени, могут свидетельствовать о зарождении повреждений или других неполадках.

Критерий II применяют для установившегося режима работы машины. При этом важно, чтобы подлежащие сравнению результаты измерений были получены приблизительно в одних и тех же условиях для одного и того же режима. Под существенным отклонением рекомендуется понимать изменение на величину, превышающую 25% верхней границы зоны B (см. таблицу 1). Превышение установленного критерия требует выяснения причины столь существенных изменений и принятия соответствующего решения.

- частота вращения ротора (безразмерная величина); - модуль функции чувствительности и границы зон устойчивости, дБ; - номинальная частота вращения; A, B, C, D - зоны устойчивости

Рисунок 11 - Оценка запаса устойчивости по

Приложение A
(справочное)

Примеры оценки запаса устойчивости. Пример 1

А.1 Испытуемый ротор

Испытательная установка и испытуемый ротор показаны на рисунках А.1 и А.2. Характеристики ротора приведены в таблице А.1.

Собственные моды и собственные частоты свободных колебаний ротора показаны на рисунке А.3.

1 - осевой АМП; 2 - радиальный АМП; 3 - вакуумная камера; 4 - ротор; 5 - двигатель

Рисунок А.1 - Испытательная установка

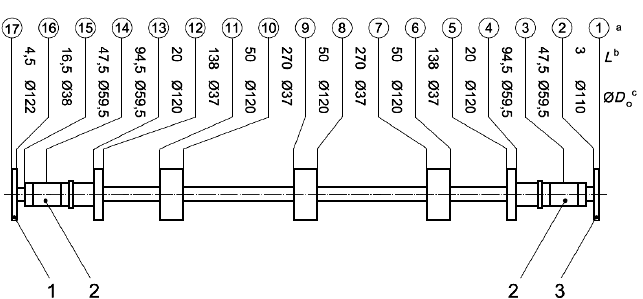
В миллиметрах

1 - ротор в осевом АМП; 2 - ротор в радиальном АМП; 3 - ротор двигателя; - точки узлов колебаний ротора; - длина элемента ротора ; - диаметр элемента ротора

Рисунок А.2 - Конструкция гибкого ротора

Таблица А.1 - Характеристики ротора

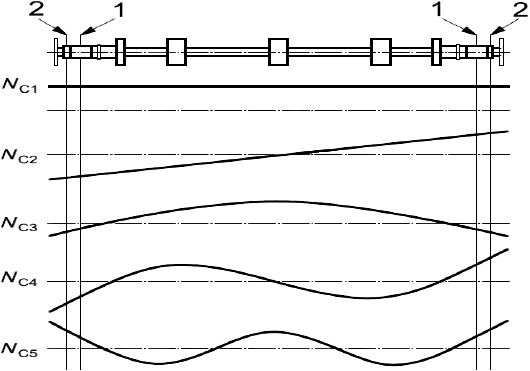
1 - плоскость АМП; 2 - плоскость датчика перемещения

Рисунок А.3 - Собственные моды и собственные частоты гибкого ротора

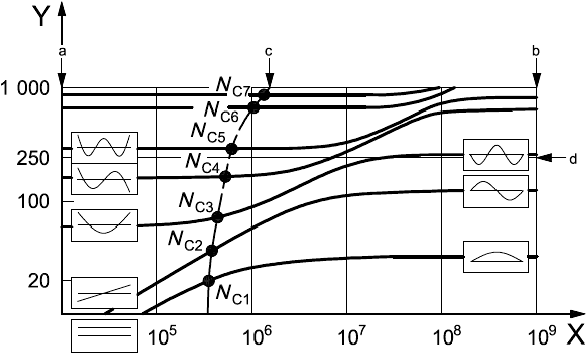
На рисунке А.4 изображен портрет критических частот ротора. Пересечения кривых собственных частот и кривой жесткости АМП дают значения собственных частот . В диапазон рабочих скоростей вращения машины (до 250 с) попадают четыре критических частоты вращения: и , соответствующие формам колебаний жесткого ротора, и , соответствующие модам изгибных колебаний гибкого ротора.

- жесткость, Н/м; - частота, Гц; - свободные концы ротора; - защемленные концы ротора; - жесткость АМП; - номинальная частота вращения

Рисунок А.4 - Портрет критических частот гибкого ротора

А.2 Контроллеры АМП

Для управления по разным осям используются контроллеры двух типов, основой каждого из которых является ПИД-регулятор.

Функциональная схема контроллера типа 1 включает в себя последовательное соединение ПИД-регулятора (передаточная функция ) и фильтра коррекции "горба" фазовой характеристики в области высоких частот [6] (передаточная функция ). Таким образом, передаточная функция контроллера имеет вид . Данный контроллер осуществляет децентрализованное управление осевым движением ротора (см. рисунок А.5). Диаграмма Боде, используемая для оценки запаса устойчивости, показана на рисунке А.6.

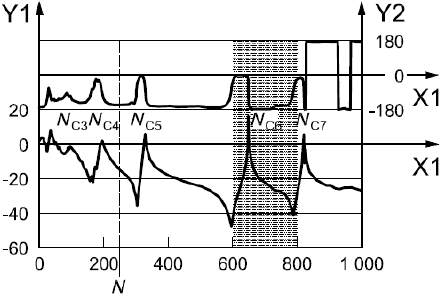
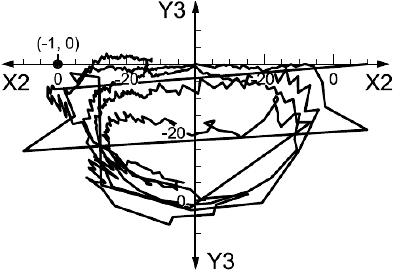
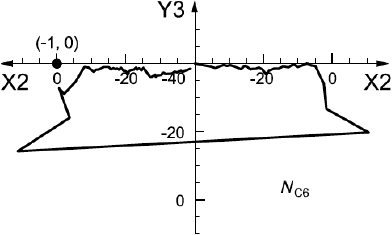
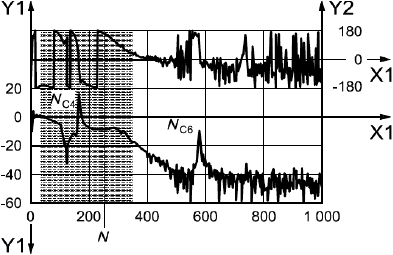
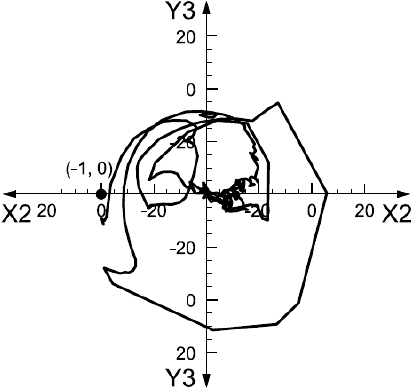
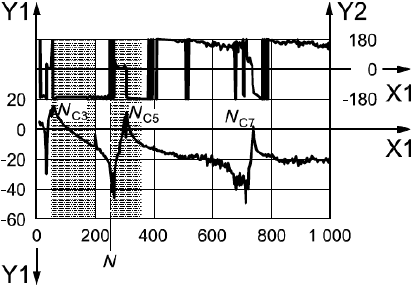
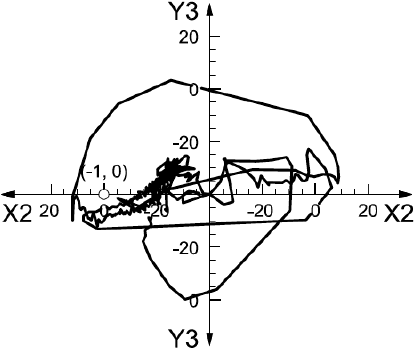
Диаграмма Боде передаточной функции разомкнутой цепи при неподвижном роторе измерена, как показано на рисунке А.6 a), с помощью двухканального БПФ-анализатора. Эта передаточная функция изображена на рисунке А.6 b) в виде диаграммы Найквиста. На рисунке А.6 c) показан участок диаграммы Найквиста в области критической частоты , равной 645 Гц [на рисунке А.6 а) данная область показана затенением]. В этом месте кривая передаточной функции близко подходит к критической точке (-1, 0), поэтому запас устойчивости системы невелик.

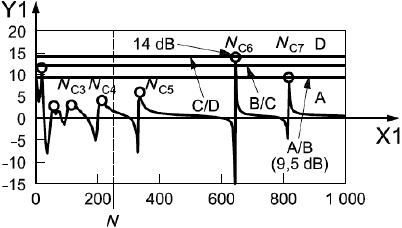
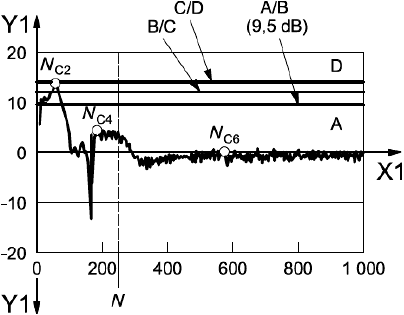
Те же результаты измерений были преобразованы в функцию чувствительности , диаграмма Боде которой приведена на рисунке А.6 d). Пиковое значение модуля функции чувствительности равно приблизительно 14 дБ, что также свидетельствует о малом запасе устойчивости (пиковое значение функции чувствительности попадает на границу зоны D).

Рисунок А.5 - Раздельное управление АМП

a) Диаграмма Боде передаточной функции разомкнутой цепи

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с

Рисунок А.6 - Оценка запаса устойчивости системы "ротор - АМП"

b) Диаграмма Найквиста передаточной функции разомкнутой цепи

с) Диаграмма Найквиста в диапазоне частот от 600 до 800 Гц

- действительная часть передаточной функции, дБ; - мнимая часть передаточной функции, дБ;

Рисунок А.6 (продолжение)

d) Функция чувствительности

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с; А, В, С, D - зоны устойчивости (см. 6.1)

Рисунок А.6 (окончание)

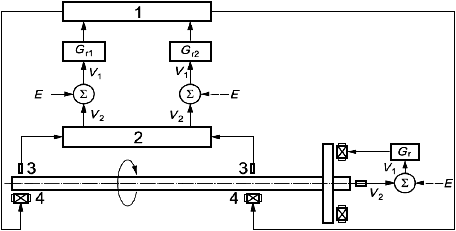
Контроллер типа 2 обеспечивает многосвязное управление (MIMO-технология) по радиальным осям двух АМП с передаточными функциями и , причем , , где - передаточная функция режекторного фильтра, а - передаточная функция фазосдвигающего фильтра (см. рисунок А.7). При этом подавляет усиление "симметричных" мод (, , , …), а - "кососимметричных" мод (, , , …).

Диаграммы Боде, используемые для оценки запаса устойчивости, показаны на рисунках А.8 и А.9 для "кососимметричных" и "симметричных" мод соответственно.

Как и в предыдущем случае, проведены измерения передаточной функции разомкнутой цепи [см. рисунки А.8 a), А.9 a)], построены диаграммы Найквиста [см. рисунки А.8 b), c), А.9 b), c)] и функции чувствительности [см. рисунки А.8 d), А.9 d)]. Как видно, кривая передаточной функции для "кососимметричной" моды находится значительно дальше от критической точки, а пики функции чувствительности ниже, за исключением пика для моды [см. рисунок А.8 d)], в то время как соответствующая кривая для "симметричных" мод близка к критической точке, а пик функции чувствительности на частоте 300 Гц высок [см. рисунок А.9 d)]. Управление "кососимметричными" модами сохраняет устойчивость системы в пределах зоны C, тогда как для "симметричных" мод значение функции чувствительности попадает в зону D.

1 - схема объединения сигналов; 2 - схема разделения сигналов; 3 - датчик перемещения; 4 - АМП

Рисунок А.7 - Многосвязное управление АМП

a) Диаграмма Боде передаточной функции разомкнутой цепи

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с

Рисунок А.8 - Оценка запаса устойчивости системы "ротор - АМП" (управление "кососимметричными" модами)

b) Диаграмма Найквиста передаточной функции разомкнутой цепи

c) Диаграмма Найквиста в диапазоне частот от 30 до 150 Гц (слева) и от 150 до 300 Гц (справа)

- действительная часть передаточной функции, дБ; - мнимая часть передаточной функции, дБ

Рисунок А.8 (продолжение)

d) Функция чувствительности

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с; A, B, C, D - зоны устойчивости (см. 6.1)

Рисунок А.8 (окончание)

а) Диаграмма Боде передаточной функции разомкнутой цепи

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с

Рисунок А.9 - Оценка запаса устойчивости системы "ротор - АМП" (управление "симметричными" модами)

b) Диаграмма Найквиста передаточной функции разомкнутой цепи

c) Диаграмма Найквиста в диапазоне частот от 40 до 200 Гц (слева) и от 250 до 350 Гц (справа)

- действительная часть передаточной функции, дБ; - мнимая часть передаточной функции, дБ;

Рисунок А.9 (продолжение)

d) Функция чувствительности

- частота, Гц; - модуль, дБ (отметки шкалы соответствуют следующим абсолютным значениям: -20 дБ =0,1; 10 дБ =0,315; 0 дБ =1; 10 дБ =3,15); - фаза, в градусах; - номинальная скорость вращения 250 с; A, B, C, D - зоны устойчивости (см. 6.1)

Рисунок А.9 (окончание)

Контроллер типа 2 обеспечивает лучшую устойчивость системы. Измерения вибрации в радиальном направлении были проведены в ходе испытаний с изменением частоты вращения ротора, и их результаты показаны на рисунке А.10.

- скорость вращения, с; - размах перемещения, мкм

Рисунок А.10 - Изменение вибрации с изменением частоты вращения ротора

Приложение B
(справочное)

Примеры оценки запаса устойчивости. Пример 2

B.1 Компрессор с магнитными подшипниками

Исследовалось поведение центробежного компрессора (см. рисунок В.1), используемого в условиях нефтеочистительного производства (см. [3] и [4]). АМП использовались в качестве опоры роторов секций низкого и высокого давления. Ротор турбинного привода имел обычную опору в виде подшипников скольжения. Подробное описание валопровода компрессора, включая собственные частоты и моды колебаний, портрет критических частот и т.д., приведено в ИСО 18439-2. Первые моды собственных колебаний валопровода имели следующие характеристики:

- 1-я мода: "симметричная" мода жесткого ротора, собственная частота 35 Гц;

- 2-я мода: "кососимметричная" мода жесткого ротора, собственная частота 82 Гц;

- 3-я мода: 1-я мода ("симметричная") изгибных колебаний гибкого ротора, собственная частота 138 Гц;

- 4-я мода: 2-я мода ("кососимметричная") изгибных колебаний гибкого ротора, собственная частота 276 Гц.

Примечание - Номинальная скорость вращения роторов 10900 мин, что соответствует частоте вращения 182 Гц.

B.2 Передаточная функция разомкнутой цепи

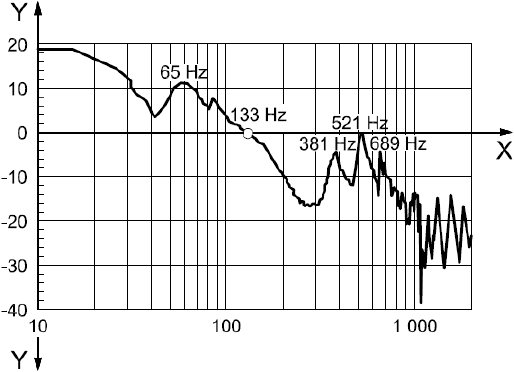
В примере использовалось раздельное управление "симметричными" и "кососимметричными" модами. Типичный вид результата измерений передаточной функции разомкнутой цепи показан на рисунке В.2. Можно предположить, что пики на частотах 381 Гц, 521 Гц и т.д. соответствуют высшим модам изгибных колебаний.

B.3 Функция чувствительности

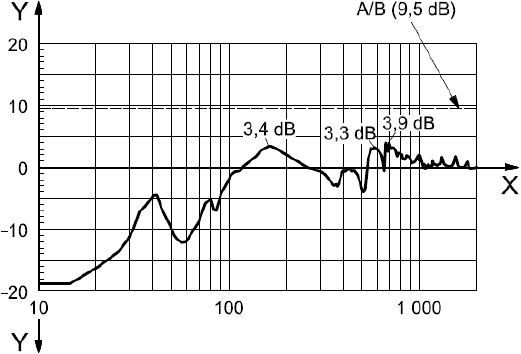
Результаты измерений были преобразованы в функцию чувствительности по формуле (4) (см. рисунок В.3). Поскольку наивысшему пику функции чувствительности соответствует значение 3,9 дБ (или 1,6 в абсолютных единицах), можно сделать вывод, что компрессор попадает в зону A (см. таблицу 1).

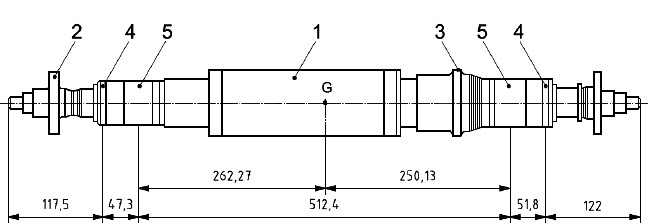
В миллиметрах

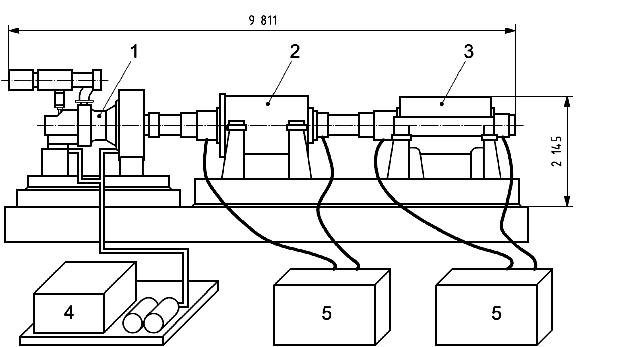
1 - турбина; 2 - секция высокого давления; 3 - секция низкого давления; 4 - система подачи масла; 5 - шкаф управления

Рисунок B.1 - Центробежный компрессор с АМП на испытательном стенде

- частота, Гц; - модуль, дБ

Рисунок В.2 - Диаграмма Боде типичной передаточной функции разомкнутой цепи

- частота, Гц; - модуль, дБ; А/В - граница между зонами устойчивости (см. таблицу 1)

Рисунок В.3 - Функция чувствительности

Приложение С
(справочное)

Примеры оценки запаса устойчивости. Исследования в условиях эксплуатации

С.1 Испытуемый ротор с АМП

В 2004 г. крупнейшей японской государственной организацией в области поддержки научных исследований NEDO с участием экспертов разных стран были организованы испытания по оценке запаса устойчивости ротора на магнитных подшипниках. Испытуемый ротор, предоставленный NEDO, и вид испытательной установки показаны на рисунке C.1. Характеристики ротора приведены в таблице C.1. Расчеты динамики ротора с используемой системой управления (контроллерами АМП) дали следующие оценки собственных частот:

- 1-я мода: "симметричная" мода жесткого ротора, собственная частота 72 Гц;

- 2-я мода: "кососимметричная" мода жесткого ротора, собственная частота 118 Гц;

- 3-я мода: 1-я мода ("симметричная") изгибных колебаний гибкого ротора, собственная частота 623 Гц;

- 4-я мода: 2-я мода ("кососимметричная") изгибных колебаний гибкого ротора, собственная частота 1241 Гц.

________________

New Energy and Industrial Technology Development Organization, 1-1 Higashi Ikebukuro, 3-chome, Toshima-ku, Tokyo 170-6028, Japan, www.nedo.go.jp.

Примечание - Номинальная скорость вращения ротора 30000 мин, что соответствует частоте 500 Гц.

Таблица С.1 - Характеристики ротора

С.2 Передаточная функция разомкнутой цепи

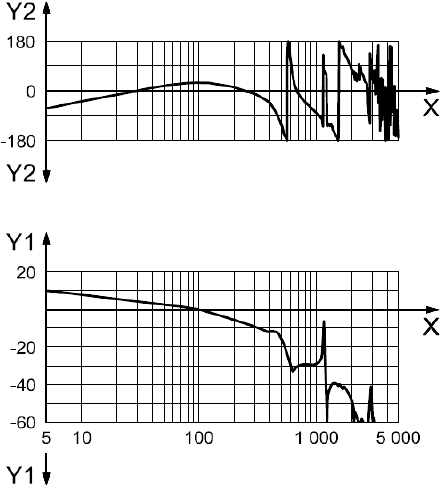
Управление АМП осуществлялось раздельно. Пример типичных результатов измерений передаточной функции разомкнутой цепи приведен на рисунке С.2.

С.3 Функция чувствительности

Результаты измерений передаточной функции разомкнутой цепи были преобразованы в функцию чувствительности по формуле (4). График функции чувствительности приведен на рисунке С.3.

В миллиметрах

a) Испытуемый ротор

1 - двигатель; 2 - диск; 3 - осевой АМП; 4 - датчик перемещения; 5 - радиальный АМП

Рисунок С.1 - Испытуемый ротор NEDO и испытательная установка

b) Испытательная установка

Рисунок С.1 (окончание)

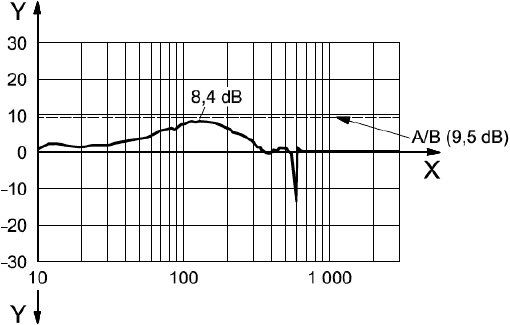
a) Управление "симметричными" модами

- частота, Гц; - модуль, дБ; - фаза, в градусах

Рисунок С.2 - Диаграмма Боде типичной передаточной функции разомкнутой цепи для ротора NEDO

b) Управление "кососимметричными" модами

- частота, Гц; - модуль, дБ; - фаза, в градусах

Рисунок С.2 (окончание)

a) Управление "симметричными" модами

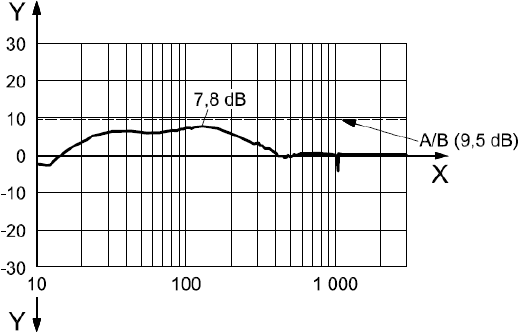
b) Управление "кососимметричными" модами

- частота, Гц; - модуль, дБ

Рисунок С.3 - Функция чувствительности ротора NEDO

Приложение D
(справочное)

Аналитические расчеты запаса устойчивости системы

Аналитический расчет запаса устойчивости системы может потребоваться на стадиях проектирования или заказа машины, т.е. до ее изготовления. Моделирование и анализ динамики системы "ротор - АМП" выходят за область применения настоящего стандарта, тем не менее ниже приведены некоторые рекомендации по данному вопросу.

В первую очередь необходимо, чтобы модель расчета поведения системы включала полное описание динамики АМП контроллеров через их передаточные функции (включая временные задержки) и учитывала полосу пропускания датчиков перемещения (моделируется фильтром нижних частот, следующим за усилителем с номинальным коэффициентом усиления). Передаточные функции элементов системы не следует преобразовывать в значения эквивалентных жесткостей и коэффициентов демпфирования, как это обычно делается при исследовании устойчивости поведения машин с подшипниками скольжения. Практика показывает, что прогнозируемый с использованием такой процедуры запас устойчивости машины будет весьма далек от наблюдаемого в действительности. Очень часто расчеты показывают неустойчивость системы, в то время как машина функционирует с большим запасом устойчивости.

Кроме того, если в диапазон частот анализа попадают собственные частоты мод изгибных колебаний ротора, то ротор необходимо моделировать как гибкий и, в частности, учитывать несовпадение в местоположении датчика перемещения и исполнительного органа АМП (магнитов). Если пренебречь тем, что датчик обычно измеряет радиальные колебания ротора не точно в той же точке вдоль оси ротора, в которой действует магнитная сила системы "ротор - статор" (см. рисунок А.3), то результаты анализа могут существенно отличаться от реального поведения системы. Причем качество таких результатов будет ухудшаться с увеличением собственной частоты моды.

Приложение E
(справочное)

Матрица разомкнутой цепи MIMO-систем управления

E.1 Передаточная функция разомкнутой цепи по схеме измерения с одним включением

В настоящем стандарте передаточная функция разомкнутой цепи определена как полученная в условиях, когда в одну из пяти цепей управления (по числу осей управления) добавлено включение возмущения, в то время как в других четырех оно отсутствует. При данных условиях измерению подлежит один входной и один выходной сигнал, что удобно реализовать с использованием двухканального БПФ-анализатора. Таким образом, настоящий стандарт требует, чтобы для АМП с пятью осями управления были проведены пять независимых измерений передаточных функций - для каждой из пяти цепей управления. Эта процедура позволяет получить пять передаточных функций разомкнутой цепи:

, …, . (Е.1)

Результаты измерений могут быть преобразованы в пять функций чувствительности по формулам:

, …, . (Е.2)

Е.2 Передаточная функция разомкнутой цепи по схеме измерения с включениями

Существует, однако, возможность добавить включения во все цепи управления одновременно и измерить многомерную передаточную функцию разомкнутой цепи с применением компьютерной обработки сигналов. В случае =5 осей управления, эта многомерная передаточная функция будет представлять собой матрицу , определяемую пятью входными и пятью выходными сигналами по формуле

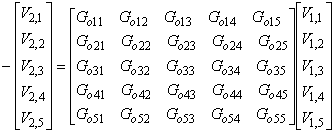. (Е.3)

Эта матрица описывает MlMO-систему управления, изображенную на рисунке Е.1. Данный подход может быть использован для машин с произвольным числом осей управления. Важно лишь, чтобы измерения всех входных и всех выходных сигналов были проведены одновременно.

Соответствующая функция чувствительности также будет иметь матричную форму в соответствии с формулой

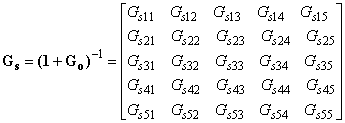. (Е.4)

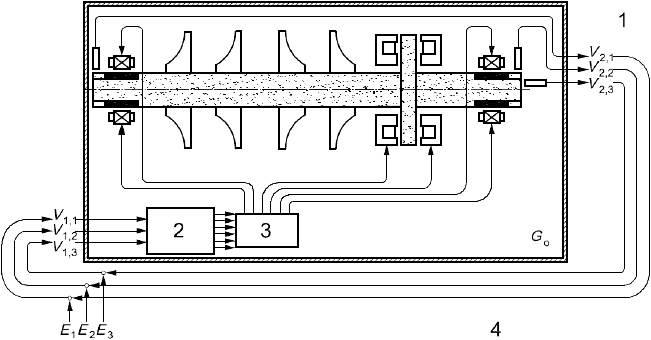
1 - сигналы с датчиков перемещения; 2 - контроллер; 3 - усилитель мощности; 4 - обычная цепь обратной связи

Рисунок Е.1 - Передаточные функции разомкнутой цепи для MIMO-системы

Е.3 Соотношение между результатами измерений передаточных функций по схемам с одним включением и с включениями

При измерении передаточной функции разомкнутой цепи 1 по схеме с одним включением определяют величину в условиях, когда в других цепях управления включения сигнала возмущения отсутствуют, т.е. , , , . Следовательно, получаемые при этом значения передаточной функции будут отличаться от тех, что рассчитаны в соответствии с формулой (3), т.е.

, . (Е.5)

Таким образом, передаточные функции разомкнутой цепи, получаемые по схеме с одним включением, не совпадают с передаточными функциями разомкнутой цепи, получаемыми по схеме с включениями.

Однако каждый диагональный элемент матрицы функции чувствительности, получаемой по формуле (Е.4), будет совпадать с соответствующей функцией чувствительности, полученной по формуле (Е.2), т.е.

, . (Е.6)

Настоящим стандартом установлена процедура оценки запаса устойчивости системы на основе измерений функции чувствительности по схеме измерений с одним включением и использованием двухканального БПФ-анализатора. Но тот же результат может быть получен с помощью схемы измерений с включениями и компьютерной обработкой сигналов, если в качестве будут взяты диагональные элементы матрицы функции чувствительности.

Приложение ДА
(справочное)

Сведения о соответствии ссылочных международных стандартов межгосударственным стандартам

Таблица ДА.1

________________

Заменен на ГОСТ ISO 21940-31-2016.

Библиография

Электронный текст документа

и сверен по:

, 2019