ГОСТ Р ИСО 16063-15-2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Вибрация
МЕТОДЫ КАЛИБРОВКИ ДАТЧИКОВ ВИБРАЦИИ И УДАРА
Часть 15
Первичная калибровка датчиков угловой вибрации методами лазерной интерферометрии
Mechanical vibration. Methods for the calibration of vibration and shock transducers. Part 15. Primary angular vibration calibration by laser interferometry
ОКС 17.160
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт метрологической службы" (ФГУП "ВНИИМС") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4, с участием Автономной некоммерческой организации "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 183 "Вибрация, удар и контроль технического состояния"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1380-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16063-15:2006* "Методы калибровки датчиков вибрации и удара. Часть 15. Первичная калибровка датчиков угловой вибрации методами лазерной интерферометрии" (ISO 16063-15:2006 "Methods for the calibration of vibration and shock transducers - Part 15: Primary angular vibration calibration by laser interferometry", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с требованиями ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
1 Область применения
Настоящий стандарт устанавливает требования к методам и средствам испытаний и измерений, используемым для первичной калибровки датчиков угловой вибрации (в том числе, со встроенными усилителями) для определения модуля и фазы комплексного коэффициента преобразования при возбуждении датчика постоянной гармонической вибрацией с применением методов лазерной интерферометрии.
Настоящий стандарт распространяется на измерения в диапазоне частот от 1 Гц до 1,6 кГц и динамическом (амплитудном) диапазоне от 0,1 до 1000 рад/с (в зависимости от частоты). Для этих диапазонов неопределенность измерения указана в разделе 3. При наличии соответствующего вибростенда для возбуждения низкочастотной угловой вибрации допускается калибровка на частотах менее 1 Гц (например, 0,4 Гц, что является опорной частотой, используемой в ряде стандартов) с амплитудами углового ускорения менее 0,1 рад/с методами 3А и 3В, установленными настоящим стандартом.
Метод счета полос с применением интерферометра типа А (метод 1А; см. раздел 8) и метод счета полос с применением интерферометра типа В (метод 1В; см. раздел 8) используются для определения модуля комплексного коэффициента преобразования в диапазоне частот от 1 до 800 Гц и в особых случаях на более высоких частотах. Метод точек минимума с применением интерферометра А (метод 2А; см. раздел 9) и метод точек минимума с применением интерферометра В (метод 2В; см. раздел 9) могут быть использованы для определения модуля коэффициента преобразования в диапазоне частот от 800 Гц до 1,6 кГц. Метод синус-аппроксимации с применением интерферометра А (метод 3А; см. раздел 10) и метод синус-аппроксимации с применением интерферометра В (метод 3В; см. раздел 10) могут быть использованы для определения модуля и фазы коэффициента преобразования в диапазоне частот от 1 Гц до 1,6 кГц. Методы 1 А, 1В и 3А, 3В обеспечивают калибровку при фиксированных амплитудах углового ускорения на разных частотах. Методы 2А и 2В обеспечивают калибровку при фиксированных амплитудах углового перемещения (при этом амплитуды угловой скорости и углового ускорения будут изменяться в зависимости от частоты).
Примечание 1 - Нумерация методов от 1 до 3 характеризует способ обработки выходного сигнала (сигналов) интерферометра по аналогии с [17]: номер 1 - для метода счета полос, номер 2 - для метода точек минимума и номер 3 - для метода синус-аппроксимации. Процедуры обработки каждого из этих сигналов могут использоваться совместно с применением интерферометров типа А и В по настоящему стандарту.
Интерферометр типа А является интерферометром Майкельсона или Маха-Цендера с уголковым отражателем, расположенным на расстоянии от оси вращения углового возбудителя. Интерферометр этого типа допускает измерения при амплитуде углового перемещения не более 3°. Интерферометр типа В является интерферометром Майкельсона или Маха-Цендера, использующим круговую дифракционную решетку, встроенную в боковую поверхность круглого измерительного стола. Этот тип интерферометра не ограничивает амплитуду углового перемещения, если дифракционные решетки нанесены на всю боковую поверхность диска (360°). Как правило, максимальное угловое перемещение в этом случае ограничивается применяемым для возбуждения угловой вибрации вибростендом.
Примечание 2 - Хотя методы калибровки, установленные настоящим стандартом, могут быть применены как к преобразователям угловой вибрации, так и к другим средствам измерения углового движения, в настоящем стандарте для упрощения описания в качестве объекта калибровки используется датчик угловой вибрации. Некоторая дополнительная информация по калибровке поворотных лазерных интерферометров приведена в 4.11 (см. также рисунок 11).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ISO 266, Acoustics - Preferred frequencies (Акустика. Предпочтительные ряды частот)
ISO 2041:1990, Mechanical vibration, shock and condition monitoring - Vocabulary (Вибрация, удар и контроль технического состояния. Словарь)
________________
Заменен на ISO 2041-2009.
ISO 16063-1:1998, Methods for the calibration of vibration and shock transducers - Part 1: Basic concepts (Методы калибровки датчиков вибрации и удара. Часть 1. Основные положения)
3 Неопределенность измерения
Применение методов, установленных настоящим стандартом, должно обеспечивать неопределенность измерения, не превышающую следующие значения:
a) для модуля коэффициента преобразования:
- 0,5% измеренного значения на опорных значениях частоты и углового ускорения,
- не более 1% измеренного значения для значений частоты и углового ускорения, отличных от опорных;
b) для фазового сдвига коэффициента преобразования:
- 0,5° на опорных значениях частоты и углового ускорения,
- не более 1° для значений частоты и углового ускорения, отличных от опорных.
Рекомендуемыми опорными значениями являются следующие:
- частота: 160, 80, 40, 16 или 8 Гц (или угловая частота : 1000, 500, 250, 100 или 50 рад/с);
- угловое ускорение (амплитуда или среднеквадратичное значение): 100, 50, 20, 10, 5, 2 или 1 рад/с.
Регулировка усилителя должна быть выбрана исходя из оптимального проведения калибровки, принимая во внимание искажения и влияние частот среза.
Под неопределенностью измерения понимается расширенная неопределенность в соответствии с ИСО 16063-1 с коэффициентом охвата 2.
4 Требования к испытательному оборудованию и средствам измерений
4.1 Общие положения
В настоящем разделе приведены рекомендуемые характеристики средств испытаний и измерений, соответствующие области применения (раздел 1) и требованиям к неопределенности измерения (раздел 3).
При необходимости может быть использовано испытательное оборудование, позволяющее реализовать требования к калибровке лишь в некотором ограниченном диапазоне частот и амплитуд. В этом случае, чтобы охватить диапазоны измерений полностью, используют разные виды испытательного оборудования (например, вибростенды).
Примечание - Аппаратура, указанная в настоящем разделе, включает в себя оборудование и средства измерений, применяемые для любого из трех методов калибровки настоящего стандарта, с указанием, в каком методе она применяется.
4.2 Генератор частоты и индикатор
Следует использовать генератор частоты, имеющий следующие характеристики:
a) неопределенность измерения частоты не более 0,05% показываемого значения;
b) стабильность частоты в пределах ±0,05% показываемого значения в течение всего времени измерения;
c) стабильность амплитуды в пределах ±0,05% показываемого значения в течение всего периода измерения.
4.3 Вибростенд для возбуждения угловой вибрации с усилителем мощности
4.3.1 Общие положения
Следует использовать вибростенд с усилителем мощности, имеющие следующие характеристики:
a) коэффициент гармоник не более 2%.
Примечание 1 - Это требование относится к возбуждению на входе калибруемого датчика.
Примечание 2 - Для метода 3А или 3В допустимы ![]() искажения;
искажения;
b) малые поперечные и угловые колебания стола вибростенда, чтобы не оказывать существенного влияния на результаты калибровки. Для интерферометра типа А может потребоваться, чтобы величина, характеризующая движение в поперечном направлении, была менее 1% тангенциальной составляющей той же величины при минимальном измеряемом угловом перемещении. Для интерферометра типа В допускается максимальное смещение стола вибростенда в поперечном направлении (с учетом эксцентриситета) 2 мкм, что может быть обеспечено, только если в качестве опоры стола вибростенда используется высокоточный подшипник с воздушным трением;
c) собственный электронный шум испытательной установки должен быть не менее чем на 70 дБ ниже максимального значения выходного сигнала;
d) стабильность амплитуды углового ускорения должна быть в пределах ±0,05% показываемого значения в течение всего времени измерения.
4.3.2 Электродинамический вибростенд для возбуждения угловой вибрации
Работа электродинамического вибростенда основана на возникновении силы Лоренца, воздействующей на электрически заряженные носители при их движении в магнитном поле.
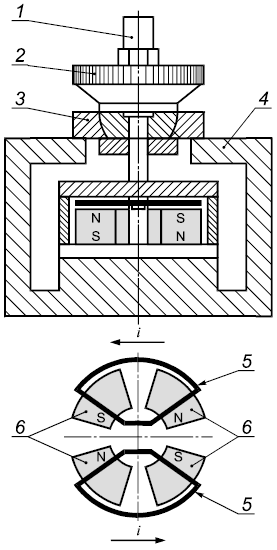
По аналогии с обычными электродинамическими вибростендами для возбуждения поступательной вибрации катушка возбуждения, расположенная в воздушном зазоре, где действует постоянное магнитное поле, может быть сконструирована таким образом, что сила Лоренца будет создавать момент силы, воздействующей на стол вибростенда с установленным на нем калибруемым датчиком. В рабочем диапазоне частот (т.е. от 1 Гц до 1,6 кГц) амплитуда угловой вибрации пропорциональна амплитуде электрического тока, проходящего через катушку. Пример вибростенда для возбуждения угловой вибрации показан на рисунке 1. Для такого вибростенда максимальная амплитуда углового перемещения не будет превышать 30° (т.е. максимальная удвоенная амплитуда будет 1 рад). Другой пример возбудителя угловой вибрации (с амплитудой 60°, т.е. 1 рад) приведен в [14].
4.3.3 Возбудитель угловой вибрации с бесколлекторным электродвигателем
В целях калибровки датчиков угловой вибрации используют специально спроектированные и изготовленные возбудители угловой вибрации на основе серийно выпускаемых электродвигателей.
Для калибровки датчиков инерционного типа, применяемых в навигационных системах, разработаны так называемые вращающиеся стенды, в которых обычно используются бесколлекторные трехфазные электродвигатели с полым валом с электронной системой управления, в частности, по угловой скорости (регуляторы угловой скорости). С помощью таких стендов удается создать сигнал гармонической угловой скорости с малым искажением. Прогресс, достигнутый за последние годы, позволяет использовать этот тип возбудителя и для возбуждения углового ускорения. Основным требованием при этом является использование подшипника с воздушным трением, как и в вибростенде, рассмотренном в 4.3.2.
Поскольку дифференцирование сигнала ведет к дополнительным искажениям формы, при калибровке угловых акселерометров может потребоваться частотно-избирательное измерение их выходного сигнала, что обеспечивается использованием методов 3А и 3В (синус-аппроксимацией).
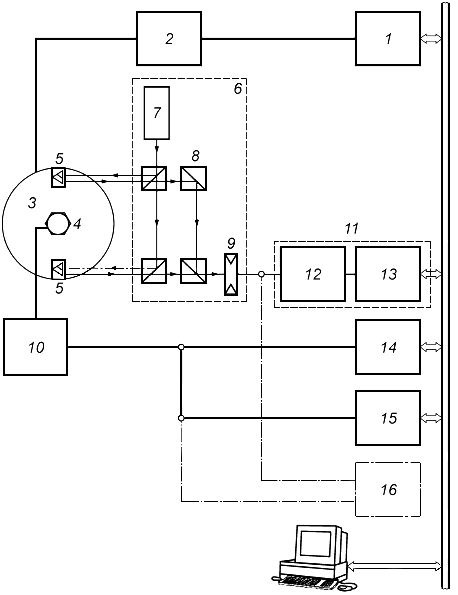
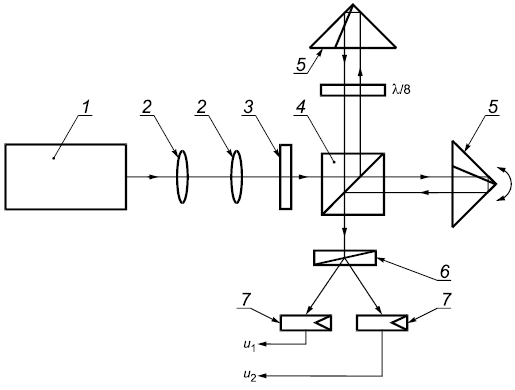
|
1 - калибруемый акселерометр; 2 - дифракционная решетка; 3 - подшипник с воздушным трением; 4 - корпус вибростенда; 5 - катушка; 6 - постоянный магнит
Рисунок 1 - Пример вибростенда для возбуждения угловой вибрации
4.4 Сейсмический блок (блоки) для вибростенда и лазерного интерферометра
Вибростенд для возбуждения угловой вибрации и интерферометр устанавливают на общем или на отдельных массивных блоках с целью предотвратить их относительное перемещение из-за колебаний грунта, а также для предотвращения чрезмерного влияния реакции опоры вибростенда на результаты калибровки.
При использовании общего блока его момент инерции должен быть по меньшей мере в 2000 раз больше момента инерции подвижной системы вибростенда. При выполнении данного условия реактивная вибрация акселерометра и интерферометра не будут превышать 0,05%. Если момент инерции сейсмического блока меньше, то колебания блока следует учитывать при расчете вибрации.
Для уменьшения искажений вследствие колебаний грунта при измерениях в диапазоне от 1 Гц до 1,6 кГц сейсмический блок (блоки) устанавливают на демпфированных пружинах, чтобы соответствующая составляющая неопределенности измерения не превышала 0,1%.
4.5 Лазер
Для калибровки используют красный гелий-неоновый лазер или одночастотный лазер с другой известной длиной волны. В лабораторных условиях (т.е. при атмосферном давлении 100 кПа, температуре 23°С и относительной влажности 50%) номинальная длина волны лазера равна 0,63281 мкм.
Если лазер имеет ручную или автоматическую компенсацию влияния условий окружающей среды, то она должна быть установлена на нуль или отключена.
4.6 Интерферометр
4.6.1 Общие положения
Интерферометр может быть использован для преобразования:
- углового перемещения в пропорциональный фазовый сдвиг
![]() выходного сигнала интерферометра;
выходного сигнала интерферометра;
- угловой скорости в пропорциональный сдвиг частоты
![]() (допплеровский сдвиг) выходного сигнала интерферометра.
(допплеровский сдвиг) выходного сигнала интерферометра.
Для обоих преобразований могут быть использованы гомодинный или гетеродинный одноканальный или двухканальный интерферометры (рисунки 3-8 и 10).
В настоящем стандарте преобразование в
![]() рассматривается как основной метод, а преобразование
рассматривается как основной метод, а преобразование в
![]() - как допустимый вариант со ссылкой на библиографический источник, где дано его подробное описание.
- как допустимый вариант со ссылкой на библиографический источник, где дано его подробное описание.
Интерферометры типов А и В воспринимают поступательную составляющую перемещения, что позволяет использовать установку для калибровки датчиков прямолинейной вибрации. Для этого вращательное движение, которое подлежит измерению, преобразуют в поступательное перемещение посредством уголковых отражателей в схеме измерения с интерферометром типа А или дифракционной решетки, установленной на вращающийся измерительный стол, в схеме измерения с интерферометром типа В. В последнем случае дифракционная решетка должна быть расположена на боковой поверхности вращающегося на воздушной опоре стола с эксцентриситетом не более 2 мкм.
Для методов 1А, 1В (рисунки 3 и 4) и методов 2А, 2В (рисунки 5 и 6) используют простой интерферометр Майкельсона с одним фотодетектором.
Интерферометр Майкельсона может быть реализован по однолучевой или двухлучевой схеме.
Для методов 3А, 3В (рисунки 7 и 8) используют модифицированный интерферометр Майкельсона с квадратурными выходными сигналами и двумя фотодетекторами для приема сигнальных лучей интерферометра. Модифицированный интерферометр Майкельсона может быть выполнен в соответствии с рисунком 9. Четвертьволновая пластина преобразует падающий линейно поляризованный свет в два измерительных луча со взаимно ортогональной поляризацией и фазовым сдвигом 90°. После интерференции с линейно поляризованным опорным лучом две компоненты со взаимно ортогональными поляризациями пространственно разделяют при помощи соответствующих оптических элементов (например, призмы Волластона или поляризационного светоделителя) и детектируют двумя фотодетекторами.
Два выходных сигнала модифицированного интерферометра Майкельсона должны иметь сдвиг нуля не более ±5% амплитуды сигнала, относительную разность амплитуд менее ±5% и отклонение разности фаз от номинального угла 90° не более ±5°. Чтобы удовлетворить этим требованиям, должны быть предусмотрены средства регулировки нуля, амплитуды сигнала и сдвига фаз между двумя сигналами интерферометра.
В случае больших угловых перемещений могут возникнуть трудности в соблюдении указанного требования к относительной разности амплитуд двух сигналов модифицированного интерферометра Майкельсона. Чтобы удовлетворить требованиям по неопределенности измерения (раздела 3), указанные выше требования должны выполняться по крайней мере для небольших угловых перемещений (до 2·10 рад). Для
![]() угловых перемещений возможны
угловых перемещений возможны ![]() допуски.
допуски.
Пример - Для углового перемещения 2,5·10 рад (что соответствует угловому ускорению 1 рад/с
на частоте 1 Гц) допуск может быть увеличен до ±10% для сдвига нуля и разности амплитуд сигналов и до ±20° для отклонения от номинального угла 90° (см. примечание 1 к 10.2).
Вышеуказанные значения допусков установлены в предположении, что коррекция погрешностей измерения с использованием интерферометра выполняться не будет. В случае применения процедуры коррекции по Хайдеману [6] границы допусков могут быть расширены.
Для методов 1А, 1В, 2А, 2В, 3А или 3В вместо интерферометра Майкельсона (модифицированного) может быть использован другой интерферометр, например гетеродинный интерферометр Маха-Цендера (модифицированный) (рисунок 10).
Интерферометр типа А (см. 4.6.2) или В (см. 4.6.3) используют с фотодетекторами, обеспечивающими прием интерференционных сигналов в необходимой полосе частот. Верхнюю границу полосы частот вычисляют, исходя из максимальной амплитуды угловой скорости
по формуле
![]() , (1)
, (1)
где - эффективный радиус (см. 4.6.2 для интерферометра типа А и 4.6.3 для интерферометра типа В);
- интервал дискретизации перемещения интерферометра.
Для интерферометра типа A ![]() для однолучевой схемы и
для однолучевой схемы и ![]() для двухлучевой схемы, где
для двухлучевой схемы, где - длина волны лазера. Для интерферометра типа В
![]() для однолучевой схемы и
для однолучевой схемы и ![]() для двухлучевой схемы, где
для двухлучевой схемы, где - постоянная решетки.
4.6.2 Интерферометр типа А (интерферометр с уголковым отражателем)
Для методов 1А и 2А используют интерферометр Майкельсона с измерительными рефлекторами совместно с фотодетекторами для приема интерференционного сигнала в заданной полосе частот (см. 4.6.1). С целью компенсации искажающих воздействий используют интерферометр с двухлучевой схемой (например, показанный на рисунках 3 и 5) с двумя уголковыми отражателями, установленными симметрично (т.е. под углом 180°).
Лазерный луч направляется к светоделителям, которые расщепляют луч на две параллельные составляющие, падающие на уголковые отражатели. После суперпозиции отраженных лучей соответствующая часть интенсивности светового излучения трансформируется фотодетектором в электрический сигнал (сигнал интерферометра).
Примечание - Двухлучевая схема обеспечивает не только компенсацию искажений (вследствие, например, вибрации земной поверхности), но и приводит к увеличению вдвое чувствительности интерферометра (интервал дискретизации составляет вместо
). Уголковые отражатели, используемые вместо плоских зеркал, позволяют компенсировать (в определенном диапазоне - см. приложение В) эффект наклона (изменения угла установки) отражателя. Более того, такой интерферометр компенсирует (в определенном диапазоне) отклонение луча в поперечном направлении без увеличения неопределенности измерения.
Квадратурный интерферометр с уголковыми отражателями, используемый в методе 3А, включает в себя измерительный и опорный рефлекторы. В варианте гомодинного интерферометра, показанного на рисунках 7 и 9, источником света является стабилизированный одночастотный лазер. Диаметр лазерного луча увеличивают линзами с целью уменьшения его расходимости. Поляризованный лазерный луч расщепляется светоделителем на измерительный и опорный лучи. Опорный луч отражается и сдвигается параллельно уголковым отражателем (опорный рефлектор). Поскольку луч пересекает замедляющую пластину дважды, разность хода составляет
. В то же время отраженный лазерный луч расщепляется на два луча, причем каждый из них имеет ортогональную поляризацию по отношению к другому, т.е. фазовый сдвиг 90° (круговая поляризация). Измерительный луч также сдвигается параллельно самому себе при отражении уголковым отражателем, размещенном на измерительном столе, сохраняя при этом линейную поляризацию. Линейно поляризованный отраженный измерительный луч и опорный луч с круговой поляризацией накладываются друг на друга. После прохождения призмы Волластона, имеющей наклон 45° по отношению к направлению поляризации отраженного измерительного луча, образуются два линейно поляризованных луча, направления поляризации которых перпендикулярны друг другу. Эти лучи преобразуются фотодетекторами в электрические сигналы, характеризующие перемещения измерительного рефлектора по закону синуса и косинуса.
4.6.3 Интерферометр типа В (интерферометр с дифракционной решеткой)
Для приема интерференционного сигнала используют интерферометр с дифракционной решеткой (например, интерферометр Майкельсона) и фотодетектором, позволяющим проводить измерения в заданной полосе частот (см. 4.6.1).
Для методов 1В и 2В используют модифицированный интерферометр Майкельсона с дифракционной решеткой (рисунки 2, 4 и 6).
Угловое ускорение, угловая скорость и угловое перемещение измеряют специальными интерферометрами, в которых использованы дифракционные решетки высокого разрешения (например, фазовые решетки в виде оптического диска с нанесенными на боковую поверхность бороздами синусоидального профиля с плотностью борозд 2400 мм или 3000 мм
) (см. [12] и [13]).
Ось диска отражающей решетки, расположенного на измерительном столе с воздушной подвеской возбудителя угловой вибрации, совпадает с осью вращения (рисунок 2). Луч света, излучаемый одночастотным стабилизированным гелий-неоновым лазером, расщепляется на два параллельных луча, падающих на решетку, симметричную относительно оси вращения, под углом, при котором отраженные лучи, соответствующие первому дифракционному максимуму (в соответствии с формулой дифракции для наклонного падения), возвращаются в направлении падающего луча. Суперпозиция лучей первого дифракционного максимума осуществляется в оптическом устройстве. Если подвижный элемент вибрационного стенда совершает угловые колебания, то эти лучи претерпевают изменения по частоте - противоположные по знаку и одинаковые по величине, пропорциональные тангенциальной скорости и, следовательно, угловой скорости подвижного элемента. Переменная составляющая интенсивности светового излучения будет периодической функцией углового перемещения.
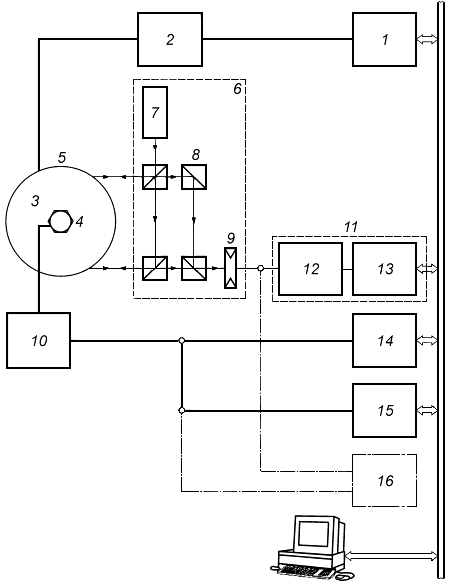
|
1 - дифракционная решетка; 2 - калибруемый датчик; 3 - интерферометр; 4 - вибростенд для возбуждения угловой вибрации
_______________
См. также рисунок 1.
Рисунок 2 - Установка для возбуждения угловой вибрации, состоящая из вибростенда и интерферометра с дифракционной решеткой (гомодинный интерферометр)
В методе 3В используется квадратурный интерферометр с дифракционной решеткой (рисунок 8).
В квадратурном интерферометре с дифракционной решеткой в однолучевой схеме луч расщепляется на опорный и измерительный лучи. Измерительный луч падает на решетку под углом, при котором отраженный луч, соответствующий первому дифракционному максимуму, возвращается в направлении падающего луча. Суперпозиция луча первого дифракционного максимума и опорного луча осуществляется в оптическом устройстве. Доминирующая переменная составляющая интенсивности излучения является гармонической функцией углового перемещения.
При высокоточных измерениях (относительная неопределенность измерения менее 0,5%) должна быть проведена однократная калибровка для конкретной дисковой решетки, используемой с данным вибростендом, для точного определения интервалов дискретизации перемещения и углового перемещения
(см. раздел 7).
4.7 Аппаратура для обработки сигнала интерферометра
4.7.1 Общие положения
При любом техническом решении общим назначением аппаратуры для обработки сигнала интерферометра является демодуляция модулированного по фазе тока или напряжения выходного сигнала фотодетектора (фотодетекторов) с целью выделения параметра (параметров) вибрации, представляющего интерес (например, амплитуды или начальной фазы гармонического углового перемещения). Для методов 1А, 1В (см. 4.7.2), методов 2А, 2В (см. 4.7.3) и методов 3А, 3В (см. 4.7.4) используется различная аппаратура.
4.7.2 Аппаратура для счета интерференционных полос (методы 1А и 1В)
Для счета интерференционных полос должна быть использована аппаратура, имеющая следующие характеристики:
a) диапазон частот от 1 Гц до требуемой максимальной частоты (обычно 20 МГц);
b) максимальная неопределенность измерения 0,01% показываемого значения.
Счетчик полос может быть заменен измерителем отношения частот, обеспечивающим такую же инструментальную неопределенность.
4.7.3 Устройство детектирования нуля (методы 2А и 2В)
Используемый полосовой фильтр или анализатор спектра должен иметь следующие характеристики:
a) диапазон частот от как минимум 800 Гц до как минимум 1,6 кГц;
b) ширина полосы анализа не более 1/6 октавы (12% среднегеометрической частоты);
c) спад частотной характеристики фильтра не менее 24 дБ на октаву;
d) отношение "полезный сигнал/шум" более 70 дБ (определяют по максимальному значению полезного сигнала);
e) динамический диапазон более 60 дБ.
Специализированное устройство детектирования нуля (не является необходимым элементом измерительной цепи в случае использования анализатора спектра) должно иметь диапазон частот от 800 Гц до 1,6 кГц. Динамический диапазон должен быть достаточным для обнаружения шума на выходе полосового фильтра.
4.7.4 Аппаратура для метода синус-аппроксимации (методы 3А и 3В)
Измерительная система должна иметь в своем составе регистратор формы сигнала с компьютерным интерфейсом, позволяющим выполнять аналого-цифровое преобразование и хранить в памяти два квадратурных выходных сигнала интерферометра и выходной сигнал акселерометра. Разрешающая способность по амплитуде, частота выборки и объем памяти должны быть достаточными для калибровки в требуемом динамическом диапазоне с неопределенностью измерения, указанной в разделе 3. Обычно для выходного сигнала акселерометра достаточно разрядности аналого-цифрового преобразования 10 бит, а для выходных квадратурных сигналов интерферометра - 8 бит. Допускается использование двух регистрирующих устройств: двухканального для выходных сигналов интерферометра и устройства с более высокой разрешающей способностью и более низкой частотой выборки для выходного сигнала акселерометра. При каждом измерении преобразование данных интерферометра и выходного сигнала датчика угловой вибрации должно начинаться и заканчиваться в одно и то же время с неопределенностью измерения, удовлетворяющей общим требованиям раздела 3.
Для наиболее короткого периода выходного сигнала интерферометра, который соответствует максимальной угловой скорости вибрации, следует обеспечить достаточное число выборочных значений (см. 10.3). При заданной амплитуде углового ускорения меньшей частоте соответствуют большие амплитуды углового перемещения, что требует ![]() частоты выборки и
частоты выборки и ![]() объема памяти. При невозможности обеспечить указанные требования амплитуду углового ускорения следует уменьшить.
объема памяти. При невозможности обеспечить указанные требования амплитуду углового ускорения следует уменьшить.
Для калибровки углового акселерометра на частоте вибрации 10 Гц и при амплитуде углового ускорения 1000 рад/с при частоте выборки свыше 20 кГц объем необходимой памяти будет превышать 4 Мбайт.
Процедура расчета для методов 3А и 3В (см. 10.4) должна быть реализована с использованием компьютера и соответствующей программы обработки данных.
4.8 Устройство измерения истинного среднеквадратичного значения выходного сигнала акселерометра
Вольтметры, используемые для измерения истинного среднеквадратичного значения выходного сигнала акселерометра, должны иметь следующие характеристики:
a) диапазон частот от как минимум 1 Гц до как минимум 1,6 кГц;
b) неопределенность измерения не более 0,1% показываемого значения.
Для вычисления амплитуды сигнала среднеквадратичное значение умножают на .
Вольтметры среднеквадратичного значения применяют в методах 1А, 1В, 2А и 2В. В методах 3А и 3В для измерения напряжения следует использовать специальную аппаратуру (см. 4.7.4). Вольтметр среднеквадратичного значения в данном случае может быть использован как вспомогательное средство.
4.9 Устройство измерения коэффициента гармоник
Для измерения искажений должно использоваться устройство, позволяющее определить коэффициент гармоник в диапазоне от как минимум 1% до 5% и имеющее следующие характеристики:
a) диапазон частот от как минимум 1 Гц до как минимум 1,6 кГц с возможностью измерения до 5-й гармоники;
b) неопределенность измерения не более 10% показываемого значения в диапазоне коэффициента гармоник от 0,5% до 5%.
4.10 Осциллограф
Применение осциллографа не является обязательным, но он может быть использован для контроля формы сигналов интерферометра и акселерометра. Диапазон частот осциллографа - от 1 Гц до как минимум 2 МГц.
4.11 Другие требования
Калибруемый датчик должен иметь жесткую конструкцию. При расчете неопределенности измерения (см. приложение А) необходимо принимать во внимание чувствительность к деформации основания, коэффициент преобразования в поперечном направлении и стабильность характеристик системы "угловой акселерометр - усилитель" (если их калибруют совместно).
При расчете неопределенности измерения должны быть учтены все факторы, влияющие на результат измерения.
Методы 1В, 2В и 3В могут применяться для калибровки лазерных виброметров углового перемещения, если параметр движения воспринимается одновременно эталонным средством измерения (см. 4.6 и 4.7) и калибруемым лазерным интерферометром. Если периоды детектирования угловой вибрации этими средствами измерений различны, то амплитуда угловой вибрации должна быть достаточно стабильна для удовлетворения требований раздела 3. Пример схемы калибровки лазерных виброметров углового перемещения показан на рисунке 11.
5 Нормальные условия окружающей среды
Калибровку проводят при следующих условиях окружающей среды:
a) комнатная температура (23±3) °С;
b) относительная влажность не более 75%.
Должны быть приняты меры к тому, чтобы на результат измерений не оказывали влияние фоновые шум и вибрация.
6 Предпочтительные опорные значения углового ускорения и частоты
Амплитуду или среднеквадратичное значение углового ускорения и частоты, равномерно покрывающие диапазоны измерений углового акселерометра, выбирают из следующих рядов:
а) угловое ускорение (методы 1А, 1В, 3А и 3В), рад/с: 0,1; 0,2; 0,5; 1; 2; 5; 10; 20; 50; 100; 200; 500; 1000 (последнее значение - только для амплитуды);
b) частота выбирается из стандартизованных третьоктавных рядов частоты (в соответствии с ИСО 266) в диапазоне от 1 Гц до 1,6 кГц или из рядов угловой частоты на основе базового значения 1000 рад/с.
7 Общие основы методов измерений
Общим для методов А1, В1, А2, В2, A3 и В3 является использование интерферометра (типа А или В) для определения перемещения в точке, расположенной на расстоянии эффективного радиуса от оси вращения круглого стола вибростенда для возбуждения угловой вибрации. По измеренной с помощью интерферометра амплитуде перемещения
вычисляют амплитуду углового перемещения
по формуле
![]() , (2)
, (2)
где - эффективный радиус, значение которого должно быть определено путем специальной калибровки интерферометра, проведенной однократно перед его применением.
Для всех методов измерение основывается на сравнении с точно известной очень малой длиной в субмикрометровом диапазоне. Для интерферометра типа А такой длиной является длина волны гелий-неонового красного лазера,
0,63281 мкм. В интерферометре типа В это период решетки
(например, для решетки на боковой поверхности оптического диска при плотности борозд 3000 мм
период решетки равен 0,33333 мкм). Значение
должно быть точно известным (по результатам измерений, проведенных изготовителем дифракционной решетки).
Примечание - Если период решетки с достаточной точностью неизвестен, то интервал дискретизации угла , который соответствует одному периоду интерференционного сигнала, может быть определен специальной калибровкой интерферометра [13]. Тогда для исключения из формулы (2) радиуса
, который не будет в дальнейшем использоваться для вычислений
, может быть использована формула
![]() для известного интервала дискретизации перемещения
для известного интервала дискретизации перемещения (например, в однолучевой схеме интерферометра В
![]() - см. рисунок 8).
- см. рисунок 8).
Все шесть методов используют значение амплитуды , полученной по формуле (2), для вычисления:
a) коэффициента преобразования по амплитуде преобразователя углового перемещения по формуле
![]() ; (3)
; (3)
b) коэффициента преобразования по амплитуде преобразователей угловой скорости по формулам:
![]() , (4)
, (4)
![]() ; (5)
; (5)
c) коэффициента преобразования по амплитуде акселерометра по формулам:
![]() , (6)
, (6)
![]() , (7)
, (7)
где - амплитуда выходного сигнала
преобразователя углового движения (например, выходное напряжение углового акселерометра);
- амплитуда угловой скорости
;
- амплитуда углового ускорения
.
Поскольку фазовый сдвиг комплексного коэффициента преобразования преобразователей угловой вибрации может быть измерен только методами 3А и 3В, процедуры определения фазового сдвига установлены в разделе 10.
8 Методы счета полос (методы 1А и 1В)
8.1 Общие положения
Эти методы применяют для определения модуля коэффициента преобразования при калибровке в диапазоне частот от 1 до 800 Гц.
Примечание - При частоте 800 Гц и амплитуде углового ускорения 1000 рад/с амплитуда углового перемещения равна 4·10
рад. Это соответствует амплитуде перемещения 2 мкм в случае, если уголковый отражатель или дифракционная решетка расположены на расстоянии 50 мм от оси вращения (т.е. дифракционная решетка находится на боковой поверхности диска диаметром 100 мм). При применении метода счета полос без использования специальных средств коррекции погрешности квантования (см. [1] и [11]) с неопределенностью измерения, указанной в разделе 3, могут быть измерены амплитуды перемещения, начиная с 2 мкм. В случае использования средств коррекции погрешности квантования методы 1А и 1В могут быть применены при меньших амплитудах. Это позволяет выполнить калибровку при заданной амплитуде углового ускорения (например, 1000 рад/с
) на более высоких частотах.
Для интерферометров типа А и В (т.е. для методов 1А и 1В) число периодов сигнала (например, максимумов интенсивности) определяется формулой
![]() , (8)
, (8)
что позволяет рассчитать по формуле
![]() , (9)
, (9)
где - амплитуда перемещения, измеренная лазерным интерферометром, которую используют при расчетах по формулам (2)-(7);
- интервал дискретизации, определяемый формулами (10) и (11) для двух вариантов интерферометра типа А и формулами (12) и (13) для двух вариантов интерферометра типа В;
- частота возбуждаемой угловой вибрации;
- средняя частота следования интерференционных полос (т.е. отношение числа полос, полученное на достаточно продолжительном периоде времени, к длительности этого периода).
Применение формул, определяющих значение [т.е. формул (10) или (11) для интерферометра типа А и формул (12) или (13) для интерферометра типа В], а также формулы (2) для преобразования перемещения в угловое перемещение позволяет рассчитать амплитуду углового перемещения
. Амплитуду угловой скорости
и амплитуду углового ускорения
рассчитывают по формулам (5) и (7) соответственно. Для вычисления коэффициента преобразования преобразователя используют формулы (3), (4) и (6).
8.2 Общая часть процедуры калибровки методами 1А и 1В
После юстировки интерферометра (см. 4.6) определяют коэффициент преобразования калибруемого датчика для заданных частот угловой вибрации и амплитуд углового ускорения (раздел 6) путем измерения частоты следования полос при помощи счетчика (см. 4.7.2) (может быть использован счет полос в соответствии с рисунком 3 или 4) или измерения отношения частоты угловой вибрации к частоте следования полос при помощи счетчика отношения.
8.3 Представление результатов (см. также раздел В.2 приложения В)
8.3.1 Метод 1А (интерферометр с уголковым отражателем)
Вычисляют амплитуду перемещения по формуле (9) на основе измерений частоты следования полос для двухлучевой схемы, показанной на рисунке 3, по формуле
![]() (10)
(10)
или для схемы с одним измерительным лучом, показанной на рисунке 7, по формуле
![]() , (11)
, (11)
где - длина волны (для гелий-неонового лазера
0,63281).
Вычисляют амплитуду углового перемещения по формуле (2), модули коэффициента преобразования
датчика углового перемещения по формуле (3), коэффициента преобразования
датчика угловой скорости по формулам (4) и (5), коэффициента преобразования углового акселерометра
по формулам (6) и (7).
8.3.2 Метод 1В (интерферометр с дифракционной решеткой)
Вычисляют амплитуду перемещения по формуле (9) на основе измерений частоты следования полос для двухлучевой схемы, показанной на рисунке 4, по формуле
![]() (12)
(12)
или для схемы с одним измерительным лучом, показанной на рисунке 8, по формуле
![]() , (13)
, (13)
где - период дифракционной решетки (т.е. ширина борозды). Например, для решетки на боковой поверхности оптического диска при плотности борозд 3000 мм
период решетки равен 0,33333 мкм.
Вычисляют амплитуду углового перемещения
по формуле (2), модули коэффициента преобразования
датчика углового перемещения по формуле (3), коэффициента преобразования
датчика угловой скорости по формулам (4) и (5), коэффициента преобразования
углового акселерометра по формулам (6) и (7).
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - уголковый отражатель; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - светоделитель; 9 - фотодетектор; 10 - усилитель; 11 - канал к счетчику отношения; 12 - счетчик полос или счетчик отношения (см. 4.7.2); 13 - вольтметр (см. 4.8); 14 - измеритель коэффициента гармоник (см. 4.9); 15 - осциллограф
Рисунок 3 - Пример измерительной системы для метода 1А (интерферометр с уголковым отражателем)
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - дифракционная решетка; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - светоделитель; 9 - фотодетектор; 10 - усилитель; 11 - канал к счетчику отношения; 12 - счетчик полос или счетчик отношения (см. 4.7.2); 13 - вольтметр (см. 4.8); 14 - измеритель коэффициента гармоник (см. 4.9); 15 - осциллограф (см. 4.10)
Рисунок 4 - Пример измерительной системы для метода 1В (интерферометр с дифракционной решеткой)
9 Методы точек минимума (методы 2А и 2В)
9.1 Общие положения
Эти методы используют для определения коэффициента преобразования по амплитуде при калибровке в диапазоне частот от 800 Гц до 1,6 кГц.
Методы, описываемые в этом разделе, основаны на измерении перемещения с использованием значений аргументов функции Бесселя первого рода первого порядка в точках ее пересечения с осью абсцисс.
Примечание - Такой же подход может быть использован для определения перемещения с использованием значений аргументов в точках пересечения функции Бесселя первого рода нулевого порядка с осью абсцисс. Но при этом потребуется обеспечить модуляцию положения опорного зеркала (см. [2]).
Регулируя амплитуду угловой вибрации до уровня, при котором составляющая частоты спектра интенсивности, равная частоте вибрации, становится равной нулю, можно вычислить амплитуду перемещения, измеряемую интерферометром, по формуле
![]() , (14)
, (14)
где - амплитуда перемещения, измеряемая интерферометром;
- аргументы, соответствующие точкам пересечения функции Бесселя с осью абсцисс, указанные в таблице 1;
- интервал дискретизации, определяемый по формулам (10) и (11) для двух вариантов интерферометра типа А и формулами (12) и (13) для двух вариантов интерферометра типа В. Для расчета значений амплитуды углового перемещения используют формулу (2). Амплитуду угловой скорости
и амплитуду углового ускорения
вычисляют по формулам (5) и (7) соответственно. Коэффициент преобразования датчика угловой вибрации вычисляют по формулам (3), (5) и (6).
Таблица 1 - Значения аргументов , соответствующих нулевым точкам функции Бесселя первого рода первого порядка
Номер точки минимума | Номер точки минимума | ||
0 | 0 | 16 | 51,04353 |
1 | 3,83170 | 17 | 54,18556 |
2 | 7,01559 | 18 | 57,32753 |
3 | 10,17346 | 9 | 60,46945 |
4 | 13,32369 | 20 | 63,61136 |
5 | 16,47063 | 21 | 66,75323 |
6 | 19,61586 | 22 | 69,89507 |
7 | 22,76009 | 23 | 73,03690 |
8 | 25,90368 | 24 | 76,17870 |
9 | 29,04683 | 25 | 79,32049 |
10 | 32,18968 | 26 | 82,46227 |
11 | 35,33230 | 27 | 85,60402 |
12 | 38,47477 | 28 | 88,74577 |
13 | 41,61709 | 28 | 91,88752 |
14 | 44,75932 | 30 | 95,02924 |
15 | 47,90146 |
9.2 Общая часть процедуры калибровки методами 2А и 2В
После юстировки интерферометра (см. 4.6) определяют коэффициент преобразования калибруемого датчика для заданных частот угловой вибрации и амплитуд углового ускорения (раздел 6). Сигнал фотодетектора (см. 4.6) пропускают через полосовой фильтр (см. 4.7.3) со среднегеометрической частотой, равной частоте угловой вибрации вибростенда. Амплитуда отфильтрованного сигнала достигает минимума при определенных амплитудах вибрации (перемещения и углового перемещения
), соответствующих аргументам
, указанным в таблице 1.
При заданной опорной частоте плавно изменяют амплитуду вибрации от нуля до значения, при котором амплитуда отфильтрованного сигнала фотодетектора после достижения максимума возвращается к минимальному значению. Полученное значение амплитуды перемещения, которое зависит от типа и конфигурации интерферометра (см. 9.3), соответствует первой точке минимума.
Измерительная система для метода точек минимума показана на рисунках 5 и 6.
Примечание 1 - Коэффициент преобразования акселерометра может быть также определен с использованием функции Бесселя первого рода нулевого порядка посредством модуляции положения опорного зеркала с частотой, которая мала по сравнению с частотой вибрации, и подстройкой среднегеометрической частоты полосового фильтра или частотного анализатора до значения, равного частоте модуляции зеркала (см. [3]).
Примечание 2 - Модуляция положения опорного зеркала может быть также применена для улучшения эффективности метода с использованием функции Бесселя первого рода первого порядка (см. [4]).
9.3 Представление результатов (см. также раздел В.3 приложения В)
9.3.1 Метод 2А (интерферометр с уголковым отражателем)
Вычисляют амплитуду перемещения ![]() для соответствующего аргумента
для соответствующего аргумента по формуле (14), где
![]() [формула (10) для двухлучевой схемы, изображенной на рисунке 3] или
[формула (10) для двухлучевой схемы, изображенной на рисунке 3] или ![]() [формула (11) для однолучевой схемы, изображенной на рисунке 7]; а
[формула (11) для однолучевой схемы, изображенной на рисунке 7]; а - длина волны гелий-неонового лазера (
0,63281 мкм).
Примечание - Вместо вычисления по формуле (14) значение амплитуды перемещения , соответствующей
-й точке минимума, может быть взято из таблицы 2.
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - уголковый отражатель; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - светоделитель; 9 - фотодетектор; 10 - усилитель; 11 - анализатор спектра (см. 4.7.3); 12 - полосовой фильтр, настроенный на частоту вибрации (см. 4.7.3); 13 - вольтметр; 14 - вольтметр (см. 4.8); 15 - измеритель коэффициента гармоник (см. 4.9); 16 - осциллограф (см. 4.10)
Рисунок 5 - Пример измерительной системы для метода 2А (гомодинный интерферометр с уголковым отражателем)
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - дифракционная решетка; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - светоделитель; 9 - фотодетектор; 10 - усилитель; 11 - анализатор спектра (см. 4.7.3); 12 - полосовой фильтр, настроенный на частоту вибрации (см. 4.7.3); 13 - вольтметр; 14 - вольтметр (см. 4.8); 15 - измеритель коэффициента гармоник (см. 4.9); 16 - осциллограф (см. 4.10)
Рисунок 6 - Пример измерительной системы для метода 2В (гомодинный интерферометр с дифракционной решеткой)
Для однолучевой схемы (рисунок 7) амплитуда , преобразуемая в амплитуду углового перемещения по формуле (2), равна значению
, взятому из таблицы 2, то есть
![]() . (15)
. (15)
Для двухлучевой схемы (рисунок 3) амплитуда , преобразуемая в амплитуду углового перемещения по формуле (2), равна половине значения
, взятого из таблицы 2, то есть
![]() . (16)
. (16)
Таблица 2 - Амплитуды перемещения для точек минимума (0,63281 мкм) для вычисления амплитуд углового перемещения
, угловой скорости
и углового ускорения
Номер точки минимума | Амплитуда перемещения | Номер точки минимума | Амплитуда перемещения |
0 | 0 | 17 | 2,7286 |
1 | 0,1930 | 18 | 2,8868 |
2 | 0,3533 | 19 | 3,0450 |
3 | 0,5123 | 20 | 3,2033 |
4 | 0,6709 | 21 | 3,3615 |
5 | 0,8294 | 22 | 3,5197 |
6 | 0,9878 | 23 | 3,6779 |
7 | 1,1461 | 24 | 3,8361 |
8 | 1,3044 | 25 | 3,9943 |
9 | 1,4627 | 26 | 4,1525 |
10 | 1,6210 | 27 | 4,3107 |
11 | 1,7792 | 28 | 4,4689 |
12 | 1,9375 | 28 | 4,6271 |
13 | 2,0957 | 30 | 4,7853 |
14 | 2,2539 | ||
15 | 2,4122 | ||
16 | 2,5704 | ||
| |||
Вычисляют амплитуду углового перемещения
по формуле (2), модули коэффициента преобразования
датчика углового перемещения по формуле (3), коэффициента преобразования
датчика угловой скорости по формулам (4) и (5), коэффициента преобразования
углового акселерометра по формулам (6) и (7).
При представлении результатов калибровки должна быть вычислена и указана неопределенность измерения в соответствии с приложением А.
10 Методы синус-аппроксимации (методы 3А и 3В)
10.1 Общие положения
Методы применяют для определения модуля и фазового сдвига коэффициента преобразования в диапазоне частот от 1 Гц до 1,6 кГц.
Примечание - Метод синус-аппроксимации может быть применен для получения коэффициента преобразования на частотах ниже 1 Гц и выше 1,6 кГц при наличии вибростенда с расширенным диапазоном частот возбуждения угловой вибрации.
В дополнение к результатам, полученным по формулам, общим для всех шести методов калибровки (раздел 7), методы 3А и 3В позволяют измерить фазовый сдвиг комплексного коэффициента преобразования датчика углового перемещения.
Начальная фаза углового перемещения
соответствует начальной фазе
перемещения
![]() . (17)
. (17)
Используя значение , полученное при помощи лазерного интерферометра, можно вычислить амплитуду начальной фазы угловой скорости
по формуле
![]() (18)
(18)
и начальную фазу углового ускорения по формуле
![]() . (19)
. (19)
Фазовый сдвиг коэффициента преобразования датчика углового перемещения вычисляют по формуле
![]() . (20)
. (20)
Фазовый сдвиг коэффициента преобразования датчика угловой скорости вычисляют по формуле
![]() . (21)
. (21)
Фазовый сдвиг коэффициента преобразования угловых акселерометров вычисляют по формуле
![]() . (22)
. (22)
В формулах (20)-(22) обозначает фазу выходного сигнала калибруемого датчика.
10.2 Процедура калибровки методами 3А и 3В (см. также раздел В.4 приложения В)
Измерительная система - в соответствии с рисунками 7, 8, 9.
Лазерный интерферометр (рисунки 7 и 8) должен быть отъюстирован так, чтобы фазы выходных квадратурных сигналов и
находились в пределах допусков, установленных в 4.6.
После юстировки интерферометра проводят измерения амплитуды и фазового сдвига коэффициента преобразования датчика для опорных значений частот и амплитуд вибрации (раздел 6) в следующем порядке.
Датчик подвергают воздействию гармонической угловой вибрации. Амплитуда перемещения должна быть достаточно большой, чтобы обеспечивать по крайней мере образование одной интерференционной полосы.
Примечание 1 - Для установки, описанной в примечании к 8.1, при амплитудах перемещения менее 0,5 мкм погрешность измерений, обусловленная изменениями квадратурных сигналов в пределах допусков, установленных в 4.6, не превышает 0,3% для модуля коэффициента преобразования и 0,3° для фазового сдвига. Уменьшить погрешность можно путем более тщательной регулировки для достижения значений меньших, чем установлено в 4.6 (см. [5]) или применением процедуры коррекции (см. [6]).
Примечание 2 - Чтобы измерить модуль и фазовый сдвиг комплексного коэффициента преобразования акселерометра при амплитудах перемещения в нанометровом диапазоне, метод синус-аппроксимации может быть применен с использованием гетеродинной техники, как описано в [7] и [8]. Это позволяет проводить калибровку при средних уровнях амплитуды ускорения на высоких частотах вибрации.
Примечание 3 - Для повышения устойчивости метода синус-аппроксимации к искажающим сигналам может быть использовано умножение значений перемещения или фазы модуляции на оконную функцию (см. [9]), если при этом будут соблюдены требования к неопределенности измерения, установленные в разделе 3.
Метод В рассматривается здесь в варианте интерферометра с дифракционной решеткой в виде оптического диска диаметром 100 мм с нанесенными на боковую поверхность бороздами с плотностью 2400 мм. Она расположена на боковой поверхности диска диаметром 100 мм, который является измерительным столом.
10.3 Сбор данных
Частоты среза низкочастотных и, если используются, высокочастотных фильтров должны быть выбраны таким образом, чтобы искажающие влияния от низкочастотной и высокочастотной фильтрации на результаты калибровки находились в пределах допусков (см. [5]). Частота выборки должна быть не ниже удвоенной максимальной частоты в спектре сигнала в соответствии с теоремой Найквиста-Котельникова.
Частота выборки выходного сигнала акселерометра может быть равна или ниже частоты выборки выходных сигналов интерферометра. Начало и конец выборки всех трех сигналов должны совпадать, а для выходных сигналов интерферометра процессы выборки должны быть точно синхронизированы, для чего используют один и тот же генератор тактовых импульсов.
Выборку квадратурных сигналов интерферометра осуществляют на периоде измерения . Интервал выборки
![]() выдерживают постоянным. В результате получают последовательности значений квадратурных сигналов интерферометра
выдерживают постоянным. В результате получают последовательности значений квадратурных сигналов интерферометра ![]() и
и ![]() , а также выходного сигнала акселерометра
, а также выходного сигнала акселерометра ![]() , которые вводят в память компьютера.
, которые вводят в память компьютера.
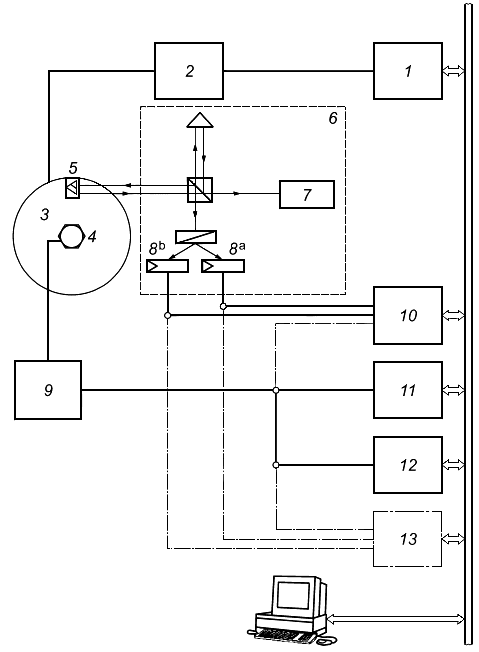
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - уголковый отражатель; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - фотодетектор; 9 - усилитель; 10 - цифровой регистратор формы сигнала (см. 4.7.4); 11 - вольтметр (см. 4.8); 12 - измеритель коэффициента гармоник (см. 4.9); 13 - осциллограф (см. 4.10); - фазовый сдвиг 0°;
- фазовый сдвиг 90°
Рисунок 7 - Пример измерительной системы для метода 3А (гомодинный интерферометр с уголковым отражателем)
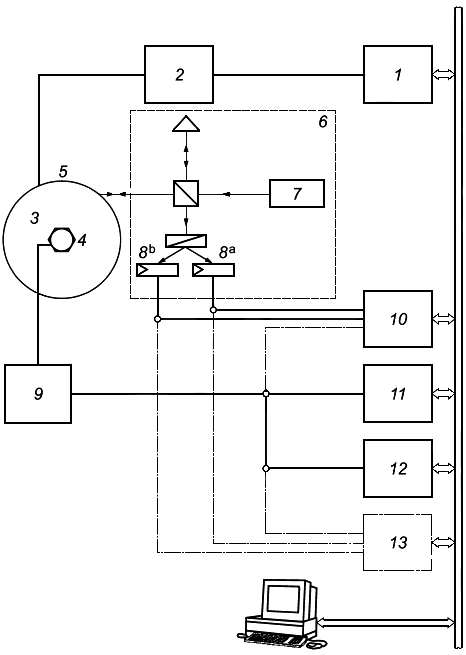
|
1 - генератор частоты (см. 4.2); 2 - усилитель мощности (см. 4.3); 3 - вибростенд (см. 4.3); 4 - калибруемый датчик; 5 - дифракционная решетка; 6 - интерферометр (см. 4.6); 7 - лазер (см. 4.5); 8 - фотодетектор; 9 - усилитель; 10 - цифровой регистратор формы сигнала (см. 4.7.4); 11 - вольтметр (см. 4.8); 12 - измеритель коэффициента гармоник (см. 4.9); 13 - осциллограф (см. 4.10); - фазовый сдвиг 0°;
- фазовый сдвиг 90°
Рисунок 8 - Пример измерительной системы для метода 3В (гомодинный интерферометр с дифракционной решеткой)
|
1 - лазер; 2 - телескоп; 3 - поляризатор; 4 - светоделитель; 5 - уголковый отражатель; 6 - призма Волластона; 7 - фотодетектор
Рисунок 9 - Модифицированный интерферометр Майкельсона с уголковым отражателем (отражателями) и квадратурным выходом
|
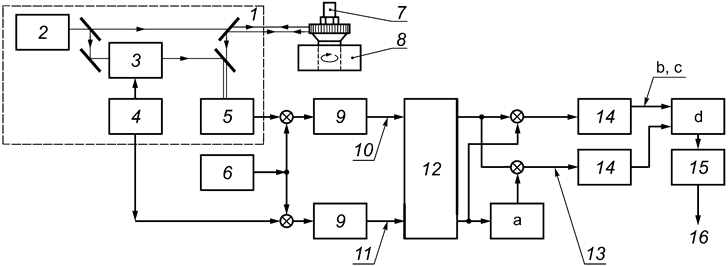
1 - интерферометр; 2 - лазер; 3 - камера Брэгга; 4 - кварцевый генератор; 5 - фотодетектор; 6 - синтезирующий генератор; 7 - калибруемый акселерометр; 8 - вибростенд с воздушной подвеской; 9 - низкочастотный фильтр; 10 - измерительный сигнал; 11 - опорный сигнал; 12 - регистратор формы сигнала (переходных процессов); 13 - квадратурные сигналы; 14 - цифровая фильтрация; 15 - алгоритмы обработки; 16 - результаты измерения (параметры вибрации и удара); а - фазовращатель (на 90°); b, с - сигналы ,
; d - преобразование arctan
![]()
Рисунок 10 - Пример измерительной системы с использованием гетеродинного интерферометра для метода 3В (гетеродинный интерферометр Маха-Цендера с дифракционной решеткой)
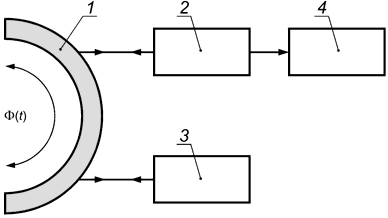
|
1 - дифракционная решетка; 2 - интерферометр; 3 - калибруемый лазерный виброметр; 4 - система обработки сигнала
Рисунок 11 - Пример схемы для калибровки лазерных виброметров для измерений угловой вибрации
10.4 Обработка данных
10.4.1 Определяют модуль и фазовый сдвиг коэффициента преобразования акселерометра в следующем порядке.
10.4.2 По выборочным значениям квадратурных сигналов интерферометра ![]() и
и ![]() вычисляют последовательность значений сигнала фазовой модуляции
вычисляют последовательность значений сигнала фазовой модуляции ![]() по формуле
по формуле
![]() , (23)
, (23)
где 0, 1, 2, ....
Целое число выбирают таким образом, чтобы избежать разрывов в сигнале фазовой модуляции.
Метод определения числа описан в [10].
Вычисляют значения перемещения ![]() по формуле
по формуле
![]() . (24)
. (24)
10.4.3 Выборочные значения перемещения подгонкой параметров ,
и
методом наименьших квадратов аппроксимируют зависимостью (синус-аппроксимация)
![]() , (25)
, (25)
где 0, 1, 2...
;
![]() ;
;
![]() ;
;
- постоянная величина;
- угловая частота вибрации
![]() ;
;
- начальный фазовый угол перемещения;
- число выборок, взятых синхронно в течение периода, указанного в 10.3.
Параметр в дальнейших преобразованиях не используют.
10.4.4 По значениям параметров и
, полученных в результате синус-аппроксимации, рассчитывают амплитуду перемещения
и начальный фазовый угол перемещения
по формулам:
![]() , (26)
, (26)
![]() . (27)
. (27)
10.4.5 По значениям и
с использованием формул (2) и (17) вычисляют амплитуду
и начальный фазовый угол
.
При калибровке датчика угловой скорости вычисляют амплитуду и начальную фазу
угловой скорости по формулам (5) и (18).
При калибровке углового акселерометра вычисляют амплитуду и начальную фазу
по формулам (7) и (19).
10.4.6 Аналогично выборочные значения выходного сигнала акселерометра ![]() аппроксимируют зависимостью
аппроксимируют зависимостью
![]() , (28)
, (28)
где ![]() ;
;
![]() ;
;
- постоянная величина;
- амплитуда выходного сигнала датчика угловой вибрации;
- начальный фазовый угол выходного сигнала датчика угловой вибрации.
Вычисляют амплитуду и начальный фазовый угол
выходного сигнала преобразователя, используя полученные значения параметров
и
, по формулам:
![]() , (29)
, (29)
![]() . (30)
. (30)
При калибровке датчика углового перемещения вычисляют значения модуля и фазового сдвига
комплексного коэффициента преобразования по значениям
и
, полученным в 10.4.6, и значениям
и
, полученным в 10.4.5, по формулам (3) и (20) соответственно.
При калибровке датчика угловой скорости вычисляют значения модуля и фазового сдвига
комплексного коэффициента преобразования по значениям
и
, полученным в 10.4.6, и значениям
и
, полученным в 10.4.5, по формулам (4) и (21) соответственно.
При калибровке углового акселерометра вычисляют значения модуля и фазового сдвига
комплексного коэффициента преобразования по значениям
и
, полученным в 10.4.6, и значениям
и
, полученным в 10.4.5, по формулам (6) и (22) соответственно.
При представлении результатов калибровки, должна быть вычислена и указана расширенная неопределенность в соответствии с приложением А. В А.1.1, А.1.2, А.1.3.1 и А.2.1 модуль комплексного коэффициента преобразования обозначен .
11 Представление результатов калибровки
В протоколе калибровки, кроме указания метода калибровки, должна быть приведена как минимум следующая информация:
a) условия окружающей среды:
- температура датчика угловой вибрации;
- температура окружающего воздуха;
b) способ крепления датчика угловой вибрации:
- материал монтажной поверхности;
- момент затяжки (если датчик крепится на шпильке);
- материал смазки, наносимой на монтажную поверхность (если смазка производилась);
- способ закрепления кабеля;
- ориентация датчика (относительно вертикальной или горизонтальной оси);
- настройки усилителя:
- коэффициент усиления;
- частоты среза фильтров;
c) результаты калибровки:
- значения опорных частот и амплитуд;
- значения модуля и фазового сдвига (если он определен) коэффициента преобразования;
- расширенная неопределенность с указанием коэффициента охвата , если его значение отлично от двух.
Приложение А
(обязательное)
Составляющие неопределенности измерения при первичной калибровке датчиков угловой вибрации методами лазерной интерферометрии
А.1 Вычисление относительной расширенной неопределенности модуля коэффициента преобразования и расширенной неопределенности фазового сдвига коэффициента преобразования для частот, амплитуд и настроек усилителя, при которых проводилась калибровка
А.1.1 Вычисление ![]() для методов 1А и 1В
для методов 1А и 1В
Согласно ИСО 16063-1 относительную расширенную неопределенность модуля коэффициента преобразования ![]() для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, вычисляют по формулам:
для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, вычисляют по формулам:
![]() ,
,
![]()
с коэффициентом охвата 2 (см. таблицу А.1).
Таблица А.1 - Составляющие неопределенности измерения для методов 1А и 1В
Составляющая стандартной неопределенности | Источник неопределенности
| Вклад в неопределенность | |
1 |
| Измерение выходного напряжения датчика (вольтметр) | |
2 |
| Влияние суммарного искажения на результат измерения выходного напряжения датчика |
|
3 |
| Влияние поперечной и нежелательной угловой вибрации на результат измерения выходного напряжения датчика (коэффициент поперечного преобразования) |
|
4 |
| Влияние дискретизации сигнала перемещения на результат измерения перемещения |
|
5 |
| Влияние гистерезиса триггера на результат измерения перемещения |
|
6 |
| Влияние фильтрации на результат измерения перемещения (спады частотной характеристики фильтра) |
|
7 |
| Влияние помех в сигнале напряжения на результат измерения перемещения (например, случайный шум в цепи фотодетектора) |
|
8 |
| Влияние искажения движения на результат измерения перемещения (например, общее искажение, относительное движение поверхности установки датчика и лазерного пятна интерферометра) |
|
9 |
| Влияние фазовых искажений на результат измерения перемещения (например, фазовый шум сигнала интерферометра) |
|
10 |
| Преобразование перемещения в угловое перемещение (функция интерферометра) |
|
11 |
| Измерение частоты вибрации (генератор частоты и показывающее устройство) |
|
12 |
| Остаточные влияния на результат измерения коэффициента преобразования (например, случайные эффекты в повторных измерениях; выборочные стандартные отклонения среднего арифметического) |
|
| |||
А.1.2 Вычисление ![]() для методов 2А и 2В
для методов 2А и 2В
Вычисление выполняют аналогично А.1.1 с использованием составляющих неопределенности, указанных в таблице А.2.
Таблица А.2 - Составляющие неопределенности измерения для методов 2А и 2В
Составляющая стандартной неопределенности | Источник неопределенности | Вклад в неопределенность | |
1 |
| Измерение выходного напряжения датчика (вольтметр) | |
2 |
| Влияние суммарного искажения на результат измерения выходного напряжения датчика |
|
3 |
| Влияние поперечной и нежелательной угловой вибрации на результат измерения выходного напряжения датчика (коэффициент поперечного преобразования) |
|
4 |
| Влияние разрешающей способности в точке минимума на результат измерения перемещения |
|
5 |
| Влияние помех в сигнале напряжения на результат измерения перемещения (например, наводки и собственный электрический шум в цепи) |
|
6 |
| Влияние искажения движения на результат измерения перемещения (например, общее искажение, относительное движение поверхности эталонного акселерометра и лазерного пятна интерферометра) |
|
7 |
| Преобразование перемещения в угловое перемещение (функция интерферометра) |
|
8 |
| Измерение частоты вибрации (генератор частоты и показывающее устройство) |
|
9 |
| Остаточные влияния на результат измерения коэффициента преобразования (например, случайные эффекты в повторных измерениях; выборочные стандартные отклонения среднего арифметического) |
|
| |||
A.1.3 Вычисление ![]() и
и ![]() для методов 3А и 3В
для методов 3А и 3В
А.1.3.1 Вычисление ![]()
Вычисление выполняют аналогично А.1.1 с использованием составляющих неопределенности, указанных в таблице А.3.
Таблица А.3 - Составляющие неопределенности измерения для методов 3А и 3В
Составляющая стандартной неопределенности | Источник неопределенности | Вклад в неопределенность | |
1 |
| Измерение выходного напряжения датчика (устройство записи, например, разрешение аналого-цифрового преобразования) | |
2 |
| Влияние фильтрации на результат измерения амплитуды выходного напряжения датчика (ограниченность полосы частот) |
|
3 |
| Влияние искажений напряжения на результат измерения выходного напряжения датчика (например, помехи и электрический шум в цепи) |
|
4 |
| Влияние поперечной и нежелательной угловой вибрации на результат измерения выходного напряжения акселерометра (коэффициент поперечного преобразования) |
|
5 |
| Влияние искажений квадратурного выходного сигнала интерферометра на результат измерения амплитуды фазовой модуляции (например, сдвиг нуля, отклонение амплитуды напряжения, отклонение от 90° номинальной разности фаз квадратурных составляющих) |
|
6 |
| Влияние фильтрации сигнала интерферометра на результат измерения амплитуды фазовой модуляции (ограниченность полосы частот) |
|
7 |
| Влияние искажения напряжения на результат измерения амплитуды фазовой модуляции (например, случайный шум в фотоэлектрических измерительных цепях) |
|
8 |
| Влияние искажения движения на результат измерения амплитуды фазовой модуляции (например, относительное движение поверхности эталонного акселерометра и лазерного пятна интерферометра) |
|
9 |
| Влияние фазовых искажений на результат измерения амплитуды фазовой модуляции (например, фазовый шум сигнала интерферометра) |
|
10 |
| Преобразование перемещения в угловое перемещение (функция интерферометра) |
|
11 |
| Измерение частоты вибрации (генератор частоты и показывающее устройство) |
|
12 |
| Остаточные влияния на результат измерения коэффициента преобразования (например, случайные эффекты в повторных измерениях; выборочные стандартные отклонения среднего арифметического) |
|
| |||
A.1.3.2 Вычисление ![]()
Согласно ИСО 16063-1 расширенную неопределенность фазового сдвига коэффициента преобразования ![]() для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, вычисляют в соответствии с [2] по формулам:
для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, вычисляют в соответствии с [2] по формулам:
![]() ,
,
![]()
с коэффициентом охвата 2 (см. таблицу А.4).
Таблица А.4 - Составляющие неопределенности измерения фазового сдвига для методов 3А и 3В
Составляющая стандартной неопределенности | Источник неопределенности | Вклад в неопределенность | |
1 |
| Измерение выходного напряжения датчика (устройство записи, например, разрешение аналого-цифрового преобразования) |
|
2 |
| Влияние фильтрации на результат измерения фазы выходного напряжения датчика (ограниченность полосы частот) |
|
3 |
| Влияние искажений напряжения на результат измерения фазы выходного напряжения датчика (например, помехи и электрический шум в цепи) |
|
4 |
| Влияние поперечной и нежелательной угловой вибрации на результат измерения фазы выходного напряжения датчика (коэффициент поперечного преобразования) |
|
5 |
| Влияние искажений квадратурного выходного сигнала интерферометра на результат измерения фазы перемещения (например, сдвиг нуля, отклонение амплитуды напряжения, отклонение от 90° номинальной разности фаз квадратурных составляющих) |
|
6 |
| Влияние фильтрации сигнала интерферометра на результат измерения фазы перемещения (ограниченность полосы частот) |
|
7 |
| Влияние искажения напряжения на результат измерения фазы перемещения (например, случайный шум в фотоэлектрических измерительных цепях) |
|
8 |
| Влияние искажения движения на результат измерения фазы перемещения (например, относительное движение поверхности эталонного акселерометра и лазерного пятна интерферометра) |
|
9 |
| Влияние фазовых искажений на результат измерения фазы перемещения (например, фазовый шум сигнала интерферометра) |
|
10 |
| Преобразование перемещения в угловое перемещение (функция интерферометра) |
|
11 |
| Остаточные влияния на результат измерения фазового сдвига коэффициента преобразования (например, случайные эффекты в повторных измерениях; выборочные стандартные отклонения среднего арифметического) |
|
| |||
А.2 Вычисление относительной расширенной неопределенности модуля коэффициента преобразования и расширенной неопределенности фазового сдвига коэффициента преобразования во всем диапазоне частот и амплитуд
А.2.1 Вычисление ![]()
Относительная расширенная неопределенность модуля коэффициента преобразования ![]() , вычисленная согласно А.1.1, А.1.2 или А.1.3.1, справедлива только для частот, амплитуд и настроек усилителя, при которых была проведена калибровка. Относительную расширенную неопределенность модуля коэффициента преобразования
, вычисленная согласно А.1.1, А.1.2 или А.1.3.1, справедлива только для частот, амплитуд и настроек усилителя, при которых была проведена калибровка. Относительную расширенную неопределенность модуля коэффициента преобразования ![]() для всего диапазона частот и амплитуд в любой момент времени между последовательными калибровками вычисляют по формулам:
для всего диапазона частот и амплитуд в любой момент времени между последовательными калибровками вычисляют по формулам:
![]() ,
,
![]()
с коэффициентом охвата 2 (см. таблицу А.5).
Таблица А.5 - Составляющие неопределенности измерения модуля коэффициента преобразования ![]()
Составляющая стандартной неопределенности | Источник неопределенности
| Вклад в неопределенность | |
1 | Неопределенность модуля коэффициента преобразования для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, в соответствии с А.1.1., А.1.2. или А.1.3.1 |
| |
2 |
| Отклонение коэффициента усиления от номинального при разных настройках усилителя |
|
3 |
| Отклонение амплитудно-частотной характеристики усилителя от постоянного значения в диапазоне частот датчика |
|
4 |
| Отклонение модуля коэффициента преобразования от постоянного значения в диапазоне частот датчика |
|
5 |
| Нелинейность усилителя |
|
6 |
| Нелинейность преобразователя |
|
7 |
| Нестабильность во времени коэффициента усиления усилителя и влияние на коэффициент усиления выходного импеданса датчика |
|
8 |
| Нестабильность во времени модуля коэффициента преобразования |
|
9 |
| Влияние изменения условий внешней среды на коэффициент усиления усилителя |
|
10 |
| Влияние изменения условий внешней среды на модуль коэффициента преобразования |
|
| |||
A.2.2 Вычисление ![]()
Расширенная неопределенность сдвига фаз коэффициента преобразования ![]() , вычисленная согласно А.1.3.2, справедлива только для частот, амплитуд и настроек усилителя, при которых была проведена калибровка. Расширенную неопределенность сдвига фаз коэффициента преобразования
, вычисленная согласно А.1.3.2, справедлива только для частот, амплитуд и настроек усилителя, при которых была проведена калибровка. Расширенную неопределенность сдвига фаз коэффициента преобразования ![]() для всего диапазона частот и амплитуд в любой момент времени между последовательными калибровками вычисляют по формулам:
для всего диапазона частот и амплитуд в любой момент времени между последовательными калибровками вычисляют по формулам:
![]() ,
,
![]()
с коэффициентом охвата 2 (см. таблицу А.6).
Таблица А.6 - Составляющие неопределенности измерения фазового сдвига комплексного коэффициента преобразования ![]()
Составляющая стандартной неопределенности | Источник неопределенности | Вклад в неопределенность | |
1 |
| Неопределенность сдвига фаз коэффициента преобразования для частот, амплитуд и настроек усилителя, при которых проводилась калибровка, в соответствии с А.1.3.2 |
|
2 |
| Отклонение коэффициента усиления от номинального при разных настройках усилителя |
|
3 |
| Отклонение фазочастотной характеристики усилителя от номинальной в диапазоне частот датчика |
|
4 |
| Отклонение сдвига фаз коэффициента преобразования от номинального в диапазоне частот датчика |
|
5 |
| Влияние амплитуды на фазочастотную характеристику усилителя |
|
6 |
| Влияние амплитуды на сдвиг фаз коэффициента преобразования |
|
7 |
| Нестабильность во времени фазочастотной характеристики усилителя и влияние на фазочастотную характеристику выходного импеданса датчика |
|
8 |
| Нестабильность во времени сдвига фаз коэффициента преобразования |
|
9 |
| Влияние изменения условий внешней среды на фазочастотную характеристику усилителя |
|
10 |
| Влияние изменения условий внешней среды на сдвиг фаз коэффициента преобразования |
|
| |||
Приложение В
(справочное)
Теоретические основы метода
В.1 Общие положения
В соответствии с ИСО 2041 и ИСО 16063-1 комплексный коэффициент преобразования датчика вибрации и удара описывается формулой
![]() , (B.1)
, (B.1)
где модуль комплексного коэффициента преобразования параметра вибрации
описывается формулой
![]() , (B.2)
, (B.2)
а фазовый сдвиг - формулой
![]() , (В.3)
, (В.3)
где - угловое перемещение
, угловая скорость
или угловое ускорение
;
,
,
и
- амплитуды соответствующих параметров вибрации;
- амплитуда выходного сигнала
датчика (например, выходного напряжения углового акселерометра).
Формулы (В.2) и (В.3) для модуля и фазового сдвига датчиков углового перемещения могут быть преобразованы в формулы:
![]() , (B.4)
, (B.4)
![]() ; (В.5)
; (В.5)
для датчиков угловой скорости - в формулы:
![]() , (B.6)
, (B.6)
![]() ; (В.7)
; (В.7)
для углового акселерометра - в формулы:
![]() , (B.8)
, (B.8)
![]() . (В.9)
. (В.9)
Параметрами вибрации, измеряемыми лазерными интерферометрами в соответствии с настоящим стандартом, являются угловое перемещение (например, амплитуда
) для всех шести методов (1А, 1В, 2А, 2В, 3А и 3В) и начальная фаза
для методов 3А и 3В. Используя значения
и
, полученные в результате измерений с использованием лазерного интерферометра, вычисляют:
- амплитуду и начальную фазу
угловой скорости по формулам:
![]() , (В.10)
, (В.10)
![]() ; (В.11)
; (В.11)
- амплитуду и начальную фазу
углового ускорения по формулам:
![]() , (В.12)
, (В.12)
![]() . (В.13)
. (В.13)
Два типа интерферометра, определенные настоящим стандартом, используют гелий-неоновый лазер, основная линия которого в спектре измерения имеет длину волны 0,63281 мкм. Для интерферометра типа А (интерферометра с уголковым отражателем) перемещение, соответствующее расстоянию между полосами (по максимуму или минимуму интенсивности) для двухлучевой схемы, приведенной на рисунках 3 и 5, определяется по формуле
![]() , (В.14)
, (В.14)
а для однолучевой схемы, приведенной на рисунке 7, - по формуле
![]() . (В.15)
. (В.15)
Стол вибростенда должен быть жестким в диапазоне частот до 1,6 кГц, поэтому начальная фаза совпадает с начальной фазой
, то есть
![]() . (В.16)
. (В.16)
Оба интерферометра (типа А и типа В) измеряют перемещение в точке, расположенной на расстоянии ("эффективный радиус") от оси вращения круглого измерительного стола вибростенда. Амплитуду углового перемещения рассчитывают по формуле
![]() , (В.17)
, (В.17)
где - амплитуда перемещения, измеряемая интерферометром.
Перемещение, измеряемое интерферометром, и понятие "эффективный радиус" поясняются ниже для каждого из двух типов интерферометров.
Для интерферометра типа А (с уголковым отражателем) должны быть, в частности, приняты во внимание три систематических эффекта, зависящие от углового перемещения, которые влияют на результат измерения.
Базовой характеристикой интерферометра с уголковым отражателем является нелинейная зависимость между амплитудой перемещения, воспринимаемой интерферометром (то есть составляющей в направлении падающего луча), и (измеряемой) амплитудой углового перемещения, определяемой формулой
![]() . (В.18)
. (В.18)
Для малых амплитуд угла вращения (при 3°) нелинейная зависимость, описанная формулой (В.18), может быть с точностью до 0,05% аппроксимирована линейной зависимостью
![]() . (B.19)
. (B.19)
Если необходима ![]() точность, то нелинейная зависимость может быть заменена полиномом, имеющим вид
точность, то нелинейная зависимость может быть заменена полиномом, имеющим вид
![]() . (B.20)
. (B.20)
Приведенные формулы справедливы в том случае, если интерферометр идеально отъюстирован, так что два входящих лазерных луча параллельны и ребра уголковых отражателей так же, как и ось вращающегося измерительного стола, перпендикулярны плоскости, образуемой двумя входящими лучами лазера. Отклонение от этих направлений приводит к систематической погрешности
измерения перемещения (так называемая "косинусная погрешность", поскольку разность хода лучей умножается на коэффициент
):
![]() , (В.21)
, (В.21)
![]() . (В.22)
. (В.22)
Кроме того, при вращательном движении возникает угол между направлением входящего лазерного луча и направлением движения уголкового отражателя, что приводит к поперечному сдвигу
лазерного луча на поверхности фотодетектора, определяемому по формуле
![]() . (В.23)
. (В.23)
Поскольку лазерный луч, перемещающийся от (фиксированного) опорного уголкового отражателя к фотодетектору не смещается, интерференционные полосы смещаются в поперечном направлении. Интерферометр с уголковым отражателем, описанный в настоящем стандарте (рисунки 3, 5 и 7), производит концентрические круглые полосы (вызываемые расходимостью между измерительным и опорным лазерными лучами). Поперечный сдвиг полос следует свести к минимуму, уменьшая по возможности расходимость лучей. Это может быть достигнуто применением телескопической системы.
Препятствием для измерения больших амплитуд углового перемещения, прежде всего, является недостаточная юстировка интерферометра из-за параллельного сдвига падающего и отраженного измерительных лучей лазера, когда уголковый отражатель вращается вокруг оси измерительного стола возбудителя.
Для интерферометра типа А радиус не является точно определимой величиной. Поскольку для предотвращения влияния наклона отражателя на результаты измерений используется уголковый отражатель, падающий и отраженный лучи смещены друг относительно друга. Другой источник неопределенности - определение
.
- расстояние между двумя уголковыми отражателями в двухлучевой схеме или расстояние между уголковым отражателем и осью вращения в однолучевой схеме.
Для интерферометра типа В (с дифракционной решеткой) перемещение, соответствующее расстоянию между двумя полосами (по максимуму или минимуму интенсивности) для двухлучевой схемы, показанной на рисунках 4 и 6, определяется по формуле
![]() , (B.24)
, (B.24)
а для однолучевой схемы, изображенной на рисунке 8, - по формуле
![]() , (В.25)
, (В.25)
где - период решетки (определенный при ее изготовлении). Например, период решетки в виде оптического диска с бороздами на боковой поверхности, нанесенными с плотностью 2400 мм
будет
1/(2400) мм = 0,4166 мкм ([13]). Формулы (В.19) и (В.20) справедливы для интерференции лучей первого дифракционного максимума, описываемого формулой
![]() , (В.26)
, (В.26)
где - порядок дифракции (
±1);
- длина волны излучения лазера;
- угол падения лазерного луча;
- угол дифрагированного лазерного луча.
Поскольку интерферометр с дифракционной решеткой воспринимает перемещение любой точки боковой поверхности круглого диска, образующего измерительный стол (то есть угловое перемещение), амплитуда углового перемещения ограничена диапазоном углов, охватываемых решеткой, если дифракционная решетка расположена только на части боковой поверхности, или каким-либо другим техническим ограничением для интерферометра типа В (например, максимальным углом поворота стола вибростенда).
Другое преимущество по сравнению с интерферометром типа А заключается в том, что радиус диска, на боковой поверхности которого расположена дифракционная решетка, является точно определенной и измеримой величиной. Однако, интерферометр типа В налагает более строгие ограничения на поперечное движение (максимальный эксцентриситет 2 мкм), чем интерферометр типа А.
В.2 Методы 1А и 1В
Для интерферометров типа А и типа В и, следовательно, для методов 1А и 1В число периодов сигнала (например, по максимальной интенсивности) определяется формулой
![]() , (B.27)
, (B.27)
из которой может быть рассчитано по формуле
![]() , (В.28)
, (В.28)
где - частота угловой вибрации вибростенда;
- (средняя) частота следования полос;
![]() .
.
Амплитуду углового перемещения рассчитывают путем использования выражения для
, то есть формул (В.14) и (В.15) для интерферометра типа А, формул (В.19) и (В.20) для интерферометра типа В и формулы (В.17) для преобразования перемещения в угол поворота. Амплитуду угловой скорости
и амплитуду углового ускорения
вычисляют по формулам (В.10) и (В.12) соответственно. Для вычисления коэффициента преобразования датчика угловой вибрации используют формулы (В.4), (В.6) и (В.8).
В.3 Методы 2А и 2В
Регулируя амплитуду угловой вибрации до уровней, при которых амплитуда составляющей интенсивности с частотой, равной частоте вибрации, становится равной нулю, вычисляют амплитуду перемещения, воспринимаемого интерферометром, по формуле
![]() , (B.29)
, (B.29)
где - аргументы, соответствующие нулевым точкам функции Бесселя, которые приведены в таблице 1. Для получения углового перемещения используют формулу (17). Амплитуду угловой скорости
и амплитуду углового ускорения
вычисляют по формулам (В.10) и (В.12) соответственно. Для вычисления коэффициента преобразования датчика угловой вибрации используют формулы (В.4), (В.6) и (В.8).
В.4 Методы 3А и 3В
При работе вибростенда, возбуждающего угловую вибрацию, гармоническое перемещение пятна, воспринимаемого интерферометрами типа А и типа В, которое находится на расстоянии "эффективный радиус" от оси вращения подвижной части вибростенда, описывается формулой
![]() . (В.30)
. (В.30)
При этом выходной сигнал датчика может быть представлен формулой
![]() . (В.31)
. (В.31)
Выходной сигнал первого фотодетектора может быть представлен в виде
![]() , (B.32)
, (B.32)
где фаза модуляции состоит из начальной фазы сигнала фотодетектора и модулирующего члена
:
![]() , (В.33)
, (В.33)
где
![]() . (B.34)
. (B.34)
Амплитуду вычисляют по формуле
![]() . (В.35)
. (В.35)
Здесь предполагается, что между перемещением и членом
![]() фазовый сдвиг отсутствует. Выходной сигнал второго фотодетектора, который является квадратурным по отношению к сигналу первого фотодетектора, описывается формулой
фазовый сдвиг отсутствует. Выходной сигнал второго фотодетектора, который является квадратурным по отношению к сигналу первого фотодетектора, описывается формулой
![]() , (B.36)
, (B.36)
где ![]() .
.
В течение времени ![]() осуществляется равномерная выборка из квадратурных сигналов. Ряды значений
осуществляется равномерная выборка из квадратурных сигналов. Ряды значений ![]() и
и ![]() , выбранные в пределах
, выбранные в пределах ![]() , имеют интервал выборки
, имеют интервал выборки ![]() .
.
По этим двум квадратурным сигналам вычисляют выборочные значения перемещения по формуле
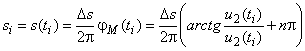 , (B.37)
, (B.37)
где 0, 1, 2...
Требуемые процедуры, в частности процедуры вычисления функции арктангенса, являются стандартными процедурами обработки оцифрованного сигнала. Параметры перемещения и
могут быть вычислены путем решения системы из
уравнений, линейных относительно параметров
![]() , (В.38)
, (В.38)
где 0, 1, 2 ...;
![]() ;
;
![]() ;
;
- постоянная величина.
соответствует числу выборочных значений, взятых в течение указанного выше интервала измерения. Параметры
,
и
вычисляют методом наименьших квадратов (синус-аппроксимация). Из этих уравнений могут быть рассчитаны амплитуда перемещения
и фазовый сдвиг
по формулам:
![]() , (В.39)
, (В.39)
![]() . (B.40)
. (B.40)
Для вычисления соответствующих значений амплитуды углового перемещения и его начальной фазы используют формулы (В.16) и (В.17). Амплитуды угловой скорости и углового ускорения
вычисляют по формулам (В.10) и (В.12) соответственно. Для вычислений модуля и фазового сдвига комплексного коэффициента преобразования датчика угловой вибрации используют формулы (В.4)-(В.9).
Приведенные выше соотношения, в особенности формулы (В.32) и (В.36), предполагают наличие идеальных условий калибровки, что на практике не выполняется. В реальных условиях сигналы фотодетекторов различаются по амплитудам ,
и сдвигам нуля
,
, а их разность фаз отклоняется от номинального значения
. Влияние неидеальности квадратурных сигналов в пределах допусков, установленных в 4.6, кратко рассмотрено в примечании 1 к 10.2 и более подробно в [7].
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ИСО 266 | - | * |
ИСО 2041:1990 | - | * |
ИСО 16063-1:1998 | IDT | ГОСТ Р ИСО 16063-1-2009 |
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
________________
Действует ГОСТ ISO 16063-1-2013.
Библиография
[1] | Von Martens H.-J. Interferometric counting methods for measuring displacements in the range 10-9 to 1 m. Metrologia, 24, No. 4, 1987, p.163-170 |
[2] | Robinson D.C., Serbyn M.R. and Payne B.F. A description of NBS Calibration Services in mechanical vibration and shock. NBS Technical Note, 1232, 1987 |
[3] | Schmidt V.A., Edelman S., Smith E.R. and Pierce E.T. Modulated photoelectric measurement of vibration. Journal of the Acoustical Society of America, 34, No. 4, 1962, p.455-458 |
[4] | Clark N.H. An improved method for calibrating reference standard accelerometers. Metrologia, 19, 1983, p.103-107 |
[5] | Link A. and Von Martens H.-J. Proposed primary calibration method for amplitude and phase response of accelerometers. ISO/TC 108/SC 3/WG 6 N 59, Sept. 1995 |
[6] | Heydemann P.L.M. Determination and correction of quadrature fringe measurement errors in interferometers. Applied Optics, 20, No. 19, 1981, p.3382-3384 |
[7] | Link A., Gerhardt J. and Von Martens H.-J. Amplitude and phase calibration of accelerometers in the nanometer range by heterodyne interferometry. SPIE, 2868, 1996, p.37-48 |
[8] | Wabinski W. and Von Martens H.-J. Time interval analysis of interferometer signals for measuring amplitude and phase of vibrations. SPIE, 2868, 1996, p.166-177 |
[9] | Sill R.D. Accelerometer calibration to 50 kHz with a quadrature laser interferometer. Proceedings NCSL, Workshop & Symposium, Session 7B, Atlanta GA July 1997, p.767-773 |
[10] | Tribolet J.M. A new phase unwrapping algorithm. IEEE Transactions on Acoustics, Speech and Signal Processing, ASSP-25, No. 2 April 1977, p.170-177 |
[11] | Von Martens H.-J. Investigations into the uncertainties of interferometric measurements of linear and torsional vibrations. Shock and vibration, 4, No. 5/6, 1997, p.327-340 |
[12] | Von Martens H.-J. and |
[13] |
|
[14] | Schlaak H.-J. Excitation of low-frequency rotational vibration. In: Journal of Low Frequency Noise, 12, 1993, No. 4, p.123-127 |
[15] | Von Martens H.-J. Generalization and analysis of the fringe-counting method for interferometric measurement of motion quantities. In: Measurement 25, 1999, p.71-87 |
[16] | Marzolf J.G. and Bull S.J. Angle Measuring Interferometer. In: The Review of Scientific Instruments, Vol. 35, No. 9, 1964, p.1212-1215 |
[17] | ISO 16063-11:1999, Methods for the calibration of vibration and shock transducers - Part 11: Primary vibration calibration by laser interferometry |
[18] | ISO 5348, Mechanical vibration and shock - Mechanical mounting of accelerometers |
[19] | BIPM/IEC/IFCC/ISO/IUPAC/IUPAP/OIML, Guide to the expression of uncertainty in measurement (GUM), 1995 |
УДК 620.178.5.05:006.354 | ОКС 17.160 |
Ключевые слова: вибрация, удар, угловая вибрация, датчики, калибровка, метод лазерной интерферометрии, неопределенность измерения | |
Электронный текст документа
и сверен по:
, 2019