ГОСТ Р ИСО/МЭК 24029-2-2024
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
Оценка робастности нейронных сетей
Часть 2
Методология использования формальных методов
Artificial intelligence. Assessment of the robustness of neural networks. Part 2. Methodology for the use of formal methods
ОКС 35.020
Дата введения 2025-01-01
Предисловие
1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "Институт развития информационного общества" (ООО "ИРИО") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 164 "Искусственный интеллект"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 28 октября 2024 г. № 1542-ст
4 Настоящий стандарт идентичен международному стандарту ИСО/МЭК 24029-2:2023* "Искусственный интеллект (ИИ). Оценка робастности нейронных сетей. Часть 2. Методология использования формальных методов" (ISO/IEC 24029-2:2023 "Artificial intelligence (AI) - Assessment of the robustness of neural networks - Part 2: Methodology for the use of formal methods", IDT).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
Введение
Нейронные сети широко применяются для выполнения сложных задач в различных ситуациях, таких как обработка изображений и естественного языка, а также прогностическое обслуживание. Модели качества системы искусственного интеллекта (ИИ) включают определенные характеристики, в том числе робастность. Например, стандарт [1], который распространяет международные стандарты серии SQuaRE [2] на системы ИИ, в своей модели качества определяет, что робастность является одной из характеристик надежности. Способность системы поддерживать свой уровень производительности в различных условиях может быть продемонстрирована с помощью статистического анализа, однако для доказательства наличия данной способности требуется проведение формального анализа. В этом отношении формальные методы могут комбинироваться с другими методами повышения доверия к робастности нейронной сети.
Формальные методы - это математические приемы для строгой спецификации и верификации программных и аппаратных систем с целью доказательства их корректности. Формальные методы используются для формального рассуждения о нейронных сетях и проверки их соответствия требуемым свойствам робастности. Например, рассмотрим классификатор на основе нейронной сети, который принимает в качестве входных данных изображение, а в качестве выходных данных возвращает метку из заданного набора классов (например, автомобиль или самолет). Такой классификатор может быть формально представлен в виде математической функции, которая принимает интенсивность пикселей изображения в качестве входных данных, вычисляет вероятности для каждого возможного класса из определенного набора и возвращает метку, соответствующую наибольшей вероятности. Затем эта формальная модель может быть использована для математического обоснования работы нейронной сети при изменении входного изображения. Например, предположим, что при наличии конкретного изображения, для которого нейронная сеть выводит метку "автомобиль", можно задать следующий вопрос: "выводит ли сеть другую метку, если значение произвольного пикселя на изображении изменяется?". Этот вопрос может быть сформулирован как формальное математическое утверждение, которое является истинным либо ложным для данной нейронной сети и изображения.
Классический подход к использованию формальных методов состоит из трех основных этапов, описанных в настоящем стандарте. На первом этапе анализируемая система формально определяется в модели, которая точно отражает все возможные варианты поведения системы. На втором этапе требование формулируется в виде математического выражения. На заключительном третьем этапе один из формальных методов, например решатель, абстрактная интерпретация или проверка с помощью модели используется для оценки соответствия системы заданному требованию, что приводит к доказательству либо к контрпримеру, либо к неоднозначному результату.
В настоящем стандарте описаны несколько доступных формальных методов. Представлены критерии, применимые для оценки робастности нейронных сетей и определены способы проверки нейронных сетей с помощью формальных методов на каждой стадии жизненного цикла системы ИИ. При использовании формальных методов могут возникнуть сложности с точки зрения масштабируемости, однако они по-прежнему применимы ко всем типам нейронных сетей, выполняющих различные задачи с несколькими типами данных. Формальные методы уже давно используются в традиционных программных системах, однако их применение по отношению к нейронным сетям началось сравнительно недавно и все еще является активной областью исследований.
Настоящий стандарт направлен на то, чтобы помочь разработчикам ИИ, которые используют нейронные сети и перед которыми стоит задача оценить их робастность на соответствующих стадиях жизненного цикла системы ИИ. Помимо формальных методов, описанных в настоящем стандарте, более детальный обзор методов оценки робастности нейронных сетей представлен в ISO/IEC TR 24029-1.
1 Область применения
Настоящий стандарт определяет методологию применения формальных методов для оценки свойств робастности нейронных сетей. Основное внимание уделяется тому, как выбирать и использовать формальные методы, а также управлять ими для подтверждения свойств робастности.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты [для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения)]:
ISO/IEC 22989:2022, Information technology - Artificial intelligence - Artificial intelligence concepts and terminology (Информационные технологии. Искусственный интеллект. Термины и определения)
ISO/IEC 23053:2022, Framework for Artificial Intelligence (AI) Systems Using Machine Learning (ML) [Экосистема разработки систем искусственного интеллекта (ИИ) с использованием машинного обучения (МО)]
3 Термины и определения
В настоящем стандарте применены термины и определения по ИСО/МЭК 22989:2022, ИСО/МЭК 23053:2022.
ИСО и МЭК поддерживают терминологические базы данных для применения в сфере стандартизации по следующим адресам:
- онлайн-платформа ИСО: доступна по ссылке: http://www.iso.org/obp;
- Электропедия МЭК: доступна по ссылке: http://www.electropedia.org/.
3.1 область (domain): Набор возможных входных данных для нейронной сети, характеризуемый атрибутами окружения.
Примеры
1 Нейронная сеть, выполняющая задачу обработки естественного языка, манипулирует текстами, состоящими из слов. Несмотря на то, что количество возможных различных текстов не ограничено, максимальная длина каждого предложения всегда ограничена. Таким образом, атрибутом, описывающим данную область, может быть максимально допустимая длина для каждого предложения.
Примечание - Атрибут используется для описания объекта с конечным числом атрибутов, даже если область может быть неограниченной.
3.2 атрибут (attribute): Свойство или характеристика объекта, которая может быть количественно или качественно различима человеком или автоматизированными средствами.
Примечание - См. [5], (3.2), измененный - "сущность" заменена на "объект".
3.3 область с конечным числом объектов (bounded domain): Множество, содержащее конечное число объектов.
Примеры
2 Количество всех допустимых предложений на английском языке бесконечно, следовательно, данная область является неограниченной.
Примечание - Количество объектов в неограниченной области бесконечно.
3.4 объект с конечным числом атрибутов (bounded object): Объект, представленный конечным числом атрибутов.
Примечание - В отличие от объекта с конечным числом атрибутов существуют объекты с неограниченным числом атрибутов.
3.5 стабильность (stability): Свойство нейронной сети сохранять неизменными выходные данные при изменении входных данных.
Примечание - В более стабильной нейронной сети выходные данные с меньшей вероятностью подвергнутся изменениям, если на входе изменения проявляются в зашумленных данных.
3.6 чувствительность (sensitivity): Степень, в которой выходные данные нейронной сети изменяются при изменении входных данных.
Примечание - В более чувствительной нейронной сети выходные данные изменятся с большей вероятностью, если изменения на входе являются информативными.
3.7 архитектура (системы) (architecture): Основные понятия или свойства системы в ее окружении, воплощенной в ее элементах, отношениях и конкретных принципах ее проекта и развития.
3.8 релевантность (relevance): Упорядоченная относительная значимость влияния одного потока входных данных на выходные данные нейронной сети по сравнению со всеми другими входными данными.
3.9 критерий (criterion): Правило, на котором могут базироваться суждение или решение, или правило, по которому продукт, услуга, результат или процесс могут быть оценены.
Примечание - Определение приведено в [6], (3.1.6).
Примечание - Определение приведено в [7], (3.54).
3.11 достижимость (reachability): Свойство, описывающее, может ли агент ИИ достичь набора состояний в заданном окружении.
3.12 кусочно-линейная нейронная сеть (piecewise neural network): Нейронная сеть, использующая кусочно-линейные функции активации.
Примечание - Примерами функций линейной активации являются Rectify linear unit или MaxOut.
3.13 бинаризованная нейронная сеть (binarized neural network): Нейронная сеть, основные параметры которой являются двоичными.
3.14 рекуррентная нейронная сеть (recurrent neural network): Нейронная сеть, в которой как выходные данные предыдущего слоя, так и результаты предыдущего шага вычислений подаются на вход текущему слою.
3.15 трансформерная нейронная сеть/трансформер (transformer neural network/transformer): Нейронная сеть, использующая механизм внимания (self-attention) для определения зависимости между входными данными во время обработки.
3.16 проверка с помощью модели (model checking): Доказательство справедливости формального утверждения теории.
3.17 структурное тестирование (structural-based testing)*: Динамическое тестирование, для которого тесты являются результатом анализа структуры элемента тестирования.
________________
* Синонимами структурного тестирования являются тестирование на основе структуры, тестирование методом прозрачного ящика.
Примечания
1 Структурное тестирование не ограничено использованием на уровне компонентов, а может использоваться на всех уровнях, например при покрытии пункта меню, как части тестирования системы.
2 Методика включает в себя тестирование ветвей, тестирование решений и тестирование операторов.
3 Определение приведено в [8], (3.80).
3.18 тестирование на основе спецификации (specification-based testing)**: Тестирование, основным базисом которого являются внешние вводы и выводы элемента тестирования, обычно на основе спецификации, а не ее реализация в исходном коде или исполняемом программном обеспечении.
________________
** Синонимом тестирования на основе спецификации является тестирование методом закрытого ящика.
Примечание - Определение приведено в [8], (3.75).
4 Сокращения
В настоящем стандарте применены следующие сокращения:
БНС - бинаризованные нейронные сети;
ГНС - графовые нейронные сети;
ИИ - искусственный интеллект;
КЛНС - кусочно-линейные нейронные сети;
МРТ - магнитно-резонансная томография;
РНС - рекуррентные нейронные сети;
РСА - радар с синтезируемой апертурой;
ЧЦЛП - частично-целочисленное линейное программирование;
ReLU - функция активации ReLU;
SMC - задача выполнимости по модулю выпуклости;
SMT - теории выполнимости по модулю.
5 Оценка робастности
5.1 Общие положения
В контексте нейронных сетей спецификации робастности обычно представляют собой различные условия, которые могут естественным или состязательным образом измениться в зависимости от сферы деятельности, где применяется нейронная сеть (см. 5.2).
Примеры
1 Рассмотрим нейронную сеть, которая обрабатывает медицинские снимки, где входные данные, поступающие в нейронную сеть, собираются с помощью медицинского устройства, которое сканирует пациентов. Получение нескольких снимков одного и того же пациента, естественно, не приводит к получению идентичных снимков. Это связано с возможным незначительным изменением положения пациента или освещения в комнате, отражением объекта или добавлением случайного шума на этапах пост-обработки изображения.
2 Рассмотрим нейронную сеть, которая обрабатывает выходные данные датчиков и бортовых камер самоуправляемого транспортного средства. Вследствие динамичной природы окружающего мира, примерами которой могут служить погодные условия, загрязнение окружающей среды и условия освещения, входные данные для нейронной сети могут иметь широкие вариации различных атрибутов.
Робастность нейронной сети, как правило, не изменяется вследствие изменений, происходящих во внешнем окружении. Затем робастность нейронной сети может быть проверена на соответствие изменениям таких условий окружения с помощью соответствующих прокси-спецификаций в сфере применения нейронной сети.
Свойства робастности могут быть локальными или глобальными [10]. Чаще всего проверяются локальные, а не глобальные свойства робастности, поскольку их легче определить. Свойства локальной робастности задаются в отношении выборки входных данных из тестового набора данных. Например, если изображение правильно классифицировано как автомобиль, свойство локальной робастности может указывать, что все изображения, сгенерированные поворотом исходного изображения на 5 градусов, также классифицируются как автомобиль. Недостатком проверки локальных свойств робастности является то, что гарантии являются локальными для предоставленной тестовой выборки и не распространяются на другие выборки в наборе данных. Свойства глобальной робастности, наоборот, определяют гарантии, которые сохраняются детерминированно для всех возможных входных данных [11]. Для сфер применения, в которых входные функции имеют семантическое значение, например системы предупреждения столкновения в воздухе, глобальные свойства могут быть заданы путем определения допустимых входных значений для входных функций, предполагаемых в реальном развертывании. Определение значимых входных значений является более сложной задачей в условиях, когда отдельные функции не имеют семантического значения. Набор свойств робастности, описанных в данном разделе, не является исчерпывающим и, возможно, в будущем будет дополнен.
5.2 Понятие области
Большинство систем ИИ, включая нейронные сети, предназначены для работы в определенном окружении, где их эксплуатационные характеристики могут быть определены и оценены (типичные показатели оценки можно найти в ISO/IEC TR 24029-1:2021, таблица 1). Робастность, являясь одним из ключевых свойств нейронной сети, неотделима от области, в которой она функционирует. Существование области с конечным числом объектов подразумевается во многих приложениях для нейронных сетей (например, классификация изображений предполагает наличие изображений определенного качества и в определенном формате).
Парадигма агента, представленная на рисунке 1 и воспроизведенная по ИСО/МЭК 22989, демонстрирует, что агент воспринимает свое окружение и предпринимает действия для достижения определенных целей. В представленной парадигме особое внимание уделяется различным концепциям агента ИИ и окружения. Понятие области отражает ограничения современной технологии, когда нейронная сеть, являясь определенным типом агента ИИ, технически способна достичь заданной цели только в том случае, если она оперирует соответствующими входными данными.
Концепция области основывается на следующих принципах:
- область определяется четко установленным набором атрибутов (т.е. область содержит объекты с конечным числом атрибутов);
- спецификация области должна быть достаточной для того, чтобы система ИИ выполняла одну или несколько заданных задач по назначению;
- данные, используемые для обучения, должны быть репрезентативными по отношению к данным, на основе которых предполагается делать заключение.
Определение области включает в себя указание всех атрибутов данных, необходимых для достижения нейронной сетью своей цели.
Некоторые популярные сферы применения нейронных сетей охватывают приложения в области зрения, обработки речи и робототехники. Для описания этих областей и, что более важно, их изменчивости, как правило, используются числовые атрибуты. Примерами могут служить форма объекта на изображении, интенсивность некоторых пикселей или амплитуда звукового сигнала.
Однако другие области могут быть выражены с помощью нечисловых атрибутов, включая обработку естественного языка, графику и масштабный код (использование автоматического обучения на основе существующего кода). В этих случаях атрибуты могут быть нечисловыми, например слова в предложении или ребра в графе.
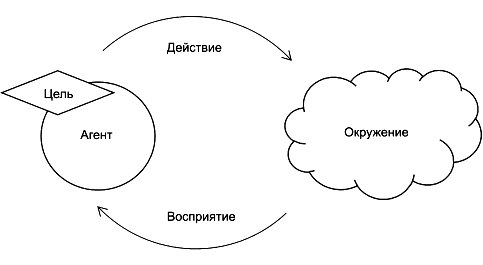 |
Рисунок 1 - Парадигма агента
Атрибуты позволяют разработчику ИИ сгенерировать в области другую сущность из уже существующей сущности. Атрибуты должны быть ограничены в спецификации робастности.
5.3 Стабильность
5.3.1 Свойство стабильности
Свойство стабильности выражает степень, в которой выходные данные нейронной сети остаются неизменными при изменении ее входных данных в определенной области. Проверка стабильности в области, где предполагается сохранение поведения, позволяет проверить, может ли сохраняться и производительность. Свойство стабильности может быть выражено в закрытой форме (например, "находится ли изменчивость ниже этого порогового значения?") либо в открытой форме (например, "какова самая большая стабильная область?").
Для доказательства того, что нейронная сеть сохраняет работоспособность при наличии зашумленных входных данных, должно быть выражено свойство стабильности. Свойство стабильности следует использовать в областях, которые, с точки зрения ожидаемого поведения, обладают некоторыми свойствами регулярности. И напротив, в хаотической системе следует избегать использования этого свойства, поскольку это не является релевантным. Однако, даже когда регулярность области нелегко подтвердить (например, в хаотической системе), свойство стабильности может быть использовано для сравнения нейронных сетей.
5.3.2 Критерий стабильности
Критерий стабильности определяет, сохраняется ли свойство стабильности в конкретной области, а не только для определенного набора примеров или для подмножества области, например для обучающих или валидационных наборов данных. Критерий стабильности может быть проверен с помощью формальных методов, описанных в 6.2.
Критерий стабильности должен определять по крайней мере область значений и пространство выходных значений, в которых он был измерен, а также ожидаемое свойство стабильности.
Критерий стабильности может быть использован в качестве одного из критериев для сравнения моделей.
Для обеспечения точности сравнения моделей необходимо соблюдение следующих требований:
- нейронные сети выполняют одинаковую задачу;
- критерий стабильности используется в той же области;
- критерий стабильности подтверждает ту же цель.
Например, для нейронной сети, выполняющей классификацию, критерий стабильности оценивает, выполняется ли конкретное решение для каждого входа в области. Для нейронной сети, выполняющей регрессию, критерий стабильности оценивает, остается ли регрессия стабильной в области.
Для применения критерия стабильности он должен опираться на ранее существовавшую информацию о предполагаемом выходе нейронной сети, которая может быть известна разработчику ИИ или может быть определена другим способом (с использованием систем моделирования или решателей). Критерий стабильности подходит для оценки робастности в области, в которой ожидаемый ответ является аналогичным. По этой причине рекомендуется использовать критерий стабильности для любого процесса принятия решений, обрабатываемого нейронной сетью (например, для классификации и идентификации).
5.4 Чувствительность
5.4.1 Свойство чувствительности
Свойство чувствительности нейронной сети выражает степень, в которой выходные данные нейронной сети изменяются при изменении ее входных данных. Для оценки робастности нейронной сети в области иногда необходимо проверять изменчивость системы. Для этой цели следует проводить анализ чувствительности для определения того, насколько сильно меняется система и какие входные данные могут повлиять на это отклонение. Затем этот анализ сравнивается с ранее определенным предполагаемым показателем производительности системы.
Анализ чувствительности должен использоваться в области, если он применяется для определения того, остается ли нейронная сеть ограниченной. Как и в случае со свойством стабильности, анализ чувствительности больше подходит для областей применения, которые обладают некоторыми свойствами регулярности.
5.4.2 Критерий чувствительности
Поскольку критерий чувствительности выражает свойство в области (а не в конкретном наборе примеров), его можно проверить с помощью формальных методов, описанных в 6.2.
Критерий чувствительности должен определять область, в которой он был измерен, и какие пороги чувствительности подлежат проверке.
Критерий чувствительности может быть использован для сравнения различных архитектур нейронных сетей или обученных моделей. Для обеспечения точности сравнения моделей необходимо соблюдение следующих требований:
- нейронные сети выполняют одинаковую задачу,
- критерий чувствительности используется в той же области,
- критерий чувствительности подтверждает ту же цель.
Критерий чувствительности особенно подходит для нейронных сетей, выполняющих задачи интерполяции или регрессии. Для таких задач критерий чувствительности позволяет получить прямое доказательство против абсолютной/эталонной истины, которая может распространяться на область.
Критерий чувствительности обычно выражается в закрытой форме как пороговое значение изменчивости в определенной области вариации входных данных.
5.5 Релевантность
5.5.1 Свойство релевантности
Свойство релевантности в нейронной сети выражает порядок влияния входных данных на выходные и может быть вычислена для каждой единицы выходных данных. Релевантность выражает индивидуальное влияние каждой единицы входных данных на результат, полученный на выходных данных. Для каждого выхода совокупность входных данных может быть отсортирована по степени их воздействия на этот выход. Свойство релевантности проверяет, удовлетворяет ли достигнутый порядок требованиям, сформулированным разработчиком ИИ. Свойство релевантности можно проверить с помощью различных методов для оценки влияния каждой единицы входных данных. В отличие от свойств стабильности и чувствительности свойство релевантности может привести к разногласиям между экспертами, ответственными за его оценку. Две нейронные сети могут иметь очень разные результаты по свойствам релевантности и по-прежнему считаться приемлемыми. Необходимо включить в протокол сравнения метод разрешения противоречивых результатов. Например, для разрешения определенных ситуаций протокол может использовать систему голосования.
Свойство релевантности следует использовать в тех случаях, когда нейронная сеть выполняет задачу, которая может быть выполнена человеком. Для таких случаев следует корректно определить и проверить обоснование выходных данных нейронной сети. Свойство релевантности определяет, можно ли гарантировать производительность системы по правильным причинам. В этом случае робастность системы будет оправдана, а не просто заявлена. Эта проверка может быть выполнена вручную человеком-оператором или автоматически с использованием эталонов, которые были проверены ранее.
5.5.2 Критерий релевантности
Критерий релевантности выражает свойство релевантности в области, которое требует демонстрации связи между каждым входом и выходом. Для этого необходим метод, способный разделить влияние каждого входа. Для достижения этой цели могут быть использованы формальные методы, основанные на символическом, логическом исчислении или вычислительных методах. Примеры формальных методов, доступных для проверки критерия релевантности, приведены в 6.2.
Критерий релевантности должен отражать область, в которой он был измерен, и ожидаемые результаты. Если ожидаемые результаты не могут быть определены априори, критерий релевантности должен по крайней мере представлять методологию оценки результатов.
Критерий релевантности может быть использован для сравнения различных архитектур нейронных сетей или результатов обучения. Для обеспечения точности сравнения необходимо соблюдение следующих требований:
- нейронные сети выполняют одинаковую задачу,
- критерий релевантности используется в той же области,
- критерий релевантности подтверждает ту же цель.
Пример - Для нейронной сети, выполняющей задачу классификации, критерий релевантности может быть использован для проверки того, расположены ли наиболее релевантные пиксели на определенной части идентифицируемого объекта (например, колеса для идентификации транспортного средства). Для нейронной сети, выполняющей прогностический анализ временных рядов, критерий релевантности может быть использован для проверки соответствия предсказанного события логическим выводам, приемлемым для разработчика ИИ (например, сигнал, оповещающий о перегреве двигателя, который вскоре выйдет из строя).
Критерий релевантности может быть выражен в различных задачах при условии, что результат может быть проанализирован разработчиком ИИ. Критерий релевантности может использоваться, например, в задачах классификации, обнаружения, интерполяции или регрессии. Проверка критерия релевантности может быть автоматизирована или же основываться на оценке человека для определения того, является ли полученный результат приемлемым. В случае если проверка основывается на оценке человека, полученное им решение может быть передано в качестве нового требования для автоматизации тестов в максимально возможной степени.
5.6 Достижимость
5.6.1 Свойство достижимости
Свойство достижимости нейронной сети выражает многоступенчатую производительность сети в сочетании с ее окружением эксплуатации. Этот тип свойств применим к системам, работающим в парадигме агента, как показано на рисунке 1. Свойство достижимости проверяет, может ли агент ИИ достичь набора состояний при использовании нейронной сети для управления собой в заданном окружении. Свойство достижимости может определить набор состояний сбоя, которых агент ИИ должен избегать, либо набор состояний цели, которых он должен достичь.
Для выражения этого типа свойства требуется определить модель окружения, описывающую влияние действия агента ИИ на его следующее состояние. Окружение может развиваться как детерминистически, так и стохастически. В детерминированном окружении свойство достижимости показывает, может ли агент ИИ достичь определенного набора состояний.
5.6.2 Критерий достижимости
Критерий достижимости выражает свойство достижимости в заданном наборе начальных состояний. Для детерминированного окружения это проверяется с помощью методов, описанных в 6.2.4. Для стохастического окружения критерий выражает вероятность достижения набора состояний. Данная вероятность может быть определена с помощью методов, описанных в 6.2.5.
Критерий достижимости должен удовлетворяться для заданного набора начальных состояний, который может быть задан как часть критерия. Для определения набора начальных состояний, для которых нейронная сеть удовлетворяет критерию, в качестве альтернативы можно использовать формальные методы. Преимущество использования критерия достижимости для оценки нейронной сети заключается в том, что он обеспечивает метрику производительности сети в замкнутом окружении. Таким образом, он может быть использован для выражения свойств безопасности высокого уровня, выходящих за рамки свойств входа-выхода.
Например, в случае с системой предупреждения столкновения в воздухе с применением нейронной сети критерий достижимости может выражать требование избегать достижения набора состояний столкновения с учетом конкретной модели окружения.
6 Применимость формальных методов к нейронным сетям
6.1 Типы рассматриваемых нейронных сетей
6.1.1 Архитектуры нейронных сетей
6.1.1.1 Общие положения
При проектировании и разработке нейронных сетей могут использоваться различные типы архитектур. Формальные методы верификации нейронных сетей зависят от их архитектуры. В 6.1.1 описываются формальные методы, разработанные для следующих архитектур нейронных сетей: кусочнолинейных, бинаризованных, рекуррентных нейронных сетей и трансформерных нейронных сетей. Хотя представленный перечень нейронных сетей не является исчерпывающим и могут появиться новые архитектуры и соответствующие формальные методы верификации, он охватывает большое количество существующих архитектур нейронных сетей и применяемых методов. Более подробная информация об упомянутых методах представлена в 6.2.
6.1.1.2 Кусочно-линейные нейронные сети
КЛНС [12] не используют нелинейные функции, такие как сигмоида или гиперболический тангенс, но они могут применять линейные преобразования, такие как полносвязные или сверточные слои, слои объединения, такие как MaxPooling, и такие операции, как пакетная нормализация или отсев, которые сохраняют кусочную линейность. КЛНС составляют большую часть современных нейронных сетей.
В [13] предложены формальные методы верификации, которые сначала преобразуют КЛНС в математически эквивалентный набор линейных классификаторов, а затем интерпретируют каждый линейный классификатор по признакам, доминирующим в его предсказании. Другие методы верификации рассматривают КЛНС как глобальную оптимизационную задачу и используют такой метод, как решатель SMT. В [14] формальная проверка робастности представлена в виде смешанной целочисленной линейной программы. Другие методы представлены в ISO/IEC TR 24029-1. Дополнительные методы проверки включают Fast-Lin - Fast-Lip [15], CROWN [16] и формальный анализ безопасности [17].
6.1.1.3 Бинаризованные нейронные сети
В БНС все операции являются двоичными, что делает эти сети эффективными с точки зрения памяти и вычислений, позволяя использовать специализированные алгоритмы для быстрого умножения двоичных матриц. С использованием такой архитектуры были созданы различные встраиваемые приложения, начиная от классификации изображений и заканчивая обнаружением объектов [18].
Формальная проверка таких БНС была достигнута путем создания точного представления БНС в виде булевой формулы таким образом, что все допустимые пары входов и выходов данной сети являются решениями булевой формулы [19]. Затем проверка достигается с помощью таких методов, как выполнимость булевых формул и целочисленное линейное программирование [18].
6.1.1.4 Рекуррентные нейронные сети
РНС обеспечивают точную и эффективную обработку последовательных данных во многих сферах деятельности, включая речь, финансы и текст. На каждом временном шаге РНС обновляет свое внутреннее состояние на основе входных данных на этом шаге и внутреннего состояния на предыдущих шагах. Окончательный результат получается по окончании последовательной обработки всех входных данных.
РНС, используемую в качестве конечного классификатора, можно рассматривать как машину с бесконечным числом состояний [20]. Для такой системы с бесконечным состоянием конечный автомат может быть обучен с использованием методов автоматизированного обучения, таких как теневая модель, аппроксимирующая рассматриваемую систему. Затем теневую модель можно использовать для проверки соответствия РНС спецификации, например с помощью методов проверки модели. Помимо проверки модели для доказательства локальной надежности РНС, используемых при классификации данных изображений, датчиков аудио и движения [21] может быть применена абстрактная интерпретация.
6.1.1.5 Трансформерные сети
Трансформерные сети - это тип моделей глубокого обучения с архитектурой кодер-декодер [22]. С помощью кодировщика трансформер начинает с генерации представлений или вложений для каждой отдельной части входа. При этом трансформатор использует модель внимания self-attention для агрегирования информации из всех других частей входа, чтобы сгенерировать новое внутреннее представление для входа. Затем этот шаг повторяется несколько раз параллельно для всех частей входа, последовательно генерируя новые внутренние представления. Декодер работает аналогично и генерирует одну часть выхода за раз. При этом декодер обращается к другим ранее сгенерированным частям выхода, а также учитывает внутренние представления, сгенерированные кодировщиком. Таким образом, трансформеры содержат сложные слои внутреннего внимания, которые создают множество проблем для верификации, включая перекрестную нелинейность и зависимость от перекрестного положения. Слои внутреннего внимания являются наиболее сложными элементами формальной верификации робастности трансформаторов.
В [23] предлагается метод формальной верификации робастности трансформеров: слой трансформера разбивается на несколько подслоев, и в каждом подслое выполняются некоторые операции над нейронами этого подслоя. Выполняемые операции в целом делятся на три категории:
- линейные преобразования,
- унарные нелинейные функции,
- операции в модели self-attention.
Каждый подслой рассматривается как содержащий n позиций в последовательности, причем каждая позиция содержит группу нейронов. Для каждой из этих позиций границы вычисляются от первого до последнего подслоя.
6.1.2 Тип входных данных нейронных сетей
6.1.2.1 Общие положения
В задачи нейронных сетей входит обработка различных типов входных данных для получения нескольких возможных типов выходных данных (см. 6.1.1). Приложения нейронных сетей работают с такими типами данных, как изображение, временной ряд, естественный язык, графики или таблицы. Хотя представленный перечень не является исчерпывающим и могут появиться новые приложения, он охватывает значительную часть типов данных, пригодных для обработки нейронными сетями.
Однако формальные методы могут иметь ограничения на то, какой тип данных может быть эффективно проанализирован. Как правило ограничения накладываются на:
- масштабируемость их вычислений в зависимости от размера входных данных (и следовательно, сети);
- характер входных данных для моделирования возмущений.
При применении формальных методов широко распространено ограничение масштабируемости. Нейронная сеть предназначена для одновременной обработки нескольких входных векторов. Однако математически доказать свойство для всей области (т.е. для каждого входного вектора) по своей сути сложнее, чем вычислить результат для некоторых точек внутри области.
Второе ограничение вытекает из характера области, представленной входными данными, и возможности моделировать формальное доказательство в данной области. Это ограничение зависит от представления атрибутов, которые используются для описания области (см. 5.2). В некоторых случаях атрибуты являются числовыми, что позволяет легко смоделировать некоторую значимую изменчивость атрибутов.
6.1.2.2 Данные изображения
Возможность обработки изображений - одна из причин недавнего успеха применения нейронных сетей. Способность нейронных сетей обрабатывать несколько типов изображений (например, с камеры, МРТ, радара, гидролокатора и РСА) различного разрешения или даже видеопотоки способствовала их широкому внедрению.
С точки зрения формального метода покрытие входного пространства определяется размером матрицы, умноженным на количество измерений каждого пикселя. Обработка больших изображений может оказаться сложной задачей для многих формальных методов, которые привязывают символ к каждому измерению каждого входа.
Для демонстрации изменений во входном пространстве для изображений можно определить несколько атрибутов. Например, освещенность изображения может быть выражена изменением интенсивности пикселей. Изменения окружения могут быть более сложными, однако при имеющейся возможности проведения аналитического определения изменения могут быть выражены непосредственно в значениях пикселей, что позволяет напрямую применять формальные методы. В случае невозможности проведения аналитического определения изменения могут быть выражены с помощью аппроксимации модели, примененной к изображению (например, с использованием маски на изображении).
6.1.2.4 Данные естественного языка
Нейронные сети могут обрабатывать типы данных естественного языка, основанных на тексте и речи. Широкомасштабное внедрение интеллектуальных аудиоустройств и способность языковых моделей генерировать легко понятный текст наглядно демонстрируют эту способность. Данные естественного языка часто проходят предварительную обработку перед передачей в нейронную сеть.
Некоторые вариации входных данных можно легко выразить формально, например путем добавления шума к записи. Другие вариации могут быть намного сложнее, например удаление или добавление слова в предложение без изменения его семантики или рассмотрение разной семантики в предложении для разных диалектов одного и того же языка. Формальные методы, применяемые в этой настройке, касаются как конвейера предварительной обработки, так и нейронной сети [21].
6.1.2.5 Графовые данные
ГНС широко применяются в молекулярной биологии, используются для выявления мошенничества и в социальных науках для обработки графовых данных для различных задач, таких как классификация узлов, предсказание связей и классификация графов. Несколько свойств робастности ГНС были определены на основе возмущающих функций узлов, а также возмущающей структурной информации, такой как добавление или удаление ребер. Возмущения, основанные на признаках, являются непрерывными и могут формально обрабатываться аналогично изменениям интенсивности пикселей в изображениях. Структурные возмущения, напротив, являясь дискретными, требуют разработки специализированных формальных методов.
6.1.2.6 Табличные данные
Многие прикладные сферы деятельности, такие как финансы, здравоохранение и логистика, в значительной степени зависят от табличных данных, что позволяет этим приложениям комбинировать данные различных типов (например, числовые, символьные, текстовые, категориальные) и выражать отношения между элементами. Табличные данные могут содержать как очень большое количество строк, так и иногда отклонения внутри каждой строки, которые почти не поддаются прогнозированию.
Применение формальных методов к табличным данным с разнородными типами данных, представленными в 6.1.2.2-6.1.2.5, может привести к описанным выше ограничениям.
6.2 Типы применимых формальных методов
6.2.1 Общие положения
6.2.1.1 Обзор типов применимых формальных методов
В 6.2 описаны существующие формальные методы, применимые к оценке робастности нейронных сетей. Эти методы могут быть классифицированы на основе следующих критериев:
- они могут быть полными или неполными;
- они могут быть детерминированными или недетерминированными;
- они могут применять верификаторы, использующие тестирование методом прозрачного ящика или закрытого ящика;
- они могут быть основаны на традиционной арифметике вещественных чисел или компьютерной арифметике вещественных чисел.
6.2.1.2 Полные или неполные верификаторы
Полные верификаторы дают точные ответы. Они доказывают свойство робастности либо приводят контрпример, демонстрирующий конкретное нарушение этого свойства. Недостаток применения полных верификаторов заключается в том, что они неэффективны при проверке робастности нейронных сетей, обеспечивающих высокую точность для сложных наборов данных. Неполные верификаторы напротив используют методы абстракции, которые масштабируются до высокоточных нейронных сетей. Однако неполные верификаторы могут не доказать, что свойство робастности действительно сохраняется.
6.2.1.3 Детерминированные или недетерминированные верификаторы
Когда детерминированный верификатор подтверждает свойство робастности, то это свойство сохраняется для каждого входа в пределах указанной области входа. Однако некоторые модели, такие как сети смешивания плотности или вариационные автокодировщики, применяемые в различных предметных областях, таких как прогнозирование запасов, распознавание речи и генерация изображений, не дают детерминированных выходных данных, а скорее создают распределение. Для таких сетей формальные методы могут быть использованы для детерминированного вычисления параметров распределения выходных данных, которые справедливы для всех входных данных (например, в виде среднего значения или стандартного отклонения), либо для предоставления формальных гарантий их робастности с высокой вероятностью.
6.2.1.4 Верификаторы, использующие тестирование методом прозрачного ящика (располагающие сведениями о модели) или закрытого ящика (не располагающие сведениями о модели)
Верификаторам, использующим тестирование методом прозрачного ящика, требуется доступ к модели (т.е. к внутреннему представлению сети), включая архитектуру и изученные параметры. Однако данные верификаторы не требуют доступа к обучающим данным или алгоритму, используемому для обучения нейронной сети. Верификаторы, использующие тестирование методом прозрачного ящика, неприменимы в областях, где развернутая модель недоступна (например, зашифрована). В таких случаях могут быть применены верификаторы, использующие тестирование методом закрытого ящика. Для функционирования таких верификаторов, использующих тестирование методом закрытого ящика, требуется только возможность запуска модели на выбранных входных данных. Это может приводить к меньшей точности этого верификатора относительно верификатора, использующего тестирование методом прозрачного ящика.
6.2.1.5 Верификаторы арифметики вещественных чисел или верификаторы компьютерной арифметики вещественных чисел
Большинство верификаторов предполагают, что вычисления нейронной сети выполняются с идеальной арифметикой вещественных чисел (т.е. без ошибок округления). Таким образом, гарантии робастности верификаторов не распространяются на фактические вычисления, выполняемые с использованием арифметики вещественных чисел с плавающей запятой, или на другую нестандартную компьютерную арифметику вещественных чисел. Голосовые верификаторы (связанные с применяемой арифметикой), напротив, учитывают семантику компьютерной арифметики вещественных чисел и гарантируют, что их выходные данные отражают выходные данные нейронной сети, возможные в рамках этой семантики. В некоторых случаях верификаторы могут также учитывать изменения в порядке вычислений (например, когда используются только операции "остаток" [24] с правильным округлением). В случаях когда операции [24] с правильным округлением не используются, тогда верификатор может приблизить округление, выполненное для каждого оператора.
6.2.2 Решатель
Решатели ЧЦЛП [25] и задача выполнимости формул в теориях (SMT) [11], [26] относятся к следующим методам верификации: детерминированной верификации, верификации методом прозрачного ящика и, как правило, к полной верификации. Они кодируют все вычисления данной нейронной сети как набор ограничений, а затем используют эти ограничения для доказательства свойств робастности.
В случаях, когда методы полной верификации недоступны, используются методы неполной верификации. Некоторые нелинейные функции активации (такие как гиперболические функции, включая сигмовидную и гиперболический тангенс) слишком сложны для точного кодирования, по этой причине решатели аппроксимируют их звуковыми абстракциями. Другие нелинейные функции активации (такие как ReLU) могут быть точно закодированы.
Для доказательства заданного свойства робастности нейронная сеть и ограничения на входные данные кодируются как задача ЧЦЛП, которая затем может быть использована для оптимизации ограничения робастности. Свойство робастности считается доказанным в случае, если границы ограничения робастности удовлетворяют ограничениям. Решатели SMT ставят проблему верификации как вопрос о выполнимости ограничения, которое выполняется либо нет.
Некоторые методы включают символическую линейную релаксацию, которая вычисляет более жесткие границы для выходов нейронной сети, отслеживая ослабленные зависимости между входами, а затем использует направленное уточнение ограничений (уточнение выходной релаксации путем разделения набора начальных или промежуточных нейронов) для проверки свойств безопасности [27]. Другие методы предлагают алгоритм, основанный на SMC, в сочетании с предварительной обработкой на основе SMC для вычисления конечных абстракций автономных систем, управляемых нейронной сетью [28].
6.2.3 Абстрактная интерпретация
Абстрактная интерпретация представляет собой общую основу для анализа больших и сложных детерминистских [29] и вероятностных [30] систем масштабируемым образом. В контексте нейронных сетей данный метод используется для обеспечения неполного, детерминированного метода прозрачного ящика, который осуществляет верификацию робастности больших нейронных сетей. Процесс верификации заключается в следующем:
- во-первых, предоставленные тестовые входные данные и спецификация робастности в совокупности определяют область, содержащую все возможные возмущенные входные данные, которые могут быть получены путем изменения входных данных на основе спецификации робастности. Эта область может быть представлена точно или приблизительно с использованием определенных геометрических фигур, таких как прямоугольники, зоноэдры и многогранники, или в виде пользовательских абстрактных областей для нейронных сетей [31];
- затем эта область распространяется через нейронную сеть таким образом, что каждый слой последовательно применяется к входной области. Входная область преобразуется в выходную, содержащую все выходные данные, доступные из входной области. В зависимости от слоя это может привести к аппроксимациям (выходные данные, которые недоступны из входной области);
- на заключительном этапе выходная область фиксирует все возможные выходные данные сети для возмущений входных данных, которые формируются в соответствии со спецификациями робастности.
В методе абстрактной интерпретации существует неизбежный компромисс между точностью и масштабируемостью. Например, простые абстрактные области, такие как ящики, могут верифицировать нейронные сети с миллионами нейронов в течение нескольких секунд, но, как правило, являются слишком неточными для верификации необходимых свойств робастности. С другой стороны, полуопределенные релаксации являются более точными, однако они не масштабируются до больших сетей. Таким образом, ключом к эффективной верификации является достижение этого компромисса.
6.2.4 Анализ достижимости в детерминированных окружениях
Методы верификации нейронных сетей на основе достижимости объединяют выходные данные решателей, описанных в 6.2.2, с методами анализа достижимости, для обеспечения гарантии производительности нейронных сетей с замкнутым циклом, функционирующих в заданном окружении. Первым шагом в этом анализе является разделение входного пространства на множество более мелких областей, называемых ячейками. Для каждой ячейки можно использовать решатели из 6.2.2, чтобы определить возможные управляющие выходы сети в определяемой ею области. Данная информация вместе с моделью окружения позволяет определить аппроксимацию сверху диапазона возможных следующих состояний для любой заданной ячейки. Повторение этого для всех ячеек в области начального состояния в течение нескольких временных шагов позволит определить аппроксимацию сверху набора достижимых состояний [32]. Другой подход к этой проблеме состоит в том, чтобы закодировать аппроксимацию сверху динамики окружения как ограничения в программе смешанных целых чисел и использовать метод верификации смешанных целых чисел из 6.2.2 для решения проблемы аппроксимации сверху выходного достижимого множества состояний [33].
6.2.5 Анализ достижимости в недетерминированных окружениях
Если окружение является стохастическим, решатели, указанные в 6.2.2, могут быть объединены с методами проверки вероятностной модели для определения вероятности достижения набора состояний. Аналогично методу, описанному в 6.2.4, входное пространство делится на набор ячеек, и каждая ячейка пропускается через решатель для определения возможных выходных данных нейронной сети. При помощи динамического программирования проверка вероятностной модели определяет вероятность достижения определенного набора состояний из заданного начального состояния [34]. Адаптируя эту структуру для работы с ячейками, а не с отдельными входными состояниями, можно получить чрезмерно приближенную вероятность достижения набора состояний при использовании нейронной сети [35].
6.2.6 Проверка с помощью модели
Проверка с помощью модели - это метод доказательства того, что формальное выражение теории справедливо при определенной интерпретации. Более подробную информацию можно найти в ISO/IEC/IEEE 24765:2017 и в [36]. Теория выражается словарем символов, состоящим из констант, функций и предикатов для построения предложений, в которых формулируются утверждения о предполагаемой семантике идеи. Теория может быть выражена предложениями логики предикатов либо шаблонами данных. Нейронные сети рассматриваются в качестве алгоритмов, предназначенных для обнаружения и использования моделей шаблонов данных. Модель шаблона данных сверяется с входными данными.
Для признания действительности проверки ей должны подвергнуться все модели. Проверка с помощью модели может быть использована в нейронных сетях для доказательства взаимосвязей между различными типами наборов, которые подчиняются некоторому соотношению.
Примеры
1 "Теория семьи" [37] подчиняется интерпретации, которая реализует принадлежность лиц, принадлежащих к семье. Таким образом, может быть доказано, что два произвольных лица являются либо не являются членами семьи. Затем предложение ‘один человек является родителем другого человека’ проверяется для всех доступных пар лиц.
2 Проверка модели была использована в [38] для доказательства существования состязательных входных данных для нейронной сети. Теория - это язык, состоящий из букв, весов и смещений, описывающих нейронную сеть. Интерпретация определяется меткой, прикрепленной к изображению буквы. Можно вычислить расстояние между каждой возможной парой букв в алфавите. Затем модель может быть проверена, чтобы убедиться в том, что каждое расстояние превышает определенный порог, установленный разработчиком ИИ. С помощью нейронной сети предопределенные разработчиком ИИ предикаты проверяются на соответствие теории.
6.3 Краткое изложение
При применении формальных методов для оценки робастности нейронных сетей необходимо учитывать некоторые аспекты. С одной стороны, архитектура нейронной сети оказывает влияние, поскольку каждый формальный метод имеет свои сильные и слабые стороны при обработке каждой математической функции, используемой в нейронной сети. С другой стороны, тип данных, используемых в качестве входных данных для нейронной сети, может оказывать влияние, поскольку изменчивость входных данных, числовой или категориальный характер и размер напрямую влияют на затратность вычислений и простоту формального анализа. Для решения этих аспектов доступно несколько формальных методов: подходы с использованием решателя, абстрактная интерпретация, анализ достижимости состояний или проверка с помощью модели.
В настоящее время наиболее распространенные архитектуры и типы данных, обрабатываемые нейронными сетями, могут быть проанализированы по крайней мере одним формальным методом. Каждый метод имеет преимущества и ограничения (например, масштабируемость) и может удовлетворять одному или нескольким критериям, описанным в разделе 5.
7 Робастность на протяжении жизненного цикла системы ИИ
7.1 Общие положения
Жизненный цикл системы ИИ, описанный в ИСО/МЭК 22989:2022, представлен на рисунке 2 и состоит из 7 стадий.
В ИСО/МЭК 22989:2022, пункт 5.19, определен набор ролей и подролей заинтересованных сторон в области ИИ, включая поставщика ИИ, производителя ИИ, разработчика ИИ, клиента ИИ и т.д. В настоящем разделе подробно описан способ оценки робастности нейронной сети в процессе проектирования и разработки, верификации и валидации, развертывания и мониторинга эксплуатации.
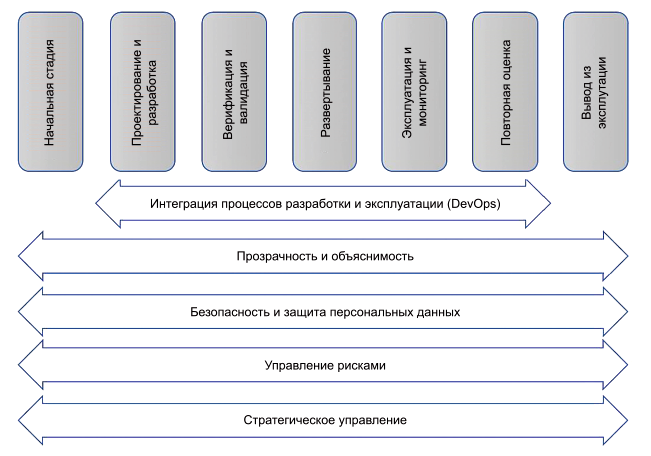 |
Рисунок 2 - Пример стадий и высокоуровневых процессов в модели жизненного цикла системы ИИ
7.2 Оценка робастности в процессе проектирования и разработки
7.2.1 Общие положения
Даже на ранней стадии разработки проверка робастности нейронной сети может помочь в ее проектировании. Узнав на ранней стадии о потенциальных недостатках в части робастности, разработчик ИИ может предпринять необходимые шаги для их устранения и, в свою очередь, избежать недостаточной робастности в дальнейшем (устранение недостатков в части робастности не рассматривается в настоящем стандарте). На этом этапе предполагается, что обучающие данные и архитектура нейронной сети все еще открыты для изменений. Формальные методы способны измерять робастность, а также выявлять источники ее потери, что предоставляет разработчику ИИ важную информацию. Например, формальные методы могут выделять особенности, изучаемые нейронной сетью для компьютерного зрения или обработки временных рядов. Формальные методы также могут выделять классы, которые нейронная сеть не различает.
7.2.2 Идентификация распознанных признаков
Идентификация признаков, распознанных нейронной сетью, позволяет разработчику ИИ лучше понять и объяснить или интерпретировать поведение нейронной сети. Таким образом, можно лучше понять, какой будет робастность нейронной сети. Знание того, какие признаки легче идентифицировать, позволяет разработчику ИИ понять, в какой степени нейронная сеть сможет выполнить свою задачу, когда ей будут представлены производственные данные.
Нейронная сеть полагается на некоторые признаки, которые она может извлечь из предоставленных ей данных, независимо от того, осуществлялось ли ее обучение с учителем, без учителя или с помощью подкрепления. Эти признаки, как правило, недоступны разработчику ИИ напрямую, и они не представлены в его структуре в удобочитаемом виде. Вместо этого они встроены в математическую модель, созданную в ходе обучения. Это означает, что признаки не могут быть выражены непосредственно в удобочитаемом виде. Они представляют собой математические артефакты, выраженные в многомерном пространстве.
Формальные методы могут использовать символьные или реляционные подходы для установления связи в области через модель от входов к выходам нейронной сети (более подробно см. 6.2). Эта связь позволяет разработчику ИИ определить степень влияния каждого входа на каждый выход. Изученные признаки в модели отвечают за силу или слабость каждой отдельной связи между входом и выходом. При наблюдении за связями можно также проследить последствия изученных признаков и следовательно лучше понимать их влияние на робастность нейронной сети.
Для идентификации некоторых из изученных признаков разработчик ИИ использует критерий релевантности. Подтверждение результата по критерию релевантности может быть выполнено вручную (посредством прямого подтверждения) либо автоматически (путем оценки соответствия целевому показателю релевантности).
В случае подтверждения вручную эксперт непосредственно оценивает результаты по критерию. Для лучшего понимания поставленной оценки следует добавить обоснование эксперта к отчету об оценке.
В случае автоматического подтверждения оценка должна основываться на четком целевом показателе релевантности данных. Следует определить явный метод для измерения уровня соответствия между релевантностью, измеряемой для любых данных, и целевым показателем релевантности. А также необходимо установить пороговое значение, чтобы проверить, насколько высок уровень соответствия. И наконец, следует указать целевой показатель релевантности.
Примечание - В процессе подтверждения личность и уровень компетентности ответственного лица могут быть установлены для отслеживания или диагностики. В случае автоматического подтверждения источник целевой релевантности также может быть использован для отслеживания или диагностики.
7.2.3 Проверка разделимости
Проверка разделимости - это метод, используемый в нейронных сетях, выполняющих классификацию. Для данных нейронных сетей роль модели заключается в прогнозировании класса на основе входных данных. Для этого классификационная модель обобщает данные между точками данных, на которых она была обучена (и за их пределами). Что касается классификатора, то чем больше модель способна разделять классы, тем эффективнее ее результат. Таким образом, робастность такой модели зависит от ее способности эффективно разделять классы.
При разработке классификатора рекомендуется использовать критерий чувствительности, чтобы определить, какие классы более или менее разделены. Для этой цели в анализе чувствительности следует использовать области, построенные вокруг точек данных в тестовых данных. Разброс значений атрибутов следует постепенно увеличивать для определения того, какие классы начинают пересекаться друг с другом. Пересечение понимается как случай, когда выходные данные нейронной сети для одного класса начинают превышать выходные данные другого класса. Процесс останавливается, когда выходные данные всех классов пересекаются со всеми другими выходными данными класса.
Результаты анализа разделимости основаны на порядке, в котором классы начинают пересекаться, и размере области, в которой начинают происходить эти пересечения. По результатам анализа чувствительности можно принять меры к обучающим данным либо к архитектуре нейронной сети. Цель состоит в том, чтобы улучшить разделимость каждого класса путем сравнительного измерения каждого анализа чувствительности.
7.3 Оценка робастности в процессе верификации и валидации
7.3.1 Общие положения
На стадии верификации и валидации нейронная сеть тестируется на соответствие ее требованиям и целям. Использование формальных методов на данной стадии не заменяет другие средства верификации и валидации (такие, как статистическое тестирование или полевые испытания). Однако формальные методы могут дать новую информацию о робастности нейронной сети в пределах конкретной области. Основное преимущество применения формальных методов на данной стадии заключается в том, что они позволяют проводить более общее доказательство робастности, поскольку это выполняется в области.
7.3.2 Покрытие частей входной области
Входная область, в которой должна работать нейронная сеть, может быть выражена с разной степенью сложности. Некоторые из них определить достаточно легко, например для нейронной сети, выполняющей задачу регрессии по определенному набору данных; все они содержатся в определенных границах. В других случаях это может быть более сложным. Например, в задачах обработки изображений входная область может характеризоваться некоторыми атрибутами (см. 5.2), но общее определение области не может быть легко определяемым математическим объектом. Формальные методы используются для некоторых форм граничных вычислений выходных данных, поэтому способ определения входной области оказывает значительное влияние на метод.
Входные области определяются атрибутами, которые указывают пространство, подлежащее валидации, с изменением тех атрибутов, которые должны быть ограничены. Затем формальные методы используются в областях или частях областей с использованием критериев робастности, описанных в разделе 5. Следует определить часть области, для которой валидация имеет смысл и дает полезную информацию для лица, проводящего оценку. Любое такое разделение входной области на части должно быть обосновано. В частности, в обосновании должно быть указано, почему выбранный критерий способен оценить робастность данного конкретного разделения входной области.
Смысл использования формальных методов в части области заключается в расширении оценки робастности в тех частях, где валидация не проводилась или была неполной. В идеале оценка проводится по всей области. Однако на практике это часто неосуществимо, будь то из-за того, что область нелегко определить как единое целое, или из-за размера области.
Следовательно, первым шагом является определение части области, для которой валидация имеет смысл и может принести полезную информацию для лица, проводящего оценку.
Данную концепцию наилучшим образом иллюстрируют два разных примера. Первый пример с легко определяемой областью, а второй - с трудно определяемой областью.
В качестве первого примера рассмотрим нейронную сеть, обученную интерполировать поведение математической функции, принимающей два входа и возвращающей один выход. Границы, определяющие область входных данных, известны, и функция, которую нейронная сеть должна имитировать, всегда определяется между этими границами. В этом примере легко определить разделение входных данных, просто определив их границы. Затем можно использовать формальные методы для проверки границ выходных данных. Поскольку функция четко определена в этой части, легко проверить, обладает ли нейронная сеть достаточной робастностью (используя критерий чувствительности). Затем все пространство может быть разделено на несколько частей, которые можно проверить по отдельности, чтобы расширить оценку робастности области.
7.3.3 Измерение воздействия возмущений
Опираясь на описание области, планируемой для использования нейронной сетью, можно определить типы возмущений, которым могут подвергаться входные данные нейронной сети. Любое возмущение может по-разному влиять на уровень производительности нейронной сети. Различное влияние на робастность нейронной сети может оказывать и их комбинация. На этапе верификации и валидации можно оценить робастность системы по случаям этих возмущений (комбинированным или нет). Используя формальные методы, можно провести более общую оценку робастности системы к этим возмущениям.
Возмущения могут быть положительными или негативными. Они также могут быть преднамеренными (например, в случае враждебной атаки) или непреднамеренными (например, в случае дефектов датчиков или изменений в окружении). Возмущения могут быть математически описаны либо только проиллюстрированы.
Пример - Возмущение размытия на изображении, как правило, основано на свертке изображения с ядром из определенных значений и строится путем применения ядра к каждому пикселю. Однако наличие капель на линзе, вызывающих некоторый дефект изображения, можно проиллюстрировать только предложив одну или несколько масок, которые искусственно добавляют капли к изображению. В первом случае эквивалентность очевидна, поскольку возмущение является математической функцией. Во втором случае применение функции в большей степени зависит от контекста и может соответствовать объединению нескольких единиц данных в одно (например, смешиванию изображения и маски).
Если настройка процесса генерации возмущенных входных данных варьируется от одного пользователя к другому, то данный процесс необходимо объяснить. Применение возмущения к входным данным нейронной сети рассматривается как применение функции к входным данным с целью их изменения.
При использовании формальных методов для оценки робастности нейронной сети к определенному возмущению одним из необходимых условий является наличие функции, описывающей процесс применения возмущения. Данная функция должна опираться по крайней мере на один ограниченный параметр. Ограниченные параметры определяются минимальными и максимальными значениями. Для соответствующих параметров должны быть установлены минимальное и максимальное отклонения. Один или несколько критериев должны быть выражены в области (см. раздел 5). Затем следует использовать формальный метод для оценки критериев в представленной области с различными допустимыми возмущениями.
Для оценки робастности нейронной сети по отношению к нескольким конкретным возмущениям можно использовать композицию функций, представляющих каждое возмущение. Предпочтительнее иметь коммутативную композицию, хотя это и не обязательно. Процесс, описанный в настоящем подразделе, затем применяется к композиции функций.
7.4 Оценка робастности в процессе развертывания
Поскольку нейронные сети являются нелинейными системами, они чувствительны к небольшим изменениям значений в своих входных данных. Эти изменения могут быть вызваны проблемами с числовой точностью, которая возникает во время работы нейронной сети. Источники проблем с числовой точностью могут быть вызваны:
- компиляторами, перестраивающими или заменяющими операции (например, использующие совмещенное умножение-сложение [39]);
- операциями по перестановке базового оборудования (например, для получения преимуществ от конвейерной обработки);
- оптимизацией, выполненной для снижения числовой точности (например, квантование, использование меньших операций с плавающей запятой или операций с фиксированной запятой);
- изменением в процессе округления;
- изменением в реализации низкоуровневого числового оператора (например, использование стандарта, отличного от стандарта IEEE 754:2019, оператор соответствия, оператор с неправильным округлением или с другой интерполяцией [24]).
Следует учитывать перечисленные проблемы при интеграции нейронной сети в систему, в которой может возникнуть один или несколько из этих источников числовых проблем. В частности, рекомендуется использовать формальные методы для проверки их воздействия. Для этой цели подойдут формальные методы для измерения границ максимальной ошибки округления, которые вызваны перестановкой операций или изменением используемой арифметики. На практике выбранные формальные методы оцениваются по каждому критерию, ранее использовавшемуся для проверки их функционирования.
Для решения описанных проблем разработчик ИИ может выполнить следующие действия:
- во-первых, разработчик ИИ должен проверить влияние выбранной используемой операции. Для этого необходимо сначала определить для каждой базовой операции, могут ли ее ошибки округления быть статически ограничены областью применения или нет:
- в случае имеющейся возможности статически привязать ошибку округления оператора, формальные верификаторы должны учитывать их в семантике, используемой для верификации нейронной сети. Например, стандартные арифметические операции с плавающей запятой, такие как сложение или деление, имеют ошибку округления, которая может быть ограничена значением единицы измерения, стоящей на последнем месте результата;
- в случае отсутствия возможности статически ограничить ошибку округления, формальные верификаторы должны полагаться на аппроксимацию сверху необходимых операций, предоставляемых разработчиком ИИ. Разработчик ИИ должен четко задокументировать гипотезу, используемую для таких аппроксимаций сверху;
- во-вторых, разработчик ИИ должен определить возможные способы, которыми процесс интеграции может изменять или перестраивать операции (будь то статически или динамически). Как только они будут идентифицированы, верификатор должен учесть эти возможные изменения. В некоторых случаях эти изменения могут быть определенными или неопределенными:
- если изменения являются определенными, то верификатор должен проанализировать нейронную сеть на соответствие ее поведению после развертывания;
- если изменения являются неопределенными, верификатор должен учесть, что они могут произойти, и определить их влияние в целом. В некоторых случаях можно определить вероятность наихудшего случая для любого порядка выполнения операции (например, когда используются только правильно округленные стандартные операции с плавающей запятой). В случаях, когда это не представляется возможным, верификатору следует полагаться на аппроксимацию сверху, вызванную этими изменениями, предоставленную разработчиком ИИ. Разработчик ИИ должен четко задокументировать гипотезу, используемую для таких аппроксимаций сверху.
7.5 Оценка робастности в процессе эксплуатации и мониторинга
7.5.1 Общие положения
Как только нейронная сеть развернута и введена в эксплуатацию, ее робастность можно контролировать. На этом этапе нейронная сеть не должна изменяться (ее веса и значения смещения для каждого нейрона фиксированы) либо она может измениться, поскольку нейронная сеть использует непрерывное обучение. В зависимости от того, изменяется ли нейронная сеть, формальные методы могут применяться для оценки робастности различными способами. С одной стороны, если нейронная сеть не изменяется, возможно провести оценку робастности в отношении новых входных данных, которые она обрабатывает. С другой стороны, если нейронная сеть меняется, следует оценить ее робастность, чтобы измерить влияние этого изменения.
7.5.2 Робастность в области эксплуатации
Когда система вводится в эксплуатацию, может быть трудно гарантировать, что она работает в предполагаемой области применения, для которой она изначально была определена и проверена. Условия эксплуатации могут изменяться без предварительного прогнозирования. Это имеет большое значение, если система работает в окружении открытого мира. На этой стадии оценка робастности может помочь определить величину отклонения от запланированной области эксплуатации. Корректирующие действия (например, оповещение оператора или переключение в отказоустойчивый режим) могут быть предприняты в том случае, если требуемый уровень робастности не достигнут.
Поскольку нейронные сети, как правило, имеют одинаковую производительность при одинаковых входных данных, мониторинг их робастности может помочь определить, являются ли входные данные все еще частью области, на которой была обучена нейронная сеть. Свойство локальной робастности может иметь аналогичный результат при аналогичных входных данных. Например, свойство стабильности (см. 5.3.1) может иметь максимальные значения на правильно классифицированных входных данных, сравнимые с максимальными значениями неправильно классифицированных входных данных. Эти подходы могут быть использованы для оценки робастности нейронных сетей в текущей области эксплуатации.
При оценке робастности нейронной сети, работающей в новой области, следует регулярно сравнивать результат применения критерия на новых входных данных с результатом применения того же критерия на предыдущей стадии жизненного цикла.
7.5.3 Изменения робастности
Использование непрерывного обучения изменяет поведение нейронной сети, поскольку могут меняться ее веса и значения смещения. Изменение внутренней структуры нейронной сети может оказать влияние (позитивное или негативное) на ее робастность.
При оценке изменений робастности нейронной сети в процессе работы следует использовать предопределенный набор критериев. Затем оценка робастности производится путем сравнения разницы в результатах по набору критериев между новой версией нейронной сети и предыдущей. Для проверки, является ли возможное снижение робастности приемлемым или нет в отношении наблюдаемой разницы, должен быть сформулирован дополнительный критерий.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO/IEC 22989:2022 | MOD | ГОСТ Р 71476-2024 (ИСО/МЭК 22989:2022) "Искусственный интеллект. Концепции и терминология искусственного интеллекта" |
ISO/IEC 23053:2022 | - | * |
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандарта: - MOD - модифицированный стандарт. | ||
Библиография
[1] | ISO/IEC 25059, Software engineering - Systems and software - Quality Requirements and Evaluation (SQuaRE) Quality Model for AI systems |
[2] | ISO/IEC 25000, Systems and software engineering - Systems and software - Quality Requirements and Evaluation (SQuaRE) - Guide to SQuaRE |
[3] | ISO/IEC TR 24029-1, Information technology - Artificial Intelligence (AI) - Assessment of the robustness of neural networks - Part 1: Overview |
[4] | ISO/IEC/IEEE 2010:2011, Systems and software engineering - Architecture description |
[5] | ISO/IEC/IEEE 5939:2017, Systems and software engineering - Measurement process |
[6] | ISO/IEC/IEEE 5289:2019, Systems and software engineering - Content of life-cycle information items (documentation) |
[7] | ISO/IEC 19794-1:2011, Information technology - Biometric data interchange formats - Part 1: Framework |
[8] | ISO/IEC/IEEE 29119-1:2022, Software and systems engineering - Software testing - Part 1: General concepts |
[9] | ISO/IEC/IEEE 4765:2017, Systems and software engineering - Vocabulary |
[10] | Leino K., Wang Z., Fredrikson M. Globally-Robust Neural Networks. Proceedings of the 38th International Conference on Machine Learning, ICML. 2021, 139, 6212-6222 |
[11] | Katz G. Barrett C., Dill D., Julian K., Kochenderfer M. Reluplex: An Efficient SMT Solver for Verifying Deep Neural Networks. 2017, International Conference on Computer Aided Verification, 10426, 97-117. doi:10.1007/978-3-319-63387-9_5 |
[12] | Szandala T. Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks. CoRR. 2020. arXiv:abs/2010.09458 |
[13] | Chu L., Hu X., Hu J., Wang L., Pei J. Exact and Consistent Interpretation for Piecewise Linear Neural Networks: A Closed Form Solution. International Conference on Knowledge Discovery & Data Mining, 2018, 24, 1244-1253. doi:10.1145/3219819.3220063 |
[14] | Bunel R., Turkaslan I., Torr P.H.S., Kohli P., Kumar M.P. A Unified View of Piecewise Linear Neural Network Verification. International Conference on Neural Information Processing Systems, 2018, 32, pp.4795-4804 |
[15] | Weng T.-W., Zhang H., Chen H., Song Z., Hsieh C.-J., Boning D., Dhillon I.S., Daniel L. Towards fast computation of certified robustness for ReLU networks. Proceedings of the 35th International Conference on Machine Learning. 2018, 80, 5276-5285 |
[16] | Zhang H., Weng T.-W., Chen P.-Y, Hsieh. C.-J., Daniel L. Efficient Neural Network Robustness Certification with General Activation Functions. Neural Information Processing Systems Conference. 2018, 31, 4944-4953 |
[17] | Wang S., Pei K., Whitehouse J., Yang J., Jana S. Efficient formal safety analysis of neural networks. Proceedings of the 32nd International Conference on Neural Information Processing Systems. 2018, 80, 6369-6379 |
[18] | Narodytska N. Formal Analysis of Deep Binarized Neural Networks. International Joint Conference on Artificial Intelligence. 2018, 27, 5692-5696. doi:10.24963/ijcai.2018/811 |
[19] | Jia K., Rinard M. Efficient Exact Verification of Binarized Neural Networks. Neural Information Processing Systems. 2020, 33, 1782-1795 |
[20] | Khmelnitsky I., Neider D., Roy R., Barbot B., Bollig B., Finkel A., Haddad S., Leucker M., Ye L. Property-directed verification of recurrent neural networks. International Symposium on Automated Technology for Verification and Analysis. 2021. arXiv:2009.10610 |
[21] | Ryou W., Chen J., Balunovic M., Singh G., Dan A., Vechev M. Scalable Polyhedral Verification of Recurrent Neural Networks. Computer-Aided Verification. 2021, 12759, 225-248. doi:10.1007/978-3-030-81685-8_10 |
[22] | Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A.N., Kaiser L., Polosukhin I. Attention is All you Need. Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems, NIPS. 2017, 30, 5998-6008 |
[23] | Shi Z., Zhang H., Chang K.-W., Huang M., Hsieh C.-J. Robustness Verification for Transformers. International Conference on Learning Representations. 2020. arXiv:2002.06622 |
[24] | IEEE 754:2019, IEEE Standard for Floating-Point Arithmetic |
[25] | Tjeng V., Xiao K., Tedrake R. Evaluating Robustness of Neural Networks with Mixed Integer Programming. The International Conference on Learning Representations. 2019 |
[26] | Katz G., Huang D.A., Ibeling D., Julian K., Lazarus C., Lim R., Shah P., Thakoor S., Wu H., Zeljic A., Dill D.L., Kochenderfer M., Barrett C. The Marabou Framework for Verification and Analysis of Deep Neural Network. Computer Aided Verification. 2019, 11561, 443-452. doi:10.1007/978-3-030-25540-4_26 |
[27] | Wang S., Pei K., Whitehouse J., Yang J., Jana S. Efficient Formal Safety Analysis of Neural Networks. International Conference on Neural Information Processing Systems. 2018, 32, 6369-6379 |
[28] | Sun X., Khedr H., Shoukry Y. Formal Verification of Neural Network Controlled Autonomous Systems. International Conference on Hybrid Systems: Computation and Control. 2019, 22, 147-156. doi:10.1145/3302504.3311802 |
[29] | Cousot P., Cousot R. Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation. Principles of programming languages. 1977, 238-252. doi:10.1145/512950.512973 |
[30] | Cousot P. Probabilistic Abstract Interpretation. Programming Languages and Systems. 2012, 7211, 169-193. doi:10.1007/978-3-642-28869-2_9 |
[31] | Singh G., Gehr T., M., Vechev M. An Abstract Domain for Certifying Neural Networks. Programming Languages . 2019, 3, 41:1-41:30. doi:10.1145/3290354 |
[32] | Julian K., Kochenderfer M. Guaranteeing safety for neural network-based aircraft collision avoidance systems. IEEE/AIAA 38th Digital Avionics Systems Conference. 2019, 603-612. doi:10.1109/DASC43569.2019.9081748 |
[33] | Sidrane C., Kochenderfer M. OVERT: Verification of nonlinear dynamical systems with neural network controllers via overapproximation. Workshop on Safe Machine Learning. 2019 |
[34] | Bouton M., Tumova J., Kochenderfer M. Point-based methods for model checking in partially observable Markov decision processes. AAAI Conference on Artificial Intelligence. 2020, 24, 10061-10068 |
[35] | Katz S., Strong C., Julian K., Kochenderfer M. Generating probabilistic safety guarantees for neural network controllers. CoRR. 2021. arXiv:abs/2103.01203 |
[36] | Ehrig H., Mahr B. Fundamentals of Algebraic Specification 1: Equations and Initial Semantics. Berlin: Springer, 1985 |
[37] | Manna Z., Waldinger R. The deductive foundations of computer programming - a one-volume version of "The logical basis for computer programming". Boston, Massachusetts: Addison-Wesley, 1993 |
[38] | Sena L.H., Bessa I.V., Gadelha M.R., Cordeiro L.C., Mota E. Incremental Bouns.ded Model Checking of Artificial Neural Networks in CUDA. Brazilian Symposium on Computing System Engineering. 2019, 1-8. doi:10.1109/SBESC49506.2019.9046094 |
[39] | Higham N.J. The Mathematics of Floating-Point Arithmetic. London Mathematical Society [online], London, UK, March 2021 [viewed 02 September 2021]. Available from: https://www.lms.ac.uk/sites/lms.ac.uk/files/files/NLMS_493_for%20web2.pdf |
[40] | Hymans C. Design and Implementation of an Abstract Interpreter for VHDL. Correct Hardware Design and Verification Methods. 2003, 2860, 263-269. doi:10.1007/978-3-540-39724-3_23 |
[41] | Banterle F., Giacobazzi R. A Fast Implementation of the Octagon Abstract Domain on Graphics Hardware. International Static Analysis Symposium. 2007, 4634, 315-332. doi: 10.1007/978-3-540-74061-2_20 |
[42] | Mirman M., Gehr T., Vechev M. Differentiable Abstract Interpretation for Provably Robust Neural Networks. Proceedings of the 35th International Conference on Machine Learning. 2018, 80, 3575-3583 |
УДК 004.8:006.354 | ОКС 35.020 | ||
Ключевые слова: искусственный интеллект, робастность, нейронная сеть | |||
