ГОСТ Р 57700.17-2018
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Численное моделирование дозвуковых течений вязких жидкостей и газов.
Валидация ПО
Numerical modeling of physical processes. Numerical simulation of subsonic flows of viscous liquids and gases. Software validation
ОКС 35.020
Дата введения 2019-01-01
Предисловие
Предисловие
1 РАЗРАБОТАН Закрытым акционерным обществом "Т-Сервисы" (ЗАО "Т-Сервисы")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 700 "Математическое моделирование и высокопроизводительные вычислительные технологии"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 6 февраля 2018 г. N 57-ст
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Цель валидации программного обеспечения (ПО) компьютерного моделирования (КМ), предназначенного для численного моделирования дозвуковых турбулентных течений жидкости или газа, заключается в подтверждении возможности ПО КМ воспроизводить характеристики реального дозвукового течения жидкости или газа. Валидация такого ПО КМ осуществляется путем решения эталонных задач. Рекомендуемые эталонные задачи перечислены в данном стандарте.
1 Область применения
Настоящий стандарт определяет общие требования к валидации программного обеспечения компьютерного моделирования, применяемого для численного моделирования турбулентного дозвукового движения (течения) жидкости или газа. Дозвуковым называют течение жидкости в том случае, если ее скорость меньше скорости звука. Турбулентным называют течение, характеризующееся наличием стохастических пульсаций. Течение может сопровождаться переносом тепла, диффузией компонентов и химическими реакциями. В зависимости от рассматриваемого диапазона условий правильную картину течения можно получать в рамках моделей несжимаемой жидкости, слабосжимаемой жидкости или сжимаемой жидкости.
Настоящий стандарт применим для валидации программного обеспечения компьютерного моделирования при проведении их сертификации.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 57188 Численное моделирование физических процессов. Термины и определения
ГОСТ Р 57700.1 Численное моделирование для разработки и сдачи в эксплуатацию высокотехнологичных промышленных изделий. Сертификация программного обеспечения. Требования
ГОСТ Р 57700.4 Численное моделирование физических процессов. Термины и определения в области механики сплошных сред: гидромеханика, газовая динамика
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и сокращения
3.1 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 57188, ГОСТ Р 57700.4-2017.
3.2 Сокращения
В настоящем стандарте применены следующие сокращения:
КМ - компьютерная модель;
ПО - программное обеспечение.
4 Общие положения
4.1 ПО, предназначенное для численного моделирования дозвуковых турбулентных течений жидкости или газа, должно адекватно интегрировать по пространству и времени или только по пространству уравнения математической модели, описывающей турбулентное дозвуковое течение жидкости и газа.
4.2 Валидация ПО, предназначенного для численного моделирования турбулентных течений жидкости или газа, осуществляется путем решения эталонных задач и тестовых задач, представляющих интерес конечного потребителя ПО КМ.
4.3 Результатом решения эталонной задачи является определенный набор характеристик, относящийся к этой задаче. Отклонение численного результата от эталонного, выраженного в некоторой норме, называют погрешностью вычислений. Возможные источники погрешности (причины отклонения) следующие:
- несоответствие математической модели рассматриваемым процессам;
- погрешность в граничных условиях;
- погрешность аппроксимации дифференциальных уравнений разностными схемами;
- ошибки округления чисел в компьютере;
- погрешность самого эталонного результата, если он получен экспериментально.
4.4 Несоответствие математической модели рассматриваемым процессам
При упрощении математической модели или при незнании реальных физических процессов в среде точность описания моделью реального течения может быть снижена.
4.5 Погрешность в граничных условиях
Любое численное моделирование турбулентных течений производится в ограниченной области расчета, на границах которой задаются граничные условия. Эти условия не всегда точно соответствуют реальным условиям в соответствующих точках пространства. Например, в численной постановке на входе в расчетную область может задаваться постоянная скорость, тогда как в эксперименте имеет место некоторое распределение скорости по входному сечению. То же самое возможно и с другими характеристиками течения.
4.6 Погрешность аппроксимации дифференциальных уравнений разностными схемами
Дискретизация уравнений математической модели неизбежно вносит погрешность в результат моделирования. Теоретическому рассмотрению данного вопроса посвящено много работ, например [1], [2]. Эта погрешность зависит от используемого численного метода и используемой конечно-разностной схемы.
4.7 Ошибки округления чисел в компьютере
Как правило, это не вносит значимой погрешности в результат моделирования, если численный метод интегрирования дифференциальных уравнений устойчив. В противном случае погрешность округления "накапливается", и это может приводить к неустойчивости решения.
4.8 Погрешность самого эталонного результата, если он получен экспериментально
Данный тип погрешности определяется согласно стандартным методикам определения ошибки эксперимента.
5 Требования к валидации ПО
5.1 Цель валидации ПО КМ, предназначенного для численного моделирования турбулентных течений жидкости или газа, заключается в подтверждении возможности ПО воспроизводить определенные особенности течения с определенной точностью, удовлетворяющей потребности конечного пользователя при решении им задач турбулентного дозвукового течения жидкости и газа.
5.2 Точность соответствия результатов решения и эталона не стандартизуется, но определяется потребностями конкретного потребителя данного ПО КМ.
5.3 Валидация применяется для:
- сертификации ПО КМ;
- проверки соответствия ПО КМ стандартам организации по использованию ПО КМ;
- анализа области применимости ПО КМ конечным пользователем для решения задач о турбулентном течении;
- анализа области применимости и создания документации ПО КМ разработчиком данного ПО КМ.
5.4 Валидационные задачи основаны на эталонных данных, полученных экспериментальным путем.
5.5 Требования к валидационным тестам и к процедуре валидации:
а) валидационные тесты для ПО КМ, предназначенного для моделирования турбулентных течений должны:
1) быть неоднократно проверены научным сообществом;
2) сопровождаться подробным описанием, обеспечивающим воспроизводимость и повторяемость процедуры получения валидационных данных;
3) соотноситься с целями и задачами применения ПО КМ для моделирования турбулентных течений конечным пользователем;
б) детальное описание процедуры валидации должно быть утверждено заинтересованной стороной и передано стороне, выполняющей валидацию;
в) процедура валидации может быть описана согласно стандарту ГОСТ Р 57700.1.
6 Рекомендуемые эталоны для проведения валидации ПО
6.1 Течение в 180-градусном повороте в трубе квадратного сечения [3]-[5]
6.1.1 Расчетная область
180° - поворотный участок трубы, гладко сопряженный с прямыми входным и выходным участками, все квадратного поперечного сечения размером 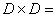 88,9х88,9 мм. Радиус поворота трубы (вдоль центральной линии)
88,9х88,9 мм. Радиус поворота трубы (вдоль центральной линии) 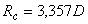 (см. рисунок 1).
(см. рисунок 1).
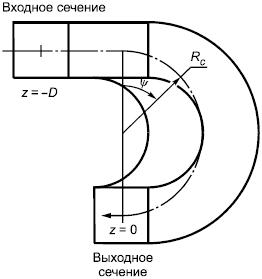
Рисунок 1 - Схема расчетной области течения в 180-градусном повороте в трубе квадратного сечения
|
Рисунок 1 - Схема расчетной области течения в 180-градусном повороте в трубе квадратного сечения
6.1.2 Параметры течения
Воздух с кинематической вязкостью: 1,72х10
м
/с.
Средняя скорость на входе: 11 м/с.
Входное число Рейнольдса: 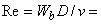 56690.
56690.
6.1.3 Условия на входе
Развитое турбулентное течение в прямой трубе квадратного сечения.
6.1.4 Результаты измерений
Ниже для пяти сечений в поворотном колене (соответствующим значениям 0,
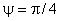 ,
, 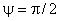 ,
, 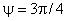 и
и 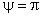 ) представлены распределения трех компонент средней скорости и трех нормальных компонент тензора напряжений Рейнольдса. Координаты в поперечном сечении
) представлены распределения трех компонент средней скорости и трех нормальных компонент тензора напряжений Рейнольдса. Координаты в поперечном сечении ,
- (
ортогональна плоскости поворота),
- координата вдоль потока (см. рисунки 2-11).
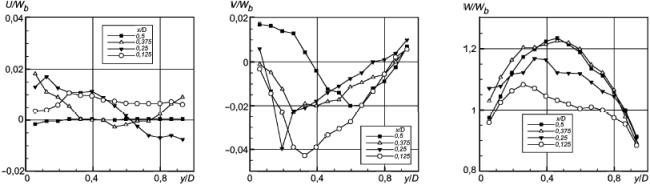
Рисунок 2 - Три компоненты скорости в сечении "пси"= 0
|
Рисунок 2 - Три компоненты скорости в сечении 0
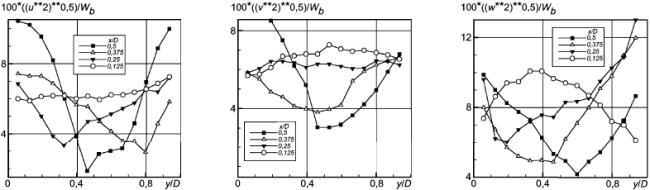
Рисунок 3 - Нормальные компоненты напряжений Рейнольдса в сечении "пси"=0
|
Рисунок 3 - Нормальные компоненты напряжений Рейнольдса в сечении 0
Рисунок 4 - Три компоненты скорости в сечении "пси"="пи"/4
|
Рисунок 4 - Три компоненты скорости в сечении 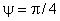
Рисунок 5 - Нормальные компоненты напряжений Рейнольдса в сечении "пси"="пи"/4
|
Рисунок 5 - Нормальные компоненты напряжений Рейнольдса в сечении 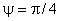
Рисунок 6 - Три компоненты скорости в сечении "пси"="пи"/2
|
Рисунок 6 - Три компоненты скорости в сечении 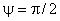
Рисунок 7 - Нормальные компоненты напряжений Рейнольдса в сечении "пси"="пи"/2
|
Рисунок 7 - Нормальные компоненты напряжений Рейнольдса в сечении 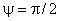
Рисунок 8 - Три компоненты скорости в сечении "пси"=3"пи"/4
|
Рисунок 8 - Три компоненты скорости в сечении 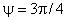
Рисунок 9 - Нормальные компоненты напряжений Рейнольдса в сечении "пси"=3"пи"/4
|
Рисунок 9 - Нормальные компоненты напряжений Рейнольдса в сечении 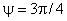
Рисунок 10 - Три компоненты скорости в сечении "пси"="пи"
|
Рисунок 10 - Три компоненты скорости в сечении 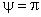
Рисунок 11 - Нормальные компоненты напряжений Рейнольдса в сечении "пси"="пи"
|
Рисунок 11 - Нормальные компоненты напряжений Рейнольдса в сечении 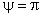
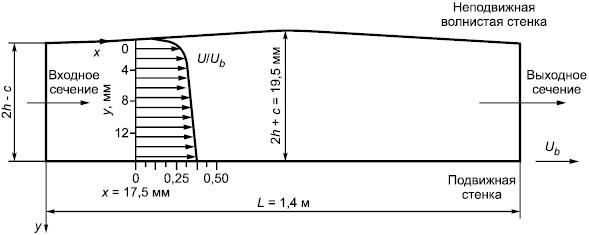
6.2 Течение Куэтта (рисунок 12) с неподвижной волнистой стенкой [6]-[9]
Рисунок 12 - Схема течения Куэтта с неподвижной волнистой стенкой
|
Рисунок 12 - Схема течения Куэтта с неподвижной волнистой стенкой
6.2.1 Расчетная область
Нижняя стенка канала движется с постоянной скоростью , волнистая верхняя стенка неподвижна. Длина канала (одного периода волнистости стенки)
1,4 м, средняя высота канала
15 мм. Форма волнистой стенки задается формулой
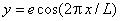 ,
, 4,5 мм.
6.2.2 Параметры течения
Воздух с кинематической вязкостью: 1,5·10
м
/с.
Скорость подвижной стенки: 8 м/с.
Число Рейнольдса: 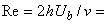 8·10
8·10.
6.2.3 Результаты измерений
Ниже для восьми поперечных сечений 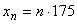 мм представлены профили продольной и поперечной скорости (
мм представлены профили продольной и поперечной скорости (,
), а также профили среднеквадратичных интенсивностей пульсаций в продольном и поперечном направлениях (
,
). Поперечная координата
направлена сверху вниз. Представленные данные покрывают область вблизи волнистой стенки и центральную часть канала (см. рисунки 13-16).
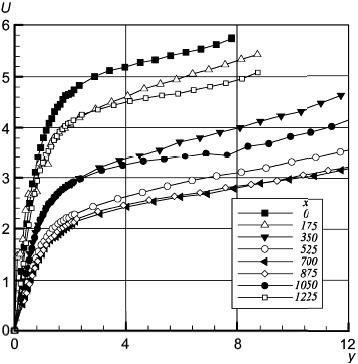
Рисунок 13 - Профили продольной компоненты скорости. Координаты x, y в мм, скорость U в м/с
|
Рисунок 13 - Профили продольной компоненты скорости. Координаты ,
в мм, скорость
в м/с
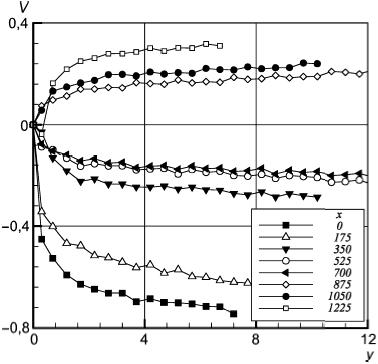
Рисунок 14 - Профили поперечной компоненты скорости. Координаты x, y в мм, скорость V в м/с
|
Рисунок 14 - Профили поперечной компоненты скорости. Координаты ,
в мм, скорость
в м/с
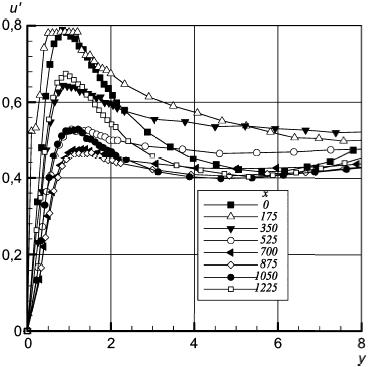
Рисунок 15 - Профили среднеквадратичных интенсивностей пульсаций в продольном направлении. Координаты x, y в мм, скорость u' в м/с
|
Рисунок 15 - Профили среднеквадратичных интенсивностей пульсаций в продольном направлении. Координаты ,
в мм, скорость
в м/с
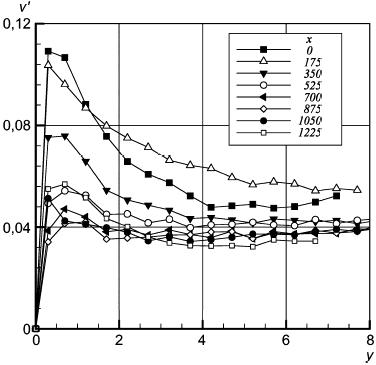
Рисунок 16 - Профили среднеквадратичных интенсивностей пульсаций v' в поперечном направлении. Координаты x, y в мм, скорость v' в м/с
|
Рисунок 16 - Профили среднеквадратичных интенсивностей пульсаций в поперечном направлении. Координаты
,
в мм, скорость
в м/с
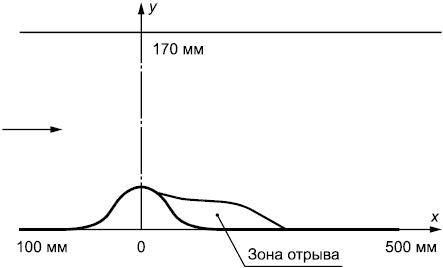
6.3 Обтекание 2D холма (рисунок 17) в канале [10]-[13]
Рисунок 17 - Схема обтекания 2D холма в канале
|
Рисунок 17 - Схема обтекания 2D холма в канале
6.3.1 Расчетная область
Препятствие в виде 2D холма размещено на нижней стенке плоского канала высотой 170 мм. Высота препятствия
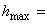 28 мм, длина
28 мм, длина 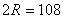 мм. Форма препятствия описывается кубическим сплайном, проведенным через следующие точки с координатами (
мм. Форма препятствия описывается кубическим сплайном, проведенным через следующие точки с координатами (,
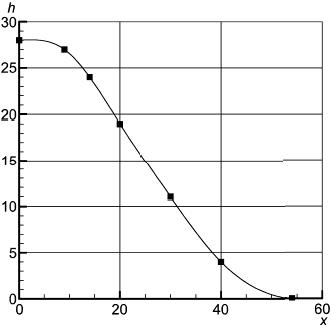
) (в мм): (±54,0), (±40,4), (±30,11), (±20,19), (±14,24), (±9,27), (0,28), и приведена на рисунке 18 (изображена только правая половина).
Рисунок 18 - Форма препятствия h(x) (x и h в мм)
|
Рисунок 18 - Форма препятствия (
и
в мм)
6.3.2 Параметры течения
Вода с кинематической вязкостью: 1·10
м
/с.
Скорость на оси входного сечения: 2,147 м/с.
Входное число Рейнольдса: 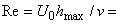 6,0·10
6,0·10.
6.3.3 Течение на входе
Развитое турбулентное течение в длинном канале.
6.3.4 Результаты измерений
Ниже представлены распределения по вертикальной координате двух компонент средней скорости ,
в нескольких сечениях вдоль потока, начиная с сечения
-50 мм и заканчивая сечением
300 мм (см. рисунки 19-21).
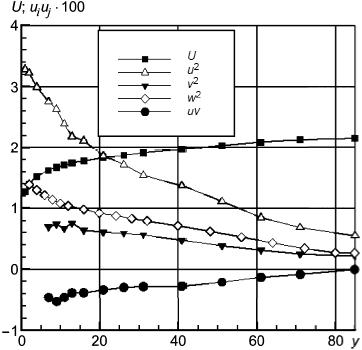
Рисунок 19 - Профиль скорости U (м/с) и профили компонент напряжений Рейнольдса u(i)u(j) (м/с) в набегающем потоке. Координата y в мм
|
Рисунок 19 - Профиль скорости (м/с) и профили компонент напряжений Рейнольдса
(м
/с
) в набегающем потоке. Координата
в мм
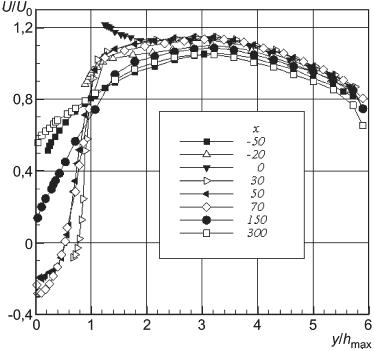
Рисунок 20 - Продольная компонента скорости в нескольких сечениях вдоль потока (x в мм)
|
Рисунок 20 - Продольная компонента скорости в нескольких сечениях вдоль потока ( в мм)
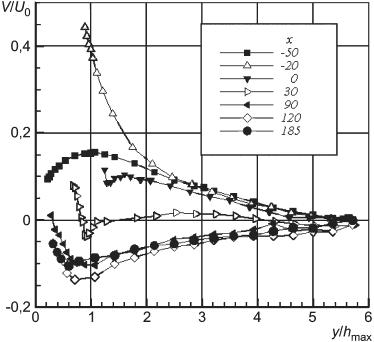
Рисунок 21 - Поперечная компонента скорости в нескольких сечениях вдоль потока (x в мм)
|
Рисунок 21 - Поперечная компонента скорости в нескольких сечениях вдоль потока ( в мм)
6.4 Круглая струя (рисунок 22), нормально падающая на плоскость [14]-[21]
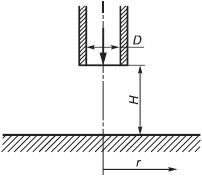
Рисунок 22 - Круглая струя, нормально падающая на плоскость
|
Рисунок 22 - Круглая струя, нормально падающая на плоскость
6.4.1 Расчетная область
Турбулентная воздушная струя вытекает из круглого сопла в окружающее воздушное пространство и падает ортогонально на плоскость. Использовались сопла с внутренним диаметром 26,5 мм и
106,1 мм. Высота струи (расстояние от плоскости до среза сопла) составляла 2
.
6.4.2 Параметры течения
Измерения проводились при двух числах Рейнольдса 23000 и
70000 (
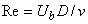 ,
,- средняя скорость на срезе сопла). Течение на выходе из сопла - развитое турбулентное течение в круглой трубе.
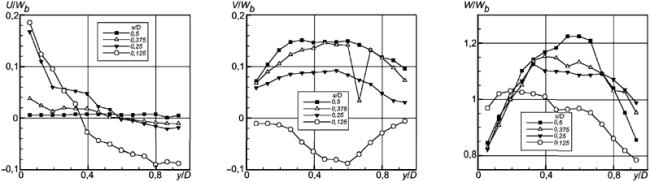
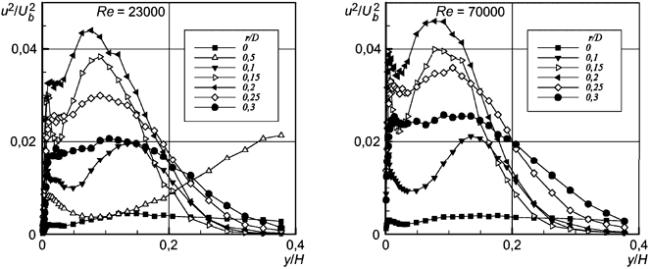
6.4.3 Результаты измерений
Ниже для двух значений числа Рейнольдса представлены результаты измерений продольной скорости , нормальных напряжений Рейнольдса
и
, а также сдвиговых напряжений Рейнольдса
. Результаты представлены как функции вертикальной координаты
(
0 соответствует стенке) для нескольких радиальных позиций относительно оси симметрии.
и
представляют собой скорость и нормальные напряжения вдоль потока, таким образом, вдоль линии
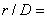 0 они соответствуют нормальной к стенке компоненте скорости, а при больших
0 они соответствуют нормальной к стенке компоненте скорости, а при больших - параллельной к стенке компоненте скорости (см. рисунки 23-26).
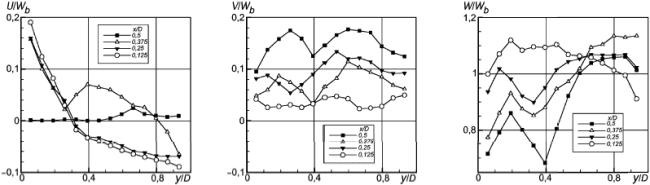
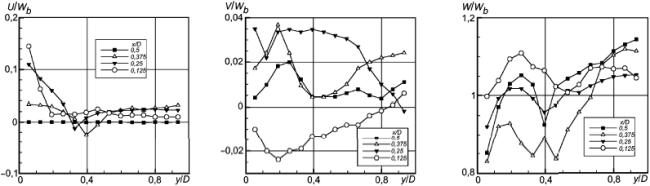
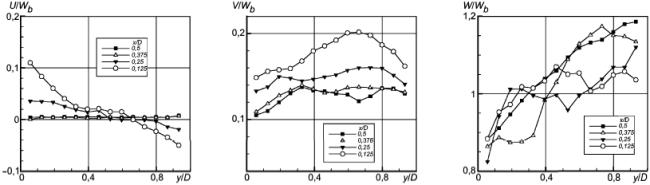
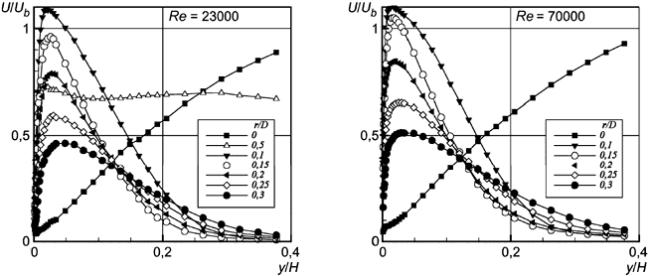
Рисунок 23 - Продольная компонента скорости
|
Рисунок 23 - Продольная компонента скорости
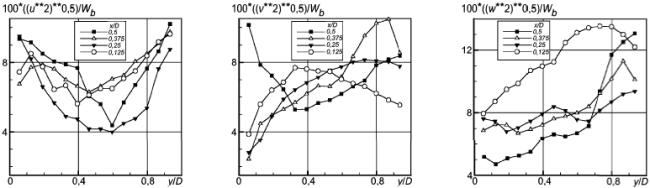
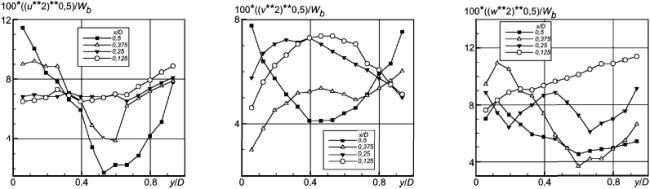
Рисунок 24 - Нормальные напряжения Рейнольдса
|
Рисунок 24 - Нормальные напряжения Рейнольдса
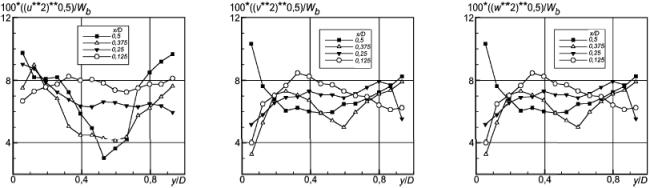
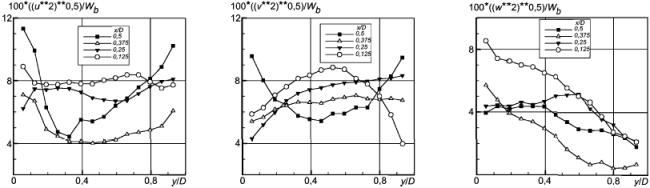
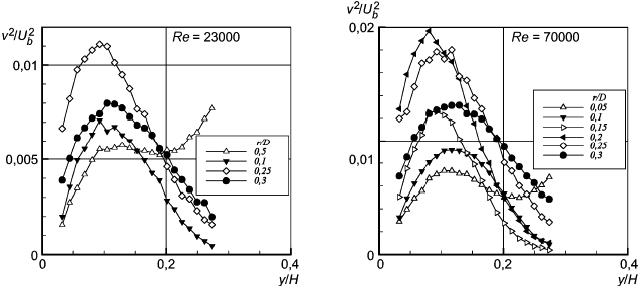
Рисунок 25 - Нормальные напряжения Рейнольдса
|
Рисунок 25 - Нормальные напряжения Рейнольдса
Рисунок 26 - Сдвиговые напряжения Рейнольдса
|
Рисунок 26 - Сдвиговые напряжения Рейнольдса
6.5 Обтекание обратного уступа (рисунок 27) [22]
Рисунок 27 - Обтекание обратного уступа
|
Рисунок 27 - Обтекание обратного уступа
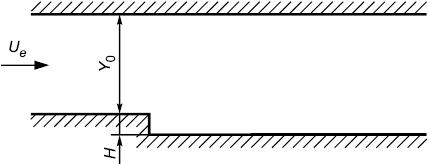
6.5.1 Расчетная область
Изучаемая конфигурация состоит из входного канала прямоугольного сечения длиной 1 м, шириной 15,1 см и высотой 10,1 см, за которым следует уступ на нижней стенке глубиной
1,27 см. Верхняя стенка горизонтальна.
6.5.2 Параметры течения
Эксперименты проводились в малошумной аэродинамической трубе при нормальных атмосферных условиях при максимальной скорости набегающего потока 44,2 м/с, что соответствует числу Маха
0,128. Число Рейнольдса, вычисленное через толщину потери импульса на расстоянии 4
вверх по потоку от ступеньки, составляет
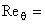 5000, что гарантирует наличие развитого турбулентного течения.
5000, что гарантирует наличие развитого турбулентного течения.
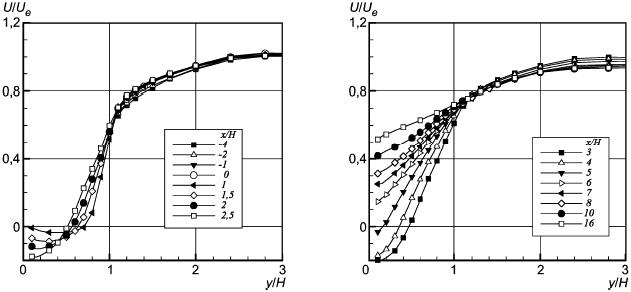
6.5.3 Результаты измерений
Ниже для нескольких сечений вдоль потока (сечение 0 соответствует положению уступа) представлены распределения по вертикальной координате
двух компонент средней скорости
,
и трех компонент тензора напряжений Рейнольдса
,
и
. Для большей части данных (кроме вертикальной компоненты скорости
) диапазон изменения
ограничен окрестностью нижней стенки, где наблюдаются наибольшие изменения характеристик вдоль потока. Кроме этого, представлены распределения коэффициента давления
вдоль нижней и верхней стенок, а также распределение коэффициента трения
вдоль нижней стенки (см. рисунки 28-33).
Рисунок 28 - Продольная компонента средней скорости
|
Рисунок 28 - Продольная компонента средней скорости
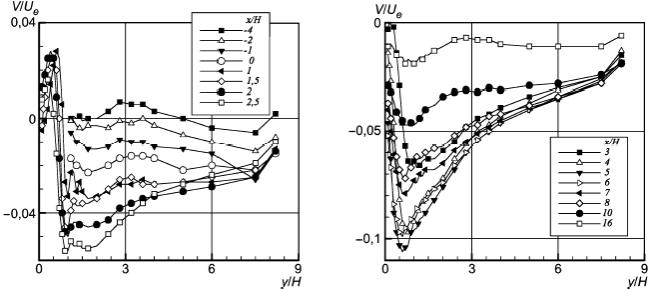
Рисунок 29 - Поперечная компонента средней скорости
|
Рисунок 29 - Поперечная компонента средней скорости
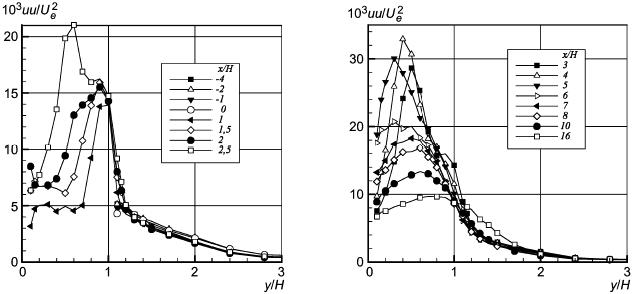
Рисунок 30 - Нормальные напряжения Рейнольдса в продольном направлении
|
Рисунок 30 - Нормальные напряжения Рейнольдса в продольном направлении
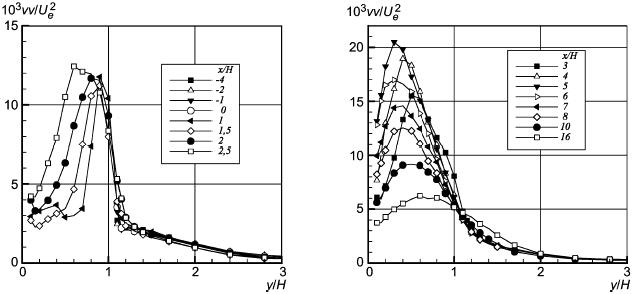
Рисунок 31 - Нормальные напряжения Рейнольдса в поперечном направлении
|
Рисунок 31 - Нормальные напряжения Рейнольдса в поперечном направлении
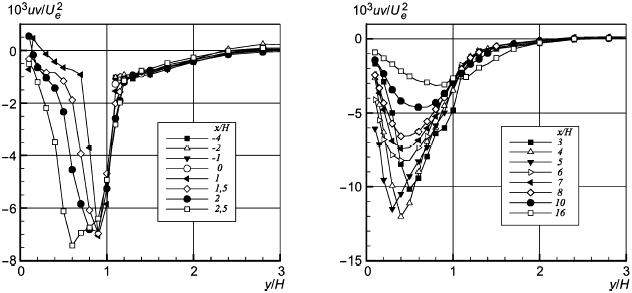
Рисунок 32 - Касательные напряжения Рейнольдса
|
Рисунок 32 - Касательные напряжения Рейнольдса
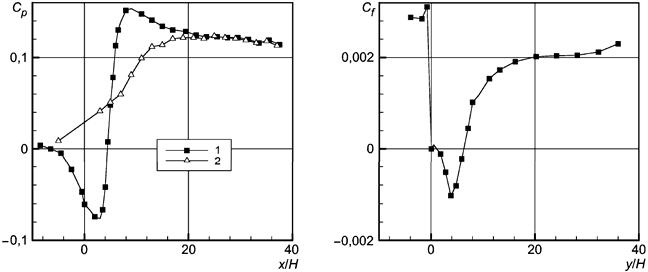
Рисунок 33 - Распределения коэффициента давления C(p) вдоль верхней и нижней стенок и коэффициента трения C("функция") вдоль нижней стенки
|
Рисунок 33 - Распределения коэффициента давления вдоль верхней и нижней стенок и коэффициента трения
вдоль нижней стенки
6.6 Обтекание кубического препятствия в канале [23]-[26]
6.6.1 Геометрия течения
Эксперименты проводились в канале прямоугольного сечения размером 60х5 см и длиной 390 см. Кубическое препятствие помещалось на нижней стенке на расстоянии 52 (
- высота канала) от входа в канал на равном расстоянии от боковых стенок.
6.6.2 Параметры течения
Эксперименты проводились в воде при числе Рейнольдса 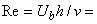 80000 (
80000 ( - средняя расходная скорость). Поток на входе искусственно турбулизовался, так что кубическое препятствие высотой
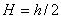 обтекалось полностью развитым турбулентным потоком.
обтекалось полностью развитым турбулентным потоком.
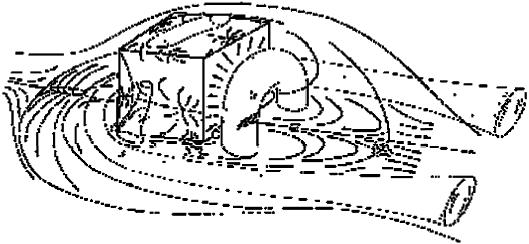
Обтекание куба несжимаемой жидкостью (см. рисунок 34) характерно наличием отрывных зон перед и за препятствием, а также на верхней грани. За препятствием возникает характерный аркообразный вихрь.
Рисунок 34 - Вихревая картина обтекания куба несжимаемой жидкостью
|
Рисунок 34 - Вихревая картина обтекания куба несжимаемой жидкостью
6.6.3 Результаты измерений
Ниже представлены результаты измерений средней скорости в трех вертикальных сечениях, параллельных боковым граням препятствия: 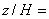 0 (плоскость симметрии),
0 (плоскость симметрии), 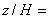 0,5 и
0,5 и 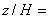 1 (положение препятствия: 0
1 (положение препятствия: 0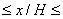 1; 0
1; 0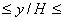 1; -0,5
1; -0,5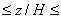 0,5). В плоскости симметрии представлены распределения продольной
0,5). В плоскости симметрии представлены распределения продольной и вертикальной
компонент скорости, в двух других сечениях даны все три компоненты скорости
,
и
(см. рисунки 35-46).
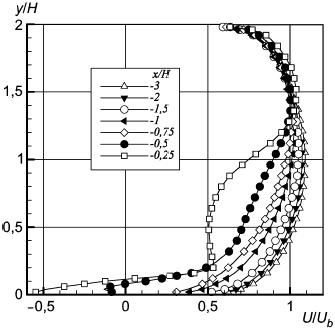
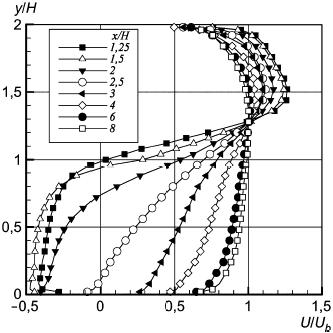
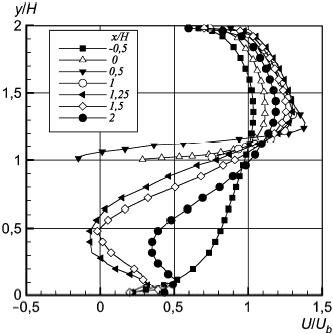
Рисунок 35 - Продольная компонента скорости перед препятствием в плоскости z/H=0
|
Рисунок 35 - Продольная компонента скорости перед препятствием в плоскости 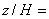 0
0
Рисунок 36 - Продольная компонента скорости над препятствием в плоскости z/H=0
|
Рисунок 36 - Продольная компонента скорости над препятствием в плоскости 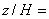 0
0
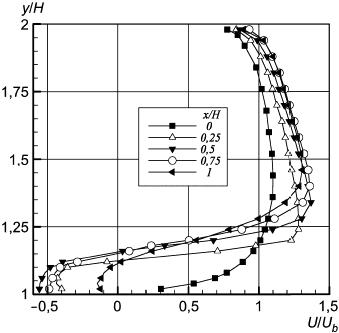
Рисунок 37 - Продольная компонента скорости за препятствием в плоскости z/H=0
|
Рисунок 37 - Продольная компонента скорости за препятствием в плоскости 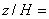 0
0
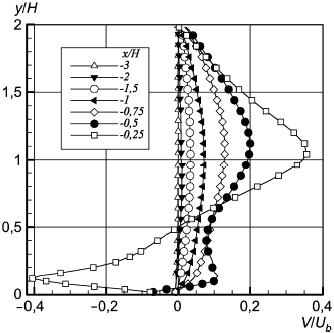
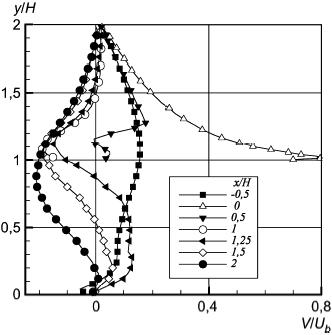
Рисунок 38 - Вертикальная компонента скорости перед препятствием в плоскости z/H=0
|
Рисунок 38 - Вертикальная компонента скорости перед препятствием в плоскости 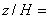 0
0
Рисунок 39 - Вертикальная компонента скорости над препятствием в плоскости z/H=0
|
Рисунок 39 - Вертикальная компонента скорости над препятствием в плоскости 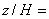 0
0
Рисунок 40 - Вертикальная компонента скорости за препятствием в плоскости z/H=0
|
Рисунок 40 - Вертикальная компонента скорости за препятствием в плоскости 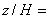 0
0
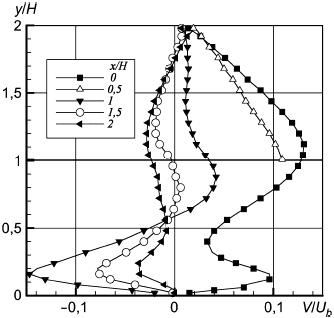
Рисунок 41 - Продольная компонента скорости в плоскости z/H=0,5
|
Рисунок 41 - Продольная компонента скорости в плоскости 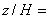 0,5
0,5
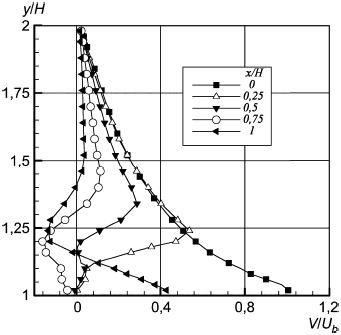
Рисунок 42 - Вертикальная компонента скорости в плоскости z/H=0,5
|
Рисунок 42 - Вертикальная компонента скорости в плоскости 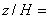 0,5
0,5
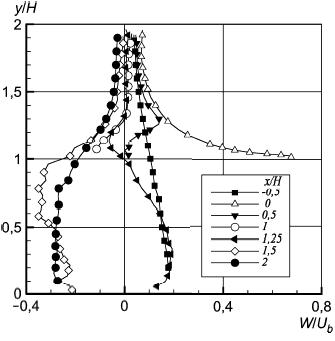
Рисунок 43 - Боковая компонента скорости в плоскости z/H=0,5
|
Рисунок 43 - Боковая компонента скорости в плоскости 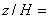 0,5
0,5
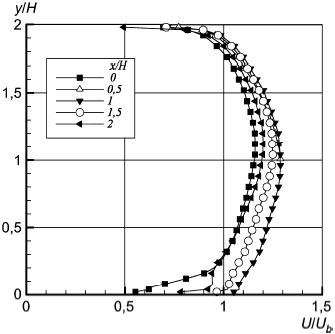
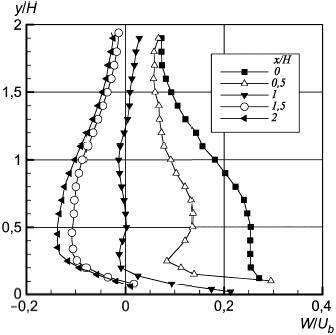
Рисунок 44 - Продольная компонента скорости в плоскости z/H=1
|
Рисунок 44 - Продольная компонента скорости в плоскости 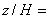 1
1
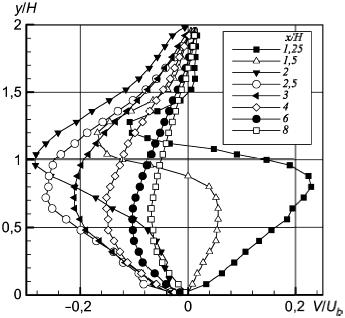
Рисунок 45 - Вертикальная компонента скорости в плоскости z/H=1
|
Рисунок 45 - Вертикальная компонента скорости в плоскости 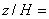 1
1
Рисунок 46 - Боковая компонента скорости в плоскости z/H=1
|
Рисунок 46 - Боковая компонента скорости в плоскости 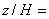 1
1
6.7 Течение (рисунок 47) в конически расширяющейся трубе [27]
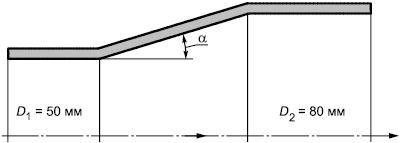
Рисунок 47 - Течение в конически расширяющейся трубе
|
Рисунок 47 - Течение в конически расширяющейся трубе
6.7.1 Расчетная область
Рассматривается турбулентное течение несжимаемой жидкости в конически расширяющейся трубе. Входной диаметр 50 мм, выходной
80 мм. Угол полураскрытия конического диффузора
18°.
6.7.2 Параметры течения
На входе в диффузор реализуется развитое турбулентное течение (рабочее тело - воздух) со скоростью на оси 2,51 м/с при числе Рейнольдса (определенном через среднюю скорость и диаметр) равном 15600.
6.7.3 Результаты измерений
Ниже для нескольких сечений вдоль трубы (0 соответствует началу расширения) представлены распределения по радиусу осевой
и радиальной
компонент средней скорости, а также распределения всех ненулевых напряжений Рейнольдса (см. рисунки 48-53).
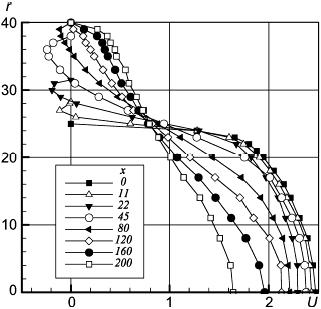
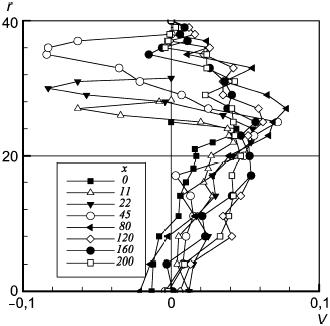
Рисунок 48 - Осевая компонента скорости; x и r в мм, U в м/с
|
Рисунок 48 - Осевая компонента скорости; и
в мм,
в м/с
Рисунок 49 - Радиальная компонента скорости; x и r в мм, V в м/с
|
Рисунок 49 - Радиальная компонента скорости; и
в мм,
в м/с
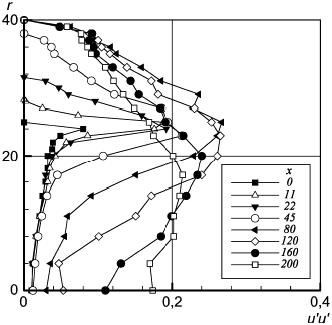
Рисунок 50 - Нормальные напряжения Рейнольдса в осевом направлении
|
Рисунок 50 - Нормальные напряжения Рейнольдса в осевом направлении; и
в мм,
в м
/с
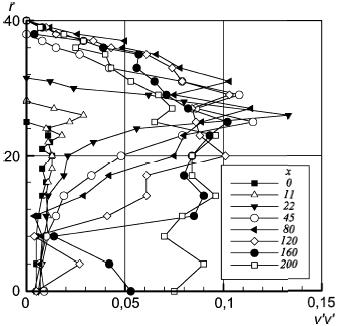
Рисунок 51 - Нормальные напряжения Рейнольдса в радиальном направлении
|
Рисунок 51 - Нормальные напряжения Рейнольдса в радиальном направлении; и
в мм,
в м
/с
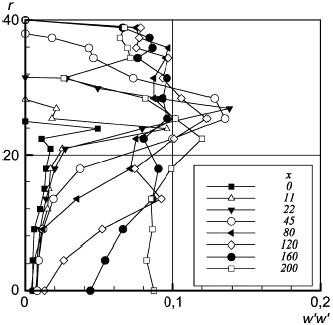
Рисунок 52 - Нормальные напряжения Рейнольдса в угловом направлении
|
Рисунок 52 - Нормальные напряжения Рейнольдса в угловом направлении; и
в мм,
в м
/с
Рисунок 53 - Сдвиговые напряжения Рейнольдса
|
Рисунок 53 - Сдвиговые напряжения Рейнольдса; и
в мм,
в м
/с
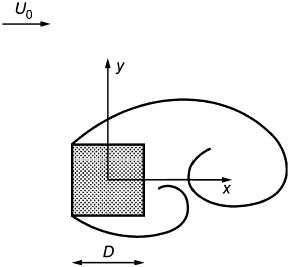
6.8 Турбулентная дорожка Кармана (рисунок 54) за квадратным цилиндром [28]-[30]
Рисунок 54 - Турбулентная дорожка Кармана за квадратным цилиндром
|
Рисунок 54 - Турбулентная дорожка Кармана за квадратным цилиндром
6.8.1 Расчетная область
Измерения проводились в замкнутом водном канале высотой 39 см и шириной 56 см в сечениях от 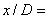 -3 (невозмущенный поток) до
-3 (невозмущенный поток) до 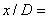 8. Диаметр цилиндра
8. Диаметр цилиндра 4 см. Результаты измерений для 20 значений фазы колебаний сходящих вихрей усреднялись по ансамблю, включающему до 400 реализаций.
6.8.2 Параметры течения
Скорость набегающего потока в центральной части ширины канала на высоте от -4
до 4
составляет
0,535 м/с, что соответствует числу Рейнольдса
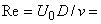 21400 при уровне турбулентности около 2%. Частота схода вихрей составляет
21400 при уровне турбулентности около 2%. Частота схода вихрей составляет 1,77 Гц, что соответствует числу Струхаля
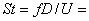 0,132.
0,132.
6.8.3 Результаты измерений
Ниже для четырех значений фазы колебаний (0, 90, 180 и 270 градусов) приводятся профили средней скорости
и
, интенсивностей пульсаций
,
, а также профили сдвиговых напряжений Рейнольдса
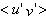 для нескольких сечений вдоль потока (сечение
для нескольких сечений вдоль потока (сечение 0 соответствует середине обтекаемого цилиндра) (см. рисунки 55-59).
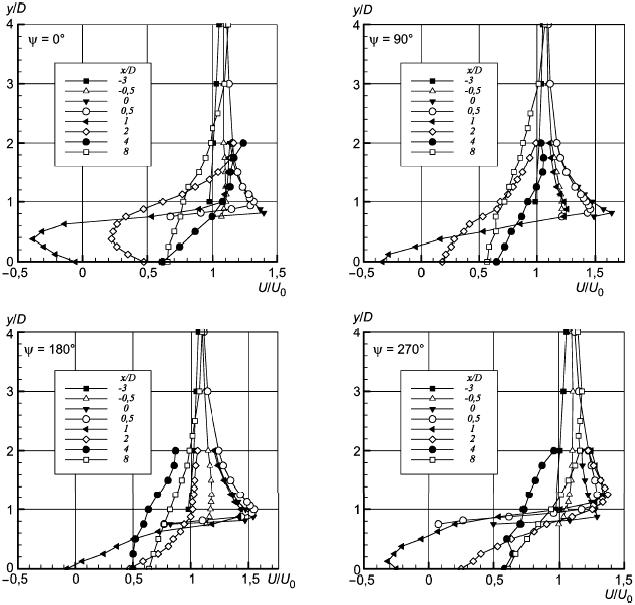
Рисунок 55 - Профили продольной компоненты средней скорости
|
Рисунок 55 - Профили продольной компоненты средней скорости
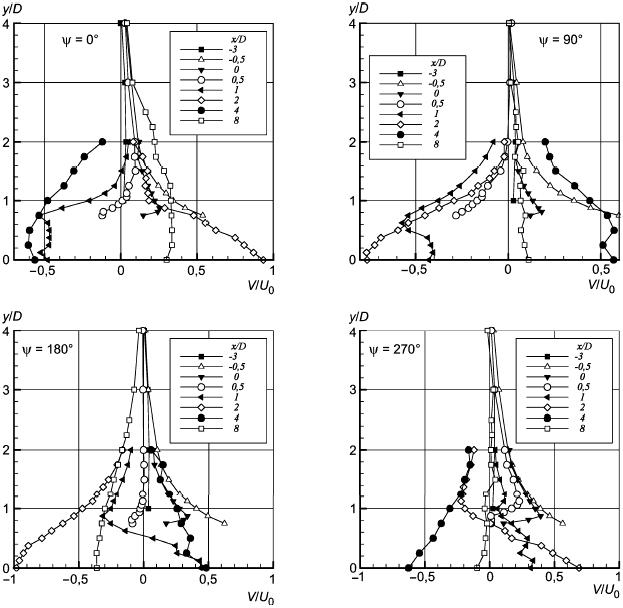
Рисунок 56 - Профили поперечной компоненты средней скорости
|
Рисунок 56 - Профили поперечной компоненты средней скорости
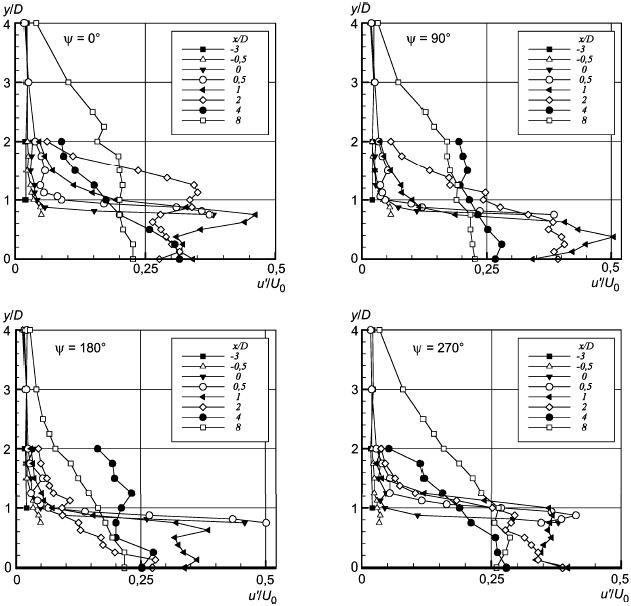
Рисунок 57 - Профили интенсивностей пульсаций скорости в продольном направлении
|
Рисунок 57 - Профили интенсивностей пульсаций скорости в продольном направлении
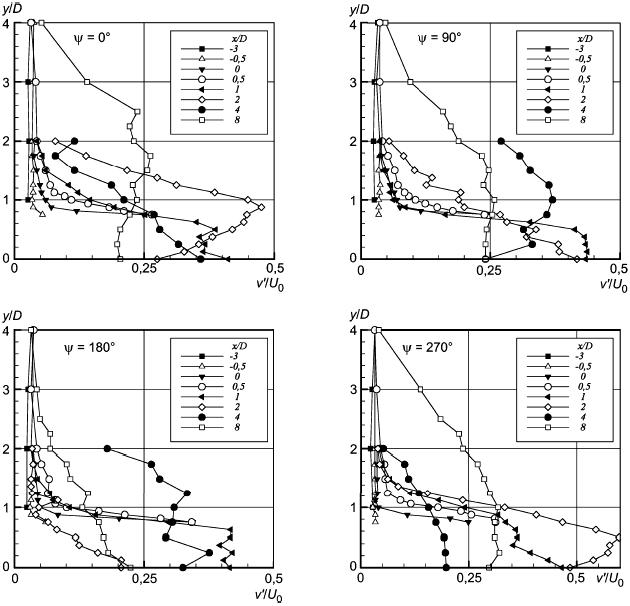
Рисунок 58 - Профили интенсивностей пульсаций скорости в поперечном направлении
|
Рисунок 58 - Профили интенсивностей пульсаций скорости в поперечном направлении
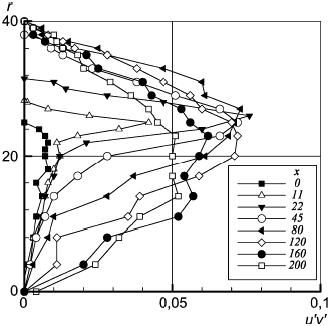
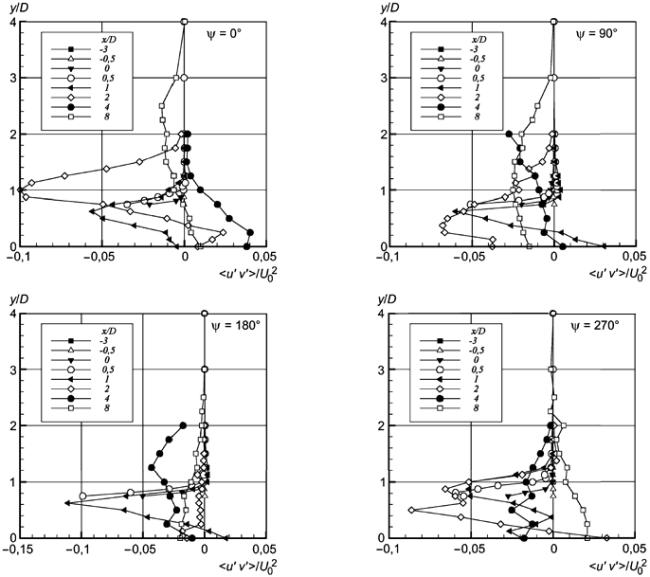
Рисунок 59 - Профили сдвиговых напряжений Рейнольдса
|
Рисунок 59 - Профили сдвиговых напряжений Рейнольдса
Библиография
[1] | Пейре Р., Тейлор Т.Д. Вычислительные методы в задачах механики жидкости. - Ленинград: Гидрометеоиздат, 1986. - 352 с. |
[2] | Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. - М.: Энергоатомиздат, 1984. - 152 с. |
[3] | Choi Y.D., Moon C., Yang S.H. Measurment of turbulent flow characteristics of square duct with a 180 degree bend by not wire anemometer. International Symp. on Engineering Turbulenze modelling and measurement, 1990. |
[4] | Choi Y.D., lacovides H., Launder B.E. Numerical computation of turbulent flow in a square-sectioned 180 deg bend. J. Fluids Engg 111, 59, 1989. |
[5] | Sotiropoulos F., Patel V.C. Evaluation of some near-wall models for the Reynolds-stress transport equations in a complex 3-d shear flow. Near wall turbulent flows, 1993, pp.987. |
[6] | Nakabayashi K., Kitoh O., Iwata H. Turbulent Couette type flow with an alternating pressure gradient. Presented at 8th Symposium on Turbulent Shear Flows, Munich, poster no. I-13, 1991. |
[7] | El Telbany M.M.M., Reynolds A.J. Velocity distributions in plane turbulent channel flows. J. Fluid Mech. 100, 1-29, 1980. |
[8] | Huffman G.D., Bradshaw P. A note on von |
[9] | Townsend A.A. Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97-120, 1961. |
[10] | Almeida G.P., Durao D.F.G. Heitor M.V. Wake flows behind two dimensional model hills. Exp. Thermal and Fluid Science, 7, p.87, 1992. |
[11] | Almeida G.P, Durao D.F.G, Simoes J.P. Heitor M.V. Laser-Doppler measurements of fully developed turbulent channel flow. Proc. 5th Symp. Appl Laser Techniques to Fluid Meet., pp.5-12, 1990. |
[12] | Snyder W.H., Hunt J.C.R. Experiments on stably and neutrally stratified flow over a model three-dimensional hill. J. Fluid Mech., Vol.96, pp.671-704, 1980. |
[13] | Castro J.P., Haque A. The structure of a turbulent shear layer bounding a separation region. J. Fluid Mech., Vol. 179, pp.439-468, 1987. |
[14] | Cooper D., Jackson D.C., Launder B.E., Liao G.X. Impinging jet studies for turbulence model assessment. Part I: Flow-field experiments. Int. J. Heat Mass Transfer, Vol.36, pp.2675-2684, 1993. |
[15] | Baughn J.W., Yan X., Masbah M. The effect of Reynolds number on the heat transfer distribution from a flat plate to an impinging jet. ASME Winter annual meeting, 1992. |
[16] | Baughn J.W., Shimizu S. Heat transfer measurement from a surface with uniform heat flux and an impinging jet. ASME Journal of Heat Transfer, Vol.111, pp.1096-1098, 1989. |
[17] | Craft T.J., Graham L.J.W., Launder B.E. Impinging jet studies for turbulence model assessment. Part II: An examination of the performance of four turbulence models. Int. J. Heat Mass Transfer, Vol.36, pp.2685-2697, 1993. |
[18] | Craft T.J., Launder B.E., Suga K. Development and application of a cubic eddy-viscosity model of turbulence. Int. J. Heat and Fluid Flow, Vol.17, pp.108-115, 1996. |
[19] | Durbin P.A. On the k-3 stagnation point anomaly. Int. J. Heat Fluid Flow, Vol.17, pp.89-90, 1996. |
[20] | Gibson M.M., Launder B.E. Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech., Vol.86, p.491, 1978. |
[21] | Craft T.J., Launder B.E. New wall-reflection model applied to the turbulent impinging jet. AIAA J., Vol.30, pp.2970-2972, 1992. |
[22] | Driver D.M., Seegmiller H.L. Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J., Vol.23, p.163, 1985. |
[23] | Martinuzzi R., Tropea С The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. //Journal of Fluid Engineering, Vol.115, p.85, 1993. |
[24] | Martinuzzi R., Psud'homme M. Higher-order correlations for the turbulent flow around a surface-mounted cube placed in a channel. TSF9, Kyoto, Japan, p.211-1, 1993. |
[25] | Martinuzzi R., Melling A., Tropea C. Reynolds stress field for the turbulent flow around a surface-mounted cube placed in a channel. TSF9, Kyoto, Japan, p.13-4-1, 1993. |
[26] | Murakami S., Mochida A., Ooka R. Numerical simulation of flow field over surface-mounted cube with various second-moment closure models. TSF9, Kyoto, Japan, p.13-5-1, 1993. |
[27] | Stieglmeier M., Tropea C., Weiser N., Nitsche W. Experiment al investigation of the flow through axisymmetric expansions // Journal of Fluids Engineering, vol.111, p.465, 1989. |
[28] | Lyn D.A., Rodi W. The flapping shear layer formed by flow separation from the forward corner of a square cylinder. J. Fluid Mech., 267, 353, 1994. |
[29] | Lyn D.A., Einav S., Rodi W., Park J.H. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. Rept. SFB 210 /E/100, 1994. |
[30] | Murakami S., Mochida A. On turbulent vortex shedding flow past 2d square cylinder predicted by CFD. Journal of wind engineering and industrial aerodynamics, 1993. |
УДК 519.642.2:006.354 | ОКС 35.020 |
Ключевые слова: моделирование, численное моделирование, физические процессы, дозвуковое течение, вязкая жидкость, вязкий газ, валидация |
Электронный текст документа
и сверен по:
официальное издание
М.: Стандартинформ, 2018


 constant in low Reynolds number turbulent flows. J. Fluid Mech. 53, Pt. 1, 45-60, 1972.
constant in low Reynolds number turbulent flows. J. Fluid Mech. 53, Pt. 1, 45-60, 1972.