ГОСТ Р 57282-2016
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Расчеты и испытания на прочность
ОПРЕДЕЛЕНИЕ ПОВРЕЖДЕННОСТИ СТАЛИ ПРИ МАЛОЦИКЛОВОМ НАГРУЖЕНИИ
Общие требования
Calculation and strength testing. Determination of damage under low-cycle fatigue of steel. General requirements
ОКС 77.040.10
Дата введения 2017-10-01
Предисловие
1 РАЗРАБОТАН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 132 "Техническая диагностика"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 24 ноября 2016 г. N 1773-ст
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
В процессе эксплуатации многие элементы конструкций работают в условиях малоцикловой усталости. На стадии до зарождения и развития макротрещины выделяют период, связанный с изменением структуры, зарождением и накоплением рассеянных микроповреждений.
В последние годы для решения задач, связанных с расчетом поврежденности материала, успешно развивается новая дисциплина - механика поврежденной среды, в рамках которой предложен ряд подходов к расчету поврежденности.
К настоящему времени сформулированы базовые уравнения термопластичности, предназначенные для описания основных эффектов, учет которых необходим для адекватного моделирования процессов накопления усталостных повреждений и расчета поврежденности на стадии до образования макродефекта в конструктивных элементах ответственных технических объектов при термосиловых нестационарных нагружениях.
Настоящий стандарт разработан с целью обеспечения методической основы применения методов механики поврежденной среды для расчета эксплуатационной поврежденности материала деталей и конструктивных элементов, подвергаемых малоцикловым воздействиям при сложных термосиловых нагружениях.
1 Область применения
Настоящий стандарт устанавливает общие требования к расчетному методу определения величины накопленной эксплуатационной поврежденности стальных конструктивных элементов, подвергаемых малоцикловым усталостным воздействиям.
Регламентируемый настоящим стандартом метод позволяет на основании подходов механики поврежденной среды сделать оценку уровня эксплуатационной поврежденности в зоне контроля при известных параметрах усталостных воздействий.
Номенклатура объектов, поврежденность материала которых может быть определена в соответствии с регламентируемым методом, устанавливается в техническом задании на контроль.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 25.505 Методы механических испытаний металлов. Метод испытаний на малоцикловую усталость при термомеханическом нагружении
ГОСТ 25859 Сосуды и аппараты стальные. Нормы и методы расчета на прочность при малоцикловых нагрузках
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и сокращения
3.1 В настоящем стандарте применены термины и определения по ГОСТ 25.505, ГОСТ 25859.
3.2 В настоящем стандарте применены следующие сокращения:
МНЦУ - многоцикловая усталость;
МПС - механика поврежденной среды;
МЦУ - малоцикловая усталость.
4 Общие положения
4.1 Рекомендуемый настоящим стандартом алгоритм расчета поврежденности при МЦУ базируется на использовании уравнений термопластичности, описывающих основные эффекты, учет которых необходим для адекватного моделирования процессов усталостной поврежденности материала конструктивных элементов при термосиловых нестационарных нагружениях.
4.2 Учитывают следующие процессы, протекающие в материале при накоплении повреждений:
- монотонное и циклическое упрочнение при пропорциональном и непропорциональном нагружении с учетом переходных циклических процессов и стабилизированного циклического поведения материала;
- изменение локальной анизотропии пластического деформирования (изменение модуля упрочнения) в результате вращения главных площадок тензора деформаций при изломе траектории деформирования (изменение направления нагружения);
- неизотермическое пластическое деформирование материала при различных законах изменения температуры и механической деформации;
- прогрессирующее изменение прочностных и жесткостных характеристик материала в процессе накопления усталостных повреждений на второй стадии развития рассеянных по объему повреждений до образования макротрещины.
5 Основные уравнения термопластичности
5.1 Тензоры напряжений и деформаций
раскладывают на шаровую (гидростатическую)
, e и девиаторную компоненты (
) и (
).
5.2 Принимают, что компоненты девиатора тензора деформаций и их приращений
являются суммой упругих
и пластических
компонент:
![]() , (1)
, (1)
![]() , (2)
, (2)
5.3 Материал считают пластически несжимаемым:
![]() , (3)
, (3)![]() . (4)
. (4)
5.4 Величина упругого изменения объема описывается соотношением:
![]() . (5)
. (5)
5.5 Рассматривают упругоизотропные среды, характеризуемые зависящими от температуры T модулем упругости Юнга E(T), коэффициентом Пуассона v(T), объемным модулем упругости K(T) и объемным модулем сдвига G(T).
5.6 Анизотропию упругих свойств, вызванную процессом накопления повреждений, не учитывают.
5.7 Связь между напряжениями () и упругими составляющими тензора деформаций (
) устанавливают на базе уравнений термоупругости:
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() , (8)
, (8)
![]() , (9)
, (9)
где - коэффициент линейного расширения, являющийся функцией температуры.
5.8 На основании гипотезы кинематического и изотропного упрочнения поверхность текучести в пространстве девиаторов напряжений представляют сферой с радиусом
и координатами центра
(тензор микронапряжений):
![]() (10)
(10)
или
![]() ;
; ![]() . (11)
. (11)
5.9 Согласно ассоциированному закону течения считают, что
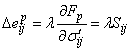 . (12)
. (12)
5.10 Принимают, что радиус поверхности текучести изменяется в зависимости от приращения длины дуги
траектории пластического деформирования и приращения температуры следующим образом:
![]() , (13)
, (13)
где ![]() ,
,
![]() , (14)
, (14)
![]() , (15)
, (15)
![]() , (16)
, (16)
![]() ,
, 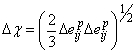 , (17)
, (17)
где 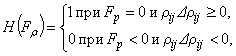
![]() ,
, ![]() , (18)
, (18) ![]() ,
, ![]() ,
, 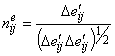 ,
, 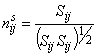 . (19)
. (19)
5.11 В уравнении (13) первый член описывает изотропное упрочнение в результате монотонного пластического деформирования (![]() =1 и
=1 и ![]() =0), второй член - изменение радиуса поверхности текучести при изменении температуры, третий член описывает циклическое упрочнение материала (
=0), второй член - изменение радиуса поверхности текучести при изменении температуры, третий член описывает циклическое упрочнение материала (![]() =0 и
=0 и ![]() =1), последний член описывает восстановление (возврат) радиуса поверхности текучести в условиях высокотемпературной выдержки (отжига).
=1), последний член описывает восстановление (возврат) радиуса поверхности текучести в условиях высокотемпературной выдержки (отжига).
5.12 Модуль изотропного упрочнения (14) учитывает изменение изотропного упрочнения материала в зависимости от направления деформирования в данной точке траектории M - угла
между вектором приращения девиатора деформации (
), имеющим направляющие косинусы
, и нормалью к поверхности текучести в точке M, определяемой направляющими косинусами
.
5.13 При пропорциональном нагружении =0, cos
=1, A=0,
![]() , где
, где - модуль изотропного упрочнения материала при одноосном растяжении образца.
5.14 При непропорциональном нагружении с углом ![]() (вектор
(вектор перпендикулярен нормали к поверхности текучести в точке нагружения) A=1,
![]() , где
, где - модуль упрочнения при нагружении по касательной к поверхности текучести ("нейтральное" нагружение).
5.15 В формуле (15) для циклического изотропного упрочнения при циклическом пропорциональном нагружении =0 и
=Q и при циклическом непропорциональном нагружении
![]() ,
, ![]() ,
, и
(0
![]() 1, 0
1, 0![]() 1) - параметры, позволяющие корректировать влияние модулей
1) - параметры, позволяющие корректировать влияние модулей ,
, Q и
на изотропное упрочнение материала.
5.16 При стационарном циклическом деформировании материала с постоянной амплитудой деформации и Т=const (=const,
![]() =0,
=0, ![]() =1,
=1, =const) радиус поверхности текучести
стремится к
=const и параметры петли гистерезиса стремятся к своему стационарному значению, определяемому значением
, которое зависит от текущих значений Т и
.
5.17 Эволюционное уравнение для изменения координат центра поверхности текучести (тензора ) имеет вид:
![]() , (20)
, (20)
где и
- модули кинематического упрочнения, являющиеся функциями температуры. Модуль
определяет перемещение центра поверхности текучести в результате приращения тензора пластических деформаций
, модуль
- его постепенную релаксацию (при
0 координаты центра
стремятся к своему начальному нулевому значению).
5.18 Модуль описывает изменение координат центра поверхности текучести в связи с повышением температуры Т:
![]() , (21)
, (21)
![]() при
при ![]() , (22)
, (22)
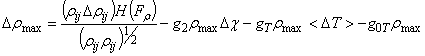 . (23)
. (23)
5.19 Соотношения (16, 17, 23) определяют изменение радиуса поверхности текучести и позволяют автоматически отделить циклическое нагружение от монотонного с помощью операторов ![]() и
и ![]() .
.
6 Рекомендуемые расчетные модели
6.1 Изотропное упрочнение
6.1.1 При ![]() в (20) и
в (20) и имеет место случай чисто изотропного нелинейного упрочнения, описываемого уравнением (13), (при этом
![]() и циклическое упрочнение также не учитывают).
и циклическое упрочнение также не учитывают).
6.1.2 Если в (14) и (15) и
, то изменение изотропного и кинематического упрочнения при непропорциональном деформировании не учитывают:
![]() , a
, a =Q (кинематическое и изотропное упрочнение, соответствующее диаграмме одноосного растяжения материала).
6.1.3 Если ![]() , то описывают линейное изотропное упрочнение.
, то описывают линейное изотропное упрочнение.
6.1.4 Если , то описывают идеально пластический материал с постоянной поверхностью текучести
![]() .
.
6.2 Кинематическое упрочнение
6.2.1 При =
=
=
0 в (13) имеет место случай чисто кинематического нелинейного упрочнения, описываемого уравнением (20).
6.2.2 Если 0 и
=const, имеет место случай линейного кинематического упрочнения.
6.3 Модель J.L.Chaboche (CHAB)
6.3.1 Основные уравнения модели CHAB имеют вид:
- уравнение поверхности текучести:
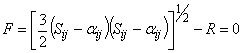 ; (24)
; (24)
- уравнение для изменения радиуса поверхности текучести:
![]() , (25)
, (25)
![]() ; (26)
; (26)
- уравнение для эволюции центра поверхности текучести
![]() , (27)
, (27)
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . (28)
. (28)
Пpимeчаниe - Уравнения (24-28) являются частным случаем уравнений (8-23) и описывают нелинейное кинематическое и изотропное упрочнение без учета циклического упрочнения при
![]() ,
, ![]() ,
, ![]() , i=1. (29)
, i=1. (29)
6.3.2 Следует учитывать, что упрочнение при монотонном деформировании носит как кинематический, так и изотропный характер; радиус поверхности текучести может как возрастать (упрочнение), так и убывать (разупрочнение).
6.3.3 Модуль упрочнения зависит от направления вектора догрузки в точке нагружения на поверхности текучести (от угла между векторами
и
).
6.3.4 При непропорциональном циклическом нагружении возникает дополнительное циклическое упрочнение по сравнению с пропорциональным циклическим нагружением с той же интенсивностью амплитуды деформаций.
6.3.5 Переходные нестационарные циклические процессы в основном зависят от изотропной части упрочнения.
6.3.6 Изотропное упрочнение (эволюция радиуса поверхности текучести ) состоит из трех типов: монотонное, циклическое пропорциональное, циклическое непропорциональное.
6.3.7 Параметры стабилизированной петли гистерезиса в основном не зависят от места стабилизации петли, предыдущей истории циклического деформирования и определяются интенсивностью амплитуды деформаций (величиной в (23) и параметрами непропорционального циклического нагружения (углом
и параметром A).
6.3.8 Закономерности циклического деформирования в стабилизированной петле в основном определяются анизотропной частью упрочнения (эволюцией ); закономерности анизотропного упрочнения для монотонных и циклических процессов могут быть различны.
6.3.9 При жестком циклическом нагружении и начальной анизотропии по амплитуде напряжений в полуциклах растяжения и сжатия наблюдается релаксация средних напряжений цикла до нуля за конечное число циклов (релаксация средних значений ).
6.3.10 Закономерности циклического деформирования описывают при помощи эволюционных уравнений (13-23) для и
.
6.3.11 На второй стадии процесса накопления рассеянных по объему усталостных повреждений наблюдается влияние поврежденности на физико-механические характеристики материала. В первом приближении это влияние может быть учтено на базе концепции деградирующего континуума введением эффективных напряжений
![]() (30)
(30)
или эффективных модулей упругости
![]() ,
, ![]() ,
, ![]() . (31)
. (31)
6.3.12 Эффективную внутреннюю переменную определяют следующим образом:
![]() . (32)
. (32)
6.3.13 Должна быть скорректирована упругая область допустимых состояний материала, определяемая поверхностью текучести. Зависимость поверхности текучести от накопленной поврежденности определяет развитие процессов пластичности поврежденного материала:
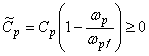 , (33)
, (33)
где ![]() 0,8.
0,8.
7 Базовые эволюционные уравнения накопления повреждений в конструкционных материалах
7.1 За физическую меру поврежденности материала принимают относительную объемную долю дефектов в эталонном элементарном объеме материала:
![]() ,
, ![]() ,
, ![]() ;
; ![]() , (34)
, (34)
где V - текущая объемная доля дефектов, - критическая объемная доля, соответствующая образованию в данном объеме материала макроскопической трещины (полной потере несущей способности материала в данном элементарном объеме).
7.2 В качестве характеристики, коррелирующей с энергией, затраченной на образование дефектов при нестационарном упругопластическом деформировании, используют работу тензора микронапряжений
на пластических деформациях
:
![]() . (35)
. (35)
7.3 В инженерных расчетах в качестве эквивалентных напряжений или деформаций, как правило, рекомендуется выбирать интенсивности соответствующих тензоров:
![]() ,
, ![]() , (36)
, (36)
или максимальные касательные (приведенные) напряжения
![]() ,
, ![]() . (37)
. (37)
7.4 Следует учитывать существенное влияние на усталостную долговечность жесткости напряженного состояния, характеризуемого интенсивностью тензора напряжений и его шаровой (гидростатической) компонентой
:
![]() . (38)*
. (38)*
_______________
* Формула соответствует оригиналу. - .
7.5 В качестве параметров жесткости напряженного состояния используют параметр или функции от
:
![]() , (39)
, (39)
![]() . (40)
. (40)
7.6 В области малоцикловой усталости при одноосном растяжении - сжатии скорость накопления усталостных повреждений связана с накопленной в данном объеме материала энергией , затраченной на образование дефектов, экспоненциальной зависимостью:
![]() . (41)
. (41)
7.7 Следует учитывать, что при непропорциональном циклическом нагружении критерии (36), (37) и критерий эквивалентных деформаций или интенсивности деформаций
![]() (42)
(42)
не являются критериями эквивалентности и могут привести к неконсервативным оценкам.
7.8 В рамках подходов МПС процесс накопления усталостных повреждений до образования макроскопической трещины считается состоящим из двух стадий:
- стадии зарождения и роста пор, при которой поры не взаимодействуют друг с другом; влияние поврежденности на физико-механические характеристики материалов отсутствует, продолжительность первой стадии характеризуется количеством циклов ;
- стадии развития поврежденности путем слияния образовавшихся микропор в микроскопические трещины, при которой наблюдается прогрессирующее влияние поврежденности на физико-механические характеристики материалов; продолжительность стадии характеризуется количеством циклов (-
).
7.9 Продолжительность первой стадии (число циклов ) тем больше, чем меньше амплитуда деформаций.
7.10 Если перестроить кривые  в кривые
в кривые 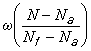 , т.е. рассматривать процесс накопления повреждений только на второй стадии, то эти кривые сольются в одну обобщенную кривую, характеризующую процесс накопления усталостных повреждений для всех амплитуд.
, т.е. рассматривать процесс накопления повреждений только на второй стадии, то эти кривые сольются в одну обобщенную кривую, характеризующую процесс накопления усталостных повреждений для всех амплитуд.
7.11 Общую структуру эволюционных уравнений накопления усталостных повреждений в элементарном объеме материала следует представлять в виде:
![]() (43)
(43)
или
![]() , (44)
, (44)
![]() ,
, ![]() , (45)
, (45)
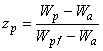 ,
, 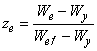 , (46)
, (46)
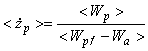 ,
, ![]() , (47)
, (47)![]() ,
, ![]() ,
,
(48)![]() ,
, ![]() ,
,
где - значение
в конце первой стадии процесса накопления усталостных повреждений,
- значение
, соответствующее пределу усталости,
и
- значения энергий, соответствующие образованию макроскопической трещины с характерным размером ~ 1 мм, когда процессы МЦУ и МНЦУ развиваются изолированно,
и r - параметры материала.
7.12 В области МЦУ <<
, z
.
7.13 В области МНЦУ =0, z=
.
7.14 В переходной области z определяется выражением (45).
7.15 Выражение для поврежденности имеет вид:
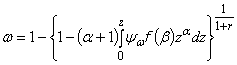 (49)
(49)
или
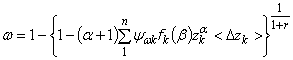 . (50)
. (50)
7.16 Другое выражение для поврежденности
![]() , (51)
, (51)
где y=Az,
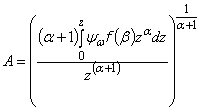 (52)
(52)
или
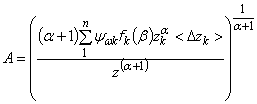 . (53)
. (53)
7.17 Для лучевых путей изотермического нагружения (=1,
![]() =const,
=const, =const,
=const)
![]() ,
, ![]() . (54)
. (54)
7.18 При чистом кручении (![]() =1,
=1, =0):
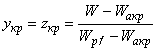 , (55)
, (55)
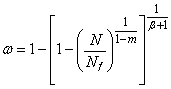 . (56)
. (56)
Пpимечание - Уравнение (56) справедливо для частного случая регулярного циклического нагружения (растяжение - сжатие). Для этого случая в уравнении (51) параметр у может быть выражен через отработанное количество циклов:
![]() . (57)
. (57)
Уравнение для регулярного циклического нагружения (56) является частным случаем уравнения (51).
8 Критерий окончания стадии развития рассеянных микроповреждений
8.1 В качестве критерия окончания стадии развития рассеянных микроповреждений (образования макротрещины) может быть принят критерий потери устойчивости процесса накопления повреждений, когда производная ![]() достигает своего критического значения
достигает своего критического значения
![]() . (58)
. (58)
8.2 При выполнении критерия (58) дальнейшее развитие процесса поврежденности зависит от любых случайных факторов, и контролировать этот процесс невозможно.
8.3 Условие (58) при одноосном растяжении - сжатии приблизительно соответствует значению
![]() . (59)
. (59)
8.4 В зависимости от свойств материала и многоосности напряженного состояния, учитываемого функцией ,
может принимать значения от 0,2 до 0,8. Кроме того, материал может быть разрушен при некотором напряженном состоянии в упругой области после некоторой истории деформирования в пластической области, в результате которой была накоплена поврежденность
<
. Для учета этого обстоятельства необходимо сформулировать силовой критерий прочности
![]() . (60)
. (60)
8.5 При =0 критерий (60) соответствует начальной предельной поверхности неповрежденного усталостью материала, а при
=
- предельной поверхности полностью поврежденного материала. Промежуточным значениям
соответствуют промежуточные поверхности (60).
8.6 Конкретизация силового критерия прочности
8.6.1 Разрушение материала наступает при условии
![]() , (61)
, (61)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
8.6.2 Предельное соотношение (61) учитывает изменяющуюся в процессе накопления повреждений роль и
: при
![]() ,
, ![]() , что соответствует возрастанию роли главного растягивающего напряжения
, что соответствует возрастанию роли главного растягивающего напряжения .
8.6.3 Образовавшаяся трещина при выполнении условия (61) перпендикулярна направлению .
УДК 620.172.1:620.179.16:006.354 | ОКС 77.040.10 | Т59 | |
Ключевые слова: поврежденность, малоцикловая усталость, эволюционные уравнения, термопластичность, тензор напряжений, поверхность текучести, упрочнение | |||
Электронный текст документа
и сверен по:
, 2016
