ГОСТ Р 8.662-2009
(ИСО 20765-1:2005)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственная система обеспечения единства измерений
ГАЗ ПРИРОДНЫЙ. ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА ГАЗОВОЙ ФАЗЫ
Методы расчетного определения для целей транспортирования и распределения газа на основе фундаментального уравнения состояния AGA8
State system for ensuring the uniformity of measurements. Natural gas. Gas phase thermodynamic properties. Methods of calculation for transmission and distribution applications on base of the AGA8 fundamental equation of state
ОКС 75.060
Дата введения 2011-01-01
Предисловие
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Российский научно-технический центр информации по стандартизации, метрологии и оценке соответствия" (ФГУП "") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 180 "Государственная служба стандартных справочных данных"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 15 декабря 2009 г. N 1043-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 20765-1:2005* "Газ природный. Расчетное определение термодинамических свойств. Часть 1. Свойства газовой фазы для целей транспортирования и распределения газа" (ISO 20765-1:2005 "Natural gas - Calculation of thermodynamic properties - Part 1: Gas phase properties for transmission and applications", MOD) путем изменения его структуры для приведения в соответствие с правилами, установленными в ГОСТ Р 1.5 (подразделы 4.2 и 4.3), а также путем изменения отдельных фраз (слов, значений, показателей, ссылок), которые выделены в тексте полужирным курсивом**.
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. -
** В оригинале документа обозначения и номера стандартов и нормативных документов отмеченные по тексту знаком "**" выделены курсивом, отмеченные по тексту знаком "***" выделены полужирным курсивом, остальные по тексту документа приводятся обычным шрифтом. Примечания изготовителя базы данных.
Внесение указанных технических отклонений направлено на учет особенностей объекта стандартизации, характерных для Российской Федерации, а также связано с целесообразностью использования ссылочных национальных и межгосударственных стандартов вместо ссылочных международных стандартов.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
Сравнение структуры настоящего стандарта со структурой указанного международного стандарта приведено в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Октябрь 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации"**. Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
1 Область применения
Настоящий стандарт устанавливает методы расчетного определения термических и калорических свойств (термодинамических свойств) природного газа, подготовленного для транспортирования и распределения по магистральным газопроводам, при условии его нахождения только в газовой фазе.
Настоящий стандарт распространяется на подготовленные для транспортирования по магистральным газопроводам газы в диапазонах давления и температуры
, при которых на практике осуществляют транспортирование и распределение газов.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 8.417*** Государственная система обеспечения единства измерений. Единицы величин
ГОСТ 31369 (ИСО 6976-1:1995) Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности, числа Воббе на основе компонентного состава
ГОСТ 31371.1 (ИСО 6974-1:2000) Газ природный. Определение состава методом газовой хроматографии с оценкой неопределенности. Часть 1. Руководство по проведению анализа
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ГОСТ 8.417***, ГОСТ 31371.1, с учетом [1]-[6], а также следующие термины с соответствующими определениями:
3.1.1 неидеальная составляющая свойства (residual property): Составляющая термодинамического свойства, которая определяется неидеальным (реальным) поведением газа или гомогенной газовой смеси, то есть представляет собой разницу между термодинамическим свойством реального газа или газовой смеси и идеально-газовой составляющей этого свойства газа или газовой смеси при тех же самых температуре и плотности.
3.1.2 калорическое свойство (caloric property): Характеристика газа или гомогенной газовой смеси, которую можно рассчитать по фундаментальному уравнению состояния (с привлечением данных об идеально-газовых значениях теплоемкости, энтальпии и энтропии).
Примечание - Вычисление калорических свойств по настоящему стандарту применимо к внутренней энергии, энтальпии, энтропии, изохорной теплоемкости, изобарной теплоемкости, коэффициенту Джоуля-Томсона, показателю изоэнтропы (адиабаты), скорости звука.
3.1.3 термическое свойство (volumetric property): Характеристика газа или гомогенной газовой смеси, которые можно рассчитать по термическому уравнению состояния.
Примечание - Настоящий стандарт распространяется на такие термические свойства, как фактор сжимаемости и плотность; перевод термина дан в соответствии с [6].
3.1.4 термодинамическое свойство (thermodynamic property): Термическое или калорическое свойство.
3.1.5 уравнение состояния (equation of state): Математическое выражение взаимосвязи между параметрами состояния газа или гомогенной газовой смеси.
Примечание - В этой части следует учитывать различия между двумя видами уравнения состояния, а именно: 1) термическим уравнением состояния, которое устанавливает взаимосвязь между такими параметрами состояния, как давление, температура и объем, занимаемый заданным количеством вещества; 2) фундаментальным уравнением состояния, которое устанавливает взаимосвязь между плотностью, температурой и свободной энергией Гельмгольца.
3.2 Обозначения
3.2.1 Условные обозначения
Условные обозначения величин приведены в таблице 1.
Таблица 1 - Условные обозначения величин
Обозначение | Наименование величины | Единицы измерений |
Константа уравнения | 1 | |
| Коэффициент уравнения состояния идеального газа | 1 |
| Коэффициент уравнения состояния идеального газа | 1 |
Коэффициент уравнения состояния реального газа | 1 | |
Второй вириальный коэффициент | м | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения | 1 | |
Параметр бинарного взаимодействия | 1 | |
Коэффициент уравнения состояния реального газа | 1 | |
Молярная изобарная теплоемкость | кДж/(кмоль·К) | |
Молярная изохорная теплоемкость | кДж/(кмоль·К) | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения состояния реального газа | 1 | |
Удельная изобарная теплоемкость | кДж/(кг·К) | |
Удельная изохорная теплоемкость | кДж/(кг·К) | |
Удельная (массовая) плотность | кг/м | |
Коэффициент уравнения состояния идеального газа | 1 | |
Энергетический параметр в расчетных уравнениях | 1 | |
Коэффициент уравнения состояния идеального газа | 1 | |
Энергетический параметр бинарного взаимодействия | 1 | |
Энергетический параметр бинарного взаимодействия | 1 | |
Молярная свободная энергия Гельмгольца | кДж/кмоль | |
Коэффициент уравнения | 1 | |
Коэффициент уравнения | 1 | |
Высокотемпературный параметр в уравнениях | 1 | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения | 1 | |
Коэффициент уравнения | 1 | |
Ориентационный параметр | 1 | |
Коэффициент уравнения состояния идеального газа | 1 | |
Ориентационный параметр бинарного взаимодействия | 1 | |
Ориентационный параметр бинарного взаимодействия | 1 | |
Молярная энтальпия | кДж/кмоль | |
Удельная энтальпия | кДж/кг | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения состояния идеального газа | 1 | |
Коэффициент уравнения состояния AGA8 | 1 | |
Параметр размера для смеси | (м | |
Параметр размера для компонента | (м | |
Параметр размера для бинарного взаимодействия | 1 | |
Температура нормировки | К | |
Молярная масса смеси | кг/кмоль | |
Молярная масса | кг/кмоль | |
Число компонентов в газовой смеси | 1 | |
Давление | МПа | |
Коэффициент уравнения | 1 | |
Коэффициент уравнения | 1 | |
Квадрупольный* параметр | 1 | |
________________ * Текст документа соответствует оригиналу. - . | ||
Универсальная газовая постоянная - 8,314510* | кДж/(кмоль·К) | |
Молярная энтропия | кДж/(кмоль·К) | |
Коэффициент уравнения | 1 | |
Удельная энтропия | кДж/(кг·К) | |
Дипольный параметр | 1 | |
Температура | К | |
Молярная внутренняя энергия | кДж/кмоль | |
Коэффициент уравнения состояния AGA8 | 1 | |
Удельная внутренняя энергия | кДж/кг | |
Коэффициент уравнения | 1 | |
Параметр бинарного взаимодействия | 1 | |
Скорость звука | м/с | |
Коэффициент уравнения | 1 | |
Параметр ассоциации | 1 | |
Молярная доля | 1 | |
Вектор значений молярной доли компонентов в смеси ( | 1 | |
Фактор сжимаемости | 1 | |
Относительная плотность | 1 | |
Относительная свободная энергия Гельмгольца | 1 | |
Показатель адиабаты | 1 | |
Коэффициент Джоуля-Томсона | К/МПа | |
Молярная плотность | кмоль/м | |
Обратная относительная температура | 1 | |
* Приведенное в настоящей таблице значение универсальной газовой постоянной | ||
3.2.2 Подстрочные индексы
Индексы в условных обозначениях величин означают следующее:
- для
-го компонента (от
1 до
);
- для второго (
-го) компонента в бинарном взаимодействии (от
2 до
);
- номер коэффициента в уравнении состояния (от
1 до 58);
0 - для идеально-газового состояния;
- для неидеальной составляющей;
- частная производная по относительной молярной плотности;
- для стандартного состояния (
298,15 K,
0,101325 МПа);
- частная производная по обратной относительной температуре.
4 Термодинамические основы метода
4.1 Сущность метода
Метод настоящего стандарта основывается на концепции, что для подлежащего транспортированию по газопроводу природного газа имеются данные о результатах анализа его полного компонентного состава, используемые для вычисления термодинамических свойств газа. Эти данные совместно с температурой и плотностью, характеризующими состояние газа, составляют комплекс входных переменных для рассматриваемого метода. На практике в качестве входных переменных более удобно использовать температуру и давление. В таком случае сначала необходимо преобразовывать эти параметры состояния в температуру и плотность.
В настоящем стандарте представлены уравнения, в которых свободная энергия Гельмгольца выражается как функция плотности, температуры и состава смеси; по этим уравнениям термодинамические свойства выражают через свободную энергию Гельмгольца и ее производные по температуре и плотности.
В настоящем методе используют результаты детального анализа молярного состава смеси, то есть должны быть указаны все компоненты, присутствующие в смеси в количествах, превышающих 0,00005 молярной доли (50 миллионных частей молярной доли). Для типичного природного газа такой анализ должен включать алканы, примерно до
или
, совместно с азотом, диоксидом углерода и гелием. Обычно изомеры алканов свыше
объединяют с нормальными изомерами с учетом молярной массы.
_______________
млн
- несистемная единица.
Для некоторых природных газов следует учитывать дополнительные компоненты, такие как углеводороды и
, водяной пар и сероводород. Для коммунально-бытовых газов необходимо учитывать наличие водорода и окиси углерода.
В настоящем методе используют результаты анализа компонентного состава, рассчитанного на 21 компонент. Эти компоненты могут присутствовать в природном газе в качестве основных или второстепенных составляющих (см. 6.2). Любой "следовой" компонент, который не входит в число 21 определяемого, можно приблизительно учитывать совместно с определяемым компонентом.
4.2 Фундаментальное уравнение состояния для свободной энергии Гельмгольца
4.2.1 Исходные положения
Примечание - Исходные положения для фундаментального уравнения состояния для свободной энергии Гельмгольца приведены в приложении А.
4.2.2 Свободная энергия Гельмгольца
Свободную энергию Гельмгольца гомогенной газовой смеси при заданных давлении и температуре выражают как сумму идеально-газовой составляющей
и неидеальной составляющей
, характеризующей поведение реального газа, согласно уравнению
![]() , (1)
, (1)
которое при безразмерном представлении свободной энергии в виде ![]() преобразуют в уравнение
преобразуют в уравнение
![]() , (2)
, (2)
где - вектор молярных долей смеси;
- обратная (безразмерная) относительная температура, связанная с температурой
по соотношению
![]() , (3)
, (3)
где L=1 K.
Поскольку, согласно статистической термодинамике, свободная энергия Гельмгольца представляет собой непосредственный результат числа и типов молекулярных взаимодействий в смеси и является тем самым непосредственной функцией молярной плотности и молярных долей молекул в смеси, в уравнения (1) и (2) в качестве входных переменных записывают соответственно - молярную плотность и
- относительную плотность, а не давление
.
Относительную плотность связывают с молярной плотностью
по уравнению
![]() , (4)
, (4)
где - смесевой параметр размера.
Идеально-газовую составляющую относительной свободной энергии Гельмгольца получают из уравнений для идеально-газовой изобарной теплоемкости (см. 4.2.2) и избыточной составляющей
из уравнения состояния AGA8 (см. 4.2.3).
4.2.3 Идеально-газовая составляющая свободной энергии Гельмгольца
Идеально-газовую составляющую свободной энергии Гельмгольца через энтальпию и энтропию
выражают в соответствии с уравнением
![]() . (5)
. (5)
В свою очередь, энтальпию и энтропию
выражают через идеально-газовую изобарную теплоемкость
по уравнениям (6) и (7), где в качестве пределов интегрирования устанавливают температуры
и
:
![]() ; (6)
; (6)
![]() . (7)
. (7)
Стандартное состояние для нулевых значений энтальпии и энтропии устанавливают при 298,15 K и
0,101325 МРа для идеальной нереагирующей газовой смеси. Константы интегрирования
и
устанавливают далее так, чтобы следовать этому условию. Стандартную (идеально-газовую) плотность
определяют по соотношению
![]() .
.
Неидеальную составляющую свободной энергии Гельмгольца ![]() определяют, используя уравнения (6) и (7), как функцию
определяют, используя уравнения (6) и (7), как функцию ,
и
, по уравнению
![]() (8)
(8)
(более подробную информацию см. в приложении В).
4.2.4 Неидеальная составляющая свободной энергии Гельмгольца
В настоящем стандарте неидеальную составляющую свободной энергии Гельмгольца получают путем использования уравнения состояния AGA8. Записывая фактор сжимаемости как функцию относительной плотности, обратной относительной температуры и молярных долей компонентов, уравнение состояния AGA8 представляют в виде следующего уравнения
![]() , (9)
, (9)
где - второй вириальный коэффициент;
- функция молярных долей компонентов;
,
,
,
- коэффициенты уравнения состояния и функции молярных долей компонентов.
Фактор сжимаемости связывают с неидеальной составляющей относительной свободной энергии Гельмгольца
согласно уравнению
![]() , (10)
, (10)
где - частная производная от
по относительной плотности при постоянных
и
.
Путем исключения , используя уравнения (9) и (10) и интегрирование по относительной плотности, приходят к уравнению для неидеальной составляющей относительной свободной энергии Гельмгольца
![]() (11)
(11)
(более подробную информацию см. в приложении С).
4.2.5 Относительная свободная энергия Гельмгольца
Исходя из возможности рассчитать все термодинамические свойства по фундаментальному уравнению состояния (2) для относительной свободной энергии Гельмгольца путем использования уравнения (8) для идеально-газовой составляющей
и уравнения (11) для неидеальной составляющей
, относительную свободную энергию Гельмгольца
представляют в виде уравнения
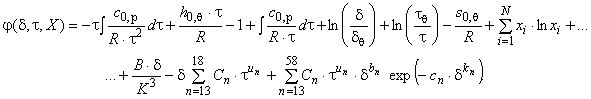 (12)
(12)
4.3 Термодинамические свойства, получаемые из свободной энергии Гельмгольца
4.3.1 Исходные положения
Каждое из термодинамических свойств можно выразить в явном виде через относительную свободную энергию Гельмгольца и различные производные от нее. Требуемые производные
,
,
,
и
определяют по уравнениям:
![]() ;
; 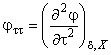 ;
; ![]() ;
; 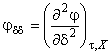 ;
; 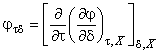 . (13)
. (13)
Каждую производную определяют в виде суммы идеально-газовой составляющей (см. приложение В) и неидеальной составляющей (см. приложение С). Вводят подстановки, приведенные в уравнениях, для упрощения получения требуемых аналитических выражений:
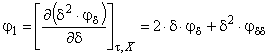 ; (14)
; (14)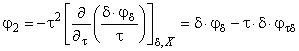 . (15)
. (15)
(более детальные выражения для ,
,
,
и
см. в приложении С; необходимые общие выражения для различных термодинамических свойств приведены в 4.3.2.1-4.3.2.9 [уравнения (17)-(26)]: в уравнениях (19)-(24) нижние символы относятся к молярным величинам (то есть отнесенным к 1 киломолю), и соответствующие верхние символы относятся к массовым величинам (то есть отнесенным к 1 килограмму); переход от молярных переменных к массовым достигается делением на молярную массу
).
Примечание - В этих уравнениях - молярная газовая постоянная; соответственно,
![]() - массовая газовая постоянная.
- массовая газовая постоянная.
Молярную массу смеси получают на основе компонентного состава
и молярных масс
компонентов по уравнению
![]() . (16)
. (16)
Значения молярных масс компонентов приведены в [7] и [8], в которых эти значения являются идентичными значениям, приведенным в ГОСТ 31369.
Примечание - Значения, приведенные для молярных масс, в большинстве случаев не идентичны современным значениям, применяемым в международной метрологической практике. Они представляют собой значения, которые были использованы в основном при получении уравнения состояния AGA8 и в этой связи оставлены без изменений; расхождения во всех случаях не превышают 0,001 кг/кмоль.
В уравнениях (20), (21) и (23)-(26) основные выражения для свойств ,
,
,
,
и
представляют в нескольких вариантах для того, чтобы полученные значения свойств можно было использовать для упрощения последующих вычислений. Такой подход можно применять в случаях, когда необходимо определять несколько или все термодинамические свойства. В каждом подпункте сначала представлены основные термодинамические соотношения, а далее вспомогательные выражения.
4.3.2 Уравнения для термодинамических свойств
4.3.2.1 Фактор сжимаемости и плотность
Выражение для фактора сжимаемости представляют согласно уравнению
![]() , (17)
, (17)
где - производная от свободной энергии Гельмгольца по относительной молярной плотности [см. также уравнение (10)]. Молярную плотность
и удельную (массовую) плотность
связывают с давлением согласно уравнению
![]() . (18)
. (18)
Значения фактора сжимаемости , рассчитываемые по настоящему стандарту, как правило, не должны отличаться от значений, рассчитываемых по стандарту [1]. Для этого выход из итерационного процесса при расчете плотности на шаге 4 блок-схемы расчета термодинамических свойств (см. рисунок F.1, приложение F) должен проводиться по критерию разности абсолютных значений рассчитанного и заданного (входного) давления; эта разность должна быть меньше 10
МПа.
4.3.2.2 Внутренняя энергия
Выражение для внутренней энергии представляют согласно уравнению
![]() . (19)
. (19)
4.3.2.3 Энтальпия
Выражение для энтальпии представляют согласно уравнению
![]() . (20)
. (20)
4.3.2.4 Энтропия
Выражение для энтропии представляют согласно уравнению
![]() . (21)
. (21)
4.3.2.5 Изохорная теплоемкость
Выражение для изохорной теплоемкости представляют согласно уравнению
![]() . (22)
. (22)
4.3.2.6 Изобарная теплоемкость
Изобарную теплоемкость определяют по уравнению
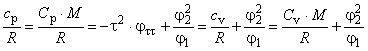 . (23)
. (23)
4.3.2.7 Коэффициент Джоуля-Томсона
Выражение для коэффициента Джоуля-Томсона представляют уравнением
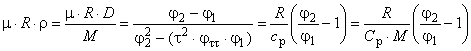 . (24)
. (24)
4.3.2.8 Показатель адиабаты
Выражение для показателя адиабаты представляют согласно уравнению
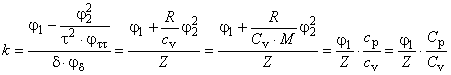 . (25)
. (25)
4.3.2.9 Скорость звука
Выражение для скорости звука представляют согласно уравнению
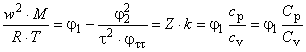 . (26)
. (26)
5 Метод расчета свойств
5.1 Входные переменные
При характеристике сущности метода, устанавливаемого в настоящем стандарте, предполагают использование относительной плотности, обратной относительной температуры и молярного компонентного состава в качестве входных переменных. На практике в качестве входных переменных обычно чаще используют абсолютное давление, абсолютную температуру и молярный компонентный состав. Соответственно, на основе этих данных необходимо сначала рассчитать обратную относительную температуру и относительную плотность. Переход от абсолютной температуры к обратной относительной температуре осуществляют, используя соотношение (3).
Переход от давления к относительной плотности проводят по 5.2.
Если вместо давления в качестве входной переменной приводят удельную (массовую) плотность
, значения
получают непосредственно без проведения процедур по 5.2, а именно, как
![]() , где
, где - молярная масса, определяемая по уравнению (16). Компонентный состав необходимо определять для следующего 21 компонента: азота, диоксида углерода, метана, этана, пропана, н-бутана, изобутана (2-метилпропана), н-пентана, изопентана (2-метилбутана), н-гексана, н-гептана, н-октана, н-нонана, н-декана, водорода, кислорода, углерода, воды, сероводорода, гелия и аргона (о допустимых пределах молярных долей компонентов, устанавливаемых рассматриваемым методом, см. 6.2). Какой-либо следовой компонент, присутствующий в газе, но не идентифицируемый в числе перечисленного 21 компонента, можно приблизительно учитывать в совокупности с подходящим из перечисленных выше (см. приложение Е). Сумма молярных долей компонентов должна быть равна единице.
Если это условие не выполняется, необходимо проверить качество проведенного компонентного анализа, в том числе на полноту учета количества компонентов. Нельзя переходить к решению последующих задач, пока не будет обнаружен источник этой проблемы. Если не установлены молярные доли гептана, октана, нонана и декана, можно использовать суммарную фракцию . Необходимо провести при этом анализ влияния подобных приближений на искажение конечных результатов.
Примечание - Если состав газа известен в объемных долях, его необходимо пересчитать в молярные доли, используя метод по ГОСТ 31369.
5.2 Переход от давления к относительной плотности
Комбинируя уравнения (4), (9) и (18), получают уравнение
![]() . (27)
. (27)
Если входные переменные выражены через давление, обратную относительную температуру и компонентный состав, используя уравнение (27), можно определить приведенную молярную плотность . Значения параметров
![]() ,
, ![]() ,
, ![]() и коэффициентов
и коэффициентов ,
,
и
уравнения (27) можно получить из уравнений и таблиц, представленных в приложении D [уравнений (D.1), (D.6) и (D.11) и таблицы D.1 соответственно] для этих характеристик. Численные значения параметров для всех индивидуальных компонентов и их бинарного взаимодействия, также требуемые для решения уравнений (D.1), (D.6) и (D.11), представлены в таблицах D.2 и D.3 соответственно.
Решение можно получить подходящим численным методом. На практике применяют стандартный алгоритм решения уравнения состояния относительно плотности как наиболее удобный и достаточно корректный. В таких алгоритмах обычно используют начальное приближение для значения плотности (часто идеально-газовое приближение) и продолжают расчеты путем итерационных вычислений и
для того, чтобы найти значение
, которое воспроизводит известное значение
в пределах заданного уровня точности. В рассматриваемом методе в качестве допустимого критерия устанавливают условие, что давление, рассчитываемое из вычисленных значений относительной молярной плотности
, должно воспроизводить исходное значение
в пределах (1/10
) МПа.
5.3 Проведение основных вычислений
Для проведения вычислений в целом необходимо выполнение нижеследующих условий.
Требуемый набор входных переменных имеется в наличии. С этим выверенным набором входных переменных: относительной плотностью , обратной относительной температурой
и компонентным составом
используют фундаментальное уравнение состояния для вычисления относительной свободной энергии Гельмгольца и других термодинамических свойств. Согласно уравнению (12) определяют относительную свободную энергию Гельмгольца как
![]() . Согласно уравнению (11) определяют неидеальную составляющую свободной энергии Гельмгольца
. Согласно уравнению (11) определяют неидеальную составляющую свободной энергии Гельмгольца как функцию относительной плотности
, обратной относительной температуры
и молярного компонентного состава
. Идеально-газовую составляющую
, определяемую уравнением (8), получают согласно уравнению (В.3) приложения В таким образом, чтобы выразить
, как представлено в уравнении
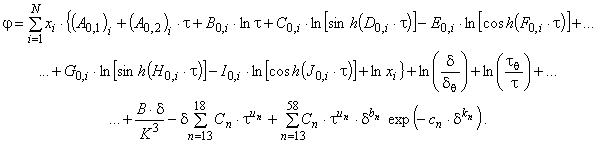 (28)
(28)
Значения всех коэффициентов ![]() ,
, ![]() и от
и от до
для идеального газа даны в приложении В для всех из 21 возможного компонента газа.
Производные от по (относительной) плотности и (обратной приведенной) температуре, которые необходимы для вычислений различных термодинамических свойств, можно получить из уравнений (С.2)-(С.6) (приложение С). Наконец, различные термодинамические свойства можно рассчитать по уравнениям (17)-(26). Значения коэффициентов
,
,
и
и параметров
, являющихся функциями молярных долей компонентов, приведены в приложении D.
Более подробное изложение процедур вычислений представлено в приложении F.
6 Условия применения
6.1 Давление и температура
Метод настоящего стандарта применим только к газам, подготовленным для транспортирования по магистральным газопроводам (см. 6.2), в диапазонах давлений и температур, при которых обычно осуществляют транспортирование и распределение газа. Соответствующие диапазоны давлений и температур представлены в таблице 2. Настоящий метод применим только к смесям в газообразном состоянии, и на него распространяется специальное ограничение, что он не должен применяться для каких-либо условий, когда расчетное значение фактора сжимаемости может быть менее 0,5.
Таблица 2 - Условия применения метода (давление и температура) для газа, подготовленного для транспортирования по магистральным газопроводам
Давление (абсолютное), МПа | 0<p<30 |
Температура, K | 250<T<350 |
6.2 Газ, подготовленный для транспортирования по магистральным газопроводам
Газом, подготовленным для транспортирования по магистральным газопроводам, следует считать природный (или ему подобный) газ, снабженный данными о компонентном составе - содержании основных и второстепенных компонентов в диапазонах молярных долей, указанных в таблице 3.
Возможные следовые компоненты природного газа и конкретные рекомендации по их учету см. приложение F. Общее суммарное содержание следовых компонентов не должно превышать 0,0005 молярной доли.
Таблица 3 - Диапазоны значений молярных долей основных и второстепенных компонентов природного газа
Порядковый номер | Компонент | Диапазон значений молярной доли |
1 | Азот |
|
2 | Диоксид углерода |
|
3 | Метан |
|
4 | Этан |
|
5 | Пропан |
|
6+7 | н-Бутан + изобутан |
|
8+9 | н-Пентан + изопентан |
|
10 | н-Гексан |
|
11 | н-Гептан |
|
12+13+14 | н-Октан + н-нонан + н-декан |
|
15 | Водород |
|
17 | Моноксид углерода |
|
18 | Вода |
|
20 | Гелий |
|
16 | Кислород |
|
19 | Сероводород |
|
21 | Аргон |
|
7 Оценка неопределенностей расчета свойств
7.1 Неопределенности расчета свойств для газа, подготовленного для транспортирования по магистральным газопроводам
7.1.1 Диаграммы неопределенностей для метана
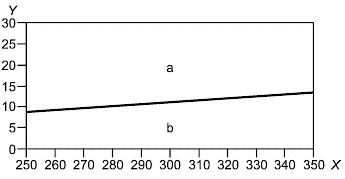
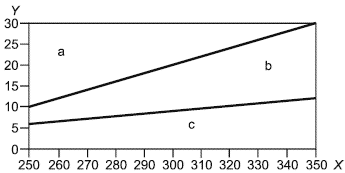
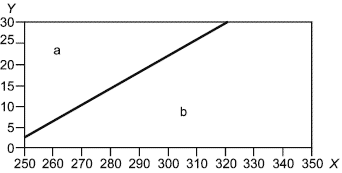
В качестве примера для неопределенностей, которые можно ожидать для смесей, содержащих молярную долю метана, близкую к единице, на рисунках 1-3 представлены соответственно диаграммы неопределенностей для фактора сжимаемости, скорости звука и энтальпии чистого метана. Неопределенность, выраженная с 95%-ной доверительной вероятностью, данная для каждой области, представляет наибольшее значение в пределах суммы неопределенности в заслуживающих доверия справочных данных и разницы между справочными данными и значениями свойства, рассчитанного методом настоящего стандарта. Использованные справочные данные рассчитаны по уравнениям, приведенным в [10].
|
- температура, K;
- давление, МПа; а - диапазон относительной расширенной неопределенности ±0,08%; b - диапазон относительной расширенной неопределенности ±0,04%
Рисунок 1 - Диаграмма расширенной неопределенности для фактора сжимаемости метана
|
- температура, K;
- давление, МПа; а - диапазон относительной расширенной неопределенности ±0,20%; b - диапазон относительной расширенной неопределенности ±0,05%
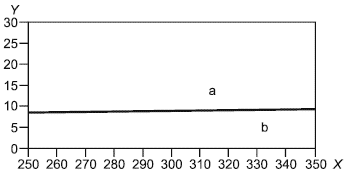
Рисунок 2 - Диаграмма расширенной неопределенности для скорости звука в метане
|
- температура, K;
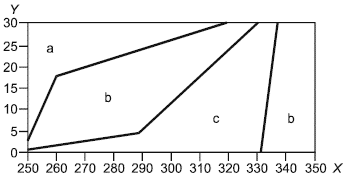
- давление, МПа; а - диапазон абсолютной расширенной неопределенности ±3 кДж/кг; b - диапазон абсолютной расширенной неопределенности ±2 кДж/кг; с - диапазон абсолютной расширенной неопределенности ±1 кДж/кг
Рисунок 3 - Диаграмма расширенной неопределенности для энтальпии метана
7.1.2 Диаграммы неопределенностей для природного газа
В качестве примера неопределенностей, которые можно ожидать для природного газа, на рисунках 4-6 представлены соответственно диаграммы неопределенностей для фактора сжимаемости, скорости звука и энтальпии. Неопределенность, выраженная с 95%-ной доверительной вероятностью, дана для каждой области наибольших отклонений (для широкого спектра природных газов) между измеренным значением свойств и значением, рассчитанным с использованием метода настоящего стандарта. Для фактора сжимаемости экспериментальные значения взяты из [10]; для скорости звука - из [11]; а для энтальпии - из [12].
Примечание 1 - Для всех газов диаграмма неопределенности для плотности идентична по форме диаграмме для фактора сжимаемости.
Примечание 2 - Для всех газов неопределенность для показателя адиабаты приблизительно в два раза больше неопределенности для скорости звука.
|
- температура, K;
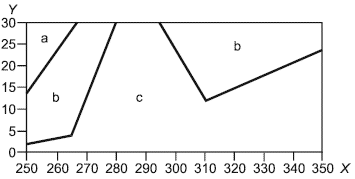
- давление, МПа; а - диапазон относительной расширенной неопределенности ±0,4%; b - диапазон относительной расширенной неопределенности ±0,2%; с - диапазон относительной расширенной неопределенности ±0,1%
Рисунок 4 - Диаграмма расширенной неопределенности для фактора сжимаемости природного газа
|
- температура, K;
- давление, МПа; а - диапазон относительной расширенной неопределенности ±2,0%; b - диапазон относительной расширенной неопределенности ±0,8%; с - диапазон относительной расширенной неопределенности ±0,2%
Рисунок 5 - Диаграмма расширенной неопределенности для скорости звука в природном газе
|
- температура, K;
- давление, МПа; а - диапазон относительной расширенной неопределенности ±0,20%; b - диапазон относительной расширенной неопределенности ±0,05%
Рисунок 6 - Диаграмма расширенной неопределенности для энтальпии природного газа
Для свойств, отличных от фактора сжимаемости, плотности (для которой диаграмма неопределенности такая же, как и для фактора сжимаемости), скорости звука и энтальпии, недостаток заслуживающих доверия (уровня рекомендуемых) экспериментальных данных делает невозможным обеспечение достоверных оценок неопределенностей. Однако можно дать некоторые рекомендации.
Для газов при низких давлениях (ниже, как правило, 1 МПа), ведущих себя подобно идеальному газу (фактор сжимаемости более чем 0,95), можно ожидать, что все калорические свойства должны быть получены с малой неопределенностью. Это следует из того факта, что в рассматриваемом частном случае большая часть каждого свойства определяется из идеально-газовой части свободной энергии Гельмгольца, которая будучи рассчитана прямо из высокоточных данных по изобарной теплоемкости идеального газа (см. приложение В), сама является высокоточной. В таком случае неопределенности для плотности, фактора сжимаемости, скорости звука, изохорной и изобарной теплоемкости, показателя адиабаты и коэффициента Джоуля-Томпсона находятся в пределах 0,1%.
7.2 Влияние неопределенностей входных переменных
Пользователь должен иметь в виду, что неопределенности входных величин (давления, температуры и молярных долей компонентов) будут давать дополнительную неопределенность при расчете любого свойства. При решении любой конкретной задачи, когда дополнительная неопределенность вносит существенные коррективы, пользователь должен определить ее значение.
8 Оформление результатов расчетов
В соответствии с единицами величин, приведенными в разделе 4, значения рассчитанных термодинамических свойств должны быть записаны с числом знаков после запятой, указанным в таблице 4. В результатах расчетов необходимо указывать значения температуры, давления (или плотности) и компонентный состав, для которых получены результаты. Использованный метод расчета должен содержать ссылку на настоящий стандарт.
Для проверки не следует использовать лишние цифры (см. пример в приложении G).
Таблица 4 - Оформление результатов
Обозначение | Свойство | Единицы величин | Количество знаков |
Фактор сжимаемости | - | 4 | |
Молярная плотность | кмоль/м | 3 | |
Плотность | кг/м | 4 | |
Молярная внутренняя энергия | кДж/кмоль | 0 | |
Удельная внутренняя энергия | кДж/кг | 1 | |
Молярная энтальпия | кДж/кмоль | 0 | |
Удельная энтальпия | кДж/кмоль | 1 | |
Молярная энтропия | кДж/(кмоль·К) | 2 | |
Удельная энтропия | кДж/(кг·К) | 3 | |
Молярная изохорная теплоемкость | кДж/(кмоль·К) | 2 | |
Удельная изохорная теплоемкость | кДж/(кг·К) | 3 | |
Удельная изобарная теплоемкость | кДж/(кг·К) | 3 | |
Коэффициент Джоуля-Томсона | К/МПа | 2 | |
Показатель адиабаты | - | 2 | |
Скорость звука | м/с | 1 |
Приложение А
(справочное)
Исходные положения для фундаментального уравнения состояния для свободной энергии Гельмгольца
Уравнение состояния [8] AGA8 было опубликовано в 1992 г. Комитетом по измерениям при транспортировке газа Американской газовой ассоциации как метод для высокоточных вычислений фактора сжимаемости. В этой связи оно является объектом рассмотрения. Для вычислений на основе уравнения состояния AGA8 всех термодинамических свойств необходимо выполнить два основных требования:
a) уравнение должно быть математически преобразовано к виду, где избыточная свободная энергия Гельмгольца представляется в явном виде, то есть в виде фундаментального уравнения состояния для свободной энергии Гельмгольца. На основе соответствующих соотношений [8] можно рассчитывать все избыточные термодинамические свойства из избыточной свободной энергии Гельмгольца и ее производных по температуре и плотности как параметров состояния;
b) для расчета калорических свойств необходимо наличие идеально-газовой составляющей свободной энергии Гельмгольца как функции температуры. В этом случае целесообразно использовать соответствующие соотношения [13], [14] для идеально-газовой изобарной теплоемкости. При этом также требуются производные свободной энергии Гельмгольца по параметрам состояния.
Преимущество применения в совокупности идеально-газовой и неидеальной составляющих свободной энергии Гельмгольца состоит в том, что производные, необходимые для вычисления термодинамических свойств, можно получить в аналитической форме. Следовательно, нет необходимости в численном интегрировании с использованием соответствующих компьютерных программ; вычислительные проблемы можно упростить и время вычисления сократить.
Предлагаемый метод вычислений следует применять в прикладных программах, в частности в программах, которые можно использовать при транспортировании и распределении газа.
Приложение В
(обязательное)
Идеально-газовая свободная энергия Гельмгольца
В.1 Вычисление идеально-газовой составляющей свободной энергии Гельмгольца
a) Идеально-газовую изобарную теплоемкость индивидуального компонента по [13], [15] можно записать в следующем виде
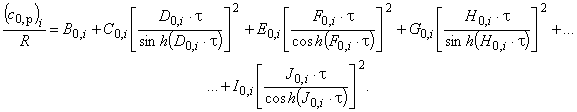 (В.1)
(В.1)
Уравнение (В.1) можно обобщить на случай -компонентной смеси, используя следующее уравнение
![]() . (В.2)
. (В.2)
b) Это уравнение для идеально-газовой изобарной теплоемкости можно включить в уравнение (8) для относительной свободной энергии Гельмгольца
. В результате получают уравнение
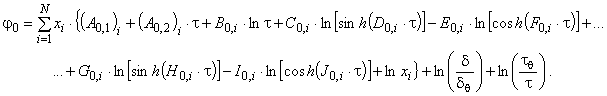 (В.3)
(В.3)
В уравнении (В.3) константы ![]() и
и ![]() связывают с константами интегрирования
связывают с константами интегрирования ![]() и
и ![]() уравнения (8) в соответствии с уравнениями:
уравнения (8) в соответствии с уравнениями:
![]() ; (В.4)
; (В.4)
![]() . (В.5)
. (В.5)
Важно отметить, что в уравнении (В.3) является функцией относительной молярной плотности
реального газа, а не относительной молярной плотности идеального газа и, следовательно, не может быть полностью рассчитана до тех пор, пока значение
неизвестно (см. приложение D). Уравнение (В.3) используют для расчета относительной свободной энергии Гельмгольца идеального газа.
c) Наиболее достоверные из известных в научной литературе данные об идеально-газовой изобарной теплоемкости [14] были использованы в качестве исходных данных для получения численных значений констант с
до
для каждого из 21 индивидуального компонента, рассматриваемого в настоящем стандарте.
Значения констант ![]() и
и ![]() , а также констант с
, а также констант с до
, используемые в уравнении (В.3), приведены в таблице В.1.
Таблица В.1 - Значения констант уравнения (В.3) для идеально-газовой составляющей свободной энергии Гельмгольца
Компонент |
|
| ||||||||||
1 | Азот | 23,26530 | -2801,72907 | 3,50031 | 0,13732 | 662,738 | -0,14660 | 680,562 | 0,90066 | 1740,06 | 0 | 0 |
2 | Диоксид углерода | 26,35604 | -4902,17152 | 3,50002 | 2,04452 | 919,306 | -1,06044 | 865,070 | 2,03366 | 483,553 | 0,01393 | 341,109 |
3 | Метан | 35,53603 | -15999,69151 | 4,00088 | 0,76315 | 820,659 | 0,00460 | 178,410 | 8,74432 | 1062,82 | -4,46921 | 1090,53 |
4 | Этан | 42,42766 | -23639,65301 | 4,00263 | 4,33939 | 559,314 | 1,23722 | 223,284 | 13,1974 | 1031,38 | -6,01989 | 1071,29 |
5 | Пропан | 50,40669 | -31236,63551 | 4,02939 | 6,60569 | 479,856 | 3,19700 | 200,893 | 19,1921 | 955,312 | -8,37267 | 1027,29 |
6 | н-Бутан | 42,22997 | -38957,80933 | 4,33944 | 9,44893 | 468,270 | 6,89406 | 183,636 | 24,4618 | 1914,10 | 14,7824 | 903,185 |
7 | Изобутан | 39,99940 | -38525,50276 | 4,06714 | 8,97575 | 438,270 | 5,25156 | 198,018 | 25,1423 | 1905,02 | 16,1388 | 893,765 |
8 | н-Пентан | 48,37597 | -45215,83000 | 4 | 8,95043 | 178,670 | 21,8360 | 840,538 | 33,4032 | 1774,25 | 0 | 0 |
9 | Изопентан | 48,86978 | -51198,30946 | 4 | 11,7618 | 292,503 | 20,1101 | 910,237 | 33,1688 | 1919,37 | 0 | 0 |
10 | н-Гексан | 52,69477 | -52746,83318 | 4 | 11,6977 | 182,326 | 26,8142 | 859,207 | 38,6164 | 1826,59 | 0 | 0 |
11 | н-Гептан | 57,77391 | -57104,81056 | 4 | 13,7266 | 169,789 | 30,4707 | 836,195 | 43,5561 | 1760,46 | 0 | 0 |
12 | н-Октан | 62,95591 | -60546,76385 | 4 | 15,6865 | 158,922 | 33,8029 | 815,064 | 48,1731 | 1693,07 | 0 | 0 |
13 | н-Нонан | 67,79407 | -66600,12837 | 4 | 18,0241 | 156,854 | 38,1235 | 814,882 | 53,3415 | 1693,79 | 0 | 0 |
14 | н-Декан | 71,63669 | -74131,45483 | 4 | 21,0069 | 164,947 | 43,4931 | 836,264 | 58,3657 | 1750,24 | 0 | 0 |
15 | Водород | 18,77280 | -5836,94370 | 2,47906 | 0,95806 | 228,734 | 0,45444 | 326,843 | 1,56039 | 1651,71 | -1,3756 | 1671,69 |
16 | Кислород | 22,49931 | -2318,32269 | 3,50146 | 1,07558 | 2235,71 | 1,01334 | 1116,69 | 0 | 0 | 0 | 0 |
17 | Моноксид углерода | 23,15547 | -2635,24412 | 3,50055 | 1,02865 | 1550,45 | 0,00493 | 704,525 | 0 | 0 | 0 | 0 |
18 | Вода | 27,27642 | -7766,73308 | 4,00392 | 0,01059 | 268,795 | 0,98763 | 1141,41 | 3,06904 | 2507,37 | 0 | 0 |
19 | Сероводород | 27,28069 | -6069,03587 | 4 | 3,11942 | 1833,63 | 1,00243 | 847,181 | 0 | 0 | 0 | 0 |
20 | Гелий | 15,74399 | -745,37500 | 2,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
21 | Аргон | 15,74399 | -745,37500 | 2,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В.2 Производные от идеально-газовой составляющей свободной энергии Гельмгольца
Для вычисления ряда термодинамических свойств необходимо иметь первые и вторые частные производные от идеально-газовой составляющей свободной энергии Гельмгольца [уравнение (В.3)] по обратной относительной температуре
. Необходимые для этого математические выражения представляют в виде уравнений:
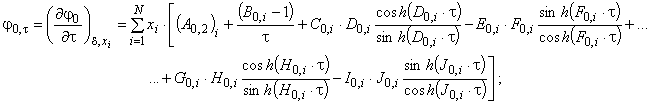 (В.6)
(В.6)
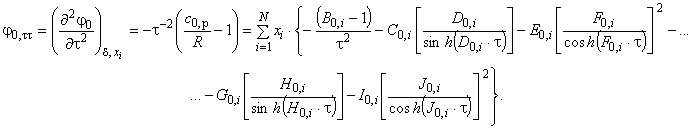 (В.7)
(В.7)
Приложение С
(обязательное)
Уравнение состояния для свободной энергии Гельмгольца
С.1 Вычисление свободной энергии Гельмгольца
Относительную свободную энергию Гельмгольца для газовой смеси заданного состава рассчитывают по уравнению
![]() , (С.1)
, (С.1)
где рассчитывают в соответствии с приложением В. Ту часть уравнения (С.1), которая учитывает неидеальную составляющую свободной энергии Гельмгольца (вся правая часть уравнения, за исключением
), определяют из уравнения (11). Уравнения для расчета функций
![]() ,
, ![]() и
и ![]() в уравнении (С.1) приведены в D.1. Значения различных констант в уравнении (С.1) даны в D.2.
в уравнении (С.1) приведены в D.1. Значения различных констант в уравнении (С.1) даны в D.2.
С.2 Производные от свободной энергии Гельмгольца
Для вычисления совокупности термодинамических свойств требуются первые и/или вторые частные производные по обратной относительной температуре и/или по относительной плотности от относительной свободной энергии Гельмгольца. Необходимые для этого математические выражения записывают в виде уравнений:
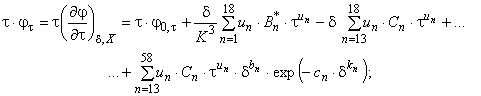 (С.2)
(С.2)
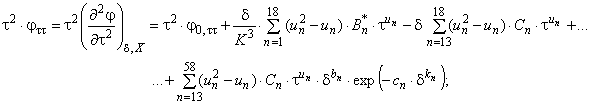 (С.3)
(С.3)
 (С.4)
(С.4)
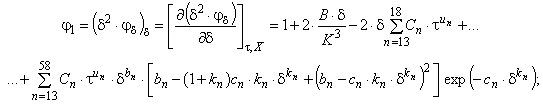 (С.5)
(С.5)
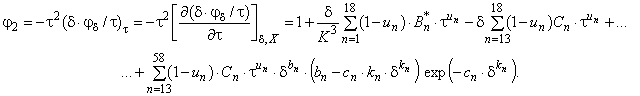 (С.6)
(С.6)
Уравнения и константы, необходимые для расчета по уравнениям (С.2)-(С.6), приведены в приложении D.
Приложение D
(обязательное)
Подробная информация по уравнению состояния
D.1 Вспомогательные уравнения
Для расчета по уравнению (С.1) необходимо определить значения второго вириального коэффициента ![]() функций
функций ![]() и параметра размера
и параметра размера ![]() . Кроме того, так как уравнение (С.1) включает в качестве аргумента относительную молярную плотность
. Кроме того, так как уравнение (С.1) включает в качестве аргумента относительную молярную плотность , необходимо получить ее значение при задании давления в качестве входной переменной. Эти шаги рассматриваются в перечислениях а)-d):
a) второй вириальный коэффициент рассчитывают по уравнениям (D.1)-(D.5) с использованием необходимых констант из таблиц D.1-D.3:
![]() , (D.1)
, (D.1)
где
![]() , (D.2)
, (D.2)
где
![]() ; (D.3)
; (D.3)
![]() , (D.4)
, (D.4)
где
![]() ; (D.5)
; (D.5)
b) функции (для
от 13 до 58) рассчитывают по уравнениям (D.6)-(D.10) с использованием необходимых констант из таблиц D.1-D.3:
![]() , (D.6)
, (D.6)
где
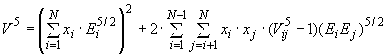 ; (D.7)
; (D.7)
![]() ; (D.8)
; (D.8)
![]() ; (D.9)
; (D.9)
![]() . (D.10)
. (D.10)
В таблице D.2 равны нулю для всех компонентов, за исключением водорода, для которого
1,0, a
равны нулю для всех компонентов, за исключением воды, для которой
![]() 1,0. Многие из параметров бинарного взаимодействия в таблице D.3 равны единице;
1,0. Многие из параметров бинарного взаимодействия в таблице D.3 равны единице;
c) смесевой параметр размера ![]() рассчитывают по уравнению (D.11) с использованием необходимых констант из таблиц D.2 и D.3
рассчитывают по уравнению (D.11) с использованием необходимых констант из таблиц D.2 и D.3
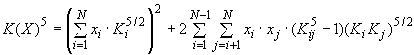 . (D.11)
. (D.11)
Многие значения равны единице;
d) относительную молярную плотность ![]() определяют в результате решения уравнения (D.12) (это уравнение получено из уравнения (27) настоящего стандарта, преобразованного к явному виду для давления)
определяют в результате решения уравнения (D.12) (это уравнение получено из уравнения (27) настоящего стандарта, преобразованного к явному виду для давления)
![]() (D.12)
(D.12)
Уравнение (D.12) решают с использованием стандартных алгоритмов расчета плотности по уравнению состояния.
D.2 Значения констант для уравнения состояния
Настоящий раздел содержит значения всех констант, необходимых для использования уравнения состояния AGA8 в уравнениях (С.1) и (D.1)-(D.12). В таблице D.1 даны значения констант самого уравнения состояния. В таблице D.2 представлены значения характеристических параметров, определяющих свойства индивидуальных компонентов смеси. В таблице D.3 даны значения параметров бинарного взаимодействия между молекулами различных компонентов смеси.
Таблица D.1 - Коэффициенты уравнения состояния
1 | 0,153832600 | 1 | 0 | 0 | 0,0 | 0 | 0 | 0 | 0 | 0 |
2 | 1,341953000 | 1 | 0 | 0 | 0,5 | 0 | 0 | 0 | 0 | 0 |
3 | -2,998583000 | 1 | 0 | 0 | 1,0 | 0 | 0 | 0 | 0 | 0 |
4 | -0,048312280 | 1 | 0 | 0 | 3,5 | 0 | 0 | 0 | 0 | 0 |
5 | 0,375796500 | 1 | 0 | 0 | -0,5 | 1 | 0 | 0 | 0 | 0 |
6 | -1,589575000 | 1 | 0 | 0 | 4,5 | 1 | 0 | 0 | 0 | 0 |
7 | -0,053588470 | 1 | 0 | 0 | 0,5 | 0 | 1 | 0 | 0 | 0 |
8 | 0,886594630 | 1 | 0 | 0 | 7,5 | 0 | 0 | 0 | 1 | 0 |
9 | -0,710237040 | 1 | 0 | 0 | 9,5 | 0 | 0 | 0 | 1 | 0 |
10 | -1,471722000 | 1 | 0 | 0 | 6,0 | 0 | 0 | 0 | 0 | 1 |
11 | 1,321850350 | 1 | 0 | 0 | 12,0 | 0 | 0 | 0 | 0 | 1 |
12 | -0,786659250 | 1 | 0 | 0 | 12,5 | 0 | 0 | 0 | 0 | 1 |
13 | 2,291290х10 | 1 | 1 | 3 | -6,0 | 0 | 0 | 1 | 0 | 0 |
14 | 0,157672400 | 1 | 1 | 2 | 2,0 | 0 | 0 | 0 | 0 | 0 |
15 | -0,436386400 | 1 | 1 | 2 | 3,0 | 0 | 0 | 0 | 0 | 0 |
16 | -0,044081590 | 1 | 1 | 2 | 2,0 | 0 | 1 | 0 | 0 | 0 |
17 | -0,003433888 | 1 | 1 | 4 | 2,0 | 0 | 0 | 0 | 0 | 0 |
18 | 0,032059050 | 1 | 1 | 4 | 11,0 | 0 | 0 | 0 | 0 | 0 |
19 | 0,024873550 | 2 | 0 | 0 | -0,5 | 0 | 0 | 0 | 0 | 0 |
20 | 0,073322790 | 2 | 0 | 0 | 0,5 | 0 | 0 | 0 | 0 | 0 |
21 | -0,001600573 | 2 | 1 | 2 | 0,0 | 0 | 0 | 0 | 0 | 0 |
22 | 0,642470600 | 2 | 1 | 2 | 4,0 | 0 | 0 | 0 | 0 | 0 |
23 | -0,416260100 | 2 | 1 | 2 | 6,0 | 0 | 0 | 0 | 0 | 0 |
24 | -0,066899570 | 2 | 1 | 4 | 21,0 | 0 | 0 | 0 | 0 | 0 |
25 | 0,279179500 | 2 | 1 | 4 | 23,0 | 1 | 0 | 0 | 0 | 0 |
26 | -0,696605100 | 2 | 1 | 4 | 22,0 | 0 | 1 | 0 | 0 | 0 |
27 | -0,002860589 | 2 | 1 | 4 | -1,0 | 0 | 0 | 1 | 0 | 0 |
28 | -0,008098836 | 3 | 0 | 0 | -0,5 | 0 | 1 | 0 | 0 | 0 |
29 | 3,150547000 | 3 | 1 | 1 | 7,0 | 1 | 0 | 0 | 0 | 0 |
30 | 0,007224479 | 3 | 1 | 1 | -1,0 | 0 | 0 | 1 | 0 | 0 |
31 | -0,705752900 | 3 | 1 | 2 | 6,0 | 0 | 0 | 0 | 0 | 0 |
32 | 0,534979200 | 3 | 1 | 2 | 4,0 | 1 | 0 | 0 | 0 | 0 |
33 | -0,079314910 | 3 | 1 | 3 | 1,0 | 1 | 0 | 0 | 0 | 0 |
34 | -1,418465000 | 3 | 1 | 3 | 9,0 | 1 | 0 | 0 | 0 | 0 |
35 | -5,99905x10 | 3 | 1 | 4 | -13,0 | 0 | 0 | 1 | 0 | 0 |
36 | 0,105840200 | 3 | 1 | 4 | 21,0 | 0 | 0 | 0 | 0 | 0 |
37 | 0,034317290 | 3 | 1 | 4 | 8,0 | 0 | 1 | 0 | 0 | 0 |
38 | -0,007022847 | 4 | 0 | 0 | -0,5 | 0 | 0 | 0 | 0 | 0 |
39 | 0,024955870 | 4 | 0 | 0 | 0,0 | 0 | 0 | 0 | 0 | 0 |
40 | 0,042968180 | 4 | 1 | 2 | 2,0 | 0 | 0 | 0 | 0 | 0 |
41 | 0,746545300 | 4 | 1 | 2 | 7,0 | 0 | 0 | 0 | 0 | 0 |
42 | -0,291961300 | 4 | 1 | 2 | 9,0 | 0 | 1 | 0 | 0 | 0 |
43 | 7,294616000 | 4 | 1 | 4 | 22,0 | 0 | 0 | 0 | 0 | 0 |
44 | -9,936757000 | 4 | 1 | 4 | 23,0 | 0 | 0 | 0 | 0 | 0 |
45 | -0,005399808 | 5 | 0 | 0 | 1,0 | 0 | 0 | 0 | 0 | 0 |
46 | -0,243256700 | 5 | 1 | 2 | 9,0 | 0 | 0 | 0 | 0 | 0 |
47 | 0,049870160 | 5 | 1 | 2 | 3,0 | 0 | 1 | 0 | 0 | 0 |
48 | 0,003733797 | 5 | 1 | 4 | 8,0 | 0 | 0 | 0 | 0 | 0 |
49 | 1,874951000 | 5 | 1 | 4 | 23,0 | 0 | 1 | 0 | 0 | 0 |
50 | 0,002168144 | 6 | 0 | 0 | 1,5 | 0 | 0 | 0 | 0 | 0 |
51 | -0,658716400 | 6 | 1 | 2 | 5,0 | 1 | 0 | 0 | 0 | 0 |
52 | 0,000205518 | 7 | 0 | 0 | -0,5 | 0 | 1 | 0 | 0 | 0 |
53 | 0,009776195 | 7 | 1 | 2 | 4,0 | 0 | 0 | 0 | 0 | 0 |
54 | -0,020487080 | 8 | 1 | 1 | 7,0 | 1 | 0 | 0 | 0 | 0 |
55 | 0,015573220 | 8 | 1 | 2 | 3,0 | 0 | 0 | 0 | 0 | 0 |
56 | 0,006862415 | 8 | 1 | 2 | 0,0 | 1 | 0 | 0 | 0 | 0 |
57 | -0,001226752 | 9 | 1 | 2 | 1,0 | 0 | 0 | 0 | 0 | 0 |
58 | 0,002850908 | 9 | 1 | 2 | 0,0 | 0 | 1 | 0 | 0 | 0 |
Таблица D.2 - Характеристические параметры индивидуальных компонентов
Компонент | Моляр- | Энергети- | Параметр размера | Ориента- | Квадру- | Высоко- | Диполь- | Пара- | |
1 | Азот | 28,0135 | 99,737780 | 0,4479153 | 0,027815 | 0,0 | 0,0 | 0,0 | 0,0 |
2 | Диоксид углерода | 44,010 | 241,960600 | 0,4557489 | 0,189065 | 0,690000 | 0,0 | 0,0 | 0,0 |
3 | Метан | 16,043 | 151,318300 | 0,4619255 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
4 | Этан | 30,070 | 244,166700 | 0,5279209 | 0,079300 | 0,0 | 0,0 | 0,0 | 0,0 |
5 | Пропан | 44,097 | 298,118300 | 0,5837490 | 0,141239 | 0,0 | 0,0 | 0,0 | 0,0 |
6 | н-Бутан | 58,123 | 337,638900 | 0,6341423 | 0,281835 | 0,0 | 0,0 | 0,0 | 0,0 |
7 | Изобутан | 58,123 | 324,068900 | 0,6406937 | 0,256692 | 0,0 | 0,0 | 0,0 | 0,0 |
8 | н-Пентан | 72,150 | 370,682300 | 0,6798307 | 0,366911 | 0,0 | 0,0 | 0,0 | 0,0 |
9 | Изопентан | 72,150 | 365,599900 | 0,6738577 | 0,332267 | 0,0 | 0,0 | 0,0 | 0,0 |
10 | н-Гексан | 86,177 | 402,636293 | 0,7175118 | 0,289731 | 0,0 | 0,0 | 0,0 | 0,0 |
11 | н-Гептан | 100,204 | 427,722630 | 0,7525189 | 0,337542 | 0,0 | 0,0 | 0,0 | 0,0 |
12 | н-Октан | 114,231 | 450,325022 | 0,7849550 | 0,383381 | 0,0 | 0,0 | 0,0 | 0,0 |
13 | н-Нонан | 128,258 | 470,840891 | 0,8152731 | 0,427354 | 0,0 | 0,0 | 0,0 | 0,0 |
14 | н-Декан | 142,285 | 489,558373 | 0,8437826 | 0,469659 | 0,0 | 0,0 | 0,0 | 0,0 |
15 | Водород | 2,0159 | 26,957940 | 0,3514916 | 0,034369 | 0,0 | 1,0 | 0,0 | 0,0 |
16 | Кислород | 31,9988 | 122,766700 | 0,4186954 | 0,021000 | 0,0 | 0,0 | 0,0 | 0,0 |
17 | Моноксид углерода | 28,010 | 105,534800 | 0,4533894 | 0,038953 | 0,0 | 0,0 | 0,0 | 0,0 |
18 | Вода | 18,0153 | 514,015600 | 0,3825868 | 0,332500 | 1,067750 | 0,0 | 1,582200 | 1,0 |
19 | Сероводород | 34,082 | 296,355000 | 0,4618263 | 0,088500 | 0,633276 | 0,0 | 0,390000 | 0,0 |
20 | Гелий | 4,0026 | 2,610111 | 0,3589888 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
21 | Аргон | 39,948 | 119,629900 | 0,4216551 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
________________
* Формула соответствует оригиналу. - .
Таблица D.3 - Параметры бинарного взаимодействия
Пара компонентов | |||||||
1 | 2 | Азот | Диоксид углерода | 1,022740 | 0,835058 | 0,982361 | 0,982746 |
1 | 3 | Азот | Метан | 0,971640 | 0,886106 | 1,003630 | 1,0 |
1 | 4 | Азот | Этан | 0,970120 | 0,816431 | 1,007960 | 1,0 |
1 | 5 | Азот | Пропан | 0,945939 | 0,915502 | 1,0 | 1,0 |
1 | 6 | Азот | н-Бутан | 0,973384 | 0,993556 | 1,0 | 1,0 |
1 | 7 | Азот | Изобутан | 0,946914 | 1,0 | 1,0 | 1,0 |
1 | 8 | Азот | н-Пентан | 0,945520 | 1,0 | 1,0 | 1,0 |
1 | 9 | Азот | Изопентан | 0,959340 | 1,0 | 1,0 | 1,0 |
1 | 15 | Азот | Водород | 1,086320 | 0,408838 | 1,032270 | 1,0 |
1 | 16 | Азот | Кислород | 1,021000 | 1,0 | 1,0 | 1,0 |
1 | 17 | Азот | Моноксид углерода | 1,005710 | 1,0 | 1,0 | 1,0 |
1 | 18 | Азот | Вода | 0,746954 | 1,0 | 1,0 | 1,0 |
1 | 19 | Азот | Сероводород | 0,902271 | 0,993476 | 0,942596 | 1,0 |
2 | 3 | Диоксид углерода | Метан | 0,960644 | 0,963827 | 0,995933 | 0,807653 |
2 | 4 | Диоксид углерода | Этан | 0,925053 | 0,969870 | 1,008510 | 0,370296 |
2 | 5 | Диоксид углерода | Пропан | 0,960237 | 1,0 | 1,0 | 1,0 |
2 | 6 | Диоксид углерода | н-Бутан | 0,897362 | 1,0 | 1,0 | 1,0 |
2 | 7 | Диоксид углерода | Изобутан | 0,906849 | 1,0 | 1,0 | 1,0 |
2 | 8 | Диоксид углерода | н-Пентан | 0,859764 | 1,0 | 1,0 | 1,0 |
2 | 9 | Диоксид углерода | Изопентан | 0,726255 | 1,0 | 1,0 | 1,0 |
2 | 10 | Диоксид углерода | н-Гексан | 0,855134 | 1,066638 | 0,910183 | 1,0 |
2 | 11 | Диоксид углерода | н-Гептан | 0,831229 | 1,077634 | 0,895362 | 1,0 |
2 | 12 | Диоксид углерода | н-Октан | 0,808310 | 1,088178 | 0,881152 | 1,0 |
2 | 13 | Диоксид углерода | н-Нонан | 0,786323 | 1,098291 | 0,867520 | 1,0 |
2 | 14 | Диоксид углерода | н-Декан | 0,765171 | 1,108021 | 0,854406 | 1,0 |
2 | 15 | Диоксид углерода | Водород | 1,281790 | 1,0 | 1,0 | 1,0 |
2 | 17 | Диоксид углерода | Моноксид углерода | 1,500000 | 0,900000 | 1,0 | 1,0 |
2 | 18 | Диоксид углерода | Вода | 0,849408 | 1,0 | 1,0 | 1,673090 |
2 | 19 | Диоксид углерода | Сероводород | 0,955052 | 1,045290 | 1,007790 | 1,0 |
3 | 5 | Метан | Пропан | 0,994635 | 0,990877 | 1,007619 | 1,0 |
3 | 6 | Метан | н-Бутан | 0,989844 | 0,992291 | 0,997596 | 1,0 |
3 | 7 | Метан | Изобутан | 1,019530 | 1,0 | 1,0 | 1,0 |
3 | 8 | Метан | н-Пентан | 0,999268 | 1,003670 | 1,002529 | 1,0 |
3 | 9 | Метан | Изопентан | 1,002350 | 1,0 | 1,0 | 1,0 |
3 | 10 | Метан | н-Гексан | 1,107274 | 1,302576 | 0,982962 | 1,0 |
3 | 11 | Метан | н-Гептан | 0,880880 | 1,191904 | 0,983565 | 1,0 |
3 | 12 | Метан | н-Октан | 0,880973 | 1,205769 | 0,982707 | 1,0 |
3 | 13 | Метан | н-Нонан | 0,881067 | 1,219634 | 0,981849 | 1,0 |
3 | 14 | Метан | н-Декан | 0,881161 | 1,233498 | 0,980991 | 1,0 |
3 | 15 | Метан | Водород | 1,170520 | 1,156390 | 1,023260 | 1,957310 |
3 | 17 | Метан | Моноксид углерода | 0,990126 | 1,0 | 1,0 | 1,0 |
3 | 18 | Метан | Вода | 0,708218 | 1,0 | 1,0 | 1,0 |
3 | 19 | Метан | Сероводород | 0,931484 | 0,736833 | 1,000080 | 1,0 |
4 | 5 | Этан | Пропан | 1,022560 | 1,065173 | 0,986893 | 1,0 |
4 | 6 | Этан | н-Бутан | 1,013060 | 1,250000 | 1,0 | 1,0 |
4 | 7 | Этан | Изобутан | 1,0 | 1,250000 | 1,0 | 1,0 |
4 | 8 | Этан | н-Пентан | 1,005320 | 1,250000 | 1,0 | 1,0 |
4 | 9 | Этан | Изопентан | 1,0 | 1,250000 | 1,0 | 1,0 |
4 | 15 | Этан | Водород | 1,164460 | 1,616660 | 1,020340 | 1,0 |
4 | 18 | Этан | Вода | 0,693168 | 1,0 | 1,0 | 1,0 |
4 | 19 | Этан | Сероводород | 0,946871 | 0,971926 | 0,999969 | 1,0 |
5 | 6 | Пропан | н-Бутан | 1,004900 | 1,0 | 1,0 | 1,0 |
5 | 15 | Пропан | Водород | 1,034787 | 1,0 | 1,0 | 1,0 |
6 | 15 | н-Бутан | Водород | 1,300000 | 1,0 | 1,0 | 1,0 |
7 | 15 | Изобутан | Водород | 1,300000 | 1,0 | 1,0 | 1,0 |
10 | 19 | н-Гексан | Сероводород | 1,008692 | 1,028973 | 0,968130 | 1,0 |
11 | 19 | н-Гептан | Сероводород | 1,010126 | 1,033754 | 0,962870 | 1,0 |
12 | 19 | н-Октан | Сероводород | 1,011501 | 1,038338 | 0,957828 | 1,0 |
13 | 19 | н-Нонан | Сероводород | 1,012821 | 1,042735 | 0,952441 | 1,0 |
14 | 19 | н-Декан | Сероводород | 1,014089 | 1,046966 | 0,948338 | 1,0 |
15 | 17 | Водород | Моноксид углерода | 1,100000 | 1,0 | 1,0 | 1,0 |
Параметры взаимодействия для любой пары компонентов, не приведенные в таблице D.3, равны 1,0.
Приложение Е
(справочное)
Учет следовых компонентов
Для того чтобы рассчитать, используя метод, устанавливаемый в настоящем стандарте, термодинамические свойства природного газа или подобной смеси, которая содержит следы одного или более компонентов, не включенных в таблицу 3, необходимо включить каждый такой следовой компонент в один из 21 основного и второстепенного компонентов, для которых было разработано уравнение AGA8. Рекомендации по такому включению даны в таблице Е.1.
Таблица Е.1 - Включение следовых компонентов
Следовой компонент | Формула | Рекомендованное включение | Номер компонента по таблице D.2 |
2,2-Диметилпропан (нео-пентан) |
| н-Пентан | 8 |
2-Метилпентан |
| н-Гексан | 10 |
3-Метилпентан |
| н-Гексан | 10 |
2,2-Диметилбутан |
| н-Гексан | 10 |
2,3-Диметилбутан |
| н-Гексан | 10 |
Этилен (этен) |
| Этан | 4 |
Пропилен (пропен) |
| Пропан | 5 |
1-Бутен |
| н-Бутан | 6 |
цис-2-Бутен |
| н-Бутан | 6 |
транс-2-Бутен |
| н-Бутан | 6 |
2-Метилпропен |
| н-Бутан | 6 |
1-Пентен |
| н-Пентан | 8 |
Пропадиен |
| Пропан | 5 |
1,2-Бутадиен |
| н-Бутан | 6 |
1,3-Бутадиен |
| н-Бутан | 6 |
Ацетилен (этин) |
| Этан | 4 |
Циклопентан |
| н-Пентан | 8 |
Метилциклопентан |
| н-Гексан | 10 |
Этилциклопентан |
| н-Гептан | 11 |
Циклогексан |
| н-Гексан | 10 |
Метилциклогексан |
| н-Гептан | 11 |
Этилциклогексан |
| н-Октан | 12 |
Бензол |
| н-Пентан | 8 |
Толуол (метилбензол) | н-Гексан | 10 | |
Этилбензол |
| н-Гептан | 11 |
о-Ксилен |
| н-Гептан | 11 |
Все остальные | - | н-Гексан | 10 |
Все остальные | - | н-Гептан | 11 |
Все остальные | - | н-Октан | 12 |
Все остальные | - | н-Нонан | 13 |
Все остальные | - | н-Декан | 14 |
Все остальные углеводороды | - | н-Декан | 14 |
Метанол (метиловый спирт) |
| Этан | 4 |
Метантиол (метилмеркаптан) |
| Пропан | 5 |
Аммиак | Метан | 3 | |
Циановодород | HCN | Этан | 4 |
Карбонилсульфид (оксисульфид углерода) | COS | н-Бутан | 6 |
Сероуглерод | н-Пентан | 8 | |
Диоксид серы | н-Бутан | 6 | |
Оксид азота | Диоксид углерода | 2 | |
Неон | Ne | Аргон | 21 |
Криптон | Kr | Аргон | 21 |
Ксенон | Xe | Аргон | 21 |
Каждая рекомендация основана на оценке того, что такое включение приводит к наилучшей точности описания полного набора термодинамических свойств. Параметры, учитываемые при такой оценке, включают молярную массу, энергетический параметр (связанный с критической температурой) и параметр размера (связанный с критическим объемом). Поскольку не существует универсального включения, которое одинаково хорошо подходило бы для всех свойств, нет ничего необычного в том, что пользователь может предпочесть какое-либо альтернативное включение для своей конкретной задачи, когда, например, надо рассчитывать только одно свойство. По этой причине рекомендации не являются обязательными. Применение метода с использованием следовых компонентов необходимо подробно документировать.
Примечание - Набор следовых компонентов по таблице Е.1 и таблице 3 настоящего стандарта соответствует ГОСТ 31369.
Приложение F
(справочное)
Реализация метода
Настоящее приложение представляет общую последовательность действий, необходимых для вычисления термодинамических свойств в соответствии с настоящим стандартом. Метод достаточно сложный, поэтому для его применения необходимо использовать компьютерные программы. В настоящем приложении обсуждаются вычислительные аспекты метода. На рисунке F.1 приведена блок-схема процесса вычислений термодинамических свойств с использованием компьютерных программ.
|
Рисунок F.1 - Блок-схема процесса вычислений термодинамических свойств
Шаг 1
Для расчета необходимо ввести молярную долю каждого компонента природного газа, абсолютную температуру
и абсолютное давление
.
В рассматриваемом методе температуру задают в градусах Кельвина (K), а давление - в мегапаскалях (МПа). Если используют какие-либо другие единицы измерения, их нужно перевести в градусы Кельвина или мегапаскали. Для этого необходимо использовать переводные коэффициенты на основе положений ГОСТ 8.417 с учетом стандарта [3].
Иногда вместо давления в качестве входной величины используют массовую плотность
. В таком случае все вычисления выполняют, как обычно, но с учетом содержания последней ступени шага 4.
Шаг 2
a) Для заданных значений , используя уравнения (D.2)-(D.5), рассчитывают значения
![]() .
.
b) Таким же образом для заданных значений , используя уравнения (D.6)-(D.10), рассчитывают значения
![]() .
.
c) По уравнению (D.11) рассчитывают значения смесевого параметра размера ![]() .
.
d) Рассчитывают следующие значения:
- относительной температуры по уравнению (3) при
![]() ;
;
- относительной плотности идеального газа при стандартных условиях по уравнению (4) при
![]() .
.
Плотность идеального газа при стандартных условиях определена в пункте 4.2.3.
Шаг 3
a) Для заданного значения по уравнению (3) рассчитывают
, а затем, используя значения
![]() [шаг 2, перечисление а)], по уравнению (D.1) рассчитывают значения второго вириального коэффициента
[шаг 2, перечисление а)], по уравнению (D.1) рассчитывают значения второго вириального коэффициента ![]() .
.
b) Таким же образом, для заданных значений , используя значения
![]() [шаг 2, перечисление b)], рассчитывают значения
[шаг 2, перечисление b)], рассчитывают значения ![]() для
для от 13 до 58.
Шаг 4
a) Подставляют рассчитанные значения ![]() ,
, ![]() и
и ![]() [шаг 3, перечисления а), b) и шаг 2, перечисление с)] соответственно в уравнение (D.12). Это уравнение для
[шаг 3, перечисления а), b) и шаг 2, перечисление с)] соответственно в уравнение (D.12). Это уравнение для , которое было задано в шаге 1, теперь содержит одно неизвестное - относительную плотность
.
b) Решают это уравнение относительно . Требуемое решение может быть получено с использованием подходящего численного метода, но на практике наиболее подходящим алгоритмом может быть стандартный алгоритм нахождения плотности из уравнения состояния. Такие алгоритмы обычно используют для первоначальной оценки плотности (часто в приближении идеального газа) и итеративным путем находят такое значение
, которое воспроизводит значение
с заранее заданной точностью. Подходящим критерием в настоящем случае является тот, при котором рассчитанное давление при заданной молярной плотности
отличается от заданного значения давления
менее чем на (1/10
) МПа.
Если в качестве входной величины вместо давления используют массовую плотность
, то
вычисляют непосредственно без итераций как
![]() , где
, где ![]() - молярная масса, рассчитанная из уравнения (16) настоящего стандарта.
- молярная масса, рассчитанная из уравнения (16) настоящего стандарта.
Шаг 5
Подставляют и
в уравнение (В.3) вместе с различными константами и функциями обратной относительной температуры
для расчета идеально-газовой части
относительной свободной энергии Гельмгольца. Используют также уравнения (В.6) и (В.7) для расчета первой и второй частных производных
по обратной относительной температуре.
Шаг 6
Используют уравнение (В.1) для расчета общей относительной свободной энергии Гельмгольца ![]() . Рассчитывают по уравнениям (С.2) и (С.4) первые частные производные
. Рассчитывают по уравнениям (С.2) и (С.4) первые частные производные и
по обратной относительной температуре и относительной плотности соответственно. Уравнение (С.3) используют для расчета второй частной производной
по обратной относительной температуре, уравнение (С.5) - для расчета
и уравнение (С.6) - для расчета
.
Шаг 7
a) Используют уравнения (17)-(26) настоящего стандарта для расчета полного набора термодинамических свойств: фактора сжимаемости ; плотности
; внутренней энергии
; энтальпии
; энтропии
; изохорной теплоемкости
; изобарной теплоемкости
; коэффициента Джоуля-Томсона
; показателя адиабаты
и скорости звука
.
b) На основе уравнений (18)-(23) можно представлять термодинамические свойства, рассчитанные на основе значений молярной (при использовании символов нижнего регистра) или массовой (при использовании символов верхнего регистра) доли. Для преобразования молярных величин в массовые используют молярную массу смеси ![]() , которую рассчитывают по уравнению (16).
, которую рассчитывают по уравнению (16).
Шаг 8
Возврат на шаг 1 (выбор новых входных переменных) или окончание вычислений.
Приложение G
(справочное)
Примеры расчетов
Следующие примеры расчетов приведены для целей проверки программных решений (таблицы G.1-G.7).
Таблица G.1 - Составы газа в молярных долях
Компонент | Газ 1 | Газ 2 | Газ 3 | Газ 4 | Газ 5 | Газ 6 | |
1 | Азот | 0,003000 | 0,031000 | 0,009617 | 0,100000 | 0,057000 | 0,117266 |
2 | Диоксид углерода | 0,006000 | 0,005000 | 0,015021 | 0,016000 | 0,076000 | 0,011093 |
3 | Метан | 0,965000 | 0,907000 | 0,859284 | 0,735000 | 0,812000 | 0,825198 |
4 | Этан | 0,018000 | 0,045000 | 0,084563 | 0,033000 | 0,043000 | 0,034611 |
5 | Пропан | 0,004500 | 0,008400 | 0,023022 | 0,007400 | 0,009000 | 0,007645 |
6 | н-Бутан | 0,001000 | 0,001500 | 0,006985 | 0,000800 | 0,001500 | 0,002539 |
7 | Изобутан | 0,001000 | 0,001000 | - | 0,000800 | 0,001500 | - |
8 | н-Пентан | 0,000300 | 0,000400 | 0,001218 | 0,000400 | - | 0,000746 |
9 | Изопентан | 0,000500 | 0,000300 | - | 0,000400 | - | - |
10 | н-Гексан | 0,000700 | - | 0,000228 | 0,000200 | - | 0,000225 |
11 | н-Гептан | - | - | 0,000057 | 0,000100 | - | 0,000110 |
12 | н-Октан | - | - | 0,000005 | 0,000100 | - | 0,000029 |
13 | н-Нонан | - | - | - | 0,000100 | - | - |
14 | н-Декан | - | - | - | 0,000100 | - | - |
15 | Водород | - | - | - | 0,095000 | - | - |
16 | Кислород | - | 0,000100 | - | 0,000100 | - | - |
17 | Моноксид углерода | - | - | - | 0,010000 | - | - |
18 | Вода | - | 0,000100 | - | 0,000100 | - | - |
19 | Сероводород | - | 0,000100 | - | 0,000100 | - | - |
20 | Гелий | - | - | - | 0,000200 | - | 0,000538 |
21 | Аргон | - | 0,000100 | - | 0,000100 | - | - |
Сумма | 1,000000 | 1,000000 | 1,000000 | 1,000000 | 1,000000 | 1,000000 |
Таблица G.2 - Результаты для газа 1
|
|
|
|
|
|
|
|
|
| ||
5 | 250 | 0,81996 | 49,295 | -280,49 | -179,06 | -2,4223 | 1,6906 | 2,8342 | 6,153 | 1,366 | 372,27 |
5 | 260 | 0,84544 | 45,971 | -260,09 | -151,32 | -2,3134 | 1,6910 | 2,7219 | 5,658 | 1,360 | 384,59 |
5 | 270 | 0,86643 | 43,196 | -240,26 | -124,51 | -2,2122 | 1,6963 | 2,6450 | 5,219 | 1,354 | 395,93 |
5 | 290 | 0,89888 | 38,764 | -201,60 | -72,61 | -2,0268 | 1,7189 | 2,5559 | 4,473 | 1,344 | 416,29 |
5 | 310 | 0,92262 | 35,331 | -163,45 | -21,93 | -1,8578 | 1,7541 | 2,5191 | 3,861 | 1,333 | 434,32 |
5 | 330 | 0,94052 | 32,558 | -125,21 | +28,36 | -1,7006 | 1,7991 | 2,5140 | 3,350 | 1,322 | 450,59 |
5 | 350 | 0,95433 | 30,253 | -86,50 | +78,77 | -1,5523 | 1,8517 | 2,5299 | 2,918 | 1,311 | 465,51 |
10 | 250 | 0,65444 | 123,524 | -353,94 | -272,98 | -3,0522 | 1,7996 | 4,3448 | 4,218 | 1,782 | 379,77 |
10 | 260 | 0,70771 | 109,834 | -323,30 | -232,25 | -2,8924 | 1,7836 | 3,8367 | 4,162 | 1,663 | 389,14 |
10 | 270 | 0,75082 | 99,693 | -295,99 | -195,68 | -2,7543 | 1,7744 | 3,4993 | 4,010 | 1,591 | 399,53 |
10 | 290 | 0,81567 | 85,439 | -247,10 | -130,06 | -2,5197 | 1,7762 | 3,1098 | 3,609 | 1,508 | 420,07 |
10 | 310 | 0,86170 | 75,657 | -202,21 | -70,03 | -2,3194 | 1,7984 | 2,9143 | 3,199 | 1,458 | 439,05 |
10 | 330 | 0,89573 | 68,371 | -159,12 | -12,86 | -2,1407 | 1,8349 | 2,8144 | 2,821 | 1,424 | 456,36 |
10 | 350 | 0,92162 | 62,653 | -116,71 | +42,90 | -1,9766 | 1,8816 | 2,7685 | 2,485 | 1,397 | 472,24 |
15 | 250 | 0,61821 | 196,147 | -418,04 | -341,57 | -3,4519 | 1,7957 | 4,5000 | 1,992 | 2,912 | 471,92 |
15 | 260 | 0,66179 | 176,182 | -382,78 | -297,64 | -3,2797 | 1,8035 | 4,2711 | 2,250 | 2,461 | 457,75 |
15 | 270 | 0,70350 | 159,598 | -350,25 | -256,26 | -3,1234 | 1,8058 | 4,0056 | 2,404 | 2,179 | 452,49 |
15 | 290 | 0,77530 | 134,830 | -292,19 | -180,93 | -2,8541 | 1,8115 | 3,5532 | 2,473 | 1,865 | 455,55 |
15 | 310 | 0,83097 | 117,682 | -240,52 | -113,05 | -2,6276 | 1,8298 | 3,2590 | 2,363 | 1,704 | 466,04 |
15 | 330 | 0,87368 | 105,145 | -192,45 | -49,79 | -2,4298 | 1,8618 | 3,0835 | 2,179 | 1,607 | 478,79 |
15 | 350 | 0,90677 | 95,519 | -146,25 | +10,79 | -2,2516 | 1,9049 | 2,9838 | 1,976 | 1,541 | 491,98 |
20 | 250 | 0,67617 | 239,112 | -455,05 | -371,41 | -3,6627 | 1,7770 | 3,9985 | 0,950 | 4,102 | 585,72 |
20 | 260 | 0,70215 | 221,406 | -421,87 | -331,54 | -3,5063 | 1,7927 | 3,9666 | 1,146 | 3,439 | 557,37 |
20 | 270 | 0,73004 | 205,063 | -389,76 | -292,23 | -3,3580 | 1,8044 | 3,8892 | 1,314 | 2,965 | 537,78 |
20 | 290 | 0,78592 | 177,345 | -329,47 | -216,69 | -3,0880 | 1,8238 | 3,6552 | 1,529 | 2,380 | 518,08 |
20 | 310 | 0,83593 | 155,978 | -274,20 | -145,98 | -2,8521 | 1,8472 | 3,4238 | 1,596 | 2,060 | 513,90 |
20 | 330 | 0,87771 | 139,550 | -222,67 | -79,35 | -2,6437 | 1,8798 | 3,2500 | 1,564 | 1,867 | 517,31 |
20 | 350 | 0,91175 | 126,664 | -173,49 | -15,59 | -2,4561 | 1,9219 | 3,1348 | 1,478 | 1,742 | 524,40 |
30 | 250 | 0,85042 | 285,176 | -495,51 | -390,31 | -3,8898 | 1,7794 | 3,4974 | 0,198 | 5,600 | 767,57 |
30 | 260 | 0,85828 | 271,697 | -465,71 | -355,30 | -3,7525 | 1,7943 | 3,5033 | 0,285 | 4,865 | 732,95 |
30 | 270 | 0,86815 | 258,660 | -436,27 | -320,29 | -3,6203 | 1,8074 | 3,4962 | 0,369 | 4,276 | 704,27 |
30 | 290 | 0,89215 | 234,343 | -378,74 | -250,73 | -3,3718 | 1,8338 | 3,4549 | 0,522 | 3,421 | 661,74 |
30 | 310 | 0,91899 | 212,820 | -323,23 | -182,27 | -3,1435 | 1,8642 | 3,3874 | 0,636 | 2,860 | 634,97 |
30 | 330 | 0,94570 | 194,277 | -269,72 | -115,30 | -2,9341 | 1,9009 | 3,3096 | 0,702 | 2,488 | 619,80 |
30 | 350 | 0,97032 | 178,527 | -217,87 | -49,83 | -2,7415 | 1,9443 | 3,2399 | 0,725 | 2,233 | 612,55 |
Таблица G.3 - Результаты для газа 2
p, МПа |
|
|
|
|
|
|
|
|
| ||
5 | 250 | 0,81260 | 52,014 | -271,30 | -175,17 | -2,2227 | 1,6407 | 2,7730 | 6,314 | 1,363 | 362,01 |
5 | 260 | 0,83929 | 48,423 | -251,33 | -148,07 | -2,1164 | 1,6406 | 2,6549 | 5,800 | 1,356 | 374,23 |
5 | 270 | 0,86121 | 45,443 | -231,98 | -121,95 | -2,0178 | 1,6455 | 2,5747 | 5,346 | 1,350 | 385,45 |
5 | 290 | 0,89498 | 40,712 | -194,31 | -71,50 | -1,8375 | 1,6675 | 2,4823 | 4,575 | 1,339 | 405,56 |
5 | 310 | 0,91961 | 37,066 | -157,20 | -22,31 | -1,6734 | 1,7020 | 2,4437 | 3,945 | 1,328 | 423,33 |
5 | 330 | 0,93815 | 34,131 | -120,03 | +26,46 | -1,5210 | 1,7460 | 2,4373 | 3,420 | 1,318 | 439,35 |
5 | 350 | 0,95244 | 31,698 | -82,41 | +75,33 | -1,3772 | 1,7973 | 2,4520 | 2,977 | 1,307 | 454,03 |
10 | 250 | 0,64076 | 131,925 | -345,46 | -269,66 | -2,8402 | 1,7534 | 4,3299 | 4,203 | 1,814 | 370,85 |
10 | 260 | 0,69620 | 116,751 | -314,83 | -229,18 | -2,6814 | 1,7366 | 3,8017 | 4,186 | 1,680 | 379,36 |
10 | 270 | 0,74112 | 105,612 | -287,73 | -193,05 | -2,5450 | 1,7264 | 3,4488 | 4,052 | 1,600 | 389,27 |
10 | 290 | 0,80858 | 90,125 | -239,57 | -128,62 | -2,3146 | 1,7263 | 3,0431 | 3,663 | 1,510 | 409,27 |
10 | 310 | 0,85633 | 79,609 | -195,61 | -70,00 | -2,1191 | 1,7470 | 2,8408 | 3,252 | 1,458 | 427,89 |
10 | 330 | 0,89156 | 71,829 | -153,56 | -14,34 | -1,9450 | 1,7821 | 2,7375 | 2,869 | 1,422 | 444,91 |
10 | 350 | 0,91833 | 65,750 | -112,23 | +39,86 | -1,7856 | 1,8272 | 2,6893 | 2,528 | 1,394 | 460,53 |
15 | 250 | 0,61032 | 207,758 | -407,94 | -335,74 | -3,2223 | 1,7438 | 4,3653 | 1,917 | 3,030 | 467,74 |
15 | 260 | 0,65329 | 186,629 | -373,37 | -293,00 | -3,0546 | 1,7529 | 4,1673 | 2,194 | 2,536 | 451,45 |
15 | 270 | 0,69507 | 168,913 | -341,36 | -252,55 | -2,9019 | 1,7560 | 3,9192 | 2,368 | 2,227 | 444,66 |
15 | 290 | 0,76800 | 142,331 | -284,21 | -178,82 | -2,6383 | 1,7614 | 3,4767 | 2,470 | 1,887 | 445,90 |
15 | 310 | 0,82503 | 123,945 | -233,50 | -112,47 | -2,4170 | 1,7784 | 3,1815 | 2,376 | 1,714 | 455,43 |
15 | 330 | 0,86891 | 110,552 | -186,46 | -50,78 | -2,2240 | 1,8090 | 3,0038 | 2,200 | 1,611 | 467,59 |
15 | 350 | 0,90295 | 100,306 | -141,36 | +8,18 | -2,0506 | 1,8504 | 2,9023 | 1,999 | 1,543 | 480,37 |
20 | 250 | 0,67318 | 251,145 | -442,98 | -363,34 | -3,4193 | 1,7252 | 3,8586 | 0,905 | 4,254 | 582,02 |
20 | 260 | 0,69828 | 232,806 | -410,74 | -324,83 | -3,2683 | 1,7412 | 3,8355 | 1,100 | 3,552 | 552,40 |
20 | 270 | 0,72551 | 215,770 | -379,46 | -286,77 | -3,1247 | 1,7531 | 3,7699 | 1,273 | 3,048 | 531,56 |
20 | 290 | 0,78093 | 186,633 | -320,57 | -213,41 | -2,8624 | 1,7725 | 3,5558 | 1,504 | 2,425 | 509,77 |
20 | 310 | 0,83125 | 164,023 | -266,51 | -144,57 | -2,6328 | 1,7952 | 3,3337 | 1,585 | 2,085 | 504,20 |
20 | 330 | 0,87364 | 146,606 | -216,12 | -79,70 | -2,4300 | 1,8265 | 3,1630 | 1,563 | 1,882 | 506,69 |
20 | 350 | 0,90832 | 132,950 | -168,11 | -17,68 | -2,2475 | 1,8671 | 3,0485 | 1,484 | 1,750 | 513,14 |
30 | 250 | 0,85223 | 297,570 | -481,33 | -380,51 | -3,6328 | 1,7290 | 3,3785 | 0,178 | 5,753 | 761,58 |
30 | 260 | 0,85951 | 283,704 | -452,42 | -346,68 | -3,5001 | 1,7437 | 3,3860 | 0,264 | 4,991 | 726,46 |
30 | 270 | 0,86884 | 270,261 | -423,84 | -312,84 | -3,3724 | 1,7563 | 3,3804 | 0,348 | 4,380 | 697,27 |
30 | 290 | 0,89195 | 245,102 | -367,95 | -245,55 | -3,1320 | 1,7818 | 3,3435 | 0,501 | 3,492 | 653,73 |
30 | 310 | 0,91822 | 222,731 | -313,95 | -179,26 | -2,9109 | 1,8113 | 3,2820 | 0,618 | 2,909 | 625,94 |
30 | 330 | 0,94465 | 203,377 | -261,85 | -114,34 | -2,7079 | 1,8467 | 3,2096 | 0,689 | 2,521 | 609,85 |
30 | 350 | 0,96924 | 186,890 | -211,36 | -50,84 | -2,5211 | 1,8887 | 3,1434 | 0,716 | 2,256 | 601,84 |
Таблица G.4 - Результаты для газа 3
|
|
|
|
|
|
|
|
|
| |||
5 | 250 | 0,76537 | 59,066 | -269,33 | -184,68 | -2,0757 | 1,6370 | 2,9473 | 7,323 | 1,346 | 337,60 | |
5 | 260 | 0,80006 | 54,331 | -248,22 | -156,20 | -1,9640 | 1,6390 | 2,7632 | 6,681 | 1,335 | 350,48 | |
5 | 270 | 0,82789 | 50,560 | -228,09 | -129,20 | -1,8621 | 1,6448 | 2,6444 | 6,123 | 1,327 | 362,19 | |
5 | 290 | 0,86987 | 44,802 | -189,42 | -77,82 | -1,6785 | 1,6676 | 2,5110 | 5,197 | 1,314 | 382,96 | |
5 | 310 | 0,89992 | 40,512 | -151,69 | -28,27 | -1,5132 | 1,7033 | 2,4532 | 4,454 | 1,303 | 401,08 | |
5 | 330 | 0,92230 | 37,133 | -114,07 | +20,58 | -1,3605 | 1,7490 | 2,4371 | 3,845 | 1,293 | 417,27 | |
5 | 350 | 0,93944 | 34,372 | -76,08 | +69,39 | -1,2169 | 1,8025 | 2,4468 | 3,338 | 1,283 | 432,01 | |
10 | 250 | 0,54763 | 165,102 | -364,22 | -303,66 | -2,7530 | 1,7569 | 5,0940 | 3,980 | 2,113 | 357,74 | |
10 | 260 | 0,61607 | 141,116 | -327,13 | -256,27 | -2,5670 | 1,7581 | 4,4023 | 4,275 | 1,818 | 358,90 | |
10 | 270 | 0,67330 | 124,338 | -295,47 | -215,05 | -2,4114 | 1,7509 | 3,8718 | 4,311 | 1,665 | 365,91 | |
10 | 290 | 0,75890 | 102,706 | -241,97 | -144,60 | -2,1594 | 1,7453 | 3,2499 | 4,028 | 1,518 | 384,45 | |
10 | 310 | 0,81833 | 89,102 | -195,19 | -82,96 | -1,9538 | 1,7610 | 2,9493 | 3,610 | 1,448 | 403,07 | |
10 | 330 | 0,86148 | 79,509 | -151,42 | -25,65 | -1,7746 | 1,7936 | 2,7981 | 3,195 | 1,405 | 420,32 | |
10 | 350 | 0,89394 | 72,244 | -108,94 | +29,48 | -1,6124 | 1,8383 | 2,7246 | 2,818 | 1,374 | 436,16 | |
15 | 250 | 0,55363 | 244,969 | -425,70 | -364,46 | -3,0925 | 1,6683 | 4,2479 | 1,522 | 4,017 | 495,98 | |
15 | 260 | 0,59147 | 220,476 | -389,85 | -321,81 | -2,9252 | 1,7245 | 4,2561 | 1,878 | 3,129 | 461,36 | |
15 | 270 | 0,63262 | 198,500 | -355,38 | -279,81 | -2,7667 | 1,7545 | 4,1247 | 2,169 | 2,584 | 441,89 | |
15 | 290 | 0,71230 | 164,138 | -292,85 | -201,46 | -2,4865 | 1,7795 | 3,7029 | 2,476 | 2,024 | 430,12 | |
15 | 310 | 0,77873 | 140,449 | -238,00 | -131,20 | -2,2521 | 1,7973 | 3,3438 | 2,498 | 1,768 | 434,56 | |
15 | 330 | 0,83089 | 123,654 | -188,16 | -66,86 | -2,0509 | 1,8254 | 3,1099 | 2,370 | 1,630 | 444,63 | |
15 | 350 | 0,87154 | 111,152 | -141,13 | -6,18 | -1,8723 | 1,8652 | 2,9713 | 2,181 | 1,544 | 456,50 | |
20 | 250 | 0,63829 | 283,304 | -455,68 | -385,08 | -3,2503 | 1,6330 | 3,6681 | 0,689 | 5,499 | 623,08 | |
20 | 260 | 0,65852 | 264,036 | -423,75 | -348,00 | -3,1048 | 1,6939 | 3,7376 | 0,883 | 4,420 | 578,61 | |
20 | 270 | 0,68213 | 245,459 | -392,00 | -310,52 | -2,9634 | 1,7329 | 3,7499 | 1,074 | 3,658 | 545,96 | |
20 | 290 | 0,73518 | 212,039 | -330,66 | -236,34 | -2,6983 | 1,7788 | 3,6430 | 1,392 | 2,727 | 507,12 | |
20 | 310 | 0,78830 | 184,992 | -273,52 | -165,40 | -2,4617 | 1,8099 | 3,4460 | 1,565 | 2,238 | 491,84 | |
20 | 330 | 0,83557 | 163,950 | -220,40 | -98,41 | -2,2522 | 1,8426 | 3,2602 | 1,609 | 1,961 | 489,08 | |
20 | 350 | 0,87537 | 147,553 | -170,21 | -34,66 | -2,0646 | 1,8828 | 3,1229 | 1,568 | 1,790 | 492,61 | |
30 | 250 | 0,83636 | 324,314 | -489,03 | -396,53 | -3,4269 | 1,6274 | 3,1918 | 0,083 | 7,038 | 806,85 | |
30 | 260 | 0,84062 | 310,260 | -460,88 | -364,19 | -3,3001 | 1,6891 | 3,2684 | 0,170 | 5,975 | 760,08 | |
30 | 270 | 0,84737 | 296,388 | -432,51 | -331,29 | -3,1760 | 1,7285 | 3,3056 | 0,255 | 5,148 | 721,87 | |
30 | 290 | 0,86661 | 269,821 | -376,14 | -264,96 | -2,9390 | 1,7791 | 3,3181 | 0,416 | 3,976 | 664,88 | |
30 | 310 | 0,89085 | 245,547 | -321,02 | -198,84 | -2,7185 | 1,8185 | 3,2888 | 0,554 | 3,220 | 627,21 | |
30 | 330 | 0,91713 | 224,056 | -267,45 | -133,55 | -2,5144 | 1,8582 | 3,2373 | 0,655 | 2,721 | 603,62 | |
30 | 350 | 0,94297 | 205,462 | -215,40 | -69,39 | -2,3256 | 1,9022 | 3,1792 | 0,711 | 2,386 | 590,21 | |
Таблица G.5 - Результаты для газа 4
|
|
|
|
|
|
|
|
|
| ||
5 | 250 | 0,86904 | 47,932 | -258,79 | -154,48 | -1,9276 | 1,5661 | 2,4858 | 4,934 | 1,388 | 380,47 |
5 | 260 | 0,88770 | 45,120 | -240,75 | -129,93 | -1,8313 | 1,5711 | 2,4268 | 4,553 | 1,381 | 391,19 |
5 | 270 | 0,90333 | 42,697 | -222,99 | -105,89 | -1,7405 | 1,5787 | 2,3846 | 4,212 | 1,375 | 401,25 |
5 | 290 | 0,92789 | 38,700 | -187,95 | -58,75 | -1,5721 | 1,6012 | 2,3351 | 3,624 | 1,363 | 419,70 |
5 | 310 | 0,94608 | 35,507 | -153,09 | -12,27 | -1,4171 | 1,6322 | 2,3170 | 3,135 | 1,352 | 436,38 |
5 | 330 | 0,95989 | 32,875 | -118,03 | +34,06 | -1,2723 | 1,6702 | 2,3194 | 2,724 | 1,341 | 451,66 |
5 | 350 | 0,97058 | 30,655 | -82,51 | +80,60 | -1,1354 | 1,7137 | 2,3362 | 2,373 | 1,330 | 465,83 |
10 | 250 | 0,76451 | 108,971 | -307,61 | -215,84 | -2,4455 | 1,6397 | 3,2234 | 3,620 | 1,644 | 388,42 |
10 | 260 | 0,79990 | 100,145 | -284,54 | -184,68 | -2,3232 | 1,6350 | 3,0195 | 3,458 | 1,591 | 398,57 |
10 | 270 | 0,82933 | 93,013 | -262,77 | -155,26 | -2,2122 | 1,6342 | 2,8720 | 3,279 | 1,553 | 408,55 |
10 | 290 | 0,87507 | 82,072 | -221,73 | -99,89 | -2,0143 | 1,6439 | 2,6846 | 2,915 | 1,500 | 427,47 |
10 | 310 | 0,90854 | 73,949 | -182,54 | -47,32 | -1,8389 | 1,6664 | 2,5828 | 2,575 | 1,463 | 444,85 |
10 | 330 | 0,93373 | 67,593 | -144,19 | +3,75 | -1,6793 | 1,6983 | 2,5303 | 2,268 | 1,435 | 460,82 |
10 | 350 | 0,95309 | 62,436 | -106,06 | +54,10 | -1,5311 | 1,7374 | 2,5087 | 1,996 | 1,412 | 475,61 |
15 | 250 | 0,73016 | 171,146 | -352,65 | -265,01 | -2,7866 | 1,6584 | 3,5832 | 2,156 | 2,200 | 439,07 |
15 | 260 | 0,76682 | 156,696 | -325,88 | -230,15 | -2,6498 | 1,6628 | 3,3901 | 2,210 | 2,024 | 440,12 |
15 | 270 | 0,79939 | 144,745 | -300,76 | -197,13 | -2,5252 | 1,6645 | 3,2203 | 2,212 | 1,901 | 443,82 |
15 | 290 | 0,85295 | 126,300 | -254,21 | -135,44 | -2,3047 | 1,6724 | 2,9664 | 2,116 | 1,744 | 455,05 |
15 | 310 | 0,89384 | 112,748 | -210,88 | -77,84 | -2,1125 | 1,6910 | 2,8071 | 1,955 | 1,648 | 468,17 |
15 | 330 | 0,92527 | 102,316 | -169,34 | -22,74 | -1,9402 | 1,7195 | 2,7118 | 1,774 | 1,582 | 481,59 |
15 | 350 | 0,94973 | 93,985 | -128,69 | +30,91 | -1,7824 | 1,7559 | 2,6588 | 1,594 | 1,534 | 494,74 |
20 | 250 | 0,76132 | 218,856 | -385,55 | -294,17 | -3,0056 | 1,6435 | 3,4981 | 1,204 | 2,925 | 517,02 |
20 | 260 | 0,78917 | 203,013 | -358,14 | -259,62 | -2,8700 | 1,6606 | 3,4071 | 1,307 | 2,608 | 506,85 |
20 | 270 | 0,81592 | 189,083 | -331,85 | -226,07 | -2,7434 | 1,6709 | 3,3011 | 1,376 | 2,379 | 501,64 |
20 | 290 | 0,86386 | 166,274 | -282,42 | -162,14 | -2,5149 | 1,6865 | 3,0987 | 1,425 | 2,080 | 500,19 |
20 | 310 | 0,90341 | 148,737 | -236,27 | -101,81 | -2,3137 | 1,7065 | 2,9428 | 1,392 | 1,898 | 505,16 |
20 | 330 | 0,93530 | 134,959 | -192,28 | -44,09 | -2,1332 | 1,7344 | 2,8364 | 1,313 | 1,777 | 513,17 |
20 | 350 | 0,96086 | 123,862 | -149,56 | +11,91 | -1,9684 | 1,7697 | 2,7694 | 1,213 | 1,691 | 522,60 |
30 | 250 | 0,90169 | 277,178 | -425,72 | -317,48 | -3,2589 | 1,6277 | 3,1843 | 0,332 | 4,207 | 674,76 |
30 | 260 | 0,91296 | 263,228 | -399,63 | -285,66 | -3,1341 | 1,6528 | 3,1774 | 0,405 | 3,733 | 652,25 |
30 | 270 | 0,92529 | 250,102 | -373,94 | -253,98 | -3,0145 | 1,6706 | 3,1554 | 0,469 | 3,361 | 634,98 |
30 | 290 | 0,95124 | 226,500 | -323,99 | -191,54 | -2,7914 | 1,6975 | 3,0844 | 0,567 | 2,830 | 612,24 |
30 | 310 | 0,97647 | 206,413 | -276,02 | -130,68 | -2,5884 | 1,7233 | 3,0021 | 0,619 | 2,482 | 600,60 |
30 | 330 | 0,99923 | 189,486 | -229,72 | -71,40 | -2,4031 | 1,7532 | 2,9292 | 0,633 | 2,244 | 595,98 |
30 | 350 | 1,01893 | 175,204 | -184,62 | -13,39 | -2,2324 | 1,7885 | 2,8744 | 0,619 | 2,073 | 595,76 |
Таблица G.6 - Результаты для газа 5
|
|
|
|
|
|
|
|
|
| ||
5 | 250 | 0,80318 | 59,396 | -242,65 | -158,47 | -1,8544 | 1,4628 | 2,5137 | 6,573 | 1,366 | 339,12 |
5 | 260 | 0,83151 | 55,166 | -224,61 | -133,98 | -1,7583 | 1,4600 | 2,3924 | 6,033 | 1,358 | 350,87 |
5 | 270 | 0,85465 | 51,685 | -207,23 | -110,49 | -1,6697 | 1,4623 | 2,3107 | 5,557 | 1,352 | 361,63 |
5 | 290 | 0,89010 | 46,204 | -173,55 | -65,34 | -1,5083 | 1,4786 | 2,2162 | 4,752 | 1,340 | 380,87 |
5 | 310 | 0,91583 | 42,009 | -140,52 | -21,49 | -1,3621 | 1,5066 | 2,1746 | 4,097 | 1,330 | 397,82 |
5 | 330 | 0,93514 | 38,648 | -107,52 | +21,85 | -1,2266 | 1,5431 | 2,1636 | 3,552 | 1,319 | 413,10 |
5 | 350 | 0,95000 | 35,869 | -74,21 | +65,18 | -1,0991 | 1,5860 | 2,1721 | 3,095 | 1,309 | 427,09 |
10 | 250 | 0,62007 | 153,875 | -313,43 | -248,44 | -2,4222 | 1,5828 | 4,0693 | 4,219 | 1,854 | 347,10 |
10 | 260 | 0,67918 | 135,079 | -284,65 | -210,62 | -2,2738 | 1,5612 | 3,5296 | 4,259 | 1,702 | 354,92 |
10 | 270 | 0,72701 | 121,518 | -259,55 | -177,25 | -2,1478 | 1,5465 | 3,1678 | 4,154 | 1,613 | 364,35 |
10 | 290 | 0,79842 | 103,018 | -215,60 | -118,53 | -1,9378 | 1,5382 | 2,7552 | 3,780 | 1,516 | 383,57 |
10 | 310 | 0,84864 | 90,670 | -175,98 | -65,69 | -1,7616 | 1,5511 | 2,5508 | 3,365 | 1,461 | 401,47 |
10 | 330 | 0,88552 | 81,627 | -138,36 | -15,85 | -1,6057 | 1,5781 | 2,4452 | 2,975 | 1,425 | 417,81 |
10 | 350 | 0,91347 | 74,608 | -101,57 | +32,47 | -1,4636 | 1,6145 | 2,3933 | 2,625 | 1,397 | 432,78 |
15 | 250 | 0,59162 | 241,909 | -371,00 | -308,99 | -2,7653 | 1,5640 | 3,9904 | 1,867 | 3,179 | 443,96 |
15 | 260 | 0,63526 | 216,627 | -339,09 | -269,84 | -2,6117 | 1,5724 | 3,8221 | 2,172 | 2,622 | 426,12 |
15 | 270 | 0,67837 | 195,347 | -309,54 | -232,75 | -2,4717 | 1,5737 | 3,5928 | 2,375 | 2,279 | 418,37 |
15 | 290 | 0,75450 | 163,524 | -257,09 | -165,36 | -2,2307 | 1,5727 | 3,1655 | 2,519 | 1,910 | 418,53 |
15 | 310 | 0,81432 | 141,736 | -211,02 | -105,19 | -2,0300 | 1,5819 | 2,8738 | 2,445 | 1,726 | 427,40 |
15 | 330 | 0,86034 | 126,024 | -168,67 | -49,64 | -1,8563 | 1,6039 | 2,6961 | 2,275 | 1,619 | 439,00 |
15 | 350 | 0,89597 | 114,097 | -128,32 | +3,14 | -1,7009 | 1,6364 | 2,5925 | 2,074 | 1,549 | 451,26 |
20 | 250 | 0,65680 | 290,535 | -402,27 | -333,43 | -2,9377 | 1,5411 | 3,4974 | 0,882 | 4,485 | 555,64 |
20 | 260 | 0,68200 | 269,040 | -372,84 | -298,50 | -2,8007 | 1,5563 | 3,4817 | 1,085 | 3,706 | 524,89 |
20 | 270 | 0,70966 | 248,978 | -344,26 | -263,93 | -2,6702 | 1,5667 | 3,4250 | 1,268 | 3,153 | 503,23 |
20 | 290 | 0,76673 | 214,554 | -290,51 | -197,30 | -2,4321 | 1,5811 | 3,2263 | 1,523 | 2,476 | 480,39 |
20 | 310 | 0,81910 | 187,877 | -241,42 | -134,96 | -2,2241 | 1,5969 | 3,0121 | 1,623 | 2,112 | 474,20 |
20 | 330 | 0,86344 | 167,428 | -195,95 | -76,50 | -2,0413 | 1,6201 | 2,8440 | 1,613 | 1,899 | 476,24 |
20 | 350 | 0,89979 | 151,484 | -152,88 | -20,85 | -1,8776 | 1,6518 | 2,7288 | 1,539 | 1,762 | 482,29 |
30 | 250 | 0,83685 | 342,041 | -436,39 | -348,68 | -3,1243 | 1,5423 | 3,0500 | 0,178 | 6,046 | 728,22 |
30 | 260 | 0,84431 | 325,979 | -410,15 | -318,12 | -3,0044 | 1,5556 | 3,0587 | 0,267 | 5,211 | 692,52 |
30 | 270 | 0,85396 | 310,360 | -384,21 | -287,55 | -2,8891 | 1,5663 | 3,0535 | 0,353 | 4,547 | 662,93 |
30 | 290 | 0,87800 | 281,044 | -333,54 | -226,80 | -2,6720 | 1,5864 | 3,0168 | 0,513 | 3,590 | 619,03 |
30 | 310 | 0,90548 | 254,934 | -284,72 | -167,04 | -2,4727 | 1,6094 | 2,9555 | 0,638 | 2,970 | 591,15 |
30 | 330 | 0,93326 | 232,354 | -237,77 | -108,65 | -2,2902 | 1,6372 | 2,8826 | 0,716 | 2,561 | 575,03 |
30 | 350 | 0,95918 | 213,156 | -192,45 | -51,70 | -2,1226 | 1,6706 | 2,8144 | 0,748 | 2,284 | 566,97 |
Таблица G.7 - Результаты для газа 6
|
|
|
|
|
|
|
|
|
| |||
5 | 250 | 0,83409 | 53,718 | -249,86 | -156,78 | -1,9766 | 1,5047 | 2,4866 | 5,831 | 1,377 | 358,07 | |
5 | 260 | 0,85765 | 50,234 | -231,91 | -132,38 | -1,8809 | 1,5060 | 2,3995 | 5,369 | 1,370 | 369,34 | |
5 | 270 | 0,87716 | 47,297 | -214,42 | -108,71 | -1,7916 | 1,5111 | 2,3387 | 4,959 | 1,364 | 379,78 | |
5 | 290 | 0,90746 | 42,565 | -180,20 | -62,74 | -1,6273 | 1,5306 | 2,2672 | 4,258 | 1,353 | 398,67 | |
5 | 310 | 0,92971 | 38,866 | -146,39 | -17,75 | -1,4772 | 1,5604 | 2,2372 | 3,680 | 1,342 | 415,50 | |
5 | 330 | 0,94651 | 35,862 | -112,50 | +26,92 | -1,3376 | 1,5981 | 2,2328 | 3,196 | 1,331 | 430,77 | |
5 | 350 | 0,95949 | 33,356 | -78,22 | +71,68 | -1,2059 | 1,6419 | 2,2458 | 2,785 | 1,320 | 444,83 | |
10 | 250 | 0,69061 | 129,758 | -309,46 | -232,39 | -2,5159 | 1,5943 | 3,5837 | 4,052 | 1,744 | 366,59 | |
10 | 260 | 0,73764 | 116,813 | -284,01 | -198,40 | -2,3825 | 1,5828 | 3,2360 | 3,953 | 1,650 | 375,82 | |
10 | 270 | 0,77613 | 106,907 | -260,85 | -167,31 | -2,2651 | 1,5765 | 2,9969 | 3,791 | 1,589 | 385,53 | |
10 | 290 | 0,83479 | 92,540 | -218,63 | -110,57 | -2,0623 | 1,5794 | 2,7096 | 3,405 | 1,514 | 404,49 | |
10 | 310 | 0,87693 | 82,410 | -179,37 | -58,03 | -1,8870 | 1,5985 | 2,5599 | 3,019 | 1,468 | 422,02 | |
10 | 330 | 0,90828 | 74,743 | -141,49 | -7,70 | -1,7297 | 1,6290 | 2,4816 | 2,666 | 1,434 | 438,08 | |
10 | 350 | 0,93223 | 68,662 | -104,13 | +41,51 | -1,5849 | 1,6679 | 2,4452 | 2,350 | 1,408 | 452,88 | |
15 | 250 | 0,65598 | 204,914 | -362,28 | -289,08 | -2,8628 | 1,5990 | 3,8350 | 2,067 | 2,659 | 441,19 | |
15 | 260 | 0,69775 | 185,235 | -332,75 | -251,77 | -2,7165 | 1,6047 | 3,6215 | 2,252 | 2,318 | 433,27 | |
15 | 270 | 0,73655 | 168,978 | -305,42 | -216,65 | -2,5839 | 1,6059 | 3,4055 | 2,351 | 2,097 | 431,46 | |
15 | 290 | 0,80222 | 144,447 | -256,08 | -152,24 | -2,3536 | 1,6102 | 3,0579 | 2,361 | 1,840 | 437,07 | |
15 | 310 | 0,85292 | 127,096 | -211,52 | -93,50 | -2,1576 | 1,6255 | 2,8339 | 2,234 | 1,699 | 447,78 | |
15 | 330 | 0,89191 | 114,173 | -169,67 | -38,29 | -1,9850 | 1,6522 | 2,6989 | 2,054 | 1,611 | 460,01 | |
15 | 350 | 0,92220 | 104,113 | -129,24 | +14,83 | -1,8287 | 1,6880 | 2,6214 | 1,860 | 1,549 | 472,47 | |
20 | 250 | 0,70695 | 253,517 | -395,37 | -316,48 | -3,0592 | 1,5823 | 3,5123 | 1,027 | 3,705 | 540,62 | |
20 | 260 | 0,73374 | 234,868 | -366,73 | -281,58 | -2,9223 | 1,5976 | 3,4611 | 1,198 | 3,165 | 519,12 | |
20 | 270 | 0,76143 | 217,944 | -339,14 | -247,37 | -2,7932 | 1,6076 | 3,3751 | 1,335 | 2,780 | 505,07 | |
20 | 290 | 0,81476 | 189,632 | -287,44 | -181,97 | -2,5595 | 1,6226 | 3,1631 | 1,493 | 2,298 | 492,26 | |
20 | 310 | 0,86115 | 167,841 | -239,84 | -120,68 | -2,3550 | 1,6413 | 2,9739 | 1,526 | 2,024 | 491,11 | |
20 | 330 | 0,89949 | 150,949 | -195,16 | -62,67 | -2,1736 | 1,6680 | 2,8360 | 1,479 | 1,854 | 495,66 | |
20 | 350 | 0,93059 | 137,565 | -152,31 | -6,92 | -2,0096 | 1,7028 | 2,7453 | 1,390 | 1,740 | 502,98 | |
30 | 250 | 0,87498 | 307,248 | -432,49 | -334,85 | -3,2743 | 1,5804 | 3,1034 | 0,229 | 5,159 | 709,77 | |
30 | 260 | 0,88365 | 292,533 | -406,36 | -303,80 | -3,1525 | 1,5973 | 3,1039 | 0,312 | 4,510 | 680,11 | |
30 | 270 | 0,89405 | 278,420 | -380,57 | -272,82 | -3,0356 | 1,6103 | 3,0917 | 0,390 | 3,994 | 656,03 | |
30 | 290 | 0,91827 | 252,383 | -330,30 | -211,43 | -2,8162 | 1,6331 | 3,0425 | 0,527 | 3,247 | 621,29 | |
30 | 310 | 0,94424 | 229,607 | -281,91 | -151,25 | -2,6155 | 1,6577 | 2,9731 | 0,622 | 2,758 | 600,30 | |
30 | 330 | 0,96930 | 210,114 | -235,30 | -92,52 | -2,4319 | 1,6873 | 2,9010 | 0,671 | 2,430 | 589,00 | |
30 | 350 | 0,99197 | 193,580 | -190,11 | -35,14 | -2,2631 | 1,7227 | 2,8401 | 0,681 | 2,202 | 584,13 | |
Приложение ДА
(справочное)
Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта
Таблица ДА.1
Структура настоящего стандарта | Структура международного стандарта ISO 20765-1:2005 |
1 Область применения (1) | 1 Область применения |
2 Нормативные ссылки (2) | 2 Нормативные ссылки |
3 Термины, определения и обозначения (-) | 3 Термины и определения |
3.1 Термины и определения (3) | - |
3.2 Обозначения (приложение А) | - |
4 Термодинамические основы метода (4) | 4 Термодинамические основы метода |
4.1 Сущность метода (4.1) | 4.1 Сущность метода |
4.2 Фундаментальное уравнение состояния для свободной энергии Гельмгольца (4.2) | 4.2 Фундаментальное уравнение состояния для свободной энергии Гельмгольца |
4.3 Термодинамические свойства, получаемые из свободной энергии Гельмгольца (4.3) | 4.3 Термодинамические свойства, получаемые из свободной энергии Гельмгольца |
5 Метод расчета свойств (5) | 5 Метод вычислений |
5.1 Входные переменные (5.1) | 5.1 Входные переменные |
5.2 Переход от давления к относительной плотности (5.2) | 5.2 Переход от давления к приведенной плотности |
5.3 Проведение основных вычислений (5.3) | 5.3 Проведение основных вычислений |
6 Условия применения (6) | 6 Условия применения |
6.1 Давление и температура (6.1) | 6.1 Давление и температура |
6.2 Газ, подготовленный для транспортирования по магистральным газопроводам (6.2) | 6.2 Газ, подготовленный для транспортирования по магистральным газопроводам |
7 Оценка неопределенностей расчета свойств (7) | 7 Оценка неопределенностей вычислений |
7.1 Неопределенности расчета свойств для газа, подготовленного для транспортирования по магистральным газопроводам (7.1) | 7.1 Неопределенности вычислений для газа, подготовленного для транспортирования по магистральным газопроводам |
7.2 Влияние неопределенностей входных переменных (7.2) | 7.2 Влияние неопределенностей входных переменных |
8 Оформление результатов расчетов (8) | 8 Оформление результатов вычислений |
Приложение А Исходные положения для фундаментального уравнения состояния для свободной энергии Гельмгольца (4.2) | Приложение А Условные обозначения и единицы величин |
Приложение В Идеально-газовая свободная энергия Гельмгольца (приложение В) | Приложение В Идеально-газовая свободная энергия Гельмгольца |
Приложение С Уравнение состояния для свободной энергии Гельмгольца (приложение С) | Приложение С Уравнение состояния для свободной энергии Гельмгольца |
Приложение D Подробная информация по уравнению состояния (приложение D) | Приложение D Подробная информация по уравнению состояния |
Приложение Е Учет следовых компонентов (приложение Е) | Приложение Е Учет следовых компонентов |
Приложение F Реализация метода (приложение F) | Приложение F Реализация метода |
Приложение G Примеры расчетов (приложение G) | Приложение G Примеры расчетов |
Приложение ДА Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта (-) | - |
Примечание - После заголовков разделов (подразделов) настоящего стандарта в скобках приведены номера аналогичных разделов (подразделов) международного стандарта. | |
Библиография
[1] | ИСО 12213-2:2006 | Природный газ. Расчетное определение фактора сжимаемости. Часть 2. Расчет на основе данных о молярном компонентном составе | |
(ISO 12213-2:2006) | (Natural gas - Calculation of calculation compression factor - Part 2: Calculation using molar-composition analysis) | ||
[2] | ИСО 14532:2004 | Газ природный. Словарь | |
(ISO 14532:2004) | (Natural gas - Vocabulary) | ||
[3] | ИСО 80000-5:2007 | Величины и единицы величин. Часть 5. Термодинамика | |
(ISO 80000-5:2007) | (Quantities and units - Part 5: Thermodynamics) | ||
[4] | ИСО 80000-9:2009 | Величины и единицы величин. Часть 9. Физическая химия и молекулярная физика | |
(ISO 80000-9:2009) | (Quantities and units - Part 9: Physical chemistry and molecular physics) | ||
[5] | Руководство 99:2007 | Международный словарь основных и общих терминов в метрологии | |
(ISO/IEC GUIDE 99:2007) | (International vocabulary of metrology - Basic and general concepts and associated terms) | ||
[6] | Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин. Сборник определений, вып.103/Комитет научно-технической терминологии АН СССР. М.: Наука, 1984. С.40 | ||
[7] | Starling K.Е. and Savidge J.L. Compressibility Factors of Natural Gas and Other Related Hydrocarbon Gases. American Gas Association Transmission Measurements Committee Report No.8, Second Edition, November 1992, and Errata No.1, June 1993, Arlington | ||
[8] | Schley P., Jaeschke M. and Busch С. Berechnung kalorische | ||
[9] | Wagner W. and De Reuck K.M. International Thermodynamic Tables of the Fluid State - 13 - Methane, Blackwell, Oxford, 1996 | ||
[10] | a) Jaeschke M. and Humphreys A.E. The GERG Databank of High Accuracy Compressibility Factor Measurements, GERG Technical Monograph TM4 (1990) and Fortschritt-Berichte VDI Series 6, No.251 (1991) b) Jaeschke M., Hinze H.-M. and Humphreys A.E. Supplement to the GERG Databank of High-Accuracy, Compression Factor Measurements, GERG Technical Monograph TM7 (1996) and Fortschritt-Berichte VDI Series 6, No.355 (1997) | ||
Примечание - Данные из [10](а) и [11](b) объединены с данными монографии GERG TM7 CD-ROM. Общее число использованных данных 7433. | |||
[11] | a) Ewing M.B. and Goodwin A.R.H. J. Chem. Thermodynamics, Vol.25, pp.1503-1511 (1993) b) Fawcett D. Thesis, Murdoch University (June 1995) c) Ingrain D., Pinvidic J.J. and Desenfant P. Gaz de France, note to GERG WG1.3, 1 October 1993 d) Montel F., Labes P., Daridon J.-L., Lagourette B. and Xans P. Proceedings of the 6th International Gas Research Conference, Cannes, France (November 1995) pp.242-250 (Govt. Institutes Inc., Rockville, Maryland) e) Le Noe O. and Desenfant P. Gaz de France, note to GERG WG1.3, 24 January 1996 f) Pack D.J. Murdoch University, note to M. Jaeschke, 27 September 1996 g) Trusler J.P.M. J. Chem. Thermodynamics, Vol.26, pp.751-763 (1994) h) Trusler J.P.M. and Costa Gomes M.F. Report to GERG WG1.3, 19 October 1995 i) Younglove B.A., Frederick N.V. and McCarty, R.D. NIST Monograph 178, January 1993 | ||
Примечание - Общее число данных, использованных из источников с [11](а) по [11](i), равно 1194. | |||
[12] | Owren G., Grini P.G., Maehlum H.S. and Jorstad O. SINTEF Energy report for GERG WG 1.3 (1 August 1996) | ||
Примечание - Общее число данных, взятых из [12], равно 206. | |||
[13] | Aly F.A. and Lee L.L. Self Consistent Equations for Calculating the Ideal Gas Heat Capacity, Enthalpy and Entropy, Fluid Phase Equilibria, Vol.6, pp.169-179, 1981 | ||
[14] | Jaeschke M. and Schley P. Ideal-Gas Thermodynamic Properties for Natural-Gas Applications, Int. J. Thermophys., Vol.16 (6), pp.1381-1392, 1995 | ||
УДК 662.76.001.4:006.354 | ОКС 75.060 |
Ключевые слова: природный газ, термодинамические свойства, метод расчета | |
Электронный текст документа
и сверен по:
, 2019