ГОСТ Р 57987-2017 Композиты полимерные. Инфракрасная спектроскопия. Многомерный количественный анализ

ГОСТ Р 57987-2017

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

КОМПОЗИТЫ ПОЛИМЕРНЫЕ

Инфракрасная спектроскопия. Многомерный количественный анализ

Polymer composites. Infrared spectroscopy. Multivariate quantitative analysis

ОКС 13.220.40

Дата введения 2018-06-01

Предисловие

1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт авиационных материалов" совместно с Автономной некоммерческой организацией "Центр нормирования, стандартизации и классификации композитов" при участии Объединения юридических лиц "Союз производителей композитов" на основе собственного перевода на русский язык англоязычной версии указанного в пункте 4 стандарта

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 497 "Композиты, конструкции и изделия из них"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 5 декабря 2017 г. N 1880-ст

4 Настоящий стандарт является модифицированным по отношению к стандарту АСТМ Е1655-05(2012)* "Стандартные практики по инфракрасному многомерному количественному анализу" (ASTM E1655-05(2012) "Standard Practices for Infrared Multivariate Quantitative Analysis") путем включения дополнительных положений, фраз, слов, ссылок, показателей, их значений и/или внесения изменений по отношению к тексту применяемого стандарта АСТМ, которые выделены курсивом**.

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей.

** В оригинале обозначения и номера стандартов и нормативных документов приводятся обычным шрифтом, кроме отмеченного в разделе "Предисловие" знаком "**". - Примечания изготовителя базы данных.

Объяснения причин внесения технических отклонений, а также оригинальный текст модифицированных структурных элементов стандарта АСТМ приведены в дополнительном приложении ДА.

Сопоставление структуры настоящего стандарта со структурой указанного стандарта АСТМ приведено в дополнительном приложении ДБ.

В настоящем стандарте исключены ссылки на стандарты АСТМ Д4855 и АСТМ Е168, т.к. они были отменены, а также стандарты АСТМ Д4057, АСТМ Д1265, АСТМ Д4177, АСТМ Д6122, АСТМ Д6299, АСТМ Д6300, АСТМ Е275, АСТМ Е961, АСТМ Е932, АСТМ Е1421, АСТМ Е1866 и АСТМ Е1944, так как они носят справочный характер.

Сведения о соответствии ссылочных национальных и межгосударственных стандартов стандартам АСТМ, использованным в качестве ссылочных в примененном стандарте АСТМ, приведены в дополнительном приложении ДВ.

Наименование настоящего стандарта изменено относительно наименования указанного стандарта АСТМ для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)

5 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации"**. Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

1 Область применения

Настоящий стандарт устанавливает общие требования к проведению многомерного количественного анализа полимерных композитов.

Настоящий стандарт может быть также применен к анализу других материалов, таких как чистые органические и неорганические вещества и их смеси, полимерные материалы (как реактопласты, так и термопласты), а также компоненты для их производства, включая смолы, отвердители, ускорители, пластификаторы и пр.

Настоящий стандарт применим к анализам, проводимым в ближней инфракрасной области (приблизительно от 780 до 2500 нм) и в средней ИК-области (приблизительно от 4000 до 400 см).

Примечание - Хотя методики, описанные в настоящем стандарте, применяются к анализу в средней и ближней областях инфракрасного спектра, многие содержащиеся в них математические и методические подходы применимы также и для многомерного количественного анализа, выполняемого с использованием других видов спектроскопии. Однако оптимальные методики многомерного количественного анализа с использованием других видов спектроскопии могут отличаться от методик, описанных в настоящем стандарте для спектроскопии в средней и ближней ИК-областях.

Метод, устанавливаемый настоящим стандартом, распространяется на анализ твердых образцов, тонко измельченных твердых веществ и жидкостей. Для сбора и обработки данных требуется использование компьютера.

Описанный метод предусматривает использование опросного листа, по которому можно проверить, отвечают ли многомерные калибровки предъявляемым в настоящем стандарте требованиям.

Для некоторых случаев многомерного спектроскопического анализа интерференционные и матричные эффекты достаточно малы, чтобы проводить калибровку с использованием смесей, содержащих значительно меньшее количество химических компонентов по сравнению с образцами, которые в конечном счете будут анализироваться. Хотя в этих упрощенных методах используются описанные в настоящем стандарте математические подходы, они не соответствуют установленным в настоящем стандарте методам, особенно в отношении обращения со статистическими выбросами. При использовании упрощенных методов допускается указание на то, что в них используются описанные в настоящем стандарте математические подходы, но они не должны претендовать на соблюдение описанных в настоящем стандарте методов.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ 27176-86 Приборы спектральные оптические. Термины и определения

ГОСТ Р 57939-2017 Композиты полимерные. Инфракрасная спектроскопия. Общие принципы

ГОСТ Р 50779.11-2000 Статистические методы. Статистическое управление качеством. Термины и определения

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ 27176 и ГОСТ Р 50779.11, а также следующие термины с соответствующими определениями:

3.1 анализ (analysis): Процесс применения калибровочной модели к спектру, предварительно обработанному в установленном порядке, для оценки значения концентрации компонента или свойства.

3.2 калибровка (calibration): Процесс, который используют для создания модели, связывающей два типа измеренных данных. Применительно к настоящему стандарту - процесс создания модели, которая соотносит значения концентрации компонентов или свойств со спектрами набора известных эталонных образцов.

3.3 калибровочная модель (calibration model): Математическое выражение или набор математических действий, соотносящих значения концентрации компонентов или свойств со спектрами набора эталонных образцов.

3.4 калибровочные образцы (calibration samples): Набор эталонных образцов, используемых для создания калибровочной модели. Стандартные значения концентрации или свойства (измеренные стандартным методом) для калибровочных образцов известны и используются при калибровке для поиска калибровочной модели, которая соотносит эти значения со спектрами.

3.5 оценка (estimate): Значение концентрации компонента или свойства, полученное в результате использования калибровочной модели при анализе спектра поглощения.

3.6 валидация модели (model validation): Процесс испытания калибровочной модели с применением проверочных образцов с целью определения отклонения между оценками модели и стандартного метода и проверки согласованности между оценками, полученными с использованием модели и стандартного метода.

3.7 многомерная калибровка (multivariate calibration): Процесс создания модели, которая соотносит значения концентрации компонентов или свойств с поглощением набора известных эталонных образцов при более чем одной длине волны или частоте.

3.8 стандартный метод (reference method): Аналитический метод, используемый для оценки значения концентрации стандартного компонента или свойства, который применяется в процедурах калибровки и валидации.

3.9 справочные значения (reference values): Значения концентрации компонента или свойства для калибровочных или проверочных образцов, определенные с использованием стандартного аналитического метода.

3.10 квалификация спектрометра/спектрофотометра (spectrometer/spectrophotometer qualification): Процедуры, с помощью которых пользователь демонстрирует, что эксплуатационные характеристики конкретного спектрометра/спектрофотометра являются пригодными для проведения многомерного анализа, для того чтобы обеспечить сходимость результатов, согласующуюся с установленной в методе.

3.11 упрощенная калибровка (surrogate calibration): Многомерная калибровка, разработанная с использованием калибровочного набора, который состоит из смесей, содержащих значительно меньшее число химических компонентов, чем анализируемые в конечном счете образцы.

3.12 упрощенный метод (surrogate method): Стандартный метод испытаний, основанный на упрощенной калибровке.

3.13 проверочные образцы (validation samples): Набор образцов, используемых при валидации модели. Проверочные образцы не являются частью набора калибровочных образцов. Значения концентрации компонента или свойства, определенные стандартным методом, сравнивают со значениями, оценка которых была проведена с использованием модели.

4 Сущность метода

Для корреляции измеренных спектров набора калибровочных образцов со значениями концентраций стандартных компонентов или свойств набора образцов применяют приемы многомерной математики. Получающуюся в результате калибровочную модель используют для спектрального анализа неизвестных образцов с целью оценки значений концентрации компонента или свойства неизвестного образца.

Множественная линейная регрессия (МЛР), регрессия на главные компоненты (РГК) и метод проекции на латентные структуры (ПЛС) являются примерами методов многомерной математики, которые широко применяют для разработки калибровочной модели. Используют и другие математические методы, но они могут не обнаруживать статистических выбросов и могут не пройти валидацию в соответствии с настоящим стандартом.

Для обнаружения статистических выбросов во время разработки калибровочной модели применяют статистические испытания. Статистические выбросы включают в себя образцы с высоким влиянием (образцы, спектры которых создают статистически значимую часть одной или более спектральных переменных, используемых в данной модели) и образцы, эталонные значения для которых несовместимы с моделью.

Валидацию калибровочной модели проводят путем использования модели для анализа набора проверочных образцов и статистического сравнения оценок для проверочных образцов со стандартными значениями, измеренными для этих образцов, таким образом, чтобы провести испытание на ошибку в модели и на согласованность модели со стандартным методом.

Статистические испытания проводят с целью обнаружения случаев, когда оцененные значения с использованием модели представляют собой экстраполяцию калибровки.

В настоящем стандарте приводятся статистические выражения для расчета повторяемости инфракрасного анализа и предполагаемой согласованности между инфракрасным анализом и стандартным методом.

5 Значение метода

Настоящий стандарт можно использовать для установления валидности результатов, полученных с помощью инфракрасного (ИК) спектрометра во время разработки калибровки. Текущая валидация оценок, получаемых в результате анализа неизвестных образцов, должна рассматриваться отдельно.

Настоящий стандарт применим для любых методов инфракрасной спектроскопии. Для количественного анализа широко применяют спектроскопию в ближней ИК-области. Многие основные принципы, описанные в настоящем стандарте, относятся к простым современным правилам спектроскопического анализа в ближней ИК-области спектра. Хотя методы отбора образцов и аппаратура могут быть разными, основные методологические принципы калибровки в равной мере применимы и для спектроскопии в средней инфракрасной области. Исследуются новые методики, которые могут усовершенствовать принципы, обсуждаемые в настоящем стандарте. Настоящий стандарт применим в части общих аспектов, включая отбор и подготовку образцов, работу приборов и интерпретацию данных.

Процедуры калибровки определяют диапазон, в котором измерения действительны, и показывают, являются ли чувствительность и линейность результатов анализа пригодными для получения значимых оценок конкретных физических или химических характеристик типов материалов, для которых разработана калибровка.

6 Многомерная калибровка - общие положения

Методика проведения инфракрасного многомерного количественного анализа включает в себя несколько стадий.

6.1 Выбор калибровочного набора

Данный набор также называют обучающим набором или спектральной библиотекой. Данный набор должен включать вариации всех химических и физических свойств, которые обычно встречаются в данном виде анализа. Выбор калибровочного набора обсуждается в разделе 17 после статистических терминов, необходимых для определения критериев выбора.

6.2 Определение концентраций и/или свойств калибровочных образцов

Химические или физические, либо те и другие, свойства образцов в калибровочном наборе должны быть правильно и точно измерены стандартным методом, чтобы безошибочно калибровать модель для предсказания свойств неизвестных образцов. Стандартные измерения обсуждаются в разделе 9.

6.3 Сбор инфракрасных спектров

Сбор оптических данных следует выполнять тщательно, чтобы одинаково представлять калибровочные образцы, проверочные образцы и анализируемые (неизвестные) образцы. Отличие в способе пробоподготовки калибровочных, проверочных и анализируемых образцов вызывают расхождения и погрешность, которые не были смоделированы в рамках калибровки. Оборудование для инфракрасного анализа рассматривается в разделе 7, а инфракрасные спектральные измерения - в разделе 8.

6.4 Расчет математической модели

Расчет математических (калибровочных) моделей может включать разнообразные способы обработки данных и алгоритмы калибровки. Наиболее распространенные линейные методики рассматриваются в разделе 12. Для оценки и оптимизации модели используются разнообразные статистические методы. Эти методы описаны в разделе 15. Статистические методы, используемые для обнаружения выбросов в калибровочном наборе, рассматриваются в разделе 16.

6.5 Валидация калибровочной модели

Для валидации эффективности конкретной калибровочной модели (уравнения) требуется применение модели для анализа отдельного набора испытываемых (проверочных) образцов и статистическое сравнение значений оценок, полученных для этих образцов, со значениями, полученными стандартным методом. Статистические испытания для валидации модели рассматриваются в разделе 18.

6.6 Применение модели для анализа неизвестных образцов

К спектрам неизвестных образцов применяется модель для оценки значений концентрации компонента и/или свойства (см. раздел 13). Для обнаружения случаев, когда анализ включает экстраполяцию модели, используется статистика выбросов (см. раздел 16).

6.7 Текущий анализ и мониторинг

После того, как установлена эффективность одного или более калибровочных уравнений, должен осуществляться их контроль на предмет сохранения правильности и точности. Одновременно должны контролироваться эксплуатационные характеристики прибора, чтобы зарегистрировать любое ухудшение его работы либо из-за самой калибровочной модели, либо из-за сбоев в работе прибора. В разделе 22 процедуры проверки эксплуатационных характеристик представлены только в общих чертах. Также там рассматривается контрольный образец для проведения контроля качества.

6.8 Перенос калибровок

Переносимые калибровки представляют собой уравнения, которые могут быть перенесены с исходного прибора, где были собраны калибровочные данные, на другие приборы, где калибровки должны использоваться для предсказания свойств анализируемых образцов. Для того чтобы калибровку можно было переносить, она должна выполнять прогнозирование после переноса без существенного ухудшения эксплуатационных характеристик, как показано установленными статистическим испытаниями. Кроме того, статистические испытания, используемые для обнаружения экстраполяции модели, не должны меняться во время переноса. Поправки на ошибку и/или отклонение должны вводиться после переноса только после статистического подтверждения. Перенос калибровок, который иногда называют стандартизацией оборудования, обсуждается в разделе 22.

7 Оборудование

7.1 Приборы для ИК измерений относятся к одной из двух категорий: приборы, которые собирают непрерывные спектральные данные в диапазонах длин волн и частот (спектрофотометры), и приборы, которые проводят измерения только при одной или нескольких дискретных длинах волн или частотах (фотометры).

7.2 Фотометры обычно имеют один или несколько фильтров по длинам волн и единственный детектор. Эти фильтры устанавливают на барабане, чтобы волны определенной длины попадали на детектор одна за другой. Аналогичным образом можно использовать и плавно регулируемые фильтры. Для сканирования измеряемой длины волны эти фильтры, линейные или кольцевые, перемещаются за входной щелью. Как вариант, фотометры могут иметь несколько источников монохроматического излучения, таких как светоизлучающие диоды, которые последовательно включаются и выключаются.

7.3 Спектрофотометры можно классифицировать по методу, которым свет разделяется на составляющие длины волн. В дисперсионных приборах обычно используется дифракционная решетка для пространственного рассеивания света в непрерывном спектре длин волн. В приборах со сканирующей решеткой она вращается таким образом, что в любой конкретный момент времени только узкая полоса частот передается на единственный детектор. Дисперсия может осуществляться перед образцом (предварительная дисперсия) или после образца (последующая дисперсия).

Доступны также спектрофотометры, в которых выбор длины волны выполнен без движущихся частей с использованием матричного фотодиодного детектора. В этом случае используется последующая дисперсия. Эту функцию также может обеспечивать решетка, хотя для этой цели используются и другие методы, такие как линейный перестраиваемый фильтр (многослойный фильтр с изменяющейся по длине толщиной, разные части которого пропускают волны разной длины). Матричный фотодиодный детектор используют для получения непрерывного спектра по длине волны без механического движения. Матричный детектор представляет собой компактную конструкцию, включающую до нескольких тысяч отдельных фотодиодных детекторов. Каждый фотодиод находится в отдельной спектральной области рассеянного луча света и детектирует волны конкретный длины.

Акустооптический перестраиваемый фильтр является непрерывной разновидностью фотометра, в котором отсутствуют подвижные оптические элементы, осуществляющие выбор длины волны. Применяют двоякопреломляющий кристалл (например, оксид теллура), в котором акустические волны выбранной частоты используются для выбора диапазона длин волн света, пропускаемого через кристалл. Изменения акустической частоты вызывают изменение шага кристаллической решетки, которое в свою очередь заставляет кристалл работать как изменяющаяся прозрачная дифракционная решетка для одной длины волны (т.е. брэгговский дифрактор). Для анализа сигнала используют единственный детектор.

Другая категория спектрофотометров для превращения модулированных сигналов света в спектральные данные использует математические преобразования. Наиболее широко известным примером служит преобразование Фурье, которое применительно к инфракрасному излучению известно как ИК-Фурье-спектроскопия. Свет разделяется на два пучка, относительные траектории которых изменяют путем применения подвижного оптического элемента (например, подвижного зеркала либо подвижного клина из материала с высоким показателем преломления). Пучки рекомбинируют, чтобы получить интерференционную картину, содержащую все исследуемые длины волн. Применяя преобразование Фурье, интерференционную картину математически переводят в спектральные данные. Метод преобразования Фурье подходит для исследования средней и ближней ИК-областей спектра. В Фурье-спектрометрах применяют один детектор.

В другом типе многоканального спектрофотометра используется преобразование Адамара. Свет сначала рассеивается решеткой, затем пропускается через диафрагму-маску, установленную на детекторе или рядом с ним. Маска кодируется по набору шаблонов. Эти шаблоны могут создаваться путем открытия и закрытия различных участков с помощью электроники, как в случае жидкокристаллического дисплея, или путем перемещения маски. Эти модуляции изменяют распределение энергии пучка, падающего на детектор. Затем для конвертации сигнала в спектральную информацию используют математическое преобразование.

7.4 Инфракрасные приборы, используемые в многомерных калибровках, должны быть установлены и применены в соответствии с инструкциями изготовителя прибора. В соответствующих случаях должны быть проведены испытания для определения эксплуатационных характеристик прибора во время калибровки по процедурам, указанным в нормативной документации. Используя те же процедуры, следует периодически проверять эксплуатационные характеристики прибора. Процедура мониторинга должна выявлять изменения эксплуатационных характеристик прибора (по сравнению с теми, что наблюдались во время регистрации калибровочных спектров), которые могут отрицательно повлиять на оценку, полученную с использованием калибровочной модели.

7.5 Для большинства случаев применения количественного анализа в инфракрасной области спектра, связанных с использованием комплексных матриц, существует единая точка зрения, что приборы сканирующего типа (дисперсионные или на базе интерферометра) имеют самые лучшие эксплуатационные характеристики благодаря стабильности и воспроизводимости современного оборудования и большему количеству спектральных данных для компьютерной обработки. Эти данные обеспечивают большую гибкость калибровки и дополнительные возможности для выбора участков спектра, менее чувствительных к сдвигам полос и внешним шумам в пределах спектрального сигнала. Сканирующие системы на базе интерферометров позволяют также получать более высокую сходимость результатов по длине волны/частоте благодаря встроенным методам калибровки длины волны/частоты и возможностям компьютерной коррекции спектра. Сканирующие приборы применяются при анализе сложных объектов, таких как корма для животных.

8 Инфракрасная спектрометрия

Многомерные калибровки основываются на законе Бера, а именно на линейной пропорциональности поглощения гомогенного образца, содержащего поглощающее вещество, концентрации поглощающего компонента. Коэффициент поглощения образца определяется как десятичный логарифм обратной величины коэффициента пропускания :

, (1)

где - коэффициент пропускания, определяемый как отношение мощности излучения, пропущенного образцом, к мощности излучения, падающего на образец.

В случае измерений, проводимых в режиме отражения, коэффициент отражения иногда заменяют на коэффициент пропускания . Коэффициент отражения определяется как отношение мощности излучения, отраженного образцом, к мощности излучения, падающего на образец.

Примечание - Зависимость является не определением, а скорее приближением, служащим для линеаризации зависимости между измеренным коэффициентом отражения и концентрацией поглощающего компонента. В некоторых случаях более подходящими могут быть другие функции линеаризации (например, Кубелки-Мунка).

Для большинства типов оборудования мощность излучения, падающего на образец, нельзя измерить напрямую. Вместо этого проводят эталонное (фоновое) измерение мощности излучения без присутствия образца в луче света.

Примечание - Во избежание путаницы эталонное измерение мощности излучения будет называться фоновым измерением, а слово "эталонное" будет использоваться только тогда, когда речь идет об измерениях с помощью стандартного метода, по которому должна проводиться калибровка в инфракрасной области спектра (см. раздел 9).

Затем проводят измерение в присутствии образца и вычисляют отношение . Фоновое измерение можно выполнять разнообразными способами в зависимости от конкретного случая и аппаратуры. Образец и держатель образца можно физически удалить из пучка света и выполнить фоновое измерение на "холостом луче". Держатель образца (кювету) можно опорожнить и выполнить фоновое измерение через "пустую кювету".

Примечание - Оптически тонкие кюветы могут потребовать осторожного обращения, чтобы избежать оптических интерференций, вызываемых многократными внутренними отражениями внутри кюветы. В случае очень толстых ячеек расхождения в показателе преломления между образцом и пустой кюветой могут изменять свойства оптической системы, например смещать точку фокусировки.

Держатель образца (кювету) можно заполнить жидкостью с минимальным поглощением в исследуемом спектральном диапазоне и выполнить фоновое измерение через "фоновую жидкость". Кроме того, пучок света можно разделить или попеременно выполнить измерение через образец и на "холостом луче", через "пустую кювету" или "фоновую жидкость". При измерениях в режиме отражения в качестве фонового измерения обычно используют отражение материала, имеющего минимальное поглощение в исследуемом диапазоне.

Конкретная используемая схема со стандартными фоновыми измерениями может отличаться для различных приборов и случаев применения. Однако для измерения всех спектров калибровочных образцов, проверочных образцов и неизвестных исследуемых образцов должна применяться одна и та же схема стандартных фоновых измерений.

Обычно образец переносят к прибору вручную и помещают в ячейку или кювету с окнами, которые пропускают излучение в исследуемом диапазоне. Также можно использовать и специальные трубки для пропускания жидкости через оптическую кювету в приборе для непрерывного анализа. В случае использования оптических волокон анализ образца можно выполнить дистанционно на удалении от прибора. Излучение посылается к образцу через оптическое волокно или пучок волокон и возвращается к прибору с помощью другого волокна или пучка волокон. Разработаны приборы, в которых используются одни и те же волокна как для передачи, так и для приема излучения, а также приборы, в которых для этих целей используются пучки волокон. Можно использовать также детекторы и источники излучения, находящиеся снаружи по отношению к прибору, и тогда требуется только одно волокно или один пучок. Для областей спектра, для которых передающие волокна недоступны, их функция может быть выполнена на ограниченном расстоянии с применением соответствующей передающей оптики.

Примечание - Если в приборе используется предварительная дисперсия света, следует принять необходимые меры предосторожности, чтобы избежать внешней засветки системы в месте расположения образца, поскольку детектирование такого света вызовет ошибки при измерении поглощения.

Хотя большинство многомерных калибровок для жидкостей предусматривает прямое измерение проходящего света, могут быть использованы и другие методы (например, нарушенное полное внутреннее отражение). Для некоторых твердых веществ (например, полимерных пленок) может использоваться измерение пропускания, в то время как другие твердые вещества (например, порошкообразные вещества) гораздо чаще анализируют методом диффузного отражения.

У большинства ИК-приборов для контроля процесса регистрации и обработки спектральных данных имеется широкий спектр регулируемых параметров. Эти параметры, такие как оптическое и цифровое разрешение и скорость сбора данных (скорость сканирования), контролируют. Детальное описание параметров сбора спектральных данных и их влияния на многомерные калибровки находится вне рамок настоящего стандарта. Однако важно, чтобы все регулируемые параметры, которые контролируют регистрацию и обработку спектральных данных, поддерживались постоянными при получении спектров калибровочных образцов, проверочных образцов и неизвестных анализируемых образцов.

Определения и более подробное описание общих методов инфракрасного микроанализа содержатся в ГОСТ Р 57939.

9 Стандартный метод и справочные значения

Инфракрасная спектроскопия требует, чтобы с помощью калибровки определялась пропорциональная зависимость между измеренными сигналами и значениями концентраций компонентов или свойств, подлежащих оценке. Во время калибровки измеряются спектры для образцов, для которых известны эти справочные значения и определяется зависимость между поглощением образца и эталонными значениями. Получаемая пропорциональная зависимость применяется затем к спектрам неизвестных образцов для оценки значений концентрации и свойств образца.

Для простых смесей, содержащих лишь несколько химических компонентов, обычно можно приготовить смеси, которые могут служить эталонами для многокомпонентной калибровки. Из-за возможного влияния поглощения других компонентов недостаточно изменить концентрацию только нескольких компонентов смеси, даже когда разрабатываются анализы лишь для одного компонента. Вместо этого должны быть изменены концентрации всех компонентов в пределах диапазона, отражающего ожидания для будущих неизвестных образцов, подлежащих анализу. Поскольку инфракрасные измерения выполняются на фиксированном объеме образца (например, на фиксированной длине пути кюветы), предпочтительно, чтобы справочные значения концентрации выражались в переводе на объемы, например в объемных процентах, граммах на миллилитр, молях на кубический сантиметр и т.д. Разработка многомерных калибровок для эталонных концентраций, выраженных иначе (например, в массовых процентах), может привести к появлению моделей, являющихся линейными приближениями к тому, что на самом деле является нелинейной зависимостью, что в свою очередь может привести к менее точным оценкам концентраций.

Для сложных смесей, таких как смеси, полученные в результате химической переработки нефти, приготовление эталонных образцов обычно нецелесообразно, и многомерную калибровку выполняют на реальных образцах. В этом случае эталонные значения, используемые при калибровке, получают с помощью стандартного аналитического метода. Точность значений концентраций компонентов или свойств, которые оцениваются путем многомерного инфракрасного анализа, зависит от правильности и точности эталонных значений, используемых при калибровке. Ожидаемая согласованность между расчетными ИК-значениями и значениями, полученными в результате отдельного эталонного измерения, не может превышать повторяемость стандартного метода, поскольку, если даже расчетное ИК-значение является истинным, измерение согласованности ограничивается сходимостью эталонных значений. Правильность справочных данных, используемых при разработке модели, и точность модели могут быть улучшены путем усреднения повторных эталонных измерений.

Примечания

1 Если эталонные значения, используемые для калибровки многомерного инфракрасного анализа, получены в одной лаборатории, необходимо, чтобы процесс измерений, используемый для получения этих значений, контролировался в части систематической погрешности и сходимости результатов с применением подходящих методов обеспечения качества. Если нет первичных эталонов, позволяющих установить систематическую погрешность процесса эталонного измерения, рекомендуется, чтобы лаборатория принимала участие в программе межлабораторных перекрестных проверок с целью демонстрации точности.

2 Свойства образцов, подобных углеводородам, получаемым при химической переработке нефти, могут с течением времени ухудшаться, если не будут тщательно соблюдаться процедуры отбора образцов и их хранения. Крайне необходимо, чтобы состав образцов, взятых для лабораторного ИК-анализа, или ИК-анализа в режиме реального времени, или для лабораторного определения справочных значений, был репрезентативным для процесса на момент взятия образцов и чтобы состав поддерживался во время хранения и переноса образцов к анализатору или в лабораторию. Всегда, когда это возможно, рекомендуется не хранить образцы в течение времени больше положенного из-за вероятного ухудшения их свойств со временем, несмотря на соблюдение мер предосторожности при отборе образцов. Ухудшение свойств образцов может вызвать изменение спектров, измеренных анализатором, и, следовательно, расчетных значений, а также свойств или характеристик, измеренных стандартным методом.

Если для получения эталонных значений используют стандартный метод с известными значениями повторяемости и воспроизводимости, необходимо только показать, что эталонное измерение на практике выполняется в соответствии с процедурами, описанными в данном методе, и что полученная повторяемость статистически сравнима с заявленной в этом методе. Если таких данных нет, то должны быть собраны данные по повторяемости, по крайней мере, на трех образцах, которые будут использованы при калибровке. Эти образцы должны выбираться таким образом, чтобы охватить диапазон значений, в котором должна быть проведена калибровка, при этом один образец должен иметь эталонное значение в нижней трети диапазона, один образец - в средней трети диапазона и один образец - в верхней трети диапазона. На каждом образце должно быть выполнено, по крайней мере, шесть эталонных измерений. Следует вычислить среднеквадратичное отклонение по измерениям и сравнить его с ожидаемым на основе заявленной повторяемости.

Когда многократные эталонные измерения выполняются на отдельном калибровочном или проверочном образце, для значений следует применять критерий Диксона (см. А.1, приложение А), чтобы определить, принадлежат ли все эталонные значения одной и той же совокупности или что одно или более значений вызывают сомнение и должны быть отброшены.

10 Простая процедура определения осуществимости калибровки

Для новых случаев применения, как правило, неизвестно, можно ли разработать соответствующую многомерную ИК-модель. В этом случае можно провести анализ осуществимости, чтобы определить наличие зависимости между ИК-спектрами и исследуемым компонентом/свойством и вероятную возможность построения модели соответствующей сходимости. Если процедура определения осуществимости калибровки завершается успешно, то ее можно расширить и валидировать. Определение осуществимости калибровки предусматривает следующие действия:

- собирают приблизительно от 30 до 50 образцов, охватывающих весь диапазон для исследуемого компонента/свойства. Нужно проявлять осторожность, чтобы избежать взаимных корреляций между основными компонентами, если только такие взаимные корреляции не существуют в исследуемых материалах всегда. Диапазон показателя концентрация/свойство должен быть не менее чем в три раза, а желательно в пять раз, больше стандартного отклонения воспроизводимости (R/2,77) стандартного анализа;

- при сборе спектральных данных на этих образцах должны быть воспроизведены колебания размера частиц, пробоподготовки и условий процесса, предполагаемых при проведении анализа. Можно прибегнуть к многократному снятию спектра одного и того же образца, если при анализе ожидаются такие изменения условий;

- стандартные анализы на этих образцах проводят с использованием принятого стандартного метода. Если диапазон значений для компонента/свойства, по крайней мере, не в пять раз больше стандартного отклонения воспроизводимости для стандартного анализа, то должно быть сделано повторных анализов на каждом образце, так чтобы диапазон, умноженный на , был по крайней мере в три раза, а желательно в пять раз, больше стандартного отклонения для стандартного анализа;

- с использованием одного или более математических методов, описанных в разделах 11 и 12, разрабатывают калибровочную модель. Калибровочную модель испытывают предпочтительно методами перекрестной проверки, такими как SECV или PRESS (см. 15.3.6). Для оценки общего качества калибровки могут быть использованы и другие статистические данные;

- если значение SECV, полученное по результатам перекрестной проверки, позволяет предположить, что может быть построена модель соответствующей сходимости, то собирают дополнительные образцы для пополнения калибровочного набора, которые будут служить проверочным набором, собирают спектры этих образцов, разрабатывают окончательную модель и проводят валидацию, как описано в разделах 13, 14 и 15.

11 Предварительная обработка данных

Для разработки многомерной калибровочной модели к спектральным данным могут быть применены различные алгоритмы предварительной обработки данных. Например, для исправления базовой линии могут быть вычислены численные производные спектров с использованием цифровых алгоритмов фильтрации. Такая фильтрация, как правило, приводит к значительному уменьшению отношения сигнал-шум. Цифровые фильтры могут также использоваться для сглаживания данных, улучшая отношение сигнал-шум за счет разрешения. Настоящий стандарт допускает использование предварительной обработки спектральных данных, если в результате получается модель, которая имеет приемлемую сходимость результатов и которая проходит проверочное испытание, описанное в разделе 21. Любой метод предварительной обработки спектральных данных должен быть автоматизирован, чтобы обеспечить получение точно воспроизводимого результата, и он должен применяться единообразно ко всем калибровочным спектрам, проверочным спектрам и спектрам неизвестных анализируемых образцов.

Одним из вариантов предварительной обработки данных является центрирование относительно среднего значения, при котором перед разработкой модели вычисляют усредненный калибровочный спектр (среднее поглощение для калибровочных спектров как функцию длины волны или частоты) и вычитают из спектров отдельных калибровочных образцов. Аналогично вычисляют усредненное эталонное значение для калибровочных образцов и вычитают его из отдельных эталонных значений для калибровочных образцов. Затем строят модель по среднецентрированным данным. Если при разработке модели использовались среднецентрированные спектральные и эталонные данные, то производят следующие действия.

При анализе неизвестного образца до применения среднецентрированной модели из спектра неизвестного образца вычитают усредненный спектр для калибровочного набора, а для получения окончательного результата к оценке среднецентрированной модели прибавляют среднее эталонное значение для калибровочного набора. При этом степени свободы при вычислении стандартной ошибки калибровки должны быть уменьшены на одну для учета степени свободы, используемой при вычислении среднего значения (см. 15.2).

12 Математические принципы многомерной калибровки

12.1 Общие положения

Для определения корреляции измеренных спектров для набора калибровочных образцов и эталонных значений (значений свойства или концентрации компонента), полученных для этого набора образцов по результатам стандартных испытаний, используют методы многомерной математики. Цель заключается в том, чтобы разработать многомерную калибровочную модель, которую можно применить к будущим, неизвестным образцам, чтобы оценить значения свойства или концентрации компонента. В настоящем стандарте описаны только линейные многомерные методы, предполагающие, что значения свойства или концентрации компонента могут быть смоделированы как линейная функция спектров образца. Существуют различные нелинейные многомерные методы, но в целом они применяются не так широко, как описанные линейные методы. Настоящий стандарт не предназначен для сравнения или противопоставления этих методов. В рамках настоящего стандарта пригодность любого конкретного математического метода оценивается только по следующим двум критериям:

- метод должен позволять создание калибровочной модели, валидацию которой можно проводить, как описано в разделе 18;

- метод должен позволять получение статистических данных, подходящих для того, чтобы определить, находятся ли анализируемые образцы вне границ диапазона, для которого модель была разработана, т.е. когда расчетные значения представляют экстраполяцию модели (см. 16.3).

Примечание - В тексте настоящего стандарта матрицы указаны прописными буквами, набранными полужирным шрифтом, векторы - строчными буквами, набранными полужирным шрифтом, а скаляры - светлыми строчными буквами. Векторы представляют собой векторы-столбцы, а их транспонированные формы - векторы-строки. Курсивными строчными буквами обозначены размеры матрицы или вектора.

Все линейные многомерные методы призваны решать одну и ту же общую проблему. Если калибровочных спектров измеряются на дискретных длинах волн (или частотах), то матрица спектральных данных определяется как матрица размера на , содержащая спектр (или как некоторая функция спектра, получаемая с помощью предварительной обработки, как описано в разделе 9) по столбцам. По аналогии с этим является вектором размера на 1, который содержит эталонные значения для калибровочных образцов. Задача линейного многомерного моделирования состоит в вычислении вектора прогноза размерностью на 1, который решает уравнение (2):

, (2)

где - результат транспонирования матрицы , полученный путем перестановки строк и столбцов;

- вектор ошибок (вектор размерности на 1, т.е. разница между эталонными значениями и их оценками ).

При этом

. (3)

Для некоторых областей применения может быть целесообразно объединить спектральные данные с другими измеренными переменными (например, температурой образца, рН, скоростью перемешивания и т.д.). Эти дополнительные разнородные переменные могут быть просто приложены к спектру каждого образца, как будто это дополнительные измеренные длины волн. В случае использования разнородных переменных важно рассмотреть возможность применения к разнородным переменным весовых коэффициентов, для того чтобы обеспечить необходимый баланс их влияния на калибровку по отношению к влиянию спектральных переменных. Включение в модель дополнительных разнородных переменных требует, чтобы эти переменные измерялись для всех будущих образцов, анализируемых с помощью данной модели.

Оценку вектора прогноза проводят для того, чтобы минимизировать сумму квадратов ошибок:

. (4)

Поскольку , как правило, не является квадратной матрицей, ее нельзя напрямую инвертировать, чтобы решить уравнение (4). Вместо этого вычисляют псевдообратную, или обобщенную обратную, матрицу :

, (5)

где - оценка методом наименьших квадратов вектора прогноза .

Следует отметить, что при использовании уравнений (2)-(5) предполагается, что ошибки в спектральных данных пренебрежимо малы по сравнению с ошибками в эталонных данных, и что существует линейная зависимость между значением концентрации компонента или свойства и спектральными данными. Если одно из этих предположений неверно, то полученные таким образом модели не дадут оптимальной оценки .

При нахождении решения уравнения (5) методом наименьших квадратов предполагается, что конкретные величины ошибки в [см. уравнение (2)] распределяются нормально с обычной дисперсией. Это будет верно, если каждое конкретное значение в представляет результат отдельного стандартного измерения и если повторяемость метода является постоянной во всем диапазоне значений в . Если значения в представляют усредненные значения более чем одного определения стандартным методом, то выражение метода наименьших квадратов в уравнении (4) неприменимо. Если эталонных значений , , , ... измеряются для калибровочного образца , то можно прибегнуть к взвешенной регрессии. Если является диагональной матрицей размера на , содержащей значений для каждого из калибровочных образцов, то взвешенная регрессия имеет вид:

, (6)

где - диагональная матрица, содержащая квадратные корни значений;

- вектор, содержащий усредненные значения эталонных значений для каждого образца.

. (7)

Если в используются усредненные значения кратных эталонных значений и применяется взвешенная регрессия, то особое внимание следует обратить на то, что необходимо снова прибавить дисперсию, удаленную при вычислении средних эталонных значений (см. раздел 11), так чтобы статистические данные для модели можно было сравнить с данными для однократного измерения эталонного значения. Конкретный метод, в котором применяется взвешенная регрессия, зависит от конкретно применяемых методов многомерной математики.

Для большинства случаев, если калибровочные спектры собирают в расширенном диапазоне длины волны (или частоты), количество конкретных значений поглощения на спектр, , будет превышать количество калибровочных спектров, . В этом случае матрицы () и () являются матрицами неполного ранга и не могут быть инвертированы напрямую. Даже в случаях, когда , колинеарность среди калибровочных спектров может сделать (*) и (*) почти вырожденными матрицами (т.е. иметь определитель, близкий к нулю). При этом прямое применение уравнений (4) и (6) может создать неустойчивую модель, т.е. модель, для которой изменения в порядке спектрального уровня шумов вызывают существенные изменения расчетных значений. Следовательно, для того чтобы решить уравнения (4) и (6), необходимо уменьшить размерность , так чтобы можно было вычислить устойчивую обратную величину. Различные линейные математические методы, используемые для многомерной калибровки, являются другим способом уменьшения размерности для того, чтобы можно было вычислить устойчивые обратные величины () и () и оценить .

________________

* Текст документа соответствует оригиналу. - .

12.2 Множественный линейный регрессионный анализ

В множественной линейной регрессии (МЛР) определенное число, , отдельных длин волн (или частот), или аналитические области, либо то и другое, выбирают так, чтобы k<=n/6. В зависимости от конкретного применения отдельная длина волны или аналитические области могут быть отдельными длинами волн с или без коррекции базовой линии, либо они могут быть линейной комбинацией нескольких длин волн (например, отношениями или интегральными площадями пиков) с или без коррекции базовой линии. Новую матрицу размера на получают путем извлечения из строк, которые соответствуют выбранным длинам волн (или частотам). Тогда калибровочным уравнением становится

, (8)

где - вектор размера на 1, содержащий набор коэффициентов регрессии, определенных при каждой из выбранных длин волн (или частот).

Решение для коэффициентов регрессии имеет вид

. (9)

Если охватывает исключительно подгруппу длин волн в , оценка полного вектора прогноза получается из путем подстановки значений из в соответствующие позиции в (соответствующие выбранным длинам волн или частотам) и установки на ноль всех других элементов (соответствующих длинам волн или частотам, исключенным при переходе из в ). Если охватывает любые интегральные площади пиков, то значение , которое подставляется в соответствующие позиции , должно быть подогнано путем деления на количество длин волн, включенных в интегральную площадь пика. Если какие-либо длины волн или интегральные площади пиков корректировались, то такая же коррекция базовой линии должна применяться к измеренному спектру для неизвестного образца до применения вектора регрессии .

Если применяется взвешенная регрессия, соответствующая форма для уравнения (9) приобретает вид

. (10)

Не все серийно выпускаемые пакеты программного обеспечения, в которых применяется МЛР, включают опции для применения взвешенных регрессий. Если модели МЛР разрабатываются с помощью таких пакетов, то усредненные величины кратных эталонных значений должны оставаться включенными в вектор , если таковые имеются. Применение усредненных значений приведет к улучшению оценки коэффициентов регрессии, но созданная модель не будет являться минимумом метода наименьших квадратов. Стандартные ошибки калибровки, вычисленные с помощью программного обеспечения, в этих случаях не будут, как правило, иметь существенного значения, поскольку они не выражены относительно единичного стандартного измерения. Стандартные ошибки калибровки следует пересчитать, используя методику, описанную в разделе 11.

Выбор числа длин волн (или частот) для применения во множественной линейной регрессии является важнейшим условием для разработки модели. Если используется слишком малое количество длин волн, то разрабатываемая модель будет иметь низкую точность. Если же используемых длин волн слишком много, то колинеарность среди значений поглощения на этих длинах волн может приводить к созданию неустойчивой модели. Оптимальное количество длин волн (или частот) для модели связано с количеством спектрально различимых компонентов в калибровочных спектрах (см. раздел 15) и обычно может быть определено только методом проб и ошибок. Как правило, количество используемых длин волн (или частот) должно быть достаточно большим для получения модели соответствующей точности, но достаточно малым для создания устойчивой модели, которая проходит валидацию.

Выбор конкретных длин волн (или частот) для включения в модель множественной линейной регрессии также является важнейшим фактором при разработке модели. Для осуществления такого выбора предложено несколько математических алгоритмов. Кроме того, выбор может быть основан на первоначальных знаниях соотношений между измеренными значениями поглощения и моделируемым свойством или компонентом. Сравнение различных методов выбора находится вне рамок настоящего стандарта. Для целей настоящего стандарта соответствующий набор длин волн определяется как набор, который создает модель требуемой точности, которая проходит процедуру валидации по методике, описанной в разделе 18.

12.3 Метод регрессии на главные компоненты (РГК)

Регрессия на главные компоненты (РГК) основана на разложении по сингулярным числам матрицы спектральных данных. Разложение по сингулярным числам имеет вид

. (11)

Матрица вкладов является матрицей размера на , которая удовлетворяет следующей зависимости:

, (12)

где - единичная матрица размера на .

, (13)

где - матрица с собственными значениями .

Матрица размера на - это матрица сингулярных значений, равных корню квадратному собственных значений, т.е.

. (14)

Матрица нагрузок - это матрица размера на , которая удовлетворяет зависимостям

, (15)

. (16)

Векторы-строки, которые составляют матрицы и , являются ортонормальными, т.е. скалярное произведение вектора на себя равно 1, а скалярное произведение на любой другой вектор в матрице равно 0.

Примечание - В некоторых случаях реализации РГК матрица данных может быть разложена как произведение только двух матриц и . Тогда или становится ортогональной, но не ортонормальной, и или .

Используя разложение по сингулярным числам, псевдообратную матрицу можно вычислить следующим образом:

. (17)

Используя псевдообратную зависимость (17), можно затем найти решение для вектора прогноза . На практике, однако, полное обращение , как указано в уравнении (17), не используют, поскольку оно содержит информацию, касающуюся спектрального шума в калибровочном спектре.

Когда анализ по основным компонентам проводят на матрице , содержащей калибровочные спектры, сигналами, поступающими от компонентов калибровочного образца, объясняется большинство случаев дисперсии в , и эти сигналы концентрируются в направлении первых векторов нагрузки, которые соответствуют собственным значениям большего размера. Хотя разделение сигнала и шума редко бывает идеальным, в создании модели лучше использовать только первые векторов. Разложение по сингулярным числам матрицы в таком случае записывается так:

, (18)

где - матрица размера на , содержащая первые столбцов ;

- матрица размера на , содержащая первые столбцов ;

- диагональная матрица размера на , содержащая первые сингулярных чисел;

, и - соответствующие матрицы, содержащие последние элементов , и .

Псевдообратная матрица затем аппроксимируется как:

. (19)

Оценка для вектора прогноза * дается тогда следующим образом:

________________

* Текст документа соответствует оригиналу. - .

. (20)*

________________

* Формула соответствуют оригиналу. - .

С другой стороны, может быть выполнена регрессия вкладов по эталонным значениям для получения набора коэффициентов регрессии :

, (21)

. (22)

Различные алгоритмы ступенчатой регрессии можно использовать для того, чтобы проверить, какие основные компоненты (какие столбцы в матрице вкладов ) показывают статистически значимую корреляцию по отношению к эталонным значениям в . Коэффициенты (элементы ) для основных компонентов, которые не показывают статистически значимой корреляции, можно установить на нулевое значение. Тогда оценка для вектора прогноза имеет вид:

. (23)

Если в векторе используется среднее значение многократных контрольных измерений, то для вычисления вектора прогноза следует применять взвешенную регрессию. Взвешенную регрессию лучше применять к вкладам в уравнениях (20) и (21), а спектры в до разложения по сингулярным числам не подвергаются взвешенной регрессии.

Если конкретных эталонных значений измеряются для -го калибровочного образца, то внесение копий спектра в матрицу или взвешивание спектра по изменят вычисляемые нагрузки. Если спектр измеряется только один раз, то неопределенность в спектральных переменных, внесенная , не отличается от неопределенности для других спектров. Взвешивание спектра до разложения по сингулярным числам обычно заставляет характеристики шума переходить в нагрузки, отрицательно влияя на модель. Взвешивание вкладов во время определения коэффициентов регрессии должным образом объясняет разницу в дисперсии среди компонентов вектора. Уравнения взвешенной регрессии принимают вид:

. (24)

. (25)

Не все серийно выпускаемые пакеты программного обеспечения, в которых применяется РГК, включают опции для применения взвешенных регрессий. Если модели РГК разрабатываются с помощью таких пакетов, то усредненные величины кратных эталонных значений следует все же включать в вектор , если таковые имеются. Применение усредненных значений позволит получить более правильные оценки коэффициентов регрессии, но созданная модель не будет минимумом наименьших квадратов. Стандартные ошибки калибровки, вычисленные с помощью программного обеспечения, в этих случаях не будут, как правило, иметь существенного значения, поскольку они не выражены относительно единичного стандартного измерения. Стандартные ошибки калибровки следует пересчитать, используя методику, описанную в 15.1.

Как и в случае длин волн в множественной линейной регрессии, выбор количества основных компонентов для использования в регрессии имеет исключительно важное значение при разработке модели. Если используется слишком мало основных компонентов, то будет разработана модель пониженной точности. В случае использования слишком большого количества основных компонентов в модель будут включаться шумовые характеристики калибровочных образцов, что приведет к неустойчивости оценок. Оптимальное количество основных компонентов для модели связано с количеством спектрально различимых компонентов в калибровочных спектрах (см. раздел 15) и обычно может быть определено только методом проб и ошибок. Как правило, количество используемых длин основных компонентов должно быть достаточно большим для получения модели соответствующей точности, но достаточно малым для создания устойчивой модели, которая проходит валидацию.

12.4 Метод проекции на латентные структуры (ПЛС)

Как и метод РГК, метод ПЛС предусматривает разложение матрицы спектральных данных в произведение матриц.

Примечание - Термин ПЛС используется для описания различных математических алгоритмов. Описанный здесь вариант представляет собой особый вид алгоритма ПЛС-1 и имеет дело только с одним набором эталонных значений за раз. Существуют алгоритмы ПЛС-2 и многоблочный ПЛС, которые можно использовать для одновременной калибровки по нескольким компонентам и/или концентрациям. За исключением особых случаев, с помощью алгоритма ПЛС-2 обычно проводят калибровки, которые не работают так, как калибровки, создаваемые с помощью алгоритма ПЛС-1, а использование многоблочного ПЛС связано со сложностями, находящимися вне рамок настоящего стандарта. Поэтому в настоящем стандарте алгоритмы ПЛС-2 и многоблочный ПЛС не рассматриваются. Были опубликованы различные описания алгоритма ПЛС-1, многие из которых немного отличаются друг от друга по практическим шагам вычислений. При реализации алгоритма ПЛС-1 должен быть сделан выбор в отношении того, подлежат ли векторы вкладов или векторы нагрузки нормализации. В следующих уравнениях нормализованы векторы вкладов. Если ни один из векторов не нормализован или нормализован вектор нагрузок вместо вектора вкладов, то для вектора прогноза будет получено другое выражение. Разница в уравнениях не должна приводить к существенной разнице в числовых значениях, полученных для вектора прогноза, равно как и в оценках, полученных на базе этого вектора.

В отличие от метода РГК, где сначала происходит разложение матрицы , а затем регрессия в сравнении с эталонными значениями, в методе ПЛС для получения разложения используется вектор . Метод ПЛС реализуется затем посредством серии шагов, которые циклически повторяются. В каждом цикле вычисляют весовой вектор (размерности на 1), вектор вкладов (размерности на 1), коэффициент регрессии (скаляр) и вектор нагрузок (размерности на 1). Индекс указывает, сколько раз был совершен полный цикл, а в начале он составляет 1.

Шаг 1 - вычисление весового вектора размером на 1, :

, (26)

. (27)

Шаг 2 - масштабирование весового вектора и вычисление нормализованного вектора вкладов размерности на 1:

, (28)

, (29)

, (30)

. (31)

Шаг 3 - осуществление регрессии вектора вкладов в сравнении с эталонными значениями для получения коэффициента регрессии :

, (32)

. (33)

Шаг 4 - вычисление вектора нагрузки размерности на 1:

, (34)

. (35)

Шаг 5 - вычисление остатков:

, (36)

. (37)

Для последующих стадий в цикле матрицу заменяют матрицей остатков из предыдущего цикла, а вектор заменяют вектором остатков . Цикл повторяют раз, чтобы получить весовых векторов, векторов вкладов и векторов нагрузки и коэффициентов регрессии. Тогда общее выражение для результатов имеет вид

, (38)

, (39)

где - матрица размерности на , содержащая как строки;

- матрица размерности на , содержащая , как отдельные строки;

- остаток из матрицы спектральных данных;

- остаток из оценки эталонных значений.

Оценка вектора прогноза представляется следующим образом:

. (40)

Если значения в векторе содержат среднее значение многократных контрольных измерений, то при разработке модели следует прибегнуть к взвешенной регрессии. К сожалению, для метода ПЛС разработка требуемой схемы взвешивания усложнена использованием в разложении . Если спектр соответствует образцу, для которого измеряются эталонные значения , то взвешивание обоих и на в шаге 1 алгоритма ПЛС будет чрезмерно подчеркивать спектральные переменные, полученные за счет . Предпочтительно выполнять взвешивание только при вычислении коэффициентов регрессии в шаге 3. Тогда уравнения (31) и (32) принимают вид

, (41)

. (42)

Остальные шаги алгоритма продолжают выполнять без изменений.

Не все серийно выпускаемые пакеты программного обеспечения, в которых применяется метод ПЛС, включают опции для применения взвешенных регрессий. Если модели ПЛС разработаны с помощью таких пакетов, то усредненные величины кратных эталонных значений, если таковые имеются, следует все же включать в вектор . Применение усредненных значений позволит получить более правильные оценки коэффициентов регрессии, но созданная модель не будет минимумом наименьших квадратов. Стандартные ошибки калибровки, вычисленные с помощью программного обеспечения, в этих случаях не будут, как правило, иметь существенного значения, поскольку они не выражены относительно единичного стандартного измерения. Стандартные ошибки калибровки следует пересчитать, используя методику, описанную в 15.2.

12.5 Выбор частоты/длины волны в моделях РГК/ПЛС

Важным этапом в разработке моделей РГК и ПЛС является выбор того, какие частоты/длины волн следует включить в модель. Калибровочная модель не обязательно должна включать данные всего спектрального диапазона, измеренные спектрометром. При анализе определенных веществ области спектра можно выбрать на основе знания того, где возникает сигнал анализируемого вещества. Однако при моделировании физических свойств или эксплуатационных характеристик рекомендуется включать максимально большое количество спектральных участков и информации. Области спектра могут исключаться из калибровочных моделей по целому ряду причин, включая высокий уровень спектрального шума, нелинейный отклик спектрометра и спектральные помехи от оптических или окружающих источников.

Спектрометры, как правило, имеют ограниченную область, в пределах которой они реагируют линейно. В дисперсионных спектрометрах линейный диапазон отклика может ограничиваться рассеянным светом. Подобным же образом в Фурье-спектрометрах диапазон линейности могут ограничивать фазовые погрешности. Если в спектральные многомерные модели включаются области с нелинейным откликом, количество переменных, необходимое для моделирования калибровочных данных, увеличивается. Нелинейность в X-блоке может ограничить переносимость модели между спектрометрами (см. раздел 22), а также устойчивость модели к техническому обслуживанию спектрометра. Из моделей всегда нужно исключать те области спектра, в которых образцы являются оптически непрозрачными.

Спектры могут содержать сигналы, возникающие из-за особенностей спектрометра, оптических характеристик образца или среды. Например, для средней ИК-области спектры часто содержат дополнительные полосы от водяного пара и диоксида углерода из-за различий в продувке. Устойчивость моделей можно иногда улучшить путем исключения спектральных областей с такими помехами. При включении областей с помехами важно или учесть эти изменения, или принять меры для физического исключения помех, например, для удаления водяного пара использовать продувку сухим воздухом.

При выборе частот/длин волн для включения в модель, возможно, будет целесообразно вычислить среднее или стандартное отклонение калибровочных спектров. Если - вектор единиц размерности на 1, то:

, (43)

. (44)

Следует собрать параллельных спектров () одного или более образцов и измерить подобное среднее значение () и значения стандартных отклонений ().

, (45)

. (46)

Отношение к целесообразно использовать при выборе частоты/длины волны для включения или удаления из модели.

Если для данной частоты/длины волны отношение к меньше 0,3, то колебания в калибровочном наборе значительно выше уровня спектрального шума, и частота/длина волны должна, как правило, включаться в модель.

Если для данной частоты/длины волны отношение к близко к единице, то колебания в калибровочном наборе сравнимы с уровнем спектрального шума, и можно говорить о реальном исключении частоты/длины волны из модели.

Остатки удобно использовать во время анализа для обнаружения компонентов, которые не представлены в калибровочных образцах. Исключение частот/длин волн может уменьшить возможности модели в обнаружении статистических выбросов.

13 Оценка значений из спектров

Если (вектор размерности на 1) является спектром образца, то расчетное значение концентрации компонента или свойства (скаляр) дается как

, (47)

где - вектор прогноза, полученный из многомерной калибровки.

Выражение в уравнении (47) связано только со скалярным произведением двух векторов для получения расчетного значения; его преимущество состоит в простоте вычислений. Однако для получения часто прибегают к другим вычислениям, поскольку они позволяют получать дополнительные параметры, требующиеся для вычисления неопределенности в расчетах, а также определять, проводится ли оценка путем интерполяции или экстраполяции калибровочной модели.

Для метода МЛР значения в , которые соответствуют выбранным длинам волн (или частот) в калибровке, вычитаются из вектора (размерности на 1). Затем получают оценку как скалярного произведения вектора и вектора коэффициентов регрессии :

. (48)

Для метода РГК вектор сначала разлагают:

, (49)

. (50)

Затем расчетные вклады (вектор размерности на 1) умножают на коэффициенты регрессии, полученные от калибровки, для определения :

. (51)

Для метода ПЛС сначала пошагово проводят разложение вектора . Для каждой скрытой переменной в модели ПЛС повторяют уравнения (52) и (53). После завершения первого цикла через уравнения (52) и (53) и заменяют на и из предыдущего цикла.

, (52)

. (53)

Затем расчетные вклады (вектор размерности на 1) умножают на коэффициенты регрессии, полученные от калибровки, для определения :

. (54)

14 Последующая обработка

Ряд методов многомерного анализа предусматривает некоторую последующую обработку оценок многомерной модели. Наиболее известным примером является такая обработка для среднецентрированных моделей (см. раздел 11), где для получения окончательной оценки к первоначальной оценке модели должны быть добавлены усредненные эталонные значения для калибровочного набора. Можно разработать модель для оценки изменений длины пути кюветы, содержащей исследуемый образец. На основе результатов оценки длины пути можно масштабировать расчетные значения концентрации и свойств.

Полное описание возможных алгоритмов последующей обработки находится вне рамок настоящего стандарта. К последующей обработке можно прибегнуть, если она позволяет получить модель адекватной точности, проходящую проверку, описанную в разделе 18, и при условии, что алгоритм последующей обработки автоматизирован для получения точно воспроизводимых результатов и одинаково применяется к результатам калибровки, валидации и анализа.

15 Статистические методы оценки и оптимизации калибровочных моделей

15.1 Общие положения

Для оценки и оптимизации характеристик моделей многомерной калибровки используют различные статистические методы. Эти статистические методы обычно применимы только к данным в калибровочном наборе, их нельзя путать со статистическими методами, применяемыми для валидации модели (см. раздел 18) и получаемыми на основе отдельно проанализированного проверочного набора. Рассматриваемые в данном разделе статистические методы не подходят для оценки ожидаемых характеристик модели многомерной калибровки при применении их для оценки значений неизвестных образцов. Для этих целей пригодны исключительно статистические методы, рассматриваемые в разделе 18.

15.2 Стандартная ошибка калибровки

Если - значения, рассчитанные для калибровочных образцов, а - соответствующие эталонные значения, тогда - это вектор ошибки калибровки, определяемый как

. (55)

Ошибки предсказания включают составляющие от ошибок в эталонных значениях для калибровочного набора, спектральные ошибки в спектрах калибровочного набора и ошибки модели (использование неправильного числа переменных, нелинейных соотношений и т.д.).

Стандартная ошибка калибровки (SEC) определяется как

, (56)

где - число степеней свободы в калибровочной модели.

Величина обычно равна , где - количество калибровочных образцов, а - число переменных (длины волн в МЛР, основные компоненты или скрытые переменные ПЛС), используемых в модели. Если спектральные данные или эталонные значения перед разработкой калибровочной модели отцентрированы относительно среднего значения (см. раздел 11), то d=n-k-1, поскольку при вычислении усредненных значений одна степень свободы теряется. Стандартную ошибку калибровки иногда называют стандартной ошибкой регрессии (SEE).

Примечания

1 Если в регрессию МЛР или в регрессию вкладов РГК в сравнении с концентрациями или свойствами включается постоянный член, то d=n-k-1, поскольку одна степень свободы связана с константой. При использовании константы необходимо соблюдать осторожность. В случае, когда анализируются чистые образцы в кюветах фиксированной длины, объемные доли всех компонентов ограничиваются тем, что в сумме они должны быть равны единице. Включение константы при этих условиях может привести к созданию матриц, близких к вырожденным, и неустойчивых моделей.

2 Для упрощенных калибровок (см. 17.6) нет зависимости между величиной SEC, вычисленной для калибровки на базе простых гравиметрических смесей и ожидаемого уровня погрешности, когда модель используют для анализа фактических образцов. Рекомендуется такие стандартные ошибки обозначать с нижним индексом как .

Стандартная ошибка калибровки используется для оценки ожидаемого совпадения значений, рассчитанных с применением калибровочных моделей, и значений, которые измерялись бы стандартным методом (см. раздел 9). К интерпретированию SEC надо подходить с некоторой осторожностью, если использованные в значения не являются однократными измерениями рекомендованным методом. Если значения в для отдельных образцов представляют среднее значение многократных контрольных измерений, то величина SEC, рассчитанная по уравнению (56), определяется не на основе контрольного измерения. Например, если все значения в являются средними значениями трех контрольных измерений, то величину SEC, рассчитанную по уравнению (56), можно использовать только для определения ожидаемого совпадения оценки в ИК-спектре и среднего значения трех контрольных измерений.

Если для некоторых или всех калибровочных образцов используются многократные справочные значения, то можно вычислить величину SEC, определяемую на основе конкретных контрольных измерений. Если является спектром -го калибровочного образца, а , ... являются независимо измеренными справочными значениями для этого образца, то для вычисления векторов прогноза предпочтительно использовать уравнение (10) взвешенной регрессии для метода МЛР, уравнения (24) и (25) для метода РГК и уравнения (41) и (42) для метода ПЛС. Независимо от того, применяется или нет взвешенная регрессия, дисперсия, устраненная вычислением усредненных значений, должна вычисляться следующим образом:

, (57)

где первое суммирование проходит по всем калибровочным образцам от =1 до , второе суммирование проходит по эталонным значениям от =1 до для -го образца, а является средним значением эталонных величин для -го образца.

В этом случае стандартную ошибку калибровки вычисляют как

. (58)

Степени свободы для взвешенной регрессии, , равны общему количеству отдельных эталонных значений, измеренных для всех образцов, минус число переменных в модели

. (59)

Если до разработки калибровки спектральные и справочные данные отцентрированы относительно среднего значения, то

. (60)

Вычисленная таким образом SEC будет опираться на конкретные контрольные измерения.

Альтернативный вариант для выражения величины SEC в случае, когда используются многократные справочные значения для образца, выражается следующим образом:

. (61)

Примечание - В уравнении (58) вектор представляет разницу между расчетным значением и справочным значением, когда справочное значение может быть средним среди более чем одного контрольного измерения. Обозначение матрицы подразумевает сумму взвешенных квадратов разности, где квадрат разности взвешивается количеством эталонных значений, включенных в среднее. Кроме того, квадрат разности между расчетным значением и каждым конкретным эталонным значением может быть вычислен и просуммирован, как в уравнении (61), и тогда член дисперсии равен нулю, поскольку средние эталонные значения в вычислении не используются.

Стандартная ошибка калибровки (SEC) является стандартным отклонением для разницы между эталонными значениями и расчетными значениями в ИК-области для образцов, входящих в калибровочный набор. Это является доказательством суммарного остатка вследствие конкретного применимого уравнения регрессии. Величина SEC будет, как правило, уменьшаться, когда увеличивается число независимых переменных, используемых в модели, указывая на то, что увеличение числа членов позволит объяснить или "подогнать" более значительные изменения данных. Статистическая величина SEC является удобной оценкой теоретической "лучшей" точности, которую можно получить для конкретного набора переменных, используемых для разработки калибровочной модели.

15.3 Оптимизация числа переменных в модели

15.3.1 Определение того, как много переменных (длин волн в методе МЛР, основных компонентов или скрытых переменных в методе ПЛС) следует использовать в модели, имеет решающее значение в разработке модели. К сожалению, строго определенных правил для этого не существует. Как правило, если используют слишком мало переменных, то получаемая модель имеет меньшую точность. В случае использования слишком большого числа переменных оценки модели могут быть неустойчивыми, т.е. небольшие изменения уровня спектрального шума в спектре могут вызвать статистически значимые изменения оценки.

15.3.2 Максимальное число переменных, которое должно использоваться при разработке многомерной калибровочной модели , зависит от количества обнаруживаемых спектрально различимых компонентов (или набора функциональных возможностей) калибровочного набора. Компоненты (набор функциональных возможностей) спектрально различимы, если они вызывают поглощения, которые линейно не коррелируются среди калибровочных образцов, и если изменение в поглощениях среди калибровочных спектров больше спектрального шума. Если в пределах калибровочного набора концентрации компонентов линейно коррелируются, то поглощения из-за этих компонентов будут также линейно коррелироваться. Даже если эти компоненты обладают свойствами изолированного поглощения, они не будут спектрально различимыми для многомерной математики и внесут самое большее одну переменную в многомерную модель. Если концентрации компонентов почти коррелируются, так что поглощения из-за компонентов коллинеарны в пределах спектрального шума, то компоненты не являются спектрально различимыми. Если компоненты присутствуют на достаточно низких уровнях, так что поглощение компонента меньше спектрального шума, то компонент спектрально необнаружим и не может внести переменную в многомерную модель. Очевидно, что для сложных матриц количество обнаруживаемых, спектрально различимых компонентов (или функциональных возможностей) часто меньше, чем количество фактических компонентов. Существуют, однако, другие источники спектральных изменений, линейно некоррелированные с компонентами образца с определенными концентрациями, но работающие как спектрально различимый компонент. Некоторыми примерами других возможных источников спектральных изменений могут служить изменения рН, размера частиц, температуры образца, размещения образца, процедуры отбора образцов, химического взаимодействия между компонентами образца, спектральной нелинейности или сдвигов полос, напряжения источников питания прибора, температуры окружающего воздуха, времени суток, месяца, времени года или года. Следует отметить, что этот перечень не является исчерпывающим.

15.3.3 Один из методов оценки максимального количества обнаруживаемых, спектрально различимых компонентов в наборе калибровочных спектров требует знания уровня спектрального шума. Уровень спектрального шума можно определить по результатам повторных измерений, проведенных на единичном образце. Например, если для одного образца получают повторные спектры, то может быть выполнен анализ методом РГК. Поскольку все спектры представляют один и тот же материал, в спектральных данных должен присутствовать только один основной компонент. Можно вычислить дисперсию в процентном выражении из-за первого основного компонента (первое собственное значение, деленное на сумму всех собственных значений). Эту дисперсию в процентном выражении можно использовать для оценки точки отсечки при определении количества основных компонентов, которые должны быть включены в модель, а именно, сумма первых собственных значений, деленная на сумму всех собственных значений, должна быть того же порядка, что и отсечка. Подобные вычисления можно выполнить, используя метод ПЛС. При использовании метода МЛР проверки коллинеарности поглощения на выбранных длинах волн обычно проводятся как часть процедуры выбора длины волны. Например, если модель создается с использованием длин волн, для которых сигналы линейно независимы, то можно проверить линейную зависимость всех длин волн, выбранных для включения в модель, на основании длин волн. Если сигналы всех возможных длин волн можно подогнать как линейную комбинацию уже отобранных длин волн в пределах уровня спектрального шума, то , как правило, представляет собой максимальное число линейно независимых длин волн, на базе которого строилась бы оптимальная модель.

15.3.4 Модели могут быть построены с использованием числа переменных, отличного от , при условии, что такие модели имеют адекватную сходимость результатов и проходят процедуру валидации.

15.3.5 Знание сходимости стандартного метода необходимо также при определении требуемого числа переменных для включения в многомерную модель. Как упоминалось ранее, согласованность между расчетными значениями в ИК-области спектра никогда не может превышать повторяемость стандартного метода, так как даже если бы расчетное значение было истинным значением, измерение согласованности было бы ограничено повторяемостью стандартного метода. Сопоставление стандартной ошибки калибровки (вычисленной на базе отдельного контрольного измерения) со стандартным отклонением, вычисленным из повторяемости стандартного метода, дает представление о максимальном числе переменных для включения в модель. Стандартные ошибки калибровки, которые меньше стандартного отклонения для стандартного метода, свидетельствуют о чрезмерно близкой подгонке данных.

15.3.6 Для оценки оптимального числа переменных, которые нужно включить в модель, используют также процедуры перекрестной проверки на достоверность. При перекрестной проверке на достоверность удаляют из матрицы данных один или несколько спектров, соответствующие им справочные значения удаляют из вектора справочных значений, и на оставшихся образцах строят модель. Затем эту модель используют для оценки значения для оставшихся образцов. Этот процесс повторяют до тех пор, пока каждый образец не останется один раз невключенным. Ошибку кросс-валидации вычисляют по формуле

, (62)

где - вектор, содержащий оценки кросс-валидации.

Сумму квадратов ошибки предсказания PRESS вычисляют по формуле

. (63)

Стандартную ошибку кросс-валидации SECV вычисляют по формуле

. (64)

Значения PRESS или SECV могут вычисляться как функции числа переменных, используемых в модели. Процедура обычно начинается с использования одной переменной, в то время как одиночный образец в калибровочный набор не включается. После разработки калибровки с использованием остающихся образцов алгоритм предсказывает исключенный образец и регистрирует разницу между справочным и расчетным значениями. Эта процедура итерируется (повторяется) для всего набора образцов, и регистрируется значение PRESS (или SECV) для модели одной переменной. Затем добавляется еще одна переменная, и процесс повторяется. Процедуру PRESS останавливают, когда достигается заранее установленное число факторов (например, от 10 до максимум 20). Калибровочная модель с наименьшими значениями PRESS (SECV) может быть выбрана как оптимальная для используемого калибровочного набора. Если более одной модели имеют близкие значения PRESS, как правило, выбирают модель с меньшим числом переменных.

Часто для определения минимального значения PRESS, соответствующего оптимальному числу переменных в калибровочной модели, применяют график зависимости значений PRESS (SECV) (ось ) от числа переменных (ось ). Минимум в этой функции может быть взят как индикация максимального числа используемых переменных. Если минимума не наблюдается, то первая точка, при которой значение PRESS или SECV достигает более или менее устойчивого уровня, может быть индикатором для включения максимального числа переменных. Сопоставление значений SECV со стандартным отклонением для повторяемости стандартного метода вновь оказывается целесообразным, поскольку значения SECV являются значительно меньше стандартного отклонения, предполагающего чрезмерно близкую подгонку данных.

Для определения значений PRESS и SECV может потребоваться большой объем вычислений и продолжительная работа ЭВМ.

Примечание - Точность вычисленных значений PRESS и SECV зависит от того, как много образцов не включаются в процедуру во время каждого цикла перекрестной проверки на достоверность. Если во время проверки на достоверность не включают более одного образца, то значения PRESS и SECV будут зависеть от комбинации пропущенных образцов. Программы перекрестной проверки на достоверность, которые не включают несколько спектров во время каждого цикла, требуют менее продолжительной работы ЭВМ, чем те, в которых единовременно пропускается один спектр. Однако результаты таких работ в меньшей степени сравнимы и воспроизводимы, чем те, в которых пропускают один спектр единовременно.

15.3.7 Вышеупомянутые методы оценивания числа переменных для использования в модели следует рассматривать только как рекомендации. Ни на один из этих методов нельзя полагаться в том смысле, что всегда будет создаваться устойчивая модель. Окончательная проверка числа параметров заключается в том, чтобы определить, можно ли провести проверку так, как описано ниже. В конечном итоге должно быть выбрано число используемых в модели переменных, позволяющих создать модель требуемой точности, и провести ее проверку на достоверность.

15.4 Границы доверительного интервала для расчетного значения

Границы доверительного интервала для значения, рассчитанного с помощью многомерной модели, определяют следующим образом

, (65)

где - значение критерия Стьюдента для числа степеней свободы в модели;

- коэффициент влияния, определяемый по 16.2.

Если значения выбирают из таблицы А.4 (приложение А) для уровня вероятности 95%, то для проверенной модели предполагается, что отдельное значение попадет в пределы диапазона от до для 95% проанализированных образцов при условии, что анализ будет представлять собой интерполяцию модели. Границы доверительного интервала для расчетного значения в уравнении (65) иногда называют доверительными полосами или доверительными интервалами оценки.

Использование уравнения (65) для оценки границ доверительного интервала является только приближением, поскольку оно игнорирует любую неопределенность спектральных данных . Границы доверительного интервала в уравнении (65) получают из предположения, что ошибки в пренебрежимо малы по сравнению с ошибками в и что спектр может быть полностью описан использованными в модели переменными. Если ошибки в спектральных данных не являются пренебрежимо малыми или если спектр содержит поглощения из-за компонентов, которых не было в калибровочном наборе, то границами доверительного интервала в уравнении (65) занижается потенциальная ошибка оценки. Предполагается, что уравнение (65) дает приемлемое приближение для границ доверительного интервала по расчетному значению для образцов, которые являются интерполяциями модели (см. 16.4).

15.5 Дополнительная статистика для оценки математических моделей

Для оценки калибровочных моделей используют разнообразные статистические испытания. Некоторые широко используемые испытания включают в себя:

- коэффициент множественной детерминации;

- коэффициент корреляции;

- критерий Фишера (F для регрессии);

- частный критерий F или для коэффициента регрессии;

- стандартная ошибка калибровки (стандартная ошибка регрессии);

- стандартная ошибка с учетом систематической погрешности.

Хотя многие из этих критериев чаще применялись к моделям МЛР, некоторые из них в равной мере применимы к моделям РГК и ПЛС. Подробная информация по этим тестам и относящимся к ним терминам дается в приложении Б.

16 Статистика выбросов

16.1 Общие положения

Во время калибровки применяют статистику выбросов для идентификации образцов, имеющих необычно высокое влияние на многомерную регрессию. При проведении анализа к статистике выбросов прибегают, чтобы обнаружить образцы, которые представляют экстраполяцию модели.

16.2 Коэффициент влияния

Коэффициент влияния является скалярной мерой того, лежит ли спектральный вектор в пределах многомерного параметрического пространства, используемого в модели. Коэффициент влияния используется для обнаружения выбросов во время калибровки, для обнаружения экстраполяции модели во время проведения анализов и при оценке неопределенности расчетного значения.

Примечание - В серийно выпускаемых пакетах программного обеспечения используются многочисленные вариации коэффициента влияния. Коэффициент влияния иногда называют матрицей проекции на пространство регрессоров, или расстоянием Махаланобиса, (хотя фактически это квадрат расстояния). В различных серийно выпускаемых пакетах программного обеспечения может использоваться вместо . Отдельные пакеты программного обеспечения могут выполнять масштабирование (или ) по (или , если отцентрировано к среднему значению) для получения статистики, независимой от количества калибровочных образцов. Если эту масштабированную статистику затем умножают на , то получают статистику с распределением F. Здесь предпочтительно использовать коэффициент влияния , поскольку он легче увязывается с числом образцов и переменных. Разработчики модели должны постараться точно проверить, что именно вычисляется. Для существуют определения, отцентрированные и не отцентрированные к среднему значению, при этом предпочтение отдается подходу с центрированием к среднему значению. Независимо от того, выполняется ли центрирование данных к среднему значению, статистику с обозначением можно эффективно использовать для обнаружения выбросов.

Если - спектральный вектор (размерности на 1), а - матрица калибровочного спектра (размерности на ), то коэффициент влияния определяется как

. (66)

Для калибровки с центрированием относительно среднего значения и в уравнении (66) заменяют на и соответственно.

Если используется взвешенная регрессия, выражение для коэффициента влияния приобретает вид

. (67)

В методе МЛР, если - вектор (размерности на 1) отобранных значений, полученных из спектрального вектора , а - матрица отобранных значений для калибровочных образцов, то коэффициент влияния определяется как

. (68)

Аналогичным образом, если используется взвешенная регрессия, выражение для коэффициента влияния приобретает вид

. (69)

В методах РГК и ПЛС коэффициент влияния для образца со спектром получают путем переноса разложений для метода РГК или для метода ПЛС в уравнении (66). Коэффициент влияния выражается как

. (70)

Примечание - Если вклады из модели РГК или ПЛС не нормализованы, то уравнение (70) приобретает вид .

Если используется взвешенная регрессия метода РГК или ПЛС, то выражение для коэффициента влияния приобретает вид

. (71)

16.3 Обнаружение статистических выбросов во время калибровки

Во время выполнения процедур калибровки можно установить два типа статистических выбросов. Первый тип выброса является образцом, который представляет предельный состав относительно остальной части калибровочного набора. Эти образцы имеют очень высокий коэффициент влияния на результаты регрессии, т.е. ими в значительной степени обусловлено определение, по крайней мере, одного из значений коэффициента регрессии. В целом нет достаточного количества данных в калибровочном наборе, позволяющих определить статистическим путем точность эталонных значений, связанных с этими образцами с высоким коэффициентом влияния. Включение их в калибровку может привести к ошибочной оценке похожих образцов, если ошибочно эталонное значение для образца с высоким коэффициентом влияния. Для второго типа выброса расчетное значение отличается от эталонного на статистически значительную величину. Такие выбросы указывают на ошибку в контрольном измерении, ошибку в спектральном измерении, опечатку в идентификации образца или транскрибировании эталонного значения или на отказ модели.

Идентификация образцов с высоким влиянием производится на основе коэффициента влияния (известного также как расстояние Махаланобиса). Для всех описанных выше типов линейной калибровки средний коэффициент влияния для спектров калибровки образца имеет значение , где - число переменных в регрессии (количество длин волн для МЛР, количество основных компонентов или число скрытых переменных для ПЛС), а - количество калибровочных образцов. В среднем каждый образец вносит спектральных переменных. Для образцов с спектр образца вносит значительную часть в определение одной из спектральных переменных и в коэффициент регрессии, связанный с этой переменной. Образцы с следует тщательно проверить и изучить на предмет исключения из калибровочного набора при разработке модели. Часто такие образцы с высоким влиянием будут неоправданно преобладать при определении коэффициентов регрессии в ущерб эксплуатационным характеристикам модели. Однако в некоторых случаях образец с высоким влиянием может дать дополнительную информацию, которая позволит улучшить эксплуатационные характеристики модели, особенно когда отношение сигнал-шум спектра пропорционально уровню влияния образцов. Коэффициент влияния является ценным индикатором образцов, которые могут отрицательно влиять на калибровку. Тем не менее лучшим критерием в принятии решения об исключении образца будет то, насколько хорошо может быть проведена проверка последующей калибровки на достоверность.

Если из калибровочного набора исключаются калибровочные спектры с и модель строится заново, то нередко для новой модели устанавливаются дополнительные спектры с . Это вероятнее всего происходит, если при исключении образцов снижается величина , но причиной могут быть и просто изменения в масштабировании многомерного пространства, вызванные изменениями величины . Говорят, что в случае периодически повторяющего применения правила для идентификации статистических выбросов испытание на выбросы "растет как снежный ком". Если такой быстрый рост происходит, это может говорить о некоторой проблеме со структурой набора спектральных данных. Следует изучить пространство переменных на предмет необычных распределений или группировок.

Испытание на выбросы можно сделать менее строгим, если во время разработки модели наблюдается указанная ниже последовательность:

a) первая модель строится на базе набора для первоначальной калибровки;

b) калибровочные спектры с исключаются из калибровочного набора;

c) с использованием того же числа переменных строится вторая модель на поднаборе калибровочных спектров;

d) для второй модели идентифицируются калибровочные спектры с .

Вторую модель следует использовать при условии, что ни один из калибровочных образцов не имеет более 0,5.

Если первая модель строится на базе набора для первоначальной калибровки, калибровочные спектры с исключают из калибровочного набора, а вторая модель с меньшим числом переменных строится на базе поднабора калибровочных спектров, то не следует автоматически делать испытание на выбросы менее строгим. Вместо этого следует перестроить первую модель с использованием меньшего числа переменных и применить указанную ранее последовательность действий к новой модели.

Для второго типа статистического выброса расчетное значение отличается на статистически значимую величину от значения из стандартного метода . Такие выбросы можно обнаружить на основании стьюдентизированных остатков. Если - разница между расчетным значением и эталонным значением для -го образца в калибровочном наборе, а - коэффициент влияния для этого образца, то стьюдентизированные остатки для -го образца вычисляются следующим образом:

. (72)

Стьюдентизированные остатки должны быть нормально распределены с общей дисперсией. Значение стьюдентизированных остатков можно сравнить со значением распределения для (или при центрировании относительно среднего значения) степеней свободы с целью определения вероятности, что ошибка в оценке соответствует ожидаемому распределению. В противном случае образец следует считать выбросом.

Если на основании стьюдентизированных остатков или с помощью других подобных испытаний образец идентифицируется как выброс, то ошибочным может быть эталонное значение. Когда это возможно, стандартное испытание следует повторить, с тем чтобы определить точное значение для образца (рекомендуются многократные испытания). Если в эталонном значении ошибки нет, то большие стьюдентизированные остатки могут указывать на ошибку в спектральном измерении, опечатку в идентификации образца или на серьезный отказ модели. При оценке концентраций компонента соответствующие спектральные помехи могут помешать точной оценке компонента для образцов данного типа. При оценке свойства определенный компонент, оказывающий существенное влияние на свойство, не может быть обнаружен. По возможности следует избегать исключения выбросов этого типа при отсутствии в эталонном значении признака ошибки, поскольку эти образцы могут лишь указывать на то, что данная модель не применима для определенного класса материалов.

16.4 Интерполяция и экстраполяция модели во время анализа

Спектры калибровочных образцов определяют набор переменных, используемых при калибровке многомерной модели. В том случае, когда анализируются неизвестные образцы, переменные, вычисленные из спектра неизвестного образца, находятся в диапазоне переменных для калибровки, а расчетное значение для неизвестного образца получается путем интерполяции модели. Если переменные для неизвестного образца находятся за пределами диапазона переменных в калибровочной модели, то оценка представляет экстраполяцию модели.

Возможны два типа экстраполяции: образец может содержать те же компоненты, что и калибровочные образцы, но в пределах концентрации, которые находятся вне рамок для калибровочного образца, либо образец может содержать компоненты, которых не было в калибровочных образцах.

Коэффициент влияния обеспечивает полезную индикацию первого типа экстраполяции. Для калибровочного набора один образец будет иметь максимальный коэффициент влияния . Это самый крайний образец в калибровочном наборе, т.е. он наиболее удален от центра пространства, определенного спектральными переменными. Если коэффициент влияния больше, чем , то оценка образца четко показывает экстраполяцию модели. При условии, что во время калибровки выбросы были исключены, распределение должно быть репрезентативным для калибровочной модели, и величину можно использовать как индикацию экстраполяции.

Примечание - Можно провести сравнение спектральных переменных для неизвестного значения по диапазону каждой спектральной переменной в калибровочной модели, при этом экстраполяцию любой отдельной переменной можно считать экстраполяцией модели. Использование коэффициента влияния как индикатора экстраполяции может не позволить обнаружить некоторые спектры, которые представляют собой незначительные экстраполяции одной или нескольких спектральных переменных; однако значительная экстраполяция любой одной переменной даст в результате высокий коэффициент влияния и позволит тем самым обнаружить экстраполяцию. Не рекомендуется в испытаниях на экстраполяцию использовать отдельные переменные, поскольку это может неоправданно ограничить диапазон образцов, к которым модель применима.

Второй тип экстраполяции модели, а именно присутствие нового компонента, может быть обнаружен сравнением оценки неизвестного спектра, выведенного из модели, с измеренным спектром неизвестного компонента.

Для метода РГК оценка спектра неизвестного компонента может быть вычислена как

, (73)

где - вектор вкладов.

Точно так же для метода ПЛС

. (74)

Разность между расчетным спектром и фактическим спектром можно вычислить следующим образом:

. (75)

Среднеквадратические спектральные остатки RMSSR для спектра можно вычислить следующим образом:

. (76)

Примечание - Некоторые коммерчески доступные пакеты программного обеспечения позволяют вычислять другие статистические величины, связанные с RMSSR, или же обозначают RMSSR иначе. Разработчик модели должен проверить, какие статистические вычисления используются в программном обеспечении для определения того, насколько хорошо модель подходит для анализируемого спектра. Значение RMSSR является примером того, как можно выполнить такое вычисление, однако могут использоваться и другие подобные статистические величины.

Значения RMSSR можно вычислить для каждого калибровочного образца. Один из калибровочных образцов будет иметь максимальное значение RMSSR, обозначаемое как . При условии, что выбросы были устранены до разработки калибровочной модели, значение можно использовать для вычисления отсечки, выше которой значения RMSSR для неизвестных спектров следует считать доказательством экстраполяции модели.

Как правило, для установления отсечки с целью индикации экстраполяции использовать значение напрямую нельзя. Для моделей РГК и ПЛС некоторые из спектральных характеристик шума для калибровочных спектров всегда включаются в спектральные переменные. Значения RMSSR, вычисленные для используемых в калибровке спектров, будут, таким образом, как правило, ниже соответствующих значений, вычисленных для спектров тех же образцов, которые в разработке модели не используются. Для оценки подходящего значения отсечки RMSSR, которая служила бы индикацией экстраполяции, рекомендуется следующая процедура.

Следует выполнить повторные спектральные измерения (по меньшей мере, семь) на нескольких (по меньшей мере, трех) калибровочных образцах. Повторные измерения должны включать все этапы процедуры измерений (например, регистрацию фонового спектра, нагружение образца и измерение спектра).

При разработке калибровочной модели должен использоваться один спектр из набора. Вычисляют значения RMSSR для спектра, используемого при калибровке. () - значение для спектра образца .

С помощью калибровочной модели анализируют остальные повторные спектры и для каждого образца вычисляют и усредняют значения RMSSR. () - среднее значение RMSSR для повторного спектра образца .

Вычисляют и усредняют отношения значений RMSSR от анализов к значениям от калибровки, а для вычисления значения отсечки умножают на среднее значение отношения

, (77)

где - количество повторных спектральных измерений.

Если значение RMSSR для анализируемого неизвестного образца превышает значение , то анализ образца представляет экстраполяцию модели.

Для множественной линейной регрессии статистику, сравнимую с RMSSR, вычислить нельзя. Следовательно, метод МЛР не позволяет обнаружить экстраполяцию второго типа, а именно, присутствие нового компонента, которого не было в калибровочных образцах. Следует быть внимательным при применении метода МЛР в системах, где калибровочный набор, используемый при разработке модели МЛР, может не представлять всего диапазона составов образцов, которые можно встретить во время анализов. В этих случаях метод МЛР следует дополнить другими методами, позволяющими определить, оказывается ли анализируемый образец в диапазоне калибровки. Например, для этих целей можно использовать статистику выбросов от моделей РГК, разработанных на том же калибровочном наборе.

Примечание - Для моделей ПЛС вычисление остатков, таких как RMSSR, не всегда является подходящим индикатором выбросов. Если во время калибровки значительный процент спектральной дисперсии (Х-блок) из-за сигнала не используется в модели, то остатки модели для вычисления могут содержать существенные дополнения вследствие поглощения компонента в калибровочном образце. В таких случаях значения , вычисленные на основании таких значений , могут быть слишком большими, чтобы обнаружить экстраполяцию из-за новых химических компонентов в анализируемых образцах.

Процедуру, описанную в 15.3.3, можно использовать для оценки процента общей дисперсии Х-блока, вызываемой сигналом. Если включенная в модель дисперсия значительно меньше дисперсии сигнала, то разработчик модели может пожелать дополнить модель ПЛС моделью РГК, построенной на тех же самых данных. Тогда статистическое значение RMSSR по модели РГК используют для обнаружения выбросов. Число переменных, используемых в модели РГК, должно быть достаточным, чтобы учесть дисперсию сигнала.

Если спектры калибровочного образца создают множественные кластеры в пределах пространства переменной, спектр анализируемого неизвестного компонента может иметь величину меньше, чем , но тем не менее попадать на относительно свободную часть калибровочного спектра. В этом случае анализируемый образец содержит те же самые компоненты, что и калибровочные образцы (поскольку образец не является статистическим выбросом RMSSR), но с комбинациями, которые не представлены в калибровочном наборе. Спектр неизвестного компонента не принадлежит ни к каким кластерам спектров калибровочного образца, а результаты, получаемые от применения модели, могут быть недействительными или менее точными, чем результаты для образцов, которые обязательно оказываются в пределах этих кластеров. По этой причине желательно прибегнуть к испытанию на расстояние до ближайшего соседа, чтобы обнаружить неизвестные образцы, которые приходятся на незаполненные участки калибровочного пространства.

В методе ближайшего соседа измеряется расстояние РБС между анализируемым спектром и отдельными спектрами калибровочного набора .

. (78)*

________________

* Формула соответствует оригиналу. - .

Для метода МЛР значение РБС вычисляется как

. (79)*

________________

* Формула соответствует оригиналу. - .

Для методов РГК и ПЛС (с независимыми вкладами) значение РБС вычисляется как

. (80)*

________________

* Формула соответствует оригиналу. - .

Значения РБС вычисляются для всех спектров калибровочного образца. Определяется максимальное значение РБС. Это значение представляет собой наибольшее расстояние между спектрами калибровочного образца.

Во время анализа вычисляется значение РБС для спектра неизвестного образца относительно калибровочных спектров. Если вычисленное значение больше максимального значения РБС, то максимальное расстояние между спектром технологического образца и калибровочными спектрами больше самого большого расстояния между спектрами калибровочного образца, а спектр неизвестного образца оказывается в пределах редко заполненного участка калибровочного пространства. Такие образцы называются статистическими выбросами ближайшего соседа.

17 Выбор калибровочных образцов

17.1 Для разработки многомерной модели идеальный набор калибровочных образцов должен содержать:

a) образцы, являющиеся примерами всех химических компонентов, присутствие которых ожидается в образцах, подлежащих анализу с использованием этой модели, чтобы анализ включал интерполяцию модели;

b) образцы, для которых диапазон изменений концентраций химических компонентов превышает диапазон изменений, ожидающихся для подлежащих анализу образцов с использованием этой модели, чтобы анализ включал интерполяцию модели;

c) образцы, для которых концентрации химических компонентов равномерно распределены по всему диапазону их изменений;

d) достаточное количество образцов для статистического определения зависимостей между спектральными переменными и моделируемыми концентрациями компонента или свойствами.

Примечание - Если требуется усовершенствовать калибровочную модель для неизвестных образцов в пределах конкретного участка(-ов) калибровочного пространства, это можно сделать путем включения большего количества калибровочных образцов в участок(-ки) калибровочного пространства, где требуется такое усовершенствование. Вместо этого может оказаться целесообразнее разбить калибровочное пространство на подпространства и разработать для каждого подпространства отдельные калибровки.

17.2 Для простых смесей калибровочные образцы обычно можно приготовить так, чтобы они отвечали вышеуказанным критериям. Для сложных смесей получить идеальный калибровочный набор трудно, а то и вовсе невозможно. Статистические испытания, используемые для обнаружения выбросов, предотвращают возможность получения неидеальных калибровочных наборов. Значения RMSSR позволяют обнаружить, когда анализируемые образцы содержат компоненты, не представленные в калибровочном наборе (нарушение перечисления b). Коэффициент влияния позволяет обнаружить, когда в анализируемых образцах концентрации находятся за пределами, представленными в калибровочном наборе (нарушение перечисления с). Обнаружение выбросов при разработке модели дает возможность установить компоненты, для которых диапазон концентраций в калибровочном образце неравномерен (нарушение перечисления с).

17.3 Количество образцов, требующихся для калибровки многомерной модели в ИК-области спектра (см. перечисление d), зависит от сложности анализируемых образцов. Если подлежащие анализу образцы содержат всего несколько компонентов разной концентрации, то число спектральных переменных будет незначительным, и относительно небольшого калибровочного набора будет достаточно, чтобы определить зависимость между переменными и концентрациями или свойствами. Если же в анализируемых образцах наблюдаются расхождения у большего количества компонентов, то для разработки модели требуется большее количество калибровочных образцов. Установить соответствие набора калибровочных образцов можно только после разработки модели и оценки числа требуемых для модели спектральных переменных.

17.4 Если многомерная модель разработана с использованием трех или менее переменных, то после устранения статистических выбросов калибровочный набор должен содержать, как минимум, 24 образца.

17.5 Если многомерная модель разработана с использованием (>3) переменных, то после устранения статистических выбросов калибровочный набор должен содержать минимум 6 спектров. Если модель центрируется относительно среднего значения, то должны оставаться, как минимум, 6(+1) спектров.

Примечание - Число 6 выбирается, чтобы обеспечить, по меньшей мере, 20 степеней свободы в модели для статистических испытаний и гарантировать, что имеется достаточное количество образцов для определения зависимости между спектральными переменными и значениями концентрации или свойства.

17.6 Для некоторых видов спектроскопического анализа возможна калибровка с использованием весовых или объемных смесей, которые содержат значительно меньшее количество компонентов, чем образцы для окончательного анализа. Для этих упрощенных методов описанная здесь статистика выбросов непригодна, поскольку все фактические образцы по определению являются выбросами относительно упрощенных калибровок. Таким образом, упрощенные методы не могут точно отвечать требованиям настоящего стандарта. Упрощенные методы должны, однако, в целом соответствовать описанным здесь требованиям по количеству и диапазону калибровочных образцов. В случае высоколинейных систем, в которых для создания калибровочного пространства используется эмпирическое моделирование, упрощенные калибровки могут успешно разрабатываться с количеством образцов, меньшим обычно требуемых здесь 6. Надежное эмпирическое моделирование должно гарантировать, что все компоненты независимо варьируются в пределах требуемого диапазона. Упрощенные калибровки можно успешно использовать при условии, что они полностью прошли проверку на достоверность и надлежащим образом контролируются после применения. Однако, упрощенные методы могут потребовать более тщательной проверки на достоверность, а также более жесткого контроля по сравнению с полноценными методами.

18 Валидация многомерной модели

18.1 Общие положения

Валидация многомерной модели ИК-области спектра выполняется с использованием модели для анализа набора из проверочных образцов и путем статистического сравнения оценок для этих образцов с известными эталонными значениями. Валидация требует тщательных испытаний модели, чтобы гарантировать, что ее работа оправдывает ожидания, основанные на статистике калибровочного набора.

18.2 Набор проверочных образцов

Идеальный набор проверочных образцов для валидации многомерной модели должен содержать:

a) образцы, являющиеся примерами всех химических компонентов, которые предположительно должны присутствовать в образцах, подлежащих анализу с применением модели;

b) образцы, для которых диапазон изменений концентраций химических компонентов сравним с диапазоном изменений, ожидаемых для образцов, анализируемых с использованием модели;

c) образцы, для которых концентрации химических компонентов равномерно распределены по всему диапазону их изменений. При этом особое внимание следует уделять тому, чтобы гарантировать включение в проверочный набор образцов, которые хотя бы иногда могут быть в числе образцов, подлежащих анализу с применением модели;

d) достаточное количество образцов для статистического определения зависимостей между спектральными переменными и моделируемыми концентрациями компонента или свойствами.

Для простых смесей проверочные образцы обычно можно приготовить так, чтобы они отвечали данным критериям. Для сложных смесей получить идеальный проверочный набор трудно, а то и вовсе невозможно.

Количество образцов, необходимое для валидации многомерной модели в ИК-области спектра, зависит от сложности модели. В процедуре валидации следует использовать только образцы, анализ которых показал, что они являются интерполяциями модели. Если в модели используются пять или менее спектральных переменных, то рекомендуются, как минимум, 20 интерполяционных образцов. Если в модели используются >5 спектральных переменных, то при валидации количество используемых интерполяционных образцов должно быть, как минимум, 4. Кроме того, проверочные образцы должны:

- охватывать диапазон значений концентраций или свойств, на который была разработана модель, т.е. охват и стандартное отклонение в диапазоне значений концентраций или свойств для проверочных образцов должны составлять, по меньшей мере, 95% охвата и стандартного отклонения в диапазоне значений концентраций или свойств в модели, а значения концентраций или свойств для проверочных образцов должны быть, насколько это возможно, равномерно распределены по всему диапазону;

- охватывать диапазон спектральных переменных, для которого была разработана модель, т.е. если диапазон спектральной переменной в калибровочной модели распространяется от a до b, а стандартное отклонение спектральной переменной равно c, то спектральные переменные для проверочных образцов должны покрывать, по меньшей мере, 95% диапазона от a до b и должны быть, насколько это возможно, равномерно распределены по всему диапазону таким образом, чтобы стандартное отклонение спектральных переменных, рассчитанное для проверочных образцов, составляло бы не менее 95% от величины c.

Установление соответствия проверочного набора обычно требует проведения анализа набора для того, чтобы можно было определить для него спектральные переменные. Образцы, анализы которых являются экстраполяциями модели, включаться в проверочный набор не должны. Если проверочный набор не соответствует вышеперечисленным критериям, то должны быть взяты дополнительные проверочные образцы.

Где это целесообразно, рекомендуется готовить отдельный проверочный набор, включающий образцы с выбросами. Данный проверочный набор с выбросами можно использовать для проверки эффективности любого процесса выявления выбросов, который может быть частью калибровки, и для выявления типа и масштабов проблем, которые можно было бы ожидать, если бы оценку выброса (для которого калибровка не действительна по определению) нужно было непредвиденно провести путем калибровки.

18.3 Измерение и анализ спектров для валидации

Спектры проверочных образцов следует собирать, используя точно такие же процедуры, какие использовались для сбора спектров калибровочных образцов. Эталонные значения для проверочных образцов должны быть получены тем же стандартным методом, который применяли для калибровочных образцов. Спектры должны быть проанализированы с применением многомерной модели для оценки концентраций компонентов или свойств. Затем следует провести статистические вычисления, как описано в разделах 18 и 19.

18.4 Ошибка валидации

Если (вектор размерности на 1) - оценки, полученные путем анализа спектров проверочных образцов, и - соответствующие значения, измеренные стандартным методом, то ошибку валидации вычисляют по формуле

. (81)

Если для некоторых проверочных образцов известны многократные эталонные значения, то среднее значение отдельных контрольных измерений может быть использовано в , а дисперсия, исключенная путем вычисления средних значений, должна вычисляться с помощью уравнения (56).

18.5 Дисперсия ошибки валидации

Дисперсию ошибки проверочных измерений вычисляют по формуле

, (82)

где равно нулю, а - единичная матрица, если в используются отдельные контрольные измерения.

18.6 Стандартная ошибка валидации

Стандартную ошибку валидации вычисляют по формуле

, (83)

где - общее количество эталонных значений, имеющихся для всех проверочных образцов;

- стандартное отклонение разности между эталонными значениями и расчетными значениями в ИК-спектрах образцов из проверочного набора. Стандартную ошибку валидации иногда называют стандартной ошибкой предсказания или, что неверно, стандартной ошибкой регрессии SEE.

Испытания на стьюдентизированные остатки могут быть применимы к оценкам проверочного набора для обнаружения возможных ошибок в эталонных значениях.

18.7 Систематическая погрешность валидации

Среднюю погрешность для оценки проверочного набора, , вычисляют по формуле

, (84)

где =1, если были использованы отдельные эталонные значения, или же это число эталонных значений, которые были усреднены для -го проверочного образца, если используются средние значения;

- общее количество эталонных значений, используемых в вычислениях.

18.8 Стандартное отклонение ошибок валидации

Стандартное отклонение ошибок валидации вычисляют по формуле

. (85)

При этом =1 и =0, если при вычислении используются отдельные контрольные измерения.

18.9 Значимость систематической погрешности валидации

Для установления факта наличия статистически значимой систематической погрешности при оценке валидации прибегают к -критерию. Значение вычисляют по формуле

. (86)

Значение сравнивают с критическими значениями из таблицы А1.4 (Приложение А1) для степеней свободы.

Если значение меньше критического значения , то ожидается, что анализы на базе многомерной модели дадут практически тот же самый результат, что и измерения, произведенные с помощью стандартного метода при условии, что анализ представляет интерполяцию модели.

Если вычисленное значение больше табулированных значений , то вероятность того, что оценка по многомерной модели не даст тех же средних результатов, что и стандартный метод, составляет 95%. Тогда ставится под сомнение сама применимость многомерной модели. Для решения вопроса с выявленной возможной статистической погрешностью требуется провести более детальное изучение модели.

18.10 Валидация соответствия модели и стандартного метода

Следует вычислить границы доверительного интервала на оценках для проверочных образцов и определить, находятся ли отдельные эталонные значения для проверочных образцов в диапазоне от до . Если более 5% эталонных значений выходят за границы этого диапазона, то основанные на значении SEC оценки границ доверительного интервала являются спорными, и требуется продолжить испытания, чтобы доказать соответствие между моделью и стандартным методом.

Для доказательства соответствия между моделью и стандартным методом можно использовать и другой метод. Этот метод предпочтительней, когда сходимость результатов стандартного метода в пределах интервала эталонных значений, используемых при калибровке, не постоянна, но может быть применим даже в том случае, когда сходимость постоянна. Если - воспроизводимость стандартного метода на уровне , то вычисляют процент эталонных значений, для которых

. (87)

Если 95% эталонных значений или более находятся в пределах этого интервала, то оценки, полученные для многомерной модели в ИК-области спектра, согласуются с оценками, полученными стандартным методом, так же, как они согласовывались бы с оценками другой лаборатории, повторяющей контрольные измерения.

18.11 Использование упрощенных калибровок

Для многомерных анализов с использованием упрощенных калибровок часто применяют процедуру, подобную той, что описана в настоящем стандарте для валидации, с целью проверки правильности выполнения калибровки прибора. Эта процедура квалификации прибора обычно включает в себя анализ весовых или объемных смесей, которые содержат значительно меньшее количество компонентов, чем образцы для окончательного анализа. Нет априорной зависимости между стандартной ошибкой, вычисленной по этой процедуре, и ошибкой, ожидаемой при использовании модели применительно к реальным образцам. Во избежание недоразумений рекомендуется такую процедуру называть не валидацией, а квалификацией спектрометра/спектрофотометра. Кроме того, рекомендуется стандартную ошибку, получаемую по этой процедуре, называть стандартной ошибкой квалификации (), а не стандартной ошибкой валидации SEV.

19 Сходимость расчетных значений в ИК-области спектра

Сходимость значений, рассчитанных из многомерной модели в ИК-области спектра, вычисляется по результатам повторных спектральных измерений. Количество образцов, для которых производятся повторные измерения, должно быть равно, по крайней мере, числу переменных, используемых в модели, и никогда не должно быть меньше трех. Образцы, используемые для повторных спектральных измерений, должны охватывать, по меньшей мере, 95% диапазона значений концентраций или свойств, используемых в модели. Когда это возможно, образцы должны отбираться таким образом, чтобы обеспечивать некоторые вариации по каждой переменной. Для каждого образца должно быть собрано, по меньшей мере, шесть спектров. Следует проанализировать спектры и провести оценку значений. Следует вычислить среднюю оценку для каждого образца и получить стандартное отклонение среди оценок. Если - оценка для -го спектра из всех спектров для -го образца, то средняя оценка для этого образца будет равна

. (88)

Стандартное отклонение повторных оценок вычисляют по формуле

. (89)

Значение вычисляют с использованием значений стандартного отклонения, вычисленных по уравнению (86):

, (90)

где

, (91)

, (92)

, (93)

- количество образцов, для которых были выполнены повторные измерения.

Значение , вычисленное по уравнению (90), сравнивают с критическим значением из таблицы статистики (см. таблицу А.5, приложение А) для степеней свободы. Если вычисленное значение меньше критического значения, то все дисперсии для повторных измерений принадлежат к той же совокупности, и среднюю дисперсию, вычисленную по уравнению (92), можно использовать как показатель повторяемости измерения в ИК-области спектра. Ожидается, что анализ в ИК-области спектра имеет повторяемость порядка .

Если вычисленное значение больше критического значения хи-квадрат, то повторяемость оценки ИК-анализа может меняться в зависимости от состава образца. В этом случае ожидается, что ИК-анализ будет иметь повторяемость не хуже, чем , где - максимальное значение для повторных измерений.

20 Основные источники ошибки при калибровке и анализе

20.1 Основные источники ошибки в спектральных измерениях

В таблице 1 приведены некоторые возможные источники ошибки, которая может случиться во время спектральных измерений, и возможные пути решения таких проблем.

Таблица 1 - Основные источники ошибки в спектральных измерениях

20.2 Ошибки, связанные с отбором образцов

В таблице 2 перечислены ошибки, возникающие из-за проблем с отбором образцов, и возможные пути решения этих проблем.

Таблица 2 - Ошибки, связанные с отбором образцов

20.3 Источники ошибки в калибровке

В таблице 3 приведены источники ошибки в разработке калибровочной модели и возможные способы минимизации этих ошибок.

Таблица 3 - Источники ошибки в калибровке

20.4 Ошибки в анализе

В таблице 4 приведены факторы, которые могут обуславливать дополнительные ошибки в расчетных значениях для неизвестных образцов, и возможные способы минимизации таких ошибок.

Таблица 4 - Ошибки в анализе

21 Чувствительность многомерной модели по длине волны (частоте)

Важнейшим условием для исполнения многомерной калибровки часто является стабильность длины волны спектрометра. Оценка чувствительности многомерной модели к изменениям в шкале длин волн является важным параметром, по которому можно судить об эксплуатационных характеристиках прибора. Чувствительность модели по длине волны можно грубо оценить с помощью следующей процедуры:

- идентифицируют образцы в калибровочном наборе, которые представляют крайние значения каждой из спектральных переменных;

- если спектры собраны с цифровым разрешением , то каждый спектр смещают на и на ;

- используя калибровочную модель, анализируют смещенные спектры и вычисляют изменения в оценках между спектрами и ;

- идентифицируют спектр с наибольшим изменением при сдвиге. Если оценки равны и , соответственно, то чувствительность модели по длине волн (частоте) может быть подсчитана как

. (94)

Значение, вычисленное по уравнению (94), представляет собой сдвиг по длине волны, который в худшем случае (для наиболее чувствительного спектра) вызовет изменение в оценке порядка 5% стандартной ошибки калибровки.

Примечание - Чувствительность модели по длине волны, вычисленная в разделе 12, будет зависеть от разнообразных факторов, включая оптическое и цифровое разрешение прибора относительно ширины полосы измеряемого образца. Вычисление чувствительности по длине волны проводят для получения эффективного инструмента диагностики для анализов, выполняемых на анализаторе одного и того же типа. Стабильность анализатора по длине волны можно сравнить со значением в уравнении (88) как средством мониторинга работы анализатора. Поскольку значение в уравнении (88) зависит от специфических параметров прибора, его, как правило, не следует использовать для сравнения пригодности анализаторов для конкретного применения.

22 Перенос калибровки и нормирование прибора

Перенос калибровки относят к процессу, посредством которого с использованием данных одного или более спектрометров модель разрабатывают, по возможности модифицируют и применяют для анализа спектров, собранных на дополнительных спектрометрах. Перенос калибровки может потребовать сбора спектральных данных для общего образца или образцов на обоих приборах и разработки некоторой функции переноса с применением ее к спектрам или модели либо к оценке, полученной с помощью модели. Полное описание методик переноса калибровки выходит за рамки настоящего стандарта.

Нормирование прибора представляет собой процесс, в котором спектры, собранные на другом приборе, математически подгоняют, пытаясь сделать так, чтобы они совпадали со спектрами, собранными на приборе, на котором калибровка была разработана. Нормирование прибора может потребовать также фактической регулировки приборной части для того, чтобы добиться такого совпадения. Нормирование прибора - это одно из средств достижения переноса калибровок.

Перенос калибровки или нормирование прибора может потребоваться, когда было проведено техническое обслуживание прибора, если такое обслуживание вызывает изменение чувствительности, достаточно значительное, чтобы изменить значения, рассчитанные с помощью модели. Можно представить, что калибровка переносится от одного прибора (до технического обслуживания) к другому прибору (после технического обслуживания).

Когда разработана процедура переноса калибровки или нормирования прибора, необходимо показать, что работа модели во время переноса не ухудшилась. Для того чтобы доказать, что процедура переноса калибровки или нормирования прибора не нарушает работу модели, необходимо провести валидацию перенесенной модели, как это описано в разделе 18. Каждая процедура переноса калибровки или нормирования прибора должна быть испытана, по крайней мере, один раз путем выполнения полной валидации перенесенной модели. Как только будет продемонстрирована успешность конкретной процедуры переноса калибровки или нормирования прибора для конкретного типа прибора, то для оценки дополнительных процедур переноса и нормирования могут быть использованы образцы для контроля качества.

23 Контроль качества калибровки

Когда для оценки концентраций компонента или свойств, либо того и другого используется многомерный анализ в ИК-области спектра, желательно периодически испытывать процедуру проведения анализа (прибор и модель), чтобы гарантировать, что исполнение анализа не меняется. Для проведения таких испытаний иногда необходимо выбрать один или более образцов для контроля качества, которые будут использоваться для этих целей. Подробное рассмотрение методов, используемых для проверки работы анализатора в ИК-области спектра, находится вне рамок настоящего стандарта.

Для контроля качества анализа можно использовать контрольные образцы (материалы, для которых эталонные значения были измерены с помощью стандартного метода) при условии, что анализ контрольных образцов предусматривает интерполяцию модели. Расчетные значения по ИК-области спектра для контрольных образцов сравнивают с эталонными значениями, используя установленные процедуры или альтернативные методы статистических испытаний. Как правило, такие испытания требуют, чтобы расчетные значения по ИК-области спектра и эталонные значения согласовывались в пределах границ доверительных интервалов, определенных в 15.3. Поскольку границы доверительных интервалов основываются на величине SEC, и поскольку над величиной SEC зачастую преобладает ошибка в исходном измерении, эти процедуры могут не обеспечивать самой чувствительной индикации изменений в исполнении анализа. Вместо этого можно использовать образцы контроля качества.

Образцы для контроля качества зачастую используются для отслеживания изменений в исполнении анализа (прибора и модели), после того как была проведена проверка анализа. Материалы для контроля качества следует идентифицировать в то время, когда разрабатывается модель, по следующим критериям:

- материалы для контроля качества должны быть химически и физически совместимы с анализируемыми материалами таким образом, чтобы не вносить загрязнений в анализируемые образцы и не создавать проблем, связанных с безопасностью;

- материалы для контроля качества должны быть химически устойчивыми при хранении и отборе образцов. При использовании смесей должен быть известен состав смеси и должны быть установлены способы ее воспроизводства;

- спектры материала для контроля качества должны быть совместимы с моделью. Полосы поглощения для материала для контроля качества не должны превышать линейный диапазон прибора в областях, используемых в калибровочной модели. Спектры материала для контроля качества должны быть по возможности такими же, как спектры калибровочных образцов. Однако, анализ образца для контроля качества может быть экстраполяцией модели.

Спектральные данные по материалу для контроля качества собирают в течение такого же периода времени, как и период сбора спектров калибровочных и проверочных образцов. Обращаться с материалом для контроля качества следует точно так же, как и с другими образцами, так чтобы колебания в спектрах были репрезентативными по отношению к колебаниям, происходящим во время сбора спектров для неизвестных образцов. Для каждого измерения следует использовать отдельные образцы. Должно быть собрано не менее 20 спектров.

Примечание - Если спектры материала для контроля качества собирают в течение слишком короткого временного интервала, наблюдаемые в спектрах колебания будут меньше обычно встречающихся в случае применения модели к неизвестным, а набор пределов контроля качества на базе этих спектров будет чрезмерно ограниченным.

Спектры для материала для контроля качества анализируют с применением калибровочной модели, при этом вычисляют среднее значение :

, (95)

где - количество спектров, собранных для материала для контроля качества.

Стандартное отклонение для расчетных значений вычисляют по формуле

. (96)

Критерий Диксона может быть применен к отдельным расчетным значениям для идентификации выбросов в расчетах по уравнениям (95) и (96).

Материал для контроля качества анализируется периодически, когда анализом (прибором и моделью) пользуются для анализа неизвестных. С материалом для контроля качества обращаются точно так же, как и с анализируемым неизвестным образцом. Расчетное значение для материала для контроля качества сравнивают с . Ожидается, что расчетное значение будет в пределах от до в течение 95% времени, где - значение критерия Стьюдента для -1 степеней свободы и 95% доверительного интервала.

Если анализ материала для контроля качества является интерполяцией модели, то величина должна соответствовать повторяемости ИК-анализа, как определено в разделе 19. Если анализ материала для контроля качества является экстраполяцией, то величина может быть несколько выше, чем величина , вычисленная в разделе 19. Однако, поскольку контрольные границы все еще основываются на повторяемости спектрального измерения и не зависят от стандартного метода, то ожидается, что они, как правило, будут строже тех, что получаются от контрольных образцов.

Использование поправок на систематическую погрешность и уклон для улучшения статистики калибровки и прогноза для многомерных ИК-моделей целесообразно при условии, что калибровка проходит полную повторную проверку сразу после внесения поправок на систематическую погрешность и уклон. Поправки на систематическую погрешность и уклон являются еще одной формой переноса калибровки, и с ними нужно обращаться так же, как с любым другим переносом калибровки. Ошибки прогноза, требующие продолжения внесения поправок на систематическую погрешность и уклон, указывают на отклонение от стандартного метода или на изменения в характере образцов, обращении с образцами, подаче образца, функции отклика прибора или стабильности длины волны. Если на этапе мониторинга контроля качества калибровочная модель нарушается, следует оценить работу прибора, проводя соответствующие испытания для определения эксплуатационных характеристик прибора, и нужно решить любую обнаруженную проблему с прибором. Если используются контрольные образцы, с помощью стандартного метода следует выполнить проверки, чтобы гарантировать правильность эталонных значений. В случае проведения технического обслуживания прибора для восстановления калибровки следует придерживаться переноса калибровки или калибровки прибора, либо того и другого вместе.

24 Усовершенствование модели

Иногда в действующую модель желательно добавить дополнительные калибровочные образцы, чтобы расширить область применимости модели. Новые калибровочные образцы могут содержать те же компоненты, что и исходные калибровочные образцы, но с большими предельными концентрациями или с новыми компонентами, отсутствующими в исходных калибровочных образцах. Новые калибровочные образцы могут заполнять пустоты в исходном калибровочном пространстве.

При усовершенствовании модели матрица , содержащая исходные калибровочные спектры, пополняется спектрами дополнительных калибровочных образцов, а вектор , содержащий значения свойства или состава для калибровочных образцов, пополняется значениями для дополнительных калибровочных образцов.

Процедуры по выбросам, описанные в 16.3, должны применяться к усовершенствованным моделям таким же образом, как они применяются к новым моделям. Следовательно, если для расширения диапазона калибровки добавляют дополнительные модели, может оказаться необходимым добавить несколько образцов каждого нового типа для того, чтобы избежать исключения дополнительных образцов как выбросов.

Когда калибровочная модель усовершенствуется, она должна заново пройти процедуру валидации. Требования по проверочным образцам для усовершенствованной модели такие же, как и для исходной модели (см. раздел 18). Спектры, использованные для валидации исходной модели, можно применять и для валидации усовершенствованной модели, но они должны быть дополнены для охвата соответствующего диапазона, как описано в 18.2. Процент новых образцов, добавленных к проверочному набору для усовершенствованной модели, должен быть, по крайней мере, таким же большим, как и процент новых образцов, добавленных в калибровочный набор.

25 Опросный лист по многомерной калибровке

Следующий опросный лист составлен в помощь пользователю для установления соответствия многомерной калибровки требованиям, изложенным в настоящем стандарте.

Если на все следующие вопросы в перечислениях a-e получены ответы в утвердительной форме, то можно сказать, что калибровка разработана и ее валидация проведена в соответствии с требованиями настоящего стандарта.

Если на любой из следующих вопросов в перечислениях a-e получены отрицательные ответы, то нельзя сказать, что калибровка разработана и ее валидация проведена в соответствии с требованиями настоящего стандарта. В случае применения для калибровки методов МЛР, РГК или ПЛС-1 можно сказать, что калибровка произведена с использованием математических методов, описанных в настоящем стандарте.

a) следующие вопросы относятся к математической методике, используемой при калибровке:

1) использовался ли при калибровке математический метод МЛР, РГК или ПЛС-1 (см. разделы 12 и 13)?

2) включала ли методика калибровки возможность обнаружения выбросов с высоким влиянием с использованием такой величины как коэффициент влияния (см. 16.2)?

3) включала ли методика проведения анализа возможность обнаружения выбросов с помощью такой статистики, как статистика, базирующаяся на спектральных остатках (см. 16.4)?

b) следующие вопросы относятся к калибровочной модели, где - количество образцов в калибровочном наборе, а - число переменных в модели (длины волн в МЛР, главные компоненты или латентные структуры в ПЛС).

1) было ли , если модель не отцентрирована относительно среднего значения, или , если модель отцентрирована относительно среднего значения (см. 17.5)?

2) равнялось ли количество образцов в калибровочном наборе, по меньшей мере, 24 (см. 17.4)?

c) следующие вопросы относятся к валидации модели:

1) использовался ли отдельный набор проверочных образцов для проверки калибровки (см. 18.2)?

2) исключались ли из набора проверочных образцов проверочные спектры, которые были выбросами на основе их влияния (расстояния Махаланобиса) или спектральных остатков (см. 18.2)?

3) превышало ли количество проверочных образцов 4, если модель не была отцентрирована относительно среднего значения, или 4(+1), если модель была отцентрирована относительно среднего значения (см. 18.2)?

4) равнялось ли количество проверочных образцов, по меньшей мере, 20 (см. 18.2)?

5) охватывали ли проверочные образцы 95% диапазона калибровочных образцов (см. 18.2)?

6) если SEC является стандартной ошибкой калибровки, приходятся ли 95% результатов для проверочных образцов на эталонных значений, где - это стьюдентизированное значение для степеней свободы ( для моделей, отцентрированных относительно среднего значения), а - коэффициент влияния (см. 18.10)?

7) показывают ли результаты валидации статистически незначимую погрешность (см. 18.9)?

d) определялась ли точность модели с использованием контрольных образцов и повторных измерений на образец (см. раздел 19)?

e) если методика калибровки и анализа включает предварительную и последующую обработку, выполняются ли эти расчеты автоматически (см. разделы 11 и 14)?

Приложение А1
(обязательное)

Статистическая обработка

А1.1 Функции критерия Диксона для исключения выбросов

Это испытание является простым и весьма эффективным методом определения того, происходят ли все полученные данные из одной и той же совокупности (с неизвестным средним значением и стандартным отклонением) и вызывает ли сомнение одна или более измерительных точек, которые следует исключить.

При использовании данного метода испытаний значения N определений сводят в таблицу в порядке возрастания величины и обозначают как , , , ... .

Значения в крайних точках табличных данных и проверяют по очереди в соответствии с числом значений в таблице.

Выбирают необходимое выражение (таблица А1.1) в соответствии с количеством определений (N) и тем, верхний или нижний предел необходимо определить.

Таблица А1.1 - Формулы для определения выбросов для различных значений количества определений

Заменяя соответствующие значения в выбранном уравнении, вычисляют значение и сравнивают его со значением в таблице А1.2 для соответствующего количества определений (N).

Исключают значение, если вычисленное значение больше, чем табличное значение.

Таблица А1.2 - Критические значения для исключения несогласованного измерения

Среднестатистическое стандартное отклонение, как показано на рисунке А1.1, означает стандартное отклонение метода испытаний. Оно устанавливается путем усреднения стандартных отклонений большого числа образцов, испытанных большим числом лабораторий. Образцы должны охватывать диапазон пригодности метода испытаний и включать материалы разного состава, если последний оказывает какое-либо влияние на воспроизводимость результатов.

Стандартное отклонение образца - это стандартное отклонение, вычисленное из данных, которые были получены группой лабораторий, проводивших испытания одного и того же образца одним методом. Понятно, что оно может быть значительно ниже или значительно выше, чем традиционное стандартное отклонение метода испытаний. Поэтому стандартное отклонение образца может быть менее достоверным (из-за этих случайных колебаний), чем среднестатистическое стандартное отклонение при определении пределов доверительного интервала среднего значения результатов нескольких определений.

Рисунок А1.1 - Номограмма числа определений для получения нужных пределов доверительных интервалов

Если среднестатистическое стандартное отклонение неизвестно, его можно заменить стандартным отклонением образца, используя номограмму и умножая затем значение, определенное по шкале доверительного интервала 95%, на приведенный в таблице А1.3 коэффициент для числа результатов в среднем для получения надежных пределов доверительного интервала 95%.

Таблица А1.3 - Значения коэффициента в зависимости от числа результатов

Для нахождения числа необходимых определений в среднем для выдачи конкретных пределов доверительного интервала кладут поверочную линейку поперек номограммы таким образом, чтобы ее край проходил через точку на правой шкале, соответствующую стандартному отклонению для испытания и через нужную точку на шкале пределов доверительного интервала. Считывают число требуемых определений из левой шкалы.

Для нахождения пределов доверительного интервала для среднего значения, используя число определений в среднем, кладут поверочную линейку от этой точки на левой шкале через точку на правой шкале, соответствующую стандартному отклонению. Считывают пределы доверительного интервала с промежуточной шкалы.

Значения коэффициентов в зависимости от степени свободы приведены в таблицах А1.4-А1.6.

Таблица А1.4 - F-распределение: степени свободы числителя

Таблица А1.5 - Значения при уровне вероятности 5%

Таблица А1.6 - Критические значения для (t-1) степеней свободы и доверительного уровня 95%

Приложение А2
(обязательное)

Статистические испытания, общие для методов спектроскопии в ближней ИК-области спектра

А2.1 Общие символы

На всем протяжении настоящего стандарта для обозначения скалярных величин используют строчные буквы. Для обозначения векторов используют строчные буквы, набранные полужирным шрифтом, а для обозначения матриц - прописные буквы, набранные полужирным шрифтом. Курсивные буквы используют для обозначения размерности векторов и матриц. Например:

- Скалярное эталонное значение для -го образца.

- Расчетное значение у для -го образца на основе регрессионной модели.

- Среднее значение для всех образцов.

- Вектор эталонных значений для образцов.

- Спектральный вектор длины для -го образца.

- Матрица спектров, строк матрицы содержат спектры длины для образцов.

- Количество образцов, используемых в калибровочной модели.

- Количество частот или длин волн, используемых в калибровочной модели.

- Число переменных, используемых в калибровочной модели.

- Количество повторных измерений на образце.

- Сигма прописная обозначает суммирование всех значений в скобках.

- Коэффициент множественной детерминации (-квадрат).

- Коэффициент простой корреляции для линейной регрессии для любого набора измерительных точек; он равняется корню квадратному значения -квадрат

- Систематическая погрешность или значение отрезка на оси для любой калибровочной функции, соответствующей данным по , . При вычислениях стандартной ошибки с поправкой на систематическую погрешность последняя равна разности между средними эталонными аналитическими значениями и прогнозными значениями в ИК-области.

А2.2 Статистические термины

Сумма квадратов для регрессии:

. (А2.1)

Сумма квадратов для остатка:

. (А2.2)

Средний квадрат для регрессии:

. (А2.3)

Средний квадрат для остатка:

. (А2.4)

Общая сумма квадратов:

. (А2.5)

А2.3 Критериальная статистика

А2.3.1 Общие положения

Статистика, которая рассмотрена ниже, чаще всего применялась к моделям МЛР. Эта статистика предполагает, что при разработке модели данные были отцентрированы относительно среднего значения. Подобную статистику можно вывести для моделей РГК и ПЛС, а также для моделей, которые не отцентрированы относительно среднего значения.

А2.3.2 Коэффициент множественной детерминации

Коэффициент множественной детерминации называют также статистикой -квадрат или общим объяснимым изменением. Эта статистика позволяет определять величину изменения данных, которая соответствующим образом моделируется с помощью калибровочного уравнения как общая доля от 1,0. Таким образом, величина =1,00 указывает на то, что калибровочное уравнение моделирует 100% изменение в пределах данных. Величина =0,50 показывает, что 50% изменений в расхождениях между фактическими значениями для измерительных точек и прогнозными или расчетными значениями для этих точек объясняют калибровочным уравнением (математической моделью), а 50% изменений необъяснимы. При разработке калибровок пробуют среднеквадратические значения, приближающиеся к 1,0. Значения -квадрат можно оценить, используя простой метод, описанный в общих чертах ниже.

Величину определяют по уравнению

. (А2.6)

Если - стандартное отклонение погрешностей при измерении стандартным методом, а - стандартное отклонение эталонных значений, использованных при калибровке (мера диапазона, охватываемого справочными данными), то значения , превышающие 1 - , скорее всего, указывают на чрезмерно близкую подгонку данных.

А2.3.3 Статистика критерия Фишера для регрессии

Эту статистику называют также -статистикой для регрессии или критерий t-квадрат. Значение критерия увеличивается по мере того, как уравнение начинает моделировать или подгонять большее количество изменений данных. Когда -квадрат сохраняется постоянным, значение критерия увеличивается с увеличением количества образцов. При уменьшении количества длин волн, используемых в уравнении регрессии, значение критерия стремится к увеличению. Исключение маловажной длины волны из уравнения вызовет увеличение значения критерия для регрессии.

Статистика критерия Фишера может находить применение также в распознавании подозрительных выбросов в наборе калибровочных образцов; если при исключении образца значение критерия уменьшается, образец не являлся выбросом. Эта ситуация является результатом того, что образец не влияет на полное соответствие калибровочной линии данным, хотя в то же время уменьшает количество образцов (). И наоборот, если исключение единичного образца увеличивает общее значение критерия для регрессии, образец считается подозрительным выбросом. Значение критерия определяется как средний квадрат для регрессии, деленный на средний квадрат для остатка (см. статистические термины в таблице А1.2, приложение А1).

Значение критерия для регрессии определяется по уравнению:

. (А2.7)

А2.3.4 Значение критерия Стьюдента (для регрессии)

Эта статистика эквивалентна -статистике при определении корреляции между и данными . Ее можно использовать для установления истинной корреляции между расчетным значением в ИК-области и первичным химическим анализом для образца. Ее применяют для проверки предположения, что корреляция действительно существует, и она только случайно не возникла. Большое значение (обычно более десяти) указывает на действительную (статистически значимую) корреляцию между и .

Значение для регрессии вычисляют по формуле

. (А2.8)

А2.3.5 Частный критерий Фишера или критерий -квадрат для коэффициента регрессии

Данный критерий показывает, способствует ли добавление конкретной длины волны (независимой переменной) и соответствующего ей коэффициента регрессии (множителя) сколько-нибудь существенному увеличению возможностей уравнения в части моделирования данных (включая остающееся необъяснимое изменение). Небольшие значения критерия Фишера или критерия говорят о том, что добавление в уравнение длины волны не дает никакого реального улучшения.

Если несколько длин волн (переменных) имеют низкие значения критериев или (меньше, чем 10 или 100 соответственно), может быть, потребуется удалить каждую из подозрительных длин волн, отдельно или комбинированно, чтобы определить, какие длины волн являются наиболее критическими для прогнозирования значений компонентов. В том случае, когда определению важной длины волны мешает корреляция между членами совокупности по другой длине волны, произойдет резкое увеличение частного критерия , когда будет исключена маловажная длина волны, и когда больше не будет высокой степени корреляции между переменными, все еще остающимися в уравнении регрессии.

Статистику по критерию иногда называют отношением фактического коэффициента регрессии для конкретной длины волны к стандартному отклонению этого коэффициента. Описанное значение частного критерия равно данному значению критерия -квадрат; обратите внимание на то, что вычисленное таким образом значение критерия сохраняет знак коэффициента, в то время как все значения критерия положительные.

Частный критерий Фишера для коэффициента регрессии вычисляют по формуле

. (А2.9)

А2.3.6 Стандартная ошибка с поправкой на систематическую погрешность

Измерения стандартной ошибки с поправкой на систематическую погрешность предусматривают описание дисперсии, приписываемой случайной необъяснимой ошибке. Величина систематической погрешности рассчитывается как средняя разность между эталонным и расчетным значениями в ИК-области спектра:

. (А2.10)

Стандартную ошибку с поправкой на систематическую погрешность вычисляют по формуле

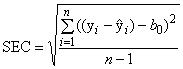. (А2.11)

Подобные значения с поправкой на систематическую погрешность можно вычислить для SECV.

А2.3.7 Стандартное отклонение повторяемости RSD

Величину RSD называют также стандартным отклонением разности (SDD) или стандартной ошибкой разности для повторных измерений (SD повторных измерений). Величину RSD вычисляют с целью обеспечения точной оценки изменений в аналитическом методе из-за отбора образцов, подачи образца и ошибок анализа. Величину RSD можно использовать как показатель сходимости в стандартном аналитическом методе.

Величину RSD* вычисляют по формуле

________________

* Текст документа соответствует оригиналу. - .

. (А2.12)*

________________

* Формула соответствуют оригиналу. - .

А2.3.8 Чувствительность к смещению

Чувствительность к смещению, называемая также систематическим изменением или показателем систематического изменения (ISV), равна сумме всех коэффициентов регрессии. Чем больше значение, тем выше чувствительность к разнице размера частиц среди образцов или к изотропным (зеркальным) рассеивающим свойствам образцов. Чувствительность к смещению используется для сравнения двух или более уравнений на их "слепоту" к изменениям по смещению между образцами. Уравнения с большими значениями чувствительности к смещению указывают на то, что колебания размеров частиц в пределах набора данных могут вызывать большие отклонения в аналитических результатах.

Величину ISV вычисляют по формуле

. (А2.13)

А2.3.9 Чувствительность к случайному изменению

Такую статистику называют также показателем случайного изменения (IRV). Чувствительность к случайному изменению вычисляется как сумма квадратов значений всех коэффициентов регрессии. Чем больше значение, тем выше чувствительность к таким факторам, как плохая точность по длине волны, колебания температур в образцах и приборе и электронные помехи. Чем выше значение, тем меньше вероятность успешного переноса уравнения на другие приборы.

Для вычисления IRV используют выражение:

. (А2.14)

А2.3.10 Стандартная ошибка лаборатории SEL для стандартных химических методов

Величину SEL можно определить, используя один или больше образцов, должным образом разделенных на аликвоты и проанализированных параллельно в одной или нескольких лабораториях. Среднее аналитическое значение для повторов на единичном образце вычисляют по формуле

. (А2.15)

Величину SEL вычисляют по формуле

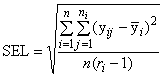, (А2.16)

где индекс представляет разные образцы, а индекс разные измерения на одном и том же образце.

Данную методику можно использовать как в случае повторных измерений, выполненных в одной лаборатории, так и в случае совместных исследований, проведенных несколькими лабораториями. С некоторой осторожностью следует отнестись к применению формулы (А2.16). Если все аналитические результаты получены одним аналитиком в одной лаборатории, то повторяемость анализов определяется как SEL, где - значение критерия Стьюдента для доверительного уровня 95% и степеней свободы. Если аналитические результаты получены от нескольких аналитиков и нескольких лабораторий, то же самое вычисление дает воспроизводимость анализа. Для многих аналитических испытаний величина SEL может изменяться по величине у. Значения SEL, вычисленные для образцов с разным , можно сравнить с помощью критерия Фишера, чтобы определить, показывают ли значения SEL статистически значимое отклонение как функцию .

Приложение ДА
(справочное)

Оригинальный текст невключенных структурных элементов примененного стандарта АСТМ

ДА.1

1 Область применения

1.2 В общих чертах представлены процедуры сбора и обработки данных для создания калибровок ИК спектрометров. Описываются определения, термины и методы калибровки. Описываются критерии для обоснования эксплуатационных характеристик калибровочной модели.

1.7 В качестве стандартных единиц измерения приняты единицы в системе СИ. В данный стандарт не включены другие единицы измерения.

1.8 Перед данным стандартом не стоит задача рассмотрения всех факторов опасности, при наличии таковых, связанных с его применением. Принятие соответствующих мер по безопасности и определение применимости нормативных ограничений перед использованием лежит в зоне ответственности пользователя данного стандарта.

Примечание - Исключение данных пунктов связано с тем, что их положения носят справочный характер.

ДА.2

7 Оборудование

7.1 Полное описание всех применимых типов инфракрасной измерительной аппаратуры находится за пределами действия данного документа. Здесь приводятся только общие сведения.

7.6 Описания конструкций аппаратуры, имеющих отношение к ссылкам (1) и (2), даются в ссылках (3) и (4). Другая аппаратура, по эксплуатационным характеристикам подобная аппаратуре, описанной в этих ссылках, приемлема для всех методов анализа в ближней инфракрасной области спектра, описанных в данной методике.

7.7 Информацию по измерению эксплуатационных характеристик спектрофотометров в ультрафиолетовой, видимой и ближней инфракрасной области спектра см. в Практике Е275. Информацию по измерению эксплуатационных характеристик светорассеивающих инфракрасных спектрофотометров см. в Практике Е932. Информацию по измерению эксплуатационных характеристик Фурье-спектрофотометров в средней инфракрасной области см. в Практике Е1421. Информацию по измерению эксплуатационных характеристик Фурье-спектрофотометров в ближней инфракрасной области спектра см. в Практике Е1944. Информацию по спектрофотометрам, к которым настоящая методика не применима, см. в Руководстве Е1866.

Примечание - Исключение данных пунктов связано с тем, что их положения носят справочный характер.

ДА.3

9 Стандартный метод и справочные значения

9.5 Если стандартный метод, используемый для многомерной калибровки, является установленным ASTM методом, а образцы, используемые при калибровке, были проанализированы по совместной программе испытаний (например, октановые числа, полученные от признанных групп обмена), то эталонные значения, полученные по совместной программе испытаний, можно использовать напрямую, а среднеквадратичные отклонения, установленные по совместной программе испытаний, можно использовать как оценку сходимости справочных данных.

9.6 Стандартные методы, не являющиеся методами ASTM, можно использовать для многомерной калибровки в ИК-анализах, но в этом случае разработчик метода обязан установить сходимость стандартного метода, используя процедуры, подобные тем, что подробно описаны в Практике Е691, Руководстве по определению данных по сходимости для методов ASTM по нефтепродуктам и смазочным маслам и Практике D6300.

Примечание - Исключение данных пунктов связано с тем, что их положения носят справочный характер.

ДА.4

16.3 Обнаружение статистических выбросов во время калибровки

Примечание 17 - Если масштабирование коэффициента влияния выполнено, как описано в (25), то для обнаружения статистического выброса можно прибегнуть к критерию Фишера.

Примечание - Исключение примечания связано с тем, что его положения носят справочный характер.

Приложение ДБ
(справочное)

Сопоставление структуры настоящего стандарта со структурой примененного в нем стандарта АСТМ

Таблица ДБ.1

Приложение ДВ
(справочное)

Сведения о соответствии ссылочных национальных и межгосударственных стандартов стандартам АСТМ, использованным в качестве ссылочных в примененном стандарте АСТМ

Таблица ДВ.1

Электронный текст документа

и сверен по:

, 2017