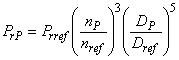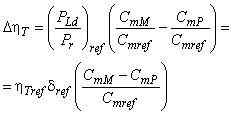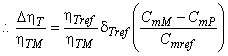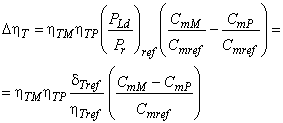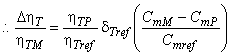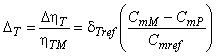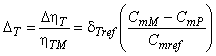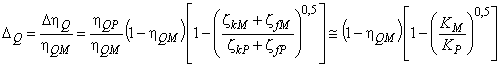ГОСТ Р 55002-2012
(МЭК 62097:2009)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
МАШИНЫ ГИДРАВЛИЧЕСКИЕ РАДИАЛЬНЫЕ И ОСЕВЫЕ
Метод преобразования эксплуатационных характеристик модели в рабочие характеристики опытного образца
Hydraulic machines, radial and axial. Performance conversion method from model to prototype
ОКС 27.140
Дата введения 2014-01-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184 "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский институт энергетических сооружений" (ОАО "НИИЭС") на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом ТК 330 "Процессы, оборудование и энергетические системы на основе возобновляемых источников энергии"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 20 сентября 2012 г. N 381-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 62097:2009* "Машины гидравлические радиальные и осевые. Метод преобразования рабочих характеристик модели в рабочие характеристики опытного образца" (IEC 62097:2009 Hydraulic machines, radial and axial - Performance conversion method from model to prototype), при этом дополнительные слова (фразы, показатели и их значения), включенные в текст стандарта для учета потребностей национальной экономики Российской Федерации и особенностей российской стандартизации, выделены полужирным курсивом**, а объяснения причин их включения приведены в сносках.
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей;
** В бумажном оригинале обозначения и номера стандартов и нормативных документов приводятся обычным шрифтом. - Примечания изготовителя базы данных.
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомления и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Настоящий стандарт устанавливает производительность опытного образца гидравлических машин на основе результатов тестирования модели с учетом масштабного эффекта, включая влияние шероховатости поверхности.
Настоящий стандарт рекомендуется использовать для оценки результатов испытаний моделей гидравлических машин согласно договору между владельцем установки и предприятием, предоставляющим услуги оценки. При оценке результатов испытаний модернизированных машин, имеющих высокую шероховатость рабочих поверхностей, необходимо руководствоваться данными, представленными в приложении D настоящего стандарта.
В настоящем стандарте отдельно рассмотрены потери удельной гидравлической энергии, потери на трение диска и потери на внутренние утечки рабочей жидкости через уплотнения и зазоры. Улучшение рабочих характеристик гидравлической установки достигнуто за счет учета зависимости потерь на трение от числа Рейнольдса (Re) и фактора шероховатости поверхности (Ra).
Введение в действие настоящего стандарта послужит также к созданию доказательной базы действующих и разрабатываемых в настоящее время технических регламентов.
1 Область применения
Настоящий стандарт применяется для определения эффективности и рабочих характеристик гидравлической машины на основе результатов испытаний моделей с учетом масштабного эффекта, включая влияние шероховатостей поверхности.
Настоящий стандарт рекомендуется использовать для оценки результатов испытаний моделей гидравлических машин согласно договору испытаний гидравлических машин.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 4.425-86 Система показателей качества продукции. Турбины гидравлические. Номенклатура показателей
ГОСТ 23956-80 Турбины гидравлические. Термины и определения
ГОСТ 28842-90 (МЭК 41-63, МЭК 607-78) Турбины гидравлические. Методы натурных приемочных испытаний
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяют в части, не затрагивающей эту ссылку.
3 Термины и определения, обозначения и сокращения
3.1 Термины и определения
В стандарте используется Международная система единиц физических величин (СИ). Все значения выражены в основных единицах СИ или в соответствующих производных. По письменному соглашению сторон возможно использование любой другой системы единиц.
В настоящем стандарте применены термины по ГОСТ 4.425, ГОСТ 23956, ГОСТ 28842, а также следующие термины с соответствующими определениями:
3.1.1 выработка электроэнергии на турбине или входящая мощность насоса (turbine output or pump input): Механическая мощность, производимая валом турбины или насоса, относящая механические потери соответствующих подшипников и уплотнителей валов на гидравлическую машину (см. рисунки А.1 и А.2).
3.1.2 гидравлическая мощность (hydraulic power): Мощность, доступная для производства энергии (турбина) или передаваемая воде (насос), определяется в соответствии с формулой:
![]() .
.
3.1.3 гидравлический диаметр (hydraulic diameter): Площадь поперечного сечения, умноженная на 4, разделенная на длину окружности сечения.
3.1.4 гидравлический КПД (hydraulic efficiency): Определяется в соответствии с формулами:
- для турбин: ![]() ;
;
- для насосов: ![]() .
.
3.1.5 делительный диаметр (reference diameter): Делительный диаметр гидравлической машины.
3.1.6 динамическая вязкость (dynamic viscosity): Количественная характеристика механического поведения жидкости.
3.1.7 индекс масштабируемой потери гидравлической энергии для секции каждого компонента (scalable hydraulic energy loss index for each component passage): Определяется в соответствии с формулой:
![]() .
.
3.1.8 индекс масштабируемой потери на трение диска (scalable disc friction loss index): Определяется в соответствии с формулой:
![]() .
.
3.1.9 исходная масштабируемая потеря гидравлической энергии (reference scalable hydraulic energy loss): Значение для модели с гладкой поверхностью, работающей при исходном числе Рейнольдса Re=7·10
.
3.1.10 исходная масштабируемая потеря гидравлической энергии в секции компонента (reference scalable hydraulic energy loss in component passage): для секции каждого компонента.
3.1.11 исходная потеря на трение диска (reference disc friction loss): Значение для модели с относительно гладкой поверхностью, работающей при исходном числе Рейнольдса Re=7·10
.
3.1.12 кинематическая вязкость (kinematic viscosity): Отношение динамической вязкости к плотности жидкости. Значения представлены в виде функции температуры.
3.1.13 кинетическая потеря удельной гидравлической энергии (kinetic loss of specific hydraulic energy): Потеря удельной гидравлической энергии, вызываемая гидравлическими явлениями, отличными от трения поверхности, такими как турбулентность, разделение потока, резкое изменение водотока и т.д.
3.1.14 коэффициент мощности (power coefficient): Определяется в соответствии с формулой:
![]() .
.
3.1.15 коэффициент потери на трение диска (disc friction loss coefficient): Коэффициент потери на трение для вращающегося диска. Определяется в соответствии с формулой:
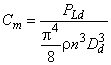 ,
,
где D - диаметр ступицы или обода рабочего колеса (большее из двух).
3.1.16 коэффициент потери на трение потока в трубе (friction loss coefficient for pipe flow): Коэффициент потери на трение для трубы. Определяется в соответствии с формулой:
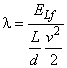 ,
,
где d - диаметр трубы, м;
L - длина трубы, м.
3.1.17 коэффициент потери на трение для плоской пластины (friction loss coefficient for a flat plate): Коэффициент потери на трение для плоской пластины. Определяется в соответствии с формулой:
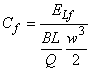 ,
,
где В - ширина плоской пластины, м;
L - длина плоской пластины, м;
Q - расход, проходящий по пластине, м/с;
w - относительная скорость потока, м/с.
3.1.18 коэффициент расхода (leakage flow rate): Объем воды, протекающий за единицу времени через зазоры уплотнителя рабочего колеса.
3.1.19 коэффициент распределения потерь (loss distribution factor): Отношение масштабируемой потери к общим потерям. Определяется в соответствии с формулой:
![]() .
.
3.1.20 коэффициент стока (discharge coefficient): Определяется в соответствии с формулой:
![]() .
.
3.1.21 коэффициент скорости потока для секции каждого компонента (flow velocity factor for each component passage): Отношение максимальной относительной скорости потока в секции каждого компонента к периферийной скорости u. Определяется в соответствии с формулой:
![]() .
.
3.1.22 коэффициент энергии (energy coefficient): Определяется в соответствии с формулой:
![]() .
.
3.1.23 КПД удельной гидравлической энергии (specific hydraulic energy efficiency): Определяют в соответствии с формулами:
- для турбин: ![]() ;
;
- для насосов: ![]() ,
,
в соответствии с рисунками А.1 и А.2.
3.1.24 крутящий момент рабочего (или крыльчатого) колеса (runner/impeller torque), Р: Крутящий момент, передаваемый через муфту рабочего колеса/крыльчатого колеса и вала, соответствующий механической энергии рабочего колеса/крыльчатого колеса.
3.1.25 массовый расход (mass flow rate): Масса воды, протекающая через любое сечение системы за единицу времени.
3.1.26 механический КПД (mechanical efficiency): Определяется в соответствии с формулами:
- для турбин: ![]() ;
;
- для насосов: ![]() ,
,
в соответствии с рисунками А.1 и А.2.
3.1.27 механическая мощность рабочего (или крыльчатого) колеса (mechanical power of runer/impeller): Мощность, передаваемая между валом и рабочим (крыльчатым) колесом посредством муфты.
3.1.28 машины осевого типа (axial flow machines): Турбины Каплана, капсульные турбины и пропеллерные турбины с неподвижными лопастями.
3.1.29 машины радиального типа (radial flow machines): Турбины Френсиса и реверсивные турбонасосы типа Френсис.
3.1.30 мощность рабочего (или крыльчатого) колеса (power of runner/impeller): Мощность, производимая рабочим колесом и определяемая в соответствии с формулой:
![]() или
или ![]() .
.
Мощность, производимую крыльчатым колесом, определяют по формуле:
![]() или
или ![]() .
.
3.1.31 объемный КПД (volumetric efficiency): Определяют в соответствии с формулами:
- для турбин: ![]() ;
;
- для насосов: ![]() ,
,
в соответствии с рисунками А.1 и А.2.
3.1.32 относительная масштабируемая потеря гидравлической энергии (relative scalable hydraulic energy loss): Масштабируемая потеря удельной гидравлической энергии, разделенная на Е, зависящая от числа Рейнольдса и шероховатости (в большинстве случаев выражается в %), определяется в соответствии с формулой:
![]() .
.
3.1.33 относительная немасштабируемая потеря гидравлической энергии (relative non-scalable hydraulic energy loss): Немасштабируемая потеря удельной гидравлической энергии, разделенная на E, остающаяся постоянной независимо от числа Рейнольдса и шероховатости, определяется по формуле:
![]() .
.
3.1.34 относительная потеря на трение диска (relative disc friction loss): Потеря на трение диска P, разделенная на Р
, определяется в соответствии с формулой:
![]() .
.
3.1.35 периферийная скорость (peripheral velocity): Периферийная скорость на делительном диаметре.
3.1.36 песочная шероховатость (sand roughness): Эквивалентная песочная шероховатость [11].
3.1.37 плотность воды (density of water): Масса на единицу объема воды.
3.1.38 полезный напор турбины или высота нагнетания насоса (turbine net head or pump delivery head): Определяется в соответствии с формулой:
![]() .
.
3.1.39 потери энергии в подшипнике (bearing loss power): Потеря энергии, вызываемая трением опорного подшипника и уплотнителя вала.
3.1.40 потеря на трение диска (disc friction loss): Потеря энергии, вызываемая трением о внешнюю поверхность рабочего (или крыльчатого) колеса.
3.1.41 потеря удельной гидравлической энергии в стационарной части (specific hydraulic energy loss in stationary part): Потеря удельной гидравлической энергии в стационарной части, включающая в себя потери на трение и кинетические потери.
3.1.42 потеря удельной гидравлической энергии на рабочем (или крыльчатом) колесе (specific hydraulic energy loss in runner/impeller): Потеря удельной гидравлической энергии на рабочем (или крыльчатом) колесе, включающая потери на трение и кинетические потери.
3.1.43 потеря удельной гидравлической энергии на трение (friction loss of specific hydraulic energy): Потеря удельной гидравлической энергии, вызываемая трением на поверхности водотоков.
3.1.44 приращение КПД (efficiency step-up): Разница между КПД в двух случаях функционирования со сходными гидравлическими условиями.
3.1.45 размерный коэффициент для потери на трение диска (dimension factor for disc friction loss): Отношение диаметра ступицы рабочего колеса или обода рабочего колеса к делительному диаметру определяется по формуле:
![]() .
.
3.1.46 размерный коэффициент для секции каждого компонента (dimension factor for each component passage): Отношение гидравлического диаметра секции каждого компонента к делительному диаметру.
3.1.47 расход (discharge): Объем воды, протекающий за единицу времени через любое сечение системы.
3.1.48 расход машины (discharge of machine): Поток, проходящий через сечение высокого давления, определяется в соответствии с формулой:
![]() .
.
3.1.49 скорость вращения (rotational speed): Количество оборотов за единицу времени.
3.1.50 соотношение приращения КПД (efficiency step-up ratio): Соотношение приращения КПД к КПД модели определяется по формуле:
![]() .
.
3.1.51 средняя арифметическая шероховатость (arithmetical mean roughness): Отклонение от профиля поверхности, представленное средним арифметическим значением.
3.1.52 средняя скорость (mean velocity): Значение расхода, разделенное на площадь поперечного сечения водовода.
3.1.53 удельная гидравлическая энергия машины (specific hydraulic energy of machine): Удельная энергия воды, имеющаяся между уравнительными секциями высокого и низкого давления первой и второй машины, с учетом влияния коэффициента сжатия.
3.1.54 удельная гидравлическая энергия рабочего (или крыльчатого) колеса (specific hydraulic energy of runner/impeller):
- для турбин: Удельная гидравлическая энергия, производимая рабочим колесом;
- для насосов: Удельная гидравлическая энергия, производимая крыльчатым колесом.
3.1.55 удельная скорость (specific speed): Определяется в соответствии с формулой:
![]() .
.
3.1.56 ускорение из-за силы тяжести (acceleration due to gravity): Местное значение гравитационного ускорения в месте исследования, выраженное функцией высоты и широты.
3.1.57 фактор мощности (power factor): Определяется по формуле:
![]() .
.
3.1.58 фактор скорости (speed factor): Определяется по формуле:
![]() .
.
3.1.59 фактор стока (discharge factor): Определяется по формуле:
![]() .
.
3.1.60 число Рейнольдса (Reynolds number): Определяется по формуле:
![]() .
.
3.1.61 число Рейнольдса для элементов узла (Reynolds number of component passage): Определяется по формуле:
![]() .
.
3.1.62 чистый расход (net discharge): Объем воды, проходящий через рабочее (или крыльчатое) колесо за единицу времени. Определяется как:
- для турбин: ![]() ;
;
- для насосов: ![]() .
.
3.1.63 эксплицитная формула (explicit formula): Раскрытая, развернутая формула.
3.1.64 энергетический КПД (КПД трения диска) [power efficiency (disc friction efficiency)]: Определяется в соответствии с формулами:
- для турбин: ![]() ;
;
- для насосов: ![]() ,
,
в соответствии с рисунками А.1 и А.2.
3.2 Обозначения и сокращения
3.2.1 Перечень индексов
М - модель;
Р - опытный образец;
Е - удельная энергия;
СО - компонент;
SP - спиральная камера;
Q - объемный параметр;
SV - статорная колонна;
T - момент трения диска;
GV - направляющая лопаток;
ref - ссылка;
RU - рабочее колесо;
d - гидравлический диаметр;
DT - отсасывающая труба;
u - скорость;
ST - стационарная часть;
h - гидравлический параметр;
opt - оптимальная точка;
off - нерасчетная точка
3.2.2 Термины, условные обозначения и единицы измерения
Массовый расход | кг | |
C | Коэффициент потери на трение для плоской пластины | - |
С | Коэффициент потери на трение диска | - |
D | Делительный диаметр | м |
d | Индекс масштабируемой потери гидравлической энергии для секции каждого компонента | - |
d | Гидравлический диаметр | м |
d | Индекс масштабируемой потери на трение диска | - |
Е | Удельная гидравлическая энергия машины | Дж·кг |
Е | Потеря удельной гидравлической энергии на трение | Дж·кг |
E | Кинетическая потеря удельной гидравлической энергии | Дж·кг |
E | Потеря удельной гидравлической энергии на рабочем (или крыльчатом) колесе | Дж·кг |
E | Потеря удельной гидравлической энергии в стационарной части | [Дж·кг |
Е | Удельная гидравлическая энергия рабочего (или крыльчатого) колеса | Дж·кг |
E | Коэффициент энергии | - |
g | Ускорение из-за силы тяжести | м·с |
Н | Полезный напор турбины или высота нагнетания насоса | м |
k | Песочная шероховатость | м |
n | Скорость вращения | с |
n | Фактор скорости | - |
N | Удельная скорость | - |
Р | Выработка электроэнергии на турбине или входящая мощность насоса | Вт |
P | Фактор мощности | - |
P | Гидравлическая мощность | Вт |
P | Потеря на трение диска | Вт |
P | Потери энергии подшипника | Вт |
Р | Механическая мощность рабочего колеса/крыльчатого колеса | Вт |
P | Коэффициент мощности | - |
Р | Мощность рабочего колеса/крыльчатого колеса | Вт |
Q | Расход | м |
q | Коэффициент расхода | м |
Q | Расход машины | м |
Q | Фактор расхода | - |
Q | Чистый расход | м |
Q | Коэффициент расхода | - |
Ra | Средняя арифметическая шероховатость | м |
Re | Число Рейнольдса | - |
Rе | Число Рейнольдса для элементов узла | - |
Т | Крутящий момент рабочего колеса/крыльчатого колеса | Н·м |
и | Периферийная скорость | м·с |
v | Средняя скорость | м·с |
V | Коэффициент распределения потерь | - |
Соотношение приращения КПД | - | |
Относительная масштабируемая потеря гидравлической энергии | - | |
| Исходная масштабируемая потеря гидравлической энергии в секции компонента | - |
Исходная масштабируемая потеря гидравлической энергии | - | |
Относительная немасштабируемая потеря гидравлической энергии | - | |
Относительная потеря на трение диска | - | |
Исходная потеря на трение диска | - | |
Приращение КПД | - | |
КПД удельной гидравлической энергии | - | |
Гидравлический КПД | - | |
Механический КПД | - | |
Объемный КПД | - | |
Энергетический КПД (КПД трения диска) | - | |
Размерный коэффициент для элементов каждого узла | - | |
Размерный коэффициент для потери на трение диска | - | |
Коэффициент скорости потока для элементов каждого узла | - | |
Коэффициент потери на трение для потока по трубам | - | |
Динамическая вязкость | Па·с | |
Кинематическая вязкость | м | |
Плотность воды | кг·м |
4 Масштабный эффект
4.1 Основные положения
4.1.1 Масштабируемые потери
Одной из основных особенностей расчетной формулы, представленной в настоящем стандарте, является отдельное рассмотрение трех компонентов КПД. Данными компонентами являются КПД гидравлической энергии , объемный КПД
и энергетический КПД
. В настоящем стандарте рассматривается эффект масштабирования в отношении каждого из данных компонентов КПД.
В настоящем стандарте в отношении машин радиального потока во внимание принимается только масштабирование на потери, соответствующие компонентам КПД ( и
), а в отношении машин осевого потока только
.
Среди потерь, соответствующих данным компонентам КПД, эффекту масштаба вследствие разницы между числом Рейнольдса и коэффициентом относительной шероховатости поверхности подвержены потери, в настоящем стандарте указанные как "масштабируемые потери":
- потеря особой гидравлической энергии вследствие трения Е;
- потеря на утечку q;
- потеря на трение диска P.
Функцией удельной скорости для каждого типа машин в настоящем стандарте считается отношение относительной величины каждой масштабируемой потери к соответствующему параметру рабочих характеристик, за исключением расхода.
Сумма потерь на трение в различных частях машины выражается как сумма потерь на трение в каждом компоненте, а именно - в соответствии с формулой ![]() .
.
Масштабный эффект на данную потерю возникает вследствие различия числа Рейнольдса и относительной шероховатости у модели и опытного образца, оценивается по формуле (1).
Потеря удельной гидравлической энергии называется кинетической потерей или немасштабируемой потерей и выражается формулой ![]() .
.
Принято, что отношение E к Е
остается одинаковым в модели и опытном образце.
Масштабный эффект потери на утечку q является результатом изменения коэффициента потери на трение зазора уплотнителя рабочего (или крыльчатого) колеса. В большинстве случаев сама потеря на утечку является небольшой, и масштабный эффект на данную потерю также является очень незначительным.
Если геометрия уплотнителя поддерживается в гомологическом состоянии в модели и в опытном образце в соответствии с критериями, приведенными в таблице 3, масштабный эффект потери на утечку не принимают во внимание, и опытного образца считается идентичным аналогичному показателю модели в соответствии с Е.3 приложения Е.
Для Е масштабный эффект на трение диска P
является результатом разницы между числом Рейнольдса и относительной шероховатостью внешней поверхности рабочего (или крыльчатого) колеса между моделью и опытным образцом. В связи с наличием радиального потока и деформации граничного слоя в пределах ограниченной площади между рабочим (или крыльчатым) колесом и стационарными частями масштабный эффект P
немного отличается от эффекта масштабирования на Е
. В настоящем стандарте принято, что масштабный эффект на трение диска может быть оценен с помощью формулы (7) масштабного эффекта (в соответствии с приложением D).
При условии рассмотрения машин осевого потока потеря на трение на поверхности корпуса рабочего колеса ничтожна мала, и ее масштабный эффект не принимается во внимание.
Если геометрия модели не сходна с геометрией опытного образца, настоящий стандарт рекомендует использовать поправочную формулу для , приведенную в Е.2 приложения Е.
Плотность потока энергии, проходящего через гидравлическую машину, и различные потери, возникающие в процессе преобразования энергии в гидравлической машине, могут быть проиллюстрированы графиками потока, представленными на рисунке А.1 (см. также [4]).
4.1.2 Основные формулы масштабного эффекта для определения потерь на гидродинамическое трение
Формула масштабирования потерь учитывает влияние шероховатости поверхности. На физическом уровне качество поверхности может быть описано формулой Кольбрука. Путем некоторых преобразований и упрощения неявная формула Кольбрука может быть преобразована в представленное ниже выражение [4, 6]:
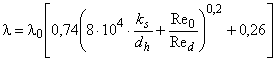 , (1)
, (1)
где Re=7·10
;
=0,0085;
k - песочная шероховатость;
d - диаметр водотока;
Re - число Рейнольдса для водотока, определяемое по формуле:
![]() .*
.*
________________
* Формула соответствует оригиналу. Вероятно, должно быть "![]() ". - .
". - .
На практике шероховатости поверхности модели и опытного образца представлены среднеарифметической шероховатостью Ra, указанной в 4.2.2. Для соотношения песочной шероховатости k и Ra на данный момент имеются несколько вариантов вычислений. В настоящем стандарте соотношение установлено формулой:
![]() . (2)
. (2)
Примечание - Для поверхностей с высокой шероховатостью следует учитывать условия, приведенные в формуле (2) и в примечании 2 к В.1 приложения В.
Тогда формула (1) выглядит следующим образом:
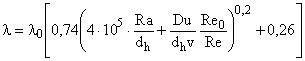 . (3)
. (3)
Способ перехода от модели к опытному образцу представлен на рисунке 1. Кривая Р изображает способ приращения опытного образца с высокой шероховатостью поверхности, Р
- образца с приемлемой шероховатостью, Р
- с гладкой поверхностью. В случае с Р
возможно снижение КПД по сравнению с моделью.
Рисунок 1 - Основной способ приращения с учетом шероховатости поверхности
Для расчета разницы гидравлического КПД между двумя рабочими точками М и Р со сходными гидравлическими условиями при разных числах Рейнольдса и разными условиями шероховатости поверхности с помощью формулы (3) может быть выведена формула [также см. приложение А.2 (2)]:
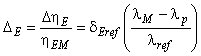 . (4)
. (4)
Формула Кольбрука применима и для потока в трубопроводе, но для достижения более высокой точности целесообразнее применять следующее уравнение:
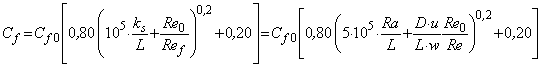 , (5)
, (5)
![]() ,
,
где Re=7·10;
С=0,0032;
Re - число Рейнольдса для пластины, определяемое по формуле:
![]() ,
,
L - длина плоской пластины;
w - относительная скорость потока на плоской пластине.
Путем замены в формуле (4) на С
, представленный в формуле (5), формула (4) может быть применена для расчета масштабного эффекта потери на трение лопастей рабочего колеса машин осевого потока.
Аналогичную формулу коэффициента потери на трение для трения диска выводят следующим образом [9] (в соответствии с приложением D):
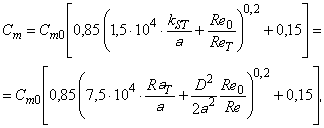 (6)
(6)
где Re=7·10;
С=0,0019;
k - эквивалентная песочная шероховатость, соотносится с Ra
в виде зависимости k
=5Ra
, где Ra
- средневзвешенное значение среднеарифметического отклонения профиля шероховатости внешней поверхности рабочего колеса и поверхности стационарной части, выходящей на рабочее колесо, в соответствии с формулой (13);
Re - число Рейнольдса для диска, определяемое по формуле:
![]() ,
,
где а - радиус ступицы или обода рабочего колеса (берется большее из двух значений), м, вычисляемый по формуле:
![]() ,
,
здесь - угловая скорость диска, рад/с.
С помощью формулы (6) можно получить формулу приращения для энергетического КПД (трение диска) [также см. приложение А.2 (4)]:
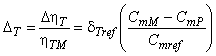 . (7)
. (7)
4.2 КПД удельной гидравлической энергии
4.2.1 Формула приращения
Масштабируемые потери по формуле (4) относятся к потерям модели с гладкой поверхностью (при R
=7·10
) и выражены в виде зависимости удельной скорости от типа гидравлической машины. Они стандартизированы и приведены в приложении В для машин радиального потока и приложении С для машин осевого типа.
Путем подстановки формулы (3) масштабного эффекта в формулу (4) выводят следующую формулу индивидуального приращения для компонента машины (см. также В.2 приложения В):
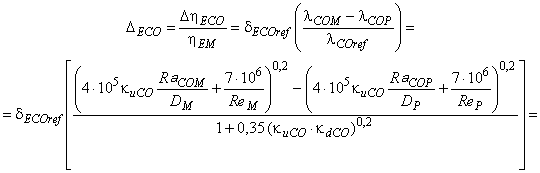
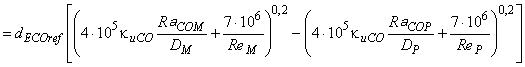 , (8)
, (8)
где ![]() - нормированная исходная масштабируемая потеря для каждого элемента узла при условии, что число Рейнольдса машины Re
- нормированная исходная масштабируемая потеря для каждого элемента узла при условии, что число Рейнольдса машины Re равно исходному числу Рейнольдса (Re
=7·10
) (см. также А.2 (2) приложения А и В.2 (2) приложения В);
- коэффициент скорости потока для элемента каждого узла в соответствии с приложением В;
- размерный коэффициент для элемента каждого узла в соответствии с приложением В;
d![]() - индекс масштабируемой потери для элементов каждого узла (см. В.2 приложения В), определяемый по формуле:
- индекс масштабируемой потери для элементов каждого узла (см. В.2 приложения В), определяемый по формуле:
![]() .
.
Для машин радиального потока формула (8) позволяет рассчитать индивидуальные приращения различных узлов с использованием показателей d![]() и
и , которые устанавливают для каждого отдельного узла от спиральной камеры до отсасывающей трубы.
Значения d![]() и
и для секции каждого узла турбины Френсиса и турбонасоса стандартизированы и представлены в 5.3.1 и 5.3.2.
Для машин осевого потока масштабируемая потеря делится на потери в лопастях рабочего колеса и на стационарных частях. При этом коэффициент приращения КПД для масштабируемой потери стационарных частей рассчитывается аналогично с машинами радиального потока по формуле 8. Также допускается, что ![]() . Значение
. Значение приведено в 5.3.
Как было указано в 4.1.2, формула масштабного эффекта для плоской пластины (5) может быть использована и для лопастей рабочего колеса. Ее также можно применять к лопастям рабочего колеса, преобразовав в формулу (8) введением модифицированного фактора скорости потока ![]() вместо
вместо :
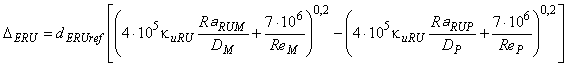 . (9)
. (9)
Затем приращение удельной гидравлической энергии для всей машины может быть рассчитано по формуле:
![]() . (10)
. (10)
Структура формулы подходит для всех типов гидравлических машин. Она может также быть использована как для турбин, так и для насосов.
4.2.2 Требования к применению формулы индивидуального приращения для компонентов машины
Для всех стационарных частей машин осевого типа в качестве репрезентативного используют значение шероховатости, приведенное в формуле:
![]() . (11)
. (11)
Согласно формуле (8) достичь более значительного увеличения КПД можно посредством тонкой полировки опытного образца. Однако шероховатость опытного образца должна быть не менее шероховатости, ожидаемой после определенного периода эксплуатации (т.е. гарантийного периода). Следует иметь в виду, что очень тонкая полировка является нерентабельной, как показано на рисунке 2.
Рисунок 2 - Критерии МЭК по шероховатости поверхности в соответствии с данными таблиц 1 и 2
В таблицах 1а, 1b и 2а, 2b представлены максимальные рекомендуемые значения шероховатости для рабочего колеса опытного образца и направляющих лопаток новых турбин. Данные рекомендуемые значения заменяют собой значения, приведенные в МЭК 60193.
Таблица 1а - Рекомендуемые значения коэффициента шероховатости поверхности рабочего колеса для новых турбин ()
Е | ||||||||
Делительный диаметр, м | 1-2 | 2-4 | 4-7 | 7-10 | ||||
Зона | А | В | А | В | А | В | А | В |
Шероховатость Ra (сторона нагнетания) | 2,3 | 3,2 | 6,3 | 12,5 | 12,5 | 25 | 12,5 | 25 |
Шероховатость Ra (сторона всасывания) | 2,3 | 2,3 | 2,3 | 3,2 | 3,2 | 6,3 | 6,3 | 6,3 |
Таблица 1b - Рекомендуемые значения коэффициента шероховатости поверхности рабочего колеса для новых турбин ()
Е>3000 Дж·кг | ||||||||
Делительный диаметр, м | 1-2 | 2-4 | 4-7 | 7-10 | ||||
Зона | А | В | А | В | А | В | А | В |
Шероховатость Ra (сторона нагнетания) | 2,3 | 2,3 | 2,3 | 3,2 | 3,2 | 6,3 | 6,3 | 6,3 |
Шероховатость Ra (сторона всасывания) | 1,6 | 1,6 | 2,3 | 2,3 | 2,3 | 3,2 | 3,2 | 4,5 |
Примечание - а) Хотя в данных таблицах представлены только 2 зоны А и В, подразумевается, что вдоль приточного края лопастей дополнительная зона часто полируется таким образом, что образуется очень низкая степень шероховатости с целью предотвращения образования полостей.
b) Данные значения шероховатости могут казаться избыточными для данных зон. Однако вышеуказанные значения были установлены на основе сравнения коэффициентов потерь по шероховатости поверхности, наблюдаемых на машинах различного размера с различным значением числа Рейнольдса. Таким образом, более крупные машины имеют большее значение числа Рейнольдса, и при их эксплуатации допускается более высокий показатель шероховатости. Однако целесообразнее использовать более низкие значения шероховатости, чем рекомендуемые значения, если участникам проекта это кажется более практичным и экономически обоснованным для данного проекта.
Примечание - В отношении шероховатости поверхности вдоль обода и ступицы рабочего колеса рекомендуется использовать среднее значение между значениями зоны "Сторона нагнетания" и зоной "Сторона всасывания".
Рисунок 3 - Лопасти и борт рабочего колеса турбины Френсиса
Примечание - Рекомендуется использовать значения шероховатости, указанные в таблице 1 для зоны "Забора лопастей" для обеих сторон (сторона нагнетания и сторона всасывания) лопастей рабочего колеса для машин осевого потока.
Рисунок 4 - Осевой поток лопасти рабочего колеса
Таблица 2а - Рекомендуемые значения шероховатости направляющей лопатки опытного образца для новых турбин ()
Е | ||||||||
Делительный диаметр, м | 1-2 | 2-4 | 4-7 | 7-10 | ||||
Зона | А | В | А | В | А | В | А | В |
Шероховатость Ra | 2,3 | 2,3 | 2,3 | 6,3 | 3,2 | 12,5 | 6,3 | 12,5 |
Таблица 2b - Рекомендуемые значения шероховатости направляющей лопатки опытного образца для новых турбин ()
Е>3000 Дж·кг | ||||||||
Делительный диаметр, м | 1-2 | 2-4 | 4-7 | 7-10 | ||||
Зона | А | В | А | В | А | В | А | В |
Шероховатость Ra | 1,6 | 2,3 | 2,3 | 2,3 | 2,3 | 3,2 | 3,2 | 6,3 |
Примечание - В случае с шероховатостью поверхности вдоль верхней и нижней части направляющей лопатки рекомендуется использовать среднее значение между А и В.
Рисунок 5 - Направляющие лопатки
При использовании формулы (8) для исследования моделей необходимо убедиться в выполнении условий договора по КПД и шероховатости, причем значения шероховатости поверхностей Ra необходимо использовать в формуле в соответствии со следующими условиями:
- Шероховатость поверхностей модели.
Известно, что на компонентах модели наблюдается высокая однородность качества поверхности. Если выполняется это условие, будет достаточно от двух до четырех точек замера на поверхности. В случае с повторяющимися поверхностями, например статорными колоннами, направляющими лопатками или лопастями рабочего колеса, рекомендуется провести замеры минимум на двух повторяющихся поверхностях.
- Шероховатость поверхностей опытного образца.
В качестве значений шероховатости поверхности опытного образца необходимо использовать проектные значения шероховатости поверхности опытного образца, предоставляемые поставщиком. Необходимо провести замеры, когда компоненты турбины собирают на заводе, а также убедиться, что среднее значение измеренной шероховатости каждого элемента узла равно или меньше проектного значения шероховатости узла.
При использовании формулы (8) для оценки повышения КПД в рамках проекта модернизации шероховатость компонентов опытного образца должна быть измерена на существующей установке. Повышение КПД посредством замены некоторых узлов может быть оценено посредством сравнения значений КПД, рассчитанных на основе коэффициентов шероховатости, полученных по результатам замеров на существующих узлах, и с использованием проектных значений для новых узлов.
При проведении проектов по обновлению оборудования данные о шероховатости поверхностей, не планируемых к замеру, предоставляет владелец в спецификации. В случае измерения неровных поверхностей старых турбин необходимо учитывать рекомендации, представленные в приложении для значений Ra более 50 .
Для спиральной камеры, статорных колонок и отсасывающей трубы точки замеров следует выбирать таким образом, чтобы добиться точного среднего значения шероховатости. В случае с направляющими лопатками и рабочим колесом точки замеров следует выбирать таким образом, чтобы добиться среднего значения шероховатости в области высокой скорости потока секций данных компонентов.
Шероховатость поверхности следует измерять в условиях, идентичных условиям эксплуатации. Шероховатость окрашенной поверхности измеряют поверх слоя краски.
4.2.3 Расчет КПД удельной гидравлической энергии
После определения шероховатости поверхности для секции того или иного узла, соответствующей скорости потока данной секции, возможно рассчитать КПД удельной гидравлической энергии для всей турбины без расчета
для компонентов. Данное вычисление описано в В.3 приложения В для машин радиального типа и в С.10 приложения С для машин осевого типа. Эти упрощенные формулы допускается использовать согласно условиям договора между сторонами.
4.3 КПД мощности. Трение диска
4.3.1 Формула приращения
Трение диска оказывает значительное влияние на КПД радиальных машин с низкой удельной скоростью. Приведенная ниже формула (12) получена путем подстановки формулы (6) в формулу (7). Она определяет диапазон значений КПД мощности машин радиального типа, возникающих вследствие различных значений числа Рейнольдса и шероховатости поверхности, в соответствии с приложением D.
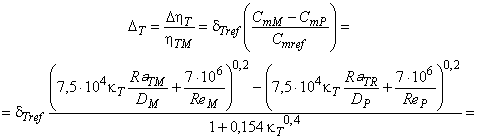
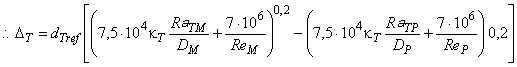 , (12)*
, (12)*
_______________
* Формула соответствует оригиналу. - .
![]()
![]() ,
,
где - размерный коэффициент для диска, связанный с потерей на трение, определяемый по формуле:
![]() ,
,
Ra - репрезентативное значение шероховатости, полученное с помощью формулы (13).
Масштабируемая потеря на трение диска d, представленная в формуле (12), относится к модели при исходном значении числа Рейнольдса Re
=7·10
с гладкой поверхностью. Значения d
и
были приняты в качестве функции от типа и удельной скорости машины радиального типа. Они стандартизированы и установлены в 5.4.
Для машин осевого типа трение поверхности корпуса рабочего колеса ничтожно мало. Поэтому в настоящем стандарте значение для машин осевого типа принято равным нулю.
4.3.2 Шероховатость поверхностей модели и опытного образца
Правила, приведенные в 4.2.2, могут быть использованы для вычисления значений шероховатости поверхности трения диска. В настоящем пункте приведены требования в отношении точек замера.
Известно, что значение шероховатости на внешней стороне ступицы и обода рабочего колеса влияет на величину силы трения диска. Исходя из этого, рекомендуется располагать точки замера шероховатости следующим образом:
а) ступица рабочего колеса: две или более точек на внешней стороне;
б) обод рабочего колеса: две или более точек на внешней стороне;
в) стационарная часть: четыре или более точек в зонах, выходящих на точки замера на рабочем колесе.
Шероховатость вращающейся части имеет определяющее влияние на момент трения диска. В формуле (12) следует использовать средневзвешенное значение шероховатости Ra в соответствии со следующей формулой:
![]() , (13)
, (13)
где Ra - средняя шероховатость, измеренная на вращающейся части;
Ra - средняя шероховатость, измеренная на стационарной части.
4.4 Объемный КПД
Оценка зависимости объемного КПД от числа Рейнольдса указывает на то, что данная зависимость незначительна в случае, если геометрическая конфигурация зазоров, лабиринтов, балансировочных отверстий/труб подобна в модели и в опытном образце. Следовательно, если геометрия уплотнителя модели выполнена подобным образом и в опытном образце (с отклонениями в пределах, указанных в таблице 3), считается, что объемный КПД является одинаковым в модели и в образце (формулы расчетов приведены в Е.3 приложения Е).
Таблица 3 - Допустимое отклонение геометрии уплотнителей модели от уплотнителей опытного образца
Размер и конструкция | Допустимое отклонение от опытного образца |
Радиальный зазор уплотнителей рабочего колеса* | 0...плюс 20% |
Диаметр уплотнителя | ±5% |
Осевая длина зазоров уплотнителей* | От 0 до минус 20% |
Количество уступов или борозд | Должно быть одинаковым |
Форма уступов или борозд (в соответствии с приложением D) | Должна быть гомологичной |
Примечание - В случае с машинами осевого типа слова, отмеченные "*", следует интерпретировать как "Зазор венца лопатки" и "Толщина венца лопатки" соответственно. В отношении радиального зазора и толщины венца лопатки применяют только эти два критерия. | |
Однако достаточно сложно изготовить уплотнители рабочего колеса, которые абсолютно соответствовали бы форме соответствующего опытного образца. В подобных случаях расход на утечку следует рассчитывать отдельно для модели и для опытного образца, а затем необходимо соответствующим образом откорректировать объемный КПД. В данном случае допускается использовать следующую формулу:
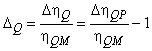 . (14)
. (14)
Если между заинтересованными сторонами не установлены особые требования относительно расчета , допускается применять формулу, представленную в Е.2 приложения Е.
5 Основные положения по увеличению КПД турбин
5.1 Основные положения
В настоящем пункте представлены значения d![]() и
и , используемые для расчета КПД удельной гидравлической энергии, и значения d
и
, используемые для расчета приращения КПД мощности (трение диска). Они относятся к исходному значению числа Рейнольдса Re
=7·10
и соответствуют машинам с гладкой поверхностью.
5.2 Удельная скорость
Гидравлическая машина любого типа характеризуется своей удельной скоростью в точке максимального КПД. Следовательно, необходимо рассчитать удельную скорость N тестируемой машины в момент ее максимального КПД:
![]() или
или 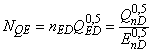 , (15)
, (15)
где n - скорость вращения с;
Q - сток машины, м
/с;
E - удельная гидравлическая энергия машины, Дж·кг.
Для гидронасоса, работающего в реверсивном режиме, проводят расчет удельной скорости в каждой точке максимального значением КПД при работы в режиме турбины или насоса, данные значения используют как исходные для определения масштабируемых потерь при работе турбины или насоса соответственно. Значения удельной скорости на разных машинах разных производителей в одних и тех же условиях эксплуатации опытного образца идентичны, и возможно заранее зафиксировать в спецификации значения d![]() ,
, , d
и
. Также необходимо определить общие значения d
![]() ,
, , d
и
для сравнительного модельного испытания.
5.3 Параметры для увеличения КПД удельной гидравлической энергии
Исследуемая гидравлическая машина описывается показателем своей удельной скорости, коэффициенты d![]() и
и для модели с гладкой поверхностью, требуемые для использования в формуле приращения, могут быть определены посредством уравнений, приведенных в таблицах 4-7.
Данные формулы применимы в пределах диапазона удельной скорости, представленного в примечании к каждой таблице.
Примечание - В случае выхода удельной скорости за пределы данных диапазонов уравнения не подтверждаются аналитическими или экспериментальными данными и могут быть некорректными. Однако даже в случае выхода за пределы границ данных диапазонов прилагаемые ведомости Excel предлагают значения приращения, рассчитываемые на основе данных формул. Указанные значения приращения приведены справочно. Если их используют для оценки результатов испытаний моделей согласно договору, то заинтересованным сторонам необходимо согласовать это заранее.
5.3.1 Турбины Френсиса
Таблица 4 - Индекс масштабируемой потери d![]() и фактор скорости
и фактор скорости для турбин Френсиса
Секция компонента | d | |
Спиральная камера | d |
|
Статорные колонны | d |
|
Направляющие лопатки | d |
|
Рабочее колесо | d |
|
Отсасывающая труба | d |
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
5.3.2 Турбонасосы
5.3.2.1 Работа в режиме турбины
Таблица 5 - Индекс масштабируемой потери d![]() и фактор скорости
и фактор скорости для турбонасосов в режиме турбины
Секция компонента | d | |
Спиральная камера | d |
|
Статорные колонны | d |
|
Направляющие лопатки | d |
|
Рабочее колесо | d |
|
Отсасывающая труба | d |
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
5.3.2.2 Работа в режиме насоса
Таблица 6 - Индекс масштабируемой потери d![]() и фактор скорости
и фактор скорости для турбонасосов в режиме насоса
Секция компонента | d | |
Спиральная камера | d |
|
Статорные колонны | d |
|
Направляющие лопатки | d |
|
Рабочее колесо | d |
|
Отсасывающая труба | d |
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
5.3.3 Машины осевого потока
Таблица 7 - Индекс масштабируемой потери d![]() и фактор скорости
и фактор скорости для машин осевого потока
Секция компонента | d | |
Рабочее колесо | d |
|
Все стационарные части | d |
|
Примечание - Вышеприведенные формулы действительны для 0,25 | ||
5.4 Параметры для увеличения КПД мощности. Трение диска
Для расчета Т и
(в соответствии с D.3 приложения D) используются уравнения, приведенные ниже. Данные уравнения применимы в пределах диапазона удельной скорости, указанного для каждого уравнения.
Примечание - В случае выхода за пределы данных диапазонов удельной скорости формулы становятся необоснованными с точки зрения аналитических или экспериментальных данных и могут быть некорректными. Однако даже в случае выхода за пределы границ данных диапазонов они могут быть использованы для оценки результатов испытаний моделей согласно договору по согласованию заинтересованных сторон.
1) Турбины Френсиса:
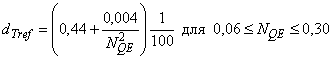 , (16)
, (16)
![]() или 1,0 (используют большее из двух значений). (17)
или 1,0 (используют большее из двух значений). (17)
2) Турбонасосы:
a) при работе в режиме турбины:
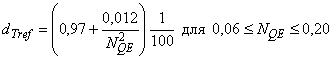 ; (18)
; (18)
![]() или 1,0 (используют большее из двух значений); (19)
или 1,0 (используют большее из двух значений); (19)
b) При работе в режиме насоса:
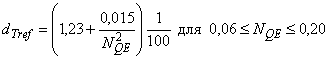 ; (20)
; (20)
![]() или 1,0 (используют большее из двух значений). (21)
или 1,0 (используют большее из двух значений). (21)
6 Преобразование характеристик модели в рабочие характеристики опытного образца. Основные формулы
6.1 Основные положения
Формулы, приведенные в 6.2-6.6, относятся к преобразованию рабочих характеристик гомологической модели в рабочие характеристики опытного образца для сходных гидравлических условий.
На основе дополнительных данных модели и опытного образца, таких как n, D, g и , могут быть рассчитаны соответствующие рабочие характеристики опытного образца.
В случае с нерасчетными точками в формулах (22)-(33) следует использовать ,
и
, рассчитанные для точки максимального КПД. Необходимо отметить, что данное преобразование обеспечивает немного меньшее приращение КПД для нерасчетных точек по сравнению с точкой максимального КПД.
6.2 Гидравлический КПД
Гидравлический КПД опытного образца гидравлической машины может быть рассчитан с помощью формулы:
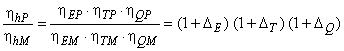 . (22)
. (22)
Математическое преобразование приводит к множителю ![]() . После сокращения членов второго и более высокого порядков может быть применена представленная ниже формула. Она отражает несущественное отклонение от точной формулы, но приводит к постоянному значению суммы:
. После сокращения членов второго и более высокого порядков может быть применена представленная ниже формула. Она отражает несущественное отклонение от точной формулы, но приводит к постоянному значению суммы:
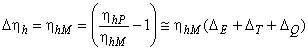 . (23)
. (23)
В случае с машинами осевого потока с аналогичными интервалами, ![]() . Вышеприведенная формула преобразуется в:
. Вышеприведенная формула преобразуется в:
![]() (24)
(24)
или
![]() . (25)
. (25)
В случае если гидравлический КПД модели выше, чем принятый максимальный гидравлический КПД (
![]() ), считается, что нормированные значения потерь, принятые в настоящем стандарте (d
), считается, что нормированные значения потерь, принятые в настоящем стандарте (d![]() , d
, d,
![]() ), равномерно уменьшаются посредством умножения их на
), равномерно уменьшаются посредством умножения их на ![]() . Если данные значения приращения используют для оценки результатов договорных модельных испытаний, участникам договора необходимо определить это заранее.
. Если данные значения приращения используют для оценки результатов договорных модельных испытаний, участникам договора необходимо определить это заранее.
Примечание - "Принятый максимальный гидравлический КПД ![]() " определяется как КПД, возникающий при значениях
" определяется как КПД, возникающий при значениях ,
и объемного КПД
, представленных в настоящем стандарте, основываясь на предположении об отсутствии кинетических потерь.
![]() .
.
6.3 Удельная гидравлическая энергия
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений.
Работа в режиме турбины (в соответствии с примечанием к 6.6):
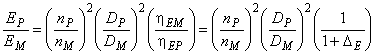 . (26)
. (26)
Работа в режиме насоса:
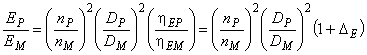 . (27)
. (27)
6.4 Расход воды
В гидравлически идентичных условиях расход преобразуется по следующим формулам.
Работа в режиме турбины (в соответствии с примечанием к 6.6):
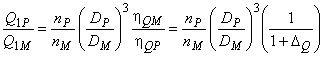 . (28)
. (28)
Работа в режиме насоса:
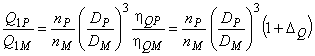 . (29)
. (29)
6.5 Крутящий момент
В гидравлически идентичных условиях крутящий момент конвертируется посредством следующих уравнений.
Работа в режиме турбины (в соответствии с примечанием к 6.6):
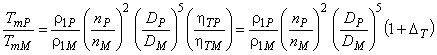 . (30)
. (30)
Работа в режиме насоса:
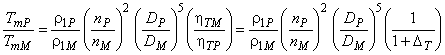 . (31)
. (31)
6.6 Мощность
В гидравлически идентичных гомологических условиях мощность преобразуется посредством следующих уравнений.
Работа в режиме турбины (в соответствии с примечанием к 6.6):
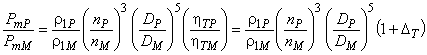 . (32)
. (32)
Работа в режиме насоса:
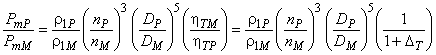 . (33)
. (33)
Примечание - Обычно при расчете рабочих характеристик турбины в первую очередь рассчитывают значение n, соответствующее указанному напору опытного образца турбины Е
. Затем с помощью графиков рабочих характеристик модели определяют значения
и Q
(и/или P
), соответствующие данному n
.
В данном преобразовании значение n рассчитывают на основе следующей формулы с учетом масштабного эффекта на Е
:
![]() .
.
Затем значения и Q
(и/или P
) модели конвертируют в значения опытного образца.
Для конвертирования используют формулу (22).
Для конвертирования других рабочих характеристик, таких как Q и P
, используются следующие формулы с учетом масштабного эффекта:
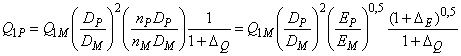
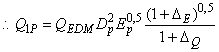
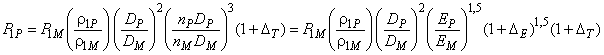
![]() .
.
6.7 Требуемые исходные данные
Исходные данные, требуемые для расчета рабочих характеристик опытного образца, подробно представлены в таблице 8.
Таблица 8 - Исходные данные, требуемые для расчета рабочих характеристик опытного образца
Исходные данные | Модель | Опытный образец | Примечание | ||
а) для конвертирования точки максимального КПД | |||||
Эксплуатационные данные | Делительный диаметр | D | D | ||
Скорость | n | n | n | ||
Сток | Q | - | |||
Удельная гидравлическая энергия | E | - | или H | ||
Гидравлический КПД | - | ||||
Температура воды | t | t | |||
Данные для приращения | Шероховатость | Спиральная камера | Ra | Ra | |
Статорные колонны | Ra | Ra | |||
Направляющие лопатки | Ra | Ra | |||
Лопасти рабочего колеса | Ra | Ra | |||
Шероховатость | Отсасывающая труба | Ra | Ra | ||
Данные для приращения | Внешняя поверхность рабочего колеса | Ra | Ra | ||
Стационарная часть, выходящая на рабочее колесо | Ra | Ra | |||
Размеры, приведенные ниже, необходимы, только если геометрия уплотнителя рабочего колеса модели отличается от опытного образца | |||||
Данные для изменения | Зазоры уплотнителя | С | С | Внешний уплотнитель, сторона ступицы | |
С | С | Внутренний уплотнитель, сторона ступицы | |||
С | С | Внешний уплотнитель, сторона обода | |||
С | С | Внутренний уплотнитель, сторона обода | |||
Радиус уплотнителей | R | R | Внешний уплотнитель, сторона ступицы | ||
R | R | Внутренний уплотнитель, сторона ступицы | |||
R | R | Внешний уплотнитель, сторона обода | |||
R | R | Внутренний уплотнитель, сторона обода | |||
Длина уплотнителя | L | L | Внешний уплотнитель, сторона ступицы | ||
L | L | Внутренний уплотнитель, сторона ступицы | |||
L | L | Внешний уплотнитель, сторона обода | |||
L | L | Внутренний уплотнитель, сторона обода | |||
b) для расчета режима работы турбины/насоса | |||||
Общее | Плотность воды | ||||
Для расчета рабочих характеристик турбины | Скорость | n | n | n | |
Расход | Q | ||||
Удельная гидравлическая энергия | E | или H | |||
Мощность | (P | ||||
Гидравлический КПД | |||||
Для расчета рабочих характеристик насоса | Скорость | n | n | ||
Расход | Q | ||||
Удельная гидравлическая энергия | E | E | или H | ||
Мощность | (P | ||||
Гидравлический КПД | |||||
| |||||
7 Алгоритм расчета
Порядок преобразования рабочих характеристик гидравлической модели в рабочие характеристики опытного образца включает в себя следующие шаги:
- шаг 1 Расчет удельной скорости N в точке максимального КПД.
- шаг 2 Расчет индекса масштабируемой потери d![]() и индекса скорости
и индекса скорости каждого компонента в соответствии с полученным ранее значением N
.
- шаг 3 Расчет индекса потери d и измерительного индекса
для приращения потери на трение диска.
- шаг 4 Определение качества поверхности, выраженного в Ra.
- шаг 5 Определение геометрических данных уплотнителей рабочего колеса, если они не являются подобными.
- шаг 6 Расчет индивидуальных значений приращения по формуле:
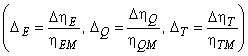 .
.
- шаг 7 Расчет рабочих характеристик опытного образца.
Прилагаемая схема отражает весь процесс, начиная с расчета удельной скорости и заканчивая расчетом рабочих характеристик опытного образца.
Шаг 1 | Расчет удельной скорости N в точке максимального КПД: |
Шаг 2 | Расчет индекса масштабируемой потери d и индекса скорости каждого компонента |
Шаг 3 | Расчет индекса потери d и измерительного индекса для приращения потери на трение диска |
Шаг 4 | Определение качества поверхности, выраженного в Ra |
Шаг 5 | Определение геометрических данных уплотнителей рабочего колеса, если они не являются гомологическими |
Шаг 6 | Расчет индивидуальных значений приращения с помощью формул (8)-(10), (12), (14): : формулы (8)-(10) : формула (12) : формула (14) |
Шаг 7 | Расчет рабочих характеристик опытного образца с помощью формул (22)-(33). Ниже приведен пример для работы в режиме турбины: , |
Рисунок 6 - Шаги расчета значений приращения
Приложение А
(обязательное)
Основные формулы и их приближенные выражения
А.1 Основные положения структуры потерь и масштабного эффекта
Формулы расчета масштабного эффекта, указанные в настоящем стандарте, получены на следующей основе.
А.1.1 Структура потерь и составляющие производительности
Как показано на рисунках А.1 и А.2, потери в гидравлических машинах классифицируются на основании четырех составляющих потерь.
Четыре составляющие:
- Удельные потери гидравлической энергии E;
- Потери при утечке q;
- Потери на трение диска P;
- Потери на трение в подшипниках P.
В зависимости от каждого типа потери выделяются следующие составляющие производительности:
- КПД удельной гидравлической энергии ;
- коэффициент заполнения ;
- коэффициент полезного действия ;
- механический коэффициент полезного действия .
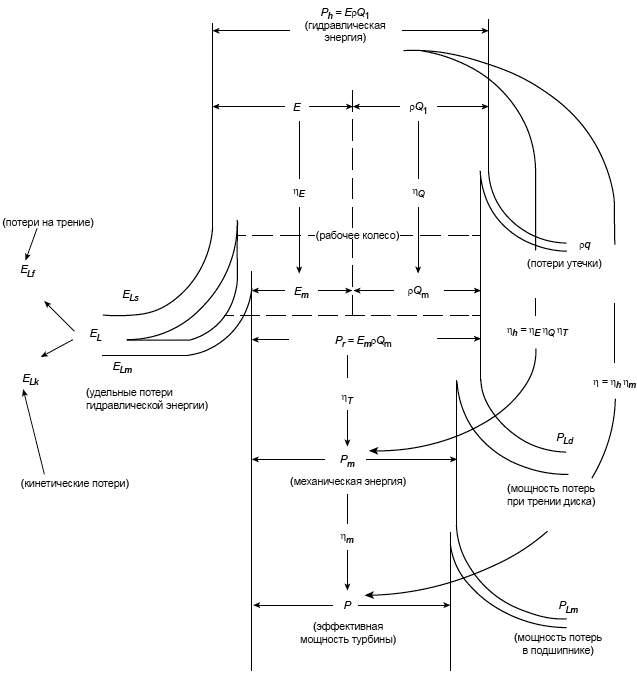
Рисунок А.1 - Диаграмма движения потока в турбине
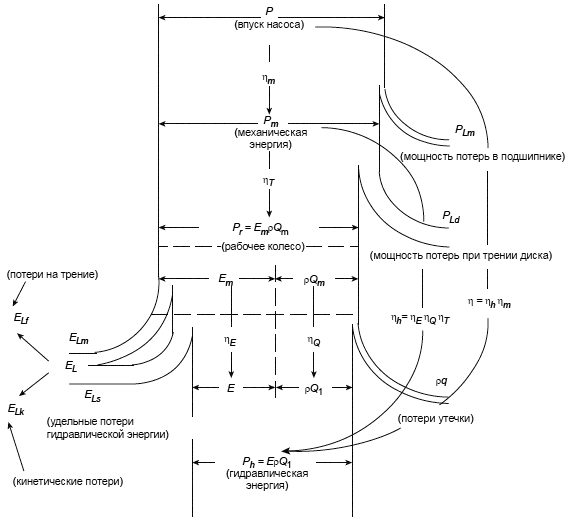
Рисунок А.2 - Диаграмма движения потока насоса
Коэффициент P/P
(для турбины) или P
/P
, (для насоса) определяется как гидравлический коэффициент полезного действия
, что выражается как произведение
,
и
.
В настоящем стандарте масштабный эффект рассматривают с точки зрения гидравлического коэффициента полезного действия , при этом механический коэффициент полезного действия
в настоящем стандарте не учитывается.
А.1.2 Аналогичные условия эксплуатации
Аналогичные условия эксплуатации рабочего (или крыльчатого) колеса в модели и опытном образце достигаются при условии аналогичных треугольников скоростей на входе и выходе рабочего (или крыльчатого) колеса. Однако аналогичность треугольников скоростей на входе и выходе невозможно поддерживать одновременно ввиду различного давления. Теоретическими расчетами доказано, что при условии достижения аналогичных треугольников скоростей на стороне высокого давления рабочего (или крыльчатого) колеса отклонение треугольника скоростей на стороне низкого давления незначительно и не влияет на производительность. Таким образом, для настоящего стандарта принимают, что аналогичные условия эксплуатации в модели и опытном образце достигаются, когда треугольник скоростей поддерживается на стороне высокого давления рабочего (или крыльчатого) колеса [2]. Если таких условий удается достичь в модели и опытном образце, параметры производительности рабочего (или крыльчатого) колеса Е, Q
и Р
можно преобразовывать в соответствии с законом подобия, который приводится ниже, без каких-либо поправок на масштабный эффект:
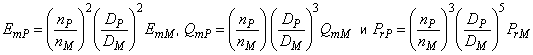 . (А.1)
. (А.1)
А.1.3 Изменение производительности [7]
Когда ,
и
опытного образца отличаются от тех же параметров модели вследствие масштабного эффекта, параметры производительности опытного образца можно рассчитать по следующим формулам (Е
, Q
и Р
аналогичны для модели и опытного образца):
- для турбин:
![]()
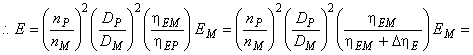
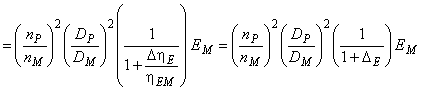 , (А.2)
, (А.2)
![]()
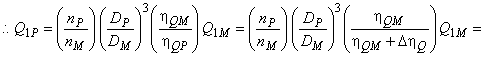
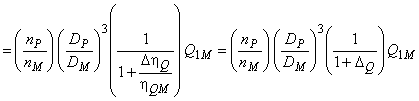 , (А.3)
, (А.3)
- для насосов:
![]()
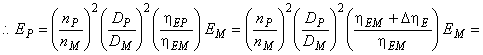
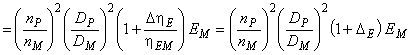 . (А.4)
. (А.4)
![]()
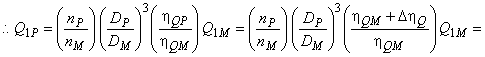
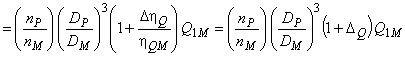 . (А.6)
. (А.6)
![]()
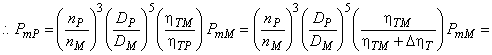
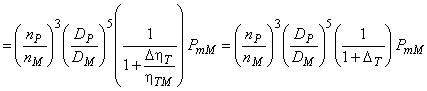 . (А.7)
. (А.7)
Масштабный эффект производительности нерасчетных точек сложен. В настоящем стандарте принимается, что производительность в нерасчетных точках рассчитывают тем же способом, что и при использовании формул (А.2)-(А.7) с ,
и
, полученными в точке максимальной эффективности.
А.1.4 Масштабируемые потери
Как указано в 4.1.1, следующие потери зависят от масштабного эффекта на разницу числа Рейнольдса и относительной шероховатости:
- удельные потери гидравлической энергии, обусловленные трением, Е;
- потери расходом, q;
- потери, вызванные трением диска, P.
Значение масштабируемых потерь основывалось на предположении о соотношении их с общими потерями, обозначаемыми как V, которое могло быть представлено как некая постоянная величина для каждого типа гидравлических машин. Данное предположение привело к большому значению масштабируемых потерь для турбин с низкой производительностью и в результате дало необоснованно высокое увеличение.
Настоящий стандарт, однако, принимает, что относительная величина каждой масштабируемой потери для каждого параметра соответствующей производительности, за исключением слива (![]() и
и ![]() ), дается как функция удельной скорости для каждого типа машины. Это позволяет рассчитать масштабный эффект по каждому компоненту эффективности отдельно, а также рассчитать изменения каждого параметра производительности, как указано в разделе 3.
), дается как функция удельной скорости для каждого типа машины. Это позволяет рассчитать масштабный эффект по каждому компоненту эффективности отдельно, а также рассчитать изменения каждого параметра производительности, как указано в разделе 3.
А.2 Погрешность формулы расчета масштабного эффекта
А.2.1 Коэффициент масштабируемых потерь по удельной гидравлической энергии и удельная производительность гидравлической энергии
Необходимо отметить, что идентичные показатели, которые можно напрямую перенести с модели на опытный образец путем применения закона гидравлического подобия, составляет Е, а не Е. Для более простого объяснения формулы отклонения в таблицу А.1 введены новые параметры
и
, обеспечивающие использование Е
.
Таблица А.1 - Соотношение и
и удельной производительности гидравлической энергии
Турбина | Насос | |
Определение |
|
|
Определение |
|
|
Новое определение |
Поскольку Е | |
Поскольку Е | ||
Соотношение между |
|
|
Смещение |
|
|
Новое определение нием |
|
|
| ||
А.2.2 Пошаговое увеличение удельной производительности гидравлической энергии
Как показано в А.2.1, выражается различными уравнениями для турбин и для насосов. Это вызвано отличием в выражении
; для турбин Е
выступает как числитель, а для насосов Е
- знаменатель. Кроме того, необходимо отметить, что немасштабируемые потери как
- это общая величина для модели и для опытного образца, a
- нет. Масштабируемые потери
могут быть увеличены на коэффициент трения от модели к опытному образцу, а
- нет.
Соответственно, может быть выведена следующая формула для с учетом формулы масштабного эффекта, представленная в таблице А.2.
Таблица А.2 - Расчет гидравлической энергии с учетом формулы масштабного эффекта
Турбина | Насос | |
|
Так как |
Так как |
Конвертирование потери по трению |
Где | |
|
|
|
| Так как | Так как |
Формула приблизитель- ности, применимая в данном стандарте | Так как | Так как |
Необходимо отметить, что уравнение для получения для турбин отличается от уравнения для насосов. Однако путем введения формулы приблизительности (нижние ячейки таблицы) для турбин и для насосов в настоящем стандарте используется общая формула.
А.2.3 Пошаговое увеличение коэффициента наполнения
Как и для , уравнение для
выражено по-разному для турбин и для насосов. Поскольку показатель расхода, который напрямую переносится на опытный образец, равен Q
(а не Q
), коэффициент потери по утечке q превышает Q
и выражается, как показано в таблице А.3, суммой пошагового увеличения коэффициента наполнения
.
Таблица А.3 - Пошаговое увеличение коэффициента наполнения
Турбина | Насос | |
Определение |
|
|
Конвертирование потери по утечке q |
где Область зазора затвора через несколько секций Когда размеры затвора и связанных деталей геометрически гомологичны, | |
|
|
|
Формула приблизитель- ности, применяемая в настоящем стандарте | Поскольку и | |
А.2.4 Пошаговое увеличение коэффициента мощности (трение диска)
В данном случае мощность рабочего (или крыльчатого) колеса Р идентична и переносится с модели на опытный образец в соответствии с законом гидравлического подобия (не Р
). Соответственно, масштабируемые потери по трению диска
, которые определяются как (Р
/Р
) увеличиваются по следующим формулам:
Таблица А.4 - Пошаговое увеличение коэффициента мощности
Турбина | Насос | |
Определение |
|
|
Условия гомологич- ности | Поскольку Р | |
Определение |
|
|
Выражение |
|
|
Пошаговое увеличение | Поскольку 1) и Р
| |
|
| |
Формула приблизи- тельности, применимая в данном стандарте | Так как | Так как |
Как видно из таблицы А.4, формула получения для турбин и насосов различна. Однако в результате применения формулы приблизительности (нижние ячейки таблицы) общая формула может быть использована и для турбин, и для насосов.
Приложение В
(обязательное)
Масштабный эффект на удельные потери гидравлической энергии машин радиального типа
В.1 Масштабный эффект на потери на трение
В.1.1 Масштабный эффект на коэффициент потери на трение
Значения масштабного эффекта незначительно отличаются для плоской пластины и трубы. Настоящий стандарт устанавливает, что коэффициент потери на трение в различных проходах машин радиального типа варьируется согласно формуле Кольбрука, описывающей поток в трубе.
Ввиду того, что оригинальная формула Кольбрука дается как имплицитная функция (см. рисунок В.1), невозможно получить значение коэффициента потери простым вычислением. В настоящем стандарте предлагается новая формула, предложенная Нихтавицем, которая представляет собой эксплицитную функцию и дает практически те же значения, что и формула Кольбрука [4, 6].
Новая формула:
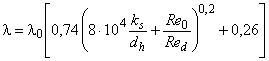 , (В.1)
, (В.1)
где Re=7·10
;
=0,0085;
k - шероховатость песка;
d - гидравлический диаметр трубы/канала/водовода;
Re - число Рейнольдса в трубе;
![]() .*
.*
________________
* Формула соответствует оригиналу. Вероятно, должно быть ![]() . - .
. - .
Сравнение оригинальной формулы Кольбрука и новой формулы показано на рисунке В.1
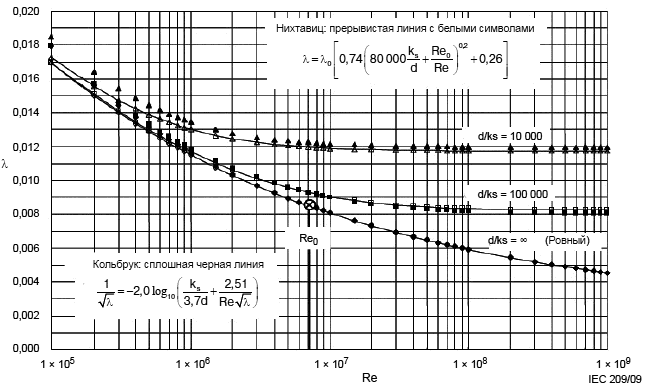
Рисунок В.1 - Коэффициент потерь против числа Рейнольдса и шероховатости поверхности
Примечание 1 - В некоторых экспериментах с шероховатостью песка наблюдается, что потери по трению на неровной поверхности, имеющей шероховатость в определенном диапазоне, те же самые, что и на совершенно ровной поверхности. В данном случае ограничение по шероховатости называют "допустимая шероховатость", а поверхность, имеющая шероховатость в установленных рамках, считается "гидравлически ровной" (см. кривые В и С на рисунке В.2).
В отношении коэффициента потери по неровной поверхности о некоторых экспериментально полученных результатах, отраженных на рисунке В.2, говорили в прошлом. По данным результатам характеристики коэффициента потери по трению отражают другую тенденцию в переходной зоне между категориями ровных и шероховатых поверхностей [13-16].
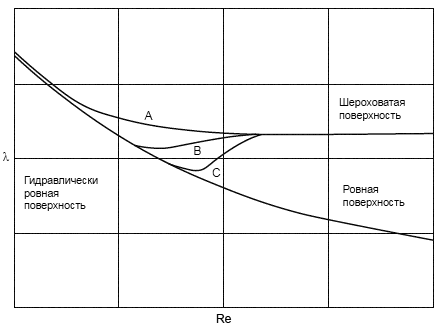
Рисунок В.2 - Различные характеристики в переходной зоне
Кривая А рассматривается в экспериментах с вполне шероховатой трубой (Муди) или турбиной шероховатой модели (Генри) [17]. Они отражают, что допустимая шероховатость очень мала и характеристики потери по трению показаны в виде асимптотической кривой. Формула Кольбрука описывает данные характеристики. В данном случае допустимая шероховатость практически равна нулю.
Зависимость В отражает данные по шероховатости песка, полученные опытным путем (Никурадзе). В данном случае допустимая шероховатость приводится приблизительно:
![]() .
.
Характеристики, выраженные кривой С, получены в результате опытов с рифленой поверхностью или с зернистой поверхностью, образованной отдельными острыми песчинками. В данном случае допустимая шероховатость становится выше.
Настоящий стандарт рассматривает допустимую шероховатость в очень маленьком проценте, и формулу Кольбрука допускается применять для расчетов масштабного эффекта потерь на трение.
В.1.2 Соотношение шероховатости песка k и среднеарифметической шероховатости Ra
Соотношение шероховатости песка k и среднеарифметической шероховатости Ra широко описано в современной литературе [14]. Однако для целей настоящего стандарта принято, что среднеарифметическую шероховатость возможно преобразовать в шероховатость песка следующим уравнением:
![]() . (В.2)
. (В.2)
Примечание 2 - В случае использования устаревших опытных образцов машин с поверхностями, значительно поврежденными коррозией, где значения Ra превышают 50 , рекомендуется учитывать следующие факторы при расчетах шероховатости поверхности.
Во-первых, расчет шероховатости вызывает сложность. В старых машинах значения шероховатости часто превышают существующие шкалы переносных измерительных приборов. В данных ситуациях рекомендуется брать в расчет изложницы в наиболее характерных местах, используя соответствующий пластичный материал, и измерять шероховатость изложниц с помощью прибора измерения координат для нахождения эквивалентного значения Ra. Другие способы измерения также допускается использовать (как, например, глубиномеры, эталоны для измерения шероховатости и т.д.) по согласованию сторон. Однако в данной ситуации эквивалентная шероховатость Ra должна определяться с наибольшей тщательностью, поскольку на нее влияют профиль шероховатости и плотность рассеянной пустоты.
Во-вторых, необходимо тщательно отобрать основные значения шероховатости из результатов измерения. Основываясь на научных знаниях в этой области, считают, что глубокие пустоты не влекут за собой больших потерь, а отражают их измеренные значения. Действительно, линии потока, пересекающие данные области, продвигаясь через пустоты, не достигают их дна, а значит, не создают больших потерь. Соответственно, в данном случае рекомендуется игнорировать области с глубокими пустотами при измерении шероховатости (глубокими пустотами считаются углубления более 1,5 мкм).
При условии учета вышеупомянутых замечаний соотношение шероховатости песка k и среднеарифметической шероховатости Ra в соответствии с формулой (В.2) [или формулой 2] допускается также применять в случае с поверхностями, значительно поврежденными коррозией.
Тогда формула (В.1) примет следующий вид:
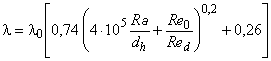 , (В.3)
, (В.3)
B.2 Расчет суммарной удельной гидравлической энергии узлов машины радиального типа
В.2.1 Коэффициент потери на трение каждого узла [9]
В случае применения формулы (В.3) для каждого узла получаем:
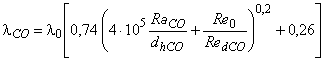 , (В.4)
, (В.4)
где индекс СО - обозначения отдельного узла;
Re - число Рейнольдса при прохождении жидкости через узел;
![]() .*
.*
________________
* Формула соответствует оригиналу. Вероятно, должно быть ![]() . - .
. - .
Число Рейнольдса для машины может быть записано как:
![]() ,
,
где u - окружная скорость рабочего (или крыльчатого) колеса на делительном диаметре;
D - делительный диаметр машины.
Число Рейнольдса для прохождения компонентов может быть выражено следующим образом:
![]() .
.
Путем замены Re в формуле (В.4) получают:
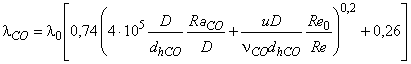 . (В.5)
. (В.5)
При введении двух новых эффектов и
формулу (В.5) можно записать следующим образом:
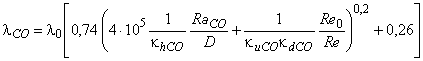 , (В.6)
, (В.6)
где - фактор размера при проходе компонента;
![]() , (В.7)
, (В.7)
- фактор скорости потока при проходе компонента;
![]() . (В.8)
. (В.8)
Когда даны геометрические размеры прохода основного потока воды, как указано на рисунке В.3, можно рассчитать значения и
по формулам (В.9) и (В.10) соответственно.
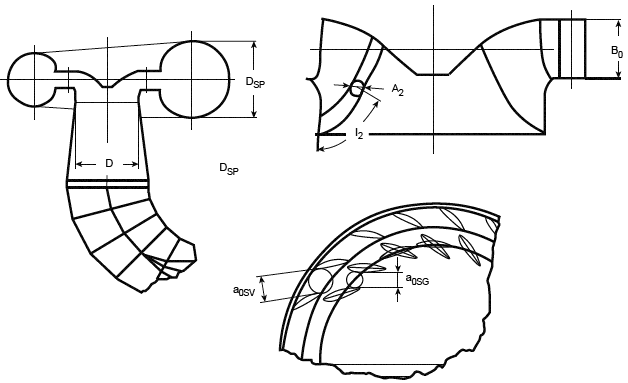
Рисунок В.3 - Показательные размеры прохождения компонентов
Фактор скорости потока:
![]() ,
,![]() ,
,![]() ,
,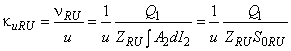 ,
,
![]() . (В.9)
. (В.9)
Фактор размеров:
![]() ,
,![]() ,
,![]() ,
,
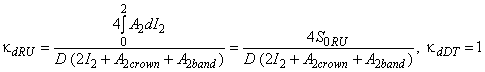 , (В.10)
, (В.10)
где S - площадь поперечного сечения трубопровода между лопастями рабочего колеса на выпускной секции;
Z - число крыльев или лопастей.
Значения и
рассчитывают для машин средней конструкции, которые используют в промышленности в настоящее время. Их стандартизованные значения указаны в С.5 приложения С.
В.2.2 Отклонение от формулы масштабного эффекта для узловой схемы машины
Стандартная масштабируемая потеря определяется для каждого прохода компонента как масштабируемая потеря ровной поверхности, работающей по уравнению Re
=Re
. Это означает, что значения
![]() соотносятся с
соотносятся с ![]() . Соответственно, уравнение, приведенное в таблице А.2, 2), может быть представлено для каждого прохода компонентов в следующем виде:
. Соответственно, уравнение, приведенное в таблице А.2, 2), может быть представлено для каждого прохода компонентов в следующем виде:
 . (В.11)
. (В.11)
![]() выражается следующим образом с помощью формулы (В.6):
выражается следующим образом с помощью формулы (В.6):
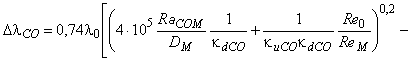
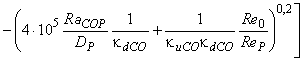 , (В.12)
, (В.12)
![]() - коэффициент потери, когда число Рейнольдса машины - это Re
- коэффициент потери, когда число Рейнольдса машины - это Re или число Рейнольдса прохода компонентов -
![]() .
.
Поскольку Re= Re
=7·10
и шероховатость поверхности эталонной машины ровная (а именно,
![]() )
) ![]() может быть представлено следующим образом:
может быть представлено следующим образом:
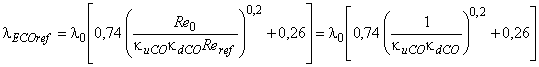 . (В.13)
. (В.13)
Тогда получается путем замены
![]() и
и ![]() в формулах (В.11), (В.12) и (В.13).
в формулах (В.11), (В.12) и (В.13).
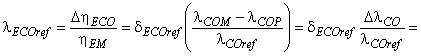
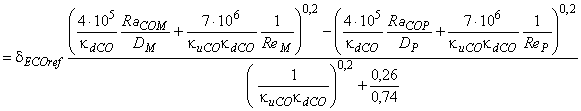
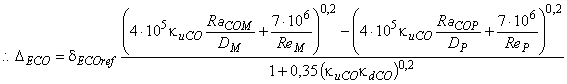 . (В.14)
. (В.14)
В целях упрощения вышеуказанная формула может быть написана следующим образом:
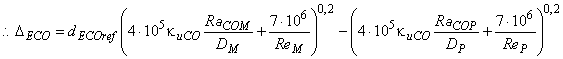 . (В.15)
. (В.15)
Значения ![]() приведены в В.4, а значения
приведены в В.4, а значения и
- В.5. Значения
![]() , которые рассчитываются из
, которые рассчитываются из ![]() и
и и
, указаны в В.6.
Затем рассчитывают суммарную удельную гидравлическую энергию для всей турбины по следующей формуле:
![]() . (В.16)
. (В.16)
В.3 Суммарное увеличение энергии для всей турбины
Объединив формулу (В.15) с формулой (В.16) и введя коэффициент исходной скорости С, получают:
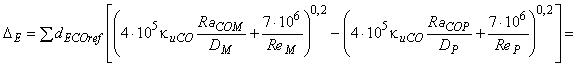
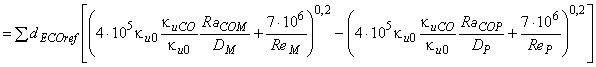 .
.
Если значения ![]() для всех модельных компонентов можно считать одинаковыми и заменить на
для всех модельных компонентов можно считать одинаковыми и заменить на ![]() , соответственно, заменить эти значения для проходов компонентами опытных образцов на
, соответственно, заменить эти значения для проходов компонентами опытных образцов на ![]() , формула примет следующий вид:
, формула примет следующий вид:
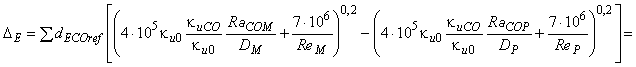
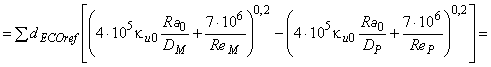
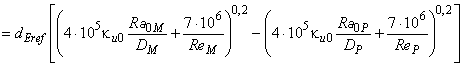 . (B.17)
. (B.17)
Формулу (B.17) допускается использовать для прямого пошагового увеличения удельной энергии по всей турбине.
Ввиду того, что потери по трению в рабочем колесе и направляющих лопастях составляют две трети общих потерь по трению, среднее значение и
используется в качестве коэффициента исходной скорости
. Кроме того, среднее значение Ra
и Ra
используют как эталонную шероховатость Ra
машины.
![]() , (В.18)
, (В.18)
![]() . (В.19)
. (В.19)
Значения ![]() и
и рассчитываются на основе d
![]() ,
, и
, указанных в (В.5) и (В.6), представлены в таблице (В.1).
Таблица В.1 - Расчетные значения индексов d,
Радиально-осевая турбина (турбина Френсиса) | Турбонасос | |
Работа в режиме насоса | Работа в режиме турбины | |
d | d | d |
|
|
|
Для применения формулы (В.17) необходимо сохранить ![]() и
и ![]() . Другими словами, шероховатость поверхности каждого прохода компонентов должна оставаться в рамках
. Другими словами, шероховатость поверхности каждого прохода компонентов должна оставаться в рамках ![]() и
и ![]() . Значения
. Значения ![]() , полученные на основе значений
, полученные на основе значений , представлены в (В.5), а требуемая шкала шероховатости для использования формулы (В.17) указана в таблице В.2.
Таблица В.2 - Критерии для шероховатости поверхности для применения формулы прямого пошагового увеличения
Уз- |
| Требуемый предел шероховатости поверхности | ||||||
Турбина Френсиса | Турбонасос (Т) | Турбонасос (Н) | модель | опытный образец | ||||
диапазон | средн. | диапазон | средн. | диапазон | средн. | |||
SP | 3,00 ~ 2,31 | 2,69 | 2,92 ~ 2,58 | 2,75 | 2,56 ~ 2,06 | 2,31 | (2,0 ~ 4,0)Ra | <3,0Ra |
SV | 1,40 ~ 2,03 | 1,60 | 1,78 ~ 2,56 | 2,03 | 1,53 ~ 2,04 | 1,72 | (1,5 ~ 3,0)Ra | <2,5Ra |
GV | 0,87 ~ 1,25 | 0,99 | 0,88 ~ 1,01 | 0,93 | 0,95 ~ 1,26 | 1,07 | (0,7 ~ 1,3)Ra | <1,3Ra |
RU | 1,17 ~ 0,83 | 1,01 | 1,16 ~ 1,00 | 1,08 | 1,06 ~ 0,83 | 0,94 | (0,7 ~ 1,3)Ra | <1,3Ra |
DT | 4,86 ~ 2,33 | 3,40 | 4,26 ~ 2,94 | 3,54 | 3,89 ~ 2,37 | 3,03 | (2,5 ~ 4,5)Ra | <4,0Ra |
Значения слева указывают самую низкую удельную скорость N | ||||||||
B.4 Относительные потери на машинах радиального типа
В.4.1 Основные положения
На основе изложенного в В.2 масштабируемые потери, рассматриваемые в настоящем стандарте, определяют для каждого отдельного компонента (спиральная камера, статорные колонны, направляющие лопасти, рабочее колесо, отводящая труба) следующим образом:
![]() ,
,
где ![]() - масштабируемое соотношение потерь удельной гидравлической энергии каждого компонента;
- масштабируемое соотношение потерь удельной гидравлической энергии каждого компонента;
Е - удельные потери гидравлической энергии, вызванные трением поверхности каждого компонента на точке максимальной эффективности, при фиксированном числе Рейнольдса;
Е - удельная гидравлическая энергия машины.
Для подсчета потери по трению в водоводах используют различные методы, представленные в [7].
Для спиральной камеры и отводящей трубы:
- потери на трения рассчитывают по модели эквивалентной трубы в соответствии с формулой Кольбрука, диаграммой Муди, формулой Блазиуса или формулой Никурадзе.
Для статорных колонн и направляющих лопастей:
- потери на трение прямоугольного водовода определяют как для плоской плиты;
- расчет пограничного слоя основан на распределении скорости основного потока, полученного в результате анализа невязких жидкостей в кубических футах в сутки (1 м=23,8 кубического фута).
Для рабочего колеса:
- расчет пограничного слоя основан на распределении скорости основного потока, невязких жидкостей в кубических метрах в сутки (1 м=23,8 кубического фута).
Оценку потери на трения путем расчета пограничного слоя проводят одним из следующих способов:
- интеграция потери энергии вследствие касательного напряжения в пограничном слое через всю область поверхности;
- рассеивание энергии скорости, полученной вследствие энергии скорости потока ниже по течению по тыльной стороне лопасти или крыла, которая может быть рассчитана на основе плотности энергии в пограничном слое.
Значения ![]() ,
, ,
и d
![]() , указанные в приложении В, подтверждены аналитическими и экспериментальными данными для следующих удельных скоростей:
, указанные в приложении В, подтверждены аналитическими и экспериментальными данными для следующих удельных скоростей:
- для турбин Френсиса | 0,06 |
- для турбонасосов | 0,06 |
Вне указанных интервалов данные значения могут быть некорректными. Соответственно, если уравнение суммы в настоящем стандарте применимо к уравнению тестовых результатов контрактной модели вне вышеуказанных удельных ограничений скоростей, заинтересованные стороны должны оговорить это в контракте.
Общие потери на трении по всей турбине ![]() , используемые для прямого пошагового увеличения гидравлической эффективности по всей турбине, также показаны в нижней части рисунков.
, используемые для прямого пошагового увеличения гидравлической эффективности по всей турбине, также показаны в нижней части рисунков.
В.4.2 Относительные масштабируемые потери гидравлической энергии турбины Френсиса
Значения ![]() , рассчитываемые для некоторых типичных моделей, зависят от удельных скоростей, как указано ниже. Для удобства зависимости в основном линейные.
, рассчитываемые для некоторых типичных моделей, зависят от удельных скоростей, как указано ниже. Для удобства зависимости в основном линейные.
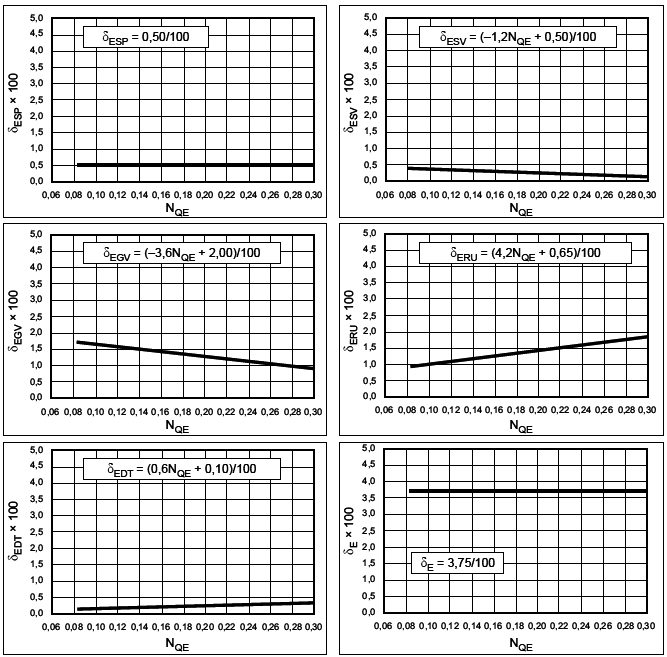
Рисунок В.4 - Относительные масштабируемые потери гидравлической энергии в каждом компоненте турбины Френсиса
Необходимо отметить, что абсцисса N представляет собой удельную скорость без учета размеров, определенную по ГОСТ 28842, которая задана как
![]() , где n - скорость вращения, с
, где n - скорость вращения, с, и Е - удельная гидравлическая энергия машины, Дж кг
.
В.4.3 Относительные масштабируемые потери гидравлической энергии обратимого турбонасоса
Значения соотношения масштабируемых потерь для турбонасосов рассчитывают отдельно для каждой работы турбины или насоса. Они зависят от удельной расчетной скорости точки максимальной эффективности в работе турбины или насоса соответственно.
а) При работе в режиме турбины
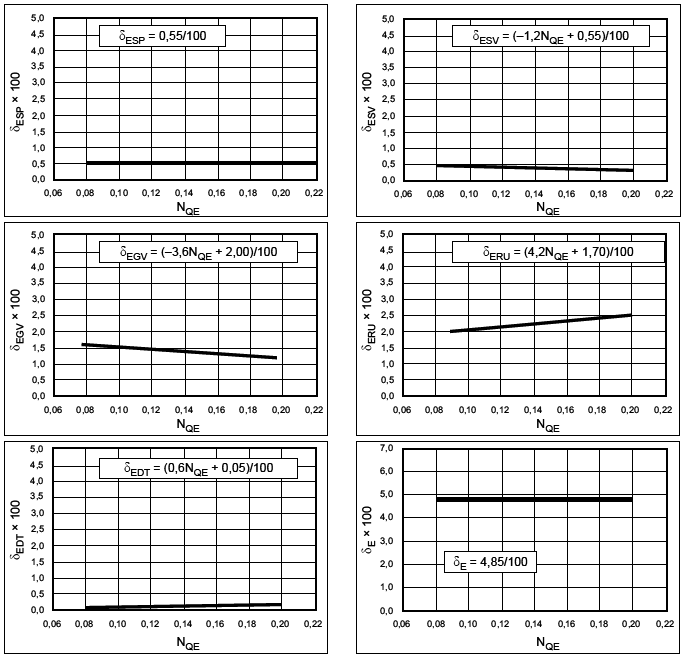
Рисунок В.5 - Относительные масштабируемые потери гидравлической энергии в каждом элементе турбонасоса при работе в режиме турбины
b) При работе в режиме насоса
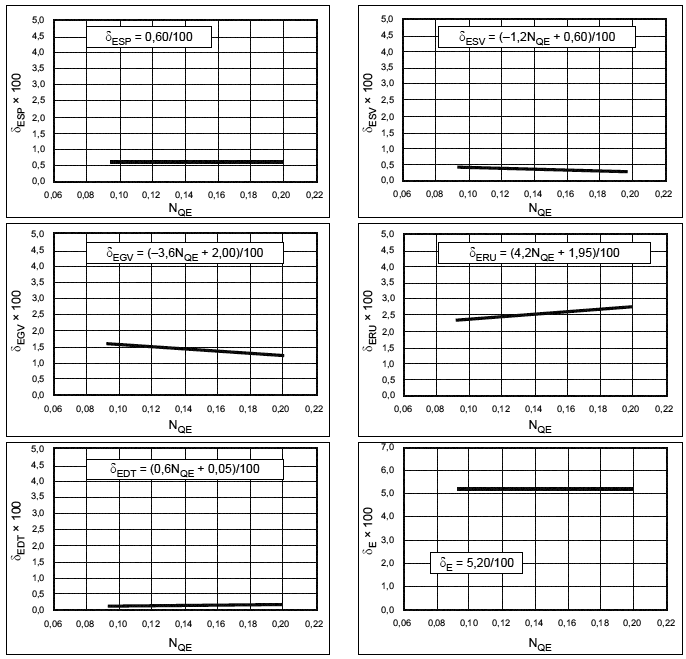
Рисунок В.6 - Относительные масштабируемые потери гидравлической энергии в каждом компоненте турбонасоса при работе в режиме насоса
В.5 Коэффициент скорости потока и размерный коэффициент для
машин радиального типа [9]
В.5.1 Основные положения
На основании стандартных геометрических данных для гидравлических машин рассчитывают коэффициент скорости потока , как указано в формуле (В.9), а также размерный коэффициент
, как указано в формуле (В.10), приведенной в В.2. Поскольку данные параметры используют для расчета d
![]() и формулой окончательного масштабного эффекта [формула (8) или формула В.17] в отношении экспонента 0,2, некоторое отклонение допустимо. Соответственно, рассчитываемые результаты приблизительно выражены в линейной зависимости для упрощения.
и формулой окончательного масштабного эффекта [формула (8) или формула В.17] в отношении экспонента 0,2, некоторое отклонение допустимо. Соответственно, рассчитываемые результаты приблизительно выражены в линейной зависимости для упрощения.
В.5.2 и
для турбины Френсиса
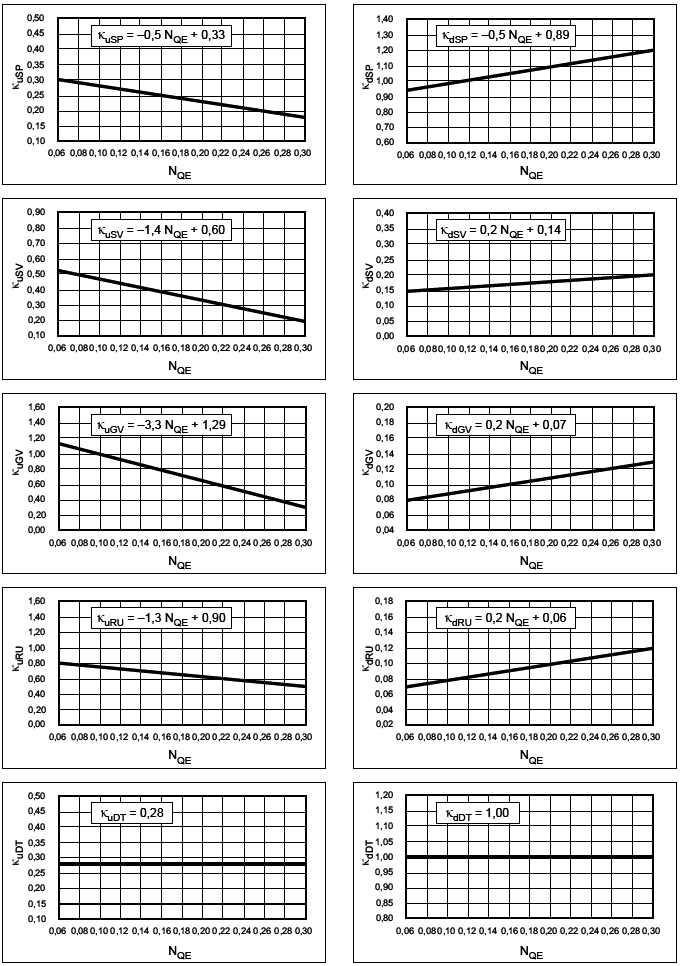
Рисунок В.7 - и
для каждого компонента турбины Френсиса
В.5.3 и
для турбонасоса
а) При работе в режиме турбины
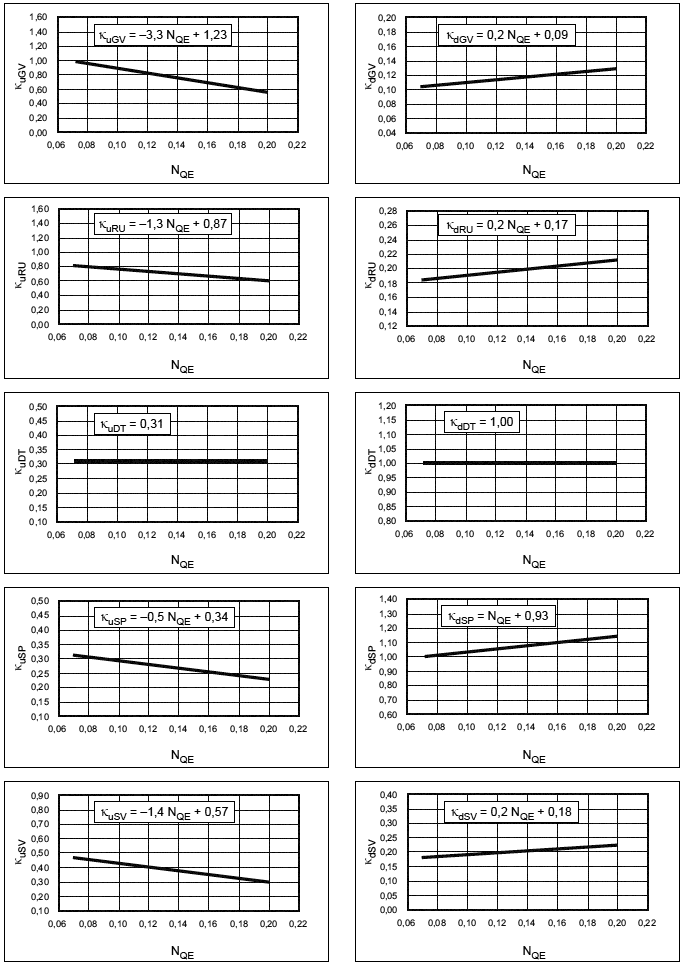
Рисунок В.8 - и
для каждого компонента турбонасоса при работе в режиме турбины
b) При работе в режиме насоса
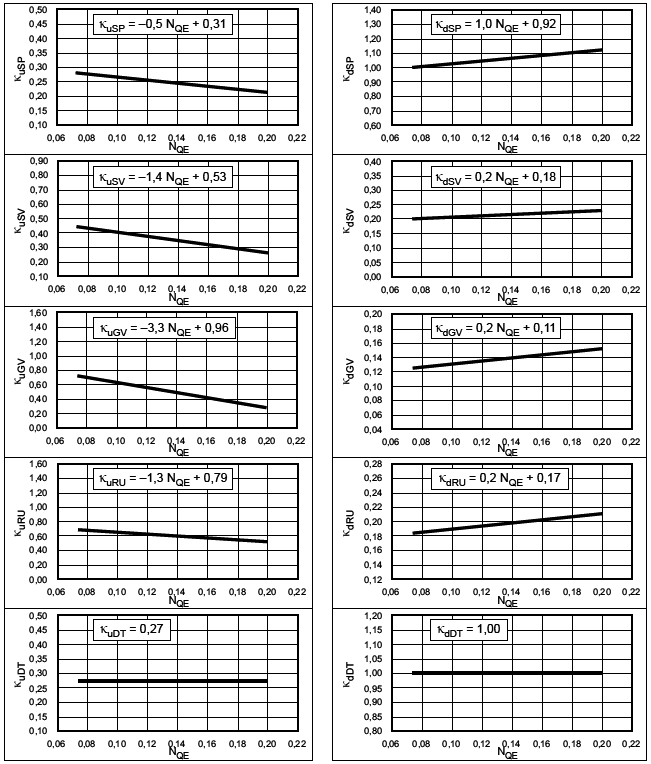
Рисунок В.9 - и
для каждого компонента турбонасоса при работе в режиме насоса
В.6 Коэффициент масштабированных потерь d![]()
В.6.1 Основные положения
На основе ![]() фактора скорости потока
фактора скорости потока и фактора размеров
коэффициент масштабируемых потерь d
![]() рассчитывают по схеме, указанной в 4.2.1. Рассчитываемые результаты d
рассчитывают по схеме, указанной в 4.2.1. Рассчитываемые результаты d![]() для удобства рассматривают в линейной зависимости.
для удобства рассматривают в линейной зависимости.
Общий коэффициент масштабируемых потерь d![]() , который предназначен для использования в прямом пошаговом увеличении удельной эффективности гидравлической энергии всей турбины (в соответствии с В.3 настоящего приложения), также показан в нижней части рисунков.
, который предназначен для использования в прямом пошаговом увеличении удельной эффективности гидравлической энергии всей турбины (в соответствии с В.3 настоящего приложения), также показан в нижней части рисунков.
B.6.2 d![]() и d
и d для турбины Френсиса
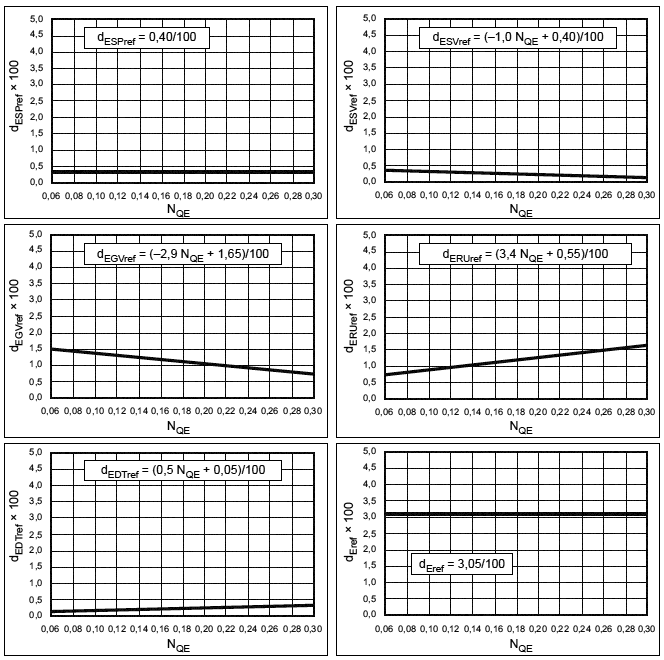
Рисунок В.10 - d![]() и d
и d для турбины Френсиса
B.6.3 d![]() и d
и d для турбонасоса
а) При работе в режиме турбины
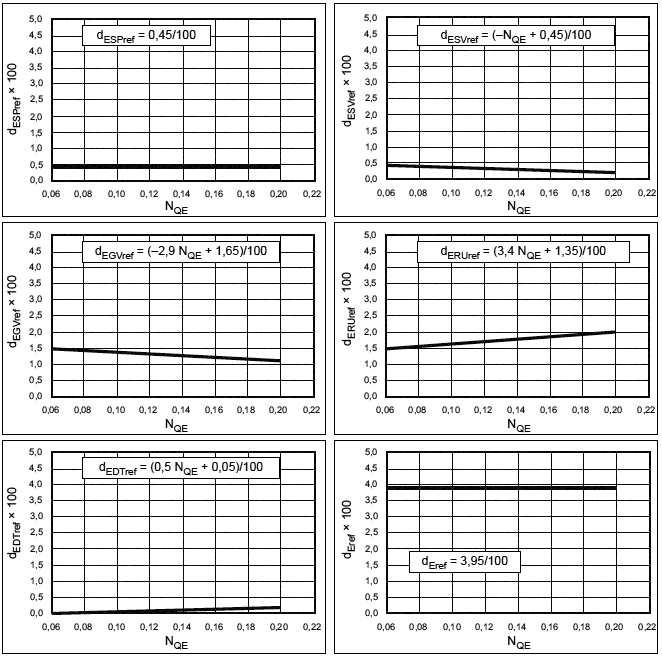
Рисунок В.11 - d![]() и d
и d для турбонасоса при работе в режиме турбины
b) При работе в режиме насоса
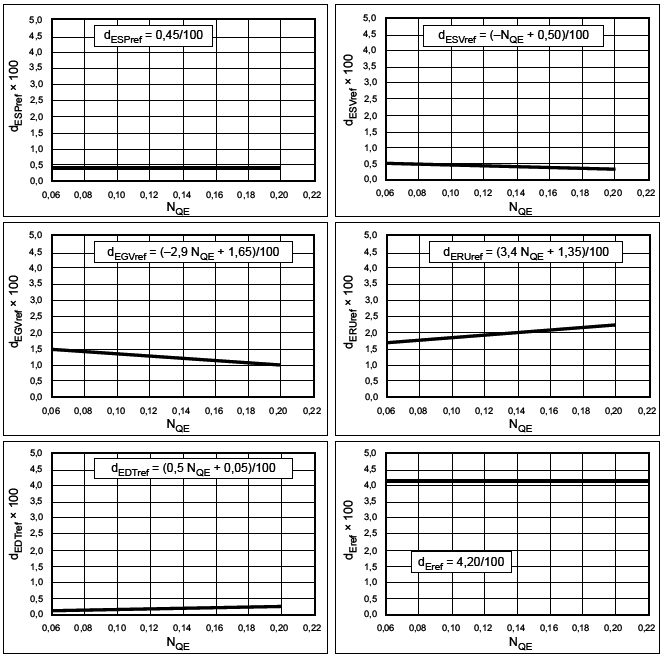
Рисунок В.12 - d![]() и d
и d для турбонасоса при работе в режиме насоса
Приложение С
(обязательное)
Масштабный эффект на удельные потери энергии машин осевого типа [10]
С.1 Масштабируемые потери машин осевого потока
Несмотря на то что в настоящее время отсутствует методика детального анализа масштабируемых потерь машин осевого типа, настоящий стандарт предписывает, что указанные потери можно рассматривать с двух сторон: для одной объектом будут лопасти рабочего колеса, для другой - другие стационарные компоненты.
Для масштабируемых потерь на лопастях рабочего колеса используют формулу расчета масштабного эффекта для плоской плиты [формула (5)]. Для стационарных деталей используют формулу для расчета потока в трубе [формула (1)], так же как и для турбин радиального потока.
С.2 Формула расчета масштабного эффекта для лопастей рабочего колеса [9]
Ниже приведена формула масштабного увеличения для лопастей рабочего колеса, выведенная из формулы расчета масштабного эффекта для плоской плиты:
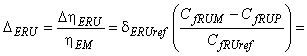

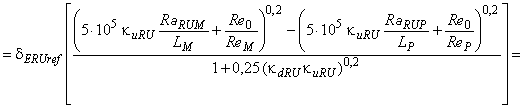
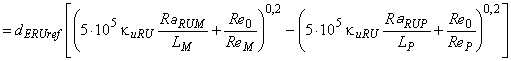 , (С.1)
, (С.1)
где ![]() - стандартизованные исходные масштабируемые потери для лопастей рабочего колеса при условии, что число Рейнольдса для машин Re
- стандартизованные исходные масштабируемые потери для лопастей рабочего колеса при условии, что число Рейнольдса для машин Re равно эталонному числу Рейнольдса (7·10
);
L - длина лопасти рабочего колеса;
w - относительная скорость потока на выходе рабочего колеса;
u - скорость лопастей рабочего колеса на периферии;
![]() - коэффициент скорости потока, проходящего через лопасти рабочего колеса:
- коэффициент скорости потока, проходящего через лопасти рабочего колеса:
![]() ,
,
![]() - стандартизованный фактор размеров для проходов лопастей рабочего колеса:
- стандартизованный фактор размеров для проходов лопастей рабочего колеса:
![]() ;
;
d![]() - коэффициент масштабируемых потерь для лопастей рабочего колеса:
- коэффициент масштабируемых потерь для лопастей рабочего колеса:
![]() . (С.2)
. (С.2)
Формула (С.1) может быть преобразована в формулу (С.3), как указано ниже, путем введения измененного фактора скорости потока ![]() . Данная формула аналогична формуле (8), которая применяется ко всем водоводам машин радиального потока, а также к стационарным частям машин осевого потока.
. Данная формула аналогична формуле (8), которая применяется ко всем водоводам машин радиального потока, а также к стационарным частям машин осевого потока.
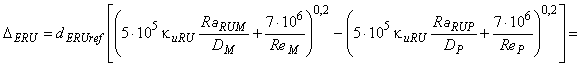
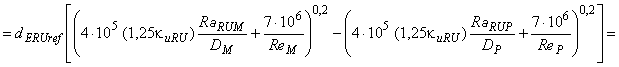
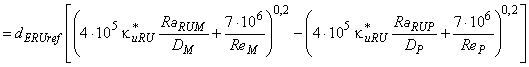 , (С.3)
, (С.3)
где ![]() - модифицированный фактор скорости потока для лопастей рабочего колеса:
- модифицированный фактор скорости потока для лопастей рабочего колеса:
![]() .
.
Поскольку примерно равен 1,03 для всех осевых машин,
![]() принимается как:
принимается как:
![]() . (С.4)
. (С.4)
С.3 Формула расчета масштабного эффекта для неподвижных деталей
Ниже приведена формула масштабного увеличения для получения , выведенная из формулы расчета масштабного эффекта для потока в трубе [формула (1)]. Данная формула приведена в основном тексте как формула (8).
При использовании формулы (8) при расчете масштабируемых потерь всех стационарных деталей применяют следующие два упрощения:
a) Фактор скорости потока, представляющий скорость потока во всех стационарных частях, принимают за 0,8 фактора скорости потока в проходе направляющих лопастей . Значение
приблизительно составляет 0,29 для низкой удельной скорости и 0,19 для высокой удельной скорости осевых машин.
Затем она упрощается для целей настоящего стандарта таким образом, что принимают за 0,24 для всех осевых машин, принимая среднюю величину.
b) Шероховатость для всех стационарных частей может быть приведена как среднеарифметическое значение шероховатости направляющих лопастей и статорных колонн.
Затем применяют следующую формулу пошагового увеличения для расчета масштабируемых потерь стационарных деталей:
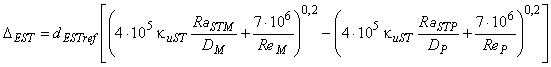 , (С.5)
, (С.5)
где - фактор скорости потока для стационарных деталей:
![]() , (С.6)
, (С.6)
Ra - исходная шероховатость стационарных деталей:
![]() . (С.7)
. (С.7)
С.4 Масштабный эффект для других неучтенных элементов, влияющих на эффективность
С.4.1 Коэффициент наполнения
Если радиальный зазор рабочего колеса идентичен опытному образцу, масштабный эффект допускается не учитывать в расчете, а принимать равным нулю.
Поскольку влияния на , производимое негомологичными радиальными зазорами, точно неизвестно, то не дают никаких формул для коррекции негомологичных радиальных зазоров. Соответственно, первостепенным требованием является сохранить идентичность радиального зазора между турбинами модели и опытного образца в рамках погрешностей, приведенных в таблице 3.
С.4.2 Коэффициент полезного действия при трении дисков
Поскольку потери по трению диска в корпусе рабочего колеса незначительны, принимают равным нулю.
С.5 Пошаговое увеличение гидравлического коэффициента полезного действия
Как указано выше, для машин осевого типа учитывают только масштабный эффект по удельной гидравлической энергии. Затем число пошагового увеличения гидравлической энергии рассчитывают по следующей формуле:
![]()
в соответствии с формулой (25).
Таким образом,
![]() . (С.8)
. (С.8)
С.6 Определение коэффициента ![]() для турбин осевого типа
для турбин осевого типа
Несмотря на то что в настоящее время отсутствует методика детального анализа относительных масштабируемых потерь гидравлической энергии, ![]() , в машинах осевого потока, некоторые справочные издания приводят приблизительные величины. Один из подобных источников представляет масштабируемые потери в точке максимальной эффективности турбин Каплана, как показано на рисунке С.1, в соответствии с [7].
, в машинах осевого потока, некоторые справочные издания приводят приблизительные величины. Один из подобных источников представляет масштабируемые потери в точке максимальной эффективности турбин Каплана, как показано на рисунке С.1, в соответствии с [7].
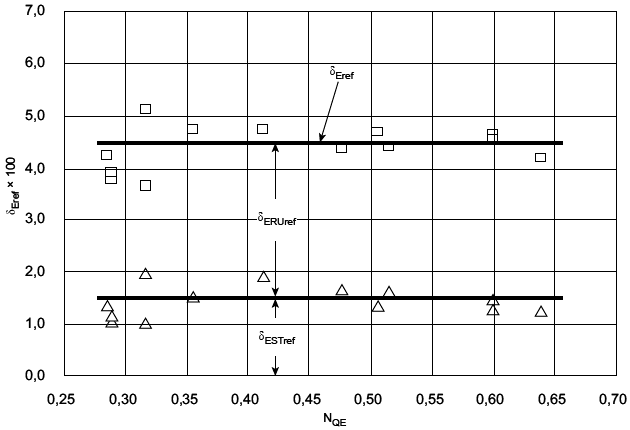
![]() - масштабируемые потери в стационарных деталях;
- масштабируемые потери в стационарных деталях; ![]() - масштабируемые потери в лопастях рабочего колеса;
- масштабируемые потери в лопастях рабочего колеса; - общие масштабируемые потери для всей турбины
Рисунок С.1 - ![]() турбин Каплана
турбин Каплана
Согласно рисунку С.1 зависимость ![]() и
и от удельной скорости очень незначительна. Например, для целей настоящего стандарта приняты следующие постоянные значения для всех турбин Каплана:
![]() , (С.9)
, (С.9)![]() , (С.10)
, (С.10)![]() . (С.11)
. (С.11)
Данные значения также применимы для пропеллерных турбин (с неподвижными лопастями).
Примечание - JSME (Японское общество инженеров-механиков) S008-1999 [7] представляет три отдельных значения масштабируемых потерь для лопастей рабочего колеса, отводной трубы и других стационарных деталей турбины Каплана. Однако известно, что его значение для стационарных деталей немного недооценено. Соответственно, масштабируемые потери JSME, измененные путем внесения разумных корректирующих факторов, приняты в настоящем стандарте. Они перегруппированы в две отдельные группы: потери по лопастям рабочего колеса и потери по всем стационарным деталям, включая отводящую трубу.
С.7 Определение ![]() для гидротурбин капсульного типа
для гидротурбин капсульного типа
Масштабируемые потери лопастей рабочего колеса капсульных гидротурбин считаются такими же, как и для турбины Каплана, соответственно, ![]() =0,030.
=0,030.
Что касается масштабируемых потерь в стационарной части, в настоящее время отсутствуют данные, позволяющие определить потери по трению в стационарной части капсульных турбин. Однако считается, что потери по трению в части верхнего бьефа, включая кольцевой проход вокруг капсули, меньше, чем такой же проход в спиральной камере турбины Каплана. С другой стороны, потери по трению в области направляющей лопасти рассматривают как несколько большие, чем в турбинах Каплана, вследствие более узких водотоков. В настоящее время нет данных по точным суммам данного вычитания или добавления потерь по трению в сравнении с турбинами Каплана.
Оценки показывают, что потери на трение в стационарной части капсульной турбины и турбины Каплана составляют приблизительно 1,0-2,0% соответственно. Если принять, что вышеупомянутые вычитание или добавление взаимовычитаются, то ошибка в расчетах ![]() нe превысит 0,5%.
нe превысит 0,5%.
Тогда возможная ошибка в сумме пошагового увеличения, рассчитанного на основе ![]() , будет в пределах 0,05-0,1%. Значит, данное предположение приемлемо.
, будет в пределах 0,05-0,1%. Значит, данное предположение приемлемо.
Из вышеприведенных допущений следует, что ![]() и
и для капсульных турбин имеют те же значения, что и для турбин Каплана.
С.8 Отклонение коэффициента масштабируемых потерь гидравлической энергии,
С.8.1 Коэффициент масштабируемых потерь для лопастей рабочего колеса
Независимо от удельной скорости машины или числа лопастей рабочего колеса значения ![]() и
и определены по кромке лопасти и приблизительно равны следующему:
![]() , (С.12)
, (С.12)
![]() . (С.13)
. (С.13)
Затем d выводится путем применения формулы (В.2):
![]() . (С.14)
. (С.14)
С.8.2 Коэффициент масштабируемых потерь для стационарных частей
Определить и
для всех стационарных частей достаточно сложно. Соответственно, вместо расчета d
![]() c помощью
c помощью и
значение d
![]() оценивают как соотношение
оценивают как соотношение ![]() и d
и d![]() для стационарных частей турбин радиального потока.
для стационарных частей турбин радиального потока.
На основе значений ![]() и d
и d![]() для стационарных частей турбины Френсиса с высокой удельной скоростью (N
для стационарных частей турбины Френсиса с высокой удельной скоростью (N=0,30), а также для частей турбонасосов с обратным ходом и высокой удельной скоростью (N
=0,20) мы можем получить соотношение
![]() , как показано в таблице С.1.
, как показано в таблице С.1.
Таблица С.1 - Соотношение ![]() для турбин Френсиса и турбонасосов
для турбин Френсиса и турбонасосов
FT (N | PT (T) (N | PT (P) (N | ||||
d | d | d | ||||
SP | 0,50 | 0,40 | 0,55 | 0,45 | 0,60 | 0,45 |
SV | 0,14 | 0,10 | 0,31 | 0,25 | 0,36 | 0,30 |
GV | 0,92 | 0,78 | 1,28 | 1,07 | 1,28 | 1,07 |
DT | 0,28 | 0,20 | 0,17 | 0,15 | 0,17 | 0,15 |
ST= | 1,84 | 1,48 | 2,31 | 1,92 | 2,41 | 1,97 |
| 0,804 | 0,831 | 0,817 | |||
Среднее значение вышеуказанного соотношения ![]() составляет приблизительно 0,82. Соответственно, значение d
составляет приблизительно 0,82. Соответственно, значение d для стационарных частей машин осевого потока определяют следующим образом:
![]() . (С.15)
. (С.15)
С.9 Формулы масштабирования для машин осевого типа
Как было объяснено в С.2, формула пошагового увеличения для лопастей рабочего колеса [формула (С.3)] может быть выражена формулой, сходной с формулой (С.5) для стационарных частей или формулой (8) для турбин радиального типа. Соответственно, формула (8) может быть применена к лопастям рабочего колеса и стационарным частям машин осевого типа.
Параметры для расчета ![]() в случае с машинами осевого типа приведены в таблице С.2.
в случае с машинами осевого типа приведены в таблице С.2.
Таблица С.2 - Параметры для расчета ![]() в случае с машинами осевого типа
в случае с машинами осевого типа
CO | d | |
RU | 0,024 5 | 1,29* |
ST | 0,012 3 | 0,19 |
* Значение, маркированное "*", является первоначально названным | ||
Примечание - Измененный фактор скорости потока для лопастей рабочего колеса | ||
Значение шероховатости для стационарной части, Ra, берется как среднее арифметическое значений шероховатости на направляющих лопастях и статорных колоннах [см. формулу (С.7)].
После того как по вышеуказанной формуле получены значения ![]() и
и на основе формулы (С.8) выводят сумму пошагового увеличения гидравлической энергии для всей машины.
Значения ![]() ,
, ,
и d
![]() , приведенные в настоящем приложении, подкрепляются аналитическими и экспериментальными данными для диапазона удельной скорости, 0,25
, приведенные в настоящем приложении, подкрепляются аналитическими и экспериментальными данными для диапазона удельной скорости, 0,25![]() 0,70.
0,70.
Вне указанного диапазона значения могут быть неправильными. Соответственно, если уравнения пошагового увеличения будут применять для оценки тестовых результатов модели вне вышеуказанного диапазона удельной скорости, эти условия должны быть прописаны в договоре.
С.10 Прямое пошаговое увеличение для всех турбин
Как и в способе прямого пошагового увеличения для машин радиального типа, способ пошагового увеличения для машин осевого типа приводится далее.
Для того чтобы представить всю машину, необходимо определить коэффициент исходной скорости потока и типичную шероховатость Ra
машины.
Как показано на рисунке С.1, масштабируемые потери на рабочем колесе в два раза больше, чем потери на стационарных частях. Принимая этот факт во внимание, и Ra
определяют следующим образом:
![]() , (C.16)
, (C.16)
![]() . (C.17)
. (C.17)
В соответствии с В.3 приложения В, если 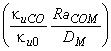 рабочего колеса и стационарной части модели может считаться одинаковой и равно выраженной через
рабочего колеса и стационарной части модели может считаться одинаковой и равно выраженной через ![]() , а в опытном образце будет выражена как
, а в опытном образце будет выражена как ![]() , можно вывести следующую формулу для расчета прямого пошагового увеличения для всей турбины:
, можно вывести следующую формулу для расчета прямого пошагового увеличения для всей турбины:
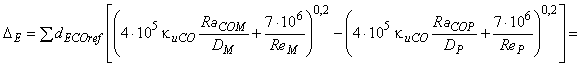
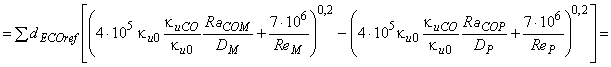
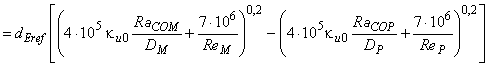 , (С.18)
, (С.18)
где
![]() . (С.19)
. (С.19)
Приложение D
(обязательное)
Влияние масштабных факторов на потери на трение
D.1 Формула расчета коэффициента потерь по трению диска
Как установлено в приложении В, новая формула, предложенная Нихтавицем, позволяющая рассчитать коэффициент потерь для потока в трубе, дает практически такие же значения, что и формула Кольбрука (см. рисунок В.1). В настоящее время имеет смысл предположить, что подобная формула также может описать коэффициент потерь по трению диска.
Общая формула для расчета коэффициента потерь, предложенная Нихтавицем [9], имеет следующий вид:
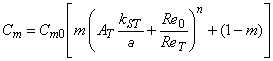 . (D.1)
. (D.1)
Однако для случая с дисковым потоком формулы введения приблизительности, схожей с формулой Кольбрука, не существует. Соответственно, вышеуказанная общая формула применялась для измерений физической модели, выполненной Фукуда [18] и другими [15, 19]. Было найдено, что наибольшего соответствия экспериментальным результатам достигают при следующих коэффициентах:
C=0,0019
Re=7·10
A=1,5·10
m=0,85
n=0,2,
где а - максимальный радиус ступицы или обода рабочего колеса, м;
D - максимальный диаметр ступицы или обода рабочего колеса, м;
- фактор размера диска
![]() ;
;
Re - число Рейнольдса диска
![]() ;
;
- угловая скорость диска, рад/с.
Примечание - Поскольку потери на трения диска пропорциональны пятой части диаметра диска, больший диаметр ступицы или обода рабочего колеса имеет значительное влияние на потери по трению диска. Соответственно, фактор размера для диска определяется большим диаметром или ступицы, или обода рабочего колеса.
Таким образом, основное уравнение для расчета коэффициента потери по трению принимает следующий вид:
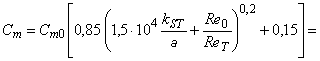
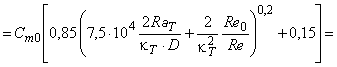
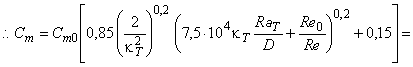
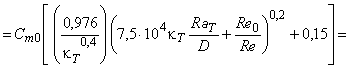
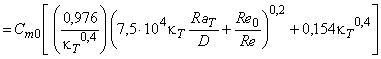 , (D.2)
, (D.2)
где k - песочная шероховатость диска, взятая как среднее значение по обеим сторонам рабочего колеса и стационарной части
![]() ;
;
Ra - среднеарифметическое значения шероховатости внешней поверхности рабочего колеса и стационарной части, обращенной к рабочему колесу, м:
![]() . (D.3)
. (D.3)
Ra - среднеарифметическая шероховатость, измеренная рядом с внешней периферией ступицы или обода рабочего колеса, м;
Ra - среднеарифметическая шероховатость, измеренная на стационарной части со стороны точек измерения ступицы или обода рабочего колеса, м.
Примечание - Эксперименты, проведенные Курокава [3, 20], указывают на то, что шероховатость вращающейся части имеет доминирующее влияние на крутящий момент при потере по трению диска рабочего колеса, чем шероховатость стационарной части. Эффект шероховатости при потере по трению диска может быть представлен средневзвешенным значением шероховатости обеих сторон, как показано в формуле (D.3).
D.2 Формула увеличения коэффициента полезного действия
Как показано в А.2, формула пошагового увеличения коэффициента полезного действия принимает следующий вид:
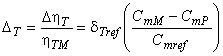 . (D.4)
. (D.4)
Коэффициент потери по трению С для презентационной модели с
![]() при ссылке на число Рейнольдса Re
при ссылке на число Рейнольдса Re=7·10
получают по следующей формуле:
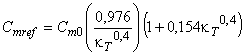 . (D.5)
. (D.5)
Путем замены С и С
в формуле (D.4), формуле (D.2) и С
в формуле (D.5) мы получаем:
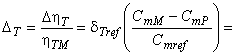
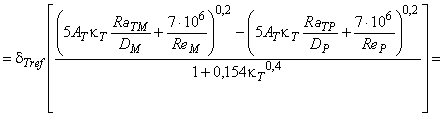
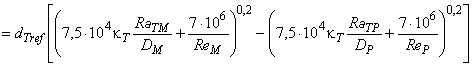 , (D.6)
, (D.6)
где 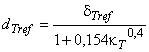 .
.
D.3 Нормированный коэффициент размера и коэффициент потерь на трении диска d
D.3.1 Коэффициент потерь по трению диска
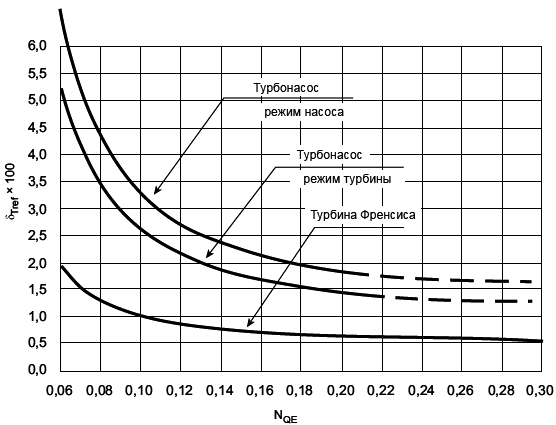
Рисунок D.1 - Коэффициент потери на трении диска
Данные кривые построены по следующим формулам:
- для турбины Френсиса:
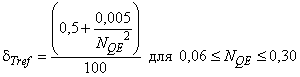 ; (D.7)
; (D.7)
- для турбонасоса при работе в режиме турбины (Т):
 ; (D.8)
; (D.8)
- для турбонасоса при работе в режиме насоса (Н):
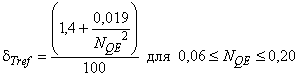 . (D.9)
. (D.9)
Примечание - Вышеуказанные формулы не подтверждаются аналитическими и экспериментальными данными вне диапазона удельных скоростей, указанного для каждой из формул. Однако данные уравнения могут быть использованы вне указанных диапазонов удельных скоростей и могут быть использованы для расчетов пошагового увеличения в тестовом режиме для моделей, указанных в договоре по согласованию заинтересованных сторон.
D.3.2 Фактор размеров диска
Значения , рассчитанные для некоторых типичных моделей, находятся в зависимости от удельной скорости и показаны ниже. Для удобства принята линейная зависимость.
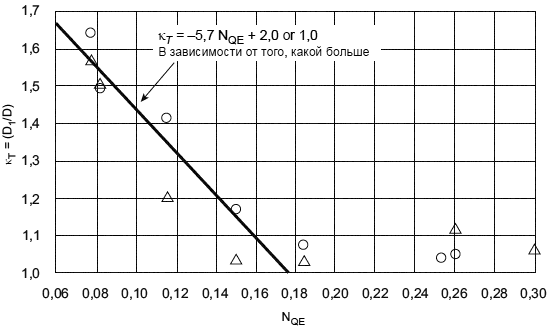
а) Фактор размеров диска для турбины Френсиса
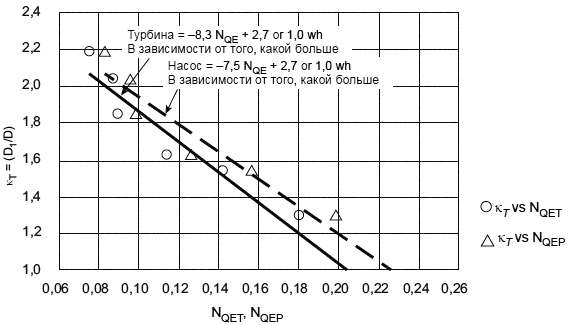
b) Фактор размеров диска для турбонасоса при N
=N
=0,06-0,20
Рисунок D.2 - Фактор размеров диска
D.3.3 Коэффициент потери по трению диска d
Путем объединения и
получают значения d
как функции удельной скорости. Они показаны на рисунке D.3. Для удобства они приведены к приблизительным значениям с помощью гиперболических уравнений.
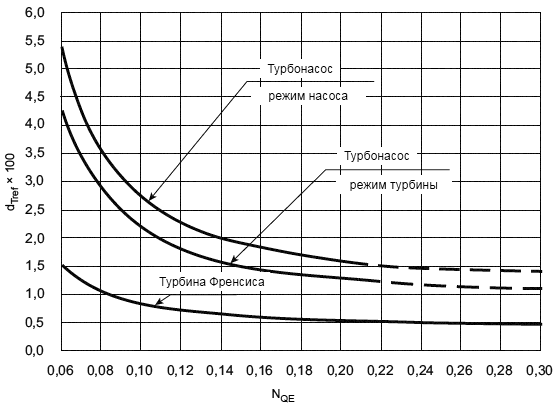
Рисунок D.3 - Коэффициент потери по трению диска d
Данные графики построены по следующим формулам:
- для турбины Френсиса:
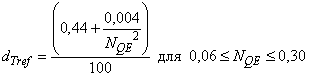 ; (D.10)
; (D.10)
- для турбонасоса при работе в режиме турбины (Т):
 ; (D.11)
; (D.11)
- для турбонасоса при работе в режиме насоса (Н):
 . (D.12)
. (D.12)
Примечание - Вышеуказанные уравнения не подтверждаются аналитическими и экспериментальными данными вне диапазона удельных скоростей для каждой из формул. Однако данные уравнения могут быть использованы вне указаных диапазонов удельных скоростей и могут быть использованы для расчетов пошагового увеличения тестовых результатов контрактной модели по согласованию заинтересованных сторон.
Приложение Е
(обязательное)
Оценка потерь утечки через уплотнения для моделей и образца
Е.1 Коэффициент потерь уплотнителя рабочего колеса
В основном тексте стандарта дается только пошаговое увеличение для герметичного уплотнителя (=0). Однако вследствие того, что достаточно трудно изготовить модель, а также из-за наличия структурных ограничений по установке сенсоров и т.д. конструкция уплотнителя модели не может удовлетворять требованиям, приведенным в таблице 3. В данном случае процедура, описанная в настоящем приложении, может использоваться для оценки коэффициента наполнения опытного образца по взаимному согласию заинтересованных сторон.
Введен эквивалентный коэффициент потерь без учета размеров уплотнителя, K, который выражен следующей формулой:
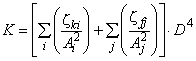
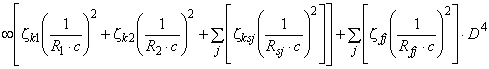 , (Е.1)
, (Е.1)
где - коэффициент потерь
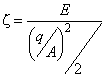 ;
;
q - поток утечки через рассматриваемый уплотнитель.
Примечание - Это не общий поток утечки через оба уплотнителя на ступице или ободе рабочего колеса;
А - площадь поперечного сечения зазора уплотнителя;
R - радиус уплотнителя;
c - радиальный зазор уплотнителя;
i - типичные 1, 2 или s;
j - число шагов/прорезов или зазоров уплотнителя;
Индексы:
k - кинетические потери;
f - потери по трению или объемы каждого зазора уплотнителя;
1 - объемы на входе с уплотнителем;
2 - объемы на выходе с уплотнителем;
s - объемы на промежуточном шаге или прорезе.
При расчете коэффициента потери K по формуле, представленной выше, коэффициенты потери предписаны в стандарте следующим образом:
Потери на уплотнителе на входе: Потери на уплотнителе на выходе: Промежуточный шаг или прорез: Потери по трению где Примечание - Масштабирование по |
|
|
На рисунке Е.1 приведены типичные примеры конструкции уплотнения рабочего колеса со стороны ступицы, а на рисунке Е.2 - со стороны обода.
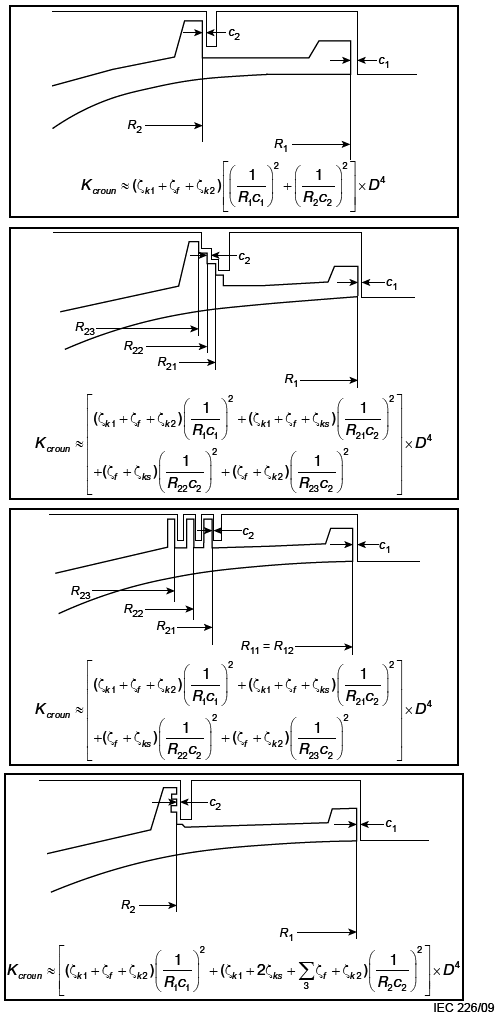
Рисунок Е.1 - Примеры типичной конструкции уплотнения рабочего колеса (сторона ступицы)
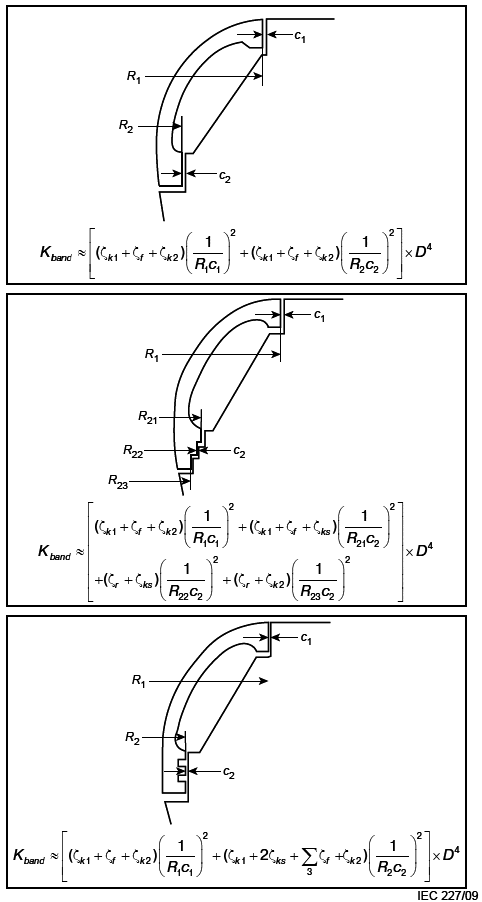
Рисунок Е.2 - Примеры типичной конструкции уплотнения рабочего колеса (сторона обода)
Значение коэффициента потери K описывается формулой (Е.1) и рассчитывается индивидуально для внешних и внутренних уплотнений на стороне ступицы рабочего колеса и на стороне обода соответственно. Затем коэффициент общих потерь K рассчитывают для всей машины по следующему уравнению:
![]() , (Е.3)
, (Е.3)
где с - величина коэффициента потерь без учета размера по уплотнителям ступицы рабочего колеса;
b - величина коэффициента потерь без учета размера по уплотнителям обода рабочего колеса.
Примечание - Формула (Е.3) получена в результате предположения, что дифференциальное давление по уплотнениям рабочего колеса на обеих сторонах (ступицы и обода) идентично. Формула не учитывает градиент давления в пространстве между рабочим колесом и стационарной частью, а также интервал потерь в балансировочных люках или балансировочных трубах.
Если значения дифференциального давления по уплотнителям рабочего колеса на обеих сторонах (ступицы и обода) не идентичны, данная формула неприменима. В данном случае требуется детальный анализ.
Е.2 Общая формула для расчета для негомологичных уплотнителей
Путем использования типичных коэффициентов потерь для модели и опытного образца общая формула для 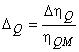 примет следующий вид [см. (А.2) и (А.3)]:
примет следующий вид [см. (А.2) и (А.3)]:
Для турбины:
Для насоса:
|
|
|
где K - типичный коэффициент потерь для модели;
K - типичный коэффициент потерь для опытного образца.
В формуле (E.4) принята как 0,99 для настоящего стандарта.
Е.3 Оценка масштабного эффекта в случае с гомологичным неизогнутым уплотнителем
В случае с гомологичным уплотнителем нормальной неизогнутой конструкции:
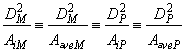 .
.
Соответственно:
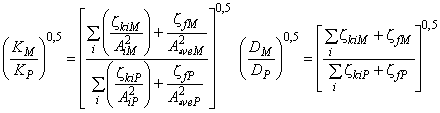 .
.
В конструкции уплотнителя нормального неизогнутого типа  .
.
Если учитывается масштабирование по ,
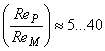 (при обычных тестовых условиях модели), то получаем
(при обычных тестовых условиях модели), то получаем 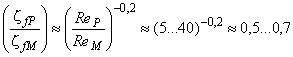 .
.
Поскольку кинетические потери не масштабируются, ![]() .
.
Соответственно, в случае с гомологическим неизогнутым уплотнителем, когда масштабный эффект по учитывается:
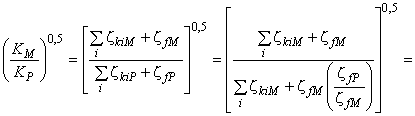
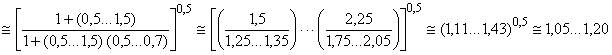 .
.
Так как (![]() ,
, для гомологического неизогнутого уплотнителя допускается рассчитывать следующим образом:
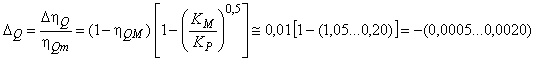
![]() %
%
Для упрощения в настоящем стандарте принимается =0%.
Е.4 Уплотнение номинальной формы с разными радиальными зазорами
В качестве примера рассмотрим случай, когда радиусы уплотнения идентичны, а радиальные зазоры - нет. Соответственно:
![]() . (E.5)
. (E.5)
Отношение коэффициента потерь для модели к коэффициенту потерь для опытного образца 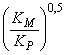 , используемое в формуле (D.4), может быть представлено следующим образом:
, используемое в формуле (D.4), может быть представлено следующим образом:
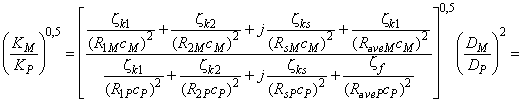
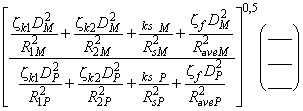 . (E.6)
. (E.6)
С помощью формулы (Е.5) и числитель для модели, и знаменатель для опытного образца в формуле (Е.6) тождественны. Соответственно, вышеуказанную формулу можно записать в виде:
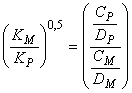 . (Е.7)
. (Е.7)
Соответственно:
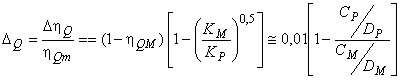 . (Е.8)*
. (Е.8)*
_______________
* Формула соответствует оригиналу. - .
Поскольку известно, что радиальный зазор уплотнения опытного образца меньше, чем в модели, коэффициент наполнения опытного образца становится больше, чем в модели.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам Российской Федерации, использованным в настоящем стандарте в качестве нормативных ссылок
Обозначение ссылочного национального стандарта Российской Федерации | Степень соответствия | Обозначение и наименование ссылочного международного стандарта |
NEQ | МЭК 60193:1999 "Турбины гидравлические, аккумулирующие насосы и турбонасосы. Приемочные испытания на модели" | |
- | ||
- | ||
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - NEQ - неэквивалентные стандарты. | ||
Библиография
[1] | МЭК 60193:1999 Гидравлические турбины, гидроагрегаты и турбонасосы. Приемные испытания прототипа |
[2] | Ida, Т. (Ида Т.). Анализ масштабного эффекта на характеристики производительности гидравлических турбин (Часть 1. Формулы масштаба гидравлической производительности и коэффициенты потери распределения в радиально-осевых прототипных турбинах и турбонасосах), J. Гидр. исследования, 1989, т.27, N 6, с.809 |
[3] | Kurokawa, J., et al (Курокава Дж. и др.). Эффекты неровности на потоке вдоль закрытого вращательного диска, Bull. JSME, 1978, т.21, N 162, с.1725 |
[4] | Nichtawitz, А. (Нишхтавиц А.). Обсуждения процедур повышения напряжения в гидравлическом оборудовании, Proc. IAHR Симпозиум - Пекин, 1994, с.841 |
[5] | Ida, Т. (Ида Т.). Новые формулы для увеличения гидравлической эффективности гидравлических турбин, J. Гидр. исследования, 1995, т.33, N 2, с.147 |
[6] | Nichtawitz, А. (Нишхтавиц А.). Дальнейшее развитие формулы увеличения напряжения с учетом неровности поверхности, Proc. IAHR Симпозиум - Валенсия, 1996, с.342 |
[7] | JSME S-008:1999 Метод конверсии производительности для гидравлических турбин и турбонасосов, 1999 |
[8] | Tanaka, Н. et al. (Танака X. и др.). Новая формула увеличения эффективности для дальнейшего международного стандарта по электротехнике, Proc. (CD-ROM), IAHR Симпозиум - Шарлоттес, 2000 |
[9] | Nichtawitz, A. et al. (Нишхтавиц А. и др.). Отклонения от формул для международного стандарта по электротехнике по увеличению эффективности, Proc. AHR Симпозиум - Стокгольм, 2004, т.А, А12-2 |
[10] | Tanaka, Н. et al. (Танака X. и др.). Формула увеличения эффективности для дальнейшего международного стандарта по электротехнике - Теоретическое основание и характеристики, Proc. IAHR Симпозиум - Стокгольм, 2004, т.А, А12-1 |
[11] | Schlichting, Н. (Шлихтинг Х.). Теория пограничного слоя, McGraw Hill, 1979, 7-е изд., с.623 |
[12] | Kurokawa, J. et al. (Курокава Дж. и др.). Точное определение волюметрической и механической эффективности и поведения протекания радиально-осевой турбины и радиально-осевого турбонасоса, Proc. IAHR Симпозиум - Пекин, 1994, т.2, с.889 |
[13] | Robertson, J.М. et al. (Робертсон Дж. М. и др.). Турбулентный поток в неровных трубах, I & ЕС Fundamentals, 1968, т.7, N 2, ст.253 |
[14] | Akaike, S., et al. (Акаике С. и др.). Полностью развитый гидравлический поток в двухмерных каналах с неровной стенкой, Proc. 10-я конференция по гидрооборудованию, Будапешт, 1995, с.21 |
[15] | Daily, J.W. et al. (Дейли Дж.В. и др.). Эффекты размеров комнаты в вынужденном потоке и фрикционное сопротивление закрытых вращательных дисков, Trans. ASME, Ser. D, 1960, т.82, N 1, с.217 |
[16] | Idelchik, I.Е. (Идельчик И.). Руководство по гидравлической сопротивляемости, Издательство Springer-Verlag, 1986, 2-е изд. |
[17] | Henry, Р. (Генри P.). Influence de la Rugosite sur ie Rendament d'un Modele Reduit de Turbine Francis, Proc. IAHR Симпозиум - Токио, 1980, т.1, с.677 |
[18] | Fukuda, Н. (Фукуда X.). Влияние неровности поверхности рабочего колеса на работу радиально-осевой турбины, Bull. JSME, 1964, т.7, N 26, с.346 |
[19] | Nece, R.Е. et al. (Несе Р.Е. и др.). Влияние неровности на фрикционное сопротивление закрытых вращательных дисков, Trans. ASME, Ser. D, 1960, т.82, N 3, с.553 |
[20] | Kurokawa, J. et al. (Курокава Дж. и др.). Осевое давление, потери от течи и момент трения турбооборудования с радиальным потоком, Proc. Конференция по турбинам и насосам (NEL, Глазго), 1976, т.1, с.1 |
УДК 621.22:006.74 | ОКС 27.140 | |
Ключевые слова: машины гидравлические, машины радиальные и осевые, турбонасосы, аккумулирующие насосы, методы преобразования рабочих характеристик опытного образца и модели | ||
Электронный текст документа
и сверен по:
, 2015

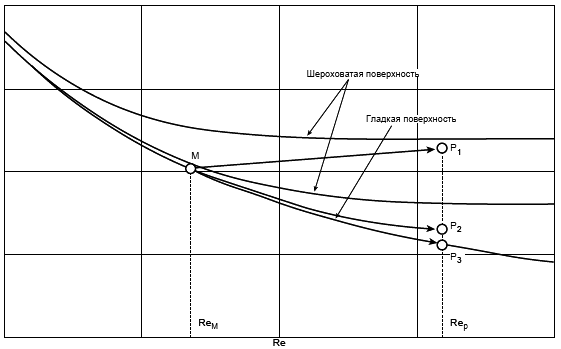

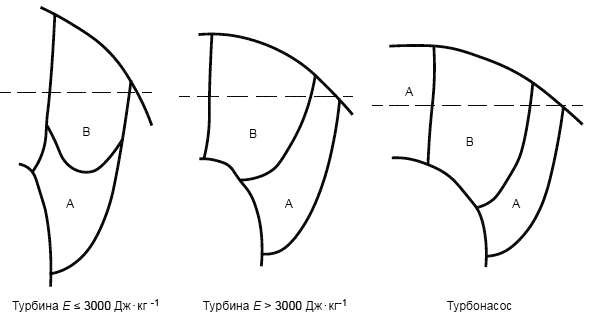
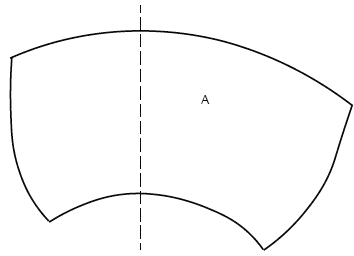
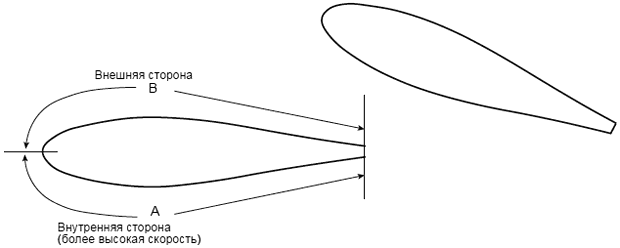
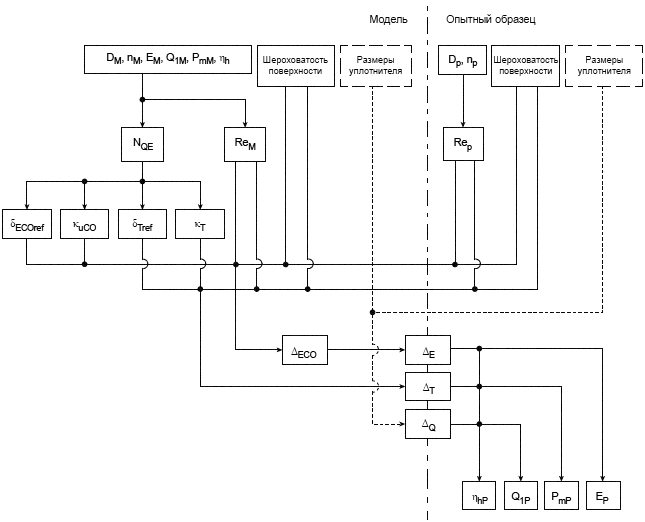
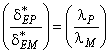
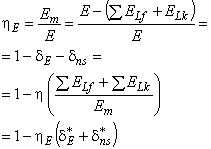
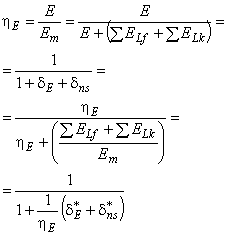
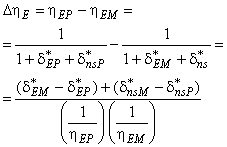
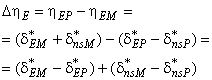
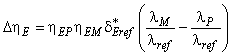
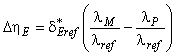
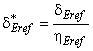
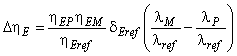
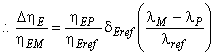
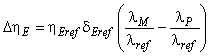
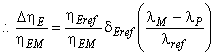
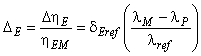
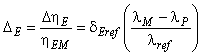
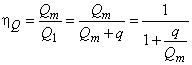
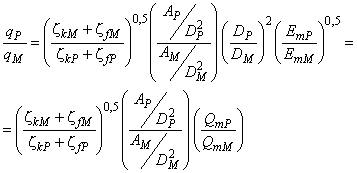
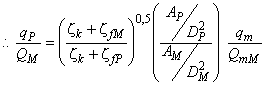 ,
,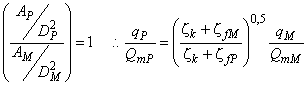
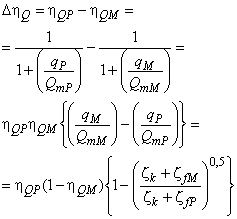
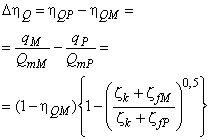
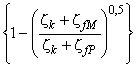 очень маленькие величины, сумму пошагового увеличения коэффициента наполнения (отрицательного) обычно не принимают в расчет.
очень маленькие величины, сумму пошагового увеличения коэффициента наполнения (отрицательного) обычно не принимают в расчет.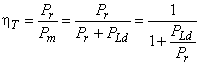
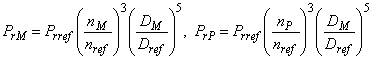
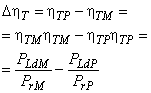
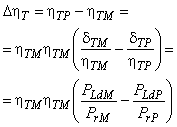
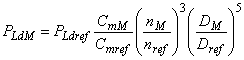 ;
;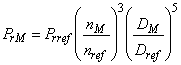 ;
;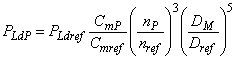 ;
;