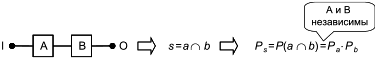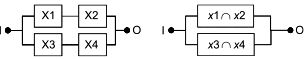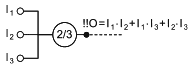ГОСТ Р МЭК 61078-2021
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Надежность в технике
СТРУКТУРНАЯ СХЕМА НАДЕЖНОСТИ
Dependability in technics. Reliability block diagrams
ОКС 03.120.01;
03.120.99
Дата введения 2022-01-01
Предисловие
1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 119 "Надежность в технике"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 21 сентября 2021 г. N 989-ст
4 Настоящий стандарт идентичен международному стандарту МЭК 61078:2016* "Структурная схема надежности" (IEC 61078:2016 "Reliability block diagrams", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ Р 51901.14-2007 (МЭК 61078:2006)
6 ПЕРЕИЗДАНИЕ. Октябрь 2022, апрель 2023 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
Введение
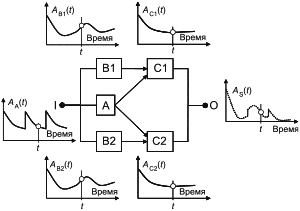
Структурная схема надежности (RBD) является наглядным представлением путей успешного функционирования системы. На этой схеме показаны логические связи функционирующих компонентов (представленных в виде блоков), необходимые для успешной работы системы (далее - "успех системы"). Следовательно, RBD эквивалентна логическому уравнению булевых переменных, а вероятностные вычисления в основном связаны с ситуацией, когда значения вероятностей успеха/отказа блоков постоянны.
Существует много различных методов анализа надежности, одним из которых является RBD. Таким образом, цель каждого метода и их индивидуального или совместного применения состоит в оценке коэффициента готовности, вероятности безотказной работы, частоты отказов и других применимых показателей надежности, которые должны быть изучены аналитиком до принятия решения об использовании RBD. Следует также рассмотреть результаты, получаемые каждым методом, данные, необходимые для выполнения анализа, сложность анализа и другие факторы, указанные в настоящем стандарте.
Если блоки RBD не зависят друг от друга и порядок, в котором происходят отказы, не имеет значения, то вычисление вероятностей может быть распространено на показатели, зависящие от времени, включая восстанавливаемые и невосстанавливаемые блоки (или компоненты). В этом случае должны быть рассмотрены три показателя, связанные с успешной работой системы: вероятность безотказной работы системы , коэффициент готовности
и частота отказов
. Для систем, включающих восстанавливаемые компоненты, вычисления
и
могут быть довольно простыми, однако вычисление
подразумевает рассмотрение зависимостей в системе (см. 3.34), которые могут быть учтены в математической структуре RBD. Тем не менее в отдельных случаях доступна аппроксимация
.
Метод RBD связан с анализом дерева отказов [1] и с марковскими методами [2]:
Базовая математика одинакова для RBD и анализа дерева отказов (FTA): RBD ориентирована на успех системы, FT - на отказ системы. Всегда можно преобразовать RBD в FT и наоборот. С математической точки зрения модели RBD и FT представляют собой две стороны одного и того же логического выражения. Поэтому математические разработки и ограничения для обоих методов одинаковы.
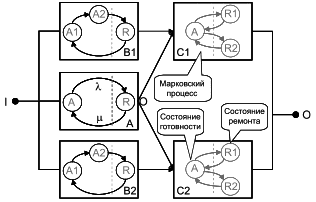
Если коэффициент готовности одного блока может быть рассчитан с использованием отдельного марковского процесса [2], независимо от других блоков,
может быть использован в качестве входных данных для расчетов, связанных с RBD, включая этот блок. Подход, в котором RBD обеспечивает логическую структуру, а марковские процессы обрабатывают вычисления значений коэффициентов готовности блоков, называется подходом "RBD-управляемых марковских процессов".
Для систем, в которых необходимо учитывать порядок возникновения отказов, или когда ремонтируемые блоки не являются независимыми друг от друга, или если вероятность безотказной работы системы не может быть рассчитана аналитическими методами, применимо моделирование Монте-Карло или другие методы моделирования, такие как динамические RBD, методы Маркова [2] или сети Петри [3].
1 Область применения
Настоящий стандарт устанавливает:
- требования к применению структурной схемы надежности (RBD) при анализе надежности;
- процедуры моделирования надежности системы с помощью структурной схемы надежности;
- способ использования RBD для качественного и количественного анализа;
- процедуры использования модели RBD для расчета коэффициента готовности, частоты отказов и показателей безотказности для систем различного типа с постоянными (или зависящими от времени) вероятностями успеха/отказа блоков, а также для невосстанавливаемых или восстанавливаемых блоков;
- некоторые теоретические аспекты и ограничения при вычислении коэффициента готовности, частоты отказов и показателей безотказности;
- связь с анализом дерева отказов (см. МЭК 61025 [1]) и методами Маркова (см. МЭК 61165 [2]).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты [для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения)].
IEC 60050-192, International Electrotechnical Vocabulary - Part 192: Dependability (Международный электротехнический словарь. Часть 192. Надежность) (доступно по адресу: http://www.electropedia.org)
IEC 61703, Mathematical expressions for reliability, availability, maintainability and maintenance support terms (Математические выражения для показателей безотказности, готовности, ремонтопригодности и обеспеченности техническим обслуживанием)
3 Термины и определения
В настоящем стандарте применены термины по МЭК 60050-192, а также следующие термины с соответствующими определениями:
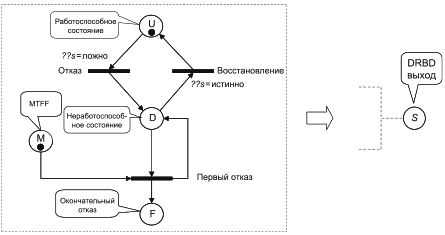
3.1 структурная схема надежности RBD (reliability block diagram RBD): Логическое, графическое представление системы, показывающее, как состояния успеха ее подсистем (представленных блоками) и их комбинации влияют на состояние успеха системы.
Примечание 1 - Метод RBD был разработан в то время, когда термин "безотказность объекта" использовался как общий термин, характеризующий успешное функционирование, то есть надежность объекта. Этот общий термин теперь заменен термином "надежность объекта". Он используется в таких выражениях, как "разработка надежности", "исследование надежности", "структурная схема надежности". Термин "надежность", используемый в RBD, не означает, что этот метод позволяет напрямую рассчитывать показатель надежности сложной системы по показателям надежности составляющих ее блоков (см. 10.3.1.4).
Примечание 2 - RBD - ориентированный ациклический граф (т.е. граф без петель), представляющий логические связи между состоянием успеха системы и состоянием успеха составляющих ее блоков. Эта логическая структура в основном представлена простыми последовательными и параллельными графическими структурами (см. разделы 4 и 7).
Примечание 3 - Метод RBD может быть расширен для представления систем с несколькими состояниями (т.е. имеющих более двух состояний), но эти расширения не могут быть обработаны в структуре булевой логики.
[МЭК 60050-192:2015, 192-11-03, термин модифицирован, добавлены примечания]
3.2 булева модель (Boolean related model): Математическая модель, в которой состояние системы представлено логической функцией булевых переменных, представляющих состояния компонентов системы.
Примечание - Булева переменная a имеет только два значения, логическая функция нескольких булевых переменных также имеет только два значения. Эти два значения могут быть, например, {0, 1}, {работоспособное состояние и неработоспособное состояние}, {истина, ложь}, {работа, отказ} и т.д. Основная математика, лежащая в основе логических функций, - это булева алгебра.
3.3 RBD-управляемый марковский процесс (RBD driven Markov process): Марковский процесс, моделируемый RBD, состоящий из блоков, моделируемых отдельными субмарковскими моделями, не зависящими друг от друга.
Примечание 1 - Лежащая в основе RBD логика позволяет объединить индивидуальные коэффициенты готовности блоков для вычисления коэффициента готовности системы. Если блок моделируют небольшими индивидуальными марковскими процессами (например, с количеством состояний менее 10), RBD эквивалентна марковскому процессу, соответствующему системе, имеющей миллионы состояний. Это является основой большинства вероятностных расчетов, выполняемых с помощью RBD. Такой марковский процесс, построенный с использованием RBD, называется "RBD-управляемым марковским процессом".
Примечание 2 - Независимый марковский процесс разработан в [2].
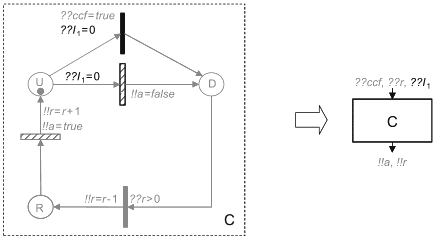
3.4 динамическая RBD; DRBD (dynamic RBD, DRBD): Структурная схема надежности, где предположение о независимости блоков не выполнено.
3.5 некогерентная RBD (non-coherent RBD): Структурная схема надежности, моделирующая немонотонную логическую функцию.
Примечание 1 - Некогерентная RBD - это RBD, где блоки могут появляться как в прямом, так и в обратном состояниях (см. таблицу 3). В этом случае некоторые из минимальных путей успеха (см. 3.15) могут включать некоторые блоки в неработоспособном состоянии, а некоторые минимальные пути отказа - некоторые блоки в работоспособном состоянии. Понятия минимальных наборов соединений более не действительны и должны быть заменены понятием простых импликантов.
Примечание 2 - В некогерентной RBD минимальный путь успеха может стать путем отказа при ремонте, блока в неработоспособном состоянии, а минимальный путь отказа может стать путем успеха при дальнейшем отказе одного блока в работоспособном состоянии. Поэтому такие RBD называют "некогерентными".
3.6 объект (item): Предмет рассмотрения.
Примечание - В настоящем стандарте термин "объект" охватывает главным образом систему, смоделированную RBD, и блоки RBD.
[МЭК 60050-192:2015, 192-01-01]
3.7 блок (block): Базовый элемент, используемый при построении RBD.
Примечание 1 - Блок имеет только два состояния (работоспособное и неработоспособное состояние) и может представлять собой любой объект (например, компоненты, функции, подсистемы) с двумя состояниями (восстанавливаемый или невосстанавливаемый). По аналогии и для упрощения формулировок восстанавливаемый/невосстанавливаемый блок представляет собой восстанавливаемый/невосстанавливаемый объект, отказ/ремонт блока представляет отказ/ремонт моделируемого объекта и работоспособное/неработоспособное состояние блока представляет работоспособное/неработоспособное состояние моделируемого объекта.
Примечание 2 - Количество состояний может быть увеличено и быть более двух для представления системы с количеством состояний (более двух), но такие расширения RBD не могут быть обработаны в рамках булевой логики.
Примечание 3 - Для целей настоящего стандарта блоки подразделяют на "элементарные блоки" или просто "блоки" и "составные блоки", состоящие из нескольких "элементарных блоков" (см. таблицу 3).
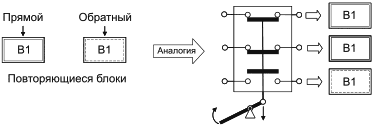
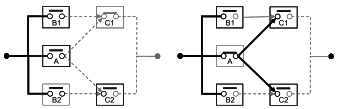
3.8 повторяющийся блок (repeated block): Блок, появляющийся в RBD более одного раза.
Примечание 1 - Повторяющиеся блоки представляют собой одни и те же физические объекты. Их не следует путать с дублированными блоками, представляющими различные, но сходные физические объекты, используемые для резервирования.
Примечание 2 - Повторяющиеся блоки могут появляться в прямом или обратном состоянии (т.е. блок появляется в работоспособном состоянии в одной части RBD и в неработоспособном состоянии в другой части RBD, или наоборот). Такие блоки очень полезны для представления RBD сложной системы или для представления RBD в виде путей успеха или отказа (см. 8.2).
3.9 работоспособное состояние (up state, available state): Состояние, в котором объект способен выполнять установленные функции.
Примечание 1 - Отсутствие необходимых внешних ресурсов может помешать работе, но не влияет на работоспособное состояние объекта.
Примечание 2 - Работоспособное состояние связано с готовностью объекта.
Примечание 3 - Объект одновременно может находиться в работоспособном состоянии по одним функциям и в неработоспособном состоянии по другим функциям.
Примечание 4 - Термин "работоспособный объект" означает объект, пребывающий в работоспособном состоянии.
Примечание 5 - В области применения RBD состояние блока идентично состоянию компонента, смоделированного этим блоком. Поэтому блок в работоспособном состоянии соответствует компоненту в работоспособном состоянии. Тот же подход применяют к RBD и соответствующей системе.
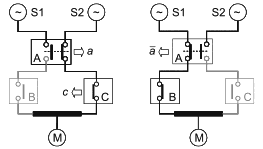
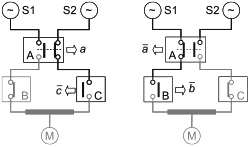
Примечание 6 - В RBD по аналогии с электрической схемой блок в работоспособном состоянии рассматривают как виртуальный переключатель в закрытом положении, а блок в неработоспособном состоянии - как виртуальный переключатель в открытом положении.
[МЭК 60050-192:2015, 192-02-01; термин модифицирован, добавлены примечания 5 и 6]
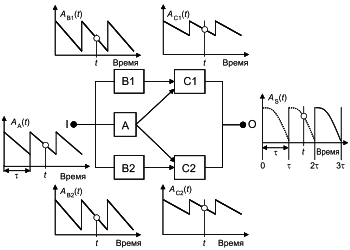
3.10 продолжительность работоспособного состояния (up time): Продолжительность периода времени, в течение которого объект пребывает в работоспособном состоянии.
[МЭК 60050-192:2015, 192-02-02]
3.11 средняя продолжительность работоспособного состояния MUT (mean up time MUT): Математическое ожидание продолжительности работоспособного состояния.
3.12 неработоспособное состояние (down state, unavailable state): Состояние объекта, в котором он не способен выполнить хотя бы одну требуемую функцию из-за внутренней неисправности или профилактического технического обслуживания.
Примечание 1 - Неработоспособное состояние связано с неготовностью объекта.
Примечание 2 - Термин "неработоспособный объект" обозначает объект в неработоспособном состоянии.
Примечание 3 - По отношению к RBD состояние блока соответствует состоянию компонента (соответственно системы), моделируемого этим блоком (соответственно этой RBD). Поэтому блок в неработоспособном состоянии на RBD соответствует компоненту (соответственно системе) в неработоспособном состоянии.
Примечание 4 - В RBD блок в неработоспособном состоянии может быть интерпретирован как открытый электрический переключатель.
[МЭК 60050-192:2015, 192-02-20]
3.13 продолжительность неработоспособного состояния (down time): Продолжительность периода времени, в течение которого объект пребывает в неработоспособном состоянии.
[МЭК 60050-192:2015, 192-02-21]
3.14 средняя продолжительность неработоспособного состояния MDT (mean down time MDT): Математическое ожидание продолжительности неработоспособного состояния.
[МЭК 60050-192:2015, 192-08-10]
3.15 путь успеха, набор соединений (success path, tie set): Набор блоков, причем каждый блок в наборе находится в работоспособном состоянии, что приводит к тому, что RBD обеспечивает состояние успеха системы.
Примечание - Термин "набор соединений" использован по аналогии с электрической схемой, в которой блоки в работоспособном состоянии составляют замкнутый электрический контур от входа в RBD до выхода из нее.
________________
Если RBD представить в виде электросхемы, в которой все блоки являются переключателями с двумя состояниями (переключатель замкнут, переключатель разомкнут), то набор соединений - это такой набор блоков в состоянии успеха (переключатель замкнут), при котором вся электрическая цепь замкнута (система находится в работоспособном состоянии).
3.16 минимальный набор соединений (minimal tie set): Такой набор соединений, при котором отказ (обрыв в электрическом контуре) одного (любого) из блоков набора приводит к отказу всей RBD (системы).
________________
Если RBD представить в виде электросхемы, в которой все блоки являются переключателями с двумя состояниями (переключатель замкнут, переключатель разомкнут), то набор обрывов - это такой набор, при котором вся электрическая цепь разомкнута (система находится в неработоспособном состоянии).
Примечание 1 - В минимальном наборе соединений необходимо, чтобы для сохранения работоспособного состояния системы каждый блок набора находился в работоспособном состоянии.
Примечание 2 - Порядок минимального набора соединений определяет количество блоков в работоспособном состоянии: минимальный набор соединений порядка 1 включает 1 блок в работоспособном состоянии, порядка 2 - 2 блока в работоспособном состоянии и т.д.
3.17 путь отказа, набор обрывов (failure path, cut set): Набор блоков, причем каждый блок в наборе находится в неработоспособном состоянии, что приводит к тому, что RBD обеспечивает неработоспособное состояние системы.
Примечание - Термин "набор обрывов" дан по аналогии с электрической схемой, в которой блоки в неработоспособном состоянии составляют незамкнутый электрический контур входа в RBD до выхода из нее.
3.18 минимальный набор обрывов (minimal cut set): Такой набор обрывов, при котором восстановление одного (любого) из блоков набора приводит к восстановлению RBD (системы).
Примечание 1 - В минимальном наборе обрывов для сохранения RBD в неработоспособном состоянии необходимо, чтобы каждый блок набора находился в неработоспособном состоянии.
Примечание 2 - Порядок минимального набора обрывов определяет количество блоков в неработоспособном состоянии: минимальный набор обрывов порядка 1 включает 1 блок в неработоспособном состоянии, порядка 2 - 2 блока в неработоспособном состоянии и т.д.
3.19 непересекающийся набор элементов (disjoint set of elements): Набор булевых элементов, пересечения которых пусты.
Пример - Например, если представляет собой набор непересекающихся наборов обрывов, то
![]() , и, следовательно,
, и, следовательно, ![]() .
.
Примечание 1 - Термин "элемент" применен здесь в значении, используемом в теории множеств, т.е. член заданного набора объектов.
Примечание 2 - Непересекающиеся элементы несовместны: когда один истинен, другой ложен и наоборот. Это описывает взаимоисключение и, следовательно, полную зависимость между элементами.
3.20 готовность объекта <item> (availability): Способность объекта выполнять требуемые функции в заданных условиях, в заданный момент или период времени при условии, что все необходимые внешние ресурсы обеспечены.
[МЭК 60050-192:2015, 192-01-23]
3.21 мгновенный коэффициент готовности (instantaneous availability, point availability): Вероятность того, что объект находится в данный момент времени в работоспособном состоянии.
[МЭК 60050-192:2015, 192-08-01; термин модифицирован]
3.22 мгновенный коэффициент неготовности (instantaneous unavailability point unavailability): Вероятность того, что в данный момент времени объект находится в неработоспособном состоянии.
[МЭК 60050-192:2015, 192-08-04; термин модифицирован]
3.23 средний коэффициент готовности ![]() (mean availability average availability): Среднее значение мгновенного коэффициента готовности за заданный период времени
(mean availability average availability): Среднее значение мгновенного коэффициента готовности за заданный период времени ![]() .
.
[МЭК 60050-192:2015, 192-08-05]
3.24 средний коэффициент неготовности ![]() (mean unavailability average unavailability): Среднее значение мгновенного коэффициента неготовности за заданный период времени
(mean unavailability average unavailability): Среднее значение мгновенного коэффициента неготовности за заданный период времени ![]() .
.
Примечание - Средний коэффициент неготовности инструментальной системы безопасности (см. МЭК 61508 [5]) также называется "средняя вероятность отказа по запросу" (аббревиатура: ![]() ).
).
[МЭК 60050-192:2015, 192-08-06; термин модифицирован, заменено примечание 1]
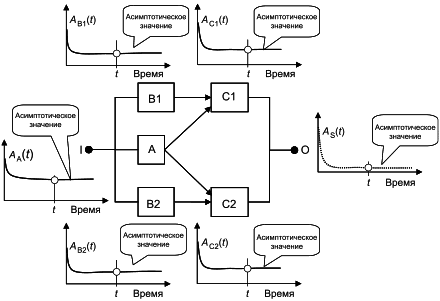
3.25 стационарный (асимптотический) коэффициент готовности ,
(steady state availability, asymptotic availability): Предел, если он существует, мгновенного коэффициента готовности, когда время стремится к бесконечности.
Примечание - В некоторых случаях стационарный коэффициент готовности может быть представлен в виде отношения MUT/(MUT+MDT). См. ГОСТ 27.010.
[МЭК 60050-192:2015, 192-08-07]
3.26 безотказность (объекта) (reliability): Свойство объекта без отказов выполнять требуемые функции в течение заданного периода времени в заданных условиях.
[МЭК 60050-192:2015, 192-01-24; термин модифицирован, примечания исключены]
3.27 вероятность безотказной работы ![]() ,
, (reliability): Вероятность того, что в течение периода времени
![]() в заданных условиях объект будет функционировать в соответствии с установленными требованиями.
в заданных условиях объект будет функционировать в соответствии с установленными требованиями.
Примечание - - вероятность безотказной работы за период времени [0,
].
[МЭК 60050-192:2015, 192-01-24; термин модифицирован, примечания заменены]
3.28 вероятность отказа ![]() ,
, (unreliability): Вероятность того, что в течение периода времени
![]() при работе в заданных условиях объект откажет.
при работе в заданных условиях объект откажет.
Примечание 1 - - вероятность отказа за период времени [0,
].
Примечание 2 - Вероятность отказа связана с вероятностью безотказной работы соотношением ![]() .
.
3.29 мгновенная интенсивность отказов, интенсивность отказов (instantaneous failure rate, failure rate): Предел, если он существует, отношения условной вероятности того, что отказ невосстанавливаемого объекта произойдет за период времени
![]() к
к , когда
стремится к нулю, при условии, что в течение периода времени [0,
] отказ не произошел.
Примечание 1 - Это определение является адаптированным определением IEC 60050-192 и охватывает восстанавливаемые объекты:
- если объект не имеет внутреннего встроенного резервирования, то интенсивность отказов идентична интенсивности отказов невосстанавливаемого объекта;
- если объект имеет внутреннее встроенное резервирование, он может оставаться в работоспособном состоянии при отказе некоторых резервированных частей. Эти отказы можно ремонтировать до тех пор, пока весь объект не перейдет в неработоспособное состояние из-за отказа следующей части.
Примечание 2 - Термины "интенсивность отказов" (3.29), "условный параметр потока отказов" (3.30) и "безусловный параметр потока отказов" (3.31) выглядят похожими, они отличаются условными событиями в их определениях. Даже если эти параметры в некоторых случаях имеют близкие числовые значения, их не следует путать, поскольку они различны по смыслу.
[МЭК 60050-192:2015, 192-05-06; термин модифицирован, заменены примечания]
3.30 мгновенный условный параметр потока отказов; условный параметр потока отказов; интенсивность отказов Весселя (instantaneous conditional failure intensity, conditional failure intensity, Vesely failure rate): Предел, если он существует, отношения условной вероятности того, что отказ объекта произойдет в течение периода времени
![]() к
к когда
стремится к нулю, при условии, что объект находится в работоспособном состоянии в момент времени
=0.
Примечание - См. примечание 2 к 3.29.
3.31 мгновенный безусловный параметр потока отказов, безусловный параметр потока отказов; частота отказов (instantaneous unconditional failure intensity, unconditional failure intensity, failure frequency): Предел, если он существует, отношения условной вероятности того, что отказ произойдет в течение периода времени
![]() , к
, к , когда
стремится к нулю, при условии, что объект находился в работоспособном состоянии в момент времени 0.
Примечание 1 - См. примечание 2 к определению интенсивности отказов (3.29).
Примечание 2 - Этот параметр эквивалентен параметру потока отказов в МЭК 60050-192:2015 (192-05-08). Наименование термина изменено, чтобы отличать его от термина "условный параметр потока отказов" (3.30).
3.32 средняя частота отказов (0, Т) (average failure frequency): Количество отказов объекта в единицу времени, усредненное за заданный период времени
.
Примечание 1 - Если - количество отказов объекта за период [0,
] , то средняя частота отказов за этот период равна
![]() .
.
Примечание 2 - Если - средняя наработка между отказами объекта (см. МЭК 60050-192) изделия, то среднее количество отказов за период времени [0,
] равно
![]() . Следовательно,
. Следовательно, ![]() .
.
Математически ![]() - среднее значение
- среднее значение за период [0,
]. Следовательно,
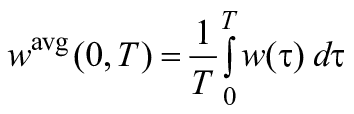 .
.
3.33 средняя наработка до отказа MTTF (mean operating time to failure MTTF): Математическое ожидание наработки объекта до отказа.
Примечание 1 - В случае невосстанавливаемых объектов, если наработка до отказа подчиняется экспоненциальному распределению (то есть интенсивность отказов постоянна), МТТF численно равна величине, обратной интенсивности отказов. Это также верно для восстанавливаемых объектов, если после восстановления их можно считать "как новые".
[МЭК 60050-192, 192-05-11; термин модифицирован, примечание 2 исключено]
3.34 системная зависимость; холистическая зависимость (systemic dependency, holistic dependency): Зависимость между частями системы, когда систему рассматривают как единое целое.
Пример 1 - Единственная ремонтная бригада устанавливает системную зависимость между ремонтируемыми объектами: когда объект отказал, он может быть отремонтирован только в том случае, если ремонтная бригада не занята ремонтом другого объекта, относящегося к системе.
Пример 2 - Вероятность безотказной работы системы R(t) может быть представлена в виде вероятности того, что система будет находиться в работоспособном состоянии в момент времени t при условии, что она не отказывала в течение периода времени [0, t]. Поэтому могут быть сохранены только последовательности событий, которые не приводят к неработоспособному состоянию в течение периода времени [0, t], а последовательности событий, которые включают переходы "работоспособное состояние" "неработоспособное состояние"
"работоспособное состояние", должны быть исключены из расчетов. Это означает в отношении расчета R(t), что объект, переходящий в неработоспособное состояние, подлежит ремонту только в том случае, когда система остается в работоспособном состоянии в течение времени ремонта объекта. Поэтому в отношении расчета R(t) объект подлежит (или не подлежит) ремонту в зависимости от состояний других блоков, и это составляет системные зависимости между всеми блоками RBD, моделирующей систему.
Примечание 1 - Системная зависимость не может быть описана как локальное свойство отдельных объектов системы.
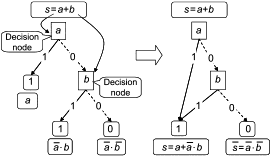
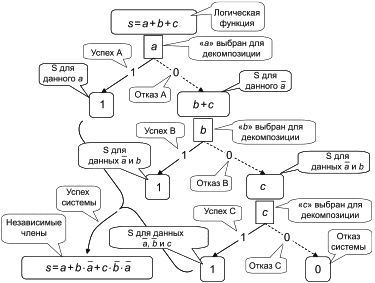
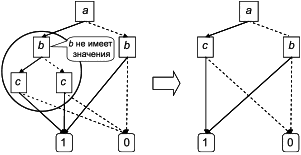
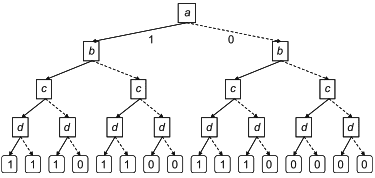
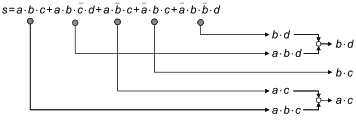
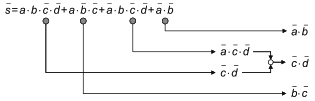
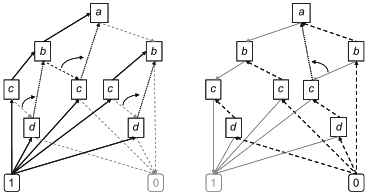
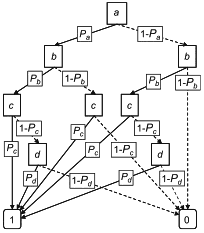
3.35 бинарная диаграмма принятия решений BDD (binary decision diagram BDD): Компактное дерево принятия решений, основанное на декомпозиции Шеннона булева выражения.
|
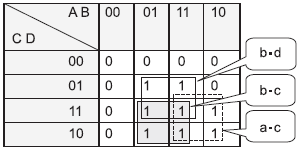
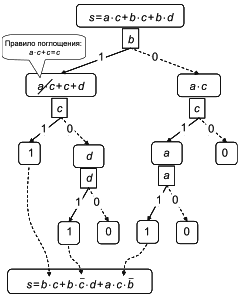
Рисунок 1 - Декомпозиция Шеннона простого булева выражения и результирующая BDD
Примечание 1 - На рисунке 1 показано, как простое булево выражение s=a+b может быть преобразовано в дерево решений с использованием декомпозиции Шеннона, и затем как соответствующая BDD может быть получена путем сбора частей, дающих одно и то же значение (0 или 1) булева выражения.
Примечание 2 - С точки зрения математики BDD - это корневой направленный ациклический граф. Это структура данных, представляющая булевы выражения в виде объединений отдельных членов. Это, в свою очередь, приводит к точным вероятностным расчетам. Это подход к вероятностному расчету на основе булевых моделей. Более подробная информация о BDD приведена в [33].
4 Условные обозначения, сокращения и аббревиатуры
Таблица 1 - Сокращения
Аббревиатура/сокращение | Значение |
BDD | бинарная диаграмма принятия решений |
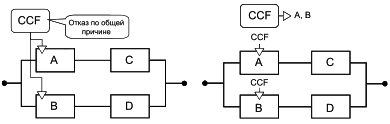
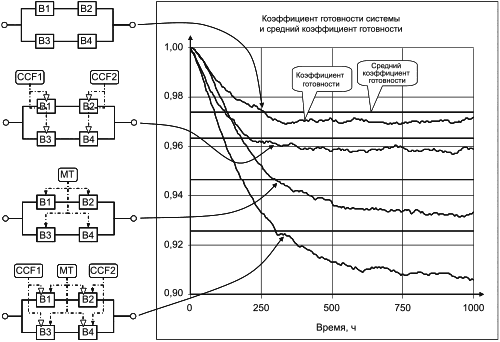
CCF | отказ по общей причине |
FMEA | анализ видов и последствий отказов |
FT, FTA | дерево неисправностей, анализ дерева неисправностей |
MTTF | средняя наработка до отказа |
MTTR | среднее время восстановления |
DBRD | динамическая структурная схема надежности |
| средний коэффициент неготовности |
PAND | вентиль очередности И |
PN | сеть Петри |
RBD | структурная схема надежности |
SEQ | последовательный вентиль |
Таблица 2 - Обозначения
Условное обозначение | Значение |
S | Система, смоделированная с помощью RBD |
| Блоки, используемые в RBD. S зарезервировано для системы, другие буквы используют для блоков |
s=S в работоспособном состоянии | Логическая переменная, указывающая, что система S находится в работоспособном состоянии. Это также событие "Система S находится в работоспособном состоянии" |
s=S в неработоспособном состоянии | Логическая переменная, указывающая на то, что система S находится в неработоспособном состоянии. Это также событие "Система S находится в неработоспособном состоянии" |
x=X в работоспособном состоянии | Логическая переменная, указывающая, что блок X находится в работоспособном состоянии. Это также событие "Х находится в работоспособном состоянии" |
x=X в неработоспособном состоянии | Логическая переменная, указывающая на то, что блок X находится в неработоспособном состоянии. Это также событие "X находится в неработоспособном состоянии" |
( | Минимальные пути успеха (минимальные наборы соединений), минимальные пути отказа (минимальные наборы обрывов) |
( | Непересекающиеся пути успеха (непересекающиеся наборы соединений), непересекающиеся пути отказа (непересекающиеся наборы обрывов) |
Функция вероятности | |
| Постоянная вероятность того, что система S находится в работоспособном состоянии |
| Постоянная вероятность того, что система S находится в работоспособном состоянии |
| Постоянная вероятность того, что блок X находится в работоспособном состоянии |
| Постоянная вероятность того, что блок X находится в неработоспособном состоянии |
| Условная вероятность того, что система S находится в работоспособном состоянии, блок X находится в работоспособном состоянии |
| Условная вероятность того, что система S находится в работоспособном состоянии при условии, что блок X находится в неработоспособном состоянии |
Зависящие от времени вероятности того, что система S находится в работоспособном состоянии | |
Зависящая от времени вероятность того, что блок X находится в работоспособном состоянии | |
Зависящие от времени вероятности того, что система S находится в неработоспособном состоянии | |
Зависящая от времени вероятность того, что блок X находится в неработоспособном состоянии | |
P(OK, | Вероятность состояния OK в момент времени |
| Текущий момент времени |
| Продолжительность времени |
[ | Период времени |
| Коэффициент готовности системы S в момент времени |
| Средний коэффициент готовности системы S за период времени [ |
| Средний коэффициент готовности системы S за период времени [0, |
| Коэффициент готовности блока X в момент времени |
| Коэффициент готовности |
| Средний коэффициент готовности блока X за период времени [ |
| Средний коэффициент готовности блока X за период времени [0, |
| Коэффициент неготовности системы S в момент времени |
| Средний коэффициент неготовности системы S за период времени [ |
| Средний коэффициент неготовности системы S за период [0, |
| Коэффициент неготовности блока X в момент времени |
| Коэффициент готовности |
| Средний коэффициент неготовности блока X за период времени [ |
| Средний коэффициент неготовности блока X за период времени [0, |
| Вероятность безотказной работы системы S за период времени [0, |
| Вероятность отказа системы S за период времени [0, |
Плотность распределения наработки до отказа системы S | |
| Вероятность безотказной работы блока X за период времени [0, |
| Вероятность отказа блока X за период времени [0, |
| Функции плотности наработки до отказа блока X |
| Постоянная и зависящая от времени интенсивности отказов системы S |
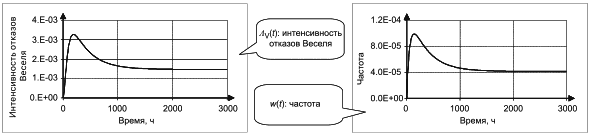
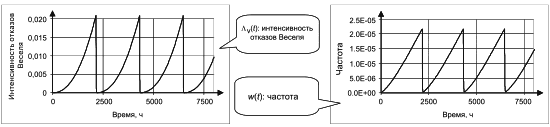
| Условный параметр потока отказов (интенсивность отказов Веселя) системы в целом |
Безусловный параметр потока отказов (частота отказов) системы S в момент времени | |
| Математическое ожидание количества отказов системы S за период времени [0, |
| Средний безусловный параметр потока отказов (средняя частота отказов) системы S за период времени [0, |
| Постоянная и зависящая от времени интенсивность отказов блока X |
| Безусловный параметр потока отказов (частота отказов) блока Х, в момент времени |
| Математическое ожидание количества отказов блока Х за период времени [0, |
| Средний безусловный параметр потока отказов (средняя частота отказов) блока X за период времени [0, |
Интенсивность отказов неработающего блока X | |
| Постоянная или зависящая от времени интенсивности ремонта блока X |
| Количество способов выбора r блоков из n блоков без учета порядка: |
|
|
"0", "1" | Символы, используемые в таблицах истинности, карте Карно, декомпозиции Шеннона и бинарных диаграммах принятия решений для обозначения неработоспособного состояния (отказа) и работоспособного состояния блоков или системы |
| Булевы операторы, обозначающие логическое И; например, |
| Булевы операторы, обозначающие логическое ИЛИ; например |
| "Невозможное" событие и "определенное" событие |
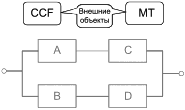
При составлении структурной схемы надежности (RBD) рекомендуется использовать условные обозначения, приведенные в таблице 3.
Таблица 3 - Графическое представление RBD: логические структуры
Графическое представление | Значение |
Вход. | |
| RBD - это направленный граф. Направление каждого соединения от входа к выходу (например, слева направо). При необходимости для исключения ошибок стрелки могут быть добавлены |
| (Элементарный) блок: группировка оборудования, компонентов или других элементов системы |
| Последовательная структура: система находится в работоспособном состоянии, если A и B находятся в работоспособном состоянии. |
| Параллельная структура (полное активное резервирование): система находится в работоспособном состоянии, если A или B находятся в работоспособном состоянии. |
| Вентиль НЕ: выход вентиля равен 0, если его вход равен 1, и наоборот |
| Вентили перехода: выхода и входа с одним и тем же именем. |
| Составной блок: группировка элементарных блоков. Это может быть полезно для упрощения RBD и указания частей, нуждающихся в дальнейшей разработке, или сбора независимых отдельных блоков в структуру, не зависящую от остальной части RBD |
| Повторяющиеся блоки: один и тот же блок, представляющий данный элемент, появляется в нескольких местах RBD либо в прямом состоянии, либо в обратном состоянии, т.е. если блок А в прямом состоянии находится в работоспособном состоянии, то блок в обратном состоянии находится в неработоспособном состоянии, и наоборот. |
| Внешний элемент, взаимодействующий с одним или несколькими блоками RBD. |
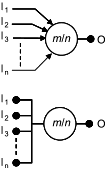
| Логика успеха большинства (обозначение m/n): по крайней мере, m из n блоков необходимо для успешного функционирования системы с активным резервированием. |
Таблица 4 - Графическое представление RBD: небулевы структуры/DRBD
Графическое представление | Значение |
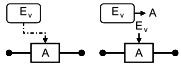
| Резервирование замещением: B начинает функционирование, когда A отказывает |
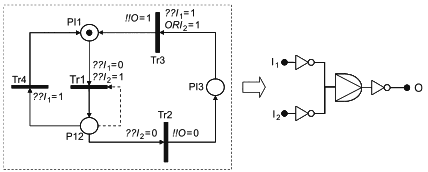
| Функциональные зависимости: состояние A зависит от события |
| Полная функциональная зависимость: если происходит событие |
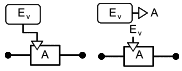
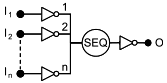
| Вентиль очередности И: выход переходит в неработоспособное состояние, когда входы переходят неработоспособное состояние в порядке |
| Последовательный вентиль: выход переходит в неработоспособное состояние, если входы переходят в неработоспособное состояние: неработоспособное в порядке |
5 Предварительные рассмотрения, основные предположения и ограничения
5.1 Общие положения
В моделях RBD систем используют логические связи между состоянием успеха (работоспособным состоянием) системы (в общей RBD) и состоянием успеха (работоспособным состоянием) ее компонентов (блоков RBD). Таким образом, RBD формирует логическую формулу, именно поэтому RBD не обязательно аналогична физической структуре системы (например, два резервных запорных клапана, расположенные последовательно на одной трубе, представлены в RBD двумя блоками, расположенными параллельно друг другу).
Во-первых, RBD может быть использована для целей качественного анализа путем выявления комбинаций блоков в работоспособном состоянии, позволяющих системе находиться в работоспособном состоянии (путей успеха или наборов соединений) или комбинаций блоков, находящихся в неработоспособном состоянии, ведущих к неработоспособному состоянию системы (путей отказа или наборов обрывов).
Во-вторых, RBD может быть использована для вероятностных расчетов, и поскольку это статическое представление (при отсутствии зависимости от времени), то вероятностные правила в основном связаны с блоками с постоянными вероятностями успеха или отказа.
Метод можно распространить на зависящие от времени вероятностные расчеты. Это может быть трудно для расчета вероятности безотказной работы, но для расчета коэффициента готовности и частоты при условии, что блоки не зависят друг от друга, нет никаких ограничений, кроме математических трудностей, связанных с распределением, которое может быть использовано для описания наработки до отказа или ремонта блоков. Это позволяет, например, смоделировать коэффициент готовности/неготовности каждого из блоков с помощью аналитических формул, результаты которых объединяют в соответствии с логикой RBD для определения коэффициента готовности системы (RBD). Если эти аналитические формулы получены с помощью марковских процессов, RBD эквивалентна глобальному марковскому процессу, моделирующему всю систему. Такая модель называется "RBD-управляемым марковским процессом". Это основа большинства вероятностных расчетов с помощью RBD.
5.2 Предварительные условия и основные предположения
RBD представляет собой направленный ациклический граф (т.е. граф без петель или обратных связей), который можно начертить, используя основные логические структуры, представленные в таблице 3. RBD используют для моделирования состояния системы на основе следующих основных предположений:
a) система имеет только два состояния: работоспособное (состояние успеха) и неработоспособное (состояние отказа);
b) блоки RBD моделируют компоненты системы или ее части (например, группы компонентов). Каждый блок имеет только два состояния: работоспособное (состояние успеха) или неработоспособное (состояние отказа);
c) RBD представляет собой логику, связывающую состояние успеха системы с состоянием успеха ее составных частей (блоков);
d) каждый блок не зависит от других блоков.
Приведенные выше предположения должны быть, как правило, выполнены для применения аналитических расчетов (т.е. расчетов по формулам), разработанных в настоящем стандарте. Если предположения не выполнены, аналитические расчеты могут быть заменены моделированием методом Монте-Карло или другими методами, такими как марковский анализ [2], сети Петри [3] или динамические RBD, описанные в 12.2 и приложении Е.
5.3 Ограничения
Предположения, приведенные в 5.2, представляют собой некоторые ограничения, но существуют и другие, менее очевидные ограничения при рассмотрении вероятностей, зависящих от времени. В частности, пользователям настоящего стандарта следует знать о проблемах, связанных с требованием независимости, которое должно быть выполнено всегда, например:
a) последовательные события не входят в область применения булевых моделей. Они в принципе не могут быть обработаны RBD. Тем не менее в простых случаях, таких как резервирование замещением, можно преодолеть эту проблему, рассматривая составные блоки (см. таблицу 3 и 7.5.3) независимо от других блоков;
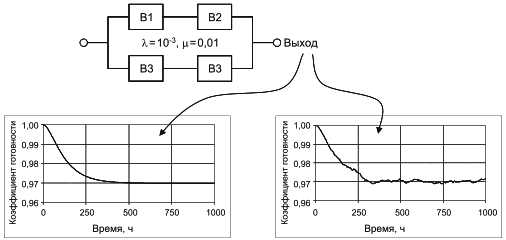
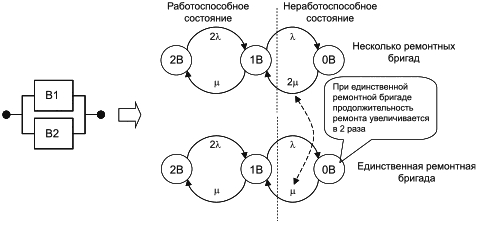
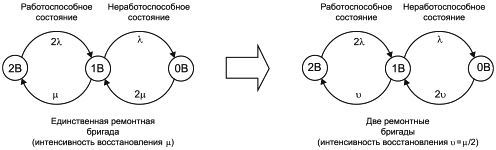
b) расчеты коэффициента готовности или частоты восстанавливаемых систем предполагают, что ремонты блоков не зависят друг от друга, т.е. для ремонта каждого блока имеется своя ремонтная бригада;
c) расчеты показателей безотказности восстанавливаемых систем предполагают, что отказавший блок может быть восстановлен только в том случае, если система при возникновении отказа все еще работает. Это вводит системные зависимости между состояниями блоков, а также между состояниями блоков и системы (см. пункт 10.3.1.4). Это нарушает предположение, описанное в 5.2 d); поэтому, за исключением частных случаев и приближений, аналитические расчеты показателей безотказности, как правило, невозможны.
При условии выполнения предположений, приведенных в 5.2, метод RBD можно использовать непосредственно для качественного анализа и расчетов коэффициента готовности и частоты, но для расчета показателей безотказности он может быть использован только в частных случаях.
Следует отметить, что при выполнении вероятностных расчетов доступны хорошие аппроксимации с низкими вероятностями (например, отказа компонентов/блоков), которые не могут быть использованы при высоких вероятностях (например, вероятностях успеха компонентов/блоков). Поэтому для преодоления этого ограничения лучше работать с вероятностями отказа (коэффициента неготовности), а не с вероятностями успеха (коэффициента готовности).
6 Установление состояний успеха/отказа системы
6.1 Общие положения
Необходимым условием построения моделей безотказности системы является четкое понимание путей функционирования системы и ее компонентов. Система часто требует более одного определения успеха/отказа. Эти определения должны быть установлены и перечислены. RBD может быть выполнена на разных уровнях: уровне системы, уровне подсистем (модулей) или уровне сборочных единиц. Если RBD создают для дальнейшего анализа (например, для FMEA), должен быть выбран уровень, подходящий для такого анализа.
Кроме того, должно быть четко установлено следующее:
- функции, которые должны быть выполнены;
- параметры работы и их допустимые пределы;
- условия окружающей среды и эксплуатации.
После определения успеха/отказа системы следующим этапом является определение логических блоков для разделения системы в соответствии с целью анализа безотказности. Отдельные блоки могут представлять собой подструктуры системы и, в свою очередь, могут быть представлены своими RBD (сокращение системы, см. 11.2).
Для количественной оценки RBD существуют различные методы. В зависимости от типа структуры могут быть применены простые булевы методы (см. 7) и/или анализ наборов путей и обрывов (см. 8). Расчеты могут быть выполнены с использованием аналитических методов (например, базовые методы расчета коэффициента готовности компонент) или с помощью моделирования методом Монте-Карло. Преимущество моделирования методом Монте-Карло заключается в том, что вероятности событий в RBD могут быть не объединены аналитически, так как само моделирование учитывает, функционирует блок или отказал (см. 12.2 и F.5).
Поскольку RBD описывает логические соотношения, необходимые для функционирования системы, то RBD не обязательно отражает физические связи аппаратного обеспечения, хотя RBD обычно следует, насколько это возможно, физическим связям системы.
6.2 Детальные рассмотрения
6.2.1 Работа системы
Возможно использование системы в нескольких функциональных режимах. Если для каждого режима использована отдельная система, такие режимы должны быть обработаны независимо от других режимов, и соответственно для них следует использовать отдельные модели безотказности. Поэтому, если одна и та же система выполняет все функции, следует использовать отдельные RBD для каждого типа операций. Четкие формулировки того, что представляет собой успех/отказ системы для каждого аспекта работы системы, являются обязательным условием.
6.2.2 Условия окружающей среды
Требования к работе системы должны сопровождаться описанием условий окружающей среды, в которых система должна функционировать. Также должно быть включено описание всех условий, воздействию которых система будет подвергаться в процессе эксплуатации, транспортировки, хранения и использования.
Конкретный элемент оборудования часто используют в нескольких условиях окружающей среды, например на борту корабля, в самолете или на земле. Если это так, то оценки показателей безотказности могут быть выполнены каждый раз с использованием одной и той же RBD, но с использованием соответствующей интенсивности отказов компонента (блока) для каждой среды.
6.2.3 Рабочие циклы
Должно быть установлено соотношение между календарным временем, временем работы и циклами включения/выключения. Если можно предположить, что процесс включения и выключения оборудования не способствует возникновению отказов, а также, что интенсивность отказов оборудования в периоды неиспользования ничтожно мала, тогда необходимо учитывать только фактическое время работы оборудования.
Тем не менее в некоторых случаях процесс включения и выключения сам по себе является основной причиной возникновения отказов оборудования, и оборудование может иметь более высокую частоту отказов в период неиспользования, чем в процессе эксплуатации (например, из-за влажности и коррозии). В сложных случаях, когда только части системы включаются и выключаются, могут быть более подходящими методы моделирования, отличные от RBD (например, Марковский анализ или сети Петри).
7 Элементарные модели
7.1 Разработка модели
Первый этап - это определение успеха/отказа системы. Если использовано более одного определения для успеха или отказа каждого из них, может потребоваться отдельная RBD. Следующим этапом является разделение системы на блоки для отражения логических связей таким образом, чтобы каждый блок статистически не зависел от других. Следует постараться сделать блоки как можно больше, гарантируя при этом, что каждый блок не включает (предпочтительно) резервирование.
Следующий этап заключается в построении RBD в соответствии с определением успеха/отказа системы, которая соединяет блоки и формирует путь успеха (см. 3.15). Как указано на схеме, различные пути успеха между входом и выходом проходят через комбинации блоков, которые должны функционировать для функционирования системы.
Примечание - На практике в зависимости от конфигурации системы может возникнуть необходимость в повторных построениях RBD (каждый раз учитывая этапы, упомянутые выше), прежде чем будет создана и отработана подходящая структурная схема.
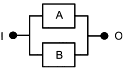
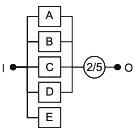
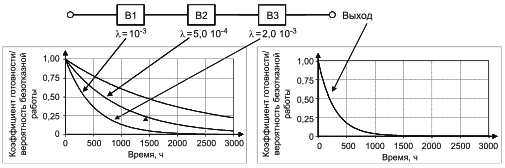
7.2 Последовательные структуры
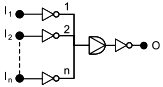
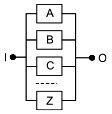
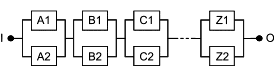
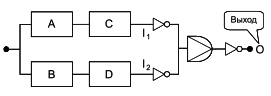
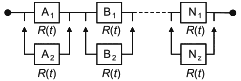
Если для функционирования системы необходимо, чтобы все блоки функционировали, то в соответствующей RBD все блоки соединены последовательно, как показано на рисунке 2.
|
Рисунок 2 - Последовательная структурная схема надежности
На этой схеме "I" - вход, "O" - выход и A, B, C, ... Z - блоки, которые вместе составляют систему. RBD такого типа называют "последовательные RBD" или "последовательные модели". Такая структура моделирует следующую логическую функцию:
![]() , (1)
, (1)
где a, b, c и z представляют собой состояния успеха блоков A, B, C и Z (см. таблицу 2) и s - состояние успеха соответствующей системы.
7.3 Параллельные структуры
Другой тип RBD необходим, когда для успеха системы достаточно состояния успеха только одного компонента системы (т.е. одного блока). Это тот случай, когда используют резервные компоненты.
Модель представляет параллельную структуру, такую как представленная на рисунке 3, которая включает несколько резервных блоков. В этой структуре система не работает тогда и только тогда, когда все блоки находятся в неработоспособном состоянии.
|
Рисунок 3 - Параллельная структурная схема надежности
Такая структура моделирует следующую логическую функцию:
![]() . (2)
. (2)
7.4 Сочетание последовательных и параллельных структур
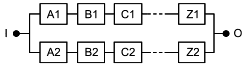
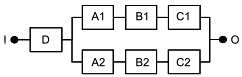
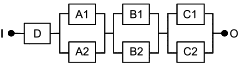
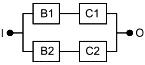
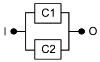
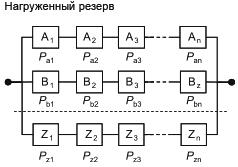
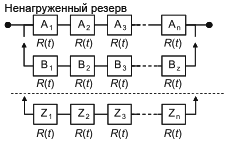
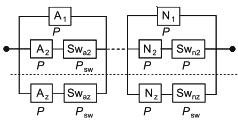
Базовые структуры, представленные на рисунках 2 и 3, могут быть использованы для моделирования RBD более сложных систем. Например, если вся RBD, представленная на рисунке 2, дублирована (т.е. резервирована), то получается RBD, показанная на рисунке 4. Если каждый блок в RBD, представленный на рисунке 2, резервирован, получается RBD, показанная на рисунке 5. RBD такого типа называют "последовательно-параллельные RBD" или "последовательно-параллельные модели". Следует заметить, что термины "дублированный", "резервный" и "параллельный" очень близки по смыслу, но не являются синонимами.
1) Дублирование относится к способу построения RBD и означает повторение аналогичных структур. Например, на рисунке 4 показано дублирование структуры, представленной на рисунке 2, а на рисунке 5 - только дублирование компонентов. На самом деле параллельные структуры (B1, B2), (C1, C2) и т.д. являются последовательным дублированием параллельной структуры (А1, А2);
2) резервирование означает, что если один компонент выходит из строя, то его функцию может выполнить другой. Например, A1 и A2 на рисунке 5 являются резервированными;
3) параллельность связана с логикой структуры системы и ее графическим представлением. Например, A1 и A2 на рисунке 5 являются резервированными.
|
Рисунок 4 - Параллельная структура, выполненная из дублированных последовательных подструктур
Такая структура моделирует следующую логическую функцию:
![]() . (3)
. (3)
|
Рисунок 5 - Последовательная структура, состоящая из последовательного соединения параллельных структур
Такая структура моделирует следующую логическую функцию:
![]() . (4)
. (4)
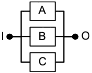
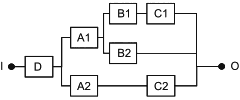
RBD, используемые для моделирования безотказности систем, часто представляют собой более сложные комбинации последовательных и параллельных структур. Например, дублированная линия связи, содержащая три ретранслятора (A1, B1, C1 и A2, B2, C2) и общий блок питания (D), может иметь вид, представленный на рисунках 6 и 7.
|
Рисунок 6 - Общая последовательно-параллельная структурная схема надежности
Такая структура моделирует следующую логическую функцию:
![]() . (5)
. (5)
|
Рисунок 7 - Общая последовательно-параллельная структурная схема надежности
Эта структура моделирует следующую логическую функцию:
![]() . (6)
. (6)
В соответствии с предполагаемой статистической независимостью, установленной выше, отказ любого блока не приводит к изменению вероятности отказа какого-либо другого блока внутри системы. В частности, отказ резервного блока не влияет на источники питания системы.
7.5 Другие структуры
7.5.1 Структуры типа m из n
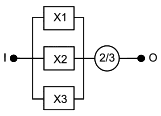
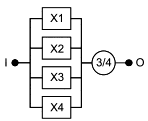
Часто возникает необходимость моделирования системы, определение успеха которой устанавливает, что для функционирования системы необходимо функционирование не менее m из n элементов, соединенных параллельно. Такие логические структуры часто называют структурами "мажоритарного голосования" или структурами "m из n". Например, см. RBD, показанные на рисунках 8 и 9.
|
Рисунок 8 - Структура резервирования 2 из 3
|
Рисунок 9 - Структура резервирования 3 из 4
Таким образом, на рисунке 8 для успешного функционирования системы требуется функционирование не менее двух блоков, а на рисунке 9 для успеха системы необходимо функционирование не менее трех блоков. В обоих случаях допускается отказ одного объекта, но отказ двух и более объектов не допустим.
Такие структуры моделируют следующие логические функции:
резервирование 2/3:
![]() ; (7)
; (7)
- резервирование 3/4:
![]() . (8)
. (8)
Эти логические функции не могут быть представлены простой комбинацией элементарных последовательных и параллельных структур.
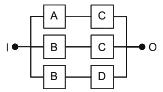
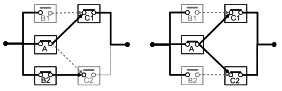
7.5.2 Конструкции с общими блоками
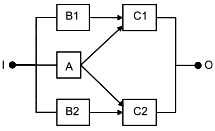
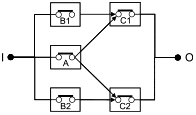
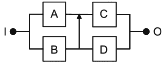
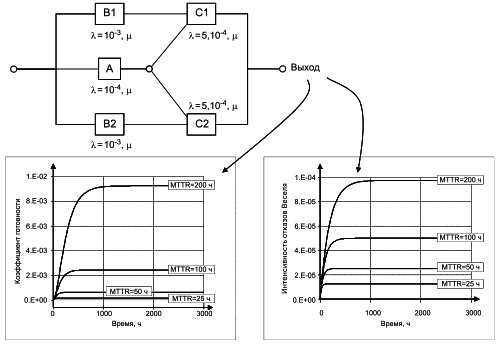
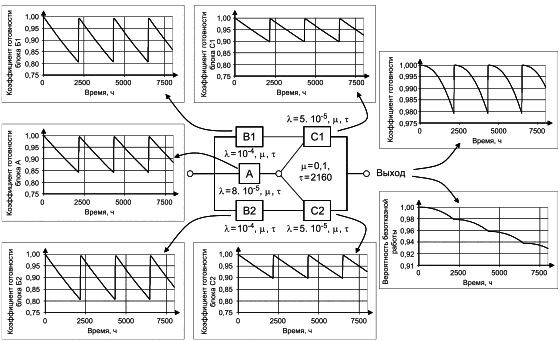
Большинство RBD являются понятными, а условия успеха системы очевидны. Однако не все RBD могут быть сведены к комбинациям последовательных или параллельных структур с блоками, появляющимися только один раз. RBD на рисунке 10 - пример, в котором блок A является общим для двух путей.
|
Рисунок 10 - Схема, которую нелегко представить последовательным и/или параллельным расположением блоков
Такая структура моделирует следующую логическую функцию:
![]() . (9)
. (9)
Схема не требует объяснений. Для успеха системы достигаются блоки B1 и C1, или блоки А и С1 или блоки А и С2, или блоки В2 и С2. На рисунке 10 представлена схема подачи топлива на двигатели легкого самолета. Блок B1 представляет собой поставку топлива на левый двигатель (С1), блок В2 представляет собой подачу топлива на правый двигатель (С2), а блок А представляет собой общую резервную поставку на оба двигателя. Определение успеха устанавливает, что для функционирования необходимо, чтобы работал хотя бы один двигатель самолета, а для отказа самолета должны отказать оба двигателя.
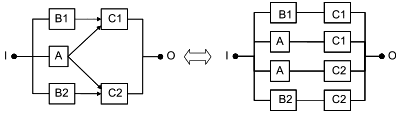
Следует отметить, что на всех приведенных выше схемах (рисунки 2-10) ни один блок не появляется на диаграмме более одного раза. Процедуры разработки выражений для RBD данного типа приведены в разделе 8.2. На рисунках 18 и 19 приведены последовательно-параллельные RBD, эквивалентные рисунку 10, где реализованы повторяющиеся блоки.
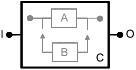
7.5.3 Составные блоки
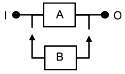
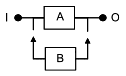
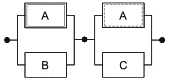
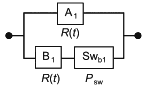
На рисунке 11 показана модель системы с холодным резервированием замещением, где объект В начинает работать при отказе объекта А при идеальном переключении с А на В. В соответствующей RBD блоки А и В не являются независимыми, и это нарушает фундаментальное предположение о независимости блоков, которое лежит в основе настоящего стандарта.
|
Рисунок 11 - Пример RBD с зависимыми блоками
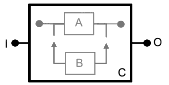
Поскольку блоки А и В не могут быть рассмотрены независимо друг от друга, необходимо рассмотреть их в целом, это можно сделать с помощью составного блока, такого как блок C, представленный на рисунке 12.
|
Рисунок 12 - Пример составного блока
Составной блок С имеет два состояния: успех/отказ. Тогда, если он не зависит от других блоков RBD, он может быть обработан как единый блок. Конечно, вероятности его отказа/успеха должны быть рассчитаны с учетом блоков А и В и зависимости между ними.
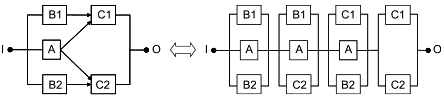
7.6 Большие RBD и использование вентилей перехода
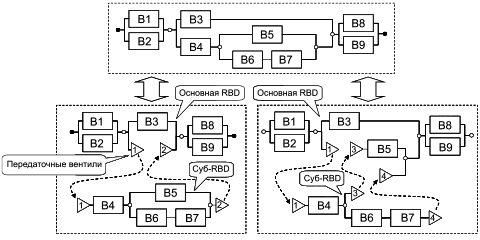
RBD, относящиеся к промышленным системам, могут быть слишком большими, чтобы их можно было нарисовать целиком на одном листе бумаги. В этом случае они могут быть разделены на несколько более мелких частей (суб-RBD), связанных с помощью использования вентилей перехода.
|
Рисунок 13 - Использование вентилей перехода и суб-RBD
На рисунке 13 приведены два примера использования вентилей перехода в каждой из двух RBD, нижняя часть рисунка эквивалентна RBD в верхней части. Они делятся на две части: основная RBD и суб-RBD. Следует отметить, что суб-RBD не обязательно должна иметь только один вход и один выход.
На общую базовую логическую функцию такое разделение не влияет, но это позволяет рисовать большую RBD на нескольких отдельных страницах. Как выбрать деление RBD, сохраняя при этом хорошее понимание всего RBD и его суб-RBD, решает аналитик.
8 Качественный анализ: минимальные наборы соединений и обрывов
8.1 Аналогия с электросхемой
RBD может быть использована в первую очередь для целей качественного анализа путем идентификации:
- комбинаций блоков в работоспособном состоянии, приводящих к тому, что система находится в работоспособном состоянии (пути успеха или наборы соединений),
- комбинаций блоков в неработоспособном состоянии, приводящих к тому, что система находится в неработоспособном состоянии (пути отказа или наборы обрывов).
|
Рисунок 14 - Аналогия между блоком и электрическим выключателем
Примечание - При построении RBD, соответствующей физической электрической схеме, положение физического переключателя может отличаться от его представления с помощью аналогии, приведенной на рисунке 14. Например, закрытый физический переключатель может быть представлен открытым виртуальным переключателем, так как он находится в нерабочем состоянии.
Для этого очень полезна аналогия с электрической схемой, показанная на рисунке 14. Она состоит в том, что каждый блок эквивалентен электрическому переключателю, который замкнут, когда блок находится в работоспособном состоянии, и открыт (разомкнут), когда блок находится в неработоспособном состоянии. Это сделано для того, чтобы показать эквивалентность рисунков 10 и 15, на рисунке 15 каждый блок смоделирован с помощью электрического переключателя.
|
Рисунок 15 - Аналогия с электрической схемой
Когда электрическая цепь замкнута, электрический сигнал проходит по RBD от входа к выходу. Поэтому любая комбинация (набор) замкнутых переключателей, позволяющих сигналу проходить по модели RBD от входа до выхода, моделирует состояние успеха системы. Это путь успеха в отношении состояния системы или набор соединений, обеспечивающий замкнутость электрической цепи.
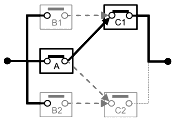
|
Рисунок 16 - Пример минимального пути успеха (набор соединений)
На рисунке 16 показан один из путей успеха () RBD, показанной на рисунке 15. Этот путь успеха минимален, поскольку если А отказывает или С1 отказывает, система в целом также отказывает, т.е. успех A и успех C1 необходимы и достаточны для того, чтобы система находилась в состоянии успеха.
В B.3.1 приведены другие примеры минимальных и не минимальных наборов соединений.
Свойства булевой алгебры обеспечивают общее представление о работоспособном состоянии системы , как объединение минимальных наборов соединений RBD (
). Это приводит к следующей формуле:
![]() . (10)
. (10)
Если электрическая цепь разомкнута (в ней имеется обрыв), электрический сигнал от входа не может пройти по RBD до выхода. Поэтому любая комбинация (набор) открытых переключателей, препятствующих прохождению сигнала от входа до выхода, моделирует неработоспособное состояние системы. Это путь отказа в отношении состояния системы или набор обрывов в отношении электрической цепи.
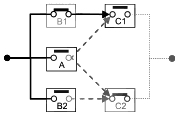
|
Рисунок 17 - Пример минимального пути отказа (набор сечений)
На рисунке 17 показан один из путей отказа, ![]() , RBD, приведенной на рисунке 15. Этот путь отказа (набор обрывов) минимален, поскольку если любой блок из A, B2 или C1 восстанавливается (выключатель закрывается), система также восстанавливается, т.е. отказы A, B2 и C1 необходимы и достаточны для того, чтобы система находилась в состоянии отказа.
, RBD, приведенной на рисунке 15. Этот путь отказа (набор обрывов) минимален, поскольку если любой блок из A, B2 или C1 восстанавливается (выключатель закрывается), система также восстанавливается, т.е. отказы A, B2 и C1 необходимы и достаточны для того, чтобы система находилась в состоянии отказа.
В B.3.1 приведены другие примеры минимальных и неминимальных наборов обрывов.
Свойства булевой алгебры обеспечивают общее представление неработоспособного состояния , как объединение наборов минимальных обрывов (
) в RBD:
![]() . (11)
. (11)
Следовательно, из формул (10) и (11) следует тождество:
![]() . (12)
. (12)
Минимальные наборы обрывов и минимальные наборы соединений могут быть получены путем расширения логической формулы, соответствующей RBD. За исключением простых случаев, это не так просто сделать вручную, но существуют мощные алгоритмы, реализованные в виде программных пакетов RBD.
8.2 Последовательно-параллельное представление с минимальными путями успеха и наборами обрывов
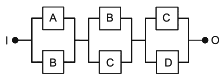
Тождество (12) обеспечивает два эквивалентных способа представления RBD на основе его минимальных наборов соединений или минимальных наборов обрывов.
Применительно к RBD, представленной на рисунке 10, это приводит к двум эквивалентным логическим формулам (подробные пояснения см. в B.3.2):
![]() , (13)
, (13)
![]() . (14)
. (14)
Затем эта RBD может быть заменена эквивалентными представлениями, приведенными на рисунке 18 (на основе наборов соединений) или на рисунке 19 (на основе наборов обрывов), на которых некоторые блоки повторяются несколько раз.
|
Рисунок 18 - Эквивалентные RBD с минимальными путями успеха
На рисунке 18 представлено четыре набора соединений второго порядка (см. 3.16, примечание 2):
![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
|
Рисунок 19 - Эквивалентные RBD с минимальными наборами обрывов
Рисунок 19 состоит из одного набора обрывов второго порядка ![]() и трех наборов обрывов третьего порядка:
и трех наборов обрывов третьего порядка:
![]() ,
, ![]() и
и ![]() .
.
8.3 Качественный анализ минимальных наборов обрывов
Для проведения качественного анализа целесообразно рассматривать минимальные наборы обрывов, а не минимальные наборы соединений. Это можно показать с помощью приведенного выше примера: наборы обрывов второго порядка ![]() более вероятны, чем наборы обрывов третьего порядка
более вероятны, чем наборы обрывов третьего порядка ![]() ,
, ![]() и
и ![]() . Поэтому с качественной точки зрения минимальный набор обрывов
. Поэтому с качественной точки зрения минимальный набор обрывов ![]() является слабым местом системы и должен быть улучшен в первую очередь.
является слабым местом системы и должен быть улучшен в первую очередь.
Таким образом, порядок выполнения качественного анализа может быть следующим:
a) определение минимального набора обрывов из логического уравнения отказа системы;
b) сортировка минимальных наборов обрывов в соответствии с возрастанием их порядка;
c) фокусировка на минимальные наборы обрывов самого низкого порядка для улучшения системы.
Когда для блоков известны вероятности отказа, минимальные наборы обрывов могут быть более точно отсортированы на этапе b) путем вычисления вероятности возникновения каждого из них.
9 Количественный анализ: блоки с постоянной вероятностью отказа/успеха
9.1 Последовательные структуры
На рисунке 20 показана связь булевой формулы базовой (последовательной) структуры с вероятностными расчетами.
|
Рисунок 20 - Связь между базовой последовательной структурой и вероятностными расчетами
Данная вероятностная формула в основном установлена для независимых блоков с постоянными вероятностями. Она выражает вероятность успеха системы в виде функции вероятностей успеха блока A (
) и блока B (
). Таким образом, модели RBD в первую очередь могут быть использованы для систем, содержащих независимые блоки с постоянной вероятностью работоспособного состояния.
На этом этапе неуместно говорить о показателях безотказности, готовности или частоте отказов системы, поскольку такие вероятностные меры определяют только для систем с зависимостью состояния от времени.
Формула, приведенная на рисунке 20, может быть легко распространена на использование в таких системах, как показанные на рисунке 2 (см. B.4.1). Если блоки A, B, ..., Z являются независимыми, то вероятность успеха системы задается простым уравнением:
![]() , (15)
, (15)
то есть произведением вероятностей успеха всех блоков, составляющих RBD.
В общем случае для n последовательных блоков
![]() .
.
9.2 Параллельные структуры
На рисунке 21 показана связь булевой формулы базовой параллельной структуры и вероятностных вычислений.
Так же как для базовой последовательной структуры, формула для базовой параллельной структуры установлена для постоянных вероятностей и независимых блоков как функция
и
.
Как бы то ни было, формулу, показанную на рисунке 21, нелегко распространить более чем на два компонента (см. формулу Сильвестра-Пуанкаре в 11.7 и B.4.2). К счастью, можно заметить, что ![]() . Это показывает, что система отказывает, когда отказывают A и B.
. Это показывает, что система отказывает, когда отказывают A и B.
|
Рисунок 21 - Связь параллельной структуры и вероятностных вычислений
Следовательно, вероятность успеха системы () задана формулой:
![]() . (17)
. (17)
Формула (17) может быть легко распространена на n параллельных блоков (см. B.4.2), т.е.:
- вероятность отказа:
![]() ; (18)
; (18)
- вероятность успеха:
![]() . (19)
. (19)
9.3 Комбинация последовательных и параллельных структур
Формулы (15) и (17) могут быть объединены, и это в простых случаях можно сделать вручную, но приведенные выше расчеты, как правило, нелегко выполнить вручную. К счастью, существуют мощные алгоритмы, реализованные в программных пакетах RBD. Они основаны на методах, описанных в B.5, B.6 или B.7.
9.4 Структуры m/n (идентичные элементы)
Структура m/n проанализирована в B.4.4. Если блоки идентичны (с одной и той же вероятностью успеха p у каждого), то вероятность успеха системы задана формулой:
![]() , (20)
, (20)
а вероятность отказа задана формулой:
![]() . (21)
. (21)
Если n=2m-1 (например, 1/1, 2/3, 3/5 и т.д.), система находится в работоспособном состоянии, если m блоков находятся в работоспособном состоянии, и система находится в неработоспособном состоянии, если m блоков находятся в неработоспособном состоянии. Эти структуры симметричны по отношению к событиям успеха и отказа. Некоторые подобные структуры, например структуру 2/3, широко используют для обеспечения безопасности системы.
Если n элементов не идентичны, рекомендуется использовать более общую процедуру (см. 11.8.2).
10 Количественный анализ: блоки с зависящими от времени вероятностями отказа/успеха
10.1 Общие положения
Расчеты, разработанные для постоянных вероятностей в 9, могут быть легко распространены на зависящую от времени вероятность системы при условии, что вероятности блоков
не зависят друг от друга. Это означает, что отказ (или ремонт) любого блока не должен влиять на вероятность отказа или ремонта любого другого блока в системе. Из этого следует, что для ремонта блоков должно быть достаточно ресурсов, когда два или более человек ремонтируют конкретный блок и ни один из них не мешает другому. При этом отказы и ремонты отдельных блоков считаются статистически независимыми событиями. Расчеты вероятности успеха системы, зависящей от времени, подробно описаны в приложении С.
Так как вероятность того, что объект находится в данный момент времени в работоспособном состоянии, является его мгновенным коэффициентом готовности ![]() и
и ![]() . Этот результат справедлив и для сложных структур и больших RBD (см. 11 и приложение В) при условии, что блоки не зависят друг от друга в каждый момент времени. Формулы, разработанные для случая постоянной вероятности, применимы для расчетов коэффициентов готовности и неготовности.
. Этот результат справедлив и для сложных структур и больших RBD (см. 11 и приложение В) при условии, что блоки не зависят друг от друга в каждый момент времени. Формулы, разработанные для случая постоянной вероятности, применимы для расчетов коэффициентов готовности и неготовности.
- Последовательные структуры:
![]() ,
, ![]() . (22)
. (22)
- Параллельные структуры:
![]() ,
, ![]() . (23)
. (23)
- Структура m/n:
![]() ,
, ![]() . (24)
. (24)
Расчеты коэффициентов готовности и неготовности, описанные выше, не простые, но расчеты вероятности безотказности работы и вероятности отказа еще более сложные. Это связано с определением понятия вероятности безотказной работы: ![]() (S в работоспособном состоянии в течение периода времени [0, t). Это означает, что только последовательности событий системы, которые не переводят систему в неработоспособное состояние, используют для вычисления
(S в работоспособном состоянии в течение периода времени [0, t). Это означает, что только последовательности событий системы, которые не переводят систему в неработоспособное состояние, используют для вычисления . Поэтому последовательности событий системы, которые включают последовательность "работоспособное состояние"
"неработоспособное состояние"
"работоспособное состояние", должны быть исключены из расчетов. Это означает, что часть системы, перешедшая в неработоспособное состояние, ремонтируется только в том случае, если система остается в работоспособном состоянии в течение ремонта этой части. Таким образом, что касается расчета
, то части системы (например, компоненты) восстанавливают или нет в зависимости от состояния системы (т.е. от состояний других частей). Это представляет собой зависимости между частями системы и, следовательно, между блоками моделирования этих частей в RBD системы. Это происходит в случае резервирования восстанавливаемых объектов. Это является основной трудностью в понимании настоящего стандарта: за исключением RBD, состоящей из последовательных блоков, вероятность безотказной работы системы
не может быть рассчитана путем объединения вероятности безотказной работы
![]() ее отдельных блоков. Формулы, установленные выше, в соответствии с гипотезой независимости больше не справедливы. Это более подробно рассмотрено в 10.3.1.4.
ее отдельных блоков. Формулы, установленные выше, в соответствии с гипотезой независимости больше не справедливы. Это более подробно рассмотрено в 10.3.1.4.
10.2 Невосстанавливаемые блоки
10.2.1 Общие положения
Если блок X невосстанавливаемый, вероятность его работоспособности в момент времени t равна вероятности отсутствия отказов в период времени [0, ]. Поэтому вероятность безотказной работы объекта
![]() равна его коэффициенту готовности
равна его коэффициенту готовности ![]() .
.
Если в системе нет восстанавливаемых блоков, система, состоящая из этих блоков, тоже является невосстанавливаемой. Тогда ее коэффициент готовности и вероятность безотказной работы идентичны и ![]() .
.
10.2.2 Простой невосстанавливаемый блок
Вероятность безотказной работы объекта X связана с его интенсивностью отказов ![]() следующей зависимостью:
следующей зависимостью:
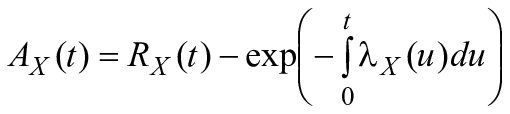 , (25)
, (25)
где ![]() - интенсивность отказов блока X в точке
- интенсивность отказов блока X в точке , где
- фиктивная переменная.
Если постоянна, формула (25) существенно упрощается:
![]() , (26)
, (26)
следовательно,
![]() . (27)
. (27)
10.2.3 Невосстанавливаемые составные блоки
Невосстанавливаемый составной блок С может быть обработан как единое целое и как простой невосстанавливаемый блок С при условии, что для него установлен коэффициент готовности ![]() . Следует заметить, что в этом случае
. Следует заметить, что в этом случае ![]() .
.
Это можно проиллюстрировать составным блоком, представленным на рисунке 12. Это соответствует холодному резерву системы со следующими параметрами:
- - постоянная интенсивность отказов блока А,
![]() - функция плотности вероятности его наработки до отказа;
- функция плотности вероятности его наработки до отказа;
- - постоянная интенсивность отказов блока B, когда он находится в пассивном (бездействующем) состоянии, либо в состоянии холодного резерва, либо в состоянии пониженной мощности;
- - постоянная интенсивность отказов блока B, когда он находится в активном состоянии после его запуска при отказе блока А.
Примечание - В следующих расчетах переключение считается совершенным, примеры моделирования несовершенного переключения приведены в 10.3.1.2 (рис.23) и C.3.3.
Такая система проанализирована в C.3.3 со следующими результатами:
- если интенсивность с резервированием в состоянии бездействия предполагается равной нулю, то коэффициент готовности системы равен:
![]() , (28)
, (28)
- если интенсивности отказов равны (![]() и
и ![]() ), формула для вероятности безотказной работы системы может быть представлена в виде:
), формула для вероятности безотказной работы системы может быть представлена в виде:
![]() . (29)
. (29)
Если в идеальных условиях, показанных выше, имеется n резервных объектов (вместо одного), последнее выражение принимает вид:
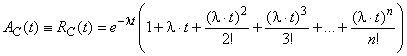 . (30)
. (30)
Формулы (28), (29) или (30) могут быть использованы для составного блока C, как формула (26) для обычных блоков. Тем не менее эти формулы трудно установить, и следует использовать другие процедуры (анализ Маркова, например, для анализа систем с резервированием) (см. 10.3.1.2).
10.2.4 RBD с невосстанавливаемыми блоками
Коэффициент готовности/вероятность безотказной работы: при условии, что блоки не зависят друг от друга, коэффициент готовности/вероятность безотказной работы RBD могут быть рассчитаны путем комбинирования коэффициента готовности/вероятность безотказной работы блоков (см. 10.2.2 и 10.2.3) в соответствии с RBD и с использованием формул, представленных в 10.1.
Частота: система, содержащая невосстанавливаемые компоненты, может отказать только один раз. Вероятность отказа за период времени [0, ] равна
![]() , а средняя частота отказов
, а средняя частота отказов ![]() равна
равна ![]() , она уменьшается и стремится к нулю с возрастанием времени.
, она уменьшается и стремится к нулю с возрастанием времени.
10.3 Восстанавливаемые блоки
10.3.1 Расчет коэффициента готовности
10.3.1.1 Простой блок
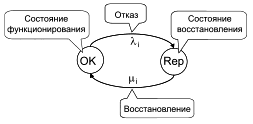
При восстановлении i-го блока его коэффициент готовности зависит как от интенсивности отказов, так и от ресурсов ремонта. Ресурсы ремонта, как правило, распределяют на уровне системы, и если они ограниченны, это создает в системе зависимость между блоками. Таким образом, блоки являются независимыми только тогда, когда ресурсы ремонта не ограниченны. В этом случае блок может быть восстановлен в любое время, даже когда один или несколько блоков уже восстанавливают. Это предположение подразумевает, в частности, наличие такого количества ремонтных бригад, сколько блоков в системе.
Коэффициент готовности блока может быть выражен формулой (простой или сложной). В простейшем случае восстановленные блоки характеризуются постоянной интенсивностью отказов
и постоянной интенсивностью ремонта
, что приводит к классической формуле:
![]() . (31)
. (31)
Эта аналитическая формула может быть заменена эквивалентным графом Маркова, представленным на рисунке 22, где ![]() , где
, где ![]() - вероятность работоспособного состояния в момент времени
- вероятность работоспособного состояния в момент времени .
|
Рисунок 22 - Граф Маркова коэффициента готовности для простого восстанавливаемого блока
Примечание - Граф Маркова, предназначенный для вычисления коэффициента готовности, называется "графом Маркова коэффициента готовности".
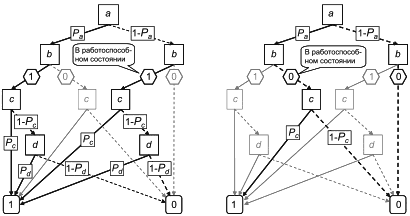
10.3.1.2 Восстанавливаемые составные блоки
Восстанавливаемый составной блок C может быть обработан как единое целое и как простой восстанавливаемый блок, при условии, что для него установлен коэффициент готовности ![]() . Следует заметить, что в этом случае
. Следует заметить, что в этом случае ![]() .
.
Это можно проиллюстрировать составным блоком, представленным на рисунке 12 и уже проанализированным в 10.2.3 в случае невосстанавливаемого блока. Если компоненты А и В считаются теперь восстанавливаемыми, то формула для коэффициента готовности ![]() блока C может быть установлена с помощью графа Маркова, приведенного на рисунке 23.
блока C может быть установлена с помощью графа Маркова, приведенного на рисунке 23.
|
Рисунок 23 - Резервирование замещением
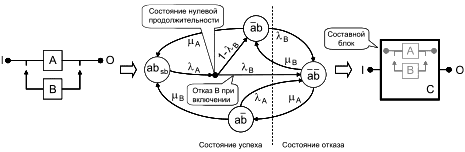
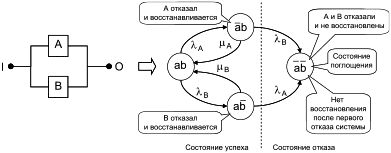
В этом графе C восстанавливают после отказа (см. переходы из состояния отказа в состояние успеха); таким образом, это граф Маркова коэффициента готовности (см. 10.3.3 для сравнения с графом Маркова "вероятность безотказной работы"). Этот граф Маркова можно использовать для установления коэффициента готовности ![]() составного блока C или даже как вход в RBD (см. C.3).
составного блока C или даже как вход в RBD (см. C.3).
В этом графе Маркова отказ механизма переключения и обнаружения моделируют, используя вероятность того, что блок B отказывает при включении при отказе A. Поскольку этот отказ возникает после отказа компонента А, было введено состояние нулевой продолжительности. Из этого состояния B немедленно включается (вероятность
![]() ) или отказывает (вероятность
) или отказывает (вероятность ).
Граф Маркова, показанный на рисунке 23, моделирует зависимости между блоками А и В:
- B включается только после отказа А;
- B может отказать при включении по запросу при отказе А;
- B возвращается в состояние резервирования, как только А и В находятся в работоспособном состоянии.
Эти зависимости между А и В не могут быть учтены путем объединения отдельных коэффициентов готовности А и В, поэтому С следует рассмотреть в целом. Если блоки А и В рассмотрены отдельно, получают классическую последовательную структуру вне области применения RBD. Объединение А и В в составной блок С позволяет управлять последним как отдельным блоком в структуре RBD.
Этот принцип является общим и может быть реализован при наличии нескольких блоков. Если количество зависимых блоков увеличивается, следует использовать другие методы, такие как динамические RBD (см. 12.2), марковские процессы [2] или сети Петри [3].
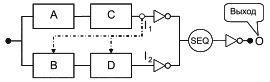
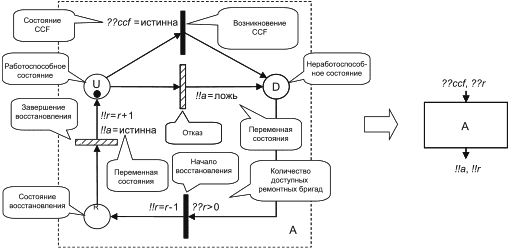
10.3.1.3 Периодически проверяемые блоки
По отношению к функциям безопасности системы, безопасности применимы только к коэффициенту готовности и коэффициенту неготовности. Поэтому обычно такие системы имеют только два состояния. Их главная особенность: несмотря на то, что они остаются в большинстве случаев в режиме ожидания, они должны реагировать с высоким коэффициентом готовности при появлении запроса по обеспечению безопасности.
Компоненты такой системы безопасности периодически проверяют на обнаружение отказов, которые могут возникнуть, когда система находится в состоянии резерва. Таким образом, коэффициент готовности периодически проверяемого компонента является максимальным сразу после проверки, где возможно, были обнаружены и устранены отказы, а затем он уменьшается до следующей проверки. Типичная пилообразная кривая коэффициента готовности такого блока представлена на рисунке 24. Она может быть смоделирована многофазным марковским процессом (см. рисунок C.4). Полная RBD c периодически проверяемыми блоками также представлена на рисунке С.5.
|
Рисунок 24 - Типовой коэффициент готовности периодически проверяемого блока
Форма коэффициента готовности блоков не меняет принципа расчета, они могут быть объединены, как описано выше, для расчета коэффициентов готовности и неготовности
системы в целом. Это очень полезно для выполнения расчета среднего коэффициента неготовности (например,
![]() ), требуемого стандартами функциональной безопасности (например, МЭК 61508 [5] или МЭК 61511 [6]), в соответствии с 10.3.2.
), требуемого стандартами функциональной безопасности (например, МЭК 61508 [5] или МЭК 61511 [6]), в соответствии с 10.3.2.
10.3.1.4 Сложные восстанавливаемые блоки (RBD-управляемые марковские процессы)
При условии выполнения требований независимости идею, представленную на рисунках 22 и 23, использования небольших марковских графов с небольшим количеством состояний для моделирования коэффициента готовности блоков можно легко распространить на все блоки RBD.
Это позволяет строить большие Марковские модели (включающие миллионы состояний), выполненные из небольших индивидуальных субмарковских моделей (включающих несколько состояний каждая), объединенных в соответствии с логикой RBD. Следовательно:
- графы Маркова обеспечивают коэффициенты готовности блоков;
- RBD обеспечивает логику, используемую для объединения коэффициентов готовности блоков.
Такие модели называются "RBD-управляемыми марковскими процессами".
Более подробная информация приведена в C.4.
10.3.2 Расчет среднего коэффициента готовности
Еще одним полезным параметром расчета на основе RBD является средний коэффициент готовности системы ![]() за заданный период [0,
за заданный период [0, ]. Это может быть сделано путем интегрирования мгновенного коэффициента готовности системы
:
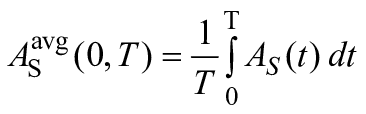 . (32)
. (32)
В общем случае такие расчеты действительно невозможно выполнить вручную, но в настоящее время для проведения необходимых расчетов доступны пакеты программ RBD.
Тем не менее в определенных условиях достигается устойчивое состояние, в котором вероятность того, что выходит из работоспособного состояния из-за отказа, равна вероятности того, что
вернется в работоспособное состояние за счет ремонта. Если оно существует, стационарное состояние коэффициента готовности
![]() достигает асимптотического значения
достигает асимптотического значения .
Это происходит:
- когда отказы быстро обнаруживают и устраняют (т.е. ![]() );
);
- если интенсивности отказов и ремонтов (,
) постоянны.
Например, в случае, представленном на рисунке 22, стационарный коэффициент готовности блока равен ![]() .
.
Если все блоки достигают стационарных состояний, система также достигает стационарного состояния (см. рисунки 25 и C.3), где ![]() . Затем вне периода перехода уравнение (32) дает долгосрочный средний коэффициент готовности системы:
. Затем вне периода перехода уравнение (32) дает долгосрочный средний коэффициент готовности системы: ![]() .
.
Поэтому, когда RBD достигает стационарного состояния, коэффициенты готовности блоков в стационарном состоянии становятся постоянными и для прогнозирования коэффициента готовности системы в стационарном состоянии могут быть использованы формулы, установленные в 9. Это выполняют простой заменой постоянной вероятности постоянными значениями
.
|
Рисунок 25 - Пример достижения RBD стационарного состояния
Внимание: приведенные выше расчеты справедливы только при наличии асимптотических коэффициентов готовности блоков. Они не действительны с обычными средними коэффициентами готовности.
Затем, если RBD не достигает стационарного состояния, средний коэффициент готовности должен быть вычислен по общей формуле (32).
Особый случай возникает, когда RBD используют на повторяющихся этапах, таких как:
- чередование сезонов: зима, весна, лето, осень;
- тестовые интервалы для периодически проверяемых объектов.
|
Рисунок 26 - Пример RBD с рекуррентными этапами
На рисунке 26 показана система с тремя рекуррентными этапами, когда один и тот же паттерн из трех этапов повторяется с интервалом времени, равным ![]() . Коэффициент готовности такой системы не имеет асимптотического значения, но средний коэффициент готовности
. Коэффициент готовности такой системы не имеет асимптотического значения, но средний коэффициент готовности ![]() обычно достигает предельного значения, когда
обычно достигает предельного значения, когда достаточно велико
![]() . (33)
. (33)
Поскольку ![]() уменьшается при увеличении
уменьшается при увеличении , то
![]() дает хорошую гарантированную аппроксимацию среднего коэффициента готовности за период времени [0,
дает хорошую гарантированную аппроксимацию среднего коэффициента готовности за период времени [0, ], охватывающий несколько наборов из рекуррентных этапов.
Поэтому методы, описанные в настоящем стандарте, могут быть использованы для расчета среднего коэффициента неготовности систем безопасности, и это обеспечивает связь со стандартами функциональной безопасности (МЭК 61508 или МЭК 61511), которые требуют таких расчетов для инструментальных систем безопасности, где средний коэффициент неготовности называется ![]() (средняя вероятность отказа по запросу). Это описано в C.4 и C.5.
(средняя вероятность отказа по запросу). Это описано в C.4 и C.5.
10.3.3 Расчет вероятности безотказной работы
При рассмотрении восстанавливаемых блоков расчет вероятности безотказной работы подразумевает, что ремонт блоков в системе (RBD) необходимо рассматривать только до тех пор, пока система остается в работоспособном состоянии (см. В 10.1).
Это может быть проиллюстрировано простой системой резервирования, смоделированной RBD в левой стороне рисунка 27. Что касается расчета , то при отказе блока B он может быть отремонтирован, только если S находится в работоспособном состоянии (т.е. если блок А находится в работоспособном состоянии). Точно так же, если блок А отказывает, он может быть восстановлен только в том случае, если S находится в работоспособном состоянии (т.е. если B находится в работоспособном состоянии). Поэтому, когда один блок выходит из строя, его восстановление зависит от состояния системы S, которое, в свою очередь, зависит от состояния всех блоков. Эту зависимость между блоками системы моделируют в виде графа Маркова, представленного в правой части рисунка 27. Он эквивалентен RBD, представленной в левой стороне рисунка.
Простая резервная система состоит из двух резервных блоков, А и В, и имеет 4 состояния: состояния успеха ,
и
и состояние отказа
. Система безотказна в течение заданного периода [0, t ] только в том случае, если она все время остается в состоянии успеха. Таким образом, состояния
,
и
являются "безотказными" состояниями только в том случае, если они возникают в результате переходов между ними. Это означает, что для расчетов вероятности безотказной работы в момент времени t переход из состояния
в период времени [0, t] не допустим. Состояние
- это состояние поглощения, наличие состояния поглощения характеризует Марковский граф вероятности безотказной работы.
В этом графе блок А может быть восстановлен до состояния , но не до состояния
, и блок B может быть отремонтированным в состоянии
, но не в состоянии
. Поэтому восстановление отказа блока зависит от состояния системы в целом, это называют "системной зависимостью".
|
Рисунок 27 - RBD и эквивалентный Марковский граф для расчетов вероятности безотказной работы
Теперь уже невозможно рассчитать вероятность безотказной работы системы путем объединения отдельных вероятностей успеха блоков.
Коэффициент готовности блоков, ![]() , не может быть использован, так как это дает коэффициент готовности системы, а не вероятность безотказной работы системы.
, не может быть использован, так как это дает коэффициент готовности системы, а не вероятность безотказной работы системы.
Вероятности безотказной работы блоков ![]() не могут быть использованы, так как это дает вероятность безотказной работы системы с невосстанавливаемыми блоками (потому что вероятность безотказной работы восстанавливаемого компонента такая же, как и вероятность безотказной работы невосстанавливаемого компонента с той же интенсивностью отказов).
не могут быть использованы, так как это дает вероятность безотказной работы системы с невосстанавливаемыми блоками (потому что вероятность безотказной работы восстанавливаемого компонента такая же, как и вероятность безотказной работы невосстанавливаемого компонента с той же интенсивностью отказов).
Поэтому, за исключением конкретного случая, разработанного далее, другие методы, такие как моделирование методом Монте-Карло (например, DRBD, см. 12.2 и приложение Е), сети Маркова [2] или Петри [3] должны быть использованы вместо метода RBD.
Единственный случай, когда вычисление вероятности безотказной работы возможно, - это ситуация, когда восстановление системы происходит быстро (т.е. ![]() ) и полностью (т.е. полностью устраняют каждую неисправность). Это значит, что при отказе блока ремонт начинается сразу и длится очень недолго. В этом случае система достаточно быстро достигает стационарного состояния, и ее коэффициент готовности
) и полностью (т.е. полностью устраняют каждую неисправность). Это значит, что при отказе блока ремонт начинается сразу и длится очень недолго. В этом случае система достаточно быстро достигает стационарного состояния, и ее коэффициент готовности достигает своего асимптотического значения
. В этом стационарном состоянии условный параметр потока отказов
(также называемый интенсивностью отказов Веселя) является постоянным и обеспечивает хорошее приближение интенсивности отказов системы
. Затем вероятность безотказной работы системы и вероятность отказа системы определяют по классическим формулам:
![]() .
.
Например, на рисунке 27 при достижении стационарного состояния свойства марковских процессов позволяют получить хорошую аппроксимацию и
:
![]() . (34)
. (34)
Это не простая формула, хотя сама система очень простая. Для более крупных RBD интенсивность отказов Веселя может быть получена с помощью условных вероятностей, которые могут быть рассчитаны с применением программного обеспечения RBD. Способ определения условных и безусловных параметров отказов по RBD подробно описан в C.6, а более подробные расчеты надежности вероятности безотказной работы приведены в С.7.
10.3.4 Вычисление частоты
Если блоки восстанавливаемые, еще одной полезной вероятностной мерой является средняя частота отказов системы за заданный период времени [0, ], которая равна
при возникновении
отказов, эту среднюю частоту отказов вычисляют с помощью среднего значения безусловного параметра потока отказов системы
![]() . Частоту отказов можно рассчитать в любом случае, но это трудно сделать вручную. Для этого были разработаны специальные алгоритмы, их принцип разъясняется в С.6.
. Частоту отказов можно рассчитать в любом случае, но это трудно сделать вручную. Для этого были разработаны специальные алгоритмы, их принцип разъясняется в С.6.
11 Булевы методы количественного анализа больших моделей
11.1 Общие положения
Можно оценить коэффициент готовности всех рассмотренных систем путем применения подходящей формулы из набора (15)-(24). Однако, если количество блоков увеличивается, соответствующие RBD может быть неудобно оценивать по приведенным выше формулам. Вычисления являются более сложными, и необходимо использовать другие математические подходы.
Такие подходы представляют собой несколько способов обработки булевых уравнений для того, чтобы сделать расчеты возможными. Как правило, они могут быть использованы вручную на небольших RBD, но большинство из них могут быть выполнены с помощью программного пакета, если количество блоков велико. Они основаны на следующих методах:
- сокращение RBD до более простых структур;
- использование теоремы полной вероятности;
- использование логических таблиц истинности;
- использование карт Карно;
- использование декомпозиции Шеннона и бинарных диаграмм принятия решений;
- использование общих формул Сильвестра-Пуанкаре.
Для последующих процедур применяется условие независимости, установленное в 5.2 d), приведенные ниже формулы позволяют выполнить расчет постоянной вероятности с помощью прямого преобразования для расчета коэффициента готовности с применением 10.1 и приложения С.
Следует отметить, что моделирование методом Монте-Карло также может быть использовано для сложных RBD. Детали использования таких процедур в настоящем стандарте не рассмотрены, динамические RBD описаны в 12.2 и приложении Е.
11.2 Метод редукции RBD
RBD, моделирующая промышленную систему, может выглядеть очень сложной. Однако тщательный анализ, как правило, позволяет сгруппировать отдельные блоки RBD в статистически независимые блоки. Это означает, что в данной системе нет двух (или более) групп, содержащих один и тот же блок.
|
Рисунок 28 - Иллюстрация группировки блоков для редукции
Это можно проиллюстрировать с помощью RBD, приведенной на рисунке 28.
Рисунок 28 можно сократить до диаграмм, приведенных на рисунке 29, которые состоят из четырех выделенных пунктирными линиями групп блоков X1, X2, X3 и X4, как показано на рисунках 10, 8, 37 и 9 соответственно.
|
Рисунок 29 - Редуцированные структурные схемы надежности
Следовательно, конечный коэффициент готовности системы можно определить следующим образом (см. 9.2):
![]() . (35)
. (35)
Метод редукции трудно автоматизировать, но он очень полезен для расчетов вручную.
11.3 Использование теоремы полной вероятности
При работе с RBD такого типа, как показанная на рисунке 10 с общим блоком А, можно реализовать подход, основанный на теореме полной вероятности.
Два взаимоисключающих событий и
образуют полный набор событий (т.е.
![]() ) и теорема полной вероятности может быть записана следующим образом:
) и теорема полной вероятности может быть записана следующим образом:
![]() . (36)
. (36)
В уравнении (36) - вероятность успеха системы,
- вероятность успеха системы при условии, что конкретный элемент
работает,
- вероятность успеха системы при условии, что конкретный элемент
отказал. Формула (36) может быть применена к блоку А, приведенному на рисунке 10, это приводит к следующему соотношению:
![]() . (37)
. (37)
Например, если объект А отказал, RBD, приведенная на рисунке 10, превращается в RBD, показанную на рисунке 30, таким образом:
![]() .
.
|
Рисунок 30 - Представление рисунка 10 при отказе объекта А
Аналогично, если A работает, RBD, приведенная на рисунке 10, превращается в RBD, приведенную на рисунке 31, так что ![]() .
.
|
Рисунок 31 - Представление рисунка 10 при работающем объекте А
Следовательно,
![]() . (38)
. (38)
Если ![]() и
и ![]() , приведенная выше формула (38) упрощается:
, приведенная выше формула (38) упрощается:
![]() . (39)
. (39)
Эта процедура может быть распространена на взаимоисключающих событий
, ...
, вероятность которых в сумме равна единице (т.е.
![]() ), тогда
), тогда ![]() . Это выражение можно использовать в RBD с повторяющимися блоками (см. 11.8.1.2). Наличие n повторяющихся блоков приводит к 2
. Это выражение можно использовать в RBD с повторяющимися блоками (см. 11.8.1.2). Наличие n повторяющихся блоков приводит к 2 членов в формуле для
. Поэтому данный метод полезен при работе RBD с ограниченным количеством повторяющихся блоков, например для структур m/n.
11.4 Использование таблиц истинности
Пути успеха системы, изображенные с помощью RBD, могут быть описаны булевыми выражениями. Например, логическое выражение для системы, состоящей из трех объектов, A, B и C, резервирующих друг друга, когда для работоспособности системы достаточно одного объекта, может быть представлено параллельной RBD, показанной на рисунке 32, или булевым выражением (40):
![]() (40)
(40)
|
Рисунок 32 - RBD системы из трех резервированных объектов
Применение формулы Сильвестра-Пуанкаре (см. 11.7 и B.5) к трем независимым событиям дает следующий результат:
![]() . (41)
. (41)
Формула (41) содержит семь членов для трех блоков (т.е. трех событий ,
и
). Количество слагаемых увеличивается экспоненциально при увеличении количества вовлеченных событий.
Чтобы предотвратить увеличение количества членов в формуле можно заменить события ,
и
эквивалентными комбинациями непересекающихся событий (см. 11.7), это можно сделать, используя таблицу истинности системы, соответствующую состояниям блоков А, В и С.
Таблица 5 - Применение таблицы истинности к примеру, представленному на рисунке 32
Номер | Блок | Система | Непересе- | Консенсус | |||
состояния | А | B | C |
| кающиеся члены |
| |
1 | 0 | 0 | 0 | 0 |
|
|
|
2 | 0 | 0 | 1 | 1 |
|
|
|
3 | 0 | 1 | 0 | 1 |
| ||
4 | 0 | 1 | 1 | 1 |
|
|
|
5 | 1 | 0 | 0 | 1 |
| ||
6 | 1 | 0 | 1 | f |
|
|
|
7 | 1 | 1 | 0 | 1 |
|
| |
8 | 1 | 1 | 1 | 1 |
|
|
|
Примечание - 1=работоспособное состояние, 0=отказ. | |||||||
В данной таблице истинности идентифицировано 8 непересекающихся событий, представляющих 8 возможных состояний системы: состояние номер 1 соответствует отказу системы, а состояния от 2-8 - работоспособным состояниям системы.
Опять имеется семь членов для обработки, и поэтому это разложение на непересекающиеся члены не очень эффективно для расчета . Следует отметить, что обычно нет связи между количеством членов формулы Сильвестра-Пуанкаре и количеством непересекающихся событий в таблице истинности.
Некоторые непересекающиеся события могут быть объединены (см. колонку "Консенсус" в таблице 5). На первом этапе термины 7 и 8, 5 и 6, 3 и 4 были объединены и получены четыре непересекающихся события. На втором этапе события 5-7 объединены в одно событие и получено три непересекающихся события:
![]() . (42)
. (42)
Наконец, вероятность отказа системы можно рассчитать следующим образом:
![]() . (43)
. (43)
Формула (43) может быть непосредственно использована для оценки коэффициента готовности системы:
![]() . (44)
. (44)
Следует отметить, что в таблице 5 указано только одно событие, приводящее систему в неработоспособное состояние ![]() . Поэтому расчет вероятности отказа оказывается проще, чем расчет вероятности успеха:
. Поэтому расчет вероятности отказа оказывается проще, чем расчет вероятности успеха:
![]() , (45)
, (45)
![]() . (46)
. (46)
Формулы (44) и (46) эквивалентны.
Для системы из блоков таблица истинности имеет 2
строк, и поэтому данный подход может стать громоздким, хотя принцип его работы довольно прост. Эта проблема в какой-то степени преодолевается с помощью карт Карно (см. 11.5), но на самом деле она решается с помощью декомпозиции Шеннона и бинарных диаграмм принятия решений (см. 11.6). Детальное описание общего применения булевых методов приведено в приложении B.
11.5 Использование карт Карно
Карты Карно [8], [9], [10], [11] были разработаны для упрощения логического вывода уравнения, соответствующего таблице истинности. Поэтому их можно использовать и для RBD.
Принцип использования таких карт показан далее на картах, соответствующих RBD, представленной на рисунке 10. Данная RBD состоит из 5 блоков. Так как карты Карно легче использовать для четырех переменных, карта разделена на две непересекающиеся ситуации:
- А находится в работоспособном состоянии (таблица 6);
- А находится в неработоспособном состоянии (таблица 7).
Таблица 6 - Карта Карно, соответствующая рисунку 10, когда A находится в работоспособном состоянии
|
Таблица 7 - Карта Карно, соответствующая рисунку 10, когда А находится в неработоспособном состоянии
|
В таблицах 6 и 7 блоки разделены на две группы (B1 B2 и C1 C2), а состояния компонентов представлены таким образом, что изменяется только одно состояние при переходе в следующую колонку или в следующую строку. Таким образом, комбинации, которые можно упростить, объединяют. Например, в таблице 6 комбинации, обведенные прямоугольником из сплошной линии, представляют только С2, так как состояния С1, В1 и В2 не имеют значения. Аналогично комбинации, обведенные пунктирной линией, представляют только C1, так как состояния C2, B1 и B2 не имеют значения. Из этого следует:
![]() , (47)
, (47)
где представляет собой систему S в работоспособном состоянии при условии, что блок A находится в работоспособном состоянии, а
и
представляют собой различные состояния, соответствующие блокам C1 и C2. В соответствии с картой Карно, представленной в таблице 7, можно записать следующую формулу:
![]() , (48)
, (48)
где представляет систему S в работоспособном состоянии при условии, что A находится в неработоспособном состоянии, а
,
,
и
представляют собой различные состояния, соответствующие блокам B1, B2, C1 и C2.
В результате можно записать:
![]() . (49)
. (49)
И наконец, коэффициент готовности системы можно вычислить по следующей формуле:
![]() (50)
(50)
Карты Карно имеют такое же количество членов (), что и исходные таблицы истинности, но они являются более компактными и позволяют лучше идентифицировать комбинации, которые могут быть объединены. Это очень полезно для определения минимальных наборов соединений или обрывов.
11.6 Использование декомпозиции Шеннона и бинарных диаграмм принятия решений
Как таблицы истинности и карты Карно, декомпозиция Шеннона позволяет идентифицировать непересекающиеся члены булева уравнения.
На рисунке 33 показан принцип декомпозиции Шеннона булевой функции (1 из 3), соответствующей RBD, представленной на рисунке 32.
|
Рисунок 33 - Декомпозиция Шеннона, эквивалентная таблице 5
Декомпозицию выполняют в несколько этапов:
1) Выбирают порядок появления переменной в логической функции (здесь порядок a, b, c);
2) для каждой переменной рисуют две ветви (успех и отказ);
3) если состояние системы (успех или отказ) достигнуто, то декомпозицию прекращают, в противном случае продолжают со следующей переменной;
4) определяют пути, ведущие к состоянию успеха (или отказа) системы.
На рисунке 33 показано три непересекающихся пути успеха: ![]() ,
, ![]() . Это тот же результат, что и из таблицы истинности, но получен более простым способом. Декомпозиция не является уникальной и зависит от выбранного порядка переменных.
. Это тот же результат, что и из таблицы истинности, но получен более простым способом. Декомпозиция не является уникальной и зависит от выбранного порядка переменных.
|
Рисунок 34 - Бинарная диаграмма принятия решений, эквивалентная таблице 5
Если работоспособное и неработоспособное состояния собраны, декомпозиция Шеннона обеспечивает построение бинарной диаграммы принятия решений (BDD), показанной на рисунке 34. Такие диаграммы обеспечивают очень компактное представление булевых уравнений с непересекающимися членами. Они очень удобны для вычислений и представляют современный способ (см. [31], [32] [33]) вероятностных вычислений на булевых моделях (например, RBD и деревья неисправностей).
11.7 Использование формулы Сильвестра-Пуанкаре
При увеличении количества компонентов простые формулы и расчеты вручную становятся неприменимыми из-за комбинаторного взрыва.
Как это указано в 8, RBD может быть представлена набором путей успеха (минимальным набором соединений).
Затем могут быть выполнены вероятностные вычисления для этих наборов соединений с помощью формулы Сильвестра-Пуанкаре (см. B.4.2 и B.5.2), которая является обобщением основной формулы ![]() :
:
![]() . (51)
. (51)
Аналогичный расчет (см. B.5.3) может быть выполнен с использованием путей отказов (минимальных наборов обрывов):
![]() . (52)
. (52)
Формула Сильвестра-Пуанкаре представляет собой альтернативную сумму, результат которой сходится к точному значению, когда количество рассматриваемых членов возрастает. Различие состоит в том, что формула (51), которая обрабатывает вероятности ![]() , близкие к 1, сходится очень медленно, а формула (52), которая обрабатывает вероятности
, близкие к 1, сходится очень медленно, а формула (52), которая обрабатывает вероятности ![]() , сходится довольно быстро. В этом случае первый член формулы (52) дает завышенную оценку вероятности отказа:
, сходится довольно быстро. В этом случае первый член формулы (52) дает завышенную оценку вероятности отказа:
 . (53)
. (53)
Это приближение широко используют, когда вероятности отказов блоков низкие, что обычно справедливо для компонентов систем безопасности. Это основа вычислений, выполняемых многочисленными пакетами программ для расчетов коэффициента готовности и вероятности безотказной работы по RBD или деревьям неисправностей.
Тем не менее трудности использования формулы (51) можно преодолеть путем преобразования наборов соединений в эквивалентные наборы непересекающихся членов ![]() , так как
, так как ![]() .
.
В этом случае формула Сильвестра-Пуанкаре (51) сводится к ее первому члену:
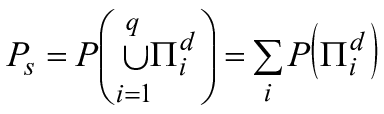 . (54)
. (54)
То же может быть сделано с формулой (52) путем замены минимальных наборов обрывов () на эквивалентный набор непересекающихся членов (
). В результате формула Сильвестра-Пуанкаре сокращается до одного члена:
![]() . (55)
. (55)
Непересекающиеся наборы можно найти с помощью таблиц истинности (11.4), карт Карно (11.5) или декомпозиции Шеннона и бинарных диаграмм принятия решений (11.6). В настоящее время идентификация непересекающихся членов булева уравнения основана на бинарной диаграмме принятия решений (BDD), описанной в 11.6. Это обеспечивает мощные алгоритмы, способные обрабатывать очень большие RBD, содержащие много повторяющихся или неповторяющихся блоков.
11.8 Примеры применения RBD
11.8.1 Модели с повторяющимися блоками
11.8.1.1 Представление набора обрывов и соединений
В разделе 7 ни один блок в RBD не появлялся более одного раза. Иногда может быть выгодно использовать структурные схемы такого же типа, как показанная на рисунке 35.
В левой части рисунка 35 показана обычная RBD с четырьмя блоками: блоки C и D, казалось бы, моделируют два функционально сходных объекта, действующих как копии один другого, но объект А может питать только объект С, а объект B может питать два объекта, C и D.
В средней и правой частях рисунка 35 приведены две эквивалентные RBD, моделирующие не только физическое расположение объектов. Для RBD очень важно с правой стороны указывать стрелки, чтобы устранить неопределенность, которая возникает на такой схеме.
|
Рисунок 35 - RBD, использующая стрелки для определения пути успеха системы
Пути успеха системы a•c, b•c, b•d, смоделированной на рисунке 35, могут быть использованы для построения эквивалентной RBD, в которой некоторые блоки появляются более одного раза. Если все пути успеха отказали, это приводит к отказу системы. Таким образом, RBD может быть представлена в виде параллельного сочетания путей успеха. Это показано на рисунке 36.
|
Рисунок 36 - Альтернативное представление рисунка 35 с использованием повторяющихся блоков и путей успеха системы
Альтернативно для построения эквивалентного RBD могут быть использованы пути отказов (например, минимальные наборы обрывов системы) ,
,
. Это сделано на рисунке 37. Если все компоненты одного из минимальных наборов обрывов приводит к отказу системы, на рисунке 37 приведена последовательная комбинация таких минимальных наборов обрывов.
RBD на рисунках 36 и 37 иллюстрируют концепции, рассмотренные в 8.2: любая RBD может быть представлена параллельной комбинацией путей успеха или последовательной комбинацией минимальных наборов обрывов.
|
Рисунок 37 - Альтернативное представление рисунка 35 с использованием повторяющихся блоков и минимальных наборов обрывов
Блоки В и С повторяются в обоих вариантах RBD, представленных на рисунках 36 и 37. Было бы неправильно рассматривать блоки как независимые друг от друга. Вместо этого могут быть применены методы, приведенные в 11.3, 11.5 и 11.6.
11.8.1.2 Применение теоремы полной вероятности
Метод полной вероятности, описанный в 11.3, примененный к RBD, представленной на рисунке 36, и распространенный на два повторяющихся компонента, дает:
 (56)
(56)
В формуле (56) означает, что система S работоспособна при условии, что события x и y истинны.
Следует отметить, что количество членов равно , если
блоков повторяются. Это означает, что данный метод применим только для небольшого количества повторяющихся блоков.
Рисунку 36 соответствует ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() (57)
(57)
11.8.1.3 Применение карты Карно
Другой способ работы с RBD, представленной на рисунке 35, заключается в разработке таблиц истинности или, что еще лучше, карты Карно (см. 11.5), которая представлена в таблице 8. Из этой карты Карно можно непосредственно найти минимальные пути успеха системы. Их идентифицируют три прямоугольника, выделенные в таблице 8.
![]() . (58)
. (58)
Таблица 8 - Карта Карно, соответствующая рисунку 35
|
Таким образом, карта Карно - хороший способ идентификации путей успеха, которые уже были представлены на рисунке 36. Метод полезен с точки зрения качественного анализа, но эти пути успеха не являются непересекающимися, а это означает, что формула Сильвестра-Пуанкаре не может быть упрощена для вероятностных расчетов.
11.8.1.4 Выполнение декомпозиции Шеннона
Декомпозиция Шеннона была выполнена на рисунке 38, и было идентифицировано три непересекающихся пути успеха:
![]() . (59)
. (59)
С точки зрения булевой алгебры формулы (59) и (58) эквивалентны, но формула (59), состоящая из непересекающихся членов, непосредственно приводит к коэффициенту готовности системы:
![]() . (60)
. (60)
Результат декомпозиции Шеннона зависит от порядка переменных, используемых для ее выполнения, и поэтому для другого порядка переменных (см. В.7, где был проанализирован тот же RBD) могут быть найдены другие эквивалентные выражения.
|
Рисунок 38 - Декомпозиция Шеннона, соответствующая рисунку 35
11.8.2 Модели m из n (неидентичные объекты)
Процедура, описанная в 9.4, в данном случае неприменима, поскольку блоки не идентичны. В качестве примера рассмотрим систему 2/5 с RBD, представленной на рисунке 39.
|
Рисунок 39 - Структура 2 из 5 с неидентичными объектами
Коэффициент готовности такой системы можно оценить с помощью методов, описанных в 11.3, 11.4, 11.5 или 11.6. Среди них таблица истинности, описанная в 11.4, требует 32 записи, из которых шесть приводят к отказу
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тогда коэффициент неготовности может быть определен по формуле
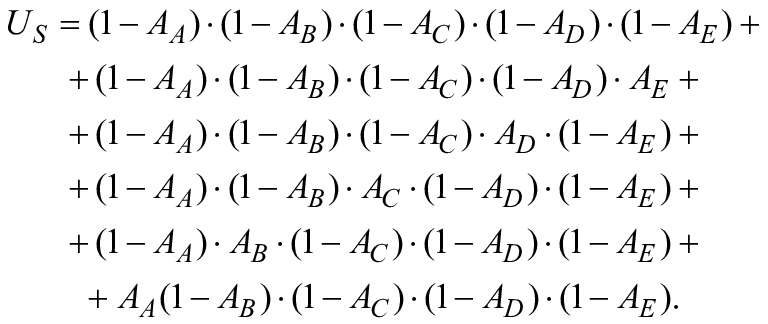 (61)
(61)
Следовательно, можно определить ![]() .
.
В формуле (61) ,
и
,
для расчетов показателей, зависящих от времени, могут быть заменены на
,
![]() и
и ,
.
12 Обобщенные методы блок-схемы надежности
12.1 Некогерентные структурные схемы надежности
Некогерентные структурные схемы являются обобщением RBD, представляющим монотонные логические функции для RBD, представляющих немонотонные логические функции. Это может соответствовать, например, отказавшим системам, восстановленным следующим отказом, или работающим системам, отказавшим в результате дальнейшего ремонта. Как правило, это нереально для физических систем, но часто происходит с "логическими" системами или моделями, сгенерированными автоматически.
Основное отличие от обычной RBD состоит в том, что данный блок может появляться в двух своих состояниях (работоспособное и неработоспособное). Как показано на рисунке 40, для этой цели был введен новый символ.
|
Рисунок 40 - Прямой и обратный блок
Функционирование "обратного" блока можно показать с помощью аналогии с электрической цепью на рисунке 40 если В1 находится в работоспособном состоянии (переключатель замкнут), обратный блок В1 находится в неработоспособном состоянии (переключатель открыт), и наоборот. Это также иллюстрирует электрическая схема, представленная на рисунке 41.
|
Рисунок 41 - Пример электрической схемы с переключателем А
Номинальная схема такой системы представлена в левой стороне рисунка 41. В отношении питания двигателя M от S2 из схемы легко заметить, что A находится в работоспособном состоянии, когда контакт в направлении S2 находится в работоспособном состоянии, когда контакт в направлении S2 замкнут, и в неработоспособном состоянии, когда тот же контакт открыт (разомкнут).
Двигатель M может питаться от источника питания S2 или, если это невозможно, от источника питания S1. Благодаря переключателю А двигатель не может питаться от S1 и S2 одновременно, это позволяет предотвратить короткое замыкание между источниками.
На рисунке 41 выделено два пути успеха, обеспечивающих питание двигателя М:
- А переключен на S2 и выключатель С замкнут: ;
- A переключен на S1 и переключатель B замкнут: .
Аналогично на рисунке 42 показаны пути отказа той же электрической системы:
- A переключен на S2 и переключатель C разомкнут: ;
- A переключен на S1 и переключатель B разомкнут: .
|
Рисунок 42 - Электрическая схема: пути отказа
A, B и C являются компонентами с двумя состояниями, такая электрическая система может быть смоделирована с помощью RBD показанной на рисунке 43 (для простоты S1, S2 и M считаются совершенными). Эта RBD, основана на путях отказа, в ней использованы повторяющиеся блоки в прямом и в обратном состояниях для моделирования двух положений переключателя А.
|
Рисунок 43 - Пример RBD с блоками в прямом и обратном состояниях
Логическая структура RBD на рисунке 43 является довольно общей и может быть применена в других ситуациях. Например, состояние блока А может влиять на значение физического параметра :
- если блок А находится в работоспособном состоянии (номинальное функционирование), ниже заданного порога
, В тормозит работу и делает C способным работать;
- если блок А отказывает, то становится больше
, это тормозит функционирование С и делает В способным работать.
- Такая RBD соответствует следующему логическому уравнению: ![]() .
.
- Данное уравнение обеспечивает три пути успеха: ![]() ,
, ![]() ,
, ![]() .
.
Это показывает, что в дополнение к двум путям успеха, указанным выше, на рисунке 41, существует и третий путь успеха: . В этом случае состояние А не имеет значения.
В отличие от обычной ситуации пути успеха формируют не только с блоками в работоспособном состоянии. Это приводит к следующим побочным эффектам:
- если данная система находится, например, в работоспособном состоянии ![]() , она переходит в неработоспособное состояние
, она переходит в неработоспособное состояние ![]() , когда A переходит в работоспособное состояние. Другими словами, состояние успеха
, когда A переходит в работоспособное состояние. Другими словами, состояние успеха ![]() является отказом, когда А отремонтирован;
является отказом, когда А отремонтирован;
- если система находится, например, в неработоспособном состоянии ![]() , она переходит в работоспособное состояние
, она переходит в работоспособное состояние ![]() , когда A переходит в неработоспособное состояние. Другими словами, состояние отказа системы
, когда A переходит в неработоспособное состояние. Другими словами, состояние отказа системы ![]() восстанавливается, когда А отказывает.
восстанавливается, когда А отказывает.
Эти обратные состояния являются типичными свойствами некогерентных RBD, моделирующих немонотонные логические функции. Это приводит к трудностям, когда для качественного анализа необходимы минимальные пути успеха. Например, пути отказа ,
,
можно легко идентифицировать по рисунку 43. Последний путь отказа не так очевиден и не может быть найден классическими алгоритмами минимальных наборов обрывов.
Для некогерентных RBD понятия минимальных наборов обрывов и минимальных наборов соединений больше не поддерживаются. Их следует заменить понятием первичных импликантов:
- три пути успеха ![]() ,
, ![]() ,
, являются тремя основными импликантами, соответствующими путям успеха системы;
- пути дерева отказов ![]() ,
, ![]() ,
, ![]() являются тремя основными импликантами, соответствующими отказам системы.
являются тремя основными импликантами, соответствующими отказам системы.
Это означает, что популярные алгоритмы, основанные на использовании минимальных наборов обрывов или минимальных наборов соединений, не допустимы для вероятностных расчетов некогерентных RBD.
|
Рисунок 44 - BDD, эквивалентная рисунку 43
Как показано на рисунке 44, подход BDD легко может быть реализован для некогерентных RBD. Нет никакой разницы между BDD, построенной для когерентной RBD, и BDD на рисунке 44, которая может быть использована для вероятностного расчета RBD, представленной на рисунке 43, точно так же, как если бы она была когерентной. Таким образом, использование BDD позволяет преодолевать трудности, возникающие при использовании минимальных наборов соединений или обрывов. Тем не менее программное обеспечение RBD редко способно обрабатывать простые импликанты.
12.2 Динамические структурные схемы надежности
12.2.1 Общие положения
Динамическая структурная схема надежности (DRBD) - это распространение общих RBD на RBD, включающие блоки, взаимодействующие между собой или с внешними объектами. Цель аналогична цели динамических деревьев неисправностей (см. [16] и [17]), но с точки зрения успеха.
RBD, разработанные в предыдущих разделах для моделирования восстанавливаемых систем (например, RBD-управляемые марковские процессы, описанные в с.4), очевидно, являются динамическими моделями, но термин DRBD обычно используют для обозначения RBD, удовлетворяющих всем основным предположениям 5, за исключением последнего, касающегося независимости блоков (см. 5.2 d)).
Некоторые динамические взаимодействия уже встречались в настоящем стандарте при рассмотрении резервирования заменой структур m/n и вычислении вероятности безотказной работы восстанавливаемых систем.
Динамическим деревьям неисправностей было уделено больше внимания, чем динамическим RBD, но проблемы у них схожие. Поэтому настоящий стандарт предлагает адаптировать и применять графические символы, обычно используемые для динамических деревьев неисправностей.
Некоторые типы динамических взаимодействий рассмотрены в [15], но на практике их очень мало. Воздействие таких взаимодействий может быть:
- локальным: состояния блоков подвержены влиянию, но логические правила обычных RBD применимы для установления состояния системы в целом;
- системным: логические правила обычных RBD не применимы для установления состояния системы в целом.
12.2.2 Локальные взаимодействия
Взаимодействия, которые влияют только на состояния блоков, можно разделить на следующие категории:
- взаимодействия между блоками в DRBD;
- взаимодействия между объектами, внешними по отношению к DRBD, и блоками DRBD.
Событие, происходящее на одном блоке или на внешнем объекте (иногда называемое триггерным событием), воздействует на состояние одного или нескольких других блоков DRBD.
Новый символ необходим для того, чтобы отразить разницу между внешними объектами, которые не относятся к RBD, и блоками, принадлежащими RBD. Он представлен на рисунке 45, где выявлены отказы по общей причине (CCF) и представлена группа технического обслуживания (MT).
|
Рисунок 45 - Символ для обозначения внешних объектов
Ниже приведены примеры локальных взаимодействий:
Функциональная зависимость:
- отказ по общей причине: при возникновении CCF все связанные блоки немедленно отказывают. Это указывает на сильную функциональную зависимость, которая может быть смоделирована, как показано на рисунке 46;
- потеря энергии: при потере энергии все связанные блоки немедленно останавливаются (неработоспособное состояние). Потеря энергии также представляет собой сильную функциональную зависимость;
- зависимость от ремонтной бригады: если несколько блоков ремонтирует одна и та же ремонтная бригада, то отказавший блок должен ждать ремонта, если ремонтная бригада занята восстановлением другого неисправного блока. Это представляет собой функциональную зависимость, которую можно смоделировать, как показано на рисунке 48;
- коллективный ремонт: несколько блоков ремонтируют в рамках одной ремонтной операции;
- резервирование заменой: если резервированный блок отказывает, начинает работать резервный блок (см. рисунок 11);
- запасные части: при отказе резервированного блока для ремонта могут потребоваться запасные части. Поэтому ремонт возможен только при наличии хотя бы одной запасной части. Кроме того, запасная часть, используемая для ремонта одного блока, становится недоступной для ремонта другого блока;
- последовательные блоки: если один из последовательных блоков отказывает или находится в ремонте, остальные могут быть восстановлены (например, потому, что выход отказавшего блока необходим для работы следующих последовательных блоков)
- другие зависимости.
События, которые могут происходить только в заданном порядке (одно событие не может произойти раньше другого):
- ремонт блока не может начаться до отказа блока. Такая функциональная зависимость уже была обработана в обычных RBD для вычисления коэффициента готовности, вероятности безотказной работы и частоты отказов;
- для заданного набора блоков (,
, ...,
) ремонт начинается только тогда, когда отказали все блоки;
- блоки становятся невосстанавливаемыми после отказа системы в целом. Это происходит при выполнении вероятностных расчетов;
- в более общем смысле для набора событий (,
, ..,
) это означает, что
не может произойти, пока не произошло
;
не может произойти до тех пор, пока не произошло
;
не может произойти до тех пор, пока не произошло
. Другими словами,
тормозит
;
тормозит
;
тормозит
. Поэтому события могут происходить только в последовательности
,
, ..,
. Это могут быть ситуации, когда электрическое устройство не может быть запущено до включения электропитания или устройство в режиме холодного резерва не может быть активировано до выхода из строя основного устройства. Такое взаимодействие аналогично последовательным вентилям (часто обозначаемым SEQ), используемым в анализе динамического дерева неисправностей (см. SEQ в таблице 4);
12.2.3 Системные динамические взаимодействия
Системные динамические взаимодействия не обязательно подразумевают функциональные зависимости между блоками, которые могут вести себя независимо друг от друга. Они появляются, когда обычные логические правила не могут быть использованы.
Примерами могжет служить следующее:
- структура m/n: эта логическая схема была рассмотрена (см. 7.5.1 и 9.4), для ее моделирования введен специальный логический вентиль;
- события, которые должны происходить в заданном порядке:
- запрос, запускающий действие, выполняемое заданным блоком B: если запрос возникает до отказа B, действие выполняется, и система остается в работоспособном состоянии; если запрос возникает после отказа B, действие не выполняется, и система отказывает;
- запорный клапан, защищающий систему от избыточного давления: опасное событие возникает только тогда, когда клапан открыт до того, как давление было снижено выше запорного клапана;
- в более общем случае для набора событий ,
, ..,
выход происходит только в случае, если события происходят в заданном порядке, в противном случае выход не происходит. Это взаимодействие аналогично "вентилю очередности И" (часто обозначаемому PAND), используемому при анализе динамического дерева неисправностей, которое также может быть использовано для DRBD. Взаимодействие может быть представлено в виде вентиля, объединяющего вход нескольких блоков.
Специальные вентили необходимы для представления системных динамических зависимостей, таких как, например, m/n, вентили PAND или SEQ, приведенные в таблице 4, которые являются популярным распространением динамических деревьев неисправностей.
Вентиль m/n уже был рассмотрен, а вентили PAND и SEQ будут рассмотрены далее (см. рисунки 49-52). Символы, обычно используемые в динамических деревьях неисправностей, здесь были применены, но вентиль NOT был введен во входы и выходы для обеспечения согласованности с логикой RBD.
12.2.4 Графическое представление динамических взаимодействий
В соответствии с 12.2.2 и 12.2.3 количество видов возможных динамических взаимодействий практически бесконечно. Поэтому, несмотря на то что были предприняты некоторые попытки предложения графических символов для отдельных случаев (см. [15], [16] и [17]), это не охватывает все ситуации, и в настоящем стандарте могут быть предложены только некоторые основные графические элементы.
|
Рисунок 46 - Динамическое взаимодействие CCF и блоков RBD
На рисунке 46 показаны сильные взаимодействия (т.е. сильные функциональные зависимости) между внешними объектами и некоторыми блоками: блоки А и В отказывают, если происходит отказ по общей причине, представленный внешним блоком.
|
Рисунок 47 - Различные способы представления динамического взаимодействия между блоками
На рисунке 47 показаны два способа представления взаимодействия (т.е. функциональных зависимостей) между блоками: состояние блоков C и D зависит от состояния блока A.
Те же способы реализованы на рисунке 48 для представления взаимодействия между единственной ремонтной бригадой и восстанавливаемыми блоками.
|
Рисунок 48 - Динамическое взаимодействие между одной ремонтной бригадой и блоками RBD
Эти простые графические представления направлены на то, чтобы показать, что существует некоторая динамика взаимодействия между блоками и внешними объектами. Пунктирные линии в левой стороне рисунков 47 и 48 могут быть использованы, если необходимо указать лишь несколько взаимодействий в RBD. Если существует много взаимодействий, которые необходимо представить, вариант, приведенный в правой стороне рисунков 46, 47 и 48, является более четким. Свойства и особенности взаимодействий должны быть установлены в другом месте. Основное применение данных методов представления взаимодействий должно поддерживать графическое представление RBD и обеспечивать хорошую идентификацию внешних объектов.
На рисунке 49 показано, как можно использовать вентиль в DRBD: выход O дает неработоспособное состояние только в том случае, если переходит в неработоспособное состояние вниз прежде, чем
переходит в неработоспособное состояние.
|
Рисунок 49 - Применение вентиля PAND
Функционирование вентиля PAND показано на рисунке 50. Вентиль PAND эквивалентен пяти состояниям конечного автомата, изображенным в левой стороне рисунка:
- состояние 1: и
находятся в работоспособном состоянии. Тогда выход O находится в работоспособном состоянии;
- состояние 2: сначала переходит в неработоспособное состояние, а
все еще находится в работоспособном состоянии. Тогда выход O находится в работоспособном состоянии;
- состояние 3: сначала переходит в неработоспособное состояние, а
все еще находится в работоспособном состоянии. Тогда выход O находится в работоспособном состоянии;
- состояние 4: и
перешли в неработоспособное состояние, но
перешел первым. Тогда выход O находится в работоспособном состоянии;
- состояние 5: и
перешли в неработоспособное состояние, но
перешел первым. Тогда выход O перешел в неработоспособное состояние.
|
Рисунок 50 - Эквивалентный конечный автомат и пример его хронограммы для вентиля PAND
Если входы и
изменяются в диапазоне от 1 до 0, выход вентиля PAND (рисунок 49) изменяется в соответствии с правилами этого конечного автомата. Можно записать, например, хронограмму, представленную в правой стороне рисунка 50. Анализ сети Петри, моделирующей такой конечный автомат, приведен в приложении Е и на рисунке F.6.
На рисунке 51 показано, как можно использовать в DRBD вентиль SEQ: как и для вентиля PAND, выход O переходит в работоспособное состояние только в том случае, если переходит в неработоспособное состояние до того, как
переходит в работоспособное состояние. Разница в том, что
не может перейти в неработоспособное состояние до того, как
перейдет в неработоспособное состояние. Таким образом, отказы B и D тормозятся до тех пор, пока
находится в работоспособном состоянии, и это обозначают с помощью динамических взаимодействий, изображенных пунктирными линиями.
|
Рисунок 51 - Применение вентиля SEQ
Функционирование показано на рисунке 52. Вентиль SEQ эквивалентен пяти состояниям конечного автомата, изображенного в левой стороне рисунка. Состояния такие же, как и для вентиля PAND, за исключением того, что нет перехода из состояния 1 в состояние 2 для того, чтобы упорядочить отказы: - первый, затем
.
|
Рисунок 52 - Эквивалентный конечный автомат и пример хронограммы вентиля SEQ
Как показано на хронограмме, не может отказать до отказа
.
Сеть Петри, моделирующая тот же самый конечный автомат, проанализирована в приложении Е (рисунки Е.6 и Е.7).
12.2.5 Вероятностные расчеты
В литературе предлагается выполнять вероятностный расчет с использованием марковского подхода (см. [2], [29] и [30]). Тем не менее построение марковского процесса для всего DRBD быстро ограничивается комбинаторным взрывом количества состояний. Поэтому такой подход должен быть ограничен небольшим количеством независимых частей DRBD, как это уже было отмечено для RBD-управляемых марковских процессов, описанных в С.4.
Другой подход, предлагаемый в литературе, заключается в том, чтобы установить связь между DRBD и конечным автоматом (машиной с конечным количеством событий или сетью Петри). Это более эффективный подход, чем марковский подход, но аналитические расчеты уже невозможны и следует применять моделирование Монте-Карло.
RBD-управляемые сети Петри, описанные в приложении Е, являются эффективным способом соединения подходов RBD и PN для решения задач динамических RBD и расчетов.
Приложение А
(справочное)
Краткое описание формул
Предупреждение: формулы, представленные в таблице А.1, предназначены для пользователей, осведомленных о лежащих в основе гипотезах, математике и ограничениях при выполнении аппроксимации.
Примечание - В таблице А.1 часто использованы термины "нагруженный" и "ненагруженный". Первый термин использован для обозначения того, что соответствующий блок (который может состоять из компонента, подсистемы, системы и т.д.) функционирует под напряжением (приведен в действие) и, следовательно, подвержен отказу. Термин "ненагруженный" использован для обозначения того, что блок или соответствующие блоки не работают и не отказали.
Таблица А.1 - Пример уравнений для вычисления вероятности успеха базовых конфигураций
Базовая конфигурация | Формула для |
1 Последовательные структуры | А Общий случай |
| Постоянные вероятности: |
| В
|
2 Параллельные структуры | А Нагруженный резерв. Общий случай |
| Постоянные вероятности: |
| В
|
| D Ненагруженный резерв |
3 Последовательно-параллельные структуры (резервированная система) | А Нагруженный резерв. Общий случай |
| Постоянные вероятности: |
| В Нагруженный резерв
|
| F Ненагруженный резерв
|
4 Параллельно-последовательные структуры (резервированные элементы) |
|
А Нагруженный резерв. Общий случай | |
| Постоянные вероятности: |
|
|
| В Нагруженный резерв |
| H Для |
Ненагруженный резерв
| D Ненагруженный резерв для |
5 Параллельно-последовательные структуры (резервированные элементы) | A Нагруженный резерв |
| Для |
|
|
Примечание 1 - В случае невосстанавливаемых блоков | |
Приложение В
(справочное)
Методы булевой алгебры
B.1 Предварительные замечания
Помимо использования булевых таблиц истинности (см. 11.4) и бинарных диаграмм принятия решений (см. 11.5), анализ RBD использует в основном обычные алгебраические математической формулы. Однако булева алгебра в целом также может быть использована для целей такого анализа и во многих случаях она более эффективна и прямолинейна. В частности, использование булевой алгебры вполне может быть самым простым подходом:
a) для RBD, содержащей повторяющиеся блоки (см. рисунок 37);
b) RBD, содержащей стрелки направлений (см. рисунки 10 и 35);
c) особенно сложной системы;
d) более простого построения логического выражения успеха (или отказа) системы, чем построение RBD;
e) систем, содержащих слишком большое количество блоков, чтобы их можно было обработать по простым формулам.
Приведенное выше перечисление d) заслуживает особого внимания. Для многих систем и сетей перечисление комбинации успеха (отказа) оборудования в булевых терминах часто является более простой задачей, чем построение соответствующей RBD. Используя с самого начала булев подход к анализу системы, риск возникновения ошибок при построении RBD системы полностью исключается.
Приведенное выше перечисление е) может быть связано с RBD, моделирующей промышленные системы с большим количеством компонентов и приводящим к комбинаторному взрыву членов, которые должны быть учтены в формуле. Это особенно важно в тех случаях, когда необходимо также использовать большое количество повторяющихся блоков.
B.2 Обозначения
Символы и
, обозначающие логические "ИЛИ" и "И", в булевой алгебре играют ту же роль, что и сложение (+) и умножение (·) в обычной алгебре. Поэтому в дальнейшем оказалось более удобным использовать символ "+" для обозначения логического "ИЛИ" и знака "•" для обозначения логического "И"
. Как обычно черточка над булевой переменной означает обратную или дополняющую переменную: например,
- обозначает "не а". Например,
![]() следует интерпретировать как "a И
следует интерпретировать как "a И И, не
И
ИЛИ
И
". Область применения символов должна быть понятной.
________________
Примечание - Преимущество такого обозначения становится очевидным в приложении В, где часто встречаются выражения вида
![]() . Запись этого выражения с использованием символов теории множеств:
. Запись этого выражения с использованием символов теории множеств: ![]() , многим читателям может показаться менее понятной.
, многим читателям может показаться менее понятной.
B.3 Анализ наборов соединений (путей успеха) и наборов обрывов (путей отказа)
B.3.1 Понятие наборов обрывов и соединений
В соответствии с 8.1, RBD можно рассматривать как электрическую цепь (см. рисунок 14), эта аналогия полезна для идентификации:
- наборов соединений, которые соответствуют замкнутой электрической цепи и представляют собой комбинации блоков в работоспособном состоянии, ведущих к работоспособному состоянию системы. Наборы соединений также есть пути "успеха" RBD;
- наборы обрывов, которые соответствуют обрыву (размыканию) электрической цепи, и представляют собой комбинации блоков в неработоспособном состоянии, ведущих к неработоспособному состоянию системы. Наборы обрывов являются путями отказов RBD.
Использование этой аналогии позволяет преобразовать RBD, представленную на рисунке 10, в электрическую схему, представленную на рисунке 15. Используя это представление, легко определить различные наборы соединений RBD, на рисунках B.1 и B.2 показаны различные примеры комбинаций закрытых переключателей, соответствующих работоспособному состоянию системы.
|
Рисунок B.1 - Примеры минимальных наборов соединений (путей успеха)
На рисунке B.1 любое размыкание (т.е. любой отказ) переключателей приводит к размыканию (обрыву) цепи и неработоспособному состоянию системы. Все замкнутые переключатели (т.е. блоки в работоспособном состоянии) необходимое и достаточное условие для того, чтобы система была в работоспособном состоянии. Эти комбинации минимальны и называются минимальными наборами соединений.
|
Рисунок B.2 - Примеры неминимальных наборов соединений (путей успеха)
На рисунке B.2 некоторые открытые переключатели (например, B2 слева или C1 справа) не изменяют работоспособное состояние системы. Не требуется, чтобы переключатели были закрыты (т.е. блоки были в работоспособном состоянии), чтобы система была в рабочем состоянии. Эти комбинации не являются минимальными и называются неминимальными наборами соединений (или просто наборами соединений).
По тому же рисунку 15 легко определить различные наборы обрывов RBD, на рисунках B.3 и В.4 показаны различные примеры комбинаций разомкнутых переключателей, соответствующих неработоспособному состоянию системы.
|
Рисунок B.3 - Примеры минимальных наборов обрывов
На рисунке B.3 любое замыкание (означает ремонт) разомкнутых выключателей приводит к замыканию цепи и переходу системы в работоспособное состояние. Все открытые переключатели (т.е. блоки в неработоспособном состоянии) необходимы и достаточны, чтобы система находилась в неработоспособном состоянии. Эти комбинации минимальны и называются минимальными наборами обрывов.
|
Рисунок B.4 - Примеры неминимальных наборов обрывов
На рисунке B.4 некоторые замыкания открытых переключателей (например, C2 слева или B2 справа) не влияют на изменение неработоспособного состояния системы. Все открытые переключатели (т.е. блоки в неработоспособном состоянии) не являются необходимыми для того, чтобы система находилась в неработоспособном состоянии. Эти комбинации не являются минимальными и называются неминимальными наборами обрывов (или просто наборами обрывов).
B.3.2 Последовательно-параллельное представление с использованием минимальных наборов соединений и обрывов
Применение свойств булевой алгебры позволяет представить работоспособное состояния системы S в виде объединения минимальных множеств соединений () из RBD, а неработоспособное состояние системы s в виде объединения минимальных наборов обрывов (
) из RBD.
Такой подход можно применить к предыдущему примеру, в котором есть четыре минимальных набора соединений, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В результате:
. В результате:
![]() . (В.1)
. (В.1)
В том же примере имеется четыре минимальных набора обрывов: ![]() ,
, ![]() ,
, ![]() ,
, ![]() что дает:
что дает:
![]() . (В.2)
. (В.2)
Эти формулы обеспечивают два варианта представления одной и той же системы. Формула (B.1) описывает состояние успеха системы, а формула (В.2) - состояние отказа системы. Формула (B.2) эквивалентна следующей формуле
![]() .
.
Преобразование (B.2) предполагает использование законов Де Моргана:
![]() ,
,
![]() .
.
Это приводит к тому, что:
![]() .
.
Таким образом:
![]() . (В.3)
. (В.3)
Получено две эквивалентных логических формулы, представляющих RBD в работоспособном состоянии. Формула (B.1) обеспечивает представление с путями успеха, а формула (B.3) (см. рисунок 18) - представление RBD с минимальными наборами обрывов (см. рисунок 19).
B.3.3 Идентификация минимальных наборов обрывов и наборов соединений
Минимальные наборы обрывов и минимальные наборы соединений могут быть получены путем обобщения логических формул, соответствующих RBD.
Это может быть сделано на примере простого RBD, как показано ниже с RBD, изображенной на рисунке B.5.
|
Рисунок B.5 - Пример RBD с наборами соединений и обрывов различного порядка
Логическая структура этой RBD обеспечивает следующую логическую формулу:
![]() . (В.4)
. (В.4)
Преобразование (B.4) приводит к следующему:
![]() и
и ![]() .
.
Поэтому данная RBD имеет три минимальных пути успеха:
![]() .
.
Минимальные наборы обрывов можно получить, дополняя (B.4) и используя законы Дe Моргана:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, найдены семь минимальных наборов обрывов:
![]() .
.
Минимальные наборы соединений и обрывов представляют собой одну и ту же информацию, но с точки зрения качественного анализа минимальные наборы обрывов более удобны, поскольку самые короткие минимальные наборы обрывов более вероятны, чем другие минимальные наборы обрывов.
Таким образом, наборы обрывов RBD, приведенной на рисунке B.5, могут быть отсортированы по порядку (см. 3.18, примечание 2):
- набор первого порядка ;
- набор второго порядка ![]() ,
, ![]() ;
;
- набор третьего порядка ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
С качественной точки зрения слабым местом этой системы, безусловно, является минимальный набор обрывов первого порядка .
За исключением простых случаев, приведенные выше расчеты на самом деле не поддаются ручной обработке, но имеются мощные алгоритмы в доступных пакетах программ для RBD. Минимальные наборы соединений и обрывов могут быть найдены с помощью, например, бинарных диаграмм принятия решений, рассмотренных в вероятностных вычислениях настоящего стандарта.
B.4 Принципы расчетов
В.4.1 Последовательные структуры
Рассмотрим систему, состоящую из n последовательных блоков (), показанную на рисунке 2. Из рисунка видно, что система в целом находится в работоспособном состоянии, когда все блоки
находятся в работоспособном состоянии. Другими словами, логическое выражение успеха системы имеет вид
![]() , (В.5)
, (В.5)
где - логическая переменная, соответствующая работоспособному состоянию блоков
.
Если блоки независимы, то вероятность того, что система находится в работоспособном состоянии, равна
![]() . (В.6)
. (В.6)
Поэтому особых вычислительных проблем при вычислении в случае последовательной структуры не существует.
Однако, если приведенная последовательная структура (B.5) относится к более крупной RBD, то этот расчет может быть сделан только в том случае, если ни один блок этой последовательной структуры не повторяется в другом месте более крупной RBD. В противном случае следует применять методы, описанные в В.5 или В.6.
B.4.2 Параллельные структуры
Рассмотрим систему из двух блоков в нагруженном резерве, такую как изображена на рисунке 21. Из рисунка можно видеть, что система в целом находится в работоспособном состоянии при условии, что A или B (или оба) находятся в работоспособном состоянии. Другими словами, логическое выражение успеха системы имеет вид
![]() , (В.7)
, (В.7)
где и
- булевы переменные, соответствующие работоспособному состоянию блоков A и B соответственно.
Для заданного времени возникает соблазн заменить
и
на
и
соответственно и переписать формулу (В.7) в виде
![]() . (В.8)
. (В.8)
Как ожидается формула (B.8) дает вероятность того, что система находится в работоспособном состоянии, но, к сожалению, это неверно, поскольку она получена из булева выражения, в котором переменные перекрываются (т.е.
![]() ). Выражение (В.8) даже не предусматривает в общем случае приемлемого приближения
). Выражение (В.8) даже не предусматривает в общем случае приемлемого приближения . Например,
=1,2 при
и
, равных 0,6. Это не верно.
Формула (В.8) должна быть дополнена следующим образом:
![]() . (B.9)
. (B.9)
В отличие от (В.8), формула (В.9) дает точный результат в любом случае.
![]() .
.
Рассмотрение структуры, состоящей из n параллельных блоков (), приводит к следующему выражению:
![]() .
.
Обобщение формулы (B.9) называют формулой Сильвестра-Пуанкаре:
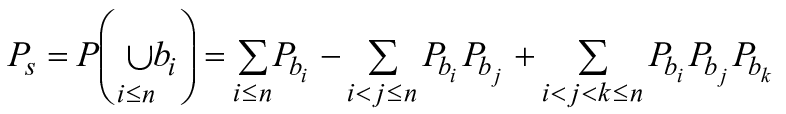 . (В.10)
. (В.10)
Это альтернативная сумма убывающих членов, которые сходятся в результате к . Количество членов сильно возрастает при увеличении n, а сходимость очень медленная, если вероятность высока. Это, к сожалению, случай, когда вероятности
работоспособного состояния блоков близки к 1. Следовательно, формула (B.10) не подходит для оценки
из-за необходимости вычисления очень большого количества членов.
К счастью, можно рассмотреть несколько вариантов. Первый - оценить вероятность того, что система находится в неработоспособном состоянии.
Например, неработоспособное состояние небольшой системы (B.7), рассмотренной выше, имеет вид ![]() , что, применяя законы де Моргана, приводит к эквивалентной форме булева выражения
, что, применяя законы де Моргана, приводит к эквивалентной форме булева выражения ![]() .
.
Если и
не зависят друг от друга, то не зависят также
и
. Тогда вероятность того, что система находится в неработоспособном состоянии имеет вид
![]() .
.
И наконец ![]() .
.
Это выражение можно легко обобщить на n параллельных блоков ![]() , то есть
, то есть ![]() , полученное с помощью применение законов де Моргана.
, полученное с помощью применение законов де Моргана.
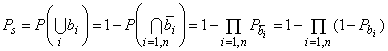 . (В.11)
. (В.11)
Формула (B.11), включающая только простые произведения для расчета параллельных структур, является более простой, чем формула Сильвестра-Пуанкаре.
B.4.3 Сочетание последовательных и параллельных структур
Формулы (B.6) и (B.11) могут быть объединены, и это в простых случаях может быть сделано вручную. Таким образом, если система имеет вид, показанный на рисунке 4, но только с тремя элементами в каждой ветви, то вероятность успеха системы равна
![]() . (В.12)
. (В.12)
Аналогично для рисунка 5:
![]() . (В.13)
. (В.13)
Для рисунков 6 и 7 можно получить вероятности успеха системы просто умножая (B.12) и (B.13) на .
Тем не менее, за исключением простых случаев по формулам (В.12) или (В.13) нелегко выполнить вручную. Существуют мощные алгоритмы, реализованные в виде пакета программ для RBD. Они основаны на методах, рассмотренных в B.5, B.6 или В.7.
B.4.4 Структура m из n (идентичные элементы)
Среди простых случаев формулы вероятности успеха системы, соответствующие рисункам 8 (2/3) и 9 (3/4), немного сложнее, чем рассмотренные в B.4.3.
Для системы 2/3, представленной на рисунке 8, формула (В.9) дает
![]()
Если блоки независимы и имеют одинаковую вероятность успеха, , то
![]() .
.
Это выражение можно преобразовать ![]() и, следовательно
и, следовательно
![]() . (В.14)
. (В.14)
Формулу (B.14) можно обобщить на структуру , состоящую из
идентичных блоков. В в этом случае для успеха системы требуется работоспособность
блоков из
, а вероятность успеха системы
имеет вид
![]() . (В.15)
. (В.15)
Применение (B.15) к логической структуре 2/4, представленной на рисунке 9, дает
![]() . (В.16)
. (В.16)
Система находится в работоспособном состоянии, если в работоспособном состоянии находится
блоков. Тогда для того, чтобы эта система находилась в неработоспособном состоянии необходимо, чтобы
![]() блоков находились в неработоспособном состоянии. Поэтому система
блоков находились в неработоспособном состоянии. Поэтому система по отношению к работоспособному состоянию является системой
![]() по отношению к неработоспособному состоянию и вероятность отказа системы
по отношению к неработоспособному состоянию и вероятность отказа системы можно получить заменами
на
![]() и
и на
![]() в формуле (B.15):
в формуле (B.15):
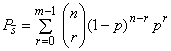 . (В.17)
. (В.17)
Конкретные ситуации.
- Если т=n-1 (например, 2/3, 3/4 и т.д.) формула (В.15) сводится к
![]() . (В.18)
. (В.18)
- Если ![]() , система симметрична относительно успеха и отказа: система находится в работоспособном состоянии, если
, система симметрична относительно успеха и отказа: система находится в работоспособном состоянии, если блоков находятся в работоспособном состоянии, и находится в неработоспособном состоянии, если
блоков находятся в неработоспособном состоянии. Это относится к структурам 1/1, 2/3, 3/5 и т.д. Благодаря этому свойству, структуру 2/3 широко используют в промышленности при проектировании систем безопасности.
Если элементов не идентичны, рекомендуется использовать более общую процедуру (см. 11.8.2).
B.5 Использование формулы Сильвестра-Пуанкаре для больших RBD и повторяющихся блоков
B.5.1 Общие положения
При наличии повторяющихся блоков может быть применена формула, разработанная в В.3 только для тех частей RBD, которые не содержат повторяющиеся блоки. Для других частей системы RBD повторяющиеся блоки должны быть должным образом учтены.
Эквивалентные RBD, состоящие из путей успеха (минимальных наборов соединений) или комбинаций отказов (минимальные наборов обрывов) являются обычно RBD с такими повторяющимися блоками. Поэтому они рассмотрены ниже.
B.5.2 Формула Сильвестра-Пуанкаре для наборов соединений
Для состояния успеха системы, имеющей путей успеха (минимальные наборы соединений), (
), можно записать
![]() .
.
Минимальные наборы соединений не являются независимыми друг от друга, и соответствующая формула Сильвестра-Пуанкаре имеет следующий вид:
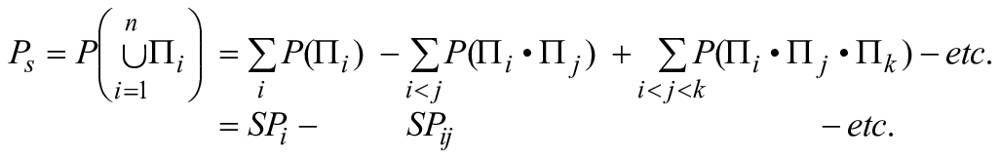 (В.19)
(В.19)
Формула (B.19) показывает, что вероятность объединения наборов соединений равна
1) сумме вероятностей множества соединений ();
2) минус сумма вероятностей пересечения наборов соединений 22 (
);
3) плюс сумма вероятностей пересечения наборов соединений 33 (
);
4) минус сумма вероятностей пересечения наборов соединений 44 (
)
5) и т.д.
Наборы соединений не являются независимыми, так как одно и то же событие может появиться в нескольких наборах соединений. Следовательно, необходимо проанализировать все пересечения множеств соединений, прежде чем выполнять вычисления для того, чтобы упростить их, когда они включают идентичные события.
Это можно показать на примере, рассмотренном в 8, который включает четыре минимальных множества соединений: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Реализация формулы (В.19) приводит к следующим результатам.
a) первый член :
![]() .
.
b) второй член :
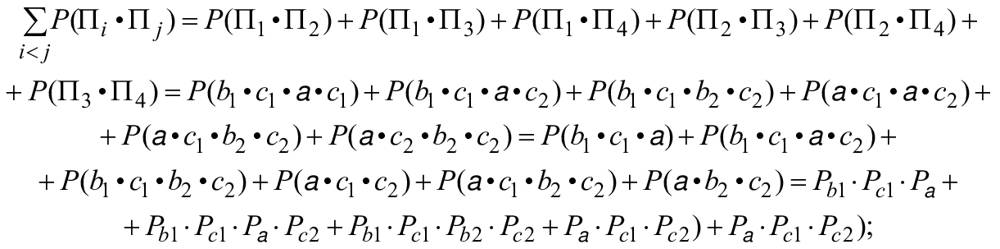
c) третий член :
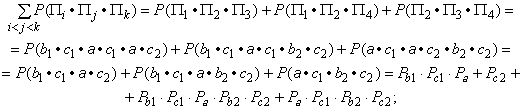
d) четвертый член :
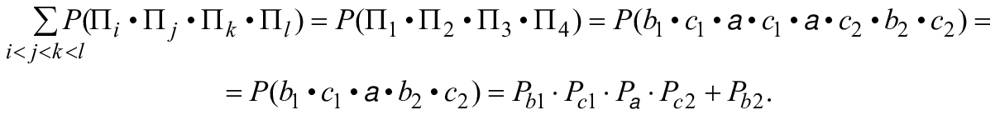
Таким образом, для четырех минимальных наборов соединений необходимо идентифицировать и составить 4+6+3+1=14 членов.
Поскольку вероятность множества соединений ![]() обычно не мала по сравнению с 1, то вероятности
обычно не мала по сравнению с 1, то вероятности ![]() ,
, ![]() тоже не маленькие и их нельзя игнорировать.
тоже не маленькие и их нельзя игнорировать.
При наличии трех событий с высокой вероятностью ![]() можно получить следующие результаты:
можно получить следующие результаты:
![]() ,
,
![]() .
.
Ни один член не является пренебрежимо малым, и все члены должны быть учтены в расчетах.
Формула (В.19) на практике не подходит для расчетов, потому что для этого требуется получить слишком много членов с подходящей аппроксимацией.
B.5.3 Формула Сильвестра-Пуанкаре для набора обрывов
Состояние отказа системы, имеющей путей отказа (минимальных наборов обрывов) (
) можно записать в виде
![]() .
.
Это приводит к соответствующей формуле Сильвестра-Пуанкаре:
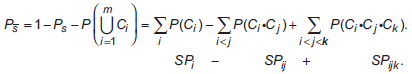 (В.20)
(В.20)
Пример из 8 также включает четыре минимальных набора обрывов
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Как и в случае с наборами соединений необходимо вычислить 14 членов, однако эта ситуация совсем другая, поскольку вероятности ![]() обычно малы по сравнению с 1.
обычно малы по сравнению с 1.
Тогда вероятности ![]() ,
, ![]() и т.д. все меньше и меньше и формула (В.20) сходится довольно быстро. Поэтому возможны аппроксимации.
и т.д. все меньше и меньше и формула (В.20) сходится довольно быстро. Поэтому возможны аппроксимации.
Из формулы ![]() видно, что результаты трех событий с высокой вероятностью (
видно, что результаты трех событий с высокой вероятностью (![]() ) и трех событий с низкой вероятностью (
) и трех событий с низкой вероятностью (![]() ) можно сравнить:
) можно сравнить:
- ![]() получается при
получается при ![]() ;
;
- ![]() получается при
получается при ![]() .
.
Тогда в случае с низкими вероятностями
- член обеспечивает верхнюю границу вероятности: 0,03,
- разность ![]() обеспечивает нижнюю границу: 0,0297, а точный результат принадлежит интервалу [0,0297, 0,03].
обеспечивает нижнюю границу: 0,0297, а точный результат принадлежит интервалу [0,0297, 0,03].
Эти результаты могут быть экстраполированы на большое количество событий:
- если вероятности высоки, сходимость очень медленная, и для получения результата должны быть рассмотрены все члены;
- если вероятности невелики, сходимость быстрая и первый член формулы Сильвестра-Пуанкаре дает приемлемый приближенный результат, а первые два члена - хороший интервал, которому принадлежит результат.
Формула Сильвестра-Пуанкаре (B.20), использующая наборы обрывов (), которые обычно включают низкие вероятности, является более хорошим кандидатом для получения приемлемого приближения, чем формула (B.19), использующая наборы соединений (
). Поэтому при выполнении вероятностных расчетов лучше рассматривать минимальные наборы обрывов (
), чем наборы соединений (
).
Чем ниже результирующая вероятность , тем быстрее происходит сходимость и в лучшем случае хорошо работает следующая аппроксимация
![]() . (В.21)
. (В.21)
Это приближение широко используют, оно является основой расчетов, выполняемых в многочисленных пакетах программ, для расчетов показателей готовности и безотказности с помощью RBD или деревьев отказов. В некоторых случаях второй член формулы Сильвестра-Пуанкаре вычисляют для определения границ интервала .
B.6 Метод дизъюнкции булевых выражений
B.6.1 Общие сведения и справочная информация
Формула (В.7) может быть записана в эквивалентном виде:
![]() . (В.22)
. (В.22)
Процесс преобразования (В.7) в (В.22) называется дизъюнкцией.
В (B.22) члены и
являются непересекающимися членами. Это означает, что
![]() и следовательно,
и следовательно, ![]() . Тогда
. Тогда сводится к известному результату:
![]() . (В.23)
. (В.23)
Следует заметить, что формулу (В.7) также можно записать в других дизъюнктивных формах, одна из которых имеет вид ![]() , что приводит к другому выражению:
, что приводит к другому выражению:
![]() . (В.24)
. (В.24)
Очевидно, что (B.23) и (B.24) эквивалентны ранее полученным формулам ![]() и
и ![]() .
.
В отличие от предыдущих выражений количество членов в формуле вероятности совпадает с количеством непересекающихся членов в булевом уравнении. Рассмотрим , представленную объединением непересекающихся путей успеха:
![]() , где
, где ![]() .
.
Тогда формула Сильвестра-Пуанкаре принимает вид
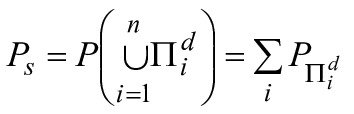 . (В.25)
. (В.25)
Аналогично, если представлена объединением непересекающихся наборов обрывов, то можно записать:
![]() , где
, где ![]() .
.
Формула Сильвестра-Пуанкаре принимает вид
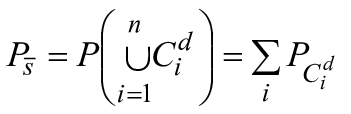 . (В.26)
. (В.26)
Поэтому и при условии минимальных наборов соединений или обрывов формулы (В.25) и (B.26) могут быть использованы для выполнения точных вычислений. Если вероятности отказа блока изменяются во времени, эти формулы могут быть использованы для расчетов показателей готовности, или неготовности
![]() .
.
Таким образом, основной целью является формирование булевых выражений для успеха или отказа системы с непересекающимися членами. Это означает, что каждый член в конечном булевом выражении не пересекается ни с одним другим членом. Более подробная информация о методе приведена в [19].
Следует отметить, что два члена взаимно не пересекаются, если хотя бы одна переменная в одном члене появляется в другом в виде своего дополнения. Например, термины ![]() и
и ![]() не пересекаются из-за переменной
не пересекаются из-за переменной . Верно и обратное. А именно два члена не являются непересекающимися (то есть пересекаются), если ни одна из переменных в одном члене не появляется в другом в виде своего дополнения. Например, два члена
![]() и
и ![]() не являются взаимно непересекающимися.
не являются взаимно непересекающимися.
B.6.2 Принцип дизъюнкции
Если два члена и
не являются непересекающимися, и требуется выполнить дизъюнкцию по отношению к ним, можно использовать несколько процедур.
Основной принцип заключается в следующем:
- выделяют все переменные в , которые не появляются в
(такие члены называют относительным дополнением
по отношению к
). Предположим, что относительным дополнением является
![]() ;
;
- затем замените на
![]() .
.
Результирующее выражение ![]() состоит из членов непересекающихся друг с другом.
состоит из членов непересекающихся друг с другом.
Например, чтобы сделать член ![]() непересекающимся с членом
непересекающимся с членом ![]() , необходимо:
, необходимо:
- найти относительное дополнение по отношению к
![]() :
:
- заменить на
![]() .
.
Теперь и
являются непересекающимися по отношению друг к другу.
B.6.3 Процедура дизъюнкции
Основная процедура дизъюнкции состоит в следующем:
a) представляют успех системы (обозначаемый ) в виде суммы произведений булевых переменных
(т.е. наборов соединений) и обозначают члены слева направо: "
,
,
, …";
________________
Для простых булевых выражений успеха системы могут быть использованы произведения одного, двух и более членов.
b) выбирают в качестве "основного" члена и сравнивают его с
;
c) при необходимости (т.е. если два члена не являются непересекающимися) делают непересекающимся по отношению к
в соответствии с В.6.2;
d) при необходимости делают непересекающимся по отношению к
;
e) продолжают процесс для остальных членов в ;
f) проверяют несколько расширенное (за счет добавленных дополнительных членов) выражение, полученное на этом этапе и упрощают его (где это возможно) с помощью правил булевой алгебры (используя такие правила, как ![]() ,
, ![]() ,
, ![]() ). Обозначают полученное выражение
). Обозначают полученное выражение , а его члены слева направо:
,
,
, …;
q) выбирают второй член () из выражения для
в качестве "основного" члена и сравнивают
с
; так действуют в соответствии с перечислениями с)-f), используя члены
. Обозначают полученное выражение
;
h) продолжают описанную выше процедуру до тех пор, пока все члены не будут использованы в качестве "основных" членов, к этому времени полученное выражение будет полностью дизъюнктивной версией исходного выражения .
Наконец, формируют набор непересекающихся членов (), относящихся к успеху системы, как описано в В.6.1. Таким образом, для вероятности успеха
или коэффициента готовности
может быть применена формула (В.25).
Такая процедура может быть использована для получения непересекающихся членов (), относящихся к отказу системы в соответствии с В.6.1. Следовательно, вероятность отказа
или коэффициент неготовности
системы можно рассчитать, применив формулу (В.26).
Описанная процедура является основной и может быть улучшена так же, как это сделано в примере, приведенном в B.6.4.
B.6.4 Пример применения процедуры дизъюнкции
Предположим, что система состоит из пяти элементов A, B, C, D и E и что a, b, c, d и e - соответствующие булевы переменные "успеха". Предположим также, что успех системы () в булевых переменных определяется следующим выражением, которое включает в себя четыре суммы произведений (т.е. четыре набора соединений):
![]() .
.
Чтобы сделать приведенное выражение непересекающимся, основная процедура, описанная в B.6.3, может быть усовершенствована и применена следующим образом:
Этап 0 - Классификация путей по возрастанию длины и в алфавитном порядке:
![]() .
.
Этап 1 - выполнение дизъюнктивной процедуры, начиная с последнего произведения () для преобразования его в непересекающееся со всеми его предшественниками:
1.1: применение процедуры к непосредственному предшественнику () путем:
- идентификация событий, принадлежащих , но не
. Это дает
,
- замена выражения в исходной формуле на
![]() ;
;
1.2: повторение этапа 1.1 для следующего члена слева ():
- идентификация событий, принадлежащих , но не
. Это дает
,
- замена выражения , измененного на этапе 1.1 (т.е.
![]() ) на
) на ![]() в исходной формуле;
в исходной формуле;
- 1.3: нет необходимости в повторении этапа 1.2 со следующим членом слева (), потому что последнее произведение
, модифицированное в
![]() , не пересекается с
, не пересекается с . Дизъюнктивная процедура, применяемая к
выполнена.
Исходная формула может быть переписана следующим образом:
![]() .
.
Этап 2 - Повторение описанной выше процедуры (этапы 1.1-1.3) для обеспечения непересекаемости с его предшественниками.
2.1. Как и ранее, применение процедуры к первому непосредственному предшественнику :
- идентификация событий, принадлежащих , но не
. Это дает b и e;
- замена выражения на
![]() в исходной формуле, имея в виду при этом (закон де Моргана), что
в исходной формуле, имея в виду при этом (закон де Моргана), что ![]() . Это дает
. Это дает ![]() .
.
2.2. Поскольку первый член декомпозиции (т.е.
![]() уже не пересекается со всеми своими предшественниками
уже не пересекается со всеми своими предшественниками и
, а второй член
![]() уже не пересекается со своим предшественником
уже не пересекается со своим предшественником , осталось сделать
непересекающимся с его вторым предшественником
:
- идентификация событий, принадлежащих , но не
![]() . Это дает
. Это дает ;
- замена выражения ![]() на
на ![]() в исходной формуле, которая принимает вид:
в исходной формуле, которая принимает вид:
![]() .
.
Этап 3 - Повторение дизъюнктивной процедуры для обеспечения непересекаемости с его единственным предшественником
:
- идентификация событий, принадлежащих , но не
. Это дает
;
- замена выражения на
![]() в исходной формуле.
в исходной формуле.
Этап 4 - Поскольку первое произведение (здесь ) всегда остается неизменным, процедура завершена и дает следующую конечную сумму непересекающихся произведений:
![]() .
.
Получено пять непересекающихся членов
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В соответствии с B.6.1 можно записать в виде
![]() .
.
Поэтому вероятность успеха или коэффициента готовности
системы могут быть вычислены по формуле (В.25)
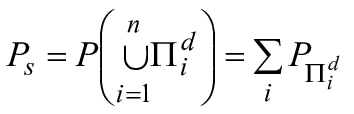 .
.
![]()
Количество непересекающихся членов зависит от порядка, в котором использованы пути успеха при применении алгоритма дизъюнкции. Все результаты эквивалентны, но получены более или менее быстро. Теоретического оптимума не существует, и выбор может быть основан на эвристике, которая хорошо работает. Использование алфавитного порядка является примером такой эвристики.
Конечно, такая же процедура может быть использована с минимальными наборами обрывов для поиска непересекающихся наборов (), позволяющих вычислять вероятность отказа
или коэффициент неготовности
) системы по формуле (В.26):
![]() .
.
B.6.5 Комментарии
Наиболее важной особенностью процедур, описанных в В.6.4, является то, что последовательность этапов, необходимых для выполнения дизъюнкции, относительно проста для программирования. Улучшенную процедуру описанную в B.6.4, часто используют на современных компьютерах, где довольно сложные булевы выражения с суммами произведений могут быть преобразованы мгновенно. Сведений, приведенных в настоящем стандарте, достаточно для написания соответствующей программы.
Еще одной важной особенностью является то, что процедура, направленная на дизъюнкцию булевых выражений, может быть применена с той же эффективностью к булевым выражениям при анализе дерева неисправностей.
B.7 Бинарные диаграммы принятия решений
B.7.1 Установление BDD
В настоящее время в вероятностных расчетах на основе булевых функций используют декомпозиции Шеннона булевых функций для построения бинарной диаграммы принятия решений (BDD), кодирующей все непересекающиеся комбинации, приводящие к моделируемой функции.
Булева функция, смоделированная RBD, приведенная на рисунке 6, зависит от четырех булевых переменных ,
,
и
.
Декомпозиция Шеннона аналогична таблице истинности булевой функции, моделируемой RBD.
|
Рисунок B.6 - RBD, приведенная на рисунке 35
|
Рисунок B.7 - Декомпозиция Шеннона булевой функции, представленной на рисунке B.6
Эта декомпозиция представлена в графическом виде на рисунке В.7. Процесс выполнения состоит в следующем:
1) выбирают одну из переменных (например, ) и помещают ее в верхнюю часть схемы;
2) от этой переменной рисуют две стрелки для представления двух ее возможных состояний: например, 1 слева и 0 справа (сплошные и пунктирные линии использованы для наглядности рисунка);
3) выбирают другую переменную (например, b) и соединяют ее с нарисованными стрелками. Эта переменная появляется два раза;
4) от каждой этой переменной рисуют две стрелки для представления двух ее возможных состояний;
5) выбирают другую переменную (например, c) и соединяют ее с имеющимися стрелками. Эта переменная появляется четыре раза;
6) и так далее до тех пор, пока все переменные не будут обработаны.
Тогда для переменных получается
путей. Каждый из них ведет к успеху функции (
=1) или к ее отказу
=0. Это можно узнать путем анализа соответствующей RBD.
|
Рисунок В.8 - Идентификация частей, состояние которых не имеет значения
Далее выполняют упрощение этого графика путем определения частей, состояние которых не имеет значения.
Они выделены пунктирными прямоугольниками на рисунке 8. Например, с левой стороны состояние системы не зависит от состояния переменной d и с правой стороны оно не зависит от состояний переменных c и d.
Это позволяет получить упрощенную схему, приведенную на рисунке В.9. Она не идентична схеме на рисунке 38 для той же RBD. Это связано с другим выбором порядка переменных, используемых для декомпозиции. Такое представление показывает, что декомпозиция не является уникальной и приводит к более или менее простой схеме в соответствии с выбранным порядком переменных.
|
Рисунок B.9 - Упрощение разложения Шеннона
На этой схеме можно выделить 9 путей: 5 путей ведут к успеху S и 4 - к ее отказу. Анализ этих путей по BDD позволяет определить связь между s или и состояниями переменных a, b, c и d:
![]() .
.
![]() .
.
Следующим этапом является построение BDD, связанной с RBD. Как показано на рисунке В.10 это делают просто, собирая входы с одинаковыми величинами.
|
Рисунок B.10 - Бинарная диаграмма принятия решений, соответствующая RBD, приведенной на рисунке B.6
B.7.2 Минимальные пути успеха и наборы обрывов с BDD
Один и тот же блок может появляться в различных местах, но в базовой RBD он в различных местах находится всегда в одном и том же состоянии. Это означает, что RBD является "когерентной", а соответствующая ей булева функция является "монотонной". Это означает, что если система отказала, она не может восстановиться в дальнейшем при отказе блока или если система находится в работоспособном состоянии, она не может отказать в дальнейшем при ремонте блока. В этом случае булева функция может быть представлена минимальным набором соединений (путей успеха), и ее дополнительная функция может быть представлена объединением минимальных наборов обрывов (путей отказа).
Если булева функция немонотонна, то понятия минимальных наборов соединений или обрывов не подходят и должны быть заменены понятием "простой импликант". Разница в том, что минимальный набор соединений состоит только из комбинации блоков в работоспособном состоянии (а минимальный набор обрывов - только из комбинации блоков в неработоспособном состоянии), тогда как простой импликант может состоять из комбинации блоков в работоспособном и неработоспособном состояниях. Простые импликанты не могут быть сведены к минимальным наборам соединений или обрывов, их не следует путать с непересекающимися членами, рассмотренными в В.7.1, эквивалентными объединению минимальных наборов соединений или обрывов.
Следовательно, если булева функция монотонна и - путь успеха, содержащий отказавшие блоки, удаление отказавших блоков также обеспечивает путь успеха. Например, если
![]() , то
, то тоже путь успеха.
Аналогично, если - набор обрывов, содержащий блоки в работоспособном состоянии, то удаление этих блоков также обеспечивает набор обрывов: например, если
![]() - набор обрывов, то
- набор обрывов, то также набор обрывов.
Таким образом, непересекающиеся пути успеха, определенные в B.7.1, могут быть использованы для идентификации путей успеха, связанных с булевой функцией. Это показано на рисунке 11.
|
Рисунок B.11 - Определение путей успеха (наборов соединений) по RBD
Среди найденных наборов соединений некоторые являются не минимальными наборами, которые включены (с точки зрения булевой алгебры) в минимальные наборы соединений. Наконец найдены три минимальных пути успеха, аналогичны тем, что были идентифицированы ранее.
|
Рисунок B.12 - Определение путей отказа (наборов обрывов) по RBD
На рисунке B.12 показано, как минимальные наборы обрывов могут быть найдены из булева уравнения отказа системы. Принцип точно такой же, как и для путей успеха. Найдено три минимальных набора обрывов, они идентичны ранее найденным.
BDD также является эффективным методом идентификации минимальных наборов соединений или обрывов.
Принцип идентификации соединений (путей успеха) показан в левой части рисунка В.13. Он справедлив только тогда, когда BDD соответствует "когерентной" RBD, как объяснено в В.7.2.
Процесс включает начало состояния успеха системы и исследование графика снизу вверх в обратном порядке (переменных) по отношению к использованному при построении BDD. При исследовании ветви, если переменная обнаружена в состоянии отказа, то ее обходят и вводят новую линию с переменной чуть выше. И так далее. При рассмотрении графика в левой стороне выявлен следующий набор соединений: ![]() ,
, ![]() ,
, ,
,
,
![]() . Некоторые из этих комбинаций не являются минимальными, а одна комбинация появляется дважды.
. Некоторые из этих комбинаций не являются минимальными, а одна комбинация появляется дважды.
|
Рисунок B.13 - Наборы обрывов и соединений, выявленные по BDD
Аналогично, принцип поиска наборов обрывов (путей отказа) показан в правой части рисунка В.13. Процесс состоит из начала состояния отказа системы и исследования графа снизу вверх в обратном порядке (переменных) по отношению к использованному при построении BDD. При исследовании ветви если переменная в работоспособном состоянии, то ее обходят и вводят новую линию с переменной чуть выше. И так далее. При рассмотрении графа с правой стороны выявлен следующий набор обрывов: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Одна из этих комбинаций
. Одна из этих комбинаций ![]() не является минимальной.
не является минимальной.
Таким образом, графы могут быть упрощены в порядке кодирования минимальных комбинаций. Это легко сделать вручную, но разработаны мощные алгоритмы для работы с большими BDD при обработке RBD с миллионами минимальных наборов соединений и обрывов.
Если булевы функции не монотонны, применение минимальных наборов соединений или обрывов не имеет смысла и должно быть заменено применением простых импликантов. Это более сложная обработка, но для решения этой проблемы также существуют мощные алгоритмы.
B.7.3 Вероятностные расчеты по BDD
В.7.3.1 Общие положения
Структура BDD, представленная на рисунке B.10, очень компактно моделирует все пути к отказу системы и пути к успеху системы. Для одной и той же RBD может быть разработано несколько эквивалентных BDD. Как и для упрощенной декомпозиции Шеннона, размер этих BDD зависит от выбора порядка исследования переменных.
Все пути, закодированные в BDD, являются непересекающимися, BDD можно использовать непосредственно для вероятностных вычислений просто заменой переменных состояния, соответствующими вероятности успеха или отказа (см. рисунок В.14).
Использование путей, ведущих к успеху системы, дает следующее выражение:
![]() .
.
Использование путей, ведущих к отказу системы, дает следующее выражение:
![]() .
.
|
Рисунок B.14 - Вероятностные расчеты по BDD
В.7.3.2 Вычисление условных вероятностей по RBD
BDD можно использовать для вычисления условных вероятностей. На рисунке B.15 показано как вычислить на левой стороне и
на правой стороне. Это основа вычислений, связанных с условным параметром потока отказов (интенсивностью Веселя), безусловным параметром потока отказов (частотой отказов) и показателей значимости (см. приложение D).
|
Рисунок B.15 - Расчет условных вероятностей с использованием BDD
B.7.4 Основные замечания по использованию BDD
Структура BDD является очень мощной для эффективного и компактного способа кодирования всех непересекающихся путей, ведущих к успеху и отказу системы. Это позволяет выполнить вероятностные вычисления без аппроксимаций.
BDD также может быть использован для кодирования минимальных наборов соединений (путей успеха) и минимальных наборов обрывов (путей отказа) при когерентных RBD или кодирования первичных импликантов при когерентных RBD.
При наличии переменных декомпозиция Шеннона (как и таблица истинности) приводит к
путям. Это невозможно обработать при больших
. Поэтому были разработаны современные алгоритмы построения BDD без построения всей декомпозиции Шеннона. Это позволяет обрабатывать сотни переменных (например, RBD с сотнями блоков) и миллиарды путей успеха или минимальных наборов обрывов. Размер зависит от выбора порядка переменных при разработке BDD и эвристик (доступных для выбора), что в некоторой степени лучше.
Использование BDD - очень эффективный способ хранения RBD в памяти компьютера и выполнения вероятностных вычислений с помощью булевых функций (например, RBD и деревья отказов).
Приложение С
(справочное)
Зависящие от времени вероятности и RBD-управляемые марковские процессы
С.1 Общие положения
Основная математика, лежащая в основе RBD - это булева алгебра, статичная по своим свойствам. Поэтому вероятностные расчеты по RBD в первую очередь связаны с постоянными значениями. Тем не менее, если блоки не зависят друг от друга во времени, формулы, разработанные для постоянных значений вероятностей, могут быть использованы непосредственно для расчета коэффициента готовности системы ![]() по коэффициентам готовности
по коэффициентам готовности ![]() блоков
блоков .
Расчеты также могут быть распространены на средний коэффициент готовности ![]() , стационарный коэффициент готовности
, стационарный коэффициент готовности , асимптотический коэффициент готовности
, частоту отказов
и только в отдельных случаях на вероятность безотказной работы
![]() .
.
Пользователь RBD должен понимать, что RBD в большей степени ориентирована на вычисление показателей готовности, чем на вероятность безотказной работы.
C.2 Принцип вычисления зависящих от времени показателей
|
Рисунок С.1 - Принцип вычисления зависящих от времени показателей
На рисунке С.1 показан принцип вычисления коэффициента готовности с использованием RBD. На этом рисунке показаны коэффициенты готовности каждого блока. Коэффициенты готовности могут быть любого вида. Единственное ограничение состоит в том, что в соответствии с основным требованием независимости в 5.2 d) блоки не должны зависеть друг от друга.
Поэтому принцип состоит в том, чтобы подобрать набор коэффициентов готовности блоков в данный момент времени (небольшие циклы на рисунке) и использовать их для вычисления коэффициента готовности системы в момент времени
с помощью логики смоделированной RBD. Эта процедура может быть использована для любого момента времени и позволяет обеспечить всю эволюцию коэффициента готовности системы
(пунктирная линия на рисунке).
За исключением очень простых случаев, эта процедура достаточно сложна при вычислении вручную, но может быть легко выполнена при использовании алгоритмов, реализованных в пакетах программ RBD/FT (например, алгоритмы, основанные на бинарных диаграммах принятия решений).
C.3 Невосстанавливаемые блоки
C.3.1 Общие положения
Принцип, описанный в С.2, очень прост в применении к RBD с невосстанавливаемыми блоками.
C.3.2 Простые невосстанавливаемые блоки
Если RBD, представленная на рисунке С.1, состоит из простых не невосстанавливаемых блоков с постоянной интенсивностью отказов, входные кривые будут иметь классическую форму:
![]() .
.
C.3.3 Составной блок: пример восстанавливаемой резервированной системы
Метод может быть применен к составному блоку, как показано на RBD, приведенной на рисунке 11, которая моделирует часто используемую форму резервирования, называемую резервированием с замещением (см. пункт 7.5.3 и первый абзац приложения А).
В самом простом случае блоки А и В являются невосстанавливаемыми и не зависят друг от друга: B начинает работать, когда A отказывает. Составной блок С можно рассматривать в целом (см. рисунок 12), а его коэффициент готовности ![]() должен быть определен как показано на рисунке С.2. Если A и B невосстанавливаемые, то C также невосстанавливаемый и поэтому
должен быть определен как показано на рисунке С.2. Если A и B невосстанавливаемые, то C также невосстанавливаемый и поэтому ![]() .
.
Коэффициент готовности ![]() такой системы может быть определен путем рассмотрения того, какие возможные события могут произойти в течение времени
такой системы может быть определен путем рассмотрения того, какие возможные события могут произойти в течение времени . Возможны следующие варианты:
- блок А находится в работоспособном состоянии в течение всего времени ;
- блок А отказывает в момент времени , блок В начинает работать в момент времени
(т.е. блок В не отказал в состоянии резервирования, переключатель не отказал до момента времени
) и не отказывает в течение периода времени [
,
].
Пусть:
- - интенсивность отказов блока А, а
![]() - соответствующая функции плотности распределения;
- соответствующая функции плотности распределения;
- - интенсивность отказов блока B, когда он находится в пассивном (спящем) состоянии, состоянии холодного или горячего резерва при низкой мощности;
- - интенсивность отказов блока B в состоянии функционирования после его запуска из-за отказа блока A;
- - интенсивность отказов переключателя S, а
![]() - вероятность безотказной работы в момент времени
- вероятность безотказной работы в момент времени .
Можно записать следующее математическое выражение:
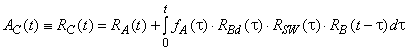 .
.
Если предположить, что все объекты имеют постоянную интенсивность отказов, то это математическое выражение принимает вид
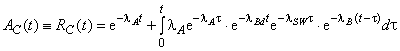 .
.
Примечание - Вероятность безотказной работы переключателя является функцией не времени, а какой-то другой переменной (количество переключений и т.д.), предпочтительно вообще не использовать функциональную зависимость, а использовать вместо нее для обозначения вероятности безотказной работы переключателя или
для обозначения вероятности отказа B по запросу.
Таким образом
![]() .
.
При предположении ![]() выражение принимает вид:
выражение принимает вид:
![]() .
.
Если интенсивность отказов элемента В в состоянии резервирования равна нулю, то коэффициента готовности рассматриваемой сиcтемы имеет вид
![]() . (С.1)
. (С.1)
Если, кроме того, обе интенсивности отказов равны (![]() и
и ![]() ), то формула для коэффициента готовности принимает вид
), то формула для коэффициента готовности принимает вид
![]() . (С.2)
. (С.2)
Если в таких идеальных условиях в резерве находится объектов (вместо одного), то эта последняя формула принимает вид
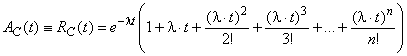 . (С.3)
. (С.3)
Следует отметить, что на практике RBD должна включать блоки, представляющие готовность и механизм чувствительности переключателя, который часто является "слабым звеном" в системах с резервированием.
Формулы (С.1), (С.2) и (С.3) могут быть использованы для составного блока С, также используют обычные формулы для обычных блоков. Тем не менее вывод этих формул является сложным, поэтому для анализа системы с резервированием, следует использовать другие процедуры, такие как марковский анализ.
С.4 RBD-управляемые марковские процессы
Как было установлено в предыдущих разделах, коэффициент готовности блоков может иметь любую форму, и, как показано на рисунке С.2, могут быть вычислены с помощью марковских процессов. Такая модель, представляющая собой смесь между RBD и марковских графов - это "RBD-управляемый марковский процесс": RBD является основой модели, а малые марковские графы обеспечивают коэффициенты готовности блоков. Это способ построения марковских процессов для больших систем, он помогает избежать комбинаторного взрыва при большом количестве состояний.
|
Рисунок C.2 - Принцип RBD-управляемых марковских процессов
Этот подход охватывает большую часть проблем, возникающих при работе с восстанавливаемыми блоками, а также большую часть случаев, когда рассматривают только постоянные интенсивности отказов и восстановлений.
На рисунке С.2 показаны коэффициенты готовности блоков, моделируемых единичными марковскими графами. Затем, после переходного периода устанавливаются асимптотические значения, и это приводит к типичной ситуации, показанной на рисунке С.3.
|
Рисунок C.3 - Типичная ситуация коэффициента готовности по RBD в случае быстрого восстановления отказов
Например, коэффициент готовности блока А, который моделируют параметры (,
), достигает асимптотического значения
![]() по истечении периода времени, равного двум или трем
по истечении периода времени, равного двум или трем ![]() (где
(где ![]() ).
).
RBD-управляемый марковский процесс также может быть реализован, когда в блоках возникают скрытые отказы, которые не обнаруживают сразу после их возникновения. В этом случае для выявления отказов и их устранения должны быть проведены периодические проверки. Это невозможно смоделировать единичными марковскими графами, как показано на рисунке С.2, вместо этого следует использовать "многоэтапные" марковские процессы.
|
Рисунок С.4 - Пример простого многоэтапного Марковского процесса
На рисунке С.4 показана простая многоэтапная марковская модель, связанная с периодическими проверками блока: каждый период времени между проверками - это этап вероятности состояний, в начале этапа рассчитывают исходя из вероятностей состояний в конце предыдущего этапа. Затем, в течение периода времени до следующей проверки коэффициент готовности блока моделируют простым марковским графом, когда отказ F является скрытым, при проведении проверки отказ обнаруживают и устраняют мгновенно. Коэффициент готовности таких периодически проверяемых блоков равен 1 сразу после проверки, а затем он уменьшается до выполнения следующей проверки, после чего он снова равен 1. Это приводит к типичным "пилообразным кривым", показанным на рисунке С.5, где все блоки проверяют через одинаковый период времени.
|
Рисунок C.5 - Типичный коэффициент готовности RBD с периодически проверяемыми блоками
Системы безопасности, реализующие периодически проверяемые компоненты, могут быть легко смоделированы таким образом. Это, в частности, типичный случай систем безопасности, описанных в МЭК 61508, МЭК 61511 и ИСО/TС 12489.
Эта комбинация отдельных марковских процессов с помощью логических комбинаций доказала свою высокую полезность как для RBD, так и для FT-подходов.
C.5 Вычисление среднего и асимптотического (стационарного) коэффициента готовности
Легко вычислить средний коэффициент готовности ![]() с помощью простого численного усреднения кривой
с помощью простого численного усреднения кривой (как показано пунктирной линией на рисунке С.1) за период времени [
].
Этот расчет справедлив в любом случае, если асимптотическое значение ![]() достигнуто, как показано на рисунке С.5; это асимптотическое значение также дает средний коэффициент готовности за время
достигнуто, как показано на рисунке С.5; это асимптотическое значение также дает средний коэффициент готовности за время , за которое коэффициенты готовности блоков достигнут асимптотических значений. Поэтому, асимптотическое значение коэффициента готовности системы также является средним коэффициентом готовности за продолжительный период времени,
![]() .
.
Если блоки очень быстро восстанавливают (![]() ), асимптотические значения достигаются очень быстро (после продолжительности времени, равной двум или трем значениям наибольшей
), асимптотические значения достигаются очень быстро (после продолжительности времени, равной двум или трем значениям наибольшей ![]() ), и этот случай является почти таким же, как и с постоянными вероятностями.
), и этот случай является почти таким же, как и с постоянными вероятностями.
Если как показано на рисунке С.5, асимптотическое значение отсутствует, то средний коэффициент готовности вычисляют по . Тем не менее, в случае повторяющихся этапов
быстро сходится. Например, для простого блока, когда восстановление не является мгновенным, устойчивое значение достигается через 2-3 периода проверки, а средний коэффициент готовности через 2-3 периода между проверками сходится к предельному значению:
![]() .
.
Модели аналогичные представленной на рисунке С.5, могут быть использованы для моделирования систем безопасности и вычисления ![]() (среднего значения вероятности отказа по запросу), требуемого стандартами функциональной безопасности МЭК 61508 и МЭК 61511 для систем безопасности, работающих в условиях редких запросов:
(среднего значения вероятности отказа по запросу), требуемого стандартами функциональной безопасности МЭК 61508 и МЭК 61511 для систем безопасности, работающих в условиях редких запросов:
![]() .
.
Если существует предельное значение, оно обычно равно ![]() , где
, где - продолжительность повторяющегося периода времени (см. 10.3.2).
C.6 Вычисление частоты
В дополнение к классическим коэффициентам готовности ![]() и вероятности безотказной работы
и вероятности безотказной работы ![]() , средняя частота отказов
, средняя частота отказов ![]() - еще один вероятностный показатель, полезный для описания свойств системы.
- еще один вероятностный показатель, полезный для описания свойств системы.
Этот параметр не существует в случае постоянных вероятностей отказа и бесполезен для невосстанавливаемых систем, однако он очень полезен при работе с восстанавливаемыми системами, которые могут отказать (и быть восстановлены) несколько раз за заданный период времени [0, ]. В этом случае, если
- количество отказов за заданный период времени, средняя частота отказов имеет вид
![]() .
.
Среднюю частоту отказов можно вычислить с помощью RBD, но математика, предполагающая вычисление показателей значимости Бирнбаума (см. D.3) не так проста, при вычислении коэффициента готовности и вероятности безотказной работы. Поэтому трудно выполнить вычисления вручную, но существуют соответствующие мощные алгоритмы, доступные для этого.
Вычисление средней частоты, выполняемое в несколько этапов.
1) Вычисляют показатели значимости Бирнбаума ![]() , соответствующих каждому блоку
, соответствующих каждому блоку . Этот показатель также называют "предельным показателем значимости" (см. приложение D).
![]() определяют на основе условных коэффициентов готовности
определяют на основе условных коэффициентов готовности ![]() и
и ![]() по следующей формуле (см. [14]):
по следующей формуле (см. [14]):
![]() . (С.4)
. (С.4)
2) Вычисляют безусловные параметры потока отказов каждого блока
. Это делают, используя интенсивность отказов
и коэффициент готовности
![]() соответствующего блока:
соответствующего блока:
![]() . (С.5)
. (С.5)
3) Вычисляют безусловную интенсивность отказов системы:
![]() . (С.6)
. (С.6)
4) Вычисляют математическое ожидание количества отказов ![]() за период [0,
за период [0, ]. Поскольку безусловный параметр потока отказов
также является частотой отказов системы в момент времени
(см. 3.31), то математическое ожидание количества отказов может быть получено простым интегрированием:
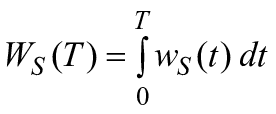 . (С.7)
. (С.7)
5) Вычисляют среднюю частоту отказов:
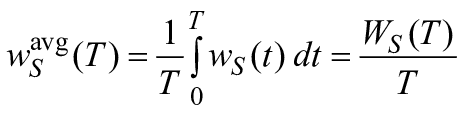 . (С.8)
. (С.8)
За исключением очень простых случаев, вычисления по формуле (С.8) могут быть выполнены вручную и только численно.
C.7 Вычисление вероятности безотказной работы
В то время как средняя частота отказов ![]() может быть вычислена в любом случае, вероятность безотказной работы системы
может быть вычислена в любом случае, вероятность безотказной работы системы может быть выведена аналитически только в очень частных случаях:
a) RBD состоит только из невосстанавливаемых блоков, и в этом случае ![]() ;
;
b) условный параметр потока отказов ![]() достигает асимптотического значения
достигает асимптотического значения .
В случае b) условный параметр потока отказов ![]() можно вывести из безусловного параметра потока отказов и коэффициента готовности системы по следующей формуле
можно вывести из безусловного параметра потока отказов и коэффициента готовности системы по следующей формуле
![]() . (С.9)
. (С.9)
![]() называют интенсивностью отказов Веселя, так как она может быть использована в качестве аппроксимации интенсивности отказов системы
называют интенсивностью отказов Веселя, так как она может быть использована в качестве аппроксимации интенсивности отказов системы ![]() при вычислении вероятности безотказной работы по классическому уравнению:
при вычислении вероятности безотказной работы по классическому уравнению:
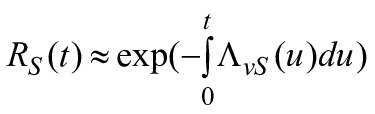 . (С.10)
. (С.10)
Конечно, это особенно полезно, когда система достигает стационарного состояния, поскольку в этом случае ![]() достигает постоянного асимптотического значения
достигает постоянного асимптотического значения ![]() . Это типичный случай RBD, аналогичной приведенной на рисунке С.3, где коэффициент готовности
. Это типичный случай RBD, аналогичной приведенной на рисунке С.3, где коэффициент готовности , безусловный параметр потока отказов
и условный параметр потока отказов
![]() достигают асимптотических значений
достигают асимптотических значений ,
,
.
В этом случае интенсивность отказов системы можно аппроксимировать
![]() , вероятность безотказной работы системы можно записать следующим образом:
, вероятность безотказной работы системы можно записать следующим образом:
![]() . (С.11)
. (С.11)
Точность аппроксимации в соответствии с формулой (С.11), очень высока, когда переходный процесс завершен. Этот переходный период является очень коротким, если отказы блоков RBD быстро обнаруживают и ремонтируют, то формулу (C.11) можно использовать по истечении периода времени, равного двум или трем значениям наибольшей MTTR блоков.
Все эти вычисления нелегко выполнять вручную, однако существуют быстрые алгоритмы на основе BDD, способные обрабатывать большие RBD для вычисления вероятности безотказной работы.
Для случаев, отличных от указанных в перечислениях a) и b), следует использовать другие методы, такие как метод моделирования Монте-Карло (например, с использованием DRBD, см. 12.2 и приложение Е), методы сетей Маркова или Петри.
Приложение D
(справочное)
Показатели значимости
D.1 Общие положения
При анализе системы полезно ранжировать компоненты в соответствии с их влиянием на вероятность успеха (или отказа) исследуемой системы. Это можно сделать с помощью одного или нескольких показателей значимости (см. [12], [13], [14], [29] и [30]).
В D.2-D.9 описаны основные показатели значимости и даны объяснения по их вычислению, если разработаны когерентные RBD. Для простоты они разработаны для случая постоянной вероятности, но когда вероятности зависят от времени (например, в случае восстанавливаемой системы), формулы аналогичны формулам для данного значения времени .
D.2 Показатель значимости Весела-Фусселла
Показатель значимости Весела-Фусселла ![]() является одним из наиболее популярных показателей значимости. Он основан на минимальных наборах обрывов системы. Он является мерой вероятности того, что при отказе системы S отказ блока
является одним из наиболее популярных показателей значимости. Он основан на минимальных наборах обрывов системы. Он является мерой вероятности того, что при отказе системы S отказ блока участвует по крайней мере в одном минимальном наборе обрывов, вызвавших отказ S. Этот показатель значимости учитывает как вероятность отказа В, так и порядок минимального набора обрывов, к которому принадлежит этот блок. Это довольно точный показатель значимости при оценке влияния компонента на вероятность отказа системы.
Рассмотрим ![]() минимальный набор обрывов, содержащий
минимальный набор обрывов, содержащий (т.е. отказ компонента
). Показатель значимости Весела-Фусселла задан формулой (D.1):
 . (D.1)
. (D.1)
Формула (D.1) не очень проста для вычислений и, если вероятность отказа системы мала (![]() ), часто используют следующее приближение:
), часто используют следующее приближение:
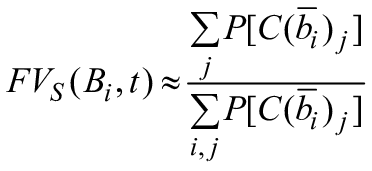 . (D.2)
. (D.2)
Формула (D.2) очень проста для расчетов вручную, когда количество минимальных наборов обрывов не слишком велико: это сумма вероятностей минимальных наборов обрывов, содержащих отказ , деленная на сумму всех минимальных наборов обрывов.
D.3 Показатель значимости Бирнбаума или предельный показатель значимости
Предельный показатель значимости ![]() называют также показателем значимости Бирнбаума. Он обеспечивает основу оценки эквивалентной интенсивности отказов (следовательно, вероятности безотказной работы) восстанавливаемой системы (см. пункт 10.3.1.4). Показатель представляет собой частную производную вероятности успеха (или отказа) системы по отношению вероятности успеха (или отказа) рассматриваемого блока системы
называют также показателем значимости Бирнбаума. Он обеспечивает основу оценки эквивалентной интенсивности отказов (следовательно, вероятности безотказной работы) восстанавливаемой системы (см. пункт 10.3.1.4). Показатель представляет собой частную производную вероятности успеха (или отказа) системы по отношению вероятности успеха (или отказа) рассматриваемого блока системы . Показатель значимости Бирнбаума обычно задан формулой (D.3):
![]() . (D.3)
. (D.3)
Формула симметрична в отношении успеха и отказа. Ее можно интерпретировать как вероятность того, что система находится в критическом состоянии (работает или отказала) из-за состояния , т.е. если S работает, отказ
приводит к отказу S, а если S отказала, то восстановление
вызывает восстановление S.
Формула (D.3) эквивалентна формуле (D.4):
![]() . (D.4)
. (D.4)
Таким образом, показатель значимости можно вычислить с помощью BDD в соответствии с 11.6 для условных вероятностей и
.
Следует отметить, что показатель значимости Бирнбаума не зависит от вероятности успеха (или отказа) компонента .
D.4 Показатель значимости Ламберта
Показатель критической значимости ![]() также называют показателем значимости Ламберта. Это нормализованный показатель значимости Бирнбаума. Он задан формулой (D.5):
также называют показателем значимости Ламберта. Это нормализованный показатель значимости Бирнбаума. Он задан формулой (D.5):
![]() . (D.5)
. (D.5)
Этот показатель значимости легко вычислить, если известен ![]() .
.
D.5 Диагностический показатель значимости
Диагностический показатель значимости ![]() представляет собой условную вероятность того, что
представляет собой условную вероятность того, что отказал при условии, что S - отказала. Этот показатель позволяет определить, какие компоненты следует рассмотреть в приоритетном порядке, если S отказывает, чтобы восстановить ее как можно скорее.
Показатель задан формулой (D.6):
![]() . (D.6)
. (D.6)
Следующая эквивалентная формула (D.7) более удобна для вычислений
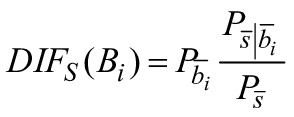 . (D.7)
. (D.7)
Этот показатель значимости связан с ![]() (см. D.6) следующим образом:
(см. D.6) следующим образом:
![]() .
.
Примечание 1 - Если значение ![]() не велико, вероятность того, что
не велико, вероятность того, что отказал, когда S отказала, является низкой. Если значение
![]() является высоким, вероятность того, что
является высоким, вероятность того, что отказал, когда S отказала также высока. Поэтому наиболее полезно проверить
с помощью промежуточных значений
![]() для диагностики отказов
для диагностики отказов .
Примечание 2 - Восстановление отказавшего компонента, идентифицированного с помощью DIF, не обязательно восстанавливает систему S.
D.6 Стоимость риска
Стоимость риска ![]() - это условная вероятность того, что S отказала при условии, что
- это условная вероятность того, что S отказала при условии, что отказал, нормализованная по вероятности отказа S. Это позволяет измерять повышение вероятности отказа S, когда
в действительности отказывает.
![]() задается формулой (D.8):
задается формулой (D.8):
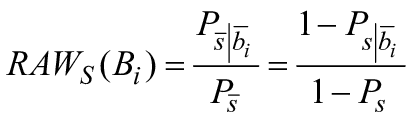 . (D.8)
. (D.8)
D.7 Стоимость снижения риска
Стоимость снижения риска ![]() - это условная вероятность того, что S отказывает при условии, что
- это условная вероятность того, что S отказывает при условии, что не откажет, нормализованная по вероятности отказа S. Этот показатель позволяет измерять снижение вероятности отказа, когда
в действительности работает.
Она задается следующей формулой (D.9):
![]() . (D.9)
. (D.9)
D.8 Дифференциальная мера значимости
Дифференциальная мера значимости ![]() - мера локальной чувствительности влияния
- мера локальной чувствительности влияния на
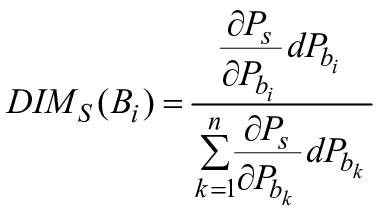 . (D.10)
. (D.10)
В формуле (D.10) ![]() заменяет
заменяет , индуцированную небольшим изменением (
) в вероятности блока
.
Дифференциальная мера значимости имеет два важных свойства:
- это аддитивная мера: ![]()
- сумма дифференциальной меры значимости всех блоков в RBD равна единице:
![]() .
.
Дифференциальная мера значимости ![]() связана с другими показателями значимости в специальных случаях:
связана с другими показателями значимости в специальных случаях:
a) равномерное изменение (критерий Н1): ![]() для
для ,
=1, 2, ...,
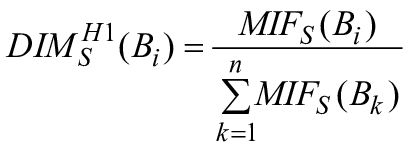
b) пропорциональные относительные изменения (критерий Н2):
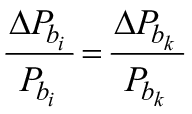 ,
, ![]() для
для ,
=1, 2, ..., n,
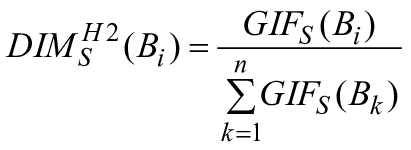 .
.
Предельный показатель значимости рассмотрен в D.3, а показатель критической значимости в D.4.
D.9 Замечания о показателях значимости
Существует много показателей значимости, разработанных для конкретных целей. Например:
![]() .
.
Среди них только показатель значимости Весела-Фусселла может быть вычислен вручную (когда ![]() и количество минимальных наборов обрывов не слишком велико). Вычисление других показателей предполагает использование условных вероятностей, которые трудно вычислить вручную, но можно вычислить, например, с помощью метода BDD, описанного в 11.6.
и количество минимальных наборов обрывов не слишком велико). Вычисление других показателей предполагает использование условных вероятностей, которые трудно вычислить вручную, но можно вычислить, например, с помощью метода BDD, описанного в 11.6.
Для работы с некогерентными RBD были разработаны и другие показатели значимости (см. 12.2). Они должны быть использованы в этом случае, поскольку описанные выше показатели значимости в данном случае не действуют, их применение может привести к противоречивым результатам.
Приложение Е
(справочное)
RBD-управляемые сети Петри
E.1 Общие положения
Одним из эффективных способов работы с динамическими RBD является совмещение подходов RBD и сети Петри. Это позволяет строить большие PN и использовать моделирование Монте-Карло для расчета исследуемых вероятностных величин.
Простейший метод состоит в моделировании блоков и внешних элементов отдельными суб-PN, которые взаимодействуют посредством использования предикатов и утверждений. Такая модель представляет собой RBD-управляемую Сеть Петри (см. справку [18]), которая
- сохраняет логическую структуру RBD для логических вычислений состояния системы по состоянию блоков;
- использует преимущества сети Петри для моделирования взаимодействий между блоками и/или внешними объектами.
E.2 Пример суб-PN, который используют в моделях RBD-управляемых PN
|
Рисунок E.1 - Пример моделирования суб-PN DRBD блока
На рисунке Е.1 приведен пример суб-PN, разработанной для использования в DRBD. Блок характеризуют:
- три состояния: работоспособное (U), неработоспособное (D) и восстановления (ремонта) (R);
- четыре перехода: (независимый) отказ, отказ по общей причине, начало ремонта (восстановления) и окончание ремонта восстановления;
- несколько предикатов и утверждений:
- два утверждения, !!а=истинно и !!a=ложно для обновления состояния блока (работоспособное или неработоспособное). Каждое состояние блока моделируют таким образом, чтобы оценить состояние системы в целом на основе логической структуры RBD,
- один предикат, ??ccf=истинно, который запускает отказ блока при возникновении CCF. Он использован для моделирования взаимодействий с внешним объектом, моделирующим CCF,
- один предикат, ??r>0, позволяющий начать восстановление, когда доступна по меньшей мере одна ремонтная бригада. Его используют для моделирования взаимодействий между блоками, которые восстанавливает одна и та же ремонтная бригада,
- одно утверждение, !!r=r-1 для уменьшения количества доступных ремонтных бригад на одну, когда начат ремонт. Это использовано для моделирования взаимодействий между блоками, которые восстанавливает одна и та же ремонтная бригада,
- одно утверждение, !!r=r+1, чтобы увеличить количество доступных ремонтных бригад на одну, когда восстановление завершено. Его используют для моделирования взаимодействий между блоками, которые восстанавливает одна и та же ремонтная бригада.
В правой части рисунка Е.1 предложено представление блока, связанного с этой суб-PN.
|
Рисунок E.2 - Пример суб-PN, моделирующей отказ по общей причине
На рисунке E.2 приведен пример суб-PN, разработанной для использования в качестве внешнего объекта DRBD. Пример моделирует отказ по общей причине, характеризующийся:
- двумя состояниями: U (работоспособное: не произошел CCF), D (неработоспособное: произошел CCF);
- двумя переходами: возникновение CCF, устранение CCF;
- несколькими предикатами и утверждениями:
- двумя утверждениями, !!ccf=true и !!ccf=false для обновления состояния CCF (не произошел или произошел). Эти утверждения используют для сбоя блоков, связанных с данными CCF,
- несколькими предикатами, ??а=истинно, ??b=истинно и т.д., которые допускают сброс CCF только после того, как все блоки, связанные с CCF, восстановлены.
В правой части рисунка Е.2 предложено представление внешнего объекта, связанного с этой суб-PN.
Суб-PN могут быть использованы для построения DRBD, как это показано на рисунке E.3.
|
Рисунок E.3 - Пример DRBD на основе RBD-управляемой PN
Эта DRBD моделирует отказ по общей причине блоков A и B и другой отказ по общей причине блоков С и D.
Ограниченное количество ремонтных бригад для восстановления четырех блоков. Количество ремонтных бригад задано начальными условиями: r=1 при моделировании одной ремонтной бригады, r=2 - при моделировании двух ремонтных бригад и т.д., r=4 эквивалентно классическому предположению, что ремонтных бригад столько же, сколько восстанавливаемых блоков.
E.3 Оценка состояния DRBD
Состояние системы задано комбинациями состояний блоков (a, b, c и d) точно так же, как для обычной RBD, используя глобальные утверждения, представленные на рисунке Е.4:
- ![]() для последовательных структур: выход блока А является работоспособным, его вход работоспособен и, если блок находится в работоспособном состоянии;
для последовательных структур: выход блока А является работоспособным, его вход работоспособен и, если блок находится в работоспособном состоянии;
- ![]() для параллельных структур: выход является работоспособным, если хотя бы один из входов работоспособен.
для параллельных структур: выход является работоспособным, если хотя бы один из входов работоспособен.
|
Рисунок E.4 - Логическое вычисление по классической структуре RBD
На рисунке 5 показано, что для вентиля 2/3 также может быть составлена простая логическая формула. Она может быть легко распространена на любой вентиль вида n/m.
|
Рисунок E.5 - Пример логических вычислений для вентиля n/m
Для вентиля PAND не существует логической формулы, но взамен можно использовать простую суб-PN, такую как представленная на рисунке Е.6. Эта PN нарисована для двух входов, но может быть легко переделана на n входов. Она эквивалентна конечному автомату, представленному на рисунке 50.
|
Рисунок E.6 - Пример суб-PN, моделирующей вентиль PAND с двумя входами
Особенности этой PN состоят в следующем:
1) вначале выход находится в работоспособном состоянии (O=1), и место Pl1 отмечено знаком 1;
2) если ложно (
=0), когда
истинно (
=1), то переход Tr1 запрещен;
3) если становится ложным (
=0), когда
истинно (
=1), это означает, что
произошло раньше
и затем немедленно срабатывает переход Tr1. Знак удаляют из Pl1 и один знак добавляют в Pl2. Это запрещает Tr1 (благодаря запрещающей стрелке в пунктирной линии) и подтверждает Tr2 и Tr4;
4) если истинно (
=1) до того, как
станет ложным, то Tr4 срабатывает, и PN возвращается в исходное состояние;
5) если становится ложным (
=0), в то время как
все еще ложно (
=0), переход Tr2 немедленно срабатывает и выход становится ложным (O=0);
6) если или
снова становятся истинными (
=1 или
=1), то срабатывает Tr3, и выход становится опять истинным (O=1);
7) если Tr3 был удален, потому что =1, то PN возвращается к этапу 2, где Tr1 запрещен;
8) если Tr3 был удален, потому что =1, то PN возвращается к этапу 3, а Tr1 срабатывает.
При этом выход sub-PN становится ложным (O=0) только в том случае, если и
ложны (
=0,
=0) в таком порядке.
Та же суб-PN может быть использована для моделирования конечного автомата, представленного на рисунке 52 для вентиля SEQ, но его недостаточно для моделирования динамического взаимодействия между и
не может перейти в неработоспособное состояние до того, как
перейдет в неработоспособное состояние. Это может быть достигнуто, например, путем моделирования блоков С и D на рисунке 51 с помощью суб-PN, аналогичных представленной на рисунке. E.7 для блока C.
|
Рисунок Е.7 - Пример запрета на отказ блока
Эта суб-PN является производной от представленной на рисунке Е.1, где переходы отказа блока (независимые отказы и отказы по общей причине) запрещают до тех пор, пока не перейдет в исходное состояние (
=0).
E.4 Вычисление коэффициента готовности, вероятности безотказной работы, частоты и MTTF
Когда модель построена, она может быть использована для вероятностных вычислений, и это может быть выполнено за счет моделирования Монте-Карло. Суб-PN, представленная на рисунке E.8, моделирует выход DRBD и может быть использована для получения всех необходимых вероятностных результатов:
- маркировка места U в момент времени t дает коэффициент готовности системы ;
- маркировка места D в момент времени t дает коэффициент неготовности системы ![]() ;
;
- средняя маркировка места U на [0, T] дает средний коэффициент готовности системы A(0, T) на [0, T];
- средняя маркировка места D на [0, T] дает средний коэффициент неготовности системы U(0, T) на [0, T];
- частота срабатывания перехода "первый отказ" дает вероятность безотказной работы системы за [0, t];
- частота срабатывания перехода "отказ" дает среднюю частоту отказов системы (0, t);
- средняя маркировка места М дает среднее время до возникновения первого отказа. Если это время достаточно велико, чтобы получить хотя бы один отказ за симуляцию, тогда это дает MTTF системы, смоделированной DRBD;
- и т.д.
|
Рисунок E.8 - Суб-PN для вычисления коэффициента готовности, вероятности безотказной работы и частоты
Приложение F
(справочное)
Числовые примеры и кривые
F.1 Общие положения
В данном приложении приведены некоторые численные примеры типовой RBD и установлены соответствующие коэффициент готовности (см. 3.21), вероятность безотказной работы (см. 3.26), условный параметр потока отказов (интенсивность отказов Весела) (см. 3.30) и безусловный параметр потока отказов (частота отказов) (см. 3.31). Приведены кривые, показывающие как эти параметры изменяются во времени.
Аналитические расчеты выполнены с использованием подхода BDD для получения результатов без аппроксимаций.
В пункте F.5 для вычисления коэффициента готовности динамических RBD, включающих несколько функциональных зависимостей, использован подход моделирования Монте-Карло.
F.2 Типовая последовательная структура RBD
F.2.1 Невосстанавливаемые блоки
На рисунке F.1 представлена типовая последовательная RBD, состоящая из трех невосстанавливаемых блоков. В этом случае вероятность безотказной работы и коэффициент готовности блоков равны, то же для системы в целом.
|
Рисунок F.1 - Коэффициент готовности вероятности безотказной работы типовой невосстанавливаемой последовательной структуры
На левой стороне рисунка представлены вероятность безотказной работы и коэффициент готовности блоков с постоянной интенсивностью отказов (экспоненциальный закон):
- блок :
![]() ч
ч;
- блок :
![]() ч
ч;
- блок :
![]() ч
ч.
На правой стороне рисунка представлены вероятность безотказной работы и коэффициент готовности системы в целом.
На рисунке F.2 показаны интенсивность отказов и частота отказов
невосстанавливаемого объекта с последовательной структурой.
В этом случае интенсивность отказов (Веселя) ![]() (условный параметр потока отказов) и интенсивность отказов
(условный параметр потока отказов) и интенсивность отказов равны и постоянны. Как и ожидалось
![]() константа.
константа.
|
Рисунок F.2 - Интенсивность отказов и частота отказов, соответствующие рисунку F.1
Таким образом, система, состоящая из трех блоков, эквивалентна одному блоку С с интенсивностью отказов ![]() .
.
|
Рисунок F.3 - Эквивалентность невосстанавливаемой последовательной структуры одному блоку
Частота отказов (безусловный параметр потока отказов) уменьшается с увеличением времени t и стремится к 0, когда t стремится в бесконечность. Это связано с тем, что являясь невосстанавливаемой, система может отказать только один раз.
F.2.2 Восстанавливаемые блоки
На рисунке F.4 представлена типовая последовательная RBD, состоящая из трех восстанавливаемых блоков. В этом случае коэффициент готовности и вероятность безотказной работы блоков различны и для блоков, и для системы в целом.
|
Рисунок F.4 - Коэффициент готовности/вероятность безотказной работы типовой восстанавливаемой последовательной структуры
На левой стороне рисунка показан коэффициент готовности блоков с постоянными интенсивностями отказов и восстановлений:
- блок :
![]() ч
ч,
![]() ч
ч;
- блок :
![]() ч
ч,
![]() ч
ч;
- блок :
![]() ч
ч,
![]() ч
ч.
Коэффициент готовности системы представлен в середине рисунка, а вероятность безотказной работы - на правой стороне рисунка.
Изменение показателей сильно отличается по сравнению с невосстанавливаемым случаем: как показанные на рисунке F.4 коэффициенты готовности блоков (левая сторона), а также коэффициенты готовности системы в целом (середина рисунка) быстро достигают асимптотических значений.
|
Рисунок F.5 - Интенсивность отказов и частота отказов, соответствующие рисунку F.4
На рисунке F.5 показаны интенсивность отказов и частота отказов
восстанавливаемого объекта с последовательной структурой. График
такой же, как и в случае без восстановления, потому что каждый отказ блока вызывает отказ системы в целом и который, с точки зрения вероятности безотказной работы не может быть отремонтирован (см. 10.3.3).
F.3 Типовая параллельная RBD
F.3.1 Невосстанавливаемые блоки
На рисунке F.6 представлена типовая RBD с параллельной структурой, состоящая из трех невосстанавливаемых блоков. В этом случае вероятность безотказной работы и коэффициент готовности блоков равны, то же справедливо для системы в целом.
|
Рисунок F.6 - Коэффициент готовности и вероятность безотказной работы типовой невосстанавливаемой параллельной структуры
На левой стороне рисунка показаны коэффициент готовности и вероятность безотказной работы блоков с постоянной интенсивностью отказов (экспоненциальный закон).
- блок :
![]() ч
ч;
- блок :
![]() ч
ч;
- блок :
![]() ч
ч.
На правой стороне рисунка показаны коэффициент готовности и вероятность безотказной работы системы в целом.
На рисунке F.7 показаны интенсивность отказов и частота отказов
невосстанавливаемой параллельной структуры. Поскольку коэффициент готовности и вероятность безотказной работы системы совпадают, интенсивность отказов и интенсивность отказов Весселя тоже совпадают:
![]() .
.
|
Рисунок F.7 - Интенсивность отказов и частота отказов, соответствующие рисунку F.6
Графики сильно отличаются по сравнению с графиками для невосстанавливаемой последовательной структуры:
- для требуется очень продолжительное время, чтобы достичь асимптотического значения, равного значению более низкой интенсивности отказов трех блоков. Это асимптотическое значение достигается, когда блоки с более высокой интенсивностью отказов уже успели отказать. Асимптотическое значение достигается очень медленно и не может быть использовано в качестве аппроксимации интенсивности отказов;
- параметр потока отказов проходит через максимальное значение, прежде чем уменьшается до нуля.
F.3.2 Восстанавливаемые блоки
На рисунке F.8 представлена типовая RBD с параллельной структурой, состоящей из трех восстанавливаемых блоков. В этом случае вероятность безотказной работы и коэффициент готовности блоков различны, то же справедливо для системы в целом.
|
Рисунок F.8 - Коэффициент готовности и вероятность безотказной работы типовой восстанавливаемой параллельной структуры
На левой стороне рисунка приведены коэффициенты готовности блоков с постоянными интенсивностями отказов и восстановлений:
- блок :
![]() ч
ч,
![]() ч
ч;
- блок :
![]() ч
ч,
![]() ч
ч;
- блок :
![]() ч
ч,
![]() ч
ч.
Коэффициент готовности системы приведен в середине рисунка, а вероятность безотказной работы - на правой стороне рисунка.
Графики сильно отличаются по сравнению с графиками для невосстанавливаемых блоков, как показано на рисунке F.8, коэффициент готовности блоков (левая сторона), а также коэффициент готовности системы в целом (середина рисунка) быстро достигают асимптотических значений.
На рисунке F.9 приведены интенсивность отказов Веселя (условный параметр потока отказов) ![]() и частота отказов
и частота отказов восстанавливаемой параллельной структуры.
|
Рисунок F.9 - Интенсивность отказов Веселя и частота отказов, соответствующие рисунку F.8
Графики восстанавливаемого и невосстанавливаемого случаев параллельной структуры сильно отличаются:
- ![]() очень быстро достигает асимптотического значения. В этом случае она становится постоянной после трех или четырех MTTR (от 30 ч до 40 ч), это асимптотическое значение может быть использовано в качестве постоянной частоты отказов при расчете вероятности безотказной работы системы;
очень быстро достигает асимптотического значения. В этом случае она становится постоянной после трех или четырех MTTR (от 30 ч до 40 ч), это асимптотическое значение может быть использовано в качестве постоянной частоты отказов при расчете вероятности безотказной работы системы;
- параметр потока отказов также очень быстро достигает асимптотического значения, которое может быть использовано для расчета средней частоты отказов системы.
F.4 RBD сложной структуры
F.4.1 RBD с непоследовательно-параллельной структурой
На рисунке F.10 приведена RBD с общим блоком, введенным в 7.5.2. Это структура не может быть сведена к простым последовательным или параллельным структурам.
|
Рисунок F.10 - Пример 1 из 7.5.2
На левой стороне рисунка и в середине рисунка приведены коэффициент готовности блоков с постоянными интенсивностями отказов и восстановлений
- блоки и
:
![]() ч
ч,
![]() ч
ч;
- блоки и
:
![]() ч
ч,
![]() ч
ч;
- блок A: ![]() ч
ч,
![]() ч
ч,
![]() .
.
Блоки являются обычными восстанавливаемыми блоками, но интенсивность восстановления блока A меньше, чем у других и этот блок также имеет вероятность работоспособного состояния в момент времени t=0, равную 0,5. В результате, как показано на рисунке F.10, график коэффициента готовности этого блока отличается от графиков коэффициентов готовности других блоков.
Графики коэффициента готовности и вероятности безотказной работы системы приведены на правой стороне рисунка. Под влиянием блока A коэффициент готовности снижается до минимума, прежде чем достичь асимптотического значения. Этот минимум соответствует МТТR блока А.
График вероятности безотказной работы обычный.
|
Рисунок F.11 - Интенсивность отказов и частота отказов, соответствующие рисунку F.10
На рисунке 11 показана интенсивность отказов Веселя (условный параметр потока отказов) ![]() и частота отказов
и частота отказов системы, представленной на рисунке F.10. Форма графиков этих параметров связана с блоком A:
![]() , также как
, также как достигают максимального значения до того, как достигают асимптотического значения.
F.4.2 Сходимость к асимптотическим значениям в зависимости от MTTR
Коэффициент готовности и эквивалентная интенсивность отказов для RBD, показанной на рисунке F.12, рассчитаны с четырьмя различными постоянными интенсивностями восстановления для того, чтобы показать влияние МТТR на скорость сходимости к асимптотическим значениям.
Блоки с RBD, представленной на рисунке F.12, имеют постоянные интенсивности отказов и восстановлений. Следовательно, к ним применим марковский подход, и поэтому коэффициент готовности системы и условный показатель потока отказов (интенсивность отказов Веселя) сходятся к асимптотическому значению.
|
Рисунок F.12 - Влияние MTTR на скорость сходимости
На рисунке F.12 четко видно, что скорость сходимости увеличивается при уменьшении MTTR. Затем, если систему быстро восстанавливают, она ведет себя так, как если бы она имела
- постоянные вероятности успеха или отказа при вычислении коэффициентов готовности и неготовности;
- постоянную интенсивность отказов при вычислении вероятности безотказной работы.
F.4.3 Система с периодически проверяемыми компонентами
На рисунке F.13 показана та же RBD, что и выше, но с периодически проверяемыми компонентами.
|
Рисунок F.13 - Система с периодически проверяемыми блоками
На левой стороне и в середине рисунка приведены коэффициенты готовности периодически проверяемых блоков, они смоделированы для следующих интервалов между проверками и постоянных интенсивностей отказов и восстановлений:
- блоки и
:
![]() ч
ч,
![]() ч
ч,
![]() ч;
ч;
- блоки и
:
![]() ч
ч,
![]() ч
ч,
![]() ч;
ч;
- блок А: ![]() ч
ч,
![]() ч
ч,
![]() ч.
ч.
Коэффициент готовности блоков - это кривые в форме зубьев пилы, и то же самое для коэффициента готовности системы в правой стороне рисунка.
Интервалы между проверками формируют особый вид кривой вероятности безотказной работы системы, приведенной в правой стороне рисунка F.13. Это все еще не возрастающая функция.
Такие RBD обычно встречаются при работе с функциональной безопасностью инструментальных систем безопасности, в которых некоторые опасные отказы обнаруживают при периодических проверках. Средний коэффициент неготовности этих систем обозначают ![]() (см. 3.24 и МЭК 61508 [5]).
(см. 3.24 и МЭК 61508 [5]).
На рисунке F.14 показаны интенсивности отказов Весселя и частота отказов системы с периодическими проверками компонентов.
|
Рисунок F.14 - Интенсивность отказов и частота отказов, соответствующие рисунку F.13
F.5 Пример динамической RBD
F.5.1 Сопоставление аналитических результатов и результатов моделирования Монте-Карло
На рисунке F.15 показана небольшая параллельно-последовательная RBD, состоящая из четырех аналогичных блоков с одинаковыми интенсивностями отказов и восстановлений: ![]() ч
ч,
![]() ч
ч.
|
Рисунок F.15 - Аналитические результаты и результаты моделирования Монте-Карло
Результаты, полученные с помощью классических аналитических расчетов на основе подхода BDD показаны в левой части рисунка F.15, а результаты, полученные с помощью моделирования методом Монте-Карло, показаны в правой стороне рисунка.
Результаты Монте-Карло были получены приблизительно за 10 c на обычном портативном компьютере, было смоделировано 50000 вариантов. Конечно, аналитическая кривая более гладкая, чем кривая, полученная методом Монте-Карло, но форма кривых одна и та же, и обе кривые обеспечивают одинаковое значение среднего коэффициента готовности 0,9739 за 1000 ч и сходимость к одному и тому же асимптотическому значению 0,97.
F.5.2 Пример динамической RBD
Несколько динамических зависимостей добавлено к предыдущей RBD, представленной в F.5.1, чтобы показать, какое влияние они могут оказать на результаты:
- отказы по общей причине на B1 и B3, и отказы по общей причине на B2 и B4
![]() ;
;
- единственная ремонтная бригада;
- единственная ремонтная бригада, и отказы по общей причине.
|
Рисунок F.16 - Влияние CCF и ограниченного количества ремонтных бригад
На рисунке F.16 четко показано, что воздействие не является незначительным и более подробно проанализировано в таблице F.1.
Таблица F.1 - Влияние функциональных зависимостей
Структура | Коэффициент готовности системы | Коэффициент неготовности системы | ||
|
|
| ||
Отсутствие функциональных зависимостей | 9,74 | 9,71 | 2,6 | 2,9 |
Наличие ССF | 9,63 | 9,59 | 3,7 | 4,1 |
Единственная ремонтная бригада | 9,47 | 9,32 | 5,4 | 6,8 |
Наличие ССF и единственной ремонтной бригады | 9,26 | 9,06 | 7,4 | 9,4 |
Эффект более заметен, когда речь идет не о коэффициенте готовности, а о коэффициенте неготовности. Например, для асимптотических коэффициентов неготовности интенсивности равны:
- для отказа по общей причине: 140%;
- для единственной ремонтной бригады: 234%;
- для обеих: 323%.
Таким образом, предположение о наличии такого количества ремонтных бригад, сколько блоков в системе оказывает влияние и не обеспечивает получение заниженных (гарантированных) оценок. Воздействие возрастает:
а) при увеличении интенсивностей отказов блоков (вероятность наличия нескольких отказов одновременно увеличивается);
b) при увеличении MTTR (вероятность отказа одного блока при ремонте другого блока возрастает);
c) при повышении порядка преобладающих минимальных наборов обрывов.
Если вероятность безотказной работы блоков очень высока, а MTTR мала, ситуации а) и b) имеют очень ограниченное влияние. Основная проблема связана с ситуацией с).
|
Рисунок F.17 - Графы Маркова, моделирующие влияние количества ремонтных бригад
Пусть RBD состоит из двух одинаковых блоков В1 и В2 с одинаковыми интенсивностями отказов и восстановлений (,
). На рисунке F.17 показаны графы Маркова, построенные при наличии двух ремонтных бригад (верхний) и одной ремонтной бригады (нижний). Эти графы Маркова имеют три состояния:
- 2B: 2 блока находятся в работоспособном состоянии;
- 1B: 1 блок находится в работоспособном состоянии и 1 блок - в неработоспособном состоянии;
- 0B: 2 блока находятся в неработоспособном состоянии (0 блоков в работоспособном состоянии).
Система отказывает при отказе B1 и B2 (состояние 0B). Продолжительность пребывания системы в этом состоянии:
- 1=MTTR при наличии только одной ремонтной бригады;
- 1/2=2
MTTR при наличии нескольких ремонтных бригад.
При наличии единственной ремонтной бригады, среднее время восстановления системы в два раза больше среднего времени восстановления системы, при наличии нескольких ремонтных бригад. Поэтому наличие единственной ремонтной бригады, подход обеспечивающий гарантированные оценки, должен заключаться в использовании MTTR вдвое большего, чем при наличии нескольких ремонтных бригад. Это показано на рисунке F.18, где граф Маркова справа (две ремонтные бригады с интенсивностью восстановления ![]() ) является аппроксимацией графа Маркова слева (единственная ремонтная бригада с интенсивностью ремонта
) является аппроксимацией графа Маркова слева (единственная ремонтная бригада с интенсивностью ремонта ). Таким образом, MTTR каждого блока с правой стороны умножена на два.
|
Рисунок F.18 - Аппроксимация для двух резервированных блоков
Такой подход является гарантированным (дает заниженные оценки коэффициента готовности), поскольку среднее время пребывания в состоянии 1B умножено на два. Тем не менее, даже в этом простом случае подход дает слишком заниженные оценки. Кроме того данный подход трудно применять для более крупных и более сложных RBD, для них лучше использовать, например RBD-управляемую PN (см. приложение Е) и моделирование Монте-Карло, которые теперь могут быть выполнены на простых портативных компьютерах.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
IEC 60050-192:2015 | NEQ | ГОСТ Р 27.101-2021 "Надежность в технике. Надежность выполнения задания и управление непрерывностью деятельности" |
IEC 61703:2016 | MOD | ГОСТ Р 27.010-2019 (МЭК 61703:2016) "Надежность в технике. Математические выражения для показателей безотказности, готовности, ремонтопригодности" |
Примечание - В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: | ||
Библиография
[1] | IEC 61025, Fault tree analysis (FTA) |
[2] | IEC 61165, Application of Markov techniques |
[3] | IEC 62551, Analysis techniques for dependability - Petri net techniques |
[4] | IEC 60812, Analysis techniques for system reliability - Procedure for failure mode and effects analysis (FMEA) |
[5] | IEC 61508:2010 (all parts), Functional safety of electrical/electronic/programmable electronic safety-related systems |
[6] | IEC 61511:2016 (all parts), Functional safety - Safety instrumented systems for the process industry sector |
[7] | ISO/TR 12489, Petroleum, petrochemical and natural gas industries - Reliability modelling and calculation of safety systems |
| Методы RBD (общие) |
[8] | Karnaugh, М. The Map Method for Synthesis of Combinational Logic Circuits. Trans. AIEE. pt I, Vol. 72, No. 9, pp.593-598, 1953 |
[9] | Me Cluskey Jr., E. Minimization of Boolean functions. Bell System Technical Journal, Vol. 35, Issue 6, pp.1417-1444, 1956 |
[10] | Veitch, E.W. A chart method for simplifying truth functions In Proceedings of the 1952 ACM national meeting, Pittsburgh, pp.127-133). ACM, 1952 |
[11] | Umezawa, Т. A method of two-level simplification of Boolean functions. Nagoya Mathematical Journal, Vol. 29, pp.201-210. 1967 |
[12] | Dutuit, Y., Rauzy, A. Efficient algorithms to assess component and gate importance in fault tree analysis, Reliability Engineering and System Safety, Vol. 72, No. 1, pp.213-222, 2001 |
[13] | Borgonovo, E. and Apostolakis, G.E. A New Importance Measure for Risk Informed Decision-Making, Reliability Engineering and System Safety, Vol. 72, No 2, pp.193-212, 2001 |
[14] | Borgonovo, E. Differential, Criticality and Birnbaum Importance Measures and Application to Basic Events, Groups and SSCs in Event Trees and Binary Decision Diagrams, Reliability Engineering and System Safety, Vol. 92, No. 10, pp.1458-1467, 2007 |
[15] | Distefano, S. System Dependability and performances: Techniques, Methodologies and Tools. Thesis of doctor in philosophy, University of Messina, Italy, 2005 |
[16] | Bobbio, A., Codetta, D. Parametric Fault trees with dynamic gates and repair boxes, RAMS 2004, pp.459-465, 2004 |
[17] | Simeu-Abazi, Z. et al. A methodology of alarm filtering using dynamic fault tree, Reliability Engineering and System Safety, Vol. 96, No. 2, pp.257-266, 2011 |
[18] | Signoret, J.-P. et al. Make your Petri nets understandable: Reliability block diagrams driven Petri nets. Reliability Engineering and System Safety, Vol. 113, pp.61-75, 2013 |
[19] | Bennetts, R.G. Analysis of Reliability Block Diagrams by Boolean Techniques, IEEE Transactions on reliability, Vol. 31, No. 2, pp.159-166, 1982 |
[20] | Barlow R.E., Proschan F. Statistical Theory of Reliability and Life Testing Probabilistic Models, New York, Holt, Rinehart and Winston, 1975 |
[21] | Billinton, R., Allan R.N. Reliability Evaluation of Engineering Systems. Concepts and Techniques. Second Edition, Springer, 1992 |
[22] | Birolini, A. Quality and Reliability of Technical Systems. Theory - Practice - Management. Berlin, Springer Verlag, 1997 |
[23] | Gaede, K.W. Zuverlassigkeit, Mathematische Modelle. Miinchen, Carl Hanser Verlag, 1977 |
[24] | Rausand, M. and Hoyland, A. System Reliability Theory - Models, Statistical Methods and Applications, second edition, Wiley, New York, 2004 |
[25] | Kaufmann, A., Grouchko, D., Cruon, R. Mathematical Models for the Study of the Reliability of Systems, New York, Academic Press, 1977 |
[26] | Kuo, W., Zuo, M.J. Optimal Reliability Modeling: Principles and Applications. New York, Wiley, 2003 |
[27] | Lewis, E.E. Introduction to Reliability Engineering, Second Edition, Wiley, New York, 1996 |
[28] | MIL-HDBK-338B, Military Handbook Electronic Reliability Design Handbook, 1 October 1998 |
[29] | Pages, A., Gondran A. System Reliability. Evaluation and Prediction in Engineering, Berlin, Springer Verlag,1986 |
[30] | Villemeur, A. Reliability, Availability, Maintainability and Safety Assessment. Volume 1. Methods and Techniques, Chichester, Wiley, 1992. Процедуры дизъюнкции (или методы произведений дизъюнкций) |
[31] | Rauzy, A. Binary Decision Diagrams for Reliability Studies. Pages 381-396, Handbook of Performability Engineering. K.B. Misra ed., Elsevier. 2008 |
[32] | Akers, B. Binary decision diagrams. IEEE Transactions on Computers, Vol. 27, issue 6, pp.509-516, 1978 |
[33] | Bryant, R. Graph based algorithms for Boolean functions manipulation. IEEE Transactions on Computers, Vol. 35, issue 8, pp.677-691, 1986 |
[34] | Abraham, J.A. An improved method for network reliability, IEEE Transactions on Reliability, Vol. 8, No.1, pp.58-61, 1979 |
[35] | Beichelt, F. Zuverlassigkeit strukturierter Systeme, Berlin, VEB Verlag Technik, 1988 |
[36] | Beichelt F., Spross L. An improved Abraham-method for generating disjoint sums IEEE Transactions on Reliability, Vol.36, No.1, pp.70-74, 1987 |
[37] | Heidtmann K.D. Smaller sums of disjoint products by subproducts inversion. IEEE Transactions on Reliability, Vol. 38, No.3, pp.305-311, 1989 |
[38] | Locks M.O. Recursive disjoint products. A review of three algorithms. IEEE Transactions on Reliability, Vol. 31, No.1, pp.33-35, 1982 |
[39] | Locks M.O. Recent developments in computing of system-reliability. IEEE Transactions on Reliability, Vol. 34, No.5, pp.425-436, 1985 |
[40] | Locks M.O. A minimizing algorithm for sum of disjoint products. IEEE Transactions on Reliability, Vol. 36, No.4, pp.445-453, 1987 |
[41] | Chatelet E., Dutuit Y., Rauzy A. and Bouhoufani T. An optimized procedure to generate sums of disjoint products, Reliability Engineering and System Safety, Vol. 65, No. 3, pp.280-294, 1999 |
[42] | Rauzy A., Chatelet E., Dutuit Y. and Berenguer C. A practical comparison of methods to assess sum-of-products. Reliability Engineering and System Safety, Vol. 79, No.1, pp.33-42, 2003 |
[43] | Luo Tong, Trivedi K.S. An improved algorithm for coherent-system reliability. IEEE Transactions on Reliability, Vol. 47, No.1, pp.73-78, 1998 |
УДК 362:621.001:658.382.3:006.354 | ОКС 03.120.01; |
| 03.120.99 |
Ключевые слова: безотказность, готовность, вероятность безотказной работы, структурная схема надежности, последовательная RBD, параллельная RBD, путь успеха, путь отказа, непересекающийся набор элементов, вероятность отказа, интенсивность отказов, интенсивность восстановления, бинарная диаграмма принятия решений | |
Электронный текст документа
и сверен по:
М.: ФГБУ "РСТ", 2023