ГОСТ Р ИСО 17123-5-2011
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственная система обеспечения единства измерений
ОПТИКА И ОПТИЧЕСКИЕ ПРИБОРЫ
Методики полевых испытаний геодезических и топографических приборов
Часть 5
Электронные тахеометры
State system for ensuring the uniformity of measurements. Optics and optical instruments. Field procedures for testing geodetic and surveying instruments. Part 5. Electronic tacheometers
ОКС 17.180.30
Дата введения 2013-01-01
Предисловие
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт физико-технических и радиотехнических измерений" (ФГУП "ВНИИФТРИ") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 206 "Эталоны и поверочные схемы"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 октября 2011 г. N 441-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 17123-5:2005* "Оптика и оптические приборы. Методики полевых испытаний геодезических и топографических приборов. Часть 5. Электронные тахеометры" (ISO 17123-5:2005 "Optics and optical instruments - Field procedures for testing geodetic and surveying instruments - Part 5: Electronic tacheometers", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Предисловие к международному стандарту ИСО 17123
ИСО (Международная организация по стандартизации) представляет собой всемирную федерацию, состоящую из национальных органов по стандартизации (комитеты - члены ИСО). Работа по разработке международных стандартов обычно ведется техническими комитетами ИСО. Каждый комитет-член, заинтересованный в теме, для решения которой образован данный технический комитет, имеет право быть представленным в этом комитете. Международные организации, правительственные и неправительственные, поддерживающие связь с ИСО, также принимают участие в работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов разрабатываются в соответствии с правилами, установленными Директивами ИСО/МЭК, часть 3.
Проекты международных стандартов, принятые техническими комитетами, направляются комитетам-членам на голосование. Для их опубликования в качестве международных стандартов требуется одобрение не менее 75% комитетов-членов, участвовавших в голосовании.
Внимание обращается на тот факт, что отдельные элементы данного документа могут составлять предмет патентных прав. ИСО не должна нести ответственность за идентификацию этих патентных прав.
Международный стандарт ИСО 17123-5 был разработан Техническим комитетом ИСО/ТК 172 "Оптика и оптические приборы", подкомитетом ПК 6 "Геодезические и съемочные приборы".
Международный стандарт ИСО 17123 состоит из следующих частей под общим наименованием "Оптика и оптические приборы. Методики полевых испытаний геодезических и топографических приборов":
- Часть 1: Теория;
- Часть 2: Нивелиры;
- Часть 3: Теодолиты;
- Часть 4: Электрооптические дальномеры (приборы EDM);
- Часть 5: Электронные тахеометры;
- Часть 6: Вращающиеся лазеры;
- Часть 7: Оптические приборы для установки по отвесу;
- Часть 8: Полевые испытания GNSS-аппаратуры в режиме "Кинематика в реальном времени" (RTK).
Приложения А и В настоящего стандарта ИСО приведены только для информации.
Введение к международному стандарту ИСО 17123
Стандарт ИСО 17123 устанавливает полевые методики для определения и оценки прецизионности геодезических приборов и вспомогательного оборудования, используемых для измерения в строительстве и геодезии. Эти испытания, в первую очередь, предназначены для полевых поверок на пригодность конкретного прибора для выполнения близких неотложных задач и на соответствие требованиям других стандартов. Эти задачи не предлагаются как испытания для приемки или выполнения оценок, более комплексных по характеру.
ИСО 17123 можно рассматривать как один из первых шагов в процессе оценки неопределенности измерения (а именно измеряемой величины). Неопределенность результата измерения зависит от ряда факторов. Эти факторы включают, помимо прочих, повторяемость (сходимость), воспроизводимость (повторяемость в разные дни) и тщательную оценку всех возможных источников погрешности в соответствии с Руководством ИСО по выражению неопределенности в измерении (GUM).
Данные полевые методики разработаны специально для применения in situ без потребности в специальном вспомогательном оборудовании и для сведения к минимуму воздействий атмосферы.
Предисловие к настоящему стандарту
Целью разработки Государственных стандартов Российской Федерации ГОСТ Р ИСО 17123-1-ГОСТ Р ИСО 17123-8 (далее - ГОСТ Р ИСО 17123), является прямое применение в Российской Федерации восьми частей международного стандарта ИСО 17123-1:2002 - ИСО 17123-8:2007 под общим наименованием "Оптика и оптические приборы. Методики полевых испытаний геодезических и топографических приборов" в практической деятельности по метрологии в области геодезических измерений: при разработке и применении методик выполнения измерений, испытаниях (в том числе при испытаниях для целей утверждения типа средства измерений), поверке и калибровке геодезических приборов.
Большинство действующих в Российской Федерации стандартов и методик, регламентирующих методы испытаний геодезической аппаратуры, были разработаны в 90-е годы прошлого века применительно к аппаратуре отечественного производства, разработанной ранее. Эти методы не охватывают все современные виды измерений в геодезии и не всегда соответствуют метрологическим и техническим характеристикам современной аппаратуры. К тому же, некоторые методы испытаний неприменимы к импортным средствам измерений (далее - СИ), составляющим в настоящее время от 90% до 95% используемой в Российской Федерации геодезической аппаратуры. Данные обстоятельства привели к необходимости разработки методов испытаний, соответствующих современному уровню.
Применение стандартов серии ГОСТ Р ИСО 17123 в геодезической и топографической практике позволит выполнять оценку метрологических характеристик всех современных видов СИ в полевых условиях, аналогичных условиям эксплуатации. Такой подход дает более достоверные значения метрологических характеристик, поскольку лабораторные испытания, как правило, дают более высокие значения прецизионности, чем те, которые можно получить в реальных условиях эксплуатации. Для импортных СИ применение этих стандартов дает возможность оценить метрологические характеристики по тем методикам, которые используются фирмами-изготовителями в процессе заводских испытаний и тестирования.
Оценки метрологических характеристик соответствуют ГОСТ Р ИСО 5725-1-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения".
1 Область применения
Настоящий стандарт устанавливает методики полевых испытаний, которые необходимо принять при определении и оценке прецизионности (повторяемости) электронных тахеометров (комбинированные станции) и вспомогательного оборудования, используемых в строительстве и геодезии. Эти испытания, в первую очередь, предназначены для полевых поверок на пригодность конкретного прибора для выполнения текущих задач и на соответствие требованиям других стандартов.
Настоящий стандарт не распространяется на комплексные по характеру испытания для приемки или выполнения оценок рабочих показателей.
2 Нормативные ссылки
Нижеследующие документы являются обязательными для применения настоящего стандарта. Для датированных ссылок используют только указанное издание. Для недатированных - последнее издание (включая любые изменения).
ISO 3534-1:2006, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Термины, используемые в теории вероятности, и общие статистические термины)
ISO 4463-1:1989, Measurement methods for building - Setting-out and measurement - Part 1: Planning and organization, measuring procedures, acceptance criteria (Методы измерения в строительстве. Монтаж и измерение. Часть 1. Планирование и организация, процедуры измерения, критерии приемки)
ISO 7077:1981, Measuring methods for building - General principles and procedures for the verification of dimensional compliance (Методы измерения в строительстве. Общие принципы и методы контроля соблюдения размеров)
ISO 7078:1985, Building construction - Procedures for setting out, measurement and surveying - Vocabulary and guidance notes (Строительство зданий. Процедуры для разбивки, измерения и топографической съемки. Словарь и примечания)
ISO 9849:2000, Optics and optical instruments - Geodetic and surveying instruments - Vocabulary (Оптика и оптические приборы. Геодезические и топографические приборы. Словарь)
Заменен на ISO 9849:2017.
ISO 17123-1:2002, Optics and optical instruments - Field procedures for testing geodetic and surveying instruments - Part 1: Theory (Оптика и оптические приборы. Методики полевых испытаний геодезических и топографических приборов. Часть 1. Теория)
________________
Заменен на ISO 17123-1:2014.
GUM Guide to the expression of uncertainty in measurement (Руководство по выражению неопределенности в измерении)
VIM International vocabulary of metrology - Basic and general concepts and associated terms (Международный словарь по метрологии. Основные и общие понятия и соответствующие термины)
3 Термины
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 4463-1, ИСО 7077, ИСО 7078, ИСО 9849, ИСО 17123-1, GUM и VIM.
4 Требования
Перед испытаниями оператор должен убедиться, что прецизионность измерительного оборудования соответствует поставленной задаче измерений.
Электронный тахеометр и вспомогательное оборудование должны быть настроены в соответствии с инструкциями изготовителя и использоваться со штативами и отражателями в соответствии с рекомендациями изготовителя.
Координаты рассматривают как наблюдаемые величины, поскольку в современных электронных тахеометрах они являются выходными величинами.
На результаты измерений влияют метеорологические условия, особенно градиент температуры. Пасмурное небо и низкая скорость ветра гарантируют наиболее благоприятные погодные условия. Фактические метеорологические данные измеряют для ввода поправок на атмосферные воздействия и в измеренные расстояния. Конкретные условия, принимаемые во внимание, могут изменяться в зависимости от того, где выполняют измерения. Эти условия должны учитывать изменения температуры, скорости ветра, облачность и видимость. Отмечают также фактические погодные условия на момент измерения и тип поверхности, над которой эти измерения выполняют. Условия, выбранные для испытания, должны совпадать с ожидаемыми условиями, в которых будут в действительности выполнены измерения (см. ИСО 7077 и ИСО 7078).
При испытаниях, проводимых в лаборатории, получают результаты, в которых практически исключены атмосферные воздействия, но стоимость таких испытаний очень высока. В этой связи их не практикует большинство пользователей. При испытаниях, проводимых в лаборатории, значения прецизионности много больше, чем те, которые получают в полевых условиях.
В настоящем стандарте (разделы 6 и 7) приведены две методики испытаний в полевых условиях. Оператор должен выбрать методику, которая наиболее соответствует конкретным требованиям проекта.
5 Принцип измерений
5.1 Методика 1. Упрощенная методика испытаний
Упрощенная методика испытаний обеспечивает оценку того, насколько прецизионность данного электронного тахеометра находится в пределах заданного допустимого отклонения согласно ИСО 4463-1.
Упрощенная методика основана на ограниченном числе измерений. Методика основана на измерениях координат ,
,
в образцовом поле без номинальных значений. В результате влияния атмосферного преломления прецизионность координат
и
и прецизионность координаты
различны и их рассчитывают по отдельности. Максимальную разность рассчитывают как показатель прецизионности.
Значимое стандартное (среднеквадратическое) отклонение получить невозможно. Если требуется более точная оценка электронного тахеометра в полевых условиях, рекомендуется применять полную методику испытания в соответствии с разделом 7.
5.2 Методика 2. Полная методика испытаний
Полную методику испытания принимают для определения наилучшего достижимого критерия прецизионности электронного тахеометра и вспомогательного оборудования в полевых условиях.
Полная методика испытаний основана на измерении координат в образцовом поле без номинальных значений. Экспериментальное стандартное (среднеквадратическое) отклонение измерения координат отдельной точки определяют методом наименьших квадратов.
При установке тахеометра для выполнения различных серий измерений особое внимание уделяют центрированию в точке на местности. Достижимая точность центрирования, выраженная в пересчете на стандартные (среднеквадратические отклонения), следующая:
- механический отвес: 1-2 мм (хуже в ветреную погоду);
- оптический или лазерный центрир: менее 1 мм (настройку проверяют в соответствии с инструкциями изготовителя);
- центрирующая рейка: 1 мм.
Рекомендуется применять принудительное центрирование для приведенных методик измерения.
Примечание - Для визирных марок, расположенных на расстоянии 100 м, смещение центра на 2 мм может привести к отклонению наблюдаемого значения до 4" (1,3 мгон). Чем короче расстояние, тем больше эффект.
Полная методика измерения, приведенная в разделе 7, предназначена для определения критерия прецизионности электронного тахеометра. Этот используемый критерий прецизионности выражают в пересчете на экспериментальные стандартные (среднеквадратические) отклонения координаты, измеренной в обеих позициях лимба зрительной трубы
![]() и
и ![]() .
.
Полную методику используют для определения:
- критерия прецизионности в эксплуатации электронных тахеометров отдельной изыскательской партией одним прибором с его вспомогательным оборудованием в данное время;
- критерия прецизионности в эксплуатации отдельного прибора в течение длительного времени;
- критерия прецизионности в эксплуатации каждого из нескольких электронных тахеометров, чтобы облегчить сравнение их соответствующих достижимых прецизионностей, которые получены в аналогичных полевых условиях.
Необходимо применить статистические критерии, чтобы определить, принадлежит ли полученное экспериментальное стандартное (среднеквадратическое) отклонение к генеральной совокупности теоретического среднеквадратического отклонения прибора
, принадлежат ли два испытанных образца к одной и той же генеральной совокупности.
6 Упрощенная методика испытаний
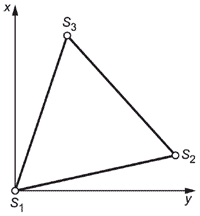
6.1 Конфигурация испытательного поля
Три точки стояния прибора (
1, 2, 3) должны быть размещены в углах треугольника (см. рисунок 1). Длину сторон треугольника следует выбирать в соответствии с поставленной задачей измерения (например, от 100 до 200 м). Высоту
рекомендуется выбирать различную, насколько позволяет поверхность земли.
|
,
,
- точки состояния прибора
Рисунок 1 - Конфигурация испытательного поля
6.2 Измерение
Прежде чем приступить к измерениям, прибор настраивают в соответствии с требованиями изготовителя. Все координаты измеряют в один и тот же день. Температуру воздуха и давление измеряют в каждой точке стояния прибора, чтобы вывести поправки за атмосферные воздействия на измерения расстояния (ввод правильного значения с коэффициентом 10). Расстояния корректируют с помощью множителя 10
для отклонения температуры на 1°С и/или давления воздуха на 3 гПа (3 мбар). Должна быть применена правильная поправка нуль-пункта в соответствии с отражательной призмой.
Устанавливают произвольную локальную систему координат (,
,
), присваивая координаты пункту стояния прибора
(например: 1000, 2000, 300). Нулевое показание горизонтального круга определяет ось
.
Из каждой точки стояния прибора (
1, 2, 3) измеряют координаты двух других точек (точки визирной цели) в локальной системе координат. Результаты измерения из точки стояния
используют как координаты точек стояния прибора для
и
соответственно для последующих измерений. Для ориентации используют только одно обратное визирование (по отношению к
).
Для ориентации используют встроенное или автономное программное обеспечение. Предпочтительно использовать такую же программу, которая будет применена на практике. Все наблюдения выполняют при одной позиции лимба зрительной трубы.
В таблице 1 представлена схема наблюдений для полевых измерений.
Таблица 1 - Схема наблюдений для упрощенной методики измерения
Точка визирования цели | Координата | Координата | Координата |
Точка стояния прибора | |||
Точка стояния прибора | |||
Точка стояния прибора | |||
| |||
6.3 Расчет
Разности координат рассчитывают следующим образом:
| |
| |
| |
| |
| (1) |
| |
| |
| |
|
и полуразность максимальных разностей
| (2) |
| (3) |
Полуразности и
не должны превышать предела допустимого отклонения
![]() и
и соответственно (согласно ИСО 4463-1) для поставленной задачи измерения. Если
![]() и
и не заданы, полуразности должны быть
![]() и
и ![]() соответственно, где
соответственно, где ![]() и
и ![]() являются экспериментальными стандартными (среднеквадратическими) отклонениями измерений
являются экспериментальными стандартными (среднеквадратическими) отклонениями измерений ,
,
соответственно, определенными в соответствии с полной методикой измерений одним и тем же прибором.
Если полуразности и
соответственно слишком велики для поставленной задачи измерения, необходимо провести дополнительные изыскания, чтобы идентифицировать основные источники отклонений.
7 Полная методика испытаний
7.1 Конфигурация испытательного поля
Три штатива, на каждом из которых размещено устройство для принудительного центрирования (
1, 2, 3), необходимо установить в углы треугольника (см. рисунок 1). Длину сторон треугольника рекомендуется выбирать в соответствии с поставленной задачей измерения (например, от 100 до 200 м). Высоты
должны быть разными, насколько позволяет поверхность земли.
7.2 Измерение
Прежде чем приступить к измерениям прибор настраивают в соответствии с требованиями изготовителя. Все координаты измеряют в один и тот же день. Чтобы устранить неопределенность в результате децентрирования, необходимо использовать принудительное центрирование.
Необходимо выполнить три серии измерений (3, для
1, ...,
), каждое из которых требует установку прибора на один из трех
3 штативов в точке
(в одну из трех точек) (набор
) измеряемого треугольника в установленном порядке, например,
![]() . Прибор следует всегда тщательно выравнивать. Не существует методики ориентации для системы координат прибора, такой как "свободное позиционирование с приведением шкалы". Чтобы обеспечить применение надежных поправок на атмосферу, температуру воздуха и давление рекомендуется измерять часто и полученные значения использовать для корректировки электронно-оптических измерений расстояния. Координаты (
. Прибор следует всегда тщательно выравнивать. Не существует методики ориентации для системы координат прибора, такой как "свободное позиционирование с приведением шкалы". Чтобы обеспечить применение надежных поправок на атмосферу, температуру воздуха и давление рекомендуется измерять часто и полученные значения использовать для корректировки электронно-оптических измерений расстояния. Координаты (,
,
) для каждой настройки прибора всегда устанавливают на нуль (0, 0, 0).
Координаты отражателей в двух других точках (
1, 2, 3) треугольника измеряют в двух позициях лимба зрительной трубы.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; 1, 2, 3;
1, 2, 3;
1, 2, 3.
Для измерения разностей координат между реперными точками устройства для принудительного центрирования учитывают разность
между высотой прибора и высотой визирной марки. Поскольку точное значение разности будет неизвестным параметром настройки (см. 7.3.2), значение
должно быть одинаковым для всех измерений. Следовательно, необходимо брать одну и ту же призму или две призмы одинакового типа.
Для простых и безошибочных расчетов необходимо выполнять последовательность измерения, приведенную в таблице 2.
Таблица 2 - Последовательность измерений
Точки | Точки | Точки | |||||||||||
| 1 | 1 | 2 |
| 1 | 2 | 1 |
| 1 | 3 | 1 | ||
| 1 | 1 | 3 |
| 1 | 2 | 3 |
| 1 | 3 | 2 |
Окончание таблицы 2
Точки | Точки | Точки | |||||||||||
| 2 | 1 | 2 |
| 2 | 3 | 1 |
| 3 | 2 | 1 | ||
| 2 | 1 | 3 |
| 2 | 3 | 2 |
| 3 | 2 | 3 | ||
| 2 | 2 | 1 |
| 3 | 1 | 2 |
| 3 | 3 | 1 | ||
| 2 | 2 | 3 |
| 3 | 1 | 3 |
| 3 | 3 | 2 |
Средние значения показаний в двух позициях I и II лимба зрительной трубы отмечают как квазинаблюдения
| |
| (4) |
| |
|
7.3 Расчет
7.3.1 Прецизионность координат и
Чтобы получить сопоставимые результаты трех серий измерений, необходимо привести каждую серию к одной и той же позиции, например, первому набору первой серии.
Поскольку координаты местоположения точки должны иметь (получить) нулевые значения, то есть (0, 0), необходимо выполнить параллельное перемещение каждого набора
| |
| (5) |
|
Для первого набора измерений (1,
1) необходимо вращение.
Таким образом, трансформированные координаты для поворота двух угловых точек и
измеряемого треугольника получают напрямую как параллельно перемещенные координаты набора
1 серии
1
![]() ;
;
![]() ;
;
2, 3.
Для каждого из следующих наборов 1, 2, 3 серий
1, 2, 3 выполняют поворот
с центром в точке
.
Наиболее доступный способ - вращение в полярных координатах. Для каждой визирной марки 2, 3 прямоугольные координаты преобразуют в полярные координаты
| (6) |
| (7) |
Ориентацию каждого набора серии
можно выразить средним значением
| (8) |
Следовательно, угол поворота равен
| (9) |
И, таким образом, новая ориентация будет
| (10) |
Преобразованные координаты затем рассчитывают как
| (11) |
| (12) |
Вычисленные координаты и
получают в виде
| (13) |
| (14) |
Для 36 остатков такого вычисления:
| (15) |
| (16) |
сумма квадратов остатков равна
| (17) |
Поскольку существуют восемь параметров вращения и четыре усредненные координаты углов треугольника, точки и точки
, число неизвестных параметров в вычислении равно
8+4=12. Таким образом, число степеней свободы будет
![]() . (18)
. (18)
Стандартное (среднеквадратическое) отклонение одной координаты или
, наблюдаемой в одной из двух позиций лимба зрительной трубы, будет
| (19) |
и наконец
| (20) |
7.3.2 Прецизионность координат
Поскольку координата точки
установлена на нуль, неизвестные в вычислении представляют собой координаты
и
точек
и
и разность высот
высоты прибора и высоты визирной марки. Вычисление методом наименьших квадратов дает систему нормальных уравнений с решением в явном виде согласно уравнениям (21)-(23).
Три неизвестных параметра вычисления (3) являются координатами
и
.
| (21) |
| (22) |
и разность будет равна
| (23) |
С этими тремя параметрами 18 остатков вычисления рассчитывают следующим образом:
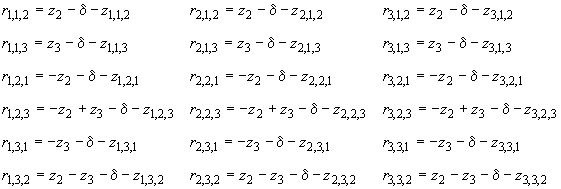 (24)
(24)
Получают сумму квадратов остатков
 . (25)
. (25)
С числом степеней свободы
![]() . (26)
. (26)
Наконец, стандартное (среднеквадратическое) отклонение одной координаты , измеренной в одной из позиций лимба зрительной трубы
![]() . (27)
. (27)
7.4 Статистические испытания
7.4.1 Общие положения
Статистические испытания рекомендованы только для полной методики испытания.
Для интерпретации результатов статистические испытания выполняют, используя экспериментальное стандартное (среднеквадратическое) отклонение координаты, измеренной на треугольнике.
Чтобы ответить на следующие вопросы:
a) Будет ли рассчитанное стандартное (среднеквадратическое) отклонение меньше, чем соответствующее значение
, установленное изготовителем, или меньше, чем другое предварительно определенное значение
?
b) Принадлежат ли два экспериментальных стандартных (среднеквадратических) отклонения и
, определенные для двух разных образцов измерения, к одной и той же генеральной совокупности, предположив, что оба образца имеют одинаковое число степеней свободы
?
Экспериментальные стандартные (среднеквадратические) отклонения и
получают из:
- двух выборок измерений, выполненных на одном и том же приборе разными наблюдателями;
- двух выборок измерений, выполненных на одном и том же приборе в разное время;
- двух выборок измерений, выполненных на разных приборах.
Для следующих испытаний уровень доверия ![]() и, согласно предназначению измерений, предполагается, что число степеней свободы
и, согласно предназначению измерений, предполагается, что число степеней свободы ![]() 24 для координат
24 для координат и
, и
15 для координаты
.
Таблица 3 - Статистические испытания
Вопрос | Нуль-гипотеза | Альтернативная гипотеза |
а) | ||
b) |
|
|
7.4.2 Ответ на вопрос а)
Нуль-гипотезу, утверждающую, что экспериментальное стандартное (среднеквадратическое) отклонение меньше или равно теоретическому или предварительно определенному значению
, не отвергают, если выполнены следующие условия:
для | для | |
|
| (28) |
|
| (29) |
|
| (30) |
|
| (31) |
|
| (32) |
В противном случае нуль-гипотезу отвергают.
7.4.3 Ответ на вопрос b)
В случае двух разных образцов испытание показывает, принадлежат ли два экспериментальных стандартных (среднеквадратических) отклонения и
к одной и той же генеральной совокупности. Соответствующую нуль-гипотезу
![]() не отвергают, если выполнены следующие условия:
не отвергают, если выполнены следующие условия:
для | для | |
|
| (33) |
|
| (34) |
|
| (35) |
|
| (36) |
В противном случае нуль-гипотезу отвергают.
Число степеней свободы и, таким образом, соответствующие экспериментальные значения ![]() ,
, ![]() и
и ![]() (взятые из справочников по статистике) изменяют, если анализируют другое число измерений.
(взятые из справочников по статистике) изменяют, если анализируют другое число измерений.
Приложение А
(справочное)
Пример упрощенной методики испытания
А.1 Измерения
В таблице А.1 все измерения компилированы согласно схеме наблюдений, приведенной в таблице 1.
Наблюдатель: | С.Миллер |
Погода: | частичная облачность (5/8), 18°С |
Атмосферное давление | 995 гПа |
Тип прибора и номер: | NN ххх 630401 |
Дата: | 2001-03-15 |
Таблица А.1 - Измерения
1 | 2 | 3 | 4 | 5 |
1000,000 | 2000,000 | 300,000 | ||
984,076 | 2082,959 | 302,227 | ||
883,478 | 2015,557 | 286,794 | ||
984,076 | 2082,959 | 302,227 | ||
883,480 | 2015,549 | 286,795 | ||
1000,000 | 1999,999 | 300,002 | ||
883,478 | 2015,557 | 286,794 | ||
1000,000 | 2000,000 | 300,002 | ||
984,082 | 2082,955 | 302,228 |
А.2 Расчет
В соответствии с уравнением (1) разность координат рассчитывают следующим образом:
0,000,
-0,006,
-0,002,
-0,001,
0,004,
0,008,
0,000,
-0,001,
-0,001.
Согласно уравнению (2) полуразность максимальных разностей
![]() 0,008.
0,008.
Согласно уравнению (3)
0,0005.
Приложение В
(справочное)
Пример полной методики испытания
В.1 Измерения координат и
Таблица В.1 содержит в столбцах 2 и 3 измеренные координаты и
.
Таблица В.1 - Измерения и остатки (HZ)
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
1 1 1 | 0,000 | 0,000 | 0,000 | 0,000 | |||||||
2 | -0,007 | 63,994 | -0,007 | 63,994 | 1,570906 | -0,0070 | 63,9940 | 0,0014 | 0,0056 | ||
3 | 55,003 | 31,999 | 55,003 | 31,999 | 0,526906 | 55,0030 | 31,9990 | -0,0023 | 0,0002 | ||
| |||||||||||
1 2 1 | 30,689 | -56,157 | 0,000 | 0,000 | |||||||
2 | 0,000 | 0,000 | -30,689 | 56,157 | 2,070937 | 1,570911 | 63,9955 | -0,0073 | 63,9955 | 0,0017 | 0,0042 |
3 | 63,615 | -1,707 | 32,926 | 54,450 | 1,026927 | 0,526901 | 63,6312 | 55,0008 | 31,9974 | -0,0001 | 0,0019 |
| -0,500026 | ||||||||||
1 3 1 | -2,791 | -63,570 | 0,000 | 0,000 | |||||||
2 | -56,651 | -29,000 | -53,860 | 34,570 | 2,570969 | 1,570930 | 63,9999 | -0,0086 | 63,9999 | 0,0029 | -0,0002 |
3 | 0,000 | 0,000 | 2,791 | 63,570 | 1,526920 | 0,526882 | 63,6312 | 55,0015 | 31,9963 | -0,0008 | 0,0029 |
| -1,000039 | ||||||||||
2 1 1 | 0,000 | 0,000 | 0,000 | 0,000 | |||||||
2 | -18,919 | 61,133 | -18,919 | 61,133 | 1,870921 | 1,570909 | 63,9935 | -0,0072 | 63,9935 | 0,0016 | 0,0061 |
3 | 43,088 | 46,823 | 43,088 | 46,823 | 0,826915 | 0,526903 | 63,6315 | 55,0011 | 31,9977 | -0,0004 | 0,0016 |
| -0,300012 | ||||||||||
2 2 1 | 63,846 | -4,519 | 0,000 | 0,000 | |||||||
2 | 0,000 | 0,000 | -63,846 | 4,519 | 3,070931 | 1,570906 | 64,0057 | -0,0070 | 64,0057 | 0,0014 | -0,0061 |
3 | 35,818 | 52,606 | -28,028 | 57,125 | 2,026931 | 0,526906 | 63,6305 | 55,0001 | 31,9973 | 0,0006 | 0,0020 |
| -1,500025 | ||||||||||
2 3 1 | -56,645 | 28,992 | 0,000 | 0,000 | |||||||
2 | -2,797 | 63,567 | 53,848 | 34,575 | 0,570791 | 1,570830 | 63,9925 | -0,0022 | 63,9925 | -0,0034 | 0,0072 |
3 | 0,000 | 0,000 | 56,645 | -28,992 | -0,473058 | 0,526981 | 63,6333 | 55,0001 | 32,0028 | 0,0006 | -0,0036 |
| 1,000039 | ||||||||||
3 1 1 | 0,000 | 0,000 | 0,000 | 0,000 | |||||||
2 | -9,038 | -63,365 | -9,038 | -63,365 | 4,570711 | 1,570801 | 64,0063 | -0,0003 | 64,0063 | -0,0053 | -0,0067 |
3 | -58,964 | -23,916 | -58,964 | -23,916 | 3,526920 | 0,527011 | 63,6296 | 54,9960 | 32,0026 | 0,0047 | -0,0034 |
| -2,999910 | ||||||||||
3 2 1 | 58,201 | 26,638 | 0,000 | 0,000 | |||||||
2 | 0,000 | 0,000 | -58,201 | -26,638 | 3,570823 | 1,570863 | 64,0073 | -0,0043 | 64,0073 | -0,0013 | -0,0077 |
3 | 6,216 | 63,335 | -51,985 | 36,697 | 2,526908 | 0,526948 | 63,6326 | 55,0006 | 32,0007 | 0,0001 | -0,0015 |
| -1,999960 | ||||||||||
3 3 1 | -2,791 | -63,573 | 0,000 | 0,000 | |||||||
2 | -56,651 | -28,999 | -53,860 | 34,574 | 2,570916 | 1,570903 | 64,0020 | -0,0068 | 64,0020 | 0,0012 | -0,0024 |
3 | 0,000 | 0,000 | 2,791 | 63,573 | 1,526922 | 0,526909 | 63,6342 | 55,0032 | 31,9994 | -0,0025 | -0,0001 |
| -1,000013 | ||||||||||
-0,0056 | 63,9996 | ||||||||||
55,0007 | 31,9992 | ||||||||||
|
| | |||||||||
Условия измерений: | |
Наблюдатель: | С.Миллер |
Погода: | солнечно, 12°С; |
Атмосферное давление | 976 гПа |
Прибор, тип и номер: | NN ххх 630401 |
Дата: | 2001-03-12 |
В.2 Расчет
В соответствии с формулой (6) рассчитывают углы ориентации для каждого направления и записывают в столбец 6 таблицы В.1 (в данном примере значения углов приведены в радианах). Расстояния
рассчитывают по формуле (7) и записывают в столбец 8 таблицы В.1. Уравнение (8) задает угол ориентации
каждой серии. Для угла поворота
по формуле (9) рассчитывают новую ориентацию
по формуле (10) и записывают в столбец 7 таблицы B.1. Для
и
преобразованные координаты
и
, рассчитывают по формулам (11) и (12) и записывают в столбцы 9 и 10 таблицы В.1. По уравнениям (13) и (14) вычисляют координаты
и
точек
и
(приведены внизу столбцов 9 и 10 таблицы В.1). Рассчитывают остатки по формулам (15) и (16) (столбцы 11 и 12 таблицы В.1). В итоге уравнение (17) дает
![]() м
м
и по формулам (19) и (20) получают экспериментальное стандартное (среднеквадратическое) отклонение координаты, измеренной в двух позициях лимба зрительной трубы, измеренное в одном наборе измерений в двух позициях I и II лимба зрительной трубы
![]() м.
м.
В.3 Измерения координаты
Таблица В.2 содержит координаты в столбце 4.
Таблица В.2 - Измерения и остатки ()
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||||
1 | 1 | 2 | 2,615 | 2 | 1 | -1 | 1 | 0 | -1 | -0,0010 | ||||
1 | 3 | 5,658 | 1 | 2 | -1 | 0 | 1 | -1 | 0,0056 | |||||
1 | 2 | 1 | -2,714 | -2 | -1 | -1 | -1 | 0 | -1 | 0,0016 | ||||
2 | 3 | 3,004 | -1 | 1 | -1 | -1 | 1 | -1 | -0,0036 | |||||
1 | 3 | 1 | -5,767 | -1 | -2 | -1 | 0 | -1 | -1 | 0,0050 | ||||
3 | 2 | -3,097 | 1 | -1 | -1 | 1 | -1 | -1 | -0,0018 | |||||
2 | 1 | 2 | 2,616 | 2 | 1 | -1 | 1 | 0 | -1 | -0,0020 | ||||
1 | 3 | 5,657 | 1 | 2 | -1 | 0 | 1 | -1 | 0,0066 | |||||
2 | 2 | 1 | -2,712 | -2 | -1 | -1 | -1 | 0 | -1 | -0,0004 | ||||
2 | 3 | 3,004 | -1 | 1 | -1 | -1 | 1 | -1 | -0,0036 | |||||
2 | 3 | 1 | -5,763 | -1 | -2 | -1 | 0 | -1 | -1 | 0,0010 | ||||
3 | 2 | -3,094 | 1 | -1 | -1 | 1 | -1 | -1 | -0,0048 | |||||
3 | 1 | 2 | 2,618 | 2 | 1 | -1 | 1 | 0 | -1 | -0,0040 | ||||
1 | 3 | 5,661 | 1 | 2 | -1 | 0 | 1 | -1 | 0,0026 | |||||
3 | 2 | 1 | -2,711 | -2 | -1 | -1 | -1 | 0 | -1 | -0,0014 | ||||
2 | 3 | 3,005 | -1 | 1 | -1 | -1 | 1 | -1 | -0,0046 | |||||
3 | 3 | 1 | -5,764 | -1 | -2 | -1 | 0 | -1 | -1 | 0,0020 | ||||
3 | 2 | -3,101 | 1 | -1 | -1 | 1 | -1 | -1 | 0,0022 | |||||
Неизвестные параметры: | 2,6632 | 5,7128 | 0,0492 |
| ||||||||||
Условия измерения: | Наблюдатель: | С.Миллер | ||||||||||||
Погода: | солнечно, 12°С | |||||||||||||
Атмосферное давление | 976 гПа | |||||||||||||
Номер прибора | NN ххх 630401 | |||||||||||||
Дата: 2001-03-12 | ||||||||||||||
В.4 Расчет
Для простого и безошибочного расчета трех неизвестных параметров по формулам (21)-(23) коэффициенты приведены в столбцах 5-7 таблицы В.2. Складывают произведения чисел в столбце 4 таблицы В.2 на соответствующие числа в столбцах 5, 6 или 7. Например, для
расчет суммы значений в столбце 4 умножают на значения в столбце 6.
![]() м.
м.
Для простого расчета остатков по формуле (24) значения неизвестных параметров повторяют в столбцах 8-10 в первой строке таблицы В.2, и в следующих строках приведены коэффициенты этих неизвестных параметров. Отсюда расчет, например для , представляет собой
![]() м.*
м.*
_______________
* Формула соответствует оригиналу. - .
По формуле (25) рассчитывают
![]() м
м
и по формуле (27) получают
![]() м.
м.
В.5 Статистические испытания
В.5.1 Статистическое испытание согласно вопросу а)
Критерий для и
![]() мм;
мм;
![]() мм;
мм;
![]() ;
;
4,2 мм5,0 мм·1,23;
4,2 мм6,2 мм.
Поскольку выполнено вышеуказанное условие, нуль-гипотезу, утверждающую, что экспериментальное среднеквадратическое отклонение ![]() мм меньше или равно значению от изготовителя
мм меньше или равно значению от изготовителя ![]() мм, не отвергают на доверительном уровне 95%.
мм, не отвергают на доверительном уровне 95%.
Критерий для
![]() мм;
мм;
![]() мм;
мм;
![]() ;
;
3,8 мм5,0 мм·1,29;
3,8 мм6,45 мм.
Поскольку выполнено вышеуказанное условие, нуль-гипотезу, утверждающую, что экспериментальное среднеквадратическое отклонение ![]() мм меньше или равно значению от изготовителя
мм меньше или равно значению от изготовителя ![]() мм, не отвергают на доверительном уровне 95%.
мм, не отвергают на доверительном уровне 95%.
В.5.2 Статистическое испытание согласно вопросу b)
Критерий для и
![]() мм;
мм;
![]() мм;
мм;
![]() ;
;
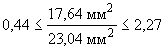 ;
;
![]() .
.
Поскольку выполнено вышеуказанное условие, нуль-гипотезу, утверждающую, что экспериментальные стандартные (среднеквадратические) отклонения ![]() мм и
мм и ![]() мм принадлежат к одной и той же генеральной совокупности, не отвергают на доверительном уровне 95%.
мм принадлежат к одной и той же генеральной совокупности, не отвергают на доверительном уровне 95%.
Критерий для
![]() мм;
мм;
![]() мм;
мм;
![]() ;
;
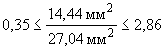 ;
;
![]() .
.
Поскольку выполнено вышеуказанное условие, нуль-гипотезу, утверждающую, что экспериментальные стандартные (среднеквадратические) отклонения ![]() мм и
мм и ![]() мм принадлежат к одной и той же генеральной совокупности, не отвергают на доверительном уровне 95%.
мм принадлежат к одной и той же генеральной совокупности, не отвергают на доверительном уровне 95%.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1:2006 | - | * |
ISO 4463-1:1989 | - | * |
ISO 7077:1981 | - | * |
ISO 7078:1985 | - | * |
ISO 9849:2000 | - | * |
ISO 17123-1:2002 | IDT | ГОСТ Р ИСО 17123-1-2011 "Государственная система обеспечения единства измерений. Оптика и оптические приборы. Методики полевых испытаний геодезических и топографических приборов. Часть 1. Теория" |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандарта: - IDT - идентичный стандарт. | ||
УДК 528.5.528.02:006.354 | ОКС 17.180.30 |
Ключевые слова: геодезия, геодезические измерения, испытания геодезических приборов | |
Электронный текст документа
и сверен по:
, 2019

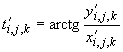 ,
,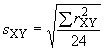
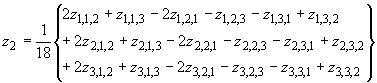 ,
,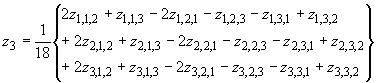 ,
,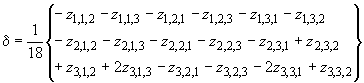 .
. 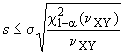 ;
;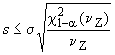 ;
;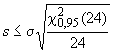 ;
;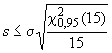 ;
;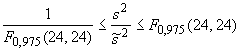 ;
;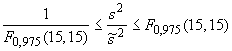 ;
;