ПНСТ 838-2023/ИСО/МЭК 23053:2022
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Искусственный интеллект
СТРУКТУРА ОПИСАНИЯ СИСТЕМ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА, ИСПОЛЬЗУЮЩИХ МАШИННОЕ ОБУЧЕНИЕ
Artificial Intelligence. Framework for artificial intelligence systems using machine learning
ОКС 35.080
Срок действия с 2024-01-01
до 2027-01-01
Предисловие
1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "Институт развития информационного общества" (ИРИО) на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 164 "Искусственный интеллект"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 15 ноября 2023 г. N 57-пнст
4 Настоящий стандарт идентичен международному стандарту ИСО/МЭК 23053:2022* "Структура описания систем искусственного интеллекта (ИИ), использующих машинное обучение (МО)" (ISO/IEC 23053:2022 "Framework for Artificial Intelligence (AI) - Systems Using Machine Learning (ML)", IDT).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16-2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за 4 мес до истечения срока его действия, разработчику настоящего стандарта по адресу: 119991, Российская Федерация, Москва, Ленинские горы, д.1 и в Федеральное агентство по техническому регулированию и метрологии по адресу: 123112, Москва, Пресненская набережная, д.10, стр.2.
В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе "Национальные стандарты" и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
Введение
Системы искусственного интеллекта (ИИ) - технические системы, генерирующие такие результаты, как контент, прогнозы, рекомендации или решения для заданного набора целей, определенных человеком. ИИ охватывает широкий спектр технологий, отражающих различные подходы к решению отмеченных сложных задач.
Машинное обучение (МО) - это направление ИИ, использующее вычислительные методы для того, чтобы дать системам возможность учиться на основе данных и опыта. Таким образом, системы МО разрабатываются путем оптимизации алгоритмов, обеспечивающей соответствие обучающим данным и повышение эффективности посредством максимизации вознаграждения. Методы МО включают глубокое обучение, также рассматриваемое в настоящем стандарте.
В настоящем стандарте использованы такие термины, как знание, обучение и решения, однако не ставится цель антропоморфировать МО.
Целью настоящего стандарта является описание структуры систем ИИ, использующих МО. Благодаря установлению единых терминологии и набора понятий для таких систем настоящий стандарт предоставляет основу для понятного объяснения как непосредственно систем, так и различных предложений, касающихся их проектирования и использования. Настоящий стандарт предназначен для широкой аудитории, включающей как экспертов, так и лиц, не имеющих практического опыта. Однако некоторые пункты (приведенные в разделе 5) включают более детальные технические описания.
Настоящий стандарт также создает фундамент для других стандартов, рассматривающих конкретные аспекты систем МО и их компонентов.
1 Область применения
Настоящий стандарт определяет для области искусственного интеллекта (ИИ) и машинного обучения (МО) структуру для описания типовой системы ИИ, использующей технологии МО. Данная структура описывает компоненты системы и их функции в экосистеме ИИ. Настоящий стандарт распространяется на организации различных типа и размера, в том числе на государственные и частные организации, органы государственной власти и некоммерческие организации, внедряющие или эксплуатирующие системы ИИ.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт [для датированной ссылки применяют только указанное издание ссылочного стандарта, для недатированной - последнее издание (включая все изменения]:
ISO/IEC 22989, Information technology. Artificial intelligence. Artificial intelligence concepts and terminology (Информационные технологии. Искусственный интеллект. Термины и определения, связанные с искусственным интеллектом)
3 Термины и определения
В настоящем стандарте применены термины и определения по ИСО/МЭК 22989.
ИСО и МЭК поддерживают терминологические базы данных для применения в сфере стандартизации по следующим адресам:
- онлайн-платформа ИСО: доступна по ссылке: http://www.iso.org/obp;
- Электропедия МЭК: доступна по ссылке: http://www.electropedia.org/.
3.1 Создание и использование моделей
3.1.1 классификационная модель (classification model): <машинное обучение> Модель машинного обучения, где ожидаемый результат для заданных входных данных представляет собой один или несколько классов.
3.1.2 регрессионная модель (regression model): <машинное обучение> Модель машинного обучения, где ожидаемый результат является непрерывной функцией входных данных.
3.1.3 обобщение (generalization): <машинное обучение> Способность обученной модели генерировать правильные результаты на основе новых входных данных.
Примечание 1 - Наиболее обобщающей моделью машинного обучения является модель, которая обеспечивает приемлемую точность генерации результатов на новых входных данных.
Примечание 2 - Обобщение тесно связано с переобучением. Переобученная модель машинного обучения не способна к корректному обобщению данных, поскольку с наибольшей точностью соответствует набору обучающих данных.
3.1.4 переобучение (overfitting): <машинное обучение> Создание модели, с наибольшей точностью соответствующей обучающим данным и не способной к обобщению при использовании новых наборов данных.
Примечание 1 - Переобучение может возникнуть, если обученная модель извлекла уроки из несущественных признаков обучающих данных (т.е. признаков, обобщение которых не приводят к полезным результатам), обучающие данные содержат много шума (например, имеют чрезмерное количество выбросов) или обученная модель чрезмерно сложна для определенных обучающих данных.
Примечание 2 - Признаком переобучения модели является значительная разница между ошибками, измеренными на обучающих данных и на отдельных тестовых и валидационных данных. На производительность переобученных моделей особенно влияет значительная разница между обучающими и эксплуатационными данными.
3.1.5 недообучение (underfitting): <машинное обучение> Создание модели, недостаточно соответствующей обучающим данным и генерирующей неверные результаты при использовании новых данных.
Примечание 1 - Недообучение может возникнуть при неверно выбранных признаках, при недостаточном времени на обучение или когда модель слишком проста для обучения на большом объеме обучающих данных ввиду ее ограниченной способности (т.е. выразительной силы).
3.2 Инструменты
3.2.1 метод обратного распространения ошибки (backpropagation): Метод обучения нейронной сети, использующий ошибку на выходном слое для корректировки и оптимизации весов связей на предыдущих последовательных слоях.
3.2.2 скорость обучения (learning rate): Размер шага для метода градиентного спуска.
Примечание 1 - Скорость обучения определяет, насколько быстро модель сходится к оптимальному решению, что делает ее важным гиперпараметром для нейронных сетей.
3.3 Данные
3.3.1 класс (class): Определяемая человеком категория элементов, являющихся частью набора данных и имеющих общие атрибуты.
Пример - "Телефон", "стол", "стул", "шарикоподшипник" и "теннисный мяч" являются классами. К классу "стол" относят: рабочий стол, обеденный стол, письменный стол, журнальный стол, верстак.
Примечание 1 - Классы обычно являются целевыми переменными и обозначаются именем.
3.3.2 кластер (cluster): Автоматически группируемая категория элементов, являющихся частью набора данных и имеющих общие атрибуты.
Примечание 1 - Наличие имен для кластеров не обязательно.
3.3.3 признак (feature): <машинное обучение> Измеримое свойство объекта или события, связанное с заданным набором характеристик.
Примечание 1 - Признаки играют роль в обучении и генерации результатов.
Примечание 2 - Признаки предоставляют машиночитаемый способ описания соответствующих объектов. Поскольку алгоритм не будет возвращаться к самим объектам или событиям, представления признаков разработаны таким образом, чтобы содержать всю полезную информацию.
3.3.4 расстояние (distance): <машинное обучение> Измеренное расстояние между двумя точками в пространстве.
Примечание 1 - В машинном обучении обычно применяется евклидова метрика.
3.3.5 неразмеченный (unlabelled): Свойство образца, не включающего целевую переменную.
4 Сокращения
В настоящем стандарте применены следующие сокращения:
АОК | - | анализ основных компонентов; |
ГСД | - | глубокая сеть доверия; |
ГСНС | - | глубокая сверточная нейронная сеть; |
ДКП | - | долгая краткосрочная память; |
ИИ | - | искусственный интеллект; |
МБ | - | машины Больцмана; |
МО | - | машинное обучение; |
НС | - | нейронная сеть; |
ОПЗ | - | отрицательная прогностическая значимость; |
ПДн | - | персональные данные; |
ППЗ | - | положительная прогностическая значимость; |
РНС | - | рекуррентная нейронная сеть; |
РХП | - | рабочие характеристики приемника; |
САО | - | средняя абсолютная ошибка; |
СГ | - | сопряженный градиент; |
СГС | - | стохастический градиентный спуск; |
СНС | - | сверточная нейронная сеть; |
УРБ | - | управляемый рекуррентный блок; |
API | - | интерфейс прикладного программирования; |
AUC | - | площадь под кривой; |
CapsNet | - | капсульная нейронная сеть; |
FFNN | - | нейронная сеть с прямой связью; |
FNR | - | доля ложных отрицательных классификаций; |
FPR | - | доля ложных положительных классификаций; |
MDP | - | марковский процесс принятия решений; |
NNEF | - | формат обмена нейронными сетями; |
ONNX | - | открытая библиотека программного обеспечения; |
PHI | - | личная или охраняемая медицинская информация; |
REST | - | передача состояния представления; |
SVM | - | метод опорных векторов; |
TNR | - | доля истинно отрицательных классификаций; |
TPR | - | доля истинно положительных классификаций. |
5 Общие положения
В ИСО/МЭК 22989 определено МО как процесс оптимизации параметров модели с помощью вычислительных методов, чтобы поведение модели отражало данные или опыт. С начала 1940-х гг. проводят исследования по моделированию нейронов (т.е. НС) и разрабатывают компьютерные программы, способные обучаться на основе данных. МО - это расширяющая область знаний, в рамках которой разрабатывают новые приложения в различных отраслях промышленности. Данный прогресс возможен благодаря доступности больших объемов данных и вычислительных ресурсов. Методы МО включают использование НС и глубокого обучения.
В ИСО/МЭК 22989 экосистема ИИ представлена с точки зрения ее функциональных уровней, где МО является ее неотъемлемым компонентом. На рисунке 1 показана система ИИ, включая компоненты модели, программные средства и методы, а также ее данные.
В разделе 6 более подробно описаны различные компоненты системы МО.
В разделе 7 описаны различные подходы МО, а также их зависимость от обучающих данных.
В разделе 8 представлен конвейер МО: процессы, связанные с разработкой, развертыванием и эксплуатацией модели МО.
Подраздел 6.5 и раздел 7 содержат значительный объем технической информации по сравнению с остальной частью настоящего стандарта. Наличие достаточного опыта работы в технической сфере способствует лучшему пониманию содержания настоящего стандарта у пользователя.
6 Система машинного обучения
6.1 Общие положения
На рисунке 1 изображены элементы системы МО. Они определяют роли и их функции, специфичные для МО, которые могут быть реализованы разными организациями (например, разными поставщиками). Примеры, представленные на рисунке 1, не являются исчерпывающим перечнем. Дальнейшие пояснения по каждому разделу, представленному на рисунке 1, приведены в разделе 6.
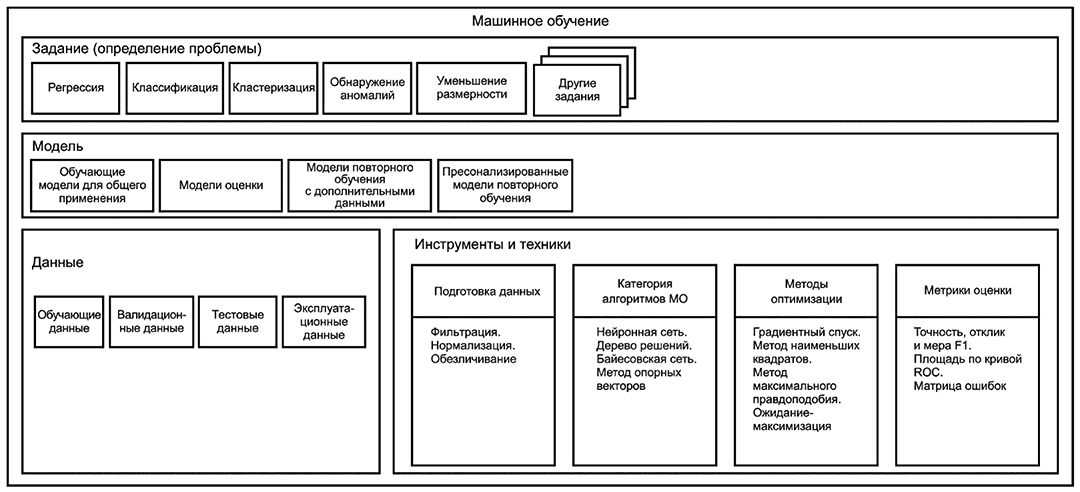 |
Рисунок 1 - Элементы системы МО
На рисунке 1 подэлементы создания и использования модели можно рассматривать как многоуровневый подход, т.е. приложения построены на основе моделей, применяемых для выполнения заданий. Создание и использование моделей, в свою очередь, зависит от программных средств и методов, а также от данных.
Одна система МО может включать комбинацию нескольких моделей МО. Компоненты системы могут быть описаны с точки зрения их входных и выходных данных, намерений и функций. Компоненты можно тестировать независимо друг от друга.
Результатом работы модели МО в процессе эксплуатации являются сгенерированные результаты и принятые решения. Предварительно обученная модель - это модель МО, обученная на момент ее получения. В некоторых случаях созданная модель может быть применена для выполнения аналогичного задания из другой области. Перенос обучения - это метод модификации предварительно обученной модели МО для выполнения другого похожего задания.
В настоящем стандарте термин "приложение" относится как к целевому использованию одной или нескольких моделей МО, так и к конкретному программному обеспечению, реализующему такое применение. Для создания приложений модели МО обычно интегрируются с другими программными компонентами. Приложения, использующие МО, различаются по типам обрабатываемых входных данных и по типам выполняемых заданий. В некоторых приложениях МО может генерировать результаты или принимать решения на высоком уровне, а в других - решать узкоспециализированные задачи.
Различия во входных данных и заданиях, а также такие факторы, как варианты развертывания, точность и надежность, приводят к разным архитектурам приложений. Приложения ИИ могут использовать собственные шаблоны проектирования или следовать шаблонам проектирования конкретной проектной области.
Логика приложения определена форматом входных и выходных данных и в некоторых случаях преобразованием и потоком данных между используемыми моделями МО. Выбор алгоритмов МО и методов подготовки данных всегда зависит от заданий приложения.
6.2 Задание
6.2.1 Общие положения
Термин "задание" обозначает действия, которые необходимо предпринять для достижения конкретной цели. В МО под этим подразумевается определение задачи, которую необходимо решить с помощью модели МО. Приложение МО может быть использовано для выполнения одного или нескольких заданий. Вместо того чтобы решать задачи с помощью определенной функции, представленной в виде набора шагов и реализованной в программном коде, можно применить обученную модель МО к эксплуатационным данным. В сущности, обученная модель МО реализует целевую функцию, являющуюся аппроксимацией гипотетической функции, которую мог бы написать программист для решения задачи.
Постановка задания МО включает в себя определение проблемы, формата данных и признаков.
Описанные в последующих пунктах задания приведены в качестве примеров, и их список не является исчерпывающим.
6.2.2 Регрессия
Задание по регрессии (регрессионному анализу) включает в себя вычисление значений непрерывной функции путем определения ее параметров, посредством обучения модели, наиболее соответствующей набору обучающих данных. В заданиях регрессии обученная регрессионная модель представляет пользовательское пространство. Когда обученную модель применяют к новой совокупности эксплуатационных данных, эту совокупность проецируют в пользовательское пространство, определяемое с помощью обученной регрессионной модели.
Регрессию в основном используют при прогнозировании численных значений для реальных процессов на основе предыдущих измерений или наблюдений за этими процессами. Варианты использования регрессии включают прогнозирование:
- динамики цен на фондовом рынке;
- возраста зрителя потокового видео;
- количества простат-специфического антигена в организме на основе различных клинических измерений.
6.2.3 Классификация
В задании по классификации отнесен объект с присущей ему совокупностью параметров (входных данных) к определенной(ому) категории или классу. Классификация может быть бинарной (т.е. истина или ложь), многоклассовой (т.е. один элемент из нескольких возможных) и многозначной (т.е. любое количество элементов из нескольких возможных). Например, классификация может быть использована, чтобы определить, чем является объект на изображении - кошкой, собакой или представителем совершенно другого вида. Как правило, классы являются элементами дискретного неупорядоченного множества, из-за чего задача не может быть решена с помощью регрессии. Например, медицинский диагноз с конкретным набором симптомов может быть определен как {инсульт, передозировка лекарственными препаратами, эпилептический приступ}, классы не упорядочены и отсутствует непрерывный переход от одного класса к другому.
Варианты использования классификаций включают:
- классификацию документов и фильтрацию почтового спама, когда документы группируются в несколько классов. Например, спам-фильтр использует два класса, а именно "спам" и "неспам";
- классификацию образца по видам. Например, классификационная модель МО может прогнозировать разновидность цветка на основе данных о длине и ширине чашелистика и лепестка;
- классификацию изображений. При наличии набора изображений (например, мебели) можно использовать систему МО для распознавания и присвоения имен объектам на этих изображениях.
6.2.4 Кластеризация
Задания по кластеризации включают в себя группировку совокупностей входных данных. В отличие от заданий по классификации в заданиях по кластеризации классы не заданы заранее, а определены в процессе кластеризации. Кластеризация может быть использована в качестве одного из этапов подготовки данных для выявления однородных данных, которые затем можно применять в качестве обучающих данных для МО с учителем. Кластеризация также может быть применена для обнаружения выбросов и аномалий путем выявления совокупностей входных данных, не похожих на другие. Примеры заданий по кластеризации включают сортировку и организацию файлов.
6.2.5 Обнаружение аномалий
Обнаружение аномалий включает в себя выявление совокупностей входных данных, не соответствующих ожидаемым закономерностям. Обнаружение аномалий может быть полезно для приложений по выявлению мошенничества или необычной активности. Для обнаружения аномалий модель МО определяет, является ли некоторая совокупность входных данных типичной для данного распределения.
6.2.6 Уменьшение размерности
Уменьшение размерности заключается в уменьшении количества атрибутов (размерностей) для конкретной совокупности данных при сохранении большей части полезной информации.
Уменьшение размерности может стимулировать выделение наиболее полезных признаков набора данных и тем самым способствовать снижению затрат на вычисления.
Уменьшение размерности смягчает различные негативные последствия хранения наибольшего количества признаков, известные под общим наименованием "проклятие размерности". Уменьшение размерности также полезно для изучения данных и анализа моделей.
Методы уменьшения размерности включают уменьшение размерности без учителя, с учителем и полуконтролируемое [1].
6.2.7 Другие задания
Существует множество других заданий с различными целями и желаемыми результатами. Для конкретного приложения существует свой набор специфических заданий. Примеры других заданий включают семантическую сегментацию текста или изображений, машинный перевод, распознавание или синтез речи, локализацию объектов и генерацию изображений.
На стадии планирования задание заключается в оптимизации последовательности действий агента(ов) посредством наблюдения за состоянием окружающей среды.
Несмотря на разнообразие заданий сформулирован ряд концепций, позволяющих установить связь между отдельными заданиями данной группы. Одной из таких концепций является структурное прогнозирование, где задания сформулированы таким образом, чтобы искомый результат модели представлял собой структурированный объект, а не одно значение.
Для структурного прогнозирования необходимы вычислительные методы, способные выявлять закономерности в полученном результате путем их явного моделирования или совместного описания структуры в целом, и модель, которая внутренне моделирует закономерности.
Варианты использования структурного прогнозирования включают:
- построение дерева парсинга для предложений на естественном языке;
- перевод предложения с одного языка на другой язык;
- пргнозирование структуры белка;
- семантическая сегментация изображения.
6.3 Модель
В ИСО/МЭК 22989:2022 (3.2.11) определена модель МО как математическая модель, которая генерирует вывод или прогнозирование на основе входных данных. Модель МО включает в себя структуру данных и программное обеспечение для обработки этой структуры, причем оба параметра определены выбранным алгоритмом МО. Модель конфигурируется входными и выходными данными, необходимыми для решения поставленной задачи.
Модель наполняется ("обучается") для представления соответствующих статистических свойств обучающих данных. В процессе обучения модель эффективно "учится" решать задачи при помощи обучающих данных с целью применения полученных знаний в реальном мире.
Модели МО выдают результаты, являющиеся аппроксимациями оптимальных решений. Для выполнения такой аппроксимации алгоритмы МО используют методы статистической оптимизации. Полученное в результате применения данных методов сопоставление входных и выходных данных модели отражает закономерности, полученные на основе обучающих данных. Закономерности могут относиться к корреляциям, причинно-следственным связям или категориям объектов данных. Модели МО являются результатом использования обучающих данных. Таким образом, если используемые данные неполны или отражают существующие социальные предрассудки и/или предвзятость, то это найдет отражение и в работе модели. Поэтому следует внимательно относиться к наборам данных, применяемым для обучающей модели. Логика, созданная в процессе МО и представленная обученной моделью, не задается программистом, а эволюционирует в процессе обучения.
Для проверки работоспособности модели ее оценивают с помощью оценочных метрик.
Повторное обучение заключается в обновлении обученной модели путем обучения на других обучающих данных. Необходимость в повторном обучении возникает из-за многих факторов, включая отсутствие достаточно большого количества обучающих данных, дрейф данных и дрейф концепции.
При дрейфе данных точность сгенерированных моделью результатов со временем снижается из-за изменений в статистических характеристиках эксплуатационных данных. В этом случае модель следует повторно обучить с помощью новых обучающих данных, которые наиболее отражают эксплуатационные данные.
При дрейфе концепции граница принятия решения перемещается, что также снижает точность генерируемых результатов, даже если данные не изменились. В случае дрейфа концепции целевые переменные в обучающих данных необходимо разметить заново, а модель - повторно обучить.
Повторное обучение также может происходить с целью переноса обучения, оптимизации или модификации модели МО.
Некоторые модели отличаются простотой настройки, что позволяет повторно их обучать и оптимизировать для конкретных вариантов использования или применять в представленном виде. В качестве примера можно привести доступную на рынке модель машинного перевода, которую можно повторно обучить для перевода юридических документов.
Непрерывное обучение - это частный случай повторного обучения, когда производительность модели постоянно развивается в результате непрерывного обучения модели на эксплуатационных данных. В таких случаях может возникнуть необходимость постоянного мониторинга работы модели или введения "ограничителей", определяющих приемлемое поведение модели.
6.4 Данные
На рисунке 2 представлена диаграмма, на которой показано разделение всех данных на четыре взаимоисключающие категории:
a) набор обучающих данных, используемый для оценки параметров моделей-кандидатов;
b) набор валидационных данных, также называемый набором данных разработки в зависимости от области ИИ (например, в обработке естественного языка), используемый для выбора наиболее подходящей модели в соответствии с критерием эффективности;
c) набор тестовых данных, используемый для проверки способности модели к обобщению и определяющий ее производительность с будущими данными;
d) эксплуатационные данные, состоящие из оперативных данных, которые будут использованы моделью для получения результатов. Распределение эксплуатационных данных может отличаться от распределения наборов обучающих, валидационных и тестовых данных.
Наборы обучающих, валидационных и тестовых данных могут быть дополнены искусственно смоделированными и возмущенными данными.
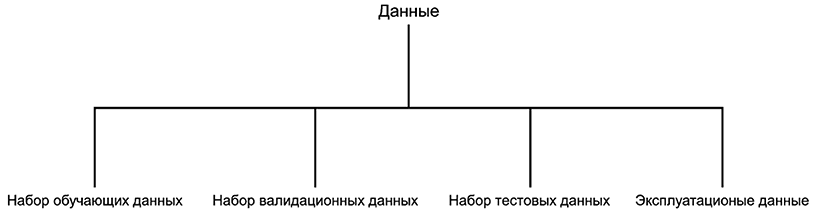 |
Рисунок 2 - Взаимосвязь понятий: данные и наборы данных
Перечисленные типы данных могут состоять только из входных данных или из входных данных с метками (ожидаемых выходных данных). Валидационные и тестовые данные часто размечены, а эксплуатационные данные, как правило, не размечены. Разметка обучающих данных зависит от подхода МО: они могут быть неразмеченными, частично размеченными или полностью размеченными. Размеченные обучающие данные позволяют алгоритму МО выявить статистические связи между входными переменными и целевой переменной. Неразмеченные обучающие данные позволяют алгоритму МО самостоятельно выявлять статистические корреляции и структуру входных данных.
Валидационные и тестовые данные используют для статистических показателей результативности (которые рассмотрены в 6.5.5), но их применение отличается: валидационные данные используют для настройки гиперпараметров, в то время как тестовые данные предназначены для оценки модели. Целью тестовых данных является проверка корректного функционирования или обобщения обученной модели на эксплуатационных данных. Обученные модели, не способные достаточно четко обобщать, называют переобученными (по отношению к обучающим данным).
Следует отметить, что использование термина "тестовые данные" ограничено спецификой процессов МО и отличается от применения данного термина в контексте проверки и валидации интегрированной системы, использующей компоненты МО, когда этот термин будет означать любые данные, применяемые для целей проверки и валидации без отношения к МО. Следует обратить внимание на то, что специфическое для МО использование термина "валидационные данные" не связано с процессами верификации и валидации, поскольку данный термин относится к созданию модели.
Чтобы обеспечить надежное применение процессов МО, обучающие, валидационные и тестовые данные должны представлять собой непересекающиеся наборы данных. Наборы обучающих, валидационных и тестовых данных могут быть получены из одного набора данных путем разделения либо приобретены по отдельности. В идеальной конфигурации все наборы данных имеют одинаковое статистическое распределение, но в зависимости от варианта использования и подхода МО может потребоваться иное распределение.
Для достоверной оценки обученной модели тестовые данные должны иметь распределение, максимально приближенное к распределению эксплуатационных данных.
Эксплуатационные данные доступны модели только после ее развертывания. Для того чтобы модель генерировала точные результаты, эксплуатационные данные должны иметь распределение, аналогичное распределению обучающих и валидационных данных, хотя существуют специальные методы, которые могут смягчить снижение производительности в случае расхождения.
Со временем распределение эксплуатационных данных может дрейфовать, что может потребовать повторного обучения модели на новых данных. Когда модель должна быть динамически адаптирована к новым закономерностям в эксплуатационных данных, модель можно постоянно обучать повторно, используя информацию, полученную из эксплуатационных данных. Примеры представлены в 6.3.
6.5 Инструменты
6.5.1 Общие положения
Для создания модели МО используют инструменты, относящиеся к категориям подготовки данных, алгоритмов МО, методов оптимизации и оценивающих метрик. Производительность модели МО оценивают с помощью инструментов, обобщающих оценивающие метрики.
Создание моделей МО часто требует выполнения высокопроизводительных вычислений в связи с потребностями в вычислительных мощностях и с использованием больших наборов обучающих данных. Производительность вычислительных систем и систем хранения данных также может влиять на скорость создания и обучения моделей МО.
Фундаментальные задачи в области МО включают статистический анализ, разработку алгоритмов и оптимизацию. Статистический анализ основан на принципах построения математических моделей, полученных на основе обучающих данных. Проектирование алгоритмов - это способ реализации алгоритмических приемов, используемых для построения модели МО. Оптимизация модели МО также является важной задачей при реализации МО. Следующей задачей является понимание потенциала и возможностей МО. Поскольку МО опирается на данные, то оно во многих случаях будет воспроизводить, усиливать и распространять присущие данным недостатки и проявления необъективности и предвзятости.
6.5.2 Подготовка данных
Подробная информация о подготовке данных представлена в 8.3.
6.5.3 Категории алгоритмов МО
6.5.3.1 Общие положения
Выбор алгоритма МО определяет схему вычислений модели МО и подход к ее обучению.
Алгоритмы могут быть использованы для различных целей МО, в том числе:
- для представления информации на стадии подготовки данных с целью дальнейшего выделения признаков;
- создания модели МО.
На рисунке 3 показаны примеры различных категорий алгоритмов МО.
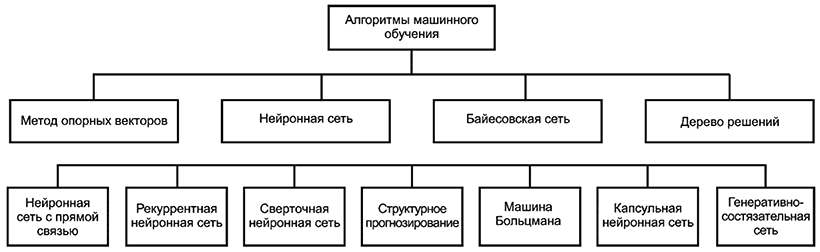 |
Рисунок 3 - Примеры различных категорий алгоритмов МО
Для определения структуры модели МО и подхода к ее обучению часто недостаточно ограничиться выбором только алгоритма МО. Для многих алгоритмов также следует выбрать гиперпараметры.
Гиперпараметры - это характеристики алгоритма МО, влияющие на его процесс обучения. Гиперпараметры могут быть использованы в процессах оценки параметров модели. Примеры гиперпараметров для НС включают количество слоев сети, ширину каждого слоя и тип функции активации. Один из практических подходов к определению оптимального набора гиперпараметров среди всех возможных комбинаций заключается в проведении случайного поиска с помощью функции ограничений и измерении производительности на наборе валидационных данных. Этот шаг называется выбором модели или настройкой гиперпараметров.
6.5.3.2 Нейронная сеть
6.5.3.2.1 Общие положения
________________
Между выходным и входным слоями НС могут существовать скрытые слои, и в этом случае сеть называется многослойным перцептроном или многослойной НС. Термины "глубокая нейронная сеть" и "глубокое обучение" относятся к НС с большим количеством скрытых слоев. Глубокое обучение - это подход к созданию насыщенных иерархических представлений посредством обучения НС с большим количеством скрытых слоев. Этот процесс позволяет НС постепенно совершенствовать конечный результат. Глубокое обучение может уменьшить или устранить необходимость в выделении признаков, поскольку наиболее значимые признаки определяются автоматически.
НС можно разделить на три общих типа: дискриминационные, генеративные и гибридные (комбинация двух первых типов).
НС можно рассматривать как коннекционистский подход. Коннекционизм использует сеть взаимосвязанных единиц, которые обычно являются простыми вычислительными единицами [2]. Поведение сети можно отрегулировать путем изменения весов каждой связи, что, как описано выше, достигается путем обучения. Узлы сети обрабатывают информацию параллельно.
Глубокое обучение может потребовать значительного времени и вычислительных ресурсов. Для работы НС МО часто требуется значительное количество вычислительной мощности и памяти. Снижение сложности модели может быть полезным для использования НС в мобильных и встроенных устройствах. Влияние времени выполнения и потребление энергии можно свести к минимуму, а в некоторых случаях такое снижение даже позволяет запускать НС в реальном времени на мобильных устройствах, не полагаясь на облачные сервисы. Сжатие весов или сжатие архитектуры может значительно снизить сложность модели при сохранении практически одинаковой производительности.
6.5.3.2.2 Нейронные сети с прямой связью
Нейронные сети с прямой связью (FFNN) являются наиболее простыми архитектурами НС. Они передают информацию от входного слоя к выходному только в одном направлении. Между нейронами внутри одного слоя связь отсутствует. Два соседних слоя обычно "полностью связаны", т.е. каждый нейрон одного слоя связывается с каждым нейроном последующего слоя. Каждая связь имеет свой весовой коэффициент. FFNN обычно обучаются методом обратного распространения ошибки с использованием размеченных обучающих данных, где каждая выборка размечается эталонными данными для получения ожидаемого значения выходных данных. Разница между фактическим результатом, полученным FFNN, и эталонными данными называется ошибкой [3]. Метод обратного распространения ошибки заключается в использовании ошибки на выходном слое для корректировки весов связей из предыдущих последовательных слоев. Метод часто используют совместно с алгоритмом градиентного спуска [4].
6.5.3.2.3 Рекуррентная нейронная сеть
6.5.3.2.3.1 Общие сведения
Рекуррентные нейронные сети (РНС) [5] - это НС, предназначенные для работы с последовательными входными данными, вводимыми в упорядоченной последовательности и в тех случаях, когда порядок данных в последовательности имеет значение. Примерами подобных входных данных являются динамические последовательности, такие как потоки звука и видео, а также статические последовательности, такие как текст и отдельные изображения. В целом РНС пригодны для использования во многих областях, поскольку большую часть форматов данных без временной шкалы (т.е. в отличие от звука и видео) можно представить в виде последовательности. Изображение или строка текста могут подаваться по одному пикселю или символу, поэтому зависящие от времени веса используются для данных, появляющихся раньше по последовательности, а не по времени.
РНС обладают свойством фиксирования текущего состояния, на которое влияет прошлое обучение. Ввод входных данных должен быть осуществлен в виде последовательности проходов в течение определенного времени, и РНС сохраняет информацию из одного прохода для ее использования в последующих проходах, т.е. РНС обладает памятью. Таким образом, в рамках текущего прохода в РНС у нейронов на одном слое имеются не только взвешенные связи от нейронов с предыдущего слоя, но и входные данные от нейронов из предыдущих проходов. РНС широко используются в распознавании речи, машинном переводе, прогнозировании временных рядов и распознавании изображений. В целом РНС наиболее подходят для оптимизации или дополнения информации, например для автозаполнения.
РНС пригодны для обработки последовательных входных данных переменной длины или для выходных последовательных данных переменной длины. К распространенным типам РНС относятся сети с ДКП и сети с УРБ, являющиеся упрощенным вариантом сетей с ДКП.
6.5.3.2.3.2 Сети долгой краткосрочной памяти
Сети ДКП - это разновидность РНС, разработанная для решения задач, требующих запоминания информации с разницей во времени как в большую, так и в меньшую сторону, что делает их пригодными для обучения долгосрочным связям. Они разработаны для решения задачи исчезающего градиента в РНС, связанной с методом обратного распространения ошибки. Каждая ячейка сети ДКП имеет внутреннюю память и скрытое состояние. Обучение РНС построено на использовании метода обратного распространения ошибки, но при данном подходе может возникать проблема исчезающего или взрывающегося градиента [6]. Во время обучения веса РНС обновляются на основе частной производной функции ошибок на каждой итерации обучения. Производная может быть либо предельно маленькой, в результате чего РНС фактически не поддается обучению, либо чрезмерно большой, в результате чего РНС становится крайне неустойчивой.
Сеть ДКП предназначена для обучения долгосрочным зависимостям и имеет архитектуру, основанную на комбинации нейронов, с ячейкой (обладающей памятью), входным фильтром, выходным фильтром и фильтром забывания. С каждым нейроном связана ячейка памяти, содержащая информацию о его предыдущем состоянии. Функция фильтров заключается в защите информации путем остановки или пропускания ее потока. Входной фильтр определяет, сколько информации из предыдущего слоя будет храниться в ячейке. Выходной фильтр на другом конце определяет, какая часть информации о данной ячейке передается в следующий слой. Фильтр забывания позволяет сети очистить ее внутреннее состояние. Например, если входные данные представляют собой абзац текста и в нем начинается новое предложение, может возникнуть необходимость в том, чтобы сеть забыла некоторые символы из предыдущего предложения. Поскольку каждый из нейронов сети ДКП имеет отдельный вес для каждого из фильтров, данная сеть сложнее других видов НС, в результате чего сети ДКП обычно требуют больше ресурсов для обучения и работы. Сети ДКП способны обучаться сложным последовательностям, например имитации литературного стиля Шекспира или сочинению музыки.
6.5.3.2.4 Сверточная нейронная сеть
Сверточные нейронные сети - это тип НС, включающий минимум один сверточный слой для фильтрации полезной информации из входных данных. СНС в основном используют для обработки изображений [7] и разметки видео, но также применяют и с другими типами входных данных, такими как аудио или текст (иногда с использованием рекуррентных версий или рекуррентных СНС). Шаблоны связей СНС для обработки изображений напоминают структуру зрительной коры головного мозга у животных. В отличие от РНС каждый нейрон, расположенный на одном слое СНС, связан только с нейронами на предыдущем слое и не получает информацию о своем предыдущем состоянии. Набор входных нейронов одного нейрона называется его рецептивным полем. В случае СНС НС обычно содержит различные типы слоев, включая сверточные и объединяющие слои. Входные данные для СНС должны иметь топологию в виде сетки. Это могут быть изображения (двумерная сетка) или временные ряды (одномерная сетка). Сверточные слои рассматривают входные данные как вектор или матрицу (например, двумерное изображение) и применяют к ним свертку, которая представляет собой скользящее скалярное произведение или взаимнокорреляционную функцию, где вектор или матрица, называемая ядром, применяются к входным данным. Определенная свертка предназначена для извлечения определенных характеристик из входных данных и создает карту характерных признаков для следующего слоя СНС. Такой подход позволяет сделать СНС позиционно инвариантной по отношению к признакам входных данных, что предпочтительнее при работе с изображениями реального мира.
Объединяющие слои уменьшают размерность своей входной информации либо локально (обработка небольшого количества входных данных), либо глобально, обрабатывая все входные данные с предыдущего слоя. Объединение позволяет эффективно отсеять несущественные детали. Для получения наилучшего результата можно последовательно использовать несколько сверточных и объединяющих слоев.
Полностью связанные слои обычно используют рядом с выходом СНС. На практике СНС часто содержат в конце FFNN для дальнейшей обработки данных, что позволяет получить нелинейные абстракции.
6.5.3.2.5 Структурный перцептрон
Структурный перцептрон представляет собой расширение алгоритма перцептрона, используемого в НС. Структурные перцептроны используют один слой нейронов несколько раз подряд для генерации различных частей результата. Процедура обучения структурного перцептрона отражает этот принцип: одна целевая переменная применена для оценки нескольких сгенерированных результатов одновременно.
6.5.3.2.6 Глубокая машина Больцмана
Машины Больцмана - это сети из двоичных единиц {0,1}, состоящие из набора видимых единиц и набора скрытых единиц. Связи существуют только между соседними единицами. МБ являются двунаправленными, и их можно обучить неизвестным вероятностным распределениям. МБ полезны в распознавании объектов и речи, являясь генеративным алгоритмом.
Простейшая форма МБ называется ограниченной машиной Больцмана (ОМБ). Сеть, в которой несколько слоев ОМБ располагаются подряд, называется глубокой машиной Больцмана (ГМБ). Глубокие сети доверия (ГСД) похожи на ГМБ, но в них также присутствуют слои нейронов (т.е. однонаправленные связи).
6.5.3.2.7 Капсульная нейронная сеть
Капсульные нейронные сети (CapsNet) - это НС, использующие динамическую маршрутизацию и способные обучаться на разреженных данных. Они нивелируют некоторые ограничения СНС, заменяя нейроны структурами-капсулами, состоящими из наборов тесно переплетенных нейронов, обновляющихся одновременно. Связи между капсулами также усовершенствованы, чтобы сети CapsNet могли четче отражать иерархические отношения и создавать представления более высокого порядка. Сети CapsNet относятся к дискриминативному типу.
6.5.3.2.8 Генеративно-состязательная сеть
Генеративно-состязательные сети (ГСС) - это НС, содержащие один или несколько генераторов, пытающихся создать наиболее репрезентативные для набора данных образцы, и один или несколько дискриминаторов, пытающихся отличить сгенерированные образцы от реальных. Компоненты генератора и дискриминатора обучаются вместе, чтобы усовершенствовать внутренние представления сети.
ГСС могут быть использованы для выполнения различных заданий (например, классификации), а также для других целей, таких как генерация модельных данных или адаптация к новой области.
6.5.3.3 Байесовская сеть
Байесовские сети - это графовые модели, используемые для генерации прогнозов о зависимостях между переменными. Они могут быть использованы при вычислении вероятности для причин или переменных, способных оказать влияние на результат. Подобная причинность чрезвычайно полезна в таких сферах, как постановка медицинского диагноза. Байесовские сети также подходят для анализа данных, работы с неполными данными и смягчения переобучения моделей по данным. Байесовские сети опираются на байесовскую вероятность: вероятность события рассматривается как степень веры в наступление события. Существуют различные методы байесовской статистики, которые можно использовать совместно с байесовскими сетями для определения причинности или анализа данных. Байесовские сети часто используют графическое представление переменных, называемое ориентированными ациклическими графами. Свойство этих графов заключается в том, что, следуя по связям между переменной x и другими переменными, граф не возвратится к переменной x. Дополнительная информация о байесовских сетях приведена в [8].
6.5.3.4 Наивный байесовский алгоритм
Наивный байесовский алгоритм - это метод классификации, основанный на теореме Байеса. Теорема определяет вероятность наступления события, основываясь на знаниях о предшествующих связанных с ним событиях. Они помогают повысить точность определения того, произойдет ли событие. Например, постановка медицинского диагноза может быть более точной, если учесть образ жизни пациента - сидячий или активный. Наивный байесовский алгоритм классификации предполагает, что признаки данных статистически независимы друг от друга. Преимущество данного метода классификации заключается в том, что он относительно прост и не требует большого набора данных для обучения.
6.5.3.5 Метод опорных векторов
Метод опорных векторов (SVM) - это метод МО, широко используемый для классификации и регрессии. Классификатор SVM помечает образцы, разделяя их на две категории, и затем относит новые совокупности входных данных либо к одной, либо к другой категории. SVM - это алгоритмы классификации по наибольшему отступу. Они создают гиперплоскость для разделения данных на два класса, обеспечивая максимальное расстояние между классифицирующей плоскостью и ближайшими точками данных. Точки, находящиеся ближе всего к границе, называются опорными векторами. Перпендикулярное расстояние между опорными векторами и гиперплоскостью составляет половину отступа SVM. Сети SVM также используют ядерные функции для распределения данных из входного пространства в более высокоразмерное (иногда бесконечное) пространство, в котором будет выбрана классифицирующая гиперплоскость.
Обучение SVM включает в себя максимизацию отступа соответственно данным из различных категорий, находящихся на противоположной стороне гиперплоскости. На практике такие SVM с жестким отступом используют редко. Классификатор с жестким отступом работает только в том случае, если данные линейно разделимы во вложенном пространстве. Всего один образец данных может сделать невозможным нахождение разделяющей гиперплоскости. Классификаторы с мягким отступом, наоборот, позволяют образцам данных нарушать отступ (т.е. располагаться на другой стороне гиперплоскости). Классификаторы с мягким отступом пытаются достичь максимального отступа, ограничивая при этом нарушение отступа. Примерами применения SVM являются категоризация неразмеченных данных, а также составление прогнозов и распознавание закономерностей.
При использовании SVM для регрессии цель обратна цели классификатора SVM. В регрессии SVM цель состоит в том, чтобы поместить как можно больше совокупностей данных внутрь отступа, ограничив при этом нарушения отступа (т.е. количество образцов данных, выходящих за пределы отступа).
6.5.3.6 Деревья решений
Деревья решений используют древовидную структуру решений для кодирования возможных исходов. Алгоритм дерева решений широко применяют для классификации и регрессии. Дерево состоит из узлов принятия решения и листовых узлов. Каждый узел принятия решения имеет как минимум две ветви, где листовые узлы представляют собой окончательное решение или классификацию. Как правило, узлы упорядочиваются по решению с сильнейшей прогнозирующей переменной. Входные данные необходимо распределить по различным факторам, чтобы получить наилучший результат. Деревья решений являются аналогом блок-схем, где в каждом узле принятия решения может быть задан какой-либо вопрос, чтобы определить, к какой ветви следует перейти.
6.5.4 Методы оптимизации МО
6.5.4.1 Общие положения
Методы оптимизации МО используют для подбора параметров модели МО к данным МО. Сложность оптимизации МО состоит в том, чтобы найти оптимальные параметры модели МО для минимизации конкретной функции потерь для конкретных данных МО. Большинство следующих методов опираются на использование функции потерь (иногда называемой "функция затрат"), чтобы определить, сходится ли модель с приемлемым решением. Распространенные методы оптимизации МО описаны в нижеприведенных пунктах.
Помимо методов оптимизации существуют другие методы, способные повысить соответствие модели МО данным. Одним из таких аспектов является выбор более подходящей функции потерь. Например, можно использовать метод регуляризации - это техника для борьбы с переобучением и для снижения высокой дисперсии при генерации результатов путем введения новых выражений в потерю. Принцип работы состоит в наложении штрафа за сложность модели и в предпочтении более общей, менее точной модели.
6.5.4.2 Метод градиентного спуска
Градиентный спуск - это итерационный метод поиска минимума функции: при единовременной подаче всего набора данных параметры обновляются постепенно и в том же направлении, что и первая производная (градиент) функции. Решением выступает глобальный оптимум, когда целевая функция является выпуклой. Расчет обновленных параметров с использованием не всего набора данных, а случайных выборок меньшего объема называется стохастическим градиентным спуском (СГС). СГС снижает затраты на вычисления, но при этом существует риск получить решение, попавшее в локальный минимум. Размер итерационного шага градиента называется скоростью обучения.
Метод импульса вводит скорость в качестве переменной для обозначения направления и скорости изменения параметра в его пространстве; эта операция сохраняет влияние предыдущего направления обновления для следующей итерации. Ускоренный метод градиентного спуска Нестерова использует адаптивное выражение импульса, что приводит к более быстрому схождению.
Регулировка скорости обучения путем изменения размера шага обновления каждого параметра улучшает эффективность метода градиентного спуска. Это явление называется адаптивной скоростью обучения. Примером может служить AdaGrad (адаптивный градиентный алгоритм), который автоматически настраивает скорость обучения.
Избыточная информация в обучающих данных может привести к медленной сходимости при использовании метода СГС. Стохастический средний градиент поддерживает состояние параметра для записи суммы последних градиентов. Эта сумма случайным образом обновляется на каждой итерации и в каждом цикле заменяет старый градиент новым. Подобный подход позволяет снизить уровень дисперсии.
6.5.4.3 Метод Ньютона
В методе Ньютона использованы первая производная (градиент) и матрица вторых производных, также называемая матрицей Гессе, для аппроксимации целевой функции квадратичной функцией. Метод Ньютона подгоняет локальную поверхность текущего положения к квадратичной поверхности; этот метод противопоставляется методу градиентного спуска, который подгоняет текущую локальную поверхность к плоскости.
6.5.4.4 Сопряженный градиент
При использовании метода СГ вычисляют векторное произведение Гессе без непосредственного расчета матрицы Гессе, как в методе Ньютона. Метод СГ генерирует новое направление поиска, используя только предыдущий вектор. Это позволяет избежать вычислительных штрафов, связанных с вычислением обратной матрицы Гессе.
6.5.4.5 Гауссовские процессы
Гауссовский процесс - это набор случайных переменных с последовательными совместными гауссовскими распределениями. Гауссовский процесс основан на теореме Байеса и статистическом обучении. Его преимущества заключаются в гибком непараметрическом выводе и высокой интероперабельности, однако он также характеризуется сложностью в применении и высоким требуемым объемом памяти.
6.5.4.6 Аппроксимация методом наименьших квадратов
Аппроксимация методом наименьших квадратов - это метод подгонки полиномиальной функции к заданным данным посредством минимизации квадрата суммы разностей между результатами полиномиальной функции и заданными данными. Для достижения надлежащего результата порядок полинома должен соответствовать данным измерений. Аппроксимация методом наименьших квадратов может работать пакетно с полным набором данных или рекурсивно с растущим набором данных.
6.5.4.7 Оценка максимального правдоподобия
Оценка максимального правдоподобия - это метод оценки параметров распределения вероятностей путем максимизации функции правдоподобия. Для построения вероятностной модели на основе наблюдаемых данных в методе оценки максимального правдоподобия выбирают гипотезу, максимизирующую вероятность наблюдаемых данных с учетом гипотезы. В общем виде данный метод не использует априорные знания для предпочтения определенной гипотезы. В методе оценки максимального правдоподобия для вычислений часто используют логарифм функции правдоподобия.
6.5.4.8 Ожидание-максимизация
Ожидание-максимизация - это итерационный метод для изучения параметров модели со скрытыми переменными, не наблюдаемыми в данных. Он заключается в чередовании шагов ожидания (оценка скрытых переменных на основе текущих параметров) и шагов максимизации (повторная оценка параметров для оптимизации вероятности данных, учитывая текущее значение скрытых переменных) для достижения сходимости.
6.5.5 Метрики оценки МО
6.5.5.1 Общие положения
Задания МО (обсуждаемые в 6.2) обычно определяют подходящие метрики оценки. Понимание варианта использования модели необходимо для выбора подходящих метрик оценки. Для адекватного выражения и изучения результативности модели может потребоваться несколько метрик. Применение только одной метрики, даже агрегированной как мера F1, без тщательной проверки базовых результатов является рискованным. Кроме того, несбалансированность классов в обучающих данных - это вмешивающийся фактор, способный исказить различные метрики.
Существует множество метрик, отражающих результативность обученных моделей, таких как:
- доля правильных ответов, рабочие характеристики приемника (ROC), матрица ошибок, точность, отклик и мера F1 могут быть использованы для оценки алгоритмов классификации;
- средняя абсолютная ошибка (САО), среднеквадратичная ошибка, относительная абсолютная ошибка, относительная квадратичная ошибка, средняя ошибка "ноль-единица" и коэффициент детерминации являются общими метриками для регрессионных моделей;
- метрики оценки для моделей кластеризации включают среднее расстояние до центра кластера, среднее расстояние до другого центра, количество точек и максимальное расстояние до центра кластера.
Нижеприведенные подпункты описывают примеры таких метрик, но не содержат их исчерпывающий список.
6.5.5.2 Точность, отклик, чувствительность и специфичность
При оценивании эти метрики обычно используют в парах, так как они дополняют друг друга: либо ППЗ и ОПЗ, в данном случае называемые точностью и откликом; либо TPR и TNR, в данном случае называемые чувствительностью и специфичностью.
Существует множество способов применения данных определений, и значение терминов различается в зависимости от того, является ли классификация бинарной или многоклассовой. В бинарной классификации один класс выбирают в качестве положительного, и определения применяют только к этому классу. Так, например, термин "точность" обозначает точность положительного класса, а точность другого класса не вычисляет. В многоклассовой классификации определения поочередно применяют ко всем классам, а точность обозначает некоторую комбинацию точности для каждого класса.
6.5.5.3 Мера F1
Мера F1 выражает производительность модели через комбинацию отклика и точности и определяется средним гармоническим значением точности и отклика. Наилучшее значение меры F1 равно 1, что означает достижение идеальной точности и отклика.
6.5.5.4 Доля правильных ответов
Доля правильных ответов выражает количество правильных классификаций модели из общего числа неправильных и правильных классификаций.
В основном эта метрика актуальна для бинарных классификаций. В многоклассовой классификации она может обозначать либо точность каждого класса, либо точность модели. Точность каждого класса равна отклику этого класса, поэтому термин "отклик" является предпочтительным. В метрике доли правильных ответов модели не учтен тот класс, к которому принадлежит образец, и рассмотрена только правильность или ошибочность его классификации путем суммирования результатов всех образцов без исключения. Однако эта метрика обычно менее информативна, чем точность и отклик или мера F1.
В многозначной классификации термин "доля правильных ответов" часто обозначает долю правильных ответов для подмножества, т.е. долю правильных ответов в прогнозировании правильного набора меток (в целом).
6.5.5.5 Рабочие характеристики приемника и площадь под кривой
Рабочие характеристики приемника (ROC) моделируются в виде кривой, отражающей способность модели различать классы. График строится как соотношение между TPR и FPR. Любая точка на кривой может быть выбрана в качестве рабочей точки для модели, что позволяет получить информацию о TPR и FPR. Таким образом, в зависимости от области применения и значимости, придаваемой TPR и FPR, рабочая точка может быть выбрана для максимизации предпочтительной точности и отклика. На рисунке 4 показан пример кривой ROC.
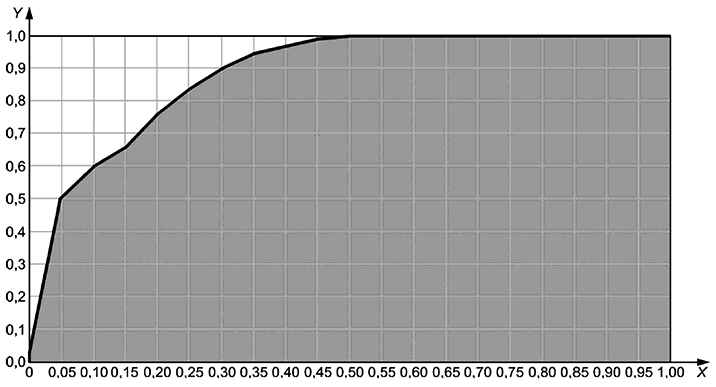 |
X - доля ложных положительных классификаций;
Y - доля истинных отрицательных классификаций;
Рисунок 4 - Кривая рабочих характеристик приемника
Площадь под кривой ROC (AUC) является мерой эффективности по всем пороговым значениям классификации. Ее значение неизменно находится в диапазоне [0, 1] и может использоваться для ранжирования моделей. Чем выше значение AUC, тем совершеннее генерация результатов. Наилучший возможный AUC равен 1,0, а наихудший ожидаемый AUC - 0,5 (поскольку диагональ обозначает случайные сгенерированные результаты). Любое значение менее 0,5 означает, что пользователь может поступить прямо противоположно рекомендациям модели, чтобы получить значение более 0,5 [9]. AUC инвариантен к масштабу и порогу классификации, что может быть положительным или отрицательным свойством в зависимости от применения. AUC обычно используют при несбалансированности классов в обучающих данных. На рисунке 4 показан пример AUC в виде серой области под кривой ROC.
6.5.5.6 Матрица ошибок
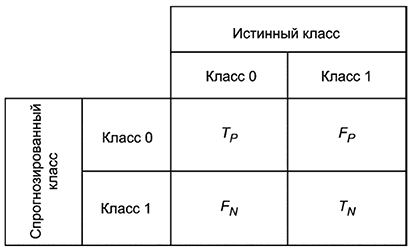 |
Рисунок 5 - Матрица ошибок
6.5.5.7 Коэффициент Каппа
Коэффициент Каппа (называемый также коэффициентом Каппа Коэна) позволяет измерить межрейтинговую надежность для качественных элементов. В МО коэффициент Каппа используется для измерения соответствия между классификацией модели и метками эталонных данных. Он также пригоден для проверки соответствия нескольких моделей и отбраковывания моделей с низким уровнем соответствия. Коэффициент Каппа полезен в случае несбалансированности наборов данных, поскольку он выражает производительность модели относительно случайного угадывания с использованием целевого распределения приложения.
Коэффициент k {0,1} измеряет степень межнаблюдательского соглашения. Измерение степени, в которой сборщики данных (оценщики) присваивают одинаковые значения или баллы одной и той же переменной или наблюдаемому объекту, называется межрейтинговой надежностью. Данная метрика отражает вероятность того, что оценщики ввиду субъективности угадывают значение переменных из-за неопределенности.
Несмотря на то что иногда данный способ используют в качестве метрики результативности модели, он разработан не для этих целей, и в научной литературе его применение не рекомендуется [10], [11].
6.5.5.8 Коэффициент корреляции Мэтью
7 Подходы к машинному обучению
7.1 Общие положения
Методы МО можно разделить на три подхода: МО с учителем, МО без учителя и МО с подкреплением. Полуконтролируемое МО, МО с самоконтролем, перенос обучения и ансамблевое обучение появились на основе нескольких подходов МО одновременно и заслуживают отдельного рассмотрения.
Подходы МО, описанные в следующих подразделах, могут задействовать несколько методов МО, как показано на рисунке 6. Некоторые из используемых методов описаны в разделе 6. Списки методов на рисунке 6 являются примерными, и в настоящем стандарте представлены не все существующие методы. Как показано на рисунке 6, некоторые методы использованы в нескольких подходах МО, например НС использованы во всех подходах МО.
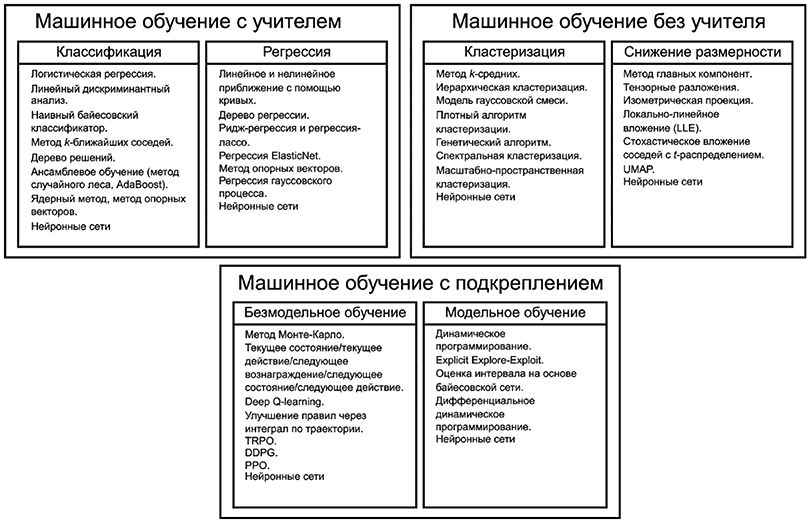 |
Рисунок 6 - Методы МО, разбитые по группам "машинное обучение с учителем", "машинное обучение без учителя" и "машинное обучение с подкреплением"
7.2 Машинное обучение с учителем
При МО с учителем модели МО обучают с использованием размеченных данных. Размеченные данные состоят из образцов, входные данные которых сопоставлены с правильными, или истинными, выходными данными. Таким образом, обучающие данные организованы в виде пар входных переменных и "истинных" выходных данных. В различных контекстах истинные выходные данные также называют метками, целевыми переменными или эталонными данными. Для создания модели при обучении с учителем, как показано на рисунке 7, алгоритм подгоняется к входным и выходным данным.
Рисунок 7 - Создание модели МО с помощью МО с учителем
Метки могут быть частью исходных данных, но зачастую возникает необходимость генерировать метки вручную или с помощью других технологий ИИ. В зависимости от целевого задания МО метки могут принимать различные формы:
- для классификации требуются категориальные метки (категория, к которой принадлежит совокупность данных, например "собака" или "здание");
- для регрессии требуются числовые метки (непрерывные значения, такие как степень, правдоподобие или вероятность);
- в случае структурного прогнозирования метки могут принимать форму структурированного объекта (например, последовательность, изображение, дерево или граф).
Типичный процесс МО с учителем представлен на рисунке 8, где показаны различные процессы создания, оценки и использования модели МО. Стадия "создание наборов данных и моделей" включает в себя подготовку, обучение и выбор модели, а также данных, необходимых для ее создания или оценки. На стадии "оценка модели" модель тестируется с использованием метрик для оценки ее работы и соответствия. На стадии "применение модели" модель применяют с эксплуатационными данными для генерации результатов. Горизонтальные области соответствуют трем стадиям, а вертикальные обозначают, с чем связаны изображенные компоненты и процессы - с данными, моделью или инструментами.
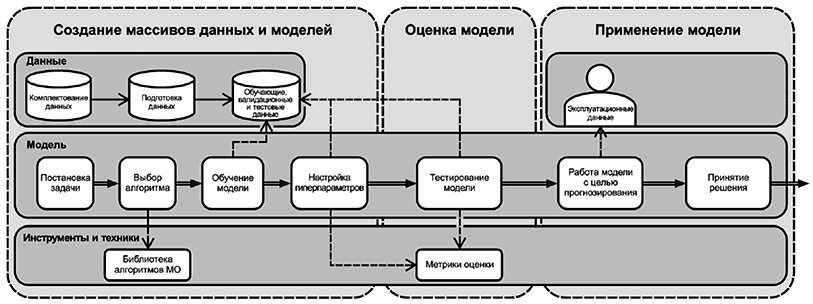 |
Рисунок 8 - Типичный процесс МО с учителем
Результативность и надежность обученной модели в значительной степени зависят от разнообразия обучающих данных (например, различные категории пешеходов), от качества обучающих данных (например, эффекты освещения или разрешение фотографий) и точности меток (например, правильная разметка пешехода на пешеходном переходе). Все свойства данных для МО с учителем подвержены появлению ошибок, поэтому данному процессу необходимо уделять пристальное внимание на протяжении всего цикла - от создания набора данных до тестирования модели.
7.3 Машинное обучение без учителя
В отличие от МО с учителем в процессе МО без учителя входные данные сопоставляют с выходными напрямую, без обучения на размеченных данных. Однако процесс обучения похож на процесс МО с учителем, показанный на рисунке 8. В процессе обучения без учителя, как показано на рисунке 9, алгоритм подгоняется к входным данным только для создания модели, без предварительного доступа к меткам. Метки обычно являются побочным продуктом обучения модели.
В заданиях по кластеризации с использованием, например, алгоритма k-средних образцы непрерывно проходят через алгоритм кластеризации, пока не будет достигнуто минимальное расстояние от каждого образца до центроида. В заданиях по уменьшению размерности с применением, например, алгоритма анализа основных компонентов (АОК) вычисляется дисперсия каждого признака во входных данных и возвращается предопределенное количество признаков с наибольшей дисперсией. Разработанные таким образом модели можно использовать для выявления сходства, закономерностей или аномалий, а также для уменьшения размерности (когда наиболее статистически значимые признаки определены независимо от метки). Обучение без учителя часто приводит к обнаружению дополнительных знаний об объекте исследования.
Рисунок 9 - Создание модели МО с помощью МО без учителя
Варианты использования МО без учителя включают:
- обнаружение кластеров в наборе входных данных;
- обнаружение латентных факторов. У данных высокой размерности зачастую необходимо уменьшить размерность, спроецировав данные на подпространство более низкой размерности, которое захватывает "сущность" данных;
- выявление корреляций в наборе измерений нескольких переменных;
- ретуширование дефектов на поврежденных или иным образом искаженных изображениях;
- анализ потребительской корзины, определяющий группы товаров, которые обычно приобретают или продают вместе.
7.4 Полуконтролируемое машинное обучение
Полуконтролируемое МО определяют как "МО, использующее в обучении как размеченные, так и неразмеченные данные". Полуконтролируемое МО - это гибрид МО с учителем и без учителя.
Один из подходов к полуконтролируемому обучению заключается в создании и использовании псевдометок для усовершенствования общей производительности модели. В таком случае модель сначала обучается на размеченных данных. Затем обученную модель используют для генерации псевдометок для неразмеченных образцов данных. В итоге формируется набор обучающих данных с размеченными и псевдоразмеченными образцами, который применяют для повторного обучения модели. Такой подход называется самообучением.
Полуконтролируемое обучение полезно в тех случаях, когда разметка всех образцов в большом наборе обучающих данных чрезмерно затратна с точки зрения времени или стоимости.
7.5 Машинное обучение с самоконтролем
Машинное обучение с самоконтролем - это подход к обучению на неразмеченных данных с использованием алгоритмов, которые обычно применяют в МО с учителем. Данный подход реализуется посредством использования неявных меток, таких как непосредственно входные данные (например, изображение для создания похожего), часть входных данных (например, одно слово из входного предложения) или другая метка, которую можно легко сгенерировать из необработанных данных (например, неперемешанная версия последовательности, которая не перемешана искусственно). Обычно он применяется для больших объемов данных.
Машинное обучение с самоконтролем чаще всего используют для обучения представлениям: конечные выходные данные модели отбрасывают, а промежуточные выходные данные могут повторно использоваться в качестве входных данных для другой модели МО. Этот подход особенно полезен для обработки неструктурированных данных и дает возможность снизить затраты на выделение признаков.
Следует отметить, что МО с самоконтролем не относится к самообучению, которое является специфическим методом полуконтролируемого МО.
7.6 Машинное обучение с подкреплением
Обучение с подкреплением отличается от других подходов, так как его принцип заключается в том, что модель инициализируется в определенном состоянии, выполняется действие, определяется вознаграждение за это действие, и модель переходит в новое состояние, которое пытается максимизировать вознаграждение. Обучение может быть использовано для инициализации модели или для определения правил, применяемых моделью для выполнения действий.
Машинное обучение с подкреплением - это процесс обучения одного или нескольких агентов взаимодействию со средой для достижения заранее определенной цели. В МО с подкреплением агенты МО обучаются посредством повторяемого процесса проб и ошибок. Цель агента - найти стратегию (т.е. построить модель) для получения наилучшего вознаграждения от среды. Среда предоставляет косвенную обратную связь после каждой пробы (как результативной, так и нерезультативной). Агент корректирует свое поведение (т.е. свою модель) на основе обратной связи. Данный процесс показан на рисунке 10. Агент определяет, какие взаимодействия стабильно предоставляют максимальное вознаграждение за его действия по достижению цели.
Действия агента и его взаимодействие со средой обычно моделируют в виде марковского процесса принятия решений (MDP). На рисунке 10 показан типичный MDP. Алгоритмы МО с подкреплением не предполагают знания точной математической модели MDP (но в некоторых техниках ее пытаются аппроксимировать). Алгоритмы МО с подкреплением обычно направлены на большие модели MDP, для которых не подходят точные методы. В отличие от МО с учителем пары входных данных, сопоставленные с размеченными истинными выходными данными, не требуются. Вместо этого задача состоит в использовании метода проб и ошибок и схождении результатов к определенной цели посредством отсроченного вознаграждения. Каждый раз, когда модель генерирует результат, рассчитывают вознаграждение и проводят дальнейшие пробы для оптимизации вознаграждения. Вознаграждение обычно представляет собой полученное в результате расчетов число, отражающее степень близости системы к достижению цели в рамках данной пробы. В некоторых случаях моделируется дополнительная информация о среде либо агенту предоставляется дополнительная информация для улучшения результатов обучения. Цель, или определение результата, обычно определяет разработчик системы.
Машинное обучение с подкреплением может также сочетаться с МО с учителем: обучение на размеченных данных используют для инициализации модели, а подкрепление - для определения последующих правил, которые агент будет применять для выполнения действий.
В некоторых случаях (например, в случае структурного прогнозирования) применение МО с подкреплением может зависеть от предварительного наличия набора данных (в том числе размеченного), поскольку он необходим для создания среды: в таких случаях среда выступает в качестве посредника информации, включенной в набор данных.
Машинное обучение с подкреплением облегчает применение непрерывного обучения, поскольку обучающая среда может быть как симулированной, так и реальной средой, присутствующей на стадии эксплуатации, при условии наличия достаточного количества информации для вычисления вознаграждения на данной стадии.
Машинное обучение с подкреплением часто используют в управлении. Управление - это применение МО с подкреплением для взаимодействия со средой. Обнаружение правил, максимизирующих вознаграждение при выполнении действий, следующих данным правилам, позволяет планировать действия и осуществлять оптимальное управление.
Варианты использования МО с подкреплением включают игру в видео- и настольные игры, где целью является максимизация полезности игровых ходов и, таким образом, получение контроля над исходом игры.
Рисунок 10 - Типичный процесс машинного обучения с подкреплением
7.7 Перенос обучения
Перенос обучения - это набор методов, направленных на хранение и извлечение знаний, полученных из данных, предназначенных для решения какой-либо задачи, с целью их применения в решении другой задачи, которая может быть отчасти связана с предыдущей (например, выполнение такого же задания в другой области). Например, знания, полученные при распознавании номеров домов на изображениях улиц, можно использовать для распознавания рукописных номеров.
Примером данной парадигмы обучения является метод тонкой настройки, когда модель, обученная для решения одной задачи, перепрофилируется и обучается для решения новой задачи. Например, модель, обученная распознавать мебель и предметы, можно настроить на распознавание обстановки (например, гостиная, пляж, кухня и т.д.) посредством обучения на фотографиях из новой области.
Для переноса обучения разработаны и другие методы, например синтез совокупностей, алгоритмы, основанные на признаках, и методы регуляризации [13].
На практике перенос обучения опирается на другие подходы к обучению и добавляет в них дополнительные шаги по хранению и извлечению знаний для дальнейшего повторного использования. Как показано на рисунке 11, методы переноса можно применять до, во время или после обучения.
Рисунок 11 - Типичные процессы переноса обучения
8 Конвейер машинного обучения
8.1 Общие положения
Для достижения конкретной прикладной цели с помощью МО создают, рассчитывают и оценивают модель МО. Процесс обычно включает в себя данные, алгоритмы и вычислительные ресурсы. В данном подразделе представлен пример конвейера МО, включая процессы, применяемые на каждом этапе. Перед началом работы с конвейером необходимо дать задание или поставить задачу, которую необходимо решить, чтобы установить конкретные цели и требования. Подробное определение задачи (включая, например, точное определение входного и выходного форматов) поможет выбрать подходящие алгоритмы МО и получить соответствующие наборы данных, необходимые для обучения модели МО.
На рисунке 12 показаны конкретные процессы МО, присутствующие в разработке, проверке, развертывании и эксплуатации модели МО, и их связь со стадиями жизненного цикла системы ИИ. Ко всему конвейеру МО применимы следующие аспекты:
- управление рисками;
- безопасность и защита персональных данных;
- подотчетность, прозрачность и объяснимость;
- безопасность, устойчивость, надежность и справедливость.
Рисунок 12 - Конвейер МО и его сопоставление с жизненным циклом системы ИИ
Описание стадий конвейера, показанных на рисунке 12, и процессы, происходящие в рамках каждой из стадий, приведены в следующих пунктах. Проектирование и создание модели МО состоит из нескольких последовательных и непоследовательных этапов. Процесс начинается с подготовительной работы, включающей в себя три этапа: получение и подготовка набора данных, выделение исполнительных признаков и выбор алгоритма. Данные процессы не зависят друг от друга и могут быть осуществлены в любом порядке или одновременно. Однако в зависимости от конкретного варианта использования могут существовать дополнительные технические ограничения, которые устанавливают определенный порядок процессов или создают необходимость их повтора. Например, анализ набора данных может помочь выделить признаки, а детализация выделенных признаков - определить выбор алгоритма, который в большей или меньшей степени полагается на них. Однако выбор алгоритма может ограничить тип или детализацию меток для аннотирования собранных данных. В таком случае его необходимо выбрать в первую очередь.
Фактическое создание модели происходит после выполнения всех подготовительных шагов, включающих в себя разработку одной или нескольких пробных моделей и выбор наиболее соответствующей из них.
8.2 Комплектование данных
Начальной стадией создания, развертывания и эксплуатации модели МО является комплектование данных. Данные являются ключевым компонентом в жизненном цикле модели МО, так как от них зависят обучение и последующий анализ. Их получение и подготовка требуют пристального внимания, поскольку укомплектованные данные должны соответствовать целям модели. Обучающие данные - часто это подмножество более крупной совокупности данных, которое дает представление об этой совокупности. Данные, используемые для обучения моделей МО с учителем, включают одну или несколько меток или целевых переменных, которые отражают достоверную информацию о записи или образце данных. Например, каждое электронное письмо в наборе писем для обучения может быть помечено как "спам" или "неспам".
Для определения точности и других показателей эффективности моделей МО потребуются валидационные и тестовые данные. Валидационные и тестовые данные можно получить вместе с обучающими данными, либо ими могут стать аналогичные наборы данных, полученные другими способами.
Тип необходимых данных зависит от решаемой задачи. Например, для прогнозирования продаж может потребоваться доступ к транзакционным данным. Для классификации изображений может понадобиться доступ к файлам изображений. Аналогичным образом задача, которую необходимо решить, определяет, какая информация (т.е. какие признаки) нужна(ы) в наборе данных. После определения источника данных приобретаются (т.е. покупаются или собираются) необходимые данные. Они могут поступать из нескольких источников, из хранилища статических данных или из потока данных. К распространенным источникам обучающих данных относят транзакции, датчики, запросы, изображения, документы, аудиофайлы и социальные сети.
8.3 Подготовка данных
Данные редко можно сразу использовать для обучения моделей МО, т.к. в них могут содержаться требования к данным для обучения. Подготовка данных обычно занимает значительное количество времени и усилий, затрачиваемых на разработку модели, и может включать использование ряда автоматизированных инструментов для форматирования и очистки различных наборов данных. Благодаря форматированию данные обретают форму, пригодную для использования конкретной системой. Очистка данных может включать в себя удаление их дубликатов и ложных данных (непригодных для решения задачи), а также дополнение недостающих данных. На этой стадии обрабатываются данные, содержащие ошибки и выбросы. Процесс подготовки данных также включает в себя их обезличивание. Даже если полученные данные уже обезличены ранее, вследствие особенностей обработки данных на этой стадии (например, вследствие объединения наборов данных) может потребоваться проведение их повторного обезличивания. Примеры этих процессов представлены в следующих абзацах об изучении, обработке, очистке, подстановке, нормализации и масштабировании, составлении набора данных, разделении данных и разметке. Данные процессы могут происходить в иной последовательности.
Изучение: изучение исходных данных. Цель - получить представление, которое поможет определить, какие процессы необходимы для подготовки данных к обучению модели. Например, к таким представлениям относятся: форма набора данных, типы данных, среднее значение, дисперсия и диапазон числовых данных, наличие индекса, признаков и меток.
Изучение распределения данных по признакам также способствует выбору действий по подготовке данных. Например, анализ распределения может помочь выявить выбросы, взаимосвязи и закономерности в данных. Эти характеристики можно использовать для выбора правильных действий по улучшению подготовки данных, а сравнение распределений обучающих данных и эксплуатационных или входных данных может помочь заинтересованным сторонам системы ИИ предвидеть эффективность планируемого решения.
Обработка данных: обработку данных проводят для создания структурированного, упорядоченного набора данных. Процесс обработки данных в таблицах включает объединение, разделение и создание граф, изменение типов и форматов данных, удаление, замену или добавление символов в строках, а также создание или переименование заголовков граф.
________________
Подстановка данных: подстановка данных обозначает процесс очистки с использованием подставленных значений для замены отсутствующих данных. Подстановка может быть однократной и многократной. Однократная подстановка (например, методы hot-deck, cold-deck, регрессия и среднее значение) непосредственно генерирует целевое значение для использования при условии отсутствия существенной неопределенности в отношении отсутствующих значений. Множественная подстановка отражает наличие неопределенности в отношении отсутствующих значений в модели подстановки, генерируя целевое значение путем рассмотрения нескольких подстановочных значений, случайно выбранных из незначительно отличающихся моделей.
Нормализация и масштабирование: значительные различия в диапазоне числовых признаков в наборе данных могут привести к тому, что признаки окажутся несопоставимыми при обучении модели МО. С одной стороны, нормализация может быть использована для приведения отдельных образцов данных к единичной норме (от 0 до 1). С другой стороны, масштабирование может быть применено для того, чтобы создать нормальное распределение из отдельных образцов или сжать образцы в заданный диапазон.
Масштабирование или нормализацию можно применять к данным для обеспечения соответствия результатов модели.
Примерами методов нормализации данных являются:
- нормализация min-max: линейное преобразование данных для приведения их в соответствие с минимальным и максимальным значениями (зачастую ноль и единица);
- нормализация Z-score: данные масштабируются на основе среднего и стандартного отклонений;
- десятичное масштабирование: перемещение десятичной точки значений атрибутов.
Составление набора данных: составление набора данных обозначает выбор или компиляцию данных, полученных из различных источников, в единый набор данных. Такое составление обычно выполняют с учетом признаков, выделенных для обучения, и достаточного распределения и представления объектов для обучения намеченным признакам.
Разделение наборов данных: моделям МО необходимы обучающие и валидационные данные для обучения модели, а также тестовые данные для ее оценки. Наборы обучающих, валидационных и тестовых данных должны быть непересекающимися. В некоторых случаях все данные приобретаются отдельными способами. Если данные получены из одного(их) источника(ов), необходимо разделить имеющиеся данные на отдельные наборы. Валидационная и тестовая части обычно значительно меньше, чем обучающая.
Разметка: разметка данных - это процесс присвоения целевой переменной образцу. Связывание данных с соответствующими метками позволяет сформировать эталонные данные. Разметка данных может быть основана на извлечении значимой информации из образца, например количества людей на изображении. Образец также может быть дополнен информацией о его содержании для создания метки (например, спорят ли два человека, изображенные на картинке). Данные могут быть размечены человеком вручную или в некоторых вариантах использования - компьютером автоматически.
Разметка данных может потребоваться для обучения, например, в случае МО с учителем или для оценки моделей, созданных не только путем обучения с учителем. В таких случаях соответствующие данные будут включать одну или несколько меток или целевых переменных, которые представляют собой эталонные данные о записи или образце.
Обезличивание - это процесс устранения связи между набором идентифицирующих атрибутов и субъектом данных, как описано в ИСО/МЭК 20889. Процесс может потребоваться для удаления ПДн, если ПДн включена в набор данных. В частности, для использования медицинских данных для обучения модели МО может потребоваться обезличивание персональных данных, особенно относящихся к таким специальным категориям, как данные о здоровье субъекта ПДн. Кроме того, проверка на засорение обучающих наборов данных имеет решающее значение для избавления от данных, которые могут привести к вредоносным или нежелательным результатам. Если наборы обучающих данных неполные или искажают распределение, необходимое для обучения, то получаемые результаты могут быть необъективными или дискриминационными.
8.4 Моделирование
Моделирование - это процесс разработки обученной и протестированной модели МО, готовой к развертыванию.
Выделение признаков: признаки - это количественные дескрипторы элементов в наборе данных, часто рассматриваемые как заголовки столбцов в табличных данных. Признаки могут быть числовыми, текстовыми, непрерывными или категориальными. Категориальные признаки могут быть номинальными или порядковыми. Примеры: дата, время, имя, адрес, возраст и сумма продаж. Разработка признаков - это процесс выбора, характеризации и оптимизации признаков для использования в модели МО. Примеры разработки признаков включают:
- кодирование: для эффективности и доступности использования текстовые и категориальные признаки часто преобразуют в числовые идентификаторы;
- преобразование типа данных: может возникнуть необходимость преобразования типа данных признака для соответствия требованиям конкретной модели;
- уменьшение размерности: высокая размерность входных данных может осложнить использование некоторых алгоритмов МО. Поэтому может возникнуть необходимость уменьшить количество атрибутов на выборку (часто путем поочередного использования другой модели МО) (см. 6.2.6);
- отбор признаков: основа отбора признаков заключается в содержании в данных избыточных или неактуальных признаков, которые могут быть удалены. Некоторые признаки вносят шум в модель или искажают сгенерированные моделью результаты, поэтому их необходимо удалить. Выбор правильных признаков важен для производительности конкретной модели МО. Необходим выбор атрибутов переменных из имеющихся наборов данных, включая следующие причины, но не ограничиваясь ими:
- упрощение моделей для облегчения их интерпретации;
- сокращение времени обучения;
- обеспечение подходящей размерности. Наборы данных с большим количеством признаков могут столкнуться с "проклятием размерности", когда определенные признаки вносят шум в модель или искажают сгенерированные ею результаты;
- уменьшение переобучения модели.
Существует несколько алгоритмов отбора признаков, которые можно использовать для выбора наиболее оптимальных и полезных из них. Первый метод заключается в том, чтобы исключить признаки, интуитивно не имеющие отношения к решаемой задаче. Второй метод заключается в визуализации данных, чтобы установить, какие признаки оказывают незначительное влияние на производительность модели. В некоторых случаях могут потребоваться обучение и тестирование модели с определенными признаками и без них, чтобы определить разницу в результативности. Некоторые алгоритмы МО, например деревья решений, включают отбор признаков как часть процесса обучения.
Выбор алгоритма: на этой стадии необходимо выбрать алгоритм МО, соответствующий заданию (например, классификация, регрессия, кластеризация, рекомендация). Алгоритмы МО - это основа для создания модели МО. Для каждого типа заданий МО существует несколько алгоритмов, и постоянно появляются новые методы. Библиотеки или коллекции алгоритмов МО находятся в общем доступе. В некоторых случаях может быть необходимо или предпочтительно создать новый алгоритм либо модифицировать существующий. Один или несколько алгоритмов могут быть выбраны из библиотеки или созданы для решения определенной задачи или выполнения определенного задания. Применение алгоритма, указанного в библиотеке, зачастую описывают в документации к этой библиотеке. В большинстве случаев научная и сравнительная литература общедоступна.
Можно также использовать совокупность моделей, где окончательное решение основано на функции, применяемой к решениям, полученным от каждой модели.
________________
Выбор модели: также известный как настройка гиперпараметров, выбор модели - это процесс использования набора валидационных данных для оценки и оптимизации гиперпараметров для определения значений, обеспечивающих наиболее соответствующие результаты для выбора надлежащей модели. Для автоматизации настройки гиперпараметров можно применять такие методы, как поиск по сетке и случайная оптимизация параметров. Кроме того, некоторые методы имеют встроенную возможность обучения и оценки модели с использованием сетки значений для заданных параметров.
Кросс-валидация используется, если данных мало и отдельные наборы данных для обучения и проверки слишком малы. Кросс-валидация k-fold часто используется для настройки гиперпараметров. При данной кросс-валидации исходное обучающее множество разбивается на k подмножеств (групп). Для каждой группы модель обучается на объединении других групп, а затем с помощью этой группы измеряется ошибка ее результата. Отдельный случай, когда каждая группа состоит только из одного образца, называется поэлементной кросс-валидацией (leave-one-out). Кросс-валидация может помочь предотвратить переобучение в результате утечки данных.
Такие методы, как Mallow’s Cp, информационный критерий Акаике и байесовский информационный критерий, также могут быть использованы для сравнения эффективности различных моделей без явного вычисления этой эффективности.
8.5 Верификация и валидация
Оценка модели: оценка модели - это процесс сравнения результатов, сгенерированных моделью на основе тестовых данных с фактическими метками в данных. Существует множество показателей, позволяющих оценить эффективность обученных моделей. Их описание приведено в 6.5.5.
Обычно тестируется несколько моделей, чтобы определить, какие из них наиболее отвечают первоначальным целям проектирования в сочетании со снижением рисков, выявленных в ходе разработки и использования. Однако такую практику следует применять с особой осторожностью, т.к. она отличается от процесса выбора модели, который не следует проводить на тестовых данных. Сравнительную оценку следует проводить только для нескольких моделей, существенно отличающихся друг от друга (например, на основе разных обучающих данных, разных алгоритмов МО или разных подходов МО, а не только разных гиперпараметров). В противном случае существует значительный риск переобучения под тестовые данные, что приведет к переоценке эффективности модели.
Валидация системы: валидация системы - это проверка того, отвечает ли обученная и развернутая модель всем потребностям заинтересованных сторон и были ли достоверны первоначальные предположения о среде, на основе которых получены признаки. Процесс не связан с валидационными данными, используемыми для настройки гиперпараметров на стадии проектирования и разработки.
8.6 Развертывание модели
После обучения и оценки модели МО ее необходимо внедрить в рабочую среду, где она может быть использована для генерации результатов на эксплуатационных данных. Модели МО могут быть развернуты как веб-приложения (где доступ к ним осуществляется через REST API) или как нативные приложения.
Пакетирование: обученные модели МО традиционно развертывают на серверах, кластерах или виртуальных машинах. Существует несколько открытых форматов для представления моделей МО или обмена ими, например: открытая библиотека программного обеспечения (ONNX) [15] и формат обмена нейронными сетями (NNEF) [16]. В последнее время модели развертывают в готовых к запуску контейнерах, упакованных со всеми зависимыми факторами, что существенно упрощает развертывание. Благодаря быстрому увеличению вычислительной мощности и емкости памяти устройств обученные модели МО развертывают на таких устройствах, как беспилотные летательные (а также основанные на других принципах движения) аппараты.
Среда выполнения: при разработке моделей МО часто используют такие высокоуровневые языки программирования, как R или Python. Затем обученная модель может быть развернута в любой среде выполнения, имеющей соответствующий уровень абстракции, например в интерпретаторе или компиляторе just-in-time. Среда выполнения модели может быть более низкоуровневой, чем среда разработки. Пристальное внимание необходимо уделить среде выполнения и тому, как она может отличаться от среды разработки.
Оптимизация: модель может быть оптимизирована для целевой платформы, например, путем изменения типов данных с точных на приближенные или с машинно-независимых на те, которые изначально поддерживаются целевой платформой (например, приведение весов нейросети к целочисленным значениям). Оптимизация также может происходить путем перегруппировки или объединения операций, для которых доступны эффективные аппаратные реализации. В зависимости от типа и степени оптимизации может потребоваться новая оценка оптимизированной модели, следовательно, возврат к стадии верификации и валидации.
8.7 Эксплуатация
После развертывания обученной модели ее можно использовать как самостоятельное приложение или как функцию для интеграции в другие приложения. Модели МО применяют в пакетном режиме с фиксированными наборами эксплуатационных данных или в непрерывном режиме с потоками эксплуатационных данных в реальном времени. Результат модели может быть отправлен обратно в приложение, а в некоторых случаях - интерпретирован человеком.
Обслуживание и восстановление работоспособности: на стадии эксплуатации модели МО и соответствующему приложению необходимы техническое обслуживание и восстановление работоспособности, аналогичные другим системам ИИ или обычным программным системам. Специфика МО на этой стадии связана с процессами обновления и мониторинга.
Обновление: процесс повторного обучения осуществляется с использованием обучающих данных, которые отражают характеристики текущих эксплуатационных данных. Обновления могут также реализовать изменения алгоритмов, которые, в зависимости от изменения, могут потребовать частичного повторного обучения или обучения новой модели с нуля.
Мониторинг: работа модели МО обычно контролируется во время эксплуатации, поскольку такие факторы, как дрейф данных, дрейф концепции или неправильное обобщение, могут оказать влияние на ее работу. В случае непрерывного обучения могут потребоваться дополнительные меры обслуживания, а мониторинг может включать новые мероприятия по оценке качества модели МО.
8.8 Машинное обучение на примере конвейера МО
Процессы конвейера МО можно применять к различным методам обучения и разработки моделей МО. В этом подразделе процессы рассмотрены в отношении МО с учителем.
На рисунке 13 представлены различные субкомпоненты системы МО и показано, как эти процессы могут сочетаться друг с другом. Следует отметить, что не все процессы, описанные в конвейере МО, изображены на рисунке 13, поскольку на нем представлен упрощенный пример. Некоторые процессы могут быть выполнены в другом порядке или одновременно. Кроме того, на рисунке показано использование инструментов на различных стадиях разработки модели, а также их зависимость от данных. Проводят различие между использованием инструментов для разработки моделей и работой процессов над данными.
Рисунок 13 - Пример процесса МО с учителем на основе конвейера МО
На рисунке 13 в верхнем слое модели представлены этапы процесса для системы, использующей МО с учителем. В среднем слое программных средств и методов находятся инструменты и элементы обработки данных, необходимые для выполнения этапов процесса; в нижнем слое данных - различные элементы данных, необходимые для всего конвейера.
Создание модели первоначально включает в себя такие этапы, как "определение задачи" и "формулирование задания", которые устанавливают цели и требования к решению. Затем следует этап "выбор алгоритма", целью которого является выбор метода МО, наиболее подходящего для обеспечения требуемого решения. Этап "обучение модели" включает в себя создание обученной пробной модели путем использования размеченных обучающих данных. При выборе модели вычисляют метрики оценки на валидационных данных для выбора окончательной модели МО среди пробных вариантов.
Оценка модели основана на метрике оценки тестовых данных для анализа эффективности обученной модели. За завершением данных процессов следует проверка системы.
Использование модели включает этап "запуска обученной и развернутой модели", на котором развертывается обученная модель, причем модель работает на эксплуатационных данных для приложения МО. В результате запуска модели на эксплуатационных данных система генерирует результаты и принимает решения на основе результата модели.
Повторное обучение модели может происходить либо с помощью непрерывного обучения, либо на основе оценки производительности обученной модели в процессе использования. Оценка работы может указывать на необходимость дополнительного обучения, в том числе для некоторых видов эксплуатационных данных, где производительность не соответствует требованиям, установленным для системы.
Пример, приведенный на рисунке 13, можно применять для описания потоков данных и связанных с ними инструкций об использовании данных, как показано в приложении А. В таких инструкциях содержатся классификация и формат инструкции об использовании данных, описанный в ИСО/МЭК 19944-1.
Приложение A
(справочное)
Пример потока данных и инструкции об использовании данных для процесса машинного обучения с учителем
A.1 Общие положения
Приложение демонстрирует использование ИСО/МЭК 19944-1 для описания потоков данных и разработки инструкций об использовании данных для МО. Содержание данного приложения является примерным и при необходимости может быть доработано. Применяя ИСО/МЭК 19944-1 к процессам МО, можно разработать структурные элементы и фундаментальные положения, необходимые для подотчетности и прозрачности ИИ.
A.2 Потоки данных в процессе машинного обучения с учителем
A.2.1 Общие положения
В этом пункте приведены примеры описания потока данных, основанные на процессе МО, показанном на рисунке 13.
Следует отметить, что потоки данных в A.2.2 не описываются как потоки между функциональными компонентами в рамках эталонной архитектуры облачных вычислений (ИСО/МЭК 17789), а вместо этого представляют собой вид потоков данных на различных стадиях процессов разработки конвейера МО и модели МО.
A.2.2 Описания потоков данных
A.2.2.1 Поток данных 1
Следующий поток данных показан на рисунке 13 и описан следующим образом:
Данные собирают из одного или нескольких источников с целью создания набора данных для МО. Чтобы подготовить набор данных к стадии обучения модели в конвейере МО, к нему применяют множество процессов.
Такие процессы описаны в 8.3.
A.2.2.2 Поток данных 2
Следующий поток данных показан на рисунке 13 и описан следующим образом:
Для МО с учителем необходимо определить истинное значение целевой переменной. Значение целевой переменной называется ее меткой. На практике один посредник может быть использован в качестве эталонных данных, а несколько посредников могут привносить ошибки и смещения.
A.2.2.3 Поток данных 3
Следующий поток данных показан на рисунке 13 и описан следующим образом:
После развертывания и запуска модели к ней применяют эксплуатационные данные. Модель генерирует выходные данные обычно с вероятностями, присвоенными результатам модели. Эти результаты, в свою очередь, могут быть использованы для принятия решений либо автоматизированно, либо для учета в качестве рекомендаций по принятию решений.
A.3 Использование данных в машинном обучении
A.3.1 Общие положения
В этом пункте показаны примеры инструкций об использовании данных на основе структуры инструкции о применении данных, описанной в ИСО/МЭК 19944-1:2020, 10.2. Следующие примеры использования данных в рамках МО с учителем основаны на потоках данных, описанных в A.2.2 и приведенных на рисунке 13.
A.3.2 Пример инструкции об использовании данных A
В данном примере рассмотрен вариант использования МО в страховой компании. В рамках потока данных, описанного в A.2.2.1 (поток данных 1), можно сформулировать нижеприведенный пример инструкции об использовании данных.
Пример - Инструменты подготовки данных используют анонимизированные финансовые данные из заявлений о страховании жилья, чтобы улучшить и подготовить полученные данные для разработки модели МО.
A.3.3 Пример инструкции об использовании данных B
В данном примере рассмотрен вариант использования МО в системах распознавания объектов автоматизированного дорожного транспортного средства. В рамках потока данных, описанного в A.2.2.2 (поток данных 2), можно сформулировать нижеприведенный пример инструкции об использовании данных.
Пример - Процесс "обучения модели" использует агрегированные и размеченные данные датчиков с бортовых камер автомобиля для обучения модели МО распознаванию объектов.
A.3.4 Пример инструкции об использовании данных C
В данном примере рассмотрен вариант использования МО в системах прогнозируемого обслуживания авиационного двигателя. Такие системы включают в себя датчики температуры, предназначенные для контроля работы двигателя. В рамках потока данных, описанного в A.2.2.3 (поток данных 3), можно сформулировать нижеприведенный пример инструкции об использовании данных.
Пример - Данные датчиков входного устройства, полученные от установленных на двигателе датчиков температуры, используются моделью МО для прогнозирования отказа компонентов и усовершенствования характеристик двигателя и его обслуживания.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO/IEC 22989 | - | * |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык международного стандарта ISO/IEC 22989. | ||
Библиография
[1] | Stuhlsatz A., Lippel J., Zielke T., Feature Extraction With Deep Neural Networks by a Generalized Discriminant Analysis. IEEE Transactions on Neural Networks and Learning Systems. 2012, 23 (4), 596-608. doi: 0.1109/tnnls.2012.2183645 |
[2] | MacLennan B.J. Connectionist Approaches. International Encyclopaedia of the Social & Behavorial Sciences. 2001, 2568-2573. doi: 10.1016/b0-08-043076-7/00537-4 |
[3] | Rosenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review. 1958, Nov, 65(6):386-408. doi: 10.1037/h0042519 |
[4] | Rumelhart D., Hinton G., Williams R. Learning representations by back-propagating errors. Nature 1986, 323, 533-536. doi: 10.1038/323533a0 |
[5] | Elman Jeffrey L. Finding structure in time. Cognitive science. 1990, 14.2, 179-211. doi: 0.1016/0364-0213(90)90002-E |
[6] | Hochreiter Sepp, Schmidhuber . Long short-term memory. Neural computation.1997, 9.8, 1735-1780. doi: 10.1162/neco.1997.9.8.1735 |
[7] | Lecun Y., Bottou L., Bengio Y., Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998, 86(11), 2278-2324. doi: 10.1109/5.726791 |
[8] | Heckerman D. A Tutorial on Learning with Bayesian Networks. Innovations in Bayesian Networks. Studies in Computational Intelligence, 156. Berlin, Heidelberg: Springer. 2008. doi: 10.1007/978-3-540-85066-3_3 |
[9] | Fawcett T. ROC graphs: Notes and practical considerations for researchers. Machine learning. 2004, 31, 1-38 |
[10] | Delgado R. Tibau X.A. Why Cohen’s Kappa should be avoided as performance measure in classification. PloS one. 2019, 14(9). doi: 10.1371/journal.pone.0222916 |
[11] | Giles M.Foody. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sensing of Environment. 2020, 239. doi: 10.1016/j.rse.2019.111630 |
[12] | ISO/IEC 19944-1:2020, Cloud computing and distributed platforms. Data flow, data categories and data use. Part 1. Fundamentals |
[13] | Yang Q., Zhang Y., Dai W., Pan S. Transfer Learning. Cambridge: Cambridge University Press.2020.doi: 10.1017/9781139061773 |
[14] | ISO/IEC 20889, Privacy enhancing data de-identification terminology and classification of techniques |
[15] | Open neural network exchange. https://onnx.ai/ |
[16] | Neural network exchange format. https://www.khronos.org/nnef |
[17] | ISO/IEC 17789, Information technology. Cloud computing. Reference architecture |
УДК 004.8:006.354 | ОКС 35.080 | |
Ключевые слова: машинное обучение, искусственный интеллект, модель, инструменты, данные, верификация, валидация, моделирование | ||
