ГОСТ Р ИСО 4355-2016
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОСНОВЫ ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Определение снеговых нагрузок на покрытия
Bases for design of structures. Determination of snow loads on roofs
ОКС 91.080.01
Дата введения 2017-07-01
Предисловие
1 ПОДГОТОВЛЕН Акционерным обществом "Научно-исследовательский центр "Строительство" (АО "НИЦ "Строительство"), Центральным научно-исследовательским, проектно-конструкторским и технологическим институтом им.В.А.Кучеренко (ЦНИИСК им.В.А.Кучеренко) на основе официального перевода на русский язык англоязычной версии указанного в пункте 4 международного стандарта, который выполнен Федеральным государственным унитарным предприятием "Российский научно-исследовательский центр информации по стандартизации, метрологии и оценке соответствия" (ФГУП "")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 "Строительство"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 декабря 2016 г. N 2013-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 4355:2013* "Основы строительных конструкций. Метод определения снеговых нагрузок на крыши" (ISO 4355:2013 "Bases for design of structures - Determination of snow loads on roofs", IDT).
Наименование настоящего стандарта изменено относительно наименования указанного европейского стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных европейских стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
Введение
Интенсивность и распределение снеговой нагрузки на покрытия могут быть описаны как функции климатических условий, топографических особенностей, формы сооружения, материала кровли, потока тепла через покрытие и времени. В настоящее время для определения таких функций имеется весьма ограниченный набор данных локального характера, вследствие чего в рамках настоящего стандарта было принято решение о рассмотрении вышеуказанной задачи в полувероятностной постановке.
Значения коэффициентов формы будут зависеть от климатических условий, в особенности от продолжительности снегового сезона, от ветра, топографии местности, геометрии рассматриваемого сооружения и окружающих зданий, материала кровли, изоляции здания и т.п. Снег может перераспределяться под действием ветра, талая вода может стекать на отдельные участки и снова замерзать; снег может сползать или перемещаться.
Для обеспечения возможности применения ИСО 4355 в каждой стране должны быть установлены национальные данные о географическом распределении веса снегового покрова на ее территории в виде карт и/или другой информации. Процедуры статистической обработки метеорологических данных описаны в приложении А.
1 Область применения
В настоящем стандарте устанавливаются методы определения снеговой нагрузки на покрытия.
ИСО 4355 может служить основой для разработки национальных стандартов по определению снеговых нагрузок на покрытия.
Статистические данные по весу снегового покрова в виде карт районирования, таблиц или формул следует принимать по национальным стандартам.
Коэффициенты формы, представленные в настоящем стандарте, предназначены для применения при проектировании и поэтому могут использоваться непосредственно в тех случаях, когда отсутствует обоснование применения иных значений.
Для определения снеговых нагрузок на покрытия нестандартной формы или форм, не охватываемых настоящим стандартом, рекомендуется проводить специальные исследования. Такие исследования могут включать в себя испытания на масштабных моделях в аэродинамической трубе или в водяном лотке, специально оборудованных для воспроизведения явления снегонакопления, и должны включать в себя методы учета местных метеорологических статистических данных.
Примеры использования численных методов, исследований на масштабных моделях и сопутствующих методов статистического анализа описаны в приложении G.
Приложения, в которых описаны методы определения характеристического значения веса снегового покрова, коэффициента защищенности, термического коэффициента и нагрузок на снегозадерживающие преграды, являются справочными ввиду ограниченного количества документальных источников и доступных научных результатов.
В некоторых регионах в отдельные зимы с аномальными погодными условиями могут быть жесткие условия нагружения, не предусмотренные настоящим стандартом.
Указание стандартных процедур и средств измерений не входит в задачи настоящего стандарта.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт*, целиком или по частям, который является обязательным к применению. Для датированной ссылки применяют только указанное издание. Для недатированной ссылки применяют последнее издание документа, на который имеется ссылка (включая все поправки).
_______________
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
Примечание 2 - В метеорологии применяется также термин-эквивалент "вес снегового покрова земли" (weight of the ground snow cover).
Примечание 1 - Значение s зависит также от защищенности кровли и теплового режима здания.
Примечание 2 - Данное определение относится к площади горизонтальной проекции покрытия.
4 Снеговые нагрузки на покрытия
4.1 Обобщенная функция, описывающая интенсивность и распределение снеговой нагрузки на покрытия
где обозначения представлены в разделе 3.
4.2 Приближенные формы представления снеговой нагрузки на покрытия
где "+" обозначает совместное действие.
Воздействие различных параметров упрощается при введении мультипликативных функций:
Базовая нагрузка характеризует нагрузку на горизонтальное покрытие и нагрузку на наветренную сторону скатного покрытия. Поскольку ветер может иметь любое направление, в качестве базовой рассматривается симметричная нагрузка на симметричное покрытие и, следовательно, определяется также основная часть общей нагрузки на подветренную сторону покрытия.
Нагрузкой от переноса называется дополнительная нагрузка, которая может накапливаться на подветренной стороне покрытия вследствие перемещения снежной массы по покрытию.
Нагрузкой от сползания (скольжения) называется нагрузка, которая образуется в результате соскальзывания снега с верхнего покрытия на нижнее покрытие или на нижнюю часть покрытия.
4.3 Частичное загружение, вызванное таянием, сползанием, перераспределением и удалением снега
Всегда следует учитывать снеговую нагрузку, возникающую из-за значительной неравномерности вследствие удаления снега, его перераспределения, сползания, таяния и т.п. (например, отсутствие снеговой нагрузки на отдельных частях покрытия).
Учет этих факторов особенно важен для конструкций, чувствительных к неравномерному нагружению (например, криволинейные покрытия, арки, купола, ригельные покрытия, неразрезные балочные системы), которые рассматриваются в других разделах настоящего стандарта.
4.4 Неустойчивость при затоплении водой
Покрытия следует проектировать таким образом, чтобы предотвратить неустойчивость при затоплении водой. Для плоских покрытий (или покрытий с малым уклоном) необходимо исследовать их прогибы под действием снеговых нагрузок с оценкой вероятности неустойчивости при затоплении покрытия дождем поверх снега или образующейся талой водой.
5 Характеристическое значение веса снегового покрова
Измерения веса снегового покрова следует проводить на ненарушенном участке, не подверженном локальному переносу.
При практическом применении характеристическое значение веса снегового покрова следует определять стандартными пошаговыми значениями, которые принимают в качестве базовых значений при составлении карт районирования, как описано в приложении А.
6 Коэффициенты для задания снеговой нагрузки
6.1 Коэффициент защищенности
Для покрытий непрямоугольной формы в качестве размеров W и L могут приниматься меньшее и большее измерения по двум осям прямоугольной системы координат. Например, для эллиптической формы W измеряют по малой оси эллипса, a L - по его большой оси.
Общее представление о коэффициентах защищенности в графической форме приведено на рисунке 2.
Рисунок 1 - Прямоугольная форма покрытия
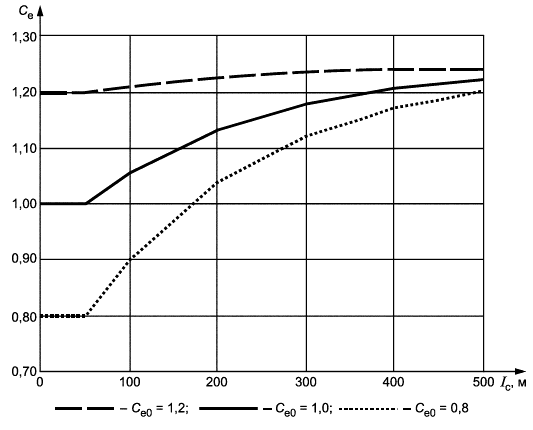
6.2 Термический коэффициент
6.3 Коэффициент по материалу поверхности кровли
Количество снега, сползающего с покрытия, зависит в определенной мере от свойств материала кровли (см. 6.4.2).
6.4 Коэффициенты формы
6.4.1 Общие принципы
Коэффициенты формы определяют распределение снеговой нагрузки по поперечному сечению строительного объекта и зависят главным образом от геометрических свойств покрытия.
Для зданий, имеющих в плане прямоугольную форму, распределение снеговой нагрузки в направлении, параллельном карнизам, считается равномерным, что соответствует предполагаемому направлению ветра перпендикулярно карнизам.
Представленные в приложении В коэффициенты формы для отдельных типов покрытий иллюстрируются применительно к определенному направлению ветра. Так как преобладающие направления ветра могут не совпадать с направлениями ветра во время сильных снегопадов, все покрытия следует проектировать исходя из предположения, что ветер при снегопадах может иметь любое направление по отношению к расположению покрытия.
6.4.2 Базовый коэффициент по нагрузке
Базовый коэффициент по нагрузке представлен графически на рисунке 3.
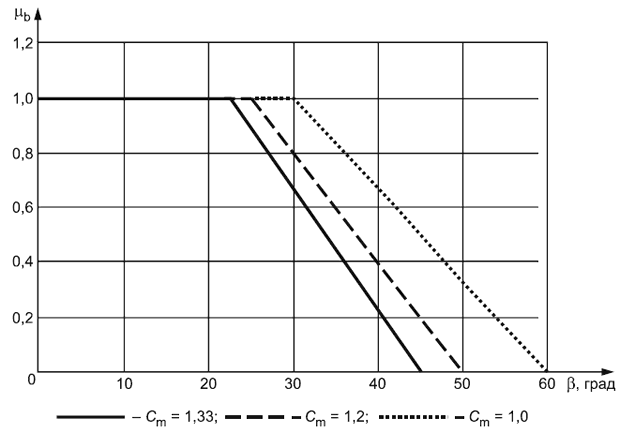
6.4.3 Коэффициент переноса нагрузки
6.4.4 Коэффициент сползания нагрузки
Нагрузка от снега, сползающего с верхней части покрытия на его нижнюю часть или на нижнюю часть многоуровневой кровли, будет зависеть от массы снега, которая может соскользнуть вниз, и от геометрии кровли.
Распределение нагрузки от сползания (скольжения) и ее распространение по покрытию будет зависеть помимо геометрической формы покрытия также от свойств сползающего снега и от силы трения на верхней поверхности кровли, с которой он сползает.
Значения этого коэффициента для разных случаев, в которых должна быть учтена нагрузка от сползания, приведены в приложении В.
Одновременно с нагрузкой от сползания (скольжения) следует принимать во внимание и ударное воздействие от сползающей нагрузки.
Приложение А
(справочное)
Предпосылки определения некоторых параметров снеговой нагрузки
А.1 Карты районирования веса снегового покрова
_______________
Вследствие изменчивого характера снеговой нагрузки предпочтительнее построение карт районирования веса снегового покрова с базовыми значениями для каждой зоны, обычно относящимися к фиксированной высоте над уровнем моря, а не использование непрерывного поля изолиний. Такой подход рекомендуется еще и потому, что в пределах климатологически заданных районов нередко может наблюдаться особое изменение снеговой нагрузки в зависимости от высоты.
Исследования показали, что в прибрежных зонах снеговая нагрузка зависит не только от высоты, но и от расстояния до береговой черты.
Примечание 1 - Если это более целесообразно, то ежегодную вероятность превышения допускается принимать меньше, чем 0,02.
Примечание 2 - Важные исследования, которые были выполнены по определению характеристических значений веса снегового покрова, описаны в работах [3], [4], [5] ,[6], [7]. Об обработке статистических данных см. А.3.
А.2 Использование базовых метеорологических данных
А.2.1 Соотношение между весом снегового покрова и его высотой
В США [9] используют следующую функциональную зависимость между весом снегового покрова и его высотой:
В формуле (А.1) учтен факт того, что максимальный вес снегового покрова необязательно имеет место в тот же день, что и максимальная высота снегового покрова.
А.2.2 Плотность снега
Средняя плотность снегового покрова по-прежнему остается важным параметром для определения снеговой нагрузки, так как на многих метеостанциях предпочитают регистрировать высоту снегового покрова, а не значения запасов воды в снеговом покрове.
В России и бывшем СССР [10] была предложена формула (А.2):
d - высота снегового покрова, м;
Т - средняя температура, °С, за период снегонакопления (предположительно не ниже минус 25°С);
v - средняя скорость ветра, м/с, за тот же период.
В Японии [11] используют формулу для эквивалентной плотности снегового покрова земли с периодом повторяемости 100 лет:
d - высота снегового покрова, м;
В США для выражения плотности снега используется формула (А.4), связывающая плотность снега в определенный момент времени с весом снегового покрова в тот же момент времени:
Формула (А.4), выраженная через высоту снегового покрова, примет вид:
d - высота снегового покрова, м.
В Германии на основе наблюдений Германской службы погоды (Deutscher Wetterdienst DWD) [12] была разработана следующая формула:
где d - высота снегового покрова, м;
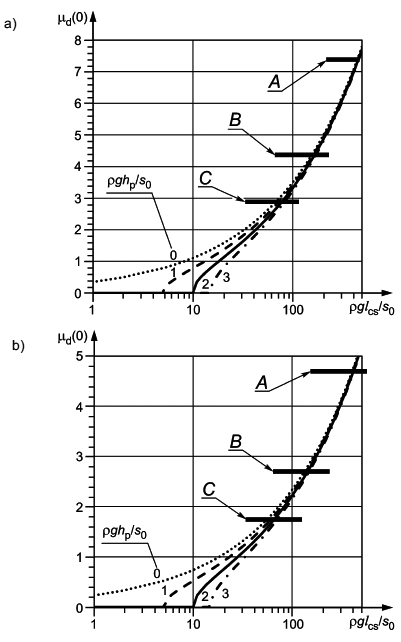
На рисунке А.1 представлены в графической форме для сравнения формулы плотности снега (А.1), (А.2), (А.3), (А.5) и (А.6) [14].
Примечание 1 - Для формулы (А.2) показаны два варианта: а) для средней температуры Т=минус 10°С при средней скорости ветра v=4 м/с; b) для средней температуры Т=минус 20°С при средней скорости ветра v= 4 м/с.
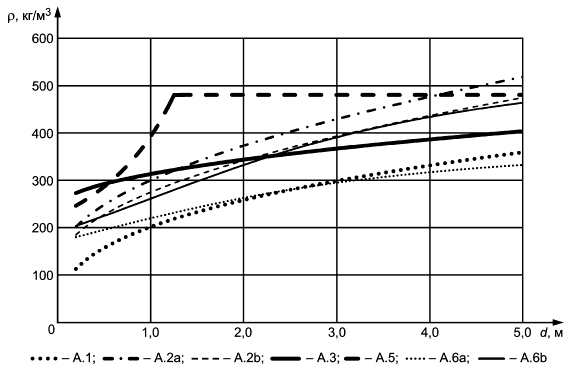
А.2.3 Интенсивность снегопада за короткие периоды времени
Для корректного проектирования покрытий с высокими тепловыми потерями определенный интерес может представлять информация об интенсивности снегопада за короткие периоды времени (24 ч и менее).
Обычно в таких случаях доступны только показания дождемеров различного типа. Однако подобные показания применительно к снегопаду никогда не следует использовать без поправок на ветер, который воздействует на измерительный прибор. Рекомендации по корректировке указанных данных, разработанные на основе наблюдений в странах Северной Европы, приведены в [15].
А.2.4 Добавочная нагрузка от дождевых осадков поверх снегового покрова
Примечание - Этот пункт заимствован из нормативных документов Американского общества инженеров гражданского строительства ASCE 7-10.
А.2.5 Учет климатических изменений
При разработке национальных карт районирования по весу снегового покрова важно отметить, что некоторая совокупность ежегодных экстремальных или пиковых значений, превышающих определенный порог, может содержать случайный позитивный или негативный тренд. Оценка возможного влияния климатических изменений призвана учесть эту случайность, для чего могут быть разработаны различные сценарии климатических изменений, позволяющие получить информацию об основных формах трендов, подлежащих анализу.
А.3 Статистическая обработка исходных данных
При использовании статистических методов обработки исходных данных об измерении веса снегового покрова следует иметь в виду, что значимость таких региональных данных во многом зависит от метода наблюдений и защищенности площадки наблюдений. Поэтому при расчете снеговой нагрузки необходимо обращать особое внимание на то, является ли метеорологическая станция типичной для данного региона.
А.3.1 Статистические распределения
Для климатических регионов с постоянным снеговым покровом в течение зимнего сезона наиболее подходящую основу для обработки данных о ежегодных максимумах веса снегового покрова представляет статистика экстремальных значений. Для климатических регионов, в которых наблюдается более одного независимого периода с постоянным снеговым покровом за зимний сезон, статистическая устойчивость оцениваемых параметров может быть улучшена за счет использования пиковых значений, превышающих определенный порог. Так как ограниченные наборы параметров неизбежно несут в себе и случайную информацию, бывает крайне трудно выявить "истинное" вероятностное распределение и соответствующие ему "истинные" параметры. Поэтому для оценки ежегодных вероятностей непревышения рекомендуется использовать распределение экстремальных значений типа 1 (распределение Гумбеля). Для климатических регионов, в которых снеговой покров образуется не каждый год, при обработке данных следует использовать только ненулевые значения веса снегового покрова. При этом особое внимание нужно обращать на данные тех наблюдений, в которых зафиксированы аномально большие значения, причисляемые к статистическим выбросам.
А.3.2 Возможная климатическая зависимость при выборе распределений
Исследования показывают, что наилучшее соответствие местных данных логарифмически нормальному распределению или распределению типа 1 обусловлено определенными климатическими условиями региона [4].
Если детальный сравнительный анализ различных распределений оказывается невозможным, то для регионов, в которых ежегодные экстремальные значения веса снегового покрова формируются путем снегонакопления на протяжении длительного периода зимнего сезона, рекомендуется выбирать распределение типа 1. Для регионов, в которых экстремальные снеговые нагрузки являются результатом только одного или нескольких снегопадов, целесообразно использовать логарифмически нормальное распределение.
Консерватизм обоих указанных распределений зависит от значений коэффициента вариации, т.е. при вычислении значений веса снегового покрова с большим периодом повторяемости при низких значениях коэффициента вариации более консервативным является распределение типа 1, а при высоких значениях - логарифмически нормальное распределение.
При сравнении различных методов параметрической оценки для рассматриваемого периода повторяемости может быть использована стандартная ошибка вычислений.
Часто рассматриваемый период повторяемости превышает длину имеющегося ряда наблюдений для максимумов веса снегового покрова. Хорошая степень соответствия теоретического распределения выборочным данным при этом не всегда будет основана на экстраполированных значениях, соответствующих большим периодам повторяемости. При принятии решений рекомендуется также учитывать и реальные климатические условия.
Приложение В
(обязательное)
Распределение снеговой нагрузки на отдельные типы покрытий
В.1 Простые двускатные покрытия
Распределение снеговой нагрузки на простые двускатные покрытия показано на рисунке В.1. Для несимметричных простых двускатных покрытий каждую сторону покрытия следует рассматривать как половину соответствующего симметричного покрытия.
Рисунок В.1 - Распределение снеговой нагрузки на простое двухскатное покрытие
Базовое нагружение:
Неравномерное нагружение:
Базовая часть нагрузки:
Часть нагрузки вследствие переноса:
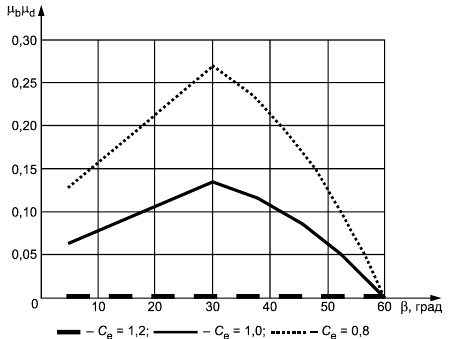
В.2 Простые плоские и односкатные покрытия
Рисунок В.3 - Распределение снеговой нагрузки для односкатного покрытия
В.3 Многопролетные покрытия
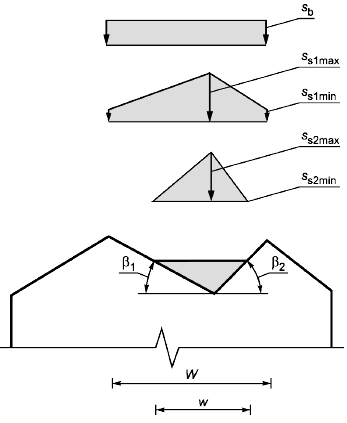
Рисунок В.4 - Распределение снеговой нагрузки для многопролетного покрытия
Случай базовой нагрузки:
Нагрузка от сползания, случай 1:
Нагрузка от сползания, случай 2:
В.4 Простые криволинейные покрытия, стрельчатые арки и купола
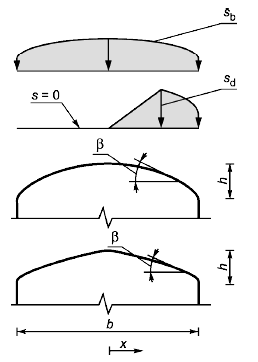
Рисунок В.5 - Распределение базовой нагрузки и нагрузки от переноса для криволинейных покрытий
Случай базовой нагрузки:
Случай нагрузки от переноса:
Коэффициент переноса нагрузки для куполов (см. рисунок В.6):
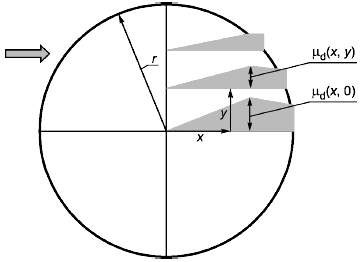
Примечание - Стрелкой указано направление ветра.
Рисунок В.6 - Коэффициент переноса нагрузки на купола в плане
Для нижних покрытий (рисунок В.7) базовую часть нагрузки определяют по формуле
где
здесь х - расстояние по горизонтали от перепада;
h - высота перепада.
Случай а: перепад расположен по направлению ветра, и снег сносится с верхнего покрытия на защищенную область у перепада.
Случай b: перепад обращен навстречу ветру, и снег переносится по нижнему покрытию в область перепада.
Случай с: концевая область перепада обращена по направлению ветра, и снег переносится в защищенную область перепада из-за угла.
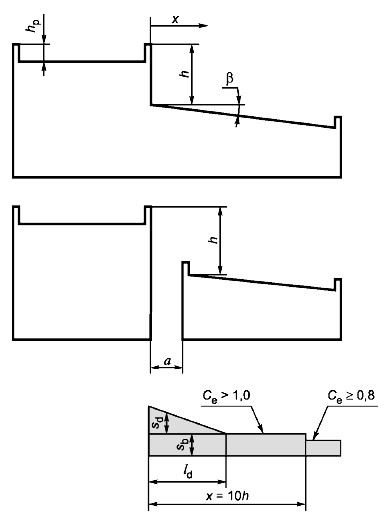
Рисунок В.7 - Распределение снега и коэффициенты по снеговой нагрузке для примыкающих покрытий нижнего уровня
Длину зоны повышенных снегоотложений определяют по формуле
Максимальная нагрузка от переноса задается следующими выражениями:
g - ускорение силы тяжести.
х | ||
0 | 1,0 | |
1,0 | ||
1,0 | 0 | |
0,8 | 0 |
где L - больший размер исходной области переноса снега.
Если верхнее покрытие двускатное, то размеры W и L основаны на общих размерах верхнего покрытия для случая а).
Примечание - Измерения L и W, показанные на рисунке, будут меняться местами в зависимости от того, какое из них больше.
Рисунок В.8 - Случаи снегопереноса и параметры для покрытий нижнего уровня
Параметр | Случай а) | Случай b) | Случай с) |
1,0 | 0,67 | 0,67 | |
Высота парапета верхнего покрытия | Высота парапета нижнего покрытия | Высота парапета нижнего покрытия | |
W и L - меньшее и большее измерения верхнего покрытия соответственно | W и L - меньшее и большее измерения исходной области сноса соответственно на нижнем покрытии для подветренного перепада | W и L - меньшее и большее измерения исходной области сноса соответственно на нижнем покрытии для наветренного перепада |
Для наружного угла, где сходятся две грани перепадов (см. рисунок В.10), треугольную нагрузку от переноса у менее нагруженной области перепада принимают распространяющейся радиально от угла. Для внутреннего угла нагрузки от переноса, вычисляемые для каждого перепада, следует прикладывать по биссектрисе угла, как показано на рисунке В.11.
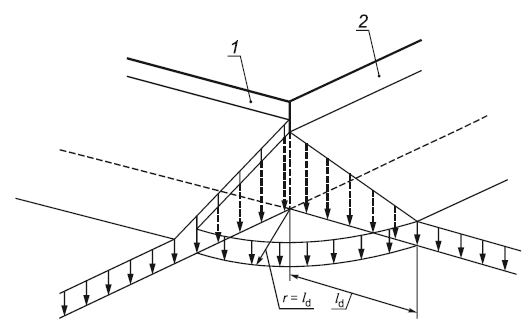
Рисунок В.10 - Снеговая нагрузка от переноса для наружного угла
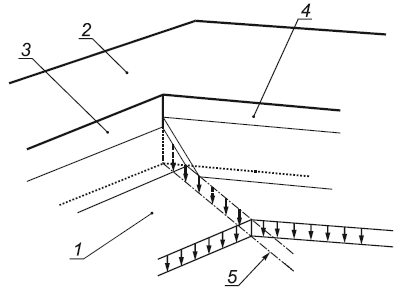
1 - нижнее покрытие; 2 - верхнее покрытие; 3 - грань перепада 1; 4 - грань перепада 2; 5 - биссектриса угла между двумя гранями перепада
Рисунок В.11 - Снеговая нагрузка от переноса возле внутреннего угла
Если покрытие сооружения находится на расстоянии менее 5 м от покрытия соседнего более высокого здания, оно должно быть рассчитано на отсеченную часть треугольного распределения снеговой нагрузки от переноса, как показано на рисунке В.7.
где
Рисунок В.12 - Коэффициент сползания снеговой нагрузки
Снеговую нагрузку от сползания следует рассматривать совместно с базовой нагрузкой и с половиной нагрузки от переноса. Следует отметить, что вышеуказанная снеговая нагрузка от сползания не включает в себя ударного воздействия снега при его падении на нижнее покрытие.
В.6 Дополнительная нагрузка от переноса и сползания на землю или на покрытие нижнего уровня, действующая на верхнее арочное или двускатное покрытие
Покрытие нижнего уровня следует проверять на нагрузку от сползания, как альтернативный случай нагружения случаям, рассмотренным в В.5. При этом необходимо учитывать и ударные воздействия (см. рисунок В.13).
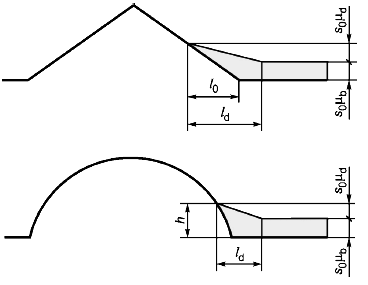
Рисунок В.13 - Добавочные нагрузки от переноса и сползания, действующие на верхнее арочное или двускатное покрытие
g - ускорение силы тяжести.
В.7 Покрытия с локальными преградами
Рисунок В.14 - Коэффициент нагрузки от переноса для локальных преград
Приложение С
(справочное)
Определение коэффициента защищенности для малых покрытий
С.1 Общие положения
Ветер, дующий во время снегопада, может вызвать уменьшение равномерно распределенной снеговой нагрузки на покрытие по сравнению с весом снегового покрова земли. Однако локальный максимум неравномерной снеговой нагрузки на покрытие может существенно превышать вес снегового покрова.
Сильный ветер при отсутствии снегопада может также вызвать равномерное уменьшение или перераспределение существующего снегового покрова на покрытии, что в значительной мере зависит от температуры окружающего воздуха и от предыстории температурного режима слоя снега. Перенос снега прекращается при определенном пороговом значении скорости ветра. Такой порог повышается с ростом температуры окружающего воздуха, поскольку известно, что силы сцепления между частицами снега с повышением температуры возрастают.
Все описанные выше явления широко известны как по практическим наблюдениям, так и по результатам аналитических исследований. Важные физические исследования в этой области описаны в работе [16], а результаты нескольких исследовательских программ наблюдения за снеговыми нагрузками на здания изложены в работах [17], [18] и [19]. Результаты исследований снегопереноса с использованием водяного лотка и аэродинамической трубы представлены в работах [20], [21], [22] и [23]. Комбинированные исследования с использованием аэродинамической трубы и компьютерного моделирования описаны в работах [24] и [25].
С.2 Защищенность при воздействии зимних ветров
В качестве главного параметра переноса снега лучше всего использовать среднюю частоту превышения скоростью ветра порогового значения (5 м/с), а не среднее месячное значение скорости ветра. Это объясняется тем, что интенсивность переноса как выпадающего, так и старого снега зависит от появления относительно сильного ветра во время снегопада, а снегопады часто сопровождаются сильным ветром.
К нормальному типу местности относятся пригородные, городские или лесные территории. К защищенной местности относятся площадки, полностью защищенные другими более высоки ми сооружениями или деревьями во всех направлениях.
Зимние ветровые режимы, представленные в таблице С.1, следует рассматривать, как правило, с учетом средних значений за три наиболее холодных месяца года.
Таблица С.1 - Категории зимних ветров
Среднее число дней месяца N с ветром, скорость которого хотя бы однократно превышает 5 м/с в течение 10-минутного периода | Категория защищенности местности | ||
| Открытая | Нормальная | Защищенная |
N<1 | II | I | I |
1 N 10 | III | II | I |
10<N | III | III | II |
Данные о повторяемости ветра есть на метеостанциях, которые регистрируют скорость ветра на открытой местности на высоте 10 м над уровнем земли.
С.3 Зимний температурный режим
В регионах с относительно теплым зимним климатом обычно возможен перенос снега только во время снегопада. В таких регионах снегопады сопровождаются самой низкой температурой зимнего периода, что не характерно для холодных регионов. Этим объясняются трудности вывода общей переменной, отражающей температуру во время снегопадов в разных климатических условиях. Из практических соображений параметр, используемый в настоящем приложении, представляет собой самую низкую среднюю месячную температуру года. Следует иметь в виду, что данный параметр принимает более низкие значения, чем средняя температура зимнего сезона по С.5.
Следует использовать среднемесячные температуры наиболее холодного месяца года, приведенные в таблице С.2.
Таблица С.2 - Категории зимних температур
Средняя температура и наиболее холодного месяца года, °С | Категория зимних температур |
>2,5 | А |
-2,5 2,5 2,5 2,5 | В |
<-2,5 | С |
С.4 Коэффициент защищенности
Коэффициент защищенности может быть определен по таблице С.3 после выбора категорий зимних ветров и температур, представленных в таблицах С.1 и С.2 соответственно, и откорректирован согласно местной топографии.
Категория зимних температур | Категория зимних ветров | ||
I | II | III | |
А | 1,2 | 1,1 | 1,0 |
В | 1,1 | 1,0 | 0,9 |
С | 1,0 | 0,9 | 0,8 |
С.5 Альтернативный способ определения коэффициента защищенности
при скорости ветра | м/с; | (С.1) | |
при скорости ветра | 2 м/с <v< 8 м/с; | (С.2) | |
при скорости ветра | м/с, | (С.3) |
где v - средняя скорость ветра, м/с, на высоте 10 м над уровнем земной поверхности в период снегопадов.
Примечание - Коэффициенты защищенности в С.4 и таблице С.3 изменяются в диапазоне от 0,8 до 1,2. В указанном выше отечественном подходе коэффициент защищенности изменяется в диапазоне от 0,4 до 1,0. Поэтому для использования в рамках настоящего стандарта коэффициенты для территории Российской Федерации нуждаются в модификации.
С.6 Климатические условия с неежегодным выпадением снега
Для климатических условий, в которых снег выпадает не каждый год, более надежный подход к анализу зимних ветров и температур состоит в учете лишь тех ситуаций, когда известно значение веса снегового покрова. Наконец, для оценки вероятности сценария формирования расчетной снеговой нагрузки требуется анализ ветровых и температурных условий.
Приложение D
(справочное)
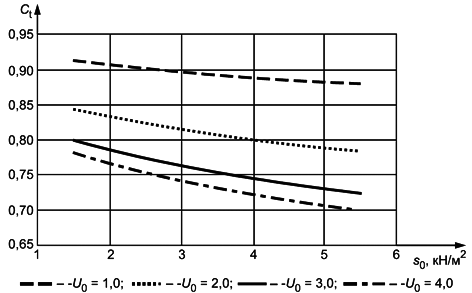
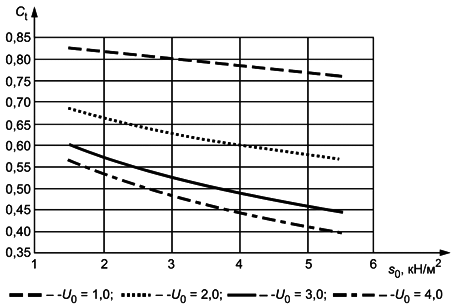
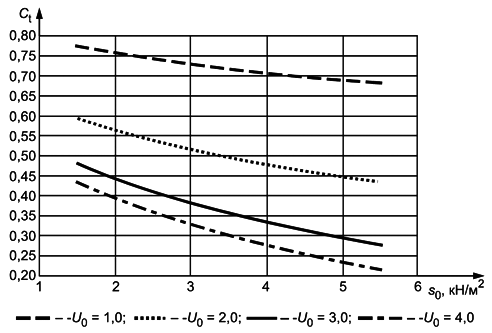
Определение термического коэффициента
_______________
_______________
Во всех случаях следует проводить проверку возможности отвода талой воды с поверхности покрытия без риска его обледенения.
Приложение Е
(справочное)
Снегозащитные устройства на покрытии
Е.1 Общие положения
Силы, действующие на снегозащитные ограждения, ассоциируемые со снеговой нагрузкой на двускатное покрытие, являются в основном компонентами массы снега вдоль поверхности покрытия, сил трения и сил сжатия на карнизах. Силы сцепления и растяжения играют важную роль при примерзании снега к поверхности кровельного материала, если снег задерживается за конек или за какое-либо иное препятствие на поверхности покрытия.
Трение и сцепление являются основными силами сопротивления. Образование тонкого слоя талой или дождевой воды на поверхности кровли ведет к ослаблению этих сил.
Е.2 Статическая нагрузка
g - ускорение силы тяжести.
Е.3 Высота снегозащитного ограждения
Высота ограждения, достаточная для предотвращения сползания снега с покрытия, зависит, главным образом, от высоты снегового покрова на покрытии, уклона покрытия и трения между отдельными слоями снега. Если трение относительно невелико, то сползание верхнего слоя возможно уже при уклонах порядка 25°.
Е.4 Динамическая нагрузка
Динамическая сила, создающая нагрузку от сползающего снега на снегозащитное ограждение, может быть рассчитана теоретически с помощью модели в виде цепи или каната, которые скользят вдоль поверхности покрытия с нулевым трением.
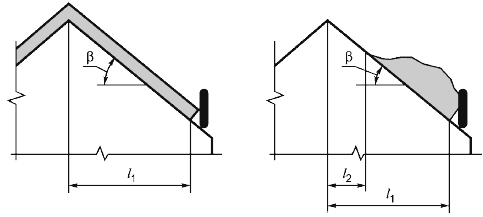
Рисунок Е.1 - Параметры, подлежащие рассмотрению при определении динамических сил, действующих на снегозащитное ограждение
Приложение F
(справочное)
Снеговые нагрузки на покрытие с использованием системы контроля снегового покрова
F.1 Общие положения
При использовании достаточно надежного устройства или метода контроля снеговая нагрузка на покрытие может быть понижена посредством реализации концепции, представленной ниже.
F.2 Снеговая нагрузка на покрытие, оснащенное системой контроля
Снеговую нагрузку на покрытие, оснащенное системой контроля, рассчитывают по формуле
F.3 Вес снегового покрова с накоплением в течениеnдней
F.3.1 Формула для веса снегового покрова с накоплением в течениеnдней
g - ускорение силы тяжести.
F.3.2 Репрезентативная высота снегового покрова с накоплением в течениеnдней
F.4 Контролируемая снеговая нагрузка
Приложение G
(справочное)
Альтернативные методы определения снеговых нагрузок на покрытия, на которые методы, предписанные настоящим стандартом, не распространяются
В основе аналитического прогнозирования снеговых нагрузок на покрытия, рассматриваемых в настоящем стандарте и его приложениях, лежат в основном полномасштабные наблюдения за процессом снегонакопления на покрытиях распространенных простых форм, включая допущения для неравномерных нагрузок, которые могут возникать вследствие переноса и сползания. Для покрытий нестандартных форм и эксплуатируемых в нестандартных окружающих условиях, для форм, не охватываемых настоящим стандартом, и для большепролетных покрытий, для которых снеговые нагрузки существенно влияют на соотношение стоимости и безопасности, рекомендуется проводить модельные испытания в аэродинамических трубах, водяных лотках и/или специальные математические исследования.
Физический процесс снегонакопления реализуется благодаря выпадению осадков с ветром или без ветра, перераспределению существующего снегового покрова или сочетанию обоих факторов. Снос снега происходит вследствие его сноса ветром, таяния и сползания. Снеговые нагрузки в любой конкретный момент времени зависят от предыстории вышеуказанных процессов в предыдущие часы, дни и недели. Длительность данной предыстории весьма значима и зависит от местных климатических условий зимнего сезона. В тех регионах, для которых характерны длительные холодные периоды, следует принимать во внимание более длительную предысторию.
Для прогнозирования снеговых нагрузок могут использовать как теоретические, так и физические модели рассматриваемых процессов. Существует несколько разновидностей снега с различными конечными скоростями, углами, при которых снег сохраняется и может отрываться и переноситься ветром. Все эти варианты следует учитывать при выборе методов моделирования.
Методы моделирования снеговой нагрузки подразделяют на три категории:
1) методы, при которых последовательность отдельных снегопадов моделируется с помощью масштабных моделей, а частицы вводятся в аэродинамическую трубу или водяной лоток для имитации снежных частиц и их аккумуляции;
2) методы, в рамках которых скоростные режимы ветра анализирует с помощью масштабных моделей, а перенос и накопление снега выводят посредством численного анализа на основе учета полевых данных о скоростях снегопереноса и другой информации. При таком подходе физические имитаторы снеговых частиц не используют;
3) подходы, основанные на использовании численных методов динамики жидкостей, включая эффекты взаимодействия снежных частиц с воздушным потоком.
Все вышеперечисленные методы полезны для выявления возможных необычных снегоотложений, возникающих под действием ветров избранных направлений. Однако в тех климатических регионах, где температуры ниже точки замерзания держатся в течение длительных периодов, максимальные снеговые нагрузки могут быть результатом снегонакопления после многочисленных снегопадов и переноса снежных масс с различных направлений на протяжении большей части зимнего сезона. В таких случаях желательно прослеживать картину накопления снега на временной базе от 1 до 3 часов, распознавая последствия каждого снегопада и ветровой обстановки. Для отслеживания событий снегопада, переноса снега, таяния, повторного замерзания, выпадения дождя, просачивания и стока талой и дождевой воды следует применять численные методы. Здесь лучше всего подходит метод 2, который позволяет проводить быстрый пересчет снеговой нагрузки с использованием почасовых записей метеоданных и характеристик теплопередачи кровли, благодаря чему открывается возможность вероятностных прогнозов экстремальных нагрузок. Однако методы 1 и 3 способны обеспечить более детальное рассмотрение определенных форм снегоотложений при отдельных событиях. Поэтому часто оказывается целесообразным совместное использование разных методов. Примеры применения альтернативных методов прогнозирования можно найти в публикациях [21-25], [27] и [30].
В связи с тем, что во всех методах прогнозирования присутствуют различные численные упрощения, касающиеся процессов снегонакопления, важно, чтобы эти методы опирались на данные полевых наблюдений (см., например, [28] и [29]).
Приложение ДА
(справочное)
Сведения о соответствии ссылочного международного стандарта национальному стандарту
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 2394:1998 | IDT | ГОСТ Р ИСО 2394-2016 "Конструкции строительные. Основные принципы надежности" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандарта: - IDT - идентичный стандарт. | ||
Библиография
[1] | H i H. Snow load on Gable roofs, Results from Snow Load Measurements on Farm Building in Norway , Proceedings of the 1st. International Conference on Snow Engineering, CRREL Special Report No. 89-6, pp.95-104, 1989 (Xy X. Снеговые нагрузки на двускатные покрытия. Результаты измерений в норвежском сельскохозяйственном строительстве. Труды 1-й Международной конференции по технике снегозащиты. Специальный отчет Научно-исследовательской лаборатории по регионам с холодным климатом, N 89-6 за 1989 г., стр.95-104) |
[2] | THIIST., & O’ROURKE M. (2012), A model for the distribution of snow load on gable roofs, in Proc. of 7th Int. Conf. on Snow Engineering, Fukui, Japan (Фиис Т. и О’Рурк М. Модель распределения снеговых нагрузок на двускатные покрытия. Труды 7-й Международной конференции по технике снегозащиты, Фукуи, Япония, 2012) |
[3] | NEWARK M.J., WELSH L.E., MORRIS R.J., DNES V. Revised ground snow loads for the 1990 National Building Code of Canada. Can. J. Civ. Eng. 1989, 16 pp.267-278 (Ньюарк М. Дж. и др. Пересмотр веса снегового покрова для Национальныx строительных норм Канады 1990 г. Канадский журнал по гражданскому строительству, N 16,1989, стр.267-278) |
[4] | ELLINGWOOD В. (1984), Probabilistic models for ground snow accumulation, in Proc. of 41st Eastern Snow Conference, New Carrolton, Maryland, USA (Эллингвуд Б. (1984), Вероятностные модели накопления веса снегового покрова земли. Труды 41-й Восточной конференции, Нью-Кэрролтон, Мэриленд, США) |
[5] | IZUMI M., MIHASHI H., TAKAHASHI Т. Statistical Properties of the Annual Maximum Series and a New Approach to Estimate the Extreme Values for Long Return Periods. Proceedings of the 1st. International Conference on Snow Engineering, CRREL Special Report No. 89-6, pp.25-34, 1989 (Ицуми М., Михаши Х., Такахаши Т. Ежегодные статистические характеристики и новый подход к оценке временных рядов экстремальных значений при длительных периодах повторяемости. Труды 1-й Международной конференции по технике снегозащиты. Специальный отчет Научно-исследовательской лаборатории по регионам с холодным климатом, N 89-6 за 1989 г., стр.25-34) |
[6] | ZURANSKI J., & SOBOLEWSKI A. Snow Loads in Poland. Scientific Papers of the Building Research Institute, Warszawa, 2009 (Журанский Дж., Соболевский А. Снеговые нагрузки в Польше. Сборник научных статей Варшавского Инженерно-строительного института, Варшава, 2009) |
[7] | KASPERSKI М. (2012), A consistent approach for estimating the design value of the snow load on the ground from confined ensembles, in Proc. of 7th Int. Conf. on Snow Engineering, Fukui, Japan [Касперски М. Согласованный подход к оценке расчетного значения веса снегового покрова на основе ограниченных наборов данных. - В Трудах 7-й Международной конференции по технике снегозащиты, Фукуи, Япония) |
[8] | WORLD METEOROLOGICAL ORGANIZATION. Guide to meteorological instruments and methods of observation. WMO No. 8. WMO, Geneva, Switzerland, 2010 (Всемирная метеорологическая организация. Руководство по метеорологическим приборам и методам наблюдения. WMO N 8, ВМО, Женева, Швейцария, 2010) |
[9] | ASCE 7-88:1990, Minimum design loads for buildings and other structures (ISBN 0-87262-742-X) (ASCE 7-88:1990, Минимальные расчетные нагрузки для зданий и других сооружений) |
[10] | ОТСТАВНОВ В.А., И ГОХБЕРГ. Особенности расчета легких трехслойных панелей кровли. Промышленное строительство, 1970, N 9, Москва, СССР |
[11] | ARCHITECTURAL INSTITUTE OF JAPAN. Recommendations for Loads on Buildings, Tokyo, Japan 1993, 1996, 2004 (ISBN 4-8189-0405-8, 4-8189-0459-7, 4-8189-0556-9) [Архитектурный институт Японии. Рекомендации по нагрузкам на здания, Токио, Япония, 1993, 1996, 2004 (ISBN 4-8189-0405-8, 4-8189-0459-7, 4-8189-0556-9] |
[12] | M. Angaben von Schneelasten, geographisch nach Zonen gegliedert den Eurocode "Lasten". Landesstelle Baustatik, Baden- , , 1989 (Гренцер М. Географическое районирование снеговых нагрузок к Еврокоду "Нагрузки", Региональное отделение по строительству, Вюртемберг, Тюбинген, 1989) |
[13] | JCSS, Probabilistic Model Code Part 2: Load Models, 2.12 Snow Load, 99-CON-DYN/M0097 February 2002 UCSS-VROU-07-02-96 (JCSS, Нормы вероятностного моделирования. Часть 2. Модели нагрузки, 2.12 Снеговая нагрузка, 99-CON-DYN/M0097 Февраль 2002 1JCSS-VROU-07-02-96) |
[14] | TAKAHASHI T., TSUTSUMI Т., CHIBA T., MIHASHI H. (2012), Review of Formula on Snow Density, in Proc. of the 7th Int. Conf. on Snow Engineering, Fukui, Japan (Такахаши Т., Цуцуми Т., Чиба Т., Михаши Х. (2012). Анализ формулы плотности снега. - В Трудах 7-й Международной конференции по снегу в строительстве, Фукуи, Япония) |
[15] | The Coordinating Committee for Hydrology in Norden (KOHYNO). The improvement of point precipitation data on an operational basis. NHP-Report No. 17, 1986, Nordic Hydrological Programme, Stockholm, Sweden (Норденский координационный комитет по гидрологии. Уточнение данных о выпадении осадков в отдельных пунктах на операционной основе. NHP - Доклад N 17, 1986, Северная гидрологическая программа, Стокгольм, Швеция) |
[16] | SCHMIDT R.A. Threshold wind-speeds and elastic impact in snow transport. J. Glaciol. 1980, 26 (Шмидт Р.А. Пороговые скорости ветра и упругое соударение при переносе снега. Гляциологический журнал, N 26, 1980) |
[17] | OTSTAVNOV V.A., & ROSENBERG L.S. Consideration of wind effect in standardization of snow load. CIB Committee W23 in Basic Structural Engineering - Requirements for Buildings, 1969 (Отставнов В.А. и Розенберг Л.С. Учет воздействия ветра при нормировании снеговой нагрузки. Комитет W23 CIB по проектированию зданий и сооружений. Требования к зданиям, 1969) |
[18] | O’ROURKE M., KOCH P., REDFIELD R. Analysis of roof snow load case studies: Uniform loads. Cold Regions Research & Engineering Laboratory, CRREL Report 83-1, 1983 (О’Рурк М., Коч П., Редфилд Р. Анализ монографий о случаях снеговых нагрузок на покрытия: равномерно распределенные нагрузки. Научно-исследовательская лаборатория по регионам с холодным климатом. Отчет 83-1 за 1983 г.) |
[19] | TAYLOR D.A. A survey of snow loads on roofs of arena-type buildings in Canada. Can. J. Civ. Eng., 1979, 6 (Тейлор Д.А. Обзор снеговых нагрузок на покрытия зданий аренного типа в Канаде. Канадский журнал по гражданскому строительству, 6, N 1, 1979) |
[20] | ISYUMOV N. An approach to the prediction of snow loads. Ph.D. thesis, University of Western Ontario, London, Canada, 1979 (Изюмов Н. Подход к прогнозированию снеговых нагрузок. Кандидатская диссертация, Университет Западного Онтарио, Лондон, Канада, 1979) |
[21] | ANNO Y., TOMABECHI T. Development of a snowdrift wind tunnel. Cold Regions Science and Technology, No. 10, 1985 (Анно Я., Томабечи Т. Разработка аэродинамической трубы для моделирования снегопереноса. Наука и техника холодных регионов, N 10, 1985) |
[22] | O’ROURKE M., DEGAETANO A., TOKARCZYK J.D. Snow Drifting Transport Rates from Water Flume Simulation. J. Wind Eng. Ind. Aerodyn. 2004 December, 92 pp.1245-1264 (О’Рурк М., Дегаэтано А., Токарчик Д. Скорости снегопереноса при моделировании в водяном лотке. - В журнале "Ветровые нагрузки в строительстве и промышленная аэродинамика", дек. 2004, 92, стр.1245-1264) |
[23] | IRWIN P.A., & WILLIAMS C.J. (1983), Application of Snow Simulation Model Tests to Planning and Design, in Proceedings of the Eastern Snow Conference, 40th Annual Meeting, Vol.48, pp.118-130 (Ирвин П.А. и Вильяме К.Д. (1983). Использование результатов модельных испытаний с применением имитаторов снега при планировании и проектировании. Труды Западной конференции по снеговым нагрузкам, 40-я ежегодная конференция, т.48, стр.118-130) |
[24] | GAMBLE S.L., KOCHANSKI W.K., IRWIN P.A. Finite Area Element Snow Loading Prediction - Applications and Advancements. J. Wind Eng. Ind.Aerodyn. 1992, 4a, pp.1537-1548 (Гэмбл С.Л., Кочанский В.К., Ирвин П.А. Прогнозирование снеговой нагрузки методом элементов конечной площади - Приложения и развитие. - В журнале "Ветровые нагрузки в строительстве и промышленная аэродинамика", 1992, 4а, стр.1537-1548) |
[25] | IRWIN P.A., GAMBLE S.L., TAYLOR D.A. Effects of Roof Size and Heat Transfer on Snow Load: Studies fort he 1995 NBC. Can. J. Civ. Eng. 1995, 22 pp.770-784 (Ирвин П.А., Гэмбл С.Л., Тейлор Д.А. Влияние размеров и теплопередачи покрытия на снеговую нагрузку. - Труды NBC за 1995 год. Канадский журнал гражданского строительства, 1995, 22, стр.770-784) |
[26] | KURAHASHI I., TOMABECHI Т., FUKIHARA М. (2000), Estimation of snow load on a large-scale inclined roof of Tajima Dome, in Proc. of the 4th International Conference on Snow Engineering, 195-199 (Курахаши И., Томабечи Т., Фукахара М. (2000). Оценка снеговой нагрузки на большегабаритное наклонное покрытие здания Таджима. - В сб. тр. 4-й Международной конференции по снеговым нагрузкам в строительстве, 195-199) |
[27] | TOMINAGAY., OKAZET., MOCHIDAA. CFD Modelling of Snowdrift Around a Building: An Evaluation of New Approach. Build. Environ. 2011, 46 pp.899-910 (Томинага Й. Оказе Т., Мочида А. Моделирование снегопереноса вокруг здания методом вычислительной гидродинамики: оценка нового подхода. - Строительство и окружающая среда, 2011, 46, стр.899-910) |
[28] | TSUTSUMI Т., CHIBA Т., TOMABECHI Т. (2012), Snowdrifts On and Around Buildings Based on Field Measurement, in Proc. of the 7th Int. Conf. on Snow Engineering, Fukui, Japan [Цуцуми Т., Чиба Т., Томабечи Т. (2012) Снегоперенос на зданиях и вокруг них на основе полевых измерений. - В сб. тр. 7-й Международной конференции по снеговым нагрузкам в строительстве, Фукуи, Япония] |
[29] | OIKAWA S., & TOMABECHI T. (2000), Daily observation of snow drifts around a model cube, in Proc. of the 4th Int. Conf. on Snow Engineering, 137-141 [Оикава С. Томабечи Т. (2000). Ежедневное наблюдение снегопереноса вокруг кубической модели. - В сб. тр. 4-й Международной конференции по снеговым нагрузкам в строительстве, 137-141] |
[30] | DELPECHP., & GUILHOT J. (2008), Quantitative assessment of snow load on complex and extended roof shapes, in Proc. of the 6th Int. Conf. on Snow Engineering, Whistler, Canada. [Делпеч П., Гуилхот Дж. (2008). Количественная оценка снеговой нагрузки на сложные покрытия и покрытия больших размеров. - В сб. тр. 6-й Международной конференции по снеговым нагрузкам в строительстве, Уистлер, Канада] |
УДК 69+624.042.4:006.354 | ОКС 91.080.01 |
Ключевые слова: сооружение, воздействие, снеговая нагрузка, характеристическое (нормативное) значение снеговой нагрузки, вес снегового покрова | |
