ГОСТ Р 70424-2022 Внутриреакторные устройства реактора с жидкометаллическим натриевым теплоносителем. Расчет на прочность на стадии проектирования

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВНУТРИРЕАКТОРНЫЕ УСТРОЙСТВА РЕАКТОРА С ЖИДКОМЕТАЛЛИЧЕСКИМ НАТРИЕВЫМ ТЕПЛОНОСИТЕЛЕМ

Расчет на прочность на стадии проектирования

Издание официальное

Москва Российский институт стандартизации 2023

Предисловие

• 1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Центральный научно-исследовательский институт конструкционных материалов «Прометей» им. И.В. Горынина Национального исследовательского центра «Курчатовский институт» (НИЦ «Курчатовский институт» — ЦНИИ КМ «Прометей»)

• 2 ВНЕСЕН Техническим комитетом по стандартизации ТК 322 «Атомная техника»

• 3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2022 г. № 1653-ст

• 4 ВВЕДЕН ВПЕРВЫЕ

• 5 Федеральное агентство по техническому регулированию и метрологии не несет ответственности за патентную чистоту настоящего стандарта. Патентообладатель может заявить о своих правах и направить в Федеральное агентство по техническому регулированию и метрологии аргументированное предложение о внесении в настоящий стандарт поправки для указания информации о наличии в стандарте объектов патентного права и патентообладателе

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru).

© Оформление. ФГБУ «Институт стандартизации», 2023

Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии

Содержание

• 1 Область применения

• 2 Нормативные ссылки

• 3 Термины и определения

• 4 Сокращения и обозначения

• 5 Общие положения

• 6 Условие обоснования прочности при анализе реализации критических событий

• 7 Расчетный дефект

• 8 Анализ реализации критического события «Зарождение трещины при циклическом нагружении по механизму усталости»

• 9 Анализ реализации критического события «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости»

• 10 Расчет подроста расчетного дефекта

• 11 Анализ реализации критических событий «Нестабильное развитие трещины», «Потеря несущей способности» и «Потеря герметичности»

• 12 Анализ реализации критического события «Недопустимое изменение геометрических размеров»

Приложение А (обязательное) Физико-механические свойства и диаграмма деформирования

Приложение Б (обязательное) Расчетные кривые усталости

Приложение В (обязательное) Уравнения для определения напряженно-деформированного состояния компонента

Приложение Г (обязательное) Процедура формирования циклов нагружения при сложном нагружении и расчет усталостного повреждения

Приложение Д (обязательное) Скорость ползучести

Приложение Е (обязательное) Радиационное распухание

Приложение Ж (обязательное) Скорость роста трещины при ползучести

Приложение И (обязательное) Процедура расчета референсного напряжения для вычисления С*-интеграла

Приложение К (обязательное) Скорость роста трещины при циклическом нагружении

Приложение Л (обязательное) Статическая трещиностойкость

Приложение М (обязательное) Процедура расчета референсного напряжения для анализа потери несущей способности и герметичности компонента

ГОСТ Р 70424—2022

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВНУТРИРЕАКТОРНЫЕ УСТРОЙСТВА РЕАКТОРА С ЖИДКОМЕТАЛЛИЧЕСКИМ НАТРИЕВЫМ ТЕПЛОНОСИТЕЛЕМ

Расчет на прочность на стадии проектирования

Pressure vessel internals of fast reactor with liquid metal sodium coolant.

Strength analysis at the design stage

Дата введения — 2023—02—01

• 1 Область применения

  • 1.1 Настоящий стандарт устанавливает требования к расчету на прочность внутриреакторных устройств реактора с жидкометаллическим натриевым теплоносителем, изготовленных из материалов аустенитного класса и подвергаемых облучению до флюенса нейтронов не более 1 • 10²⁶ нейтр/м² при Е > 0,1 МэВ [не более 4,5 смещений на атом (сна)].

  • 1.2 Настоящий стандарт применяется на стадии проектирования внутриреакторных устройств реактора с жидкометаллическим натриевым теплоносителем.

• 2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 59115.1—2021 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Термины и определения

ГОСТ Р 59115.3 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Кратковременные механические свойства конструкционных материалов

ГОСТ Р 59115.4—2021 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Длительные механические свойства конструкционных материалов

ГОСТ Р 59115.9—2021 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Поверочный расчет на прочность

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

• 3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 59115.1, а также следующие термины с соответствующими определениями:

Издание официальное

• 3.1 компонент: Часть элемента, анализируемая при выполнении расчета на прочность.

• 3.2 критическое событие: Событие, приводящее к нарушению прочности либо к недопустимому изменению размеров компонента, из следующего перечня событий:

• - зарождение трещины при циклическом нагружении по механизму усталости;

• - зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости;

• - нестабильное развитие трещины;

• - потеря несущей способности;

• - потеря герметичности;

• - недопустимое изменение геометрических размеров¹ компонента.

• 3.3 критическое событие «Зарождение трещины при циклическом нагружении по механизму усталости»: Состояние компонента, когда в какой-либо его зоне в процессе эксплуатации происходит зарождение трещины по механизму усталости.

• 3.4 критическое событие «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости»: Состояние компонента, при котором в какой-либо его зоне перестают выполняться условия прочности по критерию зарождения трещины по механизму, характеризующемуся взаимным ускорением накопления повреждений при усталости и ползучести.

• 3.5 критическое событие «Недопустимое изменение геометрических размеров»: Достижение компонентом в процессе эксплуатации такого изменения его размеров, при котором нарушается нормальное функционирование этого и (или) соседних компонентов реакторной установки.

• 3.6 критическое событие «Нестабильное развитие трещины»: Состояние компонента, когда в какой-либо его зоне в процессе эксплуатации происходит нестабильное, т. е. не требующее увеличения нагрузки, развитие в этой зоне постулированной трещины.

• 3.7 критическое событие «Потеря несущей способности»: Состояние компонента с трещиной, не работающего под избыточным давлением, при котором его дальнейшее деформирование происходит без дополнительного нагружения.

• 3.8 критическое событие «Потеря герметичности»: Состояние компонента с трещиной, работающего под избыточным давлением, при котором дальнейшее нагружение приводит к его разгерметизации.

• 3.9 повреждающая доза: Интегральная характеристика, отражающая степень радиационного повреждения металла, определяемая как накопленное за определенное время число смещений одного атома из узла кристаллической решетки под действием нейтронного и гамма-излучения.

• 4 Сокращения и обозначения

  • 4.1 Сокращения

В настоящем стандарте применены следующие сокращения:

АЭУ — атомная энергетическая установка;

ВДВ — внешние динамические воздействия;

ДХН-покрытие — диффузионно-хромированное нитридное покрытие;

КИН — коэффициент интенсивности напряжений;

МВФ — метод весовых функций;

МКЭ — метод конечных элементов;

MP3 — максимальное расчетное землетрясение;

НДС — напряженно-деформированное состояние;

ННУЭ — нарушение нормальных условий эксплуатации;

НУЭ — нормальные условия эксплуатации;

НЭК — неразрушающий эксплуатационный контроль;

ПЗ — проектное землетрясение;

РУ — реакторная установка;

сна — смещение на атом;

УПА — условия проектной аварии.

• 4.2 Обозначения

В настоящем стандарте применены следующие обозначения.

• 4.2.1 Геометрические параметры

• а, с — длина малой и большой полуоси расчетного дефекта, мм;

• а₀, с₀ — начальная длина малой и большой полуоси расчетного дефекта, мм;

• a_N и c_N — длина малой и большой полуоси расчетного дефекта после нагружения последним циклом в рассматриваемом периоде эксплуатации, мм;

• а_г и с_т — длина малой и большой полуоси расчетного дефекта на конец рассматриваемого периода эксплуатации в условиях ползучести, мм;

• ^атЛ/ ^{и с}тЛ/ — длина малой и большой полуоси расчетного дефекта, развитие которого происходит при длительном (по механизму ползучести) и циклическом (по механизму усталости) нагружениях за рассматриваемый период эксплуатации, мм;

• АН— изменение геометрического размера компонента, мм;

• [А/-/] — допускаемое изменение геометрических размеров компонента, мм;

• H_t — толщина компонента или свариваемых компонентов, мм;

• /₀ — максимально возможный размер технологического дефекта в направлении толщины свариваемых компонентов, мм;

S_K — толщина стенки компонента, мм.

• 4.2.2 Параметры нагружения

• J — J-интеграл, Н/мм;

• К| — коэффициент интенсивности напряжений первого рода, МПа • м^1/2;

• F— повреждающая доза нейтронного облучения, сна;

dF „

• --скорость набора повреждающей дозы, сна/ч;

df

Р_р — механическая нагрузка, Н;

P_s — вторичная нагрузка, зависящая от остаточных сварочных напряжений, температурных напряжений, напряжений, обусловленных радиационным распуханием, Н;

Р_Ноц— параметр Холломона;

S_o — свободное радиационное распухание;

S_o — скорость свободного радиационного распухания, ч^-1;

• S — радиационное распухание материала с учетом напряжений;

• S — скорость радиационного распухания материала с учетом напряжений, ч^-1;

Т — температура, °C;

Тдбл — температура облучения, °C;

T_t — температура, при превышении которой необходимо учитывать характеристики длительной прочности, пластичности и ползучести, °C;

t— время, ч;

At— временной интервал, ч;

t_f— время до разрушения при испытаниях на длительную прочность, ч;

c>_m, e_mL и <з_ь — общие мембранные, местные мембранные и общие изгибные напряжения соответственно, МПа.

• 4.2.3 Параметры механических и физических величин

Е^т— модуль упругости при температуре Т, МПа;

G — модуль сдвига, МПа;

К— коэффициент объемного сжатия, МПа^-1;

R_p0 2 — минимальное значение предела текучести при температуре Т, МПа;

R_m — среднее значение предела прочности, МПа;

• — минимальное значение временного сопротивления (предела прочности) при температуре Т, МПа;

R_p02 — среднее значение предела текучести, МПа;

R^t— минимальное значение условного предела длительной прочности за время t при температуре Т, МПа;

R^t — среднее значение условного предела длительной прочности за время t при температуре Т, МПа;

RT— среднее значение истинного напряжения при разрыве при длительном статическом нагружении, МПа;

RT — минимальное значение истинного напряжения при разрыве при длительном статическом нагружении, МПа;

Z⁷— относительное сужение поперечного сечения образца после разрыва при кратковременных испытаниях на растяжение, %;

ZJ— относительное сужение поперечного сечения образца после разрыва при испытаниях на длительную прочность, %;

• — истинное напряжение в момент разрушения образца при кратковременном растяжении, МПа;

Ле — приращение деформации;

z_f—деформация разрушения при кратковременных испытаниях на растяжение;

е^ — деформация разрушения при испытаниях на длительную прочность (длительная пластичность);

v — коэффициент Пуассона.

• 4.2.4 Параметры механики разрушения и повреждения

K_JC — трещиностойкость, МПа • м^1/2;

J_c— критическое значение J-интеграла, Н/мм;

С*— контурный С*-интеграл для описания роста трещины при ползучести, Н/(мм ч);

ДК — размах КИН, МПа • м^1/2;

/<тах> K_min — максимальный и минимальный КИН в цикле нагружения соответственно, МПа • м^1/2;

ДК_а и ДК_С — размахи КИН первого рода в точках а и с расчетной трещины, МПа • м^1/2;

AK_th — пороговый размах КИН первого рода, МПа ■ м^1/2;

D_n— повреждение при циклическом нагружении;

£>_т — повреждение при длительном статическом нагружении;

D_Nx — повреждение при циклическом и длительном статическом нагружении;

f_c(D_N,D_T) — критическое повреждение при длительном циклическом нагружении;

[A/_f] — допускаемое количество циклов нагружения;

г— коэффициент асимметрии цикла нагружения.

• 4.2.5 Параметры напряженно-деформированного состояния

• о — напряжение, МПа;

• о₁ — максимальное главное напряжение, МПа;

• ^aeq— интенсивность напряжений (приведенные напряжения), определяемая на основании теории Мизеса, МПа;

• о₀ — гидростатическое напряжение, МПа;

• <з_т, <з_ь, <3_mL, a_bL — общие мембранные, общие изгибные, местные мембранные и местные изгиб-ные напряжения соответственно, МПа;

• <5_ref— референсное напряжение, МПа;

• аё_р — накопленная пластическая деформация;

• c,_ref— скорость деформации ползучести, вычисленная при напряжении, равном a_ref, ч^-1.

• 5 Общие положения

  • 5.1 Прочность внутриреакторного устройства должна оцениваться на основании анализа предельных состояний компонентов, входящих в состав этого устройства.

  • 5.2 При оценке прочности компонента принимается, что зарождение в нем дефекта может происходить по механизмам усталости и ползучести.

  • 5.3 При оценке прочности компонента принимается, что рост дефекта в нем может происходить по механизмам усталости и термоактивированной ползучести с учетом влияния облучения.

  • 5.4 При оценке допустимости изменения размеров компонента принимается, что изменение его размеров может происходить за счет пластического деформирования, радиационного распухания, термоактивированной и радиационной ползучести материала.

  • 5.5 Принимается, что достижение предельных состояний компонента (см. таблицу 5.1) осуществляется при реализации следующих критических событий:

• а) зарождение трещины при циклическом нагружении по механизму усталости;

• б) зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости;

• в) нестабильное развитие трещины;

• г) потеря несущей способности;

• д) потеря герметичности;

• е) недопустимое изменение геометрических размеров компонента.

Таблица 5.1 — Предельные состояния компонента и приводящие к ним критические события

• 5.6 Оценка прочности компонента проводится с использованием номинальных размеров, установленных проектом. При этом необходимо учитывать все расчетные нагрузки и воздействия, в том числе:

• - механические нагрузки (собственный вес компонента, вес присоединенного оборудования и трубопроводов);

• - внутреннее или наружное давление;

• - нагрузки от внешних динамических воздействий, включая сейсмические воздействия и динамические воздействия техногенного происхождения;

• - температурные воздействия;

• - вибрационные нагрузки.

• 5.7 Оценка прочности компонента по предельным состояниям согласно 5.5 должна проводиться наряду с расчетами на статическую прочность, устойчивость, внешние динамические воздействия и вибропрочность.

  • 5.7.1 Расчет компонента на статическую прочность следует проводить в соответствии с ГОСТ Р 59115.9—2021 (раздел 8) при действии всех расчетных нагрузок, кроме динамических, для исключения предельных состояний «кратковременное разрушение» и «возникновение недопустимой пластической деформации по всей площади какого-либо из возможных сечений либо только по части площади сечения, но по всей толщине стенки компонента».

На основании расчета в упругой постановке определяются группы категорий напряжений. Оценка прочности компонента выполняется путем сопоставления групп категорий напряжений с допускаемыми напряжениями.

• 5.7.2 Расчет на устойчивость следует проводить для компонентов, находящихся под действием наружного давления, или при воздействии на компонент сжимающей нагрузки. Расчет проводится в соответствии с ГОСТ Р 59115.9—2021 (раздел 9) для исключения предельного состояния «потеря устойчивости (при наличии ползучести или без нее)».

Расчетом должно быть показано, что значения нагружающих факторов на компонент в условиях ползучести и без учета ползучести не достигнут значений, вызывающих потерю устойчивости.

• 5.7.3 Расчет компонента на ВДВ (включая MP3, ПЗ, воздушную ударную волну, падение летательного аппарата) следует проводить в соответствии с ГОСТ Р 59115.9—2021 (раздел 15) для исключения предельных состояний: «кратковременное разрушение», «возникновение макротрещины вследствие циклического нагружения», «возникновение недопустимой пластической деформации по всей площади какого-либо из возможных сечений либо только по части площади сечения, но по всей толщине стенки компонента» и «потеря устойчивости».

• 5.7.4 Расчет на вибропрочность следует проводить для компонентов, подвергающихся вибрационному нагружению, в соответствии с ГОСТ Р 59115.9—2021 (раздел 16) для исключения предельного состояния «возникновение макротрещины вследствие циклического нагружения».

• 5.8 Анализ реализации критических событий согласно перечислениям а) — е) 5.5 следует проводить по процедурам разделов 8—12.

• 5.9 Оценка прочности компонента должна быть проведена с учетом установленной расчетной последовательности режимов нагружения, основанной на анализе условий эксплуатации, регламентированных проектом АЭУ, с учетом всех расчетных нагрузок и воздействий, а также всех режимов эксплуатации. В один расчетный режим может быть включена группа режимов, в случае если внешние нагрузки и температуры этих режимов не отличаются более, чем на 5 % от принятых расчетных значений.

• 6 Условие обоснования прочности при анализе реализации критических событий

  • 6.1 Обоснование прочности компонента следует проводить в соответствии с проектной моделью эксплуатации РУ с учетом анализа реализации критических событий согласно перечислениям а) — е) 5.5.

  • 6.2 Обоснование прочности компонента следует проводить как для основного металла, так и для сварных швов этого компонента.

  • 6.3 Для всех сварных швов однотипных сварных соединений допускается проводить анализ прочности только для самого нагруженного шва.

  • 6.4 При обосновании прочности принимают, что на начало эксплуатации расчетный дефект отсутствует во всех компонентах, за исключением сварных швов (которые при эксплуатации не будут подвергаться периодическому НЭК), основного металла с ДХН покрытием и зон компонента, не нагруженного избыточным давлением, которые в условиях эксплуатации подвергаются многоцикловому термическому нагружению (реализация термической усталости), в результате термопульсаций, вызванных смешиванием потоков теплоносителя с разной температурой.

  • 6.5 В компоненте (как в основном металле, так и в сварных швах) должен быть проведен анализ зарождения трещины согласно перечислениям а) и б) 5.5 в соответствии с разделами 8 и 9.

  • 6.6 В самых нагруженных сварных швах, в которых не предусматривается НЭК, основном металле с ДХН-покрытием, а также в зонах компонента, не нагруженного избыточным давлением, которые в условиях эксплуатации подвергаются многоцикловому термическому нагружению, постулируют расчетные дефекты, вид, размеры и ориентацию которых следует определять согласно 7.1 и 7.2. При этом принимается, что расчетные дефекты имеются в указанных компонентах с начала эксплуатации.

Для каждого дефекта должен быть проведен анализ его возможного стабильного подроста по механизмам усталости и ползучести в соответствии с разделом 10 от начала эксплуатации до момента окончания назначенного срока службы компонента или до момента нестабильного развития дефекта (до момента реализации критического события согласно перечислению в) 5.5).

• 6.7 В сварных швах, которые будут подвергаться НЭК, и основном металле без ДХН-покрытия в момент окончания назначенного срока службы постулируют расчетные дефекты, вид, размеры и ориентацию которых следует определять согласно 7.1 и 7.3.

• 6.8 Прочность компонента обоснована, в случае если под воздействием всех видов нагружения, предусмотренных проектом, и с учетом изменения физических и механических характеристик материалов в процессе эксплуатации, за назначенный срок службы для него выполнены все следующие условия.

  • 6.8.1 Не должны реализоваться критические события согласно перечислениям а) и б) 5.5 (за исключением сварных швов, которые при эксплуатации не будут подвергаться периодическому НЭК, основного металла с ДХН-покрытием, а также зон компонента, не нагруженного избыточным давлением, которые в условиях эксплуатации подвергаются многоцикловому термическому нагружению).

  • 6.8.2 Не должны реализоваться критические события согласно перечислениям в) — д) 5.5:

• - для каждого дефекта, постулируемого по 6.6, с учетом его возможного подроста;

• - при наличии дефекта, постулируемого по 6.7.

• 6.8.3 Не должно реализоваться критическое событие согласно перечислению е) 5.5.

• 6.8.4 Анализ реализаций критических событий согласно перечислению в) — д) 5.5 следует проводить в соответствии с разделом 11, критического события согласно перечислению е) 5.5 — в соответствии с разделом 12.

• 7 Расчетный дефект

  • 7.1 В зависимости от геометрии компонента в расчетах постулируют следующие виды расчетных дефектов:

• - поверхностная полуэллиптическая трещина (рисунок 7.1а);

• - поверхностная четвертьэллиптическая трещина (рисунок 7.16).

Расчетный дефект характеризуется длиной большой полуоси (с) и длиной малой полуоси (а), а также отношением начальной длины большой полуоси с₀ к начальной длине малой полуоси а₀, равным 3.

1 — фронт трещины; а — поверхностная полуэллиптическая трещина; б — поверхностная угловая четвертьэллиптическая трещина

Рисунок 7.1 — Виды расчетного дефекта

• 7.2 В неконтролируемом сварном шве и основном металле с ДХН-покрытием начальное значение малой полуоси а₀ расчетного дефекта следует принимать равным

а₀ = /₀- ОМ)

где /₀ — максимальная глубина дефекта технологического происхождения в сварном шве или глубина дефекта для основного металла с ДХН-покрытием.

Значение² /₀ для сварного шва принимают согласно таблице 7.1. Значение /₀ для основного металла с ДХН-покрытием принимают равным 2 мм.

Значение а₀ в компоненте, не нагруженном избыточным давлением, который в условиях эксплуатации подвергается многоцикловому термическому нагружению, принимают равным 2 мм.

Таблица 7.1 — Значение /₀ для сварного шва

Конечные размеры расчетного дефекта следует определять с учетом его возможного стабильного подрастания по механизмам усталости и ползучести в соответствии с разделом 10.

• 7.3 В основном металле без ДХН-покрытия или сварном шве, который в процессе эксплуатации будет подвергаться периодическому НЭК, значение малой полуоси а₀ следует принимать равным в зависимости от толщины H_t компонента или свариваемых компонентов:

• - 1 мм, при 2 < H_t < 4 мм;

• - 0,25 H_t, при 4 < H_t < 8 мм;

• - 2 мм, при H_t более 8 мм.

Расчет стабильного подрастания расчетного дефекта по механизмам усталости и ползучести не проводят.

• 7.4 Расчетный дефект располагают перпендикулярно к поверхности компонента и ориентируют таким образом, чтобы отношение J/J_c (Ki/K_JC) было наибольшим.

• 8 Анализ реализации критического события «Зарождение трещины
  
  при циклическом нагружении по механизму усталости»

  8.1 Анализ реализации критического события «Зарождение трещины при циклическом нагружении по механизму усталости» следует проводить для зон компонента, в которых в процессе эксплуатации температура Т не превышает T_t.

  • 8.2 Анализ реализации критического события «Зарождение трещины при циклическом нагружении по механизму усталости» следует проводить для установленной последовательности режимов нагружения, основанной на анализе условий эксплуатации, регламентированных проектом, с учетом физико-механических характеристик основного металла и металла сварных швов.

  • 8.3 Весь период эксплуатации разбивают на временные интервалы Aty, так что t_y+1 = tj+ At-,j= 1 - М, где М— количество временных интервалов Aty (блоков нагружения). При этом величина Aty должна выбираться таким образом, чтобы температурные и силовые характеристики нагружения в начале и в конце интервала были одинаковыми.

  • 8.4 На каждом временном интервале At- значения характеристик механических свойств материалов компонент (предел текучести, параметры деформационного упрочнения) следует принимать в соответствии с приложением А для повреждающей дозы нейтронного облучения Fj, которая соответствует моменту времени t- (начало временного интервала Aty).

  • 8.5 На каждом временном интервале Aty свойства материалов компонент, характеризующие сопротивление усталостному разрушению (кривые усталости), следует рассчитывать в соответствии с приложением Б для повреждающей дозы нейтронного облучения F-₊₁, которая соответствует моменту времени ty₊₁ (моменту окончания временного интервала Aty).

  • 8.6 С целью определения размахов деформаций для каждого временного интервала Aty должен быть выполнен расчет НДС в упругой (для мало нагруженных компонентов, работающих при напряжениях, не превышающих предел текучести) или упругопластической постановке (для компонентов, работающих при напряжениях, превышающих предел текучести) путем пошагового прослеживания истории нагружения компонента на временном интервале Aty с использованием уравнений согласно В.2 и В.З (приложение В). Размер шага при расчете следует назначать таким, чтобы нагружение на этом шаге было близко к простому нагружению.

При расчете в упругой или упругопластической постановке не требуется учитывать остаточные сварочные напряжения и радиационное распухание, в случае если расчет на циклическую прочность проводят с использованием кривых усталости с максимальной асимметрией цикла напряжений.

При использовании кривых усталости с коэффициентом асимметрии цикла напряжений R, равным минус 1, расчет в упругой или упругопластической постановке следует проводить с учетом остаточных сварочных напряжений и радиационного распухания, при этом должно быть обосновано, что максимальное в цикле наибольшее главное напряжение о_тах не превышает величину 0,5 -Е^г Ае.

В случае использования кривых усталости с максимальной асимметрией цикла допускается проводить независимые расчеты для каждого временного интервала Aty, то есть без учета истории нагружения при t меньше t-.

• 8.7 Последовательность режимов нагружения в рассматриваемый интервал времени Aty следует определять согласно проектной модели эксплуатации РУ.

• 8.8 Формирование циклов нагружения при сложном нагружении [определение количества циклов или полуциклов нагружения и соответствующих каждому циклу (полуциклу) размахов деформаций] следует проводить в соответствии с процедурой согласно приложению Г.

При определении размахов деформаций следует рассмотреть изменение деформаций во времени в наиболее нагруженной зоне компонента с концентрацией напряжений для установленной последовательности режимов нагружения.

• 8.9 Усталостное повреждение D^_N на временном интервале Aty для наиболее нагруженных зон компонента с концентрацией напряжений рассчитывают по формуле

где N_k — характеристика к-го цикла или полуцикла с размахом деформации Аг_к (N_k = 1 в случае если с размахом Дед. существует полный цикл; N_k = 0,5 в случае если с размахом \г_к существует только полуцикл);

[N_fk] — допускаемое количество циклов при размахе деформаций Де^;

L_cs — количество циклов и полуциклов нагружения на временном интервале At-.

Значение [N_fk] следует определять по расчетным кривым усталости в соответствии с Б.З (приложение Б) с использованием значений Аг_к.

Значения N_k, L_cs и Лг_к рассчитывают согласно Г.2 (приложение Г).

Значения характеристик, используемых для расчета кривых усталости, следует принимать в соответствии с температурой Т, соответствующей максимальной температуре в цикле (полуцикле) нагружения.

• 8.10 Накопленное усталостное повреждение за весь период эксплуатации следует определять по формуле

м

D_N = ^D>_n. (8.2)

/=1

• 8.11 Критическое событие согласно перечислению а) 5.5 за назначенный срок службы не реализуется, в случае если выполнено условие

Од/<1. (8.3)

• 9 Анализ реализации критического события «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости»

  • 9.1 Анализ реализации критического события «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости» следует проводить для наиболее нагруженных зон компонента, в которых в процессе эксплуатации температура Т превышает T_t.

  • 9.2 Анализ реализации критического события «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости» следует проводить для установленной последовательности режимов нагружения, основанной на анализе условий эксплуатации, регламентированных проектом, с учетом физико-механических характеристик основного металла и металла сварных швов.

  • 9.3 Весь период эксплуатации разбивают на временные интервалы Af-, так что tj + 1 = tj + At-, j = 1 - M, где М — количество временных интервалов Af- (блоков нагружения).

Для снижения консерватизма расчет следует проводить с большим количеством временных интервалов М. Величину Afy следует выбирать таким образом, чтобы температурные и силовые характеристики нагружения в начале и в конце интервала были приблизительно одинаковыми. При уменьшении количества временных интервалов М расчетное значение усталостного повреждения будет увеличиваться и расчет повреждений будет более консервативным.

• 9.4 На каждом временном интервале Af- значения характеристик механических свойств материалов компонент (предел текучести, параметры деформационного упрочнения) следует принимать в соответствии с приложением А для повреждающей дозы нейтронного облучения F-, которая соответствует моменту времени tj (начало временного интервала At).

• 9.5 На каждом временном интервале At- свойства материалов компонент, характеризующие сопротивление усталостному разрушению (кривые усталости), следует рассчитывать в соответствии с приложением Б для повреждающей дозы нейтронного облучения Fj₊^, которая соответствует моменту времени f_y+1 (моменту окончания временного интервала Af).

• 9.6 С целью определения размахов деформаций Ае для каждого временного интервала А^-должен быть выполнен расчет НДС в вязкоупругой (для мало нагруженных компонентов, работающих при напряжениях, не превышающих предел текучести) или упруго-вязкопластической постановке (для компонентов, работающих при напряжениях, превышающих предел текучести) путем пошагового прослеживания истории нагружения компонента на временном интервале Af_y. Размер шага при расчете следует назначать таким, чтобы нагружение на этом шаге было близко к простому нагружению.

Расчет в вязкоупругой постановке проводят с использованием уравнений согласно приложению Д и радиационного распухания в соответствии с приложением Е.

Расчет в упруго-вязкопластической постановке проводят с использованием уравнений ползучести согласно приложению Д, упругопластического деформирования согласно В.2 и В.З (приложение В), и радиационного распухания в соответствии с приложением Е.

• 9.7 Последовательность режимов нагружения в рассматриваемый интервал времени Af- следует определять согласно проектной модели эксплуатации РУ.

• 9.8 Расчет усталостного повреждения следует проводить согласно 9.8.1—9.8.4.

  • 9.8.1 Формирование циклов нагружения при сложном нагружении (определение количества полуциклов нагружения и соответствующих каждому полуциклу размахов деформаций и скоростей деформирования) следует проводить в соответствии с процедурой согласно приложению Г.

При определении размахов деформаций следует рассмотреть изменение деформаций во времени в наиболее нагруженной зоне компонента с концентрацией напряжений для установленной последовательности режимов нагружения.

• 9.8.2 Усталостное повреждение на временном интервале Af- для наиболее нагруженных зон компонента с концентрацией напряжений рассчитывают согласно Г.3.6 (приложение Г) по формуле

1

D_n = 0,5k_D У -г——=г, (9.1)

n=l|_M

где [N_fn] — допускаемое количество циклов при размахе деформаций Ае_л и скорости деформирования в цикле ^_л;

L_s — количество полуциклов нагружения на временном интервале Afy, определяемое в соответствии с Г.З (приложение Г);

k_D — коэффициент, рассчитываемый согласно Г.3.5 (приложение Г).

Значение [N_fn] следует определять по расчетным кривым усталости в соответствии с Б.2 (приложение Б) с использованием значений Ае_л и £_л.

Значения Де_л и ^_л рассчитывают согласно Г.3.7 и Г.3.8 (приложение Г) соответственно.

Значения характеристик, используемых для расчета кривых усталости, следует принимать в соответствии со скоростью деформирования в полуцикле и температурой Т, соответствующей максимальной температуре в полуцикле нагружения.

• 9.8.3 Накопленное усталостное повреждение за весь период эксплуатации следует определять по формуле

м

D_n=Y^DN- (9.2)

7=1

• 9.8.4 При расчете повреждения по формуле (9.2) необходимо учитывать усталостное повреждение от циклического нагружения при температуре, не превышающей T_t. Для этого к повреждению, рассчитанному по формуле (9.2), необходимо прибавить повреждение, рассчитанное в соответствии с разделом 8.

• 9.9 Расчет повреждения, обусловленного ползучестью, для наиболее нагруженных зон компонента с концентрацией напряжений следует проводить согласно 9.9.1—9.9.3.

  • 9.9.1 По результатам упруго-вязкопластического расчета следует сформировать зависимость интенсивности напряжения <5_eq во времени с учетом изменения максимального главного напряжения о₁ и температуры Т (рисунок 9.1).

При определении зависимости o_eq(f) исключают временные интервалы с о₁ < 0 и Т< T_t. При этом значение интенсивности напряжения принимают постоянным и равным максимальному значению o_eQ(f) на временном интервале Af_;-: (о_а(?)_тах = max(o_eQ(Af_/)), где Af_z- = f_/+1 - t_t (см. рисунок 9.1).

• 9.9.2 Длительное статическое повреждение на временном интервале Af_z рассчитывают по формуле

(9.3) /=1 ^lf,i

где At, — время нагружения компонента напряжением a'_eq в течение /-го интервала при температуре Tj (учитывается только время нагружения при температурах Т > T_t);

t_fj— время до разрушения, определяемое при температуре Tj, = (o_aQ)_max и скорости набора dF

повреждающей дозы — по ГОСТ Р 59115.4;

df

К — количество интервалов нагружения на всем периоде эксплуатации, отличающихся температурой Tj или напряжением e'_eq.

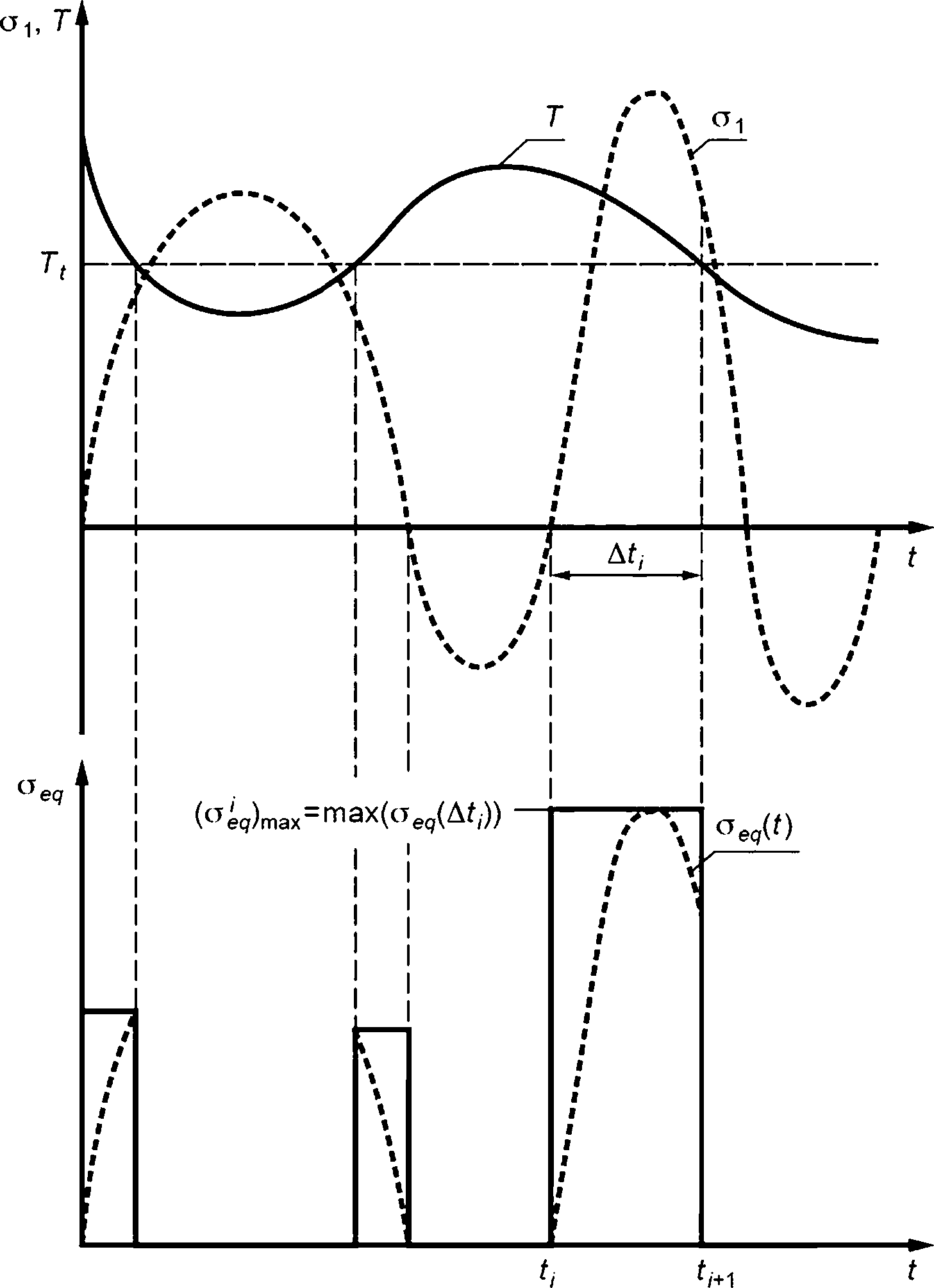
Рисунок 9.1 — Формирование зависимости (o_eQ)_max во времени с учетом изменения максимального главного напряжения о₁ и температуры Т

Значения t_fj определяют при максимальных значениях температуры Г,- = Т_тах и скорости набора повреждающей дозы на временном интервале Л?,.

Значение ^вычисляют по формуле

где значения и /^принимают по ГОСТ Р 59115.4.

• 9.9.3 Для зон компонента с остаточными сварочными напряжениями накопленное повреждение D_T следует определять по формуле

_D £

’ S(eJ_fe.)__£g_CH)

где — зависимость деформации разрушения при ползучести от средней скорости деформирования на временном интервале

^е6сн — максимальная пластическая деформация после сварки, обуславливающая остаточные сварочные напряжения; допускают принимать с&сн ⁼ 0>002.

Зависимость е^(£,) строят посредством перестроения зависимости где вместо координаты t_f используют координату £ = —. Значения определяют в соответствии с ГОСТ Р 59115.4—2021 (при-ложение Г) по формуле (Г.З) для заданных значений t_f.

Для сталей марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ зависимость eJ(£) принимают согласно ГОСТ Р 59115.4—2021 (приложение Г) по формулам (Г.1) и (Г.2).

• 9.10 Критическое событие согласно перечислению б) 5.5 за назначенный срок службы не реализуется, в случае если точка, определяемая значениями повреждений D_N и О_т, лежит внутри области, ограниченной осями 0D_T, 0D_N и кривой f_c(D_N,D_T) (рисунок 9.2).

На рисунке используются следующие обозначения:

£>_т — повреждение при длительном статическом нагружении, вычисленное согласно 9.9;

D_n — усталостное повреждение при циклическом нагружении, вычисленное согласно 9.8;

f_c(D_N,D_x) — зависимость, описывающая совокупность пар значений D_N и D_v приводящих к критическому повреждению.

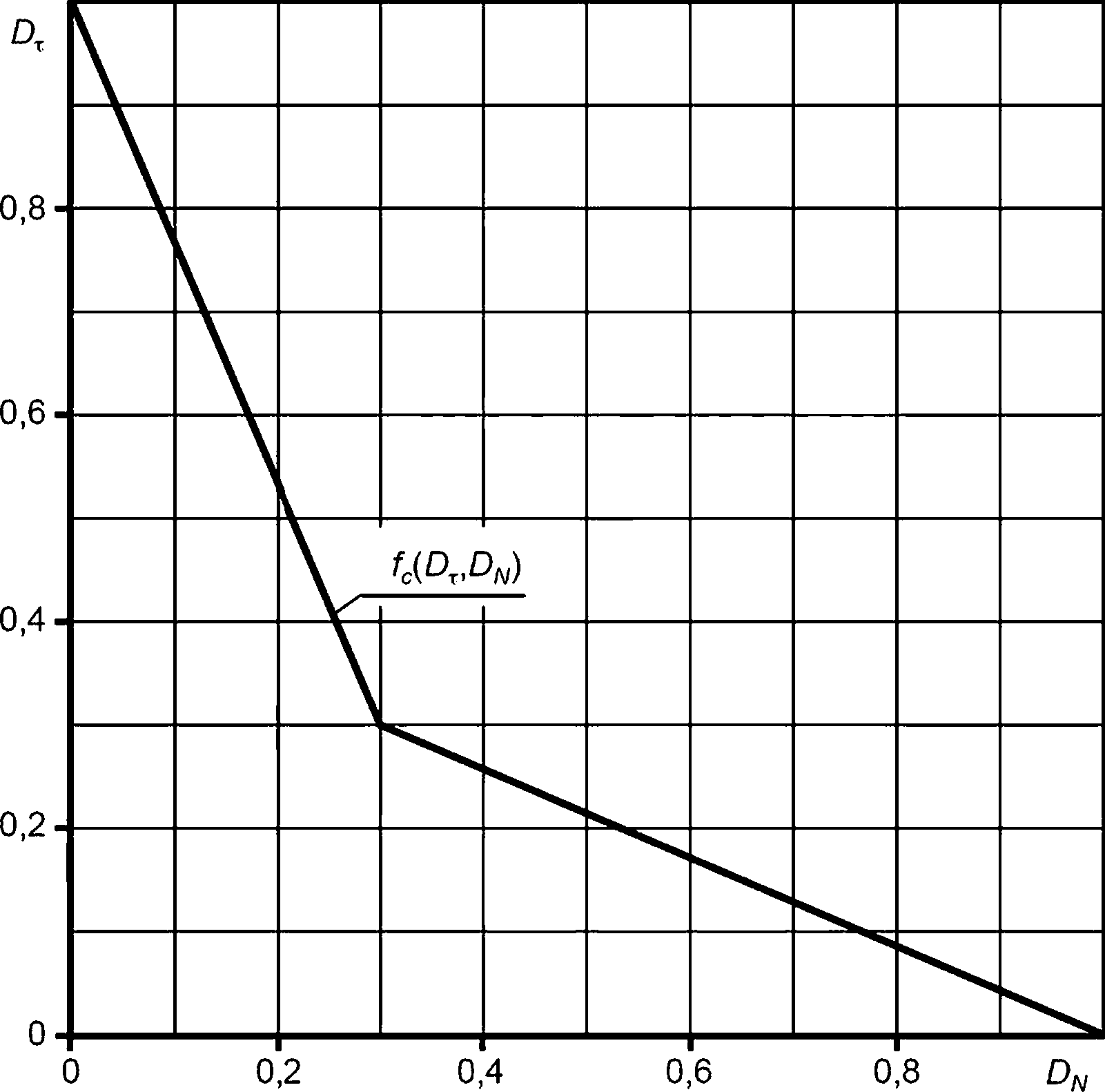
Рисунок 9.2 — Диаграмма, описывающая условие прочности при анализе критического события «Зарождение трещины при циклическом нагружении в условиях взаимодействия ползучести и усталости» для хромоникелевых сталей аустенитного класса и металла их сварных швов

• 10 Расчет подроста расчетного дефекта

  • 10.1 Общие положения при расчете подроста расчетных дефектов

    • 10.1.1 Для постулируемого согласно 6.6 поверхностного расчетного дефекта расчет подроста не проводят.

    • 10.1.2 Для постулируемого согласно 6.5 поверхностного расчетного дефекта расчет его подроста следует выполнять по механизмам усталости и ползучести. При этом расчет подроста расчетного дефекта проводят:

• - по механизму ползучести, в случае если температура Т компонента превышает 450 °C;

• - по механизму усталости, в случае если значение ЛК > K_th.

• 10.1.3 Период времени его подроста следует начинать с начала эксплуатации рассматриваемого компонента и завершать по окончанию его назначенного срока службы.

• 10.1.4 Расчет подроста расчетного дефекта следует выполнять в направлениях его большой и малой полуосей. Трещину следует располагать перпендикулярно поверхности компонента и ориентировать таким образом, чтобы ее рост был максимальным (отношение JIJ_C (Ki/K_JC) было наибольшим).

• 10.1.5 Расчет подроста расчетного дефекта следует выполнять в два этапа.

  • 10.1.5.1 На первом этапе расчета в качестве начальных размеров дефекта следует принимать его начальные длины малой и большой полуосей а₀ и с₀ согласно 7.2 и затем должен быть определен подрост этого дефекта по механизму ползучести за весь рассматриваемый период эксплуатации.

  • 10.1.5.2 На втором этапе расчета в качестве начальных размеров дефекта следует принимать его размеры, полученные на момент окончания первого этапа расчета, и затем должен быть определен подрост этого дефекта по механизму усталости за весь рассматриваемый период эксплуатации.

• 10.1.6 Анализ развития трещины по механизму ползучести следует выполнять на основе расчета в упруго-вязкопластической постановке с использованием уравнений ползучести согласно приложению Д, упругопластического деформирования согласно В.2 и В.З (приложение В), и радиационного распухания в соответствии с приложением Е.

• 10.1.7 Анализ развития трещины по механизму усталости следует выполнять на основе расчета в упругой постановке с использованием параметров линейной механики разрушения (коэффициентов интенсивности напряжений) с использованием уравнений для определения НДС согласно В.2 (приложение В).

• 10.2 Расчет подроста расчетного дефекта по механизму ползучести

  • 10.2.1 Весь рассматриваемый период эксплуатации следует разбить на временные интервалы Afy, так что f₊₁ = tj + A/у; j = 1 L, где L — количество временных интервалов A/у.

  • 10.2.2 На каждом временном интервале A/у значения характеристик механических свойств материалов следует рассчитывать в соответствии с приложением А для повреждающей дозы нейтронного облучения Fy₊₁, которая соответствует моменту времени /у₊₁ (моменту окончания временного интервала Af ).

  • 10.2.3 Для каждого временного интервала Mj должен быть выполнен расчет в вязкоупругой (для мало нагруженных компонентов, работающих при напряжениях, не превышающих предел текучести) или упруго-вязкопластической постановке (для компонентов, работающих при напряжениях, превышающих предел текучести) с учетом остаточных сварочных напряжений (при наличии таковых), радиационного распухания, ползучести и истории нагружения на временном интервале от 0 до tj.

Расчет следует проводить МКЭ (допускается использовать другие численные методы) с учетом пошагового прослеживания истории нагружения компонента. Размер шага при расчете следует назначать таким, чтобы нагружение на этом шаге было близко к простому нагружению.

При проведении расчета допускается не учитывать влияние радиационного распухания и радиационной ползучести, в случае если величина свободного радиационного распухания, рассчитанного согласно приложению Е, на момент окончания рассматриваемого периода эксплуатации составляет менее 0,1 %. При расчете свободного радиационного распухания используют наибольшие за рассматриваемый период эксплуатации повреждающую дозу и температуру нейтронного облучения в компоненте при НУЭ.

• 10.2.4 По результатам расчета следует построить зависимость референсного напряжения во времени о_ге/0-

• 10.2.5 Период нагружения A/у следует разбить на временные интервалы А/,- много меньше A/у. При этом исключают временные интервалы, при которых температура Т зоны с трещиной меньше T_t.

• 10.2.6 На каждом временном интервале А/,-значения попринимают постоянными и равными своему максимальному значению на интервале.

• 10.2.7 Для каждого временного интервала Щ должны быть рассчитаны значения КИН К’_а и К'_с в точках а и с расчетного дефекта (см. рисунок 7.1). Эти значения должны быть приняты постоянными и равными своим значениям в момент времени t, при котором б^доетнгает максимального значения на интервале А/_у. Значения К'_а и К‘_с следует рассчитывать на основании распределения нормальных к расчетному дефекту напряжений п_п, определяемых в результате расчета в упруго-вязкопластической постановке, и размеров расчетного дефекта на предыдущем временном интервале (а_/_₁ и с^). Значения К'_а и К'_с следует рассчитывать МВФ (допускается использовать другие методы), входной информацией для которого является НДС, полученное в результате расчета в упруго-вязкопластической постановке.

В случае если в компоненте рассматривается зона с остаточными сварочными напряжениями о_0СН, то для такой зоны при расчете КИН вместо о_п используется величина а_п + о_осн, где о_0СН определяется по формуле

где о_{0 2} — предел текучести материала в исходном (необлученном) состоянии;

Е^т — модуль упругости;

а_с, п_с, о₀ — параметры уравнения установившейся ползучести, принимаемые согласно приложению Д.

• 10.2.8 Подрост расчетного дефекта на временном интервале Af,- следует определять с использованием зависимостей согласно приложению Ж по формулам:

Да,-= со₂ Д_г(с_а) ^r Af,-; (10.2)

&Cj = со₁ • со₂ • A_r (С_с I -А?,-, (10.3)

где Да,- и Дс, — подросты расчетного дефекта по механизму ползучести в направлениях малой и большой полуосей за время Af,-, мм;

А_г, п_г— константы;

coi, о)₂ — коэффициенты, увеличивающие скорость роста трещины при ползучести за счет облучения;

С*, С*— С*-интеграл в точках а и с расчетного дефекта (рисунок 7.1), вычисляемый согласно приложению Ж, по формулам:

если тд_ах > T_t

<bet

0, если Г' _у < T_t ¹ 11 laA I

1СГ³ (к')² --^, если T‘>T_t l 1 i ' III d A i

®ref

0, если T^_ax < T_t

где Q_ref—деформация материала при <5_ref = c'_ref и температуре, равной максимальной T'_max на временном интервале Af, в зоне с дефектом;

К_а, К!_с — КИН в точках а и стрещины в момент времени, при котором o_refдостигает максимального значения на интервале At,. соответственно.

Расчет сопроводят в соответствии с приложением И с учетом размеров расчетного дефекта.

Значения А_г и п_г принимаются согласно таблице Ж.1 (приложение Ж).

• 10.2.9 В случае если на временном интервале At, рассчитанное значение К_а оказалось меньше 0, следует принимать К'_а равным 0. В случае если на временном интервале At,- рассчитанное значение К'_с оказалось меньше 0, следует принимать К'_с равным 0.

• 10.2.10 Текущие размеры расчетного внутреннего дефекта должны быть определены по формулам:

а,- = + Да,-;

€,-=0^ +ДС,-.

• 10.2.11 Конечные размеры а_т и с_т трещины следует определять последовательным повторением расчета согласно 10.2.6—10.2.10 до момента времени, соответствующего окончанию назначенного срока службы.

• 10.3 Расчет подроста расчетного дефекта по механизму усталости

  • 10.3.1 Для анализа развития трещины при циклическом нагружении следует определить разма-хи КИН на основании расчета в упругой постановке. При этом, в случае если расчет выполняется для компонента, в котором максимальная температура Т превышает T_t, расчет проводят с использованием начальных деформаций, полученных на этапе расчета в упруго-вязкопластической постановке при расчете роста трещины по механизму ползучести.

При проведении анализа допускается не учитывать начальные деформации, полученные на этапе расчета в упруго-вязкопластической постановке. В этом случае расчет скорости роста трещины следует проводить при коэффициенте асимметрии цикла, равном 0,95.

• 10.3.2 В качестве начальных размеров расчетного дефекта должны быть использованы длины малой и большой полуосей расчетного дефекта а_т и с_т, полученные согласно 10.2.11, в случае если проводился анализ развития трещины по механизму ползучести. В случае если расчет проводят для компонента, в котором максимальная температура Т не превышает T_t, в качестве начальных размеров дефекта следует принимать начальные длины его малой и большой полуосей а₀ и с₀ согласно 7.2.

• 10.3.3 По результатам расчета НДС в упругой постановке должны быть определены циклы нагружения, таким образом, чтобы в начале и в конце каждого /-го цикла нагружения значения КИН были одинаковыми. В случае если невозможно выделить цикл нагружения, в качестве характеристик цикла нагружения (ЛК и R) следует принимать характеристики полуцикла. При этом число циклов следует принимать равным числу полуциклов.

При проведении расчета допускается не учитывать влияние радиационного распухания, в случае если величина свободного радиационного распухания на момент окончания назначенного срока службы не превышает 0,1 %. При расчете свободного радиационного распухания следует использовать наибольшие за назначенный срок службы повреждающую дозу и температуру нейтронного облучения в компоненте при НУЭ.

• 10.3.4 Для каждого /с-го цикла (полуцикла) нагружения в точках а и с расчетного дефекта (см. рисунок 7.1) должны быть определены величины размахов КИН первого рода ЛК* и ДК£, а также коэффициенты асимметрии цикла напряжений R* и /?*.

Величины ДК^, R^k_a и ДК^к, R^k_c могут быть определены непосредственно из расчета в упругой постановке МКЭ (допускается использовать другие численные методы) или с помощью МВФ, используя в качестве исходной информации распределение напряжений в плоскости дефекта, рассчитанных при его отсутствии, а также длины малой и большой полуосей расчетного дефекта на момент окончания предыдущего цикла нагружения а_и и с^.

При проведении расчета без учета радиационного распухания коэффициенты асимметрии цикла напряжений R^k и R^k следует принимать равными 0,95.

• 10.3.5 В случае если для К-го цикла (полуцикла) нагружения рассчитанное значение /?* или R* оказалось меньше 0, следует принимать это значение равным 0. В случае если для К-го цикла нагружения рассчитанное значение R^k или R^k оказалось большим, чем 0,95, следует принимать это значение равным 0,95.

• 10.3.6 Расчет подроста дефекта по механизму усталости следует проводить только для тех циклов (полуциклов) нагружения, для которых значение ДК превышает значение ДК^, рассчитываемое в соответствии с приложением К. В случае если рассчитанное значение ДК* оказалось меньше AK_f/?(/?*), то на k-м цикле (полуцикле) нагружения следует считать, что подрост расчетного дефекта в направлении малой полуоси отсутствует. В случае если рассчитанное значение ДК* оказалось меньше AK_f/?(R*), то на к-м цикле (полуцикле) нагружения следует считать, что подрост расчетного дефекта в направлении большой полуоси отсутствует.

• 10.3.7 На основании зависимостей согласно приложению К должны быть определены величины подроста расчетного дефекта по механизму усталости за К-й цикл (полуцикл) нагружения по формулам:

/ \n_f

, если ДКо > ДКн-^а ,Т\

^{а th}\ ^а (10.8)

0, если ДКд < ДК^

•"^{Стар n}cyc ^Cf

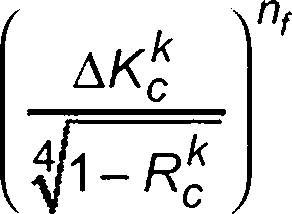
, если A/<£ > AK_th (rK,Т)

0, если ЛКр < \K_th

где ка_к и \с_к — подрост расчетного дефекта по механизму усталости в направлениях малой и большой полуосей за к-й цикл (полуцикл) нагружения, мм;

ДК^, Д/<£ — размахи КИН на к-м цикле нагружения соответственно в точках а и с трещины;

со⁵'⁴', со^стар — коэффициент ускорения роста усталостной трещины вследствие радиационного распухания и температурного старения соответственно;

^лсус — коэффициент, равный 1,0 при учете цикла и 0,5 при учете полуцикла;

C_fvi n_f— коэффициенты уравнения Пэриса;

АК_а и ЛК_С— размах КИН первого рода в вершинах расчетного дефекта на концах его малой и большой полуосей на k-м цикле (полуцикле) нагружения, МПа • м^1/2.

Значения AK_th, t£>^Sw, co^CTap, C_fn n_f следует принимать в соответствии с приложением К.

При определении значения co^Svvследует использовать значение повреждающей дозы нейтронного облучения, соответствующее моменту времени окончания к-го цикла нагружения. При определении значения C_f следует использовать значение повреждающей дозы нейтронного облучения, соответствующее моменту времени окончания к-го цикла нагружения и значение температуры, соответствующее максимальной температуре в к-м цикле нагружения.

• 10.3.8 Текущие размеры расчетного дефекта определяют по формулам:

а_к=а_к__д +&а_к; (10.10)

с_к = с_к__у + \с_к, (10.11)

где а_к и с_к — текущие размеры дефекта на к-м цикле нагружения, мм.

• 10.3.9 Конечные размеры а_тЛ/ и с_тЛ/ (при температуре Т выше T_t), или a_N и c_N (при температуре Т, не превышающей T_t) трещины при циклическом нагружении следует определять последовательным повторением расчета в соответствии с 10.3.4 — 10.3.8 до тех пор, пока не будут учтены все циклы нагружения.

• 11 Анализ реализации критических событий «Нестабильное развитие трещины», «Потеря несущей способности» и «Потеря герметичности»

  • 11.1 Анализ реализации критических событий согласно перечислениям в) — д) 5.5 следует проводить для компонента с расчетным дефектом при НУЭ, ННУЭ и УПА.

  • 11.2 Анализ реализации критического события согласно перечислению в) 5.5 проводят, в случае если температура компонента превышает 450 °C или повреждающая доза более 1 сна.

  • 11.3 Последовательность режимов нагружения следует определять согласно проектной модели эксплуатации РУ.

  • 11.4 Критическое событие согласно перечислению в) 5.5 не реализуется, в случае если в течение всего периода эксплуатации для всех режимов нагружения выполнены условия:

^nKa<^Pp’^Ps)^<KJC’ (ЦП

nK_c(P_p,P_s)<K_JC, (11.2)

где К_а(Р_р, P_s), К_с(^р_р, P_s) — значения КИН в точках а и с расчетного дефекта, рассчитанные согласно 10.2.7, с учетом механической (первичной) Р_р и вторичной P_s нагрузок, МПа; п — коэффициент запаса, п = 1,1;

K_JC — трещиностойкость, МПа • м^1/2, определяемая по формуле

Значения J_c рассчитывают в соответствии с приложением Л. Расчет значений КИН выполняется согласно 10.

• 11.5 Критическое событие согласно перечислению г) 5.5 (для компонентов, не работающих под избыточным давлением) не реализуется, в случае если в течение всего периода эксплуатации для всех режимов нагружения выполнено следующее условие

<j_fe/-(a,c,P_p) - ^Rp0,2- (11.4)

• 11.6 Критическое событие согласно перечислению д) 5.5 (для компонентов, работающих под избыточным давлением) не реализуется, в случае если в течение всего периода эксплуатации для всех режимов нагружения выполнены следующие условия:

a_ref(a,c,Pр) - ^ро,2’ (11-5)

а < 0,5S_K. (11.6)

Расчет <5_ref проводится в соответствии с приложением М с учетом размеров (а и с) расчетного дефекта и напряжений, вызванных механической нагрузкой Р

Значение Rp₀₂ принимают согласно приложению А.

• 11.7 В качестве размеров расчетного дефекта (а и с) следует принимать:

• - для постулируемого по 6.5 расчетного дефекта — значения а_тЛ/ и с_тЛ/ (при температуре Т выше T_t) или a_N и c_N (при температуре Т не превышающей T_t), определенные согласно 10.3;

• - для постулируемого по 6.6 расчетного дефекта — значения а₀ и с₀, принятые согласно 7.3.

• 12 Анализ реализации критического события «Недопустимое изменение геометрических размеров»

  • 12.1 Анализ реализации критического события согласно перечислению е) 5.5 для режимов НУЭ и ННУЭ следует выполнять путем оценки изменения геометрических размеров компонента за счет упругопластического деформирования, радиационного распухания и ползучести (термоактивированной и радиационной) посредством расчета в упругопластической (при Т < T_t) или упруго-вязкопластической постановке (при Т > T_t).

При проведении анализа допускается проводить расчеты только для режима НУЭ.

• 12.2 Весь период эксплуатации следует разбивать на временные интервалы Afy, так что f_y+1 = tj + At-, j = 1 + L, где L — количество временных интервалов Af-.

Для повышения точности и уменьшения консервативности расчетов следует увеличивать количество временных интервалов L.

• 12.3 На каждом временном интервале Щ значения характеристик механических свойств материалов следует рассчитывать в соответствии с приложением А для повреждающей дозы нейтронного облучения Fj₊i, которая соответствует моменту времени f₊₁ (моменту окончания временного интервала Af_y).

• 12.4 Для каждого временного интервала Af_y-должен быть выполнен расчет в упругопластической или упруго-вязкопластической постановке с учетом радиационного распухания, термоактивированной и радиационной ползучести, а также истории нагружения на временном интервале от 0 до tj. Определяющие уравнения для расчета НДС используют согласно приложениям В и Д; учет радиационного распухания следует проводить в соответствии с приложением Е.

• 12.5 Расчет должен быть проведен МКЭ (допускается использовать другие численные методы) с учетом пошагового прослеживания истории нагружения компонента. Размер шага при расчете следует назначать таким, чтобы нагружение на этом шаге было близко к простому нагружению.

• 12.6 Критическое событие согласно перечислению е) 5.5 за весь период эксплуатации не реализуется при условии

AH_k<[AH]_k, (12.1)

где АН_к — изменение геометрического размера компонента в к-м направлении, мм;

[А/7]^ — допускаемое изменение геометрических размеров компонента в к-м направлении, мм.

Приложение А (обязательное)

Физико-механические свойства и диаграмма деформирования

А.1 Зависимость предела текучести от температуры, повреждающей дозы нейтронного облучения и температуры облучения

А.1.1 Расчет средних значений предела текучести для исходного (необлученного, F = 0) состояния основного металла и сварного шва проводят по формуле

—о

Rpo,2 (Г) = <5_Yg + ays- МПа, при 20 °C < Т < 650 °C, (А.1)

где Gys ⁼ Р ’ e*P(~h[T + 273]), МПа;

o_yG, o_Ys — температурно-независимая и температурно-зависимая компоненты предела текучести соответственно, МПа;

[3 и h — константы материала, не зависящие от температуры.

Значения констант o_YG, fl и h приведены в таблице А.1.

Таблица А.1 — Значения констант o_yG, ЗиЛ для основного металла и металла шва сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ, 08Х18Н10Т

А.1.2 Средние значения предела текучести с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима и температуры облучения в отсутствие распухания рассчитывают по формуле

^Rp0,2 (^”^,7"^,7обл) ⁼ ^р0,2 (Т) + A/?p_{0 2} (F,Т_обл), МПа, при Т< Т_обл,

где А/?_ро 2^’Лэбл) — зависимость приращения предела текучести основного металла и металла сварного шва от повреждающей дозы нейтронного облучения и температуры облучения:

- для стали марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ и их сварных швов

^Д^ро,2(^Лбл) = А>₀₂ J¹-^exP(-°>^{094 /r}). МПа,

- для стали марки 08Х18Н10Т и ее сварного шва

ДКро,2 (^Лбл) = Ат_{0 2} • 7¹ -^ехР(-°>126 F), МПа,

K*₀₎₂(W = ^{650 + 1405}' ехр(-5,9 • 10-³ • [Т_обл + 273]).

А.1.3 Минимальные значения предела текучести с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима и температуры облучения в отсутствие распухания рассчитывают по формуле

^RpQ* (^F>^T’^To6n) = ^rIq,2(^t) + ^^Rp0,2(^F>^To6n)’ МПа, при Т< Т_обл,

где R^T_{pQ 2} — минимальное значение предела текучести для исходного состояния материала, принимаемое согласно ГОСТ Р 59115.3.

А. 1.4 Средние значения предела текучести с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима, температуры облучения и радиационного распухания рассчитывают по формуле

)=R^(F,r,T_o6„)- 1-

А. 1.5 Минимальные значения предела текучести с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима, температуры облучения и радиационного распухания рассчитывают по формуле

R^Tp_0<2(F,T,T_o6„)=R^(F,T.T_o6„y

(А. 10)

Формулы (А.2) — (А. 10) справедливы при Т< T_oQn.

А.2 Зависимость предела прочности от температуры, повреждающей дозы нейтронного облучения и температуры облучения

А.2.1 Средние значения предела прочности для исходного (необлученного, F= 0) состоянии материала рассчитывают по формулам:

-для стали марок09X18Н9, 10Х18Н9, 12Х18Н9

—о [з91 + 240 ехр(-6,95 -10^-3 тУ МПа, при 20 °C < Т < 450 °C

Rrn(T) = \ I ; (А.11)

617 - 0,49 Т, МПа, при 450 °C < Т < 650 °C

-для стали марки 08X16Н11 М3

—о _ч [463 + 153 ехр(-9,9 Ю^-3 тУ МПа, при 20 °C <7 <550 °C

Rm(T) = \ /’ ; (А.12)

1081-1,122-Т, МПа, при 550 °C < Т < 650 °C

- для стали марки 08Х18Н10Т

Ят(7) = 350 + 247-ехр(-6,6-10^-3 т), МПа, при 20 °C < Т < 400 °C. (А. 13)

А.2.2 Средние значения предела прочности с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима и температуры облучения в отсутствие распухания рассчитывают по формуле

Ят^ФФ (F,T,T_o6n) = R°_m(T) + AR_m(F,T_o6n), при Т< 7_обл, МПа,

где А/?_т(7,7_обл) — зависимость приращения предела прочности от повреждающей дозы нейтронного облучения и температуры облучения

414-^1-exp(-0,06-F), МПа, при 350 °C < 7_обл < 450 °C

(1208-1,765 • 7_0бл) ■ ^1 - ехр(-0,06-7), МПа, при 450 °C < 7_обл < 650 °C

А.2.3 Средние значения предела прочности с учетом повреждающей дозы нейтронного облучения, температуры расчетного режима, температуры облучения и радиационного распухания рассчитывают по формуле

А.З Зависимость модуля упругости от температуры

Расчет модуля упругости от температуры для стали марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08X16Н11 М3, 08Х18Н10Т проводят по формуле

Е^т = 206000 - 83 • Т, МПа.

ф($) = exp(-A_sw • Sⁿ™), (А.21)

— критическая деформация разрушения при одноосном растяжении для необлученного (исходного состояния) материала;

P_th = 6415; Т_Не = 400 °C; A_SIV = 6,55; n_sw = 0,67;

• - для сталей марок 09X18Н9,10X18Н9,12X18Н9: A_agjng = 1,490 • 1О^-4; B_agjng = 1,956; А_е = 0,53; В_£ = 0,117 сна"¹;

е? = 0,69;

• - для стали марки 08X16Н11 М3: A_agjng =1,97-10^-4; B_aging = 2,26; А_е = 0,53; В_£ = 0,117 сна^-1; е° = 0,69;

• - для стали марки 08Х18Н10Т при температуре Т меньше 450 °C: \\>(Р_Ноц) = 1; А_е = 0,41; В_е = 0,37 сна^-1; e_f° = 0,51.

Параметр Р_Но/1 вычисляют по формуле

^0//= 273)-(5,15 + lg(0)- (А.22)

А.4.2 Расчет критической деформации разрушения при кратковременных испытаниях на растяжение при Т> Т_Не проводят по формулам:

z_f = min(e(^r,ef^nt), (А.23)

где г/ — критическая деформация при транскристаллитном разрушении, расчет которой проводится по формуле (А. 18);

e^^nt — критическая деформация при интеркристаллитном разрушении

ej.^nt =ef (l-f(F))-£2(7--7-_He); (А.24)

Q(T- Т_Не) — параметр, характеризующий снижение пластичности и трещиностойкости при Т > Т_Не за счет реализации механизма высокотемпературного радиационного охрупчивания

W- Т_Не) = 1 - у(Т_Не) ■ (Т- Т_Неу, (А.25)

у(Т_Не) — коэффициент, характеризующий темп снижения пластичности и трещиностойкости

у(Т_Не) = 2,25 • 10^-5• Т_Не - 5,34 ■ 10^-3. (А.26)

Формулу (А.24) используют, в случае если концентрация гелия, образующегося в результате ядерных реакций С_Не > 1 • 10^-5 атомная доля в процентах к числу смещений на 1 атом (ат.%). При С_Не < 1 ■ 10^-5 ат.% принимается Q= 1.

А.5 Диаграмма деформирования

Расчет диаграммы деформирования проводят по формуле

(F, Т, Т_обл) = (^ф (Т, F) + A (F, Т, Т_обл)

, при

где ге_р — jdZgq ;

A(F,T,T_o6n) = b, -Ь₂-Т-Ь₃-До₀₂(Р,Т_обл), при Т>200 °C; (А.28)

-для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9: Ь₁ = 1408 МПа; Ь₂ = 1,4 МПа-°C^-1; Ь₃ = 1,6;

-для стали марки 08Х16Н11МЗ: Ь₁ = 1482 МПа; Ь₂ = 1,4 МПа - °C^-1; Ь₃ = 1,6.

Параметр деформационного упрочнения принимают в виде п_р

( А ?'^{5 п}р Т_обл) — 0,5 • —— , (А.29)

кЛ))

где А_о = 1000 МПа.

В случае если расчет по формуле (А.24) приводит к А < 0, то принимается А = 0.

Расчет диаграммы деформирования для стали марки 08Х18Н10Т выполняется по формуле (А.26), где расчет параметра деформационного упрочнения A(T,F) выполняется по формуле

Ц - »₂ Т - Ь₃ . (н_о^эфф (7, F) - о° ₂ (7-)), при Т < Т’ Ь,-Ь₂ Г-Ь₃ («о.2^Ф(^Г'-^Р)-°?,₂(^Г’))' при Т>Г’’

где = 982 МПа; Ь₂ = 1,93 МПа °C^-1; Ь₃ = 0,16; Г = 290 °C.

Параметр деформационного упрочнения п_р для стали марки 08Х18Н10Т рассчитывают на основе рассчитанных значений параметров деформационного упрочнения А, эффективного предела текучести Rg^ ^и эффектив-—эфф calc

ного предела прочности Rm путем решения относительно неизвестных величин п_р и е_о/ системы уравнений

„calc ^£ul

р^эФФ ( calc\ г\_т ^ехР1^еи/ I

где е_и/ — параметр материала.

При проведении расчетов для стационарных режимов необходимо учитывать, что текущая температура эксплуатации Т совпадает с температурой облучения Т_обл. В переходных режимах Т_обл отличается от текущей температуры эксплуатации Т. В этом случае принимается, что Т_обл соответствует температуре предшествующего стационарного режима.

Приложение Б (обязательное)

Расчетные кривые усталости

Б.1 Общие положения

Кривые усталости (кривые сопротивления усталостному разрушению) при температурах T>T_t рассчитывают согласно Б.2 с учетом скорости деформирования, при температурах T<T_t расчет проводят согласно Б.З без учета скорости деформирования.

Б.2 Расчет кривых усталости при температуре Т, превышающей T_t

Расчет кривых усталости проводят по формуле

где R_c — характеристика прочности материала;

Де — допускаемый размах деформаций;

[A/_f] — допускаемое количество циклов при размахе деформаций Де;

m, т_е — характеристики материала;

е^ — деформация разрушения;

л n_N — коэффициенты запаса по размаху деформации и числу циклов соответственно.

Показатель степени т_е вычисляют по формуле

= 0,1321 lg ^(1 + 1410'²-Z^T] , _^R-i .

где — предел выносливости.

Значения характеристик Е^Т, и Z^Tдля сталей марок 09X18Н9,10X18Н9,12X18Н9,08X16Н11 М3, 08X18Н10Т

следует принимать согласно приложению А.

Значения R^ принимают согласно ГОСТ Р 59115.3. Значения R^ и показатели степени т следует принимать по таблице Б.1.

Коэффициенты запаса прочности л_е и n_N следует принимать равными 2 и 10, соответственно, для компонентов, работающих под давлением, и равными 1,5 и 5 для компонентов, нагруженных только температурными нагрузками.

Таблица Б.1 — Значения характеристик R^ и т

Значения характеристик Е^Т, R^ и Z^T в расчетах следует принимать равными их наименьшим значениям в интервале рабочих температур рассматриваемого периода нагружения с учетом повреждающей дозы и скорости набора повреждающей дозы при нейтронном облучении.

Значение определяют по формуле

где (£) — зависимость деформации разрушения при испытаниях на длительную прочность от средней скорости деформирования £, в цикле.

Значения для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08X16Н11 М3, 08Х18Н10Т следует вычислять в соответствии с приложением А.

Допускают рассчитывать по формуле

где значения Z^T следует принимать согласно ГОСТ Р 59115.3.

Зависимость (£) строят посредством перестроения зависимости (t_f), где вместо координаты t_f исполь-е^г

зуют координату £ = —. Значения и принимают согласно ГОСТ Р 59115.4—2021 (раздел 5, приложение А). tf

Допускают определять £f_t по формуле

f Z^T

el =-In 1--*— , (Б.5)

100j ^v '

где значения Zj принимают по ГОСТ Р 59115.4.

Для сталей марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ зависимость (£) принимают согласно ГОСТ Р 59115.4—2021 (приложение Г) по формулам (Г.1) и (Г.2).

Значения характеристик E_f, и Z[ в расчетах следует принимать равными их наименьшим значениям в интервале рабочих температур рассматриваемого периода нагружения с учетом повреждающей дозы и скорости набора повреждающей дозы при нейтроном облучении.

Характеристику прочности материала R_c определяют по формуле

Значения <5_f определяют при кратковременных испытаниях на растяжение. Допускают рассчитывать a_f по формуле

оу = Rm • [l + 1,4(1 -e"^e'j], МПа.

Значения R_m для сталей марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ, 08Х18Н10Т следует вычислять в соответствии с приложением А. _

Допускают в формуле (Б.7) вместо R_m использовать значения где R^ принимают согласно ГОСТ Р 59115.3.

Зависимость R^) строят посредством перестроения зависимости R^(t_f), где вместо координаты t_f использу-^£ft(tf) —

ют координату £ = —— . Значения R^t_f) и ((f) принимают по зависимостям средних значений истинного преде-

tf

ла длительной прочности и длительной пластичности согласно ГОСТ Р 59115.4—2021 (приложение Г) по формулам (Г.6) и (ГЗ) соответственно. _

Допускают определять значения R^(t_f) по формуле

^с=^Г- (Б.8)

1-^-

100

Значения R^T_mt и 2^принимают согласно ГОСТ Р 59115.4. _

Для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08X16Н11 М3 зависимость R^T_c(t>) следует принимать согласно ГОСТ Р 59115.4—2021 (приложение_Г) по формулам (Г.4) и (Г.5).

Значения характеристик R^, a_f, /?^и R^_t в расчетах следует принимать равными их наименьшим значениям в интервале рабочих температур рассматриваемого периода нагружения.

Б.З Расчет кривых усталости при температуре Т, не превышающей температуру T_t

Б.3.1 Расчет кривых усталости проводят по формуле где E_f — деформация разрушения при кратковременных испытаниях при растяжении;

e_f(4n_w[A/_f])

г — коэффициент асимметрии цикла напряжений, г = ^С|Т|'^П

С* max

Б.3.2 Допускают проводить расчет кривых усталости без коэффициента асимметрии цикла (рассматривается случай максимальной асимметрии цикла) по формулам:

п_сЕ^т (4[N,])^m'

, если 2Rр_{0 2} -п_еДе_Л£Е^г < 0;

^ег(^4пл/ [ty])

_| Шр0,2 - ^Аел_м Е^Т

"N 7

M⁴ⁿ«К1Г" _nrn,’ ^ес™ ^2rTp0.2-о;

В формулах (Б.9) — (Б.11) R_c = o_f, где рассчитывают по формуле (Б.7); коэффициенты запаса прочности п_г и n_N следует принимать равными 2 и 10 соответственно для компонентов, работающих под давлением, и равными 1,5 и 3 для компонентов, нагруженных только температурными нагрузками.

При e._f> 0,69 следует принимать e_f = 0,69.

Б.4 Кривые усталости для металла шва рассчитывают по формуле

Ae^w = ф^е,

где (p_s — коэффициент снижения циклической прочности, принимаемый согласно ГОСТ Р 59115.9;

Де — допускаемый размах деформаций, рассчитанный согласно Б.2 или Б.З для основного металла.

Приложение В (обязательное)

Уравнения для определения напряженно-деформированного состояния компонента

В.1 Основные уравнения

Для расчета НДС используют следующие уравнения:

&ij ~ ^siJ⁺ ^ij a nv

dZjj = de^ +dE? +dE^ + 8,у de⁷” + 8,y de^sw;

о =^-^m 3 ’

[1, при / = /

О;; = 7 _Л

¹ [0, при I * J

где <5ц, Зц — компоненты тензора и девиатора действительных напряжений соответственно;

о_т — гидростатическое напряжение;

dE,y, dey, ds? , dEy — приращения компонент тензоров полных деформаций E_;y, упругих деформаций £у, пластических деформаций е? и деформаций ползучести Е,у соответственно;

dE^r, dE^sw' — приращение деформации, обусловленной температурой и радиационным распуханием соответственно.

Уравнения (В.1) — (В.4) позволяют описывать кинетику НДС компонента с учетом упруго-вязкопластического деформировании материала при известных его свойствах и заданных краевых условиях.

Для описания поведения материала в области упругого, пластического и вязкого деформирования используют уравнения согласно В.2—В.5.

В.2 Уравнения теории упругости

Уравнение, описывающее связь между напряжениями и деформациями в пределах упругости, записывают в виде

^£ij ⁼ +

Е^т

^гяе 5см^:

к =

Е^т = Е^т(Т) — модуль упругости;

G = G(T) — модуль сдвига;

К= К(Т) — коэффициент объемного сжатия;

v — коэффициент Пуассона, v = 0,3.

• В.З Уравнения теории пластичности

Для описания пластического деформирования на основе теории течения с нелинейным кинематическим упрочнением используют уравнения, приведенные ниже. Расчет эквивалентных напряжений проводят с использованием энергетической теории Мизеса.

Компоненты тензора приращений пластических деформаций при активном нагружении определяют на основе ассоциированного (с условием пластичности) закона течения в соответствии с уравнениями:

d _deP ₌ 2^i₃

^IJ 2 p_eQ ^Р"

^deeo = ^de/7 ’>

^еЧ у 2 V

P/y - ^sij ~ Pij’

/з

PeQ=^2^^:

$ij — компоненты девиатора активных напряжений;

р_е£? — интенсивность активных напряжений;

Sjj — компоненты девиатора действительных напряжений;

р_;у — компоненты микронапряжения.

Уравнение поверхности текучести принимают в виде

где С_р0 — радиус поверхности текучести, С_р0 = R_po2^ ^sij ~ ~ ® пт

o_zy — компоненты тензора действительных напряжений;

5_;у — символ Кронекера.

Уравнение для приращения микронапряжений dp_zy принимают в виде

^dPv =9i^d^-92P//^ds£r

где g₁ и д₂ — параметры, зависящие от температуры и повреждающей дозы.

• В.4 Уравнения теории ползучести

Для описания ползучести используют уравнения согласно приложению Д.

• В.5 Определение параметров д₁ и д₂ в уравнении пластичности с нелинейным кинематическим упрочнением

Параметры д₁ и д₂ следует определять из диаграммы пластического деформирования с использованием формул (В.12) — (В.14).

В соответствии с формулой (А. 18) (приложение А) для описания диаграмм пластического деформирования используют зависимость, которая для одноосного растяжения может быть представлена формулой

°и~°о,2 = ^A (zu)ⁿ' (В. 15)

где для одноосного случая = ае_р; = o_eQ;

А и п — параметры материала, зависящие от температуры Т расчетного режима.

Для одноосного растяжения и кинематического упрочнения уравнение (В.12) принимают в виде

Ри ⁼ 3(^11 ^_С_р0). (В.16)

Из уравнения (В.20) с учетом (В. 19) получим

2 / _п \^п

Ри = з^ (еи) • (В-17)

Интегрируя уравнение (В.14) с учетом растяжения (> 0), получим

^ри ⁼y^L[¹-^exp(-^g2^en)]- (В-18)

Параметры д₁ и д₂ определяют методом наименьших квадратов на основе уравнений (В.22) и (В.20) путем минимизации среднеквадратичной ошибки, заданной уравнением

n ( _д г min У — 1-ехр

ЙДй!.

где в качестве входной информации используют численные значения ;

Л/— количество значений деформации

Приложение Г (обязательное)

Процедура формирования циклов нагружения при сложном нагружении и расчет усталостного повреждения

Г.1 Процедура определения профиля циклического нагружения при нестационарном нагружении

Г.1.1 Определяют профиль циклического нагружения, т. е. изменение деформации от времени во времени, в рассматриваемой зоне компонента при исследуемом режиме нагружения или группе режимов нагружения по следующей процедуре.

Г.1.2 Рассматриваемый режим (группа режимов) нагружения разбивают на блоки таким образом, чтобы термосиловые условия нагружения (силовые нагрузки и температура) в начале и в конце блока были бы одинаковыми. Определение профиля нагружения проводят для каждого блока отдельно.

Г.1.3 Рассчитывают эквивалентную деформацию (т) на первом шаге нагружения в текущий момент времени т по формуле (используется критерий Мизеса)

где е_х(т), е_у(т), e_z(t), у_ху(т), y_yz, y_zx(z) — компоненты деформации в системе координат XYZ, рассчитанные с учетом упругой и пластической деформации, и деформации ползучести;

v — коэффициент Пуассона, v = 0,3.

Еу

т = и рассчитывают приращение деформации на первом шаге по формуле

(Г.2)

где — время, при котором достигается максимальное значение (т).

Значению Де<¹) присваивают знак плюс.

Г.1.5 Рассчитывают эквивалентное приращение деформаций на втором шаге по формуле

где

;т>г<¹).

Г.1.6 На втором шаге нагружения определяют момент времени при котором достигается максимум

де_х 1<²>

Ле_у

Де₂

_Л г и приращение

△Yxy

&Ууг

△Yzx .

деформации Де<²> по формуле

Де⁽²⁾ = max Де^²⁾ (т) = Де^ (т)|^₍₂₎ • (Г.4)

Значению Де<²> присваивают знак минус.

Г.1.7 Определяют вектор деформаций, отвечающий концу второго шага нагружения (моменту времени №), по формуле

Г.1.8 Расчет Де^ для л-го шага нагружения выполняют аналогично Г.1.5—Г.1.7.

Рассчитывают эквивалентное приращение деформаций по формуле

1

£_у ^ez

Уху yyz Yzx

— вектор деформаций, отвечающий концу (л - 1) шага нагружения.

Г.1.9 На л-м шаге нагружения определяют момент времени при котором достигается максимум Де^(т),

Ле(^п)=(-1)^{п 1} max Де^(т) = (-1)^{п 1}ДеЦ(т)| . (Г.7)

Г.1.10 Определяют вектор деформаций, отвечающий концу n-го шага, по формуле

При определении компонент деформаций система координат должна быть зафиксирована.

Г.1.11 Строят профиль циклического нагружения, то есть зависимость е<^л> от номера шага нагружения в соответствии с формулой

_е(п) _{= е}(п-1) _+Де(п) (R9)

При этом принимают, что в начальный момент рассматриваемого блока нагружения и в конечный момент е = 0, т. е.

_е(0) _=е(л/₍) _=0> (г.10)

где N_t— последний шаг рассматриваемого блока нагружения.

Г.2 Формирование циклов нагружения по методу «стока»

Г.2.1 Формирование циклов нагружения проводят для каждого блока нагружения отдельно на основании зависимости е(^л\

Г.2.2 Циклы нагружения при нестационарном нагружении формируют по методу «стока» («дождя»), алгоритм которого представлен ниже. Блок-схема данного алгоритма представлена на рисунке Г.1.

Г.2.3 Алгоритм определения размахов деформаций Де, характеристик цикла (Л/ = 1) или полуцикла (Л/ = 0,5) с размахом деформаций Де, суммарного количества циклов и полуциклов нагружения по методу «стока» состоит в следующем.

Используемые обозначения:

X — размах деформации на текущем шаге; У — предыдущий размах, примыкающий к размаху деформации X; S — точка старта в истории (начальное значение S = a); N — характеристика цикла или полуцикла с размахом деформаций Де (Л/ = 1 или Л/ = 0,5); L_cs — суммарное количество циклов и полуциклов нагружения (количество точек максимума или минимума).

• 1) Определяют текущую точку (а, b или с) максимума или минимума на основании данных зависимости е<^л\ В случае если больше данных нет, то переход к шагу 6).

• 2) В случае если определено менее трех точек, то переход к шагу 1). Иначе, формируют размахи X и У, используя три определенных точки (а, Ь, и с) максимумов и минимумов: У = |е<^а> - е<^ь>|; X = |е<^ь> - е<^с>|.

• 3) Сопоставляют абсолютные значения размахов X и У.

При X < У переход к шагу 1).

При X > У переход к шагу 4).

• 4) В случае если размах У содержит точку старта S, то переход к шагу 5. Иначе, размах У считают как один цикл (Л/= 1); точки максимума и минимума размаха У исключают из рассмотрения и далее переход к шагу 2).

• 5) Размах У считают как полуцикл (Л/ = 0,5); исключают первую точку в размахе У (минимум или максимум); точку старта S перемещают на вторую точку размаха У (S = 5); далее переход к шагу 2).

• 6) Каждый размах, который не был учтен, считают как полуцикл (Л/ = 0,5).

Г.2.4 При расчете размахов деформаций Де, характеристики N с размахом деформаций Де и суммарного количества циклов и полуциклов нагружения L„_s, в соответствии с Г.2.3 следует руководствоваться положениями настоящего пункта и графиком зависимости г^^п>, представленным на рисунке Г.2.

• 1. S = а; У= |е<^э> - е(^ъ)|; X = |е(^ъ) - е<^с)|; X > Y. Yсодержит точку S, т. е. точку а. Считают |е(^а) - е<^ь>| как полуцикл и исключают точку a; S = Ь.

• 2. У = |e(^fe) - е<^с)|; X = |е(^с) - e^I; X < Y.

• 3. Y= |е<^с) - е^|; X = Ie^ - в(^е>|; X > Y. Считают |е(^с) - е^| как один цикл и исключают точки end. Цикл формируют парой размахов |е(^с> - £<^d)| и частью |е^ - £<^е>|.

• 4. У = |е<^й> - Е<^е)|; X = |Е<^е) - е^|; У > X.

• 5. У= |Е<^е) - £<0|; Х= |е<0 _ _е<9)|; У>Х.

• 6. У = |е^ - £<0)|; X = (е^) - е(^л)|; Х> У. Считают |е^ - e^I как один цикл и исключают точки Гид. Цикл формируют парой размахов |е^ - £^)| и частью |Е<^е> - е<%

• 7. У = |е<^ъ) - Е(^е)| ; X = |c(^e> - е<^л>| ; X > У. У содержит точку S, т. е. точку Ь. Считают |е<^ь> - Е<^е>| как полуцикл и исключают точку Ь; S = е.

• 8. У = |Е<^е) - е(^л)|; X = |е<^л) - ; У > X. Больше данных нет.

• 9. Считают |Е<^е> - е(^л>| как полуцикл, |е(^л> - е<'’>| считают как полуцикл.

• 10. Конец расчета.

Результаты данного расчета приведены в таблице Г.1.

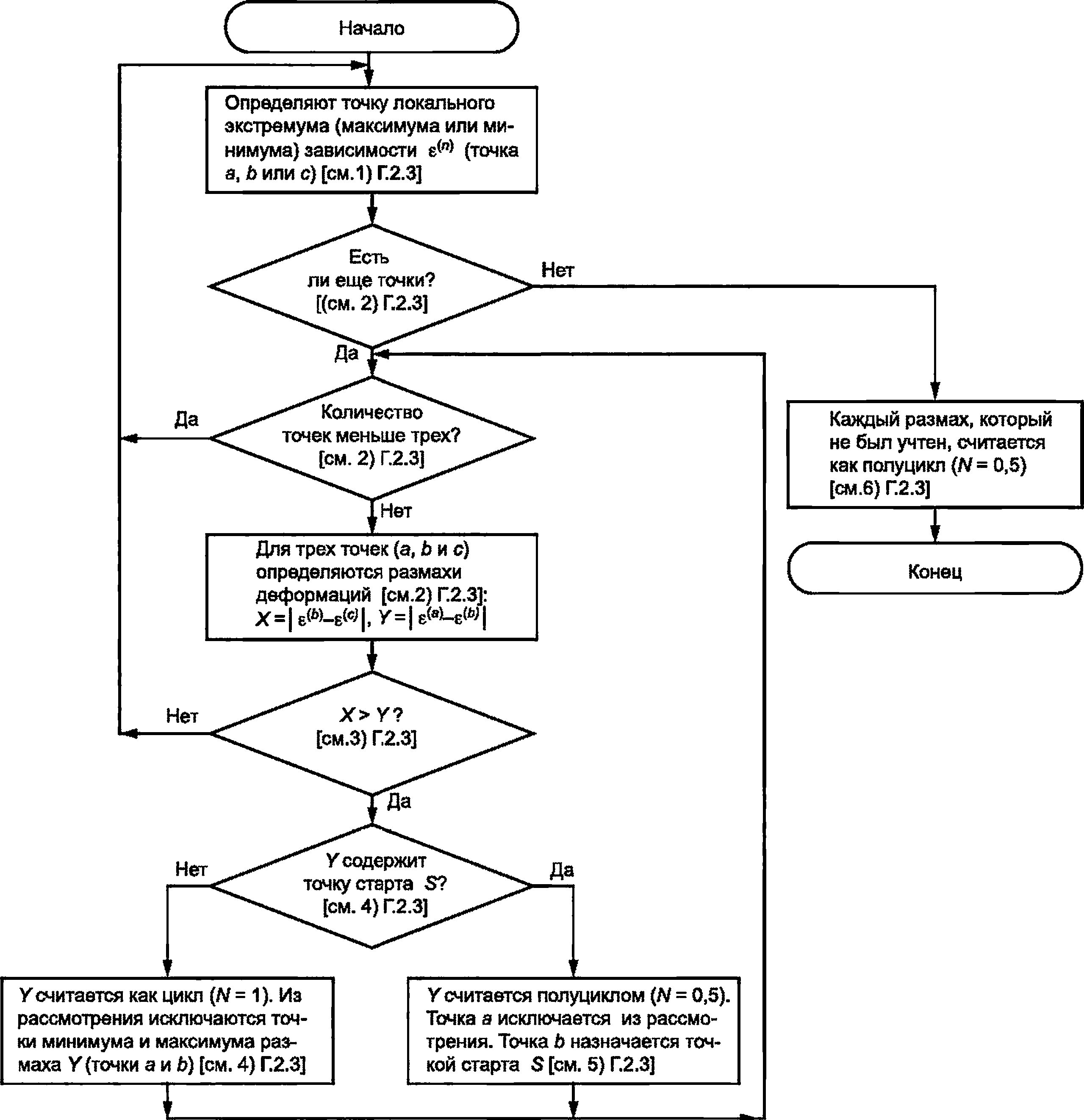
Рисунок Г.1 — Блок-схема алгоритма метода «стока» (метод «дождя»)

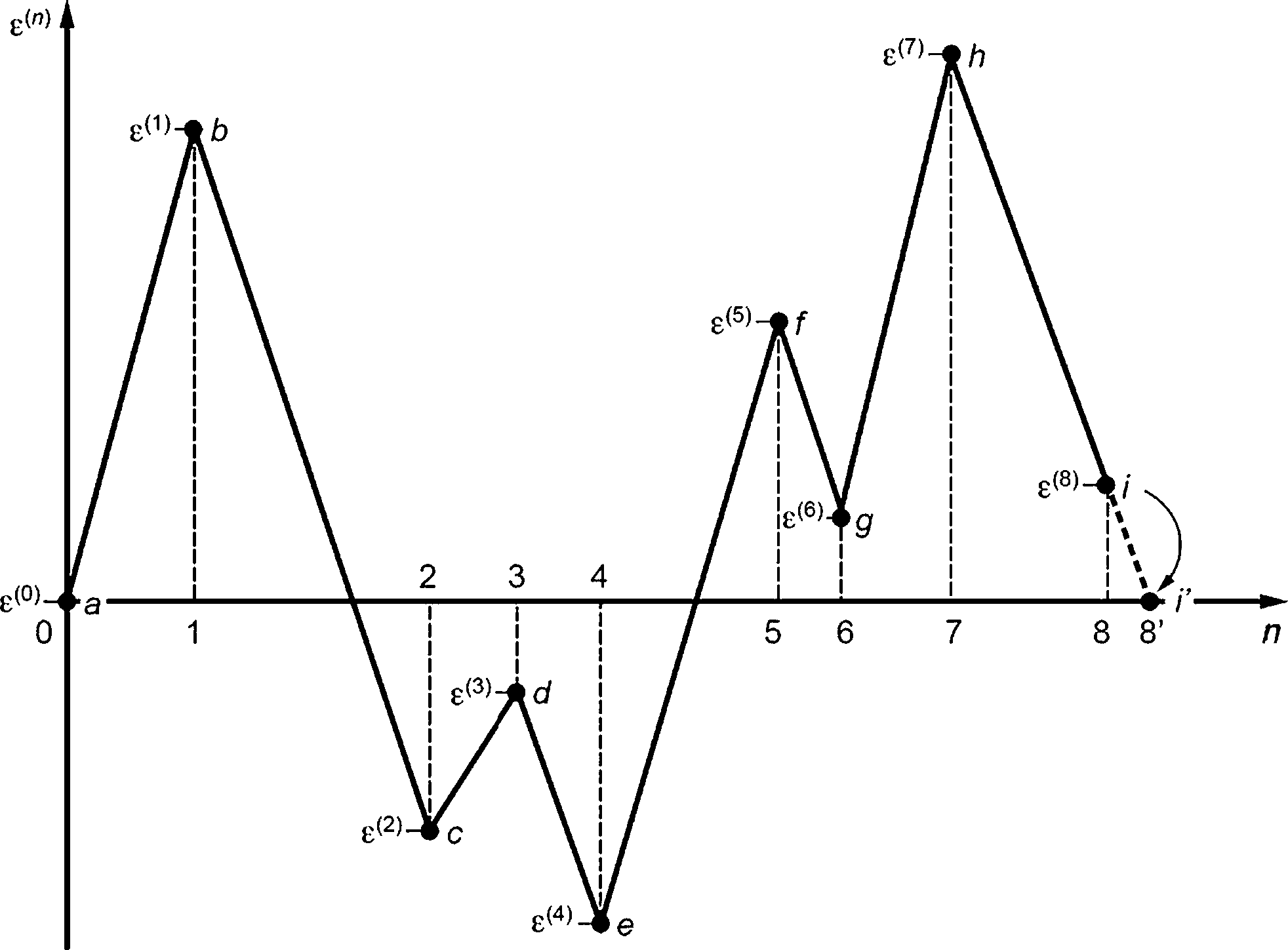
Рисунок Г.2 — Зависимость от номера шага нагружения и применение метода «стока» для определения размахов деформаций Де, характеристики Л/с размахом деформаций Де и суммарного количества циклов и полуциклов нагружения L_cs = 6

На рисунке Г.2 расчетное значение е<⁸) соответствует л = 8, принятое значение е<⁸> = 0 соответствует п = 8’.

Таблица Г.1 — Размах деформаций Де^, цикл (полуцикл) N_k с размахом деформации Аг_к и суммарное количество циклов и полуциклов нагружения L_cs для зависимости (см. рисунок Г.2) (к— порядковый номер цикла или полуцикла)

Г.З Расчет усталостного повреждения при ползучести

• Г.3.1 Расчет усталостного повреждения при Т > T_t следует проводить с учетом приоритетного рассмотрения циклов нагружения с наибольшим размахом деформаций в соответствии с процедурой, приведенной ниже. Учет изменения температуры и скорости деформирования следует проводить при переходе от полуцикла к полуциклу.

Г.3.2 Весь период нагружения рассматривают как совокупность полуциклов, характеризующуюся размахом деформаций, скоростью деформирования и температурой.

На первом этапе проводят вычисление повреждения О_сток по методу «стока» и повреждения О_Полуцикл’ Р^ас‘ считываемого на основе рассмотрения нагружения как совокупности полуциклов. Расчет повреждений проводят при таких скоростях деформирования и температуре, при которых они не будут оказывать влияние на повреждения ^сток ^и Цполуцикл⁴

На втором этапе проводят вычисление коэффициента k_D, который учитывает более консервативную оценку повреждения, рассчитанного по методу «стока» по отношению к повреждению, рассчитанному как сумма повреждений на каждом полуцикле.

На третьем этапе проводят вычисление повреждения на каждом полуцикле с учетом влияния скорости деформирования и температуры и с использованием коэффициента k_D.

Г.3.3 Расчет повреждения О_сток проводят с использованием циклов, сформированных по методу «стока» согласно Г.2, по формуле

о = у-Я* ^сток

где N_k — характеристика к-го полуцикла или цикла с размахом деформации Де^ (N_k = 0,5 в случае если с размахом Де^ существует только полуцикл; N_k = 1 в случае если с размахом Де_к существует полный цикл), рассчитываемая согласно Г.2.3;

[/V_fJ — допускаемое количество циклов, определяемое по кривой усталости при размахе деформаций Де_к, определяемом согласно Г.2, максимальной скорости деформирования с, за весь рассматриваемый период эксплуатации и минимальной температуре эксплуатации Т.

Г.3.4 Рассчитывают повреждение О_{полуцикл} при рассмотрении нагружения как совокупности полуциклов, сформированных согласно Г.3.7, по формуле

где L_s — количество полуциклов нагружения на рассматриваемом периоде эксплуатации, определяемое согласно Г.3.7;

[N_{f n}] — допускаемое количество циклов, определяемое по кривой усталости при размахе деформаций Де_л, рассчитываемом согласно Г3.7, максимальной скорости деформирования £ за весь период эксплуатации и минимальной температуре эксплуатации Т.

Г.3.5 Рассчитывают поправочный коэффициент k_D, учитывающий более консервативную оценку повреждения по методу «стока» по отношению к повреждению, рассчитанному согласно Г.3.4, по формуле

°^сток . (Г. 13)

Цю л у цикл

Г.3.6 Повреждение за весь рассматриваемый период нагружения рассчитывают по формуле

Ц j

Од/= 0,5k₀ i=— =г. (Г. 14)

n=iL^/v,nJ

Расчет допускаемого количества циклов [N_fn] проводят по кривой усталости при размахе деформаций Ае_л, рассчитанном согласно Г.3.7, с учетом скорости деформирования £_л, рассчитанной согласно Г.3.8, и температуры Т, соответствующей максимальной температуре в л-м полуцикле.

Г.3.7 Размах деформации Ае_л л-го полуцикла рассчитывают с использованием зависимости сформированной согласно Г.1, по формуле

Ае_л = |е<^л) - е<^л-1 )|, л = 1, ..., L_s, (Г.15)

где Де_л — размах деформации в л-м полуцикле.

Г.3.8 Скорость деформирования ^_л в л-м полуцикле рассчитывают по формуле

„ Де_п

(г.1б) А?_л

где Af_n — длительность л-го полуцикла, Af_n = tW - А^л-1);

А^л), ^^л-1) — значения времени, соответствующие значениям е(^л) и е<^л-1).

При определении значения Af_n не учитывают время работы компонента на стационарном режиме.

Приложение Д (обязательное)

Скорость ползучести

Д.1 Обозначения

кф — коэффициент ускорения скорости ползучести при облучении;

Sj:— компоненты девиатора действительных напряжений, МПа;

Т_а — абсолютная температура, К;

Т — температура, °C;

df— приращение времени, ч;

Еу — компоненты тензора деформаций ползучести;

de,у —приращения компонент тензора деформаций ползучести;

• — компоненты тензора скоростей деформаций ползучести, ч^-1;

^>eq — интенсивность скорости деформации ползучести материала в исходном состоянии, ч^-1;

• <5jj— компоненты тензора напряжений, МПа;

Pij—компоненты микронапряжения, МПа;

5,У—символ Кронекера;

в_т — гидростатическая компонента тензора напряжений, МПа;

°eq — интенсивность действительных напряжений, МПа.

Д.2 Уравнение термоактивированной ползучести (при Т> T_t), основанное на теории упрочнения, принимают

в виде

Д.З Интенсивность скорости деформации ползучести рассчитывается по формуле

М^С(Е_сГ, 4-1 °0 )

о₀ = 100 МПа.

Константы а_с, п_с, т_с и е_м для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9 и 08X16Н11 М3 при различных температурах приведены в таблице Д.1.

Таблица Д.1 — Значения констант в уравнениях скорости ползучести для стали марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ

где ^eqx — скорость ползучести при температуре Т_ах (Т_а2 > Т_ах > Т_а^);

Т_ах, T_aV Т_а2 — абсолютные температуры в градусах К;

^eqi > ^>eq2 — скорости ползучести, рассчитанные по формуле (Д.8) в соответствии с параметрами, указанными в таблице Д.1, при температурах Т_а1 и Т_а2 соответственно.

Формула (Д.13) применяется для материала в исходном состоянии. При определении скорости ползучести для облучаемого материала значение скорости, полученное по формуле (Д.13), умножается на коэффициент к_ф.

Д.5 Для описания радиационной ползучести (при Т < T_t) интенсивность скорости деформации ползучести используется в виде

(НС \

^e"dT ^{+ t}° J °^е<?’ ^Ч”^1, (Д-¹⁴)

где В = 1 • 10^-6 (МПа • сна)"¹; со = 2,7 10^-3 (МПа)~¹;

S — скорость распухания, определяемая в соответствии с приложением Е, ч^-1.

Д.6 Скорость ползучести, используемая при расчете релаксации напряжений и скорости роста трещины при Т> T_t, принимают в виде

( А^Пс

-т¹ . (Д.15)

°0 )

где о₀ = 100 МПа.

Значения Ь_с при различных температурах приведены в таблице Д.1.

Приложение Е (обязательное)

Радиационное распухание

(Е.4)

Р = 8,0-10-³ МПа-¹; и = 0,15;

Cjj — компоненты тензора напряжений;

• <5_eq — интенсивность напряжений, рассчитываемая по формуле (Д.10).

• Е.2 Температурно-дозовая зависимость свободного радиационного распухания рассчитывается по формулам:

-для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9

S_o = с • F^nv • exp

где с = 1,63 • 10^-4 сна^-п* ; n_v = 1,88; г = 1,1 • 1О^{-4 О}С~²; Т_т = 470 °C;

-для стали марки 08X16Н11 М3 где c_D1 = 9,8-10"⁵ сна^-п; = 2,310^-4 °C"²; Т_тах1 = 470 °C;

c_D2 = 9,610“⁵ сна^-п; г₂ = 1,510^-4 Х"²; Т_тах2 = 565 °C;

п = 1,88; T_diff= 513 °C.

Расчет радиационного распухания проводится в случае, если величина S_o, рассчитанная по формулам (Е.5) и (Е.6), превышает 1,0-10^-4.

Приложение Ж (обязательное)

Скорость роста трещины при ползучести

Скорость роста трещины для необлученного материала определяется по формуле

(Ж.1)

где А_г и п_г — константы материала (значения констант для основного металла и металла сварного шва стали марок 09Х18Н9, 10Х18Н9, 12Х18Н9 и 08Х16Н11МЗ приведены в таблице Ж.1);

/ — длина трещины, мм;

t — время, ч;

С* — контурный интеграл, определяемый по формуле

С* = ГI Wriy - сицП: 1 d s, (Ж.2)

П ^Эх1 J

где Г — криволинейный контур, начинающийся на одном берегу трещины и заканчивающийся на другом берегу трещины, по которому ведется интегрирование;

^9

W — J ^тп ‘-imn >

0

dl/;

Uj = -jy- — скорость перемещения в направлении х_;-;

^х1> ^х2 — декартовые координаты;

fij — компонента единичного вектора, перпендикулярного к элементу ds;

ds — элемент контура Г;

• <з_тп — компоненты тензора напряжений;

^•тп’ — компоненты тензора скоростей деформаций ползучести.

Таблица Ж.1 — Значения коэффициентов А_г и п_г для основного металла и металла сварного шва сталей марок 09Х18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ

С*-интеграл может быть рассчитан по упрощенной формуле

где К, — КИН первого рода, МПа • м^1/2;

c_ref — референсное напряжение, определяемое в соответствии с приложением И, МПа;

• — скорость ползучести необлученного материала, расчет которой приводится согласно Д.5 (приложение Д),

^ПРИ ^eQ ⁼ ^efH%q ^{= a}ref-^4-1-

Расчет ^_ге/-при температурах, не указанных в таблице Д.1, проводится по формуле (Д.13) (приложение Д), где вместо подставляется £,_ref.

Скорость роста трещины при ползучести под действием нейтронного облучения определяется по формуле

(dn

Ьт ^=С°Г^С°2- -77

'°^г'обл

где со₁ и (о₂ — параметры, увеличивающие скорость роста трещины при ползучести за счет облучения

(о< =1 + 6,1-10⁴/q—, ¹

где ку рассчитывается по формулам:

• - для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9

к< = 1188-3,97-7+ 3,34 -10^-3 - Т², —;

сна

• -для стали марки 08X16Н11 М3

к< = 1294- 4,26 ■ 7 + 3,52 • 10^-3• Т², —;

• ¹

(о₂ =1 + k₂(0,22F)ⁿ“;

• к₂ рассчитывается по формулам:

-для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9

к₂ = 27,2 - 8,5 • 10^-2 • 7 + 7,06 ■ 10“⁵ • 7²; = 1,362 - 1,72 • 10^-3 • 7;

-для стали марки 08X16Н11 М3

к₂ = 2,42;п_ю = 1,02 - 1,079-10"³- 7, (Ж.10)

где 7 — температура, °C.

Формулы (Ж.5) и (Ж.8) применяются для диапазона температур от 450 °C до 600 °C, диапазона скоростей набора повреждающей дозы от 0 до 1 сна/год и диапазона повреждающих доз от 0 до 45 сна.

В случае если 450 °C < 7 < 500 °C, расчет по формулам (Ж.5) и (Ж.8) проводится при 7 = 500 °C.

Приложение И (обязательное)

Процедура расчета референсного напряжения для вычисления С*-интеграла

В выбранном для оценки сечении компонента, в котором расположен дефект или предполагается его наличие (плоскость дефекта лежит в плоскости сечения), расчетным или аналитическим методом определяют распределение напряжений o_n(x,f) нормальных к плоскости сечения в момент времени / (см. рисунки И.1 и И.2). В расчетах учитывают как механические, так и вторичные нагрузки. Расчет НДС компонента проводят без дефекта.

Полученное в расчете произвольного вида напряжение о_п(х,/) представляют в текущий момент времени в виде мембранной и изгибной составляющих, и аппроксимируют вдоль оси х на отрезке от х = -h/2 до х = а - h/2. (а — глубина трещины) формулой

<7n(x) = G_m-Gbf2^, (И.1)

где с_ти о₆ — константы, значения которых определяются методом наименьших квадратов. Референсное напряжение определяют по формуле

(1 - ^)^1,58 ~- ^)^3,16 ■ 4⁺°^_ ^^)3,14 ■ 04?

ас h-(c + h)'

При с_т < 0 принимают <з_т = 0.

При <з_ь < 0 принимают в_ь = 0.

Расчет по формуле (И.2) проводят при изменении a/h от 0 до 0,8.

В случае четвертьэллиптической трещины в формуле (И.2) размер h определяют согласно рисунку И.2 и принимают, что с = а.

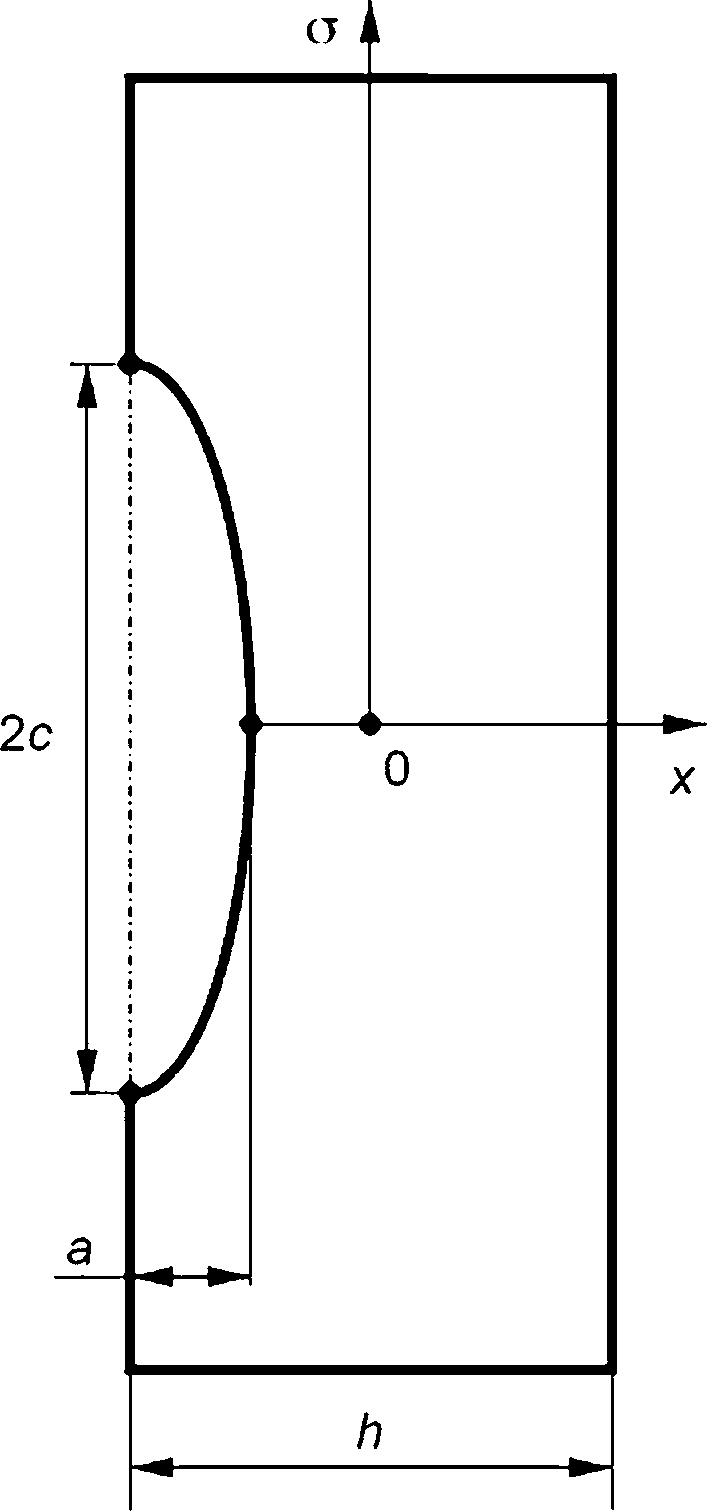
а — глубина трещины; 2с — длина оси полуэллиптической трещины; h — толщина

Рисунок И.1 — Полуэллиптическая поверхностная трещина

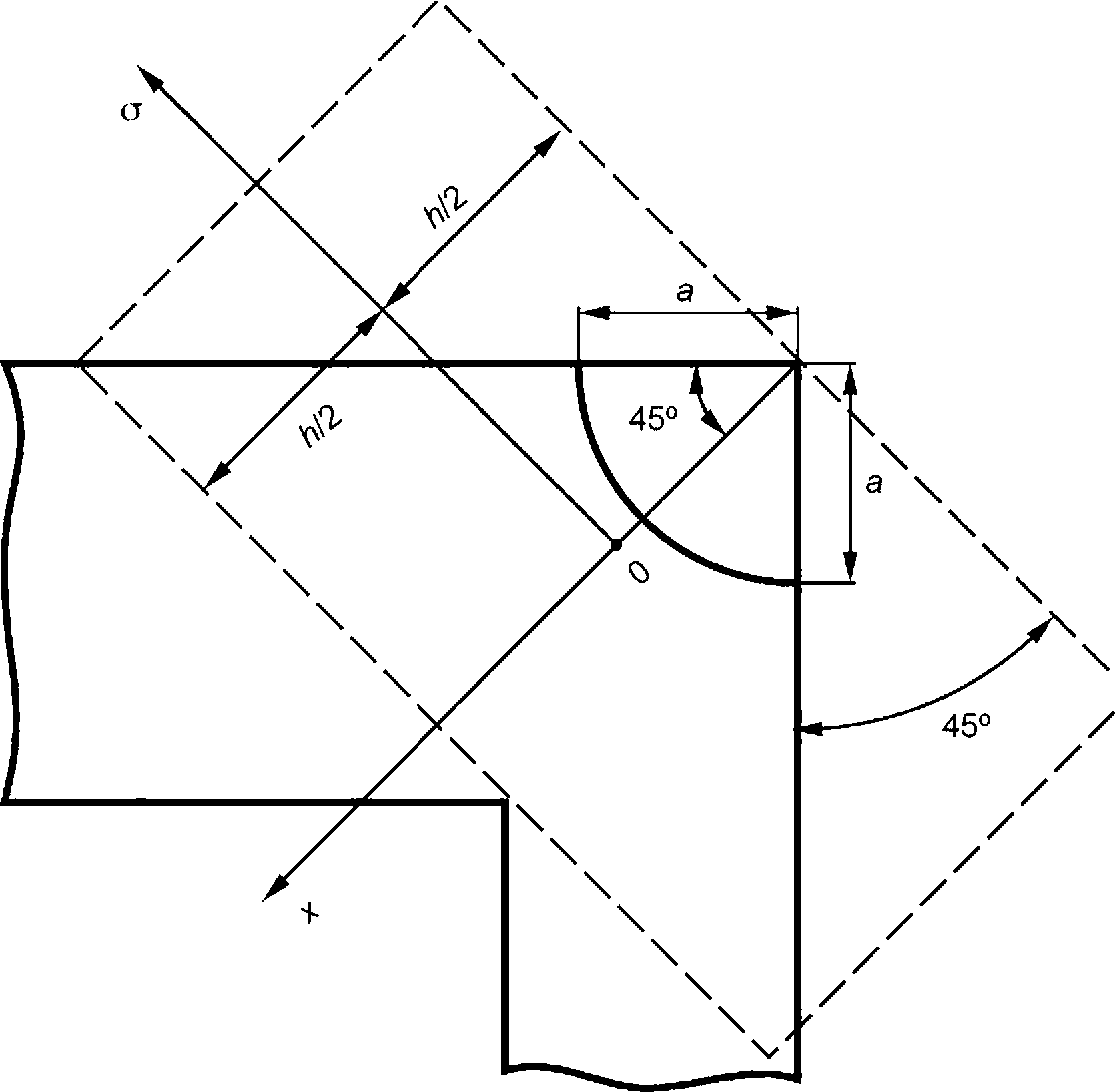
а — глубина трещины; h — расчетный параметр

Приложение К (обязательное)

Скорость роста трещины при циклическом нагружении

К.1 Скорость роста трещины (мм/цикл) при циклическом нагружении в исходном состоянии при температурах от 20 °C до 650 °C определяется по формуле

0, при ЛК < ДК_№

где R— коэффициент асимметрии цикла нагружения, R =

• - при R < 0 принимают R = 0;

• - при R > 0,95 принимают R = 0,95;

C_f— коэффициент уравнения Пэриса;

n_f— коэффициент уравнения Пэриса, n_f = 3,3;

^max ^min> ^ПР^И ^min ^>

/^max> ^ПРИ ^min — 0

Значение C_f для основного металла и металла сварного шва сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08Х16Н11МЗ, облученных до повреждающих доз 45 сна, определяется по формулам:

• - для основного металла

• 5,20- Ю"⁹, при Т <350 °C

C_f = 1 ; (К.З)

[5,20-10^-9 ехр(0,342 (7-350)°-³⁵⁶), при 7" >350 °C

• - для металла сварных швов при повреждающей дозе F не более 4 сна

5,20 Ю'⁹, при 7 <350 °C

c_f = 1 ; (к.4)

[5,20-10^-9 ехр(0,342 (7-350)°’³⁵⁶), при 7 >350 °C

• - для металла сварных швов при повреждающей дозе F свыше 4 сна

1,56-Ю’⁸, при 7 <350 °C

C_f = I • (К.5)

1,56 • 10’⁸ • ехр(0,342 • (7 - 350)°’³⁵⁶), при 7 > 350 ° С

К.2 Скорость роста трещины при циклическом нагружении с учетом термического старения и радиационного распухания определяется по формуле

IdA/J ldA/J_MCX

где со^=[(1-ДД5))ф(5)]-¹-⁶⁵;

^стар _{= [ч/(Рно//)]}-1,б5.

2/3

<p(S) — снижение критической деформации разрушения от распухания

0(S) = exp[-A_swS^j;

A_sw = 6,55; n_sw= 0,67.

у(Р_Ноц) рассчитывается по формуле (А. 12) (приложение А).

К.З Значения ДК_/Л рассчитываются по формуле

AK_f/7 = AKJ, • (1 - 0,65 • R), где ДК« — пороговый размах КИН первого рода при R = 0, МПа • м^1/2, вычисляемый по формулам:

при 20 °C < Г <550 °C

- для металла сварных швов

ГЗ,85, при 20 °C < Т < 550 °C [2,50, при 550 °C < Т < 600 °C’

G_z — номер (балл) зерна, определяемый на основе технических условий, указанных в конструкторской документации.

Формула (К. 12) применима для значений G_z в диапазоне от 4 до 8; в случае если G_z < 4, расчет по формуле (К.12) проводится при G_z = 4. В случае если балл зерна в конструкторской документации не указан, то следует принимать G_z равным 8.

Приложение Л (обязательное)

Статическая трещиностойкость

Л.1 Статическая трещиностойкость в терминах критического значения J-интеграла при Т< Т_Не определяется по формуле

J_c, при J_c > 1,0

0, при S > 0,12

Н/мм,

Gflow 2

Т_Не = 400 °C.

Значение параметра Cj принимается равным 0,27 для основного металла и 0,19 для металла сварных швов.

Расчет R_p0 2(Е,Т,Т_обл) и R_m(F,T,T₀Q_n) выполняется согласно А.1 (приложение А).

Расчет у(Р_Ноц) Для сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9 и 08X16Н11 М3 выполняется по формуле (А.19) (приложение А).

Расчет у(Рноц) Для сварных швов сталей марок 09X18Н9, 10Х18Н9, 12Х18Н9, 08X16Н11 М3 выполняется по следующим формулам:

- для сварного шва, прошедшего термическую обработку посредством аустенизации и выполненного с использованием сварочной проволоки марки Св-02Х17Н10М2-ВИ или электрода марки А-2 (А-2Т):

^aging ' ^PHoll ⁺ Paging' ^ПРИ Р^ < Рн_оц 8350

а₁ • ехр ——--- + а₄, при Р_Ноц > 8350

\^РНо11~^аз)

1, при Р_Но11 < P_th

где A_agjng = 8,75 • 10"⁵; B_aging = 1,56; а, = 1,82; а₂ = 1076; а₃ = 9502; а₄ = 0,12;

-для сварного шва, не прошедшего термическую обработку посредством аустенизации и выполненного с использованием сварочной проволоки марок Св-02Х17Н10М2-ВИ, Св-04Х17Н10М2 или электродов марок А-1 (А-1Т), А-2 (А-2Т), а также для сварного шва, прошедшего термическую обработку посредством аустенизации и выполненного с использованием сварочной проволоки марки Св-04Х17Н10М2 или электрода марки А-1 (А-1Т):

^aging ' ^PHoll ^{+ P}aging' ^ПР^{И P}th ^{< Р}Но11 - 8200

а₁ • ехр -------- + а₄, при Р_Ноц > 8200

\^РНо11~^аЗ )

1, при Р_Но11 < P_th

где A_anjnn = 2,44 ■ 10 ⁴; B_aninn = 2,56; а_и = 0,81; а₂ = 725; а-, = 9498; а₄ = 0,1.

' ' ciyifiy dyiliy I £. О Ч

Расчет радиационного распухания S выполняется согласно приложению Е.

Л.2 Статическая трещиностойкость при Г> Т_Не определяется по формуле j_c=min(jf^ans,jg^f),

где = Cj ■ c_flow (F, T) ■ [0,1 + 0,9 • ехр (-0,3 • F)] • Q (7 - Т_Не); (Л .8)

Q(T - Т_Не) рассчитывается по формуле (А.25) (приложение А).

Приложение М (обязательное)

Процедура расчета референсного напряжения для анализа потери несущей способности и герметичности компонента

М.1 Выбор схемы расчета референсного напряжения

При выборе схемы расчета референсного напряжения c_ref следует учитывать геометрические характеристики рассматриваемого компонента и принимать во внимание соотношение среднего радиуса (г_т) цилиндрической поверхности стенки компонента и его толщины (h). При rjh > 20 референсное напряжение c_ref рассчитывают на основании расчетной схемы полуэллиптической или четвертьэллиптической поверхностной трещины в пластине. При r_m/h < 20 референсное напряжение o_ref рассчитывают в зависимости от предполагаемой ориентации дефекта: по схеме внутренней полуэллиптической поверхностной трещины в диаметральной плоскости цилиндра или по схеме внутренней полуэллиптической или четвертьэллиптической поверхностной трещины по образующей цилиндра.

В расчетах учитывают только механические нагрузки. Расчет НДС компонента проводят без дефекта.

М.2 Полуэллиптическая поверхностная трещина в пластине

В выбранном для оценки сечении компонента, в котором расположен дефект или предполагается его наличие (плоскость дефекта лежит в плоскости сечения), расчетным или аналитическим методом определяют распределение напряжений a_n(x,t) нормальных к плоскости сечения в момент времени t (рисунок М.1).

Полученное в расчете произвольного вида распределение напряжения c_n(x,t) представляют в текущий момент времени t в виде мембранной и изгибной составляющих, вычисляемых по формулам (М.1) и (М.2) (рисунок М.2).

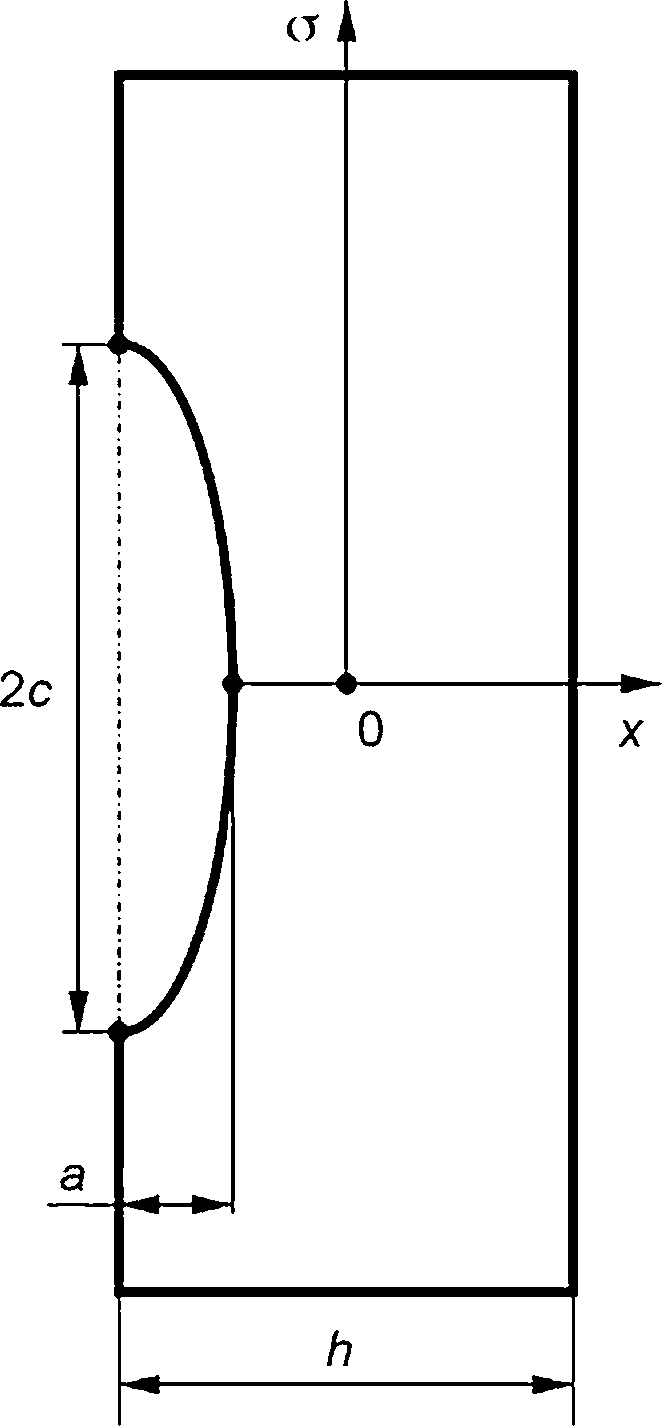
а — глубина трещины; 2с — длина оси полуэллиптической трещины; h — толщина

Рисунок М.1 — Полуэллиптическая поверхностная трещина в пластине

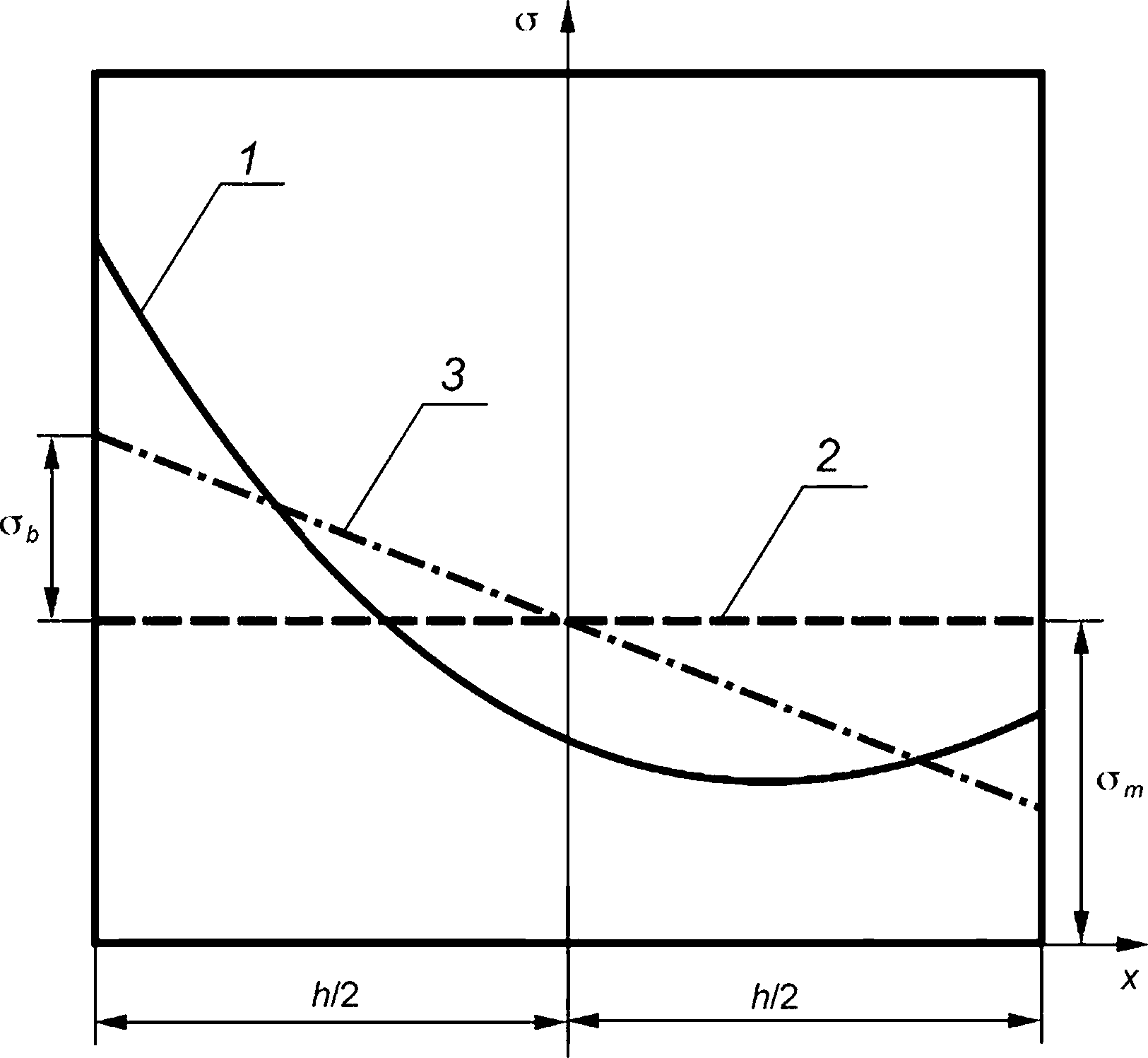
Рисунок М.2 — Распределение по толщине стенки напряжения о_п (7) и его мембранной в_т (2) и изгибной а_ь (3) составляющих

Мембранное напряжение рассчитывают по формуле

₁ ь/2

<3m=T J o(x)dx. п ^J

-h/2

Максимальное изгибное напряжение рассчитывают по формуле

6 ^h/2

<’ь=-т J oW-x-dx.

^h -1/2

Таким образом, общее (нормальное) напряжение представляют в виде формулы

(М.З)

Референсное напряжение определяют по формуле

ас h-(c + h)'

При о_т < 0 принимают <з_т = 0.

При с_ь < 0 принимают с_ь = 0.

Расчет по формуле (М.4) проводят при изменении a/h от 0 до 0,8.

М.З Внутренняя четвертьэллиптическая поверхностная трещина в узле, образованном двумя пластинами

При рассмотрении четвертьэллиптической трещины принимают, что малая и большая полуось эллипса равны между собой.

В выбранном для оценки сечении компонента, в котором расположен дефект или предполагают его наличие (плоскость дефекта лежит в плоскости сечения), расчетным или аналитическим методом определяют распределение напряжений o_n(x,f) нормальных к плоскости сечения в момент времени t (см. рисунок М.З).

Полученное в расчете произвольного вида распределение напряжения o_n(x,f) представляют в текущий момент времени t в виде мембранной и изгибной составляющих, вычисляемых по формулам (М.1) и (М.2) (см. рисунок М.2).

Референсное напряжение рассчитывают по формуле (М.4) при условии, что h определяют из рисунка М.З и с = а.

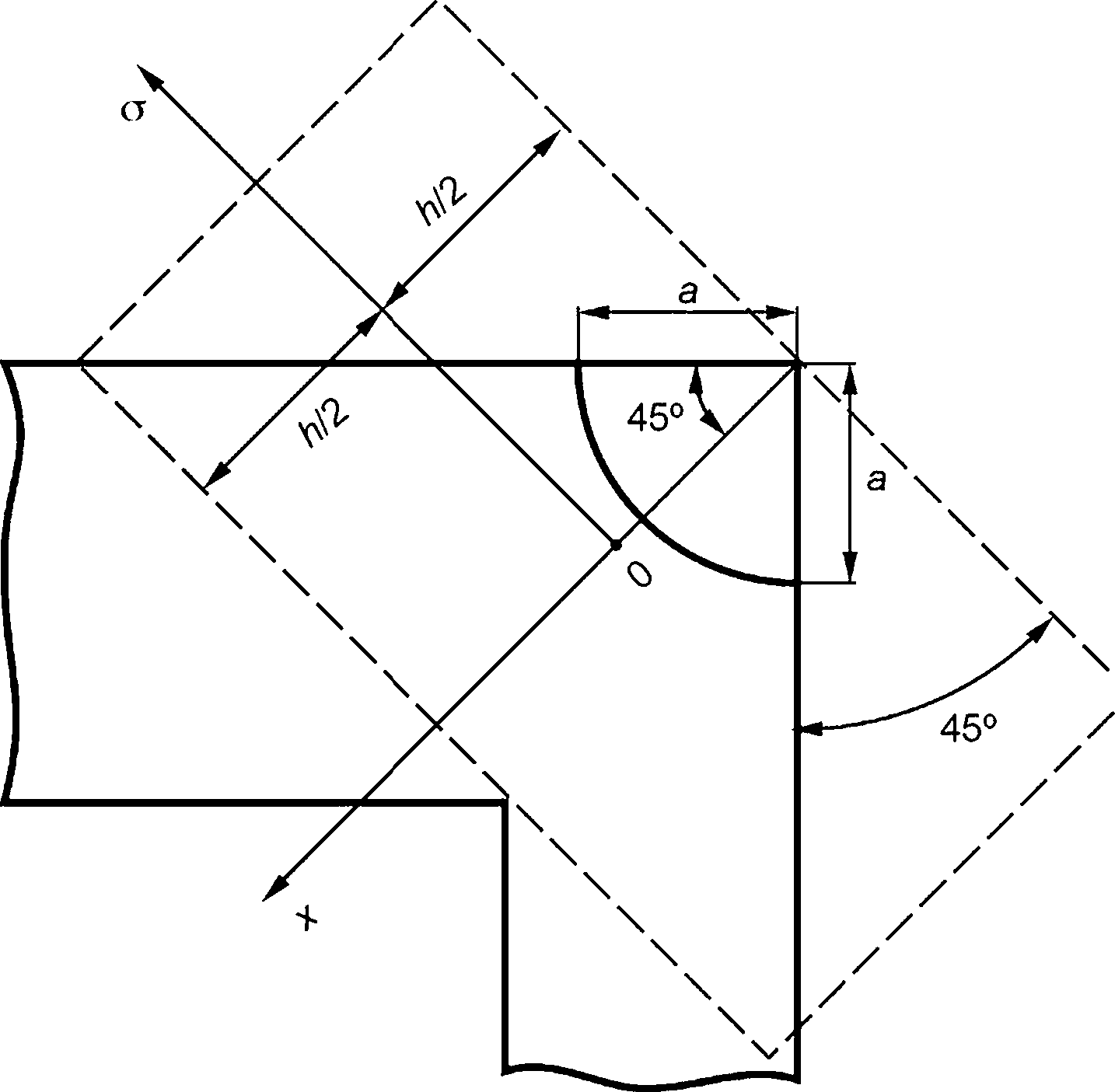
ось х — координата, по которой задается распределение нормальных к трещине напряжений; а — глубина трещины

Рисунок М.З — Четвертьэллиптическая поверхностная трещина в узле, образованном двумя пластинами, и схематизация расчетного параметра h

М.4 Внутренняя полуэллиптическая поверхностная трещина, расположенная в диаметральной плоскости цилиндра

Геометрическая схема компонента с дефектом приведена на рисунке М.4.

Референсное напряжение определяют по формуле где <з_т и (5_Ьд — соответственно мембранные и глобальные изгибные напряжения:

N

~ ! ^ътр

М •

°^ь9 ~ и/ ’ ^иитр

N — осевое усилие, Н;

М — изгибающий момент в рассматриваемом поперечном сечении трубы, Н ■ мм;

S_Tp — площадь поперечного сечения трубы, мм²;

РУ_Тр — момент сопротивления в рассматриваемом поперечном сечении трубы, мм³.

Параметры S_M, S_bg и р находят из решения системы уравнений:

_ 4 _о 2 а .

S_ba = — sinp-----sinO;

^у л 7th

' §bg ®Ьд ' $М 0-

а — глубина трещины; 2с — длина оси полуэллиптической трещины; 20 — угол трещины (в радианах), располагающийся симметрично плоскости действия изгибающего момента; г— внутренний радиус цилиндра

Рисунок М.4 — Схема расположения трещины в диаметральной плоскости цилиндра

Параметры S'_M и S'_bg находят по формулам:

Расчет по формуле (М.6) проводят при изменении а/h от 0 до 0,8 и 0 < л - р.

М.5 Внутренняя полуэллиптическая поверхностная трещина в цилиндре, ориентированная вдоль образующей

Геометрическая схема конструкции и дефекта приведена на рисунке М.5.

Референсное напряжение определяют по формуле

(М.9)

ас h-(c + h)’

— мембранная компонента напряжения, ориентированная перпендикулярно к плоскости трещины в цилиндре без трещины.

Расчет по формуле (М.9) проводят при изменении а/h от 0 до 0,8.

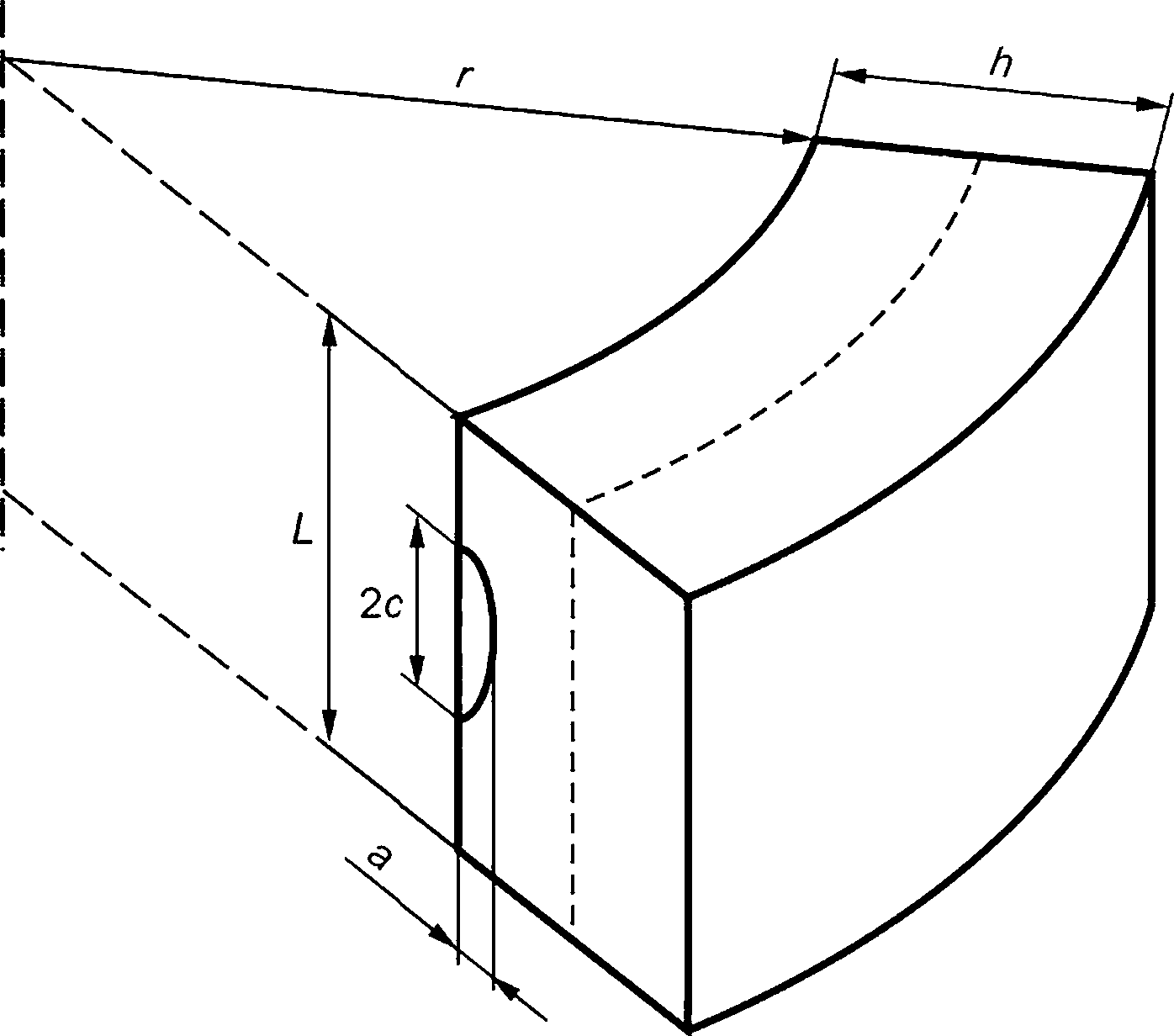
а — глубина трещины; 2с — длина оси полуэллиптической трещины; г— внутренний радиус цилиндра; L — высота цилиндра

Рисунок М.5 — Схема расположения трещины по образующей цилиндра

М.6 Внутренняя четвертьэллиптическая поверхностная трещина в узле, образованном пересечением двух цилиндров

При рассмотрении четвертьэллиптической трещины принимают, что малая и большая полуось эллипса равны между собой.

Геометрическая схема конструкции и дефекта приведена на рисунке М.6.

Референсное напряжение определяют по формуле (М.9) при условии, что h определяют из рисунка М.6 и

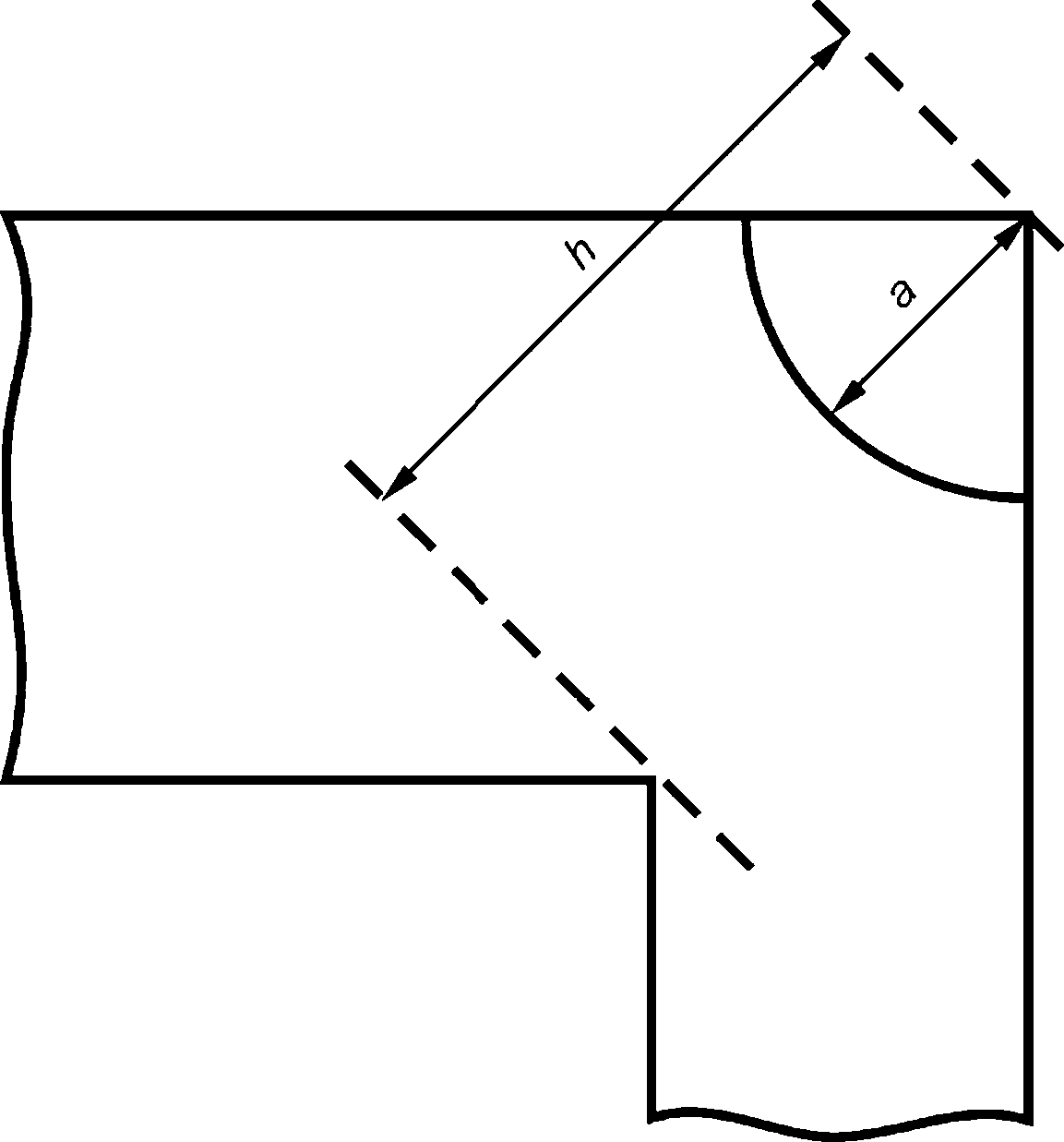
а — глубина трещины; h — расчетный параметр

Рисунок М.6 — Четвертьэллиптическая поверхностная трещина в узле, образованном двумя пересекающимися цилиндрами, и схематизация расчетного параметра h

УДК 621.039.52.034.6:006.354

Ключевые слова: реактор с жидкометаллическим натриевым теплоносителем, прочность, внутриреакторные устройства, проектирование

Редактор Л. В. Каретникова

Технический редактор В.Н. Прусакова

Корректор О.В. Лазарева

Компьютерная верстка Е.О. Астатина

Сдано в набор 29.12.2022. Подписано в печать 13.01.2023. Формат 60x84%. Гарнитура Ариал.

Усл. печ. л. 6,05. Уч.-изд. л. 5,40.

Подготовлено на основе электронной версии, предоставленной разработчиком стандарта

Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.

¹

Здесь и далее по тексту, если речь идет о размерах, понимаются номинальные размеры.

²

Здесь и далее по тексту, в случае если речь идет о значениях размеров, понимаются их номинальные значения.