ГОСТ 32298-2013
(EN 12603:2002)
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Стекло и изделия из него
Порядок определения критерия согласия и доверительных интервалов по распределению Вейбулла для значений прочности стекла
Glass and glass products. Procedures for goodness of fit and confidence intervals for Weibull distributed glass strength data
МКС 81.040.01
Дата введения 2015-01-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2009 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Институт стекла" на основе собственного аутентичного перевода на русский язык стандарта, указанного в пункте 5
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 28 августа 2013 г. N 58-П)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Киргизия | KG | Кыргызстандарт |
Молдова | MD | Молдова-Стандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
Узбекистан | UZ | Узстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 08 ноября 2013 N 1508-ст межгосударственный стандарт ГОСТ 32298-2013 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2015 г.
5 Настоящий стандарт модифицирован по отношению к европейскому стандарту EN 12603:2002* Glass in building - Procedures for goodness of fit and confidence intervals for Weibull distributed glass strength data (Стекло в строительстве. Порядок определения критерия согласия и доверительных интервалов по распределению Вейбулла для значений прочности стекла) путем изменения и дополнения отдельных фраз, слов, которые выделены полужирным курсивом**, а также изменения разделов "Область применения" и "Нормативные ссылки".
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей.
** В оригинале обозначения и номера стандартов и нормативных документов приводятся обычным шрифтом. - .
Наименование настоящего стандарта изменено относительно наименования европейского стандарта в связи с особенностями построения межгосударственной системы стандартизации.
Европейский стандарт разработан Европейским комитетом по стандартизации (CEN) ТК 129 "Стекло в строительстве".
Европейский стандарт, на основе которого подготовлен настоящий стандарт, реализует существенные требования безопасности Директивы ЕС (89/106/ЕЕС) по строительным материалам.
Перевод с английского языка (en).
Степень соответствия - модифицированная (MOD).
6 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
1 Область применения
Настоящий стандарт устанавливает методику оценки данных выборки посредством двухпараметрической функции распределения Вейбулла.
Настоящий стандарт основывается на предположении, что статистическое распределение величины, принимаемое в рассмотрение, может быть представлено единственной функцией распределения Вейбулла, даже если в некоторых случаях (например, измерение срока службы) часто наблюдается смешанное распределение. По этой причине пользователю стандарта необходимо проверить тест на критерий согласия: могут ли данные измерений по выборке быть представлены с помощью единственной функции Вейбулла. Только в этом случае может быть принята гипотеза и применен метод, описанный в данном стандарте.
Пользователь принимает решение по этому вопросу, также рассматривая все предыдущие значимые данные и общий уровень знаний в конкретной области. Каждая экстраполяция в диапазонах квантилей, не согласованная с измеренными значениями, требует особой тщательности, настолько большей, насколько дальнейшая экстраполяция превышает диапазон измерений.
Примечание - Трехпараметрическую функцию Вейбулла определяют по формуле:
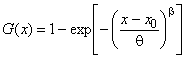 . (1)
. (1)
Если предположить х=0, получится двухпараметрическая функция Вейбулла:
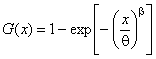 , (2)
, (2)
которая может быть переписана в виде
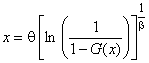 . (3)
. (3)
Расчеты могут основываться на любой нецензурированной или цензурированной выборках. Существует несколько способов цензурирования. В настоящем стандарте рассматривается только следующий способ цензурирования:
- данное число r<n образцов, для которых были измерены значения величины x.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на [1] и [2].
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов по указателю "Национальные стандарты", составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом, следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применяются термины и определения, установленные в [1].
4 Обозначения
В настоящем стандарте применены следующие обозначения:
X - рассматриваемая величина;
x, x, x
- значения величины X;
G(x) - функция распределения X= процент неблагоприятного исхода;
x,
,
- параметры трехпараметрической функции Вейбулла;
- опознавательный знак, указывающий на оценку параметра (например,
,
,
);
1- - уровень доверия;
l - значение, используемое в критерии согласия;
L - значение, используемое в критерии согласия;
n - объем выборки;
r - количество образцов, значения величин x которых были измерены;
Примечание - Выборка упорядочена, т.е. ![]() ;
;
f, f, f
- степень свободы;
k, k
- множители, используемые в оценивании
;
c - множитель, используемый в оценивании
;
s-int(0,84n)= наибольшему целому числу <0,84n;
,
- ордината и абсцисса на диаграмме Вейбулла;
- функция распределения хи-квадрат;
y, ,
- вспомогательные коэффициенты, используемые в оценивании границ доверительного интервала G(x);
А, В, С - константы, используемые при оценивании ;
H(f) - переменная, используемая при оценивании
;
T, T
![]() - коэффициенты, используемые при оценке доверительных интервалов значений
- коэффициенты, используемые при оценке доверительных интервалов значений .
Нижние индексы:
un - нижняя граница доверительного интервала;
оb - верхняя граница доверительного интервала;
z - доверительный интервал, ограниченный с двух сторон.
5 Критерий согласия
Отсортировать r значений величины х по возрастанию.
Вычислить для каждого значения от i=1 до i=r-1:
 . (4)
. (4)
Вычислить значение величины:
 , (5)
, (5)
где [r/2] - символ, используемый для обозначения наибольшего целого числа, меньшего или равного r/2.
Отвергнуть гипотезу, что данные из распределения Вейбулла на - уровне значимости, если:
![]() . (6)*
. (6)*
_______________
* Формула соответствует оригиналу. - .
Значения квантиля F распределения можно найти, например, в [2].
6 Точечная оценка для параметров  и
и  распределения
распределения
6.1 Цензурированная выборка
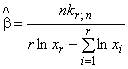 (7)
(7) (8)
(8)
Коэффициенты k и С
приведены в таблицах 1 и 2.
Таблица 1 - Коэффициент k
n | r/n | ||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
5 | 0,2231 | 0,4813 | 0,8018 | ||||||
10 | 0,1054 | 0,2172 | 0,3369 | 0,4667 | 0,6098 | 0,7715 | 0,9616 | 1,202 | |
20 | 0,0513 | 0,1583 | 0,2721 | 0,3944 | 0,5277 | 0,6756 | 0,8448 | 1,048 | 1,316 |
30 | 0,0684 | 0,1759 | 0,2904 | 0,4137 | 0,5482 | 0,6979 | 0,8697 | 1,077 | 1,357 |
40 | 0,0770 | 0,1848 | 0,2996 | 0,4233 | 0,5584 | 0,7090 | 0,8822 | 1,092 | 1,378 |
50 | 0,0821 | 0,1901 | 0,3051 | 0,4291 | 0,5646 | 0,7158 | 0,8898 | 1,101 | 1,391 |
60 | 0,0855 | 0,1936 | 0,3088 | 0,4330 | 0,5687 | 0,7202 | 0,8949 | 1,108 | 1,400 |
70 | 0,0879 | 0,1961 | 0,3114 | 0,4357 | 0,5717 | 0,7235 | 0,8985 | 1,112 | 1,406 |
80 | 0,0898 | 0,1980 | 0,3134 | 0,4378 | 0,5739 | 0,7259 | 0,9012 | 1,115 | 1,410 |
90 | 0,0912 | 0,1995 | 0,3149 | 0,4394 | 0,5756 | 0,7277 | 0,9033 | 1,118 | 1,414 |
100 | 0,0924 | 0,2007 | 0,3162 | 0,4407 | 0,5770 | 0,7292 | 0,9050 | 1,120 | 1,417 |
k | 0,10265 | 0,21129 | 0,32723 | 0,45234 | 0,58937 | 0,74274 | 0,92026 | 1,1382 | 1,4436 |
d | -1,0271 | -1,0622 | -1,1060 | -1,1634 | -1,2415 | -1,3540 | -1,5313 | -1,8567 | -2,6929 |
d | 0,000 | 0,030 | 0,054 | 0,089 | 0,145 | 0,242 | 0,433 | 0,906 | 2,796 |
Асимптотическая оценка для больших n: k | |||||||||
Таблица 2 - Коэффициент С
n | r/n | ||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
10 | -2,880 | -1,826 | -1,267 | -0,8681 | -0,5436 | -0,2574 | 0,0120 | 0,2837 | 0,5846 |
20 | -2,547 | -1,658 | -1,147 | -0,7691 | -0,4548 | -0,1727 | 0,0979 | 0,3776 | 0,7022 |
30 | -2,444 | -1,605 | -1,108 | -0,7364 | -0,4253 | -0,1443 | 0,1269 | 0,4098 | 0,7446 |
40 | -2,394 | -1,578 | -1,089 | -0,7202 | -0,4106 | -0,1301 | 0,1415 | 0,4262 | 0,7664 |
50 | -2,365 | -1,562 | -1,077 | -0,7105 | -0,4018 | -0,1216 | 0,1503 | 0,4360 | 0,7796 |
60 | -2,345 | -1,522 | -1,069 | -0,7040 | -0,3959 | -0,1159 | 0,1562 | 0,4426 | 0,7885 |
70 | -2,331 | -1,544 | -1,064 | -0,6994 | -0,3917 | -0,1118 | 0,1604 | 0,4473 | 0,7949 |
80 | -2,321 | -1,539 | -1,060 | -0,6959 | -0,3886 | -0,1088 | 0,1635 | 0,4509 | 0,7998 |
90 | -2,313 | -1,534 | -1,056 | -0,6932 | -0,3861 | -0,1064 | 0,1660 | 0,4537 | 0,8035 |
100 | -2,307 | -1,531 | -1,054 | -0,6911 | -0,3841 | -0,1045 | 0,1679 | 0,4559 | 0,8065 |
c | -2,2504 | -1,4999 | -1,0309 | -0,67173 | -0,36651 | -0,08742 | 0,18563 | 0,47589 | 0,83403 |
а | -5,5743 | -3,0740 | -2,2859 | -1,9301 | -1,7619 | -1,7114 | -1,7727 | -2,0110 | -2,7773 |
а | -7,201 | -1,886 | -0,767 | -0,335 | -0,091 | 0,111 | 0,369 | 0,891 | 2,825 |
Асимптотическая оценка для больших n: С | |||||||||
6.2 Нецензурированная (полная) выборка
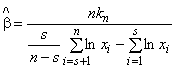 , (10)
, (10)![]() . (11)
. (11)
Коэффициент k приведен в таблице 3.
Таблица 3 - Коэффициент k
n | k |
2 | 0,6931 |
3 | 0,9808 |
4 | 1,1507 |
5 | 1,2674 |
6 | 1,3545 |
7 | 1,1828 |
8 | 1,2547 |
9 | 1,3141 |
10 | 1,3644 |
11 | 1,4079 |
12 | 1,4461 |
13 | 1,3332 |
14 | 1,3686 |
15 | 1,4004 |
16 | 1,4293 |
17 | 1,4556 |
18 | 1,4799 |
19 | 1,3960 |
20 | 1,4192 |
21 | 1,4408 |
22 | 1,4609 |
23 | 1,4797 |
24 | 1,4975 |
25 | 1,5142 |
26 | 1,4479 |
27 | 1,4642 |
28 | 1,4796 |
29 | 1,4943 |
30 | 1,5083 |
31 | 1,5216 |
32 | 1,4665 |
33 | 1,4795 |
34 | 1,4920 |
35 | 1,5040 |
36 | 1,5156 |
37 | 1,5266 |
38 | 1,4795 |
39 | 1,4904 |
40 | 1,5009 |
41 | 1,5110 |
42 | 1,5208 |
43 | 1,5303 |
44 | 1,4891 |
45 | 1,4984 |
46 | 1,5075 |
47 | 1,5163 |
48 | 1,5248 |
49 | 1,5331 |
50 | 1,5411 |
51 | 1,5046 |
52 | 1,5126 |
53 | 1,5204 |
54 | 1,5279 |
55 | 1,5352 |
56 | 1,5424 |
57 | 1,5096 |
58 | 1,5167 |
59 | 1,5236 |
60 | 1,5304 |
1,5692 |
7 Оценка данных и критерии
7.1 Диаграмма Вейбулла
График вероятностей для распределения Вейбулла составляется таким образом, чтобы функция распределения двухпараметрического распределения Вейбулла была представлена прямой линией.
Ось ординат градуирована в соответствии с функцией:
 (12)
(12)
и ось абсцисс согласно функции:
![]() или
или ![]() . (13)
. (13)
Примечание - Такие формы доступны. Как правило, надо использовать диаграммы с интервалом G значений от G=1х10=0,1% до G=0,999=99,9%. Необходимый диапазон x-значений зависит от величины параметра формы
.
7.2 Графическое представление оцениваемой функции распределения
Точки оценок параметра формы и параметра масштаба
задают прямую линию на диаграмме Вейбулла. Этот способ подходит, чтобы определить данную прямую по двум следующим точкам:
х= G(x)=0,6321=63,21%, (14)
х = х0,01005
G(x)=0,01=1%. (15)
Эту прямую линию следует нанести на диаграмму.
7.3 Нанесение данных выборки на диаграмму Вейбулла
7.3.1 Однозначность
Размер цензурированной или нецензурированной выборки дает r или n значений x величины X. Эти значения x
следует упорядочить для формирования упорядоченной выборки.
Каждое значение x упорядоченной выборки следует сопоставить с оценкой:
![]() . (16)
. (16)
Таким образом, точки, представляющие измеренные значения выборки, следует графически нанести на диаграмму Вейбулла.
7.3.2 Классифицированные значения
В случае очень большого объема выборки диапазон измеренных х-значений может быть разделен на интервалы, как правило, содержащие одинаковое количество значений. Долю х-значений, просуммированную в каждом рассматриваемом интервале, следует нанести на верхнюю границу этого интервала.
7.4 Оценка выборочных данных
Прямую линию, построенную согласно 7.2, и точки, которые представляют измеренные значения выборки, построенные согласно 7.3, можно сравнивать визуально.
Систематические отклонения могут быть подробно проанализированы с учетом фундаментальных технических и научных знаний и результатов ранее выполненных соответствующих исследований. Например, если распределение значений величины может быть аппроксимировано кусочно-прямыми линиями с различным наклоном, можно предположить смешанное распределение Вейбулла. Это можно принять как свидетельство того, что несколько основных механизмов определяют значения величины x. Такое подробное рассмотрение выходит за рамки настоящего стандарта.
8 Доверительный интервал
Уравнения следующих подпунктов применимы в том случае, когда доверительные интервалы ограничены с двух сторон (индекс z). В том случае, когда доверительные интервалы ограничены только с одной стороны, /2 должна быть заменена на
в следующих уравнениях.
Уровень доверия (1-) выбирает пользователь настоящего стандарта.
8.1 Доверительный интервал для параметра формы
Верхняя граница доверительного интервала для параметра формы при уровне доверия (1-
):
 , (17)
, (17)
и нижняя граница:
 , (18)
, (18)
f следует получить с помощью умножения данных из таблицы 4, зная размер выборки n.
Таблица 4 - Значения функции f/n
n | r/n | |||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
10 | 0,211 | 0,434 | 0,671 | 0,926 | 1,200 | 1,497 | 1,825 | 2,174 | 2,701 | |
20 | 0,103 | 0,316 | 0,543 | 0,784 | 1,042 | 1,320 | 1,621 | 1,946 | 2,277 | 2,891 |
30 | 0,137 | 0,351 | 0,579 | 0,821 | 1,080 | 1,360 | 1,661 | 1,985 | 2,303 | 2,958 |
40 | 0,154 | 0,369 | 0,597 | 0,840 | 1,100 | 1,380 | 1,682 | 2,004 | 2,315 | 2,991 |
50 | 0,164 | 0,380 | 0,608 | 0,851 | 1,111 | 1,392 | 1,693 | 2,015 | 2,320 | 3,009 |
100 | 0,185 | 0,401 | 0,629 | 0,873 | 1,135 | 1,415 | 1,718 | 2,037 | 2,330 | 3,045 |
h | 0,2052 | 0,4218 | 0,6514 | 0,8959 | 1,1577 | 1,4391 | 1,7416 | 2,0598 | 2,3394 | 3,085 |
h | -2,052 | -2,111 | -2,175 | -2,244 | -2,314 | -2,376 | -2,390 | -2,205 | -0,856 | |
h | 0,000 | 0,008 | 0,002 | -0,016 | -0,064 | -0,188 | -0,526 | -1,682 | -7,928 | |
Асимптотическая оценка для больших n: f | ||||||||||
Величины ![]() и
и ![]() - квантиль распределения хи-квадрат с числом степеней свободы f
- квантиль распределения хи-квадрат с числом степеней свободы f. Значения приведены в таблице 5.
Таблица 5 - 2,5% и 97,5% квантилей для распределения
Число степеней свободы | p | ||
2,5% | 97,5% | ||
1 | 0,000982 | 5,02 | |
2 | 0,0506 | 7,38 | |
3 | 0,216 | 9,35 | |
4 | 0,484 | 11,1 | |
5 | 0,831 | 12,8 | |
6 | 1,24 | 14,4 | |
7 | 1,69 | 16,0 | |
8 | 2,18 | 17,5 | |
9 | 2,70 | 19,0 | |
10 | 3,25 | 20,5 | |
11 | 3,82 | 21,9 | |
12 | 4,40 | 23,3 | |
13 | 5,01 | 24,7 | |
14 | 5,63 | 26,1 | |
15 | 6,26 | 27,5 | |
16 | 6,91 | 28,8 | |
17 | 7,56 | 30,2 | |
18 | 8,23 | 31,5 | |
19 | 8,91 | 32,9 | |
20 | 9,59 | 34,2 | |
21 | 10,3 | 35,5 | |
22 | 11,0 | 36,8 | |
23 | 11,7 | 38,1 | |
24 | 12,4 | 39,4 | |
25 | 13,1 | 40,6 | |
26 | 13,8 | 41,9 | |
27 | 14,6 | 43,2 | |
28 | 15,3 | 44,5 | |
29 | 16,0 | 45,7 | |
30 | 16,8 | 47,0 | |
40 | 24,4 | 59,3 | |
50 | 32,4 | 71,4 | |
60 | 40,5 | 83,3 | |
70 | 48,8 | 95,0 | |
80 | 57,2 | 106,6 | |
90 | 65,6 | 118,1 | |
100 | 74,2 | 129,6 | |
Приближение для f>30 | p | 2,5% | 97,5% |
u | -1,9600 | 1,9600 | |
| |||
8.2 Доверительный интервал для значения функции распределения G(x) при заданном значении х величины X
Границы двустороннего доверительного интервала для G при уровне доверия (1-) для рассматриваемого значения х величины X следует вычислять с помощью трех вспомогательных факторов у,
и
.
Уравнение для вспомогательного фактора у:
 . (19)
. (19)
Уравнение для вспомогательного фактора :
![]() . (20)
. (20)
Константы А, В, С должны быть получены путем деления значений, полученных из таблицы 6, учитывая размер выборки n.
Таблица 6 - Константы A.n, B.n и C.n
n | r/n | |||||||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0.9 | 1,0 | |
В.n | ||||||||||
10 | 9,488 | 4,609 | 2,979 | 2,161 | 1,667 | 1,336 | 1,096 | 0,9197 | 0,7405 | |
20 | 19,49 | 6,324 | 3,686 | 2,552 | 1,920 | 1,515 | 1,234 | 1,028 | 0,8784 | 0.6919 |
30 | 14,62 | 5,691 | 3,455 | 2,436 | 1,851 | 1,471 | 1,204 | 1,008 | 0,8683 | 0,6761 |
40 | 13,00 | 5,420 | 3,350 | 2,382 | 1,819 | 1,450 | 1,189 | 0,9981 | 0,8641 | 0,6687 |
50 | 12,18 | 5,269 | 3,290 | 2,350 | 1,800 | 1,437 | 1,181 | 0,9925 | 0,8619 | 0,6647 |
60 | 11,70 | 5,173 | 3,251 | 2,330 | 1,787 | 1,429 | 1,175 | 0,9888 | 0,8605 | 0,6616 |
80 | 11,14 | 5,058 | 3,204 | 2,305 | 1,772 | 1,419 | 1,168 | 0,9840 | 0,8590 | 0,6584 |
100 | 10,83 | 4,991 | 3,177 | 2,290 | 1,763 | 1,413 | 1,164 | 0,9816 | 0,8580 | 0,6564 |
9,746 | 4,742 | 3,070 | 2,232 | 1,728 | 1,390 | 1,148 | 0,9710 | 0,8549 | 0,6482 | |
С.n | ||||||||||
10 | 17,58 | 6,109 | 2,868 | 1,474 | 0,7502 | 0,3344 | 0,0826 | -0,0694 | -0,1981 | |
20 | 49,91 | 10,75 | 4,505 | 2,254 | 1,184 | 0,5975 | 0,2500 | 0,0373 | -0,0856 | -0,2216 |
30 | 35,98 | 9,397 | 4,107 | 2,089 | 1,102 | 0,5533 | 0,2253 | 0,0245 | -0,0883 | -0,2206 |
40 | 31,36 | 8,819 | 3,927 | 2,012 | 1,064 | 0,5323 | 0,2136 | 0,0185 | -0,0891 | -0,2262 |
50 | 29,06 | 8,499 | 3,825 | 1,967 | 1,041 | 0,5200 | 0,2068 | 0,0150 | -0,0894 | -0,2238 |
60 | 27,68 | 8,296 | 3,750 | 1,938 | 1,026 | 0,5120 | 0,2023 | 0,0127 | -0,0895 | -0,2271 |
80 | 26,10 | 8,050 | 3,680 | 1,900 | 1,008 | 0,5020 | 0,1970 | 0,0100 | -0,089 | -0,2287 |
100 | 25,30 | 7,910 | 3,630 | 1,880 | 0,9980 | 0,4960 | 0,1940 | 0,0080 | -0,089 | -0,2292 |
22,19 | 7,383 | 3,450 | 1,801 | 0,9562 | 0,4734 | 0,1807 | 0,0019 | -0,0891 | -0,2309 | |
A.n | ||||||||||
10 | 39,04 | 12,052 | 5,609 | 3,233 | 2,172 | 1,650 | 1,384 | 1,255 | 1,170 | |
20 | 140,7 | 23,96 | 9,136 | 4,666 | 2,850 | 2,000 | 1,570 | 1,350 | 1,248 | 1,159 |
30 | 100,4 | 20,96 | 8,416 | 4,410 | 2,743 | 1,949 | 1,546 | 1,339 | 1,248 | 1,165 |
40 | 87,06 | 19,68 | 8,088 | 4,292 | 2,692 | 1,925 | 1,534 | 1,335 | 1,249 | 1,161 |
50 | 80,39 | 18,97 | 7,901 | 4,223 | 2,662 | 1,911 | 1,528 | 1,332 | 1,249 | 1,165 |
60 | 76,40 | 18,52 | 7,781 | 4,179 | 2,643 | 1,902 | 1,524 | 1,331 | 1,249 | 1,162 |
60,53 | 16,50 | 7,219 | 3,967 | 2,550 | 1,859 | 1,503 | 1,323 | 1,251 | 1,162 | |
| ||||||||||
Уравнение для дополнительного фактора :
![]() , (21)
, (21)
где f и Н (f
) определяются из таблицы 7.
Примечание - и f
зависят от значения
, объема выборки n, и соотношения r/n,
и f
являются независимыми от
.
Таблица 7 - f и H(f
) как функции от
0,221 | 0,490 | 1,645 | 1,774 | 1,923 | 2,096 | 2,299 | 2,541 | 2,681 | |
f | 10,00 | 5,000 | 2,000 | 1,900 | 1,800 | 1,700 | 1,600 | 1,500 | 1,450 |
H(f | 0,103 | 0,213 | 0,577 | 0,611 | 0,650 | 0,693 | 0,742 | 0,798 | 0,830 |
2,834 | 3,003 | 3,191 | 3,401 | 3,636 | 3,901 | 4,201 | 4,543 | 4,935 | |
f | 1,400 | 1,350 | 1,300 | 1,250 | 1,200 | 1,150 | 1,100 | 1,105 | 1,000 |
H(f | 0,863 | 0,900 | 0,940 | 0,983 | 1,030 | 1,081 | 1,138 | 1,201 | 1,270 |
Математические функции: | |||||||||
| f | ||||||||
H(f | |||||||||
2 | f | ||||||||
H(f | |||||||||
Тогда границы доверительного интервала для G:
верхняя граница:
 ; (22)
; (22)
нижняя граница:
 . (23)
. (23)
8.3 Доверительный интервал для параметра масштаба
8.3.1 Метод для всех выборок
Границы двусторонних доверительных интервалов для параметра масштаба при уровне доверия (1-
) рассчитывается методом итераций:
 , (24)
, (24)
 . (25)
. (25)
Итерации могут быть начаты с ![]() .
.
После каждой итерации новые значения ![]() и
и ![]() рассчитываются по методу, описанному в 8.2.
рассчитываются по методу, описанному в 8.2.
Итерации должны быть прекращены, когда два последовательных значения как , так и
равны с требуемой точностью. Например, для оценки результатов испытаний прочности разница меньше 0,1% дает достаточную точность.
8.3.2 Метод для нецензурированной выборки
В случае нецензурированной (полной) выборки могут быть использованы следующие простые уравнения:
 , (26)
, (26) (27)
(27)
с коэффициентами T и Т
![]() , взятыми из таблицы 8.
, взятыми из таблицы 8.
Таблица 8 - Коэффициент Т
n | р=1- | p= | ||||||
0,975 | 0,95 | 0,9 | 0,75 | 0,25 | 0,1 | 0,05 | 0,025 | |
5 | 1,4897 | 1,107 | 0,772 | 0,349 | -0,444 | -0,888 | -1,247 | -1,5675 |
6 | 1,2233 | 0,939 | 0,666 | 0,302 | -0,385 | -0,740 | -1,007 | -1,3247 |
7 | 1,0642 | 0,829 | 0,598 | 0,272 | -0,344 | -0,652 | -0,874 | -1,1437 |
8 | 0,9548 | 0,751 | 0,547 | 0,251 | -0,313 | -0,591 | -0,784 | -1,0096 |
9 | 0,8738 | 0,691 | 0,507 | 0,235 | -0,289 | -0,544 | -0,717 | -0,9122 |
10 | 0,8114 | 0,644 | 0,475 | 0,222 | -0,269 | -0,507 | -0,665 | -0,8387 |
11 | 0,7603 | 0,605 | 0,448 | 0,211 | -0,253 | -0,477 | -0,622 | -0,7790 |
12 | 0,7176 | 0,572 | 0,425 | 0,202 | -0,239 | -0,451 | -0,587 | -0,7326 |
13 | 0,6815 | 0,544 | 0,406 | 0,194 | -0,228 | -0,429 | -0,557 | -0,6894 |
14 | 0,6502 | 0,520 | 0,389 | 0,187 | -0,217 | -0,410 | -0,532 | -0,6572 |
15 | 0,6235 | 0,499 | 0,374 | 0,180 | -0,208 | -0,393 | -0,509 | -0,6266 |
16 | 0,5989 | 0,480 | 0,360 | 0,175 | -0,200 | -0,379 | -0,489 | -0,6016 |
17 | 0,5778 | 0,463 | 0,348 | 0,170 | -0,193 | -0,365 | -0,471 | -0,5795 |
18 | 0,5577 | 0,447 | 0,338 | 0,165 | -0,187 | -0,353 | -0,455 | -0,5566 |
19 | 0,5405 | 0,433 | 0,328 | 0,161 | -0,181 | -0,342 | -0,441 | -0,5356 |
20 | 0,5254 | 0,421 | 0,318 | 0,157 | -0,175 | -0,332 | -0,428 | -0,5187 |
22 | 0,4958 | 0,398 | 0,302 | 0,150 | -0,166 | -0,314 | -0,404 | -0,4907 |
24 | 0,4719 | 0,379 | 0,288 | 0,144 | -0,158 | -0,299 | -0,384 | -0,4669 |
26 | 0,4509 | 0,362 | 0,276 | 0,138 | -0,150 | -0,286 | -0,367 | -0,4450 |
28 | 0,4326 | 0,347 | 0,265 | 0,134 | -0,144 | -0,274 | -0,352 | -0,4249 |
30 | 0,4156 | 0,334 | 0,256 | 0,129 | -0,139 | -0,264 | -0,338 | -0,4098 |
32 | 0,4014 | 0,323 | 0,247 | 0,125 | -0,134 | -0,254 | -0,326 | -0,3951 |
34 | 0,3879 | 0,312 | 0,239 | 0,122 | -0,129 | -0,246 | -0,315 | -0,3801 |
36 | 0,3755 | 0,302 | 0,232 | 0,118 | -0,125 | -0,238 | -0,305 | -0,3687 |
38 | 0,3648 | 0,293 | 0,226 | 0,115 | -0,121 | -0,231 | -0,296 | -0,3578 |
40 | 0,3544 | 0,285 | 0,220 | 0,113 | -0,118 | -0,224 | -0,288 | -0,3479 |
42 | 0,3450 | 0,278 | 0,214 | 0,110 | -0,115 | -0,218 | -0,280 | -0,3394 |
44 | 0,3346 | 0,271 | 0,209 | 0,108 | -0,112 | -0,213 | -0,273 | -0,3289 |
46 | 0,3286 | 0,264 | 0,204 | 0,105 | -0,109 | -0,208 | -0,266 | -0,3219 |
48 | 0,3210 | 0,258 | 0,199 | 0,103 | -0,106 | -0,203 | -0,260 | -0,3136 |
50 | 0,3136 | 0,253 | 0,195 | 0,101 | -0,104 | -0,198 | -0,254 | -0,3073 |
52 | 0,3067 | 0,247 | 0,191 | 0,099 | -0,102 | -0,194 | -0,249 | -0,3019 |
54 | 0,3012 | 0,243 | 0,187 | 0,097 | -0,100 | -0,190 | -0,244 | -0,3939 |
56 | 0,2953 | 0,238 | 0,184 | 0,096 | -0,098 | -0,186 | -0,239 | -0,2887 |
58 | 0,2895 | 0,233 | 0,181 | 0,094 | -0,096 | -0,183 | -0,234 | -0,2840 |
60 | 0,2839 | 0,229 | 0,177 | 0,092 | -0,094 | -0,179 | -0,230 | -0,2788 |
62 | 0,2791 | 0,225 | 0,174 | 0,091 | -0,092 | -0,176 | -0,226 | -0,2735 |
64 | 0,2743 | 0,221 | 0,171 | 0,089 | -0,091 | -0,173 | -0,222 | -0,2687 |
66 | 0,2697 | 0,218 | 0,169 | 0,088 | -0,089 | -0,170 | -0,218 | -0,2647 |
68 | 0,2656 | 0,214 | 0,166 | 0,087 | -0,088 | -0,167 | -0,215 | -0,2612 |
70 | 0,2618 | 0,211 | 0,164 | 0,085 | -0,086 | -0,165 | -0,211 | -0,2573 |
72 | 0,2573 | 0,208 | 0,161 | 0,084 | -0,085 | -0,162 | -0,208 | -0,2530 |
74 | 0,2542 | 0,205 | 0,159 | 0,083 | -0,084 | -0,160 | -0,205 | -0,2495 |
76 | 0,2504 | 0,202 | 0,157 | 0,082 | -0,083 | -0,158 | -0,202 | -0,2456 |
78 | 0,2466 | 0,199 | 0,155 | 0,081 | -0,081 | -0,155 | -0,199 | -0,2427 |
80 | 0,2438 | 0,197 | 0,153 | 0,080 | -0,080 | -0,153 | -0,197 | -0,2391 |
85 | 0,2352 | 0,190 | 0,148 | 0,077 | -0,078 | -0,148 | -0,190 | -0,2326 |
90 | 0,2286 | 0,185 | 0,143 | 0,075 | -0,075 | -0,144 | -0,184 | -0,2260 |
95 | 0,2218 | 0,179 | 0,139 | 0,073 | -0,073 | -0,139 | -0,179 | -0,2197 |
100 | 0,2162 | 0,175 | 0,136 | 0,071 | -0,071 | -0,136 | -0,174 | -0,2132 |
110 | 0,2056 | 0,166 | 0,129 | 0,067 | -0,067 | -0,129 | -0,165 | -0,2027 |
120 | 0,1962 | 0,159 | 0,123 | 0,064 | -0,064 | -0,123 | -0,158 | -0,1946 |
8.4 Доверительный интервал для значения x величины X заданного значения G(x) функции распределения
8.4.1 Метод для всех выборок
Доверительный интервал для х заданной G(x) может быть вычислен путем решения трансцендентного уравнения:
![]() . (28)
. (28)
Эти уравнения могут быть решены путем варьирования переменной х процедурой, описанной в 8.3.1, в качестве метода последовательных приближений.
Однако в большинстве случаев доверительные интервалы для х могут быть быстрее определены для заданного значения G(х) по диаграмме Вейбулла. Для этой цели границы доверительного интервала, определенные в соответствии с 8.2, например G(x) и G
(x), должны быть рассчитаны для ограниченного числа значений х и нанесены на диаграмму Вейбулла. В пределах графика на диаграмме Вейбулла доверительные интервалы для х, задаваемого G(x), могут быть определены напрямую.
Эта процедура становится неточной при малых значениях G(x), как в случаях, когда степень свободы f распределения хи-квадрат принимает значения меньше 1. Предельные кривые доверительного интервала функции распределения G(x) должны быть линейно экстраполированы, графически или численно.
Графическая экстраполяция позволяет непосредственно определить границы доверительного интервала х из диаграммы Вейбулла.
Для численного определения доверительного интервала заданного значения по точкам следует выбирать значения
![]() , и для этого
, и для этого доверительный интервал функции распределения G(x
) рассчитывается по 8.2 для получения доверительных интервалов
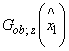 и
и  .
.
Выбранное значение должно соответствовать приблизительно нижней границе диапазона измеренных значений х.
Тогда границы доверительного интервала значения следует вычислять с использованием следующих уравнений:
 , (29)
, (29)
 . (30)
. (30)
8.4.2 Метод для нецензурированной выборки
Для G0,632 могут быть использованы следующие простые уравнения:
 , (31)
, (31)
 . (32)
. (32)
Значения и
должны быть рассчитаны в соответствии с 8.3.1 или 8.3.2.
Этот упрощенный метод расчета приводит к более осторожной оценке доверительного интервала х, по сравнению с более точным методом экстраполяции, как описано в 8.4.1.
В выборках, где 20 и
5, и для значений G<0,1 должны быть использованы следующие уравнения, дающие лучшее приближение к точному методу, описанному в 8.4.1:
 , (33)
, (33)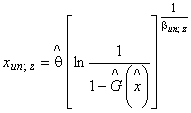 . (34)
. (34)
Приложение А
(информационное)
Примеры
А.1 Нецензурированная выборка
А.1.1 Данные
Таблица А.1 - Результаты эксперимента по определению напряжения разрушения
Номер образца | Напряжение разрушения, N/mm |
1 | 41,26 |
2 | 42,54 |
3 | 44,31 |
4 | 44,43 |
5 | 44,67 |
6 | 45,02 |
7 | 45,37 |
8 | 46,08 |
9 | 46,08 |
10 | 46,55 |
11 | 47,86 |
12 | 48,21 |
13 | 48,21 |
14 | 48,31 |
15 | 49,63 |
16 | 50,34 |
17 | 50,43 |
18 | 50,69 |
19 | 50,78 |
20 | 51,05 |
21 | 51,05 |
22 | 51,05 |
23 | 51,76 |
24 | 53,17 |
А.1.2 Статистическая оценка
А.1.2.1 Точечное оценивание
Метод описан в 6.2.
Из таблицы 3, для n=24 , k=1,4975:
s=int(0,84x24)=20.
Отсюда =18,67 и
=49,26 N/mm
.
А.1.2.2 Оценка доверительных интервалов
Для коэффициента доверия 95% доверительные интервалы: 1-/2=0,975 и
/2=0,025.
а) Метод определения доверительного интервала для параметра формы приведен в 8.1.
Из таблицы 4, с помощью линейной интерполяции, f/n=2,918, так что f
=70,03.
Из таблицы 5, ![]() =95,05 и
=95,05 и ![]() =48,78.
=48,78.
Отсюда =25,34 и
=13,01.
б) Метод определения доверительных интервалов для G(х) приведен в 8.2, и результаты вычислений приведены в таблице А.2.
Таблица А.2 - Результаты вычислений согласно 8.2
G(x) |
| y | f | H(f |
|
| G | G | ||
99 | 53,46 | -1,5276 | 0,08670 | 24,054 | 0,04215 | 4,8054 | 39,433 | 12,440 | 99,96 | 91,67 |
95 | 52,24 | -1,0966 | 0,06243 | 33,026 | 0,03058 | 3,0869 | 50,757 | 19,067 | 99,13 | 83,17 |
80 | 50,53 | -0,4752 | 0,04608 | 44,395 | 0,02269 | 1,6452 | 64,679 | 27,887 | 90,90 | 64,42 |
63,21 | 49,26 | 0 | 0,04838 | 42,331 | 0,02381 | 1,0241 | 62,179 | 26,259 | 77,78 | 47,02 |
10 | 43,67 | 2,2488 | 0,2343 | 9,4985 | 0,1090 | 0,1177 | 19,751 | 2,973 | 21,71 | 3,62 |
1 | 38,5 | 4,6013 | 0,7380 | 3,6005 | 0,3027 | 0,01359 | 10,426 | 0,377 | 3,86 | 0,14 |
Рисунок 1 показывает значения G(x), G, G
из таблицы А.2, графически нанесенные на вейбулловскую (вероятностную) бумагу соответственно для каждого
из таблицы А.2, вместе с результатами данных предела прочности из таблицы А.1.
с) Метод определения доверительных интервалов параметра масштаба приводится в 8.3.
Таблица А.3, полученная с использованием метода 8.3.1, показывает результаты последовательных итераций для определения и
.
Таблица А.3 - Результаты последовательных итераций согласно п.8.3.1
Номер итерации | ||
0 | 49,26 | 49,26 |
1 | 50,47 | 48,19 |
2 | 50,44 | 48,08 |
3 | 50,44 | 48,06 |
После трех итераций разница достаточно мала, что позволяет остановить итерационный процесс.
Отсюда =50,44 N/mm
и
=48,06 N/mm
.
Тем не менее, так как это нецензурированная выборка, упрощенная процедура, описанная в п.8.3.2, также может быть использована.
Из таблицы 8, Т![]() =-0,4669 и Т
=-0,4669 и Т![]() =0,4719.
=0,4719.
Отсюда =50,51 N/mm
и
=48,03 N/mm
.
д) С коэффициентом доверия 95% доверительные интервалы для х при G=0,1% могут быть определены либо графически из рисунка А.1, или численно методом, описанным в 8.4.1.
Графическая экстраполяция на рисунке А.1 дает:
x=38,0 N/mm
=34,0 N/mm
x
=30,1 N/mm
.
Для численного метода удобно полагать =38,50 N/mm
, что соответствует
=1%. По таблице А.2 уже были проведены расчеты и получено:
 =3,86% и
=3,86% и  =0,14%.
=0,14%.
Отсюда x=38,00 N/mm
и x
=29,03 N/mm
.
Существует хорошее соответствие между графическим и численным методами.
Для нецензурированной выборки упрощенный метод, описанный в 8.4.2, может быть использован.
Поскольку n>20, G<0,1 и >5, полученные из А.1.2.1 значения
могут быть использованы в уравнениях 8.4.2.
Отсюда x=31,51 N/mm
и x
=28,97 N/mm
.
Это также дает хорошее соответствие между графическим и полным численным методами.

Рисунок А.1 - Оценка выборки из таблицы А.1
А.2 Цензурированная выборка
А.2.1 Данные
Та же выборка, что приведена в таблице А.1, используется для этого примера, но предполагается, что образцы не могут иметь напряжение разрушения больше 50 N/mm. Таким образом, данные принимают вид, показанный в таблице А.4.
Таблица А.4 - Результаты эксперимента для определения напряжения разрушения
Номер образца | Напряжение разрушения, N/mm |
1 | 41,26 |
2 | 42,54 |
3 | 44,31 |
4 | 44,43 |
5 | 44,67 |
6 | 45,02 |
7 | 45,37 |
8 | 46,08 |
9 | 46,08 |
10 | 46,55 |
11 | 47,86 |
12 | 48,21 |
13 | 48,21 |
14 | 48,31 |
15 | 49,63 |
16 | >50 |
17 | >50 |
18 | >50 |
19 | >50 |
20 | >50 |
21 | >50 |
22 | >50 |
23 | >50 |
24 | >50 |
Уровень цензурирования определяется значениями: n=24 , r=15 и r/n=0,625.
А.2.2 Статистическая оценка
А.2.2.1 Точечное оценивание
Метод описан в 6.1.
Для n=24 и r/n=0,625, из таблицы 1, k=0,7271 и, из таблицы 2, С
=-0,0937.
Отсюда =14,67 и
=49,95 N/mm
.
А.2.2.2 Оценка доверительных интервалов
Для коэффициента доверия 95% доверительные интервалы: 1-/2=0,975 и
/2=0,025.
а) Метод определения доверительного интервала для параметра формы приведен в 8.1.
Из таблицы 4, с помощью линейной интерполяции, f/n=1,411, так что f
=33,86.
Из таблицы 5, ![]() =51,80 и
=51,80 и ![]() =19,69.
=19,69.
Отсюда, =22,44 и
=8,53.
б) Метод определения доверительного интервала для G(х) приведен в 8.2.
Из таблицы 6, В=0,05951, С=0,02062 и А=0,0781.
Результаты вычислений приведены в таблице А.5.
Таблица А.5 - Результаты вычислений согласно 8.2
G(x) |
| y | f | H(f |
|
| G | G | ||
99 | 55,43 | -1,5271 | 0,2799 | 8,1008 | 0,1285 | 5,2362 | 13,215 | 2,232 | 99,98 | 76,37 |
95 | 53,83 | -1,0966 | 0,1950 | 11,225 | 0,0917 | 3,2841 | 22,239 | 3,948 | 99,85 | 68,50 |
80 | 51,60 | -0,4768 | 0,1113 | 18,855 | 0,0540 | 1,7002 | 32,659 | 8,809 | 94,74 | 54,81 |
63,21 | 49,95 | 0 | 0,0781 | 26,595 | 0,0381 | 1,0388 | 42,680 | 14,278 | 81,12 | 42,75 |
10 | 42,85 | 2,2492 | 0,2864 | 7,9377 | 0,1312 | 0,1203 | 17,440 | 2,149 | 23,23 | 3,20 |
3 | 39,37 | 3,4917 | 0,6596 | 3,9331 | 0,2753 | 0,0401 | 11,023 | 0,4661 | 10,63 | 0,474 |
2 | 38,28 | 3,9036 | 0,8239 | 3,3067 | 0,3318 | 0,0281 | 9,899 | 0,2982 | 8,07 | 0,253 |
1 | 36,50 | 4,6021 | 1,1487 | 2,5804 | 0,4348 | 0,0155 | 8,521 | 0,147 | 4,99 | 0,088 |
На рисунке 2 приведены значения величин G(x), G и G
из таблицы А.5, нанесенные на бумагу Вейбулла соответственно каждому значению
из таблицы А.5, вместе с результатами данных прочности из таблицы А.4.
с) Метод определения доверительных интервалов параметра масштаба приведен в 8.3.1.
В таблице А.6 приведены результаты последовательных итераций для определения и
.
Таблица А.6 - Результаты последовательных итераций согласно 8.3.1
Номер итерации | ||
0 | 49,95 | 49,95 |
1 | 51,98 | 48,24 |
2 | 52,54 | 48,30 |
3 | 52,75 | 48,30 |
4 | 52,84 | 48,30 |
5 | 52,88 | 48,30 |
После пяти итераций, разница достаточно мала, что позволяет остановить итерационный процесс.
Отсюда =52,88 N/mm
и
=48,30 N/mm
.
д) С коэффициентом доверия 95% доверительные интервалы для х при G=0,1% могут быть определены либо графически на рисунке А.1, либо численно методом, описанным в 8.4.1.
Графическая экстраполяция на рисунке А.2 дает:
x=35,8 N/mm
,
=30,2 N/mm
, x
=25,3 N/mm
.
Для численного метода удобно полагать ![]() =39,37 N/mm
=39,37 N/mm, что соответствует
=3%. Из таблицы А.5, расчеты уже были произведены и получено:
 =10,63%,
=10,63%,  =0,474%.
=0,474%.
Отсюда x=36,73 N/mm
и x
=22,63 N/mm
.
Существует хорошее соответствие между графическим и численным методами.

Рисунок А.2 - Оценка выборки из таблицы А.4
Приложение В
(справочное)
Вейбулловская (вероятностная) бумага

В.1 - Диаграмма Вейбулла
Библиография
[1] | ИСО 3534 | Статистика - Словарь и условные обозначения. |
_____________________
| ||
ISO 3534 | Statistics - Vocabulary and symbols | |
[2] | ИСО 2854:1976 | Статистическое представление данных - Методы оценки и проверки гипотез о средних и дисперсиях. |
ISO 2854:1976 | Statistical interpretation of data - Techniques of estimation and tests relating to means and variances. | |
[3] | Бейн Л.Дж.: Статистический анализ надежности и испытание на стойкость (долговечность) модели. Теория и методы: Марсель Деккер Издательство: 1978 | |
Bain L.J.: Statistical Analysis of Reliability and Life Testing Models; Theory and Methods: Marcel Dekker Publishing Comp.: 1978. | ||
[4] | МЭК 56 (ЦС) 162 | Методика для проверки степени согласия, доверительных интервалов и нижней доверительной границы для данных распределения Вейбулла. |
IEC 56 (СО) 162 | Procedures for goodness-of-fit tests, confidence intervals and lower confidence limits for Weibull distributed data. | |
[5] | ДИН 55303-7 | Статистический анализ данных - Часть 7: Опыт и метод испытаний двухпараметрической функции распределения Вейбулла. |
DIN 55303-7 | Statistische Auswertung von Daten - Teil 7: Schatz- und Testverfahren bei zweiparametriger Weibull-Verteilung. | |
УДК 666.151:006.354 | МКС 81.040.01 | MOD |
Ключевые слова: прочность; распределение Вейбулла; критерий согласия; доверительный интервал; уровень доверия; цензурированная выборка | ||
Электронный текст документа
и сверен по:
, 2015
