ГОСТ 13088-67 Колориметрия. Термины, буквенные обозначения

ГОСТ 13088-67

Группа T35

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

КОЛОРИМЕТРИЯ

Термины, буквенные обозначения

Colorimetry. Terms, alphabetical symbols

Дата введения 1968-01-01

ПЕРЕИЗДАНИЕ*. Март 1990 года

_______________

* ГОСТ 13088-67 утвержден Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР 24.07.67. (Информация приведена из официального издания, М.: Издательство стандартов, 1967 год). - Примечание "КОДЕКС".


Термин	Буквенное обозначение	Определение
I. Физическое и математическое определение цвета
1. Цвет (в колориметрии)	Общепринятые для векторных величин и (в рукописях)	Цвет есть аффинная векторная величина трех измерений, выражающая свойство, общее всем спектральным составам излучения, визуально неразличимым в колориметрических условиях наблюдения. Под словом "излучение" следует понимать также свет, отраженный и пропускаемый несамосветящимися телами. Примечание. Колориметрические условия наблюдения физические условия визуального сравнения, в которых любые одинаковые по спектральному составу излучения неразличимы глазом.
2. Цветовое равенство	-	Полная визуальная неотличимость друг от друга (тождество) полей зрения в колориметрических условиях наблюдения.
3. Цветовое уравнение	или	Векторное уравнение, выражающее результаты опыта, проведенного в колориметрических условиях наблюдения.
4. Трехцветная система измерения цвета	Через три единичных вектора (три основных цвета), например: Система	Совокупность трех линейно-независимых цветов через которые любой цвет может быть выражен с помощью цветового уравнения (числа могут быть и отрицательными; см. приложения 1 и 2)
5.Основные цвета (единичные векторы координатной системы)	Соответствующие векторные обозначения, например	Три условно выбранные линейно-независимые цвета системы измерения, выполняющие роль единичных векторов
6. Координаты цвета	Обозначения, принятые для скалярных величин, например, или	Три числа, указывающие, в каких количествах следует смешать излучения, отвечающие единичным цветам, чтобы получить колориметрическое равенство с измеряемым цветом
7. Функции сложения (кривые сложения) цветов	Как координаты цвета, но с указанием функциональной зависимости от длины волны . Например, или	Совокупность координат цветов монохроматических излучений фиксированного относительного распределения энергии, представленная в виде функциональной зависимости от длины волны
8. Средний стандартный наблюдатель	-	Наблюдатель, для которого значения кривых сложения цветов совпадают со значениями, указанными в табл.1 приложения 2
9. Координаты цветностей	Малыми буквами, соответствующими буквам выбранной системы координат. Например, для системы	Отношение каждой из координат цвета к их сумме: ; ; или ; ; . Координата обычно опускается как зависимая поскольку
10. Координаты цветностей монохроматических излучений	В соответствии с требованиями п.9, но с указанием функциональной зависимости от длины волны . Например, .	Координаты цветностей монохроматических излучений с указанием функциональной зависимости от длины волны
11. Реальные цвета	См. п.1	Цвета любых физически осуществимых излучений
12. Нереальные цвета	См. п.1	Цветовые векторы, задаваемые в виде линейных комбинаций векторов реальных цветов, такие, однако, которым не соответствуют никакие реальные излучения
13. Оптимальные цвета	См. п.1	Цвета тел, у которых по всей видимой области спектра пропускания (или отражения) коэффициент пропускания или коэффициент отражения , а спектра поглощения - или , причем имеется не более двух точек разрыва (скачка пропускания от 0 до 1).
14. Цветовое пространство	-	Пространство аффинных цветовых векторов (реальных и нереальных)
15. Цветовой конус	-	Часть цветового пространства, составляющая всю область реальных цветов, ограниченная конической поверхностью бесконечной протяженности (с вершиной в начале координат), представляющей собой геометрическое место цветов монохроматических излучений
16. Цветовое тело	-	Часть цветового конуса, заключающая в себе вce цвета прозрачных и отражающих предметов в условиях данного освещения. Поверхность цветового тела представляет собой геометрическое место оптимальных цветов
17. Цветовой треугольник	-	Часть плоскости, проходящей через концы единичных векторов выбранной системы измерения, представляющая собой геометрическое место положительных координат цветности
18. График цветностей	-	Прямоугольный треугольник, катеты которого являются осями изменения координат цветности
19. Линия цветностей спектральных излучений	-	След пересечения поверхности цветового конуса с плоскостью цветового треугольника; геометрическое место точек, отвечающих цветности спектральных излучений
II. Источники света, применяемые в колориметрии (см. приложение 3)
20. Источник света		Источник, спектральная плотность излучения которого в видимой области спектра постоянна
21. Источник света		Источник, относительное спектральное распределение энергии которого в видимой области спектра соответствует излучению абсолютно черного тела при температуре 2854 °К в пределах допуска, установленного ГОСТ 7721-89
22. Источник света		Источник, относительное спектральное распределение энергии которого в видимой области спектра соответствует излучению абсолютно черного тела при температуре 4800 °К в пределах допуска, установленного ГОСТ 7721-89
23. Источник света		Источник, относительное спектральное распределение энергии которого в видимой области спектра соответствует излучению абсолютно черного тела при температуре 6500 °К в пределах допуска, установленного ГОСТ 7721-89
III. Дополнительные колориметрические термины
24. Порог цветоразличения	-	Наименьшее воспринимаемое глазом различие в цвете (в значительной степени зависит от условий наблюдения)
25. Пороговый эллипсоид	-	Область цветового пространства, ограниченная эллипсоидальной поверхностью, на которой располагаются цвета, отличающиеся от цвета, соответствующего центру эллипсоида, на один порог цветоразличения
26. Равноконтрастный цветовой график	-	График цветностей, в котором расстояние между любыми двумя точками пропорционально числу порогов цветоразличения
27. Ахроматические, серые цвета	-	Ряд цветов, расположенных в цветовом пространстве на прямой линии, проходящей через начало координат и цвет белой поверхности в условиях данного освещения
28. Дополнительные цвета	-	Цвета, которые при сложении дают ахроматический цвет
29. Метамерные излучения	-	Излучения различного спектрального состава, но одинаковые по цвету (визуально неразличимые)
30. Идеально белая поверхность	-	Поверхность, рассеивающая излучения любых длин волн видимого спектра одинаково по всем направлениям и без поглощения

ПРИЛОЖЕНИЕ 1

ОБЩИЕ РАСЧЕТНЫЕ ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ

Расчетные формулы приведены в буквенной форме для того, чтобы представлять различные функции сложений, основные цвета и коэффициенты преобразований.

Расчеты цвета по спектру излучения

а) Формула расчета координат цвета излучения по его спектральному составу :

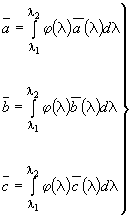, (1)

где - кривые сложения произвольной трехцветной системы , т.е. координаты монохроматических излучений единичной мощности;

- координаты цвета по системе для излучения со спектральным распределением .

Для наиболее употребительных систем и в приложении 2 приведены числовые значения ординат функций сложения. Для других систем функции сложения подлежат предварительному расчету по формулам (2) и (3) настоящего приложения и стандартным кривым сложения .

б) Векторные (цветовые) уравнения, связывающие основные цвета одной системы с основными цветами другой системы:

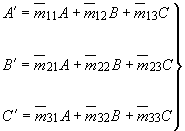, (2)

где - координаты цвета по системе ;

- координаты цвета по системе ;

- координаты цвета по системе .

При градуировке приборов коэффициенты являются координатами основных цветов градуируемого прибора по какой-либо стандартной системе, например, . Эти коэффициенты определяют по формуле (1) настоящего приложения, полагая в них , или , или , где - распределение энергии в спектре примененного в приборе источника света, а - спектральные характеристики применяемых светофильтров. Коэффициенты могут быть также получены измерением цветов на приборе с основными цветами ;

в) Скалярные уравнения преобразования координат цвета при переходе от одной системы координат к другой:

, (3)

где - вычисляемые координаты цвета по системе ;

- известные координаты того же цвета по системе .

Следует иметь в виду, что коэффициенты скалярных уравнений (3), связывающие координаты произвольного цвета по системе с координатами того же цвета по системе существенно иные, чем коэффициенты векторных уравнений (2), связывающих основные цвета (единичные векторы) тех же систем.

ПРИЛОЖЕНИЕ 2

НАИБОЛЕЕ ЧАСТО ПРИМЕНЯЕМЫЕ СИСТЕМЫ ЦВЕТОВЫХ ИЗМЕРЕНИЙ

1. Линейные системы

Система . Система, основные цвета которой задаются как монохроматические излучения длины волны 700 нм для , 546,1 нм - для и 435,8 нм - для , взятых в таких мощностях, чтобы удовлетворялось цветовое (векторное) уравнение:

где - цвет белой поверхности, освещенной источником .

Система характеризуется кривыми сложения (координатами цвета монохроматических излучений единичной мощности), приведенными в табл.1 приложения.

Таблица 1


Длина волны в нм
380	0,00003	-0,00001	0,00117
390	0,00010	-0,00004	0,00359
400	0,00030	-0,00014	0,01214
410	0,00084	-0,00041	0,03707
420	0,00211	-0,00110	0,11541
430	0,00218	-0,00119	0,24769
440	-0,00261	0,00149	0,31228
450	-0,01213	0,00678	0,31670
460	-0,02608	0,01485	0,29821
470	-0,03933	0,02538	0,22991
480	-0,04939	0,03914	0,14494
490	-0,05814	0,05689	0,08257
500	-0,07173	0,08536	0,04776
510	-0,08901	0,12860	0,02698
520	-0,09264	0,17468	0,01221
530	-0,07101	0,20317	0,00549
540	-0,03152	0,21466	0,00146
550	0,02279	0,21178	-0,00058
560	0,09060	0,19702	-0,00130
570	0,16768	0,17087	-0,00135
580	0,24526	0,13610	-0,00108
590	0,30928	0,09754	-0,00079
600	0,34429	0,06246	-0,00049
610	0,33971	0,03557	-0,00030
620	0,29708	0,01828	-0,00015
630	0,22677	0,00833	-0,00008
640	0,15968	0,00334	-0,00003
650	0,10167	0,00116	-0,00001
660	0,05932	0,00037	0,00000
670	0,03149	0,00011	0,00000
680	0,01687	0,00003	0,00000
690	0,00819	0,00000	0,00000
700	0,00410	0,00000	0,00000
710	0,00210	0,00000	0,00000
720	0,00105	0,00000	0,00000
730	0,00052	0,00000	0,00000
740	0,00025	0,00000	0,00000
750	0,00012	0,00000	0,00000

Система . Основные цвета системы не могут быть физически реализованы (нереальные цвета). Система задается через систему следующими формулами преобразования.

Векторные цветовые уравнения, связывающие цвета с цветами :

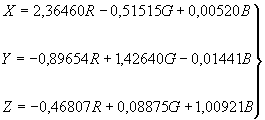(1)

Скалярные численные уравнения, связывающие координаты произвольного цвета по системе с координатами того же цвета по системе :

. (2)

По формулам (2) вычисляют данные табл.2 приложения на основании данных табл.1 (координаты цветов монохроматических излучений единичной мощности).

Примечание. Для того чтобы кривая сложения совпала с относительной кривой видности , результаты вычислений по формулам (2) умножают на 5,6504.

Таблица 2


Длина волны в нм
380	0,0014	0,0000	0,0065
390	0,0042	0,0001	0,0201
400	0,0143	0,0004	0,0679
410	0,0435	0,0012	0,2074
420	0,1344	0,0040	0,6456
430	0,2839	0,0116	1,3856
440	0,3483	0,0230	1,7471
450	0,3362	0,0380	1,7721
460	0,2908	0,0600	1,6692
470	0,1954	0,0910	1,2876
480	0,0956	0,1390	0,8130
490	0,0320	0,2080	0,4652
500	0,0049	0,3230	0,2720
510	0,0093	0,5030	0,1582
520	0,0633	0,7100	0,0782
530	0,1655	0,8620	0,0422
540	0,2904	0,9540	0,0203
550	0,4334	0,9950	0,0087
560	0,5945	0,9950	0,0039
570	0,7621	0,9520	0,0021
580	0,9163	0,8700	0,0017
590	1,0263	0,7570	0,0011
600	1,0622	0,6310	0,0008
610	1,0026	0,5030	0,0003
620	0,8544	0,3810	0,0002
630	0,6424	0,2650	0,0000
640	0,4479	0,1750	0,0000
650	0,2835	0,1070	0,0000
660	0,1649	0,0610	0,0000
670	0,0874	0,0320	0,0000
680	0,0468	0,0170	0,0000
690	0,0227	0,0082	0,0000
700	0,0114	0,0041	0,0000
710	0,0058	0,0021	0,0000
720	0,0029	0,0010	0,0000
730	0,0014	0,0005	0,0000
740	0,0007	0,0003	0,0000
750	0,0003	0,0001	0,0000

Система . Физиологическая система, функциями сложения которой являются кривые спектральной чувствительности колбочкового аппарата сетчатки глаза.

Система зональная . Система определяется основными цветами излучений, координаты которых по системе находят по формулам:

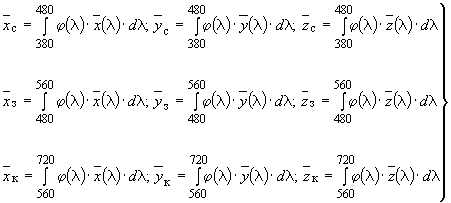
где - кривые сложения по системе ;

- спектральное распределение энергии для одного из стандартных источников света.

Примечание. Зональная система удобна для тех приложений колориметрии, когда имеют дело со смешением красок, обладающих малым рассеянием, например, в технике цветного кино.

2. Нелинейные системы

Системы барицентрические . Системы, в которых цвета изображаются на плоскости точкой с приписанным ей весом. Барицентрические координаты вычисляют по координатам соответствующей линейной системы по формулам:

; ; .

Примечание. Координата носит в литературе разные названия "количество цвета" (Гельмгольц, Максвелл), "цветовой момент" (современная немецкая литература), "модуль цвета" (в некоторых американских работах).

Цветовые расчеты в цветовом треугольнике (например, нахождение суммы двух или более цветов по принципу центра тяжести) производят всегда в барицентрической системе.

Система . Система координат типа полярной, основана на возможности получения любого цвета путем смешения монохроматического излучения (или "пурпурного", образованного смешением двух монохроматических излучений, взятых из концов видимого спектра) с тем или иным "белым" светом (см. приложение 3). Координатами при этом служат:

- длина волны используемого монохроматического излучения, - фотометрическая яркость и - "чистота цвета", определяемая соотношением , где - фотометрическая яркость монохроматической составляющей, а - общая яркость излучения.

ПРИЛОЖЕНИЕ 3

Спектральное распределение энергии в источниках и


Длина волны в нм
380	9,79	54,150	93,720
390	12,09	58,212	95,602
400	14,71	62,153	97,119
410	17,68	65,956	98,293
420	21,00	69,588	99,143
430	24,67	73,037	99,692
440	28,70	76,288	99,962
450	33,09	79,332	99,977
460	37,82	82,161	99,758
470	42,87	84,769	99,329
480	48,25	87,156	98,709
490	53,91	89,321	97,918
500	59,86	91,268	96,976
510	66,06	92,999	95,900
520	72,50	94,519	94,707
530	79,13	95,834	93,412
540	85,95	96,953	92,030
550	92,91	97,882	90,574
560	100,00	98,631	89,056
570	107,18	99,207	87,486
580	114,44	99,618	85,876
590	121,73	99,878	84,233
600	129,04	99,993	82,566
610	136,34	99,973	80,883
620	143,62	99,822	79,189
630	150,83	99,560	77,492
640	157,98	99,185	75,795
650	165,03	98,709	74,104
660	171,96	98,140	72,423
670	178,77	97,488	70,756
680	185,43	96,755	69,104
690	191,93	95,952	67,472
700	198,26	95,086	65,861
710	204,41	94,160	64,275
720	210,36	93,184	62,713
730	216,12	92,162	61,177
740	221,66	91,097	59,670
750	227,00	89,997	58,191

Текст документа сверен по:

М.: Издательство стандартов, 1990