ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСТР
34.12— 2015
Информационная технология
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
Блочные шифры
Издание официальное
Москва 2018
ГОСТ Р 34.12—2015
Предисловие
1 РАЗРАБОТАН Центром защиты информации и специальной связи ФСБ России с участием Открытого акционерного общества «Информационные технологии и коммуникационные системы» (ОАО «ИнфоТеКС»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 26 «Криптографическая защита информации»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 19 июня 2015 г. № 749-ст
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Октябрь 2018 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Фодерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (ло состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
© . оформление. 2018
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии и
ГОСТ Р 34.12—2015
Введение
Настоящий стандарт содержит описание алгоритмов блочного шифрования, которые применяются в криптографических методах защиты информации.
Необходимость разработки стандарта вызвана потребностью в создании блочных шифров с различными длинами блока, соответствующих современным требованиям к криптографической стойкости и эксплуатационным качествам.
Настоящий стандарт терминологически и концептуально увязан с международными стандартами ИСО/МЭК 10116 [1] и серии ИСО/МЭК 18033 [2]. [3].
Примечание — Основная часть стандарта дополнена приложением А.
Ill
ГОСТ Р 34.12—2015
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Информационная технология КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ Блочные шифры
Information technology. Cryptographic data security. Block ciphers
Дата введения — 2016—01—01
1 Область применения
Настоящий стандарт определяет алгоритмы базовых блочных шифров, которые применяются в криптографических методах обработки и защиты информации, в том числе для обеспечения конфиденциальности. аутентичности и целостности информации при ее передаче, обработке и хранении в автоматизированных системах.
Определенные в настоящем стандарте алгоритмы криптографического преобразования предназначены для аппаратной или программной реализации, удовлетворяют современным криптографическим требованиям и по своим возможностям не накладывают ограничений на степень секретности защищаемой информации.
Стандарт рекомендуется использовать при создании, эксплуатации и модернизации систем обработки информации различного назначения.
2 Термины, определения и обозначения
2.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями.
2.1.1
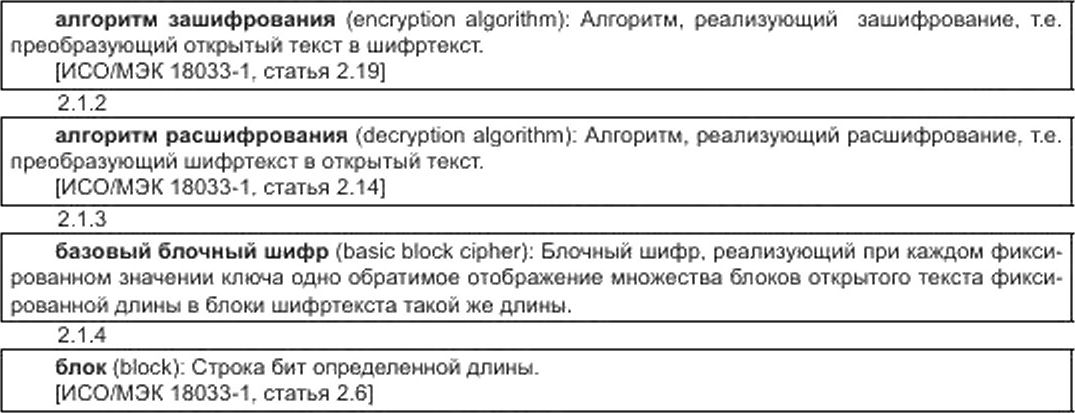
Издание официальное
1
ГОСТ Р 34.12—2015
2.1.5___________________________________________________________________________________________________________
блочный шифр (Моск cipher): Шифр из класса симметричных криптографических методов, в котором алгоритм зашифрования применяется к блокам открытого текста для получения блоков шифр-текста.
[ИСО/МЭК 18033-1. статья 2.7]
Примечание — В настоящем стандарте установлено, что термины «блочный шифр» и «алгоритм блочного шифрования» являются синонимами.
2.1.6________________________________________________________________________________________________
зашифрование (encryption): Обратимое преобразование данных с помощью шифра, которое формирует шифртекст из открытого текста.
[ИСО/МЭК 18033-1, статья 2.18]
2.1.7________________________________________________________________________________________________
итерационный ключ (round key): Последовательность символов, вычисляемая в процессе развертывания ключа шифра и определяющая преобразование на одной итерации блочного шифра.
2.1.8___________________________________________________________________________________________________________
ключ (key): Изменяемый параметр в виде последовательности символов, определяющий криптографическое преобразование.
[ИСО/МЭК 18033-1, статья 2.21]
Примечание — В настоящем стандарте рассматриваются ключи только в виде последовательности двоичных символов (битое).
2.1.9___________________________________________________________________________________________________________ открытый текст (plaintext): Незашифрованная информация.
[ИСО/МЭК 10116. статья 3.11]
2.1.10_______________________________________________________________________________________________
развертывание ключа (key schedule): Вычисление итерационных ключей из ключа шифра.
2.1.11__________________________________________________________________________________________________________
расшифрование (decryption): Операция, обратная к зашифрованию.
(ИСО/МЭК 18033-1, статья 2.13]
Примечание — В настоящем стандарте в целях сохранения терминологической преемственности по отношению к опубликованным научно-техническим изданиям применяется термин «шифрование», объединяющий операции, определенные терминами «зашифрование» и «расшифрование». Конкретное значение термина «шифрование» определяется в зависимости от контекста упоминания.
2.1.12_______________________________________________________________________________________________
симметричный криптографический метод (symmetric cryptographic technique): Криптографический метод, использующий один и тот же ключ для преобразования, осуществляемого отправителем, и преобразования, осуществляемого получателем.
(ИСО/МЭК 18033-1, статья 2.32]
2.1.13_______________________________________________________________________________________________
шифр (cipher): Криптографический метод, используемый для обеспечения конфиденциальности данных, включающий алгоритм зашифрования и алгоритм расшифрования.
[ИСО/МЭК 18033-1, статья 2.20]
2.1.14_______________________________________________________________________________________________
шифртекст (ciphertext): Данные, полученные в результате зашифрования открытого текста с целью скрытия его содержания.
(ИСО/МЭК 10116, статья 3.3]
2.2 Обозначения
В настоящем стандарте использованы следующие обозначения.
V* — множество всех двоичных строк конечной длины, включая пустую строку;
2
ГОСТ Р 34.12—2015
Vs — множество всех двоичных строк длины s. где s — целое неотрицательное число;
нумерация подстрок и компонент строки осуществляется справа налево начиная с нуля;
U * W — прямое (декартово) произведение множества U и множества IV;
|Д| — число компонент (длина) строки Ае V* (если А — пустая строка, то |Д| = 0);
А||В — конкатенация строк А, Be V. т.е. строка из V4Н0. в которой подстрока с боль
шими номерами компонент из У.д. совпадает со строкой Д. а подстрока с меньшими номерами компонент из V.B} совпадает со строкой В:
А<?кп — циклический сдвиг строки Д е У32 на 11 компонент в сторону компонент, имею
щих большие номера.
& — операция покомпонентного сложения по модулю 2 двух двоичных строк одина
ковой длины;
22, — кольцо вычетов по модулю 2s;
В — операция сложения в кольце Zjm ;
у — конечное поле GF(2)[x])p(x). где р(х) s^^^ + x^ + x + le GF(2)[x]; элемен
ты поля F представляются целыми числами, причем элементу z0 ♦ z, 9 + ... ... * z7-07 е У соответствует число z0 + 2z, + ... + 27 z7, где z. е (0.1}, / = 0. 1.....7. и 9 обозначает класс вычетов по модулю р(х). содержащий х;
Vecs; Z2» -» V,
ims; v; -> 324
АУв->Р
V:F^Va ФФ
Ф=
“ биективное отображение, сопоставляющее элементу кольца Z2s его двоичное представление, т.е. для любого элемента z е Z2i. представленного в виде z = z0 + 2 z, ♦... + 2s-1-z^,. гдег е {0.1), / = 0.1.....s-1.. выполнено равенство
Veci(z) = zs_1 ||...||z,||z0;
— отображение, обратное к отображению Vecs, т.е. Int, = VecJ;
— биективное отображение, сопоставляющее двоичной строка из Va элемент поля F следующим образом; строке z7||...||z,||z0, z.e {0.1},/ = 0.1.....7. соответствует элемент z0 ♦ z, 9 ♦ ... + z7-07 е F;
— отображение, обратное к отображению Л. т.е. V = д-’;
— композиция отображений, при которой отображение Ф действует первым;
— композиция отображений Ф5 1 и Ф. причем Ф1 = Ф.
3 Общие положения
В настоящем стандарте приведено описание двух базовых блочных шифров с длинами блоков л = 128 бит и л = 64 бит и длинами ключей к = 256 бит.
Примечания
1 На описанный в настоящем стандарте шифр с длиной блока л = 128 бит можно ссылаться как на блочный шифр «Кузнечик» («Kuznyechik»).
2 На описанный в настоящем стандарте шифр с длиной блока л = 64 бит можно ссылаться как на блочный шифр «Магма» («Magma»).
4 Алгоритм блочного шифрования с длиной блока л = 128 бит
4.1 Значения параметров
4.1.1 Нелинейное биективное преобразование
В качестве нелинейного биективного преобразования выступает подстановка - = Veca л' lnta: V8 -♦ Va, где л'; S2e -♦ 22«. Значения подстановки я' записаны ниже в виде массива л' = (к'(0). л'(1).....л'(255)):
л'= (252, 238. 221. 17, 207.110, 49. 22. 251. 196. 250. 218, 35.197, 4. 77. 233. 119. 240. 219. 147.46, 153. 186. 23. 54. 241. 187, 20. 205. 95. 193. 249. 24. 101. 90. 226. 92. 239. 33. 129, 28. 60. 66. 139. 1. 142. 79. 5. 132. 2, 174. 227, 106. 143. 160. 6. 11, 237. 152. 127, 212, 211, 31. 235. 52. 44. 81. 234. 200, 72. 171.
3
ГОСТ Р 34.12—2015
242.42.104, 162. 253, 58. 206. 204. 181.112.14, 86. 8. 12. 118, 18. 191, 114. 19. 71. 156. 183. 93.135. 21, 161, 150. 41, 16. 123. 154. 199, 243, 145, 120. 111, 157, 158, 178. 177. 50. 117. 25. 61. 255. 53. 138. 126, 109. 84. 198. 128, 195, 189. 13. 87. 223. 245. 36. 169. 62. 168. 67. 201.215. 121, 214, 246. 124. 34. 185. 3.
224. 15. 236, 222, 122. 148. 176. 188. 220. 232. 40. 80. 78. 51. 10. 74. 167, 151, 96. 115. 30. 0. 98. 68. 26,
184. 56. 130. 100, 159, 38. 65.173, 69. 70, 146. 39. 94. 85. 47, 140, 163. 165. 125. 105, 213, 149. 59. 7. 88.
179. 64, 134. 172. 29. 247. 48. 55. 107. 228. 136, 217. 231. 137. 225, 27. 131. 73. 76. 63. 248. 254. 141. 83.
170. 144. 202. 216. 133. 97. 32. 113. 103. 164. 45. 43. 9. 91. 203, 155, 37, 208, 190, 229, 108. 82. 89. 166, 116. 210, 230. 244. 180,192, 209. 102. 175, 194. 57. 75. 99. 182).
4.1.2 Линейное преобразование
Линейное преобразование задается отображением 7. V^6 -> Va, которое определяется следующим образом;
Ла15.....а0) = V(148 • Д(а15) + 32 ■ Д(а14) + 133 • Д(а,3) + 16 Д(а12) ♦
+ 194 Д(а„)* 192 Д(а10) + 1 -Д(а9) + 251 • Д(аа) + 1 ■ Д(а7) ♦ 192 Д(а6)+ (1)
+ 194 ■ д(а5) + 16 ■ Д(а4) ♦ 133 ■ Д(а3) + 32 Д(а2) + 148 • д(а,) ♦ 1 • д(а0))
для любых а( е Ve. / = 0.1.....15. где операции сложения и умножения осуществляются в поле F. а кон
станты являются элементами поля в указанном ранее смысле.
4.2 Преобразования
При реализации алгоритмов зашифрования и расшифрования используются следующие преобразования:
*М У128 | ~* ^28 | XIM(a) = А Ф а. где к. as V126; | (2) |
S; ^28 4 | ^128 | S(a) = S(a15 ||... || a0) = я(а15)||... || я(а0), где а = aJ5 ||... || аое V,2a,ae Va./=0.1.....15; | (3) |
*^28 | -* V128 | преобразование, обратное к преобразованию S. которое может быть вычислено, например, следующим образом: S-’(a) = S ’(а151|... || а0) = г’(а15)||... || n-’(a0), гдеа = а|5||...||а0е V,28. а е Va./=0. 1.....15; я 1 — подстановка, обратная к подстановке я; | (4) |
R- ^28 4 | ‘ ^128 | R(a) = R(a15 ||... || а0) = «а15.....а0)|| а,51|... || а,, где а = а,5 ||... || аое V,2a. а.е Va,/= 0.1.....15; | (5) |
^ ^>28 ^ | ^128 | Ца) = R,e(a). где а е У128; | (6) |
«’^128 | ^28 | преобразование, обратное к преобразованию R. которое может быть вычислено, например, следующим образом: R (a) = R (3i51| —1| а0) = au || а131|... || д-) || f(au, а13.....а0. а15). где а = а,5 ||... || з0 е У,2В, а, е Va. j = 0. 1.....15; | (7) |
^ v12a | 4 Vt28 | r’OJ^R-’^fa). где а е У128; | (8) |
Ф1: ^8 | Х ^128”* | ^128 х ^128 ^ <af ао) = U-SXMUa,)Ф а0. а,), где А. з0. а, е V128. | (9) |
4.3 Алгоритм развертывания ключа
Алгоритм развертывания ключа использует итерационные константы С, е V12a, /=1.2.....32. ко
торые определены следующим образом:
C. = L(Vec,2a(0)J=1.2.....32. (10)
Итерационные ключи К, е У12В, / = 1.2.....10 вырабатываются на основе ключа К = к25Ь ||... || Ао е V25B. k'G ^.1 = 0.1.....255 и определяются равенствами:
^1 = ^255 II — II ^128'
4
ГОСТ Р 34.12—2015
к2 = л,271|... || кй: (11)
^ 1- К*. 2) = ^- t>> J - ^80- П. J^. . г К21)./ = 1. 2. 3. 4.
4.4 Базовый алгоритм шифрования
4.4.1 Алгоритм зашифрования
Алгоритм зашифрования в зависимости от значений итерационных ключей Kt е У128. / = 1.2.....10
реализует подстановку Ек к о. заданную на множестве У128 в соответствии с равенством
^х,.....к10(а) = Ж10К5Х[К91... LSXIK2][K,](a), (12)
ВДвае У128.
4.4.2 Алгоритм расшифрования
Алгоритм расшифрования в зависимости от значений итерационных ключей К, е У,28. / = 1.2.....10 реализует подстановку DK, Kw. заданную на множестве V12a в соответствии с равенством
DK,.....Хи(а) = XIKJS ’f’XlKJ - S ^XI^JS V1^K10](a). (13)
гдеае V12B.
5 Алгоритм блочного шифрования с длиной блока л = 64 бит
5.1 Значения параметров
5.1.1 Нелинейное биективное преобразование
В качестве нелинейного биективного преобразования выступают подстановки х. = Vec4 x/lnt4: V4 -> V4. где л/: 2^ ->ЗД / = 0.1.....7. Значения подстановок л/ записаны ниже в виде массивов л/ = (л/(0), л'(1).... ...,яД15)М=0,1.„. ,7:
л' = (12. 4. 6. 2, 10. 5. 11.9. 14. 8. 13. 7. 0. 3, 15. 1);
л/ = (6. 8. 2. 3. 9. 10. 5. 12. 1. 14. 4. 7. 11. 13. 0. 15);
л/ = (11. 3. 5. 8. 2. 15. 10. 13. 14. 1. 7. 4. 12. 9. 6. 0);
л/ = (12. 8. 2.1. 13. 4. 15. 6. 7. 0. 10. 5. 3.14. 9.11);
л4' = (7. 15. 5.10. 8.1.6. 13. 0. 9. 3.14. 11. 4. 2. 12):
л/ = (5. 13. 15. 6. 9. 2. 12. 10. 11. 7. 8.1.4. 3. 14. 0);
л8' = (8. 14. 2. 5. 6. 9. 1, 12. 15. 4. 11. 0. 13. 10. 3, 7);
л/= (1.7.14. 13. 0. 5. 8. 3.4. 15. 10. 6.9, 12. 11. 2).
5.2 Преобразования
При реализации алгоритмов зашифрования и расшифрования используются следующие преобразования;
^32^^32 | «а) = 1(а7 ||... || а0) = л7(а?)||... || ^(аД (14) где а = а71|... || а0 е V32. а.е V4. / = 0.1.....7; |
^И: У32 -* У32 | 9И(а) = (t(Vec32(lnt32(a) 9 1пЦ2(Л)))) ^1v С15> где к. а ^ У32; |
СИ: ^2 * V32 -> У32 х уз2 | Эда,,а0) = (а0. дМ(а0)Фа,), (16) где А. а0. а,. е У32; |
GW V32 х У32 _> ум | G-H(a1.a0) = (pW(ab)®a1)||a0f (17) где к. aQ. а, е У32. |
5.3 Алгоритм развертывания ключа
Итерационные ключи К,е У32. (= 1,2..... 32 вырабатываются на основе ключа К = к255 ||... Це У256. к^ V,. г = 0.1..... 255 и определяются равенствами:
к.=к255 п ...цл224;
^2 ~ ^223 Ч "■ Ч ^192’
5
ГОСТ Р 34.12—2015
К3 = *191 Н - И *160;
^4 = *159 И — И *128’
^5 = *127 II •" II *96’
Хб=^5П" 11^4= 08)
*7 =W-11*32’-^ = *31 ll-ll^ Кмв = К„/=1,2,.... 8;
К-Мв =Кг/= 1, 28; ^24=^-'=1-2.....8.
5.4 Базовый алгоритм шифрования
5.4.1 Алгоритм зашифрования
Алгоритм зашифрования в зависимости от значений итерационных ключей К е V^. i= 1.2.....32
реализует подстановку Ек^ Кз2, заданную на множестве У64 в соответствии с равенством
^.....X^^^J^il - GfKJG^Ka^). (19)
где а = а, ||аое Уе4.а0.а, е V32.
5.4.2 Алгоритм расшифрования
Алгоритм расшифрования в зависимости от значений итерационных ключей К е У32,1- 1.2.....32 реализует подстановку D^ Xij. заданную на множестве Ve4 в соответствии с равенством
ох,.....Хз2<а> = «HKJGpg ... G(K31]G(K32](av а0). (20)
где а = а, ||аое У64. а3. а, е V3j.
б
ГОСТ Р 34.12—2015
Приложение А (справочное)
Контрольные примеры
Данное приложение носит справочный характер и не является частью настоящего стандарта.
В данном приложении двоичные строки из V*. длина которых кратна 4. записываются в шестнадцатеричном виде, а символ конкатенации (*|Г) опускается. То есть строка а е V4, будет представлена в виде
ал-1эл-2 - «0-
где а( е (0. 1.....9. а. Ь. с, d. е. 1} . / = О, 1.....г - 1 . Соответствие между двоичными строками длины 4 и шест
надцатеричными строками длины 1 задается естественным образом (таблица А.1). Преобразование, ставящее в соответствие двоичной строке длины 4г шестнадцатеричную строку длины г. и соответствующее обратное преобразование для простоты записи опускаются.
Таблица А.1 — Соответствие между двоичными и шестнадцатеричными строками
0000 | 0 |
0001 | |
0010 | 2 |
0011 | 3 |
0100 | 4 |
0101 | 5 |
0110 | 6 |
0111 | 7 |
1000 | 8 |
1001 | 9 |
1010 | а |
1011 | b |
1100 | с |
1101 | d |
1110 | е |
1111 | f |
А.1 Алгоритм блочного шифрования с длиной блока л = 128 бит
А.1.1 Преобразование S
S(ffeeddccbbaa99881122334455667700) = b66cd8887d38e8d77765aeea0c9a7efc.
S(b66cd8887d38e8d77765aeea0c9a7efc) = 559d8dd7bd06cbfe7e7b262523280d39.
S(559d8dd7bd06cbfe7e7b262523280d39) = 0c3322fed531e4630d80ef5c5a81c50b.
S(0c3322fed531e4630d80ef5c5a81c50b) = 23ae€56331842d29c5df529c13f5acda.
A.1.2 Преобразование R
«(00000000000000000000000000000100) = 94000000000000000000000000000001.
«(94000000000000000000000000000001)= 35940000000000000000000000000000.
«(5940000000000000000000000000000) = 6459400000000000000000000000000.
«(64359400000000000000000000000000) = 0d64a594000000000000000000000000.
A.1.3 Преобразование L
L(64a59400000000000000000000000000) = d456584dd0e3e84cc3166e4b7fa2890d.
L(d456584dd0e3e84cc3166e4b7fa2890d) = 79d26221b87b584cd42fbc4ffea5de9a.
L(79d26221b87b584cd42fbc4ffea5de9a) = 0e93691a0cfc60408b7b68166b513c13.
L(0e93691a0cfc60408b7b68f66b513c13) = e6a8094fee0aa204fd97bcb0b44b8580.
A.1.4 Алгоритм развертывания ключа
В настоящем контрольном примере ключ имеет значение:
К = 8899aabbccddeeff0011223344556677fedcba98765432100123456789abcdef.
К. = 8899aabbccddeeff0011223344556677,
К2 = fedcba98765432100123456789abcdef.
7
ГОСТ Р 34.12—2015
С.= 6ea276726c487ab85d27bd10dd849401.
XIC^X,) = e63bdcc9a09594475d369f2399d 1(276.
SXjC.KX,) = 0998ca37a7947aabb78(4a5ae81b748a.
LSXIC^XJ = 3d0940999db75d6a9257071d5e6144a6.
ПС^Х,. KJ = (c3d5(a01ebe36f7a9374427ad7ca8949. B899aabbccddeeff0011223344556677).
C2 = dc87ece4d890(4b3ba4eb92079cbeb02.
П^^С^Х,, K2) = (37777748e56453377d5e262d9O9O3f87, c3d5fa01ebe36(7a9374427ad7ca8949).
C3 = b2259a96b4d88e0be7690430a44(7f03.
HCJ... НС^Х,. K2) = ((9eae5f29b2815e31(11ac5d9c29fbO1.37777748e56453377d5e262d90903f87).
Cd = 7bcd1b0b73e32ba5b79cb 140(2551504, qCJ ... HCJ^. X2) = (e980089683d00d4be37dd3434699b98f. (9eae5(29b2815e31(11ac5d9c29(b01).
C5 = 156(6d791fab511deabb0c502fd18105.
F[C5]... fqC^Xp X2)= (b7bd70acea4460714(4ebe13835cf004. S980089683d00d4be37dd3434699b98().
Ce = a74a(7efab73d(160dd208608b9efe06.
^Cg]... H^KK,. K2) = (1a46ea1d6ccd236467287df93fd(974, b7bd70acea4460714(4ebe13835c(004).
C7 = C9e8819do73ba5ae50f5b570561a6a07,
Р(С7]... qC,]^. K2) = (3d4553d8e9c(ec6815ebadc40a9f(d04. 1a46ea1c(6ccd236467287df93fdl974).
Ce = (6593616e6055689adfba18027aa2a08.
<7Cr X4) = HCJ... FIC^X,. K2) = (db31485315694343228d6aef8cc78c44, 3d4553d8e9dec6815ebadc40a9ffd04).
Итерационные ключи X. j = 1.2.....10 принимают следующие значения:
X, = 8899aabbccddeef(0011223344556677,
Х2 = fedcba98765432100123456789abcde(,
Х3 = db31485315694343228d6ae(8cc78c44.
К4 = 3d4553d8e9cfec6815ebadc40a9ffd04.
Х5 = 57646468c44a5e28d3e59246f429(1ac.
X6 = bd079435165c6432b532e82834da581b,
X7 = 51e640757e8745de705727265a0098b1.
X8 = 5a7925017b9(dd3ed72a91a22286(984.
X9 = bb44e25378c73123a5(32f73cdb6e517,
X1Q = 72e9dd7416bcf45b755dbaa88e4a4043.
A,1.5 Алгоритм зашифрования
В настоящем контрольном примере зашифрование производится при значениях итерационных ключей из А. 1.4. Пусть открытый текст, подлежащий зашифрованию, равен
з= 1122334455667700ffeeddccbbaa9988.
тогда
XJXJia) = 99bb99ff99bb99fff(f(ffftfff(fffi.
SXIX^a) = e87de8b6e87de8b6b6b6b6b6b6b6b6b6.
LSX{X.l(a) = e297b686e355b0a1c(4a2f9249140830.
LSXIX^LSXIX^a) = 285e497a0862d596b36(4258a1c69072.
LSXjXJ ... LSXIX^a) = 0187a3a429b567841ad50d29207cc34e.
LSXIXJ ... LSXlX^a) = ec9bdba057d4(4d77c5d70619dcad206,
LSXJXJ ... LSXIX^a) = 1357(d11de9257290c2a1473eb6bcde1, LS^XJ ... LSXlX^a) = 28ae31e7d4c2354261027ef0b32897d(.
LSJqX7]... LSXIX^a) = 07e223d56002c013d3f5e6(714b86d2d.
LSXIXJ ... LSXlX^a) = cd8e(6cd97e0e092a8e4cca61b38b(65.
LSXJXJ ... LSXfX^a) = 0d8e40e4a800d06b2f1b37ea379ead8e.
Результатом зашифрования является шифртекст
b = XIXJZ.SXIXJ... tSXlX^a) = 7f679d90bebc24305a468d42b9d4edcd.
A.1.6 Алгоритм расшифрования
В настоящем контрольном примере расшифрование производится при значениях итерационных ключей из
А. 1.4. Пусть шифртекст. подлежащий расшифрованию, равен шифртексту. полученному в предыдущем пункте:
b= 7(679d90bebc24305a468d42b9d4edcd.
тогда
Х[Х10](Ь) = 0d8e4 0e4a800d06b2(1b3 7ea379ead8e.
8
ГОСТ Р 34.12—2015
L'1X[K10](b) = 8a6b930a52211b45c5baa43ff8b91319.
S-^-'XIK^Kb) = 76ca149eef27d1b10d17e3d5d68e5a72.
S^L ’XJKJS 'L~'X[K^(b) = 5d9b06d41b9d1d2d04df7755363e94a9.
S-'L ’XIKj ... S^1L-’XIK,J(b)= 79487192aa45709c115559d6e928016e.
S^L ’X[K7]... S VXIK^Jtb) = ae506924c8ce331bb918fc5bdfb195fa.
S 1L 1xp<fJ ... S^r’XlK,J(b) = bbffbfc8939eaaffafb8e22769e323aa.
S 'L ’xpy ... S V’XIK^Jtb) = 3cc2107cc07a8bec0f3ea0ed2ae33e4a.
S 1L ’XIK J ... S'k-’XJK^Kb) = 136f01291d0b96d591e228b72d011c36.
S ^ ^KJ ... S VXIK^Jtb) = 1c4b0c1e950182b1ce696af5c0bfc5df.
S^L ’XIK2]... S V’XIK^Kb) = 99bb99ff99bb99ffffffffffffffffff.
Результатом расшифрования является открытый текст
а = X[K1)S~’L'1Xp<2]... S-U-’XIK^Jb) = 1122334455667700ffeeddccbbaa9988.
А.2 Алгоритм блочного шифрования с длиной блока л = 64 бит
А.2.1 Преобразование f t(fdb97531) = 2a196f34. /(2a196f34) = ebd9K)3a.
1(ebd9f03a) = b039bb3d.
1(bO39bb3d) = 686954 33.
A.2.2 Преобразование g g[87654321J{fedcba98) = fdcbc20c. g[fdcbc20c](87654321)= 7e791a4b, g[7e791a4b](1dcbc20c| = c76549ec.
g(c76549ecK7e791a4b)=9791c849.
A.2.3 Алгоритм развертывания ключа
В настоящем контрольном примере ключ имеет значение:
К = Heeddccbbaa99887766554433221100f0f1f2f3f4f5f6f7f8f9fafbfcfdfeff.
Итерационные ключи К;, г = 1. 2.....32 принимают следующие значения:
Ky = ffeeddcc. | Kg = ffeeddcc. | K17 = ffeeddcc. | *25 = fcfdfeff. |
K2 = bbaa9988. | K,o= bbaa9988. | Kie = bbaa9988. | K2,3 = f8f9fafb. |
K3 = 77665544. | K„ = 77665544. | K19 = 77665544. | K27 = f41516f7. |
K4 = 33221100. | K,2 = 33221100, | K20 = 33221100. | = fO11f2f3. |
K5= 10111213. | K13 = 10111213. | K21 = ЮШ213. | K~, = 33221100. |
K6 = 14151617. | Ku = 14151617. | K22 = 14151617. | «30= 77665544. |
K7 = 18191afb. | K,5 = 1819fa1b. | K23 = 18191a1b. | K31 = bbaa9988. |
Kp = fcfdfeff. | K,6 = Icfdfeff. | K24 = fcfdfeff. | K.-& = ffeeddcc. |
А.2.4 Алгоритм зашифрования
В настоящего контрольном примере зашифрование производится при значениях итерационных ключей из А.2.3. Пусть открытый текст, подлежащий зашифрованию, равен
a = fedcba9876543210.
тогда
(а,. а0) = (fedcba98. 76543210).
GIK^ap а0) = (7654 3210. 28da3b14),
G[K2]G(K,Ka,. а0) = (28da3b14. Ы4337а5),
G[K3I... G(K1j(at. a0) = (Ы4337а5.633a7c68).
G[KJ ... G(K,](a,. a0) = (633a7c68. ea89c02c).
GIKJ ... G[K,](a?. aoj = (ea89c02c. 11fe726d).
Gpy ... G[K,](a,. a0) = (11fe726d. ad0310a4).
G[K7]... G[K,](a?. aoj = (ad0310a4. 37097125).
Gpy... G[K,](a,. a0) = (37d97f25. 46324615).
G[KcJ - G[K,](a,. a0) = (46324615. ce995f2a),
G[K~ia]... Gp^Ra,. a0) = (ce995f2a. 93c1f449).
Gp^J... GpqHa,. a0) = (93c11449. 4811c7ad).
G[K,2]... Gp^Ka,. a0) = (4811c7ad, c4b3edca).
GfK,^... Gp^Ra,. a0) = (c4b3edca. 44ca5ce1),
G[K14]... G^Ra^ a0) = (44ca5ce1,1e151b68).
9
ГОСТ Р 34.12—2015
G[X15] ... GlK^a,. а0) = (fef51b68. 2098cd86).
G[K J ... G[K,](ar a0) = (2O98cd86. 4f15b0bb),
GfKJ ... G^Na,. a0) = (4115b0bb. e32805bc), G[K J ... G[K,](ar a0) = (e32805bc. e7116722). G(K, J ... G^Na,. a0) = (e7116722. 89cadf21. GfKj ... GlK^a,. a0) = <89cadf21. bac8444d).
GIK21] ... G^Na,. a0) = (bac8444d. 11263a21), G[K22] ... G[K,](ar a0) = (11263a21, 625434c3).
GIK2J ... G^Na,. a0) = (625434c3. 8025c0a5).
GfK2J ... G[K,](ar a0) = (8025c0a5. b0d66514).
GIK2J - G^Na,. a0) = (bOd66514.47ЫЙ5И).
G[K2J ... G[K,](a,. a0) = (47b1d5f4. c78e6d50.i,
GIK27] ... G^Ka,. aj = (c78e6d50. 80251e99).
G(K2J ... GtK^a,. a0) = (80251e99. 2b96eca6).
GfK2J ... G^Ra,. a0) = (2b96eca6. O5ef44O1), GtK3j ... G^Ra,. a0) = (05ef4401.239a4577). G(K31] ... G(K,Rav a0) = (239a4577. c2d8ca3d). Результатом зашифрования является шифртекст
b = G’(K32]G[K3i] ... Gp^Ra,. a0) = 4ee901e5c2d8ca3d.
A.2.5 Алгоритм расшифрования
В настоящем контрольном примере расшифрование производится при значениях итерационных ключей из А.2.3. Пусть шифртекст. подлежащий расшифрованию, равен шифртексту. полученному в предыдущем пункте:
b=4ee901e5c2d8ca3d.
тогда
(Ьр b0) = (4ee901e5.c2d8ca3d).
вр^КР,. b0) = (c2d8ca3d. 23984577).
GpQGp^Kb,. b0) = (239а4577. 05ef4401).
GPCjJ ... G(K32Rbr b0) = (O5ef44O1, 2b96eca6).
G|K2J ... G^Rb,. b0) = (2b96eca6. 80251e99).
G(Kj ... GtK^KP,. bQ) = (80251699. c78e6d50).
G(K27] ... G^Rb^ b0) = (c78e6d50. 47b1d5M),
G[K^ ... G[K32Kbv bQ) = (47b1d5f4. b0d66514).
GV^J ... G[K32Rbr b0) = (b0d66514. 8025c0a5).
GfKJ ... G(K32Rbr bQ) = (8025c0a5. 625434c3).
G1K2J ... G^Rb,. bQ) = (625434C3.11263a21).
GfKJ ... G^Rb,. b0) = (11263a21. bac8444d).
G(K21]... G^Rb,, b0) = (bac8444d, 89cadf21).
ф<2 j ... G[K32Rbr b0) = (89cadf21.67116722).
G(K J ... G(K32Rbr b0) = (67116722. e32805bc).
GpQ ... G(K32](br b0) = (e32805bc. 4f15b0bb).
G{K,7] ... G^Rbp b0) = (4f15bObb. 2098cd86).
G(K J ... G(K32Rbv b0) = (2098cd86. 1ef51b68).
G(K J ... G(K32Rbr b0) = (1ef51b68. 44ca5ce1).
G[KJ ... G(K32](bv b0} = (44ca5ce1. c4b3edca).
GfKJ ... G[K32](br b0) = (c4b3edca. 4811c7ad).
GfKJ ... G[K32Kbr b0) = (4811c7ad. 93c 11449).
G1KJ ... GlK^Nb,- b0) = (93c1f449. ce995f2a).
G[K10] ... G(K32Kbr b0) = (ce99512a. 46324615).
в(Кэ]... GIK32](b,. b0) = <46324615. 37d97125),
G[K8]... G(K32l(b,. b0) = <37d97f25. ad0310a4),
G1K7]... GIK32](br b0) = (ad0310a4. 11fe726d).
GfKJ ... G(K32l(b,. b0) = (11fe726d. ea89c02c).
Gt/tJ ... GIK32](br b0) = (ea89c02c. 633a7c68).
G{K4]... GlK^Nb,. b0) = (633a7c68. Ы4337а5).
G(K3]... GIK32](bv b0) = (M4337a5. 28da3b14).
Gpy ... GfK^Kbp b0) = (28da3b14 .76543210).
Результатом расшифрования является открытый текст
a =G-[K1)GtK2]... G[K32](br b0) = 1edcba9876543210.
10
ГОСТ Р 34.12—2015
Библиография'
in | ИСО/МЭК 10116:2006 (ISO/IEC 10116:2006) |
Pi | ИСО/МЭК 18033-1:2005 (ISO/IEC 18033-1:2005) |
13) | ИСО/МЭК 18033-3:2010 (ISO/IEC 18033-3:2010) |
Информационные технологии. Методы обеспечения безопасности. Режимы работы для л-битовых блочных шифров (Information technology — Security techniques — Modes of operation for an o-bil block cipher)
Информационные технологии. Методы и средства обеспечения безопасности. Алгоритмы шифрования. Часть 1. Общие положения (Information technology — Security techniques — Encryption algonthms — Part 1: General)
Информационные технологии. Методы и средства обеспечения безопасности. Алгоритмы шифрования. Часть 3. Блочные шифры (Information technology — Security techniques — Encryption algorithms — Part 3: Block ciphers)
* Оригиналы международных стандартов ИСО/МЭК находятся во ФГУП «» Федерального агентства по техническому регулированию и метрологии.
11
ГОСТ Р 34.12—2015
УДК 681.3.06:006.354 ОКС 35.040
Ключевые слова: информационная технология, криптографическая защита информации, симметричный криптографический метод, зашифрование, расшифрование, блочный шифр, ключ
Редактор Л.В. Лукьянова
Технический редактор В.Н. Прусакова
Корректор И.А. Королева Компьютерная верстка Е.О. Астатина
Сдана в набор 01.10.2018. Подписана в печать 22.10.2018. Формат 60«М’/8. Гарнитура Ариал.
Уел. печ. п. 1.86. Уч.-изд. л. 1.68 Подготовлено на основе электронной версии, предоставленной разработчиком стандарта
Создано в единичном исполнении ФГУП «СТАНДАРТИИФОРМ» . 117418 Москва, Нахимовский пр-т. д. 31, к. 2.
WA-A-.gostinfo.ru infoi@gostinfo.ru
